Mesoscale connections and gene expression empower whole-brain modeling of α-synuclein spread, aggregation, and decay dynamics

SUMMARY

An emerging view regarding neurodegenerative diseases is that discreet seeding of misfolded proteins leads to widespread pathology. However, the mechanisms by which misfolded proteins seed distinct brain regions and cause differential whole-brain pathology remain elusive. We used whole-brain tissue clearing and high-resolution imaging to longitudinally map pathology in an α-synuclein pre-formed fibril injection model of Parkinson’s disease. Cleared brains at different time points of disease progression were quantitatively segmented and registered to a standardized atlas, revealing distinct phases of spreading and decline. We then fit a computational model with parameters that represent α-synuclein pathology spreading, aggregation, decay, and gene expression pattern to this longitudinal dataset. Remarkably, our model can generalize to predicting α-synuclein spreading patterns from several distinct brain regions and can even estimate their origins. This model empowers mechanistic understanding and accurate prediction of disease progression, paving the way for the development and testing of therapeutic interventions.

INTRODUCTION

Parkinson’s disease (PD) is the second most common neurodegenerative disorder. It is characterized by postural instability, tremor, rigidity, and bradykinesia (Goetz, 2011; Kalia and Lang, 2015). These clinical manifestations are caused primarily by loss of dopaminergic neurons from the substantia nigra. The hallmark pathology of PD is the presence of Lewy bodies (LB), cytoplasmic neuronal inclusions composed of misfolded aggregates of the protein α-synuclein (α-syn) (Dickson, 2012; Goedert et al., 2013; Kalia and Lang, 2015; Oliveira et al., 2021; Spillantini et al., 1997). A longstanding hypothesis about the etiopathogenesis of this debilitating disease has been the Braak hypothesis – which posits that pathological α-syn seeds form early in the disease and subsequently spread through the nervous system, correlating with the progression of motor and cognitive symptoms (Beach et al., 2009; Braak et al., 2002; Braak et al., 2003). An exciting area in neurodegenerative disease research is the emerging phenomenon of prion-like spreading of neurodegenerative disease proteins, including α-syn in PD (Aguzzi and Rajendran, 2009; Angot et al., 2010; Cushman et al., 2010; Guo and Lee, 2014; Jucker and Walker, 2013). Prions are well established as the protein-based infectious agent underlying the spongiform encephalopathies (for example, bovine spongiform encephalopathy in cattle and Creutzfeldt-Jakob disease in humans). In these rare, albeit devastating, diseases, the prion protein, PrP, converts from the normal soluble form to the aggregated self-templating infectious form. This process initiates an inexorable spread of pathology and contingent neurodegeneration throughout the brain (Aguzzi and Calella, 2009; Prusiner, 1998). But could this phenomenon extend to the more common neurodegenerative diseases like PD?

Early hints of this type of possibility came from postmortem analyses of individuals who had received fetal nigral transplants as a PD treatment and then had subsequently died several years later and come to autopsy (Kordower et al., 2008; Li et al., 2008). In some of the fetal grafts (which were only 11–16 years old at the time of autopsy), Lewy bodies, comprised of α-syn fibrils, were present. The findings were startling because they suggested the possibility that somehow α-syn aggregates from the host diseased tissue propagated to the new graft tissue. These findings were consistent with the longstanding Braak hypothesis – that PD pathology seems to spread through the brain in anatomically defined ways (Braak et al., 2003).

Although several studies have questioned this “prion-like” hypothesis owing to its inability to explain the sparsity of staged distributions in post-mortem human PD brains (Surmeier et al., 2017), studies in primary neurons and animal models demonstrate that α-syn pathology can and does spread in a cell-to-cell manner, causing impairments in excitability and ultimately leading to neuronal degeneration (Desplats et al., 2009; Hansen et al., 2011; Volpicelli-Daley et al., 2011). Injecting α-syn fibrils into α-syn overexpressing transgenic mice causes pathology and degeneration (Luk et al., 2012b). Importantly, α-syn fibrils injected into wild-type mice causes spread of pathology along anatomically interconnected brain regions, decrease in tyrosine hydroxylase-positive dopaminergic neurons, and results in motor impairments (Luk et al., 2012a). Countering the argument that these results could be a secondary consequence of a signaling pathway induced by aggregated α-syn, injection of α-syn fibrils into α-syn knockout mice causes no spread of pathology, no degeneration, and no motor impairment. Furthermore, injection of fibrils in α-syn heterozygous mice causes a reduction in pathology and a reduction in motor impairments (Luk et al., 2012a). This proves that spreading is α-syn-dependent. These observations have been extended to rats, non-human primates, and in human neurons (Bieri et al., 2019; Gribaudo et al., 2019; Paumier et al., 2015; Prusiner et al., 2015; Recasens et al., 2014; Shimozawa et al., 2017). These results point to α-syn trans-neuronal spreading playing a significant role in neurodegeneration in PD.

A picture emerges in which a small amount of α-syn fibrillar seeds (either formed spontaneously in the human brain or by direct injection into the mouse brain) can template the conversion of endogenous α-syn to an aggregated state and set in motion a flywheel that drives the nervous system inexorably toward disease. The big challenge now is to define how these aggregates spread from one brain region to the next. Are some regions selectively vulnerable? Are others resilient? These questions will need to be answered across space and time. Several recent studies have applied computational network diffusion models to predict the early stages of α-syn spreading patterns (Henderson et al., 2019a; Pandya et al., 2019), providing evidence that anatomical connectivity can accurately predict these patterns. Such spatiotemporal models will be crucial for further understanding and ultimately treating a progressive disease like PD at variable points of its progression. Recent studies have also used transgenic animal models and cell-specific labeling techniques to explore the genetic determinants behind α-syn spreading (Henderson et al., 2020; Henrich et al., 2020), indicating that levels of gene expression, such as endogenous α-syn or GBA1, are additionally important factors. However, previous studies did not quantify full three-dimensional whole-brain pathology and did not report spreading patterns beyond 6 months post-injection. We hypothesized that both a full spatial representation and tracking the later stages of spreading would be crucial in characterizing changes in pathology and degeneration that are known to occur in such progressive neurodegenerative diseases.

Here, we used tissue clearing and light-sheet fluorescence microscopy to three-dimensionally image α-syn pathology in the whole mouse brain, as well as a computational pipeline for anatomically mapping each aggregate to the Allen Reference Atlas (ARA). Merging the data into the ARA coordinate system allowed comparisons with previous studies that mapped mesoscale axonal projections between neuroanatomical regions (Oh et al., 2014) and spatial transcriptomics across many genes (Lein et al., 2007). Statistical comparisons of brain maps at various stages of disease progression revealed a biphasic spreading and decay curve with differential timing by region. Furthermore, tracking the size of each α-syn aggregate longitudinally across regions uncovered a pattern of steady increase and rapid decline of mean aggregate size per region, implying both prion-like aggregation and subsequent neurodegeneration. In order to capture these simultaneous effects, we developed a computational model that incorporates spreading, aggregation, decay, and spatial gene expression of pathology across the whole brain. The development and validation of this model provides a foundation for tracking both the origin and progression of this highly complex disease.

RESULTS

Whole-brain quantification of α-synuclein pathology using tissue clearing and light-sheet microscopy

The direct injection of α-syn pre-formed fibrils (PFF) triggers whole-brain pathology and neurodegeneration, serving as a robust model of Parkinson’s disease (Henderson et al., 2019b; Luk et al., 2012a). To track pathology throughout disease progression, we ipsilaterally injected mice aged 8–10 weeks with α-syn PFFs in the striatum, or Caudoputamen (CP), and processed mouse brains for immunohistochemistry at various timepoints up to 18 months post injection. (Figure 1A). Building off of recent advancements in three-dimensional whole-brain immunolabeling and imaging, we optimized the iDISCO+ protocol to immunolabel α-syn aggregates (using an antibody to specifically detect aggregated endogenous α-syn phosphorylated on Serine 129) (Renier et al., 2016; Renier et al., 2014) and imaged samples using a light-sheet microscope (Figures 1B and S1). We validated virtual sections from these three-dimensional datasets against traditional serial histology (Figure S2) and found them to be consistent with previous studies that used the same injection site (Bieri et al., 2019; Henderson et al., 2019a; Luk et al., 2012a), with pathology developing in both the ipsilateral striatum, intermediate layers of the cortex, and substantia nigra at both 2 and 6 months post-injection (Figure S2A). After imaging, we used a quantification pipeline building on several open source software tools, such as Ilastik (Berg et al., 2019) (machine learning library) and ClearMap (Renier et al., 2016) (registration library), to detect each α-syn aggregate and assign it to a voxel or anatomical region from the Allen Reference Atlas (Figures 1C, 1D, S3, and S4) (Oh et al., 2014). Since we were able to capture each α-syn aggregate’s three-dimensional volume (Figure 1D), we could visualize the distribution of aggregates and aggregate size across timepoints (Figure 1E). Plotting the total α-syn aggregate count in the whole brain against timepoints of months post injection (MPI) revealed a biphasic curve (Figure 1F), starting with pathological spreading (between 0–6 months post injection) followed by decay (between 8–18 months post injection). We observed a relatively larger spike of smaller aggregates at the earliest time point post injection, whereas at 4- and 8-months post injection the distribution of volumes shifted to double the mean aggregate-volume per voxel. Surprisingly, at the latest 18-month time point, this distribution shifted back to lower aggregate burden, which was not accompanied with the presence or reappearance of smaller size aggregates (Figure 1G).

Figure 1. Tissue clearing and light sheet fluorescence microscopy capture changes in whole-brain pathology at various time points post-seeding.

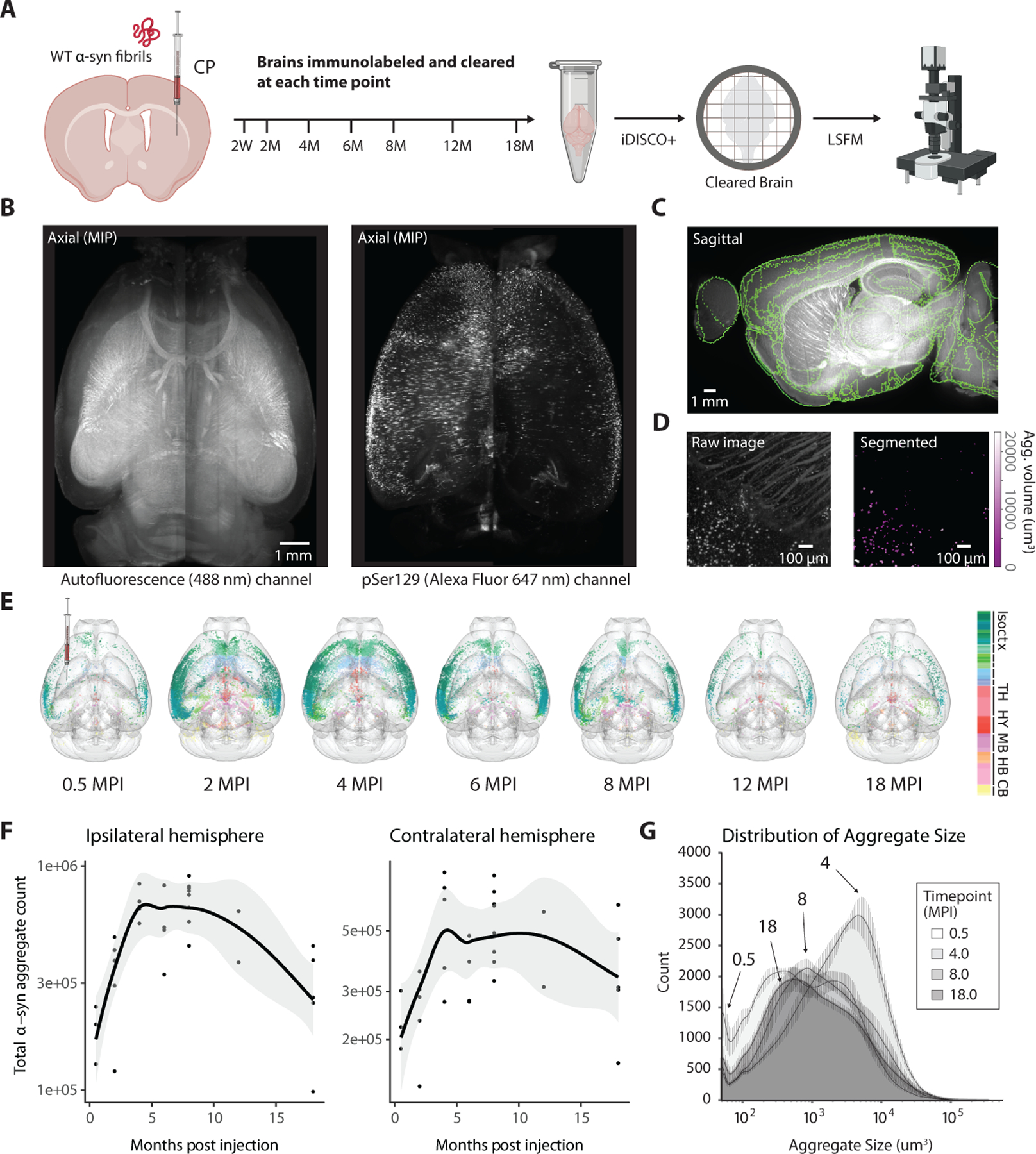
(A) α-syn PFFs were unilaterally injected into the striatum of mice, and cohorts of mice were perfused at various timepoints ranging from 2 weeks to 18 months post-injection (MPI). Each extracted mouse brain was processed for fluorescent immunolabeling of α-syn pathology and whole-brain clearing using the iDISCO+ protocol. Brains were three-dimensionally imaged by light-sheet fluorescent microscopy to visualize both the antibody fluorescence and tissue autofluorescence for anatomical mapping. (B) Axial projections of autofluorescence from an imaged mouse brain (left) and α-syn pSer129 immunolabeled pathology (right). (C) A quantitative pipeline registers the autofluorescence to an anatomical atlas, and a trained classifier (D) segments α-syn pathology. (E) Both whole-brain spreading and subsequent decline of pathology are observed in glass-brain reconstructions of representative samples at each timepoint, with each aggregate color-coded by Allen Reference Atlas region. (F) Total α-syn aggregate count versus time post-injection quantifies this trend of spreading followed by decay. Data are represented as mean ± SD. (G) Normalized density distributions of mean aggregate size at each voxel across the various timepoints depict the general increase in aggregate volume during initial apparent prion-like spread, followed by a decrease as large aggregates diminish. Data are represented as mean ± SD. Isoctx – isocortex, TH – thalamus, HY – hypothalamus, MB – midbrain, HB – hindbrain, CB – cerebellum. See also Figures S1, S3, and S4.

Statistical analysis across longitudinal groups reveals region-dependent spreading, accumulation, and decay.

To define the spatiotemporal patterns of α-syn pathology, we ran statistical comparisons at the voxel and regional levels between cohorts at various times sacrificed post-injection. Because of variability in spreading patterns across adjacent timepoints, we instead used timepoints spaced at least 3 months apart for these comparisons. Our quantitative pipeline captured both total aggregate count and mean aggregate volume for each voxel (Figure 2A). Therefore, we performed statistical comparisons for each of these two metrics between each selected pair of timepoints. Comparing total aggregate count at the voxel level (Figure 2B), we observed statistically significant clusters with widely varying rates of both spread and decay for different brain subregions. For example, when widespread pathology in the cortex has already aggregated and begins decaying by 4 months post-injection, aggregates begin to appear for the first time in various subcortical clusters, including within the thalamus and contralateral hippocampus. Statistics comparing the mean aggregate size at the voxel level demonstrate a similar initial increase both cortically and subcortically from 0.5 to 4 MPI, followed by a whole-brain decrease from 4 to 8 MPI (Figure 2B). The clusters of significant increase or decrease from the voxel-level analysis generally obeyed the boundaries of anatomical brain regions; we observed similar biphasic trends when computing both the α-syn aggregate count and mean-size metrics across regions from the Allen Brain Atlas (Figure 2C). Thus, different brain regions exhibit different spatiotemporal patterns/dynamics of α-syn spreading, accumulation, and decay.

Figure 2. Statistical analysis at both regional and voxel level demonstrates biphasic spreading and decay interleaved between cortical and subcortical areas.

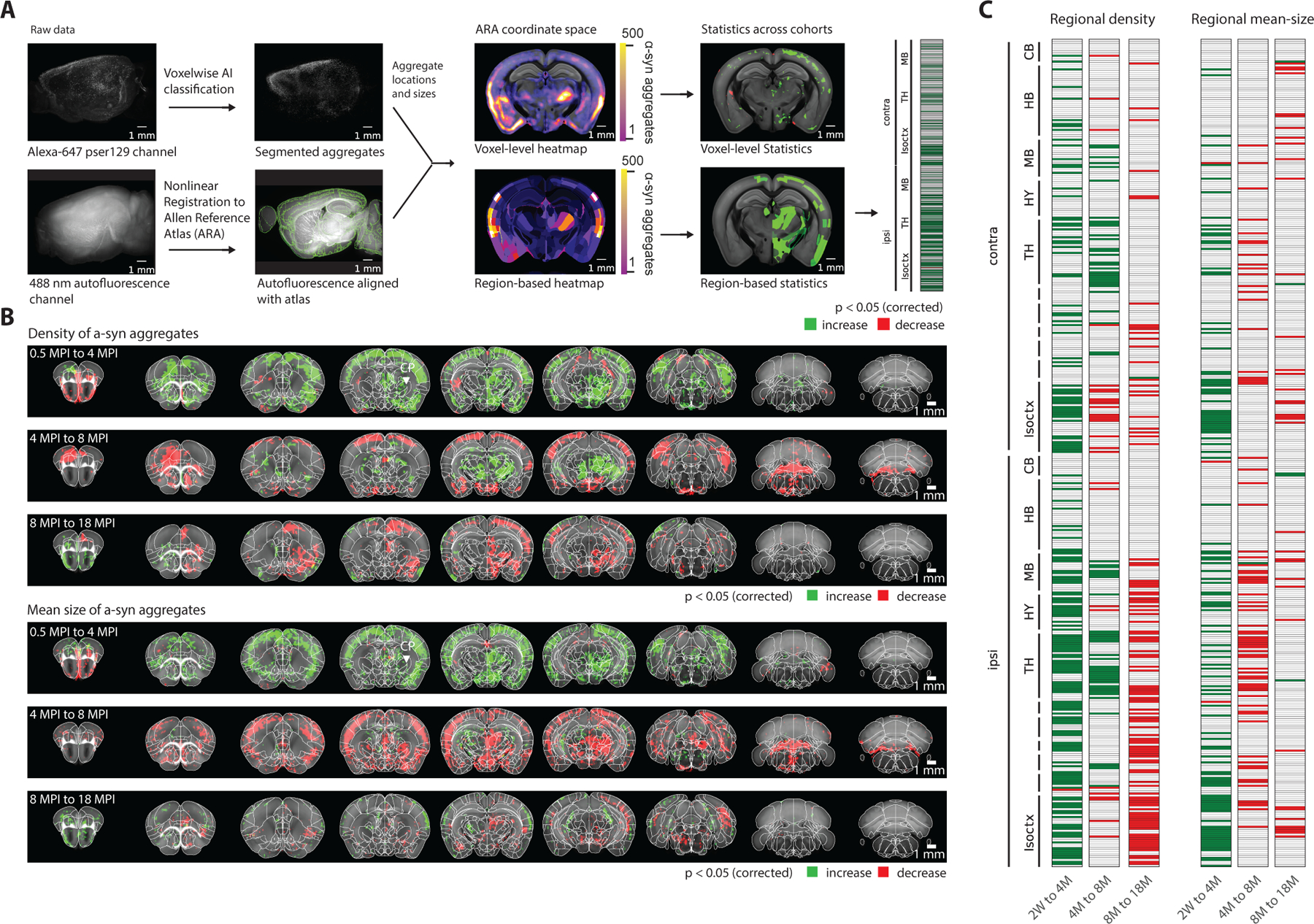
(A) The computational pipeline used for processing each brain sample consists of registration to a reference atlas, segmentation of three-dimensional aggregate volume, and using these two to map each aggregate to a neuroanatomical region or voxel in a shared coordinate space in the Allen Reference Atlas (ARA). This allows for statistical comparisons between longitudinal groups, at both the regional and brain-voxel level. (B) Voxel-level statistics using heatmaps from pairs of time points facilitates the discovery of voxel clusters with a statistically significant (p < 0.05) vulnerability to initial pathological spread, and separately accumulation of mean aggregate volume. (C) Grouping into ARA regions before statistical testing yields similar results (p < 0.05). Isoctx – isocortex, OLF – olfactory areas, HPF – hippocampal formation, CTX sp – cortical subplate, CNU – caudate nucleus, TH – thalamus, HY – hypothalamus, MB – midbrain, HB – hindbrain, CB – cerebellum. See also Figure S5 and Table S1.

Computational model of spreading

Despite being able to explain much of the initial regional variation in spreading, previous applications of computational models (Henderson et al., 2019a) only accounted for the spreading of α-syn. Thus, they are unable to generalize to later time points throughout the disease, notably even at 4 MPI where decay in pathology starts to occur (Figure 2B). To more accurately predict the progression of α-syn pathology, we developed a computational model by incorporating mechanistic insights regarding α-syn pathogenesis and trafficking from recent in vivo and in vitro studies. The key steps in this model consist of α-syn uptake into neurons, intracellular processing and interactions, and finally release of pathological α-syn. A set of differential equations model a discretized distribution of α-syn aggregate counts in each neuroanatomical region (Figure 3A). The model initially assumes quick uptake of injected α-syn fibrils into neurons within the target region. This has been confirmed by studies showing that extracellular α-syn fibrils are integrated into neurons through endocytosis (Brahic et al., 2016; Desplats et al., 2009; Henderson et al., 2019b; Konno et al., 2012). These injected fibrils are considered the smallest discrete pathological unit that can exist in the brain. However, as misfolded α-syn is processed through endo-lysosomal and cytoplasmic compartments, it can both recruit endogenous α-syn into a pathogenic fibrillar state, as well as merge with existing fibrils to form aggregates of larger size. Building off previous studies (Bieri et al., 2019), we assume retrograde spreading of any α-syn aggregate through the brain connectome, which the model incorporates as diffusion through a directed weighted graph (Figures 3B and S6A). We derived this anatomical connectivity from the Allen Connectivity Atlas (Oh et al., 2014), which includes 424 regions across the whole brain (Figures S6A and S6B; Table S1). Our model does not incorporate fragmentation of α-syn aggregates inside of the cytoplasm because previous studies have shown the fragmentation rate to be undetectably low (Gaspar et al., 2017).

Figure 3. Computational model describes spreading, aggregation, and decay.

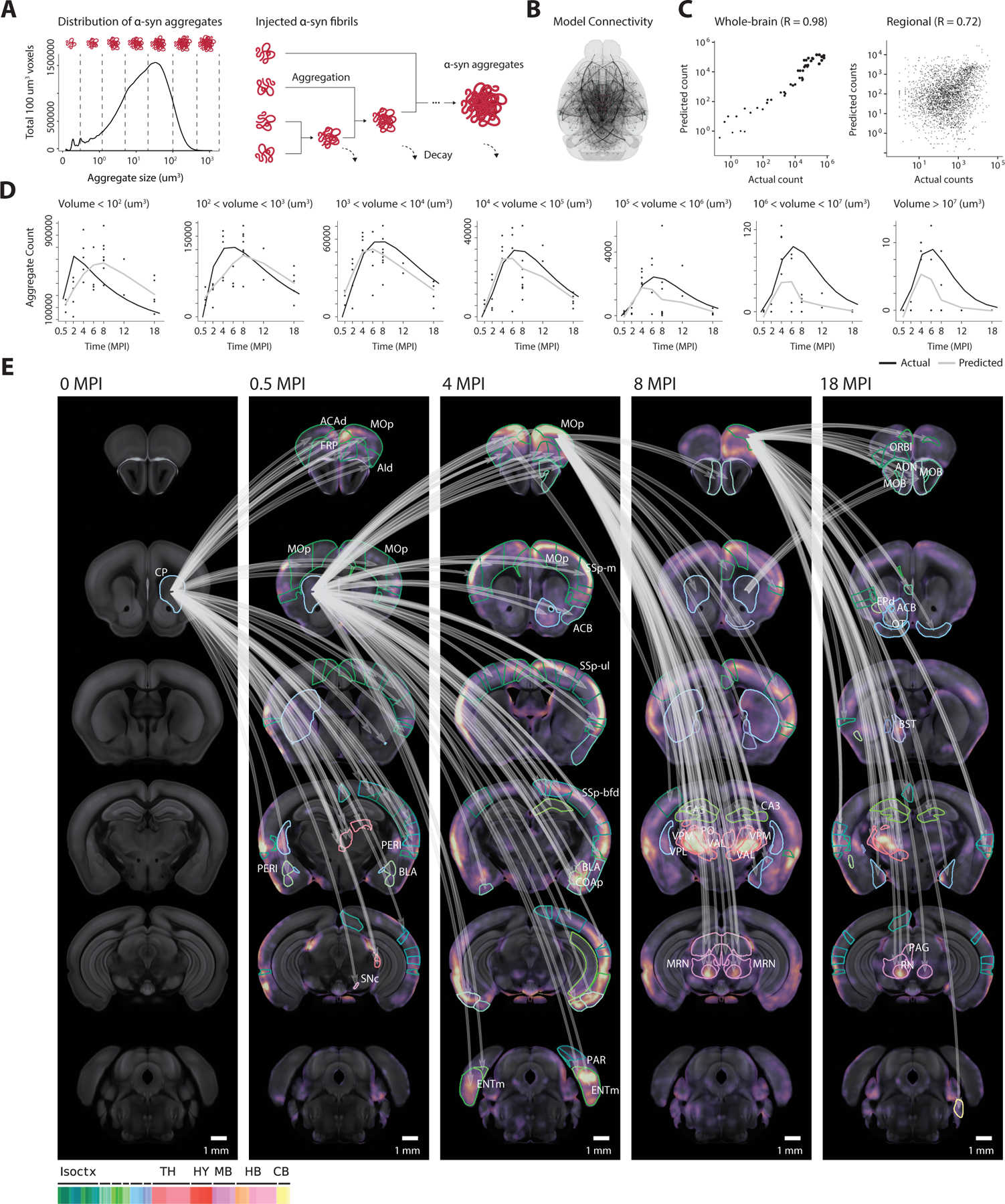
(A) To model the interactions between aggregates of various sizes, each aggregate’s volume is discretized into one of several size bins which are tracked as separate model variables in each region. Discrete-sized particles within each region can accumulate, with volumes combining additively. (B) The computational model describes the spreading of aggregates throughout the nodes of a directed graph, which relies on anatomical connectivity estimates from the Allen Connectivity Atlas. Each node represents an atlas region, with each edge representing the anatomical neuronal connectivity between the two regions. Thicker lines represent higher anatomical connections. (C) Fitted model accurately simulates both the longitudinal whole-brain counts of each discretized aggregate size (R = 0.98), and the regional counts (R = 0.72) for each size. (D) The raw time-series output from the computational model demonstrates the model’s ability to capture the dynamics of each discretized aggregate size. Black lines represent the model prediction of total aggregates of a given size, and gray lines represent the actual observed count. (E) Jacobian calculation between adjacent time points quantifies the model’s sensitivity to specific anatomical connections. The top 10% Jacobian elements for each pair of timepoints are displayed. Isoctx – isocortex, TH – thalamus, HY – hypothalamus, MB – midbrain, HB – hindbrain, CB – cerebellum. See also Figure S6.

Although we set most model parameters a priori, we fit the model’s parameters controlling the rate of spread and decay to data from α-syn PFF injection into the striatum, ranging from 0.5 to 18 MPI. Despite only being fit to maximize the model’s output in predicting the whole-brain α-syn aggregate count (Figures 3C and 3D), the resultant model additionally captures the regional variation in pathology with a high Pearson correlation coefficient of 0.72 (Figure 3C), providing evidence for the theory of a primarily retrograde neuronal spreading mechanism. We tested additional networks based on either anterograde connectivity or Euclidean distance between regions but neither could capture both whole-brain and regional variability (Figure S6C). Calculating model sensitivity through the Jacobian matrix allows for weighting of brain pathways that account for the most significant α-syn spread. This analysis highlights many retrograde pathways in the cortico-basal-ganglia-thalamo-cortical loop. Several examples with the highest Jacobian weight are early spreading from ipsilateral striatum to many cortical areas, such as the infralimbic area (ILA), main olfactory bulb (MOB), and gustatory area (GU). This is followed by spreading from the cortex to thalamus and other subcortical areas at later time points (Figure 3E).

Prediction of spreading patterns for different injection sites

After finding that our model based primarily on anatomical connectivity was able to accurately predict pathology resulting from α-syn PFFs injected into the striatum, we next tested the generalizability of this model to different seed locations (i.e., injection sites). We performed additional injections of α-syn PFFs throughout various regions of the brain and compared our model’s predictions with actual quantified pathological states. Since one of the prevailing theories behind α-synucleinopathies is that a single seeding event can result in spread throughout the nervous system, we chose a variety of distinct seed locations with relevance for Parkinson’s disease and other synucleinopathies: substantia nigra pars compacta, main olfactory bulb, and dentate gyrus (Figure 4A). Using our iDISCO immunolabeling, imaging, and computational processing pipeline, we quantified voxel-level and regional aggregate density and mean-size for brains at 0.5 MPI, 2 MPI, and 4 MPI for each seed location. These seed locations induced remarkably consistent distributions of aggregate size (Figure 4B), with the earliest 0.5 MPI maps displaying spikes of small aggregates, and this distribution tending towards larger aggregates over time. However, statistical tests from 0.5 to 4 MPI, at both the voxel and neuroanatomical level, yielded distinct spatial patterns of spreading and aggregation depending on the seed location (Figures 4C and S8B).

Figure 4. Seeding of α-syn fibrils in different brain regions results in consistent volumetric distributions of aggregate formation yet distinct spreading patterns by region, both of which are predicted by the computational model fitted to the striatal dataset.

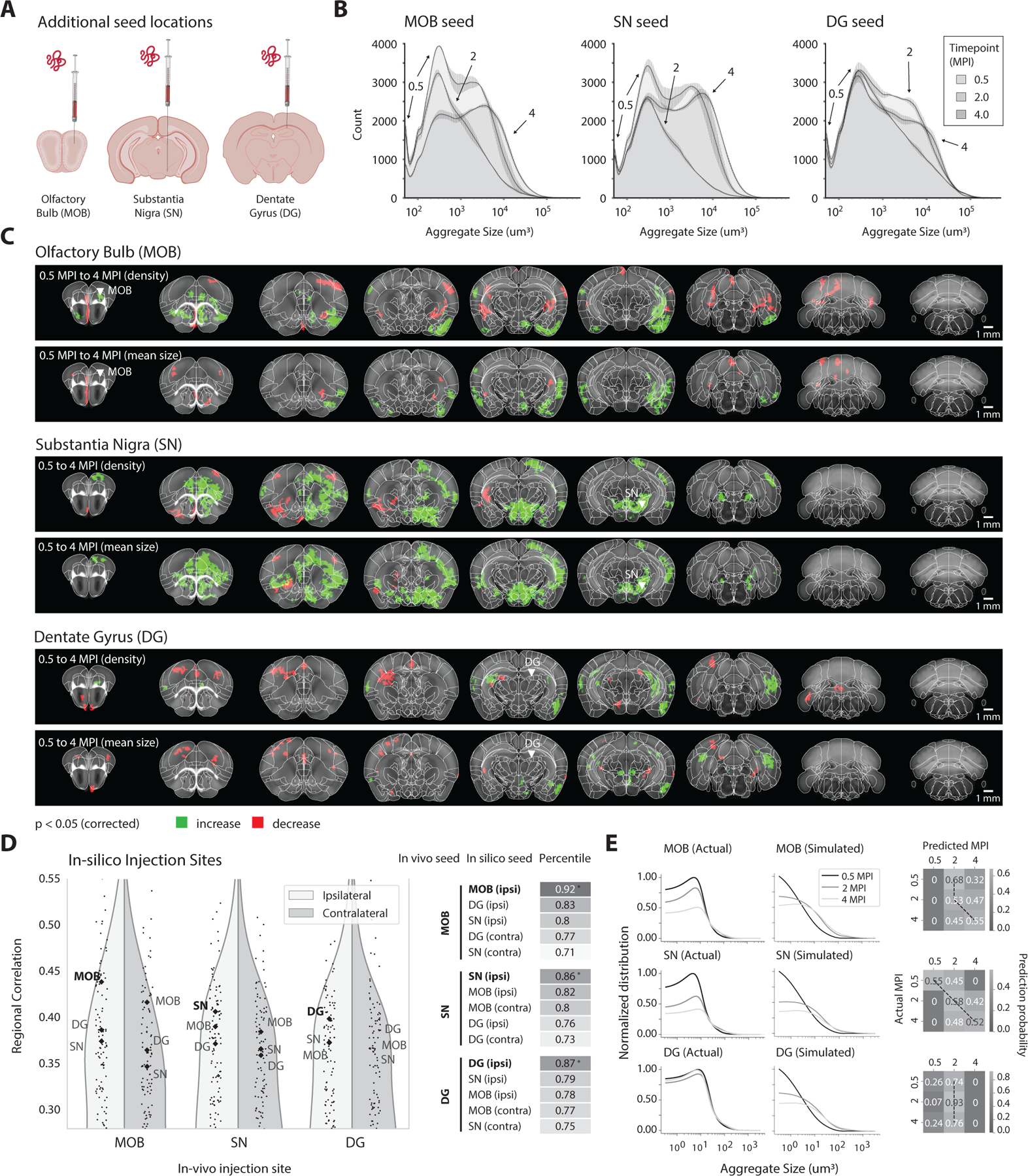
(A) α-syn PFFs are injected into new seed locations, with independent cohorts for the main olfactory bulb (MOB), substantia nigra (SN), and dentate gyrus (DG). Mice are perfused at 0.5 MPI, 2 MPI, and 4 MPI. (B) Distributions of aggregate sizes for the various seed locations demonstrate consistencies across various timepoints. 0.5 MPI samples consistently contained a higher number of small aggregates, while this distribution shifts towards larger aggregates for later time points. Data are represented as mean ± SD. However, (C) voxel-level statistics from 0.5 MPI to 4 MPI demonstrate that different seed locations result in distinct downstream spreading patterns (p < 0.05). (D) The correlation of each in vivo seed location with the model output from in silico seeding of all 424 regions in the ARA. Both ipsilateral and contralateral results for MOB, SN, and DG are labeled. In all cases, the model can accurately differentiate between unseen datasets with various distinct α-syn PFF seed locations. (E) For each additional seeding site, side-by-side comparisons of the actual and simulated histograms of aggregate volume, and confusion matrices between the actual and simulated states, demonstrate that the model can use the histogram of discretized aggregate sizes to predict the progression (MPI) since initial seeding. See also Figures S7 and S8.

We then applied our computational model to predict the regional pathological density for each discretized size bin across time. This involved modifying the initial condition of the simulated model and integrating forward in time, while keeping all parameters and hyperparameter values fixed. After iterating through each region in silico and generating the full time series of disease progression, we selected the region that best predicts the pathological state for a given dataset (Figure 4E). This method consistently predicted the correct ipsilateral hemisphere and neuroanatomical region of the initial seed from amongst all other seed locations (Figure 4E). Since all additional seed locations demonstrated consistent distributions of aggregate volume across the whole brain (Figure 4B), we hypothesized that we could also predict the duration of time since injection through inversion of this model, which we indeed found to be the case (Figure 4F).

Encoding spatial transcriptomics into the regional model

Consistent with current models (Henderson et al., 2019a), anatomical connectivity seems to be the primary driver of the patterns of α-syn spread; our computational model with edges simply weighted by anatomical retrograde connectivity was able to predict the regional spreading patterns with a high degree of correlation. But Parkinson’s disease is associated with a diverse set of genetic susceptibility factors. Do these converge on and impact α-syn spreading? The gene encoding α-syn itself, Snca, directly impacts spreading, because knockout of α-syn expression in mouse is sufficient to prevent widespread pathology following injections of α-syn PFFs, almost certainly because there is no endogenous α-syn to convert into aggregated form (Luk et al., 2012a; Luna et al., 2018; Taguchi et al., 2014). Other PD genes have also been connected to α-syn spreading. Transgenic mice engineered to express a PD-causing mutation in the Lrrk2 gene (LRRK2:G2019S) showed increased α-syn aggregation upon PFF injection (Bieri et al., 2019; Henderson et al., 2019a), as did human iPS neurons (Bieri et al., 2019).

We hypothesized that encoding regional genetic data into the computational model would allow us to rank a gene’s effects on the separate spreading and decaying steps of the model and potentially improve the model’s predictive power, as measured by the Pearson correlation coefficient of actual versus predicted regional variation. We encoded 19,893 regional gene density maps from the Allen in situ hybridization (ISH) database (Lein et al., 2007) into our previously fit computational model, using the same 424 regions spanning the whole brain (Figure 5A). Re-simulating α-syn progression with each encoded gene density map yielded a distribution of improvements they provide to each of our two model fitting parameters corresponding to spreading and decay. (Figure 5B). Interestingly, the Lrrk2 gene improved the model’s regional predictions when incorporated into the spreading parameter, and in that case ranked very highly (94^th percentile) amongst all genes. This is consistent with the hypothesis that Lrrk2 is important in vesicular trafficking pathways (Henderson et al., 2019b), and the recent evidence that reducing levels of Lrrk2 decreases α-syn aggregation (Bieri et al., 2019). The Gba gene improved the model’s regional predictions when incorporated into the decay parameter and was also ranked highly (90th percentile). Gba, which encodes the lysosomal lipid hydrolase glucocerebrosidase, is one of the most common genetic causes of PD and has been shown to be involved in modulating the susceptibility of neurons to α-syn pathology (Henderson et al., 2020).

Figure 5. Integrating spatial transcriptomics data into computational model reveals genes associated with spreading across seed locations.

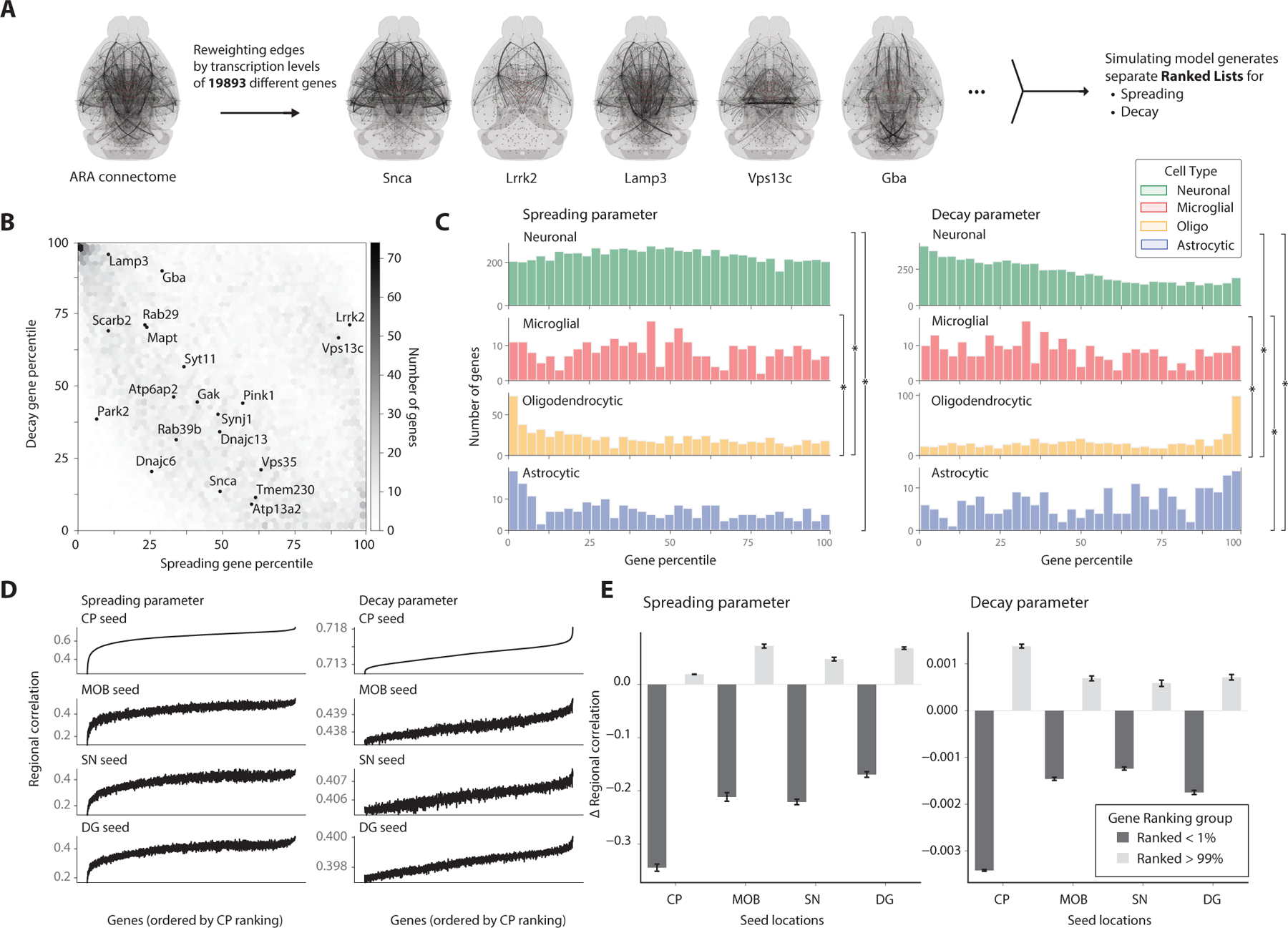
(A) Encoding region-specific gene densities from the Allen ISH database into the model allows for comparisons of each gene’s association with the spreading and decay parameters in improving predictive power. (B) Joint heatmap of the spreading and decay gene rankings depict clustering of genes that are relevant for either spreading or decay. Genes implicated in Parkinson’s Disease and synucleinopathies are additionally labeled. (C) Histograms of gene rankings for each parameter are grouped by cell type with highest transcription levels of that gene, taken from the Allen Atlas. Histograms were compared with the two-sample Kolmogorov-Smirnov test (*p < 0.05). (D) Simulation results from all genes in the Allen ISH database tested separately for the various PFF seed locations. The regional correlation between each gene’s simulated output and the entire timeseries for the seed location is reported, with the shared gene ordering on the x-axis determined by the striatum’s ranked genes in ascending order. (E) Encoding the highly ranked genes from the striatum dataset consistently improved the predictive power of the model for other seed regions, as measured by the correlation coefficient, while the bottom percentile genes consistently decreased the predictive power. Data are represented as mean ± SD.

After associating each gene with its most likely cell type using the Allen Cell Types RNA-Seq Database (Tasic et al., 2018), we explored the relationship between a gene’s cell type and its ranking. Since our model assumes a neuronal mechanism of transport, we hypothesized that genes from neuronal cell types would dominate the model’s spreading term, which is indeed the case (Figure 5C). However, for the decaying term in the model, we unexpectedly found a cluster of genes primarily expressed in oligodendrocytes, with Myelin basic protein (Mbp) being the highest ranked gene (Figure 5C). This finding is consistent with new data integrating genome-wide association studies with cell type atlases to show that oligodendrocytes play a key role in Parkinson’s disease (Bryois et al., 2020). Furthermore, accruing evidence suggests that another synucleinopathy, MSA (multiple system atrophy), an aggressive degenerative disease characterized by oligodendroglial cytoplasmic α-syn inclusions, behaves like a prion and that α-syn may indeed be the prion (Prusiner et al., 2015). Moreover, recent research suggests that the cytoplasmic milieu of oligodendrocytes promotes the formation of particularly potent α-syn seeds, which can spread to neurons (Peng et al., 2018). The enrichment of oligodendrocyte genes in our model (Figure 5C) lends further support for a role of oligodendrocytes in α-syn spreading.

Lastly, we found that using other seed locations to re-simulate the model and evaluate gene importance generated remarkably consistent rankings independent of injection site-based dataset (Figure 5D). Applying the average of the top percentile of ranked genes improved this correlation value for all injection sites, while conversely, the average of the lowest percentile of genes drastically reduced the predictive power of the model (Figure 5E). Future studies will be required to define the functional impact of these top-ranked genes on α-syn spreading but this list provides a resource for testing hypotheses.

DISCUSSION

Here, we demonstrate the ability of a mesoscale computational model to predict both the origin and progression of a neurodegenerative disease by using this computational model alongside quantitative high-resolution, whole-brain imaging. As longitudinal statistics across neuroanatomical regions and at the voxel-level demonstrated, the spreading and decay of pathology following seeding of α-syn PFFs is highly dynamic in nature, with many regions containing overlapping phases of spreading and decline. Nonetheless, our computational model is based on known mechanisms of α-syn PFF pathogenesis and accurately reconstructs the longitudinal counts of α-syn aggregates of various sizes across 424 brain regions. Retrograde anatomical connectivity can explain much of the regional variability in spread, but separately encoding 19,893 genes from a spatial transcriptomics database into the model additionally allowed us to uncover the relative involvement of genes in the model’s spreading and decaying terms. Although the incorporation of regional gene information into the models only uncovers correlative relationships between genes and the spreading and decaying of α-syn pathology, we provide evidence that the top-ranked genes in this analysis generalize to other PFF seed locations as well. With this list of genes in hand, future studies will aim to test their functional impact on α-syn spread and some may even represent therapeutic targets to slow down or stop spread.

This work confirmed many findings from previous studies that modeled the mechanisms behind α-syn spreading (Henderson et al., 2019a; Pandya et al., 2019), but also included many technological advances and novel results. A significant technological advancement included capturing a whole brain representation of α-syn pathology. We discovered that in some cases, traditional two-dimensional histological techniques used in previous studies may not adequately capture the relative α-syn aggregate counts across brain regions. Three-dimensional whole brain imaging provided a full spatial representation of α-syn pathology and allowed for the accurate quantification of aggregate morphology. This uncovered remarkably consistent distributions of aggregate volume along the longitudinal progression of disease. Additionally, exploring pathology patterns beyond 6 MPI and up to 18 MPI, which have not been extensively explored in previous studies, we were able to capture and model variable decay rates of pathology throughout the brain. While these earlier studies explored encoding genes and evaluating their effects on model fitting, our study included an unbiased exploration across a massive dataset of 19,893 genes. This exploration agreed with the known mechanisms of several genes implicated in α-syn pathology, but more importantly it provided novel hypotheses regarding the roles of all genes in the spreading and decay of pathology. Altogether, these technological advancements allowed for the novel development of a computational model that parameterized spreading, aggregation, and decay mechanisms underlying α-syn pathology changes. This model was used to predict both future and past pathological states for various seeding sites, and it can form comprehensive hypotheses around the roles of genes in each underlying parameterized mechanism.

Idiopathic PD, which represents most cases, can be seeded from various parts of both the nervous system and peripheral organs (Challis et al., 2020; Kim et al., 2019; Peelaerts et al., 2015; Sacino et al., 2014). The comparisons between in silico simulation of α-syn pathogenesis and data from various injection sites provide a testbed for this model and demonstrate its generalizability in predicting the origins and future patterns for arbitrary seeding datasets. In a broader sense, this model holds promise for analyzing human brain imaging data (such as once accurate α-syn PET ligands are developed) to wind the clock back and predict how and where α-syn pathology originated. The clock can also be wound forward to predict the future trajectory and tailor therapeutic interventions accordingly. We propose this clinical application of such a model as relevant to PD or any progressive protein-spreading neurodegenerative disorder, such as Alzheimer’s disease, amyotrophic lateral sclerosis, or frontotemporal dementia (Goedert et al., 2010; Guo and Lee, 2014; Jucker and Walker, 2013). Because our model provides a metric for predicting the in vivo seed location when given an unseen set of pathological states, being able to predict the seed location and progression given a pathological state would have high utility in clinical diagnostic and therapeutic applications for many of these neurodegenerative diseases.

We found that incorporating regional gene transcription levels into our model parameters significantly impacted how well the model fit the data. This potentially points to a gene transcription level’s role in the spreading and decay processes. Our comprehensive modeling approach allowed gene encoding into each model parameter and enabled the ranking of these genes in terms of their involvement in spreading and decay. As this aspect of our study is a proof of concept that provides rankings of genes and potential mechanisms of their contribution to spreading and decay, follow-up experimental studies manipulating these gene expressions will be needed. These rankings will also allow us to identify genes as novel targets for therapeutic intervention. We also highlight the significant finding in this study that this process produced similar rankings of genes across datasets from different pre-formed fibrils seeding locations (Figures 5D and 5E), even with these seeding locations producing vastly distinct spreading patterns of pathology (Figure 4C). This consistency supports the unique information that this approach provides, and we believe will enable future studies to explore the roles of these genes further.

Future extensions to this model could include considering additional mechanisms such as vascular, ventricular, or glial densities. Many studies have also shown spreading of seeds from both the gut and peripheral nervous system. However, owing to the current lack of quantitative atlases that connect the peripheral-to-brain or gut-brain axes, and the technological difficulty in imaging a cleared whole mouse body using light sheet microscopy, we only focused on the dynamics of pathology across the central nervous system. However, our model could integrate these datasets when they become available. Furthermore, although the encoding of genes from a spatial transcriptomics database revealed potential implications of these genes in either the spreading or decay of pathology, this analysis does not take into consideration protein expression levels, or any effects caused by genetic mutation. This computational model could help form hypotheses for further studies looking into these effects.

As our labeling approach with iDISCO utilizes polyclonal secondary antibodies, we expect that multiple polyclonal secondary antibodies bind to each primary antibody, thus providing fluorescent signal amplification. An inherent limitation in this approach is that an alpha-synuclein aggregate’s size, as measured by the three-dimensional morphology in the fluorescence channel, is not directly indicative of the actual aggregate size (nonlinear but monotonic). However, we expect this multiple binding to affect all samples equally. Given that we are performing large-scale and stringent statistics across many cohorts of mice, we expect that our statistical tests can still uncover regions of interest that show significant increase or decrease in aggregate size.

The clinical detection of pathological α-syn and other proteinaceous seeds for neurodegenerative diseases is currently performed primarily through post-mortem analysis. However, many advancements in nuclear medicine, similar to PET and SPECT radiotracers that detect amyloid depositions in vivo, will likely allow for quantitative evaluation of a patient’s pathological state. Current tracers work well for amyloid-beta and tau but are still in development for α-syn. Given the various etiologies that have been observed clinically, it will undoubtedly be essential to be able to differentiate between synucleinopathies with different origins and trajectories. The generalizability and interpretability of the computational model we present here offers unique advantages because it can both infer the progression of α-syn spreading patterns when given the current pathological state, or inversely produce the likely seed locations, and time since seeding, that led to this state. All these applications will help empower more accurate disease classification and prediction of clinical phenotypes for a wide array neurodegenerative disease.

Limitations of the Study

The methods presented in this study have demonstrated that whole-brain imaging and computational modeling can accurately describe and predict the longitudinal dynamics of pathology in neurodegenerative disease. While this model can accurately reconstruct the observed dynamics of whole brain pathology change over time across 424 neuroanatomical regions, it made several important assumptions based on recent discoveries in the literature. Specifically, these include neuronal uptake of injected α-syn fibrils (Brahic et al., 2016; Desplats et al., 2009; Henderson et al., 2019b; Konno et al., 2012), synaptic spreading of α-syn pathology (Bieri et al., 2019), prion-like aggregation of pathology into larger units, and eventual decay of this pathology (Luk et al., 2012a). Future work could extend the model to incorporate parameters that were not actively considered and test the sensitivity of the model’s predictions to these assumptions. For example, it is possible that grouping aggregate counts into the 424 neuroanatomical regions does not fully capturing the complex pathology dynamics we observed. Although we tested multiple sets of neuroanatomical regions across the atlas hierarchy of regions (Figure S6D), this number was ultimately constrained by the Allen Connectivity Atlas (Oh et al., 2014). Future studies could take full advantage of the high-resolution images obtained in our study to create more detailed models that take pathology dynamics across cortical layers or more granular anatomical regions into account.

STAR Methods

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Jin Hyung Lee (ljinhy@stanford.com).

Materials Availability

This study did not generate new unique reagents.

Data and code availability

• All data reported in this paper will be shared by the lead contact upon request.

• This paper does not report original code.

• Any additional information required to reanalyze the data reported in this work paper is available from the Lead Contact upon request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Animals

Mouse husbandry and procedures were performed in accordance with institutional guidelines and approved by the Stanford Administrative Panel on Animal Care (APLAC). 10-12-week-old male C57Bl6J mice (The Jackson Laboratory, cat# 000664) were used for stereotaxic injections. Mice were housed under specific pathogen-free conditions under a 12 h light-dark cycle, ad libitum diet and free access to water.

METHOD DETAILS

PFF preparation

The expression and purification of mouse wild-type α-syn was performed as previously described (Ghee et al., 2005). α-syn fibril formation was induced by incubation in 50mM Tris–HCl, pH 7.5, 150mM KCl buffer at 37°C under continuous shaking in an Eppendorf Thermomixer at 600rpm. α-syn fibrils were centrifuged twice at 15,000g for 10min and resuspended in PBS. All fibrils were fragmented prior to in vivo use by sonication for 20 min in 2-ml Eppendorf tubes in a Vial Tweeter powered by an ultrasonic processor UIS250v (250 W, 2.4 kHz; Hielscher Ultrasonic, Teltow, Germany). 5ug of fibrils/mouse were used for in vivo mouse experiments. The fibrils were endotoxin free, as assessed using the Pierce LAL Chromogenic Endotoxin Quantification Kit.

Fibril injections

Stereotaxic injections were performed on 10-12-week-old adult mice. Animals were placed in a stereotaxic frame and anesthetized with 2% isoflurane (2L/min oxygen flow rate) delivered through an anesthesia nose cone. Ophthalmic eye ointment was applied to prevent desiccation of the cornea during surgery. The area around the incision was trimmed, cleaned, and disinfected. A small hole was drilled above the injection site. PFF or vehicle solutions were injected unilaterally into the dorsal striatum, hippocampus, olfactory or substantia nigra using the following coordinates (from bregma): Striatum – anterior (AP) = +0.4mm, lateral (ML) = +/−1.85mm from midline, depth (DV) = −2.7mm (from dura). Olfactory bulb: AP, +4.50 mm; ML −0.75 mm; DV −1 mm. Dentate gyrus: AP −2 mm, ML = 1.5 mm, DV = −2.1 mm. Substantia nigra pars compacta: AP −3.1 mm, ML 1.2 mm, DV −3.75 mm. Mice were injected with sonicated PFFs (5µg/mouse) or PBS vehicle control. PFFs were sonicated prior to injection. 1μl volume was injected at a rate of 100nl/min using a 5μl Hamilton syringe with a 32G needle. To limit reflux along the injection track, the needle was maintained in situ for five minutes, before being slowly retrieved. The skin was closed with silk suture. Each mouse was injected subcutaneously with analgesics and monitored during recovery. Animals were sacrificed 2 weeks to 18 months post injection.

Tissue processing

Mice were anesthetized with isoflurane and transcardially perfused with 0.9% saline followed by 25ml of 4% PFA. Brains were dissected and post-fixed in 4% paraformaldehyde (PFA) pH 7.4, at 4°C for 48 hours. Brains for histology stored in 30% sucrose in 1x PBS at 4°C. PFA-fixed brains were sectioned at 35um (coronal sections) with a cryo-microtome (Leica) and stored in cryoprotective medium (30% glycerol, 30% ethylene glycol) at −20°C. Brains for iDISCO tissue clearing and labeling were stored in PBS with 0.05% sodium azide.

Tissue Clearing

Each sample was fully immunolabeled and cleared using the previously described iDISCO protocol (Renier et al., 2014), which describes the sample pretreatment, blocking, immunolabeling, and clearing steps in more detail. The methanol pretreatment step was performed for all samples. For primary immunolabeling, an anti-phospho-synuclein (pSer129) Rabbit polyclonal antibody was used at 1:1000 dilution for 7 days, while a Donkey anti-Rabbit IgG (H+L) Alexa Fluor 647nm antibody was used for secondary immunolabeling at 1:1000 dilution for 7 days. All other clearing parameters were used as previously reported (Renier et al., 2014).

Immunohistochemistry

Tissue processing and immunohistochemistry was performed on free-floating sections according to standard published techniques. 1:6 to 1:12 series of all coronal sections were used for all histological experiments. Sections were rinsed 3 times in TBST, pre-treated with 0.6% H2O2 and 0.1% Triton X-100 and blocked in 5% goat serum in TBST. Free-floating coronal sections were incubated overnight with mouse-α-syn pSer129 antibodies (81A; 1:5000, Covance/BioLegend cat# MMS-5091). After overnight incubation at 4°C, sections were rinsed 3 times in TBST. The primary antibody staining was revealed using fluorescently-labeled secondary antibodies (Thermo Fisher Scientific cat# A-21137). Sections were counter-stained with DAPI, mounted on Superfrost Plus slides (Fisher Scientific) and coverslipped using ProlongDiamond antifade mountant (Thermo Fisher Scientific cat# P36961). Images of pSer129 aggregates were acquired using a Leica DMI6000B inverted fluorescence microscope by an investigator blinded to the treatment group.

Microscopy

Each sample was imaged using an LaVision Biotec Ultramicroscope II within two days of finishing iDISCO clearing. Microscope settings of a full sheet width, numerical aperture of 0.103, mechanical step-size of 3.5 um, and light-sheet thickness of 7 um were used for all acquisitions. A 488 nm excitation laser and 460/40 nm emission filter (center wavelength/FWHM) were used for each autofluorescence acquisition. A 639 nm excitation laser and 620/60 nm emission filter were used for detecting fluorescent α-syn pathology. The left and right hemispheres of each brain sample were imaged separately. Each acquisition was in the sagittal plane. Each acquired slice had an in-plane resolution of 4.0625 × 4.0625 um, with a slice resolution of 3.5 um.

QUANTIFICATION AND STATISTICAL ANALYSIS

Registration, Segmentation, and Quantification

Upon voxel-wise binarization of the raw iDISCO α-syn fluorescence channel using a machine learning model into foreground (pathology) and background (autofluorescence), binary morphological operations are used to find the connected components. Each connected component is considered a separate α-syn aggregate, and the position (x,y,z), peak intensity (in the corresponding raw data), and volume (number of voxels) of each aggregate is saved.

The non-linear transformation resulting from the registration process is used to transform each aggregate to the Allen Reference Atlas (ARA) coordinate space. Each voxel in this coordinate space is a 100-um width cube centered at that coordinate. Since the atlas is at a lower spatial resolution (100 um) than the raw data (4.0625 um), multiple aggregates may map to a single voxel in the ARA space. For a given ARA voxel, we define the density as the total number of aggregates with centers within that voxel. We also define the total-size for a voxel as the total size of all the aggregates with centers within that voxel. We compute the mean-aggregate-size for each voxel as its total-size divided by the density. A similar calculation is performed for the total and mean intensities at each voxel. The density, mean-aggregate-size, and mean-aggregate-intensity are considered separate metrics.

To account for variations in registration quality between samples, a multidimensional Gaussian filter (σ = 15 voxels) is applied to the density, mean-aggregate-size, and mean-aggregate-intensity spatial maps to smooth the values across neighboring voxels. This filter size was empirically determined based on the registration results. Mean smoothed spatial maps for various timepoints are presented in Figures S5 and S7.

Sections from immunohistochemistry were also segmented for pathology and registered to the ARA using a similar computational pipeline, which was applied in two dimensions instead of three. For each brain section, the corresponding coronal ARA slice was first manually selected. The DAPI channel for each section was then registered to this atlas slice. Aggregates from the pSer129 channel were also detected using a machine learning model. For a given brain sample, the total aggregate count for each neuroanatomical region across all imaged histological sections was calculated. Since the histological sections only capture a sparse representation of the brain volume, each region’s aggregate count was extrapolated by dividing by the total observed volume for that region, then multiplying by the total volume of that region in the ARA.

Statistical Analysis

The smoothed maps from the image processing pipeline are used for two-sided T-tests at each voxel between samples at different timepoints. Due to the variability in the spreading patterns between adjacent time points, statistical tests were only run between time points with adequate spacing: 0.5 MPI vs 4 MPI, 4MPI vs 8 MPI, and 8 MPI vs 18 MPI. Thus, the 2, 6, and 12 MPI time points were omitted. In order to account for the large number of voxels at a 25um resolution, multiple comparison corrections were performed using the Benjamini-Hochberg method (Benjamini and Hochberg, 1995). The corrected p-values were thresholded at 0.05 for determining significance. Similar analysis was performed for counts when grouped into ARA anatomical regions.

Computational Modeling

This Smoluchowski network model has been described extensively in previous studies (Fornari et al., 2020; Wattis, 2006), and is governed by the following set of differential equations.

$$\frac{d{c}_{1,j}}{dt}=-\text{α}{\sum }_{k=1}^V{L}_{jk}{c}_{1,k}-{\text{µ}}_{1,j}{c}_{1,j}-2c_{1,j}^2\left({\text{κ}}_j+\text{ξ}{\sum }_{k=2}^{N}k{c}_{2,k}\right)-c_{1,j}{\sum }_{k=2}^N{c}_{k,j}$$

$$\frac{d{c}_{2,j}}{dt}=-2^{-\text{η}}\text{α}{\sum }_{k=1}^V{L}_{jk}{c}_{2,k}-2^{\text{λ}}{\text{µ}}_{2,j}{c}_{2,j}+c_{1,j}^2\left({\text{κ}}_j+\text{ξ}{\sum }_{k=2}^{N}k{c}_{2,k}\right)-c_{1,j}{c}_{2,j}$$

$$\frac{d{c}_{i,j}}{dt}=-i^{-\text{η}}\text{α}{\sum }_{k=1}^V{L}_{jk}{c}_{i,k}-i^{\text{λ}}{\text{µ}}_{i,j}{c}_{i,j}+c_{1,j}\left(c_{i-1,j}-c_{i,j}\right)$$

$$\frac{d{c}_{N,j}}{dt}=-N^{\text{λ}}{\text{µ}}_{N,j}{c}_{N,j}+c_{1,j}{c}_{N-1,j}$$

$c_{i,j}$ represents the total count of aggregates in the discretized size-bin indexed by I, in the brain region indexed by j. The L matrix represents the Laplacian matrix of the weighted directed graph connecting the various neuroanatomical regions of the brain, taken from the Allen Connectivity Atlas (Oh et al., 2014). As this system of differential equations has no closed form solution, numerical integration with the software package SciPy was used to solve for the state dynamics given the initial conditions. $\eta$ was chosen as a hyperparameter that slows the spread of large aggregates as the inverse power of the size, while $\lambda$ was chosen as a hyperparameter that accelerates the decay of aggregates proportionally to the power of their size. The initial values for $\alpha$ and $\mu$, which control the rate of spreading between nodes and decay at a given node, respectively, were fit by sweeping through a 2D-grid (0.001 to 1000) and selecting the values that resulted in the lowest mean-squared error between the predicted and actual counts ($\alpha =0.037$, $\mu =0.139$). In the case of $\mu =0$, $k =0$, $\text{ξ}=0$, and a one-dimensional size vector c, the above system of differential equations simplifies to the standard network diffusion model used in earlier studies (Henderson et al., 2019a; Pandya et al., 2019).

In order to quantify the model’s sensitivity to specific neuroanatomical pathways in the brain, the Jacobian matrix was calculated by taking the partial derivative of the model’s output with respect to the weight of the anatomical connection strength between two regions encoded into the model. An element of this matrix represents the relative importance of that anatomical connection in the spreading of aggregates to a specific region.

This model can be used to produce a ranking of the candidate seed locations for a given pathological state $c$ at $t=T$ MPI. To generate this ranking, each of the 424 neuroanatomical regions are used as separate seed locations at $t=0$ within the model and simulated forward in time to $t=T$ MPI. Each of the 424 simulation results are then compared with the observed state $c$ using a pairwise similarity metric. In this case, the similarity metric was the correlation coefficient between total regional aggregate counts across the observed and simulated states. The similarity metric values can then be used to sort the 424 seed locations as likely sites that lead to the observed pathological state $c$.

Similarly, the model can be used to predict the time since seeding $t=T$ MPI for a given pathological state $c$. A property of this computational model is that the distribution of simulated aggregate sizes across the whole brain is invariant to which neuroanatomical region is used as the seed location at $t=0$. Therefore, the whole-brain distribution of aggregate sizes for state $c$ can be compared with simulated distributions at various $t$ using a pairwise similarity metric without taking the seed location into account. The mean squared error was calculated between the stimulated and observed distributions. When deciding among several candidate $t$ values (0.5 MPI, 2 MPI, 4 MPI), the mean squared errors are inverted and normalized to sum to 1, providing a prediction probability for each $t$ being the correct estimate of T for the given pathological state $c$.

In order to also encode regional genetic differences and evaluate their differential effect on model performance, we reconsider the $\alpha$ (spreading) and $\mu$ (decay) parameters as regionally dependent. The spreading from a specific region is made proportional to the gene density in that region. All genes are normalized to the same range so that we are only comparing the regional distribution of gene expression relative to that gene’s total whole-brain expression. Since $\alpha$ is now considered a vector, the product of it with the Laplacian connectivity matrix $L$ has the effect of modifying the regional connectivity encoded into the model. In order to preserve the model’s previous fit to capturing the whole-brain longitudinal spread, we normalize each gene vector to have mean 1 and a standard deviation $\text{Σ}$, which is empirically set to preserve the correlation between predicted and observed whole-brain count. The normalization was chosen so that this product has the effect of maintaining the trace of the original matrix L. A derivation of this normalization preserving the trace of the Laplacian matrix is as follows: we assume the vector s is sampled from a multivariate normal distribution with mean-value 1 and standard deviation $\text{Σ}$.

$$s ~ N\left(1,\text{Σ}\right)$$

By using the definition of the matrix trace and representing s as a diagonal square matrix S, the trace of the product of S and the Laplacian matrix L results in the following, where l represents the diagonal of L.

$$Tr\left(SL\right)=Tr\left(\left[\begin{array}{ccc}{s}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & s_V\end{array}\right]L\right)=\sum _{i=1}^V{s}_i{L}_{ii}=s\cdot \text{diag}\left(L\right)=s\cdot l$$

Thus, the trace is equivalent to the dot product of s and l, which has an expectation value equivalent to the sum of the entries of l, which recovers the definition of the trace of L.

$$s\cdot l ~ N\left(1\cdot l, l \text{Σ} l\right)$$

$$\text{E}\left[s\cdot l\right]=\text{Tr}\left(L\right)$$

After each gene is encoded into the model, its net effect on the regional correlation between the simulated and actual data is compared to the baseline correlation with no genes. This provides an ordered list of genes, ranked by the relevance of their spatial expression map in improving the regional predictions the model.