Novel clinical trial designs with dose optimization to improve long-term outcomes

Abstract

Conventional designs for choosing a dose for a new therapy may select doses that are unsafe or ineffective, and fail to optimize progression free survival time, overall survival time, or remission duration. We explain and illustrate limitations of conventional dose finding designs, and make four recommendations to address these problems. When feasible, a dose-finding design should account for long-term outcomes, include screening rules that drop unsafe or ineffective doses, enroll an adequate sample size, and randomize patients among doses. As illustrations, we review three designs that include one or more of these features. The first illustration is a trial that randomized patients among two cell therapy doses and standard of care in a setting where it was assumed on biological grounds that dose-toxicity and dose-response curves did not necessarily increase with cell dose. The second design generalizes phase 1–2 by first identifying a set of candidate doses, rather than one dose, randomizing additional patients among the candidates, and selecting an optimal dose to maximize progression free survival over a longer follow up period. The third design combines a phase 1–2 trial and a group sequential randomized phase 3 trial by using survival time data available after the first stage of phase 3 to re-optimize the dose selected in phase 1–2. By incorporating one or more of the recommended features, these designs improve the likelihood that a selected dose or schedule will be optimal, and thus will benefit future patients and obtain regulatory approval.

Introduction

Preclinical development of new targeted and immunotherapy agents for cancers and other diseases has created a pressing need for clinical trials to evaluate and optimize these agents. Members of the medical research community have become aware that conventional methods for choosing the dose or schedule of a new agent are inadequate (1–6). Shah et al. (7) provided examples of several agents with recommended doses that had high toxicity rates in trials or post-marketing samples following US FDA approval. Failure of conventional designs to reliably identify safe and effective doses apply generally, and they are likely to perform poorly for cytotoxics. radiation therapy, and targeted agents (2,5,7).

We review problems with conventional dose-finding designs and recommend desirable design features to obtain better results. We review three practical dose-finding designs that reliably identify safe doses that maximize progression-free survival (PFS) time, overall survival time (OS) time, or remission duration (RD). Our goal is to motivate medical researchers to include these features in their dose-finding trials.

Background and Examples

The US FDA initiated Project Optimus (7,8), “to reform the dose optimization and dose selection paradigm in oncology drug development”. Despite widespread agreement that new dose-finding designs are needed for targeted or immunological agents, it is unclear how to structure them for many medical settings. Conventional phase 1 designs choose a maximum tolerated dose (MTD) by assigning doses to successive patient cohorts in a small trial using a 3+3 algorithm (9) or the continual reassessment method (CRM) (10,11), using dose limiting toxicity (DLT) evaluated after one or two cycles of therapy. It is well known that a 3+3 algorithm is likely to produce poor decisions (2,12,13), with a high risk of an unacceptably high toxicity rate at the MTD in later trials (7,13). Most phase I samples are too small to reliably choose an MTD or estimate its toxicity probability. For example, if two DLTs are observed in six patients treated at the MTD in phase 1, a Bayesian posterior 95% credible interval for the probability of DLT at the MTD ranges from 8% to 71%. Treating an expansion cohort at the MTD does not solve this problem, because an MTD chosen based on a small sample has a high risk of being excessively toxic. Conventional designs assume that the risk of DLT increases with dose, “monotonicity”, which may be true for some agents but not others, and a careful analysis of all preclinical data should be done to adjudicate this before choosing a design. If monotonicity does not hold, dose escalation is inappropriate, because higher doses may be less safe or provide lower anti-cancer efficacy.

Conventional phase 1 designs ignore efficacy, such as tumor shrinkage or complete remission in cancers such as leukemias, which makes it impossible to choose doses based on risk-benefit trade-offs. Phase 1–2 designs use both toxicity and early efficacy to select a doses, and are well-known to be superior to phase 1 designs (2,12,13). Phase 1–2 designs accommodate dose-response curves with a plateau due to saturation of PK exposure in the patient, whereby the response rate does not increase for higher doses, and a selected dose on a plateau by conventional phase 1 designs may expose patients unduly to a higher risk of toxicity (2). For example, if five doses have toxicity probabilities 1%, 5%, 30%, 45%, and 50%, and response probabilities 20%, 50%, 50%, 50%, and 50%, a plateau is reached at dose 2. A 3+3 algorithm or CRM with target toxicity probability 30% both are most likely to select dose 3, while dose 2 has the same response probability of 50% but much lower toxicity probability of 5%. Although superior to conventional phase 1, most phase 1–2 designs ignore PFS time, OS time, and RD evaluated over longer follow up. Because early outcomes seldom are reliable surrogates for long-term outcomes (14,15), a dose chosen in phase 1 or phase 1–2 often fails to maximize PFS, OS, or RD (16,17). Table 1 gives examples, and solutions provided by novel designs (1,18–24). For example, writing R = response and T = toxicity, the phase 1 trial of niraparib for ovarian cancer in Table 1 might be replaced by a phase 1–2 trial based on the utilities U(R, No T) =100 and U(No R, T) = 0 for the best and worst possible outcomes, with U(R, T) = 80 and U(No R, No T) = 40 for the intermediate outcomes, using estimated values of U as a basis for evaluating doses. This could be extended further to use response duration to choose a best dose, by applying the generalized phase 1–2 design, described below.

Table 1.

Examples of flaws with conventional designs and solutions provided by novel designs.

Disease	Agent	Design	References	Flaw	Solution
Philadelphia chromosome-positive leukemias	Ponatinib (oral tyrosine kinase inhibitor)	3+3	(18,19)	Pick an unsafe dose of 45 mg PO daily continuously (18), which later was modified to starting with 45 mg PO daily then 15 mg PO daily once ≤1% BCR-ABL is achieved (19)	Include a dose toxicity rate safety monitoring rule
Non-small cell lung cancer	Onartuzumab (monoclonal antibody against MET)	3+3	(20,21)	Pick a dose with a low response rate → Phase III failure	Include a dose response rate futility monitoring rule
Ovarian Cancer	Niraparib (PARP inhibitor)	Accelerated titration 3+3 design	(22,24)	Pick a dose with a high grade 3 hematologic toxicity rate	Account for toxicity grades and response using a utility function
High risk acute leukemias	Vorinostat (histone deacetylase inhibitor)	Time-to-event continual reassessment method (CRM)	(25)	Pick a dose that yielded a worse overall survival than the other doses. Limited sample size to choose among the other doses	Account for long-term overall survival and enroll adequate sample size for reliable dose selection
Clear cell renal cell carcinoma	Sitravatinib (oral tyrosine kinase inhibitor) in combination with nivolumab immunotherapy	Late-onset efficacy-toxicity	(1)	Unable to choose a dose giving better long-term survival	Account for long-term PFS or survival time when choosing a dose

As an illustration, a phase 1 trial of allogeneic stem cell transplantation for acute leukemia (25) studied six doses of vorinostat added to a standard preparative regimen, using the time-to-event CRM (26) with target toxicity probability 30%. Because very few DLTs were observed, the design rapidly escalated and selected the highest dose, level 6, as the MTD, where an expansion cohort was treated, giving per-dose sample sizes of 3, 3, 3, 4, 4, and 51. Longer follow up showed that patients treated with dose 6 had shorter OS than patients treated at doses 1 – 5. This effect persisted after accounting for prognostic variables (25,27). Since dose 6 is undesirable, but a lower dose maximizing OS cannot be determined from the small samples at dose levels 1 – 5, it is unclear what dose to use in clinical practice, or how to design a future study. This trial suggests that, in general, longer term outcomes should be considered, along with toxicity and early response, when selecting a dose.

A second illustration is phase 1–2 trial conducted to optimize the dose of sitravatinib, a tyrosine kinase inhibitor, + a fixed dose of nivolumab, an anti–programmed death agent, in clear cell renal cell carcinoma (ccRCC) (1). The “Late Onset Efficacy-Toxicity (LO-ET) design (28) was used to choose among 60-, 80-, 120-, and 150-mg doses of sitravatinib, which had final respective LO-ET desirability scores of 0.622, 0.787, 0.755, and 0.630. However, longer outcomes including PFS time and later patient-reported outcomes measuring depression, quality of life, and hope for the future all indicated that the 120 mg dose was best, rather than the nominally optimal LO-ET dose of 80 mg (1).

Recommended Features of a Dose-Finding Design

To address limitations of conventional dose-finding methods, and respond to Project Optimus, we recommend that, when feasible depending on the setting, a dose-finding design should include one or more of the following features:

Feature 1.

To choose an optimal dose, in addition to using short-term response and toxicity, a long-term outcome such as PFS time, OS time, or RD, evaluated over longer follow up should be used.

Feature 2.

Include screening rules that drop unsafe or ineffective doses. If some doses are dropped, enrich the sample sizes of remaining doses rather than reducing overall sample size.

Feature 3.

Enroll a sample large enough to make reliable inferences.

Feature 4.

If appropriate, randomize patients among doses and compare them with standard of care (SOC).

Feature (1) addresses the problem that early outcomes are imperfect surrogates for PFS, OS, or RD, so a dose maximizing response rate often does not optimize long-term outcomes. Feature (1) requires longer follow-up, often six or 12 months, to evaluate the long-term outcome. Screening rules in Feature (2) protect patients from unsafe or ineffective doses, and enrichment increases dose selection reliability. Feature (3) is motivated by the fact that the precision of any inference increases with sample size. Feature (4) ensures that between-dose comparisons are fair and, to protect patient safety, a monitoring rule that stops accrual to an excessively toxic dose should be included.

Each of the following three designs has one or more of the recommended features. The randomized controlled selection design, which is well established, is the least complex. The other two designs are novel. The generalized phase 1–2 design has intermediate complexity, and the phase 1–2/3 design is most complex. Properties of these designs are summarized in Table 2, which may provide a basis for choosing among them in a particular setting.

Table 2.

Comparisons between the three dose-finding designs

Design	Sample size requirement*	Time requirement	Phases included	Advantages	Limitations	Recommended clinical scenarios
Randomize all doses versus an active control and select the best dose	(K+1) n	Phase 1–2	1 + 2	Unbiased dose-vs-control comparisons. Can be expanded seamlessly to phase 3	Appropriate if Pr(response) and Pr(toxicity) are not monotone in dose	Randomization of all doses versus an active control is acceptable and selecting an optimal dose is the goal
Gen 1–2	K n + 10 m	Phase 1–2 + 10m more patients to estimate remission duration	1 + 2	Uses safety, response, and remission duration to optimize dose	Requires 10m more patients and 6 to 12 months longer follow up than phase 1–2	A phase 1–2 trial is planned, including longer follow- up to assess duration of response/remission
Phase 1–2/3	K n + phase 3 sample size	Phase 1–2 + Phase 1–2/3	1 + 2 + 3	Uses survival time to re-optimize the phase 1–2 dose and to do phase 3 comparison	Requires time and resources for conducting both phase 1–2 and phase 3.	A phase 3 trial is being considered, but better dose optimization is desired

^*K = number of doses considered, n = average number of patients per dose in phase 1–2, m = number of candidate doses chosen in stage 2 of a Gen 1–2 trial.

A Randomized Controlled Selection Trial to Study Cellular Therapy in COVID-19

If assuming monotonicity is not valid, randomization is more appropriate because it gives unbiased comparisons between doses. The following study (29) used a three-arm randomized controlled design (16,17) to select a best dose This design is not new (19,30), and it offers a scientifically attractive alternative to cohort-by-cohort dose-finding. The trial studied T-regulatory natural killer cells for treating COVID19-related acute respiratory distress syndrome (ARDS) (29). DLT was any regimen-related grade 3 or worse toxicity within 48 hours of infusion, and response was defined as the patient being alive and extubated at day 28. Because there was no biological or medical reason to assume monotonicity, 45 patients were randomized to 10⁸ cells, 3×10⁸ cells, or SOC, with 15 patients per arm. DLT and response were co-primary outcomes, and OS was evaluated over longer follow up. Safety monitoring rules were included to shut down a dose showing excessive toxicity compared to SOC. A schematic of the trial is given in Figure 1.

Figure 1. Schematic of the randomized trial of cellular therapy for ARDS in COVID-19.

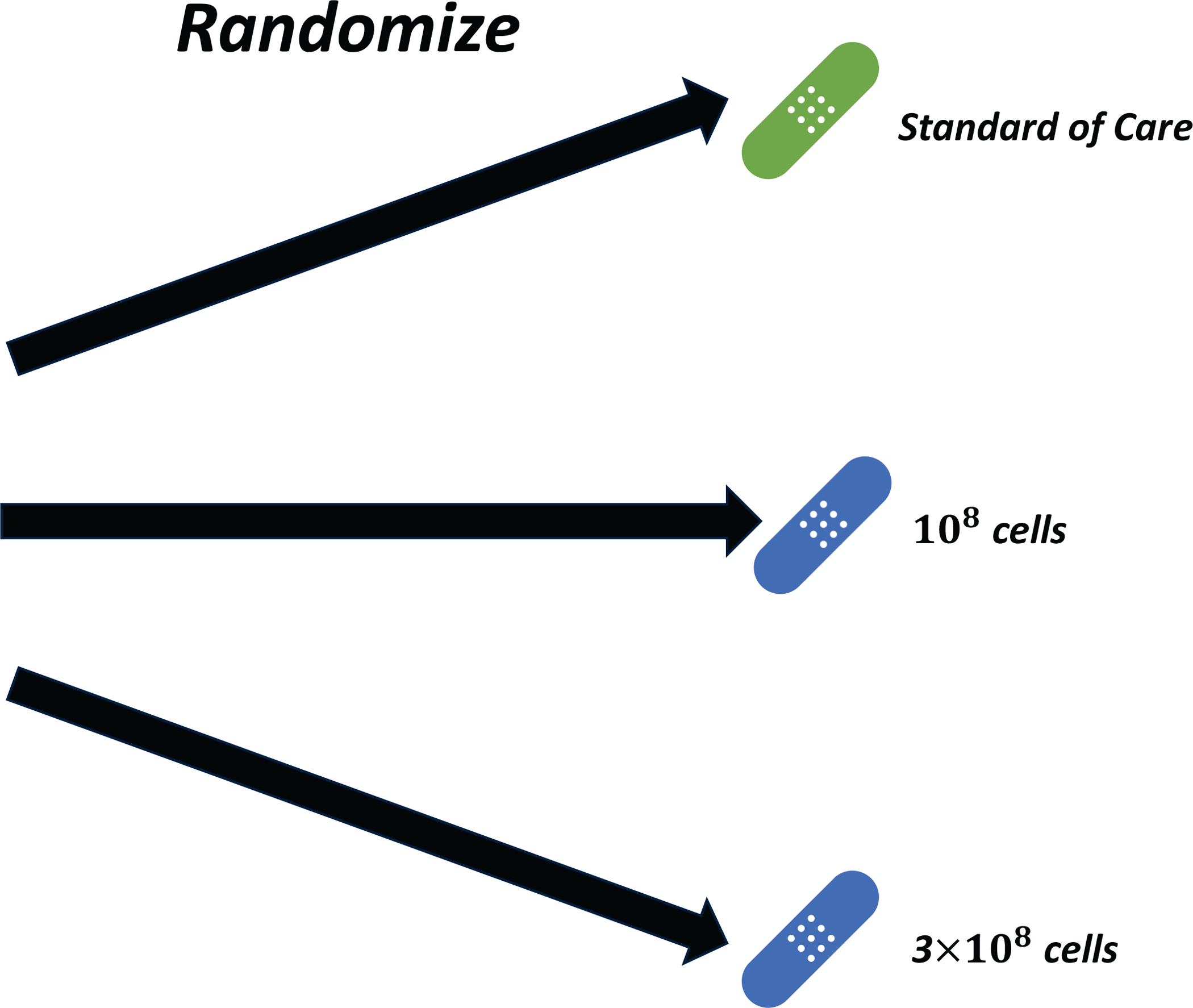
Patients were randomly assigned to different doses of cellular therapy or standard of care.

No toxicities were observed, and the response rate was highest for 10⁸ cells (9/15, 60%) and SOC (9/15, 60%) and lowest for 3×10⁸ cells (6/15, 40%) (29). Similarly, 100-day survival probabilities were 86.2% for 10⁸ cells, 77.9% for SOC, and 45.1% for 3×10⁸ cells. Because a conventional phase 1 design would have escalated to the 3×10⁸ cell arm, randomizing saved nearly 30 patients from being treated with the higher dose, 3×10⁸ cells, which had the shortest OS, and it prevented this dose from being selected.

This design is appropriate for any oncology trial of an agent when monotonicity in dose cannot be assumed. Two advantages of randomization are that the comparison between each dose of the agent and the active control is unbiased and, after the trial, patient cohorts treated with the selected dose or control may be expanded seamlessly to conduct a confirmatory randomized phase 3 trial, thus reducing phase 3 sample size. While two cell doses were considered in the COVID-19 ARDS trial, the randomized selection design is quite general. A larger number of doses, say K, may be included, and any endpoint may be used, subject to the practical requirement that the maximum sample size of (K+1)*n must be feasible, where n = number of patients per dose.

A Generalized Phase 1–2 Design to Optimize Response Duration

The following design extends phase 1–2 to include a long-term outcome. For many therapies, responders have a substantial risk of relapse. Clinical investigators aware of this problem often include a longer follow up period in a phase 1–2 dose-finding trial protocol to estimate response duration. A generalized phase 1–2 design, Gen 1–2, exploits this practice to identify a dose that maximizes the probability of long-term RD (27). The Gen 1–2 paradigm can incorporate any phase 1–2 design, and tailor trials to accommodate a variety of clinical settings. Early outcomes may be binary or ordinal variables, such as toxicity grade and disease severity levels, and numerical utilities of (R,T) = (response, toxicity) may be used for choosing doses (2,3,31–35). A Gen 1–2 design schematic is given in Figure 2.

Figure 2. Schematic of Gen 1–2 trial conduct.

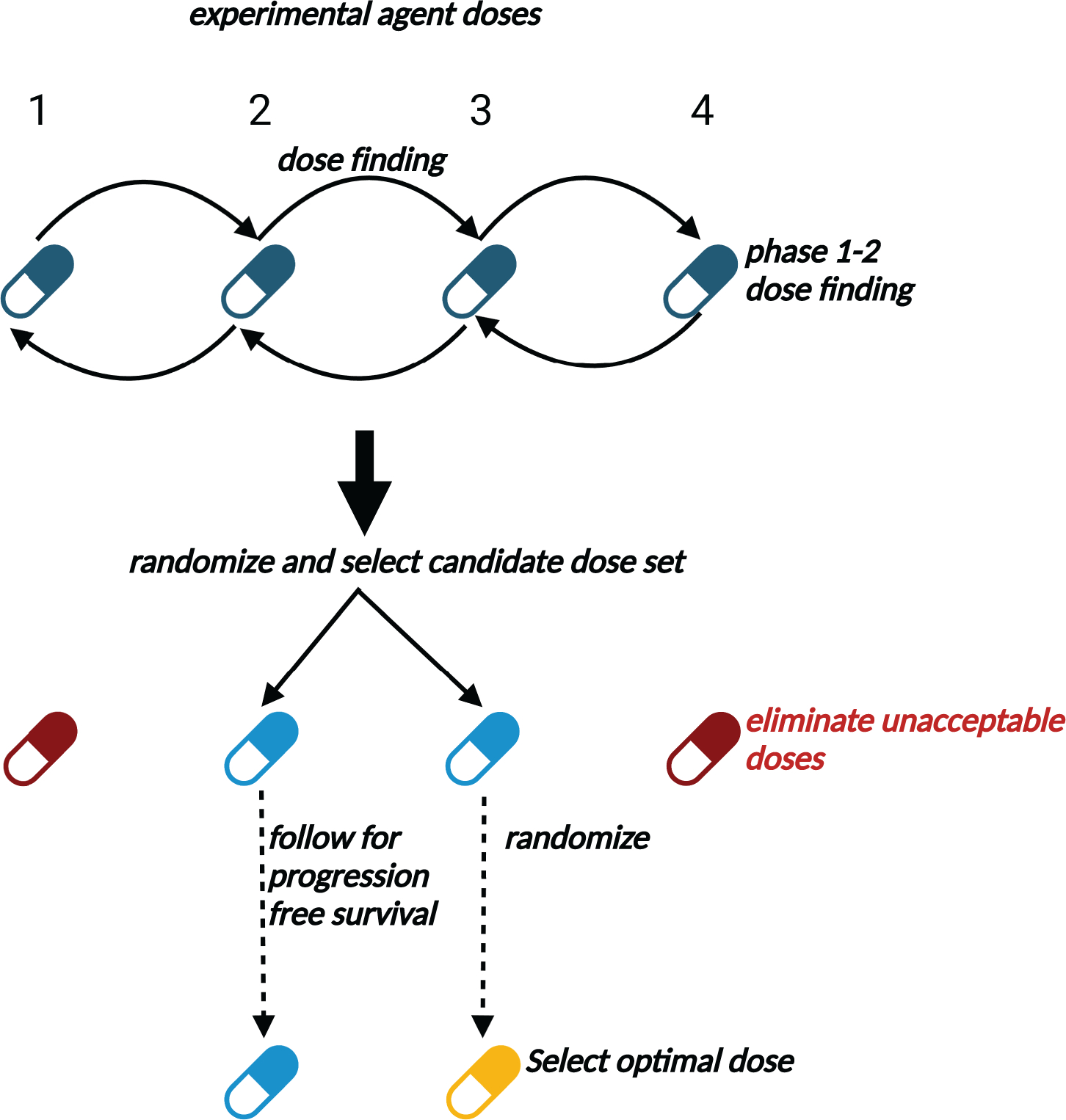
In Stage 1, doses are assigned to successive patient cohorts using typical phase 1–2 design rules to optimize early efficacy and toxicity. The set of doses found to be acceptable during Stage 1 then are randomly assigned among patients in Stage 2 to select a set of acceptable doses and eliminate unacceptable doses more accurately. Additional patients then are randomized among the remaining acceptable doses and followed over an extended time period to establish efficacy in terms of long-term outcomes such as progression-free survival. The candidate dose with the best estimated long-term outcome is ultimately chosen.

To illustrate a Gen 1–2 design, let one month be the follow up to evaluate response and toxicity, with long-term therapeutic success defined as the patient being alive with stable disease or better at six months. Stages 1 and 2 consist of a phase 1–2 trial based on toxicity and response, including rules to drop any dose having an unacceptably high toxicity or low response rate. In stage 1, doses are assigned to patient cohorts using the phase 1–2 design’s rules. Stage 2 randomizes patients among acceptable doses, and identifies a set of nearly optimal candidate doses, rather than one dose. In stage 3, additional patients are randomized among the candidates, and all patients followed to six months. The dose with largest six-month RD rate is selected as optimal. The stage 3 sample size is determined by computer simulation to obtain a desired level of reliability. Computer simulations showed that a Gen 1–2 design has optimal dose selection rates up to an order of magnitude larger than those of conventional phase 1–2 designs (27). Computer software for implementing a Gen 1–2 design is available from https://github.com/yongzang2020

A Gen 1–2 design is being used for a trial of CAR-70 NK cells as targeted immunotherapy for solid tumors at MD Anderson Cancer Center (NCT05703854 at clinicaltrials.gov). Response and toxicity are evaluated in one month. To choose an optimal dose, responders are followed to estimate the probability of long-term success, defined as being alive and in remission at six months.

A Hybrid Seamless Phase 1–2/3 Design

Korn et al. (36) considered the timing of dose optimization in drug development, and recommended that it should be done during or after phase 3. This solves the issues described above, but produces the problem that reliably comparing the rates of an outcome among multiple doses and a control in phase 3 requires a large multi-arm trial. Seamless phase 2–3 designs (37–39) address this problem by combining randomized dose selection with confirmatory testing in a large-scale trial, with reliability defined by generalized power (GP), the probability of (i) selecting a truly optimal dose that provides a meaningful survival improvement over standard therapy, and (ii) concluding in a final test that the new agent at the selected dose is superior to the standard. GP quantifies how well the entire process of dose selection and comparative testing behaves.

Chapple and Thall (37) proposed a three-stage ‘phase 1–2/3’ design that combines phase 1–2 and phase 3 in one trial. In stage 1, any phase 1–2 design based on [response, toxicity] may be used, with patients adaptively randomized among acceptably safe doses. A best acceptable dose is selected, and stage 2 begins with a phase 3 trial based on OS time, with patients randomized between a control and the new agent at the selected phase 1–2 dose. After a prespecified number of deaths in stage 2, dose is re-optimized to maximize estimated mean survival time, and phase 3 is completed with patients randomized between the control and the new agent at the re-optimized dose. A final treatment comparison is based on all response, toxicity, and survival time data (40). A phase 1–2/3 design schematic is given in Figure 3.

Figure 3. Schematic of phase 1–2/3 trial conduct.

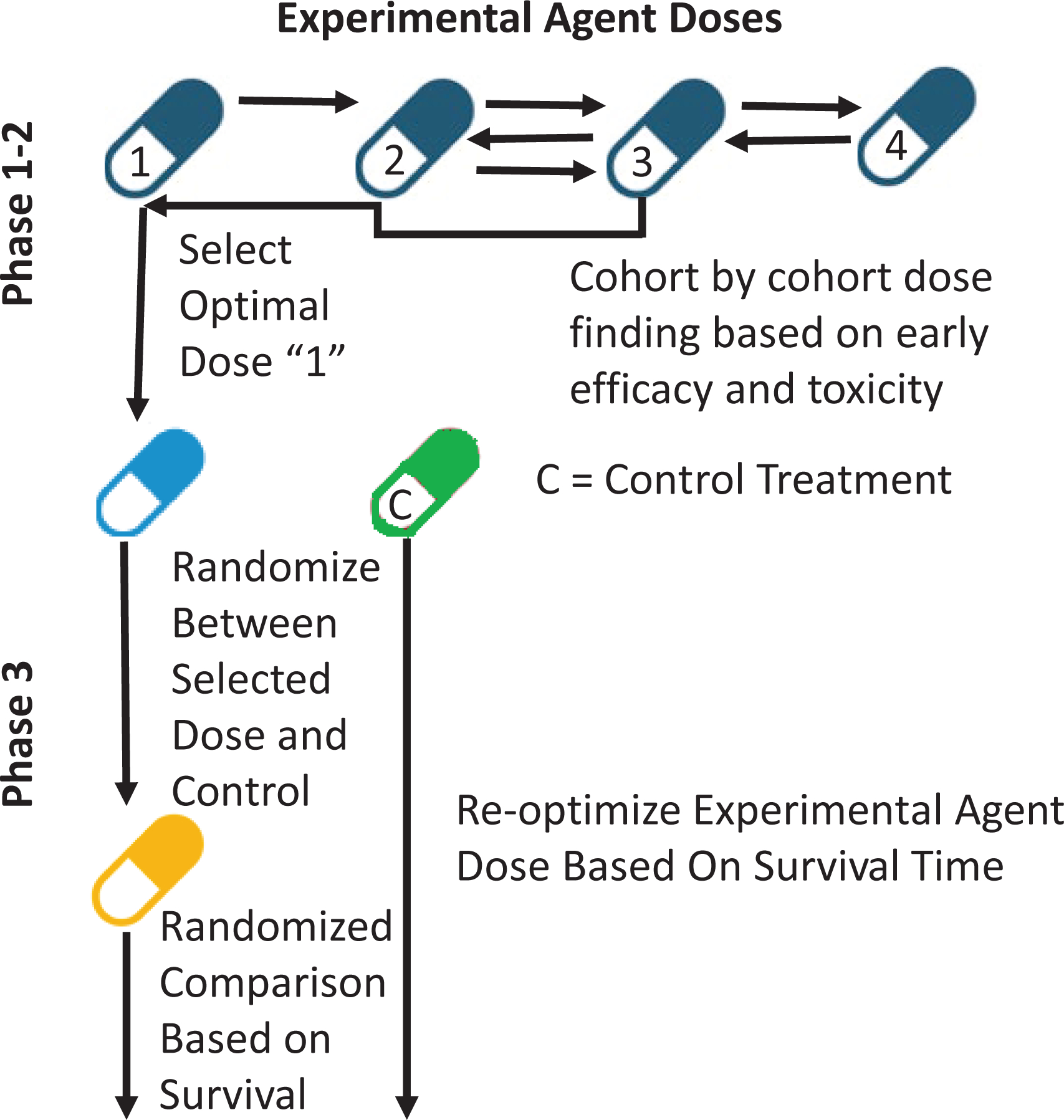
A phase 1–2 design is conducted initially to select the optimal dose based on early efficacy and toxicity. A phase 3 design subsequently is activated with patients randomly assigned to either this dose or standard of care as a control therapy. After a prespecified number of long-term outcome events occur in both the treatment and control arms, dose is re-optimized to maximize estimated long-term outcome duration using data from patients enrolled in both the phase 1–2 and phase 3 stages. A final comparison is performed at the end of the trial using efficacy, toxicity, and long term outcome data from all patients.

Computer simulations showed that a phase 1–2/3 design is greatly superior to conducting phase 3 without re-optimizing dose (37). Across a range of scenarios, dose re-optimization increases GP by 9% to 73%, and provides a substantial increase in expected survival time for patients enrolled in the trial. The price of dose re-optimization is that a phase 3 trial with N = 500 patients may require 10 to 100 additional patients to do phase 1–2/3. If eligibility criteria of the phase 1–2 and phase 3 cohorts differ, to account for heterogeneity so that patient prognosis is not conflated with dose effects, regression models for early response, toxicity, and survival time must be extended to include prognostic covariates. A similar approach can be taken in a Gen 1–2 design by extending regression models for early response and RD to include covariates. The main elaboration for phase 1–2/3 is dose re-optimization and dose switching during phase 3. The most demanding requirement is trial planning, which requires extensive computer simulations. A freely available software package, Phase123, to implement the design is available in an R package archive at https://cran.r-project.org/web/packages/Phase123/.

To use Table 2 for choosing between the three designs in a given setting, one may compute each design’s expected sample size and trial duration for particular design parameters. For example, if K=4 doses are to be studied, with on average n=15 patients per dose, then the randomized controlled selection design would require up to (4+1)15 = 75 patients. The Gen 1–2 design would require 4×15 + 10m = 70, 80, 90, or 100 patients, respectively, if m=1, 2, 3 or 4 candidate doses are chosen in stage 2. The phase 1–2/3 design would require up to 60 + (N= phase 3 sample size) patients, where N varies with the phase 3 design. For anticipated accrual rate 10 patients per month, the respective accrual durations would be approximately 75/10 = 7.5 months for the randomized selection design, 70/10 = 7 to 100/10 = 10 months for Gen 1–2, and, if N=500 for phase 3, 60/10 + (10 to 100)/10 + 500/10 = 57 to 66 months for phase 1–2/3, plus final additional follow up time added to each of these durations

Future Research

Many important issues remain, including evaluating schedules or (dose, schedule) combinations (41). A complex issue is how best to give a therapy repeatedly over multiple cycles, with later doses chosen based on each patient’s previous doses and outcomes (42,43). Additional challenges include accounting for late onset toxicity or response, and low-grade toxicities. A major issue is incorporating pharmacokinetic (PK) and pharmacodynamic (PD) parameters when evaluating doses, since the area under a PK curve quantifies systemic exposure for a given dose. This requires additional PK and PD analyses that may greatly complicate adaptive decision making during a trial. The ultimate goal is to choose personalized doses to account for patient heterogeneity (31–33,44). Several designs for personalized dose-finding have been proposed (3,45–48). Future research will integrate precision medicine approaches with the designs discussed here to incorporate information from long-term outcomes, use randomization to fairly compare doses, and conduct Gen 1–2 or phase 1–2/3 studies.

Translational Relevance.

We address limitations of conventional trial early-phase designs that hinder clinical translation of promising new agents by choosing suboptimal doses. These designs may select doses that are either unsafe or ineffective and do not optimize outcomes such as progression-free survival time, overall survival time, or remission duration. We highlight four strategies to improve this process, which include accounting for long-term outcomes, excluding doses that are unsafe or ineffective, ensuring adequate sample size, and employing randomization in dose selection. Three illustrative designs are discussed, each incorporating one or more of these recommendations. The examples provided underscore the potential of these methodologies to optimize the selected dose or schedule of a therapeutic intervention, thus enhancing patient outcomes and increasing the likelihood of securing regulatory approval. Such strategies, when effectively applied, could substantially improve dosage determination in oncology by maximizing long-term efficacy and patient safety.