Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2025 Jan 1.
Published in final edited form as: Alcohol Clin Exp Res (Hoboken). 2023 Dec 6;48(1):16–28. doi: 10.1111/acer.15232

The selection of statistical models for reporting count outcomes and intervention effects in brief alcohol intervention trials: A review and recommendations

Lin Tan 1,*, Justin M Luningham 1,*, David Huh 2, Zhengyang Zhou 1, Emily E Tanner-Smith 3, Scott A Baldwin 4, Eun-Young Mun 1
PMCID: PMC10841606  NIHMSID: NIHMS1946690  PMID: 38054529

Abstract

Background:

Understanding the efficacy and relative effectiveness of a brief alcohol intervention (BAI) relies on obtaining a credible intervention effect estimate. Outcomes in BAI trials are often count variables, such as the number of drinks consumed, which may be overdispersed (i.e., greater variability than expected based on a given model) and zero-inflated (i.e., greater probability of zeros than expected based on a given model). Ignoring such distribution characteristics can lead to biased estimates and invalid statistical conclusions.

Methods:

In this critical review, we identified and reviewed 64 papers that reported count outcomes from a systematic review of BAI trials for adolescents and young adults from 2013 to 2018. Given many statistical models to choose from when analyzing count outcomes, we reviewed the models used and reporting practices in the BAI trial literature.

Results:

A majority (61.3%) of analyses with count outcomes used linear models despite violations of normality assumptions; 75.6% of outcome variables demonstrated clear overdispersion. We provided an overview of available count models (Poisson, negative binomial, zero-inflated or hurdle, and marginalized zero-inflated Poisson regression) and formulated practical guidelines for reporting outcomes of BAIs. We developed a visual step-by-step decision guide for selecting appropriate statistical models and reporting results for count outcomes. We listed accessible resources to help researchers select an appropriate model for their data.

Conclusions:

Recent advances in count-distribution-based models hold promise for evaluating count outcomes to gauge the efficacy and effectiveness of BAIs and identify critical covariates in alcohol epidemiologic research. We recommend researchers report the distributional properties of count outcomes, such as the proportion of zero counts, and select an appropriate statistical analysis for count outcomes using the provided decision tree. By following these recommendations, future research may improve the accuracy, transparency, and reproducibility of their results.

Keywords: alcohol consumption, brief alcohol intervention, count data models, statistical reporting, young adults, Project INTEGRATE

Introduction

Over 300 clinical trials have examined the efficacy and effectiveness of brief alcohol interventions (BAIs) for adolescents and young adults since the 1980s (see Larimer et al., 2022; Mun et al., 2015, 2022b; Murphy et al., 2022; Tanner-Smith and Lipsey, 2015). Although significant variability exists in outcome measures (see Shorter et al., 2019 for a systematic review), the primary outcomes in BAI trials are typically count outcomes, such as the number of standard drinks consumed in a typical week in the past month (derived from the Daily Drinking Questionnaire [DDQ; Collins et al., 1985], the Timeline Followback [Sobell and Sobell, 1995]), or the number of alcohol-related problems experienced in the past one to three months (e.g., the summed score of dichotomized, binary responses to the Rutgers Alcohol Problems Index; White and Labouvie, 1989). Such outcomes are often bounded at zero (i.e., a non-negative integer; see Atkins et al., 2013; Huh et al., 2015). As discussed by Mun et al. (2022b), BAIs for adolescents and young adults often target diverse populations (e.g., universal, selective, or indicated approaches), which can produce count outcomes with distinct distributions, including both heavy positive skewness/overdispersion (e.g., some respondents reporting extremely high alcohol consumption so that the variability is greater than expected under a particular distribution) and zero inflation (e.g., a large proportion of respondents reporting zero drinks that exceed the expected zero proportion under a certain distribution). Therefore, conventional linear models, such as ordinary least squares (OLS) regression, that model the outcome as a continuous variable and assume normally distributed residuals may provide poor fit to data from BAI trials. This mismatch between linear regression and count data can lead to inaccurate estimation of intervention effects, incorrect standard errors, and potentially incorrect conclusions about the efficacy or effectiveness of a BAI.

Selecting an appropriate statistical model and estimating accurate BAI effect sizes are crucial for individual trials, systematic reviews, meta-analyses, and critical decision-making for clinical care. For example, the US Preventive Services Task Force (USPSTF) recommended screening and behavioral counseling interventions for unhealthy alcohol use in adults 18 or older within primary care settings because trials suggest the interventions are beneficial (USPSTF, 2018). This recommendation holds significant weight as it enables the provision of screening and behavioral counseling interventions to adults with alcohol misuse in primary care at no cost under the Patient Protection and Affordable Care Act enacted in 2010. However, if there are doubts about the evidence the USPSTF used to reach that decision because some of the effect sizes in primary trials were biased, it could create unnecessary confusion and erode public trust in the USPSTF’s recommendation and screening and behavioral counseling interventions. Therefore, identifying and disseminating best practices for analyzing and reporting outcomes of BAI trials is warranted.

Over the past two decades, numerous methodological papers have introduced appropriate count data analysis approaches to researchers in the field of substance use prevention and intervention (e.g., Atkins et al., 2013; Baggio et al., 2018; Buu et al., 2012; Horton et al., 2007; Huh et al., 2015, 2019a; Mun et al., 2022b). Furthermore, the emergent use of marginalized models for count outcomes (Long et al., 2014; Mun et al., 2022b) holds major promise for outcome evaluation in alcohol intervention and treatment trials. When appropriately used, marginalized models have greater power to detect an effect, compared with hurdle or zero-inflated models (Zhou et al., 2023a) and provide a straightforward interpretation of the efficacy and effectiveness of BAI trials (Mun et al., 2022b), because they can be used to estimate the “overall effect” on the entire population. Despite their advantages, uptake of count models in the BAI literature has been slow, and these novel models and available computing tools remain underutilized and/or inaccessible to clinical researchers. This may be due partly to the numerous possible distributions that count alcohol outcomes can assume, which has rarely been recognized or discussed in depth in the BAI literature.

Consequently, we need an explicit data reporting and model selection guide. To address this need, we aim to guide the analysis and reporting of count outcomes in the BAI and other similar alcohol intervention literature. The current paper builds upon the suggestions of Witkiewitz and colleagues (2015a, 2015b), which aimed to strengthen the design, analysis, and report of treatment trials for alcohol use disorders. More globally, there are major guidelines to improve trial design and reporting, such as the Consolidated Standards of Reporting Trials (CONSORT) 2010 (Schulz et al., 2010), additional CONSORT guidelines for multi-arm parallel-group randomized trials (Juszczak et al., 2019; Moher et al., 2010), and the recommendations by the American Psychological Association for journal article reporting standards known as the JARS (Appelbaum et al., 2018). These guidelines have been regularly updated, including a forthcoming update to CONSORT 2010 (Hopewell et al., 2022). The current paper extends the existing body of work to strengthen the methodological rigor of BAI trials in the context of various count outcome measures in the field. We provide an overview followed by concrete recommendations tailored for count outcomes in the BAI trials.

The goals of the current critical review are threefold. First, we review outcome reporting practices among papers included in a systematic review of the recent BAI trial literature to summarize the current landscape of evaluating the efficacy and effectiveness of BAIs. Second, we outline practical recommendations for checking and reporting data. Third, we provide user-friendly analytical guidance on when to use various statistical models for count outcomes and a list of available software programs, data and codes, and references for these methods.

Current Landscape: Review of Count Outcome Reporting and Analysis

Two Ph.D.-level investigators (the first two authors) independently reviewed 78 randomized and controlled quasi-experimental design studies that met the inclusion criteria of a systematic review and meta-analysis (Tanner-Smith et al., 2018; PROSPERO registration #CRD42018092348) focusing on BAIs for adolescents and young adults (ages 11–25) published between 2013 and 2018 (Tanner-Smith et al., 2023). The 78 studies had 192 reports (i.e., articles).

First, we excluded trial registrations, posters, and reports that did not examine the efficacy and effectiveness of the BAIs (e.g., protocols and cost-effective analysis reports) and reports with no count outcome variables (e.g., those reporting only binary or truly continuous outcomes), resulting in 64 reports from 54 trials with 119 count outcome variables (see Figure 1). Each report had one or more count alcohol consumption variables, such as the number of drinks consumed in a typical week. Second, we reviewed whether descriptive statistics (e.g., mean/median and standard deviation/percentile scores) and proportion of zero counts were reported for each count outcome variable. Next, we examined whether the variance was greater than two times the mean score of the outcome variable as an “approximate check of overdispersion.” Note that we adopted this arbitrary but convenient rule for the current study. Under the Poisson distribution, the variance should be equal to the mean; for example, a mean of five and a standard deviation of eight (i.e., a variance of 64) represent an overdispersion since 5 < 64. Finally, we categorized the statistical models used to assess the effectiveness of the BAI relative to the comparison group as follows: (1) analysis assuming normally distributed residuals, such as OLS regression, (2) conventional count distribution based models, such as Poisson and negative binomial (NB) regression, (3) other count distribution based models that also account for zero-inflation, such as zero-inflated and hurdle models, and (4) non-parametric models (e.g., Wilcoxon signed-rank test). Twenty percent of the reports were coded independently by the two first authors to assess interrater reliability. Cohen’s kappa for all coding ranged from 0.81 to 0.87. Cohen’s kappa estimates exceeding 0.8 indicate almost perfect agreement (Landis and Koch, 1977). When there was disagreement between two raters, disagreement was discussed with the corresponding author and resolved in meetings.

Figure 1.

Figure 1

Open in a new tab

Flow chart for reviewed reports

Review Findings

Out of the 119 outcome variables in the 64 reports, means and standard deviations were reported in most (90.8%) cases, but the proportions of zero counts were rarely reported (9.2%). This omission makes it difficult for readers to assess the distributional property of the outcome variables and whether zero inflation is present.

Upon further examining the means and standard deviations of the outcomes, we found evidence of overdispersion (i.e., defined as variance greater than two times the mean in the current study) in 75.6% of the outcome variables. A majority (61.3%) of the alcohol outcomes were analyzed using linear models such as linear regression or ANOVA. Only 31.1% of the outcome variables were analyzed using conventional count distribution based models, such as Poisson or NB regressions, with 5% analyzed by other count distribution based models, such as zero-inflated or hurdle models that account for zero inflation. Finally, 2.5% were analyzed using non-parametric models.

The widespread use of linear regression for count outcomes may be driven by researchers’ (1) unfamiliarity with and, thus, lack of checking for (and reporting of) overdispersion and zero inflation and (2) familiarity with applying conventional linear models. Linear models are generally the first and most comprehensively covered topic in introductory statistics courses and are available in nearly all statistical software packages. But as count distribution-based models have become widely available in open-source (e.g., R) and commercial (e.g., SPSS, SAS, and Stata) statistical software programs, there is a need for better guidelines for checking and reporting the outcome distribution and selecting an appropriate analytic model when analyzing count outcomes.

Data Reporting Recommendations

A consistent reporting standard can help inform how the characteristics of data (i.e., key summary statistics) are reported, increase transparency of results, and facilitate meta-analyses of trials. Although established guidelines exist for reporting data from randomized controlled trials (Butcher et al., 2022; Moher et al., 2010; Schulz et al., 2010), Table 1 presents a six-item checklist of what we recommend in BAI trial reports. Note that these recommendations can also be relevant for other intervention trials involving count outcomes. Our six recommendations are as follows:

Table 1.

Statistics reporting checklist for BAI trials with count outcomes

  1. A comprehensive description of the randomization process is reported. This should include details about the timing of randomization relative to screening/consent, the random sequence generation process, any concealment of the random generation process, and whether randomization resulted in balanced groups.

  2. Minimum, maximum, unadjusted (and adjusted, if applicable) mean, standard deviation and standard error (for adjusted mean), and sample size for each outcome variable (raw scores) are reported per randomized group at each baseline and follow-up time point.

  3. For any count outcome variables, the percent of zero observations for the variable is reported per randomized group at each baseline and follow-up time point.

  4. For any count outcome variables, the distributional properties of the variable are examined based on descriptive statistics (#2 and #3) and visual inspection of outcome distributions. Histograms, density plots, or other similar graphical tools can be used for visual inspection and reporting of outcome distributions.

  5. The mechanisms and assumptions of missing data and handling of missing data are reported. This should include details about the prevalence of missing data, assumptions about the mechanisms behind the missing data, and methods for addressing the missing data in the analysis models (e.g., maximum likelihood estimation and multiple imputations). Report the number of imputed datasets, a list of auxiliary variables used in imputation, and state whether imputations were conducted separately for groups/conditions in the trial.

  6. The software programs or packages and their versions used to conduct the analyses are reported.
Open in a new tab

(1) Provide a comprehensive description of the randomization process for the intervention/control groups. This valuable information, in addition to trial registration information, can enhance the understanding of research design and results, as suggested in the CONSORT statements (see Moher et al., 2010 for more details). However, we observed that it was sometimes unclear in BAI trial reports when randomization occurred (i.e., during screening vs. after meeting the study inclusion criteria) and whether random allocation achieved a balance between groups at baseline. If groups appear unbalanced in baseline levels of the primary outcome variables, it would be helpful to report adjusted means and standard errors of outcomes after accounting for those baseline differences. Moreover, because sample sizes can vary due to randomization and participant attrition differences, it is important to provide the total number of participants allocated to each treatment/intervention arm (i.e., sample size per group at allocation) and the number of participants included in the analysis (i.e., sample size per group in analysis). These numbers are essential for appropriately calculating effect sizes. Finally, we recommend presenting descriptive statistics for demographic and relevant study variables for each randomized group at baseline. This allows readers to examine these characteristics both within and across groups. Moreover, group-level data is important to report so that meta-analysts can evaluate risk of bias in trial results (e.g., GRADE guidelines; Guyatt et al., 2011).

(2) Provide descriptive statistics for each outcome variable, including minimum, maximum, mean, standard deviation, and number of observed sample size (n) for each randomized group at every assessment time point. As shown in our review findings described in the previous section, about 9% of outcomes lacked descriptive statistics. The descriptive statistics of outcomes are crucial for estimating effect sizes based on reported statistics, especially when effect sizes are not included in primary trials. Furthermore, descriptive statistics help gauge the presence of overdispersion in outcome variables.

(3) To better understand the outcome distribution, report percent zeros of all count outcomes for each randomized group. In the context of BAIs, it is common for a sizable number of participants to report consuming zero drinks, zero drinking days, or zero alcohol-related problems, which may indicate zero inflation (see Figure 2). Additionally, providing the proportion of zeroes may permit adjustment for the effects of zero inflation on treatment effect estimates in future meta-analytic reviews, in cases where zero-inflated outcomes were analyzed using traditional count approaches, such as the Poisson model (Zhou et al., 2021).

Figure 2.

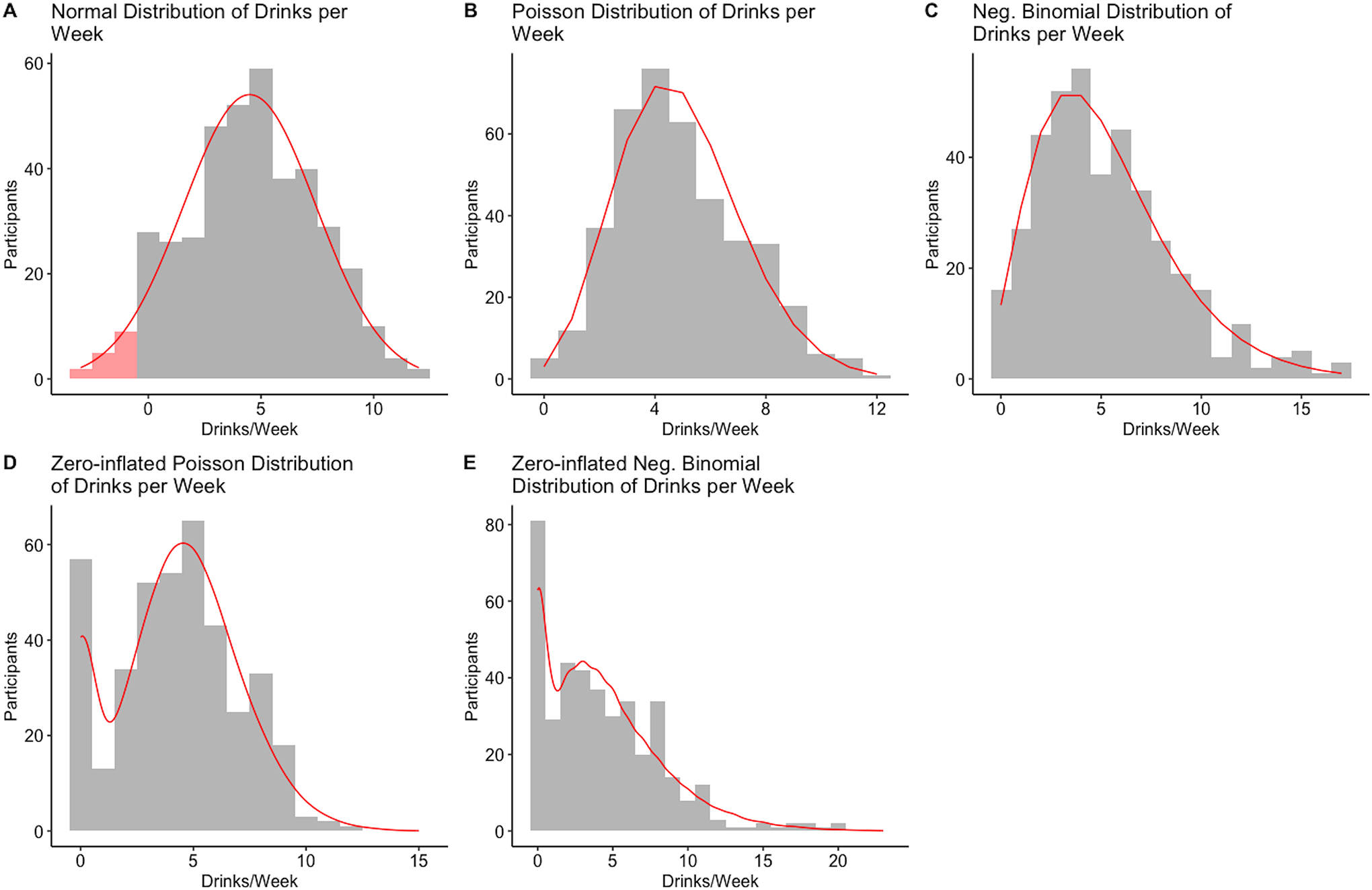
Figure 2

Open in a new tab

Visual display of typical count distributions

Notes. All five plots depict a simulated dataset of N = 400. The red curve depicts the expected density of the distribution. Figures 2A – 2E were drawn for the distribution with an average of 5 drinks per week. The red shaded area in the left tail in Figure 2A depicts negative values that would be expected under the normal distribution. The variance of the normally distributed data (2A) was 9. The Poisson data (2B and non-zero part of 2D) were generated with λ = 5. The NB data (2C and non-zero part of 2E) were generated with a mean parameter of 5 and a dispersion parameter of 3. Figures 2D and 2E had 15% zero observations.

(4) Visually inspect the distributional properties of the count outcome variables. One way to do this is by creating a histogram, which provides insight into the shape and spread of the data, allowing for the detection of overdispersion and/or zero inflation. Figure 2 offers typical examples of count distribution visualizations commonly seen in BAI studies, including normal, Poisson, NB, zero-inflated Poisson, and zero-inflated NB distributions. The actual data distribution may differ from the examples in Figure 2 if descriptive statistics (e.g., means, standard deviations, and zero proportions) differ from those we used. Whether the observed rate of zeros is inflated may require a judgment call. Due to a lack of available empirical guidance, we previously chose zero-inflated models over NB models when the observed zero rate exceeded the expected zero rate by at least 10% (Mun et al., 2022b). Since most journals allow supplemental materials online, we encourage a histogram or density plot to be reported along with all descriptive data when reporting count outcomes.

(5) Because missing data can reduce statistical power and introduce bias into estimates, report potential mechanisms of missing data and assumptions of missing data (e.g., missing completely at random, missing at random, and missing not at random). We recommend that researchers report any methods employed to handle missing data in analysis (e.g., maximum likelihood estimation and multiple imputations) and how the estimated model accounts for the missing data mechanism. In addition, report the number of imputed data sets, a list of auxiliary variables used in imputation, and state whether imputations were conducted separately for groups/conditions in the trial.

(6) Report the software programs employed for the analyses, including the specific packages and versions used. This information is particularly important because the form of certain parameters (e.g., dispersion parameter of NB distribution) can vary across different software program packages and versions. By providing these details, other researchers can accurately replicate and understand the analyses. Additionally, it is worth noting that statistical software program packages are regularly updated, which can potentially influence the estimates produced by the program.

By following this checklist and providing all relevant information, researchers can promote transparency, accuracy, and reproducibility of their findings. The improved analysis and reporting, in turn, contribute to the advancement and refinement of BAIs.

Analytic Guidance: Selecting and Implementing an Appropriate Model

The appropriate choice of a model may not be immediately clear even after visualizing and summarizing alcohol outcomes. Thus, we have summarized some guiding principles to help determine an appropriate choice in a flowchart presented in Figure 3. As a starting point, using an appropriate count-distribution based model for count outcomes is always preferred to implementing an OLS linear model assuming normally distributed residuals. Figure 2A depicts how a normal distribution of drinks per week data would typically look with an average of five drinks per week and a standard deviation of three. The red curve depicts the expected density of the distribution. The red shaded area in the left tail depicts negative values that would be expected under the normal distribution, which are impossible for a count variable such as the number of drinks.

Figure 3.

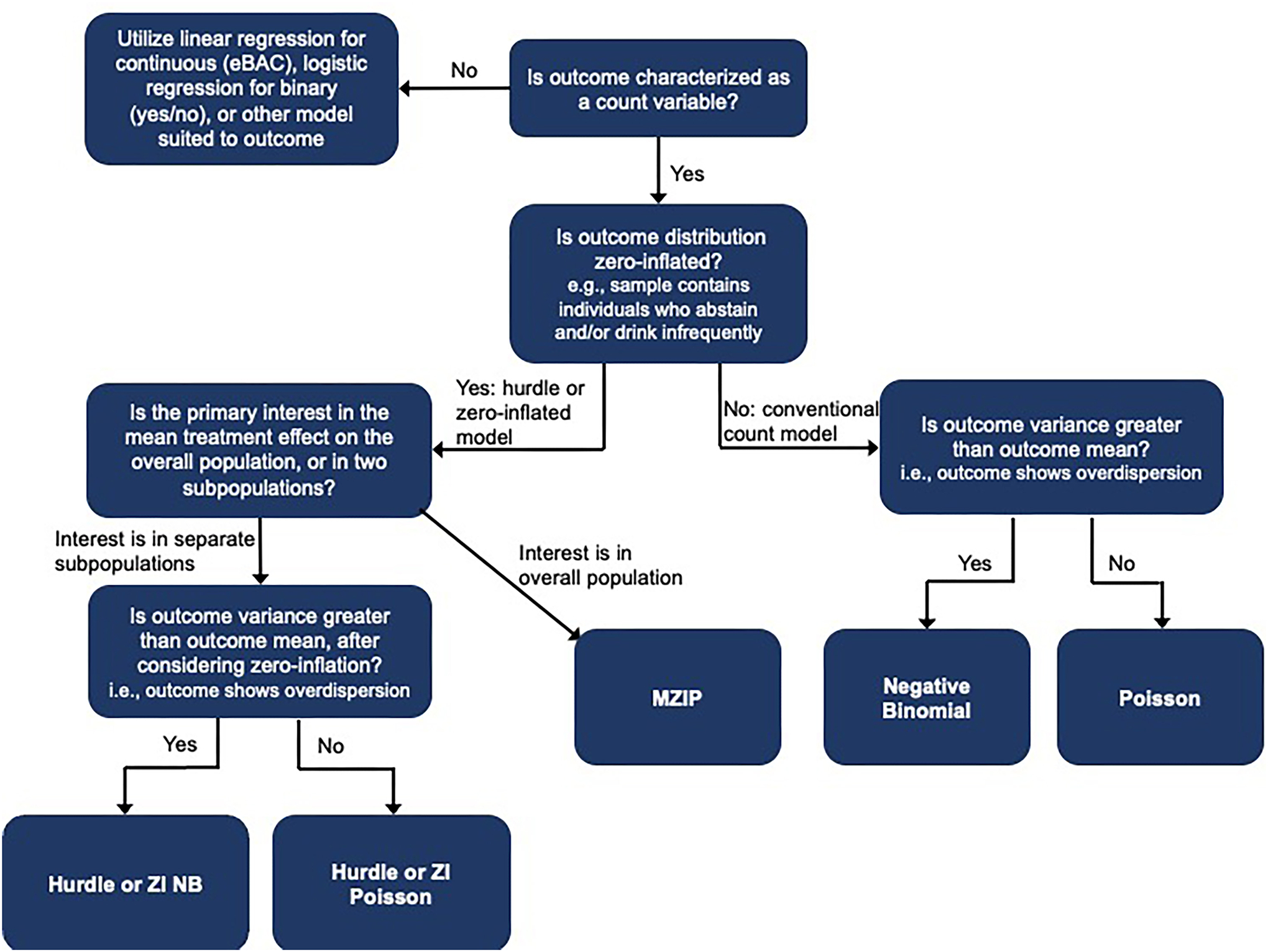
Figure 3

Open in a new tab

Decision tree for statistical models to analyze count outcomes

Notes. The decision tree included commonly used models that are appropriate and available for count and other distributions. Other methods, such as non-parametric models, are out of scope for this review but may be appropriate for the discussed data conditions. eBAC = estimated blood alcohol concentration.

The generalized linear model (GLM) uses a link function to model data that do not follow a normal distribution. OLS regression is a special case of GLM with an identity link. Other link functions include logit or log. For more information on how to interpret coefficients from GLMs and categorical data analysis, please see tutorial papers (Halverson et al., 2022; von Eye and Mun, 2003) and advanced textbooks (Agresti, 2013; von Eye and Mun, 2013). Rather than modeling the raw outcome (i.e., through an identity link) as a linear function of predictors and associated regression parameters, the GLM uses the link function to transform the expectation of the outcome variable and regresses it on a linear function of predictors. A log link is typically used for the outcome with a Poisson distribution or an NB distribution. The key characteristics of the Poisson distribution are that the values are integers that cannot go below 0, with the mean equal to the variance. The Poisson distribution may be appropriate for count outcomes, such as the number of drinks consumed per week, when the mean is roughly the same as the variance. Figure 2B depicts drinks per week data simulated from a Poisson distribution with a λ parameter (for both mean and variance) of five drinks per week. Note a slight positive skew because values are bounded at zero.

More typically, study samples include low-risk participants who occasionally drink and also those who engage in heavy episodic drinking and/or high-intensity drinking. This results in a small mean number of weekly drinks with a large variance and skewness due to a small proportion of those reporting large numbers of drinks, creating overdispersion (i.e., a count outcome with a variance greater than its mean). In such a case, NB regression is more appropriate than Poisson regression. NB regression introduces an additional dispersion parameter to account for the larger variance of the distribution. Figure 2C depicts a distribution of drinks per week data simulated under the NB distribution with a λ mean parameter of five and an overdispersion parameter of three. Compared to the Poisson distribution in Figure 2B, the NB distribution has more observations at or near zero, as well as more observations reporting many more drinks per week than average, creating a distribution with notable positive skewness. NB regression is often preferred over Poisson regression if a count outcome has a variance greater than the mean. Another straightforward approach to deciding which model to use is to fit both regression models and perform a χ2 difference test based on the difference in the log-likelihoods of the two models (Cameron and Trivedi, 2013). This test indicates whether model fit statistically significantly improves with the additional dispersion parameter. The statistical significance of the dispersion parameter can also be evaluated with a Wald test (i.e., the value of the dispersion parameter divided by its standard error; Agresti, 2013; Cameron and Trivedi, 2013), which tests the null hypothesis that the dispersion parameter equals zero.

NB is often recommended over Poisson regression because overdispersion is typically present in real-world data; this is certainly true for many alcohol outcomes. If overdispersion is not present, the NB dispersion parameter will be small, and the results will be very similar to those from Poisson regression (although, in this scenario, the NB model may face estimation challenges such as non-convergence in our experience). However, if overdispersion is present but ignored in a Poisson model, the standard errors will be underestimated, and type I errors are likely inflated (Cameron and Trivedi, 2013; Pittman et al., 2020). For additional technical details on equations and practical interpretation of NB and Poisson regression, see Atkins et al. (2013) and Mun et al. (2022b).

Next, it is imperative that researchers check for a preponderance of zeros in the count outcome. BAI trials with alcohol use outcomes may include study participants who do not drink at all and people who drink very infrequently. In this case, count outcomes related to alcohol use may have a large proportion of zero outcomes (e.g., no drinks consumed in a given week, zero episodes of heavy episodic drinking), displaying overdispersion in which the observed zero observations far exceed the expected number of zero observations (i.e., zero inflation) under a Poisson or NB distribution. One can calculate the proportion of participants with zero count responses and graphically view a histogram of the data to check for zero inflation. More formally, one can calculate the expected proportion of zeros under a Poisson or NB distribution and compare that to the observed proportion of zeros. This is also implemented in some statistical programs, such as the “check_zeroinflation” function of the glmmTMB package in R (Brooks et al., 2017; R Core Team, 2023). According to a recent simulation study, if zero inflation is present, Poisson regression tends to produce higher rates of false positive results than the nominal type I error rate of 0.05 or 5% (Zhou et al., 2023a). Two related model extensions can be applied to Poisson or NB regression to address zero inflation: zero-inflated models and hurdle models.

Zero-inflated Poisson (ZIP) or zero-inflated NB (ZINB) models posit that the data follow a mixture distribution of a point mass at zero (zero part) and a Poisson or NB distribution (count part). The zero and count parts of the zero-inflated models correspond to two underlying groups: one that produces zero outcomes and one that produces outcomes following a standard count distribution (which can include zero; Atkins and Gallop, 2007), respectively. Conceptually, zero outcomes are reported by individuals who do not drink (predictably zero; included in the “always zero” part) and by those who occasionally drink but did not drink in the measured time span (situational zero; included in the count distribution). As a result, two submodels are constructed: (1) a logistic regression submodel evaluating the probability of belonging to the “always zero” group in the zero part and (2) a Poisson or NB regression submodel evaluating the mean parameter in the count part. Panels D and E of Figure 2 depict prototypical distributions of ZIP and ZINB count data simulated under assumptions of an average of five drinks per week in the non-zero submodel and 15% zero observations. Histograms of reported drinking frequencies effectively reveal zero-inflated data because the mass of zero observations will be one of the largest frequencies of the distribution. In the ZIP distribution in Figure 2D, the zeros are the second most frequent response, and in the ZINB of Figure 2E, zeros are by far the most frequent response. This is characteristic of zero-inflated data.

Hurdle models are similar to zero-inflated models, except that the count part uses a zero-truncated Poisson or NB distribution. Thus, hurdle models strictly differentiate zero and non-zero observations from two sources (i.e., point mass at zero and a truncated count distribution). Hurdle models are formally presented in Huh et al. (2019, 2023). Because of the mixture distribution nature of the zero-inflated and hurdle models, the effects of predictors or covariates, such as a main treatment effect, are evaluated on the zero part and count part separately, introducing a challenge in interpreting the combined overall effect for the entire population.

As an extension of zero-inflated models, marginalized zero-inflated models, such as the marginalized zero-inflated Poisson (MZIP) model, are designed to estimate the effects of predictors on the overall mean for the entire distribution under the existence of excessive zeros (Long et al., 2014; Mun et al., 2022b; Zhou et al., 2023a). The MZIP model is based on the formulation of a ZIP model and can account for the zero inflation of the outcomes. Unlike a ZIP model, which relates predictors to the zero part and count part separately in the mixture distribution, the MZIP model relates predictors to the overall mean of the outcome. Therefore, the MZIP model enjoys the straightforward interpretation of predictors’ effects on the entire population and the ability to handle excessive zeros. This feature of the MZIP is attractive compared with OLS regression, which also estimates predictors’ effects on the entire population but is inconsistent with the true data-generating model. A formal presentation of Poisson, NB, ZIP, and MZIP models can be seen in Mun et al. (2022b).

If zero inflation is identified, it needs to be accounted for in the data analysis with the aforementioned zero-inflated (ZI), hurdle, or marginalized ZI models. When the effects on the overall mean of the entire population are of interest, such as the treatment effect on all participants, the marginalized ZI models (e.g., MZIP) can be considered, as they provide effect estimates on the overall mean, while accounting for zero inflation (Mun et al., 2022b; see also Tan et al., 2022a for an application to a single sample). Therefore, MZIP would be preferred over hurdle or ZINB under typical BAI effect size estimation settings, especially when the overall intervention effect on the entire population is of interest.

In other situations where the intervention effects on one or both of the subpopulations are of interest, the ZI or hurdle models can be considered because the zero part and the count part are specifically evaluated. However, the intervention effect on the “zero part” (i.e., individuals who do not drink) may not always be of clinical interest in primary BAI trials. Furthermore, intervention effect estimation in the zero subpopulation can have low statistical power (Huh et al., 2023; Kim et al., 2020; Zhou et al., 2023a). Given that the intervention effects of BAIs tend to be modest in magnitude, the power to detect an intervention effect may not be adequate when the effect is examined separately for the two submodels, especially with relatively small to modest samples (N = 200 to 300; see Zhou et al., 2023a for simulation results).

The choice between the ZI and the hurdle model ultimately depends on the researcher’s assumption about the source of the excess zeros, but some statistical guidance is also available. Typically, the Akaike Information Criterion (AIC) is used to compare model fit, and the Vuong test (Vuong, 1989) can be used for pairwise likelihood ratio tests between ZI and hurdle models. However, some research indicates that the Vuong test is less reliable than model selection based on the lowest AIC (Xu et al., 2015). Regardless, ZI and hurdle models tend to produce similar estimates (Xu et al., 2015).

Clinically, researchers should consider whether the preponderance of zeros was caused by individuals who predictably do not drink or people who did not drink during the time window asked. If researchers assume that zero responses were mostly from those who predictably report zero (i.e., those who never drink), then separating all zero responses (e.g., those who reported zero drinks) from all non-zero responses (e.g., those who reported at least one drink) in a hurdle model may be appropriate with little to no consequences. However, suppose zero responses are also from those who usually drink but did not drink within the outcome assessment period. In that case, the ZI alternative may be preferable because it will allow for zero responses in the regression model portion. For example, ZI models may be appropriate for zero drinking outcome responses if a study’s inclusion criteria required participants to endorse regular drinking. Despite subtle conceptual differences between ZI and Hurdle models, both perform roughly equivalently in data settings (Feng, 2021) that are typical for BAI trials.

Available empirical evidence on statistical performance of these models in alcohol trial research is limited. However, recent simulation work comparing the relative performance of linear models and count distribution based models – Poisson, NB, ZIP, and MZIP – indicated that under zero inflation, (1) the MZIP model had the highest statistical power, followed by the linear model with outcomes on the raw scale, NB, and ZIP model; (2) a sample size of N = 300 or greater is necessary for the MZIP and linear models in most simulation conditions with zero rate (i.e., the greater the zero rates, the less power) and effect size (i.e., the larger the effect size, the greater power) playing major determining factors; (3) the Poisson model was invalid (i.e., excessive type 1 error rate); and (4) the performance of the linear model with a log-transformed outcome variable was unsatisfactory (Zhou et al., 2023a). Although more work on statistical comparison of competing models is needed, the results cautiously suggest that lack of power is a concern for typical individual BAI trials with zero inflation and overdispersion. Though sample sizes cannot be increased or data characteristics cannot be changed by the time of analysis, researchers can select the best model for their data appropriately and report data sufficiently clearly for a meta-analysis.

In sum, several factors should be considered when selecting a statistical model to analyze count outcomes. These factors are (1) overdispersion, which is when the variance is higher than the mean; (2) zero inflation, which occurs when there is an excessive number of zero counts in the data compared to what is expected under a given distribution; (3) both zero inflation and overdispersion if both characteristics are present in the data; (4) theoretical considerations for choosing between hurdle models and ZI models when there is zero inflation; and (5) relative statistical performance and other data characteristics (e.g., sample size, effect sizes). The estimates derived from inappropriate statistical models can result in biased estimates, invalid statistical inferences, and erroneous conclusions. Once in the literature, biased estimates can also affect the conclusions of subsequent systematic reviews and meta-analyses in the field, underscoring a need to improve the evidence base from the upstream and onward.

On a related issue, the effect sizes from NB, ZIP, or MZIP models can be described using Odds Ratios (OR), Log Odds Ratios (LOR), Rate Ratios (RR), Log Rate Ratios (LRR), or in terms of % reductions in the “overall” means or OR. Examples of how effect sizes can be derived and interpreted from count and normal models can be seen in other recently published articles (Mun et al., 2022a; 2022b; Tan et al., 2023). For example, we interpreted that young adult participants allocated to a BAI (vs. control) had an average 8% reduction in standard drinks consumed in a week, an effect observed through six months post intervention. A recent tutorial (Halvorson et al., 2022) on interpreting OR and LOR may be informative for readers interested in better understanding effect sizes from these models.

Note that the recommendations in this article apply to count outcomes and not necessarily other endpoints of BAI trials (e.g., continuous measures, such as quality of life). Shorter et al. (2021) suggested that BAI trials include a core outcome set of ten measures across four distinct outcome domains, including typical frequency and quantity of alcohol consumption, frequency of heavy episodic drinking, hazardous or harmful drinking, the number of standard drinks consumed in a week, alcohol-related consequences, alcohol-related injury, use of emergency healthcare services, and quality of life. A decision tree shown in Figure 3 should help navigate analytical decisions. For example, ordinal response measures for typical frequency or quantity of alcohol use (e.g., the Alcohol Use Disorders Identification Test [AUDIT; Saunders et al., 1993] questions): “How often do you have a drink containing alcohol?” with ordinal response options ranging from 0 = “Never” to 4 = “4 or more times a week” or “How many drinks containing alcohol do you have on a typical day when drinking?” with response options ranging from 0 = “1 or 2” to 4 = “10 or more” may be appropriately analyzed using the multinomial or ordinal logistic regression model. If deriving a combined risk or severity of alcohol consumption is necessary, latent variable modeling may be adopted using indicator variables.

Available Software Packages and Implementation

Once a model is selected, researchers can apply the model using one of many statistical software programs. Recent years have seen the proliferation of user-friendly software and published tutorials for implementing regression for count outcomes (e.g., Atkins et al., 2013; Beaujean and Grant, 2016; Fávero et al., 2021). Table 2 provides an overview of available functions and arguments for popular statistical software programs, including R (version 4.3.2), SAS (version 9.4), Stata (version 18.0), SPSS (version 29), and Mplus (version 8.10). In all programs, the response variable is specified as part of the fitted model, with an additional step identifying its underlying distribution. In addition, most of these models can also be fitted with the Bayesian routines available in R, SAS, and Stata. SPSS tends to have more limited functionality than the other programs of the five. For instance, SPSS only offers conventional Poisson and NB regression as part of the standard offering; custom syntax modifications and macros would be required to fit zero-inflated models in SPSS.

Table 2.

Available software to implement different statistical models for count outcomes

R SAS SPSS Stata Mplus
Poisson Regression glm(, family = ”poisson”) PROC GENMOD / dist = POISSON;
PROC COUNTREG / dist=POISSON;		 Analyze > Generalized Linear (Mixed) Models > Generalized Linear (Mixed) Models::” Poisson loglinear” glm, family(poisson)
poisson
mepoisson		 COUNT = y*; or
COUNT = y*(p);
Negative Binomial Regression Package MASS::nb.glm() PROC GENMOD / dist = NEGBIN;
PROC COUNTREG / dist=NEGBIN		 Analyze > Generalized Linear (Mixed) Models > Generalized Linear (Mixed) Models::” Negative binomial with log link” glm, family(nbinomial)
nbreg
menbreg		 COUNT = y*(nb);
Zero-inflated Poisson Package pscl::zeroinfl() PROC GENMOD / dist = zip;
FMM / dist = POISSON;
PROC COUNTREG / dist = zip		 zip COUNT = y*(i); or
COUNT = y*(pi);
Zero-inflated Negative Binomial Package pscl::zeroinfl ( , dist = “negbin”) PROC GENMOD / dist = zinb;
PROC FMM / dist = NEGBIN;
PROC COUNTREG / dist = zinb		 zinb COUNT = y*(nbi);
Hurdle Poisson Package pscl::hurdle () PROC FMM / dist = TRUNCPOISSON tpoisson
Hurdle Negative Binomial Package pscl::hurdle () PROC FMM / dist = TRUNCNEGBIN tnbreg COUNT = y*(nbh);
Marginalized zero-inflated Poisson Package mcount::mzip()
Open in a new tab

Note.

*

indicates the response variable.

R (R Core Team, 2023) is an open-source statistical software program and, as such, contains numerous developed packages that can fit models for count data. Base R includes a function for generalized linear models, glm, which can fit Poisson regressions. The package MASS (Venables and Ripley, 2002) offers an extension of glm for NB regression, nb.glm. The pscl package implements both zero-inflated and hurdle models for Poisson and NB distributions (Jackman, 2020; Zeileis et al., 2008). The newly developed package mcount implements the MZIP model (Zhou et al., 2022). These options are widely used for count regression. In addition, the brms package (Bürkner, 2017) in R can fit Poission, NB, and ZIP models using MCMC but not the marginalized model. There may be other packages for R implementation that can fit count regression models, which can be searched on the Comprehensive R Archive Network (CRAN, http://cran.r-project.org). Note there are simulated or real data and annotated R codes that are publicly accessible to run the hurdle NB model (Huh et al., 2019b), ZIP model (Zhou et al., 2023b), and MZIP model (Mun et al., 2022c; Tan et al., 2022b).

SAS (SAS Institute Inc., 2023) contains numerous procedures that can implement the methods discussed herein as well, such as PROC GENMOD and PROC COUNTREG. PROC FMM (short for “finite mixture models”) can also fit zero-inflated and hurdle models. Note that selecting the correct distribution or regression model requires the right specification of options (following the backslash) in the procedure syntax. See Table 2 for examples. For the experienced SAS programmer, PROC NLMIXED can be used to implement the marginalized ZIP models (Long et al., 2014).

Stata (StataCorp, 2023) is a commercial statistical program that can fit traditional count models as well as their zero-inflated and hurdle model counterparts. Traditional count models can be fit using dedicated regression commands, such as “poisson” and “mepoisson” for fixed-effect and mixed-effect Poisson models, respectively. Hurdle Poisson and Hurdle NB models can be fit by dividing the count outcome into two parts (1) a dichotomous variable representing non-zero counts (=0) vs. zeroes (=1) and (2) a zero-truncated count variable representing counts when non-zero (i.e., values of 1 or higher). These two component outcomes can then be analyzed using logistic regression (e.g., logit or melogit) and a zero-truncated count regression (e.g., nbreg or menbinomial), respectively. Long and Freese (2014) discussed several methods for statistically comparing whether data are more in line with Poisson, NB, ZIP, and ZINB, with a Stata routine (i.e., countfit) that automates the comparison.

Mplus (Muthén and Muthén, 1998–2023) is another flexible statistical program for regression with count data. Mplus requires header information in its scripts about the variables and type of analysis to be used before a regression model is specified. In this header, one only needs to specify that the dependent variable is a count variable. Poisson is implemented by default, but NB can be specified within parentheses following the name of the count outcome variable, as can zero-inflated and hurdle models. Note that Mplus allows for the NB distribution only in hurdle models.

Conclusions

Although advanced statistical models appropriate for modeling count data have been developed and are available in popular software programs, the prevailing model used in the BAI trial research is linear regression, which includes ANOVA and ANCOVA as specific cases. The current study provided an accessible overview of alternative models, their assumptions, their pros and cons, and available software packages for broad implementation. We provided a checklist for reporting data, analysis, and results, and a roadmap and software list to select and implement currently available statistical models appropriate for count outcomes.

The recommendations from the current review are most relevant for the BAI field and other alcohol-related research where both sample sizes and effect sizes tend to be modest and the range of count outcomes is not extreme (e.g., 0 to 30 drinks) despite skewness and overdispersion. BAI trials, especially for young adults, tend to cover heterogeneous populations of individuals on a wide range of alcohol consumption spectrum, even within trials. Hence, BAI trials are more likely to exhibit both zero inflation and overdispersion. In other fields where primary outcomes of interest are count variables, such as number of days in hospital, episodes of unprotected sex, number of days using tobacco or other substances, and tracking discrete adverse events, among numerous other outcomes, the recommendations presented in the current study would be relevant. However, how critical the current recommendations are in other substance use intervention trials or epidemiologic research may need to be carefully evaluated depending on the factors (e.g., overdispersion, zero inflation, effect size) we discussed.

The current recommendations are based on established and cutting-edge methods that have been well characterized and demonstrated. It is important to note that methodological advances are ongoing, with possible extensions and automation, which would be meaningful clinically and computationally. For example, our group recently proposed a novel semiparametric method that can automatically account for different levels of dispersion and zero inflation (from no zero value to excessive zeros) for count data in marginalized models (Zhou et al., 2023c). This proposed method is based on the generalized estimating equation (GEE; Liang and Zeger, 1986) approach to variance estimation and directly models the overall mean of count outcomes. Because of the flexibility, this method can be particularly attractive for meta-analysis of individual participant data from heterogeneous trials with count outcomes. Future extensions to accommodate more than two subgroups or longitudinal data would also be meaningful.

The importance of reporting credible and accurate effect size estimates cannot be overstated. Underestimated or overestimated intervention effects, especially with incomplete or unclear trial data reporting in primary studies, pose a challenge as they can add noise and bias to data. It is even more critical for meta-analysis because whether each trial resulted in a statistically significant outcome is less important in a meta-analysis. Although it may be possible to correct biased effect size estimates under a specific data situation (e.g., not accounting for zero inflation; Zhou et al., 2021) and derive effect size estimates directly using individual participant data (e.g., Mun et al., 2022a, 2022b, Tan et al., 2023), no broadly applicable measures exist with aggregate data. Because many individual BAI trials are likely underpowered (see Zhou et al., 2023a for simulation results), large intervention effects are more likely in small trials, and meta-analyses tend to be more robust, large-scale meta-analysis has an important role in providing evidence of comparative effectiveness and heterogeneity of treatment effects. Toward this goal, we call for the field to continue improving reporting standards to ensure the generation of trustworthy evidence.

Given that systematic reviews and meta-analyses of aggregate data will remain important for clinical and policy decision-making for the foreseeable future, we need to improve the prevailing outcome reporting standard. It would also be helpful to have a better consensus about which core outcome measures should be assessed and reported in BAI trials. Shorter et al. (2019) found that no single outcome was common in all BAI trials included in a systematic review. Variability in outcome measures across existing BAI trials can result in trials being excluded from a meta-analysis due to a lack of common outcomes. Subsequently, Shorter et al. (2021) suggested that BAI trials include a core outcome set of ten measures. Improved overlap of core outcome measures across trials would facilitate efforts to synthesize credible and accurate intervention effects from more trials and compare the relative effectiveness of different BAI strategies. We also note a need to extend existing statistical models and improve their accessibility to further meet emerging challenges faced in BAI clinical research and meta-analyses. With the strengthened outcome reporting standard in the current review, we can trust and utilize the body of evidence in clinical research.

Funding:

The project described was supported by grants R01 AA019511 and K02 AA028630 from the National Institute on Alcohol Abuse and Alcoholism (NIAAA). The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIAAA or the National Institutes of Health.

Footnotes

Conflict of Interest: The authors have no conflict of interest to declare.

References

  1. Agresti A (2013) Categorical Data Analysis. 3rd ed. John Willey & Sons, Hoboken. [Google Scholar]
  2. Appelbaum M, Cooper H, Kline RB, Mayo-Wilson E, Nezu AM, Rao SM (2018) Journal article reporting standards for quantitative research in psychology: The APA Publications and Communications Board Task Force report. Am Psychol 73:3–25. [DOI] [PubMed] [Google Scholar]
  3. Atkins DC, Baldwin SA, Zheng C, Gallop RJ, Neighbors C (2013) A tutorial on count regression and zero-altered count models for longitudinal substance use data. Psychol Addict Behav 27:166–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Atkins DC, Gallop RJ (2007) Rethinking how family researchers model infrequent outcomes: A tutorial on count regression and zero-inflated models. J Fam Psychol 21:726–735. [DOI] [PubMed] [Google Scholar]
  5. Baggio S, Iglesias K, Rousson V (2018) Modeling count data in the addiction field: Some simple recommendations. Int J Methods Psychiatr Res 27:e1585. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Beaujean AA, Grant MB (2016) Tutorial on using regression models with count outcomes using R. Pract Assess Res Eval 21:2. [Google Scholar]
  7. Brooks ME, Kristensen K, Van Benthem KJ, Magnusson A, Berg CW, Nielsen A, Skaug HJ, Machler M, Bolker BM (2017) glmmTMB balances speed and flexibility among packages for zero-inflated generalized linear mixed modeling. The R J 9:378–400. [Google Scholar]
  8. Bürkner P (2017) brms: An R package for Bayesian multilevel models using Stan. J Stat Softw 80(1):1–28. [Google Scholar]
  9. Butcher NJ, Monsour A, Mew EJ, et al. (2022) Guidelines for reporting outcomes in trial reports: The CONSORT-outcomes 2022 extension, JAMA 328:2252–2264. [DOI] [PubMed] [Google Scholar]
  10. Buu A, Li R, Tan X, Zucker RA (2012) Statistical models for longitudinal zero-inflated count data with applications to the substance abuse field. Stat Med 31:4074–4086. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Cameron AC, Trivedi PK (2013) Regression Analysis of Count Data. 2nd ed. Cambridge University Press, New York. [Google Scholar]
  12. Collins RL, Parks GA, Marlatt GA (1985) Social determinants of alcohol consumption: The effects of social interaction and model status on the self-administration of alcohol. J Consult Clin Psychol 53:189–200. [DOI] [PubMed] [Google Scholar]
  13. Fávero LP, Souza RdF, Belfiore P, Corrêa HL, Haddad MF (2021) Count data regression analysis: concepts, overdispersion detection, zero-inflation identification, and applications with R. Pract Assess Res Eval 26:13. [Google Scholar]
  14. Feng CX (2021) A comparison of zero-inflated and hurdle models for modeling zero-inflated count data. J Stat Distrib Appl 8: 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Guyatt GH, Oxman AD, Vist G, Kunz R, Brozek J, Alonso-Coello P, Montori V, Akl EA, Djulbegovic B, Falck-Ytter Y, Norris SL, Williams JW Jr, Atkins D, Meerpohl J, Schünemann HJ (2011) GRADE guidelines: 4. Rating the quality of evidence--study limitations (risk of bias). J Clin Epidemiol 64(4): 407–415. [DOI] [PubMed] [Google Scholar]
  16. Halvorson MA, McCabe CJ, Kim DS, Cao X, King KM (2022) Making sense of some odds ratios: A tutorial and improvements to present practices in reporting and visualizing quantities of interest for binary and count outcome models. Psychol Addict Behav 36:284–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Hopewell S, Boutron I, Chan A-W, Collins GS, de Beyer JA, Hróbjartsson A, Nejstgaard CH, Østengaard L, Schulz KF, Tunn R, Moher D (2022) An update to SPIRIT and CONSORT reporting guidelines to enhance transparency in randomized trials. Nature Med 28:1740–1743. [DOI] [PubMed] [Google Scholar]
  18. Horton NJ, Kim E, Saitz R (2007) A cautionary note regarding count models of alcohol consumption in randomized controlled trials. BMC Med Res Methodol 7:9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Huh D, Baldwin SA, Zhou Z, Park J, Mun E-Y (2023) Which is better for individual participant data meta-analysis of count outcomes with many zeroes, one-step or two-step analysis? A simulation study. Multivariate Behav Res. Online first, 10.1080/00273171.2023.2173135 [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Huh D, Mun E-Y, Walters ST, Zhou Z, Atkins DC (2019a) A tutorial on individual participant data meta-analysis using Bayesian multilevel modeling to estimate alcohol intervention effects across heterogeneous studies. Addict Behav 94:162–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Huh D, Mun E-Y, Walters ST, Zhou Z, Atkins DC (2019b) Data and code for: A tutorial on individual participant data meta-analysis using Bayesian multilevel modeling to estimate alcohol intervention effects across heterogeneous studies (2019), Mendeley Data, V2, doi: 10.17632/4dw4kn97fz.2 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Huh D, Mun E-Y, Larimer M, White HR, Ray AE, Rhew I, Kim S-Y, Jiao Y, Atkins DC (2015) Brief motivational interventions for college student drinking may not be as powerful as we think: An individual participant-level data meta-analysis. Alcohol Clin Exp Res 39:919–931. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Jackman S (2022) pscl: Political science computational laboratory [CRAN Web site]. Available at: https://cran.r-project.org/web/packages/pscl/pscl.pdf.
  24. Juszczak E, Altman DG, Hopewell S, Schulz K. Reporting of multi-arm parallel-group randomized trials: Extension of the CONSORT 2010 statement. JAMA. 2019;321(16):1610–1620. [DOI] [PubMed] [Google Scholar]
  25. Kim S-Y, Huh D, Zhou Z, Mun E-Y (2020) A comparison of Bayesian to maximum likelihood estimation for latent growth models in the presence of a binary outcome. Int J Behav Dev 44:447–457. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Landis JR, Koch GG (1977) The measurement of observer agreement for categorical data. Biometrics 33: 159–174. [PubMed] [Google Scholar]
  27. Larimer ME, Kilmer JR, Cronce JM, Hultgren BA, Gilson MS, Lee CM (2022) Thirty years of BASICS: Dissemination and implementation progress and challenges. Psychol Addict Behav 36:664–677. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Liang KY, Zeger SL (1986) Longitudinal data analysis using generalized linear models. Biometrika 73(1): 13–22. [Google Scholar]
  29. Long JS, Freese J (2014) Regression models for categorical dependent variables using Stata (3 edition). Stata Press. [Google Scholar]
  30. Long DL, Preisser JS, Herring AH, Golin CE (2014) A marginalized zero-inflated Poisson regression model with overall exposure effects. Stat Med 33:5151–5165. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Moher D, Hopewell S, Schulz KF, et al. (2010) CONSORT 2010 Explanation and elaboration: Updated guidelines for reporting parallel group randomised trials. J Clin Epidemiol 63:E1–E37. [DOI] [PubMed] [Google Scholar]
  32. Mplus [computer program]. Version 8. Los Angeles, CA: Muthén & Muthén; 1998–2023. [Google Scholar]
  33. Mun E-Y, de la Torre J, Atkins DC, White HR, Ray AE, Kim S-Y, Jiao Y, Clarke N, Huo Y, Larimer ME, Huh D, Project INTEGRATE Team (2015) Project INTEGRATE: An integrative study of brief alcohol interventions for college students. Psychol Addict Behav 29:34–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Mun E-Y, Li X, Lineberry S, Tan Z, Huh D, Walters ST, Zhou Z, Larimer ME, in collaboration with Project INTEGRATE Team (2022a) Do brief alcohol interventions reduce driving after driving among college students? A two-step meta-analysis of individual participant data. Alcohol Alcohol 57: 125–135. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Mun E-Y, Zhou Z, Huh D, Tan L, Li D, Tanner-Smith EE, Walters ST, Larimer ME (2022b) Brief alcohol interventions are effective through 6 months: Findings from marginalized zero-inflated Poisson and Negative Binomial models in a two-step IPD meta-analysis. Prev Sci. Online first, 10.1007/s11121-022-01420-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Mun E-Y, Zhou Z, Huh D, Tan L, Li D, Tanner-Smith EE, Walters ST, Larimer ME (2022c) Brief alcohol interventions are effective through 6 months: Findings from marginalized zero-inflated Poisson and negative binomial models in a two-step IPD meta-analysis. Mendeley Data, V1, doi: 10.17632/h2sd5y6fxp.1 [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Murphy JG, Gex KS, Dennhardt AA, Miller AP, O’Neill SE, Borsari B (2022) Beyond BASICS: A scoping review of novel intervention content to enhance the efficacy of brief alcohol interventions for emerging adults. Psychol Addict Behav 36:607–618. [DOI] [PubMed] [Google Scholar]
  38. Pittman B, Buta E, Krishnan-Sarin S, O’Malley SS, Liss T, Gueorguieva R (2020) Models for analyzing zero-inflated and overdispersed count data: An application to cigarette and marijuana use. Nicotine Tob Res 22:1390–1398. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. R: A language and environment for statistical computing [computer program]. Vienna, Austria: R Core Team; 2023. [Google Scholar]
  40. SAS [computer program]. Cary, NC: SAS Institute Inc.: 2023. [Google Scholar]
  41. Saunders JB, Aasland OG, Babor TF, De la Fuente JR, Grant M (1993) Development of the alcohol use disorders identification test (AUDIT). WHO collaborative project on early detection of persons with harmful alcohol consumption-II. Addiction 88: 791–804. [DOI] [PubMed] [Google Scholar]
  42. Schulz KF, Altman DG, Moher D, the Consort Group (2010) CONSORT 2010 statement: Updated guidelines for reporting parallel group randomised trials. BMC Med 8:18. [DOI] [PubMed] [Google Scholar]
  43. Shorter GW, Bray JW, Giles EL, O’Donnell AJ, Berman AH, Holloway A, Heather N, Barbosa C, Stockdale KJ, Scott SJ, Clarke M, Newbury-Birch D (2019) The variability of outcomes used in efficacy and effectiveness trials of alcohol brief interventions: A systematic review. JSAD 80: 286–298. [PubMed] [Google Scholar]
  44. Shorter GW, Bray JW, Heather N, Berman AH, Giles EL, Clarke M, Barbosa C, O’Donnell AJ, Holloway A, Riper H, Daeppen JB, Monteiro MG, Saitz R, McNeely J, McKnight-Eily L, Cowell A, Toner P, Newbury-Birch D (2021) The “Outcome Reporting in Brief Intervention Trials: Alcohol” (ORBITAL) core outcome set: International consensus on outcomes to measure in efficacy and effectiveness trials of alcohol brief interventions. JSAD 82: 638–646. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Sobell LC, Sobell MB (1995) Alcohol consumption measures, in Assessing Alcohol Problems: A Guide for Clinicians and Researchers. Vol. 2 (Allen JP, Columbus M eds), pp. 75–99. National Institute on Alcohol Abuse and Alcoholism, Bethesda, MD. [Google Scholar]
  46. Stata Statistical Software [computer program]. College Station, TX: StataCorp LLC; 2023. [Google Scholar]
  47. Tan L, Friedman Z, Zhou Z, Huh D, White HR, Mun E-Y (2022a) Does abstaining from alcohol in high school moderate intervention effects for college students? Implications for tiered intervention strategies. Front Psychol 13: 993517. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Tan L, Friedman Z, Zhou Z, Huh D, White HR, Mun E-Y (2022b) Data and code for: Does abstaining from alcohol in high school moderate intervention effects for college students? Implications for tiered intervention strategies. Mendeley Data, V1, doi: 10.17632/vnpw693nnd.1 [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Tan Z, Tanner-Smith EE, Walters ST, Tan L, Huh D, Zhou Z, Luningham JM, Larimer ME, Mun EY (2023) Do brief motivational interventions increase motivation for change in drinking among college students? A meta-analysis of individual participant data. Alcohol Clin Exp Res 47(8): 1433–1446. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Tanner-Smith EE, Lipsey MW (2015) Brief alcohol interventions for adolescents and young adults: A systematic review and meta-analysis. J Subst Abuse Treat 51: 1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Tanner-Smith EE, Mun E-Y, Walters ST, Darlington T (2018) Effectiveness of brief alcohol interventions for adolescents and young adults. PROSPERO 2018 CRD42018092348 Available from: https://www.crd.york.ac.uk/PROSPERO/display_record.php?RecordID=92348
  52. Tanner-Smith EE, Xing A, Lin L, Huh D, Mun EY (2023) The comparative effectiveness of brief alcohol interventions for adolescents and young adults: A systematic review and network meta-analysis. Alcohol Clin Exp Res 47(S1): 34. [Google Scholar]
  53. US Preventive Services Task Force (2018) Screening and behavioral counseling interventions to reduce unhealthy alcohol use in adolescents and adults: US Preventive Services Task Force recommendation statement. JAMA 320(18):1899–1909. [DOI] [PubMed] [Google Scholar]
  54. Venables WN, Ripley BD (2002) Modern Applied Statistics with S. 4th ed. Springer, New York. [Google Scholar]
  55. von Eye A, Mun E-Y (2003) Characteristics of measures for 2 × 2 tables. Understanding Statistics 2(4): 243–266. [Google Scholar]
  56. von Eye A, Mun E-Y (2013). Log-linear modeling: Concepts, interpretation, and applications. New York: Wiley. [Google Scholar]
  57. Vuong QH (1989) Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica 57:307–333. [Google Scholar]
  58. White HR, Labouvie EW (1989) Towards the assessment of adolescent problem drinking. J Stud Alcohol 50:30–37. [DOI] [PubMed] [Google Scholar]
  59. Witkiewitz K, Finney JW, Harris AHS, Kivlahan DR, Kranzler HR (2015a) Guidelines for the reporting of treatment trials for alcohol use disorders. Alcohol Clin Exp Res 39:1571–1581. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Witkiewitz K, Finney JW, Harris AHS, Kivlahan DR, Kranzler HR (2015b) Recommendations for the design and analysis of treatment trials for alcohol use disorders. Alcohol Clin Exp Res 39:1557–1570. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Xu L, Paterson AD, Turpin W, Xu W (2015) Assessment and selection of competing models for zero-inflated microbiome data. PLoS ONE 10: e0129606. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Zeileis A, Kleiber C, Jackman S (2008) Regression models for count data in R. J Stat Software 27:1–25. [Google Scholar]
  63. Zhou Z, Li D, Huh D, Mun E-Y (2022) mcount: Marginalized count regression models. [CRAN Web site]. Available at: https://cran.r-project.org/web/packages/mcount/mcount.pdf Accessed December 21, 2022.
  64. Zhou Z, Li D, Huh D, Xie M, Mun E-Y (2023a) A simulation study of the performance of statistical models for count outcomes with excessive zeros. https://arxiv.org/abs/2301.12674v4 [DOI] [PMC free article] [PubMed]
  65. Zhou Z, Li D, Huh D, Xie M, Mun E-Y (2023b) Script for Zhou et al. (2023). A simulation study of the performance of statistical models for count outcomes with excessive zeros. Mendeley Data, V1, doi: 10.17632/r5bztdd766.1 [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Zhou Z, Li D, Huh D, Xie M, Chen Y, Mun E-Y (2023c). A generalized estimating equations approach to variance estimation for a family of count distributions: A unifying method. [Poster]. Presented at Joint Statistical Meeting, August 2023, Toronto, Canada. [Google Scholar]
  67. Zhou Z, Xie M, Huh D, Mun E-Y (2021) A bias correction method in meta-analysis of randomized clinical trials with no adjustments for zero-inflated outcomes. Stat Med 40 (26): 5894–5909. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES