Abstract
Introduction:
Low-density cholesterol (LDL-C) has long been estimated by the Friedewald formula (LDL-F); however, this method underestimates LDL-C in patients with hypertriglyceridemia (HTG) or low LDL-C levels. The Martin (M-LDL-C) and Sampson (S-LDL-C) formulas partially resolve these limitations. Recently, Sampson et al. developed a new equation (eS-VLDL-C) that includes ApoB. This new equation could be particularly useful in FCHL, which is characterized by the predominance of triglyceride rich VLDL and a discordance between LDL-C and ApoB.
Materials and methods:
Very low-density lipoproteins (VLDL-C) was measured in 336 patients with FCHL by sequential ultracentrifugation. LDL-C was estimated by subtracting VLDL-C estimated by the different equations from non-HDL cholesterol. Spearman correlations, R2, mean squared error (RMSE), and bias were used to compare the accuracy of the different equations. Concordance of the estimated LDL-C values with LDL-C thresholds and ApoB were also assessed by their kappa coefficients and by ROC analysis.
Results:
Overall population had a mean age of 47 years, and 61.5% were women. 19.5% had type 2 diabetes, hypertension in 20.8%, and only 12.2% were on statin treatment. Both S-LDL-C and eS-LDL-C performed similarly, and better than M-LDL-C and F-LDL-C. In the Bland-Altman analysis, eS-LDL-C showed the lowest bias, and better performance in HTG, and better concordance with LDL-C treatment goals compared to other formulas (eg ρ: 0.87 95%CI 0.84-0.89).
Conclusions:
The LDL-S and LDL-eS equations estimate the concentration of LDL-C with greater accuracy than other formulas. The LDL-eS had best performance in estimating LDL-C with lower RMSE than other formulas.
Keywords: Low-density lipoproteins, cholesterol, triglycerides, Familial Combined Hyperlipidemia, Cardiovascular Risk
Introduction:
Decades of both basic and epidemiological research have established a causal relationship between high levels of cholesterol, especially Low-Density-Lipoprotein Cholesterol (LDL-C), and cardiovascular disease (CVD).1,2 Until recently, LDL-C was routinely calculated with the Friedewald equation. It was first described 50 years ago and depends on the results from the standard lipid panel, namely Total Cholesterol [TC], High-Density-Lipoprotein Cholesterol [HDL], and triglycerides, [TG])3. However, the Friedewald equation (Shown in table 1) introduces errors by assuming that the TG content of Very-Low-Density Lipoprotein (VLDL-C) corresponds to a fixed ratio of TG/5; even though the TG content in VLDL can vary considerably depending on its size. 4 Taking this into consideration, Martin et al. developed an improved equation (Shown in table 1) in 2013 that considers a variance of this ratio through an adjustable factor depending on the TG and Non-HDL strata.5 The variable factors in the Martin Equation are based on the vertical auto profile (VAP) method, which has limitations on high TG samples.6This is a potential problem for populations with mixed dyslipidemia, such as Familial combined hyperlipidemia (FCHL) , one of the most common forms of dyslipidemia. FCHL is characterized by fluctuations in serum lipid concentrations and might present as mixed hyperlipidemia, isolated hypercholesterolemia, hypertriglyceridemia or as a normal serum lipid profile in combination with abnormally elevated levels of apolipoprotein B (ApoB).7 Given the limitations of estimating LDL-C in hypertriglyceridemia, the fluctuation of TG in FCHL may make the accurate longitudinal assessment of LDL-C difficult. Nevertheless, LDL-C levels are important for decision-making around treatment goals, as LDL-C is the main cardiovascular disease marker used to estimate CVD risk in patients with FCHL.8 Furthermore, the most recent multi-society guidelines now endorse the use of non-fasting samples for lipid screening, which can potentially add to the inaccuracy of calculated LDL-C in hypertriglyceridemic persons.9
Table 1.
Summary of the most relevant LDL-C formulas
In 2020, Sampson et al. (Shown in table 1) developed another formula for VLDL-C utilizing three terms: 1) a linear TG contribution (related to mean VLDL lipid composition); 2) an interaction term for cholesterol enrichment of VLDL by cholesterol ester transfer protein (CETP); and 3) a correction factor to account for low cholesterol content of chylomicrons and nascent LDL. This equation had a better accuracy of VLDL-C estimation when compared to ultracentrifugation (BQ) than Friedewald or Martin formula, particularly for hypertriglyceridemic patients with TG between 400-800mg/dL. It was also recently shown to be more accurate at both low and high LDL-C values than other equations, particularly when TG is elevated.11
All of the formulas for assessing LDL-C are inherited limited by its ability to calculate VLDL-C, due to the ratio of triglycerides and cholesterol content of VLDL. This particular issue is more relevant in populations where VLDL content are altered as in type III dysbetalipoproteinemia and FCHL. Hence, other efforts for improving the accuracy of estimation of lipid parameters as VLDL-C has been done, for example, Sampson et al.10 (Shown in table 1) recently enhanced their formula by adding ApoB(e-Sampson) as an independent variable. This new formula, which was based on a general dyslipidemic population, uses the same terms as the original Sampson-NIH (Sampson) equation for VLDL-C but adds ApoB and an interaction term between ApoB and TG.10 With this new formula, one can accurately assess the cholesterol to TG ratio in VLDL for identifying patients with Type III Dysbetalipoproteinemia. Although this formula was first described for type III dysbetalipoproteinemia it has never been tested for accuracy in other populations. In this study, we first describe the accuracy of the new enhanced Sampson-NIH formula for VLDL-C and then used to calculate LDL-C in a Mexican FCHL population.
Methods:
Study population
The cases were selected from a cohort of families with FCHL studied in the Lipid Clinic at the Instituto Nacional de Ciencias Médicas y Nutrición, Salvador Zubirán in Mexico City. FCHL was diagnosed using the following criteria: Apo B level > 90th percentile for Mexican population (> 108 mg/dl for men and > 99mg/dl for women) and hypercholesterolemia (total cholesterol > 200 mg/dl) and/or hypertriglyceridemia (triglycerides > 150 mg/dl) along with dyslipidemia in three first-degree relatives (6). All subjects had either a personal orfamily history of premature coronary heart disease (before 55 and 65 y in men and women, respectively) and each participant had at least one first-degree relative with a different hyperlipidemic phenotype. Exclusion criteria included VLDL-C (mmol/L)/triglycerides (mmo/L) ratio > 0.69 and Apo B < 90th percentile (type III hyperlipoproteinemia) (10), presence of tendinous xanthomas or more than 8 points of the Dutch Lipid Clinical Network criteria, history of an acute illness within previous six weeks, pregnancy, or the presence of any disease or medication known to significantly influence lipid parameters other than statins. The Human Research Ethics Committee of the Instltuto National de Ciencias Médicos y Nutrición, Salvador Zubirán approved the study and all participants gave written informed consent. All methods and procedures were done in accordance with the Declaration of Helsinki.
Laboratory measurements
Blood samples were obtained after an 8–12 hour fast. Cholesterol, triglycerides, HDL cholesterol, and apolipoprotein B were measured in serum using colorimetric assays (Unicel DxC 600 Synchron Clinical System Beckman Coulter). VLDL lipoproteins were isolated using sequential ultracentrifugation (BQ-VLDL-C [Optimal Beckman LE80-K]) of 40,000 RPM at 4°C for 18 hours. Serum aliquots (3.5 mL) were centrifuged at background density of 1.006 Kg/L; VLDL-C and VLDL-triglycerides levels in the ultracentrifugal top fraction were analyzed by colorimetric assays (Unicel DxC 600 Synchron Clinical System Beckman Coulter). To approximate a gold standard for comparative evaluations LDL-C was calculated using VLDL-C measured by ultracentrifugation. LDL and VLDL cholesterol were calculated using the Friedewald’s equation (VLDL-F, LDL-F), Sampson’s method (VLDL-S, LDL-S), enhanced Sampson’s method (VLDL-eS, LDL-eS), and the calculation proposed by Martin et al. (VLDL-M, LDL-M) from their original publications. The Enhanced Sampson is an VLDL-C formula for which we calculated the eS-LDL-C by subtracting eS-VLDL-C and HDL-C from total cholesterol. Concordance between LDL-C estimated using measured VLDL-C by ultracentrifugation as: (LDL–C=TC–[HDL–C+VLDL–C]).
Statistical Analysis:
The statistical analysis involved comparing proportions and medians, using chi-square and Mann-Whitney U tests. The variables were described using median and interquartile range. Spearman correlations were performed to evaluate the degree of linear association between VLDL-C, eS-VLDL-C, S-VLDL-C, M-VLDL-C, and F-VLDL-C. R2, root-mean-square error (RMSE), and mean bias from Bland-Altman plots were used to estimate the degree of linear fit. M-LDL-C, S-LDL-C, eS-LDL-C and F-LDL-C targets were dichotomized for each patient and compared to targets obtained by LDL-C estimated using VLDL-C by ultracentrifugation using the kappa coefficients and mean bias was estimated using Bland-Altman analyses only in individuals with triglycerides < 800mg/dL; a sensitivity analysis was performed only in subjects who had previous statin treatment to estimate significant deviances. Also, correlations and concordance of lipid goals according to the differing phenotypes of FCHL were evaluated, namely isolated hypercholesterolemia and mixed dyslipidemia. Performance of each estimation method for lipid goals of LDL-C < 100 mg/dL, LDL-C < 70 mg/dL were evaluated using areas under the receiving operating characteristic curve (AUROC). A two-tailed p-value < 0.05 was considered significant as statistically significant. Statistical analyses were performed using the SPSS software (version 24.0) and R software (Version 3.6.2, https://www.R-project.org)
Results
Study population
A total of 336 patients with confirmed FCHL diagnosis and ApoB and VLDL-C measurements were included (Table 2). The median age of the population was 47 (35-57) years and 61.6% of patients were female. Overall, 19.5% and 20.8% of patients had type 2 diabetes mellitus (T2DM) and hypertension, respectively. Only 12.2% of population were on statin treatment. In terms of FCHL phenotypes, 136 (40.5%) and 200 (59.5%) participants had isolated hypercholesterolemia and mixed dyslipidemia phenotypes respectively. When comparing both phenotypes, the mixed dyslipidemia group was observed to generally be older, have a lower proportion of women, and have a higher prevalence of T2DM, hypertension, and statin treatment (p <0.05). The mixed dyslipidemia group also had higher ApoB, LDL-C, VLDL-C, and non-HDL cholesterol levels (p < 0.001).
Table 2.
Biochemical and clinical characteristics of patients with FCHL in the overall population and stratified by FCHL dyslipidemia phenotype.
| Variables | Overall n = 336 |
Isolated hypercholesterolemia n = 136 |
Mixed dyslipidemia n = 200 |
| Sex (Female) | 207 (61.6%) | 101 (74.3%) | 106 (53%) |
| Age (y) | 47 (35-57) | 43 (32-56) | 48 (37-58) |
| Type 2 Diabetes (%) | 65 (19.5%) | 10 (7.4%) | 55 (27.5%) |
| Hypertension (%) | 70 (20.8%) | 21 (15.4%) | 49 (24.5%) |
| Total Cholesterol (mg/dL) | 209 (179.5-242-5) | 179 (160-199) | 226.5 (206-266.5) |
| HDL Cholesterol (mg/dL) | 42 (35-48) | 46.5 (41-54) | 38 (33-44) |
| No-HDL Cholesterol (mg/dL) | 168 (133-198) | 129.5 (112-154.5) | 188 (168.5-227) |
| Triglycerides (mg/dL) | 184.5 (108-312) | 99.5 (73-124) | 271 (206-394.5) |
| Apolipoprotein B (mg/dL) | 116(90-136) | 87 (73.1-103.5) | 128(114-148) |
| VLDL-Triglycerides (mg/dL) | 120.8 (61.3-239.2) | 54 (34-73.8) | 211 (114-327) |
| VLDL-Cholesterol (mg/dL) | 32.4(16.5-52.5) | 14.74(9.139-19.65) | 49.03 (36.09-66.86) |
| VLDL-Cholesterol Martin (mg/dL) | 32.9 (21.3-46) | 19.69(16.09-22.87) | 43.48(34.61-56.43) |
| VLDL-Colesterol enhanced Martin (mg/dL) | 33.3 (21.4-46.3) | 19.9 (16-22.9) | 43.4(34.5-58.5) |
| VLDL-Cholesterol Sampson (mg/dL) | 35.4(18.7-54.7) | 16.65(12.1-21.15) | 51.65 (37.9-69.55) |
| VLDL-Colesterol enhanced Sampson (mg/dL) | 30.8(19.1-51.5) | 17.65 (12.3 - 22.35) | 46 (35.3 - 65.45) |
| VLDL-Cholesterol Friedewald (mg/dL) | 36.5 (21.5-61.9) | 19.8(14.6-24.3) | 54.2 (41.2-78.9) |
| LDL-Cholesterol (mg/dL) | 127.7 (106.4-151.5) | 114.2 (98.36 - 136.7) | 139.0 (119.5 - 161.6) |
| LDL-Cholesterol Martin (mg/dL) | 130 (106.2-151.32 | 109.4(95.09-131.1) | 142.8(121.8-161.9) |
| LDL-Cholesterol enhanced Martin (mg/dL) | 130.2 (106.4-151.4) | 109.8(95-132) | 142.4(120.9-160.6) |
| LDL-Cholesterol Sampson (mg/dL) | 128 (101.3-146) | 112.2 (95.75 - 133.9) | 134.6 (110.9 - 157.2) |
| LDL-Cholesterol enhanced Sampson (mg/dL) | 128.6 (104.3-152.7) | 114(96.95 - 133.6) | 138.4(116.5-161.3) |
| LDL-Cholesterol Friedewald (mg/dL) | 122.6 (97.2-146) | 109.4(94.6-130.6) | 128.8(102.3 -153.4) |
| Statins (%) | 41 (12.2%) | 5 (3.7%) | 36 (18%) |
Performance comparison of VLDL-C equations
For VLDL-C measured by ultracentrifugation, the Sampson formula had the best correlation (ρ= 0.95, 95%CI 0.94-0.96), followed by e-Sampson (ρ= 0.94, 95%CI 0.91-0.95), then Friedewald, and Martin, respectively (ρ= 0.93, 95%CI 0.91-0.95, ρ= 0.93, 95%CI 0.91-0.94, respectively). For the isolated hypercholesterolemia phenotype, the Friedewald formula had the best correlation (ρ= 0.82, 95%CI 0.75-0.88), followed by Sampson (ρ= 0.80, 95%CI 0.72-0.85), Martin (ρ= 0.79, 95%CI 0.72-0.85), and finally e-Sampson (ρ= 0.75, 95%CI 0.70-0.79). For mixed dyslipidemia phenotype, the Sampson formula presented the best correlation (ρ= 0.88, 95%CI 0.85-0.91), followed by e-Sampson (ρ= 0.85, 95%CI 0.82-0.88), Martin (ρ= 0.83, 95%CI 0.79-0.87), and finally Friedewald (ρ= 0.82, 95%CI 0.76-0.86).
Regarding RMSE, e-Sampson was comparatively lower than Sampson, Martin, and Friedewald--in that order--and RMSE was lower for all, but in the same proportion, when we analyzed the population with Tg <800mg/dL or only mixed dyslipidemia (Fig 1). The Bland-Altman analysis showed a smaller bias in the e-Sampson formula (d = 1.39, 95%CI −0.22,0.96), followed by Sampson (d = −1.49, 95%CI −2.52,−3.56), Martin (d = 3.19, 95%CI 0.33,1.76), and Friedewald (d = −4.80, 95%CI −7.48,−6.14), compared to VLDL-C measured by ultracentrifugation. The mean absolute difference (MAD) was lower for Sampson, followed by eSampson, Martin and Friedewald’s (8.68, 8.78, 11.33 and 15.38 respectively).
Figure 1.
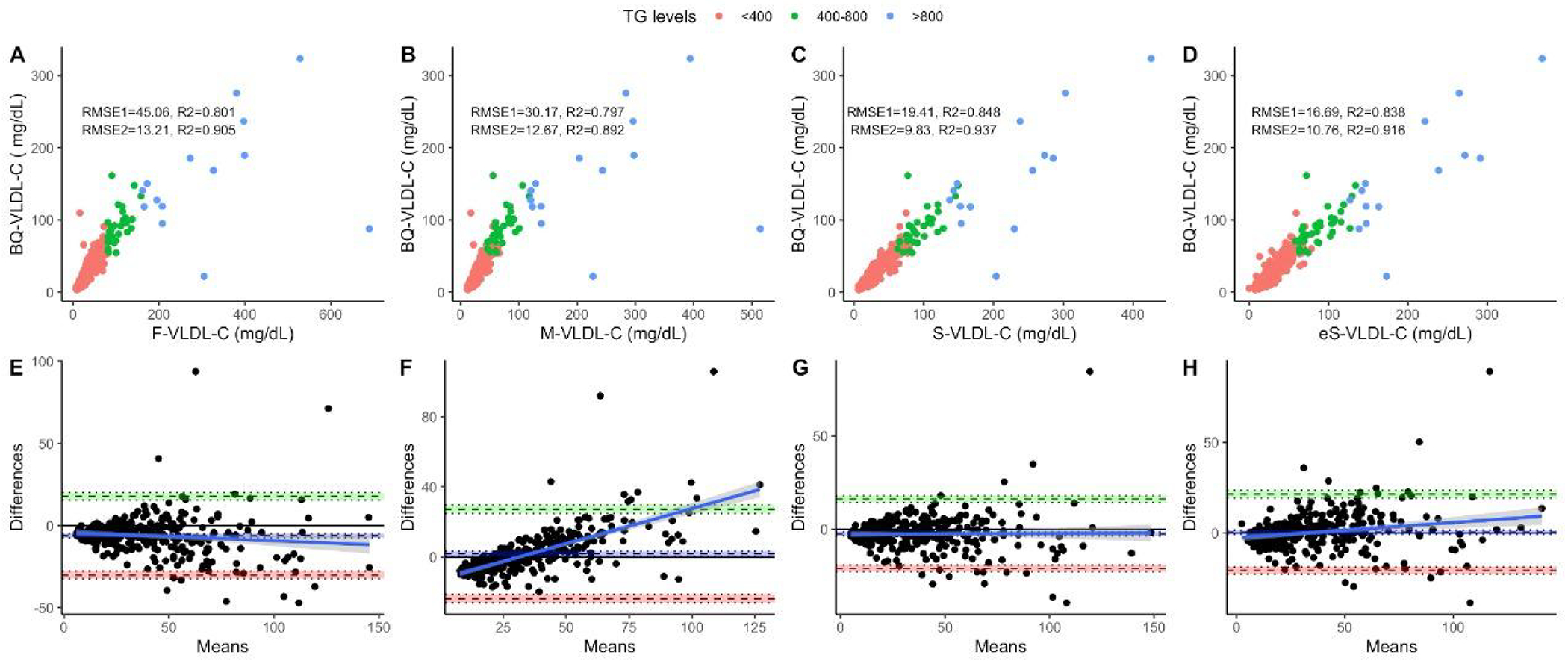
Performance metrics for all three formulas compared to VLDL-C measured by ultracentrifugation in the overall population, showing RMSE for the overall population (RMSE1, n = 336) and for subjects with triglycerides < 800mg/dL (RMSE2, n = 322) comparing VLDL-C measured and calculated by Friedewald’s (a), Martin’s (b) Original Sampson’s (c) and the Enhanced Sampson’s equation (d). The figure also shows Bland-Altman plots showing bias and limits of agreement for VLDL-C estimated using Friedewald’s (e), Martin’s (f) Original Sampson’s (g) and the Enhanced Sampson’s equation (h). Triglycerides groups <400mg/dL (n = 286), 400-800 mg/dL (n = 35), >800 mg/dL (n = 14). Abbreviations = RMSE: Root of Mean Squared Error; 95%CI: 95% Confidence Interval; BQ-VLDL-C: VLDL-C by sequential ultracentrifugation, F-VLDL-C: VLDL-C estimated by the Friedewald’s equation; M-VLDL-C: VLDL-C estimated by Martin’s formula; S-VLDL-C: VLDL-C estimated by Sampson’s formula, e-VLDL-C: VLDL-C estimated by enhanced Sampson’s formula
LDL-C comparative assessment:
For LDL-C estimates, Sampson’s and e-Sampson formula had the highest correlation for estimated LDL-C albeit with narrower confidence interval in the latter (ρ = 0.91, 95%CI 0.90–0.94, ρ=0.91, 95%CI 0.90-0.93 respectively)--followed by Martin’s (ρ = 0.90, 95%CI 0.87–0.91) and Friedewald’s (ρ = 0.89, 95%CI 0.87–0.991) formulas. Even though the R2 was higher for Sampson formula, the LDL-C estimation errors (RMSE) was comparatively lower for e-Sampson’s formula (Table 3). When only analyzing individuals with triglycerides < 800mg/dL, e-Sampson performed with a similar R2 and RMSE as Sampson but higher than any other formula (R2= 0.918, RMSE=10.72). This could be due a limitation in ApoB assay when triglycerides are >800mg/dL (10) (Fig. 2A–D). Bland-Altman analyses showed smaller bias for Martin’s formula (d = −0.99, 95%CI −2.39-0.40), followed by Sampson’s (d = 2.42, 95%CI 1.37-3.46), e-Samspon (d= 6.00, 95%CI 2.67-9.33), and Friedewald’s formulas (d = 6.91, 95%CI 5.67-8.15, Figs. 1E–G) compared to estimated LDL-C by measured VLDL-C by ultracentrifugation. The MAD was lower for eSampson followed by Sampson, Martin and Friedewald’s (8.78, 8.88, 11.27 and 15.32 respectively).
Table 3:
Performance metrics for all four formulas compared to LDL-C estimated using VLDL-C measured by ultracentrifugation in the overall population
| Overall population (n=336) | ||||
|---|---|---|---|---|
| Metric | F-LDL-C | M-LDL-C | S-LDL-C | eS-LDL-C |
| p (95%CI) | 0.90 (0.87-0.91) | 0.89 (0.87-0.91) | 0.91 (0.90-0.94) | 0.92 (0.90-0.93) |
| p with ApoB (95%CI) | 0.66 (0.60-0.72) | 0.80 (0.77-0.84) | 0.79 (0.75-0.83) | 0.87 (0.84-0.89) |
| R2 | 0.80 | 0.80 | 0.85 | 0.84 |
| RMSE | 45.06 | 30.17 | 19.41 | 17.62 |
| Bias (95%CI) | 6.91 (5.67-8.15) | −0.99 (−2.39-0.40) | 2.42 (1.37-3.46) | −0.22 (−1.40-0.96) |
Figure 2.
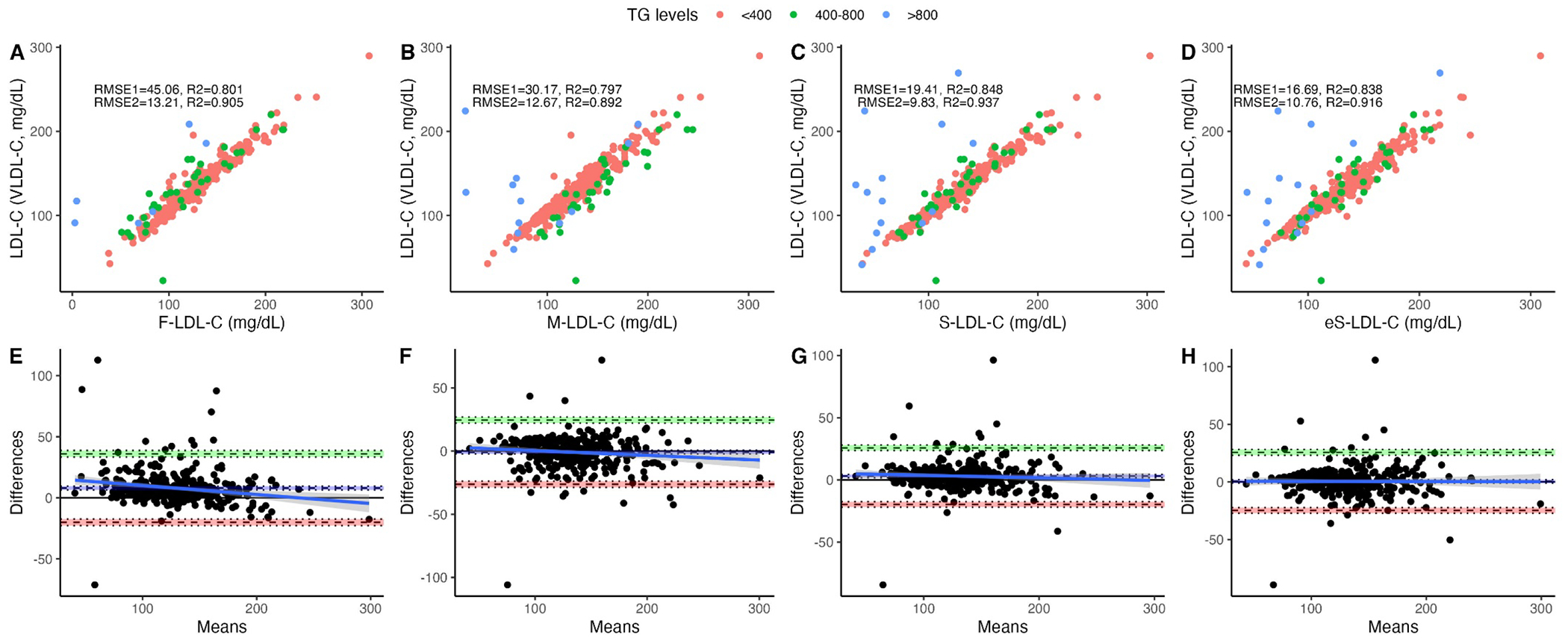
Performance metrics for LDL-C estimated using VLDL-C measured and calculated by Friedewald’s (a), Martin’s (b) Original Sampson’s (c) and the Enhanced Sampson’s (d) equations as well as Bland-Altman plots showing bias and limits of agreement for VLDL-C estimated using Friedewald’s (e), Martin’s (f) Original Sampson’s (g) and the Enhanced Sampson’s equation (h). Identical subjects as in Figure (1).
When we compared the performance of the formulas through triglyceride levels, both Sampson and e-Sampson showed a better correlation in LDL and were very similar between them (Table 4). However, all four formulas had a similar LDL correlation in those patients with triglycerides <400 mg/dL (LDL-S: ρ 0.99, 95%CI 0.98-0.99, LDL-eS ρ 0.99, 95%CI 0.98-0.99, LDL-M: ρ 0.98, 95%CI 0.98-0.99, LDL-F: ρ 0.99, 95%CI 0.98-0.99). However, there was a better correlation in Sampson and e-Sampson when triglycerides were >400 mg/dL (LDL-S: 0.87, 95%CI 0.84-0.90, LDL-eS: 0.87, 95%CI 0.84-0.89, LDL-M: 0.85, 95%CI 0.81-0.89, LDL-F: 0.84, 95%CI 0.80-0.89).
Table 4.
Performance metrics for all four formulas compared to LDL-C estimated using VLDL-C measured by ultracentrifugation stratified by FCHL dyslipidemia phenotype
| Metric | Isolated Hypercholesterolemia (n=136) |
Mixed Dyslipidemia (n=200) |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| F-LDL-C | M-LDL-C | S-LDL-C | eS-LDL-C | F-LDL-C | M-LDL-C | eM-LDL-C | S-LDL-C | eS-LDL-C | |
| p (95%CI) | 0.98 | 0.98 | 0.98 | 0.99 | 0.84 | 0.85 | 0.87 | 0.87 | 0.87 |
| (0.98-0.99) | (0.98-0.99) | (0.98-0.99) | (0.98-0.99) | (0.80-0.89) | (0.81-0.89) | (0.84-0.90) | (0.84-0.90) | (0.84-0.89) | |
| p with ApoB (95%CI) | 0.87 | 0.88 | 0.92 | 0.87 | 0.64 | 0.73 | 0.76 | 0.75 | 0.87 |
| (0.84-0.90) | (0.86-0.91) | (0.90-0.94) | (0.84-0.89) | (0.58-0.70) | (0.68-0.78) | (0.70-0.80) | (0.70-80) | (0.84-0.89) | |
| R2 | 0.97 | 0.97 | 0.98 | 0.97 | 0.71 | 0.72 | 0.76 | 0.77 | 0.76 |
| RMSE | 6.31 | 6.78 | 5.14 | 5.57 | 44.89 | 29.87 | 29.38 | 19.14 | 16.32 |
| Bias (95%CI) | 4.92 | 5.19 | 3.27 | 2.61 | 18.5 | −0.1 | −0.3 | 6 | 0.89 |
| (4.24-5.60) | (4.44-5.93) | (2.59-3.95) | (1.79-3.47) | (10.9-26.1) | (−5.5-5.2) | (−5.6-4.9) | (2.7-9.3) | (−2.0-3.8) | |
Comparison of LDL-C formulas for LDL-C therapeutic goals
When we evaluated the LDL-C control goals of <100mg/dL (n = 64), the highest concordance and AUROC were observed with the e-Sampson formula (Table 5). Although in isolated hypercholesterolemia phenotype, the concordance was higher for Sampson, e-Sampson was only slightly inferior, and all formulas had a similar AUROC (Table 6). In mixed dyslipidemia phenotype, the e-Sampson formula was superior to the rest of the formulas, but Sampson had a slightly better AUROC. At the lower LDL-C goal used for secondary prevention (<70mg/dL, n = 8), the e-Sampson formula was again superior in both concordance and AUROC to the rest of the formulas.
Table 5:
Comparison of lipid targets for all four formulas compared to LDL-C estimated using VLDL-C measured by ultracentrifugation in the overall population
| Overall population | |||||
|---|---|---|---|---|---|
| Metric | F-LDL-C | M-LDL-C | S-LDL-C | eS-LDL-C | |
| LDL-C goal < 100 mg/dL (n=64) | κ (95%CI) | 0.70 (062-0.79) | 0.73 (0.64-0.82) | 0.80 (0.72-0.88) | 0.82 (0.75-0.90) |
| AUC (95%CI) | 0.96 (0.94-0.98) | 0.95 (0.93-0.98) | 0.97 (0.96-0.99) | 0.97 (0.95-0.99 | |
| LDL-C goal < 70 mg/dL (n=8) | κ (95%CI) | 0.32 (0.11-0.55) | 0.51 (0.24-0.79) | 0.46 (0.20-0.73) | 0.70 (0.44-0.98) |
| AUC (95%CI) | 0.95 (0.89-1) | 0.91 (0.76-1) | 0.94 (0.86-1) | 0.95 (0.85-1) | |
Table 6:
Comparison of lipid targets for all four formulas compared to LDL-C estimated using VLDL-C measured by ultracentrifugation in the FCHL dyslipidemia phenotype
| Isolated Hypercholesterolemia (n=38) |
Mixed Dyslipidemia (n=26) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Métric | F-LDL-C | M-LDL-C | S-LDL-C | eS-LDL-C | F-LDL-C | M-LDL-C | eM-LDL-C | S-LDL-C | eS-LDL-C | |
| LDL-C goal <100 mg/dL | κ (95%CI) | 0.78 (0.63-0.86) |
0.78 (0.67-0.89) |
0.81 (0.70-0.91) |
0.80 (0.69-0.91) |
0.65 (0.51-0.78) |
0.63 (0.47-0.80) |
0.63 (0.47-0.79) |
0.78 (0.66-0.91) |
0.83 (0.72-0.95) |
| AUC (95%CI) | 0.99 (0.97-1) |
0.99 (0.98-1) |
0.99 (0.98-1) |
0.99 (0.98-1) |
0.96 (0.93-0.99) |
0.95 (0.93-0.98) |
0.96 (0.93-0.98) |
0.97 (0.94-0.99) |
0.96 (0.93-0.99) |
|
| LDL-C goal <70 mg/dL | κ (95%CI) | 0.80 (0.41-1.0) |
0.56 (0.12-1) |
0.80 (0.41-1) |
1 (1-1) | 0.22 (0.00-0.45) |
0.49 (0.14-0.84) |
0.34 (0.02-0.71) |
0.36 (0.05-0.66) |
0.59 (0.23-0.96) |
| AUC (95%CI) | 0.99 (0.99-1) |
1.00 (1-1) | 1.00 (1-1) | 1.00 (1-1) | 0.94 (0.85-1) |
0.91 (0.77-1) |
0.92 (0.81-1) |
0.94 (0.85-1) |
0.95 (0.86-1) |
|
Analytical error grids
In order to assess the potential impact of the different LDL-C equations on clinical decision-making, we used error grid analysis11 for all the samples with TG levels between 200-800 mg/dL. Figure 3A shows that differences between the estimated LDL-C and sequential ultracentrifugation LDL-C (BQ-LDL-C) values that were greater than the 12% proportional total allowable error goal for LDL-C11, but did not result in a change in patient classification at the low (70 mg/dL) and high (190 mg/dL) LDL-C cut-points were classified as pure analytical errors. On the other hand, errors that caused a patient to be classified incorrectly at either of these cut-points, regardless of the magnitude of the difference between the estimated and BQ-LDL-C values, were classified as clinically relevant errors.
Figure 3. Error Grid Analysis for overall population.
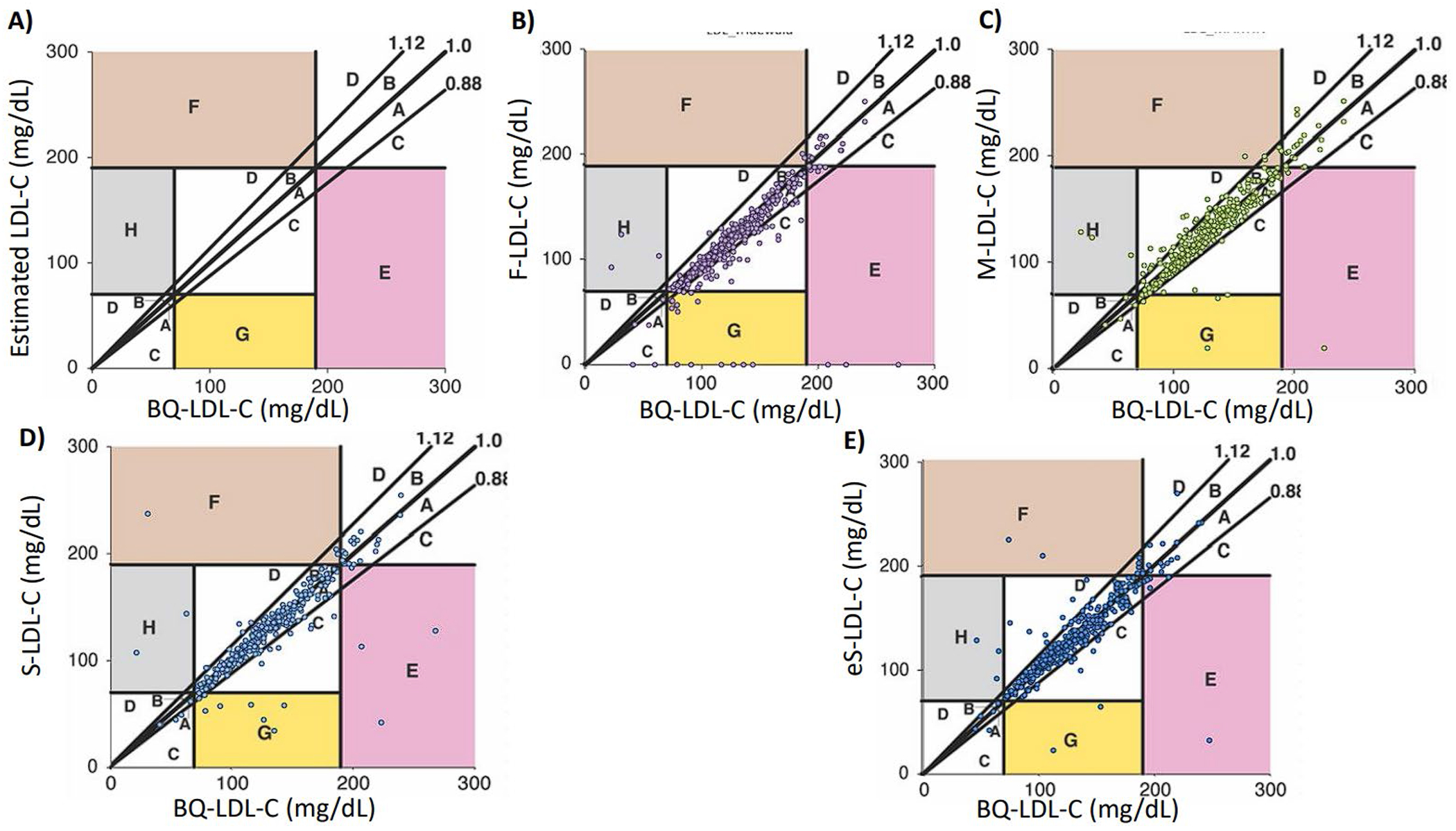
Definition of errors are shown in (Panel A). a: Within 12% proportional error and below regression line, b: Within 12% proportional error and above regression line, c: Greater than 12% proportional error but no impact on patient management and below regression line, d: Greater than 12% proportional error but no impact in patient management and above regression line, e: Underestimation of LDL-C at high LDL-C cut-point leading to error in patient management, f: Overestimation of LDL-C at high LDL-C cut-point leading to error in patient management, g: Underestimation of LDL-C at low LDL-C cut-point leading to error in patient management, h: Overestimation of LDL-C at low LDL-C cut-point leading to error in patient management. Negative values are shown as zero. Numbers in colored zones (e, f, h and g) indicate the total number of clinically relevant misclassifications (10). Overall patients (N = 336) LDL-C was calculated for Friedewalds (Panel B), Martin or enhanced Martin if TG >400 mg/dL (Panel C), Sampson’s (Panel D) or calculated enhanced Sampson’s (Panel E). Abbreviations: LDL-C: Low density lipoprotein cholesterol, BQ-LDL-C: ultracentrifugation measured LDL-C.
In terms of errors that could potentially change patient management decisions, the S-LDL-C results were predicted to have a total of 5.34% clinically relevant errors, which was lower than the errors observed with eS-LDL-C (5.63%), M-LDL-C and eM-LDL-C (5.63%) F-LDL-C (8.6%). The clinically relevant errors associated with F-LDL-C tended to underestimate LDL-C at the low LDL-C cut-point, while M-LDL-C and eM-LDL-C more often overestimated LDL-C at both the low and high LDL-C cut-points.
Discussion:
In the 2018-Multisociety Guideline on cholesterol management9, LDL-C is used to monitor lipid lowering therapies and it is recommended that patients at very high-risk or secondary prevention be treated to reach an LDL-C less than 70 mg/dl (<1.8 mmol/l). According to the 2019 European Atherosclerosis Society guidelines this same group of patients should be treated to reach an LDL-C less than 55 mg/dl (<1.4 mmol/l). Therefore, an accurate calculation and monitoring of LDL-C levels is crucial for effectively managing dyslipidemias and reducing cardiovascular risk. Inaccurate LDL-C calculations can lead to incorrect treatment decisions, potentially putting patients at risk for adverse cardiovascular events. Given the challenges of estimating LDL-C in hypertriglyceridemia, inaccurate LDL-C results leading to inappropriate treatment decisions is more likely to occur in patients with mixed dyslipidemia, particularly when using the Friedewald’s formula.12
Familial combined hyperlipidemia is a type of dyslipidemia that can present with several different phenotypes over time. Typically, these patients have elevated LDL-C and TG levels above the 90th percentile for their age and sex.13,14 Several studies have shown that S-LDL-C was better in LDL-C estimation on patients with hypertriglyceridemia11,15. This new formula improves marginally the estimation of VLDL-C and therefore the calculation of LDL-C, especially in hypertriglyceridemia, which may be particularly valuable for FCHL because of fluctuations in their lipid profile.16 More accurate LDL-C estimations would allow better decision-making in the introduction of new lipid-lowering treatments, which is clinically relevant due to the new treatments that produce very low LDL-C levels.15,17–19
Recent studies have also shown that elevated levels of VLDL-C can explain nearly half of residual CV risk when LDL-C is low.20 This suggests a need to reevaluate the current guideline emphasis on predominantly reducing LDL-C and place importance in decreasing triglyceride-rich remnants. Moreover, plasma ApoB and non-HDL-C measurements may be more clinically valuable, as they encompass LDL, IDL, VLDL and Lp(a).
Our current findings suggest that S-LDL-C and eS-LDL-C perform equally but have a higher correlation for measured LDL-C and VLDL-C (Figure 4). Martin’s formula had the smallest bias, followed by S-LDL-C, eS-LDL-C, and finally F-LDL-C. When analyzing all individuals with triglycerides between 40 and 400 mg/dL, eS-LDL-C and S-LDL-C performed comparable, slightly better than M-LDL-C, and all better than F-LDL-C. However, when triglycerides were between 400 and 800 mg/dL, S-LDL-C and eS-LDL-C had a better correlation with LDL-C. Overall, these findings provide information on the comparative performance of different formulas in estimating LDL-C and highlight the importance of considering triglyceride levels when selecting a formula.
Figure 4.
Low-density cholesterol (LDL-C) has long been estimated by the Friedewald formula (LDL-F); however, this method underestimates LDL-C in patients with hypertriglyceridemia (HTG) or low LDL-C levels. The Martin (M-LDL-C) and Sampson (S-LDL-C) formulas partially resolve these limitations. Recently, Sampson et al. developed a new equation (eS-VLDL-C) that includes ApoB. This new equation could be particularly useful in combined familial hyperlipidemia (FCHL), which is characterized by the altered VLDL TG and cholesterol composition. (Elaborated with Biorender). LDL-C calculated by Friedewald’s (a), Martin’s (b) Original Sampson’s (c) and the Enhanced Sampson’s (d) equations. (Created with Biorender)
It is important to consider that to implement this new formula, an ApoB must be measured concomitantly with the lipid profile, which would increase laboratory costs. The latest multi-society guidelines still do not support the routine use of ApoB9, although several studies have now shown that it is a more accurate cardiovascular risk marker than LDL-C21–23. In individuals with mild to moderate hypertriglyceridemia and diabetes, obesity, and metabolic syndrome, discordance with LDL-C and nonHDL-C can occur as a result of the predominance of small, dense, and cholesterol-poor LDLs24. Therefore, LDL cholesterol may not accurately reflect the concentration of LDL particles or their effect on CV risk24–26. Discordance causes LDL-C to underestimate the true risk of CVD, while in these conditions, ApoB more accurately reflects the causal effect of LDLs and other atherogenic lipoproteins on CV risk.4,13,22,24,27–29. Furthermore, using ApoB instead of LDL-C for follow-up in patients with FCHL may also improve treatment adherence and patient outcomes. By focusing on a biomarker that reflects the number of atherogenic lipoprotein particles, clinicians can better tailor their therapy to individual patients and monitor their response to treatment more closely. Using ApoB as a goal parameter may lead to better outcomes, fewer adverse events, and improved patient satisfaction.
Until we have agreed upon guidelines for ApoB target goals, the use of ApoB for improving LDL-C estimation by the eS-LDL-C equation could be useful in FCHL. The difference, however, between S-LDL-C and eS-LDL-C was relatively small so the small improvement in LDL-C estimation may not be sufficient to justify the extra cost of ApoB testing. The eSLDL-C, however, did result in less errors that would change the clinical management of patients, supporting its possible use for at least when making lipid-medication changes. Our results also clearly show that among all the equations tested that F-LDL-C offers very little advantage over the other equations when TG are elevated. Interestingly, it had, however, the best correlation to the reference method for the hypercholesterolemic phenotype. Perhaps the higher cholesterol to TG ratio in this subgroup of FCHL was not frequently present in the populations used to create the other equations and hence the newer equations did not work as well for this phenotype. If a larger FCHL population was available, it may be possible to develop a separate new equation just for this particular type of FCHL or for FCHL in general, but the downside is that it would increase the complexity of estimating LDL-C. The Martin equation did appear by most metrics to be superior to the Friedewald equation particularly for hypertriglyceridemic samples but not to either the original or enhanced Sampson equation as has been previously described11.
Strengths and Limitations:
One of the most important strengths of this study is that we used the gold standard for VLDL-C measurement, VLDL-C measured by ultracentrifugation, and evaluated the performance of these equations compared to VLDL-C and LDL-C in a Mexican population with high variability in lipid profiles. The novelty of this study is that the es-VLDL-C has never been tested in other population than type III dyslipidemia, but in this study we proved that it further improves the estimation of LDL-C. One limitation is that a non-direct method was used to measure LDL-C or remnants. To reduce this bias, LDL-C was calculated using VLDL-C measured by ultracentrifugation to approximate a gold standard for comparative evaluations. The relatively small number of participants is also a limitation. This assessment is especially important in-patient follow-up. However, the new e-Sampson formula offers a small improvement in LDL-C estimation, which does not justify it’s cost for this purpose, as well as better concordance with treatment goals to reduce cardiovascular risk. There is a need for further research to validate these findings in larger, more diverse populations.
Conclusions:
In conclusion, the adapted e-Sampson formula, from eS-VLDL-C, offers an improvement in more accurate LDL-C estimation but comparable to original Sampson. The routine use of either eS-LDL-C, if ApoB available, or S-LDL-C perform better with actual LDL-C levels through different phenotypes. Evaluation in isolated hypercholesterolemia is equally comparable between all formulas. However, in mixed dyslipidemia, either e-Sampson or original Sampson offer an improvement in both LDL-C estimation and the appropriate interpretation of treatment goals. To ensure accurate cardiovascular risk assessment, it is recommended to discontinue the routine use of the Friedewald’s formula and instead choose a more reliable LDL-C formula such as Sampson or eSampson which demonstrate superior performance.
Highlights:
Fluctuation of TG in FCHL may make the accurate calculation of LDL-C difficult
The most common way of reporting LDL-C is through Friedewlad’s equation which it’s accuracy is limited when TG are >150mg/dL
Other formulas as Martin’s, Sampson’s and Enhanced Sampson’s offer a better accuracy over Friedewald’s
To ensure accurate cardiovascular risk assessment, it is recommended to discontinue the routine use of the Friedewald’s formula and instead choose a more reliable LDL-C formula such as Sampson or eSampson
Sources of Funding
RZ receives direct funding from Fundación para la Salud y la Educación Salvador Zubirán and Asociación Ale. AV, FD, IC and CA have no source of funding. AR and MS were supported from intramural DIR funds from the National Heart, Lung and Blood Institute at the National Institutes of Health.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Disclosures
Authors have nothing to disclose.
Declaration of interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Data Statement
Data that support the findings of this study are available from the corresponding author, CA, upon reasonable request.
References
- 1.Ference BA, Ginsberg HN, Graham I, Ray KK, Packard CJ, Bruckert E, Hegele RA, Krauss RM, Raal FJ, Schunkert H, Watts GF, Borén J, Fazio S, Horton JD, Masana L, Nicholls SJ, Nordestgaard BG, van de Sluis B, Taskinen M-R, Tokgözoglu L, Landmesser U, Laufs U, Wiklund O, Stock JK, Chapman MJ, Catapano AL. Low-density lipoproteins cause atherosclerotic cardiovascular disease. 1. Evidence from genetic, epidemiologic, and clinical studies. A consensus statement from the European Atherosclerosis Society Consensus Panel. Ear Heart J. 2017;38:2459–2472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Austin MA, Breslow JL, Hennekens CH, Buring JE, Willett WC, Krauss RM. Low-density lipoprotein subclass patterns and risk of myocardial infarction. JAMA. 1988;260:1917–1921. [PubMed] [Google Scholar]
- 3.Friedewald WT, Levy RI, Fredrickson DS. Estimation of the concentration of low-density lipoprotein cholesterol in plasma, without use of the preparative ultracentrifuge. Clin Chem. 1972;18:499–502. [PubMed] [Google Scholar]
- 4.Langlois MR, Chapman MJ, Cobbaert C, Mora S, Remaley AT, Ros E, Watts GF, Borén J, Baum H, Bruckert E, Catapano A, Descamps OS, von Eckardstein A, Kamstrup PR, Kolovou G, Kronenberg F, Langsted A, Pulkki K, Rifai N, Sypniewska G, Wiklund O, Nordestgaard BG, European Atherosclerosis Society (EAS) and the European Federation of Clinical Chemistry and Laboratory Medicine (EFLM) Joint Consensus Initiative. Quantifying Atherogenic Lipoproteins: Current and Future Challenges in the Era of Personalized Medicine and Very Low Concentrations of LDL Cholesterol. A Consensus Statement from EAS and EFLM. Clin Chem. 2018;64:1006–1033. [DOI] [PubMed] [Google Scholar]
- 5.Martin SS, Blaha MJ, Elshazly MB, Toth PP, Kwiterovich PO, Blumenthal RS, Jones SR. Comparison of a novel method vs the Friedewald equation for estimating low-density lipoprotein cholesterol levels from the standard lipid profile. JAMA. 2013;310:2061–2068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sampson M, Ling C, Sun Q, Harb R, Ashmaig M, Warnick R, Sethi A, Fleming JK, Otvos JD, Meeusen JW, Delaney SR, Jaffe AS, Shamburek R, Amar M, Remaley AT. A New Equation for Calculation of Low-Density Lipoprotein Cholesterol in Patients With Normolipidemia and/or Hypertriglyceridemia. JAMA Cardiol. 2020;5:540–548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bello-Chavolla OY, Kuri-García A, Ríos-Ríos M, Vargas-Vázquez A, Cortés-Arroyo JE, Tapia-González G, Cruz-Bautista I, Aguilar-Salinas CA. FAMILIAL COMBINED HYPERLIPIDEMIA: CURRENT KNOWLEDGE, PERSPECTIVES, AND CONTROVERSIES. Rev Investig Clin Organo Hosp Enfermedades Nutr. 2018;70:224–236. [DOI] [PubMed] [Google Scholar]
- 8.Cruz-Bautista I, Mehta R, Cabiedes J, García-Ulloa C, Guillen-Pineda LE, Almeda-Valdés P, Cuevas-Ramos D, Aguilar-Salinas CA. Determinants of VLDL composition and apo B-containing particles in familial combined hyperlipidemia. Clin Chim Acta Int J Clin Chem. 2015;438:160–165. [DOI] [PubMed] [Google Scholar]
- 9.Grundy SM, Stone NJ, Bailey AL, Beam C, Birtcher KK, Blumenthal RS, Braun LT, de Ferranti S, Faiella-Tommasino J, Forman DE, Goldberg R, Heidenreich PA, Hlatky MA, Jones DW, Lloyd-Jones D, Lopez-Pajares N, Ndumele CE, Orringer CE, Peralta CA, Saseen JJ, Smith SC, Sperling L, Virani SS, Yeboah J. 2018 AHA/ACC/AACVPR/AAPA/ABC/ACPM/ADA/AGS/APhA/ASPC/NLA/PCNA Guideline on the Management of Blood Cholesterol: A Report of the American College of Cardiology/American Heart Association Task Force on Clinical Practice Guidelines. Circulation. 2019;139:e1082–e1143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sampson M, Wolska A, Meeusen JW, Donato LJ, Jaffe AS, Remaley AT. Identification of Dysbetalipoproteinemia by an Enhanced Sampson-NIH Equation for Very Low-Density Lipoprotein-Cholesterol. Front Genet. 2022;13:935257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sampson M, Wolska A, Cole J, Zubirán R, Otvos JD, Meeusen JW, Donato LJ, Jaffe AS, Remaley AT. Accuracy and Clinical Impact of Estimating Low-Density Lipoprotein-Cholesterol at High and Low Levels by Different Equations. Biomedicines. 2022;10:3156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Boot CS, Luvai A, Neely RDG. The clinical and laboratory investigation of dysbetalipoproteinemia. Crit Rev Clin Lab Sci. 2020;57:458–469. [DOI] [PubMed] [Google Scholar]
- 13.Sniderman AD, Lamarche B, Contois JH, de Graaf J. Discordance analysis and the Gordian Knot of LDL and non-HDL cholesterol versus apoB. Curr Opin Lipidol. 2014;25:461–467. [DOI] [PubMed] [Google Scholar]
- 14.Lazarte J, Hegele RA. Pediatric Dyslipidemia-Beyond Familial Hypercholesterolemia. Can J Cardiol. 2020;36:1362–1371. [DOI] [PubMed] [Google Scholar]
- 15.Vargas-Vázquez A, Bello-Chavolla OY, Antonio-Villa NE, Mehta R, Cruz-Bautista I, Aguilar-Salinas CA. Comparative assessment of LDL-C and VLDL-C estimation in familial combined hyperlipidemia using Sampson’s, Martin’s and Friedewald’s equations. Lipids Health Dis. 2021;20:46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Naukkarinen J, Ehnholm C, Peltonen L. Genetics of familial combined hyperlipidemia. Curr Opin Lipidol. 2006;17:285–290. [DOI] [PubMed] [Google Scholar]
- 17.Martin SS, Blaha MJ, Elshazly MB, Brinton EA, Toth PP, McEvoy JW, Joshi PH, Kulkarni KR, Mize PD, Kwiterovich PO, Defilippis AP, Blumenthal RS, Jones SR. Friedewald-estimated versus directly measured low-density lipoprotein cholesterol and treatment implications. J Am Coll Cardiol. 2013;62:732–739. [DOI] [PubMed] [Google Scholar]
- 18.Meeusen JW, Snozek CL, Baumann NA, Jaffe AS, Saenger AK. Reliability of Calculated Low-Density Lipoprotein Cholesterol. Am J Cardiol. 2015;116:538–540. [DOI] [PubMed] [Google Scholar]
- 19.Mehta R, Reyes-Rodríguez E, Yaxmehen Bello-Chavolla O, Guerrero-Díaz AC, Vargas-Vázquez A, Cruz-Bautista I, A Aguilar-Salinas C. Performance of LDL-C calculated with Martin’s formula compared to the Friedewald equation in familial combined hyperlipidemia. Atherosclerosis. 2018;277:204–210. [DOI] [PubMed] [Google Scholar]
- 20.Balling M, Afzal S, Varbo A, Langsted A, Davey Smith G, Nordestgaard BG. VLDL Cholesterol Accounts for One-Half of the Risk of Myocardial Infarction Associated With apoB-Containing Lipoproteins. J Am Coll Cardiol. 2020;76:2725–2735. [DOI] [PubMed] [Google Scholar]
- 21.Shapiro MD, Tavori H, Fazio S. PCSK9: From Basic Science Discoveries to Clinical Trials. Circ Res. 2018;122:1420–1438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Pencina MJ, D’Agostino RB, Zdrojewski T, Williams K, Thanassoulis G, Furberg CD, Peterson ED, Vasan RS, Sniderman AD. Apolipoprotein B improves risk assessment of future coronary heart disease in the Framingham Fleart Study beyond LDL-C and non-FIDL-C. EurJ Prev Cardiol. 2015;22:1321–1327. [DOI] [PubMed] [Google Scholar]
- 23.Pei W, Sun Y, Rou W, Zu Q, Li Y, Zhang C, Dai J, Jia Y, Lu Z, Wu X, Liu L, Hui R. [Apolipoprotein B is associated with metabolic syndrome in Chinese pedigrees with familial hyperlipidemia]. Zhonghua Yi Xue Za Zhi. 2005;85:313–317. [PubMed] [Google Scholar]
- 24.Cantey EP, Wilkins JT. Discordance between lipoprotein particle number and cholesterol content: an update. Curr Opin Endocrinol Diabetes Obes. 2018;25:130–136. [DOI] [PubMed] [Google Scholar]
- 25.Sniderman AD, Thanassoulis G, Glavinovic T, Navar AM, Pencina M, Catapano A, Ference BA. Apolipoprotein B Particles and Cardiovascular Disease: A Narrative Review. JAMA Cardiol. 2019;4:1287–1295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Welsh C, Celis-Morales CA, Brown R, Mackay DF, Lewsey J, Mark PB, Gray SR, Ferguson LD, Anderson JJ, Lyall DM, Cleland JG, Jhund PS, Gill JMR, Pell JP, Sattar N, Welsh P. Comparison of Conventional Lipoprotein Tests and Apolipoproteins in the Prediction of Cardiovascular Disease. Circulation. 2019;140:542–552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pischon T, Girman G, Sacks FM, Rifai N, Stampfer MJ, Rimm EB. Non-high-density lipoprotein cholesterol and apolipoprotein B in the prediction of coronary heart disease in men. Circulation. 2005;112:3375–3383. [DOI] [PubMed] [Google Scholar]
- 28.Mora S, Buring JE, Ridker PM. Discordance of low-density lipoprotein (LDL) cholesterol with alternative LDL-related measures and future coronary events. Circulation. 2014;129:553–561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lawler PR, Akinkuolie AO, Ridker PM, Sniderman AD, Buring JE, Glynn RJ, Chasman DI, Mora S, Discordance between Circulating Atherogenic Cholesterol Mass and Lipoprotein Particle Concentration in Relation to Future Coronary Events in Women. Clin Chem. 2017;63:870–879. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data that support the findings of this study are available from the corresponding author, CA, upon reasonable request.


