Technical note: Impact of Dose Voxel Kernel (DVK) values on dosimetry estimates in ¹⁷⁷Lu and ⁹⁰Y Radiopharmaceutical Therapy (RPT) applications

Abstract

Background:

Radiopharmaceutical Therapy (RPT) is an increasingly adopted modality for treating cancer. There is evidence that the optimization of the treatment based on dosimetry can improve outcomes. However, standardization of the clinical dosimetry workflow still represents a major effort. Among the many sources of variability, the impact of using different Dose Voxel Kernels (DVKs) to generate absorbed dose (AD) maps by convolution with the time-integrated activity (TIA) distribution has not been systematically investigated.

Purpose:

This study aims to compare DVKs and assess the differences in the ADs when convolving the same TIA map with different DVKs.

Methods:

DVKs of 3×3×3 mm³ sampling - nine for ¹⁷⁷Lu, nine for ⁹⁰Y - were selected from those most used in commercial/free software or presented in prior publications. For each voxel within a 11×11×11 matrix, the coefficient of variation (CoV) and the percentage difference between maximum and minimum values (% maximum difference) were calculated. The total absorbed dose per decay (SUM), calculated as the sum of all the voxel values in each kernel, was also compared. Publicly available quantitative SPECT images for two patients treated with ¹⁷⁷Lu-DOTATATE and PET images for two patients treated with ⁹⁰Y-microspheres were used, including organs at risk (¹⁷⁷Lu: kidneys; ⁹⁰Y: liver and healthy liver) and tumors’ segmentations. For each patient, the mean AD to the volumes of interest (VOIs) was calculated using the different DVKs, the same TIA map and the same software tool for dose convolution, thereby focusing on the DVK impact. For each VOI, the % maximum difference of the mean AD between maximum and minimum values was computed.

Results:

The CoV (% maximum difference) in voxels of normalized coordinates [0,0,0], [0,1,0] and [0,1,1] were 5%(21%), 9%(35%) and 10%(46%) for the ¹⁷⁷Lu DVKs. For the case of ⁹⁰Y, these values were 2%(9%), 4%(14%) and 4%(16%). The CoV (% maximum difference) for SUM was 9%(33%) for ¹⁷⁷Lu, and 4%(15%) for ⁹⁰Y. The variability of the mean tumor and organ AD was up to 19% and 15% in ¹⁷⁷Lu-DOTATATE and ⁹⁰Y-microspheres patients, respectively.

Conclusions:

This study showed a considerable AD variability due exclusively to the use of different DVKs. A concerted effort by the scientific community would contribute to decrease these discrepancies, strengthening the consistency of AD calculation in RPT.

Introduction and background

In Radiopharmaceutical Therapy (RPT), three-dimensional (3D) voxel-level internal dosimetry is receiving increasing attention, driven by the interest in estimating not only the average absorbed dose (AD) to volumes of interest (VOIs), but also the AD non-uniformity due to the non-uniform spatial distribution of activity. The starting point for 3D voxel-level dosimetry is 3D voxel-level activity maps, derived from quantitative tomographic images (i.e. PET or SPECT scans) acquired at single or multiple time-points. Following voxel-level time-integration techniques, a time-integrated activity (TIA) map can be computed and, by means of one of the approaches described below, converted into a 3D AD map¹.

To date, three different approaches are available for AD map calculation²:

1. Local Energy Deposition (LED), which assumes the energy released in a voxel of the TIA map to be absorbed within the same voxel. LED typically includes the contribution of charged particles and ignores the one of photons;

2. Convolution of a Dose Voxel Kernel (DVK) with a TIA map, where a DVK is defined as a 3D voxel matrix representing the mean AD to a target voxel per decay event in the central source voxel, both of which are contained in an infinite homogeneous medium. DVKs are sometimes referred to also as Voxel S-factors (VSFs) or Voxel S-Values (VSVs);

3. Direct Monte Carlo (MC) simulation of the radionuclide decays that uses the distribution from a TIA map and tracks all the transport and interactions between the emitted radiation and the patient’s body where different materials are modeled from CT imaging.

Direct MC radiation transport is considered, at least in principle, the most accurate and personalized approach for internal dosimetry as it takes into account the heterogeneity of the tissue density and composition. Because MC simulations require relevant computational resources and expertise, however, LED and convolution algorithms are more frequently adopted for clinical dosimetry³.

DVKs are generally calculated exploiting MC simulations⁴. However, different MC codes and different processes - e.g. direct MC simulation, MC-based volume integration of a dose-point kernel (DPK), which is the radial distribution of the AD per decay event due to an isotropic point source located inside a virtually infinite and homogeneous absorbing medium, and MC-derived analytical methods - have been adopted by different authors to generate the actual DVKs from simulations. Even if some sets of DVKs have been compared to each other⁵, to our knowledge no specific investigation of the impact of using different DVKs on the AD calculation has been carried out yet in a systematic manner.

The aim of this work is to assess the differences in the ADs when convolving the same TIA map with different DVKs. This has been done using a set of 18 commonly adopted or recently developed DVKs for ¹⁷⁷Lu and ⁹⁰Y and using imaging data from patients treated with ¹⁷⁷Lu-DOTATATE and with ⁹⁰Y-microspheres.

Materials and methods

Dose voxel kernels

We used a total of 18 different DVKs with details given in Tables 1 (for ¹⁷⁷Lu) and 2 (for ⁹⁰Y). For ¹⁷⁷Lu, nine DVKs with voxel sizes of 3×3×3mm³ and matrix sizes ranging from 11×11×11 to 275×275×275 were compared. Among them, five were generated by direct MC simulation (Lanconelli⁶, Pistone⁷, Salvat, Tranel and UMICH DPM), two were derived from DPKs (Graves⁸ and Vergara⁹), and two were computed based on analytical methods (Amato¹⁰ and Pistone_AM⁷). For ⁹⁰Y, nine DVKs with voxel sizes of 3×3×3 mm³ and matrix sizes from 11×11×11 to 17×17×17 were selected. Six of the selected ⁹⁰Y DVKs were computed by direct MC simulation (Bolch¹¹, Lanconelli⁶, Pistone, Salvat, Tranel and UMICH DPM), two starting from a DPK (Graves⁸ and Vergara⁹) and one with an analytical method (Amato¹⁰). Note that because ⁹⁰Y is a pure beta emitter (i.e. there are no gamma emissions) and given that the range of its beta particles in tissue (maximum range in soft tissue: 11 mm) is much shorter than gammas, the kernel matrix size of ⁹⁰Y that accounts for a complete energy deposition of the emitted particles is smaller than for ¹⁷⁷Lu.

Table 1:

Details about the computation methods and setting adopted for all the ¹⁷⁷Lu DVKs employed in the present study.

177Lu DVKs	Matrix size	Material composition	Material density	Decay data	Beta spectrum	Calculation method	MC code for DVK or DPK generation	Number of simulated particles	Energy/range cutoff	Surrounding medium
Amato 10	11×11×11	Soft tissue	1.04 g/cm3	Radar17	Radar*17	Analytical method	Geant4 9.1	10^8	10 μm	Infinite volume
Graves 8	275×275×275	Water	1.00 g/cm3	NNDC18	Radar17	MC volume integration of DPKs	MCNP 6.2	10^6 per emission type	1 keV	Sphere of 2 m radius for DPK
Lanconelli 6	11×11×11	Soft tissue	1.04 g/cm3	Radar17§	Radar**17	Direct MC simulation	DOSXYZnrc (EGSnrc)	2.5*10^7	1 keV	Cubical region with side 16.5 cm
Pistone 7	15×15×15	Soft tissue	1.03 g/cm3	Radar17	Radar17	Direct MC simulation	GAMOS 6.2.0	10^9	100 μm	Cubical region with side 50 cm
Pistone_AM 7	15×15×15	Soft tissue	1.03 g/cm3	Radar17	Radar17	Analytical method	GAMOS 6.2.0	10^9	100 μm	Cubical region with side 50 cm
Salvat †	11×11×11	Soft tissue	1.00 g/cm3	Nucleide19	García-Toraño et al.20	Direct MC simulation	PENELOPE (version 2018)21	3*10^8	5 keV (electrons), 1 keV (photons)	Sphere of 20 cm radius
Tranel †	15×15×15	Water	1.00 g/cm3	ENSDF22	ENSDF22	Direct MC simulation	GATE 9.0	10^8	10 μm	Cubical region with side 1 m
Vergara 9	11×11×11	Soft tissue‡	1.04 g/cm3	ENSDF22	ENSDF22	MC volume integration of DPKs	GATE (version not specified)	10^8	1 μm	Cubical region with side 2.1 m
UMICH DPM †	267×267×267	Soft tissue	1.00 g/cm3	NuDat 3.023	BetaShape24	Direct MC simulation	Dose Planning Method (DPM)25	10^8 (electrons), 4*10^10 (photons)	20 keV (electrons), 4 keV (photons)	Cubical region with side 267×3mm

^†Published within this paper

^‡DVK computed by MC volume integration of DPKs in water, converted into soft tissue DVK by the Cross approximation²⁶.

^*merge of monoenergetic e- DVKs, binning: 25 keV

^**merge of monoenergetic e- DVKs, binning: 10 keV

^§Characteristic x-rays and mono-energetic excluded

Comparison of DVKs

For each voxel in a 11×11×11 matrix, the coefficient of variation (CoV) – defined as the standard deviation divided by the mean - and the percentage difference between the maximum and the minimum values across all the selected DVKs normalized by the minimum (% maximum difference) were computed. In addition, normalized DVKs were generated by dividing each DVK value by the average value obtained with all the DVKs. The total absorbed dose per decay (SUM), calculated as the sum of all the voxel values in each kernel, was also compared. Given a DVK with matrix size N×N×N, SUM was computed as:

$$SUM=\left[0\text{,}\hspace{0.17em}0\text{,}\hspace{0.17em}0\right]+{{\displaystyle \sum }}_{i=i}^{N}2\ast \left[i\text{,}\hspace{0.17em}0\text{,}\hspace{0.17em}0\right]+{{\displaystyle \sum }}_{j=1}^{N}2\ast \left[0\text{,}\hspace{0.17em}j\text{,}\hspace{0.17em}0\right]+{{\displaystyle \sum }}_{k=1}^{N}2\ast \left[0\text{,}\hspace{0.17em}0\text{,}\hspace{0.17em}k\right]+{{\displaystyle \sum }}_{i=1}^N{{\displaystyle \sum }}_{j=1}^{N}4\ast \left[i\text{,}\hspace{0.17em}j\text{,}\hspace{0.17em}0\right]\hspace{0.17em}+{{\displaystyle \sum }}_{i=1}^N{{\displaystyle \sum }}_{k=1}^{N}4\ast \left[i\text{,}\hspace{0.17em}0\text{,}\hspace{0.17em}k\right]+{{\displaystyle \sum }}_{j=1}^N{{\displaystyle \sum }}_{k=1}^{N}4\ast \left[0\text{,}\hspace{0.17em}j\text{,}\hspace{0.17em}k\right]+{{\displaystyle \sum }}_{i=1}^N{{\displaystyle \sum }}_{j=1}^N{{\displaystyle \sum }}_{k=1}^{N}8\ast \left[i\text{,}\hspace{0.17em}j\text{,}\hspace{0.17em}k\right]$$

All the DVKs used in the study are available in the Supplemental Material.

Comparison of ADs on Patient Data

Quantitative post-therapy ¹⁷⁷Lu SPECT/CT images of two patients treated with ¹⁷⁷Lu-DOTATATE¹² and ⁹⁰Y PET/CT images of two patients treated with ⁹⁰Y-microspheres¹³ were used. These data are publicly available in the University of Michigan Deep Blue Data Repository.^12,14 The ¹⁷⁷Lu-DOTATATE data is the same used in the Society of Nuclear Medicine ¹⁷⁷Lu Dosimetry Challenge.^14,15 Segmentations of organs at risk (OARs) - kidneys¹⁶ for the two ¹⁷⁷Lu-DOTATATE patients, and whole and normal liver for the two ⁹⁰Y-microspheres patients – and tumors were also provided ^14,15. For each patient, the AD maps were calculated using the different DVKs coupled with the same dosimetry software, MIM SurePlan MRT (MIM Software, USA), thereby focusing on the impact specifically of the DVK. Before performing the dosimetry, all the selected DVKs were manually imported into the software. For ¹⁷⁷Lu, SPECT images acquired at four different time-points were registered and segmentations were propagated from the reference time-point (24 h) to the others. Next, ¹⁷⁷Lu time-activity curves generated for each VOI were fitted to a sum of exponentials defined according to the Akaike Information Criterion. After the time-integration at the VOI level, ¹⁷⁷Lu TIA maps – one for each patient - were derived from the reference activity map by scaling the activity in each voxel by the ratio between the TIA computed at the VOI level to the total activity in the VOI corresponding to the voxel considered. For ⁹⁰Y, instead, a time-integration at the voxel-level considering only the physical decay was performed, as is standard because the microspheres do not redistribute. The resulting SPECT or PET-derived TIA maps, resampled to cubic voxel of 3 mm size, were converted into AD maps by means of a Fast Fourier Transform convolution with each of the selected DVKs. Finally, the AD maps were divided by a CT-based density map – also resampled to the DVK resolution – and manually multiplied by the mass density of the medium in which the DVKs were calculated to account for the difference between the latter and the actual tissue density. Excluding this last step, there was no manual intervention in the steps leading to the calculation of AD. For OARs and tumors, mean AD, D10 and D90 (i.e. the minimum AD to 10% and 90% of the volume, respectively) were computed. The average of the mean AD, D10 and D90 obtained with all the DVKs were calculated as well as the CoV and the % maximum difference. To further illustrate the variability among different DVKs, normalized mean AD were generated by dividing each mean AD by the average from all ADs.

Results

Comparison of DVKs

Figure 1 and 2 (top panels) show the selected ¹⁷⁷Lu and ⁹⁰Y DVKs as a function of the distance from the source voxel (intended as the distance from the geometric center of the source voxel, here and in the following), respectively. For ¹⁷⁷Lu, the source voxel of the DVK contributes to almost all its energy deposition, the maximum beta particle range in tissue being 2 mm. For ⁹⁰Y, in comparison, the contribution at voxels away from the source is more significant, due to the higher beta particle energy corresponding to a maximum range in tissue of 11 mm. Figure 1 and 2 (bottom panels) show the normalized DVKs as function of the distance from the source voxel. The CoV and the % maximum difference are plotted in Supplemental Fig S1.

Figure 1:

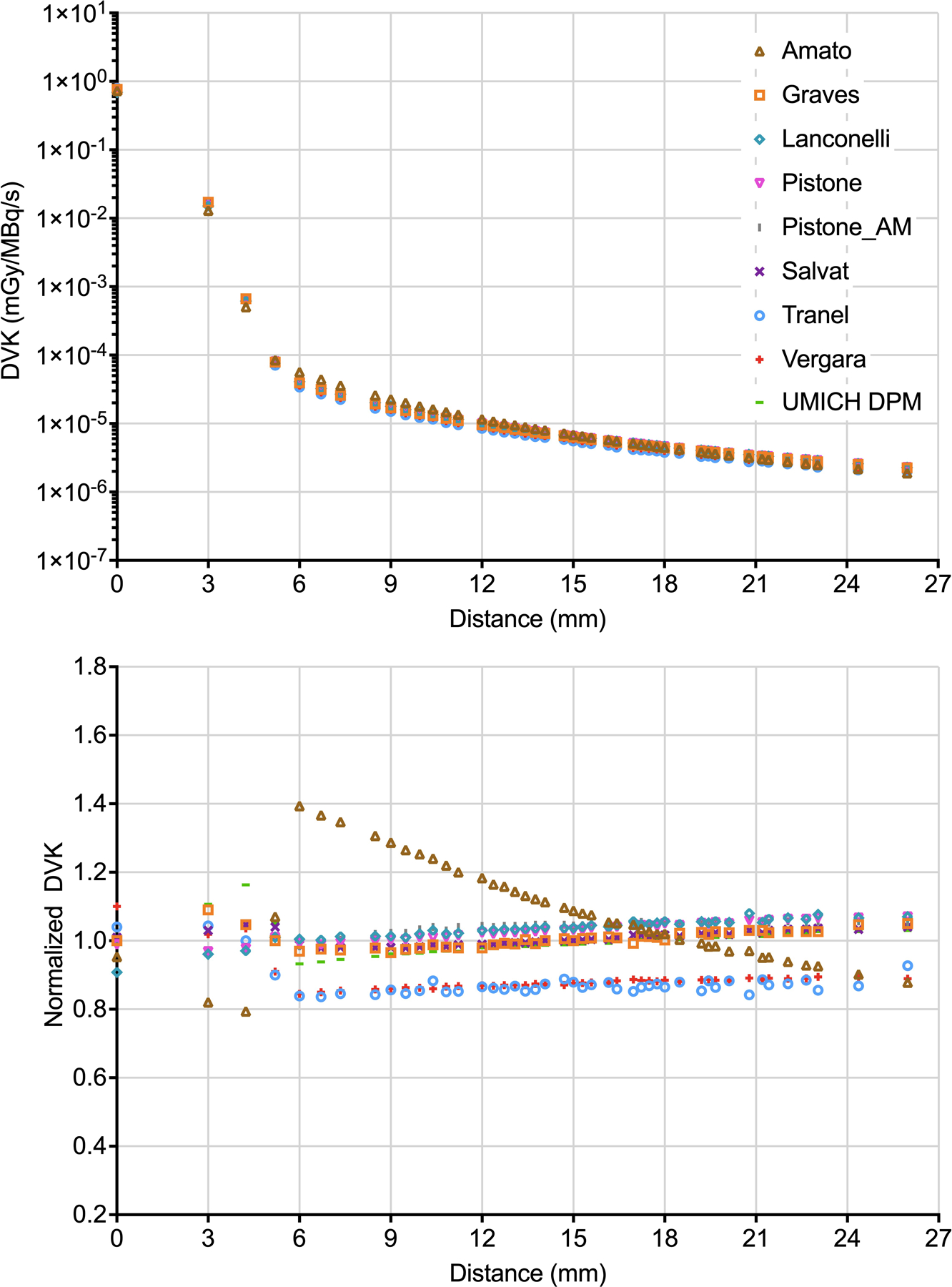
Top panel - ¹⁷⁷Lu DVKs as a function of the distance from the source voxel. Bottom panel - normalized ¹⁷⁷Lu DVKs as a function of the distance from the source voxel. For better visualization, the values at different voxels but corresponding to the same distance have been averaged.

Figure 2:

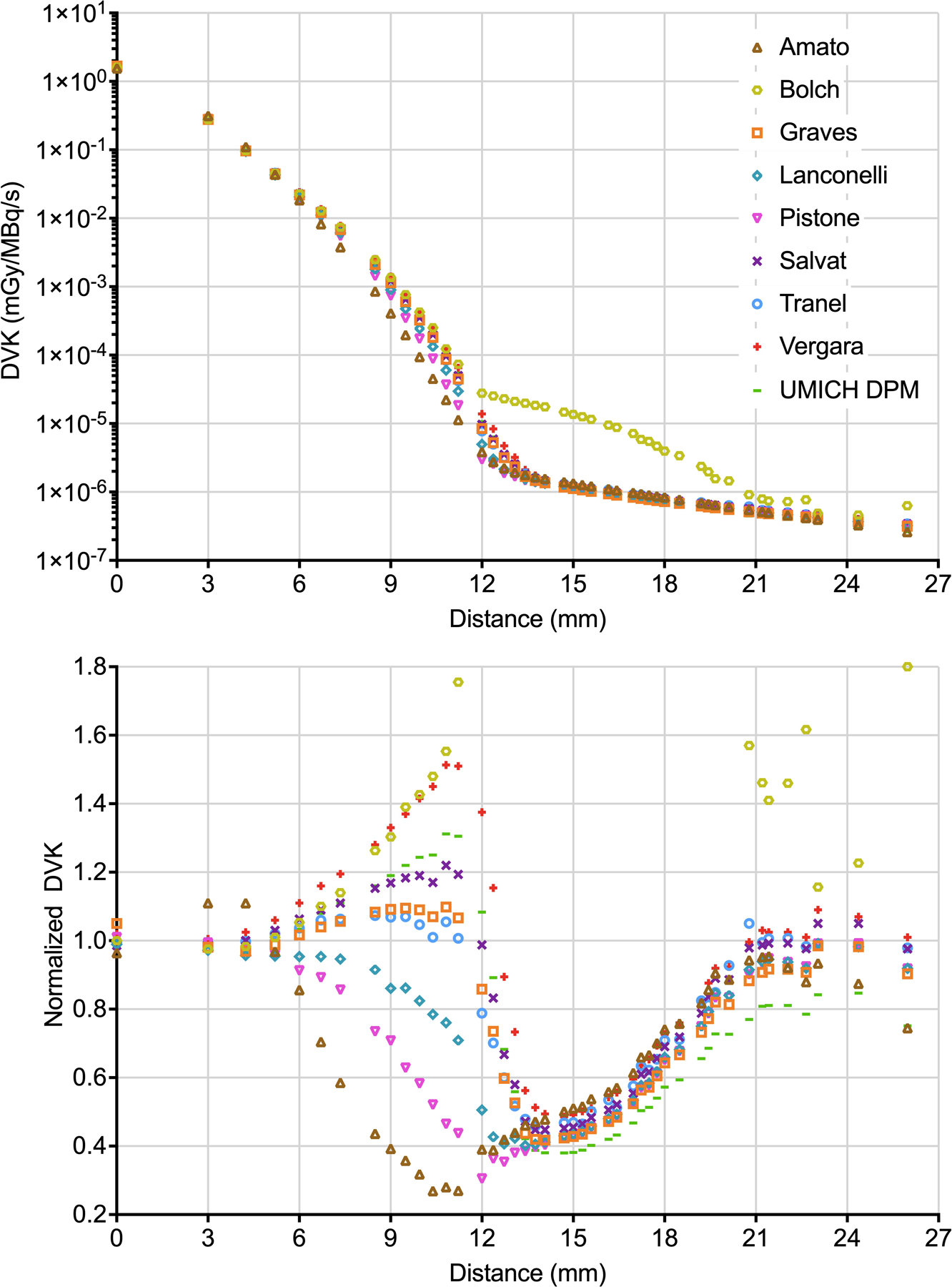
Top panel - ⁹⁰Y DVKs as a function of the distance from the source voxel. Bottom panel - normalized ⁹⁰Y DVKs as a function of the distance from the source voxel (part of data from Bolch are out of range). For better visualization, the values at different voxels but corresponding to the same distance have been averaged.

For ¹⁷⁷Lu, CoV (% maximum difference) in voxels of normalized coordinates [0,0,0] (central voxel), [0,0,1] (3 mm from the center) and [0,1,1] (4.2 mm from the center) - which are the voxels giving the maximum contribution to the AD - were 5% (21%), 9% (35%), 10% (46%), respectively. For SUM, results were 9% (33%). Maximum differences were attributable to Lanconelli/Vergara (source voxel), Amato/UMICH DPM (voxels [0,0,1] and [0,1,1]) and Lanconelli/UMICH DPM (SUM). For ⁹⁰Y, CoV (% maximum difference) results were 2% (9%), 4% (14%) and 4% (16%) at voxels of coordinates [0,0,0], [0,0,1] and [0,1,1], respectively; 4% (15%) in SUM. In this case, Amato/Graves provides the maximum difference in the source voxel, Lanconelli/Amato in the two diagonal voxels and Lanconelli/Vergara in SUM.

Comparison of ADs on Patient Data

For each patient, mean AD, D10 and D90 obtained with each selected DVK are provided in the Supplemental Tables S1–4. Average, CoV and % maximum difference of mean AD, D10 and D90 to kidneys (¹⁷⁷Lu), liver/healthy liver (⁹⁰Y) and tumors (¹⁷⁷Lu and ⁹⁰Y) are given in Table 3. Normalized mean AD are shown in Figure 3. For each VOI, maximum differences were attributable to Lanconelli/Vergara for both ¹⁷⁷Lu and ⁹⁰Y patients.

Table 3:

Average, CoV and % maximum difference of mean AD, D10 and D90 to OARs and tumors in patients treated with a) ¹⁷⁷Lu and b) ⁹⁰Y.

a)	177Lu DOTATATE : Patient 4				177Lu DOTATATE : Patient 6
	Right Kidney	Left Kidney	Tumor 1	Tumor 2	Right Kidney	Left Kidney	Tumor 1	Tumor 2	Tumor 3	Tumor 4
Mean AD
Average (Gy)	2.63	2.71	19.80	28.50	5.39	3.43	3.19	30.89	3.09	3.73
CoV	5%	5%	5%	5%	5%	5%	5%	5%	5%	5%
% maximum difference	18%	19%	18%	19%	18%	19%	19%	19%	18%	19%
D10
Average (Gy)	3.58	3.66	32.74	41.43	7.58	5.19	4.09	39.08	4.39	6.56
CoV	5%	5%	5%	5%	5%	5%	5%	5%	5%	5%
% maximum difference	18%	18%	19%	19%	19%	19%	19%	19%	18%	19%
D90
Average (Gy)	1.56	1.64	7.84	13.93	2.78	1.79	2.28	21.96	1.70	1.28
CoV	5%	5%	5%	5%	5%	5%	5%	5%	5%	5%
% maximum difference	18%	18%	18%	19%	19%	18%	19%	19%	18%	18%
b)	90Y microspheres: Patient 26						90Y microspheres: Patient 56
	Liver	Healthy liver	Tumor 1	Tumor 2	Tumor 3	Tumor 4	Liver	Healthy liver	Tumor 1	Tumor 2
Mean AD
Average (Gy)	67.57	64.68	220.04	450.38	63.52	673.57	52.59	48.39	432.42	107.22
CoV	4%	4%	4%	4%	4%	4%	4%	4%	4%	4%
% maximum difference	15%	15%	14%	14%	14%	14%	15%	15%	14%	14%
D10
Average (Gy)	180.16	172.58	328.39	727.69	122.25	1051.03	118.56	114.67	681.62	161.56
CoV	4%	4%	4%	4%	4%	4%	4%	4%	4%	4%
% maximum difference	15%	15%	14%	14%	13%	14%	15%	15%	14%	13%
D90
Average (Gy)	0.46	0.44	119.44	176.70	13.83	293.86	0.32	0.32	230.99	40.64
CoV	4%	4%	4%	4%	4%	4%	4%	4%	4%	4%
% maximum difference	14%	15%	15%	17%	17%	16%	16%	16%	16%	17%

Figure 3:

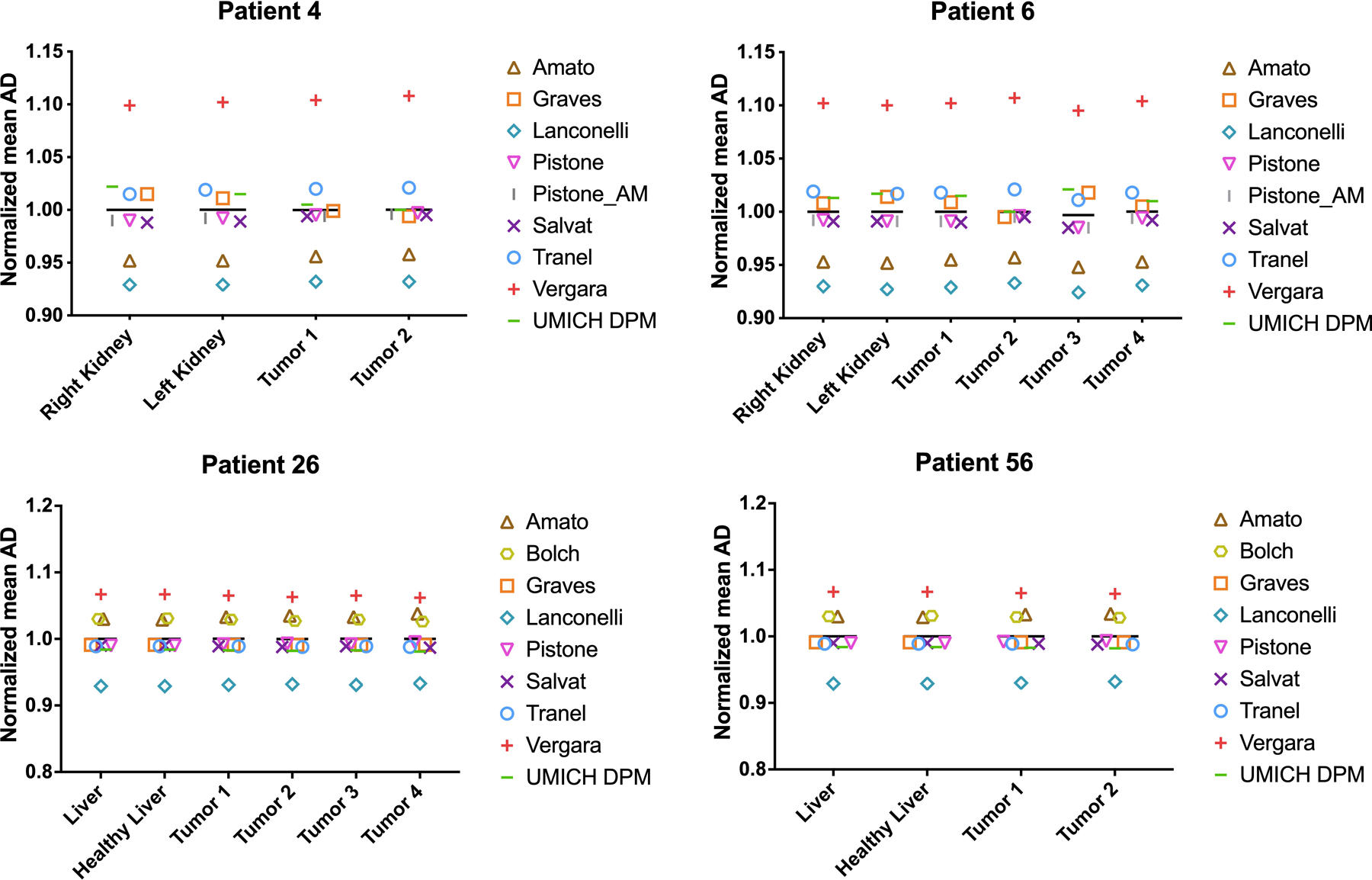
Mean AD from each kernel divided by the average value from all ADs

Discussion

There is increasing evidence that personalized dosimetry could play an important role in the optimization of RPT treatments²⁹. Multicenter trials are therefore essential to explore AD-effect relationships allowing for that optimization³⁰. The clinical dosimetry workflow, however, consists of different tasks, each of which can be performed in multiple ways. This lack of standardization prevents drawing conclusions from multicenter trials because of the discrepancies that might occur in the data among centers. The standardization of the clinical dosimetry workflow following RPT, therefore, still represents a major challenge for physicists in the field¹⁵.

Many commercial and in-house software packages are now available for the computation of the AD and comparisons among them have been performed³¹. Such comparisons, however, usually do not allow a characterization of the variability associated to a single task within the clinical dosimetry workflow, for example the variability associated with the use of different algorithms for image registration or with the method for integrating the time-activity curve. Each software, in fact, offers different and limited solutions to perform the various tasks. The identification of the major sources of variability to be reduced in view of a standardization requires each of them to be isolated and analyzed separately from all the others. In this context, we aim to study the variability introduced when using different DVKs for the computation of the AD via convolution, while being fully aware that this may not be among the major sources of variability affecting the AD.

Our comparison showed that differences in the AD due only to the use of different DVKs are not negligible, with maximum values at the VOI level of 19% and 15% in patients treated with ¹⁷⁷Lu-DOTATATE and ⁹⁰Y-microspheres, respectively. These maximum differences were associated to the same pair of DVKs (Lanconelli/Vergara), perhaps indicating that these DVKs might be less accurate than other DVKs included in this comparison. Observed discrepancies were similar in different patients and VOIs (Figure 3).

Several factors, presented in Table 1, can contribute to the observed differences among the considered DVKs: the calculation method (e.g. direct MC simulation vs MC-based volume integration of DPKs), the nuclear data (e.g. RADAR spectra vs ICRP Publication 107), the definition of material density and composition (e.g. water vs soft tissue) or the MC code (e.g. Geant4 vs Penelope) and simulation parameters, such as the number of primaries, the energy/range cut-off and the physical models. Differences in the kernel size should be also considered. The analysis of these factors and of their impact on the accuracy of DVKs is beyond the scope of this note, as our study was designed to assess variability and not accuracy.

A limitation of this study is that DVKs for only two different radioisotopes (¹⁷⁷Lu and ⁹⁰Y) were included. The inclusion of radionuclides with higher gamma emission probability and energy, e.g. 131I, would have been of interest to investigate the impact of different DVKs on the AD far from the source. Moreover, for each of the included radioisotopes, we considered patients treated with the same type of RPT (peptide receptor radionuclide therapy and radioembolization for ¹⁷⁷Lu and ⁹⁰Y, respectively), which means similar activity distributions. Finally, the results presented in this study are valid for a specific voxel size (3mm). When different voxel sizes are considered, higher or lower differences in the AD calculation can be in principle observed. Based on some limited comparisons already made, however, we can state that for voxel sizes other than 3 mm (range 2–4 mm) differences in the DVKs and mean ADs are generally of the same magnitude as those reported in this study. Exceptionally, however, AD differences up to 50% were found when including ¹⁷⁷Lu Graves’ DVKs for sizes other than 3 mm, although we are aware that recently corrections have been made after the conclusion of our study [https://zenodo.org/record/7596345#.ZBLouHaZOUk]. We therefore recommend always benchmarking the DVK chosen for each specific voxel size, even for already published datasets. As example, the few investigated DVKs for sizes other than 3 mm (2.4 mm and 4 mm) are plotted in Supplemental Fig S2–3.

The RPT dosimetry community should be made aware of the magnitude of the differences in DVKs and the associated variability in patient AD estimates. Since the use of different DVKs is only one of the many possible sources of variability affecting the AD calculation, in fact, the final variability could be considerable and potentially impair the possibility to identify dose-effect relationships from multicenter data. Additional investigations are ongoing to assess the robustness of the various methods for DVK computation and to generate a standardized set of DVKs for the AD calculation.

Conclusions

This study shows substantial differences between DVKs from different sources that propagate into not negligible variability (up to 19%) in patient-specific AD due exclusively to the use of different DVKs. Among the many sources of variability affecting the calculation of the AD, the variability introduced by using different DVKs can be easily reduced by standardization, strengthening the consistency of AD calculation in RPT.

Table2:

Details about the computation methods and setting adopted for all the ⁹⁰Y DVKs employed in the present study.

90Y DVKs	Matrix size	Material composition	Material density	Decay data	Beta spectrum	Calculation method	MC code for DVK or DPK generation	Number of simulated particles	Energy/range cutoff	Surrounding medium
Amato 10	11×11×11	Soft tissue	1.04 g/cm3	Radar17	Radar*17	Analytical method	Geant4 9.1	10^8	10 μm	Infinite volume
Bolch 11	11×11×11	Soft tissue	1.04 g/cm3	Eckerman et al.27,28	Not available	Direct MC simulation	EGS4	Not available	Not available	Cubical region with side 24.3 cm
Graves 8	13×13×13	Water	1.00 g/cm3	NNDC18	Radar17	MC volume integration of DPKs	MCNP 6.2	10^6 per emission type	1 keV	Sphere of 2 m radius for DPK
Lanconelli 6	11×11×11	Soft tissue	1.04 g/cm3	Radar17 §	Radar**17	Direct MC simulation	DOSXYZnrc (EGSnrc)	2.5*10^7	1 keV	Cubical region with side 16.5 cm
Pistone †	15×15×15	Soft tissue	1.03 g/cm3	ENSDF 22	ENSDF 22	Direct MC simulation	GAMOS 6.2.0	10^9	100 μm	Cubical region with side 50 cm
Salvat †	11×11×11	Soft tissue	1.00 g/cm3	Nucleide19	García-Toraño et al.20	Direct MC simulation	PENELOPE (version 2018)21	2*10^8	5 keV (electrons), 1 keV (photons)	Sphere of 20 cm radius
Tranel †	15×15×15	Water	1.00 g/cm3	ENSDF22	ENSDF22	Direct MC simulation	GATE 9.0	10^8	10 μm	Cubical region with side 1 m
Vergara 9	11×11×11	Soft tissue‡	1.04 g/cm3	ENSDF22	ENSDF22	MC volume integration of DPKs	GATE (version not specified)	10^8	1 μm	Cubical region with side 2.1 m
UMICH DPM †	17×17×17	Soft tissue	1.00 g/cm3	NuDat 3.023	BetaShape24	Direct MC simulation	DPM25	10^9	20 keV (electrons), 4 keV (photons)	Cubical region with side 17×3mm

^†Published within this paper

^‡DVK computed by MC volume integration of DPKs in water, converted into soft tissue DVK by the Cross approximation²⁶.

^*merge of monoenergetic e- DVKs, binning: 25 keV

^**merge of monoenergetic e- DVKs, binning: 10 keV

^§Characteristic x-rays and mono-energetic excluded