Abstract
In this study, the focus was to produce xanthan gum from pineapple waste using Xanthomonas campestris. Six machine learning models were employed to optimize fermentation time and key metabolic stimulants (KH2PO4 and NH4NO3). The production of xanthan gum was optimized using two evolutionary optimization algorithms, particle swarm optimization, and genetic algorithm while the importance of input features was ranked using global sensitivity analysis. KH2PO4 was the most important input and was found to be beneficial for xanthan gum production, while a limited amount of nitrogen was needed. The extreme learning machine model was the most adequate for modeling xanthan gum production, predicting a maximum xanthan yield of 10.34 g/l (an 11.9 % increase over the control) at a fermentation time of 3 days, KH2PO4 of 15 g/l, and NH4NO3 of 2 g/l. This study has provided important insights into the intelligent modeling of a biostimulated process for valorizing pineapple waste.
Keywords: Xanthan gum, Stimulant, Pineapple waste, Machine learning, Cross-validation, Optimization
Highlights
-
•
Valorization of pineapple waste for the biosynthesis of xanthan gum was investigated.
-
•
ML models were developed to elucidate xanthan gum production.
-
•
ELM performed best among the investigated ML models.
-
•
The highest xanthan gum yield was obtained as 10.34 g/l.
-
•
Phosphorus and nitrogen supplementation improved xanthan yield by 11.9 %.
1. Introduction
Exopolysaccharides (EPS) are naturally synthesized secondary metabolites that microorganisms produce from a carbon source, with plants and mammals being important sources. Because of their biocompatibility, biodegradability, and increased physical and biological properties, microbial EPS are being explored as a viable replacement for chemical polymers [1]. Over the past few decades, a large variety of microbial EPS have been reported with applications in numerous industries, such as food, medicine, pharmaceuticals, petroleum, environmental remediation, and cosmetics [2,3].
Xanthan gum is a water-soluble EPS, and it is the earliest bacterial EPS to be produced via aerobic fermentation of simple sugars by Xanthomonas campestris in stirred tank fermenters [2]. It is also the second microbial EPS to receive FDA approval for use as a thickener and stabilizer in food additives [4]. The structure of xanthan features a 1,4-linked β-d-glucose backbone, which has trisaccharide side chains at alternate glucose residues containing a glucuronic acid residue bridging two mannose units at the C (3) position. Terminal mannose connects to glucuronic acid via β−1,4 to α-d-mannose through the α-(1,2) linkage. About 50 % of the terminal mannose residues have pyruvic acid linked to the O (4) and O (6) positions, while acetate groups are at the O (6) position of the non-terminal mannose. Internal mannose residues contain 60–70 % acetate, while 30–40 % of terminal mannose bear pyruvate residues [5].
Despite reports of various Xanthomonas spp., such as X. malvacearum, X. phaseoli, and X. carotae, producing xanthan gum, several studies have established the superiority of X. campestris because it can utilize a wide range of carbohydrate substrates to produce xanthan gum [6]. Because of its excellent rheological properties, xanthan gum is used as a stabilizing, thickening, and suspending agent in a variety of industries, including food, medicine, pharmaceuticals, paint, cosmetics, petroleum, and agriculture [7].
For industrial-scale production of xanthan gum, there is an enormous requirement for energy in the form of a carbon source. As much as 70 % of the total xanthan gum production cost has been attributed to the carbon source [8]. For the commercial production of xanthan gum, simple sugars such as glucose and sucrose are typically used as carbon sources. With the reported cost of sourcing glucose and sucrose being in the range of $400–600/ton, it is no surprise to note the expensive cost of producing xanthan gum, which is in the range of $4000–5000/ton [9,10]. The annual production rate of xanthan gum is approximately 30,000 tons [11]. Because of the increasing cost of glucose and sucrose, it is becoming increasingly difficult for this amount to meet the annual demand, which is growing at a rate of 5–10 %. Thus, there is an urgent need to source inexpensive carbon sources that can reduce the current cost of producing xanthan gum.
For better process economics, xanthan gum can be produced from cheaper substrates with high levels of carbon. These substrates will potentially yield more xanthan gum while making the production process more economically competitive [12]. In this context, examples of inexpensive carbon sources that have been reported in the literature include whey [13], sugarcane bagasse [14], cassava bagasse [15], waste bread [16], potato waste [17], and fruit wastes [9,18,19], all geared toward the green biosynthesis of xanthan gum.
Fruit waste, in particular, is a very promising and inexpensive source of carbon for xanthan gum production. They can be easily metabolized by microorganisms to produce secondary metabolites such as xanthan gum. In addition, fruit waste has the advantages of being biocompatible and nontoxic, has abundant availability, and has a very high bioconversion rate [19].
Among fruit wastes, pineapple waste is promising and attractive for the biosynthesis of xanthan gum because it is a rich source of carbohydrates and other nutrients. Beyond that, Nigeria is ranked among the top countries producing pineapple, and thus, there is an opportunity to take advantage of the vast amounts of pineapple waste generated from pineapple consumption and processing [20]. Currently, in Nigeria and most developing countries, pineapple waste has little or no use, and the vast majority is often disposed of inappropriately, thereby constituting a source of environmental concern [21].
Despite the volume of work reported on xanthan gum production in the past decade, very few have reported its industrial-scale production due to its low yield [22]. In this regard, special attention needs to be given to the design of the fermentation process, especially the introduction of certain important nutrients needed for microbial function and stimulation. Beyond that, the nutrient composition of the fermentation medium has an impact on the molecular weight, structure, and chemical composition of the resulting xanthan gum [23]. In this context, the important medium components include nitrogen, potassium, and phosphorus sources such as NH4NO3 and KH2PO4, and this is an area that needs more attention and thus forms the motivation of the current study. Of interest in the current work is the stimulating role of NH4NO3 and KH2PO4 during xanthan gum production. A nitrogen source is important because it promotes the formation of mycelia, and in particular, ammonium salts are preferred as nitrogen sources because they contribute to pH and vegetative growth regulation [24]. On the other hand, KH2PO4 is an important source of potassium and phosphorus and plays an important role in facilitating oxidative phosphorylation, pH regulation, and the formation of the cell wall and coenzyme [25]. The choice of NH4NO3 and KH2PO4 in this study is in alignment with common practices in xanthan gum production, as evidenced by numerous literature sources [8,13,26]. This decision prioritizes simplicity and cost-effectiveness, enhancing the economic viability of producing xanthan gum from pineapple waste on a larger scale. While organic sources and alternative substrates offer merits, the selected inorganic sources ensure a straightforward and standardized approach.
Identifying the optimal levels of these stimulants can result in enhanced xanthan gum yield. A comprehensive assessment of these nutrients will enhance the understanding of the complex interrelationships between xanthan gum production and nutrient availability. This process is usually carried out using the traditional ‘one variable at a time’ approach. However, this method is not efficient because it is cumbersome, prone to error, does not consider the interaction between variables, and does not identify the true optimum. Although the regression-based tool response surface methodology (RSM) was developed to overcome these limitations, the tool itself is limited by its inability to extrapolate outside the design space, identify the global optimum, and adequately model highly nonlinear processes such as fermentation [27].
In recent reports on the biosynthesis of fermentation products, data-driven machine learning (ML) tools have been favored as a result of their highly accurate predictions. They can overcome the previously enumerated limitations of conventional tools and can model highly nonlinear and complex processes [28]. Among the ML tools reported for modeling xanthan gum production, only artificial neural networks (ANN) [[29], [30], [31]] and support vector machines (SVM) [22] have been reported, showing that only a few works have applied ML modeling for xanthan gum production. Recently, state-of-the-art ML tools that are now receiving attention include kernel ridge regression (KRR), extreme gradient boosting (XGB), extreme learning machine (ELM), and random forest (RF) [32]. These ML tools can utilize a small dataset for training, with accompanying excellent generalization capabilities and identification of the global optimum. Beyond that, these tools were chosen based on their established efficiency and effectiveness in modeling bioprocesses, especially fermentation. In selecting multiple ML tools, the aim is to comprehensively evaluate their performance and identify the most suitable one. Comparing their performance will achieve the goal of providing insights into their limitations and strengths, ensuring a robust analysis and scientific rigor. Within the limits of the authors’ literature search, no work was found that adopted these state-of-the-art ML tools in modeling the biosynthesis of xanthan gum, which represents a gap that this work intends to fill. In any case, most studies on xanthan gum biosynthesis that deploy ML do not optimize the structure of the ML tool architecture before data fitting, which often limits the performance of the tools, as seen in previous works that used ML for xanthan gum modeling [29,30,33]. Another area that does not often receive attention during the deployment of ML tools is the assessment of model uncertainty, the contribution of each input feature, and their relative level of importance, even though this can help to derive more insights from the model [34]. Global sensitivity analysis (GSA) is preferred for doing this, and it has advantages over local sensitivity analysis and analysis of variance (ANOVA) because the model uncertainty is attributed to the sources of individual variation from the input features [35]. In this context, GSA will provide useful insights into the important factors that influence xanthan gum production, thus facilitating the development of optimized xanthan gum production strategies.
Thus, in the current work, the focus was to develop ML models for predicting xanthan gum production as a function of three input features. Common ML tools such as ANN and SVM and state-of-the-art ML tools such as KRR, ELM, XGB, and RF were assessed to evaluate the one that offered the best performance in terms of prediction accuracy based on a 3-fold cross-validation for the fermentation dataset. The relative importance of the input features and their contribution to model uncertainty were evaluated using global sensitivity analysis. The ML models were implemented in Python, a very interactive programming language with simple syntax and yet very powerful computation capacity. Python has some obvious advantages compared to conventional software such as MATLAB. Python's variety of libraries makes it superior for developing advanced machine learning models. In addition, most of the machine learning projects currently developed are done with Python, which makes transfer learning possible and seamless [36].
2. Materials and methods
2.1. Collection and preparation of the substrate
Pineapple waste, which is a residue obtained from pineapple waste processing into juice, was collected from a local juice producer in Benin City, Nigeria. The waste consisted of pineapple peels and leftover pulp. The water-soluble nutrient content of the substrate was extracted with 100 ml of water (pH 7) using 100 g of homogenized pineapple waste. The resulting slurry was thoroughly agitated and then allowed to stand for 2 h. The slurry was then transferred to a domestic juicer and intermittently agitated at 1600 rpm for 2 min (twice in 1 min) to achieve homogenization [8]. The homogenized slurry was then filtered using a muslin cloth to remove the residual solids and obtain the water-soluble nutrient fraction. The extract was used as a carbon source to produce xanthan gum.
2.2. Chemical reagents
All reagents used in this study were of analytical grade, which reflects their purity and applicability for assay use. Metal salts such as zinc chloride, magnesium chloride, ammonium nitrate, potassium dihydrogen phosphate, and iron chloride were sourced from a reagent supplier in Onitsha, Nigeria.
2.3. Microorganism and media preparation
Xanthomonas campestris was used as the model microorganism to produce xanthan gum. The active strain of X. campestris isolated from spoilt tomatoes was generously donated by the Department of Microbiology, University of Benin, Nigeria. The isolate was maintained on a glucose-containing nutrient agar slant at 4 °C [8]. The composition of the fermentation medium adopted was previously reported [37]. The medium was made up of citric acid (2.1 g/l), MgCl2 (0.507 g/l), H3BO4 (0.006 g/l), FeCl3·6H2O (0.020 g/l), CaCO3 (0.020 g/l), ZnO (0.006 g/l), and Na2SO4 (0.089 g/l).
2.4. Xanthan gum biosynthesis
The water-soluble nutrient extract was used as the sole source of carbon for producing xanthan gum. It was combined with deionized water in the appropriate ratio to take the sugar concentration to 40 g/l. Xanthan gum biosynthesis was carried out in 250 ml Erlenmeyer flasks with a 100 ml working volume. The pH of the substrate was adjusted to 7 before the start of fermentation. To begin the fermentation process, the flasks were inoculated with the inoculum (5 % v/v), and the flasks were incubated with orbiter shaking at 120 rpm and 30 °C for the required number of days, which was varied between 1 and 3 for optimization purposes. KH2PO4 (0–15 g/l) and NH4NO3 (2–6 g/l) were introduced into the medium to serve as stimulants of microbial growth, and their levels were varied according to the experimental design. The experiments were carried out in triplicate to ensure reliability. In addition, separate control experiments were set up (in the absence of microbial stimulants) and monitored to investigate the actual impact of the stimulants.
2.5. Xanthan gum recovery
At the end of the fermentation period, residual microbial cells were separated from the fermentation broth through centrifugation at 10,000 rpm and 4 °C for 30 min. The recovery of xanthan was carried out by precipitation using cold isopropanol. This was done by thoroughly mixing three parts of isopropanol with one part of the supernatant. The mixture was allowed to stand for 24 h for precipitation to take place and then recentrifuged under the same conditions to separate the precipitated xanthan gum. The recovered xanthan gum was oven-dried at 50 °C until a constant weight was achieved [22].
2.6. Experimental data generation and processing
To generate the data needed for the development of the ML models, a design of experiment (DOE) was used. Specifically, a three-variable Box‒Behnken design (BBD) was used to plan the fermentation experiments for data collection. This was done to generate data that can be used to train and validate the models under varying experimental conditions [38]. The suitability of the Box‒Behnken design has been established by numerous studies based on its ability to fit the second-order model that typically serves as a starting point for the majority of chemical engineering processes [39]. In addition, the design utilizes fewer experimental runs compared to a similar design such as the central composite design. In this case, the chosen BBD resulted in 17 experiments, of which five were replicated at the center point of the input variables. The three input variables investigated were fermentation time, concentration of KH2PO4, and concentration of NH4NO3, whose range of values shown in Table 1 were determined from a combination of literature sources and preliminary experiments. The measure of the performance of the fermentation process was taken as the yield of xanthan gum. The planning of the experiment was carried out using Stat-Ease's Design Expert software (version 11).
Table 1.
Actual and coded levels of input variables.
| Variables | Symbol | Coded and actual levels |
||
|---|---|---|---|---|
| −1 | 0 | +1 | ||
| Time (d) | X1 | 1 | 2.0 | 3 |
| KH2PO4 concentration (g/l) | X2 | 0 | 7.5 | 15 |
| NH4NO3 concentration (g/l) | X3 | 2 | 4.0 | 6 |
The prediction efficiency of ML models may be negatively impacted if the data used for modeling is not standardized to have a normal distribution. In this regard, normalization of the data was carried out following the transformation procedure previously reported [40] as shown in Equation (1).
| (1) |
where and refer to the original and transformed xanthan gum production data obtained from the fermentation process for the input feature j. λ represents the transformation factor derived from the maximum likelihood estimation, and i (1 to N) represents the number of data points for each input feature. Data normalization was performed using Equation (2) [32].
| (2) |
where , and refer to the normalized data, mean of the input feature j, and standard deviation of the same input feature, respectively.
2.7. Machine learning model development
Fig. 1 shows a flowchart depicting the information flow for the development of the ML models utilized in this work. The data generated from the experimental design were stored in a data warehouse in the form of a Microsoft Office Excel Workbook. All the data engineering and machine learning were implemented using Python (version 3.7.5), with the integrated development environment (IDE) being Jupyter. All numerical operations were carried out using Numpy version 1.20.3 and Pandas version 1.1.2. The specific ML models considered in this work were ANN, SVR, ELM, KRR, RF, and XGB, and these were implemented in the Python environment using the following libraries: Scikit-learn version 0.23.2 (SVR, KRR, RF), TensorFlow version 2.4.0 (ANN), and XGBoost version 1.2.3 (XGB) [32,38]. The graphical visualization of the data was carried out using Matplotlib, a very comprehensive library for data visualization in Python. The hardware specification used to run the codes for all the ML models was an HP EliteBook with an Intel Core i5 processor with a speed of 1.9 GHz and RAM of 16 GB operating on Windows 10. A k-fold cross-validation method was used to evaluate all the ML models to assess the one with the best performance for predicting xanthan gum yield in terms of the input features. Cross-validation is an important step in the development of ML models because it reduces the chances of overfitting and improves model generalization capability. This means that the model can correctly predict the chosen output for data not previously exposed to the model. Thus, the xanthan gum yield dataset was randomly divided into k groups (folds), and the ML models were trained with k – 1 folds (representing one training dataset) and validated with the remaining fold. This method has the advantage of ensuring high prediction accuracy without bias, as the entire dataset was used for model training and validation [41]. This process was repeated k times with different combinations of training and validation datasets. In this work, 3-fold cross-validation (i.e., k = 3) was adopted. The train-test split was 70:30 (i.e., 70 percent of the data were used for training and 30 percent to test the trained models. Cross-validation was done on the whole training set. Testing was done with the test dataset which the models were not exposed to during training.
Fig. 1.
Flowchart showing the development of ML models.
2.7.1. ANN modeling
The ANN model is a feed-forward neural network consisting of three hidden layers, each with a set of neurons that can estimate a given output response (y) from the provided input data (x). Each neuron calculates a linear combination (z) of n input features (xi) with corresponding weight (wi) and bias (b), as shown in Equation (3). The selection of the right activation function is essential in the ANN modeling process because it is chiefly responsible for the mapping of the inputs to the outputs. In this regard, several activation functions, such as exponential, scaled exponential linear unit (SELU), rectified linear unit (ReLU), and leaky rectified linear unit (Leaky ReLU), were evaluated to determine which was most appropriate.
| (3) |
During the ANN process, the transformed version of the output data is forwarded from one hidden layer to another. The network is trained through an updating process that tunes the model weights to minimize model loss (ℓ), which is typically taken as the root mean square error (RMSE), as shown in Equation (4), where is the model prediction. The minimization is done through a gradient descent method where the weights are manipulated as a function of ℓ and scaled using the learning rate (λ), as shown in Equation (5).
| (4) |
| (5) |
To avoid overfitting, a 3-fold cross-validation was carried out using the output dataset. Initialization of the weights of the ANN was done using a normal distribution of each hidden layer. The ANN model was implemented in the TensorFlow version 2.4.0 library. The ANN hyperparameters were optimized using grid search cross-validation (GridSearchCV).
2.7.2. SVM modeling
A support vector machine is an ML model based on a supervised training algorithm. It works based on the development of hyperplanes in an infinite dimensional space for discriminating between data groups. It is desirable if the hyperplane is far from the closest training data points for any class [32]. SVM has been generalized to be used for regression purposes, and in this regard, it is termed support vector regression (SVR). For a given vector of input features () and vector of target outputs (), SVR produces a linearly correlated regression model of the form shown in Equation (6).
| (6) |
where w and b are the vectors of model weight and bias determined by solving Equation (7).
| (7) |
where C and are hyperparameters referring to the penalty term and error term away from the hyperplane (ε tube). Prediction by the SVR model is estimated using the Lagrangian dual method, as shown in Equation (8).
| (8) |
where and are Lagrange multipliers and K is the kernel. Various kernels that were assessed to determine the most suitable one included radial basis function (RBF), polynomial, sigmoid, and linear kernels.
2.7.3. KRR modeling
KRR combines a kernel approach with ridge regression to model nonlinear relationships between input features and output responses. The ridge regression functions by minimizing the sum of squared errors with constraint fulfillment while providing an estimate to penalize it. An important advantage of KRR is its ability to incorporate a kernel approach and regularization to capture nonlinear relationships while overcoming the challenge of overfitting [42]. Equation (9) shows a mathematical representation of KRR, where fi is defined in Equation (10).
| (9) |
| (10) |
where refers to the Hilbert normed space. The KRR expression (Equation (9)) can be expressed as an m × m kernel matrix, as shown in Equation (11).
| (11) |
| (12) |
In training the KRR model, the algorithm determines α by solving Equation (11) and then searching for the optimum values of α and λ from the set of parameters. The optimized parameters are then used in testing the model, as shown in Equation (12). Different kernels, such as linear, RBF, and polynomial kernels, were assessed to determine the most suitable one.
2.7.4. ELM modeling
Extreme learning machines, although initially developed as single-hidden-layer feedforward neural networks, can express the nonlinear relationship between input features and output/target responses. In ELM, the parameters characterizing the input and hidden layers, such as weights and bias, are randomly initialized, while the output weights are calculated using the Moore-Penrose generalized inverse [32]. The mathematical expression of the single hidden layer ELM is shown in Equation (13).
| (13) |
where is a column vector representing the output weights between the output node and the hidden layer of L nodes, while is the row vector representing the output of the hidden layer for each input feature x.
H(x) helps to map the input data of dimensional space (d) to the dimensional space of the hidden layer (L, H). The vector shown in Equation (14) represents the training data. The objective of the ELM algorithm is to minimize the training error and output weight norm, which represents an important advantage for ELM [43].
| (14) |
2.7.5. RF modeling
Random forest is an advanced decision tree-based ML algorithm. It is based on a bootstrapping and aggregation approach called bagging [42]. In the RF modeling process, each decision tree is fed a random set of replacement input data (a bootstrap sample) and grows independently based on this. The synergy derived from the aggregation of predictions from each decision tree is the major factor behind the accuracy of the RF model. The RF process takes place in three steps. The first step is the generation of n bootstrapping samples using the input variables. The second step involves building an unpruned regression tree by taking advantage of the maximum predictor split, while the last step involves the aggregation of the predictions from the n number of trees.
For a random data subset d (x,y), the decision tree iteratively partitions the variable space (x) as samples with close targets are aggregated. The data at node m is represented by dm with Nm samples. dm may be partitioned into subsets denoted as and using each candidate split θ(p, tm), where p and tm refer to a feature and threshold, respectively (Equation (15)).
| (15) |
The candidate split is defined as a loss function , as shown in Equation (16).
| (16) |
where
The minimization of Equation (16) yields the parameters θ(p, tm).
| (17) |
The recursion of Equation (17) continues for and until the maximum depth is achieved. The prediction of the RF model is thus obtained from Equation (18).
| (18) |
where K is the number of decision trees (DT) in the random forest.
2.7.6. XGB modeling
XGB is another novel and advanced decision tree-based ML algorithm that is based on the application of gradient boosting in conjunction with series-grown decision trees. It works by integrating many weak learners to develop a strong learner via additive learning. It takes advantage of automatic parallel computation to deliver improved computational accuracy during training. Equation (19) shows the prediction function for a step time (t).
| (19) |
where , , and xi represent a learner at step t, prediction at step t, prediction at step t – 1, and input data, respectively.
To prevent overfitting issues with XGB, equations are used to evaluate the model's goodness of fit with the original function, as shown in Equation (20).
| (20) |
where l, n, and Ω represent the loss function, observation number, and regularization term (Equation (21)), respectively.
| (21) |
where , , and represent the score vector, regularization parameter, and mini loss, respectively.
2.8. ML model selection and accuracy
The performance of the ML models in predicting xanthan gum yield was evaluated using established statistical indicators such as the coefficient of determination (R2 value), mean absolute error (MAE), root mean square error (RMSE), Akaike's information criterion (AIC), Willmott's index of agreement (WI), average absolute deviation (AAD), and Nash-Sutcliffe efficiency (NSE), as shown in Equations (22), (23), (24), (25), (26), (27), (28)) [42,44,45].
| (22) |
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
| (28) |
In these equations, yp,i, ya,i, , N, n, and RSS represent the model predictions, experimental values, mean of the experimental values, number of model parameters, number of data points, and residual sum of squares, respectively. Typically, high values of R2, NSE, and WI (closer to one) combined with very low values of RMSE, MAE, and AAD are desirable for good model prediction.
2.9. Algorithm-based optimization of xanthan production
Two evolutionary optimization algorithms, particle swarm optimization (PSO) and genetic algorithm (GA), were used to determine the maximum xanthan gum yield and the corresponding values of the input features. PSO is a population-based search technique that uses an iterative procedure to optimize both discontinuous and continuous functions [46]. In this method, each particle in the population, typically called a swarm, is taken as a potential solution. The spatial distribution of the particles is changed randomly until an optimal state of equilibrium is achieved. In optimizing a system of M output variables, the PSO technique considers a swarm of N particles with a randomly assigned position (x) in the multidimensional space. The velocity (v) of each particle is related to its position as shown in Equations (29), (30)):
| (29) |
| (30) |
In these equations, Pbest and Gbest are personal and global best positions, respectively, which are defined based on the minimum mean square error. c1 represents the cognitive parameter that determines the affinity of the particle to its personal best position, while c2 represents a social parameter that determines the affinity of the particle to its global best position. represents the inertia weight and measures the influence of a particle's previous velocity on its current velocity. r1 and r2 are two random variables bounded between zero and one. The values of these parameters were tuned to determine their optimal values.
Genetic algorithm is a metaheuristic technique that is motivated by the evolutionary theory of natural selection [47]. The unique advantages of GA are its capacity for optimizing real-life multivariate systems using advanced fitness functions and its ability to carry out global optimization of nonlinear systems. Its sequential deployment of initialization, selection, crossover, and mutation enables it to solve multimodal optimization problems. In the GA procedure, the generation of a population of random individuals is the beginning of the evolutionary process, which involves the high-probability selection of individuals with higher fitness values. Based on bioinspired operations such as selection, crossover, and mutation, a new generation is produced stochastically from the preceding generation. This means that the next generation is generated at random from the preceding one, although dominant individuals have a higher probability of being reproduced. The iterative method is repeated until convergence is achieved.
In this work, the search space for the optimization problem using both tools was limited to that of the experimental design generated from the input variables. Both PSO and GA were implemented in the Python environment.
2.10. Feature evaluation via global sensitivity analysis
Global sensitivity analysis was used to identify the impact of each input feature on the prediction accuracy of each ML model. The high-dimensional model representation (HDMR) method implemented in SobolGSA software (Centre for Process Systems Engineering, Imperial College London) was used for this purpose. Unlike local sensitivity analysis, which only computes the effects of input features at a specified point, global sensitivity analysis computes the effects of input features over the whole space. This means that the magnitude of the range over which each input feature is varied has a direct influence on the sensitivity to that input in global sensitivity analysis [35]. Additionally, global sensitivity analysis may be used to investigate the relationships between input features.
Global sensitivity indices were calculated using the HDMR coefficients. Any result from the model (y), i.e., xanthan gum yield, may be represented by a function, f(x), of the model's inputs (x), which are fermentation time, the concentration of KH2PO4, and the concentration of NH4NO3. The key characteristic of HDMR is the decomposition of the complete function into a sum of functions that solely depend on subsets of the input variables, as follows:
| (31) |
where N, i, j, and fo represent the number of input features, index of input features, and average value of f(x), respectively. For simplicity and ease of handling, only the first two terms of Equation (31) are usually taken into consideration because of the negligible contributions of the terms containing more than two input features. Orthogonal polynomials were used to evaluate the functions fi(x) and fij (xi,xj). The contribution of each input feature and their interaction form the basis for the estimation of the global sensitivity indices. Following Equation (31), the contribution of each term, i.e., and , to the variance of the output response can be related to the total variance () as shown in Equation (32):
| (32) |
The linear, interaction and total sensitivity indices were obtained as using Equations (33), (34), (35)):
| (33) |
| (34) |
| (35) |
These global sensitivity indices were then used to assess the relative level of importance of the input features in relation to the variance of the output response.
3. Results and discussion
3.1. ML model selection and accuracy
The experimental data generated from the fermentation process was used to train each ML model to optimize their respective hyperparameters, as shown in Table 2. The hyperparameters were optimized via a combination of a 3-fold cross-validation technique and a full-factor experimental grid search. The accuracy of the ML models corresponding to each optimized hyperparameter was assessed using key statistical metrics, as shown in Table 3.
Table 2.
Optimized values of hyperparameters for ML models.
| ML model | Hyperparameters | Final optimized value | aTotal execution time (ms) |
|---|---|---|---|
| ANN |
kernel_initializer | “normal” | 34.76 |
| model optimizer | “adam” | ||
| hidden layer 1 number of neurons | 62 | ||
| hidden layer 1 activation function | “exponential" | ||
| hidden layer 2 number of neurons | 32 | ||
| hidden layer 2 activation function | “exponential" | ||
| hidden layer 3 number of neurons | 16 | ||
| hidden layer 3 activation function | “exponential" | ||
| output layer number of neurons | 1 | ||
| output layer activation function |
“linear" |
||
| SVM |
C | 700 | 6.38 |
| ε | 0.001 | ||
| ϒ | 6 × 10−3 | ||
| kernel | “RBF” | ||
| random_state |
100 |
||
| ELM |
hidden_units | 50 | 14.74 |
| activation_function | “relu” | ||
| C | 1 | ||
| random_type |
“normal" |
||
| KRR |
α | 0.001 | 368.08 |
| kernel | “RBF” | ||
| ϒ | 1.78 × 10−2 | ||
| random_state |
100 |
||
| XGB |
learning_rate | 0.3 | 510.15 |
| n_estimators | 200 | ||
| ϒ | 0.001 | ||
| max_depth | 50 | ||
| subsample | 0.5 | ||
| colsample_bylevel | 0.7 | ||
| random_state |
100 |
||
| RF | n_estimators | 100 | 50.00 |
| max_features | 17 | ||
| max_depth | None | ||
| min_samples_split | 2 | ||
| min_samples_leaf | 1 | ||
| bootstrap | false |
Total execution time = model training time + inference time.
Table 3.
Assessment of ML model prediction.
| Parameter | ANN | SVM | ELM | KRR | XGB | RF |
|---|---|---|---|---|---|---|
| R2 | 0.9804 | 0.9760 | 0.9877 | 0.9781 | 0.9758 | 0.9583 |
| NSE | 0.9801 | 0.9733 | 0.9871 | 0.9762 | 0.9745 | 0.9336 |
| WI | 0.9950 | 0.9935 | 0.9968 | 0.9942 | 0.9933 | 0.9801 |
| MAE | 0.1155 | 0.1011 | 0.0744 | 0.1172 | 0.1105 | 0.2376 |
| RMSE | 0.1507 | 0.1744 | 0.1212 | 0.1649 | 0.1704 | 0.2752 |
| AAD (%) | 1.9787 | 1.6973 | 1.2188 | 1.9481 | 1.9211 | 3.8604 |
| AIC | −53.0090 | −48.0359 | −60.4138 | −49.9398 | −32.5365 | −32.5365 |
All the models generally displayed high predictive accuracy, as reflected in the high coefficient of determination values (R2 > 0.97). The R2 value is one of the most important measures of model fit and accuracy. A high R2 value, very close to one, is desirable. For example, the ANN model had an R2 value of 0.9804. This implies that 98.04 % of the variability in the predicted xanthan gum yield values was explained by the input features. An R2 value greater than 0.8 is an indication of an adequate model fit [48]. Thus, the R2 values obtained in this work for all the ML models investigated point to the fact that the models were able to predict xanthan gum production with a high level of accuracy. This observation was also corroborated by other statistical indices similar to the R2 value (NSE > 0.90 and WI > 0.98). The NSE metric is a better index of model accuracy than the R2 value because of the responsiveness of the variances between the experimental observations and model predictions [49]. On the other hand, Willmott's index of agreement is a standardized indicator for assessing model prediction and shows improvements over the R2 value. Low values (close to zero) are indicative of poor model accuracy, while values close to one are indicative of excellent model accuracy [50]. The values of NSE and WI shown in Table 3 showed that there was generally good agreement between the experimental observations and the model predictions for all the ML models investigated. Error measures such as RMSE, MAE, and AAD were also used to assess the accuracy of the model predictions. These error terms show the deviation of the model predictions from the actual experimental observations. Thus, they are used to demonstrate the quality of the model predictions. Low values of these error terms are preferable, and this was the case with the values reported in Table 3. The levels of fit demonstrated by all the ML models are illustrated by the parity plots shown in Fig. 2 (a - f). The clustering of the data points around the 45o line supports the desirable goodness of fit observed. Table 4 shows the comparison between the actual experimental data and the model predictions. The model predictions were generally close to the experimental observations, further corroborating the adequate model fit.
Fig. 2.
Parity plots comparing (a) ANN, (b) SVM, (c) ELM, (d) KRR, (e) XGB, and (f) RF predictions with experimental values.
Table 4.
Comparison of ML model predictions with experimental observations.
| Run no | Input features |
Response (Xanthan gum yield (g/l)) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | Experimental value | ANN prediction | SVM prediction | ELM prediction | KRR prediction | XGB prediction | RF prediction | |
| 1 | 2 | 7.5 | 4 | 5.8 | 6.2 | 6.2 | 6.1 | 6.1 | 6.1 | 6.1 |
| 2 | 2 | 0.0 | 2 | 6.7 | 6.6 | 6.6 | 6.7 | 6.6 | 6.7 | 6.3 |
| 3 | 2 | 7.5 | 4 | 6.2 | 6.2 | 6.2 | 6.1 | 6.1 | 6.1 | 6.1 |
| 4 | 3 | 0.0 | 4 | 5.7 | 5.9 | 5.7 | 5.7 | 5.7 | 5.7 | 5.9 |
| 5 | 2 | 7.5 | 4 | 6.2 | 6.2 | 6.2 | 6.1 | 6.1 | 6.1 | 6.1 |
| 6 | 1 | 7.5 | 2 | 7.2 | 7.2 | 7.2 | 7.2 | 7.2 | 7.2 | 6.9 |
| 7 | 3 | 15.0 | 4 | 7.8 | 7.6 | 7.8 | 7.8 | 7.8 | 7.7 | 7.5 |
| 8 | 2 | 15.0 | 6 | 6.9 | 6.8 | 6.7 | 6.9 | 6.7 | 6.6 | 6.4 |
| 9 | 2 | 7.5 | 4 | 5.9 | 6.2 | 6.2 | 6.1 | 6.1 | 6.1 | 6.1 |
| 10 | 2 | 0.0 | 6 | 4.5 | 4.4 | 4.2 | 4.4 | 4.2 | 4.9 | 5.0 |
| 11 | 3 | 7.5 | 2 | 7.5 | 7.5 | 7.8 | 7.7 | 7.8 | 7.5 | 7.4 |
| 12 | 2 | 7.5 | 4 | 6.3 | 6.2 | 6.2 | 6.1 | 6.1 | 6.1 | 6.1 |
| 13 | 1 | 15.0 | 4 | 6.5 | 6.4 | 6.5 | 6.4 | 6.5 | 6.4 | 6.4 |
| 14 | 2 | 15.0 | 2 | 8.3 | 8.2 | 8.3 | 8.3 | 8.3 | 8.3 | 8.0 |
| 15 | 3 | 7.5 | 6 | 6.5 | 6.4 | 6.4 | 6.5 | 6.4 | 6.4 | 6.2 |
| 16 | 1 | 7.5 | 6 | 4.6 | 4.5 | 4.6 | 4.6 | 4.6 | 4.6 | 4.6 |
| 17 |
1 |
0.0 |
4 |
4.5 |
4.2 |
4.5 |
4.5 |
4.5 |
4.5 |
4.6 |
| Control experiment | ||||||||||
| X1 = 0.00; X2 = 0.00, X3 = 0.00; Y = 9.24 g/l | ||||||||||
An assessment of the statistical metrics in Table 3 was used to discriminate between all six ML models. It was found that the extreme learning machine was the best in terms of overall performance for the prediction of xanthan gum production. The ELM model had the lowest RMSE value, indicating that it was characterized by the least loss of information compared to the actual experimental data. To confirm this observation, the Akaike information criterion was used for further model discrimination. The AIC measures prediction error and hence model quality, and it is a useful tool for model selection. The AIC strikes a balance between model simplicity and quality of fit, accounting for model accuracy while balancing the risk of overfitting and underfitting [44]. The ELM model had the lowest AIC value compared to the other ML models. This means that the ELM model was the best tradeoff between model simplicity and information capture [51]. Thus, the ELM model will be able to provide the right balance between model goodness of fit on the one hand and overfitting or underfitting on the other hand.
Although no literature exists that assessed the deployment of ELM for modeling a xanthan gum fermentation process, the excellent predictive performance of ELM has also been reported by other researchers for other fermentation processes. For example, Liu et al. [52] used ELM to calibrate pH measurements obtained from Fourier transform near-infrared (FT-NIR) spectroscopy during solid-state fermentation of crop straw. They recorded an R2 value of 0.9618 and an RMSE value of 0.1044, which was enough to give accurate pH measurements. In another study, Baron and Zhang [53], developed an ELM-based data-driven model to overcome the difficulties of developing a mechanistic model for the control of a fed-batch fermentation process. They reported enhanced model accuracy, which was useful for developing a reliable control strategy for the process. In a similar work, an extreme learning machine approach was combined with the recursive least squares (RLS) method to model and optimize a fed-batch fermentation process [54]. The RLS was integrated with the ELM model to cope with the variations in the process due to unaccounted disturbances. Their findings showed that the hybrid ELM-RLS model was able to model a simulated baker's yeast fermentation process with desirable results. In a very recent study, Zhao et al. [55] adopted a semisupervised ELM model for modeling a yeast fermentation process. They reported enhanced training speed and prediction accuracy. Also, some reports support the superiority of ELM over modeling tools such as RSM [56], SVM [57], ANN [58], and adaptive neuro-fuzzy inference system (ANFIS) [59]. From these studies, it was found that the superiority of ELM derives from its fast training speed (as it is a one-hidden-layer neural network), and remarkable capacity for generalization and accuracy, making it suitable for modeling highly nonlinear relationships such as those typically encountered in fermentation processes [60]. Compared to traditional feedforward neural networks, ELM has been reported to exhibit remarkable efficiency and generalization over a wide range of problems in different study areas [61,62]. It has also been reported in some studies that ELM has comparable or better efficiency and generalization ability compared to SVM and its variants [63].
3.2. Partial dependence plots for input-output data visualization
To assess the individual and interactive impacts of the input features on the xanthan gum predictions, one-way and 2-way partial dependence plots (PDPs) were adopted. The generation of PDPs involves constraining all data points to take the same feature value such that the partial dependence function reflects the average prediction of the output. If the feature with which the PDP was generated is unrelated to the others, the PDPs accurately depict how the feature impacts the prediction on average [64]. The major attraction to the use of PDPs lies in their intuitive nature and ease of implementation, their ability to explicitly model a causal link between input features and model outputs, and their ability to explain the relationship between outputs and inputs irrespective of the nature of the relationship. PDPs are also model-agnostic, meaning that they can be used with any model [65].
Fig. 3 shows the one-way PDP for the effect of each input on xanthan gum production. The inward tick marks on the x-axis indicate the density of the data for each feature. The tick marks are important because their absence will essentially eliminate any meaning to be derived from the PDP. From Fig. 3(a), the influence of fermentation time on xanthan gum yield was observed to increase significantly from 1 to 2 days. Although the trend continued beyond 2 days, the influence was not as significant as previously observed. Generally, increased fermentation time resulted in higher xanthan gum production. This shows that the carbon substrate was progressively and continuously converted to xanthan gum throughout the fermentation process. High xanthan production was observed at three days of fermentation. Because of the potential for resource savings, the fermentation duration needs important consideration for optimization. A similar observation has been reported by previous researchers. For instance, Psomas et al. [66] reported higher xanthan gum yields with increasing fermentation time. They recorded a maximum xanthan gum yield of 7 g/l for a fermentation time of 3 days. The importance of optimizing the fermentation time was also illustrated by Cacik et al. [67], whose optimal control strategy for minimizing fermentation time reduced the fermentation time by 16.3 %.
Fig. 3.
One-way partial dependence plot showing the impact of (a) time, (b) phosphorus source, and (c) nitrogen source on the output.
As shown in Fig. 3(b), KH2PO4, a source of phosphorus and potassium, was beneficial for xanthan gum production, as seen in the positively correlated relationship between KH2PO4 concentration and xanthan gum production. Research has shown that the production of an EPS such as xanthan gum occurs via a defensive strategy by microorganisms surviving in saline environments [68]. It is thought that the secretion of EPS serves to balance the osmotic effect experienced by microbial cells as a result of the saline environment. Potassium and phosphate ions provided by KH2PO4 play important roles in fungi-facilitated fermentation processes. Potassium ions, for example, increase fungal cell growth as well as oxidative phosphorylation [25]. Phosphates, on the other hand, are required for cell development and metabolism, as well as the synthesis of cell walls and coenzymes, among other critical intermediates [22]. They also act as essential buffers, assisting in the regulation of protoplasmic pH.
The effect of nitrogen limitation is shown in Fig. 3(c). Nitrogen limitation favored the formation of xanthan gum. This is easily explained by noting that a high concentration of nitrogen is only essential for cell maintenance and the synthesis of important cell elements such as proteins, nucleic acids, enzymes, and peptides. As is typical with the production of EPS such as xanthan gum, a high carbon-nitrogen (C/N) ratio is expected to favor the process [69]. In keeping the concentration of carbon substrate constant, as was done in this work, it is seen that low levels of nitrogen increased the C/N ratio, with the consequence of increasing the formation of the EPS. This observation has also been recorded by previous researchers [22,70].
To assess the interoperability and interaction between two features on the target response, two-way PDPs were generated, as shown in Fig. 4. The explanation for the two-way PDP is similar to that given for the one-way PDP. In Fig. 4(a), the interaction between fermentation time and phosphorus level is presented to elucidate how both features simultaneously affect xanthan gum production. There was a clear and positive influence on xanthan gum production when these two features interacted. Similar observations were recorded for Fig. 4(b and c).
Fig. 4.
Two-way partial dependence plots showing the interaction between (a) phosphorus concentration and time, (b) nitrogen concentration and time, and (c) phosphorus concentration and nitrogen concentration.
3.3. Optimization of xanthan gum production
The hyperparameters of the two evolutionary optimization algorithms used were determined as shown in Table 5, and the results were used to implement both optimization strategies with the results shown in Table 6. Both optimization algorithms predicted the same maximum xanthan gum production under very similar fermentation conditions, suggesting their reliability for optimizing the fermentation process. A maximum xanthan gum concentration of 10.34 g/l was predicted with corresponding values of fermentation time, KH2PO4 concentration, and NH4NO3 concentration of 3 days, 15 g/l, and 2 g/l, respectively. These results were validated by carrying out triplicate experiments using these values, and the average of the three experiments revealed a xanthan gum concentration of 10.31 g/l. When compared with the control experiment that did not utilize phosphorus and nitrogen supplements in the fermentation medium, the optimum xanthan production value represents an 11.91 % increase from the value of 9.24 g/l obtained (Table 4). This is a clear demonstration of the importance of these stimulants. The choice of KH2PO4 was informed by its cost-effectiveness, as phosphorus is important for xanthan gum biosynthesis. While 15 g/l may seem like a lot, KH2PO4 is a key determinant of xanthan yield. The overall impact on total xanthan production costs is less significant when considering the vital role of KH2PO4 in the fermentation process. Furthermore, while the addition of 15 g/l KH2PO4 to the medium can enhance microbial growth and potentially xanthan production, it could also impact the molecular weight, and rheological properties such as viscosity and shear-thinning behavior of the produced xanthan gum [71]. In the future, studies will be needed to investigate the economic and rheological aspects of xanthan production in the context of the nutrient medium components.
Table 5.
Optimized values of hyperparameters for optimization algorithms.
| Optimization algorithm | Hyperparameters | Final optimized value |
|---|---|---|
| PSO | Swarm size | 15 |
| c1 | 0.5 | |
| c2 | 1 × 10−4 | |
| ω | 0.5 | |
| GA | Population size | 40 |
| Bits per variable | 32 | |
| Crossover rate | 0.9 | |
| Mutation rate | 0.01 |
Table 6.
Optimization results for xanthan gum production.
| Variables | Optimization algorithm |
|
|---|---|---|
| PSO | GA | |
| Time (d) | 2.99 | 2.99 |
| KH2PO4 concentration (g/l) | 15.00 | 14.99 |
| NH4NO3 concentration (g/l) | 2.00 | 2.00 |
| Predicted xanthan yield (g/l) | 10.34 | 10.34 |
| Actual xanthan yield (g/l) | 10.31 | |
The 11.91 % increase in xanthan gum production recorded can be attributed to several reasons related to the fermentation process and metabolic engineering. For instance, KH2PO4 and NH4NO3 are important sources of phosphorus and nitrogen, respectively, and these are essential nutrients that play vital roles in the growth and metabolism of Xanthomonas campestris. Thus, the addition of KH2PO4 and NH4NO3 likely enhanced the availability of these important nutrients, thereby promoting the growth and metabolic activity of Xanthomonas campestris, which could have resulted in the overall higher production of xanthan gum [24]. In addition, KH2PO4 and NH4NO3 can act as inducers that trigger the activation of specific genes or enzymes involved in the production of xanthan gum. These inducers could possess the ability to trigger the signaling of specific metabolic pathways in Xanthomonas campestris. By possibly modulating the metabolic network of Xanthomonas campestris to favor the synthesis of xanthan gum, the inducers could have caused the increased production of xanthan gum observed [72]. Lastly, KH2PO4 can regulate fermentation medium pH by acting as a buffer, which provides a more favorable environment for the growth of Xanthomonas campestris. The existence of optimal pH conditions can enhance microbial and metabolic activity, resulting in the ultimate enhancement of xanthan gum production [25].
The optimized xanthan gum production reported herein is comparable to that reported in previous work. For instance, Psomas et al. [66] reported a maximum xanthan gum production of 7 g/l after 3 days of fermentation. In another work, Demirci et al. [16] investigated the use of different Xanthomonas strains for the biosynthesis of xanthan gum from waste bread. They reported a maximum xanthan yield of 10.3 g/l for X. axonopodis pv. vesicatoria, while close values of 12.9 and 12.5 g/l were obtained for X. campestris and X. hortorum pv., respectively. X. campestris cultivated on a biopolymer production medium yielded a xanthan gum production of 9.7 g/l [73], while xanthan gum yields of 2.8–8.3 g/l were reported by Moreira et al. [74] for X. campestris cultivated on a synthetic production medium. Li et al. [75] reported xanthan gum yields reaching 11.7 g/l for X. campestris grown solely on kitchen waste. In more recent work, Rabiya and Sen, (2022) reported a xanthan gum yield of 12.4 g/l using a modified mineral salt medium. In another recent work, Vaishnav et al. [8] recorded 11.1 g/l of xanthan gum from mixed fruit waste using X. campestris. In comparing these results with those of the current work, the differences observed might be attributed to the different microorganisms, feedstocks, and fermentation conditions employed.
3.4. Feature importance via sensitivity analysis
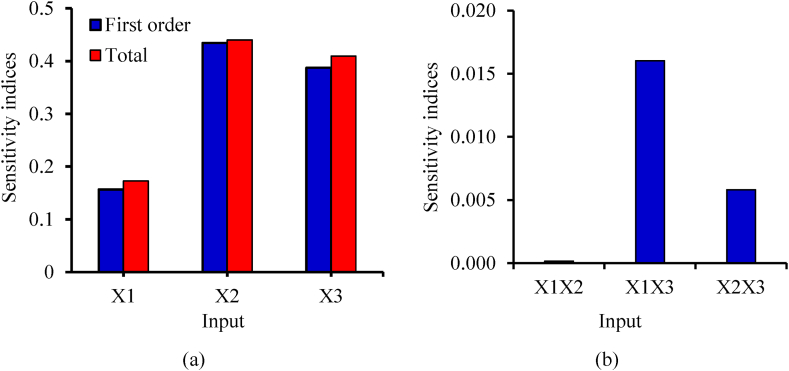
The evaluation and ranking of the input features were carried out via global sensitivity analysis. Fig. 5 shows the ranking of the inputs based on the level of their importance. Based on the first-order indices, the phosphorus source (KH2PO4) was ranked first as the most important input, with a contribution of 43.4 % to the total variance of the response (Fig. 5(a)). This was followed by the nitrogen source (NH4NO3) and fermentation time, with individual contributions of 38.7 % and 15.7 %, respectively. The overwhelming importance of KH2PO4 was also reflected in its impact on the interaction terms involving it, i.e., X1X3 and X2X3, ranking first and second, respectively (Fig. 5(b)). In any case, all the inputs were sensitive, as they all had total sensitivity indices greater than 0.1, as stipulated by Zhang et al. [76]. The fact that KH2PO4 was ranked as the most sensitive input is not a surprise considering its significant importance in the fermentation process, as already alluded to. The results obtained from a sensitivity analysis are important in providing further insights into the fermentation process for the biosynthesis of xanthan gum, and the specific details will be useful in making important decisions in ensuring maximum operational control of the fermentation process.
Fig. 5.
Sensitivity indices for (a) first and total order and (b) second-order interaction.
4. Conclusion
The current work is a comprehensive evaluation of the biosynthesis of xanthan gum from pineapple waste using Xanthomonas campestris. An extreme learning machine model was found to adequately model the relationship between fermentation time and the impact of phosphorus and nitrogen stimulants (KH2PO4 and NH4NO3) on xanthan gum production with high accuracy. A maximum xanthan gum production of 10.34 g/l was obtained with particle swarm optimization and genetic algorithm at KH2PO4 and NH4NO3 concentrations of 15 g/l and 2 g/l, respectively, for a fermentation time of 3 days. An improvement of 11.9 % was achieved in xanthan gum production with the use of KH2PO4 and NH4NO3 compared to when they were absent from the fermentation medium. An 11.9 % increase in xanthan gum production has numerous implications. The increased yield translates to improved cost efficiency, economics, and the potential commercial viability of the process. It also translates to a more stable supply chain in the case of largescale production of xanthan gum to meet the increasing demand. The sensitivity analysis showed that KH2PO4 was the most important input to the process. This work has shown that pineapple waste is a valuable resource that, when valorized, can reduce the cost of producing xanthan gum, promoting sustainable production and the circular economy. In addition, the use of microbial stimulants is an opportunity for fermentation process intensification.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Availability of data and material
Data included in article/supp. material/referenced in the article.
CRediT authorship contribution statement
Andrew Nosakhare Amenaghawon: Writing – original draft, Writing – review & editing, Supervision, Methodology, Formal analysis, Conceptualization. Shedrach Igemhokhai: Visualization, Software, Formal analysis, Data curation. Stanley Aimhanesi Eshiemogie: Visualization, Software, Formal analysis, Data curation. Favour Ugbodu: Validation, Software, Formal analysis, Data curation. Nelson Iyore Evbarunegbe: Writing – review & editing, Visualization, Software, Formal analysis, Data curation.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Ouyang B., Duan M., Zhu S., Zhou X., Zhou Y. Effect of tartary buckwheat sourdough fermented by different exogenous lactic acid bacteria on antifreeze property of frozen dough. Food Chem. Adv. 2023 doi: 10.1016/J.FOCHA.2023.100182. [DOI] [Google Scholar]
- 2.Saha I., Datta S. Bacterial exopolysaccharides in drug delivery applications. J. Drug Deliv. Sci. Technol. 2022;74 doi: 10.1016/J.JDDST.2022.103557. [DOI] [Google Scholar]
- 3.Li B., Shi Q., Miao B., Liu D., Jin S., Wang Z. Application of exopolysaccharide directionally synthesized by Xanthomonas campestris as the green selective depressant for the clean flotation of talc: statistical optimization and mechanism analysis. J. Clean. Prod. 2023;383 doi: 10.1016/J.JCLEPRO.2022.135381. [DOI] [Google Scholar]
- 4.Devi B., Devi S., Sood D., Arya P. Microbes Nat. Food Addit. Springer; Singapore: 2022. Microbial stabilizers in food processing; pp. 113–145. [DOI] [Google Scholar]
- 5.Kang J., Yue H., Li X., He C., Li Q., Cheng L., Zhang J., Liu Y., Wang S., Guo Q. Structural, rheological and functional properties of ultrasonic treated xanthan gums. Int. J. Biol. Macromol. 2023;246 doi: 10.1016/J.IJBIOMAC.2023.125650. [DOI] [PubMed] [Google Scholar]
- 6.Furtado I.F.S.P.C., Sydney E.B., Rodrigues S.A., Sydney A.C.N. Xanthan gum: applications, challenges, and advantages of this asset of biotechnological origin. Biotechnol. Res. Innov. J. 2022;6 doi: 10.4322/BIORI.202205. [DOI] [Google Scholar]
- 7.Hesari Z., Emmamzadehhashemi M.S.B., Aboutaleb E. Tragacanth and xanthan gum natural polymers for formulation of clotrimazole mucoadhesive gel. Acta Sci. Health Sci. 2023;45 doi: 10.4025/actascihealthsci.v45i1.55651. [DOI] [Google Scholar]
- 8.Vaishnav A., Upadhyay K., Koradiya M., Tipre D., Dave S. Valorisation of fruit waste for enhanced exopolysaccharide production by Xanthomonas campestries using statistical optimisation of medium and process. Food Biosci. 2022;46 doi: 10.1016/J.FBIO.2022.101608. [DOI] [Google Scholar]
- 9.Mohsin A., Zhang K., Hu J., Salim-ur-Rehman, Tariq M., Zaman W.Q., Khan I.M., Zhuang Y., Guo M. Optimized biosynthesis of xanthan via effective valorization of orange peels using response surface methodology: a kinetic model approach. Carbohydr. Polym. 2018;181:793–800. doi: 10.1016/J.CARBPOL.2017.11.076. [DOI] [PubMed] [Google Scholar]
- 10.Rashidi A.R., Azelee N.I.W., Zaidel D.N.A., Chuah L.F., Bokhari A., El Enshasy H.A., Dailin D.J. Unleashing the potential of xanthan: a comprehensive exploration of biosynthesis, production, and diverse applications. Bioproc. Biosyst. Eng. 2023;46:771–787. doi: 10.1007/S00449-023-02870-9/METRICS. [DOI] [PubMed] [Google Scholar]
- 11.Nejadmansouri M., Razmjooei M., Safdarianghomsheh R., Shad E., Delvigne F., Khalesi M. Semi-continuous production of xanthan in biofilm reactor using Xanthomonas campestris. J. Biotechnol. 2021;328:1–11. doi: 10.1016/J.JBIOTEC.2021.01.004. [DOI] [PubMed] [Google Scholar]
- 12.Dey R., Chatterji B.P. Sources and methods of manufacturing xanthan by fermentation of various carbon sources. Biotechnol. Prog. 2023:e3379. doi: 10.1002/BTPR.3379. [DOI] [PubMed] [Google Scholar]
- 13.Niknezhad S.V., Asadollahi M.A., Zamani A., Biria D., Doostmohammadi M. Optimization of xanthan gum production using cheese whey and response surface methodology. Food Sci. Biotechnol. 2015;24:453–460. doi: 10.1007/S10068-015-0060-9/METRICS. [DOI] [Google Scholar]
- 14.Prajapati J., Panchal R., Patel D., Goswami D. Biotechnol. Biol. Sci. first ed. CRC Press/Balkema; 2020. Production and characterization of xanthan gum by xanthomonas campestris using sugarcane bagasse as sole carbon source; pp. 363–367. [DOI] [Google Scholar]
- 15.Sujithra B., Deepika S., Akshaya K., Ponnusami V. Production and optimization of xanthan gum from three-step sequential enzyme treated cassava bagasse hydrolysate. Biocatal. Agric. Biotechnol. 2019;21 doi: 10.1016/J.BCAB.2019.101294. [DOI] [Google Scholar]
- 16.Demirci A.S., Palabiyik I., Apaydın D., Mirik M., Gumus T. Xanthan gum biosynthesis using Xanthomonas isolates from waste bread: process optimization and fermentation kinetics. Lebensm. Wiss. Technol. 2019;101:40–47. doi: 10.1016/J.LWT.2018.11.018. [DOI] [Google Scholar]
- 17.Soltaninejad A., Jazini M., Karimi K. Biorefinery for efficient xanthan gum, ethanol, and biogas production from potato crop residues. Biomass Bioenergy. 2022;158 doi: 10.1016/J.BIOMBIOE.2022.106354. [DOI] [Google Scholar]
- 18.Vaishnav A., Upadhayay K., Tipre D., Dave S. Utilization of mixed fruit waste for exopolysaccharide production by Bacillus species SRA4: medium formulation and its optimization. 3 Biotech. 2020;10:1–9. doi: 10.1007/S13205-020-02545-2/METRICS. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Vaishnav A.M., Upadhyay K.H., Tipre D.R., Dave S.R. Bio-prospecting of fruits waste for exopolysaccharide production by bacteria. Biotechnol. Sustain. Environ. 2021:353–371. doi: 10.1007/978-981-16-1955-7_15. [DOI] [Google Scholar]
- 20.Amenaghawon N.A., Oronsaye J.E., Ogbeide S.E. Statistical optimisation of fermentation conditions for citric acid production from pineapple peels. Niger. J. Technol. Res. 2014;9:20–26. doi: 10.4314/njtr.v9i2.5. [DOI] [Google Scholar]
- 21.Vieira I.M.M., Santos B.L.P., Santos C.V.M., Ruzene D.S., Silva D.P. Valorization of pineapple waste: a review on how the fruit's potential can reduce residue generation. Bioenergy Res. 2022;15:924–934. doi: 10.1007/S12155-021-10318-9/METRICS. [DOI] [Google Scholar]
- 22.Rabiya R., Sen R. Artificial intelligence driven advanced optimization strategy vis-à-vis response surface optimization of production medium: bacterial exopolysaccharide production as a case-study. Biochem. Eng. J. 2022;178 doi: 10.1016/J.BEJ.2021.108271. [DOI] [Google Scholar]
- 23.Sampaio I.C.F., Crugeira P.J.L., Soares L.G.P., dos Santos J.N., de Almeida P.F., Pinheiro A.L.B., Silveira L. Composition of Xanthan gum produced by Xanthomonas campestris using produced water from a carbonated oil field through Raman spectroscopy. J. Photochem. Photobiol. B Biol. 2020;213 doi: 10.1016/J.JPHOTOBIOL.2020.112052. [DOI] [PubMed] [Google Scholar]
- 24.Behera B.C. Citric acid from Aspergillus Niger: a comprehensive overview. Crit. Rev. Microbiol. 2020;46:727–749. doi: 10.1080/1040841X.2020.1828815. [DOI] [PubMed] [Google Scholar]
- 25.Amenaghawon N.A., Odika P., Aiwekhoe S.E. Optimization of nutrient medium composition for the production of lipase from waste cooking oil using response surface methodology and artificial neural networks. Chem. Eng. Commun. 2022;209:1531–1541. doi: 10.1080/00986445.2021.1980395. [DOI] [Google Scholar]
- 26.Velu S., Velayutham V., Manickkam S. Optimization of fermentation media for xanthan gum production from Xanthomonas campestris using Response Surface Methodology and Artificial Neural Network techniques. Indian J. Chem. Technol. 2016;23:353–361. [Google Scholar]
- 27.Kusuma H.S., Amenaghawon A.N., Darmokoesoemo H., Neolaka Y.A.B., Widyaningrum B.A., Anyalewechi C.L., Orukpe P.I. Evaluation of extract of Ipomoea batatas leaves as a green coagulant–flocculant for turbid water treatment: parametric modelling and optimization using response surface methodology and artificial neural networks. Environ. Technol. Innov. 2021;24 doi: 10.1016/J.ETI.2021.102005. [DOI] [Google Scholar]
- 28.Mahata C., Ray S., Das D. Optimization of dark fermentative hydrogen production from organic wastes using acidogenic mixed consortia. Energy Convers. Manag. 2020;219 doi: 10.1016/J.ENCONMAN.2020.113047. [DOI] [Google Scholar]
- 29.Zabot G.L., Mecca J., Mesomo M., Silva M.F., Prá V.D., De Oliveira D., Oliveira J.V., Castilhos F., Treichel H., Mazutti M.A. Hybrid modeling of xanthan gum bioproduction in batch bioreactor. Bioproc. Biosyst. Eng. 2011;34:975–986. doi: 10.1007/S00449-011-0548-5/METRICS. [DOI] [PubMed] [Google Scholar]
- 30.Velu S., Velayutham V. Comparative study of xanthan gum production using syntheic substrate by Xanthomonas campestris and local isolated strain. Int. J. ChemTech Res. 2014;6:2475–2483. [Google Scholar]
- 31.Velu S. Optimization of fermentation media for xanthan gum production from Xanthomonas campestris using Response Surface Methodology and Artificial Neural Network techniques. Indian J. Chem. Technol. 2016;23:353–361. doi: 10.56042/IJCT.V23I5.5211. [DOI] [Google Scholar]
- 32.Katongtung T., Onsree T., Tippayawong N. Machine learning prediction of biocrude yields and higher heating values from hydrothermal liquefaction of wet biomass and wastes. Bioresour. Technol. 2022;344 doi: 10.1016/J.BIORTECH.2021.126278. [DOI] [PubMed] [Google Scholar]
- 33.Velu S., Velayutham V., Manickkam S. Optimization of fermentation media for xanthan gum production from Xanthomonas campestris using Response Surface Methodology and Artificial Neural Network techniques. Indian J. Chem. Technol. 2016;23:353–361. http://nopr.niscair.res.in/handle/123456789/35503 [Google Scholar]
- 34.Adeyi O., Adeyi A.J., Oke E.O., Ajayi O.K., Oyelami S., Otolorin J.A., Areghan S.E., Isola B.F. Adaptive neuro fuzzy inference system modeling of Synsepalum dulcificum L. drying characteristics and sensitivity analysis of the drying factors. Sci. Rep. 2022;12:1–16. doi: 10.1038/s41598-022-17705-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Saltelli A., Jakeman A., Razavi S., Wu Q. Sensitivity analysis: a discipline coming of age. Environ. Model. Software. 2021;146 doi: 10.1016/J.ENVSOFT.2021.105226. [DOI] [Google Scholar]
- 36.Tamanna M., Uddin V., Kumar V., Yadav Kumar. Comparative study of the VINCI Robot's arm end effector matrix using Python and MATLAB. Mater. Today Proc. 2021;47:3761–3764. doi: 10.1016/J.MATPR.2021.02.429. [DOI] [Google Scholar]
- 37.Şen E., Demirci A.S., Palabiyik I. Xanthan gum characterization and production kinetics from pomace of Vitis vinifera. J. Food Process. Preserv. 2022;46 doi: 10.1111/JFPP.17098. [DOI] [Google Scholar]
- 38.Medl M., Rajamanickam V., Striedner G., Newton J. Development and validation of an artificial neural-network-based optical density soft sensor for a high-throughput fermentation system. Processes. 2023;11:297. doi: 10.3390/PR11010297. [DOI] [Google Scholar]
- 39.Umrigar V., Chakraborty M., Parikh P.A. Optimization of microwave-assisted esterification of succinic acid using Box-Behnken design approach. Environ. Sci. Pollut. Res. 2022:1–10. doi: 10.1007/S11356-022-22807-1/METRICS. [DOI] [PubMed] [Google Scholar]
- 40.Yeo I.N.K., Johnson R.A. A new family of power transformations to improve normality or symmetry. Biometrika. 2000;87:954–959. doi: 10.1093/BIOMET/87.4.954. [DOI] [Google Scholar]
- 41.Peco Chacon A.M., García Márquez F.P. In: Int. Ser. Oper. Res. Manag. Sci. García Márquez F.P., Lev B., editors. Springer; Cham: 2023. Support vector machine and K-fold cross-validation to detect false alarms in wind turbines; pp. 81–97. [DOI] [Google Scholar]
- 42.Ali M., Prasad R., Xiang Y., Yaseen Z.M. Complete ensemble empirical mode decomposition hybridized with random forest and kernel ridge regression model for monthly rainfall forecasts. J. Hydrol. 2020;584 doi: 10.1016/J.JHYDROL.2020.124647. [DOI] [Google Scholar]
- 43.Kusumo F., Silitonga A.S., Masjuki H.H., Ong H.C., Siswantoro J., Mahlia T.M.I. Optimization of transesterification process for Ceiba pentandra oil: a comparative study between kernel-based extreme learning machine and artificial neural networks. Energy. 2017;134:24–34. doi: 10.1016/J.ENERGY.2017.05.196. [DOI] [Google Scholar]
- 44.Amenaghawon A.N., Omoruyi B.O., Kenneth I., Okedi M.O., Esenogho G.O., Oyefolu P.K., Muojama O.E., Otuya I.C., Eshiemogie S.O., Okoh R., Anyalewechi C.L. Biotechnological conversion of yam peels for enhanced citric acid production: data-driven machine learning modeling and global sensitivity analysis of the impact of metabolic stimulants. Ind. Crops Prod. 2023;191 doi: 10.1016/J.INDCROP.2022.116022. [DOI] [Google Scholar]
- 45.Fan J., Zheng J., Wu L., Zhang F. Estimation of daily maize transpiration using support vector machines, extreme gradient boosting, artificial and deep neural networks models. Agric. Water Manag. 2021;245 doi: 10.1016/J.AGWAT.2020.106547. [DOI] [Google Scholar]
- 46.Sajjadi B., Asaithambi P., Raman A.A.A., Ibrahim S. Hybrid nero-fuzzy methods for estimation of ultrasound and mechanically stirring Influences on biodiesel synthesis through transesterification. Measurement. 2017;103:62–76. doi: 10.1016/J.MEASUREMENT.2017.01.044. [DOI] [Google Scholar]
- 47.Kyriklidis C., Kyriklidis M.E., Loizou E., Stimoniaris A., Tsanaktsidis C.G. Optimal Bio Marine Fuel production evolutionary Computation: genetic algorithm approach for raw materials mixtures. Fuel. 2022;323 doi: 10.1016/J.FUEL.2022.124232. [DOI] [Google Scholar]
- 48.Comber A., Brunsdon C., Charlton M., Dong G., Harris R., Lu B., Yihe L., Murakami D., Nakaya T., Wang Y., Harris P. A route map for successful applications of geographically weighted regression. Geogr. Anal. 2022;0:1–24. doi: 10.1111/GEAN.12316. [DOI] [Google Scholar]
- 49.Sharma P., Chhillar A., Said Z., Memon S. Exploring the exhaust emission and efficiency of algal biodiesel powered compression ignition engine: application of box–behnken and desirability based multi-objective response surface methodology. Energies. 2021;14:5968. doi: 10.3390/EN14185968. [DOI] [Google Scholar]
- 50.Hatami B., Ebrahimi A.A., Ehrampoush M.H., Salmani M.H., Tamaddon F., Mokhtari M. An efficient heterogeneous solid acid catalyst derived from sewage sludge for the catalytic transformation of sludge into biodiesel: preparation, characterization, and arylation process modeling. J. Clean. Prod. 2022;355 doi: 10.1016/J.JCLEPRO.2022.131809. [DOI] [Google Scholar]
- 51.Baguley T. Bloomsbury Publishing; 2018. Serious Stat: A Guide to Advanced Statistics for the Behavioral Sciences. [Google Scholar]
- 52.Liu G.H., Jiang H., Xiao X.H., Zhang D.J., Mei C.L., Ding Y.H. Determination of process variable pH in solid-state fermentation by FT-NIR spectroscopy and extreme learning machine (ELM) Spectrosc. Spectr. Anal. 2012;32:970–973. doi: 10.3964/J.ISSN.1000-0593(2012)04-0970-04. [DOI] [PubMed] [Google Scholar]
- 53.Baron C.M.C., Zhang J. Reliable on-line re-optimization control of a fed-batch fermentation process using bootstrap aggregated extreme learning machine. Lect. Notes Electr. Eng. 2020;495:272–294. doi: 10.1007/978-3-030-11292-9_14/COVER. [DOI] [Google Scholar]
- 54.Alli K., Zhang J. Adaptive optimal control of baker's yeast fermentation process with extreme learning machine and recursive least square technique. Comput. Aided Chem. Eng. 2021;50:1241–1246. doi: 10.1016/B978-0-323-88506-5.50191-1. [DOI] [Google Scholar]
- 55.Zhao M., Zhao S., Liu F. Semi-supervised hybrid modeling of the yeast fermentation process. Machines. 2023;11:63. doi: 10.3390/MACHINES11010063. [DOI] [Google Scholar]
- 56.Mujtaba M.A., Masjuki H.H., Kalam M.A., Ong H.C., Gul M., Farooq M., Soudagar M.E.M., Ahmed W., Harith M.H., Yusoff M.N.A.M. Ultrasound-assisted process optimization and tribological characteristics of biodiesel from palm-sesame oil via response surface methodology and extreme learning machine - cuckoo search. Renew. Energy. 2020;158:202–214. doi: 10.1016/J.RENENE.2020.05.158. [DOI] [Google Scholar]
- 57.Zhang L., Zhang D. vol. 1. Springer; Cham: 2016. p. 7.https://link.springer.com/chapter/10.1007/978-3-319-28397-5_20 (SVM and ELM: Who Wins? Object Recognition with Deep Convolutional Features from ImageNet). Proc. ELM-2015. [Google Scholar]
- 58.Fetimi A., Dâas A., Benguerba Y., Merouani S., Hamachi M., Kebiche-Senhadji O., Hamdaoui O. Optimization and prediction of safranin-O cationic dye removal from aqueous solution by emulsion liquid membrane (ELM) using artificial neural network-particle swarm optimization (ANN-PSO) hybrid model and response surface methodology (RSM) J. Environ. Chem. Eng. 2021;9 doi: 10.1016/J.JECE.2021.105837. [DOI] [Google Scholar]
- 59.Mousazadeh F., Naeem M.H.T., Daneshfar R., Soulgani B.S., Naseri M. Predicting the condensate viscosity near the wellbore by ELM and ANFIS-PSO strategies. J. Pet. Sci. Eng. 2021;204 doi: 10.1016/J.PETROL.2021.108708. [DOI] [Google Scholar]
- 60.Zhu X., Rehman K.U., Wang B., Shahzad M. Modern soft-sensing modeling methods for fermentation processes. Sensors. 2020;20:1771. doi: 10.3390/S20061771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Bin Huang G., Zhou H., Ding X., Zhang R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. B Cybern. 2012;42:513–529. doi: 10.1109/TSMCB.2011.2168604. [DOI] [PubMed] [Google Scholar]
- 62.Bin Huang G., Zhu Q.Y., Siew C.K. Extreme learning machine: theory and applications. Neurocomputing. 2006;70:489–501. doi: 10.1016/J.NEUCOM.2005.12.126. [DOI] [Google Scholar]
- 63.Huang G., Bin Huang G., Song S., You K. Trends in extreme learning machines: a review. Neural Network. 2015;61:32–48. doi: 10.1016/J.NEUNET.2014.10.001. [DOI] [PubMed] [Google Scholar]
- 64.Scarpone C., Brinkmann S.T., Große T., Sonnenwald D., Fuchs M., Walker B.B. A multimethod approach for county-scale geospatial analysis of emerging infectious diseases: a cross-sectional case study of COVID-19 incidence in Germany. Int. J. Health Geogr. 2020;19:1–17. doi: 10.1186/S12942-020-00225-1/FIGURES/6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Molnar C., König G., Herbinger J., Freiesleben T., Dandl S., Scholbeck C.A., Casalicchio G., Grosse-Wentrup M., Bischl B. In: Lect. Notes Comput. Sci. (Including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics) Holzinger A., Goebel R., Fong R., Moon T., Müller K.R., Samek W., editors. Springer Science and Business Media Deutschland GmbH; 2022. General pitfalls of model-agnostic interpretation methods for machine learning models; pp. 39–68. [DOI] [Google Scholar]
- 66.Psomas S.K., Liakopoulou-Kyriakides M., Kyriakidis D.A. Optimization study of xanthan gum production using response surface methodology. Biochem. Eng. J. 2007;35:273–280. doi: 10.1016/J.BEJ.2007.01.036. [DOI] [Google Scholar]
- 67.Cacik F., Dondo R.G., Marqués D. Optimal control of a batch bioreactor for the production of xanthan gum. Comput. Chem. Eng. 2001;25:409–418. doi: 10.1016/S0098-1354(00)00662-1. [DOI] [Google Scholar]
- 68.Bemal S., Anil A.C. Effects of salinity on cellular growth and exopolysaccharide production of freshwater Synechococcus strain CCAP1405. J. Plankton Res. 2018;40:46–58. doi: 10.1093/PLANKT/FBX064. [DOI] [Google Scholar]
- 69.Moshaf S., Hamidi-Esfahani Z., Azizi M.H. Optimization of conditions for xanthan gum production from waste date in submerged fermantation. Int. J. Nutr. Food Eng. 2011;5:549–552. doi: 10.5281/ZENODO.1063348. [DOI] [Google Scholar]
- 70.Vargas-García M.C., López M.J., Elorrieta M.A., Suárez F., Moreno J. Influence of nutritional and environmental factors on polysaccharide production by Azotobacter vinelandii cultured on 4-hydroxybenzoic acid. J. Ind. Microbiol. Biotechnol. 2001;27:5–10. doi: 10.1038/SJ.JIM.7000152/METRICS. [DOI] [PubMed] [Google Scholar]
- 71.Casas J.A., Santos V.E., García-Ochoa F. Xanthan gum production under several operational conditions: molecular structure and rheological properties☆. Enzym. Microb. Technol. 2000;26:282–291. doi: 10.1016/S0141-0229(99)00160-X. [DOI] [PubMed] [Google Scholar]
- 72.Gallardo R., Alves M., Rodrigues L.R. Modulation of crude glycerol fermentation by Clostridium pasteurianum DSM 525 towards the production of butanol. Biomass Bioenergy. 2014;71:134–143. doi: 10.1016/J.BIOMBIOE.2014.10.015. [DOI] [Google Scholar]
- 73.Rottava I., Batesini G., Silva M.F., Lerin L., de Oliveira D., Padilha F.F., Toniazzo G., Mossi A., Cansian R.L., Di Luccio M., Treichel H. Xanthan gum production and rheological behavior using different strains of Xanthomonas sp. Carbohydr. Polym. 2009;77:65–71. doi: 10.1016/J.CARBPOL.2008.12.001. [DOI] [Google Scholar]
- 74.Moreira A.S., Vendruscolo J.L.S., Gil-Turnes C., Vendruscolo C.T. Screening among 18 novel strains of Xanthomonas campestris pv pruni. Food Hydrocolloids. 2001;15:469–474. doi: 10.1016/S0268-005X(01)00092-3. [DOI] [Google Scholar]
- 75.Li P., Li T., Zeng Y., Li X., Jiang X., Wang Y., Xie T., Zhang Y. Biosynthesis of xanthan gum by Xanthomonas campestris LRELP-1 using kitchen waste as the sole substrate. Carbohydr. Polym. 2016;151:684–691. doi: 10.1016/J.CARBPOL.2016.06.017. [DOI] [PubMed] [Google Scholar]
- 76.Zhang W., Cho C., Piao C., Choi H. Sobol's sensitivity analysis for a fuel cell stack assembly model with the aid of structure-selection techniques. J. Power Sources. 2016;301:1–10. doi: 10.1016/J.JPOWSOUR.2015.08.076. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data included in article/supp. material/referenced in the article.