Abstract
Dementia is an escalating global health challenge, with Alzheimer's disease (AD) at its forefront. Substantial evidence highlights the accumulation of AD-related pathological proteins in specific brain regions and their subsequent dissemination throughout the broader area along the brain network, leading to disruptions in both individual brain regions and their interconnections. Although a comprehensive understanding of the neurodegeneration-brain network link is lacking, it is undeniable that brain networks play a pivotal role in the development and progression of AD. To thoroughly elucidate the intricate network of elements and connections constituting the human brain, the concept of the brain connectome was introduced. Research based on the connectome holds immense potential for revealing the mechanisms underlying disease development, and it has become a prominent topic that has attracted the attention of numerous researchers. In this review, we aim to systematically summarize studies on brain networks within the context of AD, critically analyze the strengths and weaknesses of existing methodologies, and offer novel perspectives and insights, intending to serve as inspiration for future research.
Keywords: Alzheimer's disease, brain-connectome, graph theory, deep graph neural networks
Introduction
Dementia stands as one of the most significant global health challenges in the 21st century. Currently, >50 million individuals are living with dementia worldwide (Hughes, 2017), and this number is estimated to triple, reaching 152 million by 2050 as the global population ages (International, 2019). Alzheimer's disease (AD) is the most common cause of dementia, accounting for ~60–80% of all dementia cases (Scheltens et al., 2021; World Health Organization, 2019; Alzheimer's Association, 2018). In the USA, it is forecasted that the population of Americans with either Alzheimer's dementia or mild cognitive impairment will reach 15 million in 2060 (Brookmeyer et al., 2018). At present, the total annual cost for AD and other dementias in the USA stands at $305 billion, and this figure is expected to surge to >$1.1 trillion by 2050 (Alzheimer's Association, 2018).
AD imposes not only financial burdens but also profound emotional anguish on patients and their families. As a progressive, neurodegenerative disease, AD follows a progressive disease continuum, spanning from an asymptomatic phase with biomarker evidence of AD (preclinical AD), progressing through mild cognitive impairment (MCI), and ultimately culminating in AD dementia (Jack Jr et al., 2018a). It is characterized by a range of functional, cognitive, and behavioral impairments, including memory disorders, memory loss, and challenges in decision-making, verbal communication, concentration, thinking, and judgment (Alzheimer's Association, 2018). These symptoms advance gradually over time, causing patients to progressively lose their ability to manage daily life and retain their memories. Current research identifies two primary pathological hallmarks of AD: the progressive accumulation of extracellular amyloid beta (Aβ) plaques and the presence of intracellular neurofibrillary tangles (NFTs) (Alzheimer's Association, 2018). Aβ plaques accumulate due to either reduced Aβ clearance or excessive production (Serrano-Pozo et al., 2011), typically emerging around two decades before the onset of cognitive impairment (Bateman et al., 2012; Jack Jr et al., 2018b). NFTs, on the other hand, result from the abnormal accumulation of hyperphosphorylated tau proteins (Serrano-Pozo et al., 2011) and can be detected 10–15 years before the onset of symptoms (Bateman et al., 2012; Jack Jr et al., 2018b). While there is currently no complete cure for AD due to an incomplete understanding of its etiology, pathophysiology, and progression, early diagnosis and intervention to delay dementia development can significantly benefit patients and their caregivers while also resulting in substantial cost savings for healthcare systems.
Previous research has unveiled the accumulation of pathological proteins within specific macroscale brain networks, suggesting a fundamental role of brain network architecture in the system-level pathophysiology of neurodegenerative diseases (Pearson et al., 1985; Saper et al., 1987; Braak and Braak, 1991; Jucker and Walker, 2018, 2013; Prusiner, 1998; Seeley et al., 2009; Zhou et al., 2012; Calafate et al., 2015; De Calignon et al., 2012; Grothe et al., 2016; Pereira et al., 2019; Buckner et al., 2009, 2005; Palmqvist et al., 2017; Villeneuve et al., 2015; Hoenig et al., 2018; Jones et al., 2017; Hansson et al., 2017; Bejanin et al., 2017; Ossenkoppele et al., 2016; Bero et al., 2011; Busche and Hyman, 2020; Busche et al., 2019, 2012; Wu et al., 2016). This concept, known as the network degeneration hypothesis, has gained substantial support over the last decade. Two primary mechanistic hypotheses underlie this theory: brain networks as conduits for pathological spread (Pearson et al. 1985; Saper et al., 1987; Braak and Braak, 1991; Jucker and Walker, 2018, 2013; Prusiner, 1998; Seeley et al., 2009; Zhou et al., 2012; Calafate et al., 2015; De Calignon et al., 2012; Grothe et al., 2016; Pereira et al., 2019; Buckner et al., 2009, 2005; Palmqvist et al., 2017; Villeneuve et al., 2015; Hoenig et al., 2018; Jones et al., 2017; Hansson et al., 2017; Bejanin et al., 2017; Ossenkoppele et al., 2016; Bero et al., 2011) and brain networks as drivers of disease progression (Bero et al., 2011; Busche and Hyman, 2020; Busche et al., 2019, 2012; Wu et al., 2016). Some studies (Pearson et al., 1985; Saper et al. 1987; Braak and Braak, 1991), based on post mortem human tissue analysis, have noted the frequent colocalization of abnormal protein aggregates in brain regions connected by strong anatomical links. This observation led to the proposition that pathogenic proteins originate as prion-like seeded aggregations (Jucker and Walker, 2018, 2013; Prusiner, 1998; Seeley et al., 2009; Zhou et al., 2012; Calafate et al., 2015; De Calignon et al., 2012), subsequently propagating along the neuronal pathways that constitute large-scale brain networks. This "prion-like" spreading hypothesis suggests networks act as "passive" anatomical conduits for the transport of pathological agents. Recent neuroimaging studies further support this perspective (Grothe et al., 2016; Pereira et al., 2019; Buckner et al., 2009, 2005; Palmqvist et al., 2017; Villeneuve et al., 2015; Hoenig et al., 2018; Jones et al., 2017; Hansson et al., 2017; Bejanin et al., 2017; Ossenkoppele et al., 2016; Bero et al., 2011). For example, positron emission tomography (PET) studies in AD have shown significant overlap between β-amyloid distribution and the topography of default-mode network (DMN) and fronto-parietal brain networks (Grothe et al., 2016; Pereira et al., 2019; Buckner et al., 2009, 2005; Palmqvist et al., 2017; Villeneuve et al., 2015). Likewise, there is a spatial correlation between tau-PET deposition and syndrome-specific functional networks (Hoenig et al., 2018; Jones et al., 2017; Hansson et al., 2017; Bejanin et al., 2017; Ossenkoppele et al., 2016; Bero et al., 2011). However, some recent evidence also supports an alternative hypothesis, suggesting a more "active" link between disease pathology and the dynamic properties of neuronal circuits (Bero et al., 2011; Busche and Hyman, 2020; Busche et al., 2019, 2012; Wu et al., 2016). According to this view, brain networks directly catalyze disease progression, where the functional attributes of networks dynamically influence the spread of pathological proteins and disease progression, rather than merely serving as a passive propagation pathway.
While a consensus or comprehensive understanding of the connection between neurodegeneration and brain networks is currently lacking, compelling evidence has demonstrated that pathological proteins not only accumulate in specific brain regions but also propagate further throughout the network, disrupting both the brain regions and the connections between them. Therefore, network-based studies have the potential to bridge the gap between pathological processes and emerging clinical manifestations, offering insights into the disease development mechanism. Consequently, they play a pivotal role in neurodegenerative diseases such as AD. Numerous studies aim to leverage advanced graph-based approaches to investigate brain networks for disease progression prediction and biomarker identification. In these approaches, a brain network is represented by a connection matrix, often referred to as the brain connectome, which is analyzed from a graph perspective. In this representation, nodes of the graph represent different brain regions, while edges symbolize biological or functional connections between these regions. This graph-based framework allows researchers to explore the intricate relationships and patterns within brain networks in the context of brain diseases. These graph-based approaches can be broadly categorized into two types: the traditional graph theory-based methods and the deep graph neural network-based methods. Traditional graph theory-based methods leverage established principles in mathematical graph theory to describe and analyze essential properties of intricate brain connectomes using graph measures. While these approaches have identified numerous AD-related brain connections, they struggle to effectively capture the intricate nonlinear patterns inherent in the data. On the contrary, deep graph neural network-based methods, such as graph convolutional networks (GCNs), employ deep learning techniques to capture these complex nonlinear patterns and relationships within brain connectomes. However, a drawback of deep graph neural network-based methods is their reliance on opaque black-box models. Interpreting these models requires a comprehensive understanding of the underlying mechanisms governing their decision-making processes. In this comprehensive review, our primary objective is to offer a detailed analysis and comprehensive summary of the various graph-based methods employed in the study of neurodegenerative diseases, with a particular focus on AD.
To concentrate on the latest research outcomes, we conducted a search on Google Scholar covering the period from January 2013 to June 2023, utilizing two key terms: “brain networks” and “Alzheimer's disease.” We compiled relevant studies meeting the following criteria: original peer-reviewed research studies using either graph theory or deep graph convolutional neural networks for AD prediction. Following this criterion, we identified and reviewed a total of 36 studies, which are presented in this paper. The remainder of this review is organized as follows: Brain Connectome Section introduces the foundational concepts of brain connectomes. It covers brain connectomes at three different structural scales and encompasses three distinct types of brain connectivity. Furthermore, an analysis and summary of AD-related brain connections from existing literature are presented. In Section Graph Theory-Based Approaches in AD study, the focus is on graph theory-based methods, elucidating their core principles and commonly utilized graph measures in AD-related brain networks studies. Deep Graph Neural Network-Based Approaches for AD Prediction Section shifts attention to deep graph neural network-based methods, exploring their applications and potential in the analysis of brain networks, with a particular emphasis on new findings in AD prediction. Discussion and Conclusion Section critically examines the limitations of existing research and outlines potential avenues for future work.
Brain Connectome
The definition, scales, and levels of brain connectome
The concept of brain connectome, initially proposed by Olaf Sporns, 2005, aimed to furnish a comprehensive structural depiction of the intricate network of elements and connections comprising the human brain. Its primary utility is to serve as a structural substrate for comprehending human cognitive function and interpreting neuroimaging research. This concept plays an indispensable role in supporting the exploration of intricate interrelationships of brain structure, function, and cognition. The connectome comprises two fundamental components that shape its network architecture: neural elements and neural connections. The relationship of the set of n elements can be represented by a connection matrix A = [ai,j] ∈ Rn × n, where ai,j > 0 denotes the presence of a connection between element i and j, otherwise ai,j = 0.
The elements and their connections within the connectome can vary in definition across different scales and levels of structural description. These structural descriptions typically target three distinct levels of organization. The microscale targets at the level of single neurons and synapses, while the macroscale delves into the level of anatomically distinct brain regions of interest (ROI) and inter-regional pathways. Between these extremes lies the mesoscale, which centers around neuronal populations. Single neurons have the advantage of relatively straightforward demarcation and definition. However, their sheer number, substantial variability, and rapid dynamics make them unsuitable as the fundamental elements of the connectome. By contrast, the identification and delineation of brain regions and neuronal populations pose greater challenges, as there is currently no universally accepted parcellation scheme for human brain regions. Nonetheless, anatomically distinct ROI and interregional pathways is the most practical organizational level for human connectome. This review will primarily concentrate on this particular level.
Different types of connections in the macroscale brain connectome
In the macroscale brain connectome derived from in vivo neuroimaging, connections between elements can be categorized into three types (Fig. 1): structural connectivity, representing anatomical links; functional connectivity, capturing undirected statistical dependencies; and effective connectivity, describing directed causal relationships among distributed responses (Friston, 1994). It is worth noting that this categorization is not limited to macroscale brain connectome but extends to mesoscale and microscale as well, with specific definitions dependent on the measurements and models available at each particular scale.
Figure 1:
Depictions of “connections” in a brain connectome and the resulting three types of connectivity. Structural connectivity (SC) refers to anatomical links and is usually estimated using fiber bundles derived from diffusion MRI; Functional connectivity (FC) and effective connectivity (EC) are generally inferred through the correlation of nodal activities based on BOLD-fMRI or EEG/MEG.
Structural connectivity (SC) in macroscale primarily reveals long-range fiber bundles derived from diffusion or diffusion tensor magnetic resonance imaging (MRI) (Basser et al., 1994). A structural brain network can be constructed based on these fiber bundles, associating them with the specific brain regions they interconnect (Park et al., 2004; Hagmann et al., 2007). It is worth noting that SC derived from diffusion MRI is typically undirected and cannot discern between excitatory or inhibitory connections. This stands in contrast to SC based on tracing studies, which can vary in strength or density in either direction and, in some cases, be linked to excitatory or inhibitory postsynaptic effects.
Functional connectivity (FC), on the other hand, is commonly inferred through the correlation of nodal activities based on blood oxygenation level-dependent (BOLD) functional MRI (fMRI) or coherence analysis of electro- or magnetoencephalogram (EEG/MEG) signals acquired during task performance or in a resting state. In their work, Zhang et al., 2022 provided a comprehensive summary of commonly used measurements for representing pairwise relationships between two fMRI signals. These measurements encompass correlation, partial correlation, covariance, and include both weighted and binary edges. Resting-state fMRI, in particular, has gained prominence as a foundational tool for the analysis of functional networks, thanks to the discovery of spatially organized endogenous low-frequency fluctuations within BOLD signals (Biswal et al., 1995).
Effective connectivity (EC), by contrast, delves into the realm of causal relationships within a network. It centers on the notion of one node (neuronal population) influencing another within a specific model of network dynamics. The inference of EC entails the use of a neuronal integration model, typically necessitating the estimation of model parameters (effective connectivity) that most accurately explain the observed BOLD or EEG/MEG signals. While the neuronal model is commonly constrained by SC, it is vital to note that SC does not comprehensively dictate EC. EC is dynamic, responsive to the state of the system, and contingent on experimental context. Additionally, in certain models, EC can encompass polysynaptic pathways, not solely reliant on direct axonal connections.
Methods for brain structural and functional connectivity generation
There are several commonly used methods in brain structural and functional connectivity generation. This section provides a comprehensive overview of these methods.
Generation of structural connectivity
Structural covariance network (Yun et al., 2016; Zielinski et al., 2010) and diffusion MRI derived fiber connectivity (Zhang et al., 2021, 2020a, 2019) are two commonly used approaches to generate brain structural connectivity. Structural covariance refers to the synchronized changes in morphological characteristics, including cortical thickness (CT) and cortical surface area (CSA), across brain structures that are either functionally or anatomically connected to each other. The key steps for calculating individualized structural covariance (ISC) are as follows: (i) acquisition and pre-processing of T1-weighted MRI data. The preprocessing steps are adaptable based on the specific objectives of the study. (ii) Use of open-source neuroimaging data analysis and visualization tools, such as Freesurfer, for surface reconstruction and parcellation. This results in the segmentation of the brain surface into ROI. (iii) Calculation of CT and CSA. CT can be calculated as the shortest distance between gray–white matter boundary and the gray matter–CSF boundary at each vertex and CSA can be estimated for each ROI. (iv) Use of specific formulas to calculate cortical thickness-based individualized structural covariance (CT-ISC) and cortical surface area-based ISC (CSA-ISC) values between ROI for each individual (Zielinski et al., 2010). In Equations (1) and (2), k indicates the kth individual, i and j indicate the ith and jth ROI, CTmean(i) and CTstd(i) denote the regional mean and standard deviation of CT in ROI(i) across all participants or across all normal control participants in disease related studies.
 |
(1) |
 |
(2) |
Diffusion MRI derived fiber connectivity is another commonly used method to generate brain structural connectivity. The major steps are as follows: (i) both T1-weighted MRI and diffusion MRI images are required; (ii) the same steps as the structural covariance approach are adopted to use T1 image for surface reconstruction and parcellation; (iii) diffusion MRI image is used for fiber tracking via tools such as MedINRIA and DSI-Studio; and (iv) the number of fibers connecting each pair of ROI is calculated and used to generate the structural connectivity.
Generation of functional connectivity
Various methods are commonly employed to generate functional connectivity and are categorized into knowledge-based approaches, such as the Pearson correlation coefficient (Zhang et al., 2021, 2020a, 2019; Batista-García-Ramó and Fernández-Verdecia, 2018) and partial correlation (Friedman et al., 2008), and data-driven approaches, including independent component analysis (ICA) (Zhang et al. 2018; Hutchison et al., 2010) and principal component analysis (PCA) (Ghosh-Dastidar et al., 2008; Lang et al., 2012). In other literature, these methods are also referred to as model-dependent and model-free methods, respectively. Knowledge-based approaches typically require prior knowledge about the spatial and temporal patterns of activation, as well as a model for the data generation process. These approaches usually select some ROI as seeds and generate a connectivity map of the human brain by determining whether other regions are functionally connected to these seeds according to predefined metrics. Data-driven methods serve as a complementary approach that does not rely on prior knowledge, allowing them to reveal unexpected correlations in the data.
The Pearson correlation coefficient between a pair of functional signals is a widely used functional measurement for estimating functional connectivity (Batista-García-Ramó and Fernández-Verdecia, 2018). The Pearson correlation coefficient can be calculated by Equation (3), where F = [Fi, j] ∈ RN × N denotes the functional connectivity, cov is the covariance, fi is the averaged functional signal of brain region i, and 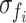 is the standard deviation of fi.
is the standard deviation of fi.
 |
(3) |
Partial correlation provides a valuable graphical depiction of functional interactions. A common method for estimating sparse inverse covariance, known as the graphical lasso (Friedman et al., 2008), utilizes partial correlation. In Friedman et al., 2008, the sparse inverse covariance matrix is determined by maximizing the L1 penalized log-likelihood of the observed data with assumption of Gaussian distribution. The graphical lasso method is then applied to learn individual sparse functional connectivity F. Specifically, for each individual, let gt,i denote functional signal of brain region i at time t, G = [gt,i] ∈ RT × N denote the functional signals over N brain regions spanning time T. The tth sample gt = [gt,1, …, gt,N]T ∈ RN is assumed to be drawn i.i.d. from some Gaussian distribution with the precision matrix F for encoding the conditional independencies between any two ROI. The empirical sample covariance is:
 |
(4) |
where  is the mean of T samples. F can be obtained by the optimization problem of the graphical Lasso:
is the mean of T samples. F can be obtained by the optimization problem of the graphical Lasso:
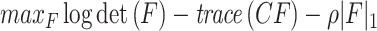 |
(5) |
where ρ is the regularization parameter to control the sparsity of F.
PCA and ICA are two typical data-driven approaches, which are based on the assumption that the activation is orthogonal (PCA) or independent (ICA) to the other signal variations. In these approaches, the brain functional data is represented by a matrix X ∈ RN × M, where M is the temporal dimension and the N is the voxel-space dimension. Before applying PCA and ICA, the mean of each row is normally subtracted from the data:  , where
, where  is a matrix that contains the row-wise means. Then the following decomposition is conducted in PCA:
is a matrix that contains the row-wise means. Then the following decomposition is conducted in PCA:
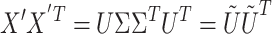 |
(6) |
where U ∈ RN × N represents the matrix of eigenimages of the N × N-dimensional correlation matrix and Σ contains the corresponding eigenvalues along its diagonal. These eigenimages identify extended areas of correlated neuronal activity. The orthogonality constraint imposed onto PCA often limits the usefulness and immediate interpretation of the eigenimages extracted. To alleviate such constraints, ICA has been considered:
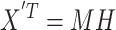 |
(7) |
The row of X′T represents spatial activity distributions and its column represents different observation time points. The spatial independent component analysis aims to discover an unmixing matrix M−1 (pseudoinverse of M) such that H = M−1X′T. In this context, H consists of rows representing independent spatial activity distributions assumed to best characterize the observations, while M contains rows representing the corresponding weights indicating how each independent component contributes to the observation at any given time point. Alternatively, when examines the columns of matrix X′T, representing pixel time courses of observed functional images, the decomposition results in independent columns of matrix M, representing independent pixel time courses reflecting temporal variations of observed neuronal activities. In this case, the columns of matrix H contain the corresponding weights. Consequently, matrix M contains temporal information in its rows, and matrix H contains spatial information in its rows, specifically the activity maps.
The impact of AD on brain networks
Existing research has extensively explored the intricate disruptions in structural and functional brain networks associated with AD. Notably, investigations into the pathological hallmarks of AD, such as amyloid plaques and hyperphosphorylated tau protein, reveal distinct regional preferences. One study (Grothe et al., 2016) uncovered a predilection for amyloid deposition in the DMN, with significant effect sizes also noted in other neocortical intrinsic connectivity networks, particularly the frontoparietal-control network. Atrophic changes exhibited specificity for an anterior limbic network, followed by the DMN, while other neocortical networks remained relatively unaffected. Hypometabolism displayed a mixed profile influenced by both amyloid and atrophy. Parallel patterns of network specificity were observed in the predementia and preclinical stages, affirming the DMN's heightened vulnerability to multimodal imaging abnormalities in AD. Another study (Hansson et al., 2017) highlighted the typical tau pattern, predominantly affecting temporal cortical areas, the precuneus–posterior cingulate, and lateral parts of the parietal and occipital cortex. This pattern notably overlapped with the dorsal attention, higher visual, limbic, and parts of the DMN. These results emphasize that tau aggregate deposition in AD predominantly affects higher-order cognitive networks over primary sensory-motor networks, challenging the specificity for the default-mode or related limbic networks.
In addition, various studies have explored the impact of AD on brain network through graph measures, further contributing to our understanding of influence of AD on brain connectivity. These studies found that individuals with AD exhibit intricate disruptions in both the FC and SC. Compared to healthy controls, AD patients show increased local efficiency, decreased global efficiency, longest characteristic path lengths, largest clustering coefficients, increased characteristic path length, and decreased intramodular connections (Dai et al., 2019, 2015; Kabbara et al., 2018; Martensson et al. 2018; Liu et al., 2012). And when compared to AD patients, MCI patients demonstrate decreased nodal centrality in the medial temporal lobe, increased nodal centrality in the occipital regions, and distinct alterations in the amygdala (Liu et al., 2012). These results indicate a widespread rewiring in AD and MCI patients, reflecting the reorganization of brain networks accompanying cognitive decline leading to AD. Furthermore, the correlation between FC and SC is heightened in connections involving the DMN and rich club, revealing overlapping and distinct network disruptions and emphasizing a strengthened correlation between FC and SC in AD (Dai et al., 2019). AD is also found to be associated with regional gray matter damage and abnormalities in functional integration between brain regions (Dai et al. 2015). The disease selectively targets highly connected hub regions, such as the medial and lateral prefrontal and parietal cortices, insula, and thalamus. This impairment is connectivity distance-dependent, particularly affecting long-range connections. Disruptions in functional connections within the default-mode, salience, and executive-control modules, as well as connections between them, significantly correlate with cognitive performance (Joo et al., 2016; Dai et al., 2015). Notably, nodal connectivity strength in the posteromedial cortex proves highly discriminative in distinguishing individuals with AD from healthy controls (Dai et al., 2015). In addition, brain networks of AD patients are characterized by lower global information processing and higher local information processing, showing significant correlation with alterations in cognitive scores (Kabbara et al., 2018).
Graph Theory-Based Approaches in AD study
Graph theory, a mathematical discipline dedicated to the study of networks, has extensive applications in various real-life contexts, often referred to as complex network analysis (Rubinov and Sporns, 2010). The fundamental idea is to characterize both local and global attributes of complex real-world networks, such as brain networks, using a concise set of meaningful and computationally feasible measures. In this section, we will introduce the prevalent network measures used to evaluate both brain structural and functional connectivity. Furthermore, we will furnish a summary and analysis of their applications in existing AD research literature.
Network measures of brain connectivity
Based on existing literature, certain measures are frequently employed in brain network studies to detect functional integration and segregation within brain networks, assess the centrality of individual brain regions or pathways, elucidate the patterns of local anatomical circuitry, and evaluate network resilience when confronted with external challenges. In the following sections, we will offer a comprehensive summary and analysis of these measures. You can find the mathematical definitions of these complex network measures, encompassing directed/undirected and binary/weighted networks, in Table 1.
Table 1:
Mathematical: definitions of complex network measures.
| Basic concepts and notation | |
| N: set of network nodes, n: number of nodes. L: set of network links, l: number of links. (i, j): link between nodes nodes i and j, (i, j ∈ N). aij: connection status between nodes i and j (aij = 1 when link (i, j) exists, aij = 0 otherwise; aii = 0 for all i ). Each undirected link was counted twice for the total number of links to avoid ambiguity with directed links. | |
| Measures of functional segregation | |
| Number of triangles around node i | Binary and undirected: 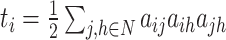 weighted: weighted: 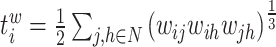 directed: directed: 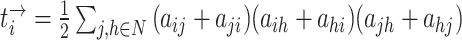
|
| Clustering coefficient | Binary and undirected (Watts and Strogatz, 1998): 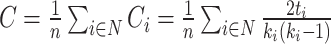 Ci: the clustering coefficient of node i (Ci = 0 for ki < 2). Weighted (Onnela et al., 2005) (see Saramäki et al., 2007 for other variants): Ci: the clustering coefficient of node i (Ci = 0 for ki < 2). Weighted (Onnela et al., 2005) (see Saramäki et al., 2007 for other variants): 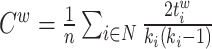 directed (Fagiolo, 2007): directed (Fagiolo, 2007): 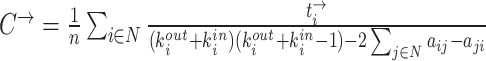
|
| Transitivity | Binary and undirected (Newman, 2003):  weighted: weighted: 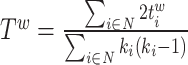 directed: directed:  Note that transitivity is not defined for individual nodes. Note that transitivity is not defined for individual nodes. |
| Modularity | Binary and undirected (Newman, 2004b): 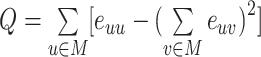 M: the network is fully subdivided into a set of nonoverlapping modules M. euv: the set of links that connect nodes in module u with nodes in module v. Weighted (Newman, 2004a): M: the network is fully subdivided into a set of nonoverlapping modules M. euv: the set of links that connect nodes in module u with nodes in module v. Weighted (Newman, 2004a): 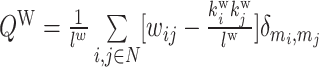 Directed (Leicht and Newman, 2008): Directed (Leicht and Newman, 2008): 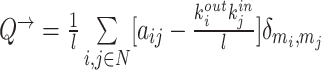
|
| Measures of functional integration | |
| Shortest path length | Binary and undirected: 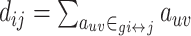 gi↔j: the shortest path (geodesic) between i and j (dij = ∞ for all disconnected pairs). Weighted: gi↔j: the shortest path (geodesic) between i and j (dij = ∞ for all disconnected pairs). Weighted:  f : a map from weight to length. f : a map from weight to length.  : the shortest weighted path between i and j . Directed: : the shortest weighted path between i and j . Directed: 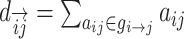 gi → j: the directed shortest path from i to j . gi → j: the directed shortest path from i to j . |
| Characteristic path length | Binary and undirected (Watts and Strogatz, 1998): 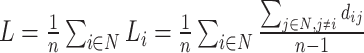 Li: the average distance between node i and all other nodes. Weighted: Li: the average distance between node i and all other nodes. Weighted:  Directed: Directed: 
|
| Global efficiency | Binary and undirected (Latora and Marchiori, 2001): 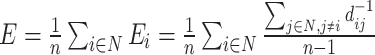 Ei: the efficiency of node i . Weighted: Ei: the efficiency of node i . Weighted: 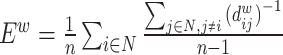 Directed: Directed: 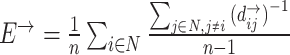
|
| Small-world brain connectivity | |
| Small-worldness | Binary and undirected (Humphries and Gurney, 2008): 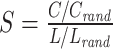 C and Crand: the clustering coefficients. L and Lrand: the characteristic path lengths of the respective tested network and a random network. Weighted: C and Crand: the clustering coefficients. L and Lrand: the characteristic path lengths of the respective tested network and a random network. Weighted: 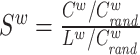 directed: directed: 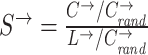 (Small-world networks often have S ≫ 1.) (Small-world networks often have S ≫ 1.) |
| Measures of centrality | |
| Degree | Binary and undirected: 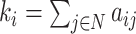 weighted: weighted: 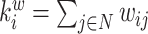 directed (out-degree of i ): directed (out-degree of i ): 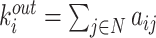 directed (in-degree of i): directed (in-degree of i): 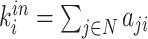
|
| Within-module degree z-score | Binary and undirected (Guimera and Amaral, 2005): 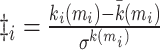 mi: the module containing node i. ki (mi): the within-module degree of i. mi: the module containing node i. ki (mi): the within-module degree of i. 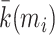 and and  : the respective mean and standard deviation of the within-module mi degree distribution. Weighted: : the respective mean and standard deviation of the within-module mi degree distribution. Weighted:  directed (out-degree): directed (out-degree):  directed (in-degree): directed (in-degree): 
|
| Participation coefficient | Binary and undirected (Guimera and Amaral, 2005): 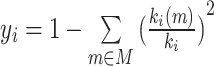 weighted: weighted: 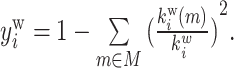 directed (out-degree): directed (out-degree): 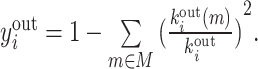 Directed (in-degree): Directed (in-degree): 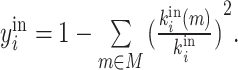
|
| Measures of network resilience | |
| Degree distribution | Binary and undirected (Barabási and Albert, 1999):  P(k): the probability of a node having degree k′: weighted: P(k): the probability of a node having degree k′: weighted:  directed (out-degree): directed (out-degree): 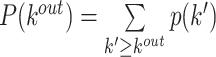 directed (in-degree): directed (in-degree): 
|
| Average neighbor degree | Binary and undirected (Pastor-Satorras et al., 2001): 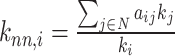 weighted: weighted: 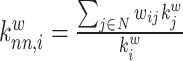 directed: directed: 
|
| Assortativity coefficient | Binary and undirected (Newman, 2002): 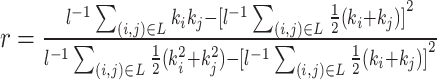 weighted: weighted: 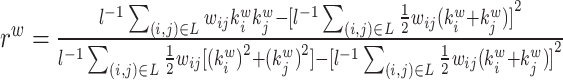 directed: directed: 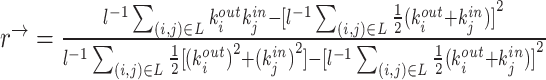
|
Measures of functional segregation
Functional segregation in the brain means specialized processing occurs in closely connected groups of brain regions. Segregation metrics assess the existence of these groups, often called clusters or modules, within networks. In anatomical and functional networks, these metrics are meaningful. Clusters in anatomical networks suggest potential functional segregation, and in functional networks they show organized statistical dependencies indicating segregated neural processing.
Simple segregation measures involve counting triangles within the network; with a great number of triangles indicating segregation. Locally, the fraction of triangles around a single node is termed a clustering coefficient, which indicates the fraction of the node's neighbors are also neighbors to each other (Watts and Strogatz, 1998). The network's mean clustering coefficient reveals the prevalence of clustered connectivity around individual node, but this measure can be skewed by nodes with fewer connections. An alternative measure, transitivity (Newman, 2003), collectively normalized, avoids this bias. Advanced segregation measures go beyond identifying tightly connected groups; they also unveil the size and composition of these groups, forming the network's modular or community structure. This entails dividing the network into groups of nodes with maximum internal links and minimum external links (Girvan and Newman, 2002). Modularity (Newman, 2004b) quantifies how effectively the network separates into these distinct, nonoverlapping groups. Optimizing the modular structure is typically done with algorithms, which may sacrifice some accuracy for computational speed. One algorithm proposed by Newman (2006) is accurate and fast enough for smaller networks. Another algorithm (Blondel et al., 2008) is faster for larger networks and can identify hierarchical modules. These algorithms have been generalized to weighted (Newman, 2004a) and directed (Leicht and Newman, 2008) networks. Some algorithms even identify overlapping modular structures, recognizing nodes that belong to multiple modules simultaneously (Palla et al., 2005).
Measures of functional integration
Functional integration in the brain refers to its capacity to rapidly combine specialized information from different regions. This concept is evaluated using integration measures, typically based on the concept of “path,” which estimate how effectively brain regions communicate. Paths represent sequences of connected nodes and links in anatomical networks, depicting potential routes for information flow between brain regions, while paths in functional networks represent sequences of statistical associations and may not necessarily reflect actual information flow within anatomical connections. Binary path length is determined by the number of links in the path, while weighted path length considers the total sum of individual link lengths. Shorter paths indicate a stronger potential for integration. The most frequently used measure of functional integration is the average shortest path length between all pairs of nodes in the network, known as the characteristic path length (Watts and Strogatz, 1998). A related measure is the average inverse shortest path length, referred to as global efficiency (Latora and Marchiori, 2001). Global efficiency can be computed even for disconnected networks, where paths between disconnected nodes are considered infinite, resulting in zero efficiency. The characteristic path length is primarily influenced by long paths, while global efficiency is primarily influenced by short paths. It is essential to note that measures such as the characteristic path length and global efficiency do not account for multiple or longer paths, which can significantly contribute to integration in larger and sparser networks (Estrada and Hatano, 2008).
Small-world brain connectivity
Anatomical brain connectivity is believed to address the dual requirements of functional integration and segregation concurrently (Tononi et al., 1994). An ideally structured anatomical network should exhibit both functionally specialized (segregation) modules and a robust number of intermodular (integration) links. This configuration is commonly referred to as a “small-world” network and is widely observed in anatomical connectivity (Bassett and Bullmore, 2006). Moreover, numerous studies investigating functional brain networks also reveal some degree of small-world organization. It is generally hypothesized that such organization represents an optimal balance between functional integration and segregation (Sporns and Honey, 2006).
Small-world networks are formally defined as networks that exhibit significantly higher clustering than random networks while maintaining approximately the same characteristic path length as random networks (Watts and Strogatz, 1998). In general, small-world networks should simultaneously demonstrate a high degree of segregation and integration. Recently, a metric called “small-worldness” was introduced to capture this property in a single statistic (Humphries and Gurney, 2008). While this metric can be valuable for providing a snapshot characterization of a network ensemble, it may also mistakenly indicate a small-world topology in networks that are highly segregated but poorly integrated. Consequently, this metric should not be generally regarded as a replacement for individual assessments of integration and segregation.
Measures of centrality
Important brain regions, often referred to as hubs, play a crucial role in facilitating functional integration and enhancing network resilience to disturbances. These hubs interact with numerous other regions, and their significance can be evaluated through various measures of node centrality.
Degree is one of the most prevalent centrality measures. The degree of a node is the count of links connected to it, which is essentially the number of its neighbors. Thus, individual degree values indicate the significance of nodes within the network. It holds a straightforward neurobiological interpretation: nodes with a high degree have extensive interactions, either structurally or functionally, with many other nodes within the network. Degree is particularly sensitive in anatomical networks characterized by nonhomogeneous degree distributions.
In modular anatomical networks, degree-based metrics that focus on within-module and between-module connectivity can help classify nodes into distinct functional groups (Guimera and Amaral, 2005). The within-module degree z-score is a localized version of degree centrality within a module. By contrast, the participation coefficient assesses the diversity of intermodular connections for individual nodes. Nodes with a high within-module degree but a low participation coefficient, often referred to as provincial hubs, are likely instrumental in facilitating modular segregation. Conversely, nodes with a high participation coefficient, known as connector hubs, play a crucial role in promoting global intermodular integration.
Various centrality measures are rooted in the idea that central nodes play a pivotal role in governing information flow within a network, often participating in numerous short paths (Freeman et al., 2002). Closeness centrality, for instance, is defined as the inverse of the average shortest path length from a node to all other nodes in the network. A closely related and often more sensitive measure is betweenness centrality, which quantifies the fraction of all shortest paths in the network that traverse a particular node. Nodes with high betweenness centrality frequently act as bridges connecting different parts of the network. The concept of betweenness centrality can also be naturally extended to edges, enabling the identification of crucial anatomical or functional connections. Certain algorithms (Brandes, 2001; Kintali, 2008) offer efficient methods for computing betweenness centrality, greatly enhancing its computational efficiency.
Measures of network resilience
Anatomical brain connectivity plays a significant role in determining how neuropathological lesions impact functional brain activity. In conditions such as stroke, the extent of functional deterioration hinges on the specific anatomical region affected, whereas in diseases such as AD, it relies on the resilience of anatomical connectivity to degenerative changes. Complex network analysis equips us with tools to assess these network resilience properties both directly and indirectly.
Indirect measures of resilience gauge anatomical features that reflect a network's vulnerability to damage. One of these features is the degree distribution (Barabási and Albert, 1999). Networks with power-law degree distributions may exhibit resilience against gradual random deterioration but can be highly sensitive to disruptions of high-degree central nodes. In practice, the degree distributions of most real-world networks deviate from perfect power-law distributions. Therefore, the extent to which these distributions resemble a power law can serve as a valuable indicator of resilience. Another indirect measure of resilience is the assortativity coefficient (Newman, 2002), which reflects the correlation between the degrees of nodes at opposite ends of an edge. Networks with a positive assortativity coefficient tend to possess a resilient core of highly interconnected, high-degree hubs. Conversely, networks with a negative assortativity coefficient often feature widely distributed and thus vulnerable high-degree hubs. Related measures of assortativity, such as the average neighbor degree (Pastor-Satorras et al., 2001) and the local assortativity coefficient (Piraveenan et al., 2008), are computed for individual nodes. Nodes with low scores on these measures can potentially compromise global network function if disrupted.
Direct assessments of network resilience typically involve evaluating the network both before and after a disruption. For instance, in the context of a progressive neurodegenerative disease, patients might undergo longitudinal imaging. Alternatively, disruptions can be computationally simulated by randomly or purposefully removing nodes and links from the network. The impact of such lesions on the network can then be assessed examining alterations in the resultant anatomical connectivity or in the simulated functional connectivity or dynamic activity that emerges (Alstott et al., 2009). In conducting such resilience tests, it is advisable to employ measures that are suitable for analyzing networks with disconnected components. For example, when assessing integration, global efficiency is preferable to characteristic path length.
Brain network measures in AD study
Graph theory analysis, coupled with a diverse range of network measures, equips us with valuable tools to quantify network properties and hence has become a popular approach to study brain networks in neurodegenerative disorders such as AD. In the realm of AD research grounded in graph theory, statistical analysis stands out as one of the most frequently employed methodologies. The core steps involve generating brain connectivity matrices for individuals at different stages of AD progression, calculating network measures, and applying statistical analyses to detect significant differences in these measures across various disease stages. These studies contribute significantly to our comprehension of how the disease impacts the brain over time.
Researchers explore the effects of AD on the brain networks from various perspectives by employing multimodal brain connectivity matrices, including structural connectivity (SC), functional connectivity (FC), and other modalities. Some studies specialize in single modality of brain connectivity (Ebadi et al., 2017; John et al., 2017; Jalili, 2017; Behfar et al., 2020; Protas et al., 2023), whereas others undertake comparative examinations involving multiple types of brain connectivity (Dai et al., 2019). Specific studies may focus on particular brain regions, while others adopt a global perspective. In Table 2, we showcase a selection of representative studies and encapsulate their pivotal findings.
Table 2:
Summary of notable graph theory-based studies in AD research.
| Work | Sample | Connectivity | Main findings |
|---|---|---|---|
| Ebadi et al. (2017) | 15NC, 15MCI, 15AD | Nodes: Brodmann areas SC: connection density of fiber derived from DTI | Acc: AD vs. NC = 80%, AD vs. MCI = 83.3%, MCI vs. NC = 70% AD vs NC (most important features): betweenness centrality at Brodmann Area 2, eigenvector centrality at Brodmann Area 1, load centrality at Brodmann Areas 2 and 27, and closeness centrality at Brodmann Area 1 AD vs MCI (most important features): Katz centrality at Brodmann Area 3, degree and closeness centrality at Brodmann Area 5, node redundancy coefficient and load centrality at Brodmann Area 4. MCI vs NC (most important features): hit centrality, page rank, betweenness centrality, and load centrality at Brodmann Area 6 along with hub centrality at Brodmann Area 1. |
| John et al. (2017) | 100AD, 135NC | Nodes: 87 cortical gray matter and subcortical regions SC: correlations of the corresponding regional volumes | AD: (first sub-graph) clustering coefficient↓, sigma (the ratio between the clustering coefficient and the characteristic path length)↓ AD: (second sub-graph) Small world propensity (SWP (Feldt Muldoon et al., 2015))↑ Neurodegenerative processes impact volumetric networks in a nonglobal fashion. |
| Jalili (2017) | 23AD, 25NC | Nodes: EEG sensor locations FC: Pearson's correlation coefficient of EEG signals | AD: local efficiency↓, modularity↓ (Global) The optimal set of measures: edge betweenness centrality, global efficiency, modularity, and synchronizability. |
| Dai et al. (2019) | 47AD, 40NC | Nodes: AAL-611 atlas SC: connection density of fiber derived from dMRI FC: Pearson's correlation coefficient of rs-fMRI | FC of AD: clustering coefficient↓, characteristic path length↑, normalized clustering coefficient↑, normalized characteristic path length↑, and small-worldne↑ (Global) SC of AD: disrupted the characteristic path length, intramodular connections in the DMN, degree↓ in the right middle frontal gyrus, insula, and middle temporal gyrus. AD: the coupling of the FC and SC in connections of the default mode network and the rich club ↑. |
| Behfar et al. (2020) | 15 young NC 15 senior NC 15 MCI | Nodes: Brainnetome Atlas FC: Pearson's correlation coefficient of rs-fMRI | Senior NC and MCI (compared to young NC): degree centrality (degree)↓ at 3 ROI: the right superior parietal lobule, rostral area 7 (Brainnetome label: SPL_R_5_1), the right and left precentral gyri caudal dorsolateral area 6 (Brainnetome label: PrG_R_6_2 and PrG_L_6_2) MCI (compared to Senior NC): degree centrality (degree)↓ in the right middle frontal gyrus, lateral areal 10 (Brainnetome label: MFG_R_7_7). |
| Protas et al. (2023) | 32AD, 115MCI, 223NC | Nodes: AAL atlas tau network: the weight indicates the difference in tau deposition between two nodes | Global strength, global efficiency, and limbic strength in the tau networks are higher in AD subjects (AD > MCI > NC). Global efficiency and global strength are significantly correlated with memory in the NC group. |
The arrows refer to an increase (↑) or a decrease (↓) of the indicated measures.
Abbreviations: DTI: diffusion tensor imaging; Acc: accuracy; NC: Normal control.
Moreover, due to variations in factors such as group size, composition, the selection of neuroanatomical atlases, and methods for creating brain connectivity matrices across different studies, the results among similar investigations often lack consistency. Therefore, some studies (Martensson et al., 2018; Xu et al., 2022) have attempted to explore the impact of various factors on graph measures by comparing different results under distinct experimental settings. This investigation aims to shed light on the stability of graph theoretical measures. Such efforts provide valuable insights into the application of graph theory in brain disease research and the analysis and interpretation of related findings.
Deep Graph Neural Network-Based Approaches for AD Prediction
Recent strides in deep learning have introduced potent and efficient models for brain network analysis, offering several substantial advantages over traditional statistical approaches. First, deep learning models possess the remarkable ability to autonomously extract relevant features from raw data. In the context of brain network analysis, this means they can automatically discern vital patterns and intricate relationships within complex connectivity data, eliminating the need for laborious manual feature engineering. This proves especially advantageous when dealing with large-scale, high-dimensional datasets. Second, brain networks often exhibit intricate, nonlinear relationships between nodes and edges, which can be challenging to model using linear techniques. Deep learning models, with their brilliant ability to capture nonlinearities through activation functions and multiple layers, are well-suited to addressing this complexity. Third, deep learning models exhibit impressive scalability, enabling them to adeptly handle vast and intricate datasets, a common characteristic of brain connectivity data. This scalability ensures that deep learning methods can efficiently manage the growing volumes of data generated in neuroscience research. Fourth, brain network analysis frequently involves integrating various data types, such as structural and functional modalities. Deep learning models can seamlessly integrate and learn from multiple modalities, providing a holistic view of brain connectivity. These compelling advantages have propelled the use and design of effective deep models in brain network studies into a popular and burgeoning field of research.
Within the expansive domain of deep models, deep graph convolutional neural networks (GCNs) (Kipf and Welling, 2016; Wu et al., 2020; Zhang et al., 2022, 2020b; Defferrard et al., 2016) have emerged as a prominent choice. This prominence is attributed to their exceptional proficiency in handling complex graph data, a quality that greatly enhances their utility in brain network analysis. The fundamental operating principle of a GCN is elucidated in Fig. 2. GCN starts with the representation of data as a graph, which can be depicted using a topology (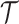 ), outlining the connections between nodes, and a feature matrix (
), outlining the connections between nodes, and a feature matrix ( ), capturing the distinctive features associated with each node. The core of GCN is the iterative message-passing process via graph convolution. This process can be formulated by
), capturing the distinctive features associated with each node. The core of GCN is the iterative message-passing process via graph convolution. This process can be formulated by 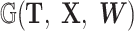 , where W = {W1, W2, ⋅⋅⋅, Wl} is the weight matrix of each convolution layer, Hl is the output of the lth convolution layer, and f(·) is the nonlinear activation function.
, where W = {W1, W2, ⋅⋅⋅, Wl} is the weight matrix of each convolution layer, Hl is the output of the lth convolution layer, and f(·) is the nonlinear activation function.
Figure 2:
The fundamental operation of a GCN. A GCN functions by first representing data as a graph, with the entire graph depicted through a topology illustrating node connectivity and a feature matrix. It then conducts iterative message passing through graph convolution, where nodes gather information from neighbors, subject it to transformation via learnable weights (Wl) and nonlinear activation functions [f(·)], and subsequently update their representations, with the final node representations used for various tasks like node or graph classification.
 |
(8) |
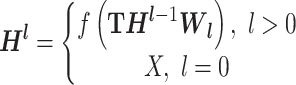 |
(9) |
In each convolution layer, Wl acts like a filter to select and aggregate information (features) from neighboring nodes along the topology and subsequently convey it back to the center node, updating its representation (Fig. 2). The incorporation of a nonlinear activation function in each convolution layer is pivotal for capturing and learning intricate patterns and relationships embedded in the graph data. Through the stacking of multiple graph convolutional layers, information from high-order neighbors, indirectly connected via other nodes, can be propagated along graph topology. After the iterations, the final node representations can be used for various tasks, such as node classification or graph classification. In essence, GCN processes graph-structured data by iteratively passing messages between nodes, allowing each node to incorporate information from its neighbors and update its own representation. This process leverages the graph structure to capture complex relationships and dependencies within the data, making it particularly useful for tasks involving graph-structured data.
Expanding on the foundational GCN graph convolution, various studies have explored innovative approaches in both structuring graph data and designing model architectures, tailored to a diverse range of applications. For graph data organization, some studies employ population-level graphs as input (Parisot et al., 2018; Huang and Chung, 2022; Li et al., 2022; Zhu et al., 2022), where each node represents an individual subject, and the edges denote correlations between subjects. For instance, Parisot et al. (2018) employed a sparse graph representation of the population, associating nodes with imaging-based feature vectors and integrating phenotypic information as edge weights. Unlike Parisot et al. (2018), which manually constructed a static affinity population graph, (Huang and Chung, 2022) introduced a framework for automatic learning to build a population graph with variational edges. Similarly, Zhu et al. (2022) also adopted a dynamic graph learning strategy to adapt the neighborhood relationship of the population graph, generating robust node embeddings and refining correlations among all data points to enhance classifier performance. Moreover, Li et al. (2022) enhanced interpretability by incorporating feature and sample interpretation modules into the population graph learning process, facilitating the interpretation of feature and sample significance. By contrast, other studies use individual-level graphs (Zhang et al., 2021, 2020a, 2019), with each node representing a ROI, and the edges signifying the connectivity or correlation between these ROI. For example, Zhang et al. (2021) proposed a deep brain connectome to simultaneously model individual structural and functional networks for brain disease analysis. The structural network served as the initialization of graph topology, while the functional information iteratively updated the topology to maximize its classification power. The resulting deep connectome effectively integrates various network connectomes and characterizes their deep relationship as an “individual connectome signature.” Both Zhang et al. (2020a) and Zhang et al. (2019) followed a similar concept, constructing individual brain networks by integrating both structural and functional networks. However, they employed distinct neural network architectures to handle fMRI time-series data. Zhang et al. (2019) utilized recurrent neural networks (RNNs) to capture temporal dependencies within fMRI sequential data, whereas Zhang et al. (2020a) incorporated an attention layer to extract disease-related features for brain network construction, enhancing the interpretability of the deep model. Moreover, specific studies adopt a hierarchical approach, concurrently incorporating both individual and population graphs (Jiang et al., 2020; Li et al., 2021a). In Jiang et al. (2020), two GCNs were employed to model the individual brain functional network and the whole population network, respectively. A compact representation of individual brain network, employed as the node embedding, was learned automatically by a graph-level embedding learning GCN. Simultaneously, the population network was acquired by updating each node embedding in the graph data through aggregating the representations of its neighbors and itself. To better study the multi-scale nature of the brain network, Li et al. (2021b) applied multiple thresholds to generate multiple connectivity networks, reflecting different levels of the topological structure of the original connectivity network. The population network was also constructed using all subjects with the same sparsity level. In general, various types of graph, including individual, population, or multi-scale graphs, are constructed to represent brain networks from a data perspective. To enhance the capacity of GCNs in handling complex multi-scale and multi-modal brain networks, advanced models or techniques such as RNNs (Zhang et al., 2020a, 2019), attention layers (Zhang et al., 2020a), and transfer learning (Li et al., 2021b) have been integrated into GCNs from a model architecture perspective. Moreover, innovative improvements to the vanilla GCNs, such as dynamic GCNs designs (Zhu et al., 2022; Zhang et al., 2021), which adaptively update graph topology or learn task-specific node/edge features during training, have been introduced, providing significant advantages over static counterparts. We have curated a selection of representative works and summarized them in Table 3 for reference.
Table 3:
Summary: of Notable GCN-Based Research in AD Study.
| Work | Dataset and sample size | Input graph | Model | Performance (accuracy) |
|---|---|---|---|---|
| Parisot et al. (2018) | ADNI: 289pMCI, 251sMCI | Graph: population. Node: Single subject with imaging based (T1) feature vectors. Edge: weighted using phenotypic information. | Vanilla spectral GCNs (Defferrard et al., 2016) | pMCI/sMCI: 0.80 |
| Zhang et al. (2019) | ADNI: 116NC, 93MCI | Graph: individual. Node: atlas-based brain region with rs-fMRI signal as features. Edge: SC. | GCRNN: combination of RNN and GCN | NC/MCI: 0.935 |
| Zhang et al. (2020a) | ADNI: 116NC, 93MCI | Graph: individual. Node: atlas-based brain region with rs-fMRI signal as features. Edge: learnable, integration of SC and rs-fMRI signal. | Deep cross-model attention network, which combine RNN, GCN, and attention layer | NC/MCI: 0.983 |
| Jiang et al. (2020) | ADNI: 99MCI, 34AD | Graph: both individual and population. Individual: FC. Population: node is single subject; edge is the learned embedding from FC. | Hi-GCN: a hierarchical GCN framework | AD/MCI: 0.785 |
| Li et al. (2021b) | ADNI: 99MCI, 34AD ABIDE: 403ASD, 468 NC | Graph: both individual and population. Individual: FC. Population: node is single subject; edge is the learned embedding from FC. | TE-HI-GCN: an ensemble of transfer hierarchical GCN. Transfer is conducted between different diseases: AD and ASD | ASD/NC: 0.765 AD/NC: 0.894 |
| Zhang et al. (2021) | ADNI: 116NC, 98MCI | Graph: individual, dynamic. Node: atlas-based brain region with FC as features. Edge: deep fusion of both structural and functional data, dynamically updated. | Deep brain connectome, multi-modal dynamic GCN | NC/MCI: 0.927 |
| Huang and Chung (2022) | ADNI: 289pMCI, 251sMCI TADPOLE: 557(NC + MCI + AD) | Graph: population. Node: Single subject. Edge: learnable variational edges using imaging and nonimaging data. | Vanilla spectral GCNs (Defferrard et al., 2016) | pMCI/sMCI: 0.7940 NC/MCI/AD: 0.8779 |
| Zhu et al. (2022) | ADNI: 51AD, 52NC, 43pMCI, 56sMCI | Graph: population, dynamic. Node: Single subject with gray matter volume as initial feature and dynamically updated. Edge: correlation of samples, and dynamically updated. | Dynamic GCN, coupling interpretable feature learning with dynamic graph learning | Refer to Fig. 2 in the paper |
| Li et al. (2022) | ADNI: 226NC, 226pMCI, 163sMCI, 186AD | Graph: population. Node: Single subject with gray matter volume as features. Edge: correlation of samples. | FSNet: a novel dual interpretable GCN, can simultaneously select significant features and samples | AD/NC: 0.844 AD/MCI: 0.736 NC/MCI: 0.718 sMCI/pMCI: 0.702 |
Abbreviations: sMCI: stable mild cognitive impairment; pMCI: progressive MCI; ASD: autism spectrum disorder.
Discussion and Conclusion
Recent advancements in AD research highlight the intricate connection between AD pathology and brain networks. Consequently, a substantial amount of research has focused on utilizing brain network-based approaches for the classification and prediction of AD conversion. This review specifically focuses on studies rooted in graph theory and deep graph convolutional neural networks. Numerous AD-related brain connections have been unveiled, accompanied by the introduction of more robust deep models. The ongoing exploration of connectome-based research has undeniably yielded valuable insights into graph data organization, analysis, and model design, laying the foundation for promising future investigations. To further deepen our understanding of AD, several critical gaps exist that require attention in future research endeavors:
Interpretability: The inherent complexity of GCNs, like other deep neural networks, renders them opaque black-box models. Interpreting these models necessitates a thorough understanding of the mechanisms governing their decision-making processes. In the realm of connectome-based AD studies, unraveling the reasoning behind the predictions made by GCN-based models is not just desirable, it is imperative. This interpretability not only facilitates the comprehension of the intricate links between brain networks and AD development mechanisms but also reinforces the trust that healthcare professionals and patients can place in these models. While strides have been made in developing interpretation techniques for graph-based deep models, such as GNNExplainer (Ying et al., 2019) and GraphLIME (Huang et al., 2022), evaluating the interpretability of these models remains a formidable challenge. This challenge stems from our limited knowledge of both brain networks and AD, making it crucial to continue exploring innovative approaches to enhance the interpretability of GCNs in medical domain.
Multimodality: To comprehensively capture the intricacies of brain networks within the context of brain diseases such as AD, it is vital to consider multimodal data. This involves integrating various types of data, including structural and functional connectivity, alongside clinical and genetic information, to form a holistic understanding of the disease's multifaceted nature. While previous research has made numerous attempts to fuse diverse modalities (Zhang et al., 2021, 2020a, 2019; Lyu et al., 2021; Wang et al., 2023), most existing multimodal studies predominantly focus on different imaging modalities. However, the growing accessibility of biomedical data from extensive biobanks, electronic health records, medical imaging, and wearable and ambient biosensors provides a significant opportunity to propel multimodal studies forward. Capitalizing on these advancements, there is a pressing need for more efficient multimodal deep models that can seamlessly integrate data from both imaging and nonimaging modalities. This includes biosensors, genetics, clinical records, and environmental factors. However, due to several key factors, effectively and seamlessly amalgamating imaging and nonimaging modalities remains a formidable challenge. One of the foremost challenges arises from the inherent heterogeneity between different modalities. Each modality possesses unique characteristics, and efficiently harmonizing and fully exploiting the potential of each modality is a central challenge in the design of multimodal models. Additionally, practical applications often grapple with the issue of missing modality. Addressing the problem of data incompleteness and effectively handling such gaps in multimodal data remains a critical concern in multimodal analysis. Developing robust strategies to handle missing data and creating models that can accommodate these real-world challenges is essential for the success of multimodal approaches in the study of AD and the whole medical imaging domain.
In conclusion, this review offers a comprehensive overview of the dynamic landscape of AD research in the context of brain network analysis. It underscores the pivotal role of brain networks in elucidating the mechanisms underpinning AD and their profound impact on the disease progression. The review has shed light on the rich spectrum of graph-based methods employed in AD investigations, classifying them into traditional graph theory-based approaches and cutting-edge deep graph neural network-based techniques. These methodologies have significantly enriched our comprehension of AD by unveiling intricate patterns within brain networks. Consequently, they have opened doors to pioneering diagnostic tools, predictive models, and the identification of potential biomarkers. However, it is crucial to acknowledge that numerous substantial challenges lie ahead. These challenges encompass issues like interpretability of complex models and the effective integration of multimodal data, especially in the context of limited medical datasets. Addressing these hurdles remains paramount for the continued advancement of AD research and its translation into clinical practice.
Acknowledgement
This work was supported by National Institutes of Health (R01AG075582, RF1NS128534).
Contributor Information
Lu Zhang, Department of Computer Science and Engineering, The University of Texas at Arlington, Arlington, TX 76019, USA.
Junqi Qu, Department of Computer Science and Engineering, The University of Texas at Arlington, Arlington, TX 76019, USA.
Haotian Ma, Department of Computer Science and Engineering, The University of Texas at Arlington, Arlington, TX 76019, USA.
Tong Chen, Department of Computer Science and Engineering, The University of Texas at Arlington, Arlington, TX 76019, USA.
Tianming Liu, Department of Computer Science, The University of Georgia, Athens, GA 30602, USA.
Dajiang Zhu, Department of Computer Science and Engineering, The University of Texas at Arlington, Arlington, TX 76019, USA.
Author contributions
Lu Zhang conceptualized and designed the structure of the review, conducted the literature search and data collection, drafted the initial manuscript, and managed the submission process. Junqi Qu, Haotian Ma, and Tong Chen conducted the literature search and edited the formulas. Tianming Liu and Dajiang Zhu reviewed and synthesized the primary findings, provided expert opinions on specific topics, and contributed to the overall coherence of the manuscript.
Conflict of interests
One of the authors, Tianming Liu, is also the editor board member of Psychoradiology. He was blinded from reviewing or making decisions on the manuscript.
References
- Alstott J, Breakspear M, Hagmann P et al. (2009) Modeling the impact of lesions in the human brain. PLoS Comput Biol. 5:e1000408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alzheimer's Association (2018) 2018 Alzheimer's disease facts and figures. Alzheimer's Dementia. 14:367–429. [Google Scholar]
- Barabási A-L, Albert R (1999) Emergence of scaling in random networks. Science. 286:509–12. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Mattiello J, Lebihan D (1994) Mr diffusion tensor spectroscopy and imaging. Biophys J. 66:259–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Bullmore E (2006) Small-world brain networks. Neuroscientist. 12:512–23. [DOI] [PubMed] [Google Scholar]
- Bateman RJ, Xiong C, Benzinger TLS et al. (2012) Clinical and biomarker changes in dominantly inherited Alzheimer's disease. N Engl J Med. 367:795–804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batista-García-Ramó K, Fernández-Verdecia C (2018) What we know about the brain structure–function relationship. Behav Sci. 8:39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behfar Q, Behfar SK, Von Reutern B et al. (2020) Graph theory analysis reveals resting state compensatory mechanisms in healthy aging and prodromal Alzheimer's disease. Front Aging Neurosci. 12:576627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bejanin A, Schonhaut DR, La Joie R et al. (2017) Tau pathology and neurodegeneration contribute to cognitive impairment in Alzheimer's disease. Brain. 140:3286–300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bero AW, Yan P, Roh JH et al. (2011) Neuronal activity regulates the regional vulnerability to amyloid-β deposition. Nat Neurosci. 14:750–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal B, Zerrin Yetkin F, Haughton VM et al. (1995) Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med. 34:537–41. [DOI] [PubMed] [Google Scholar]
- Blondel VD, Guillaume J-L, Lambiotte R et al. (2008) Fast unfolding of communities in large networks. J Stat Mech. 2008:P10008. [Google Scholar]
- Braak H, Braak E (1991) Neuropathological stageing of Alzheimer-related changes. Acta Neuropathol. 82:239–59. [DOI] [PubMed] [Google Scholar]
- Brandes U (2001) A faster algorithm for betweenness centrality. J Math Sociol. 25:163–77. [Google Scholar]
- Brookmeyer R, Abdalla N, Kawas CH et al. (2018) Forecasting the prevalence of preclinical and clinical Alzheimer's disease in the United States. Alzheimer's Dementia. 14:121–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckner RL, Sepulcre J, Talukdar T et al. (2009) Cortical hubs revealed by intrinsic functional connectivity: mapping, assessment of stability, and relation to Alzheimer's disease. J Neurosci. 29:1860–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckner RL, Snyder AZ, Shannon BJ et al. (2005) Molecular, structural, and functional characterization of Alzheimer's disease: evidence for a relationship between default activity, amyloid, and memory. J Neurosci. 25:7709–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busche MA, Chen X, Henning HA et al. (2012) Critical role of soluble amyloid-β for early hippocampal hyperactivity in a mouse model of Alzheimer's disease. Proc Natl Acad Sci USA. 109:8740–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busche MA, Hyman BT (2020) Synergy between amyloid-β and tau in Alzheimer's disease. Nat Neurosci. 23:1183–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busche MA, Wegmann S, Dujardin S et al. (2019) Tau impairs neural circuits, dominating amyloid-β effects, in Alzheimer models in vivo. Nat Neurosci. 22:57–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calafate S, Buist A, Miskiewicz K et al. (2015) Synaptic contacts enhance cell-to-cell tau pathology propagation. Cell Rep. 11:1176–83. [DOI] [PubMed] [Google Scholar]
- Dai Z, Lin Q, Li T et al. (2019) Disrupted structural and functional brain networks in Alzheimer's disease. Neurobiol Aging. 75:71–82. [DOI] [PubMed] [Google Scholar]
- Dai Z, Yan C, Li K et al. (2015) Identifying and mapping connectivity patterns of brain network hubs in Alzheimer's disease. Cereb Cortex. 25:3723–42. [DOI] [PubMed] [Google Scholar]
- De Calignon A, Polydoro M, Suárez-Calvet M et al. (2012) Propagation of tau pathology in a model of early Alzheimer's disease. Neuron. 73:685–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Defferrard M, Bresson X, Vandergheynst P (2016) Convolutional neural networks on graphs with fast localized spectral filtering. Adv Neural Info Proc Syst, 29. [Google Scholar]
- Ebadi A, Dalboni Da Rocha JL, Nagaraju DB et al. (2017) Ensemble classification of Alzheimer's disease and mild cognitive impairment based on complex graph measures from diffusion tensor images. Front Neurosci. 11:56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Estrada E, Hatano N (2008) Communicability in complex networks. Phys Rev E. 77:036111. [DOI] [PubMed] [Google Scholar]
- Fagiolo G (2007) Clustering in complex directed networks. Phys Rev E. 76:026107. [DOI] [PubMed] [Google Scholar]
- Feldt Muldoon S, Bridgeford EW, Bassett DS (2015) Small-world propensity in weighted, real-world networks. arXiv e-prints, (pp. arXiv–1505). [DOI] [PMC free article] [PubMed]
- Freeman LC et al. (2002) Centrality in social networks: conceptual clarification. Social Network: Critical Concepts in Sociology. 1:Routledge; London238–63. [Google Scholar]
- Friedman J, Hastie T, Tibshirani R (2008) Sparse inverse covariance estimation with the graphical lasso. Biostatistics. 9:432–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ (1994) Functional and effective connectivity in neuroimaging: a synthesis. Hum Brain Mapp. 2:56–78. [Google Scholar]
- Ghosh-Dastidar S, Adeli H, Dadmehr N (2008) Principal component analysis-enhanced cosine radial basis function neural network for robust epilepsy and seizure detection. IEEE Trans Biomed Eng. 55:512–8. [DOI] [PubMed] [Google Scholar]
- Girvan M, Newman MEJ (2002) Community structure in social and biological networks. Proc Natl Acad Sci USA. 99:7821–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grothe MJ, Teipel SJ (2016) Spatial patterns of atrophy, hypometabolism, and amyloid deposition in Alzheimer's disease correspond to dissociable functional brain networks. Hum Brain Mapp. 37:35–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guimerà R, Amaral LAN (2005) Cartography of complex networks: modules and universal roles. J Stat Mech. 2005:P02001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagmann P, Kurant M, Gigandet X et al. (2007) Mapping human whole-brain structural networks with diffusion mri. PLoS One. 2:e597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansson O, Grothe MJ, Strandberg TO et al. (2017) Tau pathology distribution in Alzheimer's disease corresponds differentially to cognition-relevant functional brain networks. Front Neurosci. 11:167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoenig MC, Bischof GN, Seemiller J et al. (2018) Networks of tau distribution in Alzheimer's disease. Brain. 141:568–81. [DOI] [PubMed] [Google Scholar]
- Huang Q, Yamada M, Tian Y et al. (2022) Graphlime: local interpretable model explanations for graph neural networks. IEEE Trans Knowl Data Eng. 35:1–6., [Google Scholar]
- Huang Y, Chung ACS (2022) Disease prediction with edge-variational graph convolutional networks. Med Image Anal. 77:102375. [DOI] [PubMed] [Google Scholar]
- Hughes J (2017) This Is One of the Biggest Global Health Crises of the 21st Century. In World Economic Forum. [Google Scholar]
- Humphries MD, Gurney K (2008) Network ‘small-world-ness’: a quantitative method for determining canonical network equivalence. PLoS ONE. 3:e0002051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison RM, Mirsattari SM, Jones CK et al. (2010) Functional networks in the anesthetized rat brain revealed by independent component analysis of resting-state fMRI. J Neurophysiol. 103:3398–406. [DOI] [PubMed] [Google Scholar]
- International AD (2019) World Alzheimer Report 2019: Attitudes to Dementia. Alzheimer's Disease International: London. [Google Scholar]
- Jack CR Jr, Bennett DA, Blennow K et al. (2018a) Nia-aa research framework: toward a biological definition of Alzheimer's disease. Alzheimer's Dementia. 14:535–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack CR Jr, Bennett DA, Blennow K et al. (2018b) Nia-aa research framework: toward a biological definition of Alzheimer's disease. Alzheimer's Dementia. 14:535–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jalili M (2017) Graph theoretical analysis of Alzheimer's disease: discrimination of AD patients from healthy subjects. Info Sci. 384:145–56. [Google Scholar]
- Jiang H, Cao P, Xu M et al. (2020) Hi-GCN: a hierarchical graph convolution network for graph embedding learning of brain network and brain disorders prediction. Comput Biol Med. 127:104096. [DOI] [PubMed] [Google Scholar]
- John M, Ikuta T, Ferbinteanu J (2017) Graph analysis of structural brain networks in Alzheimer's disease: beyond small world properties. Brain Struct Funct. 222:923–42. [DOI] [PubMed] [Google Scholar]
- Jones DT, Graff-Radford J, Lowe VJ et al. (2017) Tau, amyloid, and cascading network failure across the Alzheimer's disease spectrum. Cortex. 97:143–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joo SH, Lim HK, Lee CU (2016) Three large-scale functional brain networks from resting-state functional MRI in subjects with different levels of cognitive impairment. Psychiatry Investig. 13:1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jucker M, Walker LC (2013) Self-propagation of pathogenic protein aggregates in neurodegenerative diseases. Nature. 501:45–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jucker M, Walker LC (2018) Propagation and spread of pathogenic protein assemblies in neurodegenerative diseases. Nat Neurosci. 21:1341–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kabbara A, Eid H, El Falou W et al. (2018) Reduced integration and improved segregation of functional brain networks in Alzheimer's disease. J Neural Eng. 15:026023. [DOI] [PubMed] [Google Scholar]
- Kintali S (2008) Betweenness centrality: algorithms and lower bounds. arXiv preprint arXiv:0809.1906,.
- Kipf TN, Welling M (2016) Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907.
- Lang EW, Tomé AM, Keck IR et al. (2012) Brain connectivity analysis: a short survey. Comput Intell Neurosci. 2012:1–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latora V, Marchiori M (2001) Efficient behavior of small-world networks. Phys Rev Lett. 87:198701. [DOI] [PubMed] [Google Scholar]
- Leicht EA, Newman MEJ (2008) Community structure in directed networks. Phys Rev Lett. 100:118703. [DOI] [PubMed] [Google Scholar]
- Li H, Shi X, Zhu X et al. (2022) Fsnet: dual interpretable graph convolutional network for Alzheimer's disease analysis. IEEE Trans Emerg Top Comput Intell. 7:15–25. [Google Scholar]
- Li L, Jiang H, Wen G et al. (2021a) Te-hi-gcn: an ensemble of transfer hierarchical graph convolutional networks for disorder diagnosis. Neuroinformatics. 11:1–23. [DOI] [PubMed] [Google Scholar]
- Li L, Jiang H, Wen G et al. (2021b) Te-hi-gcn: an ensemble of transfer hierarchical graph convolutional networks for disorder diagnosis. Neuroinformatics. 11:1–23. [DOI] [PubMed] [Google Scholar]
- Liu Z, Zhang Y, Yan H et al. (2012) Altered topological patterns of brain networks in mild cognitive impairment and Alzheimer's disease: a resting-state fMRI study. Psychiatry Res Neuroimaging. 202:118–25. [DOI] [PubMed] [Google Scholar]
- Lyu Y, Yu X, Zhang L et al. (2021) Classification of mild cognitive impairment by fusing neuroimaging and gene expression data: classification of mild cognitive impairment by fusing neuroimaging and gene expression data. In The 14th Pervasive Technologies Related to Assistive Environments Conference(pp.26–32.). [Google Scholar]
- Mårtensson G, Pereira JB, Mecocci P et al. (2018) Stability of graph theoretical measures in structural brain networks in Alzheimer's disease. Sci Rep. 8:11592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman MEJ (2002) Assortative mixing in networks. Phys Rev Lett. 89:208701. [DOI] [PubMed] [Google Scholar]
- Newman MEJ (2003) The structure and function of complex networks. SIAM Rev. 45:167–256. [Google Scholar]
- Newman MEJ (2004a) Analysis of weighted networks. Phys Rev E. 70:056131. [DOI] [PubMed] [Google Scholar]
- Newman MEJ (2004b) Fast algorithm for detecting community structure in networks. Phys Rev E. 69:066133. [DOI] [PubMed] [Google Scholar]
- Newman MEJ (2006) Modularity and community structure in networks. Proc Natl Acad Sci USA. 103:8577–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onnela J-P, Saramäki J, Kertész J et al. (2005) Intensity and coherence of motifs in weighted complex networks. Phys Rev E. 71:065103. [DOI] [PubMed] [Google Scholar]
- Ossenkoppele R, Schonhaut DR, Schöll M et al. (2016) Tau pet patterns mirror clinical and neuroanatomical variability in Alzheimer's disease. Brain. 139:1551–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palla G, Derényi I, Farkas I et al. (2005) Uncovering the overlapping community structure of complex networks in nature and society. Nature. 435:814–8. [DOI] [PubMed] [Google Scholar]
- Palmqvist S, Schöll M, Strandberg O et al. (2017) Earliest accumulation of β-amyloid occurs within the default-mode network and concurrently affects brain connectivity. Nat Commun. 8:1214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parisot S, Ktena SI, Ferrante E et al. (2018) Disease prediction using graph convolutional networks: application to autism spectrum disorder and Alzheimer's disease. Med Image Anal. 48:117–30. [DOI] [PubMed] [Google Scholar]
- Park H-J, Kubicki M, Westin C-F et al. (2004) Method for combining information from white matter fiber tracking and gray matter parcellation. Am J Neuroradiol. 25:1318–24. [PMC free article] [PubMed] [Google Scholar]
- Pastor-Satorras R, Vázquez A, Vespignani A (2001) Dynamical and correlation properties of the internet. Phys Rev Lett. 87:258701. [DOI] [PubMed] [Google Scholar]
- Pearson RC, Esiri MM, Hiorns RW et al. (1985) Anatomical correlates of the distribution of the pathological changes in the neocortex in alzheimer disease. Proc Natl Acad Sci USA. 82:4531–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pereira JB, Ossenkoppele R, Palmqvist S et al. (2019) Amyloid and tau accumulate across distinct spatial networks and are differentially associated with brain connectivity. eLife. 8:e50830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piraveenan M, Prokopenko M, Zomaya AY (2008) Local assortativeness in scale-free networks. Europhys Lett. 84:28002. [Google Scholar]
- Protas H, Ghisays V, Goradia DD et al. (2023) Individualized network analysis: a novel approach to investigate tau pet using graph theory in the Alzheimer's disease continuum. Front Neurosci. 17:1089134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prusiner SB (1998) Prions. Proc Natl Acad Sci USA. 95:13363–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov M, Sporns O (2010) Complex network measures of brain connectivity: uses and interpretations. Neuroimage. 52:1059–69. [DOI] [PubMed] [Google Scholar]
- Saper CB, Wainer BH, German DC (1987) Axonal and transneuronal transport in the transmission of neurological disease: potential role in system degenerations, including alzheimer's disease. Neuroscience. 23:389–98. [DOI] [PubMed] [Google Scholar]
- Saramäki J, Kivelä M, Onnela J-P et al. (2007) Generalizations of the clustering coefficient to weighted complex networks. Phys Rev E. 75:027105. [DOI] [PubMed] [Google Scholar]
- Scheltens P, De Strooper B, Kivipelto M et al. (2021) Alzheimer's disease. Lancet North Am Ed. 397:1577–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seeley WW, Crawford RK, Zhou J et al. (2009) Neurodegenerative diseases target large-scale human brain networks. Neuron. 62:42–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serrano-Pozo A, Frosch MP, Masliah E et al. (2011) Neuropathological alterations in Alzheimer disease. Cold Spring Harb Perspect Med. 1:a006189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O, Honey CJ (2006) Small worlds inside big brains. Proc Natl Acad Sci USA. 103:19219–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O, Tononi G, Kötter R (2005) The human connectome: a structural description of the human brain. PLoS Comp Biol. 1:e42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tononi G, Sporns O, Edelman GM (1994) A measure for brain complexity: relating functional segregation and integration in the nervous system. Proc Natl Acad Sci USA. 91:5033–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villeneuve S, Rabinovici GD, Cohn-Sheehy BI et al. (2015) Existing pittsburgh compound-b positron emission tomography thresholds are too high: statistical and pathological evaluation. Brain. 138:2020–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Xu H, Wang M et al. (2023) A metabolism-functional connectome sparse coupling method to reveal imaging markers for Alzheimer's disease based on simultaneous PET/MRI scans. Hum Brain Mapp. 44:6020–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts DJ, Strogatz SH (1998) Collective dynamics of ‘small-world' networks. Nature. 393:440–2. [DOI] [PubMed] [Google Scholar]
- World Health Organization (2019) World Health Organization dementia factsheet.
- Wu JW, Hussaini SA, Bastille IM et al. (2016) Neuronal activity enhances tau propagation and tau pathology in vivo. Nat Neurosci. 19:1085–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Z, Pan S, Chen F et al. (2020) A comprehensive survey on graph neural networks. IEEE Trans Neural Netw Learning Syst. 32:4–24. [DOI] [PubMed] [Google Scholar]
- Xu F, Garai S, Duong-Tran D et al. (2022) Consistency of graph theoretical measurements of Alzheimer's disease fiber density connectomes across multiple parcellation scales. In 2022 IEEE International Conference on Bioinformatics and Biomedicine (BIBM)(pp.1323–8.). IEEE. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ying Z, Bourgeois D, You J et al. (2019) GNNExplainer: generating explanations for graph neural networks. Advances in Neural Information Processing Systems,32. [PMC free article] [PubMed] [Google Scholar]
- Yun J‐Y, Nyun Kim S, Young Lee T et al. (2016) Individualized covariance profile of cortical morphology for auditory hallucinations in first-episode psychosis. Hum Brain Mapp. 37:1051–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L, Wang L, Gao J et al. (2021) Deep fusion of brain structure-function in mild cognitive impairment. Med Image Anal. 72:102082. [DOI] [PubMed] [Google Scholar]
- Zhang L, Wang L, Zhu D (2020a) Jointly analyzing Alzheimer's disease related structure-function using deep cross-model attention network. In 2020 IEEE 17th International Symposium on Biomedical Imaging (ISBI)(pp.563–7.). IEEE. [Google Scholar]
- Zhang L, Wang L, Zhu D (2020b) Recovering brain structural connectivity from functional connectivity via multi-gcn based generative adversarial network. In Medical Image Computing and Computer Assisted Intervention– MICCAI 2020: 23rd International Conference, Lima, Peru, October 4–8, 2020, Proceedings, Part VII 23(pp.53–61.). Springer. [Google Scholar]
- Zhang L, Wang L, Zhu D (2022) Predicting brain structural network using functional connectivity. Med Image Anal. 79:102463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L, Zaman A, Wang L et al. (2019) A cascaded multi-modality analysis in mild cognitive impairment. In Machine Learning in Medical Imaging: 10th International Workshop, MLMI 2019, Held in Conjunction with MICCAI 2019, Shenzhen, China, October 13, 2019, Proceedings 10(pp.557–65.). Springer. [Google Scholar]
- Zhang W, Lv J, Li X et al. (2018) Experimental comparisons of sparse dictionary learning and independent component analysis for brain network inference from fMRI data. IEEE Trans Biomed Eng. 66:289–99. [DOI] [PubMed] [Google Scholar]
- Zhou J, Gennatas ED, Kramer JH et al. (2012) Predicting regional neurodegeneration from the healthy brain functional connectome. Neuron. 73:1216–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu Y, Ma J, Yuan C et al. (2022) Interpretable learning based dynamic graph convolutional networks for Alzheimer's disease analysis. Information Fusion. 77:53–61. [Google Scholar]
- Zielinski BA, Gennatas ED, Zhou J et al. (2010) Network level structural covariance in the developing brain. Proc Natl Acad Sci USA. 107:18191–6. [DOI] [PMC free article] [PubMed] [Google Scholar]




