Abstract

Coalbed methane (CBM) reservoirs are naturally fractured formations with cleats surrounding the coal matrix. Analyzing and predicting CBM production performance is challenging because of the complex fracture networks and gas–water two-phase flow, along with the permeability and porosity variation and time-dependent desorption. During depletion, pressure decreases and consequently stress increases, thereby decreasing cleat aperture and permeability, while the matrix shrinkage effect increases cleat width and permeability. The two effects compete with one another, and dominance depends on coal’s geomechanical properties and the change in reservoir properties. In addition, though the gas composition from CBM wells predominantly consists of methane, it contains traces of other gases like ethane, carbon dioxide, nitrogen, etc. The combined effects of pressure-dependent diffusivity, time-dependent desorption, and multicomponent sorption in a two-phase flowing CBM well make the flow dynamics in CBM reservoirs complex. A modified semi-analytical mathematical model is developed to characterize the time-dependent desorption and pressure-dependent diffusivity phenomena, also considering the dynamic variation of composition and multicomponent desorption for two-phase flow of CBM wells producing under semi-steady state conditions. The novelty of the model presented in this study lies in manifesting multicomponent sorption effects in the form of an equivalent single-component sorption phenomenon by establishing new transforms. A fully coupled mathematical model is developed that integrates multicomponent sorption effects in CBM reservoirs with pressure-dependent diffusivity and time-dependent desorption effects. The Article presents a new method to intertwine the desorption material balance of individual components with fully coupled flow equations and gives a workflow to predict and evaluate the production performance of a producing CBM well. The study reveals that a multicomponent, two-phase coalbed methane system can be represented in the form of an equivalent single-component single-phase system, thus paving the way for application of CBM flow equations valid for a single phase and single component. The results of the model have been verified using a CMG-GEM numerical simulator as well as in-field production data. This study brings out a novel computational approach for the compositional simulation of the CBM wells, which is unconditionally stable and involves less complexity than commercial simulators, without compromising the accuracy of the results. The findings of this study can help improve the understanding of the complex flow behavior of CBM reservoirs, where multiple phenomena occur simultaneously, like multicomponent sorption, two-phase flow, pressure-dependent diffusion, and time-dependent desorption.
1. Introduction
Coalbed methane (CBM) reservoirs, because of their distinctive features and high storage potential, have been the subject of growing research and investigation.1 Analyzing and predicting the production profile for CBM reservoirs is challenging because of the dual porosity model and desorption lag due to the concentration kinetics of the matrix.2−4 The production of CBM involves the processes of desorption, diffusion, and seepage, wherein the desorption process conforms to the Langmuir model,5 the diffusion process is driven by Fick’s law, and the seepage process conforms to Darcy’s flow. Several researchers have given models to characterize the CBM performance.6−14 Taking inspiration from pseudopressure functions conceptualized by Al-Hussainy et al.,15 Kamal and Six9 formulated pseudopressure transforms to incorporate two-phase flow effects in CBM reservoirs. A few other researchers proposed a type curve approach to represent two-phase flow effects and instantaneous desorption effects in CBM wells.9,12,16 These models successfully captured the macropore transport mechanism and micropore desorption characteristics of CBM reservoirs; however, the important aspect of pressure-dependent permeability and porosity in CBM reservoirs was missing in the said models.
Stewart17 was among the first researchers who extended the concept to pseudopressure transforms to define a stress-dependent pseudopressure function that assimilates within itself the stress-dependent porosity and permeability using the Palmer and Mansoori equation.18 Later on, Burgoyne and Shrivastava,13 Upadhyay and Laik,19,20 and Salmachi et al.21 incorporated the transport phenomena in both micropores (coal matrix) and macropores (cleats) with pressure-dependent diffusivity effects. However, these models are limited to capturing single-phase flow conditions and instantaneous desorption effects only. Taking inspiration from the work of Perrine,22 who defined modified a pseudopressure function for capturing multiphase flow effects in conventional hydrocarbon wells, Neelu et al.23 proposed a fully coupled semi-analytical model that describes two-phase flow effects in CBM wells along with time-dependent desorption and pressure-dependent diffusivity effects. However, the mentioned semi-analytical model is valid for evaluating and predicting the performance of CBM wells having composition limited to a single component (CH4) only.
Also, the gas desorption capacity and the orthotropic feature, which is an inherent coal property associated with the coal cleat system, exhibit a concrete essential impact on the gas production performance.24 Therefore, for a multicomponent system, gas desorption parameters (Langmuir pressure and Langmuir volume) for each individual component have been accounted for in our proposed model. Another factor to be considered is the dominant impact of pressure-propagation behavior (i.e., dynamic pressure and saturation distribution in desorption area) in prominently low-permeability (<1 millidarcy) CBM wells,25 which is not as essential in our study, as the permeability ranges are on higher side, but still taken into consideration using the two-phase flow transform, i.e., stress-dependent adjusted pressure (SDAP). Recent advanced theoretical studies on adsorption at the molecular level established using the profound physical principle of equilibrium of a particle or entities indicate the enhanced reliability of results and facilitate analysis,26 which is also the basis of our study, i.e., stress-equilibrated pressure (SEP) and desorption-equilibrated pressure (DEP) calculations, with the added benefit of field-wide-scale practical applicability.
Gas held in coal deposits is composed primarily of methane but can contain significant amounts of other gases, most notably CO2, nitrogen, and ethane. The CO2 amount in CBM gas is essential to predict so as to design completions and production surface facilities, as CO2 is corrosive in nature. However, single-component fully coupled CBM models are not applicable to such reservoirs that contain additional gases apart from methane. In addition, single-component CBM models are not valid for simulating the conditions of enhanced CBM recovery, where CO2 sequestration is implemented in CBM reservoirs for incremental methane recovery. Also, other gases, which are present in traces (like H2S27), need to be incorporated in the production performance to accurately predict the methane gas production and recovery with time.
Unlike simulating the primary recovery of CBM reservoirs using single-component CBM model, multicomponent models have to account for additional complicated phenomena28,29 in the form of multicomponent gas sorption. Several models have been proposed to describe the multicomponent adsorption behavior, such as the extended Langmuir model,30 the ideal-adsorbed-solution model,31−33 and the 2D EOS model.34,35 However, there are only a few analytical mathematical models36,37 that incorporate the multicomponent sorption behavior into the flow dynamics of CBM wells. There are numerical simulators like CMG-GEM, SIMED II, ECLIPSE, and COMET 3 that have the features of CBM modeling. CMG-GEM and SIMED II are capable of handling the simulation of multicomponent systems. On the other hand, ECLIPSE is a black oil simulator with additional features for CBM modeling; however, it can handle up to two gas components (binary gas sorption). COMET 3 simulator can handle up to three gas components.
The current study introduces an alternative and novel semi-analytical model for use in the simulation of CBM wells with features of fully coupled multicomponent sorption kinetics, unsteady desorption, and pressure-dependent diffusivity effects. In this paper, we are presenting a new mathematical model that
-
1.
Integrates the available knowledge to establish a new mathematical model that couples four major conditions that drive methane recovery from CBM wells, i.e., (1) two-phase flow, (2) pressure-dependent diffusivity, (3) unsteady time-dependent desorption, and (4) multicomponent sorption kinetics
-
2.
Gives a novel method to change multicomponent system into an equivalent single-component model by introducing new transforms, like equivalent Langmuir pressure, equivalent Langmuir volume, and equivalent Langmuir sorption strain
-
3.
Presents a material balance approach for multicomponent sorption CBM system, thus giving a method alternative to flash calculations used in compositional simulations
-
4.
Proposes a method to evaluate the performance of CBM wells and quantify key reservoir parameters, geomechanical parameters, and component specific sorption behavior (swelling/shrinkage parameters)
The workflow presented in this study can easily be programmed in python, MATLAB, FORTRAN, or any scripting language. In the following sections, we develop the fully coupled mathematical model. The semi-analytical solution of the mathematical model is achieved by developing a research code, whose performance is validated with CMG-GEM numerical simulator. The results of the semi-analytical mathematical model presented in this study have also been validated with the actual in-field production data from a CBM field.
2. Mathematical Model
In this section, we present the basic equations for multicomponent two-phase flow within CBM reservoirs that exhibit dual-porosity single-permeability behavior where fluid flow takes place in a cleat system and gas desorption–diffusion takes place in the coal matrix.
2.1. Fluid-Flow Model (Single-Component System)
In CBM reservoirs, the mass balance equation is applied in both cleat and matrix systems to describe the diffusivity equation for each phase (gas and water). Seidle38 showed that a dual-porosity system of CBM reservoirs can be reduced to an equilibrium desorption single-porosity system by incorporating sorption compressibility within the total compressibility of the system. Later on, Neelu et al.23 leveraged the concept to describe the diffusivity equation for gas and water in CBM reservoirs including nonequilibrium desorption effects.
| 1 |
| 2 |
Eqs 1 and 2 can be combined to a single equation by adding
| 3 |
where  is defined as the total system compressibility
(Ct) and
is defined as the total system compressibility
(Ct) and  is defined as the total
relative mobility
(λrt). CS is the sorption
compressibility given by
is defined as the total
relative mobility
(λrt). CS is the sorption
compressibility given by 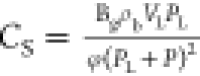
2.2. Time-Dependent Desorption Model
In this study, we are leveraging the concept used by Neelu et al.23 to incorporate time-dependent desorption effects within the total compressibility of the system. In eq 3, the nonequilibrium desorption effects are incorporated in the form of a dimensionless time delay factor (τD) given by
| 4 |
The use of a dimensionless time delay factor (τD) enables us to investigate the impact of time-dependent desorption over wide range, where τD varies from 1 to ∞ depending upon different values of desorption time (τ).
2.3. Pressure-Dependent Diffusivity Model (Single-Component System)
CBM reservoirs undergo changes in cleat porosity and permeability with pressure depletion during production from CBM wells. Pressure depletion due to production from CBM wells causes an increase in effective stress that counteracts the matrix shrinkage effects caused by gas desorption, leading to changes in cleat porosity and permeability in CBM reservoirs. Several studies have established the relationship between coal cleat porosity and pressure by combining coal geomechanics with sorption-induced coal swelling/shrinkage.18,39−41 In this study, the Palmer and Mansoori18 model is used to relate cleat porosity with pressure.
| 5 |
Using matchstick geometry model, a cubic relation can be established between cleat permeability and porosity.42 Later on, to account for the heterogeneity of the cleat network, Upadhyay and Laik19,20 and Neelu et al.23 incorporated the nth exponent relationship between cleat permeability and porosity.
| 6 |
Here, ki and φi represent the initial
cleat permeability and porosity, respectively, and α is a constant
given by 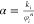 . The changes
in cleat porosity and permeability
with pressure depletion as established by eqs 5 and 6, which lead to
pressure-dependent diffusivity, can be accounted for in CBM flow equations
by substituting k = αφn in eq 3.
. The changes
in cleat porosity and permeability
with pressure depletion as established by eqs 5 and 6, which lead to
pressure-dependent diffusivity, can be accounted for in CBM flow equations
by substituting k = αφn in eq 3.
| 7 |
Neelu et al.23 presented a new pressure-transform,  , in the form of stress-dependent adjusted
pressure (SDAP) that reduces eq 7 to a single-phase diffusivity equation. The SDAP transform
includes the combined effect of two-phase flow and pressure-dependent
diffusivity. Equation 7 thus reduces to
, in the form of stress-dependent adjusted
pressure (SDAP) that reduces eq 7 to a single-phase diffusivity equation. The SDAP transform
includes the combined effect of two-phase flow and pressure-dependent
diffusivity. Equation 7 thus reduces to
| 8 |
2.4. Multicomponent Sorption Model
Yang30 presented an extended Langmuir isotherm for the multicomponent gas adsorption effects, which expresses the surface coverage of the individual component in the form of fractional proportions. The gas content of component n is given by
 |
9 |
where VLn and PLn are Langmuir volume and Langmuir pressure of the nth component, respectively, and yn is the mole fraction of nth component in gas phase.
For an n component system, the total gas content will be given by
 |
10 |
By dividing numerator and
denominator of eq 10 by  , eq 10 can be rearranged as
, eq 10 can be rearranged as
 |
11 |
By comparing eq 11 with the single-component Langmuir equation (GC = VLP/(PL + P)), we are introducing new terms “equivalent Langmuir volume (VLeq)” and “equivalent Langmuir pressure (PLeq)” in this paper to be expressed as
 |
12 |
Therefore, with the application of VLeq and PLeq, the multicomponent sorption model can be reduced to a single-component model. The transformation of a multicomponent system to a single-component system thus enables the application of eq 7, which assimilates within itself the two phase flow conditions, pressure-dependent diffusivity and time-dependent desorption effects.
2.5. Multicomponent Volumetric Strain Model
Seidle and Huitt43 and Robertson and Christiansen44 proposed a Langmuir-type equation to describe volumetric shrinkage/swelling behavior with pressure for single-component sorption.
| 13 |
Here, εL is the Langmuir sorption strain and εs is the matrix volumetric strain.
Similar to an extended Langmuir equation, eq 13 can be expressed for multicomponent sorption as
 |
14 |
By comparing eqs 13 and 14, we are introducing a new term as “equivalent Langmuir sorption strain (εLeq)” in this paper to be expressed as
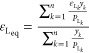 |
15 |
Therefore, with the application of εLeq and PLeq, the multicomponent volumetric strain model can be reduced to a single-component volumetric strain model, thus enabling the direct application of the Palmer and Mansoori18 model expressed in eq 5, where εL is replaced by εLeq and PL is replaced by PLeq. In this Article, we are introducing a modified form of the Palmer and Mansoori18 equation that enables the application of the equation for multicomponent sorption.
| 16 |
2.6. Semianalytical Solution for Semi-Steady State Conditions
The CBM flow equation given by eq 8 imbibes within itself the combined effects of two-phase flow, nonequilibrium desorption, and pressure-dependent diffusivity. However, the equation is limited to applications for single-component system. In this study, we are presenting a method that transforms a multicomponent system into an equivalent single-component system. The transforms (VLeq, PLeq, and εLeq) as defined above enable the application of eq 8 for multicomponent systems.
The unique feature of eq 8 is that it represents a two-phase CBM flow equation, including time-dependent desorption and pressure-dependent diffusivity effects, in the form of a single phase diffusivity equation. With the application of the Langmuir volume transform (VLeq), Langmuir pressure transform (PLeq), and Langmuir sorption strain transform (εLeq), eq 8 can be used for multicomponent systems, too. Therefore, eq 8, along with the said transforms incorporated, integrates four conditions that drive methane recovery from CBM wells: (1) two phase flow, (2) time-dependent desorption, (3) pressure-dependent diffusivity, and (4) multicomponent sorption system.
The semisteady state conditions of flow correspond to (1) no-flow boundary conditions at the outer boundary and (2) application of material balance within the drainage area of the reservoir. Since the form of eq 8 is similar to diffusivity equation for single-phase flow, its solution for semi-steady state flow conditions will also be identical to that for the single-phase solution. Neelu et al.23 presented the semi-steady state solution to eq 8 as a material balance equation and inflow equation given by
| 17 |
and
| 18 |
where tϑ–1 and tϑ denote
previous and current time steps, respectively; qt = qgBg + qwBw;  and
and  .
.
Also,
| 19 |
Equation 17 suggests that in a two-phase multicomponent CBM well flowing under the conditions of pressure-dependent permeability and time-dependent desorption, the application of the semi-analytical approach can give the average SDAP at current time step, (P̅a)ϑ, with the adjusted time (tadjusted) evaluated at every time step and the values for total fluid rate (qt), porosity (φ), and total system compressibility (Ct) used from the previous time step. For the estimation of Ct, the sorption compressibility (Cs) of the multicomponent system can be evaluated by transforming a multicomponent system into an equivalent single-component system using the concept of equivalent Langmuir volume (VLeq) and equivalent Langmuir pressure (PLeq) discussed above. Porosity (φ) at any time step is to be estimated using the equivalent Langmuir sorption strain (εLeq) in eq 16.
The novelty of this study lies in the formulation of the concept of equivalent Langmuir volume (VLeq), equivalent Langmuir pressure (PLeq), and equivalent Langmuir sorption strain (εLeq), which transforms the multicomponent sorption system into an equivalent single-component system and thus enables the application of eqs 17 and 18 to evaluate and predict the performance of a CBM well. However, it is important to note that it requires the mole fraction of the components to be known at any time step for estimating the equivalent Langmuir volume (VLeq), equivalent Langmuir pressure (PLeq), and equivalent Langmuir sorption strain (εLeq). In the following section, we develop the material balance model for estimating mole fractions at any time step.
3. Material Balance Model for Components
In this section, the material balance model for individual component is developed. This concept is partially taken from Seidle,45 in which following assumptions were made for MBE:
Water saturation is zero in cleats. Only gas is present in cleats.
Ideal gas assumption (gas deviation factor, Z = 1).
Time-dependent desorption is not considered.
Complete removal of gas after each iteration.
In this study, we are eliminating above assumptions in the material balance equation. Figure 1 shows conditions existing in a coal cleat and matrix at two consecutive time steps (the previous time step is denoted by i).
Figure 1.
MBE tank model conceptualization for multi-component desorption.
In the Figure 1, the yellow arrow shows desorption and the shaded part in orange represents the amount of gas in matrix, whereas the shaded part in green represents the amount of gas in cleat. Let us assume that at a current time step (tϑ) the adsorbed gas and free gas amount are Ga and Gf, respectively. Let us denote the corresponding amounts as in the previous time step (tϑ–1) as Gai and Gfi, respectively. Applying the material balance equation for individual components between two consecutive time steps (tϑ–1and tϑ) and considering methane, we find the total methane content (sorbed + free) at the old time step (scf/ton) is equal to the total methane content (sorbed + free) at the new time step (scf/ton) plus the produced methane content during old and new time steps (scf/ton).
| 20 |
In the equation above, the term (GaCH4 + GfCH4) represents the total methane content (sorbed + free) at the current time step. Let us denote it as GCH4. Now, eq 20 becomes
| 21 |
where
 |
 |
 |
Substituting the above expressions in eq 21, the CH4 desorption MBE can be expressed as
 |
22 |
The above equation, eq 22, represents the material balance equation applied on the methane (CH4) component. For n number of components, the above material balance equation can be written for individual components. For the ease of representation, the components are denoted in the subscript as 1, 2, 3, ..., n.
 |
23 |
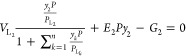 |
24 |
...
 |
25 |
Apart from the above equations, there is an additional equation that requires the sum of mole fractions to be equal to 1, i.e.,
| 26 |
The above set of (n + 1) equations can be solved simultaneously to find (n + 1) number of variables (n number of mole fractions plus the value of P, i.e., desorption-equilibrated pressure or DEP).
3.1. Method of Solving for Pressure and Mole Fraction from System of Two Desorption MBEs (Two Components)
Desorption MBEs, i.e. eqs 23–25, for binary (two) components can be conveniently rearranged as functions in two variables P (desorption-equilibrated pressure or DEP) and y2 (mole fraction of CO2, i.e., the second component):
 |
27 |
and
 |
28 |
The above simultaneous nonlinear equations in two or more variables can be solved using Newton’s method by formulating a Jacobian matrix. The detailed derivation for two or multiple variables is shown in Appendix A. The solving iterative scheme (i → i + 1) is given as
| 29 |
where
 |
 |
 |
 |
Continue iterating the pressure and mole fraction values until convergence tolerance achieved.
Now, final pressure can be estimated as the average value of the above DEP and SEP values.
The detailed methodology for solving nonlinear equations for “n” number of components is explained in Appendix A.
4. Method of Performance Prediction and Performance Evaluation of a Two-Phase Multicomponent CBM Well Considering Time-Dependent Desorption and Pressure-Dependent Diffusivity Effect Conditions
4.1. Method of Performance Prediction
The steps to predict Pwf, P̅, and the mole fraction of components for multicomponent two-phase flow CBM wells are as follows:
-
1.
At time t = 0, the initial pressure P̅ = Pi, tadjusted = 0, the initial mole fraction of individual components is known, and VL and PL of individual components are known
-
2.
Estimate μg, Z, and Bg at pressure P̅ using standard correlations for the gas phase. For μg, the Lee–Gonzalez–Eakin equation46 is used; for the Z-value, the Peng–Robinson47,48 equation-of-state (EOS) is used. Similarly, estimate μw and Bw at pressure P̅ for water.
-
3.
With known VL and PL of individual components and mole fractions of individual components, estimate VLeq, PLeq, and εLeq using eqs 12 and 15.
-
4.
Given the values of geomechanical parameters (Am and K/M),φi, and n and estimated values of εLeq and PLeq, determine the porosity (φ) at P̅ using eq 16. Also, using eq 6, estimate permeability (k) at the pressure P̅
-
5.
Define the operating constraint on the surface water rate for the well (say qw = 200 bbl/day); At time t =0, cumulative water production Wp = 0.
-
6.
Estimate gas compressibility (Cg), sorption compressibility (Cs), and the dimensionless time delay factor (τD) at pressure P̅ using
-
7.
The water material balance for CBM reservoirs gives the value of water saturation (Sw) at P̅. We is the cumulative water influx from an extraneous water source. Subject to confirmation of water influx from noncoal formations, a suitable water influx model can be attached to the CBM reservoir. We are assuming We = 0 in this example for demonstration purposes.
| 30 |
-
8.
Determine total compressibility (Ct) at pressure P̅ using

-
9.
Define Corey’s model49 (by making assumptions on krge, krwe, nw, and ng) for the relative permeability curve.
-
10.
Determine water and gas relative permeability (krw and krg, respectively) at the estimated value of Sw at P̅.
-
11.
Estimate the total mobility of reservoir fluid (λt) using
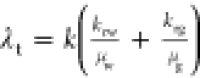 . Moreover, find the total
relative mobility
(λrt) using
. Moreover, find the total
relative mobility
(λrt) using 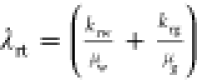 .
. -
12.Determine the surface gas flow rate (qg) using

31 -
13.Estimate total reservoir fluid rate (qt) using

32 -
14.
Say the first time time time is 5 days (say); estimate tadjusted with explicit formulation of the integral using the known values of qt, λrt, φ, and Ct from the previous time step using eq 19.
-
15.
Estimate the change in average SDAP (ΔP̅a) within a time step using eq 17.
-
16.Transform ΔP̅a to ΔP̅ using inverse SDAP transform given by

33 -
17.With known ΔP̅, find the pressure at the new time step.
The pressure at the new time step, (P̅)ϑ, is the stress-equilibrated pressure (SEP). Let us define the new pressure as P1, i.e., P1 = (P̅)ϑ.
34 -
18.
In order to determine the desorption-equilibrated pressure (DEP), use the desorption MBE for individual component as described by eq 25. Solve the system of equations, i.e., eqs 23–25, simultaneously to determine the desorption-equilibrated pressure, i.e., DEP,(say P2). The solution of the system of equations will also give mole fraction of components at the new time step (y1, y2, y3, ..., yn)
-
19.The final pressure (P̅) at the new time step can be estimated as average of both MBE pressures.

35 -
20.FBHP Pwf can be calculated as

36 
37 -
21.
Proceed to the next time step. Repeat steps 2–20.
The steps, as discussed, are implemented in PYTHON and MATLAB, which act astools that predicts the two-phase multicomponent CBM well performance with fully coupled nonequilibrium desorption and pressure-dependent diffusivity effects. The suggested steps are illustrated in detail in Table 1.
Table 1. Example of Workflow for Performance Prediction of a CBM Well Containing Three (3) Components Using Depletion and Desorption MBEs.

4.2. Method of Performance Evaluation
The semi-analytical model can also be used to evaluate the performance of a multicomponent two-phase CBM well. The data for the surface water rate (qw), cumulative produced water (Wp), and initial mole fractions of components of CBM gas are known in a producing CBM well and thus can be directly used for the implementation of the next steps. The model estimated surface gas rates (qg), reservoir pressure, flowing bottom-hole pressure (FBHP), and mole fraction of components can be compared with the observed values as a history matching process. The steps for performance evaluation are as follows:
-
1.
Given the production history, qg, qw, Gp, and Wp are available with time. Initial mole fractions of individual components are known from compositional history of CBM gas. The FBHP (Pwf) history is generated using the fluid level measurement data in CBM wells. Using standard correlations, μg, Z, Bg, μw, and Bw are known at any pressure.
-
2.
Time t = 0, P̅ = Pi, and Wp = 0. Start with an assumption on ki, φi, VL and PL of individual components, drainage area, Corey’s relative permeability parameters (krwe, krge, nw, and ng), geomechanical parameters (Am, K/M, and n), coal saturation, and the skin parameter (S). Initially, assume We = 0.
-
3.
Using VL and PL of individual components and known mole fractions of individual components, estimate VLeq, PLeq, and εLeq using eqs 12 and 15.
-
4.
Using geomechanical properties (Am and K/M), φi, n, and estimated values of εLeq and PLeq, estimate the porosity (φ) at P̅ using eq 16. Also, determine the permeability (k) at the pressure P̅ using eq 6.
-
5.
Using Wp from the production history, follow steps 5–21 as described in section 4.1. Generate a model estimated profile of qg, Pwf, P̅, and mole fraction of components (y1, y2, y3, ..., yn) and compare with the observed values on these parameters.
-
6.
Execute the steps of a multiple regression on the assumed parameters to achieve a reasonable match between observed and model-estimated qg, Pwf, P̅, and mole fraction of components.
-
7.
The presence of extraneous water influx from noncoal formations can also be confirmed using the suggested workflow of history matching. Subject to confirmation, an appropriate aquifer influx model can be integrated to the semi-analytical mathematical model presented in this paper.
The suggested steps of performance evaluation are illustrated in detail with the flowchart given in Figure 2.
Figure 2.
Performance evaluation steps.
5. Validation of Semi-Analytical Solution Using a Numerical Simulator
For detailed study, four cases of CBM reservoirs are taken, and the following different performance parameters vs time are compared using the MATLAB/Python program and simulation on the CMG-GEM Numerical Simulator:
-
1.
Total gas rate (qg in Mscf/day)
-
2.
Water rate (qw in bbl/day)
-
3.
Reservoir pressure (P̅ in psi)/flowing bottom-hole pressure (Pwf in psi)
-
4.
Mole fractions of individual components (in fraction)
-
5.
Water saturation (Sw in fraction)
-
6.
Reservoir permeability (k in millidarcy)/porosity (ϕ in fraction)
Reservoir parameters for various cases are shown in Table 2. Various parameters, including gas rate, water rate, reservoir pressure/FBHP, mole fractions of individual components, gas saturation, and permeability/porosity vs time, are compared by the semi-analytical method (MATLAB/Python) and the CMG-GEM Numerical Simulator, as shown in Figures 3–6.
Table 2. Input Parameters for Multicomponent Cases.
| parameters | case 1 | case 2 | case 3 | case 4 |
|---|---|---|---|---|
| initial reservoir pressure, Pi (psi) | 1200 | 1200 | 1200 | 1200 |
| reservoir thickness, h (ft) | 24 | 24 | 24 | 24 |
| initial cleat porosity, φi | 4.0% | 4.0% | 4.0% | 0.5% |
| initial permeability, ki (millidarcy) | 100 | 100 | 100 | 100 |
| drainage area (acres) | 80 | 80 | 80 | 80 |
| number of components | 3 | 7 | 7 | 7 |
| initial mole fraction of components | CH4= 95.0% | CH4= 95.55% | CH4= 60.0% | CH4= 95.55% |
| CO2 = 3.0% | CO2 = 2.04% | CO2 = 20.0% | CO2 = 2.04% | |
| N2 = 2.0% | N2 = 1.73% | N2 = 10.0% | N2 = 1.73% | |
| C2H6 = 0.64% | C2H6 = 2.5% | C2H6 = 0.64% | ||
| C3H8 = 0.04% | C3H8 = 2.5% | C3H8 = 0.04% | ||
| i-C4H10 = 0.04% | i-C4H10 = 2.5% | i-C4H10 = 0.04% | ||
| n-C4H10 = 0.032% | n-C4H10 = 2.5% | n-C4H10 = 0.032% | ||
| Langmuir volume of components (scf/ton) | VLCH4 = 500 | VLCH4 = 500 | VLCH4 = 500 | VLCH4 = 500 |
| VLCO2 = 900 | VLCO2 = 900 | VLCO2 = 900 | VLCO2 = 900 | |
| VLN2 = 400 | VLN2 = 400 | VLN2 = 400 | VLN2 = 400 | |
| VLC2H6 = 450 | VLC2H6 = 450 | VLC2H6 = 450 | ||
| VLC3H8 = 470 | VLC3H8 = 470 | VLC3H8 = 470 | ||
| VLi-C4H10 = 450 | VLi-C4H10 = 450 | VLi-C4H10 = 450 | ||
| VLn-C4H10 = 400 | VLn-C4H10 = 400 | VLn-C4H10 = 400 | ||
| Langmuir pressure of components (psi) | PLCH4 = 400 | PLCH4 = 400 | PLCH4 = 400 | PLCH4 = 400 |
| PLCO2 = 300 | PLCO2 = 300 | PLCO2 = 300 | PLCO2 = 300 | |
| PLN2 = 400 | PLN2 = 400 | PLN2 = 400 | PLN2 = 400 | |
| PLC2H6 = 300 | PLC2H6 = 300 | PLC2H6 = 300 | ||
| PLC3H8 = 300 | PLC3H8= 300 | PLC3H8 = 300 | ||
| PLi-C4H10 = 350 | PLi-C4H10 = 350 | PLi-C4H10 = 350 | ||
| PLn-C4H10 = 350 | PLn-C4H10 = 350 | PLn-C4H10 = 350 | ||
| relative permeability curve (Corey’s model-based) | Swc = 0.2 | Swc = 0.2 | Swc = 0.2 | Swc = 0.2 |
| Sgc = 0.01 | Sgc = 0.01 | Sgc = 0.01 | Sgc = 0.01 | |
| Krwe = 1.0 | Krwe = 1.0 | Krwe = 1.0 | Krwe = 1.0 | |
| Krge = 0.95 | Krge = 0.95 | Krge = 0.95 | Krge = 0.95 | |
| nw = 2.0 | nw = 2.0 | nw = 2.0 | nw = 2.0 | |
| ng = 2.0 | ng = 2.0 | ng = 2.0 | ng = 2.0 | |
| desorption time, τ (days) | 5 | 5 | 5 | 5 |
| initial water saturation, Swi | 1.0 | 1.0 | 1.0 | 1.0 |
| coal saturation (%) | 100% | 100% | 100% | 100% |
| equivalent Langmuir sorption strain, εLeq | 0.02 | 0.02 | 0.02 | 0.02 |
| cleat compressibility, Cf (psi–1) | 2.622 × 10–05 | 2.622 × 10–05 | 2.622 × 10–05 | 3.745 × 10–04 |
| ratio of bulk to axial modulus, K/M | 0.78 | 0.78 | 0.78 | 0.556 |
| Young’s modulus, E (psi) | 445000 | 445000 | 445000 | 445000 |
| matrix shrinkage compressibility, Am (psi–1) (Am = Cfφi) | 1.05 × 10–06 | 1.05 × 10–06 | 1.05 × 10–06 | 1.873 × 10–06 |
| exponent, n | 3 | 3 | 3 | 3 |
| skin factor, S | 0 | 0 | 0 | 0 |
| reservoir temperature, T (°R) | 530 | 530 | 530 | 530 |
| radius of wellbore, rw (ft) | 0.3 | 0.3 | 0.3 | 0.21 |
| surface water rate operating constraint (bbl/day) | 100 | 100 | 100 | 500 |
| flowing bottom-hole pressure constraint (psi) | 100 | 100 | 100 | 100 |
Figure 3.
Case 1: comparison of results from the semi-analytical mathematical model and CMG-GEM numerical simulator. (a) Surface gas rate. (b) Surface water rate. (c) Reservoir pressure and flowing bottom-hole pressure. Mole fractions of individual components (d) CH4, (e) CO2, and (f) N2 in the gas stream. (g) Water saturation. (h) Changes in cleat porosity and cleat permeability with time. Results from the semi-analytical method match closely with numerical simulator (CMG-GEM) results.
Figure 6.
Case 4: comparison of results from the semi-analytical mathematical model and CMG-GEM numerical simulator. (a) Surface gas rate. (b) Surface water rate. (c) Reservoir pressure and flowing bottom-hole pressure. Mole fractions of individual components (d) CH4, (e) CO2, (f) N2, (g) C2H6, (h) C3H8, (i) i-C4H10, and (j) n-C4H10 in the gas stream. (k) Water saturation. (l) Changes in cleat porosity and cleat permeability with time. Results from the semi-analytical method match closely with numerical simulator (CMG-GEM) results.
Figure 4.
Case 2: comparison of results from the semi-analytical mathematical model and CMG-GEM numerical simulator. (a) Surface gas rate. (b) Surface water rate. (c) Reservoir pressure and flowing bottom-hole pressure. Mole fractions of individual components (d) CH4, (e) CO2, (f) N2, (g) C2H6, (h) C3H8, (i) i-C4H10, and (j) n-C4H10 in the gas stream. (k) Water saturation. (l) Changes in cleat porosity and cleat permeability with time. Results from the semi-analytical method match closely with numerical simulator (CMG-GEM) results.
Figure 5.
Case 3: comparison of results from the semi-analytical mathematical model and CMG-GEM numerical simulator. (a) Surface gas rate. (b) Surface water rate. (c) Reservoir pressure and flowing bottom-hole pressure. Mole fractions of individual components (d) CH4, (e) CO2, (f) N2, (g) C2H6, (h) C3H8, (i) i-C4H10, and (j) n-C4H10 in the gas stream. (k) Water saturation. (l) Changes in cleat porosity and cleat permeability with time. Results from the semi-analytical method match closely with numerical simulator (CMG-GEM) results.
6. Field Validation Using in-Field Production Data
The production data from three (03) CBM wells have been considered to evaluate the reservoir performance using the proposed semi-analytical method. The wells are from the matured CBM fields of Central India, producing from Barakar coal formations. The wells are described as Well-1, Well-2, and Well-3 in this paper to maintain the confidentiality desired by the operator. Production data from wells include production rates (gas and water), FBHP (Pwf), static reservoir pressure, and mole fractions of individual components in the gas stream. The flowing bottom-hole pressure (FBHP) data are available from fluid level measurements. For limited periods, downhole pressure gauges were also installed in these wells, thus giving additional FBHP data with more accuracy. Table 3 summarizes the available data.
Table 3. Available Data from Demonstration Wells.
| well name | well radius (ft) | initial reservoir pressure Pi (psi) | cumulative coal thickness (ft) | coal saturation (%) | initial gas composition (initial gas stream) | reservoir temperature (°R) | production history |
|---|---|---|---|---|---|---|---|
| Well-1 | 0.35 | 1098 | 48.0 | 100 | CH4 = 96.7% | 590.67 | observed production rate |
| CO2 = 1.17% | • monthly gas rate | ||||||
| N2 = 1.88% | • monthly water rate | ||||||
| C2H6 = 0.25% | observed static pressure | ||||||
| Well-2 | 0.35 | 1105 | 52.0 | 100 | CH4 = 95.7% | 591.16 | • shut-in period bottom-hole |
| • pressure data | |||||||
| observed FBHP | |||||||
| CO2 = 0.82% | • fluid level measurements | ||||||
| N2 = 2.64% | • downhole pressure gauges | ||||||
| C2H6 = 0.76% | observed gas composition | ||||||
| C3H8 = 0.04% | • gas composition measurement history | ||||||
| i-C4H10 = 0.04% | |||||||
| Well-3 | 0.35 | 711 | 49.5 | 100 | CH4 = 95.55% | 541.16 | |
| CO2 = 2.04% | |||||||
| N2 = 1.73% | |||||||
| C2H6 = 0.62% | |||||||
| C3H8 = 0.04% | |||||||
| i-C4H10 = 0.01% | |||||||
| n-C4H10 = 0.01% |
The validity of the results from semi-analytical mathematical model presented here was tested using the available in-field production history from demonstration wells. The semi-analytical model was constrained to produce the observed water production rate. The model-estimated gas rates, reservoir pressure, flowing bottom-hole pressure (FBHP), and mole fractions of individual components were then compared with the observed in-field data. An iterative workflow of history matching was executed using the semi-analytical approach presented in this paper to quantify uncertain parameters like aquifer influx, a representative field-scale relative permeability curve, and geomechanical parameters, along with multicomponent sorption parameters.
7. Results and Discussion
A history matching exercise (as described in section 4.2) was undertaken to match the production history from demonstration wells. Semi-analytical mathematical model-driven history matching gives useful information on coal reservoir properties.
7.1. Discussion of Results: Well-1
The parameters established through history matching using the semi-analytical approach described in this paper give the following information on coal reservoir properties.
7.1.1. Reservoir Parameters
Reservoir parameters are as follows: Pi = 1100 psi, h = 48.0 ft, φi = 5.0% , ki = 30 millidarcy, rw = 0.35 ft, A = 105 acres, VLCH4 = 350 scf/t, PLCH4 = 400 psi, VLCO2 = 800 scf/t, PLCO2 = 300 psi, VLN2 = 310 scf/t, PLN2 = 400 psi, VLC2H6 = 380 scf/t, PLC2H6 = 400 psi, Swi = 0.92, Cf = 2.097 × 10–05 psi–1, S = 2.0, T = 590.67 °R, desorption time of 5 days, and coal saturation of 100%. Gas composition is as follows: 96.7% CH4, 1.17% CO2, 1.88% N2, and 0.25% C2H6.
7.1.2. Relative Permeability Corey’s Parameters
Corey’s parameters for permeability parameters are as follows: Swc = 0.2, Sgc = 0.01, krwe = 1.0, krge = 0.95, ng = 1.3, and nw = 1.6.
7.1.3. Geomechanical Parameters
Geomechanical parameters are as follows: εLeqi = 0.02, v = 0.4, K/M = 0.78, E = 545 000 psia, Am = 1.049 × 10–06 psi–1, and n = 3.
7.1.4. Aquifer Parameters (Extraneous Water Source)
Aquifer productivity was 28.15 bbl/psi.
The results from the semi-analytical mathematical model are compared with the observed production history (Well-1) in Figures 7–9. The observed water rate from Well-1 was used as input to the semi-analytical model, and the model gas rate was compared with the observed gas rate (Figure 7a and b).
Figure 7.
Well-1: comparison of observed data with results from the semi-analytical model. The semi-analytical model was constrained to produce the observed water rates. (a) Model water rates exactly matching with the observed water rate. (b) Comparison of observed gas rate with the model-estimated gas rate.
Figure 9.
Well-1: (a) comparison of the model CH4 mole fraction with the observed CH4 mole fraction. (b) Comparison of the model CO2 mole fraction with the observed CO2 mole fraction. (c) Comparison of the model N2 mole fraction with the observed N2 mole fraction. (d) Comparison of the model C2H6 mole fraction with the observed C2H6 mole fraction. The comparison shows that there is a close match between model values and observed values for CH4 and CO2 mole fractions. The history of the observed mole fraction of C2H6 shows that it is minutely present in the gas composition. With such small mole fractions, the possibility of measurement errors cannot be denied for C2H6. Model values of C2H6 mole fractions may seem to differ significantly with observed values; however, considering the scale of values and possibility of measurement errors with such minute mole fractions, the level of match is as expected and reasonable.
The production history from Well-1 includes the fluid-level measured flowing bottom-hole pressure (FBHP). During limited periods, a downhole gauge was also installed in the well, thus giving additional FBHP data in a more accurate form. The semi-analytical model-driven history match confirms the presence of extraneous water influx in Well-1. To quantify water influx from noncoal formations, the Carter and Tracy50 model was implemented in the semi-analytical mathematical model. With the integration of the water influx model (aquifer productivity of 28.15 bbl/psi), a good match with observed data on surface gas rate, and FBHP was achieved. (Figure 8a and b).
Figure 8.
Well-1: (a) contribution of aquifer influx to total water rate, (b) reservoir pressure and comparison of observed FBHP data with the model estimated FBHP, (c) comparison of observed relative permeability ratio with the model estimated relative permeability ratio, and (d) cleat porosity and cleat permeability changes with time.
The relative permeability ratio (krg/krw)—calculated with observed gas and water rates—was also used to describe the appropriate Corey’s model for generating a relative permeability curve for Well-1 (Figure 8c).
The multicomponent semi-analytical model presented in this paper was also used to quantify the geomechanical parameters using the production data from Well-1. The mathematical model-driven history match gives the value of Poisson’s ratio of coal as 0.4 and Young’s modulus as 545 000 psi near Well-1. The values in this range indicate the ductile behavior of the coal reservoir near Well-1. The data for Langmuir sorption stain (εL) are not known for individual components to the estimate equivalent Langmuir sorption strain (εLeq) for use in the Palmer and Mansoori equation using the method defined in eq 16 of section 2. Therefore, in the history matching exercise, the initial value of the equivalent Langmuir sorption strain (εLeqi) was regressed to achieve the best possible match. The history matching gives the initial value of equivalent Langmuir sorption strain (εLeqi) as 0.02, which changes with pressure depletion as mole fractions of components change. The semi-analytical model-driven history match confirms that the initial cleat porosity of coal reservoir is high (5.0%). High initial porosity combined with the ductile behavior of coal leads to minor cleat porosity and permeability changes in the range of pressure depletion observed in Well-1 (Figure 8d).
The semi-analytical model presented in this paper uses the material balance approach as described in section 3 to estimate the mole fraction of each component at any reservoir pressure. To test the validity of the semi-analytical solution, the model-estimated mole fractions are compared with the observed mole fraction of components given by the gas compositional history of Well-1 (Figure 9a–d).
The steps for performance evaluation for Well-2 and Well-3 follow the same methodology as those described for Well-1. The semi-analytical model-driven history matching workflow on the production history of Well-2, and Well-3 gives vital information on coal reservoir properties, relative permeability, strength of the aquifer influx (if any), geomechanical parameters, and multicomponent sorption parameters.
The parameters established through the semi-analytical model driven history match workflow on Well-2 and Well-3 are given as follows.
7.2. Well-2
7.2.1. Reservoir Parameters
Reservoir parameters are as follows: Pi = 1100 psi, h = 52.0 ft, φi = 5.0% , ki = 70 millidarcy, rw = 0.35 ft, A = 190 acres, VLCH4 = 340 scf/t, PLCH4 = 400 psi, VLCO2 = 900 scf/t, PLCO2 = 300 psi, VLN2 = 310 scf/t, PLN2 = 400 psi, VLC2H6 = 380 scf/t, PLC2H6 = 400 psi, VLC3H8 = 370 scf/t, PLC3H8 = 300 psi, VLi-C4H10 = 350 scf/t, PLi-C4H10 = 350 psi, Swi = 0.98, Cf = 2.097 × 10–05 psi–1, S = 2.0, T = 591.16 °R, desorption time of 5 days, and coal saturation of 100%. Gas composition is as follows: 95.7% CH4, 0.82% CO2, 12.64% N2, 0.76% C2H6, 0.04% C3H8, and 0.04 i-C4H10.
7.2.2. Relative Permeability Corey’s Parameters
Corey’s parameters for relative permeability are as follows: Swc = 0.2, Sgc = 0.01, krwe = 1.0, krge = 0.95, ng = 3.0, and nw = 1.1.
7.2.3. Geomechanical Parameters
Geomechanical parameters are as follows: εL = 0.015, v = 0.4, K/M = 0.78, E = 545 000 psia, Am = 1.049 × 10–06 psi–1, and n = 3
7.2.4. Aquifer Parameters (Extraneous Water Source)
Aquifer productivity is 222.866 bbl/psi.
7.3. Well-3
7.3.1. Reservoir Parameters
Reservoir parameters are as follows: Pi = 711 psi, h = 49.5 ft, φi = 5.0% , ki = 20 millidarcy, rw = 0.35 ft, A = 180 acres, VLCH4 = 340 scf/t, PLCH4 = 400 psi, VLCO2 = 900 scf/t, PLCO2 = 300 psi, VLN2 = 310 scf/t, PLN2 = 400 psi, VLC2H6 = 380 scf/t, PLC2H6 = 400 psi, VLC3H8 = 370 scf/t, PLC3H8 = 300 psi, VLi-C4H10 = 350 scf/t, PLi-C4H10 = 350 psi, VLn-C4H10 = 300 scf/t, PLn-C4H10 = 350 psi, Swi = 0.99, Cf = 2.097 × 10–05 psi–1, S = 2.0, T = 541.16 °R, desorption time of 5 days, and coal saturation of 100%. Gas composition is as follows: 95.55% CH4, 2.04% CO2, 1.73% N2, 0.62% C2H6, 0.04% C3H8, 0.01% i-C4H10, and 0.01% n-C4H10.
7.3.2. Relative Permeability Corey’s Parameters
Corey’s parameters for relative permeability are as follows: Swc = 0.2, Sgc = 0.01, krwe = 1.0, krge = 0.95, ng = 3.2, and nw = 1.5.
7.3.3. Geomechanical Parameters
Geomechanical parameters are as follows: εL = 0.015, v = 0.4, K/M = 0.78, E = 545 000 psia, Am = 1.049 × 10–06 psi–1, and n = 3.
7.3.4. Aquifer Parameters (Extraneous Water Source)
Aquifer productivity is 120.65 bbl/psi.
The history-matched plots for Well-2 and Well-3 are presented in Figures 10 and 11 of Appendix B, respectively.
Figure 10.
Well 2: comparison of results for the semi-analytical mathematical model vs observed data. (a) Surface water rate. (b) Surface gas rate. (c) Water influx from extraneous source. (d) Reservoir pressure and flowing bottom-hole pressure. Comparison of the observed mole fractions of individual components (e) CH4, (f) CO2, (g) N2, (h) C2H6, (i) C3H8, and (j) i-C4H10 in the gas stream with model-estimated data. (k) Comparison of the model-estimated relative permeability ratio with observed ratio. (l) Cleat porosity and cleat permeability vs time. The observed data match closely with semi-analytical model results. The gas compositional history suggests that methane (CH4) constitutes the major component and its changes with time are minor. Other components are only minutely present. Considering the scale of values and possibility of measurement errors with such minute mole fractions, the level of match is as expected and reasonable.
Figure 11.
Well 3: comparison of results for the semi-analytical mathematical model vs observed data. (a) Surface water rate. (b) Surface gas rate. (c) Water influx from extraneous source. (d) Reservoir pressure and flowing bottom-hole pressure. Comparison of the observed mole fractions of the individual components (e) CH4, (f) CO2, (g) N2, (h) C2H6, (i) C3H8, (j) i-C4H10, and (k) n-C4H10 in the gas stream with model-estimated data. (l) Model-estimated relative permeability ratio with the observed ratio. (m) Changes in cleat porosity and cleat permeability with time. Semianalytical model results match closely with observed data (except for mole fractions). The gas compositional history suggests that the methane (CH4) constitutes the major component and its changes with time is minor. Other components are only minutely present. Considering the scale of values and possibility of measurement errors with such minute mole fractions, the level of match is as expected and reasonable.
8. Limitations of the Mathematical Model
The mathematical model presented in this study is unique in a way that it brings out a novel approach to integrate multicomponent sorption effects, two-phase flow, and pressure-dependent diffusivity effects of CBM reservoirs. However, it also has few limitations that are listed below:
-
1.
The mathematical model is limited to applications under semi-steady state conditions of flow only; the mathematical model does not capture transient effects.
-
2.
The model has an assumption that gas molecules are not soluble in water; the mass balance equation for individual components neglects the solubility of gas in water, especially for low-pressure CBM Seams. This assumption is reasonable for CBM gas that contains mainly lighter components of hydrocarbons.51,52
9. Conclusions
In this Article, a new semi-analytical model has been developed to simulate multicomponent, two-phase flow coupled with pressure-dependent diffusivity and time-dependent desorption conditions prevailing in CBM wells. The validity of the model has been tested with numerical simulator CMG-GEM as well as in-field production data. The following key conclusions can be drawn from the application of this model:
A multicomponent sorption system can be reduced to an equivalent single-component sorption system using the novel approach of describing the equivalent Langmuir volume and pressure; moreover, a multicomponent Langmuir sorption strains can be reduced to an equivalent single-component sorption strain using the method of equivalent Langmuir sorption strain conceptualized in this paper.
The semi-analytical solutions given by mathematical model presented in this study give more computationally stable solutions than a numerical simulator. Moreover, unlike numerical simulators where repetitive adjustment of numerical parameters is needed to achieve viable solutions in multicomponent models, the semi-analytical model presented in this study gives stable solutions irrespective of the number of components, thereby saving time and being more computationally efficient.
The mathematical model finds its applications in handling multiple-component CBM simulation and, thus, overcomes the constraints of commercial CBM simulators, like ECLIPSE and COMET 3, that can process 2–3 components only.
Given the huge cost-implications of industry-standard numerical simulators, which affects the economics of small operators of CBM businesses, this semi-analytical model presents an approach that can be easily scripted into any programmable languages like Python, MATLAB, FORTRAN, etc. The presented semi-analytical model will be less expensive in comparison to numerical simulators without compromising accuracy.
Introducing multiple components, like N2, C2H6, C3H8, etc., (say “n” components) for more practical modeling in the semi-analytical method can be done by formulating desorption MBEs for each component (total “n” MBEs) and solving these “n” systems of nonlinear equations simultaneously using the proposed Newton’s method by estimating the Jacobian (n × n) matrix as shown in Appendix-A.
The multicomponent semi-analytical model can be easily extended for simulation of enhanced CBM processes like CO2 sequestration in coal.
This method can be used not only to predict the coal reservoir performance but also to evaluate the reservoir performance, such as reservoir parameters like representative relative permeability curves, the strength (productivity) of the extraneous water source (aquifer), geomechanical parameters, and multicomponent sorption parameters. It is commonly seen that CBM operators lack data on geomechanical and multicomponent sorption parameters due to cost implications of data gathering. The methodology presented in this Article will help CBM operators in quantifying these parameters using the production data gathered from CBM wells.
Though this Article uses the Palmer and Mansoori18 equation to quantify porosity at different pressures, the methodology can be executed with other geomechanical models like Shi and Durucan,39 Cui and Bustin,40 and Robertson and Christiansen.41
Acknowledgments
We express our sincere gratitude to the Computer Modelling Group (CMG), which has generously donated the reservoir simulation software to the Indian Institute of Technology (Indian School of Mines), Dhanbad, for academic and research purposes. We have used the CMG-GEM numerical simulator to verify the results of the semi-analytical model presented in this paper. We also acknowledge IIT (ISM) Dhanbad for the permission to publish this work, where the research was originally done.
Glossary
Nomenclature
- A
Drainage area of reservoir (acre)
- Am
Matrix shrinkage compressibility (psi–1)
- Bg
Gas formation volume factor (rb/scf)
- Bw
Water formation volume factor (rb/stb)
- Cf
Formation compressibility (psi–1)
- Cg
Gas compressibility (psi–1)
- Cs
Sorption compressibility (psi–1)
- Ct
Total compressibility (psi–1)
- Cti
Initial total compressibility (psi–1)
- Cw
Water compressibility (psi–1)
- GaiCH4
Adsorbed methane gas at old time step (scf/ton)
- GaCH4
Adsorbed methane gas at new time step (scf/ton)
- GfiCH4
Free methane gas at old time step (scf/ton)
- GfCH4
Free methane gas at new time step (scf/ton)
- GpCH4
Produced methane gas between the steps (scf/ton)
- GCn
Gas content of component n (scf/ton)
- GCTotal
Total gas content (scf/ton)
- h
Reservoir thickness (ft)
- Ji
Jacobian matrix
- k
Cleat permeability at pressure P (millidarcy)
- ki
Initial cleat permeability (millidarcy)
- kg
Effective gas permeability (millidarcy)
- kw
Effective water permeability (millidarcy)
- krg
Relative gas permeability (dimensionless)
- krw
Relative water permeability (dimensionless)
- K
Bulk modulus (psi)
- Psc
Pressure at standard condition (psi)
- ng, nw
Exponents for the gas–water relative permeability
- P1
Stress-equilibrated pressure (SEP) (psi)
- P2
Desorption-equilibrated pressure (DEP) (psi)
- Pi
Initial reservoir pressure (psi)
- P
Reservoir pressure (psi)
- Psc
Pressure at standard conditions (psi)
- Pd
Desorption pressure of coal (psi)
- P̅
Average reservoir pressure (psi)
- Pa
Stress-dependent adjusted pressure (psi)
- Pawf
Adjusted flowing bottom-hole pressure (psi)
- PL
Langmuir pressure (psi)
- PLCH4
Langmuir pressure of methane (psi)
- PLn
Langmuir pressure of the nth component (psi)
- PLeq
Equivalent Langmuir pressure (psi)
- (Pwf)min
Minimum flowing bottom-hole pressure (psi)
- qw
Surface water rate (stb/day)
- qg
Surface gas rate (scf/day)
- qt
Total reservoir rate at reservoir condition (rb/day)
- qti
Initial total reservoir rate at reservoir condition (rb/day)
- re
Radius of the outer boundary (ft)
- rw
Wellbore radius (ft)
- Sg
Gas saturation (dimensionless)
- Sgc
Critical gas saturation (dimensionless)
- Sw
Water saturation (dimensionless)
- Swc
Critical water saturation (dimensionless)
- Swi
Initial water saturation (dimensionless)
- S
Skin factor
- tadjusted
Adjusted time (days)
- τ
Desorption time days
- τD
Dimensionless time delay factor
- T
Reservoir Temperature (°R)
- Tsc
Temperature at standard conditions (°R)
- VL
Langmuir volume (scf/ton)
- VLCH4
Langmuir volume of methane (scf/ton)
- VLn
Langmuir volume of the nth component (scf/ton)
- VLeq
Equivalent Langmuir volume (scf/ton)
- We
Cumulative water influx (bbl)
- Wp
Cumulative water production (bbl)
- yCH4
Mole fraction of methane in the gas phase (dimensionless)
- yC2H6
Mole fraction of ethane in the gas phase (dimensionless)
- yC3H8
Mole fraction of propane in the gas phase (dimensionless)
- yi–C4H10
Mole fraction of isobutane in the gas phase (dimensionless)
- yn–C4H10
Mole fraction of n-butane in the gas phase (dimensionless)
- yCO2
Mole fraction of CO2 in the gas phase (dimensionless)
- yN2
Mole fraction of nitrogen in the gas phase (dimensionless)
- yn
Mole fraction of the nth component in the gas phase (dimensionless)
- Z
Real gas deviation factor (dimensionless)
- ZCH4
Real gas deviation factor of methane (dimensionless)
- ρb
Bulk density of coal (g/cm3)
- φi
Initial cleat porosity (dimensionless)
- φ
Average cleat porosity at pressure P (dimensionless)
- μg
Gas viscosity at pressure P (cp)
- μw
Water viscosity at pressure P (cp)
- λt
Total mobility (darcy/cp)
- λrt
Total relative mobility (cp–1)
- λrti
Initial total relative mobility (cp–1)
- α
Constant of proportionality (k and φ relation) (millidarcy)
- εL
Volumetric strain at infinite pressure
- εs
Matrix volumetric strain
- εLeq
Equivalent Langmuir sorption strain
- ϑ
Time step
Appendix A
This appendix explains the methodology to solve systems of nonlinear equations that exist in the form of a desorption material balance equation for n number of components.
As explained in section 3, the material balance equation for component i is given by
 |
38 |
The above equation is a nonlinear equation. For n components, there will be n such equations.
In addition, there will be an additional equation to ensure sum of mole fractions is equal to 1, i.e., eq 25. These functions of of “n + 1” variables can be arranged in the form
| 39 |
| 40 |
| 41 |
| 42 |
A system of multiple simultaneous nonlinear equations in multiple (say “n”) variables can be solved using Newton’s method.
By using Taylor’s series expansion (second-order terms are neglected) for the next iteration level (i → i + 1) and setting the (i + 1)th function value to be zero:
| 43 |
| 44 |
| 45 |
| 46 |
Adjusting terms in matrix form,
 |
47 |
Let,
 |
48 |
Again, upon rearranging and premultiplying the equation by Ji–1 (Jacobian matrix inverse),
 |
49 |
Therefore, solving a system of n + 1 equations using a Jacobian matrix gives the desorption-equilibrated pressure (P) and mole fraction of components (y1, y2, y3, ..., yn) at new time steps.
Appendix B
This Appendix contains the figures that compare the results from the semi-analytical model and observed data for Well-2 and Well-3 (Figures 10 and 11, respectively).
The authors declare no competing financial interest.
References
- Montgomery S. L.; Tabet D. E.; Barker C. E. Upper Cretaceous Ferron Sandstone: Major Coalbed Methane Play in Central Utah. AAPG Bull. 2001, 85 (2), 199–219. 10.1306/8626C799-173B-11D7-8645000102C1865D. [DOI] [Google Scholar]
- Warren J. E.; Root P. J. The Behavior of Naturally Fractured Reservoirs. SPE J. 1963, 3, 245–255. 10.2118/426-PA. [DOI] [Google Scholar]
- Li Y.; Wang Z.; Tang S.; Elsworth D. Re-evaluating adsorbed and free methane content in coal and its ad- and desorption processes analysis. Chemical Engineering Journal 2022, 428, 131946. 10.1016/j.cej.2021.131946. [DOI] [Google Scholar]
- Li Y.; Zhang C.; Tang D.; Gan Q.; Niu X.; Wang K.; Shen R. Coal pore size distributions controlled by the coalification process: An experimental study of coals from the Junggar, Ordos and Qinshui basins in China. Fuel 2017, 206, 352–363. 10.1016/j.fuel.2017.06.028. [DOI] [Google Scholar]
- Langmuir I. The Adsorption of Gases on Plane Surfaces of Glass, Mica, and Platinum. J. Am. Chem. Soc. 1918, 40, 1361. 10.1021/ja02242a004. [DOI] [Google Scholar]
- Nguyen V. U. A FORTRAN program for modeling methane gas desorption from coal. Comput. Geosci. 1989, 15, 695–707. 10.1016/0098-3004(89)90077-0. [DOI] [Google Scholar]
- King G. R. Material-balance techniques for coal seam and Devonian shale gas reservoirs with limited water influx. SPE Res. Eng. 1993, 8, 67–72. 10.2118/20730-PA. [DOI] [Google Scholar]
- Mohaghegh S.; Ertekin T.. A type-curve solution for coal seam degasification wells producing under two-phase flow conditions. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, Texas, 6–9 October, 1991; Society of Petroleum Engineers: Richardson, TX, 1991; Paper SPE-22673-MS. 10.2118/22673-MS [DOI]
- Kamal M. M.; Six J. L. Pressure transient testing of methane producing coalbeds. SPE Adv. Technol. Ser. 1993, 1, 195–230. 10.2118/19789-PA. [DOI] [Google Scholar]
- Jensen D.; Smith L. K.. A Practical Approach to Coalbed Methane Reserve Prediction Using a Modified Material Balance Technique. In Proceedings of the International Coalbed Methane Symposium, Tuscaloosa, Alabama, 12–16 May, 1997; University of Alabama, 1997; Paper 9765.
- Seidle J. P.A modified p/Z method for coal wells. In Proceedings of the SPE Rocky Mountain Regional Meeting, Gillette, Wyoming, 15–18 May, 1999; Society of Petroleum Engineers: Richardson, TX, 1999; Paper SPE-55605-MS. 10.2118/55605-MS [DOI]
- Salmachi A.; Yarmohammadtooski Z. Production data analysis of coalbed methane wells to estimate the time required to reach to peak of gas production. Int. J. Coal Geol. 2015, 141–142, 33–41. 10.1016/j.coal.2015.02.006. [DOI] [Google Scholar]
- Burgoyne M.; Shrivastava R. A practical workflow for characterizing stress-dependent behaviour of coal from changes in well productivity. J. Nat. Gas Sci. Eng. 2016, 33, 1025–1045. 10.1016/j.jngse.2016.03.031. [DOI] [Google Scholar]
- Yang R.; Huang Z.; Yu W.; Lashgari H. R.; Sepehrnoori K. A Semianalytical Method for Modeling Two-Phase Flow in Coalbed-Methane Reservoirs With Complex Fracture Networks. SPE Reservoir Evaluation & Engineering. 2018, 21 (3), 719–732. 10.2118/189459-PA. [DOI] [Google Scholar]
- Al-Hussainy R.; Ramey H. J.; Crawford P. B. The Flow of Real Gases Through Porous Media. J. Pet.Technol. 1966, 18, 624–636. 10.2118/1243-A-PA. [DOI] [Google Scholar]
- Thararoop P.; Karpyn Z. T.; Ertekin T. A production type-curve solution for coalbed methane reservoirs. J. Unconv Oil Gas Resour 2015, 9, 136–152. 10.1016/j.juogr.2014.12.001. [DOI] [Google Scholar]
- Stewart G.Transient testing of CBM wells. In Proceedings of the SPE Asia Pacific Oil & Gas Conference and Exhibition, Brisbane, Australia, 18–20 October, 2010; Society of Petroleum Engineers: Richardson, TX, 2010; Paper SPE-133356-MS. 10.2118/133356-MS [DOI]
- Palmer I.; Mansoori J.. How permeability depends on stress and pore pressure in coalbeds: A new model. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, Colorado, 6–9 October, 1996; Society of Petroleum Engineers: Richardson, TX, 1996; Paper SPE-36737-MS. 10.2118/36737-MS [DOI]
- Upadhyay R.; Laik S. A computational approach to determine average reservoir pressure in a coalbed methane (CBM) well flowing under dominant matrix shrinkage effect. Transp. Porous Media 2017, 116, 1167–1188. 10.1007/s11242-016-0816-6. [DOI] [Google Scholar]
- Upadhyay R.; Laik S. An Alternative Approach to Predicting Reservoir Performance in a Coalbed Methane (CBM) Well Flowing Under Dominant Matrix Shrinkage Effect. Transp Porous Media 2017, 119, 649–672. 10.1007/s11242-017-0904-2. [DOI] [Google Scholar]
- Salmachi A.; Dunlap E.; Rajabi M.; Yarmohammadtooski Z.; Begg S. Investigation of permeability change in ultradeep coal seams using time-lapse pressure transient analysis: A pilot project in the Cooper Basin. Australia. AAPG Bull. 2019, 103, 91–107. 10.1306/05111817277. [DOI] [Google Scholar]
- Perrine R. L. Analysis of Pressure Buildup Curves. Drill. Prod. Prac. 1956, 482–509. [Google Scholar]
- Neelu; Upadhyay R.; Parida B. A New Approach to Evaluate and Predict the Reservoir Performance of a Two-Phase Flow CoalBed Methane Well with Fully Coupled Time-Dependent Desorption and Pressure-Dependant Diffusivity Effects. Energy Fuels 2022, 36, 5284. 10.1021/acs.energyfuels.2c00429. [DOI] [Google Scholar]
- Sun Z.; Huang B.; Liu Y.; Jiang Y.; Zhang Z.; Hou M.; Li Y. Gas-phase production equation for CBM reservoirs: Interaction between hydraulic fracturing and coal orthotropic feature. J. Pet. Sci. Eng. 2022, 213, 110428 10.1016/j.petrol.2022.110428. [DOI] [Google Scholar]
- Sun Z.; Shi J.; Wu K.; Zhang T.; Feng D.; Li X. Effect of Pressure-Propagation Behavior on Production Performance: Implication for Advancing Low-Permeability Coalbed-Methane Recovery. SPE J. 2019, 24, 681–697. 10.2118/194021-PA. [DOI] [Google Scholar]
- Sun Z.; Huang B.; Wang S.; Wu K.; Li H.; Wu Y. Hydrogen adsorption in nanopores: Molecule-wall interaction mechanism. Int. J. Hydrogen Energy 2023, 48 (86), 33496–33508. 10.1016/j.ijhydene.2023.05.132. [DOI] [Google Scholar]
- Yang S.; Wang H.; Fu X.; Tian J.; Zhao F.; Wang Z.; Sun P.; Cao Y. Hydrogen sulfide occurrence states in China’s coal seams. Energy Explor. Exploit 2022, 40 (1), 17–37. 10.1177/01445987211033453. [DOI] [Google Scholar]
- Markham E. C.; Benton A. F. The Adsorption of Gas Mixtures by Silica. J. Am. Chem. Soc. 1931, 53, 497–507. 10.1021/ja01353a013. [DOI] [Google Scholar]
- Crank J.Mathematics of Diffusion, 2nd ed.; Oxford University Press: London, U.K., 1975. [Google Scholar]
- Yang R. T.Gas Separation by Adsorption Processes; Butterworths, Boston, MA, 1987. [Google Scholar]
- Myers A. L.; Prausnitz J. M. Thermodynamics of Mixed-Gas Adsorption. AIChE J. 1965, 11 (1), 121–127. 10.1002/aic.690110125. [DOI] [Google Scholar]
- Clarkson C. R.; Bustin R. M. Binary Gas Adsorption/Desorption Isotherms: Effect of Moisture and Coal Composition Upon Carbon Dioxide Selectivity over Methane. Int. J. Coal Geol. 2000, 42 (4), 241–271. 10.1016/S0166-5162(99)00032-4. [DOI] [Google Scholar]
- Clarkson C. R. Application of a New Multicomponent Gas Adsorption Model to Coal Gas Adsorption Systems. SPE Journal 2003, 8 (03), 236–251. 10.2118/78146-PA. [DOI] [Google Scholar]
- Zhou C.; Hall F.; Gasem K. A. M.; et al. Predicting Gas Adsorption using Two-Dimensional Equations of State. I&EC Res. 1994, 33 (5), 1280–1289. 10.1021/ie00029a026. [DOI] [Google Scholar]
- Gasem K. A. M.; Pan Z.; Mohammad S.; Robinson R. L. Two-Dimensional Equation-of-State Modeling of Adsorption of Coalbed Methane Gases. AAPG Stud. Geol. 2008, 59, 475–497. 10.1306/13171257St593392. [DOI] [Google Scholar]
- Arri L. E.; Yee D.; Morgan W. D.; Jeansonne M. W.. Modeling Coalbed Methane Production With Binary Gas Sorption. In Proceedings of the SPE Rocky Mountain Regional Meeting, Casper, Wyoming, May 18–21, 1992; Society of Petroleum Engineers: Richardson, TX, 1992; Paper SPE-24363-MS. 10.2118/24363-MS [DOI]
- Wei Z.; Zhang D. A Fully Coupled Multiphase Multicomponent Flow and Geomechanics Model for Enhanced Coalbed-Methane Recovery and CO2 Storage. SPE Journal 2013, 18 (03), 448–467. 10.2118/163078-PA. [DOI] [Google Scholar]
- Seidle J. P. Long-Term Gas Deliverability of a Dewatered Coalbed. J. Pet. technol. 1993, 45 (06), 564–569. 10.2118/21488-PA. [DOI] [Google Scholar]
- Shi J. Q.; Durucan S. A model for changes in coalbed permeability during primary and enhanced methane recovery. SPE Res. Eval. Eng. 2005, 8 (04), 291–299. 10.2118/87230-PA. [DOI] [Google Scholar]
- Cui X.; Bustin R. M. Volumetric strain associated with methane desorption and its impact on coalbed gas production from deep coal seams. AAPG Bull. 2005, 89 (09), 1181–1202. 10.1306/05110504114. [DOI] [Google Scholar]
- Robertson E. P.; Christiansen R. L.. A permeability model for coal and other fractured, sorptive-elastic media. In Proceedings of the SPE Eastern Regional Meeting, Canton, Ohio, 11–13 October, 2006; Society of Petroleum Engineers: Richardson, TX, 2006; Paper SPE-104380-MS. 10.2118/104380-MS [DOI]
- Reiss L. H.The reservoir engineering aspects of fractured formations; Editions Technip: Paris, France, 1980. [Google Scholar]
- Seidle J. P.; Huitt L. G.. Experimental Measurement of Coal Matrix Shrinkage Due to Gas Desorption and Implications for Cleat Permeability Increases. In Proceedings of the International Meeting on Petroleum Engineering, Beijing, China, November 14–17, 1995; Society of Petroleum Engineers: Richardson, TX, 1995; Paper SPE 30010. 10.2118/30010-MS [DOI]
- Robertson E. P.; Christiansen R. L.. Modeling Permeability in Coal Using Sorption-Induced Strain Data. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, Texas, October 9–12, 2005; Society of Petroleum Engineers: Richardson, TX, 2005; Paper SPE-97068-MS. 10.2118/97068-MS [DOI]
- Seidle J.Fundamentals of Coalbed Methane Reservoir Engineering. PennWell Corp.: Tulsa, OK, 2011. [Google Scholar]
- Lee A. L.; Gonzalez M. H.; Eakin B. E. The Viscosity of Natural Gases. J. Petrol. Technol. August 1966, 18, 997–1000. 10.2118/1340-PA. [DOI] [Google Scholar]
- Peng D.; Robinson D. A New Two Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15 (1), 59–64. 10.1021/i160057a011. [DOI] [Google Scholar]
- Peng D.; Robinson D. Two and Three Phase Equilibrium Calculations for Systems Containing Water. Can. J. Chem. Eng. 1976, 54, 595–599. 10.1002/cjce.5450540541. [DOI] [Google Scholar]
- Brooks R. H.; Corey A. T. Hydraulic properties of porous media. Trans. ASAE 1964, 7 (1), 0026–0028. 10.13031/2013.40684. [DOI] [Google Scholar]
- Carter R. D.; Tracy G. W. An improved method for calculating water influx. Trans. 1960, 219 (01), 415–417. 10.2118/1626-G. [DOI] [Google Scholar]
- Li J.; Li X.; Shi J. Mechanism of Liquid-Phase Adsorption and Desorption in Coalbed Methane Systems: A New Insight Into an Old Problem. SPE Res. Eval & Eng. 2017, 20 (3), 639–653. 10.2118/177001-PA. [DOI] [Google Scholar]
- Sun Z.; Shi J.; Wang K.; Miao Y.; Zhang T.; Feng D.; Sun F.; Wang S.; Han S.; Li X. The gas-water two phase flow behavior in low-permeability CBM reservoirs with multiple mechanisms coupling. Journal of Natural Gas Science and Engineering 2018, 52, 82–93. 10.1016/j.jngse.2018.01.027. [DOI] [Google Scholar]















