Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2024 Jan 22;9(5):5728–5733. doi: 10.1021/acsomega.3c08380

Experimental Study on the Chemical Reaction Characteristics in the Calcination Process of an 811 Ternary Cathode Material

Zhaodong Chen †, Haoyin Yang †, Hailong Peng ‡, Ruifeng Dou †,*, Mingzhao Zheng ‡, Weili Sun ‡, Boyang Ma †, Xunliang Liu †, Zhi Wen †
PMCID: PMC10851256  PMID: 38343958

Abstract

graphic file with name ao3c08380_0005.jpg

The research on 811 ternary cathode materials is mainly based on synthesis and modification. However, the preparation process of these materials is accompanied by complex chemical reactions, and the reaction process and corresponding kinetic analysis have not been widely explored. Under different oxygen concentrations, this study analyzed the chemical reaction mechanism of the raw material's (namely, Ni0.8Co0. 1Mn0. 1(OH)2 and LiOH·H2O mixture, which is referred to as the raw material hereinafter) calcination process by non-isothermal thermogravimetry, differential scanning calorimetry, and in situ X-ray diffraction. Based on the obtained data, multiple heating rate methods were used to calculate the reaction mechanism functions and kinetic parameters at each stage as well as the corresponding activation energy and pre-exponential factor. Results showed that four chemical reactions occurred successively during the calcination process of the raw materials with each corresponding to a different kinetic function, pre-exponential factor, and activation energy. Comparing the calcination characteristics under different oxygen concentrations showed that the activation energy was the smallest when the oxygen concentration was 60%.

1. Introduction

At present, lithium-ion batteries are the main energy suppliers for hybrid electric vehicles and pure electric vehicles in the market.1 The performance of cathode materials is an important factor that affects the charging and discharging performance of lithium batteries. Among the cathode materials, high-nickel ternary cathode materials can provide high specific capacity2,3 (more than 200 mAh/g). At the same time, because of the relatively low price and suitability for large-scale production, it has become the research focus of lithium battery cathode materials.4,5 High nickel here usually refers to cathode materials with Ni content greater than 0.6 (LiNixCoyMn1–x–yO2, x > 0.6, x + y < 1).6,7 According to the literature,8,9 the calcination preparation process of high-nickel ternary cathode materials greatly influences their microstructures and electrochemical properties, while the kinetic analysis of the calcination process is insufficient, which is not conducive to the improvement of the calcination process.

Gao et al.10 analyzed the reaction mechanism and kinetic parameters of Li1.16(Ni0.25Mn0.75)0.84O2 and the synthesized Li-rich Mn-based cathode material Li1.16(Ni0.25Mn0.75) 0.84O2 on this basis. The analysis shows that the material has a high energy density retention rate. Gang et al.11 analyzed the heat treatment process of LiNi0.82Co0.12Mn0.06O2 using various methods, such as non-isothermal thermogravimetry (TG), X-ray diffraction (XRD) testing, and particle size testing, and summarized the main chemical reactions of the material at different temperatures. They found that the crystal structure of the material continues to improve and is uniformly distributed above 600 °C. Hu et al.12 analyzed the solid-state reaction process of spinel-type cathode materials (spinel Li4Ti5O12) by non-isothermal TG. The mechanism function can be described as the Jander equation, which is a spherically symmetric three-dimensional diffusion function. Based on the kinetic parameters, the authors concluded that the formation of Li4Ti5O12/C composites is an entropy-driven one-step solid-state reaction mechanism. Han et al.13 synthesized a high-nickel LiNi0.9Co0.05Mn0.05O2 cathode material through a two-step heating treatment process. Experimental results showed that the electrochemical performance of the material is the best when the supply of lithium is 1.04 and the calcination temperature is 700 °C. Chen et al.14 found that the formation of the cathode material Li3V2(PO4)3 undergoes four stages of chemical reaction and determined that the most critical fourth-stage kinetic function is the Avrami–Erofeev equation, that is, random nucleation and subsequent growth mechanism. The enthalpy, entropy, and Gibbs free energy corresponding to that phase are also determined. Zhao et al.15 analyzed the decomposition process of LiMn2O4 under atmospheric conditions by a differential thermal analysis method and obtained the mechanism function and activation energy under four reactions. On this basis, pure LiMn2O4 with regular morphology and a high specific surface area was prepared. Llusco et al.16 analyzed the calcination process of Mg-doped LiMn2O4 and determined four reaction stages. The kinetic analysis results showed that calcination at 500 °C for 4 h and calcination at 750 °C for 12 h are the optimal processes.

Therefore, the heat treatment process can be optimized by analyzing the reaction process and calculating the kinetic parameters. However, similar analyses for 811-type ternary cathode materials (LiNi0.8Co0.1Mn0.1O2) have rarely been reported. In addition, some studies have shown that ternary cathode materials need a pure oxygen atmosphere during the calcination process.17 With regard to the effect of the oxygen concentration on the reaction process, no accurate conclusions have been found in the literature reviewed by the authors thus far.

In this study, through TG coupled with differential scanning calorimetry (DSC), XRD, and other tests, we first clarify the chemical reactions of raw materials at different temperatures. Second, the experimental results under different oxygen concentrations are studied through dynamic models, and other factors, such as the reaction mechanism function, activation energy, and pre-exponential factor, are analyzed.

2. Materials and Methods

The TG–DSC experiments were conducted using a SwissMettler TGA/DSC 3+ model simultaneous thermal analysis instrument with the raw materials as the object of study. A sample of 20–40 mg was weighed into a crucible with the following atmosphere conditions: oxygen concentrations of 20, 40, 60, 80, and 100%. The heating rate was 5 °C/min, and the maximum temperature was 1000 °C.

An in situ test was conducted by a D8 ADVANCE X-ray diffractometer on the basis of the TG–DSC experiment to determine the corresponding phase of the raw materials at different temperatures. The heating rate was 2 °C/min, and the maximum temperature was 700 °C. Twelve temperature measurement points were set, namely, 25, 200, 250, 300, 350, 400, 450, 500, 550, 600, 650, and 700 °C, to determine the substances corresponding to different temperatures.

In this study, the diffusion between solids was ignored because all experimental raw materials were ground under the premise of uniform mixing in the mixer to ensure a uniform distribution of raw materials, and the particle size of the raw materials is between 0.1 and 0.5 mm. If the diffusion effect of solid particles is considered, then this study will be extremely difficult. Based on the above considerations, this study ignored the diffusion effect of solid particles.

3. Kinetic Model

During the linear warming process, the kinetic reaction equation is expressed as follows18

3. 1

where α is the conversion rate of the substance at time t, T is the temperature corresponding to the current moment (K), t is the reaction time (min), and k(T) is a function of the temperature and is expressed as the Arrhenius equation

3. 2

where A is the pre-exponential factor (min–1), E is the apparent activation energy (J/mol), R is the universal gas constant, which is always 8.314 J/(mol K),19 and f(α) is the kinetic mechanism function20,21 and is expressed as follows

3. 3

The abovementioned formula is also the general formula of a non-isothermal kinetic reaction, and n represents the reaction order.

The heating rate (K/min or °C/min) is expressed as β = dT/dt. Thus, we substitute the heating rate and eq 2 into eq 1 to obtain the basic equation for the reaction kinetics

3. 4

where the conversion rate α is calculated by the following equation:

3. 5

where m0 is the initial mass of the material (kg), m is the mass of the material at different moments (kg), and m1 is the mass of the material after the reaction is completed (kg).

Shifting the terms of eq 4 and taking the logarithms on both sides yield:

3. 6

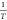In the abovementioned equation, A, R, E, and β are constants. A linear relationship exists between Inline graphic and Inline graphic. Therefore, according to the experimental data, the horizontal coordinate is set as Inline graphic, the vertical coordinate is set as Inline graphic, and the slope of the line can be determined from the activation energy E as long as the specific form of f(α) is determined. However, some studies have shown that many kinds of kinetic mechanism functions [f(α)] exist,22 and the different manifestations are mainly reflected in the value of n.23,24

Based on multiple heating rate methods, the calculation process of the kinetic parameter regression model in this study is shown in Figure 1. The main steps are as follows:

  • (1)

    Different forms of f(α) are chosen for different reaction stages and substituted into eq 6. T and the corresponding Inline graphic are experimental values measured by TG–DSC experiments.

  • (2)

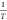    Regression is performed on the relationship between Inline graphic andInline graphic, and the correlation coefficient R is compared.

  • (3)

    The f(α) corresponding to the maximum correlation coefficient R is selected to represent the mechanism function of the reaction stage.

  • (4)

    The activation energy E is obtained from the slope (Inline graphic), and the pre-exponential factor A is obtained from the intercept Inline graphic.

Figure 1.

Figure 1

Open in a new tab

Algorithm flowchart.

4. Results and Discussion

4.1. Thermal Process Analysis of Raw Material Calcination

Figure 2 shows the TG and DSC curves of the heating process of the raw material under a 100% oxygen concentration. Four obvious mass loss curves and endothermic peaks are observed in the heating process of raw materials. The chemical reaction of raw materials is mainly divided into four stages, and the temperature ranges corresponding to the main reaction are 67–114, 220–286, 417–432, and 455–484 °C. This is basically consistent with the analysis of the LiNi0.82Co0.12Mn0.06O2 material by Gang et al.11

Figure 2.

Figure 2

Open in a new tab

TG–DSC test results.

Figure 3 shows the results of the in situ XRD detection. LiOH·H2O and Ni(OH)2 phases are detected at 25 °C (corresponding to Ni0.8Co0. 1Mn0. 1(OH)2, owing to the small contents of Co and Mn, which are the corresponding substances; ref (7) also used a similar expression method). When the temperature increases to 200 °C, the corresponding phase of LiOH is detected. Combined with the TG–DSC experiment and literature,11 the decomposition reaction of LiOH·H2O mainly occurs inside the raw material at this time, and the products are mainly LiOH and water.

Figure 3.

Figure 3

Open in a new tab

XRD test results.

At 250 °C, NiO and trace amounts of cobalt–manganese oxides are detected, which indicates that the precursor begins to decompose at 200–250 °C. This phenomenon mainly generates cobalt–manganese oxides and water. However, a small amount of Ni(OH)2 is detected, which implies that the substance is incompletely decomposed and that the reaction is still going on. Whereas Ni(OH)2 is not detected at 300 °C, indicating that the main decomposition reaction of Ni(OH)2 has basically completed, which is similar to the reaction pattern in TG-DSC experiments. The physical phases are the same at 300–400 °C, and the TG–DSC experiments do not detect any obvious heat changes; therefore, it is presumed that no new chemical reactions occur in this interval.

At 450 °C, a small amount of Li2O is detected, but the other phases do not change significantly. It is speculated that the main chemical reaction at this time is the decomposition of LiOH to produce Li2O and water. According to the results of TG–DSC, it is speculated that the main process of this reaction occurs at 400–450 °C, where an obvious endothermic peak appears. However, the XRD phase shows that LiOH is not detected at 550 °C, which means that the reaction will continue until 550 °C, while it is more intense at 400–450 °C.

When the temperature rises to 500 °C, LiNiO2 is detected (it refers to LiNi0.8Co0.1Mn0.1O2 here; owing to the small contents of Co and Mn, the corresponding material cannot be found in the Jade card). Combined with TG–DSC experiments, the decomposed oxides begin to undergo oxidation reactions between 450 and 500 °C and continue until 650 °C. However, the response is not evident in the later stages, which results in corresponding heat changes not being detected by TG–DSC.

In summary, multiple reactions occur during the heating process due to the large number of elements in the raw materials and multiple reactions may occur in the same temperature range. Combined with the known results, the main chemical reactions occurring during the heating process of the raw materials at different temperatures and the corresponding heat absorption and mass changes are summarized in Table 1.

Table 1. Calcination Reaction Mechanism Collation of Raw Materials.

temperature range (°C) main reaction equation weight loss rate (%) heat absorption (J/kg)
67–114 LiOH·H2O → LiOH + H2O 13.52 267230
220–286 Ni0.8Co0.1Mn0.1(OH)2 → 0.8NiO + 0.1MnCoO2 + H2O 8.74 133880
417–432 2LiOH → Li2O + H2O 1.57 77530
455–484 0.8NiO + 0.1MnCoO2 + 0.5Li2O + 0.25O2 → LiNi0.8Co0.1Mn0.1O2 0.95 47050
Open in a new tab

4.2. Determination of Kinetic Parameters

4.2.1. Determination of the Mechanism Function under Pure Oxygen Conditions

In order to clarify the kinetic parameters of each stage under pure oxygen conditions, first, the obtained thermogravimetric data are processed, and the corresponding conversion rate (α) and the differential conversion rate (dα/dT) at different temperatures are obtained by using the weight loss corresponding to different temperatures. According to the abovementioned analysis, different chemical reactions corresponding to different mechanism functions f(α) were obtained. After preliminary screening, five functions with higher matching degrees were selected from 15 mechanism functions.25 In order to quickly determine the kinetic function f(α) of different reaction stages, based on the regression form of eq 6, a program was written to determine f(α) by comparing the correlation coefficients corresponding to different kinetic functions. Therefore, the obtained conversion rate (α) and the differential (dα/dT) of the conversion rate at each stage are imported into the program, and the different forms of kinetic function f(α) are substituted into the program in turn for calculation. After the calculation, the correlation coefficients corresponding to different forms of f(α) (as shown in Table 2), pre-exponential factor A, and activation energy E are obtained. The different stages correspond to different mechanistic functions, which indicates that the reactions occurring in the heating process of the raw material are complex.

Table 2. Mechanism Model Fitting Results under Pure Oxygen Conditions.
numbering function name reaction mechanism F(α) f(α) R1 (first stage) R2 (second stage) R3 (third stage) R4 (fourth stage)
1 Maple one-line rule, first order stochastic nucleation and subsequent growth –ln (1 – α) 1 – α 0.9837 0.9807 0.8350 0.9580
2 second order chemical reaction, deceleration shape α-t curve (1 – α)−1 – 1 (1 – α)2 0.9644 0.9418 0.8547 0.9504
3 shrinking cylinder(area) phase boundary reaction (cylindrical symmetry) 1 – (1 – α)0.5 2 × (1 – α)0.5 0.9612 0.9994 0.7878 0.9538
4 2/3 order chemical reaction (1 – α)−0.5 2 × (1 – α)1.5 0.9737 0.9586 0.8486 0.9535
5 constricted globose phase boundary reaction (spherical symmetry) 1–(1−α)1/3 3 × (1 – α)2/3 0.9802 0.9957 0.8121 0.9595
Open in a new tab

The optimal mechanism functions corresponding to the four reactions can be determined by comparing the correlation coefficients R, and they are shown in Table 3.

Table 3. Reaction Mechanism Function for Each Stage.
reaction stage reaction temperature (°C) f(α) function name reaction mechanism
1 67–114 f = 1 – α Maple one-line rule, first order stochastic nucleation and subsequent growth
2 220–286 f = 2 × (1 – α)0.5 shrinking cylinder (area) phase boundary reaction (cylindrical symmetry)
3 417–432 f = (1 – α)2 second order chemical reaction, deceleration shape α–t curve
4 455–484 3 × (1 – α)2/3 constricted globose phase boundary reaction (spherical symmetry)
Open in a new tab

4.2.2. Determination of the Activation Energy and Pre-exponential Factor under Different Oxygen Concentrations

The abovementioned experimental conclusions indicate that oxidation reactions mainly occur in the last stages of raw material sintering. Therefore, the oxygen concentration has an important influence on the reaction of the fourth stage. If the oxygen concentration is too low, then the oxidation reaction cannot be conducted; if the oxygen concentration is too high, then the production cost is unfavorable. Therefore, after clarifying the mechanism function of each reaction stage, TG–DSC experiments were conducted by adjusting the oxygen concentration (100, 80, 60, 40, and 20%) to analyze the effect of the oxygen concentration on the calcination process of raw materials. The corresponding activation energy and pre-exponential factor at different concentrations were also determined according to the calculation idea of Figure 1. The results obtained from the fitting are listed in Table 4.

Table 4. Mechanism Functions at Different Oxygen Concentrations.
reaction stage f(α) oxygen concentration (%) R E (kJ/mol) lnA
1 f(α) = 1 – α 20 0.9597 58.302 22.182
40 0.9615 62.106 23.232
60 0.9868 66.933 29.357
80 0.9945 104.03 38.992
100 0.9837 111.016 41.904
2 f(α) = 2 × (1 – α)0.5 20 0.9729 109.12 24.279
40 0.9874 111.16 25.086
60 0.9853 109.84 24.674
80 0.9987 152.65 34.944
100 0.9994 156.16 35.708
3 f(α) = (1 – α)2 20 0.8791 131.94 25.552
40 0.8608 114.14 21.959
60 0.8284 102.04 19.104
80 0.844 97.52 18.525
100 0.8547 105.93 20.107
4 f(α) = 3 × (1 – α)2/3 20 0.9873 349.74 56.8725
40 0.9709 283.22 45.604
60 0.9893 248.57 39.3983
80 0.9898 340.62 55.144
100 0.9595 285.75 46.173
Open in a new tab

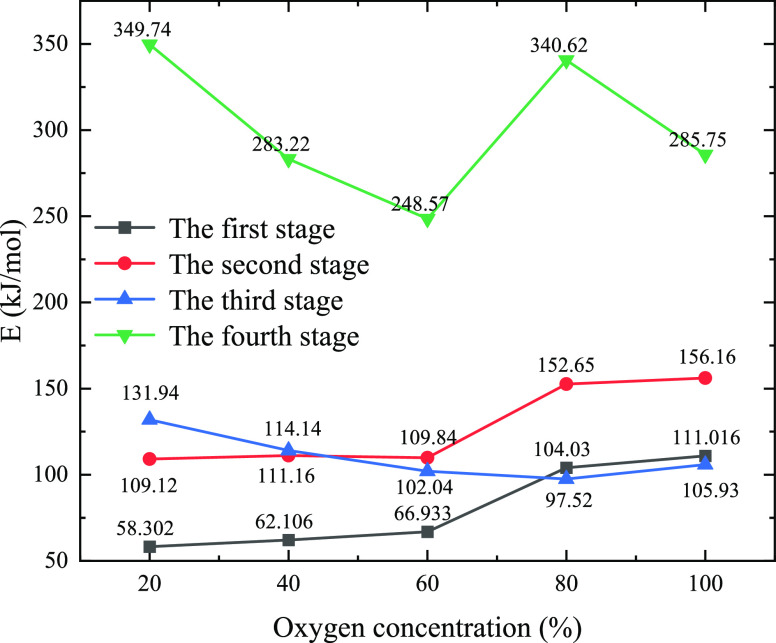
The curve of the activation energy E of the four stages with the change in the oxygen concentration is shown in Figure 4. The activation energy range for the first stage is 58.302 to 111.016 kJ/mol with a change of 52.714 kJ/mol. The activation energy range for the second stage is 109.120 to 156.160 kJ/mol with a change of 47.040 kJ/mol. The activation energy range for the third stage is 97.520–131.940 kJ/mol with a change of 34.420 kJ/mol. The activation energy range for the fourth stage is 248.570–349.740 kJ/mol with a change of 101.170 kJ/mol. The activation energy of the first, second, and third stages has smaller fluctuations under different oxygen concentrations than the fourth stage. The range of activation energy fluctuation is 34.420 to 52.174 kJ/mol, which is much smaller than that of the fourth stage. The reason is that the first, second, and third stages belong to the decomposition reaction and do not involve oxygen participation. Thus, the change law of the activation energy shows little relationship with the oxygen concentration.

Figure 4.

Figure 4

Open in a new tab

Relationship between the oxygen concentration and activation energy of the four stages of reaction.

In summary, the influence of the oxygen concentration on the activation energy of the fourth-stage chemical reaction indicates that a lower oxygen concentration can be adopted in the calcination of this type of raw material, and a 100% oxygen concentration is not necessary. Subsequently, electrochemical tests on the calcined products made under different oxygen concentrations need to be conducted.

5. Conclusions

The reaction mechanism of the calcination process of raw materials (namely, Ni0.8Co0.1Mn0.1(OH) 2 and LiOH·H2O mixture) at different oxygen concentrations was studied by non-isothermal TG analysis combined with an in situ XRD test. The following conclusions were obtained:

  • (1)

    The calcination process of raw materials is divided into four stages. The first three stages are the decomposition and dehydration of LiOH·H2O, Ni0.8Co0.1Mn0.1(OH)2, and LiOH. The fourth stage is the reaction of decomposed oxides with oxygen to form ternary cathode materials.

  • (2)

    The kinetic mechanism functions, activation energies, and pre-exponential factors were obtained for each of the four reactions at different oxygen concentrations. The reaction mechanism of the first stage is stochastic nucleation and subsequent growth. The reaction mechanism of the second stage is a phase boundary reaction (cylindrical symmetry). The reaction mechanism of the third stage is a chemical reaction, that is, a deceleration shape of the α–t curve. The reaction mechanism of the fourth stage is a phase boundary reaction (spherical symmetry).

  • (3)

    Comparing the activation energy of different oxygen concentrations shows that the activation energy of the first three stages varies from 34.42 to 52.714 kJ/mol at different oxygen concentrations, which is less than 101.17 kJ/mol in the fourth stage. However, the activation energy of the fourth stage reaction is the smallest at a 60% oxygen concentration, which is beneficial to the reaction.

In this study, the chemical reactions in the calcination process of raw materials were preliminarily analyzed by TG–DSC and in situ XRD tests, and the kinetic parameters at different concentrations were determined. Subsequently, the electrochemical properties of the raw materials at different concentrations will be discussed comprehensively, which will provide a reference for the optimization of the calcination process of the raw materials.

Acknowledgments

This research was funded by Ningbo Ronbay New Energy Technology Company.

The authors declare no competing financial interest.

References

  1. Albatayneh A.; Juaidi A.; Jaradat M.; Manzano-Agugliaro F. Future of Electric and Hydrogen Cars and Trucks: An Overview. Energies 2023, 16, 3230. 10.3390/en16073230. [DOI] [Google Scholar]
  2. Ding Y.; Mu D.; Wu B.; Wang R.; Zhao Z.; Wu F. Recent progresses on nickel-rich layered oxide positive electrode materials used in lithium-ion batteries for electric vehicles. Appl. Energy 2017, 195, 586–599. 10.1016/j.apenergy.2017.03.074. [DOI] [Google Scholar]
  3. Chang L.; Wei A.; Luo S.; Cao S.; Bi X.; Yang W.; Yang R.; Liu J. Lithium-ion battery: A comprehensive research progress of high nickel ternary cathode material. Int. J. Energy Res. 2022, 46, 23145–23172. 10.1002/er.8618. [DOI] [Google Scholar]
  4. Zha Y.; Fei Z.; Yang Z.; Meng Q.; Dong P.; Zhang Y.; Li Y. High separation efficiency of ternary cathode materials from spent lithium-ion batteries by ternary molten Li-salt method. Sustainable Mater. Technol. 2023, 35, 00575 10.1016/j.susmat.2023.e00575. [DOI] [Google Scholar]
  5. Guorong Hu; Chaopu Tan; Ke Du; et al. Preparation of high-pressure nickel-rich cathode material LiNi0.85Co0.06Mn0.06A10.0302. Chin. J. Inorg. Chem. 2017, 33 (8), 1450–1456. [Google Scholar]
  6. Song L.; Du J.; Xiao Z.; Jiang P.; Cao Z.; Zhu H. Research Progress on the Surface of High-Nickel Nickel–Cobalt–Manganese Ternary Cathode Materials: A Mini Review. Front. Chem. 2020, 8, 00761 10.3389/fchem.2020.00761. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Shen Y.; Wang P.; Chen L. Pyrolysis of cellulose with cathode materials recovered from spent binary and ternary lithium-ion batteries. Fuel 2022, 324, 124502 10.1016/j.fuel.2022.124502. [DOI] [Google Scholar]
  8. Huang C.; Xia X.; Chi Z.; Yang Z.; Huang H.; Chen Z.; Tang W.; Wu G.; Chen H.; Zhang W. Preparation of single-crystal ternary cathode materials via recycling spent cathodes for high performance lithium-ion batteries. Nanoscale 2022, 14, 9724. 10.1039/D2NR00993E. [DOI] [PubMed] [Google Scholar]
  9. Zhu X. F.; Li X.; Liang T. Q.; Liu X. H.; Ma J. M. Electrolyte perspective on stabilizing LiNi0.8Co0.1Mn0.1O2 cathode for lithium-ion batteries. Rare Metals 2023, 42 (2), 387–398. 10.1007/s12598-022-02101-2. [DOI] [Google Scholar]
  10. Gao M.; He Y.; Yan K.; Han G.; Zhuang W.; Yun F.; Lian F.; Qiu W.; Lu S. Synthesizing kinetics and characteristics of high-capacity Li1.16(Ni0.25Mn0.75)0.84O2 cathode materials for lithium-ion batteries. Ionics 2021, 27, 3729–3737. 10.1007/s11581-021-04068-z. [DOI] [Google Scholar]
  11. Gang Zhang Xu; Qian C. G. Change analysis of ternary material LiNi0.82Co0.12Mn0.06O2 during heat treatment process. Power Sources 2019, 43 (05), 747–761. [Google Scholar]
  12. Hu X.; Lin Z.; Yang K.; Deng Z. Kinetic Analysis of One-Step Solid-State Reaction for Li 4 Ti 5 O 12 /C. J. Phys. Chem. A 2011, 115, 13413–13419. 10.1021/jp2075644. [DOI] [PubMed] [Google Scholar]
  13. Han Y.; Wang T.; Yin L.; Wu Z.; Bi R.; Li B.; Yang Y. Preparation of layered Ni-rich LiNi0.9Co0.05Mn0.05O2 cathode materials with excellent electrochemical properties by controllable lithium supply and sintering. J. Energy Storage 2023, 67, 107541 10.1016/j.est.2023.107541. [DOI] [Google Scholar]
  14. Chen S.; Wu J.; Su Z.; Deng L. Kinetic Studies on the Synthesis of Monoclinic Li 3 V 2 (PO 4) 3 via Solid-State Reaction. J. Phys. Chem. A 2014, 118, 3711–3716. 10.1021/jp501516k. [DOI] [PubMed] [Google Scholar]
  15. Zhao M. S.; Song X. P. Synthesizing kinetics and characteristics for spinel LiMn2O4 with the precursor using as lithium-ion battery cathode material. J. Power Sources 2007, 164, 822–828. 10.1016/j.jpowsour.2006.11.001. [DOI] [Google Scholar]
  16. Llusco A.; Grageda M.; Ushak S. Kinetic and Thermodynamic Studies on Synthesis of Mg-Doped LiMn2O4 Nanoparticles. Nanomaterials 2020, 10, 1409. 10.3390/nano10071409. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Su M.; Chen Y.; Liu H.; Li J.; Fu K.; Zhou Y.; Dou A.; Liu Y. Storage degradation mechanism of layered Ni-rich oxide cathode material LiNi0.8Co0.1Mn0.1O2. Electrochim. Acta 2022, 422, 140559 10.1016/j.electacta.2022.140559. [DOI] [Google Scholar]
  18. Xiang K.; Li S.; Li Y.; Wang H.; Xiang R. Interactions of Li2O volatilized from ternary lithium-ion battery cathode materials with mullite saggar materials during calcination. Ceram. Int. 2022, 48, 23341–23347. 10.1016/j.ceramint.2022.04.323. [DOI] [Google Scholar]
  19. Budrugeac P.; Cucos A.; Dascălu R.; Atkinson I.; Osiceanu P. Application of model-free and multivariate nonlinear regression methods for evaluation of the kinetic scheme and kinetic parameters of thermal decomposition of low density polyethylene. Thermochim. Acta 2022, 708, 179138 10.1016/j.tca.2021.179138. [DOI] [Google Scholar]
  20. Xian X. Exploration of kinetic equation of lime sulfur absorption reaction by thermogravimetric analysis. J. Beijing Inst. Light Ind. 1994, 02, 52–58. [Google Scholar]
  21. Valenta T.; Lapčíková B.; Lapčík L. Determination of kinetic and thermodynamic parameters of food hydrocolloids/water interactions by means of thermal analysis and viscometry. Colloids Surf., A 2018, 555, 270–279. 10.1016/j.colsurfa.2018.07.009. [DOI] [Google Scholar]
  22. Pinzi S.; Buratti C.; Bartocci P.; Marseglia G.; Fantozzi F.; Barbanera M. A simplified method for kinetic modeling of coffee silver skin pyrolysis by coupling pseudo-components peaks deconvolution analysis and model free-isoconversional methods. Fuel 2020, 278, 118260 10.1016/j.fuel.2020.118260. [DOI] [Google Scholar]
  23. Tengtun X.Study on catalytic pyrolysis and pollution migration of oil-based cuttings in shale gas drilling. Chongqing university, 2019.
  24. Xueguang L.; LiuYang D. J. Pyrolysis kinetics of soybean soapstock. J. Beijing Univ. Chemical Technol. 2023, 50 (2), 1–7. [Google Scholar]
  25. Mishra R. K.; Mohanty K. Kinetic analysis and pyrolysis behaviour of waste biomass towards its bioenergy potential. Bioresour. Technol. 2020, 311, 123480 10.1016/j.biortech.2020.123480. [DOI] [PubMed] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES