Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Oct 30;127(44):21684–21694. doi: 10.1021/acs.jpcc.3c04019

High-Pressure Vibrational and Structural Properties of Ni3V2O8 and Co3V2O8 up to 20 GPa

Josu Sánchez-Martín †,*, Julio Pellicer-Porres †, Akun Liang †,‡, Jordi Ibáñez §, Robert Oliva §, Catalin Popescu ∥, Zhangzhen He ⊥, Plácida Rodríguez-Hernández #, Alfonso Muñoz #, Daniel Errandonea †
PMCID: PMC10851775  PMID: 38344684

Abstract

graphic file with name jp3c04019_0012.jpg

The vibrational and structural behaviors of Ni3V2O8 and Co3V2O8 orthovanadates have been studied up to around 20 GPa by means of X-ray diffraction, Raman spectra, and theoretical simulations. Both materials crystallize in an orthorhombic Kagomé staircase structure (space group: Cmca) at ambient conditions, and no phase transition was found in the whole pressure range. In order to identify the symmetry of the detected Raman-active modes under high pressure, single crystal samples of those materials were used in a polarized Raman and infrared setup. Moreover, high-pressure powder X-ray diffraction measurements were performed for Co3V2O8, and the results confirmed the structure stability also obtained by other diagnostic techniques. From this XRD analysis, the anisotropic compressibilities of all axes were calculated and the unit-cell volume vs pressure was fitted by a Birch–Murnaghan equation of state, obtaining a bulk modulus of 122 GPa.

1. Introduction

Metal orthovanadates following the formula M3V2O8 (M = Ni, Co, Zn, Mn, and Mg) have attracted considerable fundamental research attention for decades,1−3 due to their rich polymorphism4−7 and multiferroic properties.8−10 These qualities make them desirable materials for industrial applications. Regarding the samples studied in this work, Ni and Co orthovanadates are mainly used in nanostructured systems. Both have been investigated as catalysts in the water splitting process,11,12 as electrodes in portable power sources,13,14 in the potential improvement of electrochemical energy storage,15,16 in nitrogen fixation,17 and even in glucose detection.18

The so-called Kagomé-staircase orthorhombic structure of Ni3V2O8 and Co3V2O8 (space group: Cmca, No. 64) is formed by corrugated layers in the [010] direction of edge-sharing MO6 octahedra interconnected with VO4 tetrahedra (see Figure 1). Both compounds have four formulas per unit cell (Z = 4). The lattice parameters for Ni3V2O8 are a = 5.936(4) Å, b = 11.420(6) Å, and c = 8.240(5) Å and for Co3V2O8 are a = 6.030(4) Å, b = 11.486(2) Å, and c = 8.312(5) Å.1 It is worth mentioning that a similar polyhedral coordination is also found in metavanadates (MV2O6)19 and pyrovanadates (M2V2O7).20

Figure 1.

Figure 1

Open in a new tab

Crystal structure of the M3V2O8 orthovanadate Kagomé-staircase family. Atoms and unit-cell axis are labeled on the left. MO6 octahedra are shown in blue, and VO4 tetrahedra are shown in green.

In recent years, the high pressure (HP) community has also put the focus on this family of compounds, which have demonstrated a variety of remarkable physical behaviors under pressure. X-ray diffraction (XRD) and Raman methods were used to study Mn3V2O8 in its orthorhombic low-temperature structure; an irreversible phase transition at 10 GPa was discovered, but the new phase has not been identified yet.21 In contrast, it has been demonstrated that Zn, Ni, and Mg orthovanadates are stable up to 15,22 23,23 and 25.7 GPa,24 respectively. With different structures but the same stoichiometry, Ca and Sr orthovanadates were found to undergo different phase transitions at 9.7(1) GPa25 and 13.8 GPa,26 respectively. Alternatively, it was reported that triclinic Cu3V2O8 decomposes into CuO and V2O5 at 1.35 GPa.27 Note that the structural properties of Ni3V2O8 were recently investigated by HP powder XRD by some of the authors of the present study.24 To compare with Co3V2O8, the data from that work are included in the current investigation.

We continue the research in orthovanadates within this paper by reporting for the first time the changes in the vibrational modes of Ni3V2O8 and Co3V2O8 under HP from both experiments and density functional theory (DFT) calculations. As a previous step, polarized Raman and infrared (IR) measurements are used to properly identify the symmetry of the active modes and match them with the simulation results under ambient conditions. We also present the first HP XRD analyses of Co3V2O8. As it is situated in the periodic table between Mn (which undergoes a phase transition at 10 GPa21) and Ni (which remains stable up to 23 GPa23), it is of great interest to find out what structural changes occur under pressure. The experimental data are also supported by the corresponding DFT calculations. We determined the bulk modulus and anisotropic compressibility of this compound from the structural information we have collected. Finally, we make use of all the results obtained to compare the pressure behavior of both orthovanadates.

2. Methods

2.1. Sample Synthesis

Powder samples of Ni3V2O8/Co3V2O8 were synthesized by means of a solid-state reaction starting with NiO/CoO (99.995% purity) and V2O5 (99.9% purity). The precursors were obtained from Alfa Aesar. An Al2O3 crucible was used to heat the mixed reagents in air at 800 °C for 16 h. The product was then ground and pressed into a pellet, which was sintered at 900 °C for an additional 16 h.

For the single crystal preparation, Ni3V2O8/Co3V2O8 powders were prepared at 900 °C for 40 h by a standard/high-temperature solid-state reaction method using NiC2O4·2H2O/CoC2O4·2H2O and V2O5 as the reagents with a molar ratio of 3:1. The crystal growth was performed in an electric furnace, where Ni3V2O8/Co3V2O8 powder samples and flux V2O5 and SrCO3 (also BaCO3 for Co3V2O8) were melted homogeneously in an alumina crucible at 1000 °C and kept at 1000 °C for 10 h, cooled slowly to 800 °C/700 °C at a rate of 0.5 °C/h (making constant temperature stops several times in between), and finally cooled to room temperature at a rate of approximately 100 °C/h. The final Ni yellow crystals (∼3 × 3 × 0.5 mm3)/Co dark blue crystals (∼4 × 4 × 1 mm3) were obtained by mechanical separation from the crucible. A detailed growth procedure is described in ref (28) for Ni3V2O8 and in ref (29) for Co3V2O8.

2.2. Experimental Details

The orientation of the single crystals was carried out by using a Bruker D8 Venture diffractometer. IR spectra at ambient conditions were collected with an FTIR Bruker IFS125 HR spectrometer using a Globar light source, KBr beam splitter, and MCT detector (cut at 600 cm–1). Raman spectra were acquired in the backscattering geometry using a 632.8 nm He–Ne laser, a Jobin Yvon spectrometer combined with a thermoelectric-cooled multichannel charge-coupled device (CCD) detector with a spectral resolution of 2 cm–1, and a Semrock low-pass RazorEdge filter. A low laser power of approximately 2 mW before the diamond anvil cell (DAC) was necessary to avoid overheating the sample and wavenumber shifting. Polarizer filters were added to the Raman setup for the single crystal measurements. HP Raman measurements were performed using a DAC and a 16:3:1 methanol–ethanol–water mixture as the pressure-transmitting medium (PTM).30 The peak profile fit was achieved using a Pseudo-Voight peak profile in MATLAB software.31 The pressure gauge was determined using ruby luminescence.32

HP powder XRD measurements on Co3V2O8 were performed at the MSPD beamline of the ALBA synchrotron33 using a monochromatic beam with a wavelength of 0.4246 Å. The beam was focused down to a spot with a full width at half-maximum (fwhm) of 20 μm × 20 μm. A Rayonix CCD detector was used to collect XRD patterns with a sample-to-detector distance of 340 mm. This sample–detector distance was required to achieve a correct angular resolution, which limited our 2θ range to around 13°. The pressure was determined using the XRD reflections and the equation of state (EOS) of Cu34 with a precision of ±0.1 GPa. The PTM used for these experiments was a 4:1 methanol–ethanol (ME) mixture. The measurements thus obtained were transformed into one-dimensional patterns using the DIOPTAS suite,35 and Le Bail fittings were achieved with PowderCell.36

2.3. Ab Initio Density-Functional Theory Calculations

Ab initio calculations were performed within the framework of density functional theory (DFT)37 with the Vienna ab initio Simulation Package (VASP).38,39 The projector augmented-wave (PAW) method40,41 was employed. To ensure accurate converged results, the plane-wave kinetic cutoff was extended up to 650 and 540 eV for Ni3V2O8 and Co3V2O8, respectively. The integrations over the Brillouin zone (BZ) were carried out with a k-special point sampling grid of 6 × 6 × 4. After testing different functionals to decide which was the most accurate for each compound, the exchange-correlation energy was described by means of the generalized gradient approximation (GGA) with the Armiento and Mattsson (AM05) prescription42,43 for Ni3V2O8 and, in the case of Co3V2O8, the Perdew–Burke–Ernzerhof (PBE) functional for solids.44,45 To properly treat the strongly correlated states, the DFT + U method of Duradev et al.46 was employed. This method utilizes a single parameter, Ueff = U – J, where U and J are the effective on-site Coulomb and exchange parameters, respectively. The values used for Ueff(47) were 6.2 eV for Ni, 3.25 eV for V, and 3.32 eV for Co. In both compounds, the ferromagnetic configuration was found to be lower in energy.

The unit cell parameters and atomic positions were fully optimized to obtain, at selected volumes, the relaxed structure. For the optimization, the criteria used were as follows: the forces on the atoms were less than 3 meV/Å, and the deviations of the stress tensors from a diagonal hydrostatic form were lower than 0.1 GPa. Our ab initio calculations provide a data set of volumes, energies, and pressures (from the stress tensor) that are fitted with a Birch–Murnaghan equation of state48 to obtain the theoretical equilibrium volume, the bulk modulus, and the pressure derivatives.

Lattice-dynamic calculations of the phonon modes were carried out at the zone center (Γ point) of the BZ with the direct force-constant approach provided by Phonopy.49 These calculations provide the frequency of the normal modes, their symmetry, and their polarization vectors. This allows the identification of the irreducible representations and character of the phonon modes at the Γ-point. To include the polarization induced by atomic displacements and the generated macroscopic electric field producing the LO/TO splitting, the nonanalytical term corrections were added using a 2 × 2 × 2 supercell, with the Born effective charges and the dielectric tensor as described in the Phonopy package.49

3. Results and Discussion

3.1. Vibrational Properties of Ni3V2O8 and Co3V2O8

Both Ni and Co orthovanadates present the same crystalline structure,1 whose symmetry is described by the Cmca space group. There are two molecules in the primitive unit cell, giving rise to seventy-eight vibrational modes. Point group mmm classifies the symmetry at the zone center as follows50:

3.1.

Even (gerade) modes (Ag, B1g, B2g, and B3g) are Raman active. Ni/Co atoms located at inversion centers (those at the 4a Wyckoff position) remain at rest. One of each of the B1u, B2u, and B3u modes corresponds to acoustic modes. The rest are IR active modes with the exception of Au modes, which are silent. All these modes have been individually labeled in Tables 1 (IR active) and 4 (Raman active). The calculated atomic motions of all vibrational modes are represented in Tables S1, S2, and S3.

Table 1. Ab Initio Calculated IR Modes under Ambient Conditionsa.

  Ni3V2O8
 Co3V2O8
DFT mode ω0 (TO) ∂ω/∂P (TO) ω0 (LO) ω0 (TO) ∂ω/∂P (TO) ω0 (LO)
B11u 144 0.6(1) 145 124 –0.04(1) 125
B23u 150 0.9(1) 151 144 0.9(1) 144
B22u 174 1.0(1) 174 155 0.4(1) 154
B31u 186 1.1(1) 186 183 –0.3(1) 184
B33u 197 1.3(1) 198 184 0.9(1) 185
B32u 198 0.6(1) 199 182 –0.5(1) 182
B41u 216 1.1(1) 218 200 0.8(1) 204
B42u 221 1.4(1) 221 209 –0.8(1) 210
B43u 245 6.8(1) 261 245 1.8(1) 258
B51u 255 3.0(1) 264 247 –0.2(1) 249
B52u 290 3.5(1) 308 278 2.0(1) 288
B61u 301 2.2(1) 303 285 2.6(1) 288
B53u 308 3.8(1) 308 293 4.0(1) 293
B71u 312 2.6(1) 322 305 4.8(1) 313
B62u 316 1.6(1) 317 301 1.6(1) 303
B81u 322 4.8(1) 324 332 4.2(1) 330
B72u 323 4.6(1) 339 320 4.1(1) 339
B63u 332 4.1(1) 343 304 1.8(1) 307
B91u 369 5.1(1) 376 342 4.3(1) 354
B73u 372 4.1(1) 387 353 5.6(1) 365
B82u 404 2.9(1) 406 387 2.6(1) 390
B82u 414 4.5(1) 425 396 3.6(1) 410
B92u 442 3.5(1) 446 421 3.7(1) 422
B101u 449 3.5(1) 449 427 3.6(1) 427
B111u 653 6.5(1) 710 636 6.4(1) 691
B103u 664 6.6(1) 740 642 6.5(1) 716
B91u 793 2.6(1) 872 806 4.4(1) 860
B122u 796 6.5(1) 806 770 2.5(1) 779
B112u 814 4.4(1) 855 790 5.9(1) 823
B131u 821 2.8(1) 895 820 2.1(1) 874
B122u 883 3.8(1) 917 864 2.7(1) 893
Open in a new tab
a

Wavenumber (ω0) is expressed in cm–1 and pressure (P), in GPa. The DFT-calculated ω0 has a related uncertainty of ±5%.

Table 4. Raman Modes, Wavenumbers, and Pressure Coefficients Corresponding to the Zone-Center Active Raman Modes under Ambient Conditions for Ni3V2O8 and Co3V2O8a.

  Ni3V2O8
 Co3V2O8
  this work
 DFT
 Kesari et al.53 this work
 DFT
 Seo et al.54
mode ω0 ∂ω/∂P ω0 ∂ω/∂P ω0 ω0 ∂ω/∂P ω0 ∂ω/∂P ω0
Ag1g 121(2) 0.1(5) 121 –0.1(1) 123 111(4) 0.6(1) 111 –0.2(1)  
B11g 133(2) 0.8(3) 131 0.4(1) 135 123(5) 0.3(3) 121 0.4(1)  
B21g     154 1.4(2) 157 138(4) 0.7(6) 143 1.4(1) 136
B12g 164(3) 1.3(2) 164 1.3(1) 166 145(4) 1.8(4) 145 2.2(1)  
B31g 171(6) 1.7(8) 175 0.7(2) 177 (B3g)     169 0.4(1)  
B13g 176(3) 0.7(3) 185 0.9(1) 168 (B2g)     179 1.2(1)  
B22g 184(2) 1.1(3) 180 1.4(1) 186 (B1g)     166 0.7(1)  
B23g 209(3) 0.3(6) 205 0.3(2) 210     201 0.0(1)  
A2g 212(2) 2.5(5) 212 3.2(1) 213 185(3) 4.4(2) 204 2.6(1) 179
B33g     231 1.0(1) 230     223 0.8(1)  
B43g 255(2) 1.7(3) 252 2.0(1) 256     247 2.4(1)  
A3g 270(2) 0.9(6) 263 0.8(1) 271 258(4) 0.9(2) 260 0.4(1)  
B41g 273(2) 3.9(3) 271 3.8(1) 328 (B2g)     254 3.7(1)  
B32g 282(3)   281 4.0(1) 283 (Ag)     260 4.3(1)  
B42g 288(6) 4.2(2) 291 4.3(1) 291 (B1g) 282(5)   272 3.8(1)  
A4g 319(2) 5.6(2) 317 6.7(1) 320     306 2.3(1)  
B53g     320 6.5(1)       330 8.0(1)  
B51g 325(3) 3.8(3) 321 3.9(1) 351 (Ag) 295(6) 5.8(2) 297 4.1(1)  
A5g 347(5) 2.8(7) 340 2.9(1) 348 (B1g) 337(3) 4.8(1) 327 3.2(1) 320
B61g 351(2) 4.2(4) 349 5.0(1) (B3g) 326(5) 4.7(1) 318 4.8(1)  
B63g     372 2.3(1) 378 (B1g)     360 2.7(1)  
B73g 392(7)   387 2.9(1) 390     371 2.8(1)  
A6g 400(6) 2.2(3) 400 1.9(1) 401 385(4) 1.5(1) 386 1.7(1) 384
B71g 413(4) 3.7(2) 406 4.9(1) 413 394(5) 4.1(1) 386 4.3(1)  
B52g     442 3.1(1) 455     425 3.1(1)  
B83g 423(7)   446 2.7(1) (Ag)     425 2.3(1)  
B62g 450(6) 6.4(2) 449 4.8(1)       449 4.5(1)  
A7g 458(4) 2.7(3) 456 2.9(1) 469 (B3g) 454(4) 2.7(1) 440 2.3(1) 450
A8g 640(6) 5.6(2) 663 6.5(1) 641 629(5)   642 6.5(1) 619
B93g 675(4) 6.1(4) 695 5.8(1) 675 666(7) 4.3(7) 670 5.7(1) 666
B81g     784 3.8(1)       786 2.2(1)  
B72g 806(4)   806 3.8(1) 805 (Ag)     798 2.7(1)  
A9g 805(3) 3.9(1) 808 5.6(1) 799 (B2g) 768(6)   788 7.6(1)  
B103g 808(5)   817 5.6(1) 806     786 5.4(1)  
A10g 826(2) 2.6(1) 828 3.3(1) 825 (B3g) 814(2) 3.0(1) 817 2.2(1) 811
B113g     842 3.5(1) (Ag) 880(7)   839 2.1(1)  
Open in a new tab
a

ω0 is expressed in cm–1, and P, in GPa. The DFT-calculated ω0 has a related uncertainty of ±5%. Discrepancies in symmetry assignation with Kesari et al.53 are included in its column.

The modes with the largest wavenumbers are related to the internal modes of the VO4 tetrahedra. Taking a closer look into some of the representative modes (referring to the wavenumbers of Co3V2O8), it can be seen that A9g (Figure 2) and B121u are V–O bond stretching modes. Both have very similar calculated frequencies (789 and 770 cm–1, respectively), because their vibration pattern is very similar, but the inversion center makes the equivalent V and O movement through this point in phase or in phase opposition. Other examples of phonons related to the internal movement of the tetrahedra are the B93g, Figure 2, and B102u modes (670 and 642 cm–1, respectively). Their vibration pattern includes bending of V–O bonds. From 640 to 440 cm–1, there is a frequency gap that divides internal from external modes. The more energetic mode with a relevant Co amplitude is the A7u mode at 460 cm–1. The amplitude is, however, not large enough to be appreciated in Table S3. It is remarkable that internal modes have similar frequencies in Co and Ni compounds (a difference of less than 4%). In external modes where the M amplitude is relevant, the wavenumber differences are more pronounced. The mode with the largest Co amplitude is the B21u mode. The wavenumbers in Co and Ni compounds differ by 16% (124 and 144 cm–1, respectively). The mode B23u (144 cm–1 in the Co compound) constitutes an example of rotation of the VO4 tetrahedron, in this case having a V–O bond as an axis, Figure 2. The mode also involves a significant shift of the Co atoms. Finally, the low wavenumber mode A1g (111 cm–1, Figure 2) represents a mode where atoms in a plane roughly defined by z ≅ 0.25 vibrate in phase opposition respect to atoms in a z ≅ 0.75 plane, while atoms near z = 0 and 0.5 remain static. The large mass involved implies low frequency mode. Other similar modes are B21u (124 cm–1) and B11g (121 cm–1).

Figure 2.

Figure 2

Open in a new tab

Representative vibrational modes of M3V2O8 (M = Ni, Co) using the primitive unit cell. M is in pink, V in gray, and O in red. Blue arrows represent the key motion, while blue dots represent key atoms in still positions.

3.2. Ambient Conditions for Infrared Spectroscopy (Ni3V2O8 and Co3V2O8)

IR modes were identified using polarization and considering that B1u, B2u, and B3u modes transform as z, y, and x, respectively. The ab initio calculated IR active modes, including the transversal optic (TO) and longitudinal optic (LO) splittings and the corresponding pressure coefficients, are reported in Table 1. Furthermore, in Table 2, using the theoretical IR phonon wavenumbers and the simulated static dielectric constants (ε0), the infinite dielectric constants (ε∞) were calculated using the Lyddane-Sachs Teller relation.51

Table 2. Ab Initio Calculated Diagonal Components of the Static and Infinite Dielectric Constants of Ni3V2O8 and Co3V2O8 in Ambient Conditions.

  εxx0 εyy0 εzz0 εxx0 εyy0 εzz0
Ni3V2O8 5.1(3) 5.3(3) 5.3(3) 3.0(2) 2.8(1) 3.0(2)
Co3V2O8 6.0(3) 6.2(3) 6.0(3) 4.1(2) 3.5(2) 3.6(2)
Open in a new tab

The growth conditions of the samples favored the formation of single crystals with the largest surface perpendicular to the y-axis. The measurements were taken on the [010] surface. The spectral region for the present IR measurements covered from 600 to 4500 cm–1. Therefore, only the three highest frequency B1u modes and the last B3u for both Ni3V2O8 and Co3V2O8 single crystals were accessible. These modes were selected using polarizers, as represented in Figure 3. The dielectric constant was modeled using the following relation:

3.2. 1

where ωTO, ωLO, γTO, and γLO are the frequencies and damping factors of the transverse and longitudinal optic modes, respectively.52 Using eq 1, the reflectivity of the material, 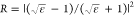Inline graphic, can be obtained, and then, the total reflectance of the sample can be calculated, considering that the body with parallel surfaces undergoes consecutive internal reflections, as follows:

3.2. 2

where α is the absorption coefficient. Equation 2 was used to fit the experimental data in Figure 3. In the spectral region where the sample is transparent, this expression simplifies to

3.2. 3

Figure 3.

Figure 3

Open in a new tab

Experimental infrared reflectivity (dots) using 3 different incident polarizations. Solid lines represent the best fit54 for each set of data.

The criteria chosen for data normalization are based on the reflectance (3) at 4500 cm–1, where the sample is transparent and the reflectance is estimated using the calculated static dielectric constant from Table 2.

The experimentally determined IR modes are gathered along with the calculated modes in Table 3. It is noticeable that both experimental and theoretical values are in good agreement, including the TO-LO splitting values.

Table 3. Theoretical and Experimental Zone-Center IR Modes for Ni3V2O8 and Co3V2O8a.

  DFT
 experimental
mode ω0 (TO) ω0 (LO) ω0 (TO) γ0 (TO) ω0 (LO) γ0 (LO)
Ni3V2O8
B111u 653 710 630(1) 24(4) 688(1) 16(3)
B93u 793 872 797(1) 19(3) 902(1) 7(3)
B121u 796 806 791(1) 14(6) 803(1) 8(4)
B131u 821 895 828(1) 6(3) 901(1) 17(4)
Co3V2O8
B111u 636 691 626(1) 11(3) 684(1) 16(3)
B93u 806 860 789(1) 10(3) 895(1) 6(4)
B121u 770 779 759(1) 25(5) 787(1) 17(5)
B131u 820 874 819(1) 8(4) 885(1) 12(5)
Open in a new tab
a

γ0 is the damping factor of the fitting in cm–1, and ω0 is expressed in cm–1. The DFT-calculated ω0 has a related uncertainty of ±5%.

3.3. Ambient Conditions for Polarized Raman (Ni3V2O8 and Co3V2O8)

First, the Raman tensors of the allowed modes are50

3.3.

The resulting selection rules provide the advantage of being able to measure the modes separately, always in the backscattering configuration, employing the previously oriented single crystals. Additionally, it must be noted that Ag and B1g/B2g/B3g modes are allowed when the backscattered signal from the single crystal sample is polarized parallel or perpendicular to the polarization of the incident laser, respectively. On the other hand, B1g/B2g/B3g modes can only be measured if the surface of incidence is oriented in the crystallographic c/b/a-axis (hereon referred to as z/y/x). Depending on the specimen, other smaller surfaces different from [010] were also available. In the case of Ni3V2O8, a single crystal with a small [001] face was measured. In addition, a third perpendicular surface could be measured, starting from the [010] plane and tilting the DAC 53° with respect to the z-axis (from now on called the ξ orientation; see Figure 4), which yielded a spectrum containing B1g and B3g modes. In the case of Co3V2O8, only the [010] and [001] surfaces were available. The Raman characterization of both compounds at room temperature was completed with a powder spectrum.

Figure 4.

Figure 4

Open in a new tab

Symmetry assignment of the Raman modes of Ni3V2O8 at ambient conditions. The vertical ticks represent the DFT calculation results, matching in color with the corresponding symmetry. The incidence direction ξ of the tilted sample is sketched. If any magnification or reduction factor is applied to the data region, it is labeled next to it.

The complete symmetry phonon assignment for Ni3V2O8 is shown in Figure 4. All 10 Ag modes were found using coincident polarization in all 3 orientations of the crystal (except for A2g, which was found only in the ξ orientation). Using crossed polarization, the B1g modes were identified when inciding along the z-axis (6 out of 8), B2g modes, with y-incidence (6 out of 7), and a mixture of B1g and B3g, in the ξ-axis (7 out of the 11 total B3g). There was no polarization leakage in any of the spectra, except for the most intense mode, A10g, which was also measured in crossed polarization at orientations z and ξ. Thus, a total of 29 modes of the 36 Raman-active modes are reported. Kesari et al. found 30 modes experimentally and performed DFT calculations.53 Overall, this work is in good agreement with this study, except that the symmetry of some nearby modes are not assigned in the same way (see B31g-B22g-B13g, A4g-B41g-B32g, A5g-B51g, B61g-B63g, A7g-B83g, A9g-B6g, and A10g-B113g in Table 4), and not all the modes detected are the same. Combining both works, there are only 3 modes not detected experimentally. The analogue study for Co3V2O8 can be seen in Figure 5, which was less successful in comparison with the Ni compound due to its higher absorption of the excitation laser, giving rise to a sizably lower Raman signal. For this crystal, the parallel polarization measurements showed 9 of the total 10 Ag modes. Using crossed polarization, 5 B1g modes were detected with z incidence and 2 B2g modes, with y incidence. In all cases, small leaked contributions to Ag modes were found. Finally, all peaks from the polarized measurements were compared with those obtained from the powder sample, which allowed us to detect 2 extra modes belonging to the B3g symmetry. The total amount of detected zone-center modes for the Co vanadate is 18 modes of the 36 available. Seo et al. were able to measure 8 modes of this compound,54 obtaining similar frequency values compared with this work. All of these mode identifications are supported by ab initio computations, showing satisfactory experiment–simulation agreement. The ambient pressure wavelength values of the vibrational modes for Ni3V2O8 and Co3V2O8, along with the calculated and literature values, are shown in Table 4.

Figure 5.

Figure 5

Open in a new tab

Symmetry assignment of the Raman modes of Co3V2O8 at ambient conditions. The vertical ticks represent the DFT calculation results, matching in color with the corresponding symmetry. The magnification of the low wavenumber region is 20×.

3.4. High-Pressure Raman Spectroscopy (Ni3V2O8 and Co3V2O8)

In the present powder vibrational HP studies, 24 modes for Ni3V2O8 are monitored up to 19.5(1) GPa and 14 modes for Co3V2O8, up to 20.4(1) GPa, as shown for selected spectra in Figures 6 and 7, respectively. Pressure coefficients under ambient conditions are presented in Table 4. The pressure coefficients were fitted using the spectra obtained near ambient conditions, where the dependence on pressure is linear. As found in previous HP XRD studies23 for Ni3V2O8, this compound does not undergo any nonisostructural phase transition in the covered pressure range. Now, this statement can also be applied to Co3V2O8.

Figure 6.

Figure 6

Open in a new tab

Raman spectra corresponding to Ni3V2O8 at selected pressures. The symmetry modes are assigned colors in the first pattern. Numbers next to the spectra indicate pressure in GPa. Downstroke data are marked with a “d”. Magnification of the first region is shown in the top left corner.

Figure 7.

Figure 7

Open in a new tab

Raman spectra corresponding to Co3V2O8 at selected pressures. The symmetry modes are assigned colors in the first pattern. Numbers next to the spectra indicate pressure in GPa. Downstroke data are marked with a “d”. Magnification of the first region is shown in the top left corner.

The pressure dependence of the calculated and experimentally measured phonon wavenumbers is shown in Figure 8 for Ni3V2O8 and in Figure 9 for Co3V2O8. It can be seen that all of the observed modes, except the A1g mode, upshift with increasing pressure. In Co3V2O8, the A8g and B93g modes were no longer differentiated out of the background because of signal attenuation as pressure increased. The experimental values of these coefficients are broadly in good agreement with those obtained in the ab initio calculations. The calculated lines in Figures 8 and 9 run parallel to the experimental points with the calculated lines generally shifted by less than 5% with respect to the measured data. Only a single crossover is observed experimentally between B62g and A7g in Ni3V2O8, which is well reproduced by the DFT calculations. All data sets collected on decompression follow the same behavior as upstroke measurements. When comparing both orthovanadates, the first dissimilarity observed is that, in spite of the larger mass of Ni, all modes in Co3V2O8 are slightly lower in wavelength (approximately 10 cm–1), while high-pressure events, such as the mode crossover, occur earlier in pressure for Ni3V2O8 (see A6g-B71g, A3g-B41g, or A6g-B73g in Figures 8 and 9). These observations suggest that Ni3V2O8 behaves as a pressurized version of Co3V2O8.

Figure 8.

Figure 8

Open in a new tab

Pressure dependence of the Raman modes of Ni3V2O8. The symmetry modes are assigned with colors on the right, matching the end of the solid line in the figure.

Figure 9.

Figure 9

Open in a new tab

Pressure dependence of the Raman modes of Co3V2O8. The symmetry modes are assigned with colors on the right, matching the end of the solid line in the figure.

3.5. High-Pressure X-ray Diffraction (Co3V2O8)

Using the XRD patterns collected for powder Co3V2O8 under HP, the orthorhombic structure (space group Cmca, number 64) was fitted from 0.0(1) to 20.0(1) GPa. Le Bail refinement55 results are shown in Figure 10 for selected pressures. The patterns shown correspond to positions of the DAC where there was no Cu signal. This compound does not exhibit any phase transition in the mentioned pressure region, as was also published for Ni3V2O8.24

Figure 10.

Figure 10

Open in a new tab

XRD patterns at selected pressures (black dots) of Co3V2O8. Le Bail fits and residuals are shown with blue and red lines, respectively. Ticks indicate the Bragg peaks for the corresponding structural phase. Pressures are indicated in the figure. The top trace corresponds to the last experiment made during decompression.

Subsequently, the pressure dependence of the unit-cell parameters and corresponding volume of the orthorhombic structure of Co3V2O8 is reported in Figure 11, using the results from the Le Bail fits55 and peak indexation with UNITCELL.56 At 10.5(1) GPa, a slight change in the evolution of all three unit-cell axes was noticed. This fact coincides with the end of the hydrostatic region of the ME pressure-transmitting media,27 which is probably the reason that the linear compressibility of each axis is reduced. This nonhydrostatic effect led us to report two separate equations of state (EOSs), one up to the hydrostatic limit of ME (9.3(1) GPa) and another up to the maximum pressure (20.0(1) GPa). Thus, the unit-cell volume was fitted using a third-order Birch–Murnaghan EOS48 employing EosFit7 software.57 The third order of the EOS was determined from the Eulerian strain-normalized pressure dependence of the data.58 All EOS parameters are reported in Table 5, along with literature ones for other Kagomé-staircase orthovanadates. The unit-cell parameters obtained by DFT calculations differ from the experimental parameters by approximately 1% in terms of absolute value. Furthermore, the bulk moduli obtained in the EOS for both calculations (129.2(7) GPa) and experiments up to 9.3(1) GPa (127.4(4) GPa) are in good agreement. Comparing these results with the bulk modulus reported for Ni3V2O8,24 it can be noticed that Co orthovanadate is more compressible than Ni orthovanadate. For this comparison, the two bulk moduli obtained by a second order EOS and under hydrostatic conditions were used, whose values are 122(4) and 143(3) GPa for Co and Ni vanadates, respectively (see Table 5). This fact agrees with the observations reported in the HP Raman section (3.4), where it was concluded that Ni3V2O8 behaves as a pressurized version of Co3V2O8. Overall, Ni and Co vanadates show bulk moduli within the range of all other Kagomé-staircase orthovanadates, with Mg3V2O8 being the highest (152(4) GPa)23 and Mn3V2O8, the lowest (106(3) GPa)21 to date.

Figure 11.

Figure 11

Open in a new tab

Pressure dependence of the unit-cell parameters (top) and volume (bottom) of Co3V2O8. Black symbols represent experimental measurements, and red lines are DFT calculations. Full circles represent upward pressure, while empty triangles release pressure data. The solid black line and dashed black line are the Birch–Murnaghan EOS fitting of the experimental unit-cell volume up to 9.7 and 20 GPa, respectively.

Table 5. EOS Parameters (Cell Volume per Formula Unit, Bulk Modulus, and Its First Derivative) for Reported Kagomé-Staircase Orthovanadates.

XRD HP experiments V0 (Å3) B0 (GPa) B0′
Co3V2O8 up to 9.3(1) GPa (this work) 575.6(3) 127(3) 2.8 (9)
575.9(2) 122(4) 4.0 (fixed)
Co3V2O8 up to 20.0(1) GPa (this work) 576.3(8) 106(7) 9.7(1.3)
574.0(6) 142(3) 4.0 (fixed)
Ni3V2O8 up to 7.6(1) GPa24 555.7(2) 139(3) 4.4(3)
555.3(2) 143(3) 4.0 (fixed)
Mn3V2O8 up to 12 GPa21 623.4(2) 116(3) 2.6(5)
624.5(5) 106(3) 4.0 (fixed)
Zn3V2O8 up to 15 GPa22 585.0(4) 115(2) 5.1(6)
585.1(1) 120(2) 4.0 (fixed)
Mg3V2O8 up to 17 GPa23 576.15(3) 141(3) 5.9(8)
576.15(3) 152(4) 4 (fixed)
DFT calculations V0 (Å3) B0 (GPa) B0′
Co3V2O8 (this work) 565.6(3) 129(7) 3.7(4)
565.9(6) 126(6) 4.0 (fixed)
Ni3V2O859 527.9 171 4.5
Zn3V2O859 563.2 136 5.4
Mg3V2O859 539.7 146 4.4
Open in a new tab

From the reported unit-cell parameters, the linear isothermal compressibility was calculated for all axes of the orthorhombic structure: 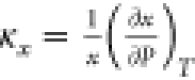Inline graphic, where x = a, b, or c. The linear compressibilities obtained are κa = 2.73(15) × 10–3 GPa–1, κb = 1.98(4) × 10–3 GPa–1, and κc = 2.29(14) × 10–3 GPa–1. The region used for the fits is from 0.0(1) to 9.3(1) GPa to guarantee that only hydrostatic data are used. When these compressibilities are compared with the experimentally obtained ones for Ni3V2O823 and simulated for other orthovanadates,59 it can be clearly appreciated that they follow the same behavior followed for this family of compounds, but the b-axis of Co3V2O8 is slightly more compressible. Once more, this can be related to the “compressed” structure of Ni3V2O8 indicated in Section 3.4, since the b-axis is mainly influenced by the layers of CoO6 octahedra (see Figure 1), which are more compressible than the NiO6 octahedra. The DFT-calculated change in bond distances within the covered pressure range can be seen in Figures S1 and S2 for both compounds.

4. Conclusions

High-pressure vibrational studies were performed for Ni3V2O8 and Co3V2O8 powders up to 19.5(1) and 20.4(1) GPa, respectively, and no phase transition was found. Polarized Raman and infrared measurements on single crystals were used to separate and identify the symmetry of the vibrational modes for both compounds under ambient conditions. Ab initio DFT calculations are reported to confirm the symmetry, ambient pressure wavenumber value, and pressure coefficients of all the experimental modes found (24 for Ni3V2O8 and 17 for Co3V2O8 out of the 36 Raman active modes). Although both Ni and Co orthovanadates present a similar vibrational behavior under pressure, it is found that Ni3V2O8 exhibits a more compact version of the structure. HP angle dispersive powder XRD analysis up to 20.0(1) GPa was also performed for Co3V2O8. Anisotropic compressibility and EOS parameters (including bulk moduli) are obtained from both the experimental results and the DFT calculations. Excellent agreement is found between the two sets of data.

Acknowledgments

The authors gratefully acknowledge the financial support from the Spanish Research Agency (AEI) and Spanish Ministry of Science and Investigation (MCIN) under Projects PID2019-106383GB-41/43, PID2022-138076NB-C41/44 and RED2022-134388-T (DOI: 10.13039/501100011033). D.E. would also like to thank the financial support of Generalitat Valenciana under grants PROMETEO CIPROM/2021/075-GREENMAT and MFA/2022/007. This study forms part of the Advanced Materials program and is supported by MCIN with funding from European Union Next Generation EU (PRTR-C17.I1) and by the Generalitat Valenciana. J.S.-M. acknowledges the Spanish Ministry of Science, Innovation and Universities for the PRE2020-092198 fellowship. C.P. acknowledges Proyectos de Generación de Conocimiento PID2021-125927NB-C21. The authors thank ALBA synchrotron for providing beam time for the HP XRD experiments (Proposal 2021095390).

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcc.3c04019.

  • Atomic motions of the acoustic and infrared active modes, the Raman active modes, and the silent modes; DFT calculated bond distances (PDF)

Author Contributions

J. Sánchez-Martín and J. Pellicer-Porres were involved in the IR experiments and analysis. J. Sánchez-Martín, J. Pellicer-Porres, and D. Errandonea were involved in the HP Raman experiments and analysis. J. Sánchez-Martín, A. Liang, J. Ibáñez, R. Oliva, C. Popescu, and D. Errandonea were involved in the HP XRD measurements and analysis. Z. He was involved in sample synthesis. P. Rodríguez-Hernández and A. Muñoz were involved in the DFT calculations. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

jp3c04019_si_001.pdf (2.5MB, pdf)

References

  1. Sauerbrei E. E.; Faggiani R.; Calvo C. Refinement of the Crystal Structures of Co3V2O8 and Ni3V2O8. Acta Crystallogr. 1973, B29, 2304. 10.1107/S0567740873006552. [DOI] [Google Scholar]
  2. Gopal R.; Calvo C. Crystal Structure of α-Zn3(VO4)2. Can. J. Chem. 1971, 49, 3056. 10.1139/v71-510. [DOI] [Google Scholar]
  3. Krishnamachari N.; Calvo C. Refinement of the Structure of Mg3(VO4)2. Can. J. Chem. 1971, 49, 1629. 10.1139/v71-266. [DOI] [Google Scholar]
  4. Wilson N. R.; Petrenko O. A.; Balakrishnan G. Magnetic phase diagrams of the Kagomé staircase compounds Co3V2O8 and Ni3V2O8. J. Phys.: Condens. Matter 2007, 19, 145257. 10.1088/0953-8984/19/14/145257. [DOI] [Google Scholar]
  5. Lawes G.; Kenzelmann M.; Rogado N.; Kim K. H.; Jorge G. A.; Cava R. J.; Aharony A.; Entin-Wohlman O.; Harris A. B.; Yildirim T.; et al. Competing Magnetic Phases on a Kagomé Staircase. Phys. Rev. Lett. 2004, 93, 247201. 10.1103/PhysRevLett.93.247201. [DOI] [PubMed] [Google Scholar]
  6. Yen F.; Chaudhury R. P.; Galstyan E.; Lorenz B.; Wang Y. Q.; Sun Y. Y.; Chu C. W. Magnetic phase diagrams of the Kagomé staircase compound Co3V2O8. Physica B Condens. Matter 2008, 403, 1487–1489. 10.1016/j.physb.2007.10.334. [DOI] [Google Scholar]
  7. Clemens O.; Rohrer J.; Nénert G. Magnetic structures of the low temperature phase of Mn3(VO4)2 - towards understanding magnetic ordering between adjacent Kagomé layers. Dalton Trans. 2016, 45, 156. 10.1039/C5DT03141A. [DOI] [PubMed] [Google Scholar]
  8. Kobayashi Y.; Yasui Y.; Sato M. Magnetic and thermal properties of Co3V2O8 and Ni3V2O8. J. Magn. Magn. Mater. 2007, 310, 1160–1161. 10.1016/j.jmmm.2006.10.336. [DOI] [Google Scholar]
  9. Koc H.; Palaz S.; Mamedov A. M.; Ozbay E. Electronic and elastic properties of the multiferroic crystals with the Kagome type lattices -Mn3V2O8 and Ni3V2O8: First principle calculations. Ferroelectrics 2019, 544, 11–19. 10.1080/00150193.2019.1598178. [DOI] [Google Scholar]
  10. Chaudhury R. P.; Yen F.; dela Cruz C. R.; Lorenz B.; Wang Y. Q.; Sun Y. Y.; Chu C. W. Pressure-temperature phase diagram of multiferroic Ni3V2O8. Phys. Rev. B Condens. Matter 2007, 75, 012407. 10.1103/PhysRevB.75.012407. [DOI] [Google Scholar]
  11. Sankar S. S.; Karthick K.; Sangeetha K.; Gill R. S.; Kundu S. Annexation of Nickel Vanadate (Ni3V2O8) Nanocubes on Nanofibers: An Excellent Electrocatalyst for Water Oxidation. ACS Sustain. Chem. Eng. 2020, 8, 4572–4579. 10.1021/acssuschemeng.0c00352. [DOI] [Google Scholar]
  12. Xing M.; Kong L.-B.; Liu M.-C.; Liu L.-Y.; Kang L.; Luo Y.-C. Cobalt vanadate as highly active, stable, noble metal-free oxygen evolution electrocatalyst. Mater. Chem. A 2014, 2, 18435. 10.1039/C4TA03776F. [DOI] [Google Scholar]
  13. Hosseini H.; Shahrokhian S. Advanced binder-free electrode based on core-shell nanostructures of mesoporous Co3V2O8-Ni3V2O8 thin layers@porous carbon nanofibers for high-performance and flexible all-solid-state supercapacitors. Chem. Eng. J. 2018, 341, 10–26. 10.1016/j.cej.2018.02.019. [DOI] [Google Scholar]
  14. Liu M.-C.; Kong L.-B.; Kang L.; Li X.; Walsh F. C.; Xing M.; Lu C.; Ma X.-J.; Luo Y.-C. Synthesis and characterization of M3V2O8 (M = Ni or Co) based nanostructures: a new family of high performance pseudocapacitive materials. J. Mater. Chem. A 2014, 2, 4919. 10.1039/c4ta00582a. [DOI] [Google Scholar]
  15. Hamidi R.; Ghasemi S.; Hosseini S. R. Ultrasonic assisted synthesis of Ni3(VO4)2-reduced graphene oxide nanocomposite for potential use in electrochemical energy storage. Ultrason. Sonochem. 2020, 62, 104869. 10.1016/j.ultsonch.2019.104869. [DOI] [PubMed] [Google Scholar]
  16. Lu Y.; Yu L.; Wu M.; Wang Y.; Lou X. W. D. Construction of Complex Co3O4@Co3V2O8 Hollow Structures from Metal-Organic Frameworks with Enhanced Lithium Storage Properties. Adv. Mater. 2018, 30, 1702875. 10.1002/adma.201702875. [DOI] [PubMed] [Google Scholar]
  17. Vesali-Kermani E.; Habibi-Yangjeh A.; Ghosh S. Efficiently enhanced nitrogen fixation performance of g-C3N4 nanosheets by decorating Ni3V2O8 nanoparticles under visible-light irradiation. Ceram. Int. 2020, 46, 24472–24482. 10.1016/j.ceramint.2020.06.232. [DOI] [Google Scholar]
  18. Kumar R.; Bhuvana T.; Rai P.; Sharma A. Highly Sensitive Non-Enzymatic Glucose Detection Using 3-D Ni3(VO4)2 Nanosheet Arrays Directly Grown on Ni Foam. J. Electrochem. Soc. 2018, 165, B1–B8. 10.1149/2.0201802jes. [DOI] [Google Scholar]
  19. Lenertz M.; Alaria J.; Stoeffler D.; Colis S.; Dinia A. Magnetic Properties of Low-Dimensional α and γ CoV2O6. J. Phys. Chem. C 2011, 115, 17190–17196. 10.1021/jp2053772. [DOI] [Google Scholar]
  20. Díaz-Anichtchenko D.; Bandiello E.; González-Platas J.; Liang A.; He Z.; Muñoz A.; Rodríguez-Hernández P.; Errandonea D.; Popescu C. Physical Properties and Structural Stability of Cobalt Pyrovanadate Co2V2O7 under High-Pressure Conditions. J. Phys. Chem. C 2022, 126, 13416–13426. 10.1021/acs.jpcc.2c03101. [DOI] [Google Scholar]
  21. Kesari S.; Garg A. B.; Clemens O.; Joseph B.; Rao R. Pressure-Induced Structural Behavior of Orthorhombic Mn3(VO4)2: Raman Spectroscopic and X-ray Diffraction Investigations. ACS Omega 2022, 7, 3099–3108. 10.1021/acsomega.1c06590. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Díaz-Anichtchenko D.; Santamaría-Pérez D.; Marqueño T.; Pellicer-Porres J.; Ruíz-Fuertes J.; Ribes R.; Ibáñez J.; Achary S. N.; Popescu C.; Errandonea D. Comparative study of the high-pressure behavior of ZnV2O6, Zn2V2O7, and Zn3V2O8. J. Alloys Compd. 2020, 837, 155505. 10.1016/j.jallcom.2020.155505. [DOI] [Google Scholar]
  23. Kesari S.; Garg A. B.; Rao R. Phonon anharmonicity and equation of state parameters of orthovanadate Mg3(VO4)2: Raman Spectroscopy and X-ray diffraction investigation. Solid State Sci. 2023, 139, 107186. 10.1016/j.solidstatesciences.2023.107186. [DOI] [Google Scholar]
  24. Díaz-Anichtchenko D.; Turnbull R.; Bandiello E.; Anzellini S.; Errandonea D. High-Pressure Structural Behavior and Equation of State of Kagome Staircase Compound, Ni3V2O8. Crystals 2020, 10, 910. 10.3390/cryst10100910. [DOI] [Google Scholar]
  25. Sánchez-Martín J.; Errandonea D.; Mosaher H. S. R.; Paszkowicz W.; Minikayev R.; Turnbull R.; Berkowski M.; Ibáñez-Insa J.; Popescu C.; Fitch A. N. The pressure and temperature evolution of the Ca3V2O8 crystal structure using powder X-ray diffraction. CrystEngComm 2023, 25, 1240. 10.1039/D2CE01676A. [DOI] [Google Scholar]
  26. Grzechnik A.; McMillan P. F. High-pressure X-ray diffraction of Sr3(VO4)2 and Ba3(VO4)2. Phys. B: Condens. Matter 1998, 252, 268–273. 10.1016/S0921-4526(98)00214-2. [DOI] [Google Scholar]
  27. Díaz-Anichtchenko D.; Turnbull R.; Bandiello E.; Anzellini S.; Achary A. N.; Errandonea D. Pressure-Induced Chemical Decomposition of Copper Orthovanadate (α-Cu3V2O8). J. Mater. Chem. C 2021, 9, 13402. 10.1039/D1TC02901K. [DOI] [Google Scholar]
  28. He Z.; Ueda Y.; Itoh M. Crystal growth of Ni3V2O8 by flux method. J. Cryst. Growth 2006, 297, 1–3. 10.1016/j.jcrysgro.2006.08.047. [DOI] [Google Scholar]
  29. He Z.; Taniyama T.; Itoh M.; Ueda Y. Flux Growth and Magnetic Anomalies of Co3V2O8 Crystals. Cryst. Growth Des. 2007, 7, 1055–1057. 10.1021/cg060539u. [DOI] [Google Scholar]
  30. Klotz S.; Chervin J.-C.; Munsch P.; Le Marchand G. Hydrostatic Limits of 11 Pressure Transmitting Media. J. Phys. D Appl. Phys. 2009, 42, 075413. 10.1088/0022-3727/42/7/075413. [DOI] [Google Scholar]
  31. Higham D. J.; Higham N. J.. MATLAB guide; Siam, 2016. [Google Scholar]
  32. Chijioke A. D.; Nellis W. J.; Soldatov A.; Silvera I. F. The Ruby Pressure Standard to 150 GPa. J. Appl. Phys. 2005, 98, 114905. 10.1063/1.2135877. [DOI] [Google Scholar]
  33. Fauth F.; Peral I.; Popescu C.; Knapp M. The New Material Science Powder Diffraction Beamline at ALBA Synchrotron. Powder Diffr. 2013, 28, S360–S370. 10.1017/S0885715613000900. [DOI] [Google Scholar]
  34. Dewaele A.; Loubeyre P.; Mezouar M. Equations of State of Six Metals Above 94 GPa. Phys. Rev. B 2004, 70, 094112. 10.1103/PhysRevB.70.094112. [DOI] [Google Scholar]
  35. Prescher C.; Prakapenka V. B. DIOPTAS: A program for reduction of two-dimensional X-ray diffraction data and data exploration. High. Press. Res. 2015, 35, 223–230. 10.1080/08957959.2015.1059835. [DOI] [Google Scholar]
  36. Kraus W.; Nolze G. POWDER CELL - a Program for the Representation and Manipulation of Crystal Structures and Calculation of the Resulting X-ray Powder Patterns. J. Appl. Crystallogr. 1996, 29, 301–303. 10.1107/S0021889895014920. [DOI] [Google Scholar]
  37. Hohenberg P.; Kohn W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864. 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
  38. Kresse G.; Furthmüller J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
  39. Kresse G.; Furthmüller J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  40. Blöchl P. E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  41. Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  42. Armiento R.; Mattsson A. E. Functional designed to include surface effects in self-consistent density functional theory. Phys. Rev. B 2005, 72, 085108. 10.1103/PhysRevB.72.085108. [DOI] [Google Scholar]
  43. Mattsson A. E.; Armiento R.; Paier J.; Kresse G.; Wills J. M.; Mattsson T. R. The AM05 density functional applied to solids. J. Chem. Phys. 2008, 128, 084714. 10.1063/1.2835596. [DOI] [PubMed] [Google Scholar]
  44. Perdew J. P.; Ruzsinszky A.; Csonka G. I.; Vydrov O. A.; Scuseria G. E.; Constantin L. A.; Zhou X.; Burke K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. 10.1103/PhysRevLett.100.136406. [DOI] [PubMed] [Google Scholar]
  45. Perdew J. P.; Ruzsinszky A.; Csonka G. I.; Vydrov O. A.; Scuseria G. E.; Constantin L. A.; Zhou X.; Burke K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2009, 102, 039902. 10.1103/PhysRevLett.102.039902. [DOI] [PubMed] [Google Scholar]
  46. Dudarev S. L.; Botton G. A.; Savrasov S. Y.; Humphreys C. J.; Sutton A. P. Electron-Energy-Loss Spectra and the Structural Stability of Nickel Oxide: An LSDA+U Study. Phys. Rev. B 1998, 57, 1505–1509. 10.1103/PhysRevB.57.1505. [DOI] [Google Scholar]
  47. Jain A.; Ong S. P.; Hautier G.; Chen W.; Richards W. D.; Dacek S.; Cholia S.; Gunter D.; Skinner D.; Ceder G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. 10.1063/1.4812323. [DOI] [Google Scholar]
  48. Birch F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. 10.1103/PhysRev.71.809. [DOI] [Google Scholar]
  49. Togo A.; Tanaka I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1. 10.1016/j.scriptamat.2015.07.021. [DOI] [Google Scholar]
  50. Kroumova E.; Aroyo M. I.; Pérez-Mato J. M.; Kirov A.; Capillas C.; Ivantchez S.; Wondratschek H. Bilbao Crystallographic Server: useful databases and tools for phase transitions studies. Ph. Transit. 2003, 76, 155–170. 10.1080/0141159031000076110. [DOI] [Google Scholar]
  51. Chaves A. S.; Porto S. P. S. Generalized Lyddane-Sachs Teller relation. Solid State Commun. 1973, 13, 865–868. 10.1016/0038-1098(73)90386-4. [DOI] [Google Scholar]
  52. Gervais F.; Piriou B. Temperature dependence of transverse and longitudinal optic modes in the α and β phases of quartz. Phys. Rev. B 1975, 11, 3944–3950. 10.1103/PhysRevB.11.3944. [DOI] [Google Scholar]
  53. Kesari S.; Rao R.; Gupta M. K.; Mittal R.; Balakrishnan G. Symmetries of modes in Ni3V2O8: Polarized Raman spectroscopy and ab initio phonon calculations. J. Raman Spectrosc. 2019, 50, 587–594. 10.1002/jrs.5539. [DOI] [Google Scholar]
  54. Seo Y.-S.; Kim S.-H.; Ahn J. S. Determination of the Local Symmetry and the Multiferroic-ferromagnetic Crossover in Ni3-xCoxV2O8 by Using Raman Scattering Spectroscopy. J. Korean Phys. Soc. 2013, 62, 116–120. 10.3938/jkps.62.116. [DOI] [Google Scholar]
  55. Le Bail A.; Duroy H.; Fourquet J. L. Ab-initio structure determination of LiSbWO6 by X Ray powder diffraction. Mater. Res. Bull. 1988, 23, 447–452. 10.1016/0025-5408(88)90019-0. [DOI] [Google Scholar]
  56. Holland T. J. B.; Redfern S. A. T. UNITCELL: a nonlinear least-squares program for cell-parameter refinement and implementing regression and deletion diagnostics. J. Appl. Crystallogr. 1997, 30, 84. 10.1107/S0021889896011673. [DOI] [Google Scholar]
  57. Gonzalez-Platas J.; Alvaro M.; Nestola F.; Angel R. EosFit7-GUI: a New Graphical User Interface for Equation of State Calculations, Analyses and Teaching. J. Appl. Crystallogr. 2016, 49, 1377–1382. 10.1107/S1600576716008050. [DOI] [Google Scholar]
  58. Angel R. J. Equations of State. Reviews in Mineralogy and Geochemistry 2000, 41, 35–59. 10.2138/rmg.2000.41.2. [DOI] [Google Scholar]
  59. Díaz-Anichtchenko D.; Errandonea D. Comparative Study of the Compressibility of M3V2O8 (M = Cd, Zn, Mg, Ni) Orthovanadates. Crystals 2022, 12, 1544. 10.3390/cryst12111544. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp3c04019_si_001.pdf (2.5MB, pdf)

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES