Abstract
Background
To construct several prediction models for the risk of stroke in coronary artery disease (CAD) patients receiving coronary revascularization based on machine learning methods.
Methods
In total, 5757 CAD patients receiving coronary revascularization admitted to ICU in Medical Information Mart for Intensive Care IV (MIMIC-IV) were included in this cohort study. All the data were randomly split into the training set (n = 4029) and testing set (n = 1728) at 7:3. Pearson correlation analysis and least absolute shrinkage and selection operator (LASSO) regression model were applied for feature screening. Variables with Pearson correlation coefficient<9 were included, and the regression coefficients were set to 0. Features more closely related to the outcome were selected from the 10-fold cross-validation, and features with non-0 Coefficent were retained and included in the final model. The predictive values of the models were evaluated by sensitivity, specificity, area under the curve (AUC), accuracy, and 95% confidence interval (CI).
Results
The Catboost model presented the best predictive performance with the AUC of 0.831 (95%CI: 0.811–0.851) in the training set, and 0.760 (95%CI: 0.722–0.798) in the testing set. The AUC of the logistic regression model was 0.789 (95%CI: 0.764–0.814) in the training set and 0.731 (95%CI: 0.686–0.776) in the testing set. The results of Delong test revealed that the predictive value of the Catboost model was significantly higher than the logistic regression model (P<0.05). Charlson Comorbidity Index (CCI) was the most important variable associated with the risk of stroke in CAD patients receiving coronary revascularization.
Conclusion
The Catboost model was the optimal model for predicting the risk of stroke in CAD patients receiving coronary revascularization, which might provide a tool to quickly identify CAD patients who were at high risk of postoperative stroke.
Introduction
Coronary artery disease (CAD) is the most common cardiovascular diseases wherein atherosclerosis occurs in one or more of the coronary arteries [1]. CAD was reported to be one of the major causes of mortality in both the developed and developing countries [2]. Currently, percutaneous coronary intervention (PCI) and coronary artery bypass grafting (CABG) are common coronary revascularization procedures [3]. With the development and application of drug-eluting stents and minimally invasive surgery, the prognosis of patients undergoing PCI or CABG was improved, but some patients still have postoperative adverse cardiovascular events, which result in worse prognosis [4]. Stroke is a cerebrovascular disorder which is the second leading cause of mortality and morbidity worldwide [5]. Stroke is a prevalent complication among surgical and ICU patients, with postoperative stroke incidence in cardiac surgery patients ranging from 0.8% to 9% [6]. Previous evidence suggested that the occurrence of stroke occurrence was associated with a significantly elevated risk of mortality in patients undergoing PCI or CABG procedures [7, 8]. Constructing predictive models to accurately identify patients receiving coronary revascularization who were at high risk of stroke is of great significance.
Recently, machine learning methods are gradually applied to the construction of clinical models in order to improve the accuracy of clinical diagnosis or prediction of diseases [9]. Machine learning method was widely applied in predicting poor prognosis after heart surgery and the risk of postoperative stroke, which presented better performance than traditional risk models such as logistic regression [10–12]. However, no studies have reported the use of machine learning to predict the risk of postoperative stroke in patients undergoing coronary revascularization.
This study intended to construct several prediction models for the risk of stroke in CAD patients who underwent coronary revascularization based on machine learning methods. The optimal prediction model was identified and the predictive value was compared with traditional logistic regression model.
Methods
Study design and population
In this cohort study, the records of 6289 CAD patients receiving coronary revascularization were obtained in Medical Information Mart for Intensive Care IV (MIMIC-IV). MIMIC-IV builds upon the success of MIMIC-III and incorporates numerous enhancements from 2008 to 2019. MIMIC-IV is a relational database that encompasses authentic hospitalizations of patients admitted to a tertiary academic medical center located in Boston, MA, USA. Each patient’s length of stay, laboratory tests, medication treatment, vital signs and other comprehensive information during their ICU stay were recorded [13]. Patients with age < 18 years old and those with the length of ICU stay less than 24 h were excluded. Finally, 5757 participants were included. The requirement of ethical approval for this was waived by the Institutional Review Board of The second hospital of Dalian medical university, because the data was accessed from MIMIC-IV (a publicly available database). The need for written informed consent was waived by the Institutional Review Board of The second hospital of Dalian medical university due to retrospective nature of the study.
Potential predictors
Age (years), gender (female or male), ethnicity (White, Black, others or unknown), insurance (Medicaid, Medicare or others), marital status (married, or no married), first care unit [Cardiac Care Unit (CCU), cardiovascular intensive care unit (CVICU) or others), family history of stroke (yes or no), personal history of stroke (yes or no), treatments (CABG and PCI, CABG alone or PCI alone), thrombolysis (yes or no), antiplatelet (yes or no), beta-blockers (yes or no), calcium channel blockers (yes or no), ventilation (yes or no), vasopressors (yes or no), Glasgow Coma Scale (GCS) score, Charlson Comorbidity Index (CCI), weight (kg), heart rate (bpm), systolic blood pressure (SBP) (mmHg), diastolic blood pressure (DBP) (mmHg), respiratory rate (bpm), temperature (°C), oxygen saturation (SpO2) (%), white blood cell (WBC) (K/uL), platelet (K/uL), hemoglobin (g/dL), red blood cell distribution width (RDW) (%), hematocrit (%), creatinine (mg/dL), international normalized ratio (INR), prothrombin time (PT) (seconds), partial thromboplastin time (PTT) (seconds), blood urea nitrogen (BUN) (mg/dL), glucose (mg/dL), calcium (mmol/L), sodium (mEq/L), chloride (mEq/L), bicarbonate (mEq/L), and lactate (mmol/L) were potential predictors. All these data were collected within 24 hours of admission to ICU.
Construction of the prediction models
Logistic regression model is a classification algorithm evolved from linear regression, and belongs to a Sigmoid function normalization model of generalized linear regression model, which is commonly used to solve binary classification problems and has strong explanatory ability [14].
Support vector machine (SVM) is a classification algorithm, and it can also be classified. Different models can be made according to different input data. If the input label is classified value, SVC() is used for classification. This algorithm improves the generalization ability of learning machine by seeking the minimum structural risk, and minimizes the empirical risk and confidence range. Its basic model is defined as the linear classifier with the largest interval on the feature space, that is, the learning strategy of support vector machine is to maximize the interval, and it can be converted into the solution of a convex quadratic programming problem [15].
Random forest is an extended variant of Bagging ensemble learning. On the basis of constructing Bagging ensemble with decision tree as a base learner, it further adds the selection of random attributes to the training process of decision tree. For each node of the base decision tree, a subset containing k attributes is randomly selected from the candidate attribute set of the node. Then an optimal attribute is selected for division. The method of prediction stage of this algorithm is Bagging strategy. The classification model uses voting method to determine the final result, and the regression model uses mean method to determine the final result [16].
Extreme Gradient Boosting (XGBoost) is an efficient gradient lifting decision tree algorithm, which is improved on the basis of the original Gradient Boosting Decision Tree. As a forward addition model, its core is to adopt the Boosting thought, which integrates multiple weak learners into a strong learner by a certain method, that is, multiple trees make decisions together, and the result of each tree is the difference between the target value and the predicted result of all the previous trees, adding up all the results to get the final result. In this way, the effect of the whole model is improved [17].
Adaptive Boosting (Adaboost) is an iterative algorithm to train different classifiers for the same training set, and then set these weak classifiers together to form a stronger final classifier. The set strategy is to increase the weight of the samples that were classified wrong by the previous round of classifiers. Reducing the weight of samples with correct classification will get more attention from the following classifiers, and then weaker classifiers can be generated. By combining these weak classifiers with majority weighted voting, the classifier with small error rate is increased, and the classifier with large error rate is reduced, so that it plays a less role in voting [18].
Naive bayes is one of the most widely used classification algorithms. It is a classifier method based on Bayesian definition and independent assumption of feature conditions. Naive Bayes algorithm is based on Bayesian principle and uses the knowledge of probability statistics to classify sample data sets. It is characterized by the combination of prior probability and posterior probability, which avoids the subjective bias of using only prior probability, and also avoids the overfitting phenomenon of using sample information alone [19].
K-nearest neighbor (KNN) is one of the most basic and simplest algorithms in the machine learning algorithm model. It can be used for classification and regression by measuring the distance between different eigenvalues. The working principle is to use the training data to partition the eigenvector space and take the partition result as the final algorithm model.
Categorical boosting (Catboost) is a kind of gradient boosting algorithm library that can handle categorical features well. It has made some improvements on the basis of the original Gradient Boosting Decision Tree. Specifically, the algorithm has two characteristics of adaptive learning rate and categorical feature processing, which can help the algorithm better control the contribution of the weak learner in each iteration. In addition, the algorithm can deal with categorical features efficiently and reasonably, so it can deal with the influence of categorical features better [20].
Outcome variable
Postoperative stroke was the outcome, which was screened according to the ICD diagnosis codes, ICD-9 (430–436, and 997020, and ICD-10 three I60-I66, I9782, I97820.
Statistical analysis
Mean ± SD was used to describe the distribution of measurement data subject to normal distribution, and t-test was used to compare the difference between groups. Median and quartiles were used to describe the distribution of measurement data that did not follow normal distribution, and Wilcoxon rank sum test was used to compare the difference between groups. The enumeration data were expressed as number and percentage of cases [n (%)], and the Chi-square test or Fisher’s exact probability were used to compare the differences between the groups. Missing values <20% were dealt by Random forest interpolation, and ≥20% were deleted (Table 1). Sensitivity analysis were performed before and after interpolation (Table 2). All the data were randomly split into the training set (n = 4029) and testing set (n = 1728) at 7:3 with the random seed if 42 [21]. Pearson correlation analysis and least absolute shrinkage and selection operator (LASSO) regression model were applied for feature screening. Variables with Pearson correlation coefficient<9 were included, and the regression coefficients were set to 0. Features more closely related to the outcome were selected from the 10-fold cross-validation, and features with non-0 Coefficient were retained and included in the final model. Eight prediction models were constructed, and the parameter settings were shown in Table 3. The predictive values of the models were evaluated by sensitivity, specificity, area under the curve (AUC), accuracy, and 95% confidence interval (CI). The confidence level alpha = 0.05. Missing value interpolation, training set and testing set split, data modeling and result visualization were completed using Python 3.9.12. Sensitivity analysis and difference comparison were performed by SAS 9.4 (SAS Institute Inc., Cary, NC, USA).
Table 1. The number and percentage of missing values.
| Variables | n | % | Total samples (n) | Manipulation |
|---|---|---|---|---|
| GCS | 6 | 0.10% | 5751 | Random forest interpolation |
| SPO2 | 6 | 0.10% | 5751 | Random forest interpolation |
| Systolic | 7 | 0.12% | 5750 | Random forest interpolation |
| Diastolic | 7 | 0.12% | 5750 | Random forest interpolation |
| Platelet | 7 | 0.12% | 5750 | Random forest interpolation |
| Heart rate | 8 | 0.14% | 5749 | Random forest interpolation |
| Chloride | 8 | 0.14% | 5749 | Random forest interpolation |
| Sodium | 9 | 0.16% | 5748 | Random forest interpolation |
| BUN | 11 | 0.19% | 5746 | Random forest interpolation |
| Creatinine | 11 | 0.19% | 5746 | Random forest interpolation |
| Hematocrit | 12 | 0.21% | 5745 | Random forest interpolation |
| Bicarbonate | 15 | 0.26% | 5742 | Random forest interpolation |
| Glucose | 16 | 0.28% | 5741 | Random forest interpolation |
| RDW | 18 | 0.31% | 5739 | Random forest interpolation |
| Hemoglobin | 18 | 0.31% | 5739 | Random forest interpolation |
| WBC | 18 | 0.31% | 5739 | Random forest interpolation |
| Calcium | 35 | 0.61% | 5722 | Random forest interpolation |
| Weight | 135 | 2.34% | 5622 | Random forest interpolation |
| PTT | 147 | 2.55% | 5610 | Random forest interpolation |
| INR | 149 | 2.59% | 5608 | Random forest interpolation |
| PT | 150 | 2.61% | 5607 | Random forest interpolation |
| Marital status | 358 | 6.22% | 5399 | Random forest interpolation |
| Temperature | 685 | 11.90% | 5072 | Random forest interpolation |
| Lactate | 734 | 12.75% | 5023 | Random forest interpolation |
| Respiratory rate | 783 | 13.60% | 4974 | Random forest interpolation |
| Lymphocytes | 2514 | 43.67% | 3243 | Deleting |
| Neutrophil | 2514 | 43.67% | 3243 | Deleting |
| ALT | 4976 | 86.43% | 781 | Deleting |
| Bilirubin total | 4977 | 86.45% | 780 | Deleting |
| AST | 4983 | 86.56% | 774 | Deleting |
| ALP | 5012 | 87.06% | 745 | Deleting |
| Albumin | 5377 | 93.40% | 380 | Deleting |
| Cholesterol | 5460 | 94.84% | 297 | Deleting |
| Cholesterol-HDL | 5464 | 94.91% | 293 | Deleting |
| Triglycerides | 5466 | 94.95% | 291 | Deleting |
| Cholesterol-LDL | 5467 | 94.96% | 290 | Deleting |
| Height | 5498 | 95.50% | 259 | Deleting |
| Ntprobnp | 5628 | 97.76% | 129 | Deleting |
| GGT | 5753 | 99.93% | 4 | Deleting |
| Troponin-I | 5757 | 100.00% | 0 | Deleting |
GCS: Glasgow Coma Scale, SPO2: oxygen saturation, BUN, blood urea nitrogen, RDW: red blood cell distribution width, WBC: white blood cell, PTT partial thromboplastin time, INR: international normalized ratio, PT prothrombin time, HDL: high density lipoprotein
Table 2. Sensitivity analysis of data before and after manipulation.
| Variables | After manipulation (n = 5757) | Before manipulation (n = 5757) | Statistics | P |
|---|---|---|---|---|
| Platelet, K/uL, Mean ± SD | 159.42 ± 51.43 | 157.92 ± 51.44 | t = 1.55 | 0.121 |
| Calcium, mmol/L, M (Q1, Q3) | 1.20 (1.11, 1.35) | 1.20 (1.11, 1.35) | Z = -0.413 | 0.679 |
| SPO2, %, Mean ± SD | 98.81 ± 2.63 | 98.82 ± 2.63 | t = -0.02 | 0.985 |
| RDW, %, Mean ± SD | 13.60 ± 0.99 | 13.57 ± 1.00 | t = 1.44 | 0.151 |
| BUN, mg/dL, M (Q1, Q3) | 16.00 (13.00, 21.00) | 16.00 (13.00, 21.00) | Z = -0.011 | 0.991 |
| Glucose, mg/dL, Mean ± SD | 139.92 ± 33.61 | 139.41 ± 34.17 | t = 0.79 | 0.427 |
| Marital status, n (%) | χ2 = 1.459 | 0.227 | ||
| Married | 3854 (66.94) | 3556 (65.86) | ||
| No married | 1903 (33.06) | 1843 (34.14) | ||
| Creatinine, mg/dL, M (Q1, Q3) | 0.90 (0.70, 1.10) | 0.90 (0.70, 1.10) | Z = 0.025 | 0.980 |
| Lactate, mmol/L, M (Q1, Q3) | 2.00 (1.60, 2.60) | 2.10 (1.50, 2.70) | Z = 1.470 | 0.141 |
| Weight, kg, Mean ± SD | 84.67 ± 16.98 | 84.51 ± 17.21 | t = 0.49 | 0.622 |
| Hemoglobin, g/dL, Mean ± SD | 10.27 ± 2.27 | 10.27 ± 2.27 | t = 0.06 | 0.955 |
| Temperature, °C, Mean ± SD | 36.35 ± 0.47 | 36.36 ± 0.51 | t = -1.75 | 0.080 |
| INR, ratio, Mean ± SD | 1.38 ± 0.19 | 1.38 ± 0.20 | t = 0.50 | 0.620 |
| Chloride, mEq/L, Mean ± SD | 105.84 ± 3.60 | 105.91 ± 3.58 | t = -0.97 | 0.334 |
| PT, seconds, Mean ± SD | 15.15 ± 2.02 | 15.12 ± 2.05 | t = 0.89 | 0.375 |
| PTT, seconds, Mean ± SD | 37.23 ± 21.82 | 36.66 ± 21.72 | t = 1.39 | 0.165 |
| Hematocrit, %, Mean ± SD | 30.77 ± 6.67 | 30.74 ± 6.66 | t = 0.25 | 0.800 |
| Heart rate, bpm, Mean ± SD | 80.04 ± 9.38 | 80.00 ± 9.52 | t = 0.19 | 0.848 |
| SBP, mmHg, Mean ± SD | 113.69 ± 16.67 | 113.49 ± 16.70 | t = 0.65 | 0.516 |
| DBP, mmHg, Mean±SD | 59.74 ± 10.73 | 59.43 ± 10.66 | t = 1.52 | 0.128 |
| Respiratory rate, bpm, Mean ± SD | 15.21 ± 2.07 | 15.18 ± 2.34 | t = 0.61 | 0.542 |
| Bicarbonate, mEq/L, Mean ± SD | 23.18 ± 2.17 | 23.19 ± 2.20 | t = -0.27 | 0.790 |
| Sodium, mEq/L, Mean ± SD | 135.76 ± 2.83 | 135.76 ± 2.84 | t = -0.10 | 0.920 |
| WBC, K/uL, M (Q1, Q3) | 12.20 (9.20, 15.50) | 12.10 (9.20, 15.50) | Z = -0.730 | 0.466 |
| GCS, score, Mean ± SD | 13.38 ± 3.54 | 13.38 ± 3.54 | t = 0.02 | 0.985 |
SD: standard deviation, M: median, Q1: 1st quartile, Q3: 3st quartile, SPO2: oxygen saturation, RDW: red blood cell distribution width, BUN, blood urea nitrogen, INR: international normalized ratio, PT prothrombin time, PTT partial thromboplastin time, SBP: systolic blood pressure, DBP: diastolic blood pressure, WBC: white blood cell, GCS: Glasgow Coma Scale
Table 3. Parameter settings for 8 machine learning models.
| Model | Logistic regression | SVM | Random forest | XGBoost | Adaboost | Naive bayes | KNN | Catboost |
|---|---|---|---|---|---|---|---|---|
| Parameter 1 | C = 1 | kernel = ’rbf’ | n_jobs = -1 | learning_rate = 0.001 | learning_rate = 0.001 | alpha = 10 | n_neighbors = 13 | objective = ‘ CrossEntropy’ |
| Parameter 2 | max_iter = 1000 | probability = True | oob_score = True | max_depth = 4 | n_estimators = 178 | weights = ‘ uniform’ | colsample_bylevel = 0.503349 | |
| Parameter 3 | n_jobs = -1 | C = 0.732536 | class_weight = ’balanced’ | n_estimators = 494 | random_state = 151 | leaf_size = 35 | depth = 4 | |
| Parameter 4 | random_state = 151 | gamma = 0.011125 | n_estimators = 300 | min_child_weight = 6 | l2_leaf_reg = 1 | |||
| Parameter 5 | solver = ’newton-cg’ | random_state = 151 | max_depth = 5 | subsample = 0.218971 | boosting_type = ‘Ordered’ | |||
| Parameter 6 | penalty = ’l2’ | random_state = 151 | reg_lambda = 1 | bootstrap_type = ‘MVS’ | ||||
| Parameter 7 | Seed = 151 | random_state = 151 | ||||||
| Parameter 8 | used_ram_limit = ‘3gb’ | |||||||
| Parameter 9 | learning_rate = 0.001 |
SVM: support vector machine, XGBoost: Extreme Gradient Boosting, Adaboost: Adaptive Boosting, KNN: K-nearest neighbor, Catboost: Categorical boosting
Results
Comparisons of the characteristics of participants with and without postoperative stroke in the training set
A total of 6289 CAD patients undergoing coronary revascularization were identified in MIMIC-IV. Among them, patients with the length of ICU stay less than 24 h were excluded (n = 532). Finally, 5757 participants were included. All patients were divided into the postoperative stroke group (n = 433) and postoperative non-stroke group according whether postoperative stroke occurred. The screen process of the participants was exhibited in Fig 1.
Fig 1. The screen process of the participants.
The percentage of patients with personal history of stroke in those with postoperative stroke was higher those without (15.86% vs 5.35%; P<0.001). The mean INR in patient with postoperative stroke was higher those without (1.41 vs 1.37; P = 0.001). The median length of stay in patents with postoperative stroke was higher those without (2.31 days vs 1.83 days; P<0.001). More detailed information was observed in Table 4.
Table 4. Comparisons of the characteristics of participants with and without postoperative stroke in the training set.
| Postoperative stroke | |||||
|---|---|---|---|---|---|
| Variables | Total (n = 4029) | No (n = 3720) | yes (n = 309) | Statistics | P |
| Age, years, Mean ± SD | 67.77 ± 10.96 | 67.45 ± 11.00 | 71.54 ± 9.85 | t = -6.94 | <0.001 |
| Gender, n (%) | χ2 = 8.998 | 0.003 | |||
| Female | 1005 (24.94) | 906 (24.35) | 99 (32.04) | ||
| Male | 3024 (75.06) | 2814 (75.65) | 210 (67.96) | ||
| Ethnicity, n (%) | χ2 = 4.675 | 0.197 | |||
| White | 2881 (71.51) | 2650 (71.24) | 231 (74.76) | ||
| Black | 162 (4.02) | 155 (4.17) | 7 (2.27) | ||
| Others | 483 (11.99) | 453 (12.18) | 30 (9.71) | ||
| Unknown | 503 (12.48) | 462 (12.42) | 41 (13.27) | ||
| Insurance, n (%) | χ2 = 13.545 | 0.001 | |||
| Medicaid | 130 (3.23) | 120 (3.23) | 10 (3.24) | ||
| Medicare | 1819 (45.15) | 1649 (44.33) | 170 (55.02) | ||
| Others | 2080 (51.63) | 1951 (52.45) | 129 (41.75) | ||
| Marital status, n (%) | χ2 = 5.110 | 0.024 | |||
| Married | 2686 (66.67) | 2498 (67.15) | 188 (60.84) | ||
| No married | 1343 (33.33) | 1222 (32.85) | 121 (39.16) | ||
| First care unit, n (%) | χ2 = 4.078 | 0.130 | |||
| CCU | 595 (14.77) | 561 (15.08) | 34 (11.00) | ||
| CVICU | 3388 (84.09) | 3117 (83.79) | 271 (87.70) | ||
| Others | 46 (1.14) | 42 (1.13) | 4 (1.29) | ||
| Family history of stroke, n (%) | - | 0.653 | |||
| No | 4010 (99.53) | 3703 (99.54) | 307 (99.35) | ||
| Yes | 19 (0.47) | 17 (0.46) | 2 (0.65) | ||
| Personal history of stroke, n (%) | χ2 = 54.537 | <0.001 | |||
| No | 3781 (93.84) | 3521 (94.65) | 260 (84.14) | ||
| Yes | 248 (6.16) | 199 (5.35) | 49 (15.86) | ||
| Treatments, n (%) | χ2 = 4.197 | 0.123 | |||
| CABG and PCI | 22 (0.55) | 21 (0.56) | 1 (0.32) | ||
| CABG alone | 3316 (82.30) | 3049 (81.96) | 267 (86.41) | ||
| PCI alone | 691 (17.15) | 650 (17.47) | 41 (13.27) | ||
| Thrombolysis, n (%) | - | 1.000 | |||
| No | 4027 (99.95) | 3718 (99.95) | 309 (100.00) | ||
| Yes | 2 (0.05) | 2 (0.05) | 0 (0.00) | ||
| Antiplatelet, n (%) | - | 0.321 | |||
| No | 3970 (98.54) | 3663 (98.47) | 307 (99.35) | ||
| Yes | 59 (1.46) | 57 (1.53) | 2 (0.65) | ||
| Beta blockers, n (%) | χ2 = 18.061 | <0.001 | |||
| No | 2933 (72.80) | 2740 (73.66) | 193 (62.46) | ||
| Yes | 1096 (27.20) | 980 (26.34) | 116 (37.54) | ||
| Calcium channel blockers, n (%) | χ2 = 22.544 | <0.001 | |||
| No | 3616 (89.75) | 3363 (90.40) | 253 (81.88) | ||
| Yes | 413 (10.25) | 357 (9.60) | 56 (18.12) | ||
| Ventilation, n (%) | χ2 = 4.717 | 0.030 | |||
| No | 176 (4.37) | 170 (4.57) | 6 (1.94) | ||
| Yes | 3853 (95.63) | 3550 (95.43) | 303 (98.06) | ||
| Vasopressors, n (%) | χ2 = 8.987 | 0.003 | |||
| No | 1060 (26.31) | 1001 (26.91) | 59 (19.09) | ||
| Yes | 2969 (73.69) | 2719 (73.09) | 250 (80.91) | ||
| GCS, score, Mean ± SD | 13.36 ± 3.55 | 13.40 ± 3.52 | 12.89 ± 3.90 | t = 2.21 | 0.028 |
| CCI, score, M (Q1, Q3) | 2.00 (1.00, 3.00) | 2.00 (1.00, 3.00) | 3.00 (2.00, 5.00) | Z = 14.468 | <0.001 |
| Weight, kg, Mean ± SD | 84.60 ± 16.96 | 84.92 ± 16.98 | 80.81 ± 16.34 | t = 4.10 | <0.001 |
| Heart rate, bpm, Mean ± SD | 80.03 ± 9.40 | 80.07 ± 9.44 | 79.58 ± 8.94 | t = 0.88 | 0.379 |
| SBP, mmHg, Mean ± SD | 113.64 ± 16.80 | 113.68 ± 16.76 | 113.17 ± 17.33 | t = 0.51 | 0.610 |
| DBP, mmHg, Mean ± SD | 59.69 ± 10.76 | 59.92 ± 10.67 | 56.98 ± 11.39 | t = 4.63 | <0.001 |
| Respiratory rate, bpm, Mean ± SD | 15.21 ± 2.08 | 15.21 ± 2.09 | 15.20 ± 1.98 | t = 0.11 | 0.916 |
| Temperature, °C, Mean ± SD | 36.34 ± 0.47 | 36.34 ± 0.47 | 36.31 ± 0.49 | t = 1.40 | 0.162 |
| SPO2, %, Mean ± SD | 98.79 ± 2.74 | 98.78 ± 2.73 | 98.88 ± 2.83 | t = -0.59 | 0.556 |
| WBC, K/uL, M (Q1, Q3) | 12.20 (9.30, 15.60) | 12.30 (9.30, 15.60) | 11.70 (8.70, 15.10) | Z = -1.343 | 0.179 |
| Platelet, K/uL, M (Q1, Q3) | 152.20 (121.00, 192.00) | 153.00 (121.00, 192.00) | 144.00 (118.00, 186.00) | Z = -1.714 | 0.086 |
| Hemoglobin, g/dL, Mean ± SD | 10.27 ± 2.28 | 10.33 ± 2.28 | 9.64 ± 2.24 | t = 5.13 | <0.001 |
| RDW, %, Mean ± SD | 13.60 ± 1.00 | 13.57 ± 1.00 | 13.86 ± 0.95 | t = -4.79 | <0.001 |
| Hematocrit, %, Mean ± SD | 30.77 ± 6.72 | 30.94 ± 6.71 | 28.79 ± 6.58 | t = 5.40 | <0.001 |
| Creatinine, mg/dL, M (Q1, Q3) | 0.90 (0.70, 1.10) | 0.90 (0.70, 1.10) | 0.90 (0.70, 1.10) | Z = -0.588 | 0.557 |
| INR, ratio, Mean ± SD | 1.38 ± 0.19 | 1.37 ± 0.19 | 1.41 ± 0.21 | t = -3.24 | 0.001 |
| PT, seconds, Mean ± SD | 15.14 ± 2.00 | 15.11 ± 1.99 | 15.51 ± 2.11 | t = -3.38 | <0.001 |
| PTT, seconds, Mean ± SD | 37.36 ± 22.21 | 37.45 ± 22.57 | 36.28 ± 17.30 | t = 1.12 | 0.266 |
| BUN, mg/dL, M (Q1, Q3) | 16.00 (13.00, 21.00) | 16.00 (13.00, 21.00) | 17.00 (14.00, 23.00) | Z = 1.946 | 0.052 |
| Glucose, mg/dL, Mean ± SD | 140.04 ± 33.37 | 140.03 ± 33.27 | 140.20 ± 34.62 | t = -0.09 | 0.932 |
| Calcium, mmol/L, M (Q1, Q3) | 1.20 (1.11, 1.35) | 1.20 (1.12, 1.36) | 1.18 (1.11, 1.33) | Z = -1.864 | 0.062 |
| Sodium, mEq/L, Mean ± SD | 135.80 ± 2.85 | 135.82 ± 2.84 | 135.58 ± 2.90 | t = 1.43 | 0.153 |
| Chloride, mEq, Mean ± SD | 105.86 ± 3.63 | 105.84 ± 3.63 | 106.09 ± 3.71 | t = -1.16 | 0.245 |
| Bicarbonate, mEq/L, Mean ± SD | 23.20 ± 2.17 | 23.22 ± 2.17 | 22.98 ± 2.17 | t = 1.83 | 0.068 |
| Lactate, mmol/L, M (Q1, Q3) | 2.01 (1.60, 2.60) | 2.01 (1.60, 2.60) | 2.01 (1.50, 2.80) | Z = 0.490 | 0.624 |
| LOS, days, M (Q1, Q3) | 1.92 (1.26, 3.11) | 1.83 (1.25, 3.07) | 2.31 (1.36, 3.64) | Z = 6.621 | <0.001 |
SD: standard deviation, M: Median, Q1: 1st quartile, Q3: 3st quartile, CCU: Cardiac Care Unit, CVICU: cardiovascular intensive care unit, CABG: coronary artery bypass grafting, PCI: percutaneous coronary intervention, GCS: Glasgow Coma Scale, CCI: Charlson Comorbidity Index, SBP: systolic blood pressure, DBP: diastolic blood pressure, SPO2: oxygen saturation, WBC: white blood cell, RDW: red blood cell distribution width, INR: international normalized ratio (INR), PT prothrombin time, PTT partial thromboplastin time, BUN, blood urea nitrogen, LOS: length of stay
Construction and the predictive values of the prediction models for the risk of stroke in CAD patients receiving coronary revascularization
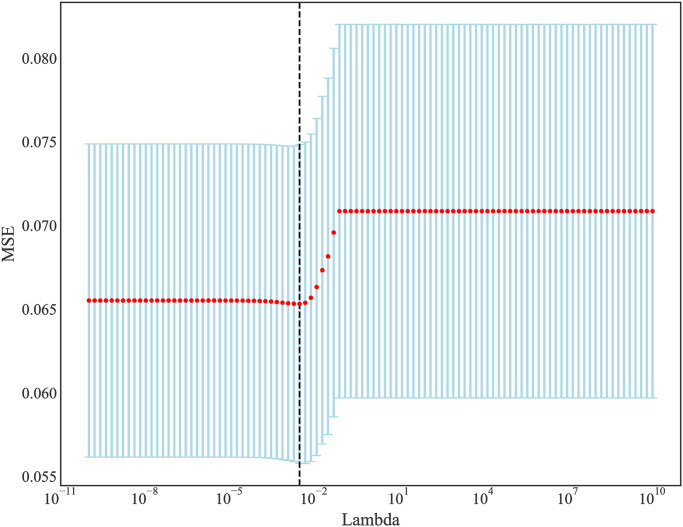
Initially, 40 features included, and 45 features were identified after one-hot encoding during the discretization of classification features. There were 39 variables with Pearson correlation coefficient<9. In order to ensure the stability and efficiency of features, valuable feature sets were selected from the 10-fold cross-validation results. As λ gradually expanded from 10−10 to 1010, the number of variables entering the model decreased. When λ was 0.002984, LASSO regression model showed the best prediction performance. Finally, 20 features with non-0 Coefficient were retained, which were age, GCS, CCI, weight, heart rate, DBP, SPO2, platelet, creatinine, INR, PTT, BUN, glucose, calcium, Ethnicity-unknown, Ethnicity-White, personal history of stroke-yes, beta-blockers-yes, calcium channel blockers-yes, and vasopressors-yes. Fig 2 presented the changes of mean-squared error (MSE), and Fig 3 showed the changes of Coefficients with Lambda in the Lasso regression.
Fig 2. The changes of MSE with Lambda in the Lasso regression.
Fig 3. The changes of Coefficients with Lambda in the Lasso regression.
The predictive values of the prediction models for the risk of stroke in CAD patients undergoing coronary revascularization
The predictive values of prediction models for stroke in CAD patients undergoing coronary revascularization were presented in Table 5. The results delineated that Catboost model presented the best predictive performance with the AUC of 0.831 (95%CI: 0.811–0.851) in the training set, and 0.760 (95%CI: 0.722–0.798) in the testing set. The AUC of the logistic regression model was 0.789 (95%CI: 0.764–0.814) in the training set and 0.731 (95%CI: 0.686–0.776) in the testing set (Table 6). The results of Delong test revealed that the predictive value of the Catboost model was significantly higher than the logistic regression model (P<0.05). The ROC curves of machine learning models in the training set and testing set were respectively shown in Figs 4 and 5.
Table 5. The predictive values of different machine learning prediction models.
| Model | Cut off | Sensitivity (95%CI) | Specificity (95%CI) | AUC (95%CI) | Accuracy (95%CI) |
|---|---|---|---|---|---|
| Logistic regression Training set | 0.076 | 0.764 (0.716–0.811) | 0.696 (0.681–0.711) | 0.789 (0.764–0.814) | 0.701 (0.687–0.715) |
| Logistic regression Testing set | 0.076 | 0.669 (0.587–0.752) | 0.671 (0.648–0.694) | 0.731 (0.686–0.776) | 0.671 (0.649–0.693) |
| SVM Training set | 0.114 | 0.417 (0.362–0.472) | 0.787 (0.774–0.800) | 0.629 (0.595–0.662) | 0.759 (0.746–0.772) |
| SVM Testing set | 0.114 | 0.331 (0.248–0.413) | 0.816 (0.797–0.835) | 0.591 (0.536–0.646) | 0.781 (0.762–0.801) |
| Random forest Training set | 0.466 | 0.877 (0.840–0.914) | 0.717 (0.703–0.732) | 0.883 (0.866–0.900) | 0.730 (0.716–0.743) |
| Random forest Testing set | 0.466 | 0.621 (0.536–0.706) | 0.734 (0.713–0.756) | 0.749 (0.712–0.786) | 0.726 (0.705–0.747) |
| XGBoost Training set | 0.339 | 0.838 (0.797–0.879) | 0.622 (0.606–0.638) | 0.814 (0.792–0.837) | 0.639 (0.624–0.653) |
| XGBoost Testing set | 0.339 | 0.782 (0.710–0.855) | 0.577 (0.553–0.601) | 0.744 (0.703–0.784) | 0.591 (0.568–0.615) |
| Adaboost Training set | 0.148 | 0.699 (0.648–0.750) | 0.671 (0.656–0.686) | 0.720 (0.696–0.743) | 0.673 (0.659–0.688) |
| Adaboost Testing set | 0.148 | 0.677 (0.595–0.760) | 0.673 (0.650–0.696) | 0.718 (0.681–0.755) | 0.674 (0.652–0.696) |
| Naïve bayes Training set | 0.071 | 0.599 (0.544–0.653) | 0.708 (0.694–0.723) | 0.708 (0.679–0.737) | 0.700 (0.686–0.714) |
| Naïve bayes Testing set | 0.071 | 0.524 (0.436–0.612) | 0.646 (0.622–0.669) | 0.629 (0.582–0.676) | 0.637 (0.614–0.660) |
| KNN Training set | 0.154 | 0.612 (0.557–0.666) | 0.798 (0.785–0.811) | 0.785 (0.761–0.809) | 0.784 (0.771–0.797) |
| KNN Testing set | 0.154 | 0.226 (0.152–0.299) | 0.906 (0.892–0.920) | 0.625 (0.573–0.677) | 0.857 (0.841–0.874) |
| Catboost Training set | 0.173 | 0.838 (0.797–0.879) | 0.662 (0.646–0.677) | 0.831 (0.811–0.851) | 0.675 (0.661–0.690) |
| Catboost Testing set | 0.173 | 0.718 (0.639–0.797) | 0.660 (0.637–0.683) | 0.760 (0.722–0.798) | 0.664 (0.642–0.687) |
Table 6. Comparisons of the prediction performance of Catboost model and logistic regression model.
| Dataset | Model | AUC (95%CI) | Statistics | P |
|---|---|---|---|---|
| Training set | Logistic regression | 0.789 (0.764–0.814) | Ref | |
| Catboost | 0.831 (0.811–0.851) | Z = 6.36 | <0.001 | |
| Testing set | Logistic regression | 0.731 (0.686–0.776) | Ref | |
| Catboost | 0.760 (0.722–0.798) | Z = 3.12 | 0.002 |
Fig 4. The ROC curves of machine learning models in the training set.
Fig 5. The ROC curves of machine learning models in the testing set.
The importance of each feature in the Catboost model was displayed in Fig 6, which depicted that CCI was the most important variable associated with the risk of stroke in CAD patients undergoing coronary revascularization.
Fig 6. Absolut summary plot showing the importance of each feature in the Catboost model.
The SHapley Additive exPlanations (SHAP) values of features in the Catboost model were visualized in Fig 7, with SHAP values on the X-axis, features on the Y-axis, and each point representing a sample. The redder color indicates a stronger effect of the feature on the outcome, while the bluer color indicates a weaker effect. CCI was an important factor that exhibited a positive correlation with the risk of stroke in CAD patients following coronary revascularization. Creatinine levels were found to be associated with the risk of stroke, as indicated by blue dots primarily concentrated in areas where SHAP values exceeded 0, suggesting that lower creatinine levels were linked to higher stroke risk. Fig 8 depicted the SHAP value analysis of each sample in the Catboost model, where blue represents negative feature contribution and red indicates positive contribution. The length of an arrow signifies the degree of influence that a feature has on output, and its reduction or increase can be observed through the scale value on the X-axis. Base value refers to the average output of the model and training data, while the number below the arrow represents the actual eigenvalue of a single sample. Referring to a single sample, we found that CCI had the reddest summary plots, indicating that patients with a CCI score of 6 might be at risk for postoperative stroke. Age exhibited the longest blue bar, suggesting that patients aged 53 might experience reduced risk of postoperative stroke. The final SHAP output value of the model was -1.58. Fig 9 illustrated the impact of each feature in the Catboost prediction model on the model’s output. The x-axis represents features, while the y-axis represents SHAP values, and each dot denotes a sample. When a feature’s SHAP value exceeded 0, the risk of postoperative stroke was increased. CCI≥2 was associated with an increased risk of stroke.
Fig 7. Summary plot for SHAP values of features in the Catboost model.
Fig 8. Force plot for SHAP values of features in the Catboost model.
Fig 9. Dependence plot for SHAP values of CCI.
Discussion
The present study constructed several prediction models for the risk of stroke in CAD patients who received coronary revascularization based on machine learning methods. The results demonstrated that Catboost model was the optimal model for predicting the risk of stroke in CAD patients who received coronary revascularization. The AUC of Catboost model was 0.831 in the training set, and 0.760 in the testing set, which were higher than the logistic regression model. The findings might provide a novel and quick tool to identify CAD patients receiving coronary revascularization treatments who were at high risk of stroke, and offer timely interventions to prevent the poor prognosis.
Previously, several prediction models were constructed to predict the risk of cardiovascular events in CAD patients receiving coronary revascularization. Zhang et al. built a nomogram for predicting major adverse cardiovascular events after PCI in coronary heart disease patients with chronic kidney disease, and the AUC value of the model was 0.612 [22]. Another prediction model for predicting major adverse cardiac and cerebrovascular events among high-risk myocardial infarction patients undergoing primary PCI had an AUC of 0.883 in the testing set [23]. A very early prediction model for stroke patients undergoing CABG had an AUC of 0.70 [24]. A multicenter Spanish study established a multivariate prediction model for perioperative in-hospital cerebrovascular accident after coronary bypass surgery, and the AUC was 0.77 [25]. The present study constructed several prediction models using machine learning method, and the Catboost model had the optimum predictive value for the risk of stroke in CAD patients who underwent coronary revascularization. The prediction model can handle irregular data, missing values and other problems well, and has good robustness, and effectively prevent overfitting, which also makes the model more general; in addition, it can match any advanced machine learning algorithm in terms of model performance [20]. The prediction model might provide an easy tool for the clinicians to quickly identify CAD patients undergoing coronary revascularization who were at high risk of stroke. The success of deep learning and machine learning has brought excitement and high expectations in revolutionary changes in health care in CAD patients [26–28]. The deep learning and machine learning algorithm could achieve more accurate results and outperform statistical methods. The findings of this study might be interesting for other researchers from different fields.
CCI is a measure of comorbidity burden that facilitates the evaluation of the prognostic significance of various clinical conditions based on their quantity and individual prognostic impact [29]. CCI has been extensively investigated in various clinical conditions and its significance as a prognostic indicator has been demonstrated. A previous study depicted that CCI was higher in patients with a more diffuse extent of CAD than those with milder disease [30]. Rashid et al. indicated that CCI >2 significantly increased the risk of mortality in acute coronary syndrome [31]. CCI was also identified to be a predictor of readmission in CAD patients [32]. CCI was reported to be highly associated with long-term survival and almost equivalent to left ventricular ejection fraction [33]. CCI was independently associated with an increase in 30-day, 1-year and 5-year cardiac death and major adverse cardiovascular events [34]. Other studies also revealed that CCI was a reliable indicator for the mortality of ischemic stroke patients [35–37]. Herein, CCI was found to be a vital predictor for the risk of stroke in CAD patients who received coronary revascularization. Age was identified to be an important variable associated with the outcomes of post-ST-segment elevation myocardial infarction patients among patients without preexisting coronary artery disease [38]. In this study, age was also related to the risk of stroke in CAD patients who received coronary revascularization.
Several prediction model for stroke risk in CAD patients with coronary revascularization treatments was constructed based on a variety of machine learning methods, which might provide certain references for early identification of high-risk patients and management of postoperative complications. Some limitations existed in this study. Firstly, although all the data were divided into the training set and testing set, the samples were from a single center, and the model should be applied with caution. Secondly, due to the limitations of the MIMIC database, some preoperative and postoperative data, and data related to liver enzymes could not be obtained. More studies were required to verify the results in this study.
Conclusions
The current study established several prediction models and identified an optimal model for the risk of stroke in CAD patients who received coronary revascularization. The prediction model might offer quick tool to identify CAD patients receiving coronary revascularization who were at high risk of stroke, and make specific treatment strategies to prevent the occurrence of stroke.
Data Availability
The datasets generated and/or analyzed during the current study are available in the MIMIC-IV database, https://mimic.physionet.org/iv/.
Funding Statement
The author(s) received funding from Dalian Medical Science research project (No. 2112012) for this work.
References
- 1.Amin AM. Metabolomics applications in coronary artery disease personalized medicine. Advances in clinical chemistry. 2021;102:233–70. Epub 2021/05/29. doi: 10.1016/bs.acc.2020.08.003 . [DOI] [PubMed] [Google Scholar]
- 2.Malakar AK, Choudhury D, Halder B, Paul P, Uddin A, Chakraborty S. A review on coronary artery disease, its risk factors, and therapeutics. Journal of cellular physiology. 2019;234(10):16812–23. Epub 2019/02/23. doi: 10.1002/jcp.28350 . [DOI] [PubMed] [Google Scholar]
- 3.King SB 3rd, Marshall JJ, Tummala PE. Revascularization for coronary artery disease: stents versus bypass surgery. Annual review of medicine. 2010;61:199–213. Epub 2009/10/15. doi: 10.1146/annurev.med.032309.063039 . [DOI] [PubMed] [Google Scholar]
- 4.Bangalore S, Kumar S, Fusaro M, Amoroso N, Attubato MJ, Feit F, et al. Short- and long-term outcomes with drug-eluting and bare-metal coronary stents: a mixed-treatment comparison analysis of 117 762 patient-years of follow-up from randomized trials. Circulation. 2012;125(23):2873–91. Epub 2012/05/16. doi: 10.1161/CIRCULATIONAHA.112.097014 . [DOI] [PubMed] [Google Scholar]
- 5.Global, regional, and national life expectancy, all-cause mortality, and cause-specific mortality for 249 causes of death, 1980–2015: a systematic analysis for the Global Burden of Disease Study 2015. Lancet (London, England). 2016;388(10053):1459–544. Epub 2016/10/14. doi: 10.1016/S0140-6736(16)31012-1 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Arnan MK, Hsieh TC, Yeboah J, Bertoni AG, Burke GL, Bahrainwala Z, et al. Postoperative blood urea nitrogen is associated with stroke in cardiac surgical patients. The Annals of thoracic surgery. 2015;99(4):1314–20. Epub 2015/02/17. doi: 10.1016/j.athoracsur.2014.11.034 . [DOI] [PubMed] [Google Scholar]
- 7.Yamamoto K, Natsuaki M, Morimoto T, Shiomi H, Matsumura-Nakano Y, Nakatsuma K, et al. Periprocedural Stroke After Coronary Revascularization (from the CREDO-Kyoto PCI/CABG Registry Cohort-3). The American journal of cardiology. 2021;142:35–43. Epub 2020/12/07. doi: 10.1016/j.amjcard.2020.11.031 . [DOI] [PubMed] [Google Scholar]
- 8.Head SJ, Milojevic M, Daemen J, Ahn JM, Boersma E, Christiansen EH, et al. Stroke Rates Following Surgical Versus Percutaneous Coronary Revascularization. Journal of the American College of Cardiology. 2018;72(4):386–98. Epub 2018/07/22. doi: 10.1016/j.jacc.2018.04.071 . [DOI] [PubMed] [Google Scholar]
- 9.Silva GFS, Fagundes TP, Teixeira BC, Chiavegatto Filho ADP. Machine Learning for Hypertension Prediction: a Systematic Review. Current hypertension reports. 2022;24(11):523–33. Epub 2022/06/23. doi: 10.1007/s11906-022-01212-6 . [DOI] [PubMed] [Google Scholar]
- 10.Tseng PY, Chen YT, Wang CH, Chiu KM, Peng YS, Hsu SP, et al. Prediction of the development of acute kidney injury following cardiac surgery by machine learning. Critical care (London, England). 2020;24(1):478. Epub 2020/08/02. doi: 10.1186/s13054-020-03179-9 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nistal-Nuño B. Machine learning applied to a Cardiac Surgery Recovery Unit and to a Coronary Care Unit for mortality prediction. Journal of clinical monitoring and computing. 2022;36(3):751–63. Epub 2021/04/17. doi: 10.1007/s10877-021-00703-2 . [DOI] [PubMed] [Google Scholar]
- 12.Zhang X, Fei N, Zhang X, Wang Q, Fang Z. Machine Learning Prediction Models for Postoperative Stroke in Elderly Patients: Analyses of the MIMIC Database. Frontiers in aging neuroscience. 2022;14:897611. Epub 2022/08/05. doi: 10.3389/fnagi.2022.897611 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Liu Q, Zheng HL, Wu MM, Wang QZ, Yan SJ, Wang M, et al. Association between lactate-to-albumin ratio and 28-days all-cause mortality in patients with acute pancreatitis: A retrospective analysis of the MIMIC-IV database. Frontiers in immunology. 2022;13:1076121. Epub 2023/01/03. doi: 10.3389/fimmu.2022.1076121 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ding C, Guo Y, Mo Q, Ma J. Prediction Model of Postoperative Severe Hypocalcemia in Patients with Secondary Hyperparathyroidism Based on Logistic Regression and XGBoost Algorithm. Computational and mathematical methods in medicine. 2022;2022:8752826. Epub 2022/08/05. doi: 10.1155/2022/8752826 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhao X, Lu Y, Li S, Guo F, Xue H, Jiang L, et al. Predicting renal function recovery and short-term reversibility among acute kidney injury patients in the ICU: comparison of machine learning methods and conventional regression. Renal failure. 2022;44(1):1326–37. Epub 2022/08/06. doi: 10.1080/0886022X.2022.2107542 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cabrera A, Bouterse A, Nelson M, Razzouk J, Ramos O, Chung D, et al. Use of random forest machine learning algorithm to predict short term outcomes following posterior cervical decompression with instrumented fusion. Journal of clinical neuroscience: official journal of the Neurosurgical Society of Australasia. 2023;107:167–71. Epub 2022/11/15. doi: 10.1016/j.jocn.2022.10.029 . [DOI] [PubMed] [Google Scholar]
- 17.Hauptman A, Balasubramaniam GM, Arnon S. Machine Learning Diffuse Optical Tomography Using Extreme Gradient Boosting and Genetic Programming. Bioengineering (Basel, Switzerland). 2023;10(3). Epub 2023/03/30. doi: 10.3390/bioengineering10030382 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sorayaie Azar A, Babaei Rikan S, Naemi A, Bagherzadeh Mohasefi J, Pirnejad H, Bagherzadeh Mohasefi M, et al. Application of machine learning techniques for predicting survival in ovarian cancer. BMC medical informatics and decision making. 2022;22(1):345. Epub 2022/12/31. doi: 10.1186/s12911-022-02087-y . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Saroj RK, Yadav PK, Singh R, Chilyabanyama ON. Machine Learning Algorithms for understanding the determinants of under-five Mortality. BioData mining. 2022;15(1):20. Epub 2022/09/25. doi: 10.1186/s13040-022-00308-8 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Qin Y, Wu J, Xiao W, Wang K, Huang A, Liu B, et al. Machine Learning Models for Data-Driven Prediction of Diabetes by Lifestyle Type. International journal of environmental research and public health. 2022;19(22). Epub 2022/11/27. doi: 10.3390/ijerph192215027 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chen Q, Pan T, Wang YN, Schoepf UJ, Bidwell SL, Qiao H, et al. A Coronary CT Angiography Radiomics Model to Identify Vulnerable Plaque and Predict Cardiovascular Events. Radiology. 2023;307(2):e221693. Epub 2023/02/15. doi: 10.1148/radiol.221693 . [DOI] [PubMed] [Google Scholar]
- 22.Zhang Y, Wang J, Zhai G, Zhou Y. Development and Validation of a Predictive Model for Chronic Kidney Disease After Percutaneous Coronary Intervention in Chinese. Clinical and applied thrombosis/hemostasis: official journal of the International Academy of Clinical and Applied Thrombosis/Hemostasis. 2022;28:10760296211069998. Epub 2022/01/25. doi: 10.1177/10760296211069998 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhao X, Liu C, Zhou P, Sheng Z, Li J, Zhou J, et al. Development and Validation of a Prediction Rule for Major Adverse Cardiac and Cerebrovascular Events in High-Risk Myocardial Infarction Patients After Primary Percutaneous Coronary Intervention. Clinical interventions in aging. 2022;17:1099–111. Epub 2022/07/27. doi: 10.2147/CIA.S358761 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Charlesworth DC, Likosky DS, Marrin CA, Maloney CT, Quinton HB, Morton JR, et al. Development and validation of a prediction model for strokes after coronary artery bypass grafting. The Annals of thoracic surgery. 2003;76(2):436–43. Epub 2003/08/07. doi: 10.1016/s0003-4975(03)00528-9 . [DOI] [PubMed] [Google Scholar]
- 25.Hornero F, Martín E, Rodríguez R, Castellà M, Porras C, Romero B, et al. A multicentre Spanish study for multivariate prediction of perioperative in-hospital cerebrovascular accident after coronary bypass surgery: the PACK2 score. Interactive cardiovascular and thoracic surgery. 2013;17(2):353–8; discussion 8. Epub 2013/05/01. doi: 10.1093/icvts/ivt102 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chan HP, Samala RK, Hadjiiski LM, Zhou C. Deep Learning in Medical Image Analysis. Advances in experimental medicine and biology. 2020;1213:3–21. Epub 2020/02/08. doi: 10.1007/978-3-030-33128-3_1 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Huang AA, Huang SY. Use of machine learning to identify risk factors for coronary artery disease. PloS one. 2023;18(4):e0284103. Epub 2023/04/15. doi: 10.1371/journal.pone.0284103 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Jee J. Machine learning-based markers for CAD. Lancet (London, England). 2023;402(10397):183. Epub 2023/07/16. doi: 10.1016/S0140-6736(23)01062-0 . [DOI] [PubMed] [Google Scholar]
- 29.Niewiński G, Graczyńska A, Morawiec S, Raszeja-Wyszomirska J, Wójcicki M, Zieniewicz K, et al. Renaissance of Modified Charlson Comorbidity Index in Prediction of Short- and Long-Term Survival After Liver Transplantation? Medical science monitor: international medical journal of experimental and clinical research. 2019;25:4521–6. Epub 2019/06/19. doi: 10.12659/MSM.914669 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Karabağ T, Altuntaş E, Kalaycı B, Şahіn B, Somuncu MU, Çakır MO. The relationship of Charlson comorbidity index with stent restenosis and extent of coronary artery disease. Interventional medicine & applied science. 2018;10(2):70–5. Epub 2018/10/27. doi: 10.1556/1646.10.2018.20 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rashid M, Kwok CS, Gale CP, Doherty P, Olier I, Sperrin M, et al. Impact of co-morbid burden on mortality in patients with coronary heart disease, heart failure, and cerebrovascular accident: a systematic review and meta-analysis. European heart journal Quality of care & clinical outcomes. 2017;3(1):20–36. Epub 2017/09/21. doi: 10.1093/ehjqcco/qcw025 . [DOI] [PubMed] [Google Scholar]
- 32.Albar HM, Alahmdi RA, Almedimigh AA, Shaik RA, Ahmad MS, Almutairi AB, et al. Prevalence of coronary artery disease and its risk factors in Majmaah City, Kingdom of Saudi Arabia. Frontiers in cardiovascular medicine. 2022;9:943611. Epub 2022/09/27. doi: 10.3389/fcvm.2022.943611 . [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 33.Sachdev M, Sun JL, Tsiatis AA, Nelson CL, Mark DB, Jollis JG. The prognostic importance of comorbidity for mortality in patients with stable coronary artery disease. Journal of the American College of Cardiology. 2004;43(4):576–82. Epub 2004/02/21. doi: 10.1016/j.jacc.2003.10.031 . [DOI] [PubMed] [Google Scholar]
- 34.Mamas MA, Fath-Ordoubadi F, Danzi GB, Spaepen E, Kwok CS, Buchan I, et al. Prevalence and Impact of Co-morbidity Burden as Defined by the Charlson Co-morbidity Index on 30-Day and 1- and 5-Year Outcomes After Coronary Stent Implantation (from the Nobori-2 Study). The American journal of cardiology. 2015;116(3):364–71. Epub 2015/06/04. doi: 10.1016/j.amjcard.2015.04.047 . [DOI] [PubMed] [Google Scholar]
- 35.Hall RE, Porter J, Quan H, Reeves MJ. Developing an adapted Charlson comorbidity index for ischemic stroke outcome studies. BMC health services research. 2019;19(1):930. Epub 2019/12/05. doi: 10.1186/s12913-019-4720-y . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bajic B, Galic I, Mihailovic N, Ristic S, Radevic S, Cupic VI, et al. Performance of Charlson and Elixhauser Comorbidity Index to Predict in-Hospital Mortality in Patients with Stroke in Sumadija and Western Serbia. Iranian journal of public health. 2021;50(5):970–7. Epub 2021/06/30. doi: 10.18502/ijph.v50i5.6114 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Falsetti L, Viticchi G, Tarquinio N, Silvestrini M, Capeci W, Catozzo V, et al. Charlson comorbidity index as a predictor of in-hospital death in acute ischemic stroke among very old patients: a single-cohort perspective study. Neurological sciences: official journal of the Italian Neurological Society and of the Italian Society of Clinical Neurophysiology. 2016;37(9):1443–8. Epub 2016/05/12. doi: 10.1007/s10072-016-2602-1 . [DOI] [PubMed] [Google Scholar]
- 38.Jang SJ, Kim LK, Sobti NK, Yeo I, Cheung JW, Feldman DN, et al. Mortality of patients with ST-segment-elevation myocardial infarction without standard modifiable risk factors among patients without known coronary artery disease: Age-stratified and sex-related analysis from nationwide readmissions database 2010–2014. American journal of preventive cardiology. 2023;14:100474. Epub 2023/03/17. doi: 10.1016/j.ajpc.2023.100474 . [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets generated and/or analyzed during the current study are available in the MIMIC-IV database, https://mimic.physionet.org/iv/.