Decision rules for personalized statin treatment prescriptions over multi-objectives

Abstract

In our previous study, we demonstrated the feasibility of producing a proactive statin prescription strategy – a personalized statin treatment plan (PSTP) – using neural networks with big data. However, its non-transparency limited result interpretations and clinical usability. To improve the transparency of our previous approach with minimal compromise to the maximal statin treatment benefit-to-risk ratio, this study proposed a five-step pipeline approach called the decision rules for statin treatment (DRST). Steps 1–3 of our proposed pipeline improved our previous PSTP model in optimizing individual benefit-to-risk ratio; Step 4 used a decision tree model (DRST) to provide straightforward rules in the initial statin treatment plan; Step 5 aimed to evaluate the efficacy of these decision rules by conducting a clinical trial simulation. We included 107,739 de-identified patient data from Optum Labs Database Warehouse in this study. The final decision rules were compact and efficient, resulting from a decision tree with only a maximum depth of 3 and 11 nodes. The DRST identified three factors that are easily obtainable at the point of care: age, low-density lipoprotein cholesterol (LDL-C) level, and age-adjusted Charlson score. Moreover, it also identified six subpopulations that can benefit most from these decision rules. In our clinical trial simulations, DRST was found to improve statin benefit in LDL-C reduction by 4.15 percentage points (pp) and reduce risks of statin-associated symptoms (SAS) and statin discontinuation by 11.71 and 3.96 pp, respectively, when compared to the standard of care. Moreover, these DRST results were only less than 0.6 pp suboptimal to PSTP, demonstrating that building DRST that provide transparency with minimal compromise to the maximal benefit-to-risk ratio of statin treatments is feasible.

Impact Statement

Clinical guidelines have provided proactive strategies to maximize statin benefits in low-density lipoprotein cholesterol (LDL-C), hence reducing the risks of atherosclerotic cardiovascular disease. However, statin treatments are associated with undesirable side effects, which in turn discourage the use of statins. A simple guideline to proactively prevent statin-associated symptoms (SAS) and statin discontinuation has yet to be developed. In this study, we illustrated an effective pipeline to build decision rules for statin treatment (DRST) to prevent SAS and statin discontinuation while maximizing statin benefits in LDL-C. We also demonstrated the feasibility of developing proactive and simple guidelines that can optimize multi-objectives in statin treatment. Our proposed pipeline (DRST) can emulate a personalized statin treatment plan (PSTP) approach that we discussed in our previous study and achieve similar patient outcome optimizations. These rules may assist future clinical guidelines in balancing the benefit-to-risk ratio in statin treatment.

Introduction

Statins have been widely used to treat the leading cause of death in the United States – atherosclerotic cardiovascular disease (ASCVD). Studies have proven the efficacy of statins in lowering low-density lipoprotein cholesterol (LDL-C), and hence, in preventing death and major adverse cardiovascular events (MACE). ¹ With that in mind, clinical guidelines have identified subgroups who would benefit from statin treatment (i.e. statin benefit groups) and recommended higher-intensity statins in hopes of reducing their ASCVD risk. ² However, statins are also associated with skeletal muscle, metabolic, neurological, and other possible side effects, known as statin-associated symptoms (SAS). ³ Existing strategies to manage potential SAS generally involve reactive strategies to revise statin treatment plans after SAS occurrence, such as altering statin treatment, discontinuing statin treatment, or changing to other lipid-lowering drugs. Failure to adhere to statin treatments can negate its benefits in reducing MACE and can increase the risk of cardiovascular events by up to 33%, especially in the older cohort. ⁴ While many cholesterol guidelines have successfully guided prescribers in optimizing patients’ LDL-C reductions, little guidance is available to help providers manage SAS and prevent statin discontinuation. Thus, developing a proactive approach to identify the optimal choice of an initial statin treatment plan that can maximize LDL-C reduction while minimizing potential SAS and discontinuation is desirable and necessary to obtain the long-term benefit of statins.

With the increasing accessibility to multiple sources of medical data, personalized medicine has been a growing field that many believed to be the next generation of healthcare.^5,6 Personalized medicine is a treatment approach that is tailored to each patient’s characteristics. By enabling optimal treatment tailored to each patient, the standard of care, as we know it today, can be redefined drastically: reducing trial and error prescribing, shifting medicine from reaction to proactive, increasing patient compliance with treatments, and reducing overall healthcare costs. ⁷ To demonstrate a personalized medicine approach in choosing statin treatments, in our previous study, ⁸ we showed the feasibility of developing a personalized statin treatment plan (PSTP) that can minimize both risks of SAS and discontinuation simultaneously. Specifically, our simulations showed that PSTP may reduce the risk of discontinuation by 4% on average with similar SAS risk when compared to the standard of care (P < 0.01). However, our previous study also pointed out that non-transparent machine learning models restricted clinical interpretability. Despite the potential benefits of the PSTP approach, clinical professionals may be skeptical of its clinical usability since it does not provide straightforward rules in prescribing a statin treatment plan. This challenge can also be seen in many personalized medicine approaches, where many stakeholders and consumers have yet to fully understand the benefits of personalized medicine due to poor transparency, limited scientific understanding of the mechanisms, and challenging economic and technology burdens. ⁶ Therefore, in this study, we aimed to improve the transparency and usability of our previous PSTP approach by generating a set of clinical decision rules that can directly map from patients’ characteristics to clinically actionable insights (i.e. the optimal choice of initial statin treatment plan).

The goal of our study is to provide simple rules for an initial statin treatment plan with minimal compromise to the maximal statin treatment benefit-to-risk ratio. Hence, it is important to (1) identify a treatment plan that minimizes risks (SAS and discontinuation) while maximizing benefits (LDL-C reduction) of taking a statin for a subpopulation and (2) identify a patient subpopulation with the maximal proportion of patients who can benefit from the recommended statin treatment plan. Given these considerations in mind, one approach to solving our problem is to use an impurity function (in our study, the Gini index) as it provides a measure of how data can be separated across subpopulations. In this study, we proposed a five-step pipeline approach called the decision rules for statin treatment (DRST) and demonstrated that its clinical efficacy (statin benefit-to-risk ratio) is comparable to that of PSTP.

Materials and methods

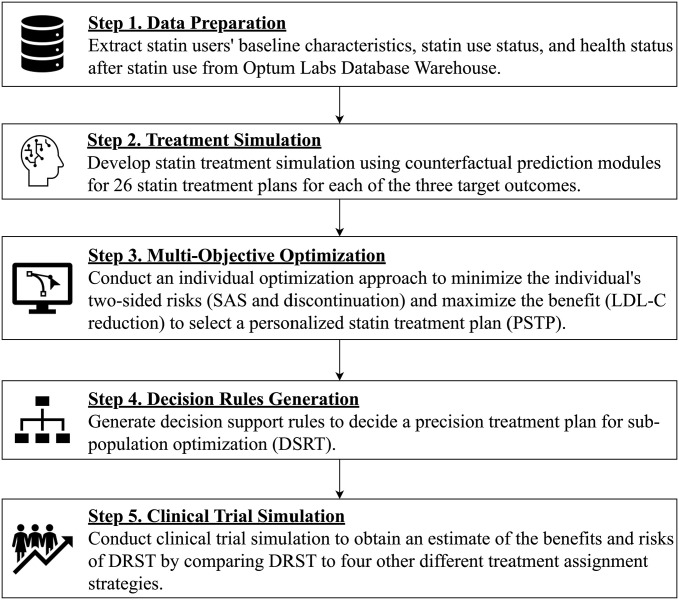
Figure 1 summarizes our proposed five-step pipeline approach to develop and assess DRST. This pipeline consists of five steps that will be further discussed in this “Methods” section: data preparation, treatment simulation, multi-objective optimization, decision rule generation, and clinical trial simulation. In summary, Steps 1–3 in this pipeline lead to a PSTP, Step 4 aims to improve knowledge base transparency by creating decision rules, and Step 5 aims to evaluate the efficacy of DRST.

Figure 1.

Proposed five-step integrated approach for the DRST. Five rectangular boxes represent five steps of the proposed pipeline. The arrows represent the workflow of the proposed pipeline. In brief, Steps 1–3 aim to produce a PSTP. Step 4 creates DRST. Step 5 aims to evaluate the efficacy of DRST by conducting a clinical trial simulation.

Previous PSTP methods

Our previous PSTP can be achieved in the first three steps in Figure 1: data preparation, treatment simulation, and multi-objective optimization. We used similar data preparation and multi-objective optimization steps that are proposed in this study but a different treatment simulation technique. Briefly, our previous study used a feed-forward neural network to simulate patient potential outcomes. However, this method cannot account for the confounding bias that might arise in observational data. Hence, in this study, apart from improving the model transparency (Step 4), we also improved our previous treatment simulation (Step 2) by adopting a counterfactual framework.

Data preparation

Details of the data source and cohort selection were described in our previous PSTP study. ⁸ Briefly, this study is a retrospective study that uses nationwide de-identified longitudinal claims and electronic health records (EHRs) from Optum Labs Database Warehouse (OLDW). Available data elements include patient history, patient demographics, patient insurance claims data, EHRs, and laboratory test results. ⁹

In our previous PSTP study, we only focused on patients with ASCVD between 2010 and 2015. In this study, we extended our study period to 2019 (i.e. this study period is 2010–2019) and expanded our scope to include three other statin benefit groups (high LDL-C, diabetes, and high ASCVD risk groups) defined by the 2013 ACC/AHA Guideline on the Treatment of Blood Cholesterol to Reduce Atherosclerotic Cardiovascular Risk in Adults ² (denoted as the “2013 ACC/AHA Guideline”). A detailed description can be found in the Supplemental Methods. We included these statin benefit groups as many studies have validated the benefits of statins in these groups and this study aimed to recommend an initial statin treatment plan to patients who are in need of starting statin treatment.

Similar to our previous PSTP study, we included all patients who had at least one prescription for any statin medication containing atorvastatin, lovastatin, fluvastatin, pravastatin, pitavastatin, simvastatin, or rosuvastatin between 2010 and 2019. The index date was defined as the patient’s first statin prescription date. The baseline period was defined as the one year preceding the index date while the follow-up period was defined as the one year following the index date. Further inclusion criteria included one-year continuous insurance enrollment in medical and pharmacy in the baseline and follow-up periods. To capture the effect of statin treatment plans on patients’ LDL-C levels, patients were required to have at least one LDL-C value recorded three months before the index and one recorded three months after the index. Patients were also required to have no history of statin use before their index dates. This allowed our study to focus on the initial clinician–patient consultation in starting appropriate statin treatment.

A total of 75 baseline clinical variables were extracted during the baseline period as predictors (Supplemental Table 1). In short, these variables consist of demographics, socioeconomic status, vital status, cholesterol levels, and comorbidity profile that includes the risk factors that were already identified in the 2013 ACC/AHA Guideline. However, due to the nature of EHRs and healthcare claim records, some of this information was missing. To mitigate bias that arises from missing data, we adopted the missing pattern approach: ¹⁰ a missing indicator was created for each variable that consists of missing values (resulting in a total of 80 variables), and the missing values were replaced by 0. The exposure of this study is patients’ initial statin treatment plan. A unique statin treatment plan was defined by a unique statin drug-dose combination. Some studies might use the term “treatment plan” to refer to a dynamic treatment regime that tailors treatment regimens to individuals over time. In this study, the statin treatment plan referred to the initial choice of statin to be prescribed. We included a total of 26 unique but commonly used statin treatment plans (Supplemental Table 2). During the one-year follow-up period, three target outcomes were captured for every patient: (1) LDL-C reduction – a continuous variable representing the change in percentage in the average LDL-C values between the three months before and after the index. That being said, if a patient has more than one LDL-C value within three months before or after the index, the average LDL-C across the three-month period is taken. This is because it is rare for a patient to be tested more than once within three months. Moreover, to keep LDL-C stabilized at a lower value after using statins, it is not fair to compare the first or the last, the highest or the lowest LDL-C value if these values are vastly different. In both cases, the average serves as a good indicator when these LDL-C values are vastly different and also representative if these LDL-C values are similar; (2) SAS – a binary variable indicating the occurrence of any severe muscle pain, newly developed diabetes mellitus, and poisoning events during the follow-up period; (3) discontinuation – a binary variable indicating if the patient had a gap of 45 days or more in their initial statin medication supply during the follow-up period.

Treatment simulation

To choose an optimal initial statin treatment plan for each patient, it is crucial to comprehend their potential outcomes of LDL-C reduction, SAS, and discontinuation for each of the 26 statin treatment plans. However, we can only obtain patient outcomes for their actual prescription using observational data. To predict patient outcomes for the statin treatments that they have never taken, we explored predictive machine learning models to predict potential outcomes for each treatment in our previous study. Specifically, in our previous study, we trained a feed-forward neural network ( $70x10x2$ ) with early stopping using patient’s actual statin prescription as one of the identified predictors (70 in previous study). During testing, we predicted patient potential outcomes (SAS and discontinuation) under each treatment by generating copies of patients predictors and cycling through all possible statin treatment options (27 in previous study) as input for each patient. However, we found that pure prediction models can suffer from confounding bias, which can distort treatment estimations for a patient whose potential treatments were not observed. To address this issue, in this study, we used a counterfactual prediction framework – Generalized Overlap Weights Using Propensity Scores. This approach is inspired by inverse probability weighting ¹¹ and aims to mitigate the potential bias that can arise from confounding factors in observational data using weighted regression models. In brief, the Generalized Overlap Weights Using Propensity Scores framework creates a balanced pseudo-population by weighting the original cohort by some weights before predicting patient potential outcomes across different treatment cohorts.

To apply our proposed framework, we first computed propensity scores for our study cohort for each of the 26 statin treatment plans (i.e. 26 propensity scores were calculated for each patient) using a feed-forward neural network with two hidden layers ( $78\times 156$ ). These propensity scores indicate the probability of a patient being treated with a particular statin treatment plan. Then, overlap weights were calculated for each patient under each of the 26 statin treatment plans using the method proposed by Li et al. ¹²

$${\mathrm{overlap}\mathrm{weights}}_{\mathrm{t}}=\frac{{\left({\sum }_{t=1}^T\frac{1}{{propensityscore}_t}\right)}^{-1}}{{propensityscore}_t}$$

where t represents the 26 statin treatment plans.

These overlap weights are essential in creating a balanced pseudo-population. A larger overlap weight represents lower certainty of being assigned to the particular treatment plan (i.e. under-represented cohort in our original population) while a smaller overlap weight represents higher certainty of being assigned to the particular treatment plan (i.e. over-represented cohort in our original population). With these 26 overlap weights for each patient, we predicted patient potential outcomes for LDL-C reduction, SAS, and discontinuation using regression models with overlap weights as sample weights for each statin treatment plan during training. Recall that both SAS and discontinuation were both binary variables; therefore, logistic regression models were trained among patients who took the particular statin treatment plan from observational data. Since LDL-C reduction is a continuous variable that represents the percentage of reduction, a linear regression model was chosen for this outcome variable. However, linear regression models do not have any boundaries in predicted values. Therefore, it can easily produce values that are out of bound (i.e. a percentage of reduction that is more than 100%). To solve this extreme extrapolation, we used an L1-regularization technique, the Least Absolute Shrinkage and Selection Operator (LASSO).

After fitting the outcome regression models, we simulated patient potential outcomes for each of the 26 statin treatment plans. This resulted in a final schedule of outcomes for LDL-C reduction, SAS, and discontinuation under 26 statin treatment plans for all patients.

Multi-objective optimization

In Step 2, three target outcomes under 26 statin treatment plans for each patient were simulated. To choose an optimal initial statin treatment plan that can maximize LDL-C reduction while minimizing SAS and discontinuation (i.e. PSTP), we used a multi-objective optimization approach to optimize three objectives simultaneously: (1) maximize LDL-C reduction, (2) minimize SAS risk, and (3) minimize discontinuation risk. In this study, we adopted the Technique for Order of Preference by Similarity to the Ideal Solution (TOPSIS). ¹³ Using this technique, the chosen optimal solution would have the smallest Euclidean distance from the ideal solution and the largest Euclidean distance from the worst solution. The ideal solution is as the name suggested, an ideal combination of the best outcomes from each objective while the worst solution is a combination of the worst outcomes from each objective. In other words, the chosen optimal solution tries to achieve the best outcomes in each objective while avoiding the worst outcomes.

As a proof-of-concept, we have chosen equal weights for all three objectives (LDL-C reduction, SAS, and discontinuation) with TOPSIS when choosing the optimal initial statin treatment plan (i.e. PSTP) for each patient. The weights used in TOPSIS represented the importance of each objective in the optimization problem. Therefore, one could adjust the weights to create a patient-centered solution, with a restricted condition that the weights add up to 1.

Decision rules generation

In the last step, we achieved individual optimization (PSTP) using a multi-objective optimization approach, TOPSIS. We recognize that our individual optimization approach in this study is more transparent than our previous PSTP approach, in which regression models are generally more translatable than neural networks. However, the clinical interpretation of 78 (three target outcome models for 26 statin treatment plans) weighted regression models on top of the multi-objective optimization technique is still not straightforward. Therefore, in this step, we aimed to further improve the clinical interpretability and optimize statin treatment for subpopulations by generating compact and simple rules that can lead to an optimal or near-optimal statin treatment assignment.

To identify the largest subpopulation that benefits from these rules, an impurity function, the Gini index was used to construct a classification decision tree to indicate which subpopulation can benefit most (while minimizing risks) from a particular treatment plan. A common decision tree is usually built top-down, that is, it starts from a root node that represents the first split that can best separate the classes (i.e. the predictor that has the lowest impurity). For each split, two paths will be created: the left and right paths. The final predicted class resides in the leaf nodes that can be traced down through the left or the right path, where every other split during the path is called a splitting node. In our study, the classes (response variable) in the classification tree were the chosen PSTP in Step 3 while the predictors were the 80 previously identified patient baseline characteristics. In other words, the cohorts that reside in the leaf nodes represent the subpopulations where the majority class represents the best statin treatment plan for that subpopulation. Therefore, the decision rules for the statin treatment plan (DRST) can be generated by following the paths from the root node to the leaf nodes. If two statin treatment plans hold the same votes, one of the statin treatment plans would be randomly assigned to the subpopulation.

To achieve the DRST, we first split our dataset into training and testing datasets in an 80:20 ratio and stratified by class. Then, we used the rpart package ¹⁴ in R version 4.2.1 to build a multiclass classification decision tree using our training dataset. The rpart (Recursive Partitioning) algorithm uses the traditional approach described above, a greedy, top-down approach. Briefly, it uses the entire training dataset and evaluates every feature (i.e. the 80 previously identified patient baseline characteristics) to find the best feature (i.e. the feature that can best minimize the impurity function) to split from the root node until termination. In our study, the impurity function is set as the Gini index and the termination criteria are set as 0% impurity, that is, when all leaf nodes are perfectly classified. In other words, the decision tree was first grown to perfect classification using the Gini index. Then, a postpruning method, called cost-complexity pruning was adopted to avoid overfitting. The optimal complexity parameter (cp) was set at 0.015 as it resulted in the least cross-validation error (Supplemental Figure 1). The other hyperparameters were set to default. Once the final decision tree was generated, we summarized the multiclass classification accuracy across training and testing datasets. We also visualized the final decision tree using the dtreeviz package ¹⁵ in Python version 3.9.16.

Clinical trial simulation

We have shown our proposed DRST pipeline from Steps 1–4. To understand the efficacy of DRST on the general population, a traditional approach is to conduct a randomized controlled trial against the current standard of care or randomization. However, conducting a randomized clinical trial is an expensive and time-consuming process, and before running a clinical trial, analyzing the benefits and risks is a crucial step. A clinical trial simulation is an alternative approach to a randomized clinical trial as it mimics the process and provides a close estimate of its benefits and risks. In this study, to evaluate the efficacy of the decision rules, we employed a clinical trial simulation framework. Five treatment arms were considered representing five different statin treatment assignment strategies: randomization, standard of care, clinical guidelines, PSTP, and DRST. These treatment assignment strategies vary in the amount of knowledge about patient baseline characteristics: randomization assumed an equal chance of getting 1 of the 26 statin treatment plans and randomly chose a statin treatment plan for each patient. We expected randomization to have the worst performance and this treatment assignment strategy served as the lower-bound reference point for performance; standard of care represented statin treatment plans that were actually prescribed to patients from the observational data; clinical guidelines assigned a random statin treatment within the recommended statin intensity based on the 2013 ACC/AHA Guideline (Supplemental Figure 2); PSTP assigned the best statin treatment plan tailored to each patient and served as the upper-bound reference point for performance; and DRST used subpopulation characteristics to assign the best statin treatment plan.

All patients were assigned to five treatment arms. This resembles the cross-over design. Then, we used the schedules of simulated outcomes from Step 2 to estimate potential patient target outcomes in LDL-C reduction, SAS, and discontinuation for each treatment arm. The average treatment effects under each treatment arm were summarized and a Tukey’s Honest Significant Difference (HSD) test was conducted to identify if the differences in means between the two treatment arms were statistically significant. To understand which subpopulation benefited most from our proposed DRST pipeline, the average treatment effects of each treatment arm were also summarized at each decision node.

Results

This study included a total of 107,739 patients and patient baseline characteristics were summarized in Table 1. The average age of our study cohort was 59 years old. The proportion of females was equal to that of males. While half of our study cohort had missing values in race, the majority of the patients were White (33%), followed by an equal number of Blacks (7%) and Hispanics (7%), then the least, Asians (2%). Our study cohort consisted of most patients with diabetes as defined in the 2013 ACC/AHA Guideline (48%), followed by patients with ASCVD (36%), patients who have high LDL-C levels (14%), and the least patients with high ASCVD risks (2%). The average Charlson comorbidity score was 0.28 while the average LDL-C was 141.17 mg/dL.

Table 1.

Patient baseline characteristics.

	Study cohort (107,739)
Age	58.86 ± 10.86
Females	55,114 (0.51)
Race
White	35,134 (0.33)
Black	7142 (0.07)
Asian	2157 (0.02)
Hispanic	7377 (0.07)
2013 ACC/AHA guidelines benefit groups
ASCVD	39,075 (0.36)
High-LDL	14,869 (0.14)
Diabetic	51,472 (0.48)
High ASCVD risk	2323 (0.02)
Charlson score	0.28 ± 0.67
Blood pressure – systolic	129.25 ± 18.15
Low-density lipoprotein cholesterol (LDL-C)	141.17 ± 44.23
High-density lipoprotein cholesterol (HDL-C)	52.52 ± 25.46
Total cholesterol	210.19 ± 53.81

ASCVD: atherosclerotic cardiovascular disease.

Patient baseline characteristics at the end of the pseudo-immortal-time period are summarized in either as number of patients, n (%) or mean ± standard deviation.

DRST

Figure 2 shows the decision rules generated for statin treatments (DRST). In total, 86,191 patient data were used to train the decision tree model and 21,548 patient data were included in testing. The training and testing accuracy was 76.987 and 76.986% respectively. The resulting decision tree for DRST was relatively small with a maximum depth of 3 and only 11 nodes. Three variables were chosen as splitting nodes: patient age at index, three-month average LDL-C before the index, and age-adjusted Charlson score before the index. Following the paths from DRST, we also identified six subpopulations: (1) patients aged ⩽ 59 years old who have an LDL-C value ⩽ 141.63 mg/dL in Node 2; (2) patients aged ⩽ 59 years old who have an LDL-C value > 141.63 mg/dL and age-adjusted Charlson score ⩽ 0.5 in Node 4; (3) patients aged ⩽ 59 years old who have an LDL-C value > 141.63 mg/dL and age-adjusted Charlson score > 0.5 in Node 5; (4) patients aged > 59 years old who have an LDL-C value ⩽ 81.90 mg/dL in Node 7; (5) patients aged > 59 years old who have an LDL-C value between 81.91 and 187.58 mg/dL in Node 9; and (6) patients aged > 59 years old who have an LDL-C value > 187.58 mg/dL in Node 10. Their optimal treatment plans that maximized LDL-C reduction while minimizing SAS and discontinuation were represented in the six leaf nodes: (1) simvastatin 20 mg and ezetimibe 10 mg in Node 2 (23.3%); (2) pitavastatin calcium 2 mg in Node 4 (11.1%); (3) rosuvastatin calcium 40 mg in Node 5 (17.8%); (4) simvastatin 5 mg in Node 7 (5.5%); (5) Simvastatin 10 mg and ezetimibe 10 mg in Node 9 (37.6%); and (6) rosuvastatin calcium 20 mg in Node 10 (4.7%).

Figure 2.

DRST. This figure illustrates the decision tree generated for DRST. There are 11 nodes that are labeled from Node 0 to Node 10 where Node 0 is the root node. At each splitting node (Nodes 0, 1, 3, 6, 8), one of the three patient baseline characteristics is chosen and its distribution is shown in a scatter plot: patient age at the index (age), three-month average LDL-C before the index (ldl_pre), and age-adjusted Charlson score before the index (dchar_score_age). The x-axis of the distribution scatter plots represents the value range of the chosen patient baseline characteristics (age, ldl_pre, or dchar_score_age) while the y-axis represents the statin treatment plans. The different statin treatment plans are also represented in different colors. By following the splitting criteria on the left or right paths of the splitting nodes, six identified subpopulations can be found in the six leaf nodes (Nodes 2, 4, 5, 7, 9, and 10). The pie charts at the leaf nodes represent the distribution of the recommended statin treatment plans from the PSTP strategy. The majority votes are displayed underneath each of the pie charts and they represent the six optimal statin treatment plans that can maximize the benefits of LDL-C reduction and minimize the risks of SAS and discontinuation for each of the identified subpopulations, respectively.

Clinical trial simulation

Recall that the decision tree generated for DRST used the statin treatment plan chosen for PSTP for each patient as response variables. Out of the available 26 statin treatment plans, only 18 of them remained under the recommendation PSTP. Out of these 18 recommended PSTP statin treatment plans, only six statin treatment plans remained in DRST. Figure 3 shows the statin treatment distribution under DRST compared to other treatment assignment strategies: standard of care, clinical guidelines, and PSTP. DRST followed the statin treatment distribution under PSTP very closely for six of the majority of treatment options but omitted the other 12 treatment options. The standard of care showed that atorvastatin was the most popular statin drug while fluvastatin and pitavastatin were not frequently prescribed. However, clinical guidelines assigned statin treatment plans evenly across moderate- and high-intensity statins, respectively.

Figure 3.

Statin treatment distribution across statin treatment assignment strategies. This is a Sankey diagram from four statin treatment assignment strategies to 26 statin treatment plans. The four nodes on the left represented four statin treatment assignment strategies: standard of care, clinical guidelines, PSTP, and DRST. The 26 nodes on the right represented 26 different statin drug-dose combinations (i.e. statin treatment plans). The thickness of the paths from left to right nodes represented the number of patients assigned to the particular statin treatment plan under the particular statin treatment assignment strategy.

Table 2 shows the average treatment effects under five different statin treatment strategies. As expected, PSTP performed the best across three targeted outcomes in our simulations: 31.51% in LDL-C reduction, 45.64% in SAS risk, and 55.10% in discontinuation risk. The second-best treatment strategy was DRST. Its performance was almost similar to PSTP with only less than 0.6 percentage point (pp) in difference: 0.53 pp (95% CI = [0.38, 0.69]) less in LDL-C reduction, 0.16 (95% CI = [0.05, 0.27]) less in SAS risk, and 0.28 pp (95% CI = [0.13, 0.43]) more in discontinuation risk. Compared to the standard of care, DRST improved LDL-C reduction by 4.15 pp (95% CI = [4.00, 4.31]) while reducing SAS risk by 11.71 pp (95% CI =[11.60, 11.82]) and discontinuation risk by 3.96 pp (95% CI = [3.81, 4.11]). However, our clinical trial simulation also showed that the clinical guidelines can improve patients’ LDL-C reduction by 1.64 pp (95% CI = [1.48, 1.78]) and SAS risk by 1.69 pp (95% CI = [1.58, 1.80]), but worsen discontinuation risk of the standard of care by 4.28 pp (95% CI = [4.13, 4.42]). In summary, both PSTP and DRST have significantly higher LDL-reduction benefits and lower SAS and discontinuation risks. The differences in all pairwise comparisons of the two treatment strategies are all statistically significant under Tukey’s HSD test (Figure 4). Note that the differences between PSTP and DRST were marginally close to the significance level, while the differences between DRST (or PSTP) and other treatment assignment strategies were the furthest away from the significance level.

Table 2.

Average treatment effects under clinical trial simulation.

	LDL-C reduction (%)	SAS risk (%)	Discontinuation risk (%)
Randomization	25.06 ± 13.75	57.69 ± 10.40	60.82 ± 11.59
Standard of care	26.83 ± 14.35	57.19 ± 5.77	59.34 ± 9.64
Clinical guidelines	28.47 ± 14.82	55.50 ± 9.60	63.62 ± 11.82
Personalized statin treatment plan (PSTP)	31.51 ± 10.97	45.64 ± 10.40	55.10 ± 14.32
Decision rules for statin treatment (DRST)	30.98 ± 11.11	45.48 ± 10.16	55.38 ± 14.36

The columns represent three target outcomes of this study: LDL-C reduction in percentage, SAS risk, and discontinuation risk. The rows represent the five statin treatment assignment strategies identified in the clinical trial simulation framework. The average treatment effects and standard deviation are summarized in each cell (mean ± standard deviation).

Figure 4.

Differences in means from Tukey’s HSD test. This diagram shows the result of the pairwise comparison testing from the Tukey’s HSD test. The three subplots (rows) represent the confidence interval plots for three target outcomes: LDL-C reduction in percentage, SAS risk, and discontinuation risk. The confidence interval plots show the 95% confidence intervals and the average differences in mean levels between the pairwise comparison testing between two of the five statin treatment assignment strategies: DRST, clinical guidelines, PSTP, randomization, and standard of care. The x-axis represents the values in differences in mean levels. The significance level centered at 0 is plotted as a vertical dotted line in each subplot. The further away the intervals are from the significance level, the more significant the pairwise comparison result is (P < 0.05).

In addition to computing the overall average treatment effects, treatment effects for each identified subpopulation (nodes of the final decision tree) were also summarized. Figure 5 shows the classification accuracy of the decision tree, the average treatment effects in LDL-C reduction, SAS risk, and discontinuation risk under five different treatment assignment strategies for each node (Figure 2). Randomization, standard of care, and clinical guidelines performed similarly in the treatment effects of LDL-C reduction, SAS, and discontinuation across all nodes. Meanwhile, PSTP produced the best outcomes in all three target outcomes in all nodes: highest LDL-C reduction, lowest SAS risk, and lowest discontinuation risk. DRST also achieved similar outcomes as PSTP in some nodes but worse in others due to the tradeoff among the three target outcomes.

Figure 5.

Performance across decision tree node. Four subplots (rows) represent the average LDL-C reduction in percentage, SAS risk, discontinuation risk, and the multi-class classification accuracy under DRST at each decision tree node. Five bars are plotted in different colors to represent five statin treatment assignment strategies in the first three subplots. The x-axis represents the decision tree nodes that were identified in Figure 2. Node 0 is the root node, Nodes 2, 4, 5, 7, 9, and 10 are leaf nodes while the others are splitting nodes. The y-axis represents the average LDL-C reduction, SAS risk, discontinuation risk, and accuracy of the decision tree, respectively.

Recall that Nodes 2, 4, 5, 7, 9, and 10 were the leaf nodes that represented the six subpopulation we have identified under DRST. All leaf nodes had higher classification accuracy than the splitting nodes, except for Node 10 – patients who were aged more than 59 years old and had a three-month average LDL-C before the index of more than 187.58 mg/dL. Despite its low accuracy of 49.7% for the subpopulation at Node 10, DRST still performed better than other treatment assignment strategies (aside from PSTP) in the average LDL-C reduction and SAS: The subpopulation in Node 10 had an average LDL-C reduction of 47.8% under DRST, which was only slightly lower than PSTP but higher than the other treatment assignment strategies. Also, the average SAS risk in Node 10 was 49.2%, which was 11.6% higher than PSTP but lower than the other treatment assignment strategies. However, with a 70.6% accuracy at Node 2, the DRST produced LDL-C reduction outcome that was completely up to par with PSTP reaching 30.3% but did not outperform randomization, standard of care, and clinical guidelines in SAS and discontinuation risk. Similarly, DRST achieved SAS and discontinuation risks that were on par with PSTP but suffered some loss in LDL-C reduction in Node 4. Interestingly, all statin treatment assignment strategies had the lowest LDL-C reduction in Node 7 – patients who were aged more than 59 years old and had a three-month average LDL-C before index less than 81.90 mg/dL indicating this subpopulation had a relatively low LDL-C at baseline. However, this subpopulation was able to achieve the lowest discontinuation risks under both PSTP and DRST.

Discussion

Our study aimed to generate a set of decision-support rules to improve the transparency and clinical usability of our previous PSTP approach ⁸ with minimal compromise to the maximal benefit-to-risk ratio of statin treatment plans. To identify the subpopulation that can benefit the most (maximal LDL-C reduction) from a particular statin treatment plan while avoiding the risks the most (minimal SAS and discontinuation), we built on our other previous works^16,17 and proposed a five-step DRST pipeline to choose the optimal initial statin treatment plan: Steps 1–3 of our proposed pipeline produced a knowledge base that optimizes individual statin treatment benefit-to-risk ratio (PSTP), Step 4 used a decision tree model (DRST) to summarize our treatment simulation and multi-objective optimization framework (Steps 1–3), and Step 5 aimed to evaluate the efficacy of these decision rules by conducting a clinical trial simulation. This study not only improved the previous PSTP approach by accounting for the confounding bias but also provided simple rules for statin treatment plans for statin benefit groups identified by the 2013 ACC/AHA Guideline. The resulting decision rules were compact and efficient. It only used three patient variables that can be easily obtained at the point of care: patient age at the visit, three-month average LDL-C before the visit, and age-adjusted Charlson score before the visit. These rules resulted from a well-generalized decision tree with only 11 nodes and a maximum depth of 3. The DRST also produced treatment effects that were only less than 0.6 pp suboptimal to PSTP across all of the three target outcomes (LDL-C reduction, SAS, and discontinuation). These results from our study demonstrated the feasibility of generating a concise yet effective set of DRST.

In our study, we found that all differences in mean levels of any combination of two treatment strategies were statistically significant under the Tukey’s HSD test (Figure 4). This is due to our relatively large sample size (107,739 per arm). However, not all were clinically significant. For instance, the differences in means between PSTP and DRST were the smallest across all comparisons for all three target outcomes. In fact, we found that the differences between PSTP and DRST were marginally close to the significance level, indicating that the significance was weaker compared to the others. However, the differences between DRST (or PSTP) and other treatment strategies were the furthest away from the significance level, indicating that these improvements in means that resulted from DRST were stronger in significance. Furthermore, we found that the statin treatment assignments under DRST closely mirrored those of PSTP for the majority of treatments under PSTP (Figure 3). Specifically, the DRST considered the major six statin treatment plans identified by the PSTP. A sensitivity analysis revealed that these major six statin treatment plans existed as one of the Pareto optimal solutions to the other statin treatment plans. A Pareto optimal solution is a solution that is not worse than the other solutions, that is, the solution cannot do better in all objectives. Recall that our multi-objective optimization framework chose a statin treatment plan that can equally optimize three targeted outcomes. Therefore, there existed other Pareto solutions (i.e. DRST, when DRST is not the same as PSTP) that can do better in some outcomes but worse in others when compared to the PSTP. For instance, a solution that can reduce SAS and discontinuation risk better than PSTP but cannot optimize LDL-C reduction as much as PSTP might exist. In this case, the DRST treatment strategy was able to identify the exact Pareto optimal solution among these major six statin treatment plans (Supplemental Figure 3). All in all, these results showed that DRST can mirror the PSTP treatment strategy or choose a Pareto optimal treatment plan for patients. As a result, DRST was able to achieve similar average treatment effects in three target outcomes as PSTP.

Interestingly, no patients were assigned atorvastatin under DRST while only a small fraction of patients were recommended atorvastatin under PSTP. Since the proportion of the patients taking atorvastatin under PSTP was small, naturally DRST did not further split to correctly classify these patients to avoid overfitting. However, the rare assignment of atorvastatin under PSTP was unexpected since it was a popular statin treatment. We further investigated in a sensitivity analysis by prioritizing discontinuation in multi-objective optimization (i.e. assigned a weight of 1 to discontinuation and 0 for SAS and LDL-C reduction). The sensitivity analysis revealed that atorvastatin was the least preferred in minimizing the risks of discontinuation. In fact, no patients were assigned atorvastatin when discontinuation was prioritized in multi-objective optimization (i.e. PSTP). Patients may discontinue the higher-intensity statin treatment, atorvastatin due to the occurrence of SAS or fear of developing side effects. A recent N-of-1 trial found that in patients who discontinued statin treatments due to side effects, 90% of the muscle symptoms were caused by negative expectations. ¹⁸ This is known as the nocebo effect. However, identifying who will experience the nocebo effect is challenging as it is highly dependent on factors that are difficult to capture and rarely exist in the EHRs: patient perceptions, exposures, or suggestions of the dose of the exposure that they receive. ¹⁹ In our study, we tried to account for the nocebo effect risk factors by including patient clinical risk factors. In contrast, less than 1% of the actual prescription was simvastatin 5 mg but it was found to be an optimal drug for most patients in prioritizing discontinuation and SAS prevention for patients who have low LDL-C levels (i.e. LDL-C less than 100 mg/dL) – Node 7 in DRST. As simvastatin 5 mg is a low-intensity and low-dose statin, it is commonly used to wean down statin side effects, and hence rarely prescribed as the initial statin prescription. Our simulation suggested that simvastatin 5 mg may have enough effect for patients with relatively lower LDL-C and may be used as an initial statin prescription.

Our study also showed that the average treatment effects under clinical guidelines were similar to that of the standard of care and randomization. This was due to the imbalance options in moderate-intensity statin treatment plans. The clinical guidelines only recommended either moderate- or high-intensity statins while the number of available moderate-intensity statins doubled the number of low- and high-intensity statins. Therefore, a moderate-intensity statin would be chosen with a higher chance. Similarly, a random choice under randomization or clinician prescription would most likely be a moderate-intensity statin, specifically atorvastatin, given its popularity. It is possible that the average treatment effects under these three treatment assignment strategies would converge to the same average. Meanwhile, DRST suggested six statin treatment plans that cover low-, moderate-, and high-intensity statins and recommended different intensity statins to different subpopulations accordingly. Furthermore, the three patient variables (age, LDL-C values, and comorbidity score) that were used in the DRST are very similar to the risk factors that were used in the clinical guidelines (age, history of ASCVD, LDL-C values, history of diabetes, and the ASCVD risk score). The chosen comorbidity score, the age-adjusted Charlson score, considers 17 comorbidities including the indication of ASCVD and diabetes in the risk score calculation. However, more specific vital status or laboratory values that were included in the ASCVD risk score were not included in the age-adjusted Charlson score calculation. Recall that the goal of clinical guidelines is to maximize LDL-C reduction and DRST aims to balance both the risks and benefits of statins. Moreover, note that ASCVD risk was also included in the decision tree training process, but was not chosen. This might suggest that the 17 comorbidities might be indicative of the risks of discontinuation and SAS.

To the authors’ best knowledge, no studies have generated a set of data-driven decision-support rules for statin treatment plans. Nonetheless, this study had a few limitations: (1) This study used de-identified claims and EHR data within OLDW. With that in mind, only claims that were submitted to a single payor or medical records available to the internal EHR system were accessible to the authors. (2) Patient outcomes were simulated under the intent-to-treat principle. Any indication of SAS and LDL-C reduction might be influenced by other statin treatments if the patient discontinued their initial statin treatment and switched to another. To provide a better estimate, SAS and LDL-C reduction could be adjusted to account for the duration of the initial statin treatment only. (3) Patients without LDL-C values recorded before and after the index were excluded from this study. Our results might not generalize if there exists a systematic difference that causes missing values in LDL-C. (4) This study used a counterfactual framework to simulate patient potential outcomes for the other 25 statin treatment plan that the patient did not take. There are a few key assumptions for this framework, specifically the no unmeasured confounding assumption. If any confounding variables were absent from this study, the effect estimates of this study would be susceptible to bias. (5) Patients might report side effects from statin that were caused by the nocebo effect. The nocebo effect might have confounded statin discontinuation that might not be captured. However, this study included clinical information that might be risk factors of the nocebo effect. Other non-clinical risk factors such as exposure to negative statin information are not available to this study. Furthermore, this study only focused on objective adverse effects from statins that are less likely to occur due to nocebo effects, hence reported SAS was most likely caused by statin treatments. (6) Our clinical trial simulation framework assumed the most optimistic scenario where dropouts and drop-ins were assumed to be none. (7) Since the accuracy of the decision tree was not ideal, the resulting decision rules should be carefully examined before adopting them in clinical practice.