Abstract
Background
Single nucleotide polymorphisms in the human leukocyte antigen (HLA) region in both maternal and fetal genomes have been robustly associated with birthweight (BW) in previous genetic association studies. However, no study to date has partitioned the association between BW and classical HLA alleles into maternal and fetal components.
Methods
We used structural equation modelling (SEM) to estimate the maternal and fetal effects of classical HLA alleles on BW. Our SEM leverages the data structure of the UK Biobank (UKB), which includes ∼270 000 participants’ own BW and/or the BW of their firstborn child.
Results
We show via simulation that our model yields asymptotically unbiased estimates of the maternal and fetal allelic effects on BW and appropriate type I error rates, in contrast to simple regression models. Asymptotic power calculations show that we have sufficient power to detect moderate-sized maternal or fetal allelic effects of common HLA alleles on BW in the UKB. Applying our SEM to imputed classical HLA alleles and own and offspring BW from the UKB replicated the previously reported association at the HLA-C locus and revealed strong evidence for maternal (HLA-A*03:01, B*35:01, B*39:06, P <0.001) and fetal allelic effects (HLA-B*39:06, P <0.001) of non-HLA-C alleles on BW.
Conclusions
Our model yields asymptotically unbiased estimates, appropriate type I error rates and appreciable power to estimate maternal and fetal effects on BW. These novel allelic associations between BW and classical HLA alleles provide insight into the immunogenetics of fetal growth in utero.
Keywords: Genetic association, structural equation modelling, human leukocyte antigen, birthweight, UK Biobank
Key Messages.
We developed a new method to partition genetic effects at classical human leukocyte antigen (HLA) loci into maternal and fetal genetic components using structural equation modelling (SEM).
The SEM model leverages the data structure of the UK Biobank (UKB), which includes participants’ own birthweight (BW) and/or the BW of their firstborn child.
Our SEM model yields asymptotically unbiased estimates, appropriate type I error rates and appreciable power to estimate maternal and fetal effects on BW.
UKB analyses revealed strong evidence for maternal and fetal effects of multiple HLA alleles on BW which provide insight into the immunogenetics of fetal growth in utero.
Background
Birthweight (BW) is widely used as a cheap but imperfect measure of intrauterine growth and development.1,2 Both high and low BW infants are at increased risk of short- and long-term morbidities. Low BW infants are at increased risk of neonatal mortality3 and cardiometabolic diseases in later life,4 which in the latter’s case, might reflect ‘developmental programming’ as a consequence of an adverse intrauterine environment.5 In contrast, high BW infants (fetal macrosomia) are at increased risk of injury during birth (e.g. delivery shoulder dystocia, obstructive labour)6 and type 2 diabetes in later life.7
BW is a complex trait influenced by both maternal and fetal genetics and environmental factors.8 Large-scale genome-wide association studies (GWAS)8–13 have identified over 200 loci associated with BW, including single nucleotide polymorphisms (SNPs) in the human leukocyte antigen [HLA, also known as major histocompatibility complex(MHC)] region on the short arm of chromosome 6.8,12 The classical HLA antigens can be divided into HLA class I (HLA-A, B and C) and class II (HLA-DP, -DQ and -DR loci).14 This area of the genome exhibits extensive and complex patterns of linkage disequilibrium and contains a set of highly polymorphic genes that encode cell-surface antigens that play a key role in specific immunity, allograft rejection and the development of many immune-mediated and autoimmune diseases (reviewed in15). These results are interesting, given that epidemiological and immunological studies have suggested that both maternal and fetal immune systems play important roles in fetal growth and development.14,16–18
One complication with interpreting the results of genetic association studies of perinatal traits, is that it is often unclear whether specific genetic associations reflect an effect of the fetal genome, an effect of the maternal genome or some mixture of both.19 Insight into this question can sometimes be obtained by performing conditional genetic association analyses (i.e. where the effect of fetal genotype is conditioned on maternal genotype and vice versa) and/or haplotype analyses of genotyped mother-offspring pairs.12 A complication, however, is that worldwide there is a paucity of cohorts with large numbers of genotyped mother-offspring pairs, meaning that these sorts of analyses are often underpowered.20 In order to address this issue, Warrington et al. (2018) developed a structural equation model that was capable of partitioning genetic effects on BW into maternal and fetal components, using the large UK Biobank (UKB) resource.21 In the UKB, genotyped participants report their own BW and the BW of their first child (females only).22 Wu et al. (2021) further extended this statistical framework to estimate parental and fetal genetic effects using summary results statistics from GWAS conducted on own and offspring BW, simultaneously accounting for sample overlap and one generation of assortative mating.23 However, these models were derived for bi-allelic variants (mostly SNPs), whereas classical HLA genes are multi-allelic. Thus, an extension of the model is required to estimate maternal and fetal effects at multi-allelic classical HLA genes.
In this manuscript, we develop a novel structural equation model to estimate the maternal and fetal genetic effects of imputed HLA alleles on offspring outcomes. We define maternal genetic effects as the effect of a mother’s genotype on the phenotype of her offspring, independent of the offspring’s genotype. In other words, maternal genetic effects on the offspring phenotype are mediated through the maternal phenotype (in the case of BW, most likely some aspect of the intrauterine environment provided by the mother). In contrast, we define fetal genetic effects as the effect of the fetus’s own genotype on their own phenotype, independent of their mother’s genotype. We conducted a simulation study to assess the bias and the type I error rate of our model, and performed asymptotic power calculations to estimate the power to detect the allelic effects and partition them into maternal and fetal allelic effects. We subsequently applied our structural equation modelling (SEM) to data from the UKB to estimate the maternal and fetal genetic effects of classical HLA alleles on BW.
Methods
Structural equation modelling
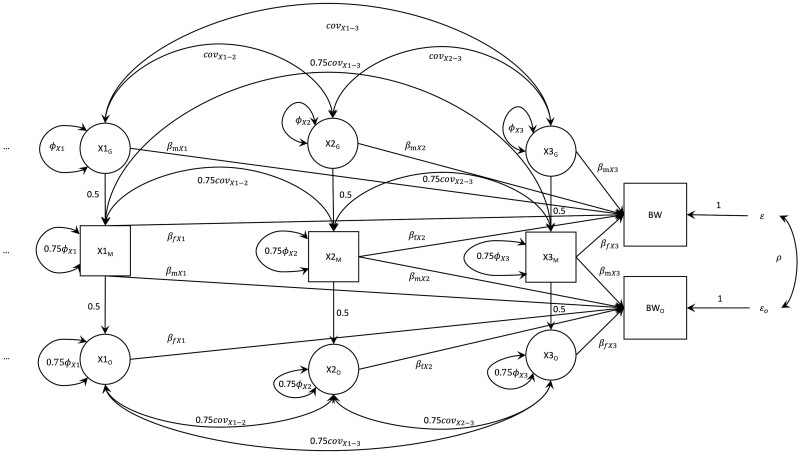
Structural equation modelling (SEM), with its ability to model the relationship between latent and observed variables, provides a natural framework for investigating the association between maternal and fetal genotypes and perinatal phenotypes.24 We illustrate the SEM we developed to estimate maternal and fetal genetic effects on BW at classical HLA alleles in the form of a path diagram in Figure 1 (see Supplementary Note 1, available as Supplementary data at IJE online for further details). To simplify explication, we assume the locus contains only four hypothetical alleles (here HLA-X0, HLA-X1, HLA-X2, HLA-X3;Figure 1) in the fictitious HLA-X gene (we use ‘HLA-X’ to avoid confusion with real HLA genes), although the model can be generalized, at least in theory, to an arbitrary number of alleles. We set the most common allele, here the HLA-X0 allele, as the ‘baseline’, and it is hence not included in the SEM to avoid collinearity. The model contains both observed variables (represented by squares in the path diagram) and latent variables (represented by circles in the path diagram). The two observed phenotypic variables are the self-reported BW of the individual (BW) and the self-reported BW of their first offspring in the case of women in the UKB (BWO). The three observed genetic variables are X1M, X2M and X3M, which represent the number of copies of each of these HLA alleles that each individual carries (the ‘M’ subscript referring to the mothers in the SEM in Figure 1). The rest of the variables are modelled as latent variables. We estimate the maternal and fetal effects of all the alleles at one locus simultaneously and the covariances across all the allele counts. However, in a more realistic scenario, not every individual reports both phenotypes (i.e. they report only BW or BWO). In order to include the maximum amount of data to optimize power, we also simultaneously modelled individuals who failed to report either their own or their offspring’s BW (Supplementary Figure S1, available as Supplementary data at IJE online). The details of model identification are described in Supplementary Note 2 (Supplementary Figure S6, available as Supplementary data at IJE online). The model was written and fitted using the OpenMx package25 (version 2.19.8) in R (version 3.6.3; the R script for conducting analysis using our model is provided in Supplementary Note 13, available as Supplementary data at IJE online).
Figure 1.
Structural equation model used for the analysis of multi-allelic human leukocyte antigen markers and birthweight (BW). Latent variables are represented by circles, observed variables by square boxes. Causal paths are indicated by unidirectional arrows, bidirectional arrows represent covariances. In order to illustrate the model, we use the fictional example of the human leukocyte antigen (HLA)-X gene. We assume there are only four alleles in the HLA-X gene (here HLA-X0, HLA-X1, HLA-X2, HLA-X3), although the model is generalizable to an arbitrary number of alleles (represented by the ellipsis ‘…’ on the left-hand side of the path model). The HLA-X0 allele is modelled as the ‘baseline’ allele (so all effects are modelled as displacements from this baseline allele), and hence is not shown in the diagram. The X1, X2 and X3 variables represent the number of copies of each of these HLA alleles that each individual carries. The ‘G’, ‘M’ and ‘O’ subscripts index alleles in the grandmaternal (latent), maternal (observed) and offspring (latent) generation respectively. The ‘m’ and ‘f’ subscripts of the path coefficients represent maternal and fetal allelic effects, respectively. The five observed variables, displayed in squares, in the analysis are: (i) the self-reported birthweight of the individual (BW) in the UKB; (ii) the self-reported BW of their first offspring (in the case of women only) in the UK Biobank (BWO); and (iii) the number of copies of the HLA-X1 (X1M), HLA-X2 (X2M) and HLA-X3 (X3M) alleles. The latent variables, displayed in circles, in the analysis are: (i) the number of copies of the relevant allele carried by the individual's mother (i.e. X1G, X2G and X3G); and (ii) the number of copies of the relevant allele carried by the individual's offspring (X1O, X2O and X3O). The variance of the allele counts in the grandmaternal (X1G, X2G, X3G), maternal (X1M, X2M, X3M) and offspring (X1O, X2O, X3O) generations are estimated as ΦX1, ΦX2 and ΦX3, respectively, and are assumed not to change across generations [i.e. variance (XG) = Φ, variance (XM) = 0.75Φ + 0.25Φ = Φ and variance (XO) = 0.75Φ + 0.25Φ = Φ)] The covariances between the different allele counts are also estimated (e.g. covX1-2, covX1-3, covX2-3) and assumed not to vary across generations [e.g. covariance (X1G, X2G) = covX1-2, covariance (X1M, X2M) = 0.75 covX1-2 + 0.25 covX1-2 = covX1-2, and covariance (X1O, X2O) = 0.75 covX1-2 + 0.25 covX1-2 = covX1-2]. The βmX1, βfX1, βmX2, βfX2, βmX3 and βfX3 are path coefficients that quantify the maternal and fetal allelic effects of each allele on BW, respectively. The residual error terms for the BW of the individual and their offspring are represented by ɛ and ɛo respectively, and the variance of both of these terms is estimated in the structural equation model. The estimated covariance between residual genetic and environmental sources of variation on BW is represented by ρ
Simulations to assess bias and type I error
We performed simulations to investigate the accuracy of our SEM to estimate both maternal and fetal effects on BW. For each scenario, we generated 1000 replicates where we analysed 80 000 genotyped individuals who had simulated phenotypic data for their own BW and the BW of their offspring. For each replicate, we generated HLA alleles for the three generations of individuals at a single locus (i.e. even though only the HLA alleles of the individual in the middle generation were modelled as an observed variable in the analysis). The variances of each allele were standardized to unit variance. The details of the simulation are described in Supplementary Note 38,26 (Supplementary Table S1, available as Supplementary data at IJE online).
Asymptotic power calculations
We also performed asymptotic power calculations using the OpenMx package (version 2.19.8 in R (version 3.6.3). We calculated the power assuming individuals with complete data (N = 80 000). In addition, we also calculated power when individuals only reported their own or their offspring’s BW. We assumed 100 000 individuals who only reported their own BW, 80 000 mothers who only reported the BW of their firstborn and 80 000 individuals who reported both (i.e. similar numbers of individuals as in the UKB). We fitted an SEM that included additional structures for individuals who only reported their own or their offspring’s BW (Supplementary Figure S1, available as Supplementary data at IJE online). The details of the power calculations are described in Supplementary Note 4.20
Application of SEM to BW data in the UK Biobank
The UK Biobank (UKB) Study is a study of over 500 000 volunteers (with 5.45% response rate of those invited27) recruited from across the UK at age 40–69 years between 2006 and 2010, with a broad range of health-related information and genome-wide genetic data.28
After a series of stringent procedures of data cleaning, 105 121 unrelated European individuals who only reported their own BW, 82 445 mothers who reported only the BW of their firstborn and 85 757 mothers who reported both were retained for subsequent analyses (Supplementary Figures S2 and S3, available as Supplementary data at IJE online; see Supplementary Note 5, available as Supplementary data at IJE online for the details of data cleaning22,28–31). Z-scores of individuals’ own BW and the BW of their first child were then generated and used for subsequent analyses. The top four principal components were included in the SEM as definition variables (Supplementary Note 9, available as Supplementary data at IJE online), which were regressed on both BW measurements and each HLA allele.
We fitted our SEM to UKB self-reported BW, offspring BW and allelic status at 11 classical imputed HLA loci (HLA-A, HLA-B, HLA-C, HLA-DRB1, HLA-DRB3, HLA-DRB4, HLA-DRB5, HLA-DQB1, HLA-DQA1, HLA-DPB1 and HLA-DPA1 (Supplementary Table S5, available as Supplementary data at IJE online) using the OpenMx package in R (version 3.6.3). For each HLA gene, alleles with a frequency lower than 0.5% across studied participants from UK Biobank were collapsed together into a single category (denoted as ‘Other’ allele, e.g. A*Other). In other words, using this coding, individuals could carry zero, one or two rare alleles at a given HLA gene.
In addition to one degree of freedom tests where we evaluated the significance of the maternal and fetal components individually, we also compared the full model with a constrained model in which we fixed the maternal and fetal effects of the allele of interest to zero (i.e. a two degree of freedom test; Supplementary Note 6, Supplementary Table S6, available as Supplementary data at IJE online). We also conducted conditional analyses whereby we augmented our SEM by including genome-wide significant SNPs in the HLA region as observed variables in the model (Supplementary Note 7, Supplementary Figure S4, Supplementary Tables S6 and S8, available as Supplementary data at IJE online). We also performed analyses using a weighted linear model to compare with the results of SEM (Supplementary Note 8, Supplementary Table S9, available as Supplementary data at IJE online).
Results
Bias and type I error rate
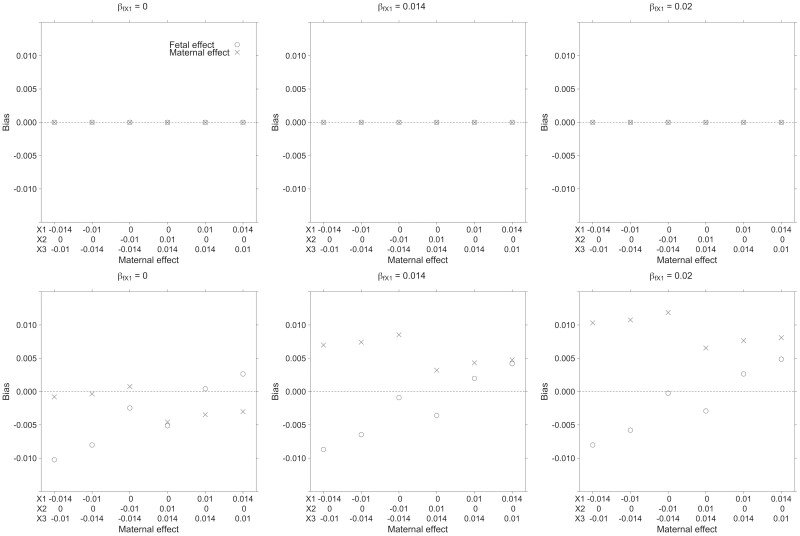
Figure 2 and Supplementary Table S1 (available as Supplementary data at IJE online) show the bias in estimating maternal and fetal allelic effects of the simulated HLA-X gene using linear regression or the SEM (results are shown for the HLA-X1 allele only, but other alleles show similar patterns). Our results suggest the SEM yields asymptotically unbiased estimates of maternal and fetal effects in contrast to ordinary least squares regression, which does not explicitly partition allelic effects into maternal and fetal components. Likewise, whereas the SEM produced well-calibrated type I error rates (≤5%) for tests of the estimated effects when the true effect size was set to zero, the type I error rates for linear regression could be inflated, e.g. when the true maternal effect was zero but fetal effects were present (or vice versa) (Supplementary Table S2, available as Supplementary data at IJE online).
Figure 2.
Simulation results showing bias in estimates of the maternal and fetal effect of the human leukocyte antigens X1 allele obtained using structural equation modelling (upper row) or ordinary least squares linear regression (lower row). The true fetal effect of human leukocyte antigen's (HLA)-X1 varies between the six panels (βfX1 = 0 left panels; βfX1 = 0.014 middle panels; βfX1 = 0.02 right panels—the fetal effects of other HLA-X alleles for each panel are listed in Supplementary Table S1, available as Supplementary data at IJE online). The effect of the maternal alleles (βmX1, βmX2, βmX3) varies across the x-axis. Across all conditions, the structural equation model returned unbiased estimates of the maternal and fetal effect size for HLA-X1 whereas ordinary least squares regression resulted in biased effect estimates. Similar patterns of results were observed for HLA-X alleles other than HLA-X1 (results not shown)
Asymptotic power calculation
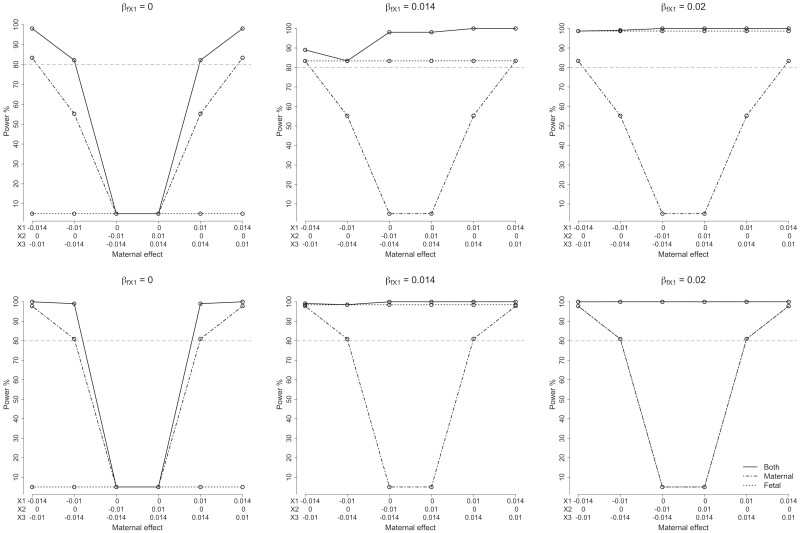
Figure 3 and Supplementary Table S3 (available as Supplementary data at IJE online) present asymptotic power to detect the effect of classical HLA alleles (i.e. a two degree of freedom test) and subsequently partition the allelic effect into maternal and fetal components (i.e. one degree of freedom tests) when the sample size is set to 80 000 mothers who report their own and their offspring’s phenotype (α = 0.05). We have excellent power (>80%) when the standardized effect of the allele of interest (HLA-X1; allele frequency = 0.1) is greater than 0.014 (the variances of all alleles have been standardized to unit variance). Even with a maternal standardized effect size as low as 0.01, the model still had >50% power to detect the partitioned maternal effect. As expected, the two degree of freedom test had more power (to detect any allelic effect at the locus) than the one degree of freedom maternal/fetal tests for all conditions we examined. The asymptotic power calculation is consistent with the results of simulation study (Supplementary Table S3, available as Supplementary data at IJE online). The addition of incomplete data (i.e. individuals who report only their own phenotype or alternatively their offspring’s phenotype, but not both) also increased power (Figure 3; Supplementary Table S4, available as Supplementary data at IJE online).
Figure 3.
Asymptotic power of the structural equation model. Power of the structural equation model to detect (i.e. a two degree of freedom test where both maternal and fetal components are set to zero) and partition the effects (one degree of freedom tests) of different combinations of underlying maternal and fetal effects (α = 0.05). The styles of the lines represent tests for fetal (dotted line), maternal (dot-dashed line) or both (solid line) components. Βm, maternal effect; βf, fetal effect. The horizontal dashed line shows the level for 80% power. The three plots on the upper row show power calculations for 80 000 samples with both own and offspring birthweight (BW). The three plots on the lower row show power calculations for 80 000 samples with both own and offspring BW, 100 000 samples with their own BW only and 80 000 samples with offspring BW only
Empirical analysis in UK biobank
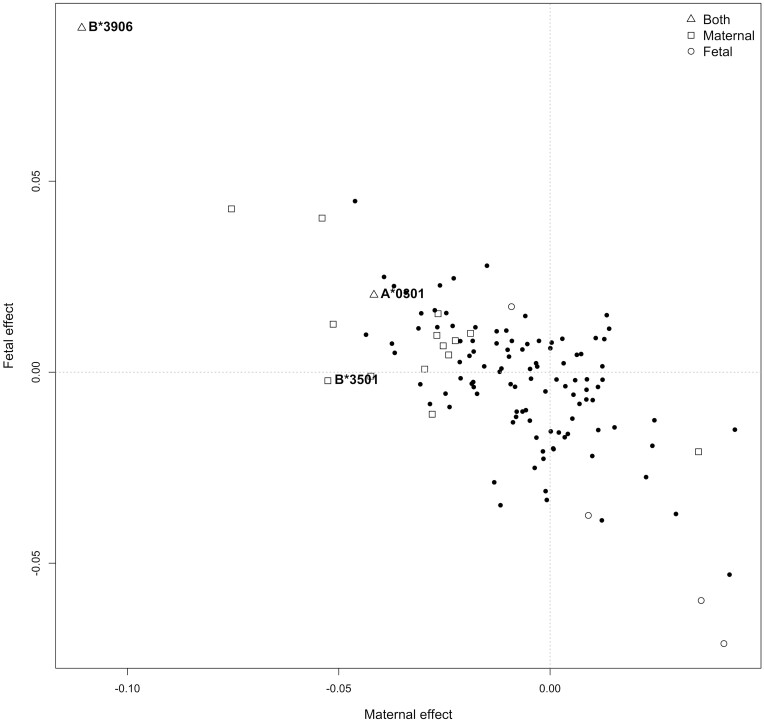
Figure 4 summarizes the results of partitioning the effects at HLA loci into maternal and fetal components in the UKB dataset. A total of 19 HLA alleles had nominally significant maternal and/or fetal effects on BW (P <0.05; Supplementary Table S7, available as Supplementary data at IJE online); 13 of the 19 alleles had evidence for a maternal effect only, four alleles primarily had evidence for a fetal effect only and two alleles had evidence of both. We further set a more stringent threshold for significance using Bonferroni correction for 50 tests (α = 0.05/50 = 0.001), on the rationale that the locus with the most coded alleles (HLA-B, 25 alleles) involved 50 statistical tests (i.e. one maternal and one fetal effect for each coded allele). Three of the alleles exhibited significant evidence for maternal effects, with P-values less than 0.001 (A*03:01, B*35:01, B*39:06, labelled in Figure 4), and the HLA- B*39:06 allele exhibited a significant fetal effect at P <0.001 (labelled in Figure 4). The allele that exhibited the most significant P-value, A*03:01, showed evidence for opposite maternal and fetal effects [i.e. maternal effect = −0.042 (−0.057, −0.026), Pm = 9.21 × 10−8; fetal effect = 0.020 (0.006, 0.035), Pf = 6.92 × 10−3]. The allele with the largest estimated maternal and fetal effects was B*39:06, which had a relatively low allele frequency of 0.69% and consequently wide confidence intervals for the effect sizes [maternal effect = −0.111 (−0.151, −0.029), Pm = 7.10 × 10−4; fetal effect = 0.090 (0.029, 0.151), Pf = 3.84 × 10−3]. We identified two nominally significant associations in the HLA-C gene, which has previously been reported to be associated with BW, including HLA-C*03:03 [maternal effect = 0.035 (0.012, 0.058), Pm = 2.62 × 10−3] and HLA-C*04:01 [maternal effect = −0.028 (−0.048, −0.008), Pm = 5.64 × 10−3]. The most significant Class II allele was DRB1*11:04, which involved only a fetal effect [fetal effect = − 0.071 (− 0.114, −0.028), Pf = 1.34 × 10−3]. Supplementary Table S8 (available as Supplementary data at IJE online) presents the results for all alleles, and Supplementary Figure S5 (available as Supplementary data at IJE online) presents the results from the SEM of the BW-associated HLA alleles at each locus.
Figure 4.
Maternal and fetal effect estimates for classical human leukocyte antigen alleles and birthweight in the UK Biobank. Fetal and maternal effect sizes estimated using the structural equation model. The shape of each dot represents whether maternal (square) and/or fetal associations (circle) passed nominal significance (P < 0.05). Triangles indicate alleles where tests for both maternal and fetal effects reached the threshold; solid dots represent alleles which did not (P < 0.05). Alleles with P < 0.001 are explicitly labelled. The observed negative correlation between maternal and fetal effect estimates is at least partially a consequence of the negative correlation between these parameters in the structural equation model
Discussion
In the current study, we formulated an SEM for estimating the maternal and fetal effects of classical HLA alleles on perinatal phenotypes. Our SEM is appropriate for analysing data structures where (unrelated) individuals with classical HLA genotypes are measured on their own phenotype and their offspring. Our simulations suggested that estimates of maternal and fetal allelic effects produced by our SEM were asymptotically unbiased. This was in contrast to analyses using ordinary least squares linear regression, which does not explicitly partition allelic effects into maternal and fetal components. Our SEM can also be used when a subset of the data has either only the individual’s own phenotype and/or only the phenotype of their offspring.
Asymptotic power calculations show that our SEM has appreciable power to partition maternal and fetal effects of common HLA alleles in a sample of at least 80 000 individuals (i.e. similar to the number of individuals in the UKB with BW information on themselves and their offspring). These results are similar to what we have observed previously in our analogous SEM that analyses bi-allelic SNP genotypes.20,21
In empirical analyses in UKB, we identified BW associations at multiple alleles at MHC class I and II loci, using data from more than 270 000 independent European individuals. We then used our SEM to partition the allelic associations into maternal and/or fetal effects. A total of 19 HLA alleles were shown to have maternal and/or fetal effects on BW (P <0.05). Most classical HLA alleles which showed association with offspring BW, exhibited negative effects relative to the most common allele at the respective locus. Previous GWAS have shown that most genome-wide significant SNPs for BW in non-MHC regions have effects that are mediated primarily through the fetal genome (or at least the estimated fetal effect is larger than the estimated maternal effect).8,21 However in the HLA region, our results suggest that many alleles have predominantly maternal effects. In addition, our results suggest that the most common maternal alleles (i.e. which were used as the baseline comparator genotype) are protective against low BW and fetal growth restriction. It is interesting to speculate whether this could be a consequence of natural selection, since HLA alleles that cause low BW might lead to a low survival rate and consequently decrease their frequencies in the population.
The classical allele with the lowest P-value was HLA-A*03:01, which exhibited a predominantly maternal effect that decreased offspring BW relative to the most common HLA-A*02:01 allele. The association was still significant after conditioning on genome-wide associated SNPs in the HLA region (P2df = 2.47 × 10−7). HLA-A*03:01 has never been directly associated with BW previously. However, it is associated with double the risk of developing multiple sclerosis.32 Studies have shown associations between multiple sclerosis and both own and offspring BW.33,34 However, if A*03:01 is truly associated with both phenotypes, then this most likely reflects genetic pleiotropy rather than a causal effect mediated through multiple sclerosis.
In addition to the putative association with the BW, HLA-A alleles are also in high linkage disequilibrium (LD) with non-classical HLA-Ib alleles (HLA-E, -F and -G), especially HLA-G.35HLA-G genotypes, playing a key role in immune tolerance throughout pregnancy (Kovats, 1990 #1006) have been associated with BW, placental weight,36 recurrent miscarriage37 and pregnancy-induced hypertension.38 It has been previously reported that the HLA-A*03 allele is in strong linkage disequilibrium with HLA-F*01:03:01, the HLA-G UTR-4 haplotype and the HLA-G*01:01 allele,39,40 which might reduce the risk of allo-immunization during pregnancy.41 However, HLA-A*03:01 shows a negative maternal effect on BW in our study, which is in contrast to the protective effect of the HLA-G and HLA-F haplotypes reported by the previous authors. However, their study only had a small sample size (N = 89) with genotyped maternal, but not fetal, HLA alleles. Larger studies are required to elucidate the role of non-classical HLA Ib alleles with fetal growth restriction and allo-immunization during pregnancy.
The HLA-B*39:06 allele displayed the largest estimated maternal and fetal effects among all associated alleles. A previous study has shown that the HLA-B*39:06 allele is associated higher risk of type 1 diabetes (T1D),42,43 especially when two specific HLA-DR/DQ haplotypes are present [DRB1*08:01-DQB1*04:02, odds ratio (OR) = 25.4; DRB1*01:01-DQB1*05:01, OR = 10.3].44 Intriguingly, DRB1*08:01, DRB1*01:01 and DQB1*05:01 were also nominally significantly associated with BW in our analysis (P2df <0.05). High BW has been previously associated with childhood-onset T1D45 and pregnancies in women with T1D have also been associated with BW extremes and preterm delivery.46,47 These associations could be partly attributable to HLA-B*39:06, as our results indicate a positive fetal and a negative maternal effect of this allele on BW.
In the conditional analysis (Supplementary Note 7, available as Supplementary data at IJE online), all the top associated classical MHC alleles remained significant in the two degrees of freedom test (P <0.001), indicating the primary associations at the HLA alleles rather than the SNPs; and independent associations on other loci might be novel findings of genetic contributions to fetal growth.
Fetal HLA-C epitopes have previously been associated with BW in observational studies,17,18 and GWAS studies have reported a BW-associated SNP rs9366778 in the HLA-C gene which exhibits a putative fetal effect.8 We detected four HLA-C alleles in the two degrees of freedom test which reached nominal significance (HLA-C*03:03, C*04:01, C*05:01, C*15:02, P <0.05). A previous study18 has suggested the existence of an interaction between paternally derived fetal HLA-C2 epitope (HLA-C molecule has a lysine at position 80; HLA-C*02/*04/*05/*06/*15),48 and maternal killer-cell immunoglobulin-like receptor (KIR) genotypes influences human BW. Future studies involving genotyped parent-offspring trios and dyads are warranted.
Although our method introduces a negative correlation between estimates of maternal and fetal genetic effects (r = −0.73), it still produces unbiased estimates of both types of parameters. Indeed, we observed a similar phenomenon in our previous SEM involving SNPs,21 as have other authors employing methodologies similar to ours.23 Such technical correlations may obscure real maternal and fetal genetic effects and make the results of partitioning difficult to interpret when sample sizes are small. However, the correlation is less of a concern when the sample size is large, and the study is well powered.
There are several limitations to our study, in that our SEM model does not consider scenarios with: (i) maternal and fetal interactions or incompatibility17,18; (ii) individual low-frequency alleles; (iii) non-classical HLA genes in MHC region: (iv) linkage disequilibrium or potential interactions between different HLA loci; (v) the possibility of dominance, epistasis, gene-environment or gene-gene interactions; (vi) potential non-transmitted paternal genetic effects on offspring BW; (vii) direct causal path between own (maternal) BW and offspring BW; and (viii) the influence of HLA-associated infertility.49,50 Furthermore, UKB only has self-reported BW and does not provide gestational age for adjustment. We have discussed these limitations in Supplementary Note 12 (available as Supplementary data at IJE online) and further investigated some important assumptions (Supplementary Notes 3, 10 and 11; Supplementary Figures S7–8; Supplementary Table S10, available as Supplementary data at IJE online). Finally, our findings warrant independent verification of the involvement of classical HLA alleles in BW aetiology in the future.
Conclusion
In conclusion, we have developed an SEM that can be used to partition the genetic association between classical HLA alleles and perinatal traits into maternal and fetal genetic components. Application of our model to individuals in the UKB revealed interesting novel allelic associations between BW and classical HLA alleles, which potentially provide insight into the immunogenetics of intrauterine fetal growth.
Ethics approval
The authors assert that all procedures contributing to this work comply with the ethical standards of the National Statement on Ethical Conduct in Human Research (Australia) and with the Helsinki Declaration of 1975, as revised in 2008, and has been approved by the University of Queensland Medicine, Law & Negligible Risk Ethics Sub-Committee. The UK Biobank has approval from the North West Multi-Centre Research Ethics Committee, which covers the UK. Participants of all studies provided written informed consent.
Supplementary Material
Acknowledgements
This research has been conducted using the UK Biobank resource (Reference 53641). The authors would like to thank the research participants of the UK Biobank. The authors would like to thank Dr John P. Kemp (Institute for Molecular Biosciences, University of Queensland, Brisbane, Australia) for his kind assistance with the definition of European ancestry.
Contributor Information
Geng Wang, Frazer Institute, Faculty of Medicine, University of Queensland, Brisbane, QLD, Australia; Institute for Molecular Bioscience, University of Queensland, Brisbane, QLD, Australia.
Nicole M Warrington, Frazer Institute, Faculty of Medicine, University of Queensland, Brisbane, QLD, Australia; Institute for Molecular Bioscience, University of Queensland, Brisbane, QLD, Australia; Medical Research Council Integrative Epidemiology Unit, University of Bristol, Bristol, UK; K.G. Jebsen Center for Genetic Epidemiology, Department of Public Health and Nursing, Norwegian University of Science and Technology, Trondheim, Norway.
David M Evans, Frazer Institute, Faculty of Medicine, University of Queensland, Brisbane, QLD, Australia; Institute for Molecular Bioscience, University of Queensland, Brisbane, QLD, Australia; Medical Research Council Integrative Epidemiology Unit, University of Bristol, Bristol, UK.
Data Availability
Human genotype and phenotype data from the UKB on which the results of this study were based were accessed with accession ID 53641. The genotype and phenotype data are available upon application to the UKB [http://www.ukbiobank.ac.uk/].
Supplementary data
Supplementary data are available at IJE online.
Author contributions
G.W. conducted the statistical analysis and drafted the manuscript. G.W., N.M.W. and D.M.E. designed the study, interpreted the results and reviewed the manuscript.
Funding
G.W. is supported by the University of Queensland Graduate School Scholarship (Australian Government Research Training Program Scholarship). N.M.W. is funded by a National Health and Medical Research Council (Australia) Investigator grant (APP2008723). D.M.E. is funded by an Australian National Health and Medical Research Council Investigator grant (APP2017942) and this work was funded by NHMRC project grants (GNT1157714, GNT1183074).
Conflict of interest
None declared.
References
- 1. Camerota M, Bollen KA.. birthweight, birth length, and gestational age as indicators of favorable fetal growth conditions in a US sample. PLoS One 2016;11:e0153800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Bollen KA, Noble MD, Adair LS.. Are gestational age, birthweight, and birth length indicators of favorable fetal growth conditions? A structural equation analysis of Filipino infants. Stat Med 2013;32:2950–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. McCormick MC. The contribution of low birthweight to infant mortality and childhood morbidity. N Engl J Med 1985;312:82–90. [DOI] [PubMed] [Google Scholar]
- 4. Barker DJ, Hales CN, Fall CH, Osmond C, Phipps K, Clark PM.. Type 2 (non-insulin-dependent) diabetes mellitus, hypertension and hyperlipidaemia (syndrome X): relation to reduced fetal growth. Diabetologia 1993;36:62–67. [DOI] [PubMed] [Google Scholar]
- 5. Barker DJ. Fetal origins of coronary heart disease. BMJ 1995;311:171–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Beta J, Khan N, Khalil A, Fiolna M, Ramadan G, Akolekar R.. Maternal and neonatal complications of fetal macrosomia: systematic review and meta-analysis. Ultrasound Obstet Gynecol 2019;54:308–18. [DOI] [PubMed] [Google Scholar]
- 7. Johnsson IW, Haglund B, Ahlsson F, Gustafsson J.. A high birthweight is associated with increased risk of type 2 diabetes and obesity. Pediatr Obes 2015;10:77–83. [DOI] [PubMed] [Google Scholar]
- 8. Warrington NM, Beaumont RN, Horikoshi M. et al. ; EGG Consortium. Maternal and fetal genetic effects on birthweight and their relevance to cardio-metabolic risk factors. Nat Genet 2019;51:804–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Freathy RM, Mook-Kanamori DO, Sovio U. et al. ; Early Growth Genetics (EGG) Consortium. Variants in ADCY5 and near CCNL1 are associated with fetal growth and birthweight. Nat Genet 2010;42:430–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Horikoshi M, Yaghootkar H, Mook-Kanamori DO. et al. ; Early Growth Genetics (EGG) Consortium. New loci associated with birthweight identify genetic links between intrauterine growth and adult height and metabolism. Nat Genet 2013;45:76–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Beaumont RN, Warrington NM, Cavadino A. et al. ; Early Growth Genetics (EGG) Consortium. Genome-wide association study of offspring birthweight in 86 577 women identifies five novel loci and highlights maternal genetic effects that are independent of fetal genetics. Hum Mol Genet 2018;27:742–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Juliusdottir T, Steinthorsdottir V, Stefansdottir L. et al. Distinction between the effects of parental and fetal genomes on fetal growth. Nat Genet 2021;53:1135–42. [DOI] [PubMed] [Google Scholar]
- 13. Horikoshi M, Beaumont RN, Day FR. et al. ; Early Growth Genetics (EGG) Consortium. Genome-wide associations for birthweight and correlations with adult disease. Nature 2016;538:248–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Bodmer JG, Marsh SG, Albert ED. et al. Nomenclature for factors of the HLA system, 1995. Tissue Antigens 1995;46:429–18. [DOI] [PubMed] [Google Scholar]
- 15. Thorsby E. A short history of HLA. Tissue Antigens 2009;74:101–16. [DOI] [PubMed] [Google Scholar]
- 16. Ober C. Current topic: HLA and reproduction: lessons from studies in the Hutterites. Placenta 1995;16:569–77. [DOI] [PubMed] [Google Scholar]
- 17. Hiby SE, Walker JJ, O'Shaughnessy KM. et al. Combinations of maternal KIR and fetal HLA-C genes influence the risk of preeclampsia and reproductive success. J Exp Med 2004;200:957–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Hiby SE, Apps R, Chazara O. et al. Maternal KIR in combination with paternal HLA-C2 regulate human birthweight. J Immunol 2014;192:5069–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Evans DM, Moen GH, Hwang LD, Lawlor DA, Warrington NM.. Elucidating the role of maternal environmental exposures on offspring health and disease using two-sample Mendelian randomization. Int J Epidemiol 2019;48:861–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Moen GH, Hemani G, Warrington NM, Evans DM.. Calculating power to detect maternal and offspring genetic effects in genetic association studies. Behav Genet 2019;49:327–39. [DOI] [PubMed] [Google Scholar]
- 21. Warrington NM, Freathy RM, Neale MC, Evans DM.. Using structural equation modelling to jointly estimate maternal and fetal effects on birthweight in the UK Biobank. Int J Epidemiol 2018;47:1229–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Sudlow C, Gallacher J, Allen N. et al. UK biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS Med 2015;12:e1001779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Wu Y, Zhong X, Lin Y. et al. Estimating genetic nurture with summary statistics of multigenerational genome-wide association studies. Proc Natl Acad Sci USA 2021;118:e2023184118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Bollen KA. Structural Equations with Latent Variables. New York: Wiley, 1989. [Google Scholar]
- 25. Neale MC, Hunter MD, Pritikin JN. et al. OpenMx 2.0: extended structural equation and statistical modeling. Psychometrika 2016;81:535–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Morris TP, White IR, Crowther MJ.. Using simulation studies to evaluate statistical methods. Stat Med 2019;38:2074–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Fry A, Littlejohns TJ, Sudlow C. et al. Comparison of sociodemographic and health-related characteristics of UK Biobank participants with those of the general population. Am J Epidemiol 2017;186:1026–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Bycroft C, Freeman C, Petkova D. et al. The UK Biobank resource with deep phenotyping and genomic data. Nature 2018;562:203–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Auton A, Brooks LD, Durbin RM. et al. ; 1000 Genomes Project Consortium. A global reference for human genetic variation. Nature 2015;526:68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Abraham G, Qiu Y, Inouye M.. FlashPCA2: principal component analysis of Biobank-scale genotype datasets. Bioinformatics 2017;33:2776–78. [DOI] [PubMed] [Google Scholar]
- 31. Manichaikul A, Mychaleckyj JC, Rich SS, Daly K, Sale M, Chen WM.. Robust relationship inference in genome-wide association studies. Bioinformatics 2010;26:2867–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Hafler DA, Compston A, Sawcer S. et al. ; International Multiple Sclerosis Genetics Consortium. Risk alleles for multiple sclerosis identified by a genomewide study. N Engl J Med 2007;357:851–62. [DOI] [PubMed] [Google Scholar]
- 33. Luetic GG, Menichini ML, Deri N. et al. High birthweight and risk of multiple sclerosis: a multicentre study in Argentina. Mult Scler Relat Disord 2021;47:102628. [DOI] [PubMed] [Google Scholar]
- 34. Dahl J, Myhr KM, Daltveit AK, Hoff JM, Gilhus NE.. Pregnancy, delivery, and birth outcome in women with multiple sclerosis. Neurology 2005;65:1961–63. [DOI] [PubMed] [Google Scholar]
- 35. Geraghty DE, Koller BH, Orr HT.. A human major histocompatibility complex class I gene that encodes a protein with a shortened cytoplasmic segment. Proc Natl Acad Sci USA 1987;84:9145–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Emmery J, Christiansen OB, Nilsson LL. et al. Associations between fetal HLA-G genotype and birthweight and placental weight in a large cohort of pregnant women - possible implications for HLA diversity. J Reprod Immunol 2017;120:8–14. [DOI] [PubMed] [Google Scholar]
- 37. Meuleman T, Drabbels J, van Lith JMM. et al. Lower frequency of the HLA-G UTR-4 haplotype in women with unexplained recurrent miscarriage. J Reprod Immunol 2018;126:46–52. [DOI] [PubMed] [Google Scholar]
- 38. Colbern GT, Chiang MH, Main EK.. Expression of the nonclassic histocompatibility antigen HLA-G by preeclamptic placenta. Am J Obstet Gynecol 1994;170:1244–50. [DOI] [PubMed] [Google Scholar]
- 39. Carlini F, Ferreira V, Buhler S. et al. Association of HLA-A and non-classical HLA Class I alleles. PLoS One 2016;11:e0163570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Alizadeh M, Picard C, Frassati C. et al. A new set of reagents and related software used for NGS based classical and non-classical HLA typing showing evidence for a greater HLA haplotype diversity. Hum Immunol 2020;81:202–205. [DOI] [PubMed] [Google Scholar]
- 41. Persson G, Picard C, Marin G. et al. Maternal HLA Ib Polymorphisms in Pregnancy Allo-Immunization. Front Immunol 2021;12:657217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Nejentsev S, Howson JM, Walker NM. et al. ; Wellcome Trust Case Control Consortium. Localization of type 1 diabetes susceptibility to the MHC class I genes HLA-B and HLA-A. Nature 2007;450:887–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Noble JA, Valdes AM, Varney MD. et al. ; Type 1 Diabetes Genetics Consortium. HLA class I and genetic susceptibility to type 1 diabetes: results from the Type 1 Diabetes Genetics Consortium. Diabetes 2010;59:2972–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Baschal EE, Baker PR, Eyring KR, Siebert JC, Jasinski JM, Eisenbarth GS.. The HLA-B 3906 allele imparts a high risk of diabetes only on specific HLA-DR/DQ haplotypes. Diabetologia 2011;54:1702–709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Bjorkman PJ, Saper MA, Samraoui B, Bennett WS, Strominger JL, Wiley DC.. The foreign antigen binding site and T cell recognition regions of class I histocompatibility antigens. Nature 1987;329:512–18. [DOI] [PubMed] [Google Scholar]
- 46. Murphy HR, Howgate C, O'Keefe J. et al. ; National Pregnancy in Diabetes (NPID) Advisory Group. Characteristics and outcomes of pregnant women with type 1 or type 2 diabetes: a 5-year national population-based cohort study. Lancet Diabetes Endocrinol 2021;9:153–64. [DOI] [PubMed] [Google Scholar]
- 47. Scott EM, Murphy HR, Kristensen KH. et al. Continuous glucose monitoring metrics and birthweight: informing management of type 1 diabetes throughout pregnancy. Diabetes Care 2022;45:1724–34. [DOI] [PubMed] [Google Scholar]
- 48. Biassoni R, Falco M, Cambiaggi A. et al. Amino acid substitutions can influence the natural killer (NK)-mediated recognition of HLA-C molecules. Role of serine-77 and lysine-80 in the target cell protection from lysis mediated by “group 2” or “group 1” NK clones. J Exp Med 1995;182:605–609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Cervan-Martin M, Tuttelmann F, Lopes AM. et al. Immune and spermatogenesis-related loci are involved in the development of extreme patterns of male infertility. Commun Biol 2022;5:1220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Huang M, Zhu M, Jiang T. et al. Fine mapping the MHC region identified rs4997052 as a new variant associated with nonobstructive azoospermia in Han Chinese males. Fertil Steril 2019;111:61–68. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Human genotype and phenotype data from the UKB on which the results of this study were based were accessed with accession ID 53641. The genotype and phenotype data are available upon application to the UKB [http://www.ukbiobank.ac.uk/].