Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Jan 25;15(5):1195–1203. doi: 10.1021/acs.jpclett.3c02980

J Coupling Constants of <1 Hz Enable 13C Hyperpolarization of Pyruvate via Reversible Exchange of Parahydrogen

Charbel D Assaf †,*, Xin Gui ‡, Alexander A Auer ‡, Simon B Duckett §, Jan-Bernd Hövener †, Andrey N Pravdivtsev †,*
PMCID: PMC10860132  PMID: 38271215

Abstract

graphic file with name jz3c02980_0006.jpg

Observing pyruvate metabolism in vivo has become a focal point of molecular magnetic resonance imaging. Signal amplification by reversible exchange (SABRE) has recently emerged as a versatile hyperpolarization technique. Tuning of the spin order transfer (SOT) in SABRE is challenging as the small 1H–13C J couplings, in the 13C-pyruvate case, result in SOT being not readily discernible. We demonstrate an experimental method using frequency-selective excitation of parahydrogen-derived polarization SOT sequence (SEPP-SPINEPT); its application led to up to 5700-fold 13C signal gain. In this way, we estimated the lifetime of two Ir–pyruvate SABRE complexes alongside the individual probing of eight small 1H–13C J couplings that connect the hydride protons in these complexes to 1- and 2-13C pyruvate spins, affording values between 0 and 2.69 Hz. Using electronic structure calculations, we define the low-energy structure of the corresponding complexes. Hence, this study demonstrates a novel approach to analyzing the spin topology of short-lived organometallic complexes.

Pyruvate (pyr) plays a significant role in cellular metabolism, lying at the junction of numerous metabolic processes within living cells.1−3 Studying the metabolic fate of pyr has attracted a great deal of attention due to its potential as a clinical tool, particularly in diagnosing cancer4 and inflammation.5 Nuclear magnetic resonance (NMR) and magnetic resonance imaging (MRI) allow the tracking of pyr metabolism in vitro and in vivo. However, these methods are insensitive to the low-spin polarization produced by the magnetic fields available today. Several techniques can increase nuclear spin polarization, known as hyperpolarization; pyr was hyperpolarized using dissolution dynamic nuclear polarization (dDNP)4,6,7 more than a decade ago. Later, parahydrogen-induced polarization with side arm hydrogenation (PHIP-SAH)8−13 was used to polarize pyr, and only recently, was this achieved by signal amplification by reversible exchange (SABRE).14−17

SABRE14 is particularly interesting because it is fast and allows continuous hyperpolarization.18−20 In contrast to PHIP-SAH, in which an unsaturated precursor is required,8−13 a chemical modification of the agent is unnecessary. These attributes make SABRE more accessible than dDNP and PHIP-SAH, leading to a rapid in vivo demonstration.21,22

In SABRE, the target substrate (here pyr) and parahydrogen (pH2) coordinate reversibly to an Ir complex (Figure 1) so that a transient J coupling is created between pyr and protons previously in pH2. These couplings allow the transfer of spin alignment to pyruvate,14,15 which can be used later for imaging or spectroscopy. We will refer to the two protons of pH2, now coordinated to the Ir complex, as IrHH. There are two main mechanisms for coherent SOT in SABRE: free evolution at (low) magnetic fields, which takes place close to level anticrossings of the involved spin states,23−27 or free evolution in combination with radiofrequency (RF) excitation at a low or high magnetic field.28−32 Polarization transfer via incoherent interactions has been demonstrated, too, but these mechanisms are usually less efficient.33−35

Figure 1.

Figure 1

Open in a new tab

SABRE hyperpolarization of 13C-pyr and IrHH protons. (A) H2, DMSO, and pyr bind to the transient, active, Ir-based SABRE complex [Ir(H)2(pyr)(DMSO)(IMes)] for [1] and [2], and [Ir(H)2(Cl)(DMSO)2(IMes)] for [3]. J couplings under appropriate conditions transfer polarization from IrHH (pH2-derived hydride protons) to pyr. There are three primary hyperpolarized complexes, [1]–[3]: two where pyr binds on equatorial, [1], or axial–equatorial, [2], sites and a third complex with an additional DMSO ligand, [3]. (B) 1H (black) and 1H{13C} (red) NMR PASADENA spectra showing polarized IrHH protons of [1]–[3] formed by supplying 8.75 bar of pH2 to the Ir catalyst precursor with either 1-13C-pyr (top) or 2-13C-pyr (bottom) in methanol-d4 at 267 K. The spectra consist of three pairs of hydride signals, with the dominant signal being from [1]. The 1H chemical shift was calibrated to CD2HOD to be 3.34 ppm.36

In the presence of H2, dimethyl sulfoxide (DMSO), pyr (CH3COCO2−, added as the sodium salt of pyruvate), and an IrIMes catalyst precursor {[IrCl(COD)(IMes)], where COD = cyclooctadiene, and IMes = 1,3-bis(2,4,6-trimethylphenyl)imidazol-2-ylidene}, three major complexes result: [Ir(H)2(pyr)(DMSO)(IMes)] complexes [1] and [2], and [Ir(H)2(Cl)(DMSO)2(IMes)] complex [3] (Figure 1). Under pH2 pressure at low temperatures, the mechanism of H2 exchange operates by opening the chelate in [1], which makes the pyruvate ligand η-1.15 New pH2 can then exchange with the already bound IrHH protons, and the chelate re-forms, resulting in the hyperpolarized signal for complex [1] (Figure 1B). A similar mechanism takes place for [2] and [3]. Additionally, DMSO ligand exchanges are most likely to occur in [2] and [3] rather than in [1], as the hydride is a good trans-labilizing ligand.

So far, the highest pH2-based polarization of 1-13C-pyr (>20%) with SABRE was achieved at 50 μT using weak RF irradiation and fully deuterated pyr.32 These impressive polarization levels highlight the potential of SABRE to enhance the sensitivity and detection of pyr for a wide range of applications.

Interestingly, J couplings mediate the polarization transfer in all coherence-driven SOTs. To optimize the SOT conditions, one must know the size of all such interactions. Unfortunately, these parameters are unknown for the SABRE active catalysts, Ir–pyr complexes [1] and [2] (Figure 1). This is due to the inability of 1H NMR to detect these couplings because of their small magnitude and line broadening due to chemical exchange. In recent work,27 these parameters were estimated using density functional theory (DFT) simulations and SOT at low magnetic fields; however, this approach has known biases.

To assess the details of the molecular structures of the complexes investigated, we carried out electronic structure calculations at the DFT level of theory. For [1]–[3] (Figure S14), geometry optimizations and normal-mode analyses were carried out for a series of possible conformers.

The relative Gibbs free energy of compound [2] (Figure 2D) is higher than that of complex [1] by 7.6 kJ/mol. In addition, the relative Gibbs free energy of isomer [2′] (Figure 2E),15 with the pyr coordinated differently than in [2], is 11.9 kJ/mol higher than that of [2] (and 19.5 kJ/mol higher than that of [1]), indicating that experimentally one likely observes [2]37 instead of [2′].15 Similarly, for [3], there is an isomer, [3′], with an energy difference of 0.4 kJ/mol, which differs by rotation of the IMes structure (Figure S14C). Hence, we will assign the observed experimental interactions to primary isomers [1]–[3].

Figure 2.

Figure 2

Open in a new tab

Quantum chemical calculations for three Ir complexes. (A) Chemical structure of complex [1] defining Ir–H2 and H–H distances. (B) Relaxed relative potential energy surface of complex [1] along the H–H and Ir–H2 distances, with contour lines increasing in 8 kJ/mol intervals. (C) Computed JH–H values when moving from dihydrogen to the dihydride complex (denoted with stars) on the PES. (D and E) Three-dimensional chemical structures and energies for complexes [2] and [2′], respectively. The computed J couplings are as follows: J[1]HH = −0.041 Hz, J[2]HH = 2.29 Hz, and J[2′]HH = 0.912 Hz. The measured values are as follows: J[1]HH = −10.48 Hz, and J[2]HH = −6.55 Hz. The eye icons highlight the region of pyruvate reorientation.

According to a previous study by Gelabert et al. on a similar iridium hydride complex,38 the Ir–H2 unit exhibits complex dynamics complicated by the motions of the two hydrogen atoms bound to Ir, giving rise to both dihydrogen and dihydride complexes in extreme cases. Therefore, a two-dimensional surface scan was performed for complex [1] (Figure 2B), where the H–H (RHH) and Ir–H2 distances (RIr–H2, the distance between Ir and the midpoint between the two hydrogen atoms) distances were varied while the Ir–Ha and Ir–Hb were kept equal (Figure 2A).

The energy minimum structure is a dihydride complex (RHH = 1.9 Å). Another very shallow minimum shows a certain degree of dihydrogen character (RHH = 1.2 Å), which is, however, 64 kJ/mol higher in energy. Both structures are true minima without imaginary frequencies. When we move from dihydrogen (RHH = 0.8 Å) to the dihydride complex (RHH = 1.9 Å), the corresponding JHH value decreases rapidly as the H-H bond breaks (Figure 2C). Note that experimentally, a negative JHH value is observed for the two now inequivalent hydride ligands; negative values were found for the dissociated hydrogens (RHH > 1.9 Å). Overall, the shallow potential energy surface implies that a more accurate estimate of the JHH value should be calculated using a Boltzmann average of all possible vibrational states at a given temperature in the anharmonic potential well and include nonclassical dynamics, the influence of a heavy transition metal atom, and its complex electronic structure.38 Hence, while structures and relative energies for such compounds are typically reasonable, the computed J coupling and chemical shift values are, as expected (Figure 2C and Tables S4 and S5), not accurate enough to replicate the experimental observations.

To measure these J couplings experimentally, one can analyze the 1H–13C J couplings by measuring 1H NMR spectra of solutions containing the activated IrIMes catalyst with sodium 1-13C-pyr or 2-13C-pyr and DMSO-d6 in methanol-d4 after the addition of pH2 to the solution. Upon hydrogen exchange and addition of pH2 to IrIMes, three pairs of antiphase resonances for the hydride ligands in Ir complexes [1]–[3] (Figure 1B) are observed. Such an NMR spectrum and the corresponding spin order are often termed under PASADENA (parahydrogen and synthesis allow dramatically enhanced nuclear alignment) conditions.39 Note that [1] and [2] are regioisomers for which in [1], pyr coordinates trans to hydride, and in [2], pyr is trans to hydride and NHC; complex [3] contains no pyr. The result of these arrangements is that the hydride ligands are chemically inequivalent, and we will refer to them as Ha and Hb as depicted in Figure 1A. Before, the chemical shifts of the pair of hydride ligands were assigned to the corresponding molecular composition (not specifying which of two hydrides has which chemical shift),15 while here, we tentatively assign the chemical shifts of protons to the nuclei in the complex as discussed below.

By bubbling pH2 through the methanol-d4 solution at a high magnetic field (9.4 T), we obtained 1H PASADENA type NMR spectra (Figure 1B), where visual inspection yields only the Ha–Hb coupling constants: J[1]HH = −10.5 Hz, J[2]HH = −6.5 Hz, and J[3]HH = −6.15 Hz. However, no visible interactions with 13C were seen, except for Hb to 2-13C-pyr in [2].

Applying 13C decoupling narrowed some lines in the 1H{13C} PASADENA spectra (Figure 1B), which let us estimate 1H–13C interactions. It proved to be possible to discern that C1 has the strongest interaction with Ha in [1], while C2 has the strongest interaction with Hb in [2] and negligible interaction with Hb [1]: 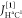Inline graphic ≅ 0.9 Hz, 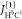Inline graphic ≅ 0.8 Hz, 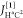Inline graphic ≅ 1.6 Hz, 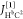Inline graphic≅ 0.2 Hz, 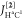Inline graphic ≅ 0.4 Hz, 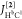Inline graphic ≅ 0.2 Hz, 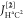Inline graphic ≅ 1.1 Hz, and 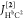Inline graphic ≅ 2.7 Hz (see Figures S6–S8). However, this method is not very reliable because its precision relies on a reproducible T2* (compromised by gas bubbling). Therefore, we propose to use SOT sequences to estimate these small interactions.40

The efficiency of RF-based SOT sequences is strongly dependent on the interplay of J couplings and sequence timings. Thus, the J couplings can be determined by varying the timings and recording the polarization.

SOT in SABRE experiments, however, is challenging due to the interplay of chemical exchange and J coupling interactions.41,42 The complex needs to exist for the duration of the SOT sequence. Cooling a sample reduced the bond rupture rate, prolonging the complex’s lifetime and the viable period for SOT.16,43 The maximum 1H PASADENA signal intensity for complex [1] was achieved at 267 K [decreasing further for lower temperatures (Figure S1)]. As [1] is assumed to be responsible for producing hyperpolarized pyr, it is the most important of the three complexes. Hence, we probed the J coupling interactions of [1] at this temperature (and lower temperatures) to decrease the exchange rate and maximize polarization.15

We started with the pH2 and insensitive nuclei polarization transfer sequence (phINEPT),44 which has already been used for SABRE to enhance 15N signals (and will be used for 13C in this work) and to measure lifetimes for Ir complexes.43,45 This approach theoretically allows one to probe the J couplings. However, when the simple phINEPT approach is used, it becomes apparent that it is virtually impossible to simultaneously measure two weak 1H–13C J coupling constants (Figure S5).

Instead, we hypothesized that frequency-selective excitations46 can be used to probe individual J coupling interactions between one of the protons and one of the 13C nuclei. To disentangle all of these interactions, we employ frequency-selective excitation of polarization with PASADENA (SEPP) followed by insensitive nuclei enhanced by polarization transfer (INEPT) with selective pulses (SP); altogether, this is a frequency-selective version of SEPP-INEPT47 [SEPP-SPINEPT (Figure 3)].48 In this sequence, we set the excitations such that no more than two spins are excited simultaneously during SOT, enabling us to probe interactions between two spins only.

Figure 3.

Figure 3

Open in a new tab

Scheme of 1H–13C selective spin order transfer sequence SEPP-SPINEPT. The spin evolution of two protons (I and S spins) and one 13C (F spin) is indicated. As a result, an antiphase 13C signal split by JSF can be observed. The amplitude of such a signal is modulated with only two interactions as sin(2πJISτ1) sin(2πJSFτ2). By fixing τ1 ≅1/(4JIS) and varying the duration of the τ2 interval, one can measure the corresponding 1H–13C interaction. The round pulses are frequency-selective pulses with different amplitudes and the same duration Δ. Additional indices for selective pulses indicate excited nuclear spins. Rectangle pulses indicate the hard pulses. During acquisition, a selective decoupling {1H} at 2.36 ppm was added to decouple the methyl group’s interaction. Due to rapid chemical exchange, the optimal τ1 can differ from 1/(4JIS) (examples in Figure S4).

A high-field SABRE experiment generates IHaZIHbZ spin order on the IrHH protons. When we probed for a JHaC interaction, we exited Ha with the first selective pulse, generating the following spin order after SEPP-SPINEPT IHaZICY sin(2πJHHτ1) sin(2πJHaCτ2). Now, if τ1 is set to the optimal value [close to 1/(4JHH) (see Figure S4)] and τ2 is varied, the effect of JHaC is mapped. This process was repeated for Hb, the second 13C spin, and the other complexes to probe the remaining interactions. Optionally, one can accelerate this approach by the simultaneous excitation of complexes [1] and [2], so that two data points result per experiment. Multimode excitation was used recently for the generation of multiple long-lived spin states.49

By fitting the measured SEPP-SPINEPT kinetics with A sin(2πJHCτ2) exp(−2τ2R), one can estimate the corresponding 1H–13C interaction, where R = kd + R2 is the superposition of the dissociation rate constant (1/kd is the lifetime of the complex) and R2 is the effective transversal relaxation time constant. This description shows that SEPP-SPINEPT is useful for asymmetric systems as it needs chemically non-equivalent IrHH protons. However, it will not be practical for the IrIMes complex with three pyridine ligands, where IrHH are chemically equivalent.14

Using this approach, we transferred polarization to 13C1 and 13C2 spins in complexes [1] (Figure 4) and [2] (Figure 5) at three temperatures (256, 261, and 267 K) and estimated corresponding 1H–13C interactions (Table 1).

Figure 4.

Figure 4

Open in a new tab

SEPP-SPINEPT applied to complex [1]. (A–D) Schemes represent selective SOT between IrHH protons (−29.10 and −27.20 ppm) and consequent polarization transfer to 13C1 (168.54 ppm) or 13C2 (206.59 ppm). (E–P) Normalized fitted integrals of absolute 13C signals of bound pyr after SEPP-SPINEPT as a function of τ2 and (Q–T) exemplary phased spectra at a maximum of polarization with signal enhancement (ε) at 267 K (black) and with {1H} decoupling (red). No polarization was observed when polarization was transferred from Hb to 13C2 (H and L). Phased spectra were integrated (dots) and fitted with A sin(2πJCHτ2) exp(−2τ2R) (lines), giving decaying R and J coupling values (Table 1). The duration of selective pulses was 10 ms, and the first delay (τ1) was 20 ms.

Figure 5.

Figure 5

Open in a new tab

SEPP-SPINEPT applied to complex [2]. (A–D) Schemes represent selective SOT between IrHH protons (−24.08 and −14.97 ppm) and consequent polarization transfer to 13C1 (165.14 ppm) or 13C2 (196.86 ppm). (E–P) Normalized fitted integrals of 13C signals of bound pyr after SEPP-SPINEPT as a function of τ2 and (Q–T) exemplary phased spectra at a maximum of polarization with signal enhancement (ε) at 267 K (black) and with {1H} decoupling (red). Phased spectra were integrated (dots) and fitted with A sin(2πJCHτ2) exp(−2τ2R) (lines), giving decaying R and J coupling values (Table 1). The duration of selective pulses was 10 ms, and the first delay (τ1) was 38 ms.

Table 1. 1H–13C Coupling Constants for Complexes [1] and [2] for Both Protons and C1 and C2 of pyr Measured with SEPP-SPINEPT (*) or SEPP-SPINEPT{1H} (†), Estimated before27 and 1H–1H Coupling Constants for Complexes [1]–[3] Measured with SEPP (‡, Figure S4)a.

  [1] [2]
δHa (ppm) –29.10 –14.97
δHb (ppm) –27.20 –24.08
δC1 (ppm) 168.54 165.15
δC2 (ppm) 206.59 196.86
JHa–Hb (Hz) –10.48‡ –6.55‡
JC1–Ha (Hz) |0.55 ± 0.02|* |0.32 ± 0.03|*
|0.53 ± 0.02|† |0.21 ± 0.04|†
–0.9727
JC1–Hb (Hz) |0.014 ± 0.00|* |0.25 ± 0.03|*
|0.006 ± 0.00|† |0.025 ± 0.33|†
0.827
JC2–Ha (Hz) |0.93 ± 0.08|* |0.41 ± 0.02|*
|0.99 ± 0.016|† |0.45 ± 0.02|†
–0.527
JC2–Hb (Hz) not observable*† |2.69 ± 0.002|*
–0.0627 |2.69 ± 0.035|†
RT=256 K (s–1) 3.16 ± 0.03* 1.36 ± 0.05*
2.96 ± 0.03† 1.47 ± 0.06†
RT=261 K (s–1) 4.19 ± 0.04* 1.56 ± 0.05*
4.06 ± 0.04† 1.58 ± 0.06†
RT=267 K (s–1) 7.05 ± 0.07* 1.91 ± 0.05*
6.73 ± 0.07† 1.96 ± 0.05†
Open in a new tab
a

The JHH values are −10.48 ± 0.02 Hz for complex [1], −6.55 ± 0.01 Hz for complex [2], and −6.03 ± 0.01 Hz for complex [3] (−21.59 and −15.56 ppm). Measurements were taken at three temperatures (256, 261, and 267 K). The reference for the 13C chemical shift was 47.63 ppm with methanol-d4.36 SEPP-SPINEPT does not provide any information about the sign of J couplings.

Exemplary SEPP-SPINEPT kinetics measured at 256, 261, and 267 K are shown in Figures 4 and 5. No signal was observed for 13C2 of [1] when polarization was transferred from Hb, meaning that the J coupling is very small and is the smallest interaction among all for both complexes [1] and [2]. The Hb–C2 interaction of [2] was visible in 1H PASADENA (Figure 1) and confirmed with SEPP-SPINEPT (Figure 5H), which equals ∼2.69 Hz and does not need additional verification.

The other six interactions (three for each complex) are <2 Hz but still facilitate transfer polarization. Cooling the sample to 256 K (the lowest available temperature for our system) allowed us to slow the chemical exchange and prolong the complex’s lifetime, enabling more accurate J coupling determinations by comparing measurements at different temperatures.

A global fitting approach was employed to enhance the accuracy of the fitting, allowing J coupling parameters and relaxation parameter R to be shared across the data sets (detailed in Table 1 and Figures S9 and S10). Variation of the temperature from 267 to 256 K more than halved effective relaxation parameter R for [1] from ∼7 to ∼3 s–1, while for complex [2], the reduction was <1 s–1, highlighting the contributions from the chemical exchange and differences between dynamics of the complexes.

In addition, parameter R in our fittings (Table 1) provides valuable estimates of exchange rates, which exhibit a strong correlation with temperature; however, it is important to acknowledge that these estimates can also be affected by the pressure-dependent association mechanism of H2 exchange and temperature-dependent T1 relaxation. Further investigations of the [H2] and [pyr] effects will be conducted separately.

Assuming that the effective relaxation of the system during the polarization transfer is ∼1 s–1 (typical order of magnitude for the relaxation time of hydride protons), the lifetimes at, e.g., 267 K are 0.16 s for complex [1] and 1 s for complex [2]. Using such relaxation estimates, the values for the enthalpy and entropy of activation are 43.4 kJ/mol and −64.39 J mol–1 K–1 for complex [1] and 41.7 kJ/mol and −88.47 J mol–1 K–1 for complex [2], respectively (Figure S11B).

In further studies, for an even better assessment of interactions and exchange, one should go to even lower temperatures, ∼250 K, where the lifetime of complex [1] is estimated to be similar to the spin–spin relaxation of the hydride protons or lower (see Figure S11A). Similar R values were obtained using the SEPP experiment (Table S1 and Figure S4).

The use of decoupling during the NMR analysis has emerged as a superior strategy, significantly outperforming the nondecoupled spectra. A selective 1H decoupling at 2.36 ppm allowed decoupling of the hydrogen interactions of the ethyl group. One can see a simplification of the spectrum at 206.59 and 196.86 ppm for 2-13C-pyr (Figures 3S,T and 4S,T). In addition, selective decoupling enhanced the accuracy of signal fitting by maximizing the intensity of the SEPP-SPINEPT signal.

Previously, all of these interactions were estimated to explain polarization transfer to 1-13C-pyr. For example, a 5 Hz interaction was estimated by Nantogma et al.,17 while the strongest interaction we found for [1] was only 0.55 Hz. In the other study,31 the minimal interaction of 0.06 Hz was assumed because no broadening of the 13C spectral lines was visible. However, as the authors explain,31 this effect may be caused by line narrowing due to rapid chemical exchange; our estimations of the chemical-exchange rates agree with this explanation. Complexes [1]–[3] are the primary complexes of the system; however, there are others visible in 1H PASADENA and 13C SEPP-SPINEPT (examples in Figure S12), indicating even greater complexity of this dynamic SABRE system.

The best estimates for the interactions so far were achieved by combining results of SOT at ultralow magnetic fields and DFT calculations.27 Our experimental methods allowed us to determine the magnitude but not the sign of the J coupling interactions. DFT calculations and low-field experiments shed some light on the signs of these interactions.27 We assigned the IrHH chemical shifts to the structure of [1] such that Ha (−29.10 ppm) and C2 (206.59 ppm) with the largest J coupling of 0.93 Hz are in the trans position; however, this is a tentative assignment, and the measurements of distances using nuclear Overhauser effects would give better structure evaluation.

The selective nature of SEPP-SPINEPT excitation sequences addresses the issue of dynamic exchange as it creates two-spin order coherence, which, in addition to decaying through relaxation, will vanish as the Ir–O13C bond to pyr breaks (the IrHH bonds in these complexes rupture after this step). Consequently, the resulting signal oscillation will experience a modulation that will dampen its amplitude, limiting the J coupling size that can be measured at any particular temperature. This reduction at the temperatures (and, therefore, bond rupture rate) selected has a minimal effect on the position of the peak maximum, which defines the measured coupling as the rate of signal damping acts on a longer time scale. Furthermore, deploying hyperpolarization helps address this detail by increasing the signal-to-noise ratio. Therefore, this approach is robust, overcoming the inherent challenges when dealing with the dynamic behavior of these critical Ir complexes. The obtained NMR parameters of the short-lived Ir complexes can be used as a benchmark for quantum chemical calculations of hydrogens near heavy metals. Also, the parameters obtained here can be used to numerically optimize SOT for even stronger hyperpolarization of pyr with SABRE. This method and these results will greatly facilitate further development of the up-and-coming SABRE technology.

Methods

Chemicals. Perdeuterated Ir precatalyst [Ir-d22] = [IrCl(COD)(IMes-d22)] was synthesized according to ref (50) [IMes = 1,3-bis(2,4,6-trimethylphenyl)imidazol-2-ylidene, and COD = cyclooctadiene], and sodium pyruvate-1-13C (13C-pyr, 490709, Sigma-Aldrich), sodium pyruvate-2-13C (13C-pyr, 490725, Sigma-Aldrich), dimethyl sulfoxide-d6 (DMSO, 00905-25, DEUTERO GmbH), and methanol-d4 (441384, Sigma-Aldrich) were used here.

Sample. Samples were prepared with a fixed ratio of substrate, catalyst, and DMSO in 450 μL of methanol-d4 and placed in a high-pressure 5 mm NMR tube (524-PV-7, DEUTERO GmbH). The ratio of the substrate, catalyst (5 mM), and DMSO was 10:1:5.

Experiment. The NMR tube was then attached to a bubbling system (similar to that used in ref (51)) and placed inside the spectrometer (Bruker Neo, 9.4 T). The solution was bubbled with parahydrogen-enriched H2 gas to a pressure of 8.7 bar. The gas was enriched to >92% pH2 in the presence of a spin-exchange catalyst (Fe2O3) at a low temperature (25 K). During acquisition, a selective decoupling {1H} of 250 Hz at 2.36 ppm was applied for 1 ms by using WALTZ-16 with a P of 0.0024 W.

Fitting. 1H PASADENA and SEPP-SPINEPT kinetics were fitted using MATLAB scripts (available in the Supporting Information). The details of the fitting functions and global fittings are available in the Supporting Information. All error margins for the fitted values are standard deviations estimated using the MATLAB nonlinear regression “nlinfit” function.

Computational Details. All quantum chemical calculations were performed with the ORCA 5.0 program package.52 Geometries were optimized at the B3LYP-D4/def2-TZVP level of theory.53−56 The optimized structures were confirmed to be true minima by harmonic vibrational frequency analyses. The NMR chemical shifts were calculated at the GIAO-ZORA-TPSSh/def2-TZVPP level of theory,57−61 and the coupling constants were calculated at the PBE/pcJ-3 level of theory,62,63 where the SARC-ZORA-TZVPP basis set was used for Ir64 and the def2-TZVPP or pcJ-3 basis set was used for all other nuclei. All basis sets were decontracted and complemented with the “Autoaux” auxiliary basis sets available in ORCA.65 Very tight convergence criteria were employed for the optimization and self-consistent field, and a tight “DefGrid3” DFT integration grid was applied. The CPCM model was used in both geometry optimizations and NMR calculations to account for solvation effects.66

Acknowledgments

The authors acknowledge funding from the German Federal Ministry of Education and Research (BMBF) within the framework of the e: Med research and funding concept (01ZX1915C), DFG (PR 1868/3-1, HO-4602/2-2, HO-4602/3, GRK2154-2019, EXC2167, FOR5042, and TRR287). MOIN CC was founded by a grant from the European Regional Development Fund (ERDF) and the Zukunftsprogramm Wirtschaft of Schleswig-Holstein (Project 122-09-053). A.A.A. and X.G. acknowledge funding by the Max-Planck-Society and the MPI für Kohlenforschung.

Data Availability Statement

The corresponding raw data can be accessed via Zenodo https://zenodo.org/doi/10.5281/zenodo.10512816.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.3c02980.

  • Additional 1H and 13C NMR spectra, SEPP and phINEPT polarization transfer sequences, and estimation of J coupling constants using 1H and 1H{13C} PASADENA spectra (PDF)

  • SEPP-SPINEPT fitting matlab scripts (ZIP)

  • Geometries of identified complexes (ZIP)

  • Transparent Peer Review report available (PDF)

Author Contributions

A.N.P.: conceptualization. C.D.A.: experiments, spin dynamics simulations, and investigation. X.G. and A.A.A.: all quantum chemistry simulations. S.B.D., A.N.P., C.D.A., and J.-B.H.: analysis, writing of the original draft, and discussion. A.N.P. and J.-B.H.: supervision and funding acquisition. All authors contributed to discussions and interpretation of the results and have approved the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

jz3c02980_si_001.pdf (3.7MB, pdf)
jz3c02980_si_004.zip (253.9KB, zip)
jz3c02980_si_005.zip (11.2KB, zip)
jz3c02980_si_007.pdf (947.4KB, pdf)

References

  1. Warburg O. On the Origin of Cancer Cells. Science 1956, 123 (3191), 309–314. 10.1126/science.123.3191.309. [DOI] [PubMed] [Google Scholar]
  2. Gray L. R.; Tompkins S. C.; Taylor E. B. Regulation of Pyruvate Metabolism and Human Disease. Cell. Mol. Life Sci. 2014, 71 (14), 2577–2604. 10.1007/s00018-013-1539-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Liberti M. V.; Locasale J. W. The Warburg Effect: How Does It Benefit Cancer Cells?. Trends Biochem. Sci. 2016, 41 (3), 211–218. 10.1016/j.tibs.2015.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Nelson S. J.; Kurhanewicz J.; Vigneron D. B.; Larson P. E. Z.; Harzstark A. L.; Ferrone M.; van Criekinge M.; Chang J. W.; Bok R.; Park I.; Reed G.; Carvajal L.; Small E. J.; Munster P.; Weinberg V. K.; Ardenkjaer-Larsen J. H.; Chen A. P.; Hurd R. E.; Odegardstuen L.-I.; Robb F. J.; Tropp J.; Murray J. A. Metabolic Imaging of Patients with Prostate Cancer Using Hyperpolarized [1–13C]Pyruvate. Sci. Transl. Med. 2013, 5 (198), 198ra108–198ra108. 10.1126/scitranslmed.3006070. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Lewis A. J. M.; Miller J. J.; Lau A. Z.; Curtis M. K.; Rider O. J.; Choudhury R. P.; Neubauer S.; Cunningham C. H.; Carr C. A.; Tyler D. J. Noninvasive Immunometabolic Cardiac Inflammation Imaging Using Hyperpolarized Magnetic Resonance. Circ. Res. 2018, 122 (8), 1084–1093. 10.1161/CIRCRESAHA.117.312535. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Ardenkjær-Larsen J. H.; Fridlund B.; Gram A.; Hansson G.; Hansson L.; Lerche M. H.; Servin R.; Thaning M.; Golman K. Increase in Signal-to-Noise Ratio of > 10,000 Times in Liquid-State NMR. Proc. Natl. Acad. Sci. U.S.A. 2003, 100 (18), 10158–10163. 10.1073/pnas.1733835100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Apps A.; Lau J. Y.C.; Miller J. J.J.J.; Tyler A.; Young L. A.J.; Lewis A. J.M.; Barnes G.; Trumper C.; Neubauer S.; Rider O. J.; Tyler D. J. Proof-of-Principle Demonstration of Direct Metabolic Imaging Following Myocardial Infarction Using Hyperpolarized 13C CMR. JACC: Cardiovascular Imaging 2021, 14 (6), 1285–1288. 10.1016/j.jcmg.2020.12.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Cavallari E.; Carrera C.; Aime S.; Reineri F. Studies to Enhance the Hyperpolarization Level in PHIP-SAH-Produced C13-Pyruvate. J. Magn. Reson. 2018, 289, 12–17. 10.1016/j.jmr.2018.01.019. [DOI] [PubMed] [Google Scholar]
  9. Cavallari E.; Carrera C.; Aime S.; Reineri F. Metabolic Studies of Tumor Cells Using [1–13C] Pyruvate Hyperpolarized by Means of PHIP-Side Arm Hydrogenation. ChemPhysChem 2019, 20 (2), 318–325. 10.1002/cphc.201800652. [DOI] [PubMed] [Google Scholar]
  10. Ding Y.; Korchak S.; Mamone S.; Jagtap A. P.; Stevanato G.; Sternkopf S.; Moll D.; Schroeder H.; Becker S.; Fischer A.; Gerhardt E.; Outeiro T. F.; Opazo F.; Griesinger C.; Glöggler S. Rapidly Signal-Enhanced Metabolites for Atomic Scale Monitoring of Living Cells with Magnetic Resonance. Chem. Methods 2022, 2, e202200023 10.1002/cmtd.202200023. [DOI] [Google Scholar]
  11. Brahms A.; Pravdivtsev A.; Stamp T.; Ellermann F.; Sönnichsen F.; Hövener J.-B.; Herges R. Synthesis of 13C and 2H Labeled Vinyl Pyruvate and Hyperpolarization of Pyruvate. Chem. - Eur. J. 2022, 28, e202201210 10.1002/chem.202201210. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hune T.; Mamone S.; Schroeder H.; Jagtap A. P.; Sternkopf S.; Stevanato G.; Korchak S.; Fokken C.; Müller C. A.; Schmidt A. B.; Becker D.; Glöggler S. Metabolic Tumor Imaging with Rapidly Signal-Enhanced 1–13C-Pyruvate-D3. ChemPhysChem 2023, 24, e202200615 10.1002/cphc.202200615. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Marshall A.; Salhov A.; Gierse M.; Müller C.; Keim M.; Lucas S.; Parker A.; Scheuer J.; Vassiliou C.; Neumann P.; Jelezko F.; Retzker A.; Blanchard J. W.; Schwartz I.; Knecht S. Radio-Frequency Sweeps at Microtesla Fields for Parahydrogen-Induced Polarization of Biomolecules. J. Phys. Chem. Lett. 2023, 14, 2125–2132. 10.1021/acs.jpclett.2c03785. [DOI] [PubMed] [Google Scholar]
  14. Adams R. W.; Aguilar J. A.; Atkinson K. D.; Cowley M. J.; Elliott P. I. P.; Duckett S. B.; Green G. G. R.; Khazal I. G.; López-Serrano J.; Williamson D. C. Reversible Interactions with Para-Hydrogen Enhance NMR Sensitivity by Polarization Transfer. Science 2009, 323 (5922), 1708–1711. 10.1126/science.1168877. [DOI] [PubMed] [Google Scholar]
  15. Iali W.; Roy S. S.; Tickner B. J.; Ahwal F.; Kennerley A. J.; Duckett S. B. Hyperpolarising Pyruvate through Signal Amplification by Reversible Exchange (SABRE). Angew. Chem., Int. Ed. 2019, 58 (30), 10271–10275. 10.1002/anie.201905483. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. TomHon P.; Abdulmojeed M.; Adelabu I.; Nantogma S.; Kabir M. S. H.; Lehmkuhl S.; Chekmenev E. Y.; Theis T. Temperature Cycling Enables Efficient 13C SABRE-SHEATH Hyperpolarization and Imaging of [1–13C]-Pyruvate. J. Am. Chem. Soc. 2022, 144 (1), 282–287. 10.1021/jacs.1c09581. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Nantogma S.; Eriksson S. L.; Adelabu I.; Mandzhieva I.; Browning A.; TomHon P.; Warren W. S.; Theis T.; Goodson B. M.; Chekmenev E. Y. Interplay of Near-Zero-Field Dephasing, Rephasing, and Relaxation Dynamics and [1–13C]Pyruvate Polarization Transfer Efficiency in Pulsed SABRE-SHEATH. J. Phys. Chem. A 2022, 126 (48), 9114–9123. 10.1021/acs.jpca.2c07150. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hövener J.-B.; Schwaderlapp N.; Lickert T.; Duckett S. B.; Mewis R. E.; Highton L. A. R.; Kenny S. M.; Green G. G. R.; Leibfritz D.; Korvink J. G.; Hennig J.; von Elverfeldt D. A Hyperpolarized Equilibrium for Magnetic Resonance. Nat. Commun. 2013, 4, ncomms3946. 10.1038/ncomms3946. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Pravdivtsev A. N.; Yurkovskaya A. V.; Vieth H.-M.; Ivanov K. L. RF-SABRE: A Way to Continuous Spin Hyperpolarization at High Magnetic Fields. J. Phys. Chem. B 2015, 119 (43), 13619–13629. 10.1021/acs.jpcb.5b03032. [DOI] [PubMed] [Google Scholar]
  20. Suefke M.; Lehmkuhl S.; Liebisch A.; Blümich B.; Appelt S. Para-Hydrogen Raser Delivers Sub-Millihertz Resolution in Nuclear Magnetic Resonance. Nat. Phys. 2017, 13 (6), 568–572. 10.1038/nphys4076. [DOI] [Google Scholar]
  21. MacCulloch K.; Browning A.; Guarin Bedoya D. O.; McBride S. J.; Abdulmojeed M. B.; Dedesma C.; Goodson B. M.; Rosen M. S.; Chekmenev E. Y.; Yen Y.-F.; TomHon P.; Theis T. Facile Hyperpolarization Chemistry for Molecular Imaging and Metabolic Tracking of [1–13C]Pyruvate in Vivo. J. Magn. Reson. Open 2023, 16–17, 100129 10.1016/j.jmro.2023.100129. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. de Maissin H.; Groß P. R.; Mohiuddin O.; Weigt M.; Nagel L.; Herzog M.; Wang Z.; Willing R.; Reichardt W.; Pichotka M.; Heß L.; Reinheckel T.; Jessen H. J.; Zeiser R.; Bock M.; von Elverfeldt D.; Zaitsev M.; Korchak S.; Glöggler S.; Hövener J.-B.; Chekmenev E. Y.; Schilling F.; Knecht S.; Schmidt A. B. In Vivo Metabolic Imaging of [1–13C]Pyruvate-D3 Hyperpolarized By Reversible Exchange With Parahydrogen. Angew. Chem., Int. Ed. 2023, 62, e202306654 10.1002/anie.202306654. [DOI] [PubMed] [Google Scholar]
  23. Pravdivtsev A. N.; Yurkovskaya A. V.; Vieth H.-M.; Ivanov K. L.; Kaptein R. Level Anti-Crossings Are a Key Factor for Understanding Para-Hydrogen-Induced Hyperpolarization in SABRE Experiments. ChemPhysChem 2013, 14 (14), 3327–3331. 10.1002/cphc.201300595. [DOI] [PubMed] [Google Scholar]
  24. Truong M. L.; Theis T.; Coffey A. M.; Shchepin R. V.; Waddell K. W.; Shi F.; Goodson B. M.; Warren W. S.; Chekmenev E. Y. 15 N Hyperpolarization by Reversible Exchange Using SABRE-SHEATH. J. Phys. Chem. C 2015, 119 (16), 8786–8797. 10.1021/acs.jpcc.5b01799. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Pravdivtsev A. N.; Kempf N.; Plaumann M.; Bernarding J.; Scheffler K.; Hövener J.-B.; Buckenmaier K. Coherent Evolution of Signal Amplification by Reversible Exchange in Two Alternating Fields (Alt-SABRE). ChemPhysChem 2021, 22 (23), 2381–2386. 10.1002/cphc.202100543. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Eriksson S. L.; Lindale J. R.; Li X.; Warren W. S. Improving SABRE Hyperpolarization with Highly Nonintuitive Pulse Sequences: Moving beyond Avoided Crossings to Describe Dynamics. Sci. Adv. 2022, 8 (11), eabl3708 10.1126/sciadv.abl3708. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Browning A.; Macculloch K.; TomHon P.; Mandzhieva I.; Chekmenev E. Y.; Goodson B. M.; Lehmkuhl S.; Theis T. Spin Dynamics of [1,2- 13 C 2 ]Pyruvate Hyperpolarization by Parahydrogen in Reversible Exchange at Micro Tesla Fields. Phys. Chem. Chem. Phys. 2023, 25, 16446–16458. 10.1039/D3CP00843F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Theis T.; Truong M.; Coffey A. M.; Chekmenev E. Y.; Warren W. S. LIGHT-SABRE Enables Efficient in-Magnet Catalytic Hyperpolarization. J. Magn. Reson. 2014, 248, 23–26. 10.1016/j.jmr.2014.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Pravdivtsev A. N.; Yurkovskaya A. V.; Zimmermann H.; Vieth H.-M.; Ivanov K. L. Transfer of SABRE-Derived Hyperpolarization to Spin-1/2 Heteronuclei. RSC Adv. 2015, 5 (78), 63615–63623. 10.1039/C5RA13808F. [DOI] [Google Scholar]
  30. Ariyasingha N. M.; Lindale J. R.; Eriksson S. L.; Clark G. P.; Theis T.; Shchepin R. V.; Chukanov N. V.; Kovtunov K. V.; Koptyug I. V.; Warren W. S.; Chekmenev E. Y. Quasi-Resonance Fluorine-19 Signal Amplification by Reversible Exchange. J. Phys. Chem. Lett. 2019, 10 (15), 4229–4236. 10.1021/acs.jpclett.9b01505. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Pravdivtsev A. N.; Buckenmaier K.; Kempf N.; Stevanato G.; Scheffler K.; Engelmann J.; Plaumann M.; Koerber R.; Hövener J.-B.; Theis T. LIGHT-SABRE Hyperpolarizes 1–13C-Pyruvate Continuously without Magnetic Field Cycling. J. Phys. Chem. C 2023, 127 (14), 6744–6753. 10.1021/acs.jpcc.3c01128. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Schmidt A. B.; Eills J.; Dagys L.; Gierse M.; Keim M.; Lucas S.; Bock M.; Schwartz I.; Zaitsev M.; Chekmenev E. Y.; Knecht S. Over 20% Carbon-13 Polarization of Perdeuterated Pyruvate Using Reversible Exchange with Parahydrogen and Spin-Lock Induced Crossing at 50 MT. J. Phys. Chem. Lett. 2023, 14 (23), 5305–5309. 10.1021/acs.jpclett.3c00707. [DOI] [PubMed] [Google Scholar]
  33. Barskiy D. A.; Kovtunov K. V.; Koptyug I. V.; He P.; Groome K. A.; Best Q. A.; Shi F.; Goodson B. M.; Shchepin R. V.; Coffey A. M.; Waddell K. W.; Chekmenev E. Y. The Feasibility of Formation and Kinetics of NMR Signal Amplification by Reversible Exchange (SABRE) at High Magnetic Field (9.4 T). J. Am. Chem. Soc. 2014, 136 (9), 3322–3325. 10.1021/ja501052p. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Pravdivtsev A. N.; Ivanov K. L.; Yurkovskaya A. V.; Petrov P. A.; Limbach H.-H.; Kaptein R.; Vieth H.-M. Spin Polarization Transfer Mechanisms of SABRE: A Magnetic Field Dependent Study. J. Magn. Reson. 2015, 261 (Suppl. C), 73–82. 10.1016/j.jmr.2015.10.006. [DOI] [PubMed] [Google Scholar]
  35. Knecht S.; Kiryutin A. S.; Yurkovskaya A. V.; Ivanov K. L. Mechanism of Spontaneous Polarization Transfer in High-Field SABRE Experiments. J. Magn. Reson. 2018, 287, 74–81. 10.1016/j.jmr.2017.12.018. [DOI] [PubMed] [Google Scholar]
  36. Fulmer G. R.; Miller A. J. M.; Sherden N. H.; Gottlieb H. E.; Nudelman A.; Stoltz B. M.; Bercaw J. E.; Goldberg K. I. NMR Chemical Shifts of Trace Impurities: Common Laboratory Solvents, Organics, and Gases in Deuterated Solvents Relevant to the Organometallic Chemist. Organometallics 2010, 29 (9), 2176–2179. 10.1021/om100106e. [DOI] [Google Scholar]
  37. Tickner B. J.; Semenova O.; Iali W.; Rayner P. J.; Whitwood A. C.; Duckett S. B. Optimisation of Pyruvate Hyperpolarisation Using SABRE by Tuning the Active Magnetisation Transfer Catalyst. Catal. Sci. Technol. 2020, 10 (5), 1343–1355. 10.1039/C9CY02498K. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Gelabert R.; Moreno M.; Lluch J. M.; Lledós A.; Heinekey D. M. Determination of the Temperature Dependence of the H–D Spin–Spin Coupling Constant and the Isotope Effect on the Proton Chemical Shift for the Compressed Dihydride Complex [Cp*Ir(P–P)H 2 ] 2+. J. Am. Chem. Soc. 2005, 127 (15), 5632–5640. 10.1021/ja043011r. [DOI] [PubMed] [Google Scholar]
  39. Bowers C. R.; Weitekamp D. P. Parahydrogen and Synthesis Allow Dramatically Enhanced Nuclear Alignment. J. Am. Chem. Soc. 1987, 109 (18), 5541–5542. 10.1021/ja00252a049. [DOI] [Google Scholar]
  40. Eshuis N.; Aspers R. L. E. G.; van Weerdenburg B. J. A.; Feiters M. C.; Rutjes F. P. J. T.; Wijmenga S. S.; Tessari M. Determination of Long-Range Scalar 1H–1H Coupling Constants Responsible for Polarization Transfer in SABRE. J. Magn. Reson. 2016, 265 (Suppl. C), 59–66. 10.1016/j.jmr.2016.01.012. [DOI] [PubMed] [Google Scholar]
  41. Adams R. W.; Duckett S. B.; Green R. A.; Williamson D. C.; Green G. G. R. A Theoretical Basis for Spontaneous Polarization Transfer in Non-Hydrogenative Parahydrogen-Induced Polarization. J. Chem. Phys. 2009, 131 (19), 194505 10.1063/1.3254386. [DOI] [PubMed] [Google Scholar]
  42. Pravdivtsev A. N.; Hövener J.-B. Coherent Polarization Transfer in Chemically Exchanging Systems. Phys. Chem. Chem. Phys. 2020, 22 (16), 8963–8972. 10.1039/C9CP06873B. [DOI] [PubMed] [Google Scholar]
  43. Pravdivtsev A. N.; Yurkovskaya A. V.; Zimmermann H.; Vieth H.-M.; Ivanov K. L. Enhancing NMR of Insensitive Nuclei by Transfer of SABRE Spin Hyperpolarization. Chem. Phys. Lett. 2016, 661 (Suppl. C), 77–82. 10.1016/j.cplett.2016.08.037. [DOI] [Google Scholar]
  44. Haake M.; Natterer J.; Bargon J. Efficient NMR Pulse Sequences to Transfer the Parahydrogen-Induced Polarization to Hetero Nuclei. J. Am. Chem. Soc. 1996, 118 (36), 8688–8691. 10.1021/ja960067f. [DOI] [Google Scholar]
  45. Vaneeckhaute E.; Tyburn J.; Kempf J. G.; Martens J. A.; Breynaert E. Reversible Parahydrogen Induced Hyperpolarization of 15 N in Unmodified Amino Acids Unraveled at High Magnetic Field. Adv. Sci. 2023, 10 (23), 2207112 10.1002/advs.202207112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Schmidt A. B.; Brahms A.; Ellermann F.; Knecht S.; Berner S.; Hennig J.; von Elverfeldt D.; Herges R.; Hövener J.-B.; Pravdivtsev A. Selective Excitation of Hydrogen Doubles the Yield and Improves the Robustness of Parahydrogen-Induced Polarization of Low-γ Nuclei. Phys. Chem. Chem. Phys. 2021, 23 (47), 26645–26652. 10.1039/D1CP04153C. [DOI] [PubMed] [Google Scholar]
  47. Sengstschmid H.; Freeman R.; Barkemeyer J.; Bargon J. A New Excitation Sequence to Observe the PASADENA Effect. J. Magn. Reson. A 1996, 120 (2), 249–257. 10.1006/jmra.1996.0121. [DOI] [Google Scholar]
  48. Pravdivtsev A.; Hövener J.-B.; Schmidt A. B. Frequency-Selective Manipulations of Spins for Effective and Robust Transfer of Spin Order from Parahydrogen to Heteronuclei in Weakly-Coupled Spin Systems. ChemPhysChem 2022, 23, e202100721 10.1002/cphc.202100721. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Sonnefeld A.; Bodenhausen G.; Sheberstov K. Polychromatic Excitation of Delocalized Long-Lived Proton Spin States in Aliphatic Chains. Phys. Rev. Lett. 2022, 10.1103/PhysRevLett.129.183203. [DOI] [PubMed] [Google Scholar]
  50. Rayner P. J.; Burns M. J.; Olaru A. M.; Norcott P.; Fekete M.; Green G. G. R.; Highton L. A. R.; Mewis R. E.; Duckett S. B. Delivering Strong 1 H Nuclear Hyperpolarization Levels and Long Magnetic Lifetimes through Signal Amplification by Reversible Exchange. Proc. Natl. Acad. Sci. U. S. A. 2017, 114 (16), E3188–E3194. 10.1073/pnas.1620457114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Pravdivtsev A. N.; Ellermann F.; Hövener J.-B. Selective Excitation Doubles the Transfer of Parahydrogen-Induced Polarization to Heteronuclei. Phys. Chem. Chem. Phys. 2021, 23 (26), 14146–14150. 10.1039/D1CP01891D. [DOI] [PubMed] [Google Scholar]
  52. Neese F.; Wennmohs F.; Becker U.; Riplinger C. The ORCA Quantum Chemistry Program Package. J. Chem. Phys. 2020, 152 (22), 224108 10.1063/5.0004608. [DOI] [PubMed] [Google Scholar]
  53. Becke A. D. A New Mixing of Hartree–Fock and Local Density-Functional Theories. J. Chem. Phys. 1993, 98 (2), 1372–1377. 10.1063/1.464304. [DOI] [Google Scholar]
  54. Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37 (2), 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  55. Caldeweyher E.; Bannwarth C.; Grimme S. Extension of the D3 Dispersion Coefficient Model. J. Chem. Phys. 2017, 147 (3), 034112 10.1063/1.4993215. [DOI] [PubMed] [Google Scholar]
  56. Weigend F.; Ahlrichs R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7 (18), 3297. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
  57. Wolinski K.; Hinton J. F.; Pulay P. Efficient Implementation of the Gauge-Independent Atomic Orbital Method for NMR Chemical Shift Calculations. J. Am. Chem. Soc. 1990, 112 (23), 8251–8260. 10.1021/ja00179a005. [DOI] [Google Scholar]
  58. Lenthe E. V.; Baerends E. J.; Snijders J. G. Relativistic Regular Two-Component Hamiltonians. J. Chem. Phys. 1993, 99 (6), 4597–4610. 10.1063/1.466059. [DOI] [Google Scholar]
  59. Van Lenthe E.; Baerends E. J.; Snijders J. G. Relativistic Total Energy Using Regular Approximations. J. Chem. Phys. 1994, 101 (11), 9783–9792. 10.1063/1.467943. [DOI] [Google Scholar]
  60. Sadlej A. J.; Snijders J. G.; Van Lenthe E.; Baerends E. J. Four Component Regular Relativistic Hamiltonians and the Perturbational Treatment of Dirac’s Equation. J. Chem. Phys. 1995, 102 (4), 1758–1766. 10.1063/1.468703. [DOI] [Google Scholar]
  61. Staroverov V. N.; Scuseria G. E.; Tao J.; Perdew J. P. Comparative Assessment of a New Nonempirical Density Functional: Molecules and Hydrogen-Bonded Complexes. J. Chem. Phys. 2003, 119 (23), 12129–12137. 10.1063/1.1626543. [DOI] [PubMed] [Google Scholar]
  62. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77 (18), 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  63. Jensen F. The Optimum Contraction of Basis Sets for Calculating Spin–Spin Coupling Constants. Theor. Chem. Acc. 2010, 126 (5–6), 371–382. 10.1007/s00214-009-0699-5. [DOI] [Google Scholar]
  64. Pantazis D. A.; Chen X.-Y.; Landis C. R.; Neese F. All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms. J. Chem. Theory Comput. 2008, 4 (6), 908–919. 10.1021/ct800047t. [DOI] [PubMed] [Google Scholar]
  65. Stoychev G. L.; Auer A. A.; Neese F. Automatic Generation of Auxiliary Basis Sets. J. Chem. Theory Comput. 2017, 13 (2), 554–562. 10.1021/acs.jctc.6b01041. [DOI] [PubMed] [Google Scholar]
  66. Barone V.; Cossi M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102 (11), 1995–2001. 10.1021/jp9716997. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz3c02980_si_001.pdf (3.7MB, pdf)
jz3c02980_si_004.zip (253.9KB, zip)
jz3c02980_si_005.zip (11.2KB, zip)
jz3c02980_si_007.pdf (947.4KB, pdf)

Data Availability Statement

The corresponding raw data can be accessed via Zenodo https://zenodo.org/doi/10.5281/zenodo.10512816.

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES