Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Jan 29;128(5):1867–1876. doi: 10.1021/acs.jpcc.3c05155

Properties of Layered TMDC Superlattices for Electrodes in Li-Ion and Mg-Ion Batteries

Conor Jason Price 1,*, Edward Allery David Baker 1, Steven Paul Hepplestone 1,*
PMCID: PMC10860140  PMID: 38352854

Abstract

graphic file with name jp3c05155_0006.jpg

In this work, we present a first-principles investigation of the properties of superlattices made from transition metal dichalcogenides for use as electrodes in lithium-ion and magnesium-ion batteries. From a study of 50 pairings, we show that, in general, the volumetric expansion, intercalation voltages, and thermodynamic stability of vdW superlattice structures can be well approximated with the average value of the equivalent property for the component layers. We also found that the band gap can be reduced, improving the conductivity. Thus, we conclude that superlattice construction can be used to improve material properties through the tuning of intercalation voltages toward specific values and by increasing the stability of conversion-susceptible materials. For example, we demonstrate how pairing SnS2 with systems such as MoS2 can change it from a conversion to an intercalation material, thus opening it up for use in intercalation electrodes.

Introduction

With the rise of renewable energy sources such as solar and wind power,1,2 and the growing popularity of electric vehicles,3,4 the need for cost-effective, efficient energy storage methods has increased dramatically. This has led to a substantial increase in battery research5 over the last two decades. Following the work of Whittingham6,7 and Goodenough8,9 in the 1970s and 1980s and the recent isolation of graphene by Novoselov and Geim,10,11 materials which possess a layered structure have received a lot of attention for energy storage. Materials such as NMC and its variants,12−17 the TMDCs,18−20 and the MXenes21−24 all demonstrate ideal electrode properties owing to the fact that their intrinsic structures possess van der Waals (vdW) gaps and provide natural channels for intercalated ions to occupy and travel through during the cycling of a cell. However, many of these materials possess voltages that lie outside ideal anode/cathode ranges, slow charging rates, and low capacities.

One clear extension to these layered materials can be achieved through the construction of superlattices and heterostructures. This allows for the utilization of not only the properties of the component materials but also the novel physics that can arise from their interface. The study of such nanocomposites has been facilitated by advances in fabrication techniques such as chemical vapor deposition,25 liquid exfoliation,26 and nucleation growth,27 which allow for monolayer control of material synthesis.28−30 The resultant electronic structure of vdW heterostructures is normally determined by Anderson’s rule31−33 with a few key considerations.34−37 The ability to predictably tailor the electronic properties has resulted in applications such as solar38−43 and photocatalytic44−46 cells, nanotransistors,47−49 and diodes.50,51

Heterostructures and superlattices have shown potential for electrode applications,52−55 with graphitic carbon being used as an additive to many MXenes56−58 and TMDCs such as MoS259,60 and SnS2.61−63 Experimental investigations have shown improvements to the cyclability,64 and first-principles studies have found a reduction in volumetric expansions;65,66 hence, there is opportunity in using superlattices to enhance the performance of intercalation electrodes. However, due to the immense number of possible combinations, no study can be exhaustive, and previous works have been limited to a few select cases of heterostructures or superlattices. Nevertheless, a comprehensive study of TMDCs and their composites is needed to better understand how superlattice construction can enhance electrode properties.

Here, we report on a theoretical modeling of TMDC superlattices, with a focus on their properties for use as electrode materials in Li- and Mg-ion cells. We present the material voltage profiles, showing how these change between single constituents and compounds, and also discuss how the thermodynamic stability of these materials upon intercalation can be used as a way to estimate the charge storage capacity. We discuss other properties that are important for electrode materials, such as volumetric expansion and the resultant electronic structure, which is important for electronic conduction. This allows us to offer insight into how a careful choice of materials in a superlattice can be used to improve these materials for electrode applications.

Methods

First-Principles Methods

In this work, first-principles techniques based on density functional theory were used to determine the structural and energetic properties of superlattice structures composed of vertically stacked layered MX2 materials and to evaluate how these properties change when intercalated with varying levels of lithium or magnesium. We focus on superlattices with 1T-phase TMDC components as these are found to be the preferred phase in their pristine and intercalated forms, though it is worth noting that the Group VI TMDCs, lithium-intercalated Group V TMDCs, and magnesium-intercalated Group IV TMDCs will prefer the H-phase structure.20 While other phases67,68 are possible for the TMDCs, such as 2H and the α-NaFeO2-like structure, their intercalation environments are similar to those of the 1T phase, so only the 1T is considered. In this stacking configuration, the layers are arranged such that the metal atoms of each TMDC layer are vertically aligned, as in the usual T-phase structure.

To investigate a range of superlattices based on TMDCs, we paired various TMDC materials with a second lattice-matched TMDC in a 1:1 match, as shown in Figure 1. To be considered “lattice-matched”, the two MX2-materials are required to have a lattice constant within 5% of each other. While the pairing of nonlattice-matched MX2-materials could be considered, there is a much larger combination space to investigate: phenomena such as moiré rotation effects,69−71 consideration of relative in-plane translations of the two atomic layers,68 and rippling72,73 are each deserving of a study of their own. Further to this, analysis of the effects of edge formation74−76 and the investigation of defects77 would also be required for a thorough description of a material in a working electrode. However, none of these can be explored until the fundamental properties of the core superlattices have been established. As such, we limit our investigation to pristine bulk superlattices formed through combinations of aligned MX2-materials with similar in-place lattice constants, with the addition of MoS2|SnS2, which shows strains between 5 and 10%. Further details of the material pairings, including the resultant strain and the formation energy, are presented in the Supporting Information.

Figure 1.

Figure 1

Open in a new tab

Schematic showing the 1:1 pairing of two lattice-matched TMDCs to form a superlattice. The layers are stacked such that the metal atoms of each layer are vertically aligned.

To achieve a finer sampling of intercalant concentrations than would be accessible through consideration of only the primitive unit cells, supercells consisting of (2 × 2 × 2) unit cells were used for the individual TMDC materials, and supercells consisting of (2 × 2 × 1) unit cells were used for the superlattice structures. Each of these corresponds to 24 atoms, eight MX2 formula units, and two TMDC layers. 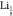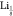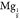These were then used as the bulk unit cells into which lithium and magnesium were intercalated for evaluation of voltages and thermodynamic stability, giving us access to a range of lithium concentrations between Inline graphic MX2 and LiMX2 in increments of Inline graphic MX2. Similarly, we can access magnesium concentrations between Inline graphic MX2 and MgMX2 in increments of Inline graphic MX2.

We determine the preferred sites of intercalation to be those with octahedral coordination, a further discussion of which is presented in the Supporting Information. Using the supercell sizes described above, we thus have access to eight potential octahedrally coordinated intercalation sites, which allow for 24 potential intercalant filling configurations. Each of these has been explored, and combinations of different concentrations have been used to emulate clustering effects.78−81 Further details of these are presented in the Supporting Information. For a given intercalant concentration, the configuration that results in the lowest energy structure is used for the evaluation of key electrode properties, such as calculation of the intercalation voltage and the assessment of the thermodynamic stability.

The calculations performed here employed the Vienna Ab initio Simulation Package (VASP).82−85 The valence electrons included for each species are indicated in the Supporting Information. The projector augmented wave method86 was used to describe the interaction between core and valence electrons, and a plane-wave basis set was used with an energy cutoff of 700 eV. All structural relaxations were completed using the Perdew–Burke–Ernzerhof (PBE)87 functional and converged to a force tolerance of 0.01 eV/Å per atom, while electronic self-consistency is considered to have an accuracy of 10–7 eV. Γ-centered Monkhorst–Pack grids88 of k-points equivalent to a 6 × 6 × 6 grid in the supercells are used throughout, and we have allowed for optimization of collinear spin. Van der Waals interactions have been addressed using the zero-damping DFT-D3 method of Grimme.89 Further calculation details are presented in the Supporting Information.

Methods for Material Evaluation

To compare different levels of lithium-intercalated superlattice (SL = MX2M′X′2) the voltage, V, can be calculated using

graphic file with name jp3c05155_m005.jpg 1

for total lithium content b2 > b1, and energy of the superlattice structure with b intercalant atoms per SL formula unit 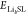Inline graphic. In this work, we consider values of 0 ≤ b ≤ 2, with b = 2 corresponding to one intercalant ion per metal atom of the host structure. z is the valency of the intercalant (z = 1 for the case of lithium, z = 2 for magnesium), and ELi is the energy of a lithium atom as found in bulk. Each occurrence of Li should be replaced with an equivalent of Mg for magnesium intercalation. Further discussion of voltage calculation is presented in the Supporting Information.

Previous first-principles works20 have assessed the stability of individual TMDCs when intercalated with lithium or magnesium, with intercalation limits depending on how favorable the formation of secondary products (for example, Li2X or MgX) is. Typically, the formation of these compounds results in material amorphization and the irreversible loss of the layered TMDC structure. Here, we have developed a generalized approach for calculating EIS, a measure of stability and hence the reversible intercalation capacity of a material. This is given by

graphic file with name jp3c05155_m007.jpg 2

for lithium intercalation and by

graphic file with name jp3c05155_m008.jpg 3

for magnesium intercalation. In both of these, ΔH(A) gives the enthalpy of formation of compound A, E(A) gives the energy of compound A, and ΔμB gives the chemical potential of elemental species B (in the intercalated SL structure) relative to its chemical potential when it is in its elemental bulk structure. EIS is assessed for each intercalant concentration, with positive values indicating that the host TMDC is thermodynamically stable with intercalation and resists conversion to Li2S, MgS, or an equivalent compound. Negative values of EIS then indicate that a material is susceptible to conversion, and the concentration at which EIS is negative gives the limit of reversible intercalation. Further discussion of EIS and its origins are provided in the Supporting Information.

Results

Volumetric Expansion

One important metric for assessing the promise of a material for electrode applications is the volumetric expansion arising from intercalation. We calculate this expansion with respect to the unintercalated structure using 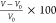Inline graphic for initial volume V0 and the final volume V. Importantly, for electrode applications, we show that there is minimal volumetric expansion with the intercalation of these superlattices and highlight this with some examples in Figure 2. When intercalated with lithium (magnesium), we see that the SnS2|SnSe2 superlattice has a total volumetric expansion of 10.9% (21.4%), for ZrS2|ZrSe2, we see a total expansion of 1.8% (3.3%), and for NbS2|TaS2, we see a total expansion of 10.2% (12.9%). Thus, the minimal expansion demonstrated by layered materials holds upon construction of the superlattice, with most superlattices expanding by less than 20% (30%). These values are comparable with other layered materials that have demonstrated success as intercalation electrodes, including LiCoO290,91 (2–3.25%), NMC92 (8.44%), and graphite93 (13.2%), as well as the <30% generally seen for the TMDCs.20

Figure 2.

Figure 2

Open in a new tab

Volume expansion with intercalation for the selected TMDC superlattices, calculated with respect to the unintercalated structures using 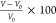Inline graphic. (a) Data for lithium intercalation and (b) magnesium intercalation. In each of these, the x-axis gives the number of intercalant ions (NLi/Mg) per metal atom of the host structure (NM + NM′).

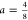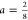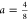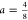We note the surprising reduction in volume expansion of ZrS2 as lithium content increases beyond Inline graphic, and this behavior extends to the superlattice structure. The same can be seen as magnesium content increases beyond Inline graphic (corresponding to the same amount of charge transfer to the host structure as Inline graphic of lithium), though the volume increases again for larger intercalant concentrations. We also notice in Figure 2b a larger increase in the volume for SnS2 and TaS2 with magnesium intercalation beyond Inline graphic, and this behavior carries over to the corresponding superlattices.

A closer evaluation shows that for lithium intercalation, the volumetric expansions of the superlattices fall within 2% of the mean of the volumetric expansion for the relevant components. Thus, if the superlattice volumetric expansion were to be estimated by calculating the mean of the volumetric expansion arising in the component TMDCs, then we could expect the result to deviate by up to a 2% error from what is observed in the actual superlattice. This close agreement is not surprising considering the vdW gaps between MX2 layers.

We note a larger expansion upon magnesium intercalation than with lithium intercalation and attribute this to the greater charge donation from magnesium than with lithium. This can be seen in Figure 2. For example, SnS2|SnSe2 expands by 10.7% when half-intercalated with magnesium and 10.9% when fully intercalated with lithium (hence having similar levels of charge donation). Similarly, ZrS2|ZrSe2 expands by 1.7% when half-intercalated with magnesium and by 1.2% when fully intercalated with lithium, and NbS2|TaS2 expands by 8.7% when half-intercalated with magnesium and by 10.2% when fully intercalated with lithium. We rationalize this as the chalcogen species in the intercalated structures have larger negative charges, and the metal species have smaller positive charges. Consequently, there is a reduced attraction between the M and X species but an increased repulsion between the X species. This leads to a “stretching” of the MX2 layers along the c-axis. Comparable results are also seen for the other superlattices considered, further details of which are presented in the Supporting Information.

Voltages

In Figure 3, we present the voltage profiles and thermodynamic stability (indicated by EIS) of the highlighted superlattices with lithium and magnesium intercalation. For comparison, we have also included the results of the relevant individual TMDCs which were presented in our previous work.20 In general, we find that the intercalation voltage of the formed superlattice is intermediate with the profiles of the component materials. This is best highlighted with lithium-intercalated SnS2|SnSe2: SnS2 is shown to have a flat voltage profile at 1.80 V, and SnSe2 has a flat voltage of 1.85 V, with a minor step at the start of intercalation of 1.89 V. The superlattice then shows an almost flat voltage of 1.83 V, intermediate in value to those of the components in both shape and magnitude. We show a similar result for lithium-intercalated NbS2|TaS2, where the more distinct features of the NbS2 and TaS2 components are reproduced, maintaining the intermediate voltage profile.

Figure 3.

Figure 3

Open in a new tab

Intercalation voltages and EIS for selected superlattices. (a) Results for lithium intercalation and (b) results for magnesium intercalation. In each of these, the top shows the voltage profile, and the bottom shows the variation of EIS with intercalation. The superlattice data is presented in purple, and the data for the component materials is color-coded in red or blue.

We note that the voltage behavior seen with magnesium intercalation is very similar to that seen with lithium intercalation, and we highlight this with the SnS2|SnSe2 and GeS2|SnS2 structures. These show that the flat voltage profiles of the component materials result in a similarly flat voltage profile in the superlattices. Further, the dramatic drop in voltage for high magnesium concentrations in ZrTe2 produces a similar drop in voltage for high magnesium concentrations in the SnSe2|ZrTe2 superlattice. This SnSe2|ZrTe2 superlattice also suggests an exciting use of superlatticing: whereas the drop seen for ZrTe2 reaches a voltage of −0.64 V, the voltage drop demonstrated by the superlattice reaches a value of −0.02 V. Although this value is still negative, it suggests that the inclusion of SnSe2, a material that retains a constant voltage across the concentration range, limits the drop shown by the superlattice. The HfS2|ZrS2 further supports this: though the HfS2 component shows a negative voltage at high concentrations, the superlattice retains a positive value due to the inclusion of the ZrS2. This effect has been observed before, both using first-principles methods94 and experimentally.64

While some materials deviate from this with voltage profiles that extend beyond the bounds of the component materials, such as with the lithium-intercalated NiS2|TiS2 and MoS2|SnS2, and the magnesium-intercalated NbS2|TaS2 and MoS2|SnS2, these deviations do not remove the underlying shape of the component materials. Further, comparing the average voltages of the superlattice with those of the components highlights that taking an average of the component materials is a reliable method to predict the voltage of the formed superlattice. These comparisons, along with the results of 41 other superlattice structures which show the same result, are presented in the Supporting Information.

As mentioned above, electrode materials should ideally have a well-defined voltage,95 and so, based only on the voltage profiles in Figure 3a, pairings such as MoS2|SnS2 can be ruled out as a promising electrode material for lithium ion batteries. As one of the components (MoS2) has a large voltage variation, the resultant voltage for the superlattice can also be expected to have a large variation. Similarly, the magnesium-intercalation voltage profiles of NbS2|TaS2, SnSe2|ZrTe2, and MoS2|SnS2 vary significantly across the magnesium concentration range due to the large variation of one or both of the component TMDCs. However, this does also suggest that a large variation seen for a TMDC can be reduced by pairing with a TMDC with a constant voltage profile. For example, TiS2 varies by 0.59 V across the concentration range considered here. However, when paired with NiS2 (which varies by 0.11 V), the variation of the resultant NiS2|TiS2 superlattice is 0.17 V. Therefore, if a particular TMDC is desirable for use as an electrode but possesses a voltage which varies significantly, its voltage could be “pinned” by pairing it with a suitable partner.

The intercalation voltage of anode materials should be lower than 2 V, ideally in the range 0.5–1.5 V,95 and for cathode materials, it should exceed 3 V.96 As the pairing of two TMDCs results in a voltage that is intermediate to both, it would be sensible to combine materials that are energetically alike. For anodes, two TMDCs with low voltages should be combined, and for cathodes, two TMDCs with high voltages should be combined. If a low-voltage TMDC (e.g., SnS2 with a voltage of 1.80 V) were to be combined with a high-voltage TMDC (e.g., ScS2 with a voltage of 3.66 V97), the voltage of the superlattice (e.g., 2.69 V, see Supporting Information) would be poor for both anode and cathode applications.

Thermodynamic Stability

The values of EIS for a range of intercalant concentrations within the superlattices are shown in Figure 3a,b. As was demonstrated with the evolution of the intercalation voltage with concentration, the evolution of EIS with intercalant concentration follows a trend that is an intermediate of the two component materials, and the value of EIS of a superlattice at a given concentration is well approximated by calculating the average of the component materials. This suggests that, as EIS is an indicator of the thermodynamic stability of a given TMDC against conversion, a highly stable material (characterized by a high, positive value of EIS) can be paired with a material that is susceptible to conversion (characterized by a low or negative value of EIS) to make a superlattice that is also resistant to conversion. This is shown with the pairing of SnS2|SnSe2, GeS2|SnS2, and MoS2|SnS2 with lithium intercalation. In each of these, SnS2 is the component with a negative value of EIS across the range of lithium concentration. However, the formed superlattices have positive values of EIS, indicating the stability that has arisen from the inclusion of a thermodynamically stable component. We see the same result of a conversion-resistant component stabilizing a conversion-susceptible component with the pairings NiS2|TiS2 and HfS2|PdS2 for magnesium intercalation.

The importance of the improved resistance to conversion is highlighted by consideration of the gravimetric charge capacity, a quantity that is crucial for characterizing a material for electrode applications. We have used the range over which EIS has a positive value to calculate the reversible gravimetric charge capacities for each of the superlattice structures, which are presented in Figure 4, along with the capacity of the component materials for comparison.20 Aside from the improvements in stability, we can also expect improvements in capacity simply due to the inclusion of a lighter material. For example, hafnium is a Period-VI element, so the specific capacity of 109.7 mA h g–1 for lithium intercalation (219.4 mA h g–1 for magnesium intercalation) is relatively low despite it possessing positive values of EIS across the intercalation range. However, combining this with a TMDC composed of a lighter transition metal, such as ZrS2 in HfS2|ZrS2, increases this to 140.5 mA h g–1 (281.0 mA h g–1). Further, superlattice construction can, in some cases, provide a reversible charge capacity that is better than either of the components. This is highlighted by the intercalation of SnS2|SnSe2: SnS2 is shown to be susceptible to conversion reactions, so the capacity is zero. However, a combination with SnSe2 (which possesses a positive EIS for both intercalants) results in a capacity of 120.9 mA h g–1 (241.8 mA h g–1). We can therefore improve not just the voltage (through “pinning”) and thermodynamic stability (by increasing EIS) of a TMDC through superlatticing but also the gravimetric charge capacity.

Figure 4.

Figure 4

Open in a new tab

Reversible gravimetric charge capacity of selected superlattices and their component TMDCs for lithium (top) and magnesium (bottom) intercalation. The superlattice results are presented in purple, and the corresponding results for the component materials are presented in red and blue. Missing bars indicate materials with zero reversible capacity.

Electronic Structure

One of the main reasons the TMDCs have received a lot of attention in recent years is for the wide range of electronic properties the family can exhibit, and their superlattices/heterostructures have been of further interest for the electronic physics that can arise from the combination of two materials.34−37 For electrode applications, electronically conductive materials are preferred so that compensating electrons from an external circuit can balance the positively charged lithium/magnesium ions.

We find that the electronic structure of a superlattice can be obtained crudely by superimposing the electronic structures of the constituent TMDC materials. As a result, combining TMDCs that offer a relative type II band alignment (staggered gap) results in a superlattice with a band gap that is smaller than either of the components, and combining a metallic TMDC with a TMDC that possesses a band gap results in a superlattice that is also metallic. Though exact band gap values can be sensitive to the choice of functional and the level of strain induced from lattice matching, this observation agrees with many previous works36 and shows that the construction of a superlattice provides a simple method through which the electrical conductivity can be improved.

The introduction of ionic species into the host structure dramatically changes the nature of interlayer bonding, however, and consequent changes to the electronic structure can be expected. Here, we investigate how the electronic structure of superlattice structures changes with intercalation. In Figure 5, we present the electronic structure density of states (DOS) for NbS2|TaS2 (5a), HfS2|ZrS2 (5b), and GeS2|SnS2 (5c). These show the electronic DOS for the intercalated superlattices, along with the limit of lithium and magnesium intercalation corresponding to one intercalant per metal atom in the host supercell. The associated electronic band structures are presented in the Supporting Information. We have qualitatively aligned to the high-energy occupied states of the unintercalated superlattice at Γ, allowing us to comment on the relative position of the highest occupied molecular orbital (HOMO) level, with further details presented in the Supporting Information. We emphasize that this is an aesthetic choice made purely for easier comparison of the highest-occupied states of the pristine and intercalated materials.

Figure 5.

Figure 5

Open in a new tab

Electronic density of states (DOS) for pristine and intercalated superlattice structures. NbS2|TaS2 data is presented in (a), HfS2|ZrS2 in (b), and GeS2|SnS2 in (c). Pristine data are presented in black, data for lithium-intercalated structures in red, and data for magnesium-intercalated structures in blue. Each has been aligned with high-energy-occupied states of the pristine superlattice material. The energy of the highest occupied state (EHOMO) is indicated with dashed lines. Corresponding band structures are presented in the Supporting Information.

We identify several broad groups describing the electronic behavior: the superlattice either (i) retains a conductive nature with intercalation, (ii) undergoes a semiconductor to conductor transition, (iii) possesses an insulating nature before intercalation and at the intercalation level corresponding to one intercalant per metal atom in the host supercell, or (iv) undergoes a conductor to semiconductor transition. The superlattice NbS2|TaS2 is an example of group (i), possessing no band gap at the start and end of intercalation. We can see from Figure 5a (and the corresponding band structure in the Supporting Information) that this is due to the HOMO lying in the middle of a linear band that extends from −0.5 eV at M to 2.5 eV between K and Γ. Electrons that are transferred from the intercalants to the host then simply occupy the unoccupied states in this band, so the HOMO level progressively rises. For HfS2|ZrS2, an example of group (ii), we see a very similar behavior, but the presence of an initial band gap means that there is a much larger initial jump in the position of the HOMO. However, the continuous range of bands beyond this allows for a gradual rise in the HOMO level, as seen for group (i). This is presented in Figure 5b. Figure 5c shows the electronic DOS for the GeS2|SnS2 superlattice and its intercalated forms, where we see the pristine structure possesses a band gap of ∼0.6 eV. Upon lithium intercalation, the HOMO shifts to intersect the two lowest-energy unoccupied states of the pristine structure, becoming metallic as with a type (ii) material. However, upon intercalation with magnesium, these states become fully occupied, and the HOMO level then sits at the bottom of a further band gap.

Though HSE and GW calculations typically offer improvements in accuracy over LDA and GGA functionals, this is not universally true for the TMDCs. Some works have found cases of GGA functionals producing band gaps closer to experimental values than HSE98 or GW99,100 calculations. Our previous work36 considered the band alignment of TMDCs and also found that HSE calculations resulted in the same conclusions as those obtained in the PBE functional. As such, we do not use these higher levels of calculation as there is not a guaranteed improvement in the results, nor do we expect any changes to the conclusions already presented.

Further Considerations

Beyond the above discussions of volumetric expansion, intercalation voltage, stability, and electronic structure, all of which are important considerations for any electrode material, we here present a brief discussion of diffusion characteristics, elastic properties, and charge transfer, as these can also play an important role in electrode function. Further details of these are presented in the Supporting Information.

Climbing-image nudged elastic band101 calculations were used to identify the octahedrally coordinated intercalation site to be the lowest in energy, with ionic diffusion predominantly occurring between adjacent octahedral and tetrahedral sites. The barriers to this diffusion in the superlattices are shown to be intermediate with their TMDC components. Thus, due to the exponential dependence on the diffusion barrier in the Arrhenius rate, the rate of diffusion through a superlattice is lower than the average of the rates of the two components but faster than the rate of the component with the largest barrier.

We also calculate the elastic tensor of the superlattices discussed above. We find all of these superlattices to be elastically stable, with the exception of magnesium-intercalated HfS2|PdS2 and magnesium-intercalated MoS2|SnS2. The bulk, shear, and Young’s moduli generally increase with the addition of an intercalant, with larger values obtained with magnesium intercalation, indicating the strengthened interaction between TMDC layers due to the addition of an ionic intercalant. The elastic values of the superlattices are again found to be intermediate to those of the component TMDCs.102

Finally, we also present charge analysis in the Supporting Information as this can offer insight into the electronic structure and intercalation properties. As there is relatively little charge transfer between component layers upon superlattice construction, there is correspondingly minimal change to the electronic structure of component TMDCs upon construction of a superlattice/heterostructure.36,37 Consequently, the evolution of the superlattice electronic structure with intercalation is very similar to what has been observed for the component materials,20 i.e., the donated electrons from intercalated lithium or magnesium gradually fill the unoccupied states of the host structure, as discussed above. We find that the charge transfer from the intercalant to the host material is intermediate to the charge transfer of the component layers, which explains the observed “averaging” of the electrode properties of volumetric expansion, voltage, and stability assessed here.

Conclusions

We have presented here the results of an investigation of intercalation into transition metal dichalcogenide superlattices with both lithium and magnesium. The volumetric expansion, electronic structure, intercalation voltages, and thermodynamic stability determined through phase diagrams have all been considered, as the information they provide is essential for the consideration of materials for use as electrodes. Upon construction of a superlattice, we find that many of these properties can be well approximated through the consideration of the equivalent properties for the component layers. For example, if the superlattice volumetric expansion were to be estimated by calculating the mean of the volumetric expansion arising in the component TMDCs, we could expect the result to deviate by up to a 2% error from what is observed in the actual superlattice, and the voltage profiles of the component materials provide bounds to the voltage profile exhibited by the constructed superlattice. Further, the unoccupied states of the host material are progressively filled with the addition of an intercalant, which follows the behavior observed with the individual TMDCs. Most interestingly, the construction of superlattices allows for many improvements to component materials: the construction of a superlattice can result in a reduction of the electronic band gap, thus improving electronic conductivity; conversion-resistant materials can be used to increase the stability of conversion-susceptible materials, extending their cyclability and lifetime; and materials can be chosen such that the overall voltage can be tuned toward specific values.

The conclusions presented in this work should also extend to other layered materials. In particular, the layered transition metal oxides offer a group of materials that are very closely related to the TMDCs used to construct the superlattices here and have already demonstrated success as electrodes. Using the ideas used here, however, they could have their voltages tuned, their intercalation stability improved, and ultimately have an increased energy storage capacity.

Acknowledgments

The authors would like to acknowledge financial support from the EPSRC (United Kingdom) (grant no. EP/L015331/1) and the Materials Chemistry Consortium (EP/L000202, EP/R029431, and EP/X035859). The authors acknowledge the use of the University of Exeter HPC facility. This work used the Isambard 2 UK National Tier-2 HPC Service (http://gw4.ac.uk/isambard/) operated by GW4 and the UK Met Office and funded by EPSRC (EP/T022078/1). We wish to acknowledge the use of the EPSRC-funded Physical Sciences Data-Science Service hosted by the University of Southampton and STFC under grant number EP/S020357/1.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcc.3c05155.

  • Further details of the methodology, including the results of nudged elastic band calculations and the derivation of limits for thermodynamic phase diagrams, calculation of strain and formation energy associated with constructing each superlattice, numerical values of the results presented in the main article, along with calculated elastic properties and charge analysis, and relevant electrode properties of an additional 41 superlattice structures (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp3c05155_si_001.pdf (5.5MB, pdf)

References

  1. Dunn B.; Kamath H.; Tarascon J.-M. Electrical Energy Storage for the Grid: A Battery of Choices. Science 2011, 334, 928–935. 10.1126/science.1212741. [DOI] [PubMed] [Google Scholar]
  2. Davies D. M.; Verde M. G.; Mnyshenko O.; Chen Y. R.; Rajeev R.; Meng Y. S.; Elliott G. Combined economic and technological evaluation of battery energy storage for grid applications. Nat. Energy 2019, 4, 42–50. 10.1038/s41560-018-0290-1. [DOI] [Google Scholar]
  3. Nykvist B.; Nilsson M. Rapidly falling costs of battery packs for electric vehicles. Nat. Clim. Change 2015, 5, 329–332. 10.1038/nclimate2564. [DOI] [Google Scholar]
  4. Castelvecchi D. Electric cars and batteries: how will the world produce enough?. Nature 2021, 596, 336–339. 10.1038/d41586-021-02222-1. [DOI] [PubMed] [Google Scholar]
  5. Cheng X. B.; Zhang R.; Zhao C. Z.; Zhang Q. Toward Safe Lithium Metal Anode in Rechargeable Batteries: A Review. Chem. Rev. 2017, 117, 10403–10473. 10.1021/acs.chemrev.7b00115. [DOI] [PubMed] [Google Scholar]
  6. Whittingham M. S. The Role of Ternary Phases in Cathode Reactions. J. Electrochem. Soc. 1976, 123, 315–320. 10.1149/1.2132817. [DOI] [Google Scholar]
  7. Whittingham M. S. Electrical Energy Storage and Intercalation Chemistry. Science 1976, 192, 1126–1127. 10.1126/science.192.4244.1126. [DOI] [PubMed] [Google Scholar]
  8. Mizushima K.; Jones P.; Wiseman P.; Goodenough J. LixCoO2 (0 < x<-1): A new cathode material for batteries of high energy density. Mater. Res. Bull. 1980, 15, 783–789. 10.1016/0025-5408(80)90012-4. [DOI] [Google Scholar]
  9. Mizushima K.; Jones P. C.; Wiseman P. J.; Goodenough J. B. LixCoO2 (0 < x < 1): A new cathode material for batteries of high energy density. Solid State Ionics 1981, 3–4, 171–174. 10.1016/0167-2738(81)90077-1. [DOI] [Google Scholar]
  10. Novoselov K. S.; Geim A. K.; Morozov S. V.; Jiang D.; Zhang Y.; Dubonos S. V.; Grigorieva I. V.; Firsov A. A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. 10.1126/science.1102896. [DOI] [PubMed] [Google Scholar]
  11. Geim A. K.; Novoselov K. S.. Nanoscience and Technology: A Collection of Reviews from Nature Journals; Co-Published with Macmillan Publishers Ltd: UK, 2009; pp 11–19. [Google Scholar]
  12. Wan D. Y.; Fan Z. Y.; Dong Y. X.; Baasanjav E.; Jun H.-B.; Jin B.; Jin E. M.; Jeong S. M. Effect of Metal (Mn, Ti) Doping on NCA Cathode Materials for Lithium Ion Batteries. J. Nanomater. 2018, 2018, 1–9. 10.1155/2018/8082502. [DOI] [Google Scholar]
  13. Kasnatscheew J.; Röser S.; Börner M.; Winter M. Do Increased Ni Contents in LiNixMnyCozO2 (NMC) Electrodes Decrease Structural and Thermal Stability of Li Ion Batteries? A Thorough Look by Consideration of the Li+ Extraction Ratio. ACS Appl. Energy Mater. 2019, 2, 7733–7737. 10.1021/acsaem.9b01440. [DOI] [Google Scholar]
  14. Nam G. W.; Park N. Y.; Park K. J.; Yang J.; Liu J.; Yoon C. S.; Sun Y. K. Capacity Fading of Ni-Rich NCA Cathodes: Effect of Microcracking Extent. ACS Energy Lett. 2019, 4, 2995–3001. 10.1021/acsenergylett.9b02302. [DOI] [Google Scholar]
  15. Li W.; Lee S.; Manthiram A. High-Nickel NMA: A Cobalt-Free Alternative to NMC and NCA Cathodes for Lithium-Ion Batteries. Adv. Mater. 2020, 32, 2002718. 10.1002/adma.202002718. [DOI] [PubMed] [Google Scholar]
  16. Phillip N. D.; Westover A. S.; Daniel C.; Veith G. M. Structural Degradation of High Voltage Lithium Nickel Manganese Cobalt Oxide (NMC) Cathodes in Solid-State Batteries and Implications for Next Generation Energy Storage. ACS Appl. Energy Mater. 2020, 3, 1768–1774. 10.1021/acsaem.9b02230. [DOI] [Google Scholar]
  17. R. N R.; Bosubabu D.; M. G. K. B.; Ramesha K. Tuning of Ni, Mn, and Co (NMC) content in 0.4(LiNixMnyCozO2)·0.4(Li2MnO3) toward stable high-capacity lithium-rich cathode materials. ACS Appl. Energy Mater. 2020, 3, 10872–10881. 10.1021/acsaem.0c01897. [DOI] [Google Scholar]
  18. Gao Y.-P.; Wu X.; Huang K.-J.; Xing L.-L.; Zhang Y.-Y.; Liu L. Two-dimensional transition metal diseleniums for energy storage application: a review of recent developments. CrystEngComm 2017, 19, 404–418. 10.1039/C6CE02223E. [DOI] [Google Scholar]
  19. Gao Y.-P.; Xu J.; Huang K.-J.; Lu H.; Pang Y.-X.; Li G.-q. An overview of the current status and prospects of cathode materials based on transition metal sulfides for magnesium-ion batteries. CrystEngComm 2021, 23, 7546–7564. 10.1039/D1CE01029H. [DOI] [Google Scholar]
  20. Price C. J.; Baker E. A. D.; Hepplestone S. P. First principles study of layered transition metal dichalcogenides for use as electrodes in Li-ion and Mg-ion batteries. J. Mater. Chem. A 2023, 11, 12354–12372. 10.1039/D3TA00940H. [DOI] [Google Scholar]
  21. Chaudhari N. K.; Jin H.; Kim B.; San Baek D.; Joo S. H.; Lee K. MXene: an emerging two-dimensional material for future energy conversion and storage applications. J. Mater. Chem. A 2017, 5, 24564–24579. 10.1039/C7TA09094C. [DOI] [Google Scholar]
  22. Greaves M.; Barg S.; Bissett M. A. MXene-Based Anodes for Metal-Ion Batteries. Batteries Supercaps 2020, 3, 214–235. 10.1002/batt.201900165. [DOI] [Google Scholar]
  23. Ming F.; Liang H.; Huang G.; Bayhan Z.; Alshareef H. N. MXenes for Rechargeable Batteries Beyond the Lithium-Ion. Adv. Mater. 2021, 33, 2004039. 10.1002/adma.202004039. [DOI] [PubMed] [Google Scholar]
  24. Chen Q. D.; Yuan S. F.; Dai J. H.; Song Y. Functionalized M2TiC2Tx MXenes (M = Cr and Mo; T = F, O, and OH) as high performance electrode materials for sodium ion batteries. Phys. Chem. Chem. Phys. 2021, 23, 1038–1049. 10.1039/D0CP01846E. [DOI] [PubMed] [Google Scholar]
  25. Sukma Aji A.; Izumoto M.; Suenaga K.; Yamamoto K.; Nakashima H.; Ago H. Two-step synthesis and characterization of vertically stacked SnS–WS2 and SnS–MoS2 p–n heterojunctions. Phys. Chem. Chem. Phys. 2018, 20, 889–897. 10.1039/C7CP06823A. [DOI] [PubMed] [Google Scholar]
  26. Coleman J. N.; Lotya M.; O’Neill A.; Bergin S. D.; King P. J.; Khan U.; Young K.; Gaucher A.; De S.; Smith R. J.; et al. Two-Dimensional Nanosheets Produced by Liquid Exfoliation of Layered Materials. Science 2011, 331, 568–571. 10.1126/science.1194975. [DOI] [PubMed] [Google Scholar]
  27. Li J.; Yang X.; Liu Y.; Huang B.; Wu R.; Zhang Z.; Zhao B.; Ma H.; Dang W.; Wei Z.; et al. General synthesis of two-dimensional van der Waals heterostructure arrays. Nature 2020, 579, 368–374. 10.1038/s41586-020-2098-y. [DOI] [PubMed] [Google Scholar]
  28. Singh J.. In Physics of Semiconductors and Their Heterostructures; Brown A. T., Ed.; McGraw-Hill, Inc, 1993. [Google Scholar]
  29. McDonnell S. J.; Wallace R. M. Atomically-thin layered films for device applications based upon 2D TMDC materials. Thin Solid Films 2016, 616, 482–501. 10.1016/j.tsf.2016.08.068. [DOI] [Google Scholar]
  30. Chen T.; Ding D.; Shi J.; Wang G.; Kou L.; Zheng X.; Ren X.; Liu X.; Jin C.; Zhong J.; Hao G. Lateral and Vertical MoSe2-MoS2 Heterostructures via Epitaxial Growth: Triggered by High-Temperature Annealing and Precursor Concentration. J. Phys. Chem. Lett. 2019, 10, 5027–5035. 10.1021/acs.jpclett.9b01961. [DOI] [PubMed] [Google Scholar]
  31. Anderson R. L. Germanium-Gallium Arsenide Heterojunctions [Letter to the Editor]. IBM J. Res. Dev. 1960, 4, 283–287. 10.1147/rd.43.0283. [DOI] [Google Scholar]
  32. Chiu M.-H.; Tseng W.-H.; Tang H.-L.; Chang Y.-H.; Chen C.-H.; Hsu W.-T.; Chang W.-H.; Wu C.-I.; Li L.-J. Band Alignment of 2D Transition Metal Dichalcogenide Heterojunctions. Adv. Funct. Mater. 2017, 27, 1603756. 10.1002/adfm.201603756. [DOI] [Google Scholar]
  33. Koda D. S.; Bechstedt F.; Marques M.; Teles L. K. Trends on band alignments: Validity of Anderson’s rule in SnS2- and SnSe-based van der Waals heterostructures. Phys. Rev. B 2018, 97, 165402. 10.1103/PhysRevB.97.165402. [DOI] [Google Scholar]
  34. Kou L.; Frauenheim T.; Chen C. Nanoscale Multilayer Transition-Metal Dichalcogenide Heterostructures: Band Gap Modulation by Interfacial Strain and Spontaneous Polarization. J. Phys. Chem. Lett. 2013, 4, 1730–1736. 10.1021/jz400668d. [DOI] [PubMed] [Google Scholar]
  35. Tang K.; Qi W. Moiré-Pattern-Tuned Electronic Structures of van der Waals Heterostructures. Adv. Funct. Mater. 2020, 30, 2002672. 10.1002/adfm.202002672. [DOI] [Google Scholar]
  36. Davies F. H.; Price C. J.; Taylor N. T.; Davies S. G.; Hepplestone S. P. Band alignment of transition metal dichalcogenide heterostructures. Phys. Rev. B 2021, 103, 045417. 10.1103/physrevb.103.045417. [DOI] [Google Scholar]
  37. Besse R.; Silveira J. F. R. V.; Jiang Z.; West D.; Zhang S.; Da Silva J. L. F. Beyond the Anderson rule: importance of interfacial dipole and hybridization in van der Waals heterostructures. 2D Materials 2021, 8, 041002. 10.1088/2053-1583/ac1902. [DOI] [Google Scholar]
  38. Ahn J.; Jeon P. J.; Raza S. R. A.; Pezeshki A.; Min S. W.; Hwang D. K.; Im S. Transition metal dichalcogenide heterojunction PN diode toward ultimate photovoltaic benefits. 2D Materials 2016, 3, 045011. 10.1088/2053-1583/3/4/045011. [DOI] [Google Scholar]
  39. Furchi M. M.; Höller F.; Dobusch L.; Polyushkin D. K.; Schuler S.; Mueller T. Device physics of van der Waals heterojunction solar cells. npj 2D Mater. Appl. 2018, 2, 3. 10.1038/s41699-018-0049-3. [DOI] [Google Scholar]
  40. Linghu J.; Yang T.; Luo Y.; Yang M.; Zhou J.; Shen L.; Feng Y. P. High-Throughput Computational Screening of Vertical 2D van der Waals Heterostructures for High-efficiency Excitonic Solar Cells. ACS Appl. Mater. Interfaces 2018, 10, 32142–32150. 10.1021/acsami.8b09454. [DOI] [PubMed] [Google Scholar]
  41. Zhao Q.; Guo Y.; Zhou Y.; Yao Z.; Ren Z.; Bai J.; Xu X. Band alignments and heterostructures of monolayer transition metal trichalcogenides MX 3 (M = Zr, Hf; X = S, Se) and dichalcogenides MX2 (M = Tc, Re; X = S, Se) for solar applications. Nanoscale 2018, 10, 3547–3555. 10.1039/C7NR08413G. [DOI] [PubMed] [Google Scholar]
  42. Din H. U.; Idrees M.; Rehman G.; Nguyen C. V.; Gan L.-Y.; Ahmad I.; Maqbool M.; Amin B. Electronic structure, optical and photocatalytic performance of SiC–MX2 (M = Mo, W and X = S, Se) van der Waals heterostructures. Phys. Chem. Chem. Phys. 2018, 20, 24168–24175. 10.1039/C8CP03933J. [DOI] [PubMed] [Google Scholar]
  43. Idrees M.; Din H. U.; Ali R.; Rehman G.; Hussain T.; Nguyen C. V.; Ahmad I.; Amin B. Optoelectronic and solar cell applications of Janus monolayers and their van der Waals heterostructures. Phys. Chem. Chem. Phys. 2019, 21, 18612–18621. 10.1039/C9CP02648G. [DOI] [PubMed] [Google Scholar]
  44. Li C.; Cao Q.; Wang F.; Xiao Y.; Li Y.; Delaunay J.-J.; Zhu H. Engineering graphene and TMDs based van der Waals heterostructures for photovoltaic and photoelectrochemical solar energy conversion. Chem. Soc. Rev. 2018, 47, 4981–5037. 10.1039/C8CS00067K. [DOI] [PubMed] [Google Scholar]
  45. Wang Z.; Luo Z.; Li J.; Yang K.; Zhou G. 2D van der Waals heterostructures of graphitic BCN as direct Z-scheme photocatalysts for overall water splitting: the role of polar π-conjugated moieties. Phys. Chem. Chem. Phys. 2020, 22, 23735–23742. 10.1039/D0CP04219F. [DOI] [PubMed] [Google Scholar]
  46. Baker E. A. D.; Pitfield J.; Price C. J.; Hepplestone S. P. Computational analysis of the enhancement of photoelectrolysis using transition metal dichalcogenide heterostructures. J. Phys.: Condens. Matter 2022, 34, 375001. 10.1088/1361-648X/ac7d2c. [DOI] [PubMed] [Google Scholar]
  47. Roy T.; Tosun M.; Cao X.; Fang H.; Lien D.-H.; Zhao P.; Chen Y.-Z.; Chueh Y.-L.; Guo J.; Javey A. Dual-Gated MoS2/WSe2 van der Waals Tunnel Diodes and Transistors. ACS Nano 2015, 9, 2071–2079. 10.1021/nn507278b. [DOI] [PubMed] [Google Scholar]
  48. Iordanidou K.; Mitra R.; Shetty N.; Lara-Avila S.; Dash S.; Kubatkin S.; Wiktor J. Electric Field and Strain Tuning of 2D Semiconductor van der Waals Heterostructures for Tunnel Field-Effect Transistors. ACS Appl. Mater. Interfaces 2023, 15, 1762–1771. 10.1021/acsami.2c13151. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Iordanidou K.; Wiktor J. Two-dimensional MoTe2/SnSe2 van der Waals heterostructures for tunnel-FET applications. Phys. Rev. Mater. 2022, 6, 084001. 10.1103/PhysRevMaterials.6.084001. [DOI] [Google Scholar]
  50. Yan R.; Fathipour S.; Han Y.; Song B.; Xiao S.; Li M.; Ma N.; Protasenko V.; Muller D. A.; Jena D.; Xing H. G. Esaki Diodes in van der Waals Heterojunctions with Broken-Gap Energy Band Alignment. Nano Lett. 2015, 15, 5791–5798. 10.1021/acs.nanolett.5b01792. [DOI] [PubMed] [Google Scholar]
  51. Liu C.-H.; Clark G.; Fryett T.; Wu S.; Zheng J.; Hatami F.; Xu X.; Majumdar A. Nanocavity Integrated van der Waals Heterostructure Light-Emitting Tunneling Diode. Nano Lett. 2017, 17, 200–205. 10.1021/acs.nanolett.6b03801. [DOI] [PubMed] [Google Scholar]
  52. Shi L.; Zhao T. S.; Xu A.; Xu J. B. Ab initio prediction of a silicene and graphene heterostructure as an anode material for Li- and Na-ion batteries. J. Mater. Chem. A 2016, 4, 16377–16382. 10.1039/C6TA06976B. [DOI] [Google Scholar]
  53. Pomerantseva E.; Gogotsi Y. Two-dimensional heterostructures for energy storage. Nat. Energy 2017, 2, 17089. 10.1038/nenergy.2017.89. [DOI] [Google Scholar]
  54. Du Y. T.; Kan X.; Yang F.; Gan L. Y.; Schwingenschlögl U. MXene/Graphene Heterostructures as High-Performance Electrodes for Li-Ion Batteries. ACS Appl. Mater. Interfaces 2018, 10, 32867–32873. 10.1021/acsami.8b10729. [DOI] [PubMed] [Google Scholar]
  55. Das P.; Fu Q.; Bao X.; Wu Z.-S. Recent advances in the preparation, characterization, and applications of two-dimensional heterostructures for energy storage and conversion. J. Mater. Chem. A 2018, 6, 21747–21784. 10.1039/C8TA04618B. [DOI] [Google Scholar]
  56. Wu X.; Wang Z.; Yu M.; Xiu L.; Qiu J. Stabilizing the MXenes by Carbon Nanoplating for Developing Hierarchical Nanohybrids with Efficient Lithium Storage and Hydrogen Evolution Capability. Adv. Mater. 2017, 29, 1607017. 10.1002/adma.201607017. [DOI] [PubMed] [Google Scholar]
  57. Ma Z.; Zhou X.; Deng W.; Lei D.; Liu Z. 3D Porous MXene (Ti3C2)/Reduced Graphene Oxide Hybrid Films for Advanced Lithium Storage. ACS Appl. Mater. Interfaces 2018, 10, 3634–3643. 10.1021/acsami.7b17386. [DOI] [PubMed] [Google Scholar]
  58. Demiroglu I.; Peeters F. M.; Gülseren O.; Çakır D.; Sevik C. Alkali Metal Intercalation in MXene/Graphene Heterostructures: A New Platform for Ion Battery Applications. J. Phys. Chem. Lett. 2019, 10, 727–734. 10.1021/acs.jpclett.8b03056. [DOI] [PubMed] [Google Scholar]
  59. Jiang H.; Ren D.; Wang H.; Hu Y.; Guo S.; Yuan H.; Hu P.; Zhang L.; Li C. 2D Monolayer MoS2 -Carbon Interoverlapped Superstructure: Engineering Ideal Atomic Interface for Lithium Ion Storage. Adv. Mater. 2015, 27, 3687–3695. 10.1002/adma.201501059. [DOI] [PubMed] [Google Scholar]
  60. Larson D. T.; Fampiou I.; Kim G.; Kaxiras E. Lithium Intercalation in Graphene–MoS2 Heterostructures. J. Phys. Chem. C 2018, 122, 24535–24541. 10.1021/acs.jpcc.8b07548. [DOI] [Google Scholar]
  61. Kim H. S.; Chung Y. H.; Kang S. H.; Sung Y. E. Electrochemical behavior of carbon-coated SnS2 for use as the anode in lithium-ion batteries. Electrochim. Acta 2009, 54, 3606–3610. 10.1016/j.electacta.2009.01.030. [DOI] [Google Scholar]
  62. Luo B.; Fang Y.; Wang B.; Zhou J.; Song H.; Zhi L. Two dimensional graphene-SnS2 hybrids with superior rate capability for lithium ion storage. Energy Environ. Sci. 2012, 5, 5226–5230. 10.1039/C1EE02800F. [DOI] [Google Scholar]
  63. Chang K.; Wang Z.; Huang G.; Li H.; Chen W.; Lee J. Y. Few-layer SnS2/graphene hybrid with exceptional electrochemical performance as lithium-ion battery anode. J. Power Sources 2012, 201, 259–266. 10.1016/j.jpowsour.2011.10.132. [DOI] [Google Scholar]
  64. Bediako D. K.; Rezaee M.; Yoo H.; Larson D. T.; Zhao S. Y.; Taniguchi T.; Watanabe K.; Brower-Thomas T. L.; Kaxiras E.; Kim P. Heterointerface effects in the electrointercalation of van der Waals heterostructures. Nature 2018, 558, 425–429. 10.1038/s41586-018-0205-0. [DOI] [PubMed] [Google Scholar]
  65. King’ori G. W.; Ouma C. N. M.; Mishra A. K.; Amolo G. O.; Makau N. W. Two-dimensional graphene–HfS2 van der Waals heterostructure as electrode material for alkali-ion batteries. RSC Adv. 2020, 10, 30127–30138. 10.1039/D0RA04725B. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. King’ori G. W.; Ouma C. N. M.; Amolo G. O.; Makau N. W. Ab initio insights into Graphene-Zirconium disulfide/diselenide heterostructure as electrode material for alkali-ion batteries. Surf. Interfaces 2021, 24, 101036. 10.1016/j.surfin.2021.101036. [DOI] [Google Scholar]
  67. Katzke H.; Tolédano P.; Depmeier W. Phase transitions between polytypes and intralayer superstructures in transition metal dichalcogenides. Phys. Rev. B 2004, 69, 134111. 10.1103/PhysRevB.69.134111. [DOI] [Google Scholar]
  68. Ribeiro-Soares J.; Almeida R. M.; Barros E. B.; Araujo P. T.; Dresselhaus M. S.; Cançado L. G.; Jorio A. Group theory analysis of phonons in two-dimensional transition metal dichalcogenides. Phys. Rev. B 2014, 90, 115438. 10.1103/PhysRevB.90.115438. [DOI] [Google Scholar]
  69. Wang D.; Liu L. M.; Zhao S. J.; Hu Z. Y.; Liu H. Potential Application of Metal Dichalcogenides Double-Layered Heterostructures as Anode Materials for Li-Ion Batteries. J. Phys. Chem. C 2016, 120, 4779–4788. 10.1021/acs.jpcc.5b11677. [DOI] [Google Scholar]
  70. Brem S.; Linderälv C.; Erhart P.; Malic E. Tunable Phases of Moiré Excitons in van der Waals Heterostructures. Nano Lett. 2020, 20, 8534–8540. 10.1021/acs.nanolett.0c03019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  71. Zhang L.; Zhang Z.; Wu F.; Wang D.; Gogna R.; Hou S.; Watanabe K.; Taniguchi T.; Kulkarni K.; Kuo T.; Forrest S. R.; Deng H. Twist-angle dependence of moiré excitons in WS2/MoSe2 heterobilayers. Nat. Commun. 2020, 11, 5888. 10.1038/s41467-020-19466-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  72. Luo S.; Hao G.; Fan Y.; Kou L.; He C.; Qi X.; Tang C.; Li J.; Huang K.; Zhong J. Formation of ripples in atomically thin MoS2 and local strain engineering of electrostatic properties. Nanotechnology 2015, 26, 105705. 10.1088/0957-4484/26/10/105705. [DOI] [PubMed] [Google Scholar]
  73. Chaves A.; et al. Bandgap engineering of two-dimensional semiconductor materials. npj 2D Mater. Appl. 2020, 4, 29. 10.1038/s41699-020-00162-4. [DOI] [Google Scholar]
  74. Davelou D.; Kopidakis G.; Kaxiras E.; Remediakis I. N. Nanoribbon edges of transition-metal dichalcogenides: Stability and electronic properties. Phys. Rev. B 2017, 96, 165436. 10.1103/physrevb.96.165436. [DOI] [Google Scholar]
  75. Li D.; Ding F. Environment-dependent edge reconstruction of transition metal dichalcogenides: a global search. Mater. Today Adv. 2020, 8, 100079. 10.1016/j.mtadv.2020.100079. [DOI] [Google Scholar]
  76. Ma H.; Zhao W.; Yuan S.; Ren H.; Zhu H.; Ma H.; Ding F.; Guo W. Reconstructed edges of T phase transition metal dichalcogenides. Mater. Today Phys. 2021, 19, 100411. 10.1016/j.mtphys.2021.100411. [DOI] [Google Scholar]
  77. Hu Z.; Wu Z.; Han C.; He J.; Ni Z.; Chen W. Two-dimensional transition metal dichalcogenides: Interface and defect engineering. Chem. Soc. Rev. 2018, 47, 3100–3128. 10.1039/C8CS00024G. [DOI] [PubMed] [Google Scholar]
  78. Van der Ven A.; Bhattacharya J.; Belak A. A. Understanding Li Diffusion in Li-Intercalation Compounds. Acc. Chem. Res. 2013, 46, 1216–1225. 10.1021/ar200329r. [DOI] [PubMed] [Google Scholar]
  79. Zhang Q.; Li R.; Zhang M.; Zhang B.; Gou X. SnS2/reduced graphene oxide nanocomposites with superior lithium storage performance. Electrochim. Acta 2014, 115, 425–433. 10.1016/j.electacta.2013.10.193. [DOI] [Google Scholar]
  80. Gao P.; Wang L.; Zhang Y. Y.; Huang Y.; Liao L.; Sutter P.; Liu K.; Yu D.; Wang E. G. High-Resolution Tracking Asymmetric Lithium Insertion and Extraction and Local Structure Ordering in SnS2. Nano Lett. 2016, 16, 5582–5588. 10.1021/acs.nanolett.6b02136. [DOI] [PubMed] [Google Scholar]
  81. Lu Y.; Li J.; Zhao Y.; Zhu X. Lithium Clustering during the Lithiation/Delithiation Process in LiFePO4 Olivine-Structured Materials. ACS Omega 2019, 4, 20612–20617. 10.1021/acsomega.9b02694. [DOI] [PMC free article] [PubMed] [Google Scholar]
  82. Kresse G.; Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  83. Kresse G.; Hafner J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. 10.1103/PhysRevB.49.14251. [DOI] [PubMed] [Google Scholar]
  84. Kresse G.; Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
  85. Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  86. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  87. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  88. Monkhorst H. J.; Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
  89. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  90. Qi Y.; Hector L. G.; James C.; Kim K. J. Lithium Concentration Dependent Elastic Properties of Battery Electrode Materials from First Principles Calculations. J. Electrochem. Soc. 2014, 161, F3010–F3018. 10.1149/2.0031411jes. [DOI] [Google Scholar]
  91. Luo J.; Dai C.; Wang Z.; Liu K.; Mao W.; Fang D.; Chen X. In-situ measurements of mechanical and volume change of LiCoO2 lithium-ion batteries during repeated charge–discharge cycling by using digital image correlation. Measurement 2016, 94, 759–770. 10.1016/j.measurement.2016.09.023. [DOI] [Google Scholar]
  92. Woodcox M.; Shepard R.; Smeu M. First principles investigation into the interwoven nature of voltage and mechanical properties of the LixNMC-811 cathode. J. Power Sources 2021, 516, 230620. 10.1016/j.jpowsour.2021.230620. [DOI] [Google Scholar]
  93. Schweidler S.; de Biasi L.; Schiele A.; Hartmann P.; Brezesinski T.; Janek J. Volume Changes of Graphite Anodes Revisited: A Combined Operando X-ray Diffraction and In Situ Pressure Analysis Study. J. Phys. Chem. C 2018, 122, 8829–8835. 10.1021/acs.jpcc.8b01873. [DOI] [Google Scholar]
  94. Fan S.; Zou X.; Du H.; Gan L.; Xu C.; Lv W.; He Y. B.; Yang Q. H.; Kang F.; Li J. Theoretical Investigation of the Intercalation Chemistry of Lithium/Sodium Ions in Transition Metal Dichalcogenides. J. Phys. Chem. C 2017, 121, 13599–13605. 10.1021/acs.jpcc.7b05303. [DOI] [Google Scholar]
  95. Eftekhari A. Low voltage anode materials for lithium-ion batteries. Energy Storage Mater. 2017, 7, 157–180. 10.1016/j.ensm.2017.01.009. [DOI] [Google Scholar]
  96. Manthiram A. A reflection on lithium-ion battery cathode chemistry. Nat. Commun. 2020, 11, 1550. 10.1038/s41467-020-15355-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  97. Price C. J.; Pitfield J.; Baker E. A. D.; Hepplestone S. P. First principles study of layered scandium disulfide for use as Li-ion and beyond-Li-ion batteries. Phys. Chem. Chem. Phys. 2023, 25, 2167–2178. 10.1039/D2CP05055B. [DOI] [PubMed] [Google Scholar]
  98. Gusakova J.; Tay K.; Gusakov V. General approach for band gap calculation of semiconductors and insulators. Phys. Status Solidi A 2016, 213, 2834–2837. 10.1002/pssa.201600517. [DOI] [Google Scholar]
  99. Jiang H. Electronic Band Structures of Molybdenum and Tungsten Dichalcogenides by the GW Approach. J. Phys. Chem. C 2012, 116, 7664–7671. 10.1021/jp300079d. [DOI] [Google Scholar]
  100. Kim H.-g.; Choi H. J. Thickness dependence of work function, ion ization energy, and electron affinity of Mo and W dichalcogenides from DFT and GW calculations. Phys. Rev. B 2021, 103, 085404. 10.1103/physrevb.103.085404. [DOI] [Google Scholar]
  101. Henkelman G.; Uberuaga B. P.; Jónsson H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. 10.1063/1.1329672. [DOI] [Google Scholar]
  102. Price C. J.; Hepplestone S. Intercalation-Dependent Elastic Properties of Transition Metal Dichalcogenides. J. Mater. Chem. C 2023, 11, 14278–14291. 10.1039/d3tc02106h. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp3c05155_si_001.pdf (5.5MB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES