Abstract
Lewontin’s paradox, the observation that levels of genetic diversity (π) do not scale linearly with census population size (Nc) variation, is an evolutionary conundrum. The most extreme mismatches between π and Nc are found for highly abundant marine invertebrates. Yet, the influences of new mutations on π relative to extrinsic processes such as Nc fluctuations are unknown. Here, we provide the first germline mutation rate (μ) estimate for a marine invertebrate in corallivorous crown-of-thorns sea stars (Acanthaster cf. solaris). We use high-coverage whole-genome sequencing of 14 parent-offspring trios alongside empirical estimates of Nc in Australia’s Great Barrier Reef to jointly examine the determinants of π in populations undergoing extreme Nc fluctuations. The A. cf. solaris mean μ was 9.13 x 10−09 mutations per-site per-generation (95% CI: 6.51 x 10−09 to 1.18 x 10−08), exceeding estimates for other invertebrates and showing greater concordance with vertebrate mutation rates. Lower-than-expected Ne (~70,000–180,000) and low Ne/Nc values (0.0047–0.048) indicated weak influences of population outbreaks on long-term π. Our findings are consistent with elevated μ evolving in response to reduced Ne and generation time length, with important implications for explaining high mutational loads and the determinants of genetic diversity in marine invertebrate taxa.
Author summary
Understanding how levels of genetic diversity levels are maintained in natural populations and their relationship to species abundance is central to many conservation problems. We address this question in ecologically important crown-of-thorns sea stars to advance our understanding about the determinants of genetic diversity in species undergoing extreme population size fluctuations or outbreaks. In this work, we report the first germline mutation rate estimate for a marine invertebrate using whole-genome sequencing of parent-offspring trios. Our results reveal that unexpectedly high mutational contributions and reduced effective population size (stronger genetic drift than predicted by abundance) shape genetic diversity in this species, despite outbreaking populations sizes exceeding 20–90 million individuals. Our results are consistent with theory on mutation rate evolution, whereby elevated mutation rates evolve in response to reduced effective population size or generation time length. Our findings highlight the potential importance of high mutation rates in maintaining extreme deleterious mutational loads observed in marine invertebrate taxa and moderate genetic diversity levels despite population declines. Such fundamental knowledge advances our understanding about the determinants of genetic diversity in large marine populations and is valuable for testing future hypotheses on mutation rate evolution across diverse animal phyla.
Introduction
Understanding how and why genetic diversity varies among taxa is a longstanding evolutionary puzzle [1]. The neutral theory of evolution predicts that genetic diversity should increase proportionally with effective population size, Ne [2], where the expected level of pairwise genetic diversity (π) at neutral sites reflects the balance between new mutations and loss via genetic drift (as reflected by Ne) and can be approximated by π = 4Neμ, where μ is the mutation rate per-base pair, per-generation. However, empirical evidence shows that the range of π observed in natural populations does not scale with ranges in census population sizes (Nc) [1,3,4]. This disparity between π and Nc variance across taxa, known as Lewontin’s paradox, contradicts theoretical expectations and challenges our understanding of how natural variation is maintained. With increasing evidence that genetic diversity is central to many conservation problems [5], including inferences about extinction risks and species responses to environmental change, our ability to understand how diversity levels are maintained and how they relate to census population sizes is critical. Yet, the determinants of π and the causative factors underlying Lewontin’s paradox are still debated well into the genomic era [4,6–9].
Population genetic studies aiming to solve Lewontin’s paradox suggest that neutral and selective processes act in combination to decouple π from Nc [9] (Fig 1). Historical demographic fluctuations and contemporary dynamics such as repeated extinctions and recolonisations or pest population outbreaks may result in founder events that substantially reduce Ne [10–12]. Positive selection [13] and the indirect effects of background selection and recombination rate variation may also reduce linked neutral diversity to levels lower than predicted by Nc [9,14,15], where the effect of these selective processes on π is expected to be greater in large populations [6,8]. Importantly, equilibrium values of π are also a function of the mutation rate, μ, which varies by orders of magnitude across animal taxa [16]. Several hypotheses seek to explain μ variation across organisms. In particular, the drift-barrier hypothesis proposes that more efficient selection against high mutation rates (relative to genetic drift) in large populations leads to maximal fine-tuning of DNA repair and replication mechanisms and predicts that reduced germline mutation rates should evolve in highly abundant taxa [17–19] (Fig 1). Alternatively, life history traits such as differences in generation time length [16] and reproductive longevity [20,21] may be important determinants of μ evolution across animal phyla, whereby longer-lived organisms have higher mutation rates compared to shorter-lived taxa (which also tend to be more abundant). While these predictions help explain lower-than-expected π in highly abundant species, the extent to which μ variation influences π relative to extrinsic processes remains unknown for most taxa.
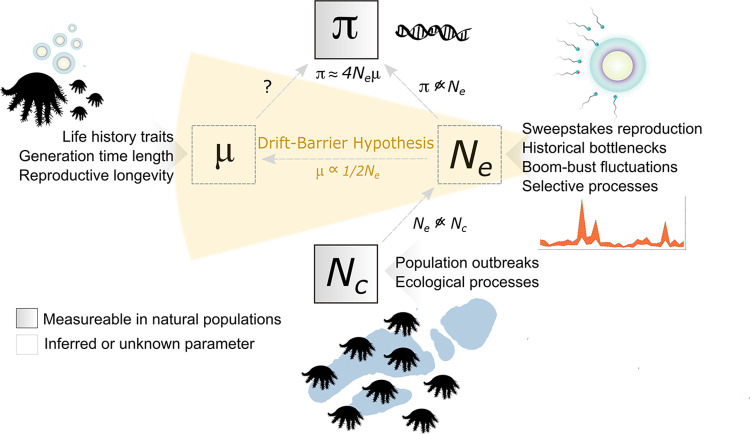
Fig 1. Conceptual diagram illustrating the relationships between evolutionary parameters underlying genetic diversity.
Under mutation-drift equilibrium, pairwise genetic diversity (π) reflects the balance between new mutations (μ) and the loss of variation via genetic drift, reflected by effective population size (Ne). In natural populations, π does not increase linearly with Ne and Ne is often smaller than census population size (Nc). μ is unknown for marine invertebrate taxa, thus the contributions of new mutations to π remain unknown. The drift-barrier hypothesis, a leading explanation for μ variation, proposes that selection against high μ is less efficient in small Ne species. This leads to an inverse relationship between μ and Ne (μ ~1/2Ne for diploid organisms) and the evolution of high μ in small Ne populations. Key evolutionary and ecological processes or traits affecting the magnitude of each parameter are shown. Several evolutionary processes act in combination to reduce Ne and thus, constrain π, decoupling it from Nc. This decoupling leads to a disparity between the range of π and Nc variance observed across taxa, known as Lewontin’s paradox. π can be measured in natural populations using DNA sequencing to calculate pairwise differences between sampled individuals and Nc can be approximated most accurately from direct observations of organisms from field surveys. μ and Ne are inferred parameters from polymorphism data.
Bentho-pelagic marine organisms have long been recognised for harbouring extreme levels of genetic diversity (π ~2–8% [3,4,22,23]). For example, prolific fecundity and long-lived planktonic larval stages, coupled with few physical barriers to gene flow in the marine environment can enable the establishment of large and genetically diverse populations [24]. While the assumption of large population sizes holds true for some marine taxa as a possible explanation for high π [25], marine invertebrates show some of the most extreme mismatches between π and Nc towards both lower [26] and higher relative genetic diversity [4,8]. High variance in larval recruitment and reproductive success (i.e., sweepstakes reproduction) among broadcast spawning adults may drastically decrease Ne relative to population size [27]. Similarly, the ‘boom-bust’ population ecologies of many marine invertebrates, whereby populations rapidly increase in density followed by dramatic declines [28,29], can decouple Ne from Nc (Fig 1). Theory suggests that long-term Ne in fluctuating populations is approximated by the harmonic mean and thus bound closer to population sizes during contraction periods [10,30,31]. From the other perspective, exceptionally high π in highly fecund and dispersive species (e.g., tunicates and mussels, [4,25,32,33]) exceeds expectations based on approximated Nc (see Fig 2 in [8]). In both cases, decomposing the determinants of π (Ne and μ) and their relationship to Nc provide deeper insights regarding the processes maintaining genetic variation in natural populations [34].
Fig 2. Germline mutation rates inferred in Acanthaster cf. solaris and other metazoan taxa.
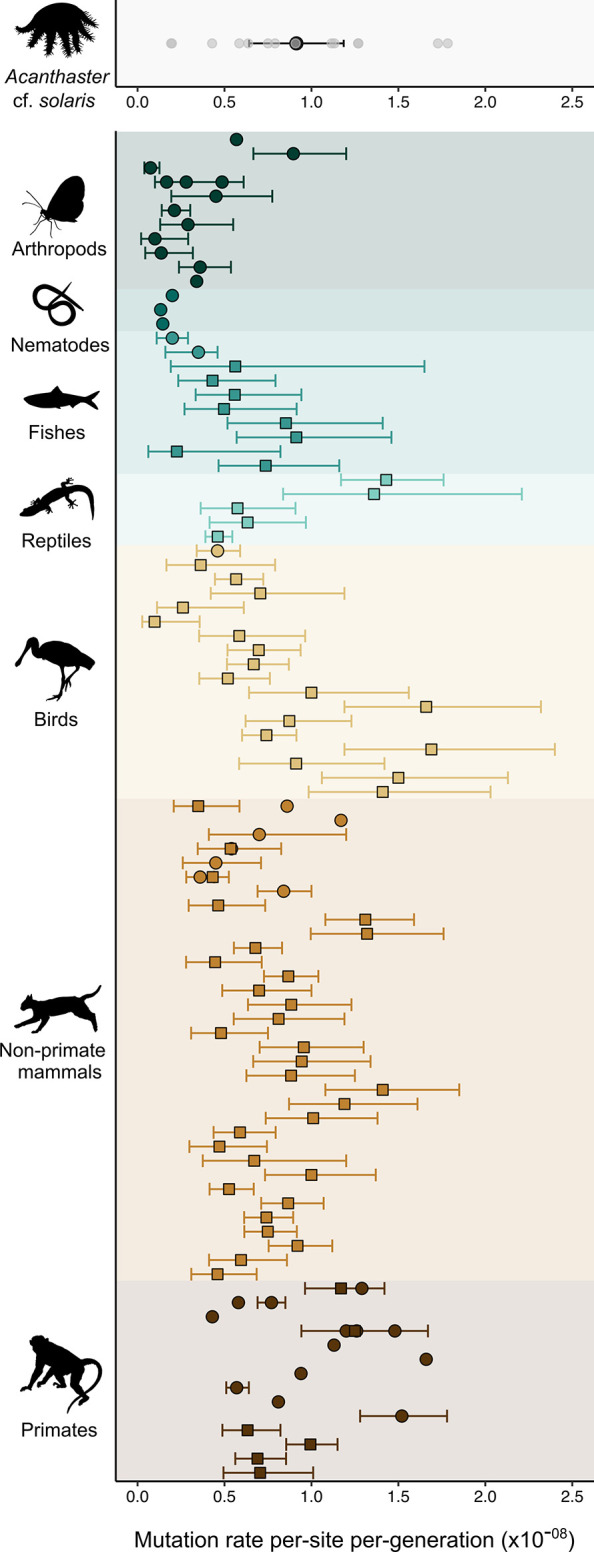
Top panel: Germline mutation rates (μ) for 14 A. cf. solaris parent-offspring trios. Individual estimates for each trio are shown in grey. The average μ is show in black and 95% confidence intervals are indicated with error bars. Lower panel: Previously published average μ estimates and 95% confidence intervals for representative metazoan groups. Mutation rates estimates from [16] are represented by squares and estimates from other publications (both pedigree-based and mutation accumulation approaches) are represented by circles. 95% confidence intervals are shown as reported or omitted if not reported. In cases where multiple estimates are available for a single taxon, 95% confidence intervals from the most recent publication are shown. Refer to S9 Table for article details. Exceedingly high mutation rate estimates (μ > 2.5 x 10−08) for Thamnophis sirtalis and Rhea pennata [16] (S9 Table) are omitted for visual purposes only. Silhouettes were sourced from Phylopic (http://phylopic.org).
Focusing on how μ affects π, determining whether high contributions of new heritable mutations underlie high π values could help explain how extreme polymorphism levels are maintained in some marine invertebrate taxa (e.g., genome-wide silent site π ~ 8.0% for Bostrycapulus aculeatus, [4] and Ciona savignyi, [3]; π ~ 5.0% for Ciona intestinalis, [33]; π ~ 2.3% for Crassostrea gigas, [23]). Marine invertebrates also show some of the highest reported rates of deleterious recessive mutations associated with early mortality (i.e., high mutational load) for animal taxa, exemplified by wild populations of mussels, oysters and abalones (e.g., [35–38]). Thus, one possible explanation for large mutational loads in marine invertebrates is that their genome-wide mutation rates are substantially higher than terrestrial animals and marine fishes [39]. Indirect measures of mutational load based on comparisons of synonymous and nonsynonymous diversity also support elevated genomic mutation rates in the marine invertebrate taxa studied (e.g., [33,37]). Despite the importance of quantifying new mutational contributions to genetic diversity, little empirical data exists on germline spontaneous mutation rates for marine organisms. The current knowledge for germline mutation rates in marine metazoans is limited to five fish taxa [16,40], and there are no direct estimates of germline mutation rates for marine invertebrates.
In this study, we decompose key evolutionary parameters (μ, Ne, Nc) in one of the world’s most intensely monitored marine invertebrate species, the corallivorous crown-of-thorns sea star (CoTS; Acanthaster cf. solaris) to advance our understanding about the determinants of π in populations undergoing extreme Nc fluctuations. (Fig 1). We present the germline mutation rate, μ, for A. cf. solaris using deep sequencing of pedigree trios of wild-caught parents and early-stage larval offspring, alongside detailed estimates of Nc calculated from 32 years of long-term field monitoring and high-resolution mapping of reef geomorphology in Australia’s Great Barrier Reef (GBR). CoTs in the genus Acanthaster are diploid, broadcast spawning asteroid echinoderms that reach sexual maturity at about two years of age when they become corallivorous [41,42]. Although CoTS are native to the Indo-Pacific Ocean, they are among the most influential keystone predators in tropical coral reef ecosystems. CoTS populations can locally reach massive adult densities during cyclical outbreak events (>1,500 individual ha-1) [43,44] during which populations can decimate coral reefs [45]. In the GBR, predation by outbreaking A. cf. solaris populations is among the leading causes of hard coral cover loss [45,46]. Population outbreaks are followed by rapid declines to population densities several orders of magnitude below outbreaking densities within a few years (~3 individual ha-1) [47,48]. Such boom-bust population fluctuations appear characteristic for echinoderm taxa and are also common to many pests and invasive species. However, empirical genomic datasets for fluctuating or outbreaking populations are rare, limiting our knowledge about the impact of population fluctuations on π and as a contributing factor to extreme cases of Lewontin’s paradox [9].
Our first aim is to directly quantify μ and infer Ne. Given the inverse predicted relationship between μ and Ne (i.e., drift-barrier hypothesis), we expect that A. cf. solaris μ is low and similar to values reported for other highly abundant invertebrates, where presumably large Ne favours the evolution of low mutation rates. Alternatively, if Ne is low, or if elevated μ underlies high mutational loads [39] and extreme polymorphism levels observed in some marine invertebrates (e.g., [4]), we may expect that A. cf. solaris μ is high relative to terrestrial animals and marine fishes. Similarly, if generation time length is an important determinant of mutation rate variation, the A. cf. solaris μ may exceed values reported for annual, shorter-lived invertebrate taxa, such as insects, and align closely with μ estimates for longer-lived organisms. A. cf. solaris are one of the most intensely monitored wild marine invertebrate taxa in the world providing far greater resolution on Nc than is typically feasible for marine invertebrate taxa, where indirect approaches for estimating Nc have been based on body size predictors of population density and distribution ranges extracted from publicly-sourced occurrence data (e.g., [6,8]). Thus, our second aim is to clarify the relationship between Ne and Nc with higher certainty to provide insight into the magnitude of genetic drift influencing π in large populations experiencing frequent outbreaks. Our study provides the first germline mutation rate estimate for a marine invertebrate, a crucial basis for interpreting genetic diversity patterns within species [17], and advances our understanding of the processes controlling levels of natural genetic variation in an ecologically significant taxon.
Methods and materials
Parental gonad collection and fertilisation
Reproductively mature A. cf. solaris were collected from John Brewer Reef (18°38’S, 147°03’E) in the Great Barrier Reef (GBR; November 2020). Specimens used for the analysis were collected by the Great Barrier Reef Marine Park Authority’s (GBRMPA) CoTS control program and were thus from areas with densities above the culling threshold (e.g., 10–15 individuals ha−1; [49,50]). Collection of gonad tissue, in vitro breeding experiments and larval rearing were performed at the National Sea Simulator (SeaSim) Experiment Rooms at the Australian Institute of Marine Science (AIMS; Townsville, Queensland) following procedures outlined in [51]. However, here we fertilised individual males and females as unique parental pairs and raised their embryos and larvae for 3–8 days. For each parental cross, we selected two larvae in the early-mid bipinnaria stage (day 3–8) or early-mid brachiolaria stage (day 8–9) (Fig A in S1 Text). DNA from individual larvae was extracted using the QIAGEN Blood and Tissue kit and following modifications for A. cf. solaris larvae from [52]. Adult DNA was extracted from gonad tissue using a modified CTAB protocol optimised for marine invertebrate tissue [53] and purified with PCR-DX Clean beads. Whole genome libraries were prepared for seven biparental families with two offspring per family to generate 14 mother-father-offspring trios including siblings. Genomic libraries were sequenced on a single lane of the NovaSeq S4 300 cycle to achieve 60X coverage using 2 x 150 bp paired reads. Refer to S1 Text for additional details on breeding experiments, DNA extraction and genomic library preparation.
Genomic data processing, variant calling and site selection
Raw reads were quality filtered using Trimmomatic (v0.39) [54]. Quality-filtered reads were mapped to the A. cf. solaris reference genome (GCF_001949145.1_OKI-Apl_1.0) [55] using the Burrow-Wheeler Aligner (v0.7.17 BWA) [56]. BAM files were sorted and indexed using Samtools v1.10 [57] and PCR duplicates were removed using picard (http://broadinstitute.github.io/picard/). The bioinformatic pipeline used for calling germline mutations from pedigree samples was initially described in [58] and follows best practices principles outlined in [59]. All scripts are available on Github (https://github.com/lucieabergeron/germline_mutation_rate). Variant calling was performed in GATK (v4.0.7.0) using HaplotypeCaller (BP-RESOLUTION) constrained to 693 scaffolds greater than 10,000 bp. Individual gVCF files were collated into a GenomicsDB for each trio using GenomicsDBImport and joint genotyping was performed using GenotypeGVCF. SNPs were filtered to remove sites following site-specific parameters: QD < 2.0; FS > 20.0; MQ < 40.0; MQRankSum < -2.0, MQRankSum > 4.0, ReadPosRankSum < -3.0, ReadPosRankSum > 3.0, SOR > 3.0. Refer to S1 Text for additional details on genomic data and variant filtering.
Detecting and filtering of de novo mutations
We detected candidate de novo mutations (DNMs) as positions with Mendelian violations using GATK SelectVariants, where one of the alleles observed in an offspring is not present in either parent. We retained sites in which: (i) parents were homozygous for the reference allele and the offspring was heterozygous (parental alternative allelic depth per site, AD = 0); (ii) all individuals within a trio have GQ > 70, DP > 0.5 * average individual depth, and DP < 2 * average individual depth; and (iii) the offspring had an allelic balance (AB) between 0.3 and 0.7. We recalled regions with candidate DNMs with bcftools (version 1.2) [60] and classified any candidates not jointly detected by GATK and bcftools as False Positive (FP) DNMs. All resulting DNMs and mutation-associated regions were manually inspected using original BAM files in Integrative Genomics Viewer [61]. We ruled out mis-mapping errors, validated homozygous parental genotypes and confirmed shared DNMs between siblings following six criteria to assign DNMs as spurious (S1 Text). Refer to S1 Text for details on DNM detection and manual curation.
Germline mutation rate estimation
To estimate the germline mutation rate, we estimated the genome portion for which we had power to detect candidate DNMs, considering all sites where mutations could be detected (i.e., number of callable sites) and corrections for the false negative rate (S1 Text). This was done by selecting every position in the VCF files (BP_RESOLUTION output) for which both parents were homozygous for the reference allele and all three individuals passed GQ and DP filters (as described above) [58]. The mutation rate was then estimated for each trio as:
where nb_DNM is the number of DNMs, nb_FP is the number of false positive mutations, C is the number of callable sites in the genome and FNR is the false negative rate.
Parental origins and mutation characteristics
We phased DNMs to their parental origins using a read-back phasing approach [62] (https://github.com/besenbacher/POOHA) to determine the proportion of male-to-female contributions (α) to DNMs. DNMs were classified by mutation type and mutations resulting in a change from C to any base were classified as CpG sites. We annotated variants and predicted their genomic location with snpEff v5.1 [63] according to the A. cf. solaris reference genome annotations [55] to assess whether the number of DNMs in each annotation category was significantly greater than expected by chance (S1 Text).
Effective population size (Ne) estimation
We used our new μ estimate and population nucleotide diversity (π) across 14 parental genomes using ANGSD (v0.934) [64] to calculate effective population size as Ne = π /(4μ). It is important to note that population genomic programs leveraging whole genome data (e.g., ANGSD [64] and Sequential Markovian coalescent approaches [65]) often rely on SNPs for inference because their mutational process is well approximated by the infinite sites model [66]. Neglecting sites with multiple mutations (e.g., tri-allelic SNPs) can bias diversity estimates [67] and may be especially relevant for high diversity species (π >>0.05) in which the infinite sites model is violated and π is no longer proportional to Ne [68]. Because our dataset of filtered variants (quality thresholds as applied to GONE analyses described below) across 14 parental genomes did not contain sites with multiple alleles, it is reasonable to assume that no or very few sites show multiple mutations affecting diversity and Ne estimates in A. cf. solaris.
We inferred historical changes in Ne (> 10,000 years ago) using Multiple Sequential Markovian Coalescent (MSMC2) analysis [65,69] The MSMC method approximates the most recent time to coalescence between haplotypes across multiple diploid phased genomes, where the coalescence rate distribution is used to infer changes in historical Ne over an extended time period into the past (several hundreds to thousands of generations) [65,70]. For this analysis, we adapted scripts from Github (https://github.com/iracooke/atenuis_wgs_pub) [71]. MSMC2 analyses were executed for each pair of phased parental genomes (4 haplotypes) using a single randomly chosen offspring for phasing. A distribution of Ne was obtained for each parental pair applying our inferred mean μ and a 2 year generation time as inferred from laboratory and field studies in A cf. solaris [41,42,72].
To infer Ne on recent timescales (< 100 generations ago) and to generate Ne estimates that are independent of our inferred μ, we used the Genetic Optimisation for Ne Estimation (GONE) method [73]. The GONE method leverages the distribution of linkage disequilibrium (LD) between pairs of loci over a range of recombination rates from SNP data to infer recent Ne changes (0–200 generation). Because LD patterns between pairs of loci at various genetic distances provide Ne information at different time points in the recent past, the GONE genetic algorithm can infer the recent Ne trajectory that best explains observed LD patterns, providing much greater resolution on contemporary Ne not captured by coalescent-based methods [70,73]. For this analysis, we used the 14 parental genomes, retained scaffolds greater than 1M bp and variants passing minimum quality criteria (S1 Text). We used the default recombination rate of 1 centimorgans per megabase and a maximum recombination rate of 0.01 (hc = 0.01) as recommended by the authors [73]. Because the GONE method considers the compounded effects of genetic drift from all previous generations, we calculated the arithmetic mean Ne between the last 10–80 generations to exclude the most recent and distant generations where estimation may not be reliable [73]. Refer to S1 Text for details on Ne estimation.
Census population size (Nc) estimation using long-term monitoring data
We inferred the size of the contemporary A. cf. solaris population in the GBR Marine Park using three decades of benthic monitoring data [74] combined with high-resolution (10 m) mapping of the reef geomorphology of the GBR to estimate the area of suitable A. cf. solaris habitat [75,76]. This mapping product characterises the geomorphic zonation of 2,164 offshore reefs [75] and 890 fringing and nearshore reefs [76] of the GBR Marine Park to a 20 m depth using classifications of physical attributes derived from remote-sensing data (sub-surface reflectance, bathymetry, slope angle) and wave modelling. As representative A. cf. solaris habitats, we only considered geomorphic categories predominantly covered by consolidated hard substrate, which is more suitable for coral colonisation. According to Roelfsema et al. [75], there are 4 geomorphic categories that are representative of significant ‘coral habitat’: ‘outer reef flat’, ‘reef slope’, ‘reef crest’, and ‘shelter reef slope’. These habitats are likely to support the greatest share of adult A. cf. solaris populations, as they provide optimal conditions for abundant shelter and food source. Refer to S1 Text for additional details. The available census data were collected using standardised benthic surveys performed between 1991 and 2022 on a selection of individual reefs. For each surveyed reef, individual counts were converted into an estimate of non-cryptic A. cf. solaris density (i.e., adult density, where adults are approximately > 15 cm diameter) (Fig B in S1 Text), and a mean value of reef-level density (individuals km-2) was calculated for each annual sample of monitored reefs. A 95% confidence interval of annual mean densities was calculated from 500 pseudo-samples generated by bootstrap for each monitored year. Finally, the confidence limits and the mean of the annual mean densities were multiplied by the total surface (3D) area of the preferred A. cf. solaris habitat of reef-building corals on the GBR (14,199 km2, S1 Text).
Results
Germline mutation rate in A. cf. solaris
High-coverage sequencing of 14 A. cf. solaris parent-offspring trios resulted in an average coverage of 59X per individual after mapping (range 37X to 91X) (S1 Table). Analyses of relatedness validated trio parent-offspring relationships (relatedness_phi ~0.25 between parents and offspring) and low parental relatedness (relatedness_phi < 0.015 between parents) (S2 Table). Variant calling in GATK resulted in 7,316,821 SNPs post-filtering (mean across trios) and 596 DNM candidates based on Mendelian violations (S3 and S5 Tables). Additional filtering for sites with no reads supporting parental alternative alleles (AD = 0) resulted in 246 variants (S4 and S5 Tables). Following variant calling with an independent approach, 141 of 246 variants passed our selection criteria as candidate DNMs. Four false positive mutations were present as low frequency variants in the population genomic dataset spanning the GBR (S6 Table). We further verified 63 out of these 141 mutations (44.7%) as true positive DNMs based on strict manual validation criteria (S6 and S7 Tables). The total number of validated DNMs (n = 63) ranged between 1 and 9 mutations per trio (S5 Table). Approximately 19.0% (12 of 63) of DNMs were shared among siblings where both shared DNMs passed selection criteria.
The average false positive rate was 42% when considering the independent variant calling approach and 31% for manual validation, resulting in a cumulative false positive rate of 73.0% (range 50% to 92% among trios; S5 Table). False positives arose largely from the incorrect absence of a heterozygous site in the parents where 1 or more reads supported the alternative allele. The high rate of false heterozygous genotypes is comparable to other values reported for non-model taxa [16] and could be due to read mapping errors, paralog mis-mapping or incorrect variant calls associated with reference genome quality [77]. The available CoTS reference genome is a scaffold-level assembly, although genome assembly quality is not expected to have large impacts on the accuracy of the mutation rate estimates [16]. Our parent-offspring trios and high coverage genomic data could be used to improve mutation rate estimates in the future with the availability of a chromosome-level assembly for A. cf. solaris or long-read technologies.
We estimated the per-site per-generation mutation rate as the number of observed true positive DNMs out of the total number of callable sites while accounting for the FNR, estimated to be 8.4% (S5 Table). The number of callable sites ranged from 196,000,000 to 294,000,000 for each trio, representing 71% of the A. cf. solaris genome on average (S5 Table), which is comparable to other studies (e.g., range for 68 taxa 17–93%, mean = 72%; see Fig S1c in [16]; ~80%; [78]; ~88% [58]). The final estimated mean germline mutation rate averaged across 14 trios was μ = 9.13 x 10−09 DNMs per-site per-generation (95% CI: 6.51 x 10−09 to 1.18 x 10−08).
Parental origins and mutation characteristics
We established parental origins for 53/63 DNMs, with 27 maternally and 26 paternally inherited phased DNM across all trios (S7 and S8 Tables). The ratio of male-female contributions (α) to DNMs was 0.96, not statistically distinguishable from 1 (Welch two sample t-test; p = 0.50; Fig CA in S1 Text). There was no effect of family grouping on between group variance (ANOVA; p = 0.33; Fig D in S1 Text). Four phased pairs of DNMs shared among siblings showed no parental bias, however the remaining two pairs of shared DNMs could not be phased to parental origins. Out of 63 DNMs, the number of transitions (n = 47) exceeded transversions (n = 16) as is typically observed in eukaryotes, yielding a transition to transversion ratio (ti/tv) of 2.94 (Fig CB in S1 Text and S7 Table). 15.9% of DNMs (10 of 63) were located in CpG sites, two of which were classified as missense mutations (Fig CB in S1 Text). Twenty-four DNMs occurred within introns (34.9%) and four DNMs within intergenic regions (6.3%), and nine variants (14.2%) fell within coding regions (missense and synonymous variants) (Fig E in S1 Text and S7 Table). There was no significant enrichment of annotation categories based on genome-wide expectations (p>0.05) after corrections for multiple tests.
Ne and Nc estimates
Based on our estimated μ and π from 14 parental individuals (π = 0.0108), we calculated the long-term Ne (π/4μ) of A. cf. solaris to be 296,000 based on equilibrium expectations. Historical Ne trajectories inferred by MSMC2 using four parental haplotypes (per larva) showed peak Ne values ~60,000 years ago, followed by a decline to a most recent minimum ~20,000 years ago, coinciding with the lowest global sea levels during the last glacial maximum (data from [79]; Fig 3). However, recent Ne estimates (< 10,000 years) are likely inflated and less reliable because there are few coalescent events expected to have occurred on these recent timescales [65]. The historical harmonic mean Ne over the last 10,000 to 1 million years was 187,141 and 238,656 over a more recent time period (10,000–100,000 years). Estimates of recent Ne using GONE that are independent of our inferred μ returned a mean Ne of 67,755 between the last 10–80 generations.
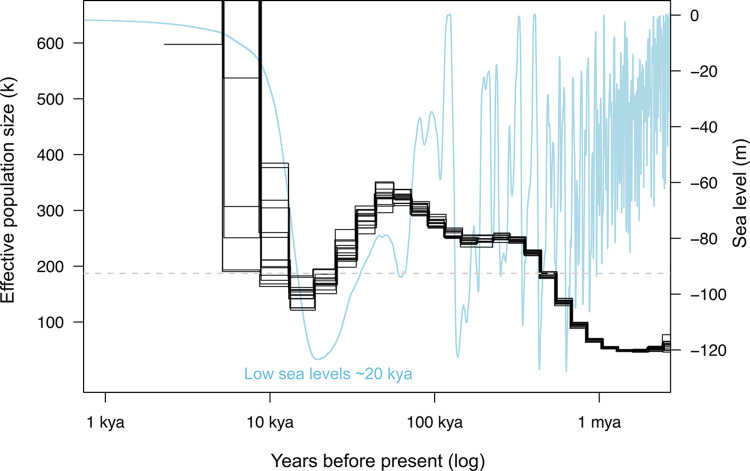
Fig 3. Historical Ne trajectories inferred in MSMC2 applying the inferred Acanthaster cf. solaris mutation rate and nucleotide diversity from 14 parental genomes (four parental haplotypes per larva).
Populations have experienced large fluctuations over the past 10,000 to 1 million years, with peak population sizes ~60,000 years ago and a most recent minimum ~20,000 years ago coinciding with the lowest global sea levels during the late Pleistocene [79]. The long-term harmonic Ne between the last 10,000 to 1 million years (~180,000) is indicated by the grey dashed line.
To better understand the ecological factors constraining Ne, we drew upon observational density estimates from 32 years of long-term monitoring surveys to calculate contemporary adult Nc in the GBR with much higher certainty than is typically feasible for marine invertebrate taxa (e.g., [8]). Increased certainty is not only due to the monitoring technique, which allows for rapid surveys of adult populations over large reef areas, but also due to high-resolution spatial mapping enabling reliable estimates of the extent of coral habitat sustaining adult A. cf. solaris populations. Between 37 and 136 individual reefs were monitored annually between 1991–2022 across the GBR (Fig 4A). Contemporary Nc estimates across 14,199 km2 of coral habitat varied between 6.7 and 14.3 million non-cryptic individuals (harmonic means of the annual 2.5th and annual 97.5th percentiles of bootstrap distributions, Fig 4B). Population sizes were 3 to 6 times higher (20–90 million individuals) during outbreaking years (Fig 4B). Considering these Nc confidence intervals, harmonic mean Ne/Nc ratios ranged between 0.0047–0.048 applying equilibrium Ne (Ne/Nc = 0.022–0.048), historical Ne (Ne/Nc = 0.014–0.030) and recent Ne (Ne/Nc = 0.0047–0.010).
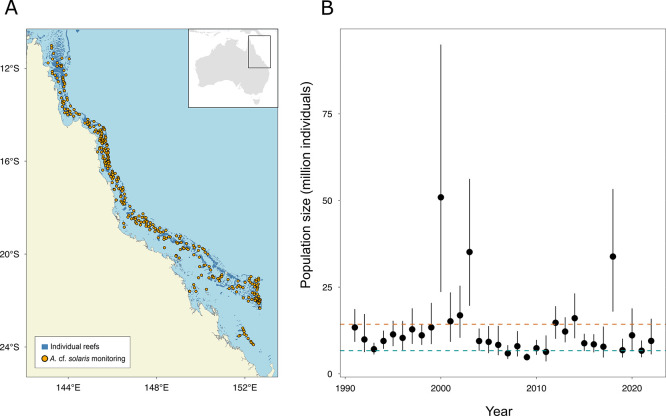
Fig 4. Recent adult Acanthaster cf. solaris abundance estimates in the Great Barrier Reef (GBR) based on long-term monitoring data.
(A) Individual reefs monitored between 1991 and 2022; (B) Contemporary abundance estimates of adult A. cf. solaris across the GBR (3,054 reefs). For each surveyed reef, individual A. cf. solaris counts were converted into a density estimate (individuals km-2), where mean reef-level density was calculated for each annual sample and a 95% confidence interval of annual mean densities was calculated from 500 pseudo-samples generated by bootstrap for each year. The confidence limits and the mean of the annual mean densities were multiplied by the total surface area of the preferred A. cf. solaris habitat of reef-building corals on the GBR to calculate census population size. Black dots indicate the average abundance, while vertical lines indicate the extent of the 95% confidence intervals of the 500 mean annual values estimated by bootstrap sampling. The blue and red dashed lines represent, respectively, the harmonic means of the 2.5th (6.7 million) and 97.5th percentiles (14.3 million) of mean annual values over 32 years of monitoring. https://geoportal.gbrmpa.gov.au/.
Discussion
Lewontin’s paradox arises from comparisons of genetic diversity (π) and census population sizes (Nc) across the tree of life. Yet, partitioning the determinants of π and characterising species-specific Nc is a difficult challenge, especially for large and fluctuating populations [4,7,9]. In this study, we estimate the germline mutation rate (μ) in Acanthaster cf. solaris crown-of-thorns sea stars and provide empirical estimates of adult Nc to interrogate the determinants of π in this species. Based on direct observations of 63 de novo mutations (DNMs) across 14 pedigree trios, the A. cf. solaris mean μ was 9.13 x 10−09 DNMs per-site per-generation (95% CI: 6.51 x 10−09 to 1.18 x 10−08). Our estimated μ exceeds previously reported values for highly abundant terrestrial and freshwater invertebrates (Fig 2). Instead, the A. cf. solaris μ aligns more strongly with values reported for vertebrate taxa, with largely overlapping 95% confidence intervals with mammals and marine fishes (Fig 2). To provide insight into the magnitude of genetic drift influencing π in large populations experiencing frequent outbreaks, we used our new μ estimate to infer historical Ne alongside more recent Ne estimates (that are independent of μ). We find that historical (Ne ~ 180,000) and recent Ne (Ne ~ 70,000) estimates are 1–2 orders of magnitude lower than typically reported for highly dispersive marine organisms (e.g., ~ 106, [25,80]) and between 2–3 orders of magnitude lower than Nc estimated from the Great Barrier Reef (GBR) (Fig 4). Our findings of elevated μ and reduced Ne in A. cf. solaris are consistent with μ evolving in response to reduced Ne (i.e., drift-barrier hypothesis), suggesting that short periods (~2–3 generations) of outbreaking population sizes exceeding 20–90 million individuals do not allow for lasting effects of selection against high mutation rates. Consistently, A. cf. solaris exhibits low Ne/Nc values (0.0047 to 0.048), indicating significant genetic drift and weak influences of contemporary demographic outbreaks on long-term π. More broadly, our findings suggest that larger contributions of new mutations to π may underlie high mutational loads observed in some marine invertebrate taxa (e.g., bivalves) [39] and may help explain high polymorphism levels in marine populations despite demographic declines [4]. Our study also provides new data valuable for further testing hypotheses about the determinants of mutation rate variation across diverse animal phyla, which are discussed below.
Low long-term Ne and high μ shape genetic diversity in crown-of-thorns sea stars
Using our new μ estimate and π from 14 parental genomes (π = 0.0108), the A. cf. solaris long-term Ne was ~296,000 based on equilibrium expectations (π/4μ). Reconstructions of historical Ne in MSMC2 returned a lower harmonic mean Ne ~180,000 over the last 10,000–1 million years and revealed significant impacts of historic climactic changes on A. cf. solaris long-term Ne. We show that A. cf. solaris have experienced large population fluctuations over the past 1 million years, with the most recent Ne minimum coinciding with the lowest global sea levels during the late Pleistocene (Ne ~ 150,000) [79] (Fig 3). Applying the GONE method, which does not rely on μ estimates, recent Ne values were even smaller (< 70,000) considering contemporary populations over last 10–80 generations. While Ne estimates in A. cf. solaris in the present study (~70,000–180,000) are similar or larger than for most terrestrial chordates (e.g., < 105,) [16], the Ne range reported here is 1–2 orders of magnitude lower than for many highly dispersive marine organisms (~106) [16,25,80], and terrestrial insects (e.g., Chironomus midges ~2.16–3.95 x 106, [81]; ~1.4 x 106, Drosophila, [77]; ~2 x 106, Heliconius; [82]). This finding adds to empirical evidence that extremely abundant marine taxa, including those with outbreaking tendencies, can sustain low Ne that is strongly decoupled from contemporary Nc, contradicting the broad notion that large marine populations are immune to the effects of genetic drift [26,83].
From a long-term evolutionary perspective, our findings of reduced Ne and elevated μ in A. cf. solaris provide new genomic results consistent with the drift-barrier hypothesis as an explanation for μ variation across taxa. The drift-barrier hypothesis predicts that the efficiency of selection on DNA repair and replication machineries is negatively correlated with the strength of genetic drift. Because the power of genetic drift is inversely proportional to Ne (~1/2Ne for diploid organisms), high mutation rates are expected to evolve in small Ne species, such that π is constrained across diverse taxa (Fig 1) [17,18]. Indeed, negative correlations between per-generation μ and Ne are evident across the tree of life [16,17] and recent work demonstrates that environmental constraints on Ne in prokaryotes can rapidly evolve elevated mutation rates, pointing to evolutionarily labile μ influencing π [19]. Thus, under the drift-barrier hypothesis, low Ne in A. cf. solaris (i.e., similar to terrestrial vertebrates) allows for a high μ to evolve because selection’s ability to maintain high-fidelity replication and repair mechanisms is compromised (relative to the magnitude of genetic drift as reflected by Ne). This observation supports a dominant role of genetic drift in evolutionary change and helps to explain Lewontin’s paradox by describing the stability of π across diverse phyla as a result of the inverse relationship between μ and Ne, rather than a reflection of relatively constant Ne [17]. With our study, it becomes clear that knowledge of temporal population size fluctuations should be incorporated into investigations of μ variation and Lewontin’s paradox to support interpretations of the processes controlling genetic diversity in natural populations [9].
The low Ne values observed in this study likely reflect historical bottlenecks or Nc minima during non-outbreaking periods. While periods of massive Nc experienced by A. cf. solaris increase opportunities for genetic diversity to be reshuffled through phases of high recombination, rare variants are ultimately lost during repeated population bottlenecks and genetic diversity can only be recovered through the generational input of new mutations or migration [10,30]. Thus, if population size changes occur at a rate higher than coalescent events (that reflect genetic drift), long-term Ne becomes independent of short-term demographic dynamics and contemporary drift [84,85]. As such, frequently fluctuating A cf. solaris populations are expected to remain far from mutation-drift equilibrium for longer periods of time [86] and a weak relationship is predicted between π and Nc [4]. Consistent with this hypothesis, our calculations of recent adult Nc resulted in low harmonic mean Ne/Nc values (0.0047 to 0.048), indicating stronger-than-expected genetic drift and weak influences of extreme population outbreaks on long-term π. It is important to note that Nc upper bounds reported here were below the distribution of Nc estimates for other echinoderms (~108−1012; [8]). Because we focused on coral habitats as defined by remote-sensing within the GBR [75], considering the full-distribution of A. cf. solaris throughout its range in the Pacific Ocean would have likely resulted in species-wide abundance estimates up to 5 x greater than our reported mean Nc. We obtained Ne estimates from a sampled population representing a small proportion of the A. cf. solaris range. However, based on absent spatial population structure in microsatellite data [87], we can infer that gene flow is high across the GBR and that Ne estimates in our present study are likely representative of the population within this region. Thus, while our Ne/Nc estimates are conservative for the species-range, we consider them to be precise for the panmictic A. cf. solaris population within the GBR [87] for which we present genomic data.
In the context of low Ne, larger contributions of new mutations to π may thus, in part, explain how moderate polymorphism levels (π = 0.0108) are maintained in A. cf. solaris, and may explain extreme polymorphism levels in marine bentho-pelagic taxa more broadly (e.g., tunicates and mussels) [4,33,68]. The combination of low Ne and elevated μ in A. cf. solaris (relative to terrestrial invertebrates; Fig 2) could also reconcile evidence for higher observed mutational loads in marine invertebrates compared to terrestrial taxa and marine fishes [39]. Populations with small Ne are expected to hold higher burdens of weakly deleterious mutations due to less efficient purifying selection [88]. For example, high mutation rates in marine invertebrates have been speculated from evidence for elevated genetic loads in Pacific oysters [38]. Similarly, low-frequency deleterious mutations and extreme dN/dS ratios in the flat oyster, Ostrea edulis, are posited as outcomes of large mutational inputs coupled with small Ne [37]. While we provide evidence for a high germline mutation rate in A. cf. solaris, the 95% confidence intervals were not distinctly greater than terrestrial animals or marine fishes for which we have μ estimates (Fig 2). This result implies that extrinsic processes sustaining reduced Ne (e.g., sweepstakes reproduction or demographic fluctuations) may have a more predominant role, than mutation rate alone, in shaping genetic load and π in A. cf. solaris and other marine invertebrate populations.
Large variance in reproductive success may be necessary to explain extremely low Ne/Nc ratios (i.e., < 1%) in A. cf. solaris and other wild populations of exploited fish and bivalves [26,34,37,80,89,90]. High skews in reproductive success may be especially relevant for shaping Ne in A. cf. solaris during non-outbreaking periods when populations can reach densities as low as ~ 3 individuals ha-1 [47,48]. Alternatively, asexual reproduction (or budding) of larvae observed in A. cf. solaris under some circumstances in the laboratory [91], may, even if occasionally, contribute to patterns of genetic diversity observed in natural CoTS populations (reviewed in [92]). Although there is limited support for this hypothesis from genetic simulations [93], an analysis of microsatellites from > 3700 individuals showed no effect of potential clonality on population genetic structure [94]. However, testing these hypotheses, and whether reaching known Allee effect thresholds may amplify reproductive variance [95] or define lower genetic diversity limits required to escape extinction [4] is challenging to evaluate in marine populations [80]. Comparisons of mutation rate and Ne estimates with closely related species that do not experience cyclical outbreaks of a similar nature (e.g., Acanthaster brevispinus) or with different mating systems (e.g., brooding Asteroids) would be informative to tease apart the relative contributions of mating strategies (e.g., [16]) versus ecologically-driven Ne fluctuations to μ variation.
Alternative hypotheses for mutation rate evolution in A. cf. solaris
There is growing evidence that differences in generation time length (e.g., [16]) and reproductive longevity (e.g., [20,21]) are important determinants of germline mutation rate evolution across animal phyla, whereby species with longer generation times have higher μ than smaller and shorter-lived organisms [96]. This alternative hypothesis could explain higher μ observed in A. cf. solaris relative to other invertebrate taxa (Fig 2; with the exception of the cyclical parthenogen Daphnia magna, 8.9 x 10−09, [97]). Compared to annual invertebrates, A. cf. solaris are longer-lived species (~8 years in the wild; [45]) where most individuals become sexually mature at 2 years of age when individuals become corallivorous [41,98]. In captivity, sexual maturity can be delayed up to 6.5 years if juveniles are confined to herbivory, implying that generation times in natural populations may be longer depending on the availability of live corals as a food resource, although similar delays in sexual maturity have not been confirmed for wild populations. Thus, the mutation rate observed in A. cf. solaris (values closer to vertebrate taxa; Fig 2) suggests that marine invertebrate taxa may not be an exception to generation time as a predictive factor, despite their phylogenetic distance and unique life history characteristics that differentiate them from most chordates, such as extreme fecundity, large population sizes and bentho-pelagic life cycles [83].
By assigning DNMs to their parental origin, we showed no significant differences in the proportion of male-to-female contributions (α~1) to germline mutations in A. cf. solaris. This result is consistent with similar male and female mutational contributions observed in ectotherm vertebrates (e.g., reptiles mean α = 1.5; fishes, mean α = 0.8; [16]), and in contrast to stronger male biases observed in mammals that experience larger numbers of mitotic cell divisions during the father’s reproductive lifetime [16,20,58]. This observed variation among ectotherms and mammals may be explained by differences in gametogenesis. Seasonally breeding reptiles and fishes produce gametes during limited periods proceeding mating or spawning activity [99,100], such that differences in the number of male and female cell divisions are expected to be reduced and therefore α is closer to 1 (e.g., [40]). Similar to fishes, in A. cf. solaris and other echinoderms, highly fecund females produce > 100 million oocytes per season [101] and undergo gametogenesis every spawning period (e.g., November to January; [102]). Although little is known about germline formation in sea stars, the source of germline stem cells (gonia) is likely present throughout the year [103,104], while gametes appear to be reabsorbed after the spawning period [105,106]. The annual renewal of oogonia after the spawning season implies that females replenish germ cells each gametogenesis cycle [104] and that males and females undergo similar numbers of cell divisions throughout their reproductive life spans. In the present study, we show that α estimates for A. cf. solaris are consistent with theory and empirical data for seasonally reproducing animals. The effect of parental age on the observed mutation rate variation among trios (Fig D in S1 Text) is not clear, however, because unlike other pedigree studies (e.g., [16]), we do not have information about the parental age of wild-caught A. cf. solaris.
Deep sequencing supports new inferences for non-model bentho-pelagic marine invertebrates
By sequencing 3-day old larvae, we demonstrate that it should be feasible to detect germline mutations in non-model bentho-pelagic organisms with long-lived planktotrophic larvae if pedigreed larvae can be maintained to the earliest developmental stages preceding planktotrophy (e.g., day 3 larvae)—the key stage impeding successful captive rearing of many bentho-pelagic species. The next main challenge in estimating genomic mutation rates is identifying extremely rare, new mutations against a background of possible sequencing errors [107]. In the present study, we used deep sequencing (60x) of many trios (>10) and applied stringent bioinformatic criteria to detect germline mutations with high certainty. First, we applied best practises workflows with conservative quality thresholds (e.g., genotype quality >70; [59]) that enabled us to reliably compare the A. cf. solaris μ with most metazoan estimates [16]. Second, we mitigated possible limitations imposed by reference genome quality (e.g., [77]) by visually inspecting BAM files and applying stringent criteria to validate individual DNM candidates. Third, our approach of screening DNMs against all sequenced trios and an independent population genomic A. cf. solaris dataset helped ensure that DNMs did not correspond to known alleles segregating in contemporary GBR populations. These measures were necessary because larval resequencing was not feasible for independent validation. Additionally, our study examined only single base pair mutations and excluded indel variants, copy number and larger structural variants that may also be important components of germline mutations as the raw material for evolution (e.g., [20,81]). Although our strict approaches for classifying DNMs may have resulted in underestimations of the A. cf. solaris mutation rate, we have high certainty in the identified DNMs and thus confidence in the resulting patterns, such as the co-occurrence of DNMs between siblings and trends in parental bias. Our conservative approach strengthens our main result that mutational rates in A. cf. solaris crown-of-thorns sea stars are high relative to other measured invertebrate taxa.
Supporting information
Fig A. Summary of A. cf. solaris fertilisation workflow and larval stages. (A) A. cf. solaris adult being dissected to extract gonads; (B) Female gonads after rinsing in FSW; (C) Mature eggs recently dislodged from the gonad tissue; (D) Fertilised eggs under the microscope presenting a clear fertilisation membrane; (E-I) Larval developmental stages. For each parental cross, we selected two larvae in the early (F) or mid (G) bipinnaria stage (Day 3–8) and early-mid brachiolaria stage (Day 8–9) (H). Fig B. Relationship between manta tow counts and SCUBA swim counts from [108]. The observed data (black dots) are expressed as a per-tow basis (200×12 m, with 2 to 15 tows/transects supporting each observation). The regression model is used to generate deterministic predictions of SCUBA swim counts (line) or stochastic predictions function of the number of tows conducted in a given area (e.g., the perimeter of a reef), illustrated here with 5 (red dots) and 25 tows (green dots). Increasing the number of tows decreases the dispersion around the deterministic model. Fig C. Variation in parental origins and mutational types for de novo mutations (DNM). (A) Per-trio proportions of DNMs phased to their parental origins and those with unknown phasing. There was no significant difference in the proportion of maternally and paternally inherited phased DNMs among trios (Welch two sample t-test; p = 0.50); (B) Distribution of DNMs classified by mutation type, where mutations resulting in a change from C to any base were classified as CpG sites. Fig D. Mutation rate estimates for 14 parent-offspring trios grouped by family. There was no effect of family grouping on between group variance (ANOVA; p = 0.33). Mutation rate data points for Trio 7 siblings are overlayed. Fig E. Annotated variants (synonymous, nonsynonymous) and their predicted genomic locations according to the A. cf. solaris reference genome annotations [55]. There was no significant enrichment of annotation categories based on genome-wide expectations (p>0.05) after corrections for multiple tests.
(PDF)
(XLSX)
(XLSX)
(XLSX)
(XLSX)
(XLSX)
(XLSX)
(XLSX)
(XLSX)
95% confidence intervals are shown as reported by authors or omitted if not reported. Highlighted mutation rate estimates are removed from Fig 2.
(XLSX)
Acknowledgments
We acknowledge the team of the Australian Institute of Marine Science’s Long Term Monitoring Program for their efforts in maintaining the online database of CoTS monitoring (https://eatlas.org.au/gbr/ltmp-data). We also thank the Great Barrier Reef Marine Park Authority for helpful advice and spatial data and Carolina Castro-Sanguino for critical advice on reef habitats and mapping. We would like to thank the QRIScould computing cluster at The University of Queensland and the GenomeDK at Aarhus University for providing computational resources for IP and LB, respectively.
Data Availability
Raw whole genome sequence data from parent-offspring trios are available on the NCBI Short Read Archive (BioProject ID PRJNA1064695). Supporting scripts and associated data are available on The University of Queensland’s Library eSpace: https://doi.org/10.48610/ad122d0. Scripts relating to mutation rate estimation are available on Github (https://github.com/lucieabergeron/germline_mutation_rate). Scripts and data relating to census population size analysis are available on Github: https://github.com/ymbozec/acanthaster_GBR_abundance. A version of this manuscript has been uploaded to the bioRxiv repository: https://doi.org/10.1101/2023.06.28.546961.
Funding Statement
This work was supported by the Australian Research Council (ARC DP190101593) granted to C.R., S.U., and G.W. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. I.P. and S.M.H. received salary from the funders.
References
- 1.Lewontin RC. The genetic basis of evolutionary change: Columbia University Press New York; 1974. [Google Scholar]
- 2.Kimura M. Theoretical foundation of population genetics at the molecular level. Theoretical population biology. 1971;2(2):174–208. doi: 10.1016/0040-5809(71)90014-1 [DOI] [PubMed] [Google Scholar]
- 3.Leffler EM, Bullaughey K, Matute DR, Meyer WK, Segurel L, Venkat A, et al. Revisiting an old riddle: what determines genetic diversity levels within species? 2012. doi: 10.1371/journal.pbio.1001388 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Romiguier J, Gayral P, Ballenghien M, Bernard A, Cahais V, Chenuil A, et al. Comparative population genomics in animals uncovers the determinants of genetic diversity. Nature. 2014;515(7526):261–3. doi: 10.1038/nature13685 [DOI] [PubMed] [Google Scholar]
- 5.Hoban S, Bruford MW, Funk WC, Galbusera P, Griffith MP, Grueber CE, et al. Global commitments to conserving and monitoring genetic diversity are now necessary and feasible. BioScience. 2021;71(9):964–76. doi: 10.1093/biosci/biab054 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Corbett-Detig RB, Hartl DL, Sackton TB. Natural selection constrains neutral diversity across a wide range of species. PLoS biology. 2015;13(4):e1002112. doi: 10.1371/journal.pbio.1002112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ellegren H, Galtier N. Determinants of genetic diversity. Nature Reviews Genetics. 2016;17(7):422–33. doi: 10.1038/nrg.2016.58 [DOI] [PubMed] [Google Scholar]
- 8.Buffalo V. Quantifying the relationship between genetic diversity and population size suggests natural selection cannot explain Lewontin’s Paradox. Elife. 2021;10:e67509. doi: 10.7554/eLife.67509 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Charlesworth B, Jensen JD. How Can We Resolve Lewontin’s Paradox? Genome biology and evolution. 2022;14(7):evac096. doi: 10.1093/gbe/evac096 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wright S. Size of population and breeding structure in relation to evolution. Science. 1938;87:430–1. [Google Scholar]
- 11.Kimura M. The neutral theory of molecular evolution: Cambridge University Press; 1983. [Google Scholar]
- 12.Chapuis M-P, Loiseau A, Michalakis Y, Lecoq M, Franc A, Estoup A. Outbreaks, gene flow and effective population size in the migratory locust, Locusta migratoria: A regional-scale comparative survey. Molecular Ecology. 2009;18(5):792–800. [DOI] [PubMed] [Google Scholar]
- 13.Gillespie JH. Is the population size of a species relevant to its evolution? Evolution. 2001;55(11):2161–9. doi: 10.1111/j.0014-3820.2001.tb00732.x [DOI] [PubMed] [Google Scholar]
- 14.Burri R. Interpreting differentiation landscapes in the light of long-term linked selection. 2017; 118–131. View Article. 2017. [Google Scholar]
- 15.Charlesworth D, Charlesworth B, Morgan M. The pattern of neutral molecular variation under the background selection model. Genetics. 1995;141(4):1619–32. doi: 10.1093/genetics/141.4.1619 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bergeron LA, Besenbacher S, Zheng J, Li P, Bertelsen MF, Quintard B, et al. Evolution of the germline mutation rate across vertebrates. Nature. 2023;615(7951):285–91. doi: 10.1038/s41586-023-05752-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lynch M. Evolution of the mutation rate. TRENDS in Genetics. 2010;26(8):345–52. doi: 10.1016/j.tig.2010.05.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lynch M, Ackerman MS, Gout J-F, Long H, Sung W, Thomas WK, et al. Genetic drift, selection and the evolution of the mutation rate. Nature Reviews Genetics. 2016;17(11):704–14. doi: 10.1038/nrg.2016.104 [DOI] [PubMed] [Google Scholar]
- 19.Wei W, Ho W-C, Behringer MG, Miller SF, Bcharah G, Lynch M. Rapid evolution of mutation rate and spectrum in response to environmental and population-genetic challenges. Nature communications. 2022;13(1):4752. doi: 10.1038/s41467-022-32353-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Thomas GW, Wang RJ, Puri A, Harris RA, Raveendran M, Hughes DS, et al. Reproductive longevity predicts mutation rates in primates. Current Biology. 2018;28(19):3193–7. e5. doi: 10.1016/j.cub.2018.08.050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wang RJ, Raveendran M, Harris RA, Murphy WJ, Lyons LA, Rogers J, et al. De novo mutations in domestic cat are consistent with an effect of reproductive longevity on both the rate and spectrum of mutations. Molecular Biology and Evolution. 2022;39(7):msac147. doi: 10.1093/molbev/msac147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Solé-Cava Ad, Thorpe J. High levels of genetic variation in natural populations of marine lower invertebrates. Biological Journal of the Linnean Society. 1991;44(1):65–80. [Google Scholar]
- 23.Zhang G, Fang X, Guo X, Li L, Luo R, Xu F, et al. The oyster genome reveals stress adaptation and complexity of shell formation. Nature. 2012;490(7418):49–54. doi: 10.1038/nature11413 [DOI] [PubMed] [Google Scholar]
- 24.Gagnaire P-A, Gaggiotti OE. Detecting polygenic selection in marine populations by combining population genomics and quantitative genetics approaches. Current Zoology. 2016;62(6):603–16. doi: 10.1093/cz/zow088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Small KS, Brudno M, Hill MM, Sidow A. Extreme genomic variation in a natural population. Proceedings of the National Academy of Sciences. 2007;104(13):5698–703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hedgecock D. Does variance in reproductive success limit effective population sizes of marine organisms. Genetics and evolution of aquatic organisms. 1994;122:122–34. [Google Scholar]
- 27.Hedgecock D, Pudovkin AI. Sweepstakes reproductive success in highly fecund marine fish and shellfish: a review and commentary. Bulletin of Marine Science. 2011;87(4):971–1002. [Google Scholar]
- 28.Uthicke S, Schaffelke B, Byrne M. A boom–bust phylum? Ecological and evolutionary consequences of density variations in echinoderms. Ecological monographs. 2009;79(1):3–24. [Google Scholar]
- 29.Strayer DL, D’Antonio CM, Essl F, Fowler MS, Geist J, Hilt S, et al. Boom-bust dynamics in biological invasions: towards an improved application of the concept. Ecology letters. 2017;20(10):1337–50. doi: 10.1111/ele.12822 [DOI] [PubMed] [Google Scholar]
- 30.Motro U, Thomson G. On heterozygosity and the effective size of populations subject to size changes. Evolution. 1982:1059–66. doi: 10.1111/j.1558-5646.1982.tb05474.x [DOI] [PubMed] [Google Scholar]
- 31.Nei M, Maruyama T, Chakraborty R. The bottleneck effect and genetic variability in populations. Evolution. 1975:1–10. doi: 10.1111/j.1558-5646.1975.tb00807.x [DOI] [PubMed] [Google Scholar]
- 32.Nydam ML, Harrison RG. Polymorphism and divergence within the ascidian genus Ciona. Molecular Phylogenetics and Evolution. 2010;56(2):718–26. [DOI] [PubMed] [Google Scholar]
- 33.Tsagkogeorga G, Cahais V, Galtier N. The population genomics of a fast evolver: high levels of diversity, functional constraint, and molecular adaptation in the tunicate Ciona intestinalis. Genome biology and evolution. 2012;4(8):852–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hare MP, Nunney L, Schwartz MK, Ruzzante DE, Burford M, Waples RS, et al. Understanding and estimating effective population size for practical application in marine species management. Conservation Biology. 2011;25(3):438–49. doi: 10.1111/j.1523-1739.2010.01637.x [DOI] [PubMed] [Google Scholar]
- 35.Mallet A, Zouros E, Gartner-Kepkay K, Freeman K, Dickie L. Larval viability and heterozygote deficiency in populations of marine bivalves: evidence from pair matings of mussels. Marine Biology. 1985;87:165–72. [Google Scholar]
- 36.Liu X, Liu X, Guo X, Gao Q, Zhao H, Zhang G. A preliminary genetic linkage map of the Pacific abalone Haliotis discus hannai Ino. Marine biotechnology. 2006;8:386–97. [DOI] [PubMed] [Google Scholar]
- 37.Harrang E, Lapègue S, Morga B, Bierne N. A high load of non-neutral amino-acid polymorphisms explains high protein diversity despite moderate effective population size in a marine bivalve with sweepstakes reproduction. G3: Genes| Genomes| Genetics. 2013;3(2):333–41. doi: 10.1534/g3.112.005181 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Plough L, Shin G, Hedgecock D. Genetic inviability is a major driver of type III survivorship in experimental families of a highly fecund marine bivalve. Molecular Ecology. 2016;25(4):895–910. doi: 10.1111/mec.13524 [DOI] [PubMed] [Google Scholar]
- 39.Plough LV. Genetic load in marine animals: a review. Current Zoology. 2016;62(6):567–79. doi: 10.1093/cz/zow096 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Feng C, Pettersson M, Lamichhaney S, Rubin C-J, Rafati N, Casini M, et al. Moderate nucleotide diversity in the Atlantic herring is associated with a low mutation rate. Elife. 2017;6:e23907. doi: 10.7554/eLife.23907 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lucas J. Growth, maturation and effects of diet in Acanthaster planci (L.) (Asteroidea) and hybrids reared in the laboratory. Journal of Experimental Marine Biology and Ecology. 1984;79(2):129–47. [Google Scholar]
- 42.Zann L, Brodie J, Berryman C, Naqasima M. Recruitment, ecology, growth and behavior of juvenile Acanthaster planci (L.) (Echinodermata: Asteroidea). Bulletin of Marine Science. 1987;41(2):561–75. [Google Scholar]
- 43.Birkeland C, Randall R. Report on the Acanthaster planci (alamea) studies on Tutuila, American Samoa. Samoa: office of marine Resources, government of Samoa; 1979. [Google Scholar]
- 44.Kayal M, Vercelloni J, Lison de Loma T, Bosserelle P, Chancerelle Y, Geoffroy S, et al. Predator crown-of-thorns starfish (Acanthaster planci) outbreak, mass mortality of corals, and cascading effects on reef fish and benthic communities. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Pratchett MS, Caballes CF, Wilmes JC, Matthews S, Mellin C, Sweatman HP, et al. Thirty years of research on crown-of-thorns starfish (1986–2016): scientific advances and emerging opportunities. Diversity. 2017;9(4):41. [Google Scholar]
- 46.De’Ath G, Fabricius KE, Sweatman H, Puotinen M. The 27–year decline of coral cover on the Great Barrier Reef and its causes. Proceedings of the National Academy of Sciences. 2012;109(44):17995–9. doi: 10.1073/pnas.1208909109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Uthicke S, Robson B, Doyle JR, Logan M, Pratchett MS, Lamare M. Developing an effective marine eDNA monitoring: eDNA detection at pre-outbreak densities of corallivorous seastar (Acanthaster cf. solaris). Science of The Total Environment. 2022;851:158143. [DOI] [PubMed] [Google Scholar]
- 48.Rogers JG, Pláganyi ÉE, Babcock RC. Aggregation, Allee effects and critical thresholds for the management of the crown-of-thorns starfish Acanthaster planci. Marine Ecology Progress Series. 2017;578:99–114. [Google Scholar]
- 49.Keesing JK. Feeding biology of the crown-of-thorns starfish, Acanthaster planci (Linnaeus): James Cook University; 1990. [Google Scholar]
- 50.Moran P, De’Ath G. Estimates of the abundance of the crown-of-thorns starfish Acanthaster planci in outbreaking and non-outbreaking populations on reefs within the Great Barrier Reef. Marine Biology. 1992;113:509–15. [Google Scholar]
- 51.Uthicke S, Liddy M, Patel F, Logan M, Johansson C, Lamare M. Effects of larvae density and food concentration on Crown-of-Thorns seastar (Acanthaster cf. solaris) development in an automated flow-through system. Scientific reports. 2018;8(1):1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Doyle JR, McKinnon AD, Uthicke S. Quantifying larvae of the coralivorous seastar Acanthaster cf. solaris on the Great Barrier Reef using qPCR. Marine Biology. 2017;164:1–12.27980349 [Google Scholar]
- 53.Panova M, Aronsson H, Cameron RA, Dahl P, Godhe A, Lind U, et al. DNA extraction protocols for whole-genome sequencing in marine organisms. Marine genomics: Methods and protocols. 2016:13–44. doi: 10.1007/978-1-4939-3774-5_2 [DOI] [PubMed] [Google Scholar]
- 54.Bolger AM, Lohse M, Usadel B. Trimmomatic: a flexible trimmer for Illumina sequence data. Bioinformatics. 2014;30(15):2114–20. doi: 10.1093/bioinformatics/btu170 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hall MR, Kocot KM, Baughman KW, Fernandez-Valverde SL, Gauthier ME, Hatleberg WL, et al. The crown-of-thorns starfish genome as a guide for biocontrol of this coral reef pest. Nature. 2017;544(7649):231–4. doi: 10.1038/nature22033 [DOI] [PubMed] [Google Scholar]
- 56.Li H. Aligning sequence reads, clone sequences and assembly contigs with BWA-MEM. arXiv preprint arXiv:13033997. 2013. [Google Scholar]
- 57.Li H, Handsaker B, Wysoker A, Fennell T, Ruan J, Homer N, et al. The sequence alignment/map format and SAMtools. bioinformatics. 2009;25(16):2078–9. doi: 10.1093/bioinformatics/btp352 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Bergeron LA, Besenbacher S, Bakker J, Zheng J, Li P, Pacheco G, et al. The germline mutational process in rhesus macaque and its implications for phylogenetic dating. GigaScience. 2021;10(5):giab029. doi: 10.1093/gigascience/giab029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Bergeron LA, Besenbacher S, Turner T, Versoza CJ, Wang RJ, Price AL, et al. The Mutationathon highlights the importance of reaching standardization in estimates of pedigree-based germline mutation rates. Elife. 2022;11:e73577. doi: 10.7554/eLife.73577 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Li H. A statistical framework for SNP calling, mutation discovery, association mapping and population genetical parameter estimation from sequencing data. Bioinformatics. 2011;27(21):2987–93. doi: 10.1093/bioinformatics/btr509 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Robinson JT, Thorvaldsdóttir H, Winckler W, Guttman M, Lander ES, Getz G, et al. Integrative genomics viewer. Nature biotechnology. 2011;29(1):24–6. doi: 10.1038/nbt.1754 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Maretty L, Jensen JM, Petersen B, Sibbesen JA, Liu S, Villesen P, et al. Sequencing and de novo assembly of 150 genomes from Denmark as a population reference. Nature. 2017;548(7665):87–91. doi: 10.1038/nature23264 [DOI] [PubMed] [Google Scholar]
- 63.Cingolani P, Platts A, Wang LL, Coon M, Nguyen T, Wang L, et al. A program for annotating and predicting the effects of single nucleotide polymorphisms, SnpEff: SNPs in the genome of Drosophila melanogaster strain w1118; iso-2; iso-3. fly. 2012;6(2):80–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Korneliussen TS, Albrechtsen A, Nielsen R. ANGSD: analysis of next generation sequencing data. BMC bioinformatics. 2014;15(1):1–13. doi: 10.1186/s12859-014-0356-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Schiffels S, Durbin R. Inferring human population size and separation history from multiple genome sequences. Nature genetics. 2014;46(8):919–25. doi: 10.1038/ng.3015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Charlesworth B, Charlesworth D. Elements of evolutionary genetics: Springer; 2010. [Google Scholar]
- 67.Sellinger T, Johannes F, Tellier A. Improved inference of population histories by integrating genomic and epigenomic data. eLife Sciences Publications, Ltd; 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Cutter AD, Jovelin R, Dey A. Molecular hyperdiversity and evolution in very large populations. Molecular ecology. 2013;22(8):2074–95. doi: 10.1111/mec.12281 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Schiffels S, Wang K. MSMC and MSMC2: the multiple sequentially markovian coalescent. Statistical population genomics: Humana; 2020. p. 147–65. doi: 10.1007/978-1-0716-0199-0_7 [DOI] [PubMed] [Google Scholar]
- 70.Nadachowska-Brzyska K, Konczal M, Babik W. Navigating the temporal continuum of effective population size. Methods in Ecology and Evolution. 2022;13(1):22–41. [Google Scholar]
- 71.Cooke I, Ying H, Forêt S, Bongaerts P, Strugnell JM, Simakov O, et al. Genomic signatures in the coral holobiont reveal host adaptations driven by Holocene climate change and reef specific symbionts. Science advances. 2020;6(48):eabc6318. doi: 10.1126/sciadv.abc6318 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Pratchett MS, Caballes CF, RiveraPosada JA, Sweatman HP. Limits to understanding and managing outbreaks of crown-of-thorns starfish (Acanthaster spp.). Oceanography and marine biology: an annual review. 2014;52:133–200. [Google Scholar]
- 73.Santiago E, Novo I, Pardiñas AF, Saura M, Wang J, Caballero A. Recent demographic history inferred by high-resolution analysis of linkage disequilibrium. Molecular Biology and Evolution. 2020;37(12):3642–53. doi: 10.1093/molbev/msaa169 [DOI] [PubMed] [Google Scholar]
- 74.AIMS. (2015). AIMS Long-term Monitoring Program: Crown-of-thorns starfish and benthos Manta Tow Data (Great Barrier Reef). 10.25845/5c09b0abf315a. accessed 14-Jul-2023. [DOI]
- 75.Roelfsema CM, Lyons MB, Castro-Sanguino C, Kovacs EM, Callaghan D, Wettle M, et al. How Much Shallow Coral Habitat Is There on the Great Barrier Reef? Remote Sensing. 2021;13(21):4343. [Google Scholar]
- 76.Castro-Sanguino C, Bozec YM, Condie SA, Fletcher CS, Hock K, Roelfsema C, et al. Control efforts of crown-of-thorns starfish outbreaks to limit future coral decline across the Great Barrier Reef. Ecosphere. 2023;14(6):e4580. [Google Scholar]
- 77.Keightley PD, Ness RW, Halligan DL, Haddrill PR. Estimation of the spontaneous mutation rate per nucleotide site in a Drosophila melanogaster full-sib family. Genetics. 2014;196(1):313–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Smeds L, Qvarnström A, Ellegren H. Direct estimate of the rate of germline mutation in a bird. Genome research. 2016;26(9):1211–8. doi: 10.1101/gr.204669.116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Bintanja R, Van de Wal R. North American ice-sheet dynamics and the onset of 100,000-year glacial cycles. Nature. 2008;454(7206):869–72. doi: 10.1038/nature07158 [DOI] [PubMed] [Google Scholar]
- 80.Waples RS. Tiny estimates of the Ne/N ratio in marine fishes: Are they real? Journal of Fish Biology. 2016;89(6):2479–504. doi: 10.1111/jfb.13143 [DOI] [PubMed] [Google Scholar]
- 81.Oppold A-M, Pfenninger M. Direct estimation of the spontaneous mutation rate by short-term mutation accumulation lines in Chironomus riparius. Evolution Letters. 2017;1(2):86–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Keightley PD, Pinharanda A, Ness RW, Simpson F, Dasmahapatra KK, Mallet J, et al. Estimation of the spontaneous mutation rate in Heliconius melpomene. Molecular biology and evolution. 2015;32(1):239–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Bierne N, Bonhomme F, Arnaud-Haond S. Editorial dedicated population genomics for the silent world: the specific questions of marine population genetics. Current zoology. 2016;62(6):545–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Nordborg M, Krone SM. Separation of time scales and convergence to the coalescent in structured populations. Modern developments in theoretical population genetics: The legacy of gustave malécot. 2002;194:232. [Google Scholar]
- 85.Sjödin P, Kaj I, Krone S, Lascoux M, Nordborg M. On the meaning and existence of an effective population size. Genetics. 2005;169(2):1061–70. doi: 10.1534/genetics.104.026799 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Kimura M. Diffusion models in population genetics. Journal of Applied Probability. 1964;1(2):177–232. [Google Scholar]
- 87.Harrison HB, Pratchett MS, Messmer V, Saenz-Agudelo P, Berumen ML. Microsatellites reveal genetic homogeneity among outbreak populations of crown-of-thorns starfish (Acanthaster cf. solaris) on Australia’s Great Barrier Reef. Diversity. 2017;9(1):16. [Google Scholar]
- 88.Nei M. Molecular evolutionary genetics: Columbia university press; 1987. [Google Scholar]
- 89.Frankham R. Effective population size/adult population size ratios in wildlife: a review. Genetics Research. 1995;66(2):95–107. [DOI] [PubMed] [Google Scholar]
- 90.Vucetich JA, Waite TA, Nunney L. Fluctuating population size and the ratio of effective to census population size. Evolution. 1997:2017–21. doi: 10.1111/j.1558-5646.1997.tb05123.x [DOI] [PubMed] [Google Scholar]
- 91.Allen JD, Richardson EL, Deaker D, Agüera A, Byrne M. Larval cloning in the crown-of-thorns sea star, a keystone coral predator. Marine Ecology Progress Series. 2019;609:271–6. [Google Scholar]
- 92.Deaker DJ, Byrne M. Crown of thorns starfish life-history traits contribute to outbreaks, a continuing concern for coral reefs. Emerging Topics in Life Sciences. 2022;6(1):67–79. doi: 10.1042/ETLS20210239 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Hart MW, Guerra VI, Allen JD, Byrne M. Cloning and selfing affect population genetic variation in simulations of outcrossing, sexual sea stars. The Biological Bulletin. 2021;241(3):286–302. doi: 10.1086/717293 [DOI] [PubMed] [Google Scholar]
- 94.Uthicke S, Pratchett MS, Messmer V, Harrison H. Limited genetic signal from potential cloning and selfing within wild populations of coral-eating crown-of-thorns seastars (Acanthaster cf. solaris). Coral Reefs. 2021;40:131–8. [Google Scholar]
- 95.Eldon B, Riquet F, Yearsley J, Jollivet D, Broquet T. Current hypotheses to explain genetic chaos under the sea. Current zoology. 2016;62(6):551–66. doi: 10.1093/cz/zow094 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Ohta T. An examination of the generation-time effect on molecular evolution. Proceedings of the National Academy of Sciences. 1993;90(22):10676–80. doi: 10.1073/pnas.90.22.10676 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Ho EK, Macrae F, Latta 4th LC, McIlroy P, Ebert D, Fields PD, et al. High and highly variable spontaneous mutation rates in Daphnia. Molecular biology and evolution. 2020;37(11):3258–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Caballes CF, Pratchett MS. Reproductive biology and early life history of the crown-of-thorns starfish. Echinoderms: Ecology, Habitats and Reproductive Biology; Whitmore E, Ed. 2014:101–46. [Google Scholar]
- 99.Schulz RW, de França LR, Lareyre J-J, LeGac F, Chiarini-Garcia H, Nobrega RH, et al. Spermatogenesis in fish. General and comparative endocrinology. 2010;165(3):390–411. doi: 10.1016/j.ygcen.2009.02.013 [DOI] [PubMed] [Google Scholar]
- 100.Gribbins K. Reptilian spermatogenesis: a histological and ultrastructural perspective. Spermatogenesis. 2011;1(3):250–69. doi: 10.4161/spmg.1.3.18092 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Babcock RC, Milton DA, Pratchett MS. Relationships between size and reproductive output in the crown-of-thorns starfish. Marine Biology. 2016;163:1–7. [Google Scholar]
- 102.Babcock R, Mundy C. Reproductive biology, spawning and field fertilization rates of Acanthatser planci. Marine and Freshwater Research. 1992;43(3):525–33. [Google Scholar]
- 103.Bouland C, Jangoux M. Origin of germinal cells and the reproductive cycle of the asteroid Asterias rubens L.(Echinodermata). Invertebrate reproduction & development. 1990;17(2):97–102. [Google Scholar]
- 104.Wessel GM, Fresques T, Kiyomoto M, Yajima M, Zazueta V. Origin and development of the germ line in sea stars. genesis. 2014;52(5):367–77. doi: 10.1002/dvg.22772 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Mercier A, Hamel J-F. Advances in marine biology: endogenous and exogenous control of gametogenesis and spawning in echinoderms. 2009. [DOI] [PubMed] [Google Scholar]
- 106.Caballes CF, Byrne M, Messmer V, Pratchett MS. Temporal variability in gametogenesis and spawning patterns of crown-of-thorns starfish within the outbreak initiation zone in the northern Great Barrier Reef. Marine Biology. 2021;168(1):13. [Google Scholar]
- 107.Yoder AD, Tiley GP. The challenge and promise of estimating the de novo mutation rate from whole-genome comparisons among closely related individuals. Molecular Ecology. 2021;30(23):6087–100. doi: 10.1111/mec.16007 [DOI] [PubMed] [Google Scholar]
- 108.Moran P, De’ath G. Suitability of the manta tow technique for estimating relative and absolute abundances of crown-of-thorns starfish (Acanthaster planci L.) and corals. Marine and Freshwater Research. 1992;43(2):357–79. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig A. Summary of A. cf. solaris fertilisation workflow and larval stages. (A) A. cf. solaris adult being dissected to extract gonads; (B) Female gonads after rinsing in FSW; (C) Mature eggs recently dislodged from the gonad tissue; (D) Fertilised eggs under the microscope presenting a clear fertilisation membrane; (E-I) Larval developmental stages. For each parental cross, we selected two larvae in the early (F) or mid (G) bipinnaria stage (Day 3–8) and early-mid brachiolaria stage (Day 8–9) (H). Fig B. Relationship between manta tow counts and SCUBA swim counts from [108]. The observed data (black dots) are expressed as a per-tow basis (200×12 m, with 2 to 15 tows/transects supporting each observation). The regression model is used to generate deterministic predictions of SCUBA swim counts (line) or stochastic predictions function of the number of tows conducted in a given area (e.g., the perimeter of a reef), illustrated here with 5 (red dots) and 25 tows (green dots). Increasing the number of tows decreases the dispersion around the deterministic model. Fig C. Variation in parental origins and mutational types for de novo mutations (DNM). (A) Per-trio proportions of DNMs phased to their parental origins and those with unknown phasing. There was no significant difference in the proportion of maternally and paternally inherited phased DNMs among trios (Welch two sample t-test; p = 0.50); (B) Distribution of DNMs classified by mutation type, where mutations resulting in a change from C to any base were classified as CpG sites. Fig D. Mutation rate estimates for 14 parent-offspring trios grouped by family. There was no effect of family grouping on between group variance (ANOVA; p = 0.33). Mutation rate data points for Trio 7 siblings are overlayed. Fig E. Annotated variants (synonymous, nonsynonymous) and their predicted genomic locations according to the A. cf. solaris reference genome annotations [55]. There was no significant enrichment of annotation categories based on genome-wide expectations (p>0.05) after corrections for multiple tests.
(PDF)
(XLSX)
(XLSX)
(XLSX)
(XLSX)
(XLSX)
(XLSX)
(XLSX)
(XLSX)
95% confidence intervals are shown as reported by authors or omitted if not reported. Highlighted mutation rate estimates are removed from Fig 2.
(XLSX)
Data Availability Statement
Raw whole genome sequence data from parent-offspring trios are available on the NCBI Short Read Archive (BioProject ID PRJNA1064695). Supporting scripts and associated data are available on The University of Queensland’s Library eSpace: https://doi.org/10.48610/ad122d0. Scripts relating to mutation rate estimation are available on Github (https://github.com/lucieabergeron/germline_mutation_rate). Scripts and data relating to census population size analysis are available on Github: https://github.com/ymbozec/acanthaster_GBR_abundance. A version of this manuscript has been uploaded to the bioRxiv repository: https://doi.org/10.1101/2023.06.28.546961.