Micro-motion characteristics of multi-feature targets on the double pulse coherent system

Abstract

In this paper, we study the micro-motion characteristics of multi-feature targets based on a double pulse coherent system under atmospheric conditions. The theoretical model for echo signal and micro-motion characteristics of a 3D target in double pulse coherent system is deduced. We discuss the influence of micro-motion characteristics, the relative size of light spot and target, target shapes, and incident direction on frequency shift. LRCS (Lidar cross-section), echo waveform, intensity and radiation energy distribution under different conditions are obtained additionally. Simulation results conclude that these parameters are of advantage to the inversion of target shape properties and motion types.

1. Introduction

In-depth analysis on the micro-motion characteristics of multi-feature targets has become an important trend [1,2] in research. Multi-feature targets not only refer to the “multi-feature” properties of the target shape, including the simple target-sphere and the complex target-cone, but also represent the “multi-feature” characteristics of micro-motion, including translation, rotation that can be manifested by angular frequency, and composite motion. This research in the time-frequency-intensity domain may provide further information for target detection, classification and recognition [3]. It can achieve the high-speed and long-distance target recognition [4,5] in complex scenes. The target signal has become a kind of interference signal for the detection system. It makes the Snr (signal-to-noise ratio) of micro-Doppler information decrease seriously. The double pulse laser [6,7] can emit higher energy under the condition that a single pulse has the same ranging ability, which is conducive to the detection of weak signals. Therefore, it is suitable for measuring the echo energy and intensity of a target. The micro-Doppler detection using a double pulse LIDAR [8] can ignore noise components introduced by the overall motion of the target through the before-and-after pulse correlation process furthermore. Lower micro-motion speeds can be measured by controlling the time interval between the front and back pulses of a pulse pair. The processing results only include the micro-Doppler frequency information of the target, which improves the Snr of useful signals and extracts high-resolution micro- Doppler spectra.

The double pulse coherent detection system can realize velocity measurement, ranging, even the processing of echo information in time domain completely [9]. Therefore, it is widely used in tracking and makes extremely accurate Doppler measurement possible. A typical double pulse coherent system consists of an active laser and a slave laser, Fig. 1.

Fig. 1.

The principle of double pulse coherent detection system.

The influence of random phase noise from lasers on detection results can be largely eliminated by the following coherence process: (1) coherence of the active laser pulse signal with the slave laser pulse signal; (2) coherence of main and echo pulse laser signal; (3) the generated echo signal can be detected by photodiode. The coherent operation is performed again in the signal processing system. The active laser produces the main oscillation signal, a portion of which is modulated into the slave laser to produce a double pulse signal. A part of the generated signal is mixed with the unmodulated signal emitted by the active laser as the local oscillator pulse laser signal. The other one acts on the target, which is reflected by the target and then mixed with the unmodulated signal as detection signal.

Reference [10] provides theoretical models for the noise caused by dual pulse detection of targets, including photon or shot noise, target correlation noise, etc. The on-site measurement results using a double pulse lidar will be compared with theoretical simulation results. In 2014, NASA's Langley Research Center developed a long-range LiDAR system, by a continuously agile double pulse waveform scheme. It is used to track rapidly moving resident space objects to achieve both millimeter level ranging accuracy and millimeter/second speed accuracy [8]. The above studies have demonstrated experimentally that double pulses have high accuracy in detecting long-distance high-speed moving targets. Due to the need for extensive testing under various environmental conditions, however, the design of double pulse coherent system consumes a lot of resources, and extends the research and development cycle [11]. The research on micro-motion characteristics of multi-feature targets on the double pulse coherent system can effectively save resources and shorten the R&D cycle. Hence, its importance cannot be overstated.

In 2016, the mechanism of dual pulse laser coherent detection has been analyzed, including the composition and structure of the detection system, as well as the working principle of the system [12]. However, the additional noise attached to impulse signal by the atmospheric turbulence [13] causes a degradation of the signal-to-noise ratio (SNR) and brings difficulties to the accurate extraction of micro-motion information.

This paper establishes a theoretical model for micro-motion characteristics of multi-feature targets on the double pulse coherent system by combining the theory of atmospheric turbulence. Of course, this method is not limited to the double pulse coherent system in Fig. 1. Physical quantities such as echo intensity, energy, phase, and frequency shift are collectively referred to as echo modulation characteristic parameters. The technical key of double pulse coherent detection lies in controlling the time interval between the front and back pulses, pulse width, and period to affect these parameters. In Section 2, the theory based on double pulse coherent system is presented, including echo signal model and micro-motion features of a target acquired by finite element method (FEM). The atmospheric transport theory imported as a propagation condition. A theoretical method of micro-motion characteristics of multi-feature targets based on a double pulse coherent system is proposed in Section 3, which is used to calculate echo modulation characteristic parameters. The simulation experiments results show: (1) motion types, the relative size of light spot and target, target shapes, and incident direction on FSTD; (2) the comparison of LRCS obtained by irradiating the target with large and tiny spots; (3) echo waveform with different target shapes (4) the radiation energy distribution and target strength of a cone being symmetrical with “burrs”. In all, echo modulation characteristic parameters can inverse shape properties and motion features, providing a theoretical basis for the micro-motion characteristics classification and target identification.

2. Method

2.1. Echo signal model in double pulse detection

We can write the intensity reflected toward the receiver as [14].

$$I_r=\frac{\underset{t\arg et}{\int }I\left(x,y,z,t\right)f_r\left(x,y,z\right)dA}{R^2}$$ (1)

where the radiant intensity from the transmitter is I(x,y,z) and f_r is the BRDF of the surface element, dA_i. The integration is performed on the luminous surface part of the target. The range z = R is the average range to the target, which is assumed to be much larger than the target size. According Eq. (1), the intensity of the emission derived to double-pulse can be written as

$$I\left(x,y,z,t\right)=I_0\mathrm{g}\left(x,y\right)s\left(z\right)=I_0\mathrm{g}\left(x,y\right)s\left\{t-2\frac{R\left(x,y\right)}{c}\right\}$$ (2)

$$I\left(x,y,z,t+\Delta T\right)=I_0\mathrm{g}\left(x,y\right)s\left(z+\Delta z\right)=I_0\mathrm{g}\left(x,y\right)s\left\{t+\Delta T-2\frac{R\left(x,y\right)}{c}\right\}$$ (3)

where g(x,y) and s(z) are the normalized transverse (spatial) and longitudinal (time) distributions respectively. ΔT is the time interval between the two pulses before and after in a pulse pair. Fig. 2 provides a simplified illustration of the double pulse measurement process. The phase at t = t₀ is Φ₀, and then becomes Φ₀+4π△s/λ. The double pulse waveform [15] essentially measures the micro-motion by the phase change between the first and second pulse caused. The range to target is measured by the amount of Δs.

Fig. 2.

The principle of pulse waveform velocity measurement.

The influence of the front and rear pulses in a pulse pair on the normalized longitudinal distribution of intensity can be ignored. Based on Eqs.(2) (2), (3), the double-pulse LIDAR equation in view of atmospheric attenuation is rewritten as.

$$P_r\left(t\right)={\eta }_{syst}{I}_r\frac{A_r}{R^2}\mu \left(r,\lambda \right)=\frac{A_r}{R^4}\mu \left(r,\lambda \right){\eta }_{syst}{I}_0\times \underset{t\arg et}{\int }\mathrm{g}\left(x,y\right)s\left(z,z+\Delta z\right)dA$$ (4)

where μ(r) is the atmospheric attenuation coefficient at a distance of r, A_r is the receiver area, η_syst is the system loss and s(z, z+△z) represents the longitudinal distribution of intensity in double-pulse detection. It can be signed by the phasebΔΦ described in detail in Section 2.2. Eq. (4) is simplified as Eq. (5).

$$P_r\left(t\right)=\frac{A_r}{R^4}\mu \left(r,\lambda \right){\eta }_{syst}{I}_0\times \underset{t\arg et}{\int }\mathrm{g}\left(x,y\right)\exp \left(j\cdot \Delta \phi \right)dA$$ (5)

The LRCS per unit area can be obtained in Eq. (6) [16].

$${\sigma }_i=4\pi \underset{t\arg et}{\int }\mathrm{g}\left(x,y\right)f_{r1}{f}_{r2}\exp \left(j\cdot \Delta \phi \right)dxdy$$ (6)

The Torrance-Sparrow model contributes to describing the reflectivity of rough targets and its BRDF is written as Eq. (7).

$$f_r\left({\theta }_i,{\theta }_r,{\phi }_r\right)=\frac{k_b{k}_r^2\cos \beta }{1+\left(k_r^2-1\right)\cos \beta }\cdot \exp \left[b{\left(1-\cos \gamma \right)}^a\right]\frac{G\left({\theta }_i,{\theta }_r,{\phi }_r\right)}{\cos {\theta }_i\cos {\theta }_r}+\frac{k_d}{\cos {\theta }_i}$$ (7)

where θ_i is the angle between the incident light and the normal vector of the small grid, θ_r is the angle between the reflected light and the normal vector of the small grid, φ_r is the azimuth of reflection, k_b, k_r, k_d, a, b are parameters influenced by the target material, β and γ are related to θ_i; θ_r; φ_r and G(θ_i,θ_r, φ_r) characterizes the geometric decay [17]. After completing the geometry operations on the target and selecting the material, the above parameters will be imported from the material library automatically. Since ΔT is small, the change in the target before and after the pulse is characterized by the angle. The algebraic sum of LRCS values in each surface element equals to the overall LRCS of a target. The LRCS carried by each face element is summed by using the FEM.

2.2. 3D target micro-motion characteristics in ideal double pulse detection theory

Fig. 3 illustrates the double-pulse waveform format, comprising a pair of pulselets. The phase difference between the first and second pulse in a pulse pair caused by the motion is [18].

$$\Delta \phi =angle\left\{\exp \left[-j2\frac{2\pi }{\lambda }\Delta TV\left(\frac{p}{f_{PRF}}\right)\right]\cdot \exp \left[j2\frac{2\pi }{\lambda }\Delta TV\left(\frac{p}{f_{PRF}}+\Delta T\right)\right]\right\}=angle\left\{\underset{A}{\int }I\left(x,y\right)\exp \left[-j2\frac{2\pi }{\lambda }\Delta TV\left(\frac{p}{f_{PRF}}\right)\right]d{A}_r\cdot \underset{A}{\int }I\left(x,y\right)\exp \left[j2\frac{2\pi }{\lambda }\Delta TV\left(\frac{p}{f_{PRF}}+\Delta T\right)\right]d{A}_{\mathrm{r}}\right\}$$ (8)

Fig. 3.

The principle of double-pulse waveform format.

Where the function angle represents the complex phase angle, p represents the serial number of pulse pair in the generated double-pulse laser signal, p = 1, 2, 3 …..., f_PRF is the repetition frequency of the pulse pair, λ is the wavelength, V(x,y) represents the spatial distribution of target micro-motion velocity, $V\left(\frac{p}{f_{PRF}}\right)$ is the target micro-motion velocity corresponding to the previous pulse and $V\left(\frac{p}{f_{PRF}}+\Delta T\right)$ is related to the latter pulse. The phase difference between the first and second pulse in one pulse pair caused by the target micro-motion is further written as

$$\Delta {\phi }_i=angle\left[\exp (-j2\frac{2\pi }{\lambda }\Delta TV\cos \left({\omega }_T\left(\frac{p}{f_{PRF}}\right)\right)\cdot \exp (j2\frac{2\pi }{\lambda }\Delta TV\left(\frac{p}{f_{PRF}}+\Delta T\right)\right]$$ (9)

where ω_T denotes the target micro-motion frequency. Taking account to translation, ω_T = 0. When the V(x,y) is a cosine function, such as rotation, the phase difference is simplified as

$$\Delta {\phi }_i=-4\frac{2\pi }{\lambda }\Delta T{V}_{est}\sin \left(\frac{{\omega }_{\mathrm{T}}\Delta T}{2}\right)\cos \left({\omega }_T\frac{p}{f_{PRF}}+\frac{{\omega }_{\mathrm{T}}\Delta T}{2}+\frac{\pi }{2}\right)$$ (10)

The instantaneous micro-Doppler velocity is

$$V_{est}=\frac{\Delta \phi }{\Delta T}\cdot \frac{\lambda }{2\pi }\cdot \frac{1}{4\sin \left(\frac{{\omega }_T\Delta T}{2}\right)}$$ (11)

The micro-Doppler frequency is

$$f_D=\frac{2V_{est}}{\lambda }=\frac{\Delta \phi }{\Delta T}\cdot \frac{1}{4\pi \sin \left(\frac{{\omega }_T\Delta T}{2}\right)}$$ (12)

The relationship between time and pulse sequence can be simplified as

$$t=\left(p-1\right)\frac{1}{f_{PRF}}+2\tau +\Delta T$$ (13)

In summary, the micro-motion characteristics of a target in a double pulse detection is obtained by Eqs. (9), (10), (11), (12), (13).

$$f_D=-\frac{2}{\lambda }V\cos \left[{\omega }_T\frac{\left(t-2\tau -\Delta T\right)f_{PRF}+1}{f_{PRF}}+\frac{{\omega }_T\Delta T}{2}+\frac{\pi }{2}\right]$$ (14)

The target is dissected into small surface elements. The micro-Doppler feature information carried by each surface element of the target is superimposed by FEM similarly. The 3D target micro-Doppler FS can be calculated.

2.3. Atmospheric transport theoretical model

The theory of 3D target micro-motion characteristics in doublepulse detection only considers the propagation of echoes in ideal gas (without attenuation). The influence of atmospheric attenuation on echoes must be inevitably considered in detection. Therefore, it is necessary to import the atmospheric attenuation model as one of propagation conditions in simulation. The following parameters should also be discussed to refine the atmospheric transport theory.

• ①Atmospheric absorption coefficient

Generally, the attenuation of laser caused by atmosphere is expressed as Eq. (15).

$$I\left(R\right)=I_0\exp \left[-{\int }_0^R\mu \left(r\right)dr\right]$$ (15)

where R is the total distance between the target and detection position. The atmospheric absorption coefficient calculated by the standard atmospheric model is less than 10⁻⁶km⁻¹ for the 1.06 μm laser [19,20]. The empirical model formula for predicting the attenuation coefficient [21] in common use is shown in Eq. (16).

$$\mu \left(\lambda \right)=\frac{3.912}{V_b}{\left(\frac{0.55}{\lambda }\right)}^a$$ (16)

where V_b is the atmospheric visibility and a is the wavelength correction factor related to visibility as shown in Eq. (17).

$$a=\{\begin{array}{l}0.585V_b^{1/3}\\ 1.3\\ 1.6\end{array}\begin{array}{l}{V}_b\le 6km\\ \text{Average}\text{visibility}\\ \text{Good}\text{visibility}\end{array}$$ (17)

• ②Relative humidity

The relative humidity [22,23] is defined as the ratio of actual water vapor pressure in the air to the saturated water vapor pressure at current air temperature. It is expressed as a percentage. Relative humidity is set to account for atmospheric conditions to make the model closer to the actual atmospheric environment [24]. The relative humidity of 0.5 can represent sunny days.

3. Simulation

3.1. Overview of the simulation

The following are computational steps of the theoretical method:

• Step 1 Draw the model

Select the 3D model and draw a target. The center of the target is at the origin.

• Step 2 Add the relevant physical field

We choose the RF field-based frequency domain model of electromagnetic waves and the sound field-based atmospheric transport model.

• Step 3 Add light source

Relevant parameters of the source are shown in Table 1. Fig. 4 shows the relation among multiple targets and light sources in different directions. The target that can be covered by the spot is called a small target (large spot), Fig. 4(a), taking a sphere as an example. The target in Fig. 4(b) that is much larger than the spot size is called a large target (tiny spot). Fig. 4(c) and (d) are diagrams of tiny cones illuminated in different incident directions. The magenta area is the irradiated surface. The shaded area is the set of masked face elements. The arrow is identical to the incident direction. Simulation parameters are shown in Table 1.

• Step4 Set boundary conditions, parameters and other necessary geometric operations

Table 1.

Simulation parameters.

Item	Specification	Remark
Material	Steel	Target
	Air	Atmosphere
Target	Cone	Radius of bottom surface: 0.3 m
		Height:1 m
	Sphere	Radius:1 m
Atmospheric absorption coefficient	10−7km−1
Reference temperature	293.15 K
Standard atmospheric pressure	101.325 kPa
Air reference pressure	20 μPa
Incident angle	60°
Pitch angle	50°
Azimuth angle	20°
Euler angle	(20°,30°,50°)
Atmospheric visibility	23 km	Sunny days
Relative humidity	0.5
The receiver area	0.3m2
Angular velocity	31.4 rad/s
Velocity	5 m/s
Double-pulse light source parameters	190ns	Time interval between two pulses within a pulse pair
	500ns	Pulse-to-pulse interval
	50ns	Pulse width
	1 μm	Wavelength
	1 kW	Peak power
	6	The serial number of pulse pair
	954 m	Distance from the light source to the target

Fig. 4.

(a) A large spot shining vertically on the sphere (b) A tiny spot shining vertically on the sphere (c) A large spot shining vertically on the cone (d) A large spot shining obliquely on the cone.

The inclusion of boundary conditions, such as optical fluctuation equations, scattering boundary conditions, perfect matching layer (PML) [25], pressure background field and target surface impedance can make the solution of finite element equations satisfy convergence. Other operations refer to data series operations, including the spatial integration, averaging, projection, normal velocity, rotation axis and coordinate system, etc.

• Step5 Add material

The target material is steel. Air is used as the material of infinite airspace.

• Step6 Mesh division and FEM solution

It is able to analyze and solve complex discretization of the dissected whole by using the FEM with a direct solver based on the LU decomposition [17]. The number of convergence is 10000. The error is 10⁻⁵. Good convergence.

• Step7 Calculation

We import the probe and set its position so that it meets the light source co-location. The study of echo modulation characteristics parameters is achieved by selecting two-dimensional coordinates/three-dimensional images and inputting related physical quantities. Azimuth and pitch angle can be obtained by setting the position of light source and camera.

3.2. Simulation experiments

Considering the coherence of double pulse [10], the relationship between time and frequency cannot be defined only by using traditional geometric method. The micro-motion target echo frequency shift [26] in double pulse detection under atmospheric conditions is obtained by Eq. (8) and Eq. (15). As the detection time increases, yet, in Eq. (18), the detection position, the area of the receiving surface, the generation time of pulse and other variables affect the phase difference.

$$\begin{array}{l}\Delta \phi =angle\{\underset{A}{\int }{I}_0\exp \left[-{\int }_0^R\mu \left(r\right)dr\right]\cdot \exp \left[-j2\frac{2\pi }{\lambda }\Delta TV\left(\frac{p}{f_{PRF}}\right)\right]d{A}_r\\ \underset{A}{\int }{I}_0\exp \left[-{\int }_0^R\mu \left(r\right)dr\right]\cdot \exp \left[j2\frac{2\pi }{\lambda }\Delta TV\left(\frac{p}{f_{PRF}}+\Delta T\right)\right]d{A}_{\mathrm{r}}\}\end{array}$$ (18)

The above equation can be written in view of the atmospheric attenuation in Section 2.3 as

$$\begin{array}{l}\Delta {\phi }_i=angle\{\underset{A}{\int }{I}_0\exp \left[-{\int }_0^R\frac{3.912}{V_b}{\left(\frac{0.55}{\lambda }\right)}^{\mathrm{a}}dr\right]\cdot \\ \left[\exp (-j2\frac{2\pi }{\lambda }\Delta TV\cos \left({\omega }_T\left(\frac{p}{f_{PRF}}\right)\right)\cdot \exp (j2\frac{2\pi }{\lambda }\Delta TV\left(\frac{p}{f_{PRF}}+\Delta T\right)\right]dA\}\end{array}$$ (19)

The above equation describes the theoretical model of the micro-motion characteristics of moving targets detected by a double pulse coherent detection under atmospheric conditions. The composite motion in this article is an attitude where both translation and rotation occur simultaneously. It can be simulated with Eq. (19). While considering only translation or rotation, it is necessary to refer to section 2.2. The overall phase information is regarded as the superposition of each face element in a target: $\Delta \phi =\sum _i\Delta {\phi }_i$. The simulation of FS is then achieved by dissecting the mesh with FEM, which is closer to reality. This paper proposes a method on micro-motion characteristics of multi-feature targets on the double pulse coherent system. We carried out simulation experiments for the effects of motion types, the relative size of spot and target, target shape, incident direction, detection frequency and other parameters on FSTD as follow.

3.2.1. Motion type

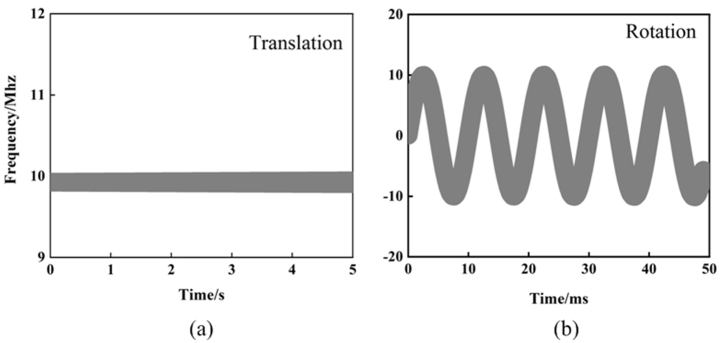
Motions used in the simulation include translation, rotation, compound motion, etc. The FS of a sphere illuminated by a large spot can be shown in Fig. 5, which is aimed to prove the correctness of this method. Small targets are generally considered for remote detection, for example, Fig, 4(a). Along x-axis in the negative direction we applied a translation speed to the sphere. It can be corroborated in Fig. 5(a) that the inter-pulse phase does not change with time when ω_T = 0, but a large FS is generated. Of course, the existence of atmospheric attenuation makes the value of FS slightly distinguish from |2V/λ|. The width of FS is about 120 KHz. Fig. 5(b) shows the FSTD curve of a small rotation sphere satisfies the cosine law. The period is 10 ms. In conclusion, the curve of FS can invert the motion type.

Fig. 5.

The FS of a sphere illuminated by a large spot under (a) translation, (b) rotation.

3.2.2. The relative size of spot and target

Next, we discuss the influence of various relative sizes of spots and targets in Fig. 4(a) and (b) on FSTD. Obviously, the shape and amplitude of the FSTD of the sphere in Fig. 4(a) with compound motion are the same as that with rotation by comparing Figs. 5(b) and Fig. 6(a). The difference is that the period of FSTD in Fig. 5(b) is smaller than that in Fig. 6(a). The curve of FS in Fig. 6(a) is getting thicker in addition. Here, the grid division is based on the wavelength unit magnitude. The complex motion inevitably leads to a change in masked face elements and the number of grids contained in the detection area per unit time, which is reflected in the thickness of the FSTD curve. This curve in Fig. 6(a) becomes thicker in the time of 0–50 ms. It characterizes that the number of face elements within the detection area is increased, i.e., the target moves away from the detector. The period has changed to T = 20 ms. Fig. 6(b) illustrates that the FSTD diagram of the sphere in Fig. 4(b) with compound motion is a thinner cosine curve since the tiny detection spot only covers a few face elements. The peak value of FS in these two figures is identical, f_Dpeak = 9.877Mhz. The thickness of FSTD curve can represent the difference between the relative size of spot and target as a result by comparing Fig. 6(a) and (b).

Fig. 6.

(a)FS of a sphere in compound motion illuminated by a large spot (b)FS of a sphere in compound motion illuminated by a tiny spot (c)LRCS of a sphere in compound motion illuminated by a large spot (d)LRCS of a sphere in compound motion illuminated by a tiny spot.

Fig. 6(c) and (d) show LRCS of the two spheres in Fig. 4(a) and (b). The scanning step is 0.01°. The magnitude of LRCS depends on the echo strength received at each point in transceiver with coherent system, satisfying $\sigma =\sum _i{\sigma }_i$. Fig. 6(c) indicates the LRCS curve of a compound motion sphere illuminated by a large spot. This curve is similar to the uniform parabola with an opening upward. The maximum value is LRCS_max(c) = 0.1615 m⁻² with the incident angle of −10°(350°) and the min. value is LRCS_min(c) = 0.00935 m⁻² with the incident angle of 3.29°. And LRCS of tiny spot is characterized in Fig. 6(d), whose curve is the non-uniform parabola with origin as symmetric center of point aggregation. The non-uniformity is due to that the received LRCS information is mainly focused on the part illuminated by spot light, leading to the thick-bottom and narrow-top of curve. The maximum value is LRCS_max(d) = 0.1802m⁻² and the min. value is LRCS_min(d) = 0.1261 m⁻². To sum up, the relative size of spot and target can also be inverted through LRCS.

3.2.3. Target shapes

The influence of target shape on echo modulation characteristics parameters is studied. The divergence angle of the light source is 2deg. The incident light shines vertically to the cone in Fig. 4(c). Fig. 7 shows the FS curve of Fig. 4(c). The reason why the curve in Fig. 7 thickens over time is the same as in Fig. 6(a). The FS peak value is low (f_Dpeak = 9.051Mhz). The period of curve (T = 22.055 ms) is not the same with Fig. 6(a). The type of FSTD is basically similar yet. Therefore, FSTD can also be used as the basis for inversion of the target shape by comparing Figs. 7 and 6(a).

Fig. 7.

The FS curve of a cone.

Echo waveform is used for characterization of shape properties in Fig. 8. Echo waveform of the sphere in Fig. 4 (a) is Gaussian, Fig. 8 (a). The peak value is 1.38 μW when t = 58.1ns. Echo waveform of the cone in Fig. 4(c) is shown as Fig. 8 (b), which is a Gaussian-like waveform with the peak to the left. The value of peak power is 1.78 μW.

Fig. 8.

The comparison of echo waveform with different target shapes:(a) sphere target, (b) cone target.

3.2.4. Incident direction

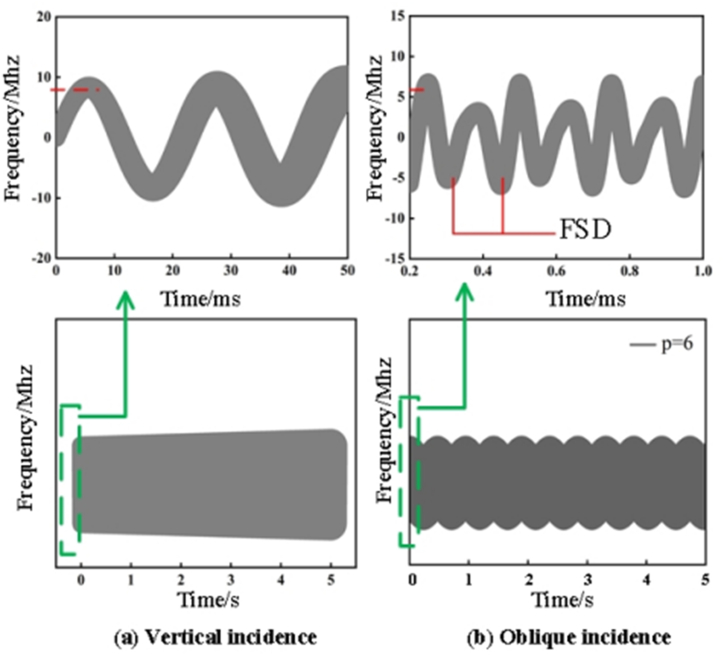
We attach great importance to the characteristics of FSTD for a compound motion cone at different incident direction. Fig. 9 indicates the FSTD of the cone in Fig. 4(c) and (d). The time range of 0–5s and the step size of 0.01s with p = 6 is shown. Apparently, Fig. 9(a) is compressed by the cosine curve getting thicker with time. The characteristics of this curve are detailed in Fig. 7 in Section 3.2.3.

Fig. 9.

The FSTD curve of compound motion cones under different incidence directions: (a) vertical incidence, (b) oblique incidence.

Fig. 9(b) indicates the FSTD of the cone in Fig. 4(d) with a compound motion, demonstrating the universality of this method. The incident light can cover the bottom and side of the cone. In general, the FSTD is compressed by a cosine-like periodic frequency shift deformation curve. The following is a detailed description of curve characteristics.

• ①Cosine-like

The detail plot provides information about the fact that the curve is actually a cosine-like curve varying with time.

• ②Frequency shift deformation(FSD)

The coherent detection of a typical target may drift at a speed other than zero in the optical path direction, leading to the frequency shift deformation. As can be seen in the detail diagram of Fig. 9(b), the amount of FSD due to the overall movement of the target away from the detector is -3Mhz.

• ③Periodicity

The period of FSTD curve is 0.25 ms, which contains an undeformed wave and a FSD. In all, the position of incident light is also a powerful means to affect FSTD by influencing the masked face elements.

Fig. 10(a) points out the radiation energy distribution of this cone to assist the target recognition. The radius of scan is 100 m. The radiation energy distribution of micro-motion cone is a hemisphere with “burrs”. The “burr” is caused by cone's narrow-top and wide-bottom shape. The magnitude of the received energy depends on the actual position of the measurement. It is obvious that the red color indicates maximum energy and dark blue is the minimum. In general, the energy detected on sunny days decreases with increasing detection distance. The meshed geometry was read and available for calculation of target strength [27], Fig. 10(b). The target intensity is characterized as a symmetric figure with “burrs”, which also coincides with the symmetry of the cone. It is not difficult to find that both the radiation energy distribution and target strength at a certain moment can be used as a reference to invert shape properties and motion features of a target.

Fig. 10.

Echo energy and intensity of the cone (a) the radiation energy distribution; (b) target strength on the radial axis.

4. Conclusion

We have demonstrated an effective implementation of studying micro-motion characteristics of multi-feature targets on the double pulse coherent system. The echo signal model and the theory of 3D target micro-motion characteristics in double pulse detection were derived by the finite element method. What we take into account is the impact of motion type, the relative size of light spot and target, target shapes and incident direction on FS for testing the correctness and universality of FSTD. What's more, LRCS, echo waveform, intensity and radiation energy distribution can be gained. To make a long story short, these parameters can invert target shape properties and micro-motion characteristics effectively. In this method, masked face elements are directly obtained by setting light source and target parameters, optimization calculation. These all provide a theoretical support for promoting the ability to identify targets, making the evaluation of their performance at perfect and laying the foundation for the double pulse coherent system.

Data availability

Data will be made available on request. The data that support the findings of this study areavailable on request from the corresponding author, Haiyang Zhang (HZhang-628-974), uponreasonable request.

CRediT authorship contribution statement

Si Chen: Writing – review & editing, Writing – original draft, Software, Methodology, Formal analysis, Data curation, Conceptualization. Haiyang Zhang: Visualization, Validation, Supervision, Resources. Lin Wang: Writing – review & editing, Data curation. Yu Fan: Validation, Project administration. Changming Zhao: Supervision, Resources.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.