Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Aug 8;62(33):13566–13572. doi: 10.1021/acs.inorgchem.3c01987

Analyzing Fluoride Binding by Group 15 Lewis Acids: Pnictogen Bonding in the Pentavalent State

Logan T Maltz 1, François P Gabbaï 1,*
PMCID: PMC10862541  PMID: 37551938

Abstract

graphic file with name ic3c01987_0005.jpg

We report the results of a computational investigation into fluoride binding by a series of pentavalent pnictogen Lewis acids: pnictogen pentahalides (PnX5), tetraphenyl pnictogeniums (PnPh4+), and triphenyl pnictogen tetrachlorocatecholates (PnPh3Cat). Activation strain and energy decomposition analyses of the Lewis adducts not only clearly delineate the electrostatic and orbital contributions to these acid–base interactions but also highlight the importance of Pauli repulsion and molecular flexibility in determining relative Lewis acidity among the pnictogens.

Short abstract

Among pentavalent pnictogen Lewis acids, antimony-based species stand out as the strongest fluoride binders. Computational activation strain and energy decomposition analyses highlight the importance of Pauli repulsion and molecular flexibility in determining this relative Lewis acidity.

Introduction

Among Lewis acids, antimony holds a special place. SbF5, in particular, is a Lewis superacid1 that has had profound impacts on chemistry as exemplified by the work of Olah involving magic acid.2 Recently, our group3 and others4 have effectively employed the unique Lewis acidity of Sb to develop transmembrane anion transporters and anion-recognition platforms. But what is it that distinguishes Sb from the other elements in the pnictogen (Pn) group? As chemists, we turn to chemical bonding and the competition between covalency and ionicity to answer this question.

Being saturated or hypervalent, pentavalent pnictogens use an empty σ*-orbital to accept electron density. At the same time, the coincident σ-hole provides Coulombic stabilization to the newly formed linkage. Scheiner details the importance of these effects in his original definition of the pnictogen bond using trivalent elements5 which has since expanded to include the interactions between any pnictogen-based Lewis acid—in the trivalent or pentavalent state—and a Lewis base.6 Obviously, the distinction between the pnictogens must rely on amplification of whichever form of bonding predominates. Is the interaction more covalent? Then we might look to relative lowest-unoccupied molecular orbital (LUMO) energies to provide insight into the increasing Lewis acidity down the group.7 Does ionicity dominate the bonding interaction? Then we might look to measures of the electrostatic potential to understand the increased Lewis acidity of Sb derivatives.

Wanting simple, intuitive descriptions of chemical bonding, we sometimes forget its complexity. Fortunately, chemists have developed models to better conceptualize complex interactions. Computational energy decomposition analysis (EDA) provides a convenient way to break an interaction into various energetic contributions: London dispersion interactions (ΔEdisp), electrostatic interactions (ΔEel), orbital interactions (ΔEoi), and Pauli repulsion (ΔEPauli). In our constant debates about the covalency or ionicity of an interaction, we often neglect London dispersion and Pauli repulsion.

Hypervalent SbF5 reminds us that with any interaction—but especially closed-shell interactions—we need to consider Pauli repulsion: the destabilizing interaction occurring when two filled orbitals interact with each other. This repulsion is the underlying electronic basis for what we term “steric interactions” and is also at play in our discussions of ionic and covalent bonding. In this paper, we contend that Pauli repulsion rivals electrostatic and orbital interaction contributions in its importance to the Lewis acidity of the pnictogens.

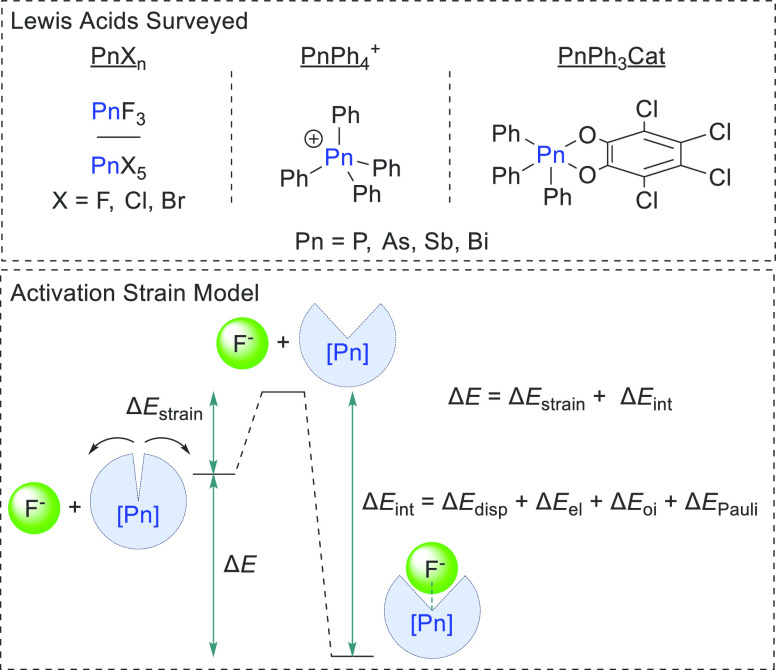
In the past decade, the utility of the activation strain model (ASM) has been repeatedly demonstrated.8 This model bifurcates the overall interaction energy ΔE into the energy necessary to strain and reorganize the interacting species into their interacting geometries (ΔEstrain) and the energy associated with allowing these strained species to interact (ΔEint).8a To fully understand the interactions in these systems, ΔEint is then parsed into its constituent components using EDA in the Amsterdam Density Functional (ADF) program (Figure 1). This method conveniently captures ΔEstrain and ΔEPauli which are important components of the overall interaction energy that are often overlooked because they are not as comfortably approachable as ΔEel and ΔEoi.

Figure 1.

Figure 1

Open in a new tab

Top: Lewis acids surveyed in this study. Bottom: diagram of the activation strain model and the energy components comprising the overall interaction energy between the Lewis acids studied and F–.

Inspired by Bickelhaupt and co-workers’ analysis of trivalent pnictogen trihalides,9 we have undertaken a similar analysis on a series of pentavalent pnictogen Lewis acids: pnictogen pentahalides (PnX5), tetraphenyl pnictogeniums (PnPh4+), and triphenyl pnictogen tetrachlorocatecholates (PnPh3Cat) (Figure 1). The last two families of compounds were selected because of their extensive use by our group as anion-binding platforms, anion sensors, and anion transporters.3 Unlike the previous work on trivalent pinctogens,9 we expanded the scope of Lewis acids beyond the homoleptic halides but narrowed the scope of Lewis bases, focusing on these acids’ interactions with fluoride (F–). As such, we are effectively decomposing fluoride ion affinities (FIAs), though we are assessing changes in electronic energy (ΔE) while FIAs are defined as changes in enthalpy (ΔH).

The computations and analyses presented in this article illustrate that despite having lower magnitudes of stabilizing contributions from ΔEel and ΔEoi, Sb displays the highest Lewis acidity (most negative ΔE) in almost every case analyzed, the only exception being the trivalent pnictogen trifluorides. This result is due to Sb also having lower magnitudes of destabilizing contributions from ΔEstrain and ΔEPauli.

Computational Methods

For computational efficiency, we optimized the initial geometries of the Lewis acids and their fluoride adducts in Orca 5.0.210 using PBEh-3c/def2-mSVP11 with the default defgrid2 settings. Frequency calculations were performed at the same level of theory to verify that all optimized structures were at a local minimum on the potential energy surface. Natural population analysis (NPA) charges were obtained through Natural Bonding Orbital calculations using NBO 7.0 at the same level of theory.12 Where possible, structures were reoptimized from previously optimized coordinates.9,13 All other structures were initially produced using either GaussView 6.1.114 or Avogadro15 or by substituting one atom for another in the input file before performing the optimization depending on which method was simpler. For the F– adducts of the PnPh3Cat species, two isomers were possible: F trans to Ph or F trans to O in the tetrachlorocatecholate. In the main text, the isomer with F trans to Ph is discussed as it is the lowest-energy isomer for Sb and similar trends are seen among both isomers. For completeness, both isomers were fully analyzed, and that data is presented in Table S1 and Graphs S7–S9.

The structures optimized in Orca were used as inputs for single-point energy calculations and EDA16 computations conducted in ADF 2022.10117 using the M06 functional18 paired with the D3 model to account for dispersion effects.19 The QZ4P basis set20 as implemented in the ADF program was used without frozen-core approximation and with good numerical quality. The zeroth-order regular approximation (ZORA) Hamiltonian was employed to account for scalar relativistic effects.21 To avoid numerical issues, the “Fix Dependencies” function in ADF was enabled for the PnPh4+ and PnPh3Cat species due to their size. ΔEstrain was determined by subtracting the single-point energy of the free Lewis acid from the single-point energy of the strained Lewis acid with no F– bound. EDA directly provided ΔEdisp, ΔEel, ΔEoi, and ΔEPauli. LUMO energies were obtained from ADF as well.

Because EDA divides the Lewis adduct into its constituent acid and the small, highly negative F– base, we used the counterpoise method as implemented in ADF to investigate the basis set superposition error (BSSE).22 The BSSE was determined to be in the narrow range of 2.88–3.74 kcal mol–1 for all species, predominantly due to F–, with the Lewis acid contributing ≤0.3 kcal mol–1 to the BSSE in all cases. In accordance with prior EDA investigations of main group Lewis acid adducts,9,23 the individual BSSEs were not incorporated in the reported energy values. As expected for a hard ion such as F–, ΔEdisp is negligible for all Lewis acids considered, reaching a maximum magnitude of −0.5 kcal mol–1 in the PnPh4+ and PnPh3Cat species which is expected given their larger surface areas (Table S1).

Results and Discussion

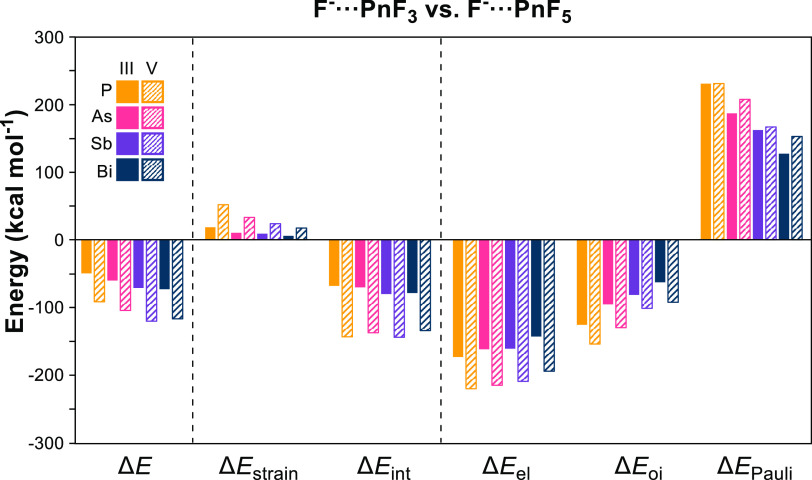
Our lab has previously demonstrated that oxidizing the pnictogen center from the +3 state to the +5 state increases its Lewis acidity.3f This conclusion is corroborated by the ∼40 kcal mol–1 increase in the magnitude of ΔE for all pnictogens going from PnF3 to PnF5 (Table 1). Gratifyingly, this data vindicates our assertion that oxidation leads to both an increase in the electrostatic contribution to the interaction through a deepening of the σ-hole and an increase in the orbital contribution through the lowering of the σ*-based LUMO (Chart 1). Moving from PnF3 to PnF5, we also see an increase in ΔEstrain and ΔEPauli as expected with an increased number of substituents attached to the central pnictogen and a decrease in the bond lengths upon oxidation. Thus, for oxidation from PnIII to PnV, the substantial increase in stabilization energy leads to greatly enhanced Lewis acidity despite a simultaneous increase in destabilizing interactions. As we will discuss, this scenario is inverted when looking at the periodic trends across the pentavalent pnictogens.

Table 1. Activation Strain and Energy Decomposition Analyses (in kcal mol–1) at Optimized Geometriesa.

Acid ΔE ΔEstrain ΔEint ΔEel ΔEoi ΔEPauli dPn···F (Å) Chargeb ELUMO (eV)c
F–···PnF3
PF3 –49.6 18.5 –68.1 –173.2 –125.6 230.7 1.738d 1.77 –2.16
AsF3 –60.1 10.2 –70.4 –161.9 –95.3 186.8 1.847d 1.84 –2.50
SbF3 –71.2 9.0 –80.2 –161.0 –81.5 162.2 1.989d 1.98 –3.03
BiF3 –72.9 5.8 –78.7 –142.9 –62.9 127.1 2.119d 2.00 –2.94
F–···PnF5
PF5 –91.6 51.8 –143.4 –220.1 –154.1 230.9 1.634 2.71 –5.49
AsF5 –104.5 33.0 –137.5 –215.1 –129.8 207.5 1.738 2.76 –6.37
SbF5 –120.3 23.7 –144.1 –209.3 –101.4 166.7 1.900 2.96 –6.52
BiF5 –116.9 17.3 –134.1 –194.2 –92.4 152.6 1.997 2.80 –7.34
F–···PnPh4+
PPh4+ –125.4 33.3 –158.7 –251.1 –155.8 248.7 1.724 1.52 –5.37
AsPh4+ –123.4 23.7 –147.1 –230.8 –118.9 203.2 1.852 1.64 –5.32
SbPh4+ –142.0 18.6 –160.6 –229.4 –102.2 171.4 2.000 1.94 –5.81
BiPh4+ –138.9 14.2 –153.0 –206.1 –84.9 138.3 2.132 1.78 –6.01
F–···PnPh3Cate
PPh3Cat –75.0 31.3 –106.3 –199.4 –170.2 263.8 1.683 1.76 –2.94
AsPh3Cat –73.2 20.6 –93.8 –180.5 –135.3 222.5 1.801 1.89 –3.13
SbPh3Cat –85.9 16.0 –101.8 –172.4 –112.9 184.0 1.955 2.23 –3.30
BiPh3Cat –78.8 12.8 –91.6 –152.1 –98.7 159.6 2.065 2.05 –3.69
Open in a new tab
a

ΔEdisp omitted for clarity.

b

NPA charge in strained acid without F–.

c

LUMO energy in strained acid without F–.

d

Smaller of two Pn···F distances.

e

Isomer with F trans to Ph. For the complete table, see Table S1 in the Supporting Information.

Chart 1. Bar Graph Depicting the Data from the Activation Strain and Energy Decomposition Analyses of the F-···PnF3 and F-···PnF5 Seriesa.

Chart 1

Open in a new tab

a ΔEdisp has been omitted for clarity.

We focus our analysis on the PnF5 series as the trends seen hold for the other series. With a ΔE of −120.3 kcal mol–1—in line with previously computed fluoride ion affinities24—SbF5 is the strongest Lewis acid in this series. Down the group, there is a 28.7 kcal mol–1 increase in the magnitude of ΔE from −91.6 kcal mol–1 for PF5. This general trend of increasing Lewis acidity down the group has been observed experimentally as well.7,25 While the destabilization from ΔEstrain decreases from 51.8 kcal mol–1 for PF5 to 23.7 kcal mol–1 for SbF5, ΔEint stays nearly constant, seeing only a 0.7 kcal mol–1 increase in magnitude.

The decrease in ΔEstrain follows from the larger size of the pnictogen center allowing increased flexibility of the coordinated ligands. This flexibility was highlighted in Moc and Morokuma’s 1997 study on hypervalent pnictogens wherein they concluded that the larger pnictogens enjoy a reduced barrier to Berry pseudorotation due to an increased ease in adjusting their Pn–F bond lengths from the ground state D3h structure to achieve the transitional C4v structure.26 Their values for the pseudorotation barrier are comparable to those calculated by Breidung and Thiel in 1992.27 During this conversion from D3h to C4v, the predominantly ligand-based highest occupied molecular orbital (HOMO) decreases in energy while the pnictogen-centered HOMO–1 increases in energy.28 Accordingly, decreasing the destabilization of the pnictogen-based HOMO–1 corresponds with a decrease in the pseudorotation barrier. Given this analysis, it seems that the most influential factor in the PnF5 series is the weaker bonds formed down the group resulting from greater atomic radius and increased orbital diffuseness which both lead to less effective orbital overlap. Steric repulsion also plays a role in decreased ΔEstrain as larger atoms allow more room between the ligands as they become compressed in the C4v geometry.

Turning our attention from ΔEstrain, we see that though the change in ΔEint is small down the group, the magnitude of ΔEint is 3-6 times greater than that of ΔEstrain and thus contributes significantly to ΔE. As expected with increased atomic radius, ΔEel decreases consistently down the group with SbF5 having an electrostatic contribution that is 10.8 kcal mol–1 less stabilizing than that for PF5. ΔEoi sees a dramatic decrease of 52.7 kcal mol–1 in stabilization going from PF5 to SbF5, which can be attributed to the increased diffuseness of the pnictogen center’s orbitals leading to decreased overlap with the incoming Lewis base due to the size mismatch. This combination of increasing atomic radius and increasing orbital diffuseness progressively favors the ionic contribution down the group with ΔEel increasing from 59% of the stabilizing contribution for PF5 to 67% for SbF5.

Despite a cumulative 63.5 kcal mol–1 decrease in stabilization from P to Sb, there is a simultaneous 64.2 kcal mol–1 decrease in ΔEPauli that more than compensates, producing a ΔEint that remains largely unchanged down the group which then allows the decrease in ΔEstrain to drive the observed differences in Lewis acidity . Similar trends are seen for the pentachloride and pentabromide species as well (Supporting Information). Noticeably lacking in this discussion, however, is Bi.

While BiF5 is more Lewis acidic than PF5 and AsF5, there is a drop in Lewis acidity going from SbF5 to BiF5 which has also been observed experimentally and has been repeatedly reproduced in FIA calculations (Table 2).7,25,26,29 The trends that exist down the group still hold when going from Sb to Bi: both stabilizing and destabilizing contributions decrease. This transition, however, does not come with the same magnitude of change in the energetic contributions—the decrease in destabilizing contributions no longer compensates as much for the decrease in stabilizing contributions. While ΔEel decreases from P to As by 2% and then from As to Sb by 3%, there is a significant 7% decrease in ΔEel from Sb to Bi. This decrease appears less consequential upon realizing that ΔEoi only decreases by 9% from Sb to Bi compared to a 22% decrease from As to Sb. As a result, Sb and Bi have similar ratios of ΔEel to ΔEoi with both having ∼32% of the stabilization energy coming from ΔEoi.

Table 2. Comparison of ΔE and FIAs (in kcal mol–1).

Acid ΔE FIA
PF3 –49.6 47.8a
AsF3 –60.1 58.3a
SbF3 –71.2 69.3a
BiF3 –72.9  
PF5 –91.6 91.9b
AsF5 –104.5 104.1b
SbF5 –120.3 117.6b
BiF5 –116.9 115.2b
Open in a new tab
a

FIAs converted from kJ mol–1 from ref (24b).

b

FIAs obtained as negatives of the reaction energy for PnF5 + F– → PnF6– in ref (26).

The major difference between Sb and Bi lies in the reduction of ΔEPauli. ΔEstrain decreases rather consistently: a 28% decrease from As to Sb and a 27% decrease from Sb to Bi. This steady decrease is likely due to the predictably weaker and longer bonds formed by the more diffuse orbitals moving down the group. ΔEPauli, on the other hand, only decreases by 8% from Sb to Bi compared to the significant 20% decrease seen from As to Sb. This inconsistency results from the unexpected trend in covalent radii. The covalent radius from As to Sb increases by 0.20 Å (1.19 vs 1.39 Å).30 Due to the lanthanide contraction, the increase from Sb to Bi is only 0.09 Å (1.39 vs 1.48 Å)—also reflected in the computed Pn–F bond lengths (Table 1).30

With a smaller-than-expected increase in size, the Bi–F bonds are closer to the incoming F– than might otherwise be anticipated leading to the smaller-than-expected decrease in Pauli repulsion. As such, the larger-than-expected Pauli repulsion is not as effectively counterbalanced by the stabilizing contributions in Bi as it is in Sb, leading to a reduction in overall Lewis acidity. Owing to the scandide contraction, a similarly small decrease of 10% in ΔEPauli is seen for the transition from P to As; however, this 10% decrease corresponds to a considerable 23.4 kcal mol-1 reduction in ΔEPauli while the 8% drop from Sb to Bi only produces a 14.1 kcal mol–1 decrease, indicating that an increase in covalent radius has a more profound effect on ΔEPauli for smaller atoms.

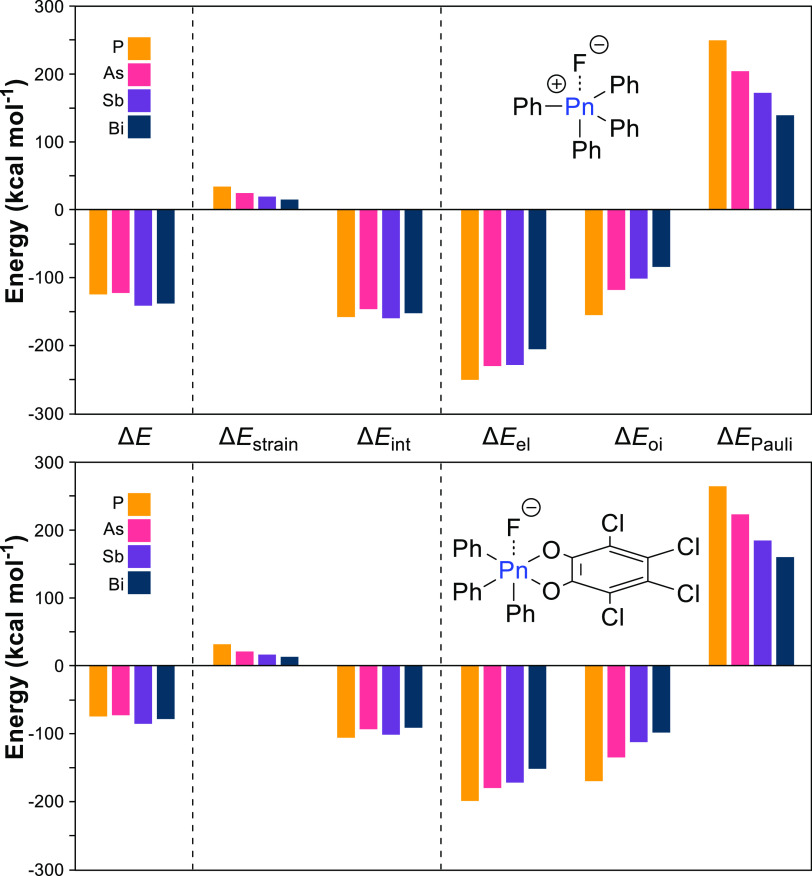
With these trends in mind, we turn to more complex pnictogen-based Lewis acids, starting with the PnPh4+ series. These cationic species serve as representative examples of pnictogen-based Lewis acids employed extensively in anion transport.3g For these cationic species—and the rest of the species studied—ΔE seems to oscillate: Sb and Bi have larger ΔE’s than P and As with Bi and As having the lower ΔE’s in these pairs (Chart 2). While this “secondary periodicity” is also seen in the ΔEint of the PnF5 series, it likely manifests in the ΔE of the PnPh4+ series due to a slight increase in the importance of ΔEel as a result of the cationic charge.31 The percentage of ΔEel’s contribution to the stabilization energy increases from 59–68% in the PnF5 series to 62–71% in the PnPh4+ series. Furthermore, ΔEel increases in magnitude by ∼20–30 kcal mol–1 for P and Sb but only ∼12–16 kcal mol–1 for As and Bi. This observed secondary periodicity results from the scandide contraction at As and the lanthanide contraction at Bi which lead to not only smaller radii than would be expected but also higher electronegativities than expected.

Chart 2. Bar Graphs Depicting the Data from the Activation Strain and Energy Decomposition Analyses of the F-···PnPh4+ (Top) and F-···PnPh3Cat (Bottom) Seriesa.

Chart 2

Open in a new tab

a ΔEdisp has been omitted for clarity.

While electronegativity seemingly decreases down the group according to the Pauling scale, Haïssinsky reminds us that electronegativity increases with oxidation state, leading to electronegativities of 2.2 for AsV, 2.1 for SbV, and >2.3 for BiV.32 This irregularity in the electronegativity is seen in the natural population analysis (NPA) charges in the strained geometries: +1.52 for P, +1.64 for As, +1.94 for Sb, and +1.78 for Bi (Table 1). Though there is a slight increase in charge from P to As, it cannot overcome the 0.12 Å increase in covalent radius,30 resulting in a large 20.3 kcal mol–1 decrease in ΔEel for this pair. The transition from Sb to Bi sees an even larger decrease of 23.3 kcal mol–1 in ΔEel due to the combination of decreased positive charge at the pnictogen center and increased covalent radius (0.09 Å).30 Ultimately, these large changes in ΔEel are reflected in ΔE due to the increased prominence of electrostatic contributions in these cationic species.

Despite the apparent increased importance of ΔEel in determining ΔE, SbPh4+—even with its lower ΔEel—is still 16.6 kcal mol–1 more acidic than PPh4+. While the stabilizing interactions (ΔEel + ΔEoi) decrease by 75.3 kcal mol–1, they are matched by a 77.3 kcal mol–1 decrease in ΔEPauli. The 14.7 kcal mol–1 decrease in ΔEstrain then drives the increased Lewis acidity of SbPh4+.

Finally, we analyzed the neutral PnPh3Cat series. Oxidation of pnictogens using ortho-chloranil has been repeatedly applied to produce active anion receptors and Lewis acid catalysts.3f,13 Due to the differing substituents, two isomers are possible upon binding F–: one where F is trans to Ph and the other with F trans to Cat. Because the same trends hold in both series (Supporting Information) and the isomer with F trans to Ph is 1.5 kcal mol–1 lower in energy for Sb, we have focused our analysis on this series. Overall, these ΔE values are lower than their PnF5 and PnPh4+ counterparts yet still higher than those seen for the pnictogen trifluorides. This decreased Lewis acidity is expected due to a reduced σ-hole and a higher-lying σ*-orbital resulting from decreased bond polarity. This reduced polarity produces a less ionic interaction as seen in the relative contributions of ΔEel and ΔEoi: ΔEoi contributes 39–46% to the stabilization energy for all pnictogens, whereas it contributes 29–41% in the PnF5 and PnPh4+ series (Chart 2). While the overall ΔE values are lower in the PnPh3Cat series, it is noteworthy that ΔEstrain is the lowest among the pentavalent pnictogen series presented in Table 1, indicating the benefits of preorganization that the catecholate provides.23 As also seen in the PnF5 and PnPh4+ series, Sb has the greatest Lewis acidity despite having the lowest magnitude of stabilizing contributions due to such a significant reduction in destabilizing contributions.

Conclusions

Though FIAs provide a way to compare the strengths of Lewis acids, activation strain analysis paired with EDA allows deeper insight into the underlying contributions to Lewis acid strength. We have confirmed that oxidation from PnIII to PnV produces an increase in ΔEel and ΔEoi due to a deeper σ-hole and a lower-energy σ*-orbital. While it was already known that Sb-based acids are strong Lewis acids, our analysis highlights the significance of increased molecular flexibility and decreased Pauli repulsion in the preeminence of Sb among the pentavalent pnictogens. Despite lower stabilizing contributions from ΔEel and ΔEoi moving down the group, Sb exhibits greater Lewis acidity due to lower destabilizing contributions from ΔEstrain and ΔEPauli. The decrease in ΔEPauli prevents drastic changes in ΔEint by offsetting the decreases in ΔEel and ΔEoi, thereby allowing the significant reduction in ΔEstrain to drive the dramatic increase in ΔE from P to Sb. Additionally, we not only confirmed the importance of electrostatic contributions for cationic Lewis acids but also demonstrated that the pnictogen bond has substantial orbital contribution. Our hope is that this work informs future applications of pnictogen-based Lewis acids.

Acknowledgments

This work was performed with support from the National Science Foundation (CHE-2108728), the Welch Foundation (A-1423), and Texas A&M University (Arthur E. Martell Chair of Chemistry). This research was conducted with the advanced computing resources provided by Texas A&M High-Performance Research Computing.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.inorgchem.3c01987.

  • Complete data table; bar graphs; and optimized structures in XYZ format (PDF)

Author Contributions

L.T.M. conducted the computational work and data analysis. F.P.G. oversaw the study. L.T.M. and F.P.G. wrote the manuscript.

The authors declare no competing financial interest.

Notes

A draft of this work has been deposited to ChemRxiv.33

Supplementary Material

ic3c01987_si_001.pdf (797.6KB, pdf)

References

  1. Greb L. Lewis Superacids: Classifications, Candidates, and Applications. Chem. - Eur. J. 2018, 24, 17881–17896. 10.1002/chem.201802698. [DOI] [PubMed] [Google Scholar]
  2. a Olah G. A.; Schlosberg R. H. Chemistry in super acids. I. Hydrogen exchange and polycondensation of methane and alkanes in FSO3H-SbF5 (″magic acid″) solution. Protonation of alkanes and the intermediacy of CH5+ and related hydrocarbon ions. The high chemical reactivity of ″paraffins″ in ionic solution reactions. J. Am. Chem. Soc. 1968, 90, 2726–2727. 10.1021/ja01012a066. [DOI] [Google Scholar]; b Olah G. A.Superacid Chemistry; Wiley: Hoboken, N.J, 2009. [Google Scholar]
  3. a Ke I.-S.; Myahkostupov M.; Castellano F. N.; Gabbaï F. P. Stibonium Ions for the Fluorescence Turn-On Sensing of F– in Drinking Water at Parts per Million Concentrations. J. Am. Chem. Soc. 2012, 134, 15309–15311. 10.1021/ja308194w. [DOI] [PubMed] [Google Scholar]; b Hirai M.; Gabbaï F. P. Lewis acidic stiborafluorenes for the fluorescence turn-on sensing of fluoride in drinking water at ppm concentrations. Chem. Sci. 2014, 5, 1886–1893. 10.1039/C4SC00343H. [DOI] [Google Scholar]; c Hirai M.; Gabbaï F. P. Squeezing Fluoride out of Water with a Neutral Bidentate Antimony(V) Lewis Acid. Angew. Chem., Int. Ed. 2015, 54, 1205–1209. 10.1002/anie.201410085. [DOI] [PubMed] [Google Scholar]; d Hirai M.; Myahkostupov M.; Castellano F. N.; Gabbaï F. P. 1-Pyrenyl- and 3-Perylenyl-antimony(V) Derivatives for the Fluorescence Turn-On Sensing of Fluoride Ions in Water at Sub-ppm Concentrations. Organometallics 2016, 35, 1854–1860. 10.1021/acs.organomet.6b00233. [DOI] [Google Scholar]; e Chen C.-H.; Gabbaï F. P. Fluoride Anion Complexation by a Triptycene-Based Distiborane: Taking Advantage of a Weak but Observable C–H···F Interaction. Angew. Chem., Int. Ed. 2017, 56, 1799–1804. 10.1002/anie.201611009. [DOI] [PubMed] [Google Scholar]; f Yang M.; Tofan D.; Chen C.-H.; Jack K. M.; Gabbaï F. P. Digging the Sigma-Hole of Organoantimony Lewis Acids by Oxidation. Angew. Chem., Int. Ed. 2018, 57, 13868–13872. 10.1002/anie.201808551. [DOI] [PubMed] [Google Scholar]; g Park G.; Brock D. J.; Pellois J.-P.; Gabbaï F. P. Heavy Pnictogenium Cations as Transmembrane Anion Transporters in Vesicles and Erythrocytes. Chem 2019, 5, 2215–2227. 10.1016/j.chempr.2019.06.013. [DOI] [PMC free article] [PubMed] [Google Scholar]; h Gonzalez V. M.; Park G.; Yang M.; Gabbaï F. P. Fluoride anion complexation and transport using a stibonium cation stabilized by an intramolecular P=O → Sb pnictogen bond. Dalton Trans. 2021, 50, 17897–17900. 10.1039/D1DT03370K. [DOI] [PubMed] [Google Scholar]
  4. a Robertson A. P. M.; Chitnis S. S.; Jenkins H. A.; McDonald R.; Ferguson M. J.; Burford N. Establishing the Coordination Chemistry of Antimony(V) Cations: Systematic Assessment of Ph4Sb(OTf) and Ph3Sb(OTf)2 as Lewis Acceptors. Chem. - Eur. J. 2015, 21, 7902–7913. 10.1002/chem.201406469. [DOI] [PubMed] [Google Scholar]; b Chitnis S. S.; Sparkes H. A.; Annibale V. T.; Pridmore N. E.; Oliver A. M.; Manners I. Addition of a Cyclophosphine to Nitriles: An Inorganic Click Reaction Featuring Protio, Organo, and Main-Group Catalysis. Angew. Chem., Int. Ed. 2017, 56, 9536–9540. 10.1002/anie.201704991. [DOI] [PubMed] [Google Scholar]; c Qiu J.; Song B.; Li X.; Cozzolino A. F. Solution and gas phase evidence of anion binding through the secondary bonding interactions of a bidentate bis-antimony(III) anion receptor. Phys. Chem. Chem. Phys. 2018, 20, 46–50. 10.1039/C7CP05933G. [DOI] [PubMed] [Google Scholar]; d Benz S.; Poblador-Bahamonde A. I.; Low-Ders N.; Matile S. Catalysis with pnictogen, chalcogen, and halogen bonds. Angew. Chem., Int. Ed. 2018, 57, 5408–5412. 10.1002/anie.201801452. [DOI] [PMC free article] [PubMed] [Google Scholar]; e Sharma D.; Balasubramaniam S.; Kumar S.; Jemmis E. D.; Venugopal A. Reversing Lewis acidity from bismuth to antimony. Chem. Commun. 2021, 57, 8889–8892. 10.1039/D1CC03038H. [DOI] [PubMed] [Google Scholar]; f Sharma D.; Benny A.; Gupta R.; Jemmis E. D.; Venugopal A. Crystallographic evidence for a continuum and reversal of roles in primary–secondary interactions in antimony Lewis acids: applications in carbonyl activation. Chem. Commun. 2022, 58, 11009–11012. 10.1039/D2CC04027A. [DOI] [PubMed] [Google Scholar]
  5. Scheiner S. A new noncovalent force: Comparison of P···N interaction with hydrogen and halogen bonds. J. Chem. Phys. 2011, 134, 094315 10.1063/1.3562209. [DOI] [PubMed] [Google Scholar]
  6. Varadwaj A.; Varadwaj P. R.; Marques H. M.; Yamashita K. Definition of the Pnictogen Bond: A Perspective. Inorganics 2022, 10, 149 10.3390/inorganics10100149. [DOI] [Google Scholar]
  7. Gillespie R. J.; Ouchi K.; Pez G. P. Fluorosulfuric acid solvent system. VI. Solutions of phosphorus, arsenic, bismuth, and niobium pentafluorides and titanium tetrafluoride. Inorg. Chem. 1969, 8, 63–65. 10.1021/ic50071a015. [DOI] [Google Scholar]
  8. a van Zeist W.-J.; Bickelhaupt F. M. The activation strain model of chemical reactivity. Org. Biomol. Chem. 2010, 8, 3118–3127. 10.1039/b926828f. [DOI] [PubMed] [Google Scholar]; b Vermeeren P.; van der Lubbe S. C. C.; Guerra C. F.; Bickelhaupt F. M.; Hamlin T. A. Understanding chemical reactivity using the activation strain model. Nat. Protoc. 2020, 15, 649–667. 10.1038/s41596-019-0265-0. [DOI] [PubMed] [Google Scholar]
  9. de Azevedo Santos L.; Hamlin T. A.; Ramalho T. C.; Bickelhaupt F. M. The pnictogen bond: a quantitative molecular orbital picture. Phys. Chem. Chem. Phys. 2021, 23, 13842–13852. 10.1039/D1CP01571K. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. a Neese F. The ORCA program system. WIREs Comput. Mol. Sci. 2012, 2, 73–78. 10.1002/wcms.81. [DOI] [Google Scholar]; b Neese F.; Wennmohs F.; Becker U.; Riplinger C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108 10.1063/5.0004608. [DOI] [PubMed] [Google Scholar]; c Neese F. Software update: The ORCA program system—Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606 10.1002/wcms.1606. [DOI] [Google Scholar]
  11. Grimme S.; Brandenburg J. G.; Bannwarth C.; Hansen A. Consistent structures and interactions by density functional theory with small atomic orbital basis sets. J. Chem. Phys. 2015, 143, 054107 10.1063/1.4927476. [DOI] [PubMed] [Google Scholar]
  12. Glendening E. D.; Badenhoop J. K.; Reed A. E.; Carpenter J. E.; Bohmann J. A.; Morales C. M.; Karafiloglou P.; Landis C. R.; Weinhold F.. NBO 7.0, Theoretical Chemistry Institute; University of Wisconsin: Madison, WI, 2018.
  13. a You D.; Zhou B.; Hirai M.; Gabbaï F. P. Distiboranes based on ortho-phenylene backbones as bidentate Lewis acids for fluoride anion chelation. Org. Biomol. Chem. 2021, 19, 4949–4957. 10.1039/D1OB00536G. [DOI] [PubMed] [Google Scholar]; b Chishiro A.; Akioka I.; Sumida A.; Oka K.; Tohnai N.; Yumura T.; Imoto H.; Naka K. Tetrachlorocatecholates of triarylarsines as a novel class of Lewis acids. Dalton Trans. 2022, 51, 13716–13724. 10.1039/D2DT02145E. [DOI] [PubMed] [Google Scholar]
  14. Dennington R.; Keith T. A.; Millam J. M.. GaussView, version 6; Semichem Inc.: Shawnee Mission, KS, 2016.
  15. Hanwell M. D.; Curtis D. E.; Lonie D. C.; Vandermeersch T.; Zurek E.; Hutchison G. R. Avogadro: an advanced semantic chemical editor, visualization, and analysis platform. J. Cheminf. 2012, 4, 17 10.1186/1758-2946-4-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. a Bickelhaupt F. M.; Nibbering N. M. M.; Van Wezenbeek E. M.; Baerends E. J. Central bond in the three CN• dimers NC-CN, CN-CN and CN-NC: electron pair bonding and Pauli repulsion effects. J. Phys. Chem. A 1992, 96, 4864–4873. 10.1021/j100191a027. [DOI] [Google Scholar]; b Bickelhaupt F. M.; Baerends E. J.. Kohn-Sham Density Functional Theory: Predicting and Understanding Chemistry. In Reviews in Computational Chemistry; John Wiley & Sons, 2000; pp 1–86. [Google Scholar]; c Krapp A.; Bickelhaupt F. M.; Frenking G. Orbital Overlap and Chemical Bonding. Chem. - Eur. J. 2006, 12, 9196–9216. 10.1002/chem.200600564. [DOI] [PubMed] [Google Scholar]
  17. te Velde G.; Bickelhaupt F. M.; Baerends E. J.; Fonseca Guerra C.; van Gisbergen S. J. A.; Snijders J. G.; Ziegler T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. 10.1002/jcc.1056. [DOI] [Google Scholar]
  18. a Zhao Y.; Truhlar D. G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 2006, 125, 194101 10.1063/1.2370993. [DOI] [PubMed] [Google Scholar]; b Zhao Y.; Truhlar D. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
  19. a Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]; b Grimme S.; Hansen A.; Brandenburg J. G.; Bannwarth C. Dispersion-Corrected Mean-Field Electronic Structure Methods. Chem. Rev. 2016, 116, 5105–5154. 10.1021/acs.chemrev.5b00533. [DOI] [PubMed] [Google Scholar]
  20. van Lenthe E.; Baerends E. J. Optimized Slater-type basis sets for the elements 1-118. J. Comput. Chem. 2003, 24, 1142–1156. 10.1002/jcc.10255. [DOI] [PubMed] [Google Scholar]
  21. van Lenthe E.; Baerends E. J.; Snijders J. G. Relativistic total energy using regular approximations. J. Chem. Phys. 1994, 101, 9783–9792. 10.1063/1.467943. [DOI] [Google Scholar]
  22. Cramer C. J.Essentials of Computational Chemistry Theories and Models, 2nd ed.; John Wiley & Sons Ltd.: Hoboken, NJ, 2004. [Google Scholar]
  23. Roth D.; Stirn J.; Stephan D. W.; Greb L. Lewis Superacidic Catecholato Phosphonium Ions: Phosphorus–Ligand Cooperative C–H Bond Activation. J. Am. Chem. Soc. 2021, 143, 15845–15851. 10.1021/jacs.1c07905. [DOI] [PubMed] [Google Scholar]
  24. a Krossing I.; Raabe I. Relative stabilities of weakly coordinating anions: A computational study. Chem. - Eur. J. 2004, 10, 5017–5030. 10.1002/chem.200400087. [DOI] [PubMed] [Google Scholar]; b Erdmann P.; Leitner J.; Schwarz J.; Greb L. An Extensive Set of Accurate Fluoride Ion Affinities for p-Block Element Lewis Acids and Basic Design Principles for Strong Fluoride Ion Acceptors. ChemPhysChem 2020, 21, 987–994. 10.1002/cphc.202000244. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Bougon R.; Bui Huy T.; Cadet A.; Charpin P.; Rousson R. Adducts of chlorine oxide trifluoride with group V element pentafluorides. Structural study of the hexafluoro anions. Inorg. Chem. 1974, 13, 690–695. 10.1021/ic50133a035. [DOI] [Google Scholar]
  26. Moc J.; Morokuma K. Ab initio MO study on the periodic trends in structures and energies of hypervalent compounds: five-, six-, and seven-coordinated XF5, XH6-, XF6-, XH72- and XF72- species containing a group 15 central atom (where X is P, As, Sb, Bi). J. Mol. Struct. 1997, 436–437, 401–418. 10.1016/S0022-2860(97)00124-5. [DOI] [Google Scholar]
  27. Breidung J.; Thiel W. A systematic ab initio study of the group V trihalides MX3 and pentahalides MX5 (M = P—Bi, X = F—I). J. Comput. Chem. 1992, 13, 165–176. 10.1002/jcc.540130208. [DOI] [Google Scholar]
  28. Gimarc B. M. The shapes and other properties of non-transition element complexes. 3. AB5. J. Am. Chem. Soc. 1978, 100, 2346–2353. 10.1021/ja00476a014. [DOI] [Google Scholar]
  29. Jupp A. R.; Johnstone T. C.; Stephan D. W. Improving the Global Electrophilicity Index (GEI) as a Measure of Lewis Acidity. Inorg. Chem. 2018, 57, 14764–14771. 10.1021/acs.inorgchem.8b02517. [DOI] [PubMed] [Google Scholar]
  30. Cordero B.; Gomez V.; Platero-Prats A. E.; Reves M.; Echeverria J.; Cremades E.; Barragan F.; Alvarez S. Covalent radii revisited. Dalton Trans. 2008, 2832–2838. 10.1039/b801115j. [DOI] [PubMed] [Google Scholar]
  31. a Biron E. V. Phenomena of secondary periodicity. Zh. Russ. Fiz.-Khim. Obshch. Ch. Khim. 1915, 47, 964–988. [Google Scholar]; b Pyykkö P. On the Interpretation of ’Secondary Periodicity″ in the Periodic System. J. Chem. Res. 1979, 380–381. [Google Scholar]; c Lipshultz J. M.; Li G.; Radosevich A. T. Main Group Redox Catalysis of Organopnictogens: Vertical Periodic Trends and Emerging Opportunities in Group 15. J. Am. Chem. Soc. 2021, 143, 1699–1721. 10.1021/jacs.0c12816. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. a Haïssinsky M. Échelle des électronégativités de Pauling et chaleurs de formation des composés inorganiques. J. Phys. Radium 1946, 7, 7–11. 10.1051/jphysrad:01946007010701. [DOI] [Google Scholar]; b Allred A. L.; Hensley A. L. Electronegativities of nitrogen, phosphorus, arsenic, antimony and bismuth. J. Inorg. Nucl. Chem. 1961, 17, 43–54. 10.1016/0022-1902(61)80184-X. [DOI] [Google Scholar]
  33. Maltz L.; Gabbaï F. P.. Analyzing Fluoride Binding by Group 15 Lewis Acids: Pnictogen Bonding in the Pentavalent State Chemrxiv 2023, 10.26434/chemrxiv-2023-t60dq. [DOI] [PMC free article] [PubMed]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ic3c01987_si_001.pdf (797.6KB, pdf)

Articles from Inorganic Chemistry are provided here courtesy of American Chemical Society

RESOURCES