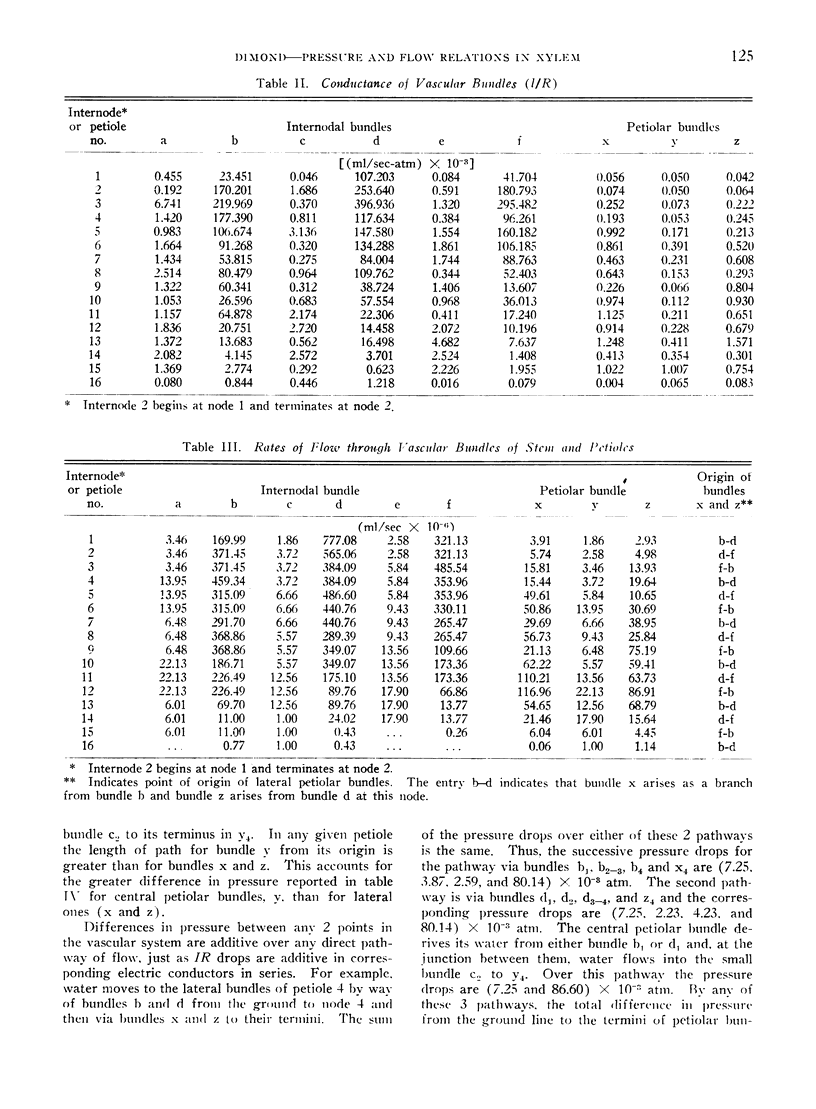
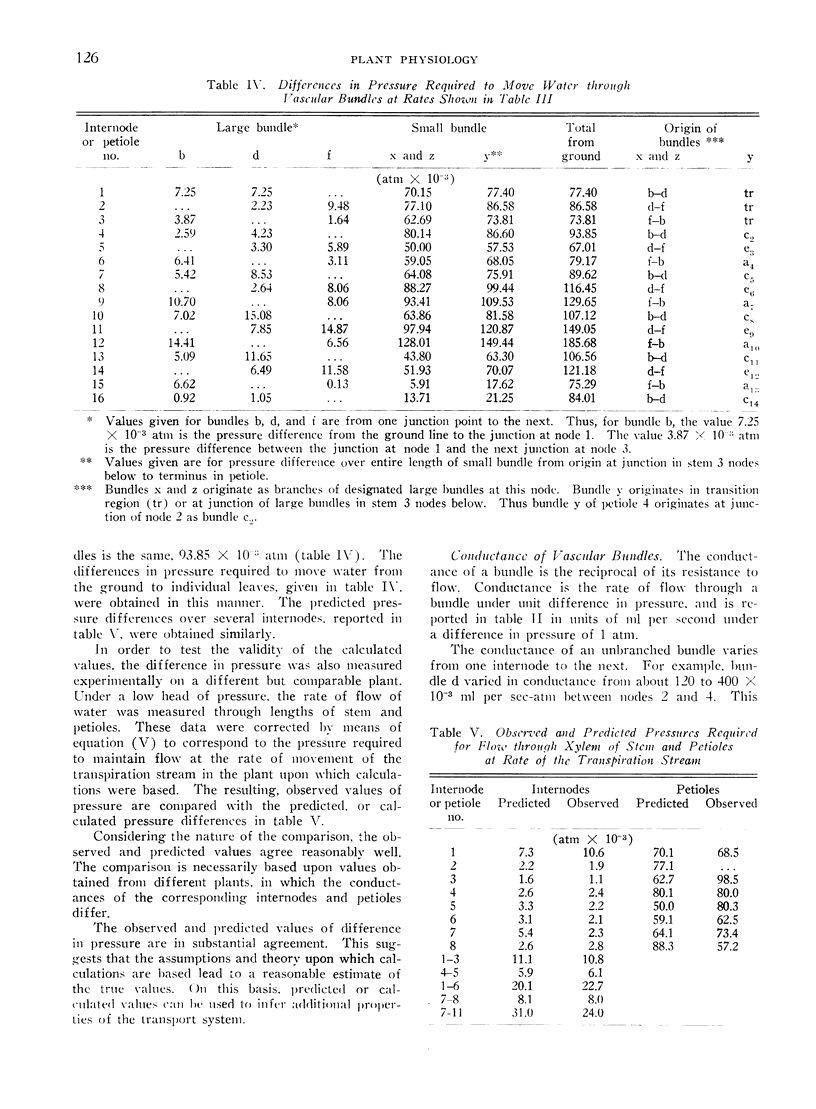
Abstract
In the tomato plant water flows through primary xylem in accordance with Poiseuille's law. This relation and the analogy between Poiseuille's and Ohm's law were employed to calculate rates of flow and differences in pressure within vascular bundles when transpiration rates from individual leaves were known. The resistance of vascular bundles to flow was calculated from a modification of Poiseuille's law and from measurements of vessels in all bundles. The rates of flow in all bundles were derived from a set of simultaneous linear equations of flow, written to correspond with the nature of the vascular network. Values of the difference in pressure associated with flow in bundles were derived from resistances and flow rates in individual bundles. These agreed substantially with values observed in a comparable plant.
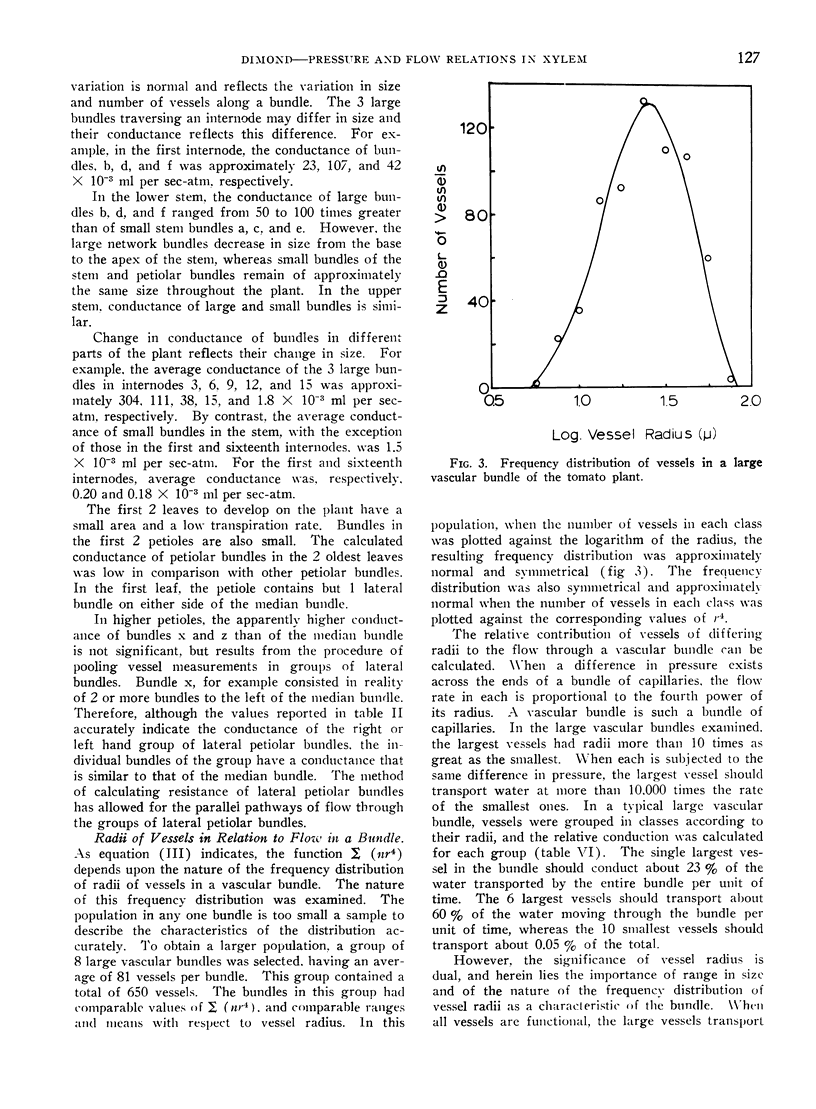
In large bundles, vessels occur in a frequency distribution that is approximately normal with respect either to the logarithms of their radii or to the fourth power of their radii. The largest vessels in a bundle transport most of the water when they are functioning.
The tomato plant contains 2 types of vascular bundle. The large bundles of the stem form a network by joining above each node in combinations of 2 at a time. The small bundles of the stem and petiolar bundles are independent of other bundles from their origins at junctions to their termini. The small bundles offer high resistance to flow, whereas the resistance of large bundles is low. The average conductance of large bundles decreases from the base to the apex of the stem. That of small vascular bundles remains low and more or less constant throughout the plant.
Only a small difference in pressure is required to maintain flow in large bundles. For lower leaves, the driving pressure required to move water to the base of a petiole is considerably less than that which moves water through petioles. The difference in pressure that maintains flow increases steadily for successively higher nodes. However, the pressure that drives flow to leaves is not always greater for higher leaves than for intermediate ones. For the plant examined, the highest leaves required a smaller amount of energy to move water from the ground than intermediate leaves did. This was also true of the power expended in moving water to individual leaves.
In the large network bundles, significant cross transfer of flow occurs at junction points from one bundic to another. Because of the interconnections between large bundles. pressure and flow relations are apparently not greatly altered when localized dysfunction occurs in the vessels of large bundles. In small, independent bundles, a localized dysfunction in vessels produces a significant effect on pressure and flow relations.
Full text
PDF









Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Bonner J. Water Transport: This classical problem in plant physiology is becoming increasingly amenable to mathematical analysis. Science. 1959 Feb 20;129(3347):447–450. doi: 10.1126/science.129.3347.447. [DOI] [PubMed] [Google Scholar]
- Scholander P. F., Bradstreet E. D., Hemmingsen E. A., Hammel H. T. Sap Pressure in Vascular Plants: Negative hydrostatic pressure can be measured in plants. Science. 1965 Apr 16;148(3668):339–346. doi: 10.1126/science.148.3668.339. [DOI] [PubMed] [Google Scholar]
- Scholander P. F., Hemmingsen E., Garey W. Cohesive Lift of Sap in the Rattan Vine: The problem of how sap rises lies stranded for lack of means to measure negative pressure in liquids. Science. 1961 Dec 8;134(3493):1835–1838. doi: 10.1126/science.134.3493.1835. [DOI] [PubMed] [Google Scholar]
- Scholander P. F., Love W. E., Kanwisher J. W. The Rise of Sap in Tall Grapevines. Plant Physiol. 1955 Mar;30(2):93–104. doi: 10.1104/pp.30.2.93. [DOI] [PMC free article] [PubMed] [Google Scholar]


