Closed-shell d¹⁰–d¹⁰ mechanochromic [AuPh(CNPh)]_n complex: quantum chemistry electronic and optical properties

Abstract

The electronic structure, spectroscopic properties, and solid state chemistry of monomer and dimers of [AuPh(CNPh)] complex were studied at post-Hartree–Fock (MP2, SCS-MP2, and CC2) and density functional theory levels. The absorption spectra of these complexes were calculated using single excitation time-dependent (TD) methods at DFT, CC2, and SCS-CC2 levels. The influences of the bulk are accounted for at the PBE-D3 level, incorporating dispersion effects. The calculated values agree with the experimental range, where absorption and emission energies reproduce experimental trends with large Stokes shifts. The aurophilic interaction is identified as a key factor influencing the spectroscopic and structural properties of these complexes. The intermetallic interactions were found as the main factor responsible for MMCT electronic transitions in the models studied.

[AuPh(CNPh)]₂ complexes are modeled, and their electronic properties, optical properties, and solid state chemistry are studied.

1. Introduction

Complexity is a new concept in chemistry^1,2 that attempts to explain how the chemistry of the system is organized at the molecular level. Since 1997, chemistry has started considering complexity^3,4 at the molecular scale. Chemistry has evolved from individual molecules to the description and manipulation of systems of molecules, giving rise to some new fields, such as the materials chemistry, supramolecular chemistry, and nanochemistry.^5,6 Theoretical and computational chemistry have helped us understand the behavior of chemical systems at the molecular scale. The systems chemistry approach indicates that the organization of the individual molecule will determine the new properties of the whole system. At the simplest level, noncovalent interactions between molecules can lead to the emergence of large structures in solid and liquid states.⁷ In the last forty years, it has been shown that gold(i) atoms can form stable self-assemblies and inorganic complexes.^8–12 Inorganic molecular assemblies based on d¹⁰ configuration complex systems represent an essential class based on exotic geometries obtained from various noncovalent interactions.^13–21 The self-assembly of molecules with gold atoms involves inter- and intramolecular interactions that lead to the formation of systems with high complexity.^22–30

This phenomenon is known as “aurophilic interaction”.^31–41 These closed-shell interactions are estimated to be energetically similar to hydrogen bonds (7–20 kJ mol⁻¹) in the case of gold(i).^42–45 The aurophilic interaction has been experimentally determined via solid-state X-ray diffraction^23–26 and NMR/absorption/emission/Raman spectroscopic measurements.^27,28 From a theoretical point of view, gold interactions can be understood as the contribution of two terms to the equilibrium distance: dispersion and ionic interactions.^31–41 The relativistic effects contribute around 20% to the energy of interaction at the MP2 level.³² However, in recent years, some researchers have proposed that the aurophilic interaction is driven by the balance between strong Pauli repulsion at close range^46–48 and orbital interaction among metallic centers. These studies also demonstrated the relevance of the dispersion term in the attractive interaction obtained in the gold–gold equilibrium distance, which is recovered in the electronic correlation. It has been stated that all dispersion forces are due to electronic correlation effects but that the electronic correlation contribution is not necessarily dispersion forces.⁴⁹ Additionally, it should be considered that same complexes have electrostatic interaction via a dipole–dipole term that dominates at the equilibrium Au–Au distance calculated from the sum of induction and dispersion terms.^50,51 The experimental results in many studies are explained by theoretical models described at the post-Hartree–Fock (MP2, spin-component-scaled (SCS)-MP2, CCSD(T)) and density functional theory (DFT) levels with dispersion correction.⁵² In the case of more extensive systems, the DFT method is usually preferred because of its better performance, although sacrificing accuracy.⁵³

The aurophilic interactions have been evidenced by absorption and emission behavior in several complexes where these interactions are present.^16–20 The photophysical properties of gold complexes undergo significant changes when Au–Au interactions are established.^21–26 Understanding these systems comes from calculating intermolecular interaction energies and determining how these lead to structures and patterns that result in specific optical properties. Thus, it is possible to rationalize the relationship between the structure and optical properties of gold complexes. In this context, the observation of absorption/luminescence has been tied to the presence of close Au–Au contacts in solid and solution.^14–26 An interesting situation occurs with solid-state luminescence when the material is subject to external influences, such as light, thermal, mechanical, and chemical.^54,55 The crystal can give rise to drastic differences in luminescence responses. One of these phenomena is known as mechanochromism. Ito and co-workers reported phenyl(phenylisocyanide)gold(i) ((C₆H₅)Au(CN–C₆H₅)) described as PhAuCNPh, which exhibits two polymorphic structures.^56–58 Rapid recrystallization of the complex gave a triclinic structure (polymorph I_b) without Au–Au contacts. Meanwhile, slow evaporation of the complex gave a tetragonal polymorph (II_y) featuring Au–Au interactions of 318 pm. Mechanical stimulus resulted in a single-crystal-to-single-crystal (SCSC) phase transformation with changes in the photoluminescence, i.e., blue to yellow-green, due to aurophilic interactions and C–H/π in the tetragonal complex. The excitation and emission spectra for polymorph complexes II_y and I_b are very different. The excitation spectrum is observed at 432 nm (2.9 eV) in II_y and 315 (4.0 eV) in I_b. The emission spectrum is observed at 567 nm (2.2 eV) in II_y and 490 nm (2.5 eV) and 460 nm (2.7 eV) in I_b. See Scheme 1.

Scheme 1. Experimental excitation and emission spectra of II_y and I_b complexes.^56–58.

Ito and co-workers⁵⁹ performed time-dependent density functional theory (TDDFT) calculations based on B3LYP using models from the tetrameric experimental structures of I_b and II_y. The results for I_b showed an excitation with metal–ligand-to-ligand charge transfer (MLLCT) character, with singlet–singlet transitions at 326, 354, 356, and 387 nm. The calculated electronic spectrum was consistent with experimental excitation peaks from 320 nm to 380 nm with an edge of 400 nm. Conversely, calculations with II_y showed an electronic spectrum with a metal–metal to ligand charge transfer (MML) facilitated by the short Au–Au distance. The main electronic transition is found at 409 nm, corresponding to HOMO → LUMO and HOMO−1 →LUMO+1. This transition can be attributed to the antibonding sigma orbital σ* (gold d_z²) to isocyanide π* transition. Moreover, Ito, Sakaki, and co-workers⁵⁹ used the same tetrameric model with quantum mechanics (QM)/molecular mechanics (MM) calculations to study ground-state structures and absorption and emission spectra at the TD-DFT B3LYP-D3 level. They used (Ph)Au(CNPh) 1 with a gold(i) isocyanide complex that formed two different polymorphic crystals I_b and I_y, analogous to I_b and II_y described above. The QM/MM calculations showed that the polymorph I_y was more stable than I_b, which agrees with experimental findings. The results show that LLCT is the lowest-energy excitation state in absorption. The π–π* local state on the CNPh moiety is the lowest-energy triplet state in the emission by I_b models. In contrast, in I_y model, the MMLCT state is the lowest-energy excitation absorption and emission state. The differences in the optical behavior between two optimized structures arise from changes in the Au–Au distance, which is shorter in I_y than in I_b.

Gold complexes have provided the opportunity to understand excited states covering broad emission colors.^56–59 Control of supramolecular chemistry systems of functional metal complexes is essential to determine the charge transport and optical properties.⁹ Herein, we focused on establishing the relationship between aurophilic interaction and experimental geometries using models of [PhAuCNPh]₂ complexes. Moreover, our second aim was to study geometrical and optical properties at post-Hartree–Fock (CC2 and SCS-CC2) and density functional theory (PBE, TPSS, and B3LYP) levels on simplified models of the two types of complexes described above: I_b and II_y. The light-absorption processes in complexes were studied using time-dependent density functional theory (TDDFT) calculations and by performing ab initio correlated calculations at the approximate spin-component-scaled approximation second-order coupled cluster (SCS-CC2). Finally, we performed calculations based on solid-state chemistry using PBE functionals to evaluate the effect of bulk on aurophilic interactions.

2. Theoretical models and calculations

We used the [PhAuCNPh] model 1 (Ph C₆H₅) to build dimers 2 and 3 of [PhAuCNPh]₂ shown in Fig. 1. The dimers have orientation II_y (2) and I_b (3), simulating the experimental geometry.⁵⁶ The geometries were fully optimized at scalar quasi-relativistic MP2, SCS-MP2, PBE (Perdew–Burke–Ernzerhof),⁶⁰ B3LYP,⁶¹ and TPSS⁶² levels in the gas phase for each fragment in the models. Grimme's dispersion correction incorporates an accurate description of weak forces when using those functionals in what is known as the DFT-D3 level with the Becke–Johnson (BJ) damping function correction.^63,64 The gold–gold interaction energy (ΔE_int) and geometric equilibrium distances (R_e) of complexes were obtained using the counterpoise correction for the basis-set superposition error (BSSE).^65,66

Fig. 1. [PhAuCNPh] (1) and dimers of [PhAuCNPh]₂: II_y (2) and I_b (3).

The calculations were carried out using Turbomole 7.0 (ref. 67) and Gaussian16 (ref. 68) program packages. We used the Turbomole program to obtain optical properties, while the Gaussian program was used to obtain equilibrium geometries and electronic properties. The 19 valence electrons (VE) of the Au quasi-relativistic (QR) pseudo-potential (PP) of Andrae⁶⁹ were employed. We used 2f-type polarization and diffuse functions on gold (α_f = 0.20, 1.19). Furthermore, C and N atoms were treated through PPs, using double-zeta basis sets with the addition of two d-type polarization functions.⁷⁰ A double-zeta basis set plus two p-type polarization functions were used for the H atom.⁷¹

Single-point calculations of equilibrium geometries were used to study excitation spectra by PBE, TPSS, and B3LYP. The excitation energy was obtained using the time-dependent perturbation theory approach (TD),⁷² which is based on the random-phase approximation (RPA) method.⁷³ The TD calculations do not evaluate the spin–orbit splitting, and values are averaged in metallic atoms described by pseudo-potentials. Moreover, excitation energies and oscillator strengths are calculated at the approximate second-order coupled cluster (CC2) and spin-component-scaled approximation (SCS-CC2)^74,75 levels. We used the equilibrium distance (R_e) estimated at MP2 and SCS-MP2 levels to calculate excitation spectra at CC2 and SCS-CC2. The SCS-MP2 methodology is an accurate and efficient tool for incorporating electronic correlation to study models at a low computational cost.⁷⁶ This method involves the Laplace transformation (LT) algorithm and reduced-virtual-space (RVS) approximation. The RVS cutoff threshold was 60 eV.⁷⁷

The optPBE functional^78,79 was used for all calculations implemented in the VASP code.^80–82 For gold, oxygen, carbon, and nitrogen atoms, electron configurations [Xe] 4f¹⁴5d¹⁰6s¹, [He] 2s²2p⁴, [He] 2s²2p², and [He] 2s²2p³ were used, respectively, and their core electrons were kept frozen and replaced by PAW-generated pseudopotentials.^83,84 The valence electrons were described with plane wave basis with a cutoff of 425 eV. The methodology was tested for the bulk of [AuPh(CNPh)]₂ II_y (2′) and [AuPh(CNPh)]₂ I_b (3′) structures using crystallographic data obtained from experimental X-ray data by Ito et al.⁵⁶ To optimize both systems in this study, the primitive cell for system 2′ was considered. This cell was identified as rhombohedral and contains 200 atoms, with dimensions a = 15.68 Å, b = 15.68 Å, c = 15.68 Å, α = 129.4, β = 129.4, and γ = 74.4. Conversely, for system 3′, it was found to be triclinic, and the unit cell contains 50 atoms with dimensions a = 6.02 Å, b = 9.07 Å, c = 11.45 Å, α = 102.2, β = 101.5, and γ = 102.4. The band structure and density of states were obtained using the VASPKIT⁸⁵ routine available in the VASP program. To generate LDOS plots, it was necessary to use the DOSCAR file, which is an output file that uses the keyword LORBIT = 11 in the input file (INCAR). Subsequently, through integration with the total number of electrons for each system, it is possible to identify the Fermi level, corresponding to the energy of the highest occupied level in a system.

3. Results and discussion

3.1. Aurophilic attractions

[AuPh(CNPh)]₂ II_y (2) and I_b (3) dimers are used for modeling aurophilic and C–H/π interactions, respectively. Au–Au and C–H/π distances, together with interaction energies, are listed in Table 1 to compare and systemize the analysis of the weak intermolecular interaction. The results reported in this study using MP2, SCS-MP2, and DFT-D3(BJ) methods are at the same level as those reported in the literature for the interaction energy and geometry.^86,87 It is known that the MP2 method tends to overestimate interaction energies and shorten Au–Au distances.^13,14 In this context, the SCS-MP2 method provides an improved description of the system, with lower interaction energies and longer Au–Au distances than with MP2, a trend observed in all dimers according to the data from Table 1. The DFT-D3(BJ) calculations generated similar geometries, where incorporating dispersion corrections (D3) allowed interaction energies and Au–Au and C–H/π distances comparable to those obtained at the MP2 level. In the II_y model, interaction energies with B3LYP are overestimated, while those with PBE and TPSS are similar to MP2. Furthermore, it is highlighted that interaction energies are all similar to those calculated by DFT for model I_b. This is because its nature does not involve an aurophilic interaction. In all I_b models, C–H/π interactions are present.

Optimized Au–Au distance and C–H/π for models II_y (2) and I_b (3) at different levels. Equilibrium distances in pm; interaction energies ΔE_Int in kcal mol⁻¹.

Model	Method	Au–Au	C–H/π	ΔEInt
[AuPh(CNPh)]2 IIy	MP2	305.2	375.9	−8.1
	SCS-MP2	325.6	392.7	−4.6
	B3LYP-D3(BJ)	299.1	375.9	−11.7
	PBE-D3(BJ)	300.6	375.9	−7.2
	TPSS-D3(BJ)	298.9	375.9	−9.2
[AuPh(CNPh)]2 Ib	MP2	514.2	299.4	−5.9
	SCS-MP2	526.6	311.7	−4.4
	B3LYP-D3(BJ)	511.8	299.4	−6.9
	PBE-D3(BJ)	512.5	299.4	−6.1
	TPSS-D3(BJ)	512.4	299.4	−6.5
Model Iy59	B3LYP-D3	317.7		−11.4
Model Ib59	B3LYP-D3	573.3		−6.2
[AuPh(CNPh)]2 IIy	Exp.56	317.7
[AuPh(CNPh)]2 Ib	Exp.56	573.3

Previous theoretical models,⁵⁹ I_b, and I_y use experimental geometry and perform calculations at the B3LYP (MM/QC) level. The magnitudes of interaction energies are in the same range as the models proposed in this study. The only difference between results reported here and previous ones is that they optimized the geometries of proposed dimers, and a model with two units was sufficient to obtain comparable results to experimental ones.

3.2. Optical properties: absorption spectra

The UV-vis spectra were calculated at CC2 and SCS-CC2 levels. Additionally, the excitation energies of the models were calculated at the TDDFT level using B3LYP, PBE, and TPSS functionals to compare their performance concerning CC2 and SCS-CC2 results. We calculated the allowed spin-singlet transition for these systems based on the ground-state structures of monomer (1) and dimers (2 and 3). The objective is to evaluate the electronic structure of the excitation state. The allowed transitions are listed in Table 2 for [AuPh(CNPh)] (1), and [AuPh(CNPh)]₂ II_y (2) and I_b (3).

Strongest singlet excitation energies calculated for models [AuPh(CNPh)] (1), II_y (2) and I_b (3) are compared to experimental data. The excitation energies and oscillator strengths have been calculated at CC2 and SCS-CC2 levels. The orbital contributions and characters of transitions are also given.

System	Method	λ calc/nm	f a	Contributionb	Transition type
[AuPh(CNPh)]	CC2	288	0.6829	43a → 44a (83)
	SCS-CC2	245	0.7011	43a → 44a (82)
	B3LYP	273	0.3881	43a → 47a (70)
	PBE	274	0.3702	43a → 47a (70)
	TPSS	269	0.3828	43a → 47a (70)
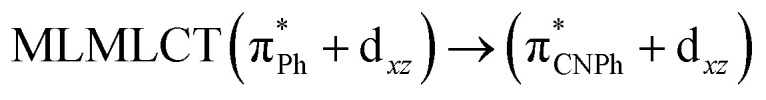
[AuPh(CNPh)]2 IIy	CC2	378	0.1387	86a → 87a (44)
				84a → 87a (19)
	SCS-CC2	320	0.1655	86a → 87a (30)
				82a → 87a (26)
	B3LYP	460	0.1066	84a → 88a (50)
				83a → 87a (26)
	PBE	459	0.1015	84a → 88a (49)
				83a → 87a (32)
	TPSS	445	0.1049	84a → 88a (50)
				83a → 87a (30)
[AuPh(CNPh)]2 Ib	CC2	255	0.7984	85a → 90a (26)
				85a → 92a (25)
				86a → 90a (17)
	SCS-CC2	244	0.7906	85a → 90a (27)
				85a → 92a (26)
				86a → 90a (15)
	B3LYP	329	0.2766	85a → 91a (32)
				85a → 92a (32)
	PBE	329	0.2572	85a → 92a (34)
				85a → 91a (30)
	TPSS	321	0.2304	85a → 92a (27)
				85a → 91a (23)
Model Iy	B3LYP	387/399
Model Ib	B3LYP	276/302/335
[AuPh(CNPh)]2 IIy	Exp.56	432
[AuPh(CNPh)]2 IIy	Exp.56	390
Ground
[AuPh(CNPh)]2 Ib	Exp.56	315

^aOscillator strength.

^bValues are |coeff.|² × 100.

The discussion of the properties of excited states is focused on principal transitions obtained from theoretical calculations. The optical properties of monomer 1 are shown in the ESI.†Table 2 shows that the same main electronic transition MLML charge transfer is obtained between PhCN, Ph, and gold orbital ligands with an antibonding component for all calculation methods used. The magnitude of the electronic transition is between 288 nm and 245 nm. The optical properties change when we analyze dimeric models. An apparent intermolecular interaction effect changes the location and type of electronic transition. The simulated spectra of models II_y (2) and I_b (3) are shown in Fig. 3 at CC2 and B3LYP levels. The results obtained with other methods were very similar. The most important molecular orbitals necessary to describe the nature of electronic transitions are shown in Fig. 4 and 5.

Fig. 3. Electronic spectra at CC2 and B3LYP levels calculated for [PhAuCNPh]₂ II_y (2) and I_b (3).

Fig. 4. Most important active molecular orbitals in the electronic transition of [AuPh(CNPh)]₂ II_y (2) at CC2 and B3LYP levels.

Fig. 5. Most important active molecular orbitals in the electronic transition of [AuPh(CNPh)]₂ I_b (3) at CC2 and B3LYP levels.

The experimental spectra of solid-state gold complexes showed a characteristic band at 432 nm for II_y and at 315 nm for I_b. TDDFT calculations with dimer models provided absorption bands in the same range concerning the experimental spectrum. The details about electronic transitions and their respective orbital contributions are listed in Table 2. Each calculated spectrum showed a principal transition that depended on the model type. [AuPh(CNPh)]₂ II_y (2) was close to the experimental value at DFT levels: B3LYP is 460 nm, PBE is 459 nm, and TPSS is 445 nm. However, for CC2 and SCS-CC2, their main bands are at 378 nm and 320 nm, respectively. The difference with DFT may be because, in CC2 and SCS-CC2 calculations, occupied and empty orbitals are more separated than in DFT. This is associated with higher energy electronic transitions. I_y model describes two main bands at 399 nm and 387 nm at B3LYP.⁵⁹ This difference with the results of this work may be because model I_y only partially optimizes the geometry.

In contrast, this situation is repeated for the [AuPh(CNPh)]₂ I_b (3) model. The principal band at B3LYP is 239 nm, PBE is 329 nm, and TPSS is 321 nm, very close to the experimental band at 315 nm. It is found that at CC2 and SCS-CC2 the main band is overestimated. Regarding the previously published theoretical model I_b, the values of its main band are at 302 nm and 335 nm at the B3LYP level. In this model, there is more coincidence between both studies.

Model II_y (2) has one principal transition at CC2 and B3LYP levels attributed to a metal ligand-to-metal–ligand charge transfer (MMCT), mainly centered among gold atoms, Ph, and CNPh from antibonding to bonding orbitals. The active molecular orbitals in the electronic transition are shown in Fig. 4. Conversely, model I_b (3) shows transitions generated between ligands with a low gold contribution. The active molecular orbitals in the electronic transition are shown in Fig. 5.

3.3. Emission energies

Aurophilic interactions are considered to be the main factor responsible for electronic spectroscopic features in most complexes, which have been proven to be highly dependent on the Au–Au distance.^50,88 This was shown in the previous section. The obtained emission energies, the Au–Au distance in the ground state and excited states (S₁ and T₁) of II_y and I_b dimers are listed in Table 3. In both models, it is observed that the Au–Au distance decreases in the different DFT methods when going from the ground state to the excited one. For the case of model II_y, the decrease in the Au–Au distance is more relevant because of the increase of its covalent character in the excited state.

Optimized Au–Au distance and R_e (pm) for models II_y and I_b [AuPh(CNPh)]₂ in S₀, S₁ and T₁ states. Transition energies (in eV) and wavelengths (in nm) for S₁ → S₀ and T₁ → S₀ emission processes in the models.

Model	Method	Au–Au (S0)	Au–Au (S1)	Au–Au (T1)	S1 → S0 eV (nm)	T1 → S0 eV (nm)
[AuPh(CNPh)]2 IIy	B3LYP-D3	300.6	273.1	279.3	1.86 (667)	2.15 (576)
	PBE-D3	300.6	275.6	280.6	1.83 (677)	2.14 (579)
	TPSS-D3	298.9	271.7	278.3	1.89 (655)	2.17 (572)
	Exp.a
[AuPh(CNPh)]2 Ib	B3LYP-D3	512.0	506.0	503.4	3.02 (407)	3.03 (409)
	PBE-D3	512.5	507.4	503.9	3.13 (396)	3.03 (409)
	TPSS-D3	512.4	507.4	503.9	3.13 (396)	3.12 (398)
	Exp.b

^a[AuPh(CNPh)]_n II_y emission band 2.19 eV (567 nm).⁵⁶

^b[AuPh(CNPh)]_n I_b emission bands 2.53 eV (490 nm), 2.72 eV (460 nm).⁵⁶

For dimer II_y, S₁ → S₀ and T₁ → S₀ emission energies are very close among the three methods. The magnitude of the emission band T₁ → S₀ reproduces that of the experimental band at 2.19 eV (567 nm). This would confirm that the photophysical process involves a spin change. The same analysis for the I_b model is more difficult since the emission cannot be seen because magnitudes are very similar between T₁ → S₀ and S₁ → S₀. Both emission bands have magnitudes similar to that of the experimental emission band (2.53 eV and 2.72 eV). The results of the two models generate quantitatively better results than those proposed through the QC/MM of Ito and co-authors.⁵⁹ For models I_y and I_b, they obtained transitions between 2.30 eV (539 nm) and 2.37 eV (523 nm) and 3.10 eV (399 nm) and 2.70 eV (459 nm), respectively.

3.4. Electronic solid state

In Fig. 2, the crystalline structures of [AuPh(CNPh)]₂ II_y and I_b (models 2′ and 3′) are depicted in their periodic forms. Crystal packing plays a crucial role in facilitating the movement of electrons in these systems. This is evident in model 2′, which has a rhombohedral structure with gold atoms closer at 3.199 Å, whereas in model 3′, with a triclinic structure, gold atoms are more distant, measuring 5.730 Å. Consequently, the proximity of gold atoms in the II_y system could facilitate the movement of electrons more efficiently than in the I_b system. This behavior of electrons agrees with results obtained for the band gap observed in Fig. 6, because the band gap value for model 2′ is 2.16 eV (574 nm). In contrast, for model 3′, it is 3.05 eV (407 nm), indicating that the movement of electrons requires less energy in model 2′ than in model 3′. These theoretical results agree with dimer systems II_y (2) and I_b (3) shown in Table 2, where the excitation energy is lower in II_y than in I_b, and the experimental data shows higher energy for system II_b than II_y. In consequence, the band gap is smaller in system II_y than in I_b, indicating that the proximity of gold atoms reduces the band gap, making II_y system more conductive. Conversely, in Fig. 6, band structures (Fig. 6a and c) and density of states (Fig. 6b and d) show the Fermi level closer to the conduction band in the II_y system, whereas in the I_b system, the Fermi level is closer to the valence band. Hence, the II_y system harbors a higher count of electrons in energy levels, enabling their unrestricted movement and engagement in electrical conduction, owing to the proximity of gold atoms. On the contrary, in the I_b system, fewer electrons are available to move and contribute to electrical conduction, leading to a more insulating behavior than II_y.

Fig. 2. Crystalline structure of [AuPh(CNPh)]₂ II_y (2′) and [AuPh(CNPh)]₂ I_b (3′).

Fig. 6. (a and c) Band structure of [AuPh(CNPh)]₂ for the II_y system (model 2′) and I_b system (model 3′). (b and d) Density of states of [AuPh(CNPh)]₂ for the II_y system (model 2′) and I_b system (model 3′).

4. Conclusion

The detailed study of [AuPh(CNPh)]₂ gold complexes in their II_y (2 or 2′) and I_b (3 and 3′) forms reveals a series of significant findings. The aurophilic interaction is identified as a critical factor influencing the spectroscopic and structural properties of complexes. Theoretical simulations employing MP2, SCS-MP2, and DFT-D3(BJ) methods provide a detailed understanding of weak intermolecular interactions and excited states. The Au2Au distances are essential, and a decrease in these distances is observed in excited states, especially in the II_y system, indicating a more covalent nature in the excited state. The results of two dimeric structures agree with solid-state results. This directly impacts photophysical properties, such as emission and absorption energies, which closely align with experimental results.

The analysis of optical and electronic properties, band gaps, and band structures offers a comprehensive insight into the relationship between aurophilic interaction and electronic behaviour of these systems. The solid states analysis confirms that the proximity of gold atoms in the II_y system facilitates electron movement, with a smaller band gap, thus this system exhibits a more conductive behaviour. Overall, these results confirm the significance of aurophilic interactions in the properties of gold complexes and demonstrate the utility of advanced theoretical approaches in understanding and predicting the properties of these systems. Previous theoretical models with MM/QM methodology complement the results presented in this work. Finally, the significant contributions of this manuscript are the understanding of the coordination chemistry and physics of excited states in gold complexes, opening new perspectives for the manipulation and application of these materials in nanotechnology and optoelectronics.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.