Abstract
The assessment of colleges’ effectiveness heavily relies on the employment status of graduates. Government-industry-university-research (GIUR) collaboration in cultivation talent is the key to improving the employment rate of college graduates. Based on the theoretical framework of the triple helix, this study develops a tripartite evolutionary game model that encompasses government, enterprises, and university research institutions. The research findings indicate (1) the evolutionary convergence of strategies among the subjects of the three-party game. (2) The attainment of a stable ideal evolution state for (1,1,1) is possible when the requisite conditions are met. This suggests that the cultivation of aligned talent in GIUR collaborations should coordinate the interests of various stakeholders. (3) Drawing inspiration from parameter-sensitive simulation, the problem of mismatch between talent cultivation and social demand can be effectively addressed through measures such as reducing the cost of cooperation, balancing the distribution of benefits, and implementing appropriate reward and punishment mechanisms. In response to these implications, we put forward some management insights and suggestions.
Keywords: Government-industry-university-research, Talent cultivation, Tripartite game
1. Introduction
China places a significant emphasis on development driven by innovation and actively pursues this strategic approach, with the aim of attaining a competitive advantage internationally and expediting China's long-term economic growth. The sole means by which a nation can attain an edge in such a fiercely competitive global milieu is to foster a heightened level of innovative talent and effectively harness the advantages of high-quality talent to bolster the high-quality development of the nation and society [1]. Currently, China has experienced a significant increase in its gross enrollment rate in higher education, rising from 30 % in 2012 to 59.6 % in 2022 [2]. This represents a substantial increase of 29.6 percentage points. Furthermore, the total number of individuals enrolled in higher education has reached an impressive 240 million. Institutions of higher education also play a crucial role in fostering innovation, adapting to societal trends, and reimagining approaches to nurturing talent and facilitating transformation [3].
However, in certain circumstances, inadequate teaching methods and curricula may not be able to fulfill this demand of businesses seeking individuals with advanced skills [4]. According to the data presented in Fig. 1, the relevance of employment to the profession for undergraduate graduates from 2017 to 2021 is found to be below 75 %. Additionally, the level of students' satisfaction with their employment is reported to be low, illustrating that the current employment rate is unsatisfactory, and the existing talent cultivation is insufficient to meet the demands of society [5]. Therefore, vigorously cultivating technical talent that is compatible with the upgrading of industrial structure and social and economic development and improving the modern higher education system has become an urgent problem [6]. The creation of a “market-oriented, enterprise is the main body, industry-university-research (IUR) collaboration" technological innovation system is more conducive to further balance between China's innovative talent training structure and modern industrial development needs.
Fig. 1.
Employment satisfaction among undergraduate graduates and relevance of profession, 2017–2021.
In this instance, the idea of “Government-Industry-University-Research” (GIUR) collaboration gives this occurrence fresh life. The foundation of this idea necessitates collaboration between numerous components and interaction across the four sectors of government, university, society, and practice. GIUR collaborative talent cultivation is an innovative behavior of complementing each other's advantages made by governments, enterprises, and university research institutions through mutual collaboration with their own resources, aiming to compensate for their knowledge inadequacy and improve their talent cultivation. During collaboration, all parties are involved spontaneously in an informal collaboration network and work together through the collaboration of each sector [7]. Universities can turn knowledge dissemination into a more direct teaching approach throughout the teaching stage by using other environments, including social businesses, as the basis of the teaching environment, which considerably enhances the skills and talents needed by society [8].
China's economic development and government policies provide a platform for collaboration between its stakeholders (namely universities), government, and industry [9]. GIUR collaboration highlights the role and responsibilities of each actor at different stages of knowledge generation and commercialization [10]. For the past few years GIUR relations, as well as the scope of collaborations, have changed in response to reforms in regulations [11]. Though GIUR relations continue to develop, the scope of government-industry collaboration decreases because of deregulation, and the tripartite relationship between universities, industry, and government shows a loose trend [12].
Cultivation of innovative talent should prioritize comprehensive collaborative education involving government, industry, and university research institutes. It is crucial to integrate innovation and entrepreneurship education with the requirements of enterprises throughout the entire talent cultivation process. This approach is necessary to address the growing demand for talent in the era of globalization [13]. As an emerging and innovative approach to talent cultivation, the GIUR talent cultivation model has the potential to enhance the quality of talent for enterprises while also addressing the issue of college student employment. This model aims to improve overall performance [14,15]. However, when considering the interests of individual groups, the industry-university-research alliance may not always opt for collaboration, as these groups often prioritize fair distribution and maximizing benefits, and there exists a significant interdependence among individuals [16].
This paper investigates the following three inquiries: (1) Does the government opt to proactively engage or adopt a hands-off approach? (2) How can a system of rewards and punishments be implemented to incentivize university research institutions and enterprises? (3) In the face of the employment rate of college students, enterprises have the option to either passively respond to government initiatives or proactively assume social responsibility by actively collaborating with universities to foster talent. In addressing these inquiries, this paper aims to address an overlooked concern by examining the tripartite evolutionary game of the stakeholders involved in the university talent cultivation system. It seeks to elucidate the strategic decisions made by the government, university research institutes, and enterprises within the framework of the innovative talent cultivation system.
This paper may contribute to the literature in the following aspects: (1) It provides a new evolutionary perspective that concentrates on the behavioral strategies of university research institutions and industry collaborating to train innovative talent under government involvement. The focus of this paper is on the evolution of strategy interactions rather than technology improvement or policy design in static situations. (2) The application of evolutionary game theory is extended, and the theory is innovatively used to analyze the process of cultivating innovative talent and the interaction among the government, university research institutions, and industry. (3) The evolutionary trajectory and the influence of key parameters are provided through numerical simulation. In addition, targeted policy recommendations are proposed based on the model results, which are of strong practical significance for innovation to enhance talent training. To the best of our knowledge, this study represents the pioneering application of an evolutionary game model to analyze the tripartite decision-making process involved in the cultivation of innovative talent through GIUR collaboration. By conducting numerical simulations to analyze the evolutionary trajectory of the evolutionarily stable strategy (ESS) and its dependence on key parameters, this paper offers valuable theoretical insights for the cultivation of innovative talent.
The subsequent sections of this paper are structured as follows. Section 2 provides an overview of the literature. Section 3 presents the theoretical framework for fostering innovative talent through collaborative GIUR, drawing upon triple helix theory. Section 4 delineates the problem and establishes the parameters while also presenting the tripartite evolutionary game model. Section 5, simulation analysis, aims to examine the effects of key parameters on the evolutionary results and trajectories. Finally, the results of the analysis are summarized, management insights are presented, and ideas and directions for future development are offered.
2. Literature review
2.1. University talent cultivation
Talent cultivation in higher education has become a critical focal point in academia. Collaboration between universities and industry is largely seen as one approach to cultivating innovative talent [17,18]. The cultivation of innovative talent requires the collaboration of universities, governments, enterprises, and other pertinent stakeholders. Successful collaboration between industry and university research institutions necessitates the alignment of the university's evolving mission with the crucial demands of the industry [19]. The incorporation of conventional academic fields with interdisciplinary technology and the integration of theoretical instruction and practical education, along with the integration of knowledge transfer and application inquiry, fosters the development of innovative talent [20].
Intel's exploratory research model facilitates collaboration and enables the simultaneous execution of projects in various locations, thereby enhancing outcomes and expediting technology transfer [21]. Rui Zhou et al. found that under the guidance of IUR collaboration, students practice more in the teaching and learning process in response to the needs of society [22]. It incorporates the “Industry-University-Research-Competition" approach, considering the viewpoints of students, teachers, and colleges. It effectively incorporates positive psychological cues and develops the “student teaching assistant" auxiliary system to enhance learning promotion efforts. Ultimately, it aims to innovate the talent cultivation system [23]. Additionally, companies have the option to establish direct collaborations with universities and their affiliated research institutions. They can also consider recommendations from universities, delegate the task of cultivating specific professionals to universities, or even offer internship opportunities for designated students pursuing professional cultivation and cultivating innovative talent [24].
With the advancement of science and technology, an increasing number of novel technologies are being utilized in the education and cultivation of innovative talent in higher education institutions. The “Internet + Education" initiative in innovative talent education can effectively guide the innovation of talent education models, allowing for greater utilization of novel technologies to enhance efficiency and performance [25]. The ongoing global pandemic caused by the coronavirus has necessitated a swift adjustment to online learning for students and educators at all levels of education [26]. Yanli Ma is incorporating artificial neural networks into the cultivation process of developing film creation talent [27]. Additionally, for the past few years, a significant body of literature has addressed the cultivation of innovative talent, emphasizing the need for colleges and universities to revise their understanding and optimize their faculty structure [28,29], the reform of educational concepts, models, and policies [30], and the reform of curricula [31,32]. Zhang, H et al. suggested dismantling institutional obstacles, fostering collaboration and talent exchange, and implementing a talent-sharing mechanism [33].
In these papers, numerous scholars have examined the issue of university talent cultivation from various perspectives. However, while a few studies [[22], [23], [24]] have explored university talent cultivation from the IUR perspective, they have not analyzed the role of the government in fostering talent through IUR collaboration, nor have they examined the influence of the interests of each main stakeholder on the development of collaborative talent. Therefore, to address this research gap, this paper aims to investigate the application of evolutionary game theory in describing the long-term dynamic process of multiplayer games within the context of GIUR collaborative talent cultivation, taking into account the constraints of limited rationality. The multiplayer evolutionary game is simulated, and its stability is subsequently analyzed. Based on the simulation analysis involving various stakeholders, an efficient stabilization control strategy is proposed and subsequently validated.
2.2. Evolutionary game theory
Game theory offers a mathematical framework for examining the dynamics of rational decision-makers' interactions, addressing a gap that is often overlooked by traditional approaches, which fail to consider the individual and social behaviors of stakeholders [34]. The aforementioned analysis tool and decision theory holds significant influence in the field of economics, as it aids in comprehending and examining conflict and collaboration within the decision-making process [35]. Traditional game theory is founded upon the assumption of complete rationality, wherein individuals always strive to maximize their utility and possess flawless introspection and inference capabilities [36]. However, this assumption diverges from the concept of bounded rationality that characterizes real individuals. At the same time, the strategy choice of participants with limited rationality is not fixed but rather influenced by the observation and comparison of benefits. These individuals could adjust their strategy choices and adapt their strategies dynamically.
The Evolutionarily Stable Strategy and the Replicating Dynamic Equation, proposed by Maynard Smith and Price [37] and Taylor and Jonker [38] in the 1970s, respectively, have been fundamental to the field of evolutionary games. These concepts have provided a solid foundation for understanding the dynamics of evolution in various contexts. Evolutionary game theory offers a solution to the limitations of traditional game theory by examining the bounded rationality of players and the dynamic nature of games. Each individual within the study is considered a bounded rational economic agent [39]. Over time, individuals engage in the process of observing and comparing the advantages, subsequently continuing to acquire knowledge and adapt their strategic decisions. This behavior exemplifies the attributes of a complex dynamic game.
At present, there is an increasing body of research that has utilized evolutionary game theory to examine the strategic interactions among various stakeholders in the fields of supply chain management [40], low-carbon economy [41], land and resources administration [42], safety management [43], and public service [44] to investigate this phenomenon. Meanwhile, evolutionary game analysis, a widely used quantitative analysis framework, has been utilized to examine the effectiveness of energy policies. Gong et al. employed an evolutionary game-theoretic model to ascertain the optimal time-of-use pricing for urban gas. Their study revealed that various gas users demonstrated varying degrees of demand responsiveness [45]. Therefore, the utilization of evolutionary game theory is deemed more appropriate for the examination of a long-term dynamic game involving bounded rational players within the context of our GIUR cultivation innovation talent cultivation system.
3. Theoretical framework based on triple helix theory
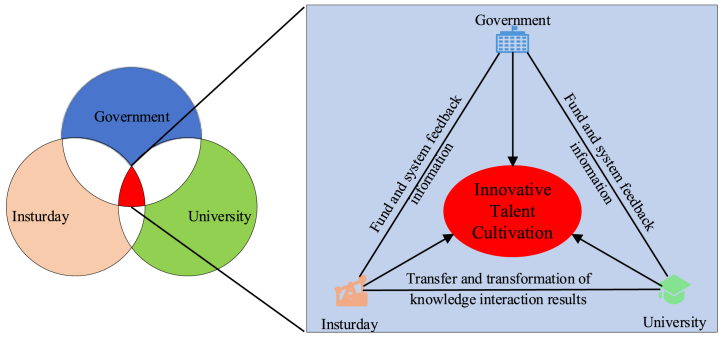
The triple helix model is a conceptual framework employed for the analysis of the interconnections among government, universities, and industries [46,47]. Etzkowitz and Leydesdorff [47] introduced the metaphor of the triple helix to conceptualize the intricate dynamics of relationships between universities, industries, and governments. The model posits the establishment and expansion of innovation in a knowledge-based society [48]. Presently, with the increasing interaction between universities and industrial activities, the roles and responsibilities of universities are expanding. According to the original talent cultivation theory, universities have traditionally been regarded as the primary institutions responsible for talent cultivation. However, this perspective is no longer in line with the current phenomenon of talent cultivation. Triple helix theory posits that universities, enterprises, and governments each play a crucial role in fostering innovative talent. According to this theory, these three entities should not only collaborate closely in innovation but also retain their distinct characteristics and independent status. This approach aims to establish a novel model of talent cultivation.
This paper utilizes Etzkowitz's triple helix theory of innovation [48] to construct a theoretical framework for examining the collaboration between government, industry, and university research institutions in fostering the development of innovative talent, as shown in Fig. 2.
Fig. 2.
Theoretical framework based on triple helix theory.
Innovative talent cultivation institutions consist of three key stakeholders: the government, industry, and university research institutions. The three subjects converge based on the principles of prior talent development and cultivation, establishing a cycle of elements through collaborative project pathways and the translation of scientific research outcomes. This approach aims to foster a triple helix relationship, wherein the capabilities of all three parties mutually influence one another; by leveraging their respective strengths, they can collectively contribute to the development of innovative talent. In the context of fostering innovative talent through collaboration, it is possible for the government, enterprises, and university research institutions to engage in talent cultivation individually and independently. However, the most crucial aspect of this practical endeavor lies in the cross-collaboration between these three entities. This collaboration serves as a catalyst for the other two parties, generating positive outcomes and fostering a collaborative initiative. The emphasis of policy promotion should be on the establishment of overlapping sectors.
4. The evolutionary game consisting of tripartite participants
4.1. Model assumptions
In the process of cultivating innovative talent, it is necessary to rely on collaboration between industry and university research institutes. In addition to the key participants who can be seen in the cultivation process, the government, the driving force behind the process, also does work that cannot be ignored. The government is equivalent to the “ripening agent", which has the incentive to promote collaboration between universities and research institutions and enterprises as soon as possible and obtain social benefits by solving the employment problems of university graduates. In a realistic environment of IUR collaboration to cultivate talent, the employment situation of graduates and the work completion degree of the participants is inspected by the government on a regular basis, and the inspection results are used as evidence for subsequent financial support. On this basis, the following assumptions are made.
-
(1)
Participating subjects. Government (G), university research institutions (S) and enterprises (E) are the three main bodies in the process of GIUR collaboration in cultivating innovative talent. At present, our country's GIUR collaborative talent cultivation is a model of government guidance, with university research institutions leading and enterprises participating. As a guide, the government mainly uses various encouraging policies to provide support to universities and research institutions and their enterprises to promote collaboration between enterprises and university research institutions to cultivate talent; enterprises are responsible for practical courses and providing internships; universities and research institutions are mainly responsible for the delivery of theoretical knowledge. In the process of collaboration, the three parties constantly play a limited and rational game and seek the best strategy in the game.
-
(2)
Collaboration strategy. If the three parties collaborate in the game of cultivating talent, the geographical boundaries of the activities of the people participating in the three parties are split, and the government can play its unique role of supervision, supervising the university research institutions and enterprises in the process of joint cultivation of talent. It can also choose not to participate in the supervision of enterprises and university research institutions' collaboration to cultivate talent and provide preferential and incentive policies. Whether or not to participate in the collaboration mainly depends on the actual situation of the two main subjects, that is, whether it is beneficial for them to participate in the collaboration, which can also be divided into two cases, and the set is expressed as (collaborative, noncollaborative). Let and denote the probability of collaboration between enterprises and university research institutions to cultivate talent, respectively; then, and denote the probability of noncollaborative between enterprises and university research institutions, respectively. Let represent the probability of government participation and represent the probability of no government participation, where .
-
(3)
Cost of collaboration. If the government does not participate in the cultivation of collaborative innovation talent, then it will not produce the total cost, and then enterprises and university research institutions become the key participants in the cultivation of talent, as the main body will inevitably put the corresponding human, talent and material resources as the total cost of production . If we take and as the cost-sharing ratios of enterprises and university research institutions, respectively, and , we can obtain the costs of enterprises and university research institutions as and , respectively. If the government chooses to participate in the process, then it will pay certain supervision and incentive costs. We set and as the monitoring and incentive costs of government participation, respectively. At the same time, because of the government's participation and because the government's own characteristics can give enterprises and university research institutions corresponding preferential policies to reduce the total investment of the two main participants, the total cost is expressed by , the amount of cost reduction is expressed by , and at the same time, the total cost paid by the two parties will become (, ). Then, and are the cost of their needed inputs and the cost of the university research institutions' inputs, respectively.
(4)Benefits of collaboration. Let and denote the benefits when enterprises and university research institutions choose not to collaborate, respectively, denote the benefits when enterprises and university research institutions collaborate with each other to cultivate talent without government involvement, denote the benefits when enterprises and university research institutions collaborate with each other to cultivate talent and government involvement, and . When both enterprises and university research institutions choose to collaborate to cultivate talent, the government can obtain an additional benefit of , the total benefit of enterprises and university research institutions is , the proportion of enterprises and university research institutions sharing this benefit is and , , the new benefit of enterprises is , and indicates the benefit of university research institutions. In addition, if there are enterprises and university research institutions that actively participate in the collaboration to cultivate talent, the government will give additional incentive funds, which is denoted by . The ratio of incentive funds for enterprises and universities is and , and ; then, the incentive funds for enterprises are , and the incentive funds for universities are . In the case that the enterprise agrees to join the collaboration to cultivate talent, but the research institution refuses to join, indicates the benefits gained by the enterprise. Conversely, if the company does not join the collaborative talent cultivation but the university research institution chooses to join, the following indicates the benefits received by the university research institution .
-
(5)
Punishment. To further control the breach of trust between enterprises and university research institutions in the process of collaboration to cultivate talent, so that the collaboration can achieve the ultimate purpose of cultivating innovative talent, we use the government to supervise, such as in the case that enterprises participate in the collaboration and university research institutions do not participate, the enterprise will get the penalty amount paid by the university research institutions when the university research institutions break the trust and breach the contract ; the position changes when the university research institutions participate in the collaboration and enterprises choose not to participate, and the university research institutions will get the penalty amount paid by the enterprises. If the enterprise is involved in the collaboration, the enterprise chooses not to participate, and the enterprise defaults on the contract, the university research institution will receive the penalty amount paid by the enterprise .
Based on the underlying assumptions, the anticipated payoffs for the government, industry, and university were illustrated in a game tree, as depicted in Fig. 3.
Fig. 3.
Tripartite game tree.
4.2. Game solution
4.2.1. Constructing the expected payoff function
Based on the data presented in Fig. 3, we conducted calculations to determine the anticipated payoffs to the government when deciding whether to engage in GIUR collaboration for talent cultivation. The expected benefits of the government “participate" strategy , the expected benefits of the “nonparticipate" strategy , and the average expected benefits of the game ,which are expressed by (1), (2), (3), respectively:
| (1) |
| (2) |
| (3) |
The expected benefits of the enterprise choosing the “collaborative" strategy , the expected benefits of choosing the “noncollaborative" strategy , and the average expected benefits of the game ,which are expressed by (4), (5), (6), respectively:
| (4) |
| (5) |
| (6) |
The expected benefits of the university choosing the “collaborative" strategy , the expected benefits of choosing the “noncollaborative" strategy and the average expected benefits of the game ,which are expressed by (7), (8), (9), respectively:
| (7) |
| (8) |
| (9) |
4.2.2. Dynamic replication equations for evolutionary games
With the above analysis, the replication dynamic equation of the enterprise is formula (10):
| (10) |
The replication dynamics equation for university research institutions is formula (11):
| (11) |
The replication dynamic equation for the government is formula (12):
| (12) |
By associating (10), (11), (12), the dynamic equations of the replication dynamics system of the government, enterprises and university research institutions are obtained as formula (13).
| (13) |
4.2.3. Stability analysis of the tripartite evolutionary game system
According to the method proposed by Friedman, the ESS [49] of the system of differential equations can be obtained from the local stability analysis of the Jacobi matrix of this system, which is obtained from formula (13) as formula (14):
| (14) |
Among them,
In the system of replicated dynamic equations, let obtain the locally stable equilibria as , , , , , , , and . According to the evolutionary game theory, the equilibrium point that satisfies all the eigenvalues of the Jacobi matrix is nonnegative and is the ESS of the replicated dynamic equation system.
The following is the first analysis of the case where the equilibrium point is when the Jacobi matrix is:
The eigenvalues of the Jacobi matrix are currently , , and . By analogy, the eigenvalues of the Jacobi matrix corresponding to each of the eight equilibrium points can be obtained by substituting them into the Jacobi matrix, as shown in Table 1.
Table 1.
Eigenvalues of the Jacobi matrix.
| Balancing point | Eigenvalue | Eigenvalue | Eigenvalue |
|---|---|---|---|
To facilitate understanding the sign of the eigenvalues corresponding to different equilibrium points without loss of generality, Assuming (1) the government's participation in monitoring and incentivizing the collaborative cultivation of talent will make the government earn more revenue and make the net revenue more than that without participation in monitoring and incentivizing the collaborative cultivation of talent, i.e., ; (2) under the condition that the government participates in monitoring and incentivizing, the net revenue of the collaborative cultivation of talent between enterprises and university research institutions is greater than that without collaboration, i.e., and ; and (3) under the condition that the government is not involved in supervision and incentives, the net benefit of collaboration between enterprises and university research institutions in cultivating talent is greater than the net benefit of not cooperating in cultivating talent, i.e., and . Based on the large number of complicated parameters in the model, the evolutionary game stabilization strategy is discussed in the following four scenarios.
Scenario 1: and means when the enterprise chooses not to participate in collaboration to cultivate talent but to cultivate talent independently with itself as the largest subject, the cost paid out, in this case, is less than the benefit, while the benefit of independent cultivation of talent by university research institutions is greater than the cost paid. From Table 2, we know that is the evolutionary equilibrium point of the game model, and the evolutionary equilibrium strategy is (collaborative, collaborative, participate).
Table 2.
Local stability of equilibrium points.
| Scenario 1 |
Scenario 2 |
Scenario 3 |
Scenario 4 |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Stability | Stability | Stability | Stability | |||||||||||||
| + | + | + | Saddle Point | – | – | + | Non-Stability Point | + | – | + | Non-Stability Point | – | + | + | Non-Stability Point | |
| + | + | – | Non-Stability Point | – | – | – | ESS | + | – | – | Non-Stability Point | – | + | – | Non-Stability Point | |
| + | – | + | Non-Stability Point | + | + | + | Saddle Point | + | + | + | Saddle Point | + | – | + | Non-Stability Point | |
| + | – | – | Non-Stability Point | + | + | – | Non-Stability Point | + | + | – | Non-Stability Point | + | – | – | Non-Stability Point | |
| – | + | + | Non-Stability Point | + | + | + | Saddle Point | – | + | + | Non-Stability Point | + | + | + | Saddle Point | |
| – | + | – | Non-Stability Point | + | + | – | Non-Stability Point | – | + | – | Non-Stability Point | + | + | – | Non-Stability Point | |
| – | – | + | Non-Stability Point | – | – | + | Non-Stability Point | – | – | + | Non-Stability Point | – | – | + | Non-Stability Point | |
| – | – | – | ESS | – | – | – | ESS | – | – | – | ESS | – | – | – | ESS | |
Scenario 2: and , that is, under the condition that the government participates in supervision and incentives, the sum of the revenue obtained by the enterprise when it chooses to collaborate and the university research institution when it chooses not to collaborate to cultivate talent, and the sum of the liquidated damages and government incentive funds paid by the university research institution is less than the cost of its investment, and the sum of the revenue obtained by the university research institution when it chooses to collaborate and the enterprise when it chooses not to collaborate to cultivate talent, and the sum of the liquidated damages and government incentive funds paid by the enterprise is less than the cost of its investment. The sum of the default and government incentive funds is less than the funds invested. Table 2 shows that the eigenvalues of the Jacobi matrices of and are nonpositive, which are the evolutionary equilibrium points of the game model, and on this basis, the system presents two stable points of and , and the corresponding evolutionary strategies are (noncollaborative, noncollaborative, participation) and (collaborative, collaborative, participate).
Scenario 3: and , i.e., the benefits of independent cultivation are greater than the costs, and the sum of the benefits gained and the liquidated damages and government incentive funds paid by the enterprise is less than the costs when the university and research institution choose to collaborate and the enterprise chooses not to collaborate in cultivating talent. From Table 2, is the evolutionary equilibrium point of the game model, and the evolutionary equilibrium strategy is (collaborative, collaborative, participate).
Scenario 4: and , i.e., the sum of the benefits gained by the enterprise when it chooses to collaborate and the university research institution when it chooses not to collaborate to cultivate talent, and the sum of the breach of contract and government incentive funds paid by the university research institution is less than the costs paid by the university research institution, and the benefits of the university research institution to cultivate talent independently are greater than the costs paid by the university research institution. From Table 2, we can see that is the equilibrium point of the model, and the corresponding strategies are (collaborative, collaborative, participate).
5. Numerical simulations
In light of the research opportunity regarding talent cultivation in private colleges and universities in Chongqing, a comprehensive study was conducted on a total of 29 colleges and universities, as well as 33 school-enterprise collaboration units in the same region. Based on an analysis of data from the “Chongqing Municipal Statistical Yearbook" and relevant research, the initial values of each external variable were determined in relation to the expenditure on the fusion of university and enterprise production and education. The values are displayed in Table 3. In this paper, Python 3.8 is utilized to simulate and analyze the decision-making process of government entities, enterprises, and university research institutions in various scenarios. The focus is primarily on factors such as the initial inclination to participate, government policies and the severity of associated penalties, as well as the distribution of benefits and cost-sharing coefficients among the final participants.
Table 3.
Parameters and assignment.
| Parameters | Parameter Meaning | Initial value |
|---|---|---|
| The total cost of cultivating talent for companies and universities when the government is not involved | 60 | |
| Total cost for companies and universities to train talents when the government is involved | 56 | |
| The cost of monitoring, when the government is involved | 8 | |
| Incentive costs when the government is involved | 5 | |
| When both enterprises and university research institutions choose to collaborate in cultivating talent, the government can gain additional benefits | 2 | |
| Government participation in collaboration between enterprises and universities to train talents to gain revenue | 40 | |
| The government does not participate in the collaboration between enterprises and universities to train talents to gain revenue | 20 | |
| Benefits when companies choose not to collaborate | 18 | |
| Benefits for university research institutions when they choose not to collaborate | 15 | |
| Enterprises and university research institutions bring total benefits | 60 | |
| Cost allocation coefficient of enterprise talent cultivation | 0.5 | |
| Cost allocation coefficients for cultivating talents in university research institutions | 0.5 | |
| Coefficient of revenue distribution for enterprise collaboration in cultivating talent | 0.5 | |
| Coefficient of revenue distribution for collaboration between universities and research institutions in cultivating talent | 0.5 | |
| Allocation factor for enterprises to receive government incentive funds | 0.5 | |
| Allocation coefficients of government incentive funds to university research institutions | 0.5 | |
| The benefits gained by enterprises when universities and research institutions choose not to collaborate in cultivating talent, but enterprises choose to collaborate in cultivating talent | 15 | |
| The benefits gained by university research institutions when university research institutions choose to collaborate in cultivating talent while enterprises choose to train talents alone | 18 | |
| Universities and research institutions pay the cost of a breach of contract | 5 | |
| Companies pay the cost of a breach of contract | 5 |
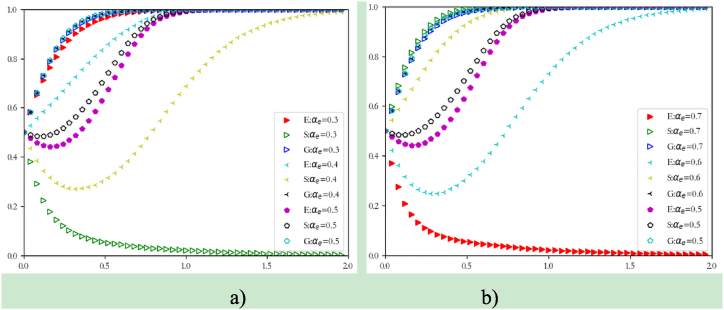
5.1. 1Influence of variations in participants' initial probabilities
Fig. 4 illustrates the simulation of the impact of variations in the initial probabilities of the three parties, i.e., enterprises, university research institutions and the government, to participate in the collaborative cultivation of talent on the collaborative cultivation of talent strategy, occurring under the condition that the remaining parameters remain unchanged. As can be seen from Fig. 4 that 0.4–0.5 is the range of the critical value of the initial probabilities of enterprises, universities and research institutions and the government. When the critical value is larger than the initial probabilities of all three parties, will converge to 1, but will converge to 0, and the final equilibrium point will converge to (0, 0, 1). The convergence speed of enterprises' probabilities to participate is much faster than university. In contrast, which will make all converge to 1, and the final equilibrium point will converge to (1, 1, 1). When the three parties' probabilities to participate remains the same, positive encouragement will gradually increase the government and universities' probabilities to participate, but the government's increase rate is more prominent. However, in the face of positive encouragement enterprises' probabilities to participate will decrease, but eventually, enterprises' probabilities to participate will decrease along with the remaining two parties' probabilities to participate. If the government is fully involved in the plan of cooperating to cultivate talent, and their interests are guaranteed, then this will directly drive the other two parties to participate, and their probabilities to participate will go up, and finally both parties will choose to participate after weighing the pros and cons. The ideal state is that the government, enterprises and university research institutions are all willing to participate, and finally, all three parties are willing to collaborate to cultivate talent, which will make the point at (1,1,1) remain stable. From the simulation analysis, when , which represents the probabilities of the three parties, is rising, then the speed of converging to 1 is significantly accelerated, and the speed of converging to 1 is slowed down, but finally, all three parties can reach the same probabilities to participate in the collaborative cultivation of talent.
Fig. 4.
Evolutionary results of simultaneous variations in probabilities to participate .
The starting point of Fig. 5 is a simulation analysis of the impact of the strategy of collaboration between university research institutions and the government in cultivating talent caused by the variations in the initial probabilities of enterprises participating based on the remaining parameters being unchanged. As can be seen from Fig. 5 that under the influence of the initial probabilities of enterprises, the values of , which represent the initial probabilities of government and university research institutions to participate, are kept in an intermediate position, and the initial probabilities of enterprises are taken from 0.3 to 0.4, and when the critical value is greater than , converges to 0, and converges to 1. The point (0,0,1) is the convergence point of the final equilibrium. Meanwhile, the expansion of will slow down the convergence speed of , and with the increase of , the convergence speed of will be accelerated rapidly; when the critical value is less than , converges to 1, but the convergence speed of is less than that of , and the point (1,1,1) is the convergence point of the final equilibrium point.
Fig. 5.
Evolutionary results of variations in probabilities to participate .
Fig. 6 shows the simulation analysis of the initial probabilities to participate of enterprises and the government subjected to variations in the initial probabilities to participate of universities and research institutions occurring under the condition that the remaining parameters remain unchanged. As can be seen from Fig. 6 that the values of , which represent the initial probabilities of government and enterprises to participate, are kept at half and half, and it can also be concluded that the initial probabilities of universities to participate value is taken at 0.3–0.4; when the critical value is greater than , converges to 1, converges to 0, and the (0,0,1) point is the final equilibrium convergence point. At this time the convergence of slows down because of the rise of the value, however, in order to make the convergence of the value accelerate rapidly, it is necessary to make so that the convergence speed of enterprises is much faster than the convergence speed of university research institutions. The critical value is less than when converges to 1, then the point (1,1,1) will be the convergence point of the final equilibrium point. In this case the convergence speed of will be accelerated because of the increase of , and it makes the convergence speed of slow down; from this change trend it can be concluded that the probabilities of enterprises to participate varies with the initial probabilities of universities and research institutions to participate in , and increases together with the increase of probabilities. The government's probabilities to participate is the opposite, but it will join eventually. According to the data in Figs. 5 and 6 that when the initial probabilities of enterprises or university research institutions to participate both increase, the likelihood of the probabilities to participate in collaborative talent cultivation continues to rise so that both parties eventually join the line of collaborative talent cultivation; only from this perspective can we know that the probabilities of enterprises to participate are largely influenced by the attitude of the universities.
Fig. 6.
Evolutionary results of variations in probabilities to participate .
Fig. 7 shows the simulation analysis of the probabilities of universities and research institutions and enterprises participating in collaboration to cultivate talent influenced by the change in the initial probabilities of the government participating , which occurs under the condition that the rest of the parameters remain unchanged. As can be seen from Fig. 7 the initial probabilities of enterprises and universities to participate in , and their values show a flat state; that is, the probabilities to participate are not very strong. The government's initial probabilities to participate in are taken at 0.2–0.3. When the critical value is greater than , converges to 0, and point (0,0,1) is the convergence point of the greatest equilibrium point. At this time, the convergence speed of will slow down, which is due to the increase of at this time, but for , when the critical value is less than , the convergence speed of converges to 1 and point (1,1,1) is the convergence point of the final equilibrium point. The convergence speed of is accelerated, which is caused by the rise of , but the convergence speed of is less than that of . Meanwhile, it can be found that the probabilities to participate of enterprises and university research institutions will be motivated following the increase of the government's initial probabilities to participate , and the increase of the government's probabilities is a positive guidance, so the government's probabilities to participate has a significant impact on the probabilities to participate of universities.
Fig. 7.
Evolutionary results of variations in probabilities to participate .
Fig. 8 shows that the rest of the parameters remain unchanged; that is, when is high, it means that both enterprises and universities have a strong initial probability of participating in collaborative talent cultivation. In this case, even if is low, will converge to 1, and finally, both enterprises and universities will join the collaborative talent cultivation team. In contrast, when both enterprises and universities are not willing to join the collaboration, that is, is very low, and even will converge to 0 with the high initial probabilities of the government alone, enterprises and universities will still not join the collaborative talent cultivation team. Meanwhile, we can see in Fig. 8 that if both enterprises and universities are not involved, will converge to 0 less quickly than , and will converge to 1. As can be seen from Fig. 8 that when the government is involved in the collaborative cultivation of talent with small preferences, whether the government is involved in the collaborative cultivation of talent has little influence on enterprises and universities, and the market demand for talent is the core factor that enterprises consider repeatedly. In contrast, universities are strongly influenced by the government's probability of participating.
Fig. 8.
Evolutionary results of simultaneous variations in probabilities to participate .
Fig. 9 is under the condition that the rest of the parameters remain unchanged, letting the government's initial probabilities to participate be fixed; if the enterprise side shows a strong initial probability of participating , the opposition of the university research institutions can be directly ignored regardless, but this does not prevent from converging to 1. At first, the enterprises' probability of participating will have a small decline, but the downward trend will be broken gradually by the rising probability of the university research institutions participating. Eventually, when the probabilities of university research institutions to participate reach a certain value, the probabilities of enterprises to participate will no longer decline but will follow the same rise of university research institutions, finally leading to the choice of both enterprises and university research institutions to join the collaboration to cultivate talent. In another situation, under the premise that university research institutions have a strong initial probability of participating , even if enterprises refuse to participate in their initiatives, will converge to 1. As can be seen from Fig. 9 the government's probability of participating remains stable, and the choices of enterprises and university research institutions have a great influence on each other, which is determined by their characteristics. When one party is willing to collaborate, the other party will choose to participate in the collaboration.
Fig. 9.
Evolutionary results for unchanging probabilities to participate .
5.2. Influence of variations in the cost of collaboration
Fig. 10 depicts a simulation illustrating the influence of variations in the cost allocation coefficient on the collaborative talent cultivation strategy between enterprises and universities, with all other parameters held constant. In Fig. 10(a)–a pivotal range of values for the cost allocation factor emerges, specifically falling between 0.3 and 0.4. Additionally, Fig. 10(b) presents an additional critical range of values for the cost allocation factor, spanning from 0.6 to 0.7.
Fig. 10.
Evolutionary results of the variations in the cost allocation factor.
In this way, there are three situations: (1) when the cost allocation coefficient is smaller than 0.3–0.4, converges to 1 and converges to 0. This is because the shared cost of university research institutions is higher than the sum of their shared benefit and the default amount paid to enterprises; at this time, , the research institutions choose not to collaborate in cultivating talent, and enterprises and the government choose to participate in collaborative talent cultivation. (2) When the cost allocation coefficient is greater than 0.6–0.7, converges to 1 and converges to 0. At this time, the shared cost of enterprises is higher than the sum of their shared revenue and the liquidated damages paid to universities, , so enterprises choose not to collaborate in cultivating talent; in contrast, universities and governments show a willing attitude. (3) When the cost allocation coefficient is between 0.4 and 0.6, converges to 1, and the cost allocation coefficient will be infinitely close to 0.5. The speed of converging to 1 is also determined by the distance between the distribution coefficient and 0.5; the closer the distance is, the faster the convergence speed. When , because the input cost of enterprises is less than that of universities and research institutions, the probabilities of universities, in this case, will drop temporarily, but it will rise at a later stage; when , the situation is just the opposite, but no matter what, enterprises and universities eventually choose to collaborate to cultivate talent. As can be seen from Fig. 10 the final strategy choice of enterprises and universities will be affected by the change in the cost allocation coefficient , and in terms of the degree of being affected, enterprises are more sensitive to its influence.
5.3. Influence of variations in the distribution of earnings
Fig. 11 illustrates the simulation with the remaining parameters held constant, exploring the impact of variations in the revenue allocation coefficient within collaborative talent development involving companies and university research institutions. In Fig. 11(a), it is evident that the range of 0.36–0.37 represents a critical interval for the income distribution factor under constant costs and a cost-sharing ratio of 0.5 each. Moving to Fig. 11(b), we observe that the range of 0.63–0.64 signifies another critical interval for the income distribution factor under constant costs and a cost-sharing ratio of 0.5 each.
Fig. 11.
Evolutionary results of the variations in the revenue distribution coefficient.
In this case, three situations will be presented. (1) There is a situation where enterprises and universities refuse to participate in collaboration to cultivate talent in the end, which is because the benefit distribution coefficient is smaller than 0.36 and converges to 0. However, in this case, the relative comparison of universities' share of benefits will be larger than that of enterprises, so the probabilities of universities' research institutions to participate will be adjusted upward because of the benefit factor, but will eventually decline due to the decline in revenue (2) When the benefit distribution coefficient is larger than 0.64, will converge to 0, which will cause both enterprises and universities not to choose to collaborate to cultivate talent. (3) When the benefit distribution coefficient is between 0.36 and 0.64, will converge to 1, the benefit distribution coefficient will be infinitely close to 0.5, and the speed of convergence of to 1 will be determined by the distance between the distribution coefficient and 0.5. When , the benefit to the enterprise is smaller than that to the university, because the benefit will make the enterprise's probabilities first decline and then rise slowly; when , the situation is the opposite, although the enterprise's benefit is higher than that of the university, but the probabilities of both parties will decline slightly, but then will increase. However, the probabilities of both parties in this case decreases slightly, and then gradually increase, so that both parties can join the collaboration in cultivating talent. As can be seen from Fig. 11 the change in revenue allocation coefficient will affect the strategy choice of enterprises and universities to join the collaborative cultivation or not, and among the three, enterprises are the most sensitive to revenue allocation because they always pursue profit maximization, so they are most affected by the allocation coefficient.
5.4. Influence of variations policy incentive
The government's probability of participating can be demonstrated in two ways: policy support and financial incentives. Policy support will alleviate the total cost of enterprises and university research institutions in joining collaborative talent development, and the financial incentive is through direct payment to enterprises and university research institutions. The starting point of Fig. 12 is based on the simulation of the impact of the amount of cost of collaborative cultivation of talent made by the government's policy support under this change on the choice of collaborative cultivation of talent strategy by enterprises and universities, with the remaining parameters unchanged. From Fig. 10, it can be concluded that 1–2 is the critical value of cost reduction . When the critical value is greater than , converges to 0, (0,0,1) point is the convergence point of final equilibrium, the increase of makes the convergence speed of slow down, and the convergence speed of is slower than the convergence speed of . The critical value of is less than , converges to 1, (1,1,1) is the convergence point of final equilibrium, the convergence speed of accelerates because of the increase of , and the convergence speed of is relative to the convergence speed of . We find that the former is slower than the latter, and we can conclude that the increase of will enhance the probabilities of enterprises and universities to participate. When the amount of is smaller, its enterprises' probabilities to participate has a downward trend, but if the government and universities' probabilities to participate continue to be strong, then the enterprises' probabilities will gradually increase, and they will finally agree to collaborate in cultivating talent. As can be seen from Fig. 12 that the final choice of enterprises and university research institutions is affected by the change in the cost reduction , and enterprises are affected more strongly than university research institutions. The reason for this is that the government's participation in the collaborative cultivation process can reduce the cost of both enterprises and universities through preferential policies, which can achieve the same benefit with less money than before. However, the impact of on enterprises is more obvious because enterprises attach great importance to benefits and losses.
Fig. 12.
Evolutionary results of variations in policy support.
Fig. 13 shows the simulation of the impact of the change in the incentive funds given by the government to universities and enterprises on their strategies to participate in the collaborative cultivation of talent, occurring under the condition that the remaining parameters remain unchanged. We find that 1–2 is the range of values of the critical value of the funding subsidy ; at the critical value greater than, converges to 0, the point (0,0,1) is the convergence point of the final equilibrium point, will let its convergence slow down because of the increase of , and the performance of university research institutions is more distinct. At the critical value less than , converges to 1, and point (1,1,1) is the convergence point of the final equilibrium. In summary, the change in government incentive funds has a profound impact on the strategy choice of enterprises and universities, but the impact on universities is stronger in comparison.
Fig. 13.
Evolutionary results of variations in incentive funding.
5.5. Influence of variations in penalties
Fig. 14 shows the simulation analysis of the impact of the change in the default penalty paid by the university to the enterprise on the strategy of the enterprise and the university to participate in the collaboration to cultivate talent, which occurs under the condition that the remaining parameters remain unchanged. The critical value of the default penalty is 2–3. When the critical value is greater than , converges to 0, and the point of (0,0,1) is the convergence point of the final equilibrium point. In this case, because of the increase in the government's probability of participating in , the convergence speed of slows down. In comparison, the convergence speed of university research institutions will be slower than the convergence speed of enterprises. When the critical value is less than , converges to 1, and the point of (1), (1), (1) is the convergence point of the final equilibrium point. The point of (1), (1), (1) is the convergence point of the final equilibrium point; in this case, the convergence speed of will be accelerated because of the increase in the government's probability of participating in , but in comparison, the convergence speed of university research institutions will be faster than that of enterprises.
Fig. 14.
Evolutionary results of the variations of default penalties in universities.
Fig. 15 shows the simulation analysis of the impact of the change in the default penalty paid by the enterprise to the university research institution on the university research institution and the enterprise on the choice of the strategy of collaboration in cultivating talent, which occurs with the remaining parameters unchanged. Fig. 15 shows that 2–3 is the range of the critical value of the default penalty . When the critical value is greater than , converges to 0, and the point (0,0,1) is the convergence point of the final equilibrium point. In this case, the convergence speed of slows down because of the increasing probabilities of the government participating in . In comparison, the convergence speed of the university research institution will be slower than that of the enterprise. The critical value is less than , converges to 1, the point (1,1,1) is the convergence point of the final equilibrium point, and the convergence speed of the university research institution will be slower than that of the enterprise. The critical value is less than , converges to 1, and the point (1,1,1) is the convergence point of the final equilibrium point. In the convergence of the final equilibrium point, in this case, the convergence speed is accelerated because of the increase in the government's probability of participating , but the convergence speed of the enterprise at this time is slower than that of the university research institution. Fig. 16 shows the simulation analysis of the impact of the simultaneous variations of the default penalty paid by the university research institution to the enterprise and the default penalty paid by the enterprise to the university research institution on the enterprises and universities' choice of collaboration strategy for cultivating talent, occurring under the condition that the remaining parameters remain unchanged. We find that the critical value of the default penalty is between 3 and 4. When the default penalty is less than this critical value, converges to 0, and the final equilibrium point converges to (0,0,1). At this time, the convergence speed slows down with the increase in the government's probability of participating , but the convergence speed of enterprises is obviously faster than that of universities; when the critical value is less than the default penalty, converges to 1, and the point (1,1,1) is the convergence point of the final equilibrium point. At the convergence point, the faster convergence rate is due to the increase in the government's probability of participating , while the convergence rate of enterprises is slower than that of universities and research institutions. In addition, the convergence rate follows the increase in the default penalty.
Fig. 15.
Evolutionary results of the variations in the penalty for corporate default.
Fig. 16.
Evolutionary results of simultaneous variations in default penalties for universities and firms.
According to the simulation in Figs. 14–16, it can be learned that what drives the probabilities of enterprises and universities to collaborate more is the increase in the penalty for breach of contract, compared to the enterprise side, which is more significantly affected by the intensity of the penalty. This is due to the nature of enterprises, which always aim at pursuing greater profitability, and when enterprises find that collaboration is harmful to themselves, their probabilities of participating then vary. However, if the punishment is too light, it will lead to the enterprise not participating in the collaborative talent cultivation program, which will lead to the chain reaction of decreasing the probabilities of universities and research institutions of participating, until the probabilities of participating completely disappear and the situation occurs that they also do not participate in collaborative talent cultivation; in contrast, when the punishment is stronger, even if the university (enterprise) does not participate in collaborative talent cultivation, the enterprise (university) will get part of the benefits. This increases the probability of enterprises (universities) participating driven by interest until the probability of universities (enterprises) participating also increases and they finally choose to collaborate in cultivating talent.
6. Conclusions and policy recommendations
6.1. Conclusions
This paper uses evolutionary game theory to construct a matrix of collaboration in cultivating talent involving the government, enterprises and university research institutions and provides a systematic interpretation of the decision and strategy deconversion process of the three parties in cooperating in cultivating talent while exploring the factors regarding the strategic choices affecting the collaboration of the three parties in cultivating talent based on the study of the values, and the following conclusions can be drawn.
-
(1)
The government, enterprises and university research institutions are influenced by the differences in the probabilities of participation among each other. Under the condition that the participation of universities and enterprises increases year by year, the dependence of both parties' probabilities to participate on the government's probabilities to participate gradually decreases. At the same time, the government's probability of participating is not influenced by the other benefits obtained by participating and not participating in the collaboration. What determines the government's probability of participating is the amount of difference in the benefits received. The government's main purpose is to promote the employment rate of college graduates, and only the outstanding benefit gap will push the government to choose the corresponding program.
-
(2)
Regarding sensitivity to penalties, cost sharing and revenue division, enterprises are more sensitive than universities. In contrast, the purpose of universities is to serve the profound development of the country and to cultivate innovative talent to serve scientific research and social construction, so the academic value of knowledge is particularly important. At the same time, a scientific and appropriate benefit distribution system is developed to encourage enterprises to join the ranks of collaboration in cultivating talent in a positive way.
-
(3)
The size of the government's incentive cost for enterprises and universities involved in the collaborative cultivation of talent affects the probabilities of the three parties participating. The lower the incentive cost is, the lower the probability of enterprises and university research institutions participating, and the higher the probability of the government participating in the collaborative cultivation of talent; the higher the incentive cost is, the higher the probability of enterprises and university research institutions participating in the collaborative cultivation of talent, and the lower the probability of the government participating. On the other hand, when the government supervision cost and incentive cost are constant, making policies to reduce the cost of cooperating with enterprises and university research institutions to cultivate talent can enhance the probabilities of both parties participating.
6.2. Policy recommendations
The collaboration between government, industry, university, and research institutions holds immense importance in fostering the cultivation of innovative talent. The strategies employed by these stakeholders significantly influence this process. The findings of the study suggest that the decision-making behavior of major stakeholders is influenced by factors such as incentives [50] and penalties, cost sharing, and benefit distribution. Consequently, this paper puts forth the subsequent policy implications.
-
(1)
To enhance the collaboration between industry, and university research institutions in talent cultivation, the government establishes a robust system of incentives and penalties. To foster collaboration, financial grants are provided to support collaborative projects, while tax incentives are offered to industries that actively participate in such initiatives. Access to state-of-the-art research facilities is facilitated as an additional reward. Conversely, entities that do not engage in cooperation are confronted with diminished research funding, exclusion from government programs, and limited access to facilities. Industries that resist collaboration may face the consequence of higher taxes, heightened regulatory scrutiny, and limited access to subsidies. This strategic integration of incentives and penalties seeks to foster a culture of collaboration, creativity, and ongoing enhancement in the domain of talent cultivation, aligning the objectives of government, industry, and university research institutions.
-
(2)
Establishing a robust mechanism to ensure the fair distribution of benefits among industry, academia, and research institutes is of paramount importance in promoting the cultivation of innovative talent. Financial benefits arising from collaborative projects, such as favorable research outcomes or groundbreaking products, may be allocated using a predetermined formula that considers the extent of participation and expertise provided by each collaborating entity. Additionally, the implementation of a shared intellectual property policy can serve to delineate the allocation of ownership and royalties, thereby safeguarding the interests of all collaborators involved.
-
(3)
Achieving a reasonable sharing of talent training costs is pivotal for promoting effective GIUR collaboration in talent cultivation. Government funding can serve as foundational support, covering a portion of the overall expenses to encourage collaboration. Industries can contribute by providing financial support, internships, and on-the-job training opportunities. On the other hand, university research institutes can leverage their educational expertise and infrastructure for training purposes. A tiered funding structure could be implemented, considering the scale and impact of collaboration. Regular assessment and reassessment of the collaborative initiatives would ensure that the burden is shared fairly, and adjustments can be made based on the evolving needs of all stakeholders. This balanced approach to sharing talent training costs promotes a sustainable and mutually beneficial ecosystem, fostering long-term cooperation between industry, academia, and research institutions.
This study has several limitations. (1) To prevent the model from becoming overly complex, we limited our consideration to a select few influential factors that are widely recognized and significant. Future research endeavors may explore student factors and incorporate demand-side stakeholders for a more comprehensive and in-depth discussion. (2) This study is grounded in a survey conducted among universities in Chongqing to establish the parameters. Subsequent research endeavors may consider broadening the survey's scope to enhance the accuracy of the findings. (3) Future research can differentiate and study public and private universities.
Data availability
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
Funding
This study is funded by Chongqing Municipal Education Science Planning Key Project "Research on the Cultivation Path of Applied Innovative Talents Based on the Integration of Industry-University-Research" ( No. 2021-GX-037).
CRediT authorship contribution statement
Jianlong Ma: Writing – original draft, Writing – review & editing, Visualization, Validation, Software, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Dongsheng Yang: Writing – review & editing, Investigation.
Declaration of generative AI and AI-assisted technologies in the writing process
During the preparation of this work the author(s) used ChatGPT in order to increase the readability of the article. After using this tool/service, the author(s) reviewed and edited the content as needed and take(s) full responsibility for the content of the publication.
Declaration of competing interest
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests:
Jianlong Ma reports financial support was provided by Chongqing Municipal Education Science Planning Project. If there are other authors, they declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Zhu Z., Cui S., Wang Y., et al. Exploration on the collaborative relationship between government, industry, and university from the perspective of collaborative innovation. Appl. Math. Nonlinear Sci. 2022;7(2):903–912. doi: 10.2478/amns.2021.2.00174. [DOI] [Google Scholar]
- 2.MOE releases statistical report on China's educational achievements in 2022 - Ministry of Education of the People's Republic of China. http://en.moe.gov.cn/news/press_releases/202304/t20230403_1054080.html (accessed 2023-October-7).
- 3.Wu N., Liu Z. Higher education development, technological innovation and industrial structure upgrade. Technol. Forecast. Soc. Change. 2021;162 doi: 10.1016/j.techfore.2020.120400. [DOI] [Google Scholar]
- 4.Özer M., Suna H.E. The linkage between vocational education and labor market in Turkey: employability and skill mismatch. Kastamonu Eğitim Dergisi. 2020;28(2):558–569. doi: 10.24106/kefdergi.704878. [DOI] [Google Scholar]
- 5.Yu X., Zhang B. Innovation strategy of cultivating innovative enterprise talents for young entrepreneurs under higher education. Front. Psychol. 2021;12 doi: 10.3389/fpsyg.2021.693576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sun C., Zhan Y., Du G. Can value-added tax incentives of new energy industry increase firm's profitability? Evidence from financial data of China's listed companies. Energy Econ. 2020;86 doi: 10.1016/j.eneco.2019.104654. [DOI] [Google Scholar]
- 7.Li E., Yao F., Xi J., et al. Evolution characteristics of government-industry-university-research cooperative innovation network for China's agriculture and influencing factors: illustrated according to agricultural patent case. Chin. Geogr. Sci. 2018;28(1):137–152. doi: 10.1007/s11769-017-0924-4. [DOI] [Google Scholar]
- 8.Msosa S.K. A comparative trend analysis of changes in teacher rate of absenteeism in South Africa. Educ. Sci. 2020;10(8):189. doi: 10.3390/educsci10080189. [DOI] [Google Scholar]
- 9.Turriago-Hoyos A., Thoene U., Torres B., et al. Product innovation, research and development and technology acquisition: a case study of the industrial sector in Colombia. Inst. Econ. 2015:85–119. [Google Scholar]
- 10.Abbas A., Avdic A., Xiaobao P., et al. University-government collaboration for the generation and commercialization of new knowledge for use in industry. Journal of Innovation & Knowledge. 2019;4(1):23–31. doi: 10.1016/j.jik.2018.03.002. [DOI] [Google Scholar]
- 11.Yoda N., Kuwashima K. Triple helix of university–industry–government relations in Japan: transitions of collaborations and interactions. J Knowl Econ. 2020;11(3):1120–1144. doi: 10.1007/s13132-019-00595-3. [DOI] [Google Scholar]
- 12.Zhuang T., Zhao S., Zheng M., et al. Triple helix relationship research on China's regional university–industry–government collaborative innovation: based on provincial patent data. Growth Change. 2021;52(3):1361–1386. doi: 10.1111/grow.12490. [DOI] [Google Scholar]
- 13.Jiang J., Tan W., Zhu X., et al. Innovative models and practices for engineering and technology talent cultivation in transnational higher education. Transform. Bus. Econ. 2021;20(1):37–52. [Google Scholar]
- 14.Teng T., Cao X., Chen H. The dynamics of inter-firm innovation networks: the case of the photovoltaic industry in China. Energy Strategy Rev. 2021;33 doi: 10.1016/j.esr.2020.100593. [DOI] [Google Scholar]
- 15.Prokop V., Hajek P., Stejskal J. Configuration paths to efficient national innovation ecosystems. Technol. Forecast. Soc. Change. 2021;168 doi: 10.1016/j.techfore.2021.120787. [DOI] [Google Scholar]
- 16.Tang Q., Wang C., Feng T. Research on the group innovation information-sharing strategy of the industry–university–research innovation alliance based on an evolutionary game. Mathematics. 2023;11(19):4161. doi: 10.3390/math11194161. [DOI] [Google Scholar]
- 17.Perkmann M., Neely A., Walsh K. How should firms evaluate success in university–industry alliances? A performance measurement system. R D Manag. 2011;41(2):202–216. doi: 10.1111/j.1467-9310.2011.00637.x. [DOI] [Google Scholar]
- 18.Ankrah S., Al-Tabbaa O. Universities-industry collaboration: a systematic review. Scand. J. Manag. 2015;31(3):387–408. doi: 10.1016/j.scaman.2015.02.003. [DOI] [Google Scholar]
- 19.Santoro M.D., Chakrabarti A.K. Building industry–university research centers: some strategic considerations. Int. J. Manag. Rev. 1999;1(3):225–244. doi: 10.1111/1468-2370.00014. [DOI] [Google Scholar]
- 20.Zhou Y., Zheng F. Study of engineering talent cultivation in emerging engineering education. Transform. Bus. Econ. 2021;20(1):21–36. [Google Scholar]
- 21.Tennenhouse D. Intel's open collaborative model of industry-university research. Res. Technol. Manag. 2004;47(4):19–26. doi: 10.1080/08956308.2004.11671637. [DOI] [Google Scholar]
- 22.Zhou R., He Z., Lu X., et al. Applying deep learning in the training of communication design talents under university-industrial research collaboration. Front. Psychol. 2021;12 doi: 10.3389/fpsyg.2021.742172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Nie Y., Wang H., Liu B., et al. Research on construction of high-quality application-oriented talent cultivation system for internet of things engineering: based on educational psychology. Front. Psychol. 2022;13 doi: 10.3389/fpsyg.2022.921840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Liao S., Zhao C., Chen M., et al. Innovative strategies for talent cultivation in new ventures under higher education. Front. Psychol. 2022;13 doi: 10.3389/fpsyg.2022.843434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Luo Y., An Z. Research on self-learning system with “internet plus education” innovative talents education mode under big data background. Comput. Appl. Eng. Educ. 2022 doi: 10.1002/cae.22525. [DOI] [Google Scholar]
- 26.Lockee B.B. Online education in the post-COVID era. Nature Electronics. 2021;4(1):5–6. doi: 10.1038/s41928-020-00534-0. [DOI] [Google Scholar]
- 27.Ma Y. Simulation of the training path of film creation talents based on artificial neural network. Soft Comput. 2023 doi: 10.1007/s00500-023-08656-1. [DOI] [Google Scholar]
- 28.Tang Z. Research on cultivation of innovative talents in colleges and universities based on fuzzy evaluation model. Wireless Commun. Mobile Comput. 2022;2022 doi: 10.1155/2022/6373351. [DOI] [Google Scholar]
- 29.An H., Xu Y. Cultivation of entrepreneurial talents through virtual entrepreneurship practice in higher education institutions. Front. Psychol. 2021;12 doi: 10.3389/fpsyg.2021.690692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zhao X., Wang X. The influence of college entrepreneurship education system on the cultivation of applied innovative talents. Front. Psychol. 2022;13 doi: 10.3389/fpsyg.2022.844234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Pock A.R., Durning S.J., Gilliland W.R., et al. Post-carnegie II curricular reform: a north American survey of emerging trends & challenges. BMC Med. Educ. 2019;19(1):260. doi: 10.1186/s12909-019-1680-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tikkanen L., Pyhältö K., Pietarinen J., et al. Lessons learnt from a large-scale curriculum reform: the strategies to enhance development work and reduce reform-related stress. J. Educ. Change. 2020;21(4):543–567. doi: 10.1007/s10833-019-09363-1. [DOI] [Google Scholar]
- 33.Zhang H., Su S., Liu Y. Higher education talents strategy in the context of regional talent hub construction: textual analysis and endosymbiotic cooperation model. Sage Open. 2023;13(1) doi: 10.1177/21582440231156152. [DOI] [Google Scholar]
- 34.Eissa R., Eid M.S., Elbeltagi E. Current applications of game theory in construction engineering and management research: a social network analysis approach. J. Construct. Eng. Manag. 2021;147(7) doi: 10.1061/(ASCE)CO.1943-7862.0002085. [DOI] [Google Scholar]
- 35.Lv J., Lin M., Zhou W., et al. How PPP renegotiation behaviors evolve with traffic changes: evolutionary game approach. J. Construct. Eng. Manag. 2021;147(5) doi: 10.1061/(ASCE)CO.1943-7862.0002024. [DOI] [Google Scholar]
- 36.Simon H.A. Harper & Brothers; New York: 1960. The New Science of Management Decision. [DOI] [Google Scholar]
- 37.Smith J.M., Price G.R. The logic of animal conflict. Nature. 1973;246(5427):15–18. doi: 10.1038/246015a0. [DOI] [Google Scholar]
- 38.Taylor P.D., Jonker L.B. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978;40(1–2):145–156. doi: 10.1016/0025-5564(78)90077-9. [DOI] [Google Scholar]
- 39.You M., Li S., Li D., et al. Evolutionary game analysis of coal-mine enterprise internal safety inspection system in China based on system dynamics. Resour. Pol. 2020;67 doi: 10.1016/j.resourpol.2020.101673. [DOI] [Google Scholar]
- 40.Babu S., Mohan U. An integrated approach to evaluating sustainability in supply chains using evolutionary game theory. Comput. Oper. Res. 2018;89:269–283. doi: 10.1016/j.cor.2017.01.008. [DOI] [Google Scholar]
- 41.Wu B., Liu P., Xu X. An evolutionary analysis of low-carbon strategies based on the government–enterprise game in the complex network context. J. Clean. Prod. 2017;141:168–179. doi: 10.1016/j.jclepro.2016.09.053. [DOI] [Google Scholar]
- 42.Xie H., Wang W., Zhang X. Evolutionary game and simulation of management strategies of fallow cultivated land: a case study in hunan province, China. Land Use Pol. 2018;71:86–97. doi: 10.1016/j.landusepol.2017.11.050. [DOI] [Google Scholar]
- 43.Li W., Lu C., Zhang Y.-W. Prospective exploration of future renewable portfolio standard schemes in China via a multi-sector CGE model. Energy Pol. 2019;128:45–56. doi: 10.1016/j.enpol.2018.12.054. [DOI] [Google Scholar]
- 44.Xue Q., Zhou L., Hao J., et al. HCI International 2018–Posters’ Extended Abstracts: 20th International Conference, HCI International 2018, Las Vegas, NV, USA, July 15-20, 2018, Proceedings, Part III 20. Springer; 2018. The research on the benefit of telemedicine to human based on evolutionary game theory; pp. 318–333. [DOI] [Google Scholar]
- 45.Gong C., Tang K., Zhu K., et al. An optimal time-of-use pricing for urban gas: a study with a multi-agent evolutionary game-theoretic perspective. Appl. Energy. 2016;163:283–294. doi: 10.1016/j.apenergy.2015.10.125. [DOI] [Google Scholar]
- 46.Leydesdorff L., Meyer M. The triple helix of university-industry-government relations. Scientometrics. 2003;58(2):191–203. doi: 10.1023/A:1026276308287. [DOI] [Google Scholar]
- 47.Etzkowitz H., Leydesdorff L. The dynamics of innovation: from national systems and “mode 2” to a triple helix of university–industry–government relations. Res. Pol. 2000;29(2):109–123. doi: 10.1016/S0048-7333(99)00055-4. [DOI] [Google Scholar]
- 48.Etzkowitz H. second ed. Routledge; London ; New York: 2018. The Triple Helix: University-Industry-Government Innovation and Entrepreneurship. [Google Scholar]
- 49.Friedman D. Evolutionary games in economics. Econometrica. 1991;59(3):637–666. doi: 10.2307/2938222. [DOI] [Google Scholar]
- 50.Li R., Fang W. University-industry-government relations of the ministry of industry and information technology (MIIT) universities: the perspective of the mutual information. PLoS One. 2019;14(2) doi: 10.1371/journal.pone.0211939. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analyzed in this study.