Confounded exposure metrics

Exposure‐response (E‐R) modeling frequently relies on the use of exposure metrics that summarize drug concentrations over time. We present simulations to demonstrate that certain commonly used exposure metrics, including average concentration up to an event time, are likely to lead to causal confounding under the very conditions that motivate their use.

Exposure‐response (E‐R) analysis modeling strategies are varied and often specific to the type of data collected in a trial. ¹ One typical and important consideration is the choice of summary exposure metric. Although models for the dynamic effects of time‐varying exposure generally permit a broader range of questions to be addressed, models using time‐aggregated summaries of exposure are often preferred for their simplicity.

One common choice of time‐aggregated exposure metric is average exposure until the event, Cavg_TE. This metric may be computed by taking the area under the curve (AUC) up to the time of event, AUC_TE, and dividing by the time of the event TE, resulting in CavgTE = AUC_TE / TE. This choice of exposure metric is generally motivated by a desire to leverage all relevant dosing and pharmacokinetic (PK) data until the event. In contexts involving dose adjustments and/or dose holidays, average concentration up to an event time (C _avgTE) may seem intuitively preferable to, for example, average concentration over the first dosing cycle (C _avgC1), or average concentration at steady‐state (C _avg,ss), both of which are insensitive to the particularities of individual dosing histories.

Exposure metrics that depended on event times or responder status have been used in recent analyses and regulatory submissions. For example, in an analysis of cabozantinib, dose modifications throughout the trial justified the use of C _avgTE in a survival analysis to show E‐R relationship for several safety end points as a function of cabozantinib exposure. ² In a slight variation, a regulatory submission for selinexor used the average dose to the event and estimated clearance to derive a “time‐averaged” AUC. ³ One of the exposure metrics considered in a regulatory filing of inotuzumab ozogamicin was C _avgTE over the time interval of treatment, which partially depended on AEs. ⁴

Unfortunately, the intuitive appeal of C _avgTE is misleading. As we demonstrate in the following simulation, the very conditions that motivate the use of such a metric (i.e., dosing patterns leading to higher or lower average exposures over time) are also conditions that will generate spurious associations between exposure and response.

To illustrate this point, we simulated a time‐to‐event response with no causal dependence on exposure, concentration, or other covariates and then analyzed (as categorical and continuous time‐to‐event end points) the simulated data using C _avgTE or average concentration in the first cycle (C _avgC1) exposure metrics. The PK data were simulated from a two‐compartment model using mrgsolve ⁵ with interindividual variability on clearance and no covariate effects. The PK parameters were chosen such that accumulation was negligible. The dose level was the same for all dose events and all patients, with a 3‐week dosing cycle. Response data were simulated using a Weibull distribution for 75% of the patients, and the remaining 25% of the patients were assigned to not have the event. After six cycles (147 days), all patients were administratively censored. The simulations were analyzed graphically, with Kaplan–Meier curves, and with logistic regression, which is available on the linked GitHub repository (https://github.com/metrumresearchgroup/confounded‐exposure‐metrics).

The distribution used to simulate the time‐to‐event response had no covariate effects nor random interindividual variability. The distribution had the highest hazard at the beginning of the trial, and then monotonically decreased (Figure 1b). Initially, high hazard rates unrelated to study drug exposure can and do occur for many AEs, for example, when studies are designed to enroll participants following acute events, when the standard of care treatment in a trial of combination therapy entails short‐term risks, or when unobserved characteristics of patients affect the baseline hazard.

FIGURE 1.

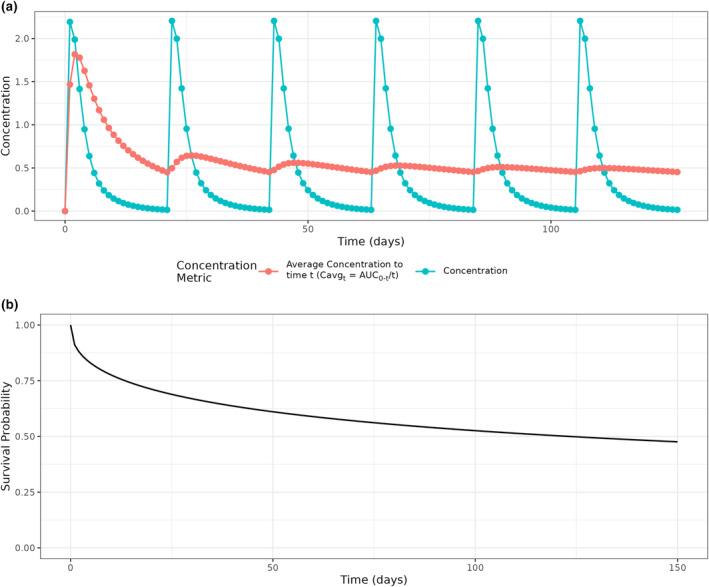
Simulation design. (a) Concentration‐time curve for a typical patient, and the average concentration (C _avg,t = AUC_0−t /t) from time zero, which is C _avgTE if an event were to occur at a specific time, t. (b) Survival curve for simulating event times for all patients, which is independent of concentration and has no covariate effects.

To illustrate how C _avgTE changes as a function of time, the average concentration from time zero through time t (C _avg,t ), or equivalently total area under the concentration curve divided by time (C _avg,t = AUC_0‐t /t), was derived for the typical patient at a grid of event times t (Figure 1a). For example, at t = 21 days, C _avg21 is C _avgC1. Two distinct trends are notable. Within each dosing cycle C _avg,t is highest near the start of the cycle and decreases over time. Overall, the highest values of C _avg,t are observed in the beginning of the first cycle.

A scatterplot of C _avgTE versus time to the event had a clear relationship between C _avgTE and event time when exposures were high, or the event time was small (Figure 2a). Continuing the hypothetical analysis, Kaplan–Meier plots stratified by C _avgTE quartile show a clear separation across the exposure groups, especially for the highest quartile of exposure (Figure 2b). A logistic regression using only C _avgTE as a predictor, that is, no covariates, also showed a clear relationship with the predicted probability of an event, ranging from ~0.1 at the lower range of exposure to ~0.9 at the highest exposures (Figure 2c). All three analysis strategies led to the same conclusion, that higher C _avgTE was associated with shorter time to the event and a higher event probability, and in 1000 replications, the true (null) causal effect was never contained inside the 95% confidence interval. Because C _avgTE was used as the exposure metric, this result would likely be interpreted as “higher exposures cause higher event rates,” with corresponding consequences for future planning and regulatory interactions. Such a conclusion is incorrect because, by design, the true causal relationship was null (flat).

FIGURE 2.

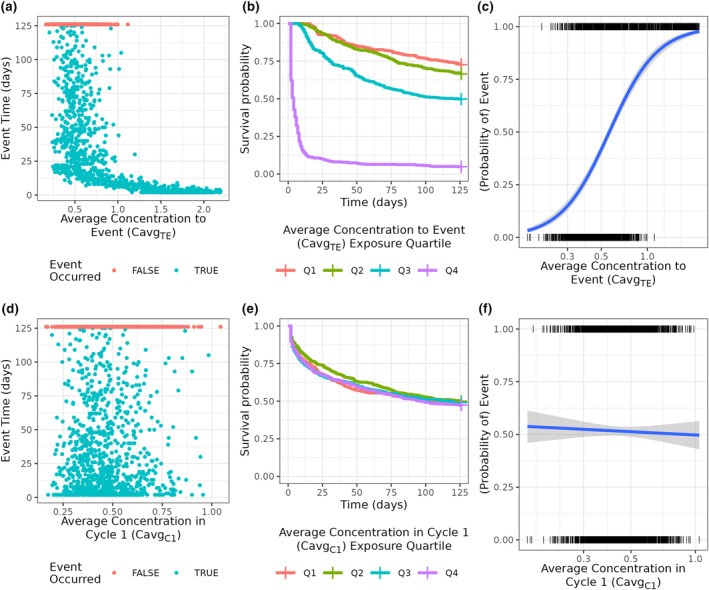
Simulation and analysis results by exposure metric used. (a–c) Analyses using average concentration to the event (C _avgTE) as the exposure metric, which show an exposure‐response (E‐R) relationship resulting from using the outcome to derive exposure. (d–f) Analyses using cycle 1 average concentration (C _avgC1) as the exposure metric, which correctly does not show an E‐R relationship. In (d) and (f) the blue line is a logistic regression fit with a 95% confidence interval.

However, using C _avgC1 led to an unbiased conclusion of the E‐R relationship. The scatterplot between C _avgC1 and event time correctly showed no association (Figure 2d). The Kaplan–Meier curves were essentially identical (Figure 2e), and the logistic regression had a negligible relationship between C _avgC1 and the probability of an event (Figure 2f). These analyses would correctly lead to the conclusion that there is no E‐R relationship. We note that use of C _avgC1 is consistent with the recommendations in Dai et al. ⁶ and Ruiz‐Garcia et al. ¹

The above‐illustrated problem with C _avgTE cannot be diagnosed using standard statistical model fit or model comparison criteria. For example, in the presence of two competing models (one using C _avgTE and one using C _avgC1), a natural approach would be to use both qualitative and quantitative model evaluation tools. For the two logistic regression models, the model using C _avgTE had an Akaike information criterion (AIC) of 2046 and the model using C _avgC1 had an AIC of 2774, indicating that using C _avgTE leads to a better fit of the data despite leading to the wrong causal conclusion.

Moreover, it is not even logically possible to correctly create certain simulation‐based diagnostics, such as Visual Predictive Checks when using C _avgTE. The required simulation logic in this case would be circular: exposure depends on when the event happens, and the latter is unknown because it can only be simulated with knowledge of the exposure. The logical impossibility of constructing such a simulation is in itself an indication that the causal question has not been properly formulated.

To build an intuition of why C _avgTE led to a biased conclusion, one may imagine two patients with identical longitudinal concentration data, but different event times. These patients will have different C _avgTE because their event times are different. One would never use the outcome as a covariate in an E‐R model, yet indirectly this is the logic when using C _avgTE. In other words, the outcome caused the exposure in the analysis instead of having the exposure cause the outcome, and the predicted probability of an outcome will be different only because their observed outcomes were different. This is a specific example of an explanatory variable that depends on the outcome, thereby introducing a spurious association between cause and effect. ⁷

Furthermore, such confounding is not limited to average concentration metrics. The same principle of conditioning on the outcome applies in other circumstances. For example, consider a drug that accumulates after each dose and maximum concentration (C _max) is the exposure metric. C _max will increase cycle by cycle because of the accumulation, so longer event times will be associated with higher exposures. Again, information about the event time was used to determine the time window for computing C _max, and therefore bias is introduced (see the GitHub repository for a simulation example).

More broadly, it has been recognized that E‐R modeling can be subject to bias due to causal confounding; for example, in the presence of unmeasured or unmodeled confounders ⁶ and immortal time bias. ⁸ , ⁹ The choice of exposure metric is another such way bias can be introduced into the analysis, as demonstrated by the preceding simulation.

Although non‐null causal relationships were not specifically considered here, the null scenario is sufficient to convincingly demonstrate that analyses based on C _avgTE are problematic. As we have shown, a non‐null association with C _avgTE is not evidence of a non‐null causal effect—a sufficiently damning analysis property in itself. Neither have we considered scenarios where multiple dose levels are available. Multiple randomized dose levels would be expected to mitigate causal bias in any exposure‐response analysis; nonetheless it would be ill‐advised to knowingly introduce analytic bias only to hope that experimental design will provide a cure for the self‐inflicted wound.

C _avgTE should be understood a priori as an exposure metric that will lead to biased analyses. Whereas there are conditions under which it will be unbiased, these are the very same conditions that would make C _avgC1 or C _avg,ss an equally valid metric, that is, scenarios with no average temporal trends in exposure. Instead, as a general approach, we suggest using exposure metrics that clearly do not depend on the outcome or intercurrent events, for example, C _avgC1, thinking clearly about how specific drug development questions lead to appropriate exposure metrics, or alternatively using models that avoid the use of summary measures of exposure altogether and instead model the dynamic effects of time‐varying exposure, as described in Ruiz‐Garcia et al. ¹ , ¹⁰ A simple rule of thumb is: “if you can't in principle simulate responses using your exposure metric, choose a different exposure metric.”

FUNDING INFORMATION

No funding was received for this work.

CONFLICT OF INTEREST STATEMENT

The authors declared no competing interests for this work. As an Associate Editor for CPT: Pharmacometrics & Systems Pharmacology, Jonathan L. French was not involved in the review or decision process for this paper.

Supporting information

Figure S1

Wiens MR, French JL, Rogers JA. Confounded exposure metrics. CPT Pharmacometrics Syst Pharmacol. 2024;13:187‐191. doi: 10.1002/psp4.13074