PopShift: A Thermodynamically Sound Approach to Estimate Binding Free Energies by Accounting for Ligand-Induced Population Shifts from a Ligand-Free Markov State Model

Abstract

Obtaining accurate binding free energies from in silico screens has been a long-standing goal for the computational chemistry community. However, accuracy and computational cost are at odds with one another, limiting the utility of methods that perform this type of calculation. Many methods achieve massive scale by explicitly or implicitly assuming that the target protein adopts a single structure, or undergoes limited fluctuations around that structure, to minimize computational cost. Others simulate each protein–ligand complex of interest, accepting lower throughput in exchange for better predictions of binding affinities. Here, we present the PopShift framework for accounting for the ensemble of structures a protein adopts and their relative probabilities. Protein degrees of freedom are enumerated once, and then arbitrarily many molecules can be screened against this ensemble. Specifically, we use Markov state models (MSMs) as a compressed representation of a protein’s thermodynamic ensemble. We start with a ligand-free MSM and then calculate how addition of a ligand shifts the populations of each protein conformational state based on the strength of the interaction between that protein conformation and the ligand. In this work we use docking to estimate the affinity between a given protein structure and ligand, but any estimator of binding affinities could be used in the PopShift framework. We test PopShift on the classic benchmark pocket T4 Lysozyme L99A. We find that PopShift is more accurate than common strategies, such as docking to a single structure and traditional ensemble docking—producing results that compare favorably with alchemical binding free energy calculations in terms of RMSE but not correlation—and may have a more favorable computational cost profile in some applications. In addition to predicting binding free energies and ligand poses, PopShift also provides insight into how the probability of different protein structures is shifted upon addition of various concentrations of ligand, providing a platform for predicting affinities and allosteric effects of ligand binding. Therefore, we expect PopShift will be valuable for hit finding and for providing insight into phenomena like allostery.

I. Introduction

Developing strategies to accelerate and simplify hit discovery in drug development is one of the core foci of computational chemistry. Because huge arcs of chemical space must be subtended, methods that scale well per ligand predominate.¹ Most of these methods are based on docking a set of compounds to a single protein structure as rapidly as possible to maximize the chemical space that can be considered. The scores predicted by these methods correlate so poorly with true binding affinities that they are typically judged by how much the high scoring compounds are enriched for tight binders compared to randomly selected compounds.^2,3 Of course, a wide range of methods have been developed to make different trade-offs between speed and accuracy. Of these, alchemical free energy calculations are some of the most physically rigorous and should, in principle, be capable of quantitatively accurate predictions.^4,5 However, routinely achieving quantitative predictions with any method remains difficult.⁶

One striking feature of all of these methods is the extent to which they assume proteins adopt a limited set of highly similar structures. Many docking algorithms do not include any protein conformational heterogeneity. The cross docking problem highlights the limitations this assumption imposes (i.e., docking a library of compounds against a protein structure obtained by removing a ligand from a ligand-bound structure is more predictive than docking against a structure obtained in the absence of ligand).⁷ To address this, some docking algorithms allow limited protein flexibility such as rotations of side-chains. However, many do not find that incorporating conformational heterogeneity in this way is worth the additional computational cost.⁸ In principle, alchemical free energy calculations should be able to deal with protein conformational heterogeneity, as every degree of freedom is allowed to move as dictated by the force field. However, in practice, alchemical free energy simulations are so short that the protein only undergoes limited fluctuations around the starting structure.⁹ Phrased differently, ignoring receptor conformational heterogeneity for the sake of computational performance is one of the key approximations of most digital screening campaigns.

Ensemble docking has emerged as a strategy to address protein conformational heterogeneity but still faces significant limitations.¹⁰ In ensemble docking, one generates a set of protein structures (often via molecular dynamics simulations) and then docks a library of compounds against each of these structures. Typically, one then ranks the compounds based on their best score against any protein structure, though there are other flavors of ensemble docking. While this ensemble docking approach recognizes that there is uncertainty in which protein structure is relevant, it still essentially assumes that a single structure is relevant in the end. It also throws out thermodynamic information from the simulations, instead giving all of the protein structures equal weight. These methods are still generally incapable of quantitative predictions and suffer from some strange pathologies. For example, it has been reported that ensemble docking against short simulations outperforms docking to a single structure but that adding more simulation data often hurts performance rather than helping.¹⁰⁻¹³ Other efforts to include conformational heterogeneity into docking have included the existence of multiple conformations using some assessment of their relative abundance, but have done so in an ad-hoc fashion.^14,15

Here, we propose a reweighting approach called PopShift, schematically depicted in Figure 1, that uses Markov state models (MSMs) of a ligand-free protein to account for the populations of different protein structures and how they are shifted upon binding to a ligand. PopShift builds on the numerous successes of simulations of apo proteins in capturing rare conformational changes. For example, we have predicted and experimentally confirmed cryptic pockets formed by motions ranging from side chain displacements to displacements of entire secondary structural elements.^14,16−18 MSMs can be viewed as a compressed representation of the system’s thermodynamic ensemble.¹⁹ Thus, MSMs representing the ligand-free protein ensemble contain all the receptor information needed to estimate ligand binding.²⁰ In order to weight the contribution of state populations in the apo context versus how tightly they bind ligand, we estimate binding to representative conformations from each state, obtaining a per-state binding free energy by averaging them. We then combine these using an “over parts” approach analogous to that used in Jayachandran, Shirts, Park, and Pande²¹ to combine these per-state affinities with weights from a ligand free MSM. Thus, instead of taking the best score against any structure, as in traditional ensemble docking, we take a correctly weighted average over all structural states. This is made tractable by the MSM, since it means we only need one or, to be more confident, a handful of binding estimates per MSM state. A related idea that treats affinity per conformation using the same math, but does not leverage an MSM to index conformational heterogeneity, is the Implicit Ligand Theory.^22,23

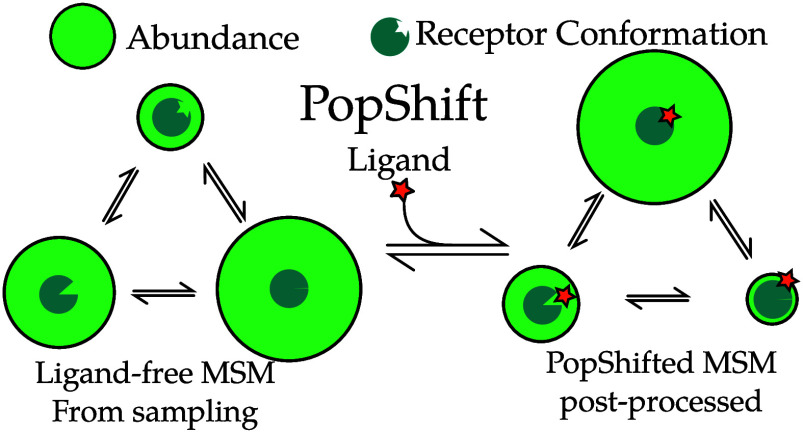
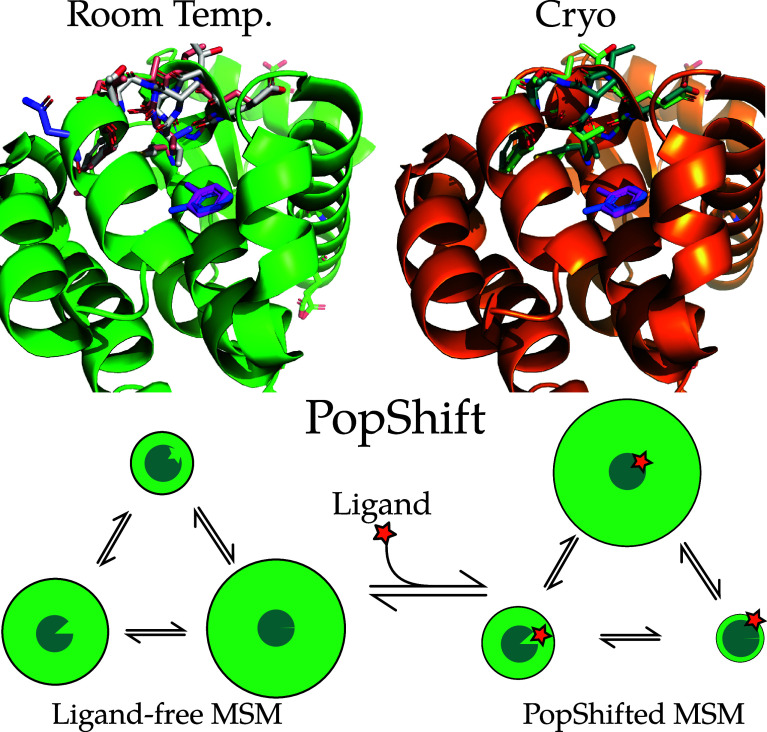
Figure 1.

Examples of conformational heterogeneity in the T4 lysozyme and a schematic of how PopShift accounts for this heterogeneity. These renders show the multiple conformations even the L99A pocket bound to toluene is capable of accessing under crystallographic study. The top section shows the room temperature structure (PDB 7L39) and a cryogenic structure from the same study (PDB 7L3A). All residues with alternative locations in the F-helix, and also toluene, are shown in sticks. Extensive alternative locations are present in both, even though this protein is reckoned to be rigid and to bind simple, largely rigid, fragments. Note that the two alternative locations for the ligand are nearly identical at both temperatures. Nearly every residue in the critical F-helix shows heterogeneity, centered on valine 111, which extends down toward the toluene. The lower panel shows a schematic of the PopShift method, showing MSM populations from a ligand free ensemble being biased by varying degrees of ligand affinity to those states to approximate the ligand-bound ensemble. The sea-blue pac-man represents the protein, with three states in equilibrium, green circle sizes indicating abundance, and the shape cut out of the pac-man representing varying degrees of pocket accessibility to the ligand, which is schematically represented by a star.

By capturing how ligands shift the relative probabilities of different protein conformations, PopShift also provides an opportunity to understand how ligands remodel their binding sites or even allosterically impact distant sites. Population-shift in response to ligand binding is, by definition, allostery. If the ligand-free MSM is a compressed representation of the perturbed model’s ensemble, then the reweighted MSM is a compressed representation of the receptor’s liganded ensemble. Thus, observables of interest can be estimated with the reweighted state probabilities to understand the allosteric mechanism. Because the expression for reweighted state probabilities includes ligand concentration, the impact on these averages can also be used to compute an EC50.

To test PopShift, we compare its performance to several other candidates on a simple-yet-subtle benchmark for protein–ligand binding, T4 Lysozyme L99A. Because this system has received extensive study over the years the field has accepted it as a first-pass benchmark for many computational protein–ligand binding methods, despite certain drawbacks (notably the poor dynamic range inherent in the ligands that have actually received ITC affinity validation).²³⁻²⁵ Indeed the literature on this receptor is deep, with quality work on the heterogeneity of the receptor and the impact this has on binding reiterated especially in the last 10 years by the Minh, Mobley, Fischer, and Shoichet groups, among others.^1,23,26,27

From a set of apo simulations we build an MSM. We then sample conformations from each MSM state, and dock to them, using the customary organic fragments from Morton, Baase, and Matthews.²⁸ We use the docking score as a heuristic for the free energy of binding to a particular conformation. We recognize that docking has severe limitations, especially for ligands with rotatable bonds. However, docking provides a simple and highly relevant starting point given its widespread use in drug discovery, and the fragments we consider here are not subject to the known issues with rotatable bonds. In the future, it will be interesting to try alternatives to docking in the PopShift framework. In PopShift, the free energies of binding are then incorporated into an affinity estimate and reweighted state probabilities. We compare these strategies to best-score docking, docking to holo crystal structures with the ligand removed, and absolute binding free energy calculations performed in the customary style with docked and hand-adjusted starting poses. We also explore how the conformational preferences of the protein are altered by the addition of ligand.

II. Results and Discussion

II.A. PopShift Performs Well Compared to Alternative in Silico Estimators of Binding Free Energies

We reasoned that modern simulations are sufficiently predictive that both structures from these simulations and their populations can inform a successful hit finding strategy.²⁹ In particular, MSMs provide a powerful and quantitatively predictive map of a protein’s conformational ensemble and therefore approximate its partition function. Thus, we hypothesized that using the populations from an MSM in an “over parts”^21,30 approach—with the MSM supplying the state populations—would allow correct incorporation of docking scores from across this sample.

To test this hypothesis, we collected three replica simulation data sets of L99A, made MSMs from them, and estimated binding affinities using PopShift and other popular alternatives. Each replica consisted of 10 simulations, 5 × 4 μs and 5 × 8 μs, started from PDB 187L with the ligand (p-xylene) removed. One MSM was made for each replica data set using TICA³¹ on the pocket residue backbone and side chain torsions, and VAMP-2³² to validate the number of clusters for k-means as has been done in Meller, Lotthammer, Smith, Novak, Lee, Kuhn, Greenberg, Leinwand, Greenberg, and Bowman.¹⁸ We docked ligands from the classic Morton, Baase, and Matthews²⁸ set against structures from each MSM state using the SMINA docking algorithm.³³ Macroscopic binding affinities were estimated using the PopShift framework; see methods (Section IV). For comparison to extant approaches, we used the conventional ensemble docking approach of taking the best score across a set of samples, and of docking compounds of interest to a holo crystal structure with ligand removed. We also performed absolute binding free energy simulations using a vanishing ligand transformation from initial hand-selected ligand poses.

We find that PopShift performs well compared to alternative docking approaches and even showed some advantages compared to alchemical free energy calculations (Figure 2). Docking each ligand to a single holo structure (the n-butylbenzene structure, PDB 186L) and then taking the minimized score as an affinity estimate gives a poor correlation to experimentally measured binding affinities and poor accuracy, as measured by the root mean squared error (RMSE) from experimental results. PopShift also outperforms simply taking the best score, a traditional ensemble docking approach, most notably for ranking. The best-score approach systematically predicts affinities that are too favorable. Although using docking to a ligand-removed crystal structure’s scores as affinity estimates exhibited slightly better correlation with experiment on this data set than the best-score approach, these scores emanating from a lone structure exhibited a similar pattern of overly favorable affinity estimates.

Figure 2.

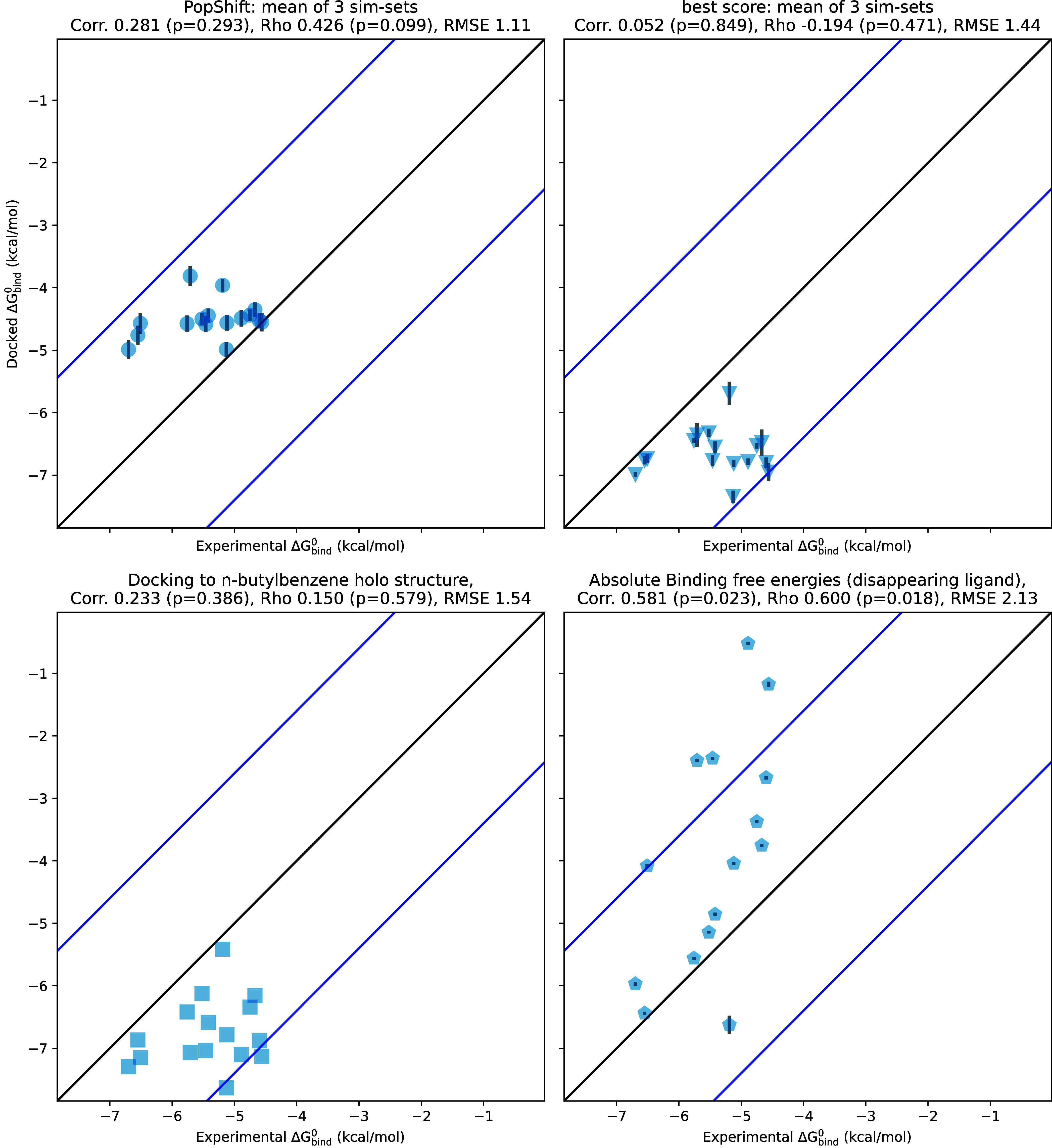
PopShift compares well to alternative predictors, such as docking to a single crystal structure, traditional “best score” ensemble docking, and alchemical free energy calculations. The x values are the experimental binding free energies for 17 ligands as measured by ITC in Morton, Baase, and Matthews.²⁸ The y values are the binding free energy estimated by each in silico method given in the panel title. Correlation is the Pearson’s correlation coefficient, rho is Spearman’s ranking coefficient, and RMSE is the root-mean-squared error in kcal/mol. The error bars on the top two panels are the standard uncertainty in the mean across the three replica data sets. The error bars on the ABFE points are those provided by alchemlyb/pymbar. Black and blue lines are visual guides and represent the 1–1 line and 2k_BT deviated values, respectively.

Absolute binding free energy estimates produced the strongest correlation and ranking results but struggled with accuracy. This is likely related to initial poses and receptor conformations failing to relax fully in the course of the windowed simulations. This interpretation is complicated by our use of the docking energy function to make affinity estimates, which is very different from the force field we used to obtain the MSM we dock to. Because docking to many samples from an MSM allows us to estimate affinity to many receptor conformations, it sidesteps the issue of having to choose a “most relevant” one to start from. This is especially important if there may be multiple thermodynamically relevant poses for the ligand.²⁷

The dynamic range of our reference data presented in Figure 2 is a concern. Given the lower RMSE for PopShift and the small dynamic range of the experimental data, it is not surprising that the RMSE when using the average PopShift prediction as an estimate for each ligand is also low (1.12). However, the value of Spearman-ρ for PopShift’s predictions suggests the method has ranking power, whereas guessing a single value for each ligand would give a ρ of zero, which is essentially what we see for the best score and holo crystal docking approaches.

Making predictions for other ligands also confirms that PopShift is not merely predicting a constant plus noise that happens to be in the right ballpark for every ligand. If experimentally measured affinities were available, we would have added these ligands ITC data taken at a particular temperature is limited for this ligand—the largest collection of these coming from the data set presented in Figure 5, from Morton, Baase, and Matthews.²⁸ The change in melting temperature induced by a broader array of ligands has been collected from several other studies by Xie, Nguyen, and Minh.²³ While we cannot directly compare our predicted affinities to these changes in melting temperature, we did predict affinities for this set of ligands and obtained predictions ranging from −5.45 to −1.15 kcal/mol. These results demonstrate that PopShift does not merely predict the same result for every ligand.

Figure 5.

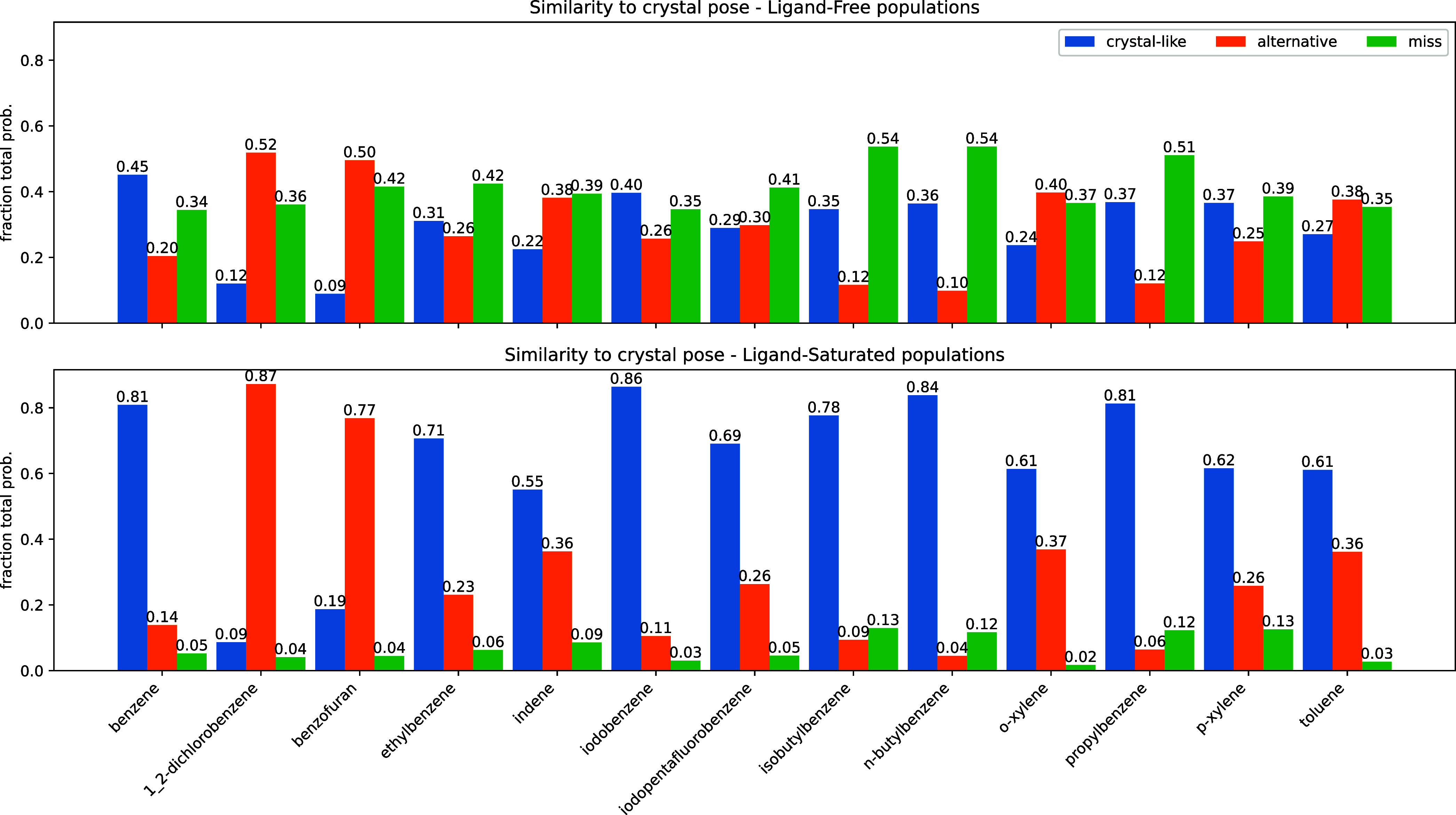
Summary of pose accuracy across all ligands studied. Each grouped bar represents the fraction of ligand poses that fall into the categories “crystal-like”, for within 2 Å symmetry-corrected RMSD³⁵ of the holo crystal structure, “alternative”, for between 2 and 4 Å RMSD from the holo crystal, and “miss”, for poses above 4. As before, the top panel represents the poses with an “apo” ensemble weighting. The lower panel provides pop-shifted reweights for the same data set.

As a further test of whether PopShift is appropriately averaging the per-state estimates of binding free energies, we also tried two additional approaches: (1) the population weighted average docking score (ΔG = ∑_iπ_iΔG_i, which we have previously called Boltzmann docking¹⁴), and (2) using eq 2, but with every state given equal probability instead of using the populations from our MSMs. The first reduction of the docking scores results in absurd values with an RMSE of 6.8 kcal/mol. This is because most states yield a positive docking score, reflecting the abundance of closed states in the apo ensemble. If one fails to account for the fact that binding makes these states exceedingly rare, then these rare complexes unrealistically dominate the prediction. The second reduction yields an RMSE of 1.40 kcal/mol and ablates the correlation to 0.29 with a p-value of 0.28, demonstrating that the equilibrium probabilities from our MSM contribute to the predictive power of PopShift.

Application of PopShift to estimate the affinity of an inhibitor called blebbistatin to a set of different myosin motor domains also supports our claim that the method is predictive.¹⁸ Our estimates of the affinity of that ligand to isoforms of myosin was between −6 and −9 kcal/mol, with an R2 of 0.82 to previous experimental measurements. PopShift also successfully predicted the result of an experiment that we performed after making our prediction. These results again show that PopShift is capable of covering a larger dynamic range than for the small set of lysozyme ligands we focus on in this work and has the potential to match experiment well.

Based on reports of poorer performance of best score aggregation on longer simulations, we were curious to know how sensitive our method is to data set size. We reasoned that larger data sets will typically include some incredibly rare conformation that, when docked to, will give a higher score than anything in a smaller data set. Without correctly accounting for such a conformation’s rarity, this will trend toward worse results with increasing sampling. Phrased differently, the best score approach is an outlier detector that is only in the correct ballpark when—by happenstance—no outlier conformations have been sampled yet. In contrast, more data from longer initial simulations should cause PopShift’s estimate to converge as the simulations do. The aforementioned outlier conformations, when correctly weighted by their rarity, will simply contribute to the overall picture of the ensemble, instead of dominating the prediction.

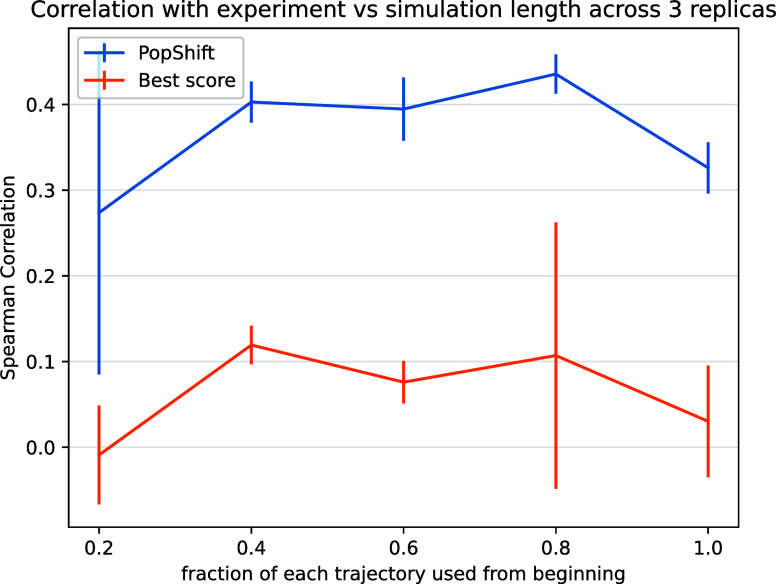
To test this notion, we truncated our data set as a series of fractions (that is, we took the first X% of each trajectory, where X corresponds to the fraction shown) and reran our analysis. Each result based on truncated data was generated by reworking that data set as though it were the full length data set, including featurization and clustering. We then inspected Pearson and Spearman correlations as a function of data set size (Figure 3). As before, we selected 20 frames per state to generate these truncated data sets. We also held cluster count fixed at 75, so that the total number of structures to dock to was not changing: only their diversity as the underlying feature trajectories became more mature and the quality of the MSMs providing the equilibrium population estimates.

Figure 3.

PopShift performs well as one varies the amount of simulation data, whereas traditional “best score” ensemble docking gives worse performance and has greater statistical variation as data is added. The data set used for MSM construction was truncated by taking the indicated fraction from the beginning of each trajectory. This can be viewed as asking the question, “what would happen if simulations had been stopped early?” The error bars arise from the standard uncertainty in the mean across the three replica data sets.

We found that PopShift is less sensitive to the extent of input data than best-score ensemble docking. Because the number of structures docked to is constant across this sweep, it highlights how additional structural heterogeneity is not correctly indexed by simply looking for the most favorable score. As we suspected, the best score gets worse with more data because it detects outliers. In other words, if an ensemble is scored by its most favorable possible interaction with a ligand, the strain or unfavorability of that conformation on the protein is neglected. If one could create an ideal binding site for a ligand by moving residues out of the way such that it has ideal contacts, it would get very favorable docking scores when that conformation was docked to, but in fact the affinity for this site would be quite low because of how badly strained the protein would be by such rearrangements. In contrast, PopShift benefits from having more data, both in terms of the mean correlation with experiment and the statistical certainty in the results. These results also emphasize that at least for macroscopic binding constant estimation, our results for PopShift are not particularly sensitive to the length of input simulations. This is consistent with prior results suggesting that thermodynamic properties of MSMs converge quickly.³⁴ Taken together, this implies that adding conformational heterogeneity to a docking campaign is best done by including a correctly weighted sample of receptor conformations if the objective is ranked estimated affinity prediction.

II.B. PopShift Retrodicts Ligand Poses and Their Relative Abundance

Given the low RMSE between PopShift’s predicted binding free energies and experimental measurements, we hypothesized that the approach also accurately predicts the pose the ligand adopts. Specifically, we reasoned that any ligand likely adopts a wide variety of different poses in different protein conformations from the ligand-free MSM. If PopShift works as intended, protein–ligand structures where the ligand resembles ligand-bound crystal structures should have significant increases in their equilibrium probabilities compared to the same protein structure in the ligand-free ensemble. In this case, the distribution of RMSDs from the reweighted ensemble should be more favorable than the distribution from the original ensemble (i.e., using the state populations from the ligand-free MSM instead of updating the populations based on the strength of the interaction between protein and ligand).

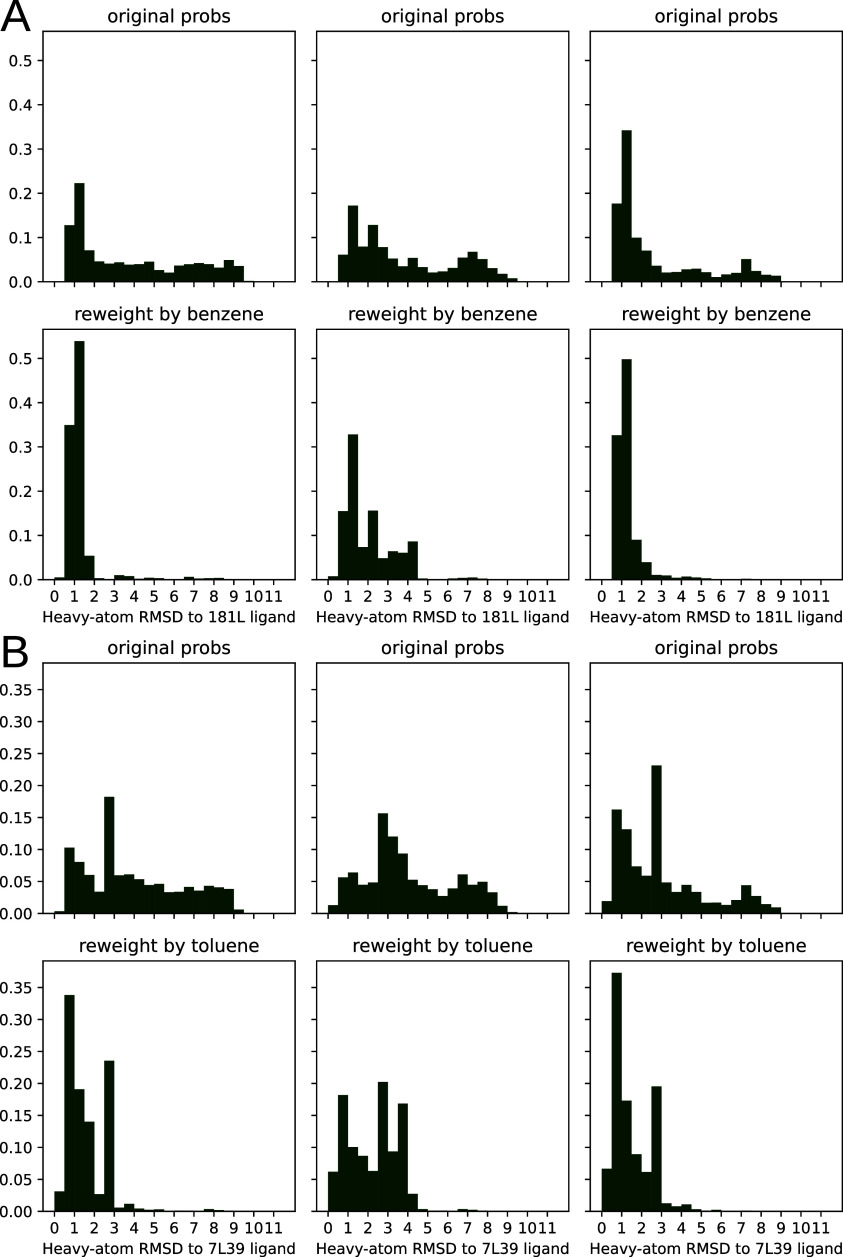
To test our hypothesis, we compared the distribution of RMSDs to the ligand-bound crystal structure before and after reweighting the states based on the interaction with ligand (Figure 4). For each sample from each MSM bin, i, we weighted its apo probability as being π_i/n, where π_i is the equilibrium probability for that bin, and n is the number of samples drawn from each bin. We used eq 5 to estimate each sample’s probability in the presence of a saturating ligand based on the docking score for that particular sample. We aligned based on pocket residue heavy atoms (residues within 5 Å of p-xylene in PDB 186L). RMSDs were then computed across all heavy atoms in the ligands. We plot both histograms for each replica in Figure 4 to convey how reproducible the results are with different sets of simulations.

Figure 4.

Population shift calculated by PopShift correctly favors ligand poses with a low RMSD to the crystal structure. The data histogrammed is the symmetry corrected RMSD³⁵ of the predicted pose to the holo crystal structure, where the structures are superimposed according to an alignment of their pocket atoms but not any ligand atoms. The RMSD histogram here is across all of the heavy atoms after this alignment. For each main panel, the three subpanel columns represent individual replica data sets. The top row provides the ligand-free equilibrium probabilities, and the lower row shows how the population is redistributed in the presence of the ligand. Main panel A provides the data for benzene, while the second panel B provides the data for toluene.

Our results for benzene and toluene show that PopShift does indeed favor low RMSD states compared with the broad heterogeneity in pose RMSDs from the original ensemble (Figure 4, panels for ligand-free populations.) Many states from the ligand-free ensemble are not compatible with the experimentally observed binding pose, resulting in RMSDs between the best scoring pose and the ligand-bound crystal structure over 4 Å. When pose RMSDs were reweighted using pop-shifted equilibrium probabilities at saturating ligand concentrations, the distribution collapses and poses become holo-like. Interestingly, for some ligands, such as toluene (Figure 4, panel B), alternative conformations appear to be present. Given the way crystal structures solved at cryogenic temperatures are known to favor low energy structures and underestimate structural heterogeneity, it is interesting to consider the possibility that the heterogeneity in poses that PopShift predicts for some ligands is real.

To test the generality of our results for the two ligands from Figure 4, we devised a means to judge how closely our predictions agree with experiments across multiple compounds. Because experimental techniques have a hard time describing conformational heterogeneity, it is possible that poses dissimilar to experiment have relevance for the thermodynamic ensemble of the complex. Thus, we chose to use three categories: one for configurations similar to the crystal pose, one for conformations that were dissimilar but likely still in the pocket, and one for conformations with clashes or completely alternative ligand placements. We reasoned this would be reasonably measured by aligning the receptor pockets but transforming the ligands by that alignment.

We binned our histograms into three categories—fraction of samples that are similar to the crystal structure’s pose (RMSD < 2 Å), others that are in some alternative pose but probably still in the binding site (2 ≤ RMSD < 4 Å), and ones that are likely in a very different pose or outside the binding site altogether (RMSD ≥ 4 Å) in Figure 5. We aligned the α-carbons of the pocket residues we used to build our MSMs, and then transformed our predicted ligand poses by that alignment transform. Thus, high-RMSD scores likely emerge from poses that have significant displacements in center of mass—that is, poses that are not properly in the binding pocket. We named the three categories of poses “crystal-like”, “alternative”, and “miss”, as abbreviations of this interpretation.

The pattern we demonstrated for benzene and toluene in Figure 4 is consistent across all the ligands we tested (Figure 5) . Poses we categorize as “miss” are quite common with apo weights, but become rare after reweighting with PopShift. With ligand saturated weights, we often observe alternative poses. It is hard to know whether these conformations exist in solution, but they are probable in the ligand biased ensemble, suggesting that they contribute nontrivially to our estimates of affinity.

II.C. PopShift Predicts How Ligands Change the Abundance of Protein Conformations

Because macroscopic affinities estimated with correctly weighted per-state affinities seem accurate, we reasoned that reweighted state probabilities might also be usefully accurate. We knew that Valine 111’s dihedral angle is able to occupy several rotameric states in apo simulations, but that the distribution is different upon ligand binding.^27,36 Thus, we hypothesized that the broad distribution from our ligand-free MSM should collapse to the binding-compatible one upon reweighting with ligand-saturated populations.

We tested this hypothesis by histogramming valine 111 angles from the receptor structures we sampled, weighted by both apo- and ligand saturated state probabilities (Figure 6). As in Figure 4, we plot both histograms for each replica to convey the reproducibility of our results.

Figure 6.

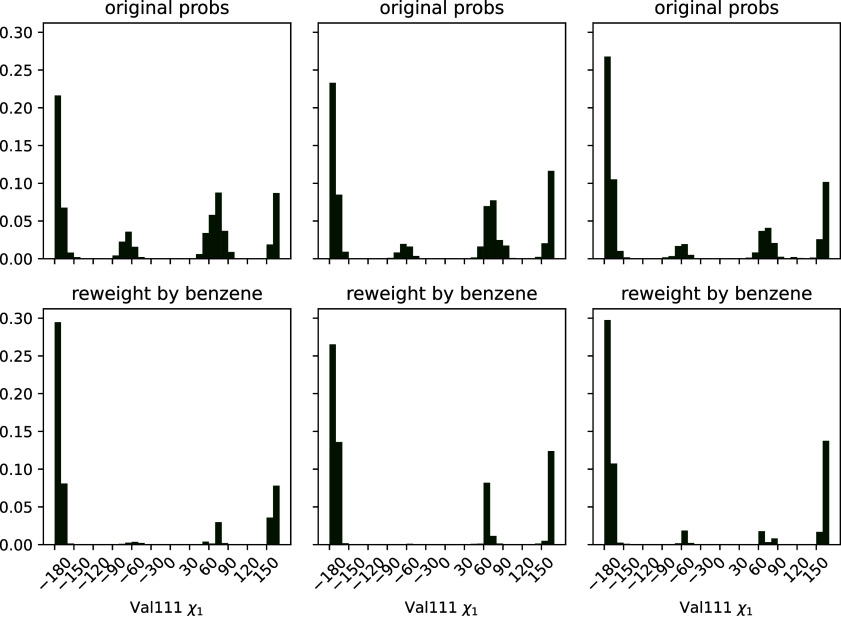
Three alternative conformations of the Val111 χ1 angle in the ligand-free MSM collapse to mostly trans population in the presence of the ligand, in agreement with the dominant pose seen crystallographically. The top row of plots is histograms of the χ1 torsion across the frames sampled from the MSM states, weighted using the ligand-free MSM equilibrium probabilities. The second row displays the same data, but weighted by the benzene-saturated equilibrium probabilities. Each column represents the results from one fully independent replica.

We find that the ligand-free protein broadly populates several different structures, but the ligand shifts the population to favor the trans state, with some population of gauche+. This angle is noted as having many different distributions in RT crystal structures for liganded T4 lysozyme L99A protein.²⁷ Trans is the angle modeled into cryo-structures from previous efforts (PDB ID 181L, 4W52).^28,37 Our plots suggest that, like room-temperature X-ray structures, the ligand-saturated ensemble is heterogeneous but does prefer certain angles, the primary of these being shared with the cryo X-ray structures. Thus, the receptor population has shifted through conformational selection to a binding-compatible ensemble.

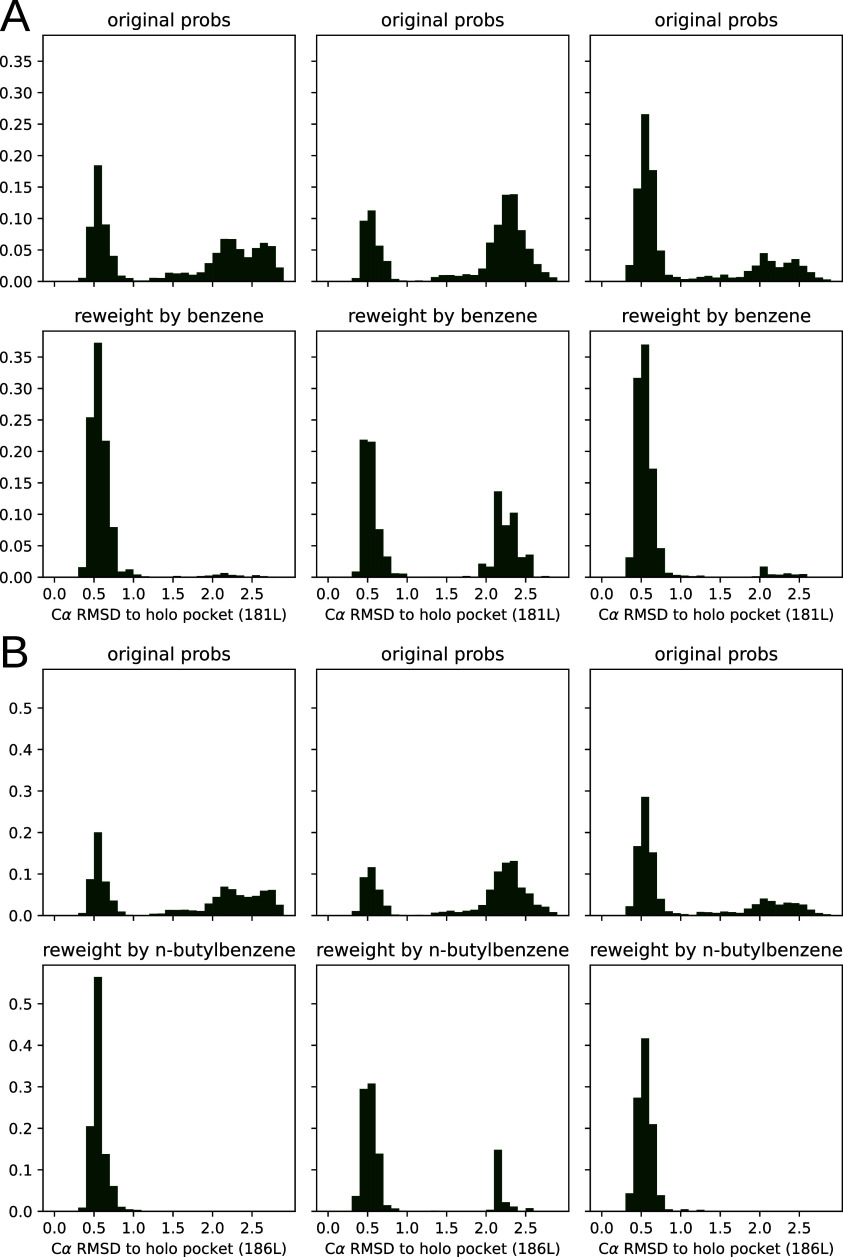
To assay this another way, we also calculated receptor α-carbon RMSD histograms to the cognate crystal structure for pocket residues (see Figure 7). Because the F-helix is known to occupy several different conformations, we reasoned that the distance from the holo structure for a large and a small ligand would be indicative of what conformations are enriched by ligand. We did this for benzene and n-butylbenzene as examples of smaller and larger ligands. We found that in both cases, as with the valine torsion histograms, our broad sampling of pocket conformations collapses to the holo-like structure in the presence of a saturating ligand.

Figure 7.

Population shift calculated by PopShift correctly favors pocket conformations with a low α carbon RMSD for the holo crystal structure. The data histogrammed is the RMSD of the predicted pocket conformation to the holo crystal structure’s pocket, where the structures are superimposed according to an alignment of their pocket atoms but not any ligand atoms. For each main panel, the three subpanel columns represent individual replica data sets. The top row shows the ligand-free equilibrium RMSD distributions and the lower row shows how the population is redistributed in the presence of ligand. Main panel A provides the data for benzene, while main panel B provides the data for n-butylbenzene.

II.D. PopShift Can Estimate Ensemble Features as a Function of Ligand Concentration

Because the histograms from Figure 4 represent unliganded and saturated conformational preferences, respectively, we hypothesized that inspecting the conformational preference as a function of ligand concentration might help with analyzing binding preferences and allosteric effects. We wanted to know at what ligand concentrations certain histogram populations become more prominent since structural features not directly corresponding to ligand binding are often relevant for drug development—particularly in the case of allosteric modulators. For example, we previously identified both activators and inhibitors that bind a cryptic pocket in the protein TEM β-lactamase.¹⁴ Looking at what structures are stabilized/destabilized by a ligand could provide a facile means to predict their effects on the structural preferences of distant sites and, ultimately, on function. If a structural feature were used as a heuristic for some mechanistic action, that feature could be used to compute an EC50.

To display this transition, we computed ligand-rmsd histograms at various ligand concentrations and stacked them by descending ligand concentration as a dilution series. To do this, we recomputed the histograms from Figure 4 using eq 5 with a range of concentrations plugged in for x (see Figure 8). Each histogram-bin’s probability was displayed using color, so that each row in the heatmap corresponds to a particular RMSD histogram at a particular ligand concentration. Bins, and therefore the X axis match those from Figure 4. We covered concentrations ranging from nM—essentially no ligand for these relatively weak binders—to 0.1 M—completely saturating for all the ligands we tried. Our predicted ligand dissociation constants for each replica are marked by an orange line.

Figure 8.

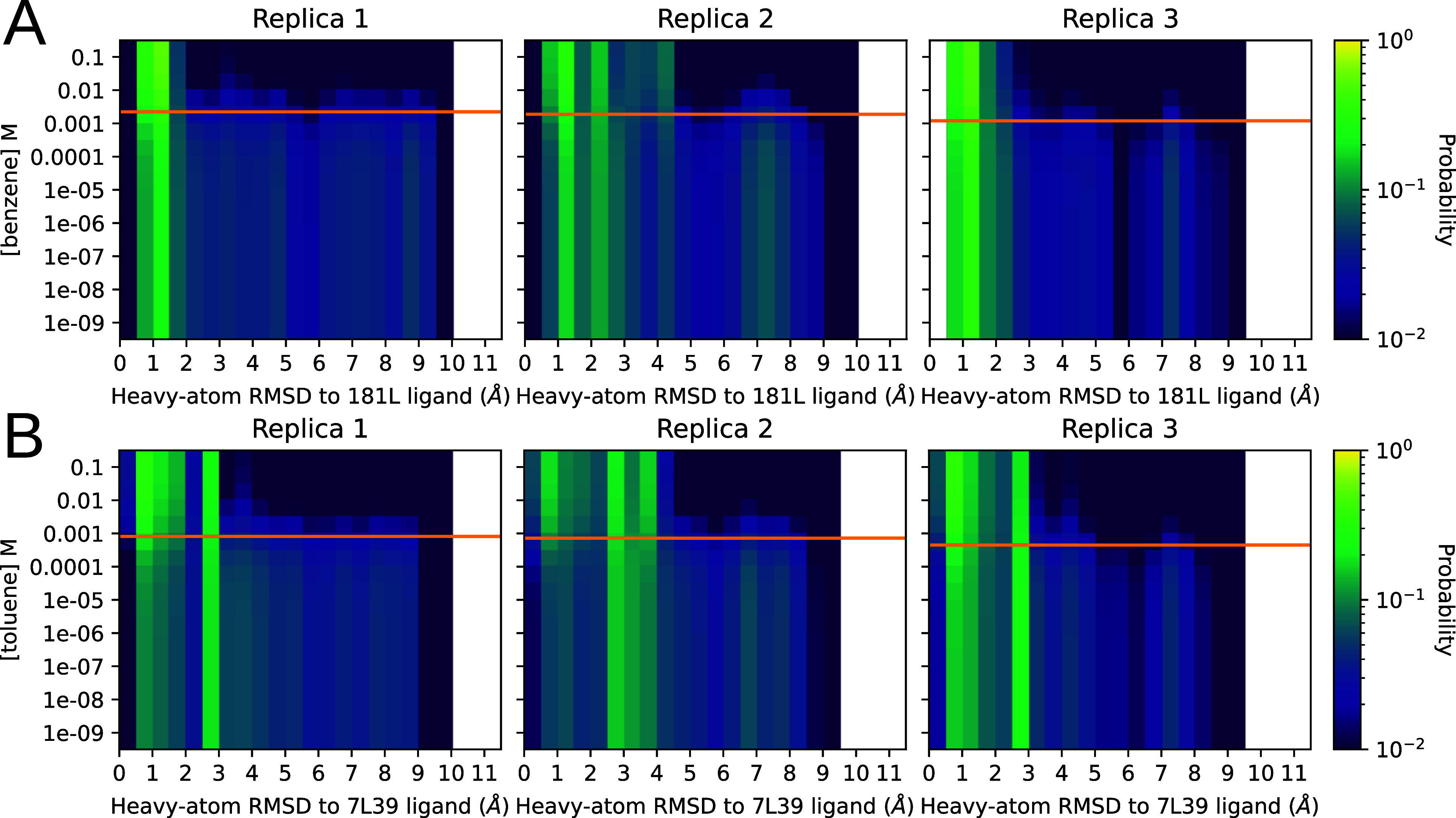
Distribution of RMSDs to a ligand-bound reference structure as the concentration of the ligand is varied. Panels A and B represent the titrations for benzene and toluene, respectively. The Y axis is ligand concentration, and the X axis is the pocket-aligned symmetry corrected³⁵ Ligand RMSD to holo crystal structure, histogrammed as before (Figure 4) . Each row in each heatmap is from the same raw data being histogrammed with different weights, computed by plugging the Y-value matching that row into eq 5. The orange line on each replica plot shows the K_D as calculated for that replica using eq 1 for reference. The heat, or intensity, is in logscale to aid visualization. The top row in each heatmap is holo-like, because it is at high ligand concentration, and the bottom row is apolike, because it is at low ligand concentration. Being able to titrate observables measurable from conformations in this way could provide exciting opportunities to understand ligand efficacy in systems with allosteric behavior.

We found that the populations of conformers outside the binding site were abundant until within an order of magnitude or so of the molecule’s K_D, where a shift happened to structures that more closely resemble the ligand-bound structure. The poses closer to the K_D on the low concentration side contain a mixture of boundlike and ligand-free-like structures. They are similar to the ligand-free weighted distribution that we see in Figure 4.

III. Conclusion

In this work, we have presented PopShift, a framework for estimating binding free energies in a manner that correctly weights the conformational heterogeneity present in the ligand binding sites of proteins. PopShift’s estimated binding free energies from docking scores perform well compared to other common methods for the simple problem of lysozyme L99A binding to small organic compounds. Our results demonstrate that adding receptor fluctuations into docking is indeed a significant improvement over making the simplifying assumption that a single protein structure encodes all of the relevant information. Further, our approach provides an approximation of the receptor–ligand complex ensemble, which has utility in mechanistic studies, such as those focused on tuning the abundance of receptor conformations known to correlate with function.

The future directions for this approach are many. PopShift of docking scores for affinity estimation is still limited by the performance of the docking scoring function. Thus, it is likely that applying PopShift to more challenging problems, such as for ligands with many rotatable bonds or charge, will require more sophisticated estimates of per-state K_D’s. Using per-state estimates from Generalized-Born or Poisson–Boltzmann rescoring, or absolute or relative binding free energy simulations, is therefore an exciting and immediate future direction for this work.³⁸ More broadly, we see opportunities to apply this framework to other perturbations to an MSM sampled from one thermodynamic state, without having to redo the sampling in those new states—such as gracefully integrating multiple protonation states for either ligand or receptor and indexing the relative free energy changes of mutations. Expansive and expensive sampling, done once for some reference model, can thus be reweighted to solve a host of important problems facing modern Biophysics.

IV. Methods

IV.A. Free Energy Formalism with MSMs

It has been shown previously that one can break up a binding free energy calculation across states discretized from simulations.^21,30,39 From Gallicchio, Lapelosa, and Levy,³⁰ (eq 22 in that work) we have

1

where K is the macroscopic binding constant, the index of the sum i runs over the n states of the discretization of state space for the receptor, π_i is the equilibrium population of that state from the ligand-free model, and K_i is the binding constant estimated for the ligand binding just to state i. Therefore, the free energy of binding becomes

2

Critically, those states need only be sampled in one ensemble; for ease of sampling, because misestimation of both binding compatible and incompatible state abundances would lead to large errors, the apo ensemble is often preferred. This is also helpful when several or possibly many binding modes may contribute relevant amounts to the overall favorability of binding.

Gallicchio, Lapelosa, and Levy³⁰ also demonstrate that one can write the probability of a state in the ligand bound ensemble as the product of its original probability and the fractional contribution it makes to the equilibrium constant defined in eq 1.

3

where π^*_i is the population of state i in the ligand bound ensemble and π_i, K_i, and K are the equilibrium population from the unbound ensemble, the affinity of the ligand to state i, and the binding constant, respectively. We can use this to compute the extent to which population shifts as a function of ligand concentration, for example, [X], as the sum of the unbound and bound population at that concentration.

4

Here w^*_i, the expression for the weight of the state, is not normalized; doing so gives

5

Equation 5 is the expression for the reweighted (shifted) population of each state as a function of the free ligand concentration. In this work we are estimating K_i by docking to each state, but other means of estimating that equilibrium constant could be used.²¹ Note that this equation has the correct limiting behavior. At high [X], the populations of the states are dominated by the favorability of binding to each state because the right-hand numerator term and the denominator both grow with [X], but the left-hand term does not. For any realistically measurable association constant (say, K > 1000) with high ligand concentrations eq 5 becomes approximately equal to eq 3. That is to say, the probability of a state in an increasingly ligand-saturated ensemble approaches the probability of that state in the ligand bound ensemble. Conversely, at very low [X] the state probabilities are very nearly the apo ones, as the right-hand term in both the numerator and denominator becomes small relative to the left-hand term. (These same expressions can be obtained from Wyman and Gill;⁴⁰ see for example chapter 4, eqs 12 and 20 through 24.)

IV.B. Lysozyme MSM Simulations and Construction

IV.B.1. Simulations

Simulations were run with Gromacs.⁴¹ Three sets of ten simulations were run starting from protein coordinates taken from PDB ID 187L using the Amber03 force field.⁴² Five of the trajectories in each set totaled 4 μs of sampling, while the other five totaled 8 μs. The protein was solvated with TIP3P explicit water in a dodecahedral box that extended one nm beyond the protein in any dimension and eight chloride ions were added to neutralize the charge.^43,44 This system was energy minimized with the steepest descent algorithm until the maximum force fell below 10 kJ/(mole*nm) using a step size of 0.01 nm and a cutoff distance of 1.2 nm for the neighbor list, Coulomb interactions, and van der Waals interactions.

The system was then equilibrated at 298 K in a 1 ns NVT simulation followed by 1 ns NPT simulation with a position restraint on all protein heavy atoms (spring constant 1,000 kJ mol^–1 nm^–2). A long-range dispersion correction was employed for both the energy and pressure. All bonds were constrained with the LINCS algorithm.⁴⁵ Cut-offs of 1.2, 0.9, and 0.9 nm were used for the neighbor list, Coulomb interactions, and van der Waals interactions, respectively. The Verlet cutoff scheme was used for the neighbor list and particle mesh Ewald was employed for the electrostatics (with a grid spacing of 0.12 nm, PME order 4, and tolerance of 1 × 10^–6).⁴⁶ The v-rescale thermostat (with a time constant of 0.1 ps) was used to hold the temperature at 298 K and the Berendsen barostat was used to bring the system to 1 bar pressure.^47,48 For the production runs, the position restraint was removed and the Parrinello–Rahman barostat was employed.⁴⁹ Snapshots were stored every 10 ps. Structures were visualized with PyMOL, and trajectories with both PyMOL and VMD.^50,51

IV.B.2. MSM Construction

MSMs were constructed using Deeptime independently for each set of 10 simulations.⁵² Clustering data was managed using the RaggedArray class from enspara.⁵³ Backbone and all χ dihedrals for any residues with heavy atoms within 5 Å of p-xylene in PDB entry 187L were selected as input features. This feature space was reduced using TICA,³¹ with lag times of 1, 2, and 5 ns and with a kinetic variance cutoff of 0.9 using commute mapping. Our final models were built from the 5 ns lag TICA features. We used k-means to cluster this reduced feature set, choosing our number of states using the cross-validation approach taken by Meller, Lotthammer, Smith, Novak, Lee, Kuhn, Greenberg, Leinwand, Greenberg, and Bowman.¹⁸ Briefly, the reduced features were clustered by splitting features into 10 train-test pairs, where k-means with a range of k was used to cluster only the training set. Test set trajectories were then assigned to clusters using euclidean distance to the k centroids resulting from the “training” clustering. MSMs were fit to the train and test pairs using the MLE method.⁵⁴ The first 10 eigenmodes of both models were then VAMP-2 scored³² using the train model, to estimate how overfit the model was to cluster count.^55,56 The number of clusters chosen for final model fitting was the point at which the VAMP-2 score of the test data starts to decline, which was k = 75 in this case. The complete set of input features was reclustered using k-means with 75 clusters, and then an MLE model was fit with a lag time of 20 ns, after scrutinizing the implied time scales of the data with various lag times.

IV.C. PopShift Workflow

The workflow used here to do the PopShift postprocessing of our ensemble docking run is as follows:

• 1.Obtain a satisfactory ligand-free MSM. (Note that for thermodynamic observables all that is really needed for step 1 is a discretized state space or clustering of input features, and an associated collection of equilibrium probabilities for each state. MSM construction, especially with a collection of shorter trajectories as we have, is a sensible path to obtaining this association, but others are possible.)
• 2.Sample a number of receptor conformations from each state of the MSM using the assignment trajectories from clustering (Frame-picking).
• 3.Align these conformations so that they will fit neatly in a docking box.
• 4.Dock to each sample, saving the ligand pose and docking score.
• 5.Compile docking scores into free energies of binding using eq 2 and the equilibrium probabilities from the ligand-free MSM.
• 6.Compute reweighted state populations from apo weights, ligand concentration of interest, and docking scores using eq 5.

IV.C.1. PopShift Implementation

To pick frames, the assignment trajectories used for model selection were sorted into lists of frames corresponding to each cluster center, and then several of these (20 for the data in Figures 2 and 3) were selected by picking indices at random. These frames were extracted from the coordinate trajectories and iteratively aligned⁵⁷ by the α-carbons of their pocket residues (defined in the same fashion as for MSM construction in Sec. IV.B.2), using LOOS.^58,59 Ligands and receptors were prepared using prepare_ligand.py and prepare_receptor.py from AutoDock tools.⁶⁰ We parallelized the preparation process by using GNU parallel.⁶¹ Docking was performed using a box with 12-Å sides centered on the centroid of the average structure of the aligned frames using SMINA.³³ Each docking run targeting each extracted conformation was performed as an independent single CPU task using Jug.⁶² We used the SMINA and Jug versions hosted on a conda forge. For SMINA the binary we used returned the following version statement (from calling smina --version): Smina Nov 9 2017. Based on AutoDock Vina 1.1.2. For Jug the version statement returned by the python module was 2.2.2. No modifications were made to the docking energy model in this study. Analysis of extracted receptor conformations and docked ligand poses was performed using python scripts involving PyLOOS.⁵⁹ Ligand RMSDs were obtained via a symmetry corrected graph theoretic algorithm implemented in the spyrmsd python package as downloaded from conda forge (version 0.6.0).³⁵ Docking scores were extracted and collated into ligand-indexed JSON associative arrays by using scripts provided in the PopShift package. OpenBabel 3.0.1 was used for ligand preparation for extended docking and to extract atomic numbers for spyrmsd.⁶³ PopShift is available as open-source software and can be found on the Bowman Lab Github: https://github.com/bowman-lab/PopShift

IV.D. Disappearing Ligand Absolute Binding Free Energy Simulations

IV.D.1. Starting Pose Selection

The binding modes of the ligand for free energy calculations were selected using 5 methods, all based on the thermodynamic cycle depicted in Figure 9. For ligands with a known crystal structure bound to T4-Lysozyme, we selected the MSM pose with an RMSD closest to that of the crystal structure. All poses had an RMSD < 2 Å to the crystal pose and thus would be considered the same binding mode.⁶⁵ The exception to this was 1,2-dichlorobenzene which did not have an MSM pose that closely matched the known crystal structure. In the case of 1,2-dichlorobenzene, we used the exact pose from the crystal structure.

Figure 9.

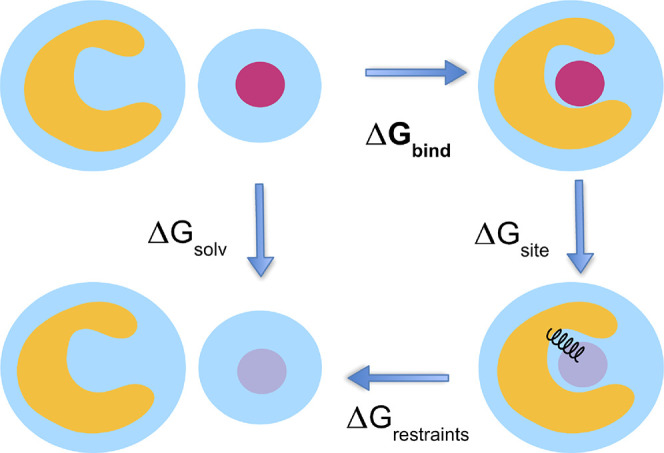
This cartoon depicts the thermodynamic cycle and transformation used for the absolute binding free energy calculations from Figure 2. We take ΔG_bind = ΔG_solv – ΔG_site – ΔG_restraints. In its weakly and noninteracting state, the ligand is free to leave the binding site. We use orientational Boresch-style restraints to reduce the phase space that must be sampled.⁶⁴

For ligands without a crystal structure, we took a known crystal structure most similar to the ligand and posed our ligand accordingly in several poses. Each pose for each ligand was simulated for 2 ns, and an RMSD analysis of the ligand throughout the trajectory as compared to the starting pose was run. The pose with the smallest change in RMSD and the smallest variance in RMSD was chosen as the most stable pose and was the pose used for the remainder of calculations. We overlaid 2-ethyltoluene with the crystal pose of o-xylene and then flipped 2-ethyltoluene so the ethyl group and methyl group would align first with the 1-methyl and 2-methyl of o-xylene as pose 1, and the 2-methyl and 1-methyl as pose 2. We overlaid 3-ethyltoluene with the crystal pose of o-xylene. We aligned the ethyl group of 3-ethyltoluene with each methyl group of o-xylene, resulting in 4 different poses. We also aligned the methyl group of 3-ethyltoluene with each methyl group of o-xylene resulting in 4 more different poses. We overlaid 4-ethyltoluene with the crystal pose of p-xylene, and then flipped 4-ethyltoluene so the ethyl group and methyl group would align first with the 1-methyl and 4-methyl of o-xylene as pose 1, and the 4-methyl and 1-methyl as pose 2. We overlaid thianaphthene with the crystal pose of indene as pose 1, and flipped the thianaphthene across its length so the sulfur would be on the opposite side as pose 2.

Lastly, for m-xylene, we began with a process similar to that of 3-ethyltoluene. We overlaid m-xylene with the crystal pose of o-xylene. We aligned the methyl groups of m-xylene with each methyl group of o-xylene resulting in 4 different poses. Again, an RMSD was used to choose the most stable pose to use for the remainder of calculations. However, upon free running free energy calculations, we observed m-xylene switching to a different stable pose after 1.5 ns, impacting the free energy calculation. For m-xylene, the stable pose found at 1.5 ns in the free energy calculation was chosen.

IV.D.2. Ligand and Protein Parameterization

The ligands were parametrized with Open Force Field version 2.0.0 and charged with AM1-BCC charges.⁶⁶ The protein (PDB 7l38) was prepared using an OpenEye Spruce to add hydrogen atoms at pH 7.0. The protonated protein was then parametrized using AMBER ff14SB and the TIP3P water model was used for the waters. GROMACS was used to solvate and add a salt concentration of 150 mM to the ligand and protein–ligand systems. Each ligand system was energy minimized and NVT equilibrated, and then a 2 ns NPT production run was performed. Each protein–ligand system was energy minimized and NVT equilibrated, then a 2 ns NPT production run was performed. The trajectory of the production run was used to select the atoms and dihedrals for the Boresch restraints to restrain the ligand to the binding site during simulation.⁶⁴

IV.D.3. Running Absolute Binding Free Energy Calculations in GROMACS

Simulations were run by using GROMACS 2021.2. For binding site simulations, we used 20 lambda windows. In this protocol, we first restrained the ligand to the binding site, turned off the Coulomb interactions, and then turned off the vdW interactions. For unbound ligand simulations, we performed absolute hydration free energies. In this protocol, we first turned off the Coulomb interactions and then turned off the vdW interactions.

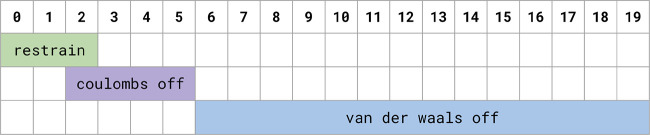
Prior to running production simulations, every lambda window was energy minimized for 5000 steps using the steepest descent and equilibrated at constant volume for 10 ps at 298.15 K. Production simulations were run for 15 ns per lambda window with an NPT ensemble. During production, replica exchange was attempted every 200 steps. See Figure 10 for a graphical representation of this schedule.

Figure 10.

This λ schedule depicts the schedule for restraining and scaling down ligand interactions (coulomb and vdW) for the protein–ligand protocol discussed in the text.

IV.D.4. Analysis of Absolute Binding Simulation Results

We obtained the free energy difference using the alchemlyb/pymbar package MBAR estimator.⁶⁷ The first nanosecond of the 15 ns of production simulations was discarded as equilibration. Each ligand was inspected for symmetry and the trajectory of the protein–ligand system in its unrestrained state was inspected to determine whether all symmetries were equally sampled.⁶⁸ The free energy difference of ligands with at least one axis of symmetry without adequate sampling of symmetries was corrected using the equation:

6

where k_B is the Boltzmann constant, T is the temperature, and σ_L is the ligand symmetry.

Data Availability Statement

Data files and scripts used to analyze results and produce figures, as well as trajectory data, will be available upon request. The data is hosted (possibly via links or other download means, depending on which data it is) at https://github.com/bowman-lab/popshift-ms-data. Software: Python command line tools written to perform the PopShift calculations discussed here are distributed as free software at: https://github.com/bowman-lab/PopShift.

Author Contributions

^⊥ (L.G.S. and B.N.) These authors contributed equally to this work.

This work was funded in part by NSF MCB-2218156, NIH NIA RF1AG067194, and the Basser Center for BRCA at the University of Pennsylvania, to G.R.B., and NIH R35GM148236 and R01GM132386 to D.L.M. G.R.B. holds a Packard Fellowship for Science and Engineering from The David & Lucile Packard Foundation.

The authors declare no competing financial interest.