Classical Exchange Polarization: An Anisotropic Variable Polarizability Model

Abstract

Polarizability, or the tendency of the electron distribution to distort under an electric field, often depends on the local chemical environment. For example, the polarizability of a chloride ion is larger in gas phase compared to a chloride ion solvated in water. This effect is due to the restriction the Pauli exclusion principle places on the allowed electron states. Because no two electrons can occupy the same state, when a highly polarizable atom comes in close contact with other atoms or molecules, the space of allowed states can dramatically decrease. This constraint suggests that an accurate molecular mechanics polarizability model should depend on the radial distance between neighboring atoms. This paper introduces a variable polarizability model within the framework of the HIPPO (Hydrogen-like Intermolecular Polarizable Potential) force field, by damping the polarizability as a function of the orbital overlap of two atoms. This effectively captures the quantum mechanical exchange polarization effects, without explicit utilization of anti-symmetrized wavefunctions. We show that the variable polarizability model remarkably improves the two-body ALMO energies and three-body energies of ion-ion and ion-water systems. Under this model, no manual tuning of atomic polarizabilities for monatomic ions is required – the gas phase polarizability can be used because an appropriate damping function is able to correct the polarizability at short range.

Graphical Abstract

I. Introduction

A key feature of many molecular systems is their chemical heterogeneity. Molecular interactions occur in a wide range of chemical environments, and at the heart of capturing the various responses is polarization. Broadly speaking, polarization refers to the change in electron density due to the local electric field. Many molecular simulation applications require polarization to accurately model the system. For example, polarization plays a critical role in ion channel simulations to reproduce the selective conduction of ions through the membrane.¹ Various properties of DNA and RNA require treatment of polarization for accurate modeling.² The amphipathic nature of lipid molecules, comprised of a charged hydrophilic head and hydrophobic tail, are thought to require polarization effects to model the vastly different chemical environments that the lipid bilayer creates.³ The importance of polarizability and polarization in both ionic and biomolecular systems is well established and can be found in various reviews.^4–10 One of the widely used polarizable force field is the AMOEBA (Atomic Multipoles Optimized Energetics for Biomolecular Applications) model, which has been developed to simulate biomolecules such as water, ions, small organic molecules, proteins, and nucleic acids.^2,11–15

Despite its success, the AMOEBA polarizable force field has struggled to accurately reproduce the polarization energy at short range (near equilibrium distance) for some interactions involving ions. The polarization energy is too negative at short range and compensating corrections to VdW parameters are needed to generate the correct equilibrium distance.^16,17 Adjustments in Thole damping factors,^18,19 polarizability,^15,19–22 electric field,^23,24 and Van der Waals parameters^11,25 are often made in polarizable force fields to damp the otherwise correct interaction energy. One major reason current models struggle is their lack of an explicit model for exchange-polarization effects. The importance of these effects for ions is well known. The chloride ion in gas phase has a polarizability of 5.482 ų. However, when placed in water, its polarizability decreases to roughly 3.25–3.5 “ų, and falls further to 2.96 ų in crystal-phase.^26–28 Because experimental polarizabilities include higher order and charge transfer effects, these values must be interpreted carefully. Nevertheless, computational studies using Hirshfeld partitioning²⁹ and localized Wannier function²⁷ have shown that (charge-transfer free) polarizabilities of monatomic ions and surrounding water molecules change depending on its chemical environment. Exchange polarization results in the diminishment in the space of allowed excited states due to exchange interactions with electrons of neighboring atoms.³⁰ Exchange polarization results from enforcing the Pauli exclusion principle on “polarized” electrons, and can be explicitly computed from perturbation theory.³¹ Whereas exchange effects in a gas-phase monomer arises solely from intra-molecular electron exchange, in condensed phase systems both the intra- and inter-molecular electron exchange must be properly accounted for.

One way to capture exchange-polarization is through variable polarizability. In this model, the polarizability of an atom is not fixed, but rather depends on the radial distance between neighboring atoms.²⁹ In spirit, this is reminiscent of Brumer and Karplus’ “effective polarizability” treatment of alkali halide dimers.³² At long range, where there is no intermolecular electron orbital overlap, the gas phase polarizability faithfully reproduces the QM polarization energy. However, as two atoms approach each other, the intermolecular electron orbitals start to overlap. In the context of perturbation theory, the overlapping ground state electrons give rise to exchange-repulsion, whereas the overlapping excited state electrons give rise to exchange-polarization and exchange-dispersion. Because exchange effects destabilize the interaction energy, the net effect is that exchange-polarization effects oppose the stabilizing classical polarization energy. If the exchange-polarization effect is not taken into consideration, the polarization energy of an interaction will be larger (more negative) than expected when compared against rigorous quantum mechanical results. For example, Giese and York showed that a variable polarizability model may need to be applied to condensed water clusters to obtain an accurate polarization response.³³ We propose that exchange-polarization effects be incorporated into classical force fields through a variable polarizability model.

A previous approach to solve this problem was to uniformly scale the atomic polarizabilities derived from QM calculations.^21,22 A constant scale factor with value between 0 and 1 is fit to reproduce the polarizability and energy of bulk phase. This gas phase polarizability is then multiplied by this scale factor to incorporate exchange-polarization effects. However, limitations to this approach are the need for a separate parameterization procedure and possible lack of transferability.³⁰ For example, a constant scale factor may not be flexible enough to capture variable polarizability effects when an ion is fully hydrated vs. when the same ion is on an interfacial boundary. The constant scaling approach to address the over-polarization problem is currently used with the AMOEBA model.^2,11–15,34 In AMOEBA the polarizability of the chloride ion is fixed to 4 ų, which is in between the gas phase and bulk phase polarizability. Other anion polarizabilities are interpolated in a similar fashion. Although this is an approximation to fit both the gas phase and bulk phase polarizabilities, it does not explicitly incorporate chemical environmental effects.

Kurnikov and Kurnikova took a different approach and introduced the variable polarizability model.³⁰ In their model, the atomic polarizabilities are damped as a function of the radial distance between neighboring atoms. The polarizability damping factor is determined by the proximity and number of neighboring atoms. The variable polarizability model can better reproduce Mg²⁺-water interaction energies and thermodynamic properties compared to a fixed polarizability model. Here we build on this variable polarizability model, with a few key differences. Whereas Kurnikov’s model starts from AMOEBA, our model is built on HIPPO,^35–38 which incorporates charge penetration effects.^39–41 This is important in reproducing the correct electrostatic potential surface. Secondly, their model exhibits a singularity in its damping function.³⁰ Instead, we use an empirical damping function that depends on the atomic orbital overlap of two atoms. Finally, we introduce an anisotropic variable polarizability model, where the polarizability damping factor depends on each neighboring atom’s position. This will be further developed in the Theory section.

In this paper, we propose an anisotropic variable polarizability model based on the overlap of hydrogen-like atomic orbitals underpinning the HIPPO model. Hydrogen-like atomic orbitals are used to represent the overlap of two atoms. We show the problem of over-polarization resides not in the electric field, but in the fixed polarizability. By including exchange-polarization effects, we are able to obtain polarization energies that closely mirror QM energies, especially for strongly polarizing cases such as ion-ion and ion-water interactions.

II. Theory

To derive the polarization energy with exchange effects, we begin with the classical, charge penetration corrected, point inducible dipole model. After introducing this model, we incorporate exchange effects in the form of variable polarizability that depends on the virtual orbital overlap $S^2$, first for the isotropic case and then for anisotropic. Hydrogen-like orbitals will be used to approximate this overlap.

A. Polarization with charge penetration correction

In the classical point inducible dipole model, atom $i$ has an inducible dipole determined by:

$${\mathit{\mu }}_i={\alpha }_i\left({\mathit{E}}_i^{\mathit{\text{perm}}}+{\mathit{E}}_i^{\mathit{\text{ind}}}\right),$$ (1)

where ${\mathit{\mu }}_i$ is the induced dipole, ${\alpha }_i$ is the polarizability, ${\mathit{E}}_i^{\mathit{\text{perm}}}$ is the electric field due to permanent multipoles, and ${\mathit{E}}_i^{\text{ind}}$ is the electric field due to induced dipoles. Because ${\mathit{E}}_i^{\text{ind}}$ depends on the induced dipole ${\mathit{\mu }}_j$ at all sites $j\ne i$, eq. 1 must be solved self-consistently until $\mathit{\mu }$ is sufficiently converged. Once the induced dipoles have been solved, the polarization energy associated with the induced dipole is⁴²

$$U^{\mathit{\text{pol}}}=-\frac{1}{2}\sum _i{\mathit{\mu }}_i\cdot {\mathit{E}}_i^{\mathit{\text{perm}}}.$$ (2)

The key to solving for the induced dipole and polarization energy is the electric field due to permanent multipoles ${\mathit{E}}_i^{\mathit{\text{perm}}}$ and induced dipoles ${\mathit{E}}_i^{\text{ind}}$

The permanent electric field ${\mathit{E}}_i^{\mathit{\text{perm}}}$ is

$${\mathit{E}}_i^{\mathit{\text{perm}}}=\sum _{i\ne j}{T}_{ij}{Z}_j+{\mathit{T}}_{ij}^{\mathit{\text{damp}}}{\mathit{M}}_j$$ (3a)

$${\mathit{M}}_j^T=\left(q_j,\hspace{1em}\left[\begin{array}{l}{d}_{j,x}\\ d_{j,y}\\ d_{j,z}\end{array}\right],\hspace{1em}\left[\begin{array}{lll}{\Theta }_{\mathrm{j},\mathrm{x}\mathrm{x}}& {\Theta }_{\mathrm{j},\mathrm{x}\mathrm{y}}& {\Theta }_{\mathrm{j},\mathrm{x}\mathrm{z}}\\ {\Theta }_{\mathrm{j},\mathrm{y}\mathrm{x}}& {\Theta }_{\mathrm{j},\mathrm{y}\mathrm{y}}& {\Theta }_{\mathrm{j},\mathrm{y}\mathrm{z}}\\ {\Theta }_{\mathrm{j},\mathrm{z}\mathrm{x}}& {\Theta }_{\mathrm{j},\mathrm{z}\mathrm{y}}& {\Theta }_{\mathrm{j},\mathrm{z}\mathrm{z}}\end{array}\right]\right)$$ (3b)

$$T_{ij}=-\nabla \left(\frac{1}{R_{ij}}\right)$$ (3c)

$${\mathit{T}}_{ij}^{\mathit{\text{damp}}}=\left[\begin{array}{lll}-\nabla & {\nabla }^2& -\frac{1}{3}{\nabla }^3\end{array}\right]\left(\frac{1}{R_{ij}}{f}_{ij}^{\mathit{\text{damp}}}\left(R_{ij}\right)\right).$$ (3d)

where $Z_j$ is the nuclear charge, ${\mathit{M}}_j$ is the multipole vector containing the monopole, dipole, and quadrupole terms, and $T_{ij},{\mathit{T}}_{ij}^{\mathit{\text{damp}}}$ are the Coulomb interaction matrices. $f_{ij}^{\mathit{\text{damp}}}$ is the hydrogen-like damping factor and is given by³⁶

$$f_{ij}^{\mathit{\text{damp}}}\left(R_{ij}\right)=1-\left(1+\frac{1}{2}{\zeta }_j{R}_{ij}\right)e^{-{\zeta }_j{R}_{ij}}.$$ (3e)

with ${\zeta }_j$ as the damping parameter. The explicit form of eq. 3a–d with all gradients solved and simplified is given in the Appendix.

According to eq. 1, the electric field due to the induced dipoles ${\mathit{E}}_i^{\text{ind}}$ must also be determined. ${\mathit{E}}_i^{\text{ind}}$ is

$${\mathit{E}}_i^{\text{ind}}=\sum _{i\ne j}{\nabla }^2\left(T_{ij}^{\mathit{\text{overlap}}}\right)\left[\begin{array}{l}{\mu }_{j,x}\\ {\mu }_{j,y}\\ {\mu }_{j,z}\end{array}\right]$$ (4a)

where $T_{ij}^{\mathit{\text{overlap}}}$ is the Coulomb interaction matrix, and ${\mu }_j$ is the induced dipole. The interaction matrix is given by

$$T_{ij}^{\mathit{\text{overlap }}}=\frac{1}{R_{ij}}{f}_{ij}^{\mathit{\text{overlap}}}\left(R_{ij}\right)$$ (4b)

where^35,36

$$f_{ij}^{\mathit{\text{overlap}}}\left(R_{ij}\right)=\left\{\begin{array}{ll}1-\left(1+\frac{11}{16}\zeta R_{ij}+\frac{3}{16}{\left(\zeta R_{ij}\right)}^2+\frac{1}{48}{\left(\zeta R_{ij}\right)}^3\right)e^{-\zeta R_{ij}},& {\zeta }_i={\zeta }_j\\ 1-A^2\left(1+2B+\frac{{\zeta }_i}{2}{R}_{ij}\right)e^{-{\zeta }_i{R}_{ij}}-B^2\left(1+2A+\frac{{\zeta }_j}{2}{R}_{ij}\right)e^{-{\zeta }_j{R}_{ij}}& {\zeta }_i\ne {\zeta }_j\end{array}\right.$$ (4c)

$$B=\frac{{\zeta }_i^2}{{\zeta }_i^2-{\zeta }_j^2}andA=\frac{{\zeta }_j^2}{{\zeta }_j^2-{\zeta }_i^2}$$

is derived from the interaction between two hydrogen-like electron densities. A subtle difference between $f_{ij}^{\mathit{\text{damp}}}$ of eq. 3e and $f_{ij}^{\mathit{\text{overlap}}}$ of eq. 4c is that $f_{ij}^{\mathit{\text{damp}}}$ is derived from a one-center integral of a hydrogen-like potential, whereas $f_{ij}^{\mathit{\text{overlap}}}$ is derived from a two-center integral of hydrogen-like potential. Because the ${\mathit{E}}_i^{ind}$ term describes the induced dipole – induced dipole interaction, it is physically appropriate to treat this electric field as a two-center damping function.^36,43 The explicit form of eq. 4a–c with all gradients solved and simplified is given in the Appendix.

Armed with the expression for ${\mathit{E}}_i^{\text{ind}}$, eq. 1 can be rewritten as

$${\mathit{\mu }}_i={\alpha }_i\left({\mathit{E}}_i^{\mathit{\text{perm}}}+\sum _{i\ne j}{\nabla }^2\left(T_{ij}^{\mathit{\text{overlap}}}\right){\mathit{\mu }}_j\right),$$ (5a)

and bringing ${\mathit{\mu }}_j$ to the left,

$$\left({\delta }_{i,j}{\alpha }_i^{-1}-\sum _{i\ne j}{\nabla }^2\left(T_{ij}^{\mathit{\text{overlap}}}\right)\right){\mathit{\mu }}_j={\mathit{E}}_i^{\mathit{\text{perm}}}.$$ (5b)

In matrix form, eq. 5b is equivalent to

$$\left(\begin{array}{cccc}{\alpha }_1^{-1}& -{\nabla }^2\left(T_{12}^{\mathit{\text{overlap}}}\right)& \cdots & -{\nabla }^2\left(T_{1N}^{\mathit{\text{overlap}}}\right)\\ -{\nabla }^2\left(T_{21}^{\mathit{\text{overlap}}}\right)& {\alpha }_2^{-1}& \cdots & -{\nabla }^2\left(T_{2N}^{\mathit{\text{overlap}}}\right)\\ ⋮& ⋮& \ddots & ⋮\\ -{\nabla }^2\left(T_{N1}^{\mathit{\text{overlap}}}\right)& -{\nabla }^2\left(T_{N2}^{\mathit{\text{overlap}}}\right)& \cdots & {\alpha }_N^{-1}\end{array}\right)\left(\begin{array}{c}{\mathit{\mu }}_1\\ {\mathit{\mu }}_2\\ ⋮\\ {\mathit{\mu }}_N\end{array}\right)=\left(\begin{array}{c}{\mathit{E}}_1^{\mathit{\text{perm}}}\\ {\mathit{E}}_2^{\mathit{\text{perm}}}\\ ⋮\\ {\mathit{E}}_N^{\mathit{\text{perm}}}\end{array}\right).$$ (5c)

which can be expressed as

$$\left({\mathit{\alpha }}^{-1}-\mathit{\Gamma }\right)\mathit{\mu }=\tilde{\mathit{T}}\mathit{\mu }={\mathit{E}}^{\mathit{\text{perm}}},$$ (5d)

Eq. 5d is of the form $\mathit{A}\mathit{x}=\mathit{b}$, and all that remains is to solve a set of linear equations for $\mathit{\mu }$, which can be done by matrix inversion, although, in practice, the preconditioned conjugate gradient is more efficient. The polarization energy eq. 2 can also be expressed using matrix notation

$$U^{\mathit{\text{pol}}}=-\frac{1}{2}{\mathit{\mu }}^T{\mathit{E}}^{\mathit{\text{perm}}}.$$ (5e)

There is another way to express the polarization energy, and we will later find it useful when we incorporate exchange effects. The polarization energy can be expressed as

$$U^{pol}=\frac{1}{2}{\mathit{\mu }}^T\left({\mathit{\alpha }}^{-1}-\mathit{\Gamma }\right)\mathit{\mu }-{\mathit{\mu }}^T{\mathit{E}}^{\mathit{\text{perm}}}$$ (6a)

Since the polarization energy is a variational minimum, it is determined by minimizing $U^{pol}$. The induced dipoles can be solved by setting the derivative of $U^{pol}$ with respect to ${\mathit{\mu }}^T$ equal to zero:

$$\frac{\partial U^{pol}}{\partial {\mathit{\mu }}^T}=\frac{1}{2}\left({\mathit{\alpha }}^{-1}-\mathit{\Gamma }\right)\mathit{\mu }+\frac{1}{2}\left({\mathit{\alpha }}^{-1}-\mathit{\Gamma }\right)\mathit{\mu }-{\mathit{E}}^{\mathit{\text{perm}}}=\left({\mathit{\alpha }}^{-1}-\mathit{\Gamma }\right)\mathit{\mu }-{\mathit{E}}^{\mathit{\text{perm}}}=0$$ (6b)

which is equivalent to eq. 5d. Therefore, we see that induced dipoles are solved by minimizing the polarization energy.

B. Isotropic polarization with exchange correction (variable polarizability)

So far, we have solved the induced dipole and polarization energy with charge penetration correction. Now, empirical exchange correction will be applied via a variable polarizability model. Eq. 6a is a very good approximation to the polarization energy in the region of no overlap. However, in the case of orbital overlap, we suggest that eq. 6a be modified to

$$U^{\mathit{\text{pol }}}=\frac{1}{2}{\mathit{\mu }}^T\left({\mathit{\alpha }}^{-1}-\mathit{\Gamma }\right)\mathit{\mu }-{\mathit{\mu }}^T{\mathit{E}}^{\mathit{\text{perm}}}+\frac{1}{2}{\mathit{\mu }}^T\left(\mathit{k}{\mathit{S}}^2\right)\mathit{\mu }$$ (7a)

where $\mathit{k}$ is a diagonal matrix of “spring constants,” and ${\mathit{S}}^2$ is a diagonal matrix of “virtual orbital overlap.” In the case of two atoms, the $\mathit{k}{\mathit{S}}^2$ matrix is represented as

$$\mathit{k}{\mathit{S}}^2=\left(\begin{array}{cc}{k}_1{S}_{12}^2& 0\\ 0& k_2{S}_{21}^2\end{array}\right)$$ (7b)

Eq. 7a can be interpreted by absorbing the spring-like term into the polarizability

$$U^{pol}=\frac{1}{2}{\mathit{\mu }}^T\left(\left({\mathit{\alpha }}^{-1}+\mathit{k}{\mathit{S}}^2\right)-\mathit{\Gamma }\right)\mathit{\mu }-{\mathit{\mu }}^T{\mathit{E}}^{\mathit{\text{perm}}}.$$ (7c)

The $\mathit{k}{\mathit{S}}^2$ term is redefined to $\mathit{k}{\mathit{S}}^2\to \frac{\mathit{k}{\mathit{S}}^2}{\mathit{\alpha }}$, for a cleaner expression,

$$U^{pol}=\frac{1}{2}{\mathit{\mu }}^T\left({\mathit{\alpha }}^{-1}\left(1+\mathit{k}{\mathit{S}}^2\right)-\Gamma \right)\mathit{\mu }-{\mathit{\mu }}^T{\mathit{E}}^{\mathit{\text{perm}}}.$$ (7d)

The equation above shows that adding in a spring-like term is equivalent to changing the polarizability as a function of the spring constant times the overlap of the virtual orbitals between two atoms. When two atoms are far apart, $k{S}^2=0$ and the exchange effects are absent. However, for nonzero overlap, $k{S}^2>0$ and the polarizability decreases to $\alpha \to \frac{\alpha }{1+k{S}^2}$. This “variable polarizability” interpretation is consistent with the fact that polarizability is different in gas phase versus bulk phase for many atoms. DFT polarizability calculations show that anion polarizability decreases when placed in bulk phase water, compared to gas phase.^26,27 This effect can be attributed to the fact that anti-symmetrizing the virtual orbitals restricts the geometric tensor space that induced dipoles can inhabit.

Now that we have a physical picture of the model, we can evaluate the virtual orbital overlap $S_{ij}$ of eq. 7b by using hydrogen-like orbitals

$${\varphi }_i=\sqrt{\frac{q_i{\zeta }_{\mathrm{i}}^3}{8\pi }}{e}^{-\frac{{\zeta }_{i}R}{2}}$$ (8a)

and taking the two-center integral

$$S=\int {\varphi }_i{\varphi }_{j}dv.$$ (8b)

Plugging eq. 8a into eq. 8b,

$$S=\int {\varphi }_i{\varphi }_{j}dv=\sqrt{q_i{q}_j{\zeta }_i^3{\zeta }_j^3}\frac{1}{8\pi }\int e^{\frac{1}{2}\left(-{\zeta }_i-{\zeta }_j\right)R}dv=\sqrt{q_i{q}_j{\zeta }_i^3{\zeta }_j^3}\cdot f_{ij}^{rep}\left(R\right)$$ (8c)

The $f^{rep}\left(R\right)$ function can be evaluated using the two-center Coulson integrals.⁴⁴ In the case of two identical atoms ${\zeta }_i={\zeta }_j$,

$$f^{rep}\left(R\right)=\frac{1}{{\zeta }^3}\left(1+\frac{\zeta R}{2}+\frac{1}{3}{\left(\frac{\zeta R}{2}\right)}^2\right)e^{-\frac{\zeta R}{2}}$$ (8d)

Whereas two heteroatoms yield the more complicated expression

$$f_{ij}^{rep}\left(R\right)=\frac{1}{2X^{3}R}\left[{\zeta }_i\left(RX-2{\zeta }_j\right)e^{-\frac{{\zeta }_{j}R}{2}}+{\zeta }_j\left(RX+2{\zeta }_i\right)e^{-\frac{{\zeta }_{i}R}{2}}\right]$$ (8e)

$$X={\left(\frac{{\zeta }_i}{2}\right)}^2-{\left(\frac{{\zeta }_j}{2}\right)}^2.$$ (8f)

Not only is eq. 8e cumbersome to calculate, but it also has a poor limiting behavior as $f_{ij}^{rep}\left(R\right)$ does not approach one as $R\to 0$. Van Vleet, et al.⁴⁵ also recognized that eq. 8e was cumbersome to compute, and used a Waldman-Hagler style analysis⁴⁶ to show that the eq. 8e can be approximated by the simpler eq. 8d by using the geometric mean combination rule

$$\zeta =\sqrt{{\zeta }_i{\zeta }_j}.$$ (8g)

By using eq. 8d for heteroatoms, and using eq. 8g to combine the damping parameter, the expression is simpler and has a well-behaved limiting behavior as $R\to 0$.

C. Anisotropic polarization with exchange correction

Consider the NaCl dimer again. Suppose that Cl⁻ sits at the origin, and Na⁺ is located on the z-axis at $z=2.37$ Å, which is the equilibrium distance of NaCl dimer in gas phase. The presence of Na⁺ changes the polarizability of Cl⁻, but because the virtual orbital overlap is in the $z$ direction, the anisotropy must be properly taken care of. In other words, because Na⁺ is on the $z$ axis, we expect a modification of the ${\alpha }_{zz}$ polarizability, but not of the ${\alpha }_{xx}$ and ${\alpha }_{yy}$ polarizabilities. The inverse polarizability tensor of Cl⁻ changes as follows:

$${\alpha }_{Cl}^{-1}=\left(\begin{array}{ccc}{\alpha }^{-1}& 0& 0\\ 0& {\alpha }^{-1}& 0\\ 0& 0& {\alpha }^{-1}\end{array}\right)\to \left(\begin{array}{ccc}{\alpha }^{-1}& 0& 0\\ 0& {\alpha }^{-1}& 0\\ 0& 0& {\alpha }^{-1}\left(1+k{S}^2\right)\end{array}\right)$$ (9)

In the case of multiple atoms, the $k{S}^2$ terms are added up in a pairwise manner in its local frame, and then rotated to the global frame. Since the polarization energy is rotationally invariant, we start with eq. 7a:

$$U^{pol}=\frac{1}{2}{\mathit{\mu }}^T\left({\mathit{\alpha }}^{-1}-\Gamma \right)\mathit{\mu }-{\mathit{\mu }}^T{\mathit{E}}^{\mathit{\text{perm}}}+\frac{1}{2}{\mathit{\mu }}^T\left(\mathit{k}{\mathit{S}}^2\right)\mathit{\mu }$$ (7a)

Since the first two terms are already rotationally invariant, only the third term must be treated carefully. In the local frame, the radial distance between two atoms is set as the $z$ axis. The third term of eq. 7a is

$$\frac{1}{2}{\mathit{\mu }}_L^T{\left(\mathit{k}{\mathit{S}}^2\right)}_L{\mathit{\mu }}_L=\frac{1}{2}{\left(\begin{array}{l}{\mu }_x\\ {\mu }_y\\ {\mu }_z\end{array}\right)}_L^T{\left(\begin{array}{ccc}{\alpha }^{-1}& 0& 0\\ 0& {\alpha }^{-1}& 0\\ 0& 0& {\alpha }^{-1}\left(1+k{S}^2\right)\end{array}\right)}_L{\left(\begin{array}{l}{\mu }_x\\ {\mu }_y\\ {\mu }_z\end{array}\right)}_L$$ (10a)

where the “L” subscripts denote local frame. In the global frame, a rotation matrix $R$ rotates the induced dipoles and the rank-2 $\mathit{k}{\mathit{S}}^2$ tensor:

$$\frac{1}{2}{\mathit{\mu }}_G^T{\left(\mathit{k}{\mathit{S}}^2\right)}_G{\mathit{\mu }}_G=\frac{1}{2}{\left({\mathit{R}}^T{\mathit{\mu }}_{\mathrm{L}}\right)}^T{\left(\mathit{k}{\mathit{S}}^2\right)}_G\left({\mathit{R}}^T{\mathit{\mu }}_{\mathrm{L}}\right)$$ (10b)

Since this energy is invariant under rotation,

$$\frac{1}{2}{\mathit{\mu }}_L^T{\left(\mathit{k}{\mathit{S}}^2\right)}_L{\mathit{\mu }}_L=\frac{1}{2}{\left({\mathit{R}}^T{\mathit{\mu }}_{\mathrm{L}}\right)}^T{\left(\mathit{k}{\mathit{S}}^2\right)}_G\left({\mathit{R}}^T{\mathit{\mu }}_{\mathrm{L}}\right).$$ (10c)

It follows that

$${\left(\mathit{k}{\mathit{S}}^2\right)}_G={\mathit{R}}^T{\left(\mathit{k}{\mathit{S}}^2\right)}_L\mathit{R}$$ (10d)

which is expected since $\mathit{k}{\mathit{S}}^2$ is a rank-2 tensor.

By summing up all the pairwise $\mathit{k}{\mathit{S}}^2$ terms, the total $\mathit{k}{\mathit{S}}^2$ in the global frame can be computed

$${\left(k{S}^2\right)}_G^{Tot}=\sum _{j>i}{\mathit{R}}_{ij}^T{\left(k{S}_{ij}^2\right)}_L{\mathit{R}}_{ij}$$ (11a)

and the polarization energy is given by a slight modification of eq. 7a:

$$U^{pol}=\frac{1}{2}{\mathit{\mu }}^T\left({\mathit{\alpha }}^{-1}-\mathit{\Gamma }\right)\mathit{\mu }-{\mathit{\mu }}^T{\mathit{E}}^{\mathit{\text{perm}}}+\frac{1}{2}{\mathit{\mu }}^T{\left(\mathit{k}{\mathit{S}}^2\right)}_G^{Tot}\mathit{\mu }$$ (11b)

III. Methods

The HIPPO force field is derived directly from a model electron density obtained from ab initio results and electronic structure theory but then parameterized to improve agreement with target experimental data. The energy terms in HIPPO consist of exchange-repulsion, electrostatics, polarization, charge transfer, and dispersion.^{35–37 38} The variable polarizability model is a modification to the existing polarization model. The HIPPO energy terms are computed with Tinker Version 8.⁴⁷

Quantum calculations and parameterization

Various energy decomposition analysis (EDA) schemes such as Symmetry-Adapted Perturbation Theory (SAPT)⁴⁸ and Absolutely Localized Molecular Orbital (ALMO)⁴⁹ can be used to parameterize a force field. Both SAPT and ALMO have naturally built-in exchange-polarization. SAPT accomplishes this by applying the anti-symmetry operator for each perturbation term,^{48,50, 51} and ALMO does this by working with the already relaxed anti-symmetrized wavefunctions. In our paper, we choose to use ALMO as a reference for the polarization energy. Although both SAPT and ALMO reproduce values that closely mirror the CCSD(t)/CBS limit interaction energies,^49,52 using ALMO EDA in force field development is advantageous for two reasons. Firstly, ALMO polarization energy respects the variational principle inherent to the self-consistent field approximation, which can be directly compared to the variational polarization energy used in many force fields. Secondly, the clean separation between polarization and charge transfer allows for a straightforward parameterization using classical force fields. ALMO’s definition of polarization and charge transfer is intuitive: polarization is the relaxation of electron density where electrons are tied to their local molecular orbitals, whereas charge transfer is the further relaxation of electron density where electrons are allowed to be delocalized to other molecular orbital centers.

The ALMO EDA cleanly separates out charge transfer from polarization by three sets of QM calculations. First the energy of the dimer system is computed using frozen localized molecular orbitals $\left(E_{FRZ,LMO}\right)$. Then, the localized molecular orbitals are allowed to relax, and the energy of the dimer system is computed using the relaxed localized molecular orbitals ($\left.E_{RLX,LMO}\right)$. Finally, the orbitals are allowed to become delocalized, and the energy of the dimer system is computed using the relaxed delocalized molecular orbitals $\left(E_{RLX,DMO}\right)$. Polarization is defined as the difference between $E_{RLX,LMO}$ and $E_{FRZ,LMO}\left(\Delta E_{POL}=E_{RLX,LMO}-E_{FRZ,LMO}\right)$, and charge transfer is defined as the difference between $E_{RLX,DMO}$ and $E_{RLX,LMO}\left(\Delta E_{CT}=E_{RLX,DMO}-\right.\left.E_{RLX,LMO}\right)$⁴⁹

The total interaction energy and EDA were computed for various water-water, water-ion, and ion-ion configurations. The geometry of each configuration with a local minimum was optimized at the level of MP2/aug-cc-pVTZ. The electric field was computed at the level of MP2/aug-cc-pVTZ. These calculations were computed with Psi4.⁵³ The ALMO EDA scheme⁴⁹ was used to decompose the interaction energy as the “classically interpretable” electrostatic, exchange-repulsion, polarization, charge transfer, and dispersion energy components. As recommended by Mao, et al.⁴⁹ the energy components were computed by the ALMO-EDA-II method at the level of ωB97X-V/def2-TZVPPD using Q-Chem5.⁵⁴

HIPPO calculations in this paper were performed with Tinker Version 8.⁴⁷ The electrostatic, exchange-repulsion, polarization, charge transfer, and dispersion energy components were initially fit to ALMO-EDA-II components. Then, the parameters for each component were relaxed to fit for the total energy. A simple Levenberg-Marquardt least-squares algorithm was used to fit both the energy components and total energy.

IV. Results

The key to solving the polarization energy is the polarizability $\alpha$ and permanent electric field ${\mathit{E}}^{\mathit{\text{perm}}}$. Therefore, prior to computing the polarization energy, the electrostatic parameters must be determined. The various Na⁺, K⁺, Cl⁻, Br⁻, and water configurations used for parameterization and testing are displayed in Figure 1. Figure 2 shows the electrostatic energy of Na⁺, K⁺, Cl⁻, Br⁻, and water. The anisotropic, charge penetration corrected electrostatic energy matches the ab initio ALMO perfectly (data not presented, but fits SAPT electrostatic energy equally well). Since the electrostatic energy is computed from the potential, this implies that the HIPPO electric potential accurately represents its ab initio counterparts.

Figure 1: Geometry of distance scans for two-body and three-body systems.

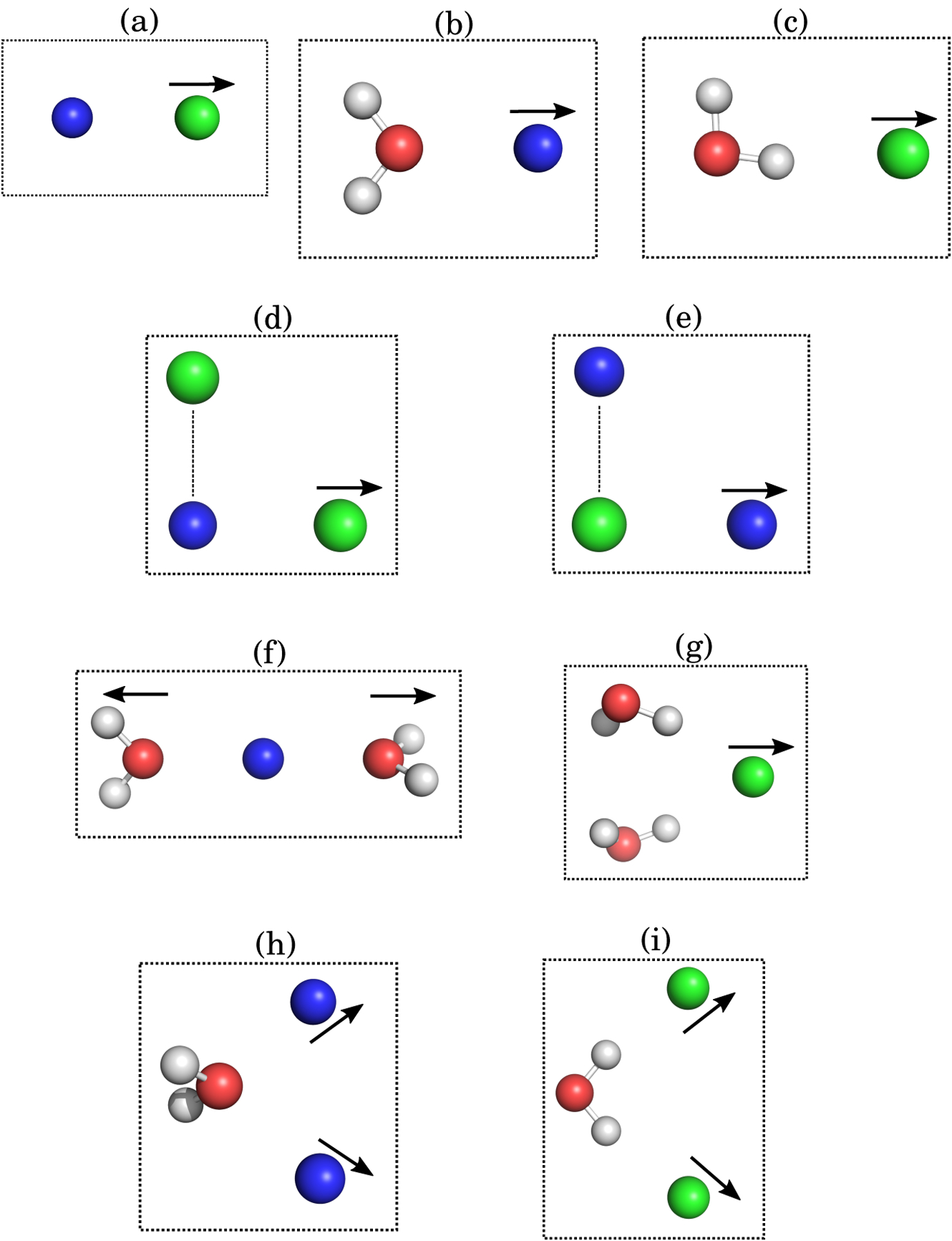
(a) M⁺ – X⁻, (b) M⁺ – H₂O, (c) X⁻ – H₂O, (d) X⁻ – M⁺ – X⁻, (e) M⁺ – X⁻ – M⁺, (f) H₂O – M⁺ – H₂O, (g) H₂O – X⁻ – H₂O, (h) M⁺ – H₂O – M⁺, and (i) X⁻ – H₂O – X⁻. M⁺ = Na⁺/K⁺ and X⁻ = Cl⁻/Br⁻.

Figure 2: Dimer electrostatic energy.

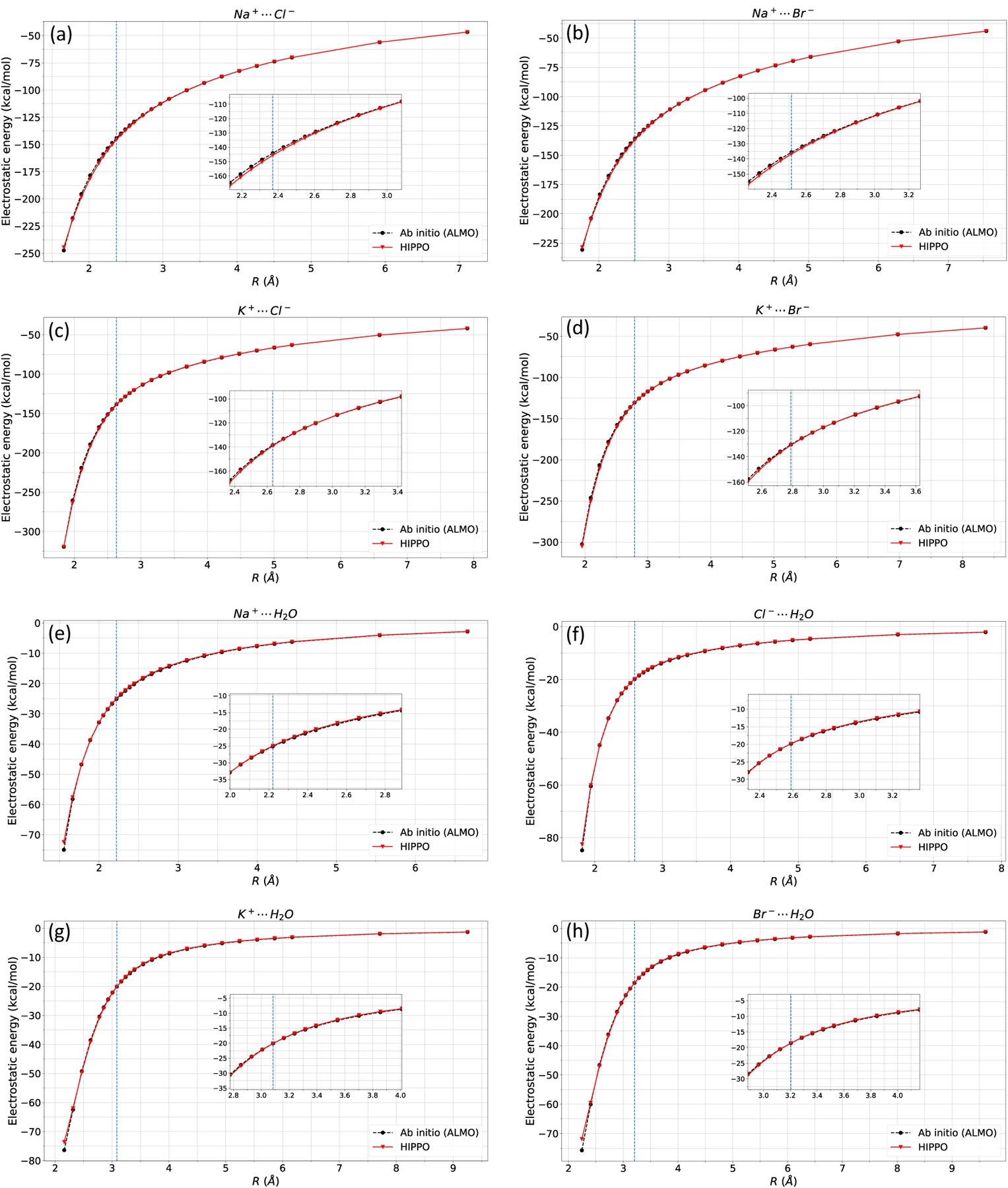
Electrostatic energy of a) Na-Cl, b) Na-Br, c) K-Cl, d) K-Br, e) Na-Water, f) Cl-Water, g) K-water, and h) Br-water dimer. Electrostatic parameters reproduce ab initio data. The vertical line indicates equilibrium distance.

The gas phase polarizabilities are used for all ions and water. The polarizabilities for Na⁺, K⁺, Cl⁻, Br⁻, and Br⁻ are set to 0.157, 0.830, 5.482, and 7.268 ų, respectively.^26,55,56 The polarizabilities for O and H (water) are chosen to reproduce the experimental gas phase water polarizability of ${\alpha }_{xx}=1.528,{\alpha }_{yy}=1.415,{\alpha }_{zz}=1.468$ ų.^14,57 Having determined ${\mathit{E}}^{\mathit{\text{perm}}}$ and $\alpha$, the induced electric field ${\mathit{E}}^{\text{ind}}$ and induced dipole $\mathit{\mu }$ are solved in a self-consistent fashion. Once $\mathit{\mu }$ is found, the energy is computed from eq. 2. Figure 3 highlights the limitation of the fixed polarizability model. Four different polarization energies for the sodium chloride dimer are computed. The ALMO polarization energy is compared to HIPPO with and without variable polarizability and to polarization energy computed from the ab initio electric fields. For the latter method, the ab initio electric field was computed using a grid around each isolated Na⁺ and Cl⁻ ion. Eq. 1 and 2 were used to solve for the “ab initio” induced dipole and polarization energy. Figure 3 shows that the fixed polarizability model exactly replicates the polarization energy computed from the ab initio field. Close agreement of HIPPO electrostatic energy with ab initio electrostatic energy already indicated that the electric field is robust; this is an additional confirmation that the problem with over-polarization does not lie in the electric field. On the other hand, the variable polarizability model fixes the problem of over-polarization. Agreement at equilibrium distance is within 0.1kcal/mol – additionally, the shape of the polarization curve is correct up to short-range. Note that all four models perform equally well at the region of no overlap, beyond 3.5 Å. It is within the region of overlap where inclusion of variable polarizability, which is due to exchange polarization, becomes important.

Figure 3: Na-Cl polarization energy.

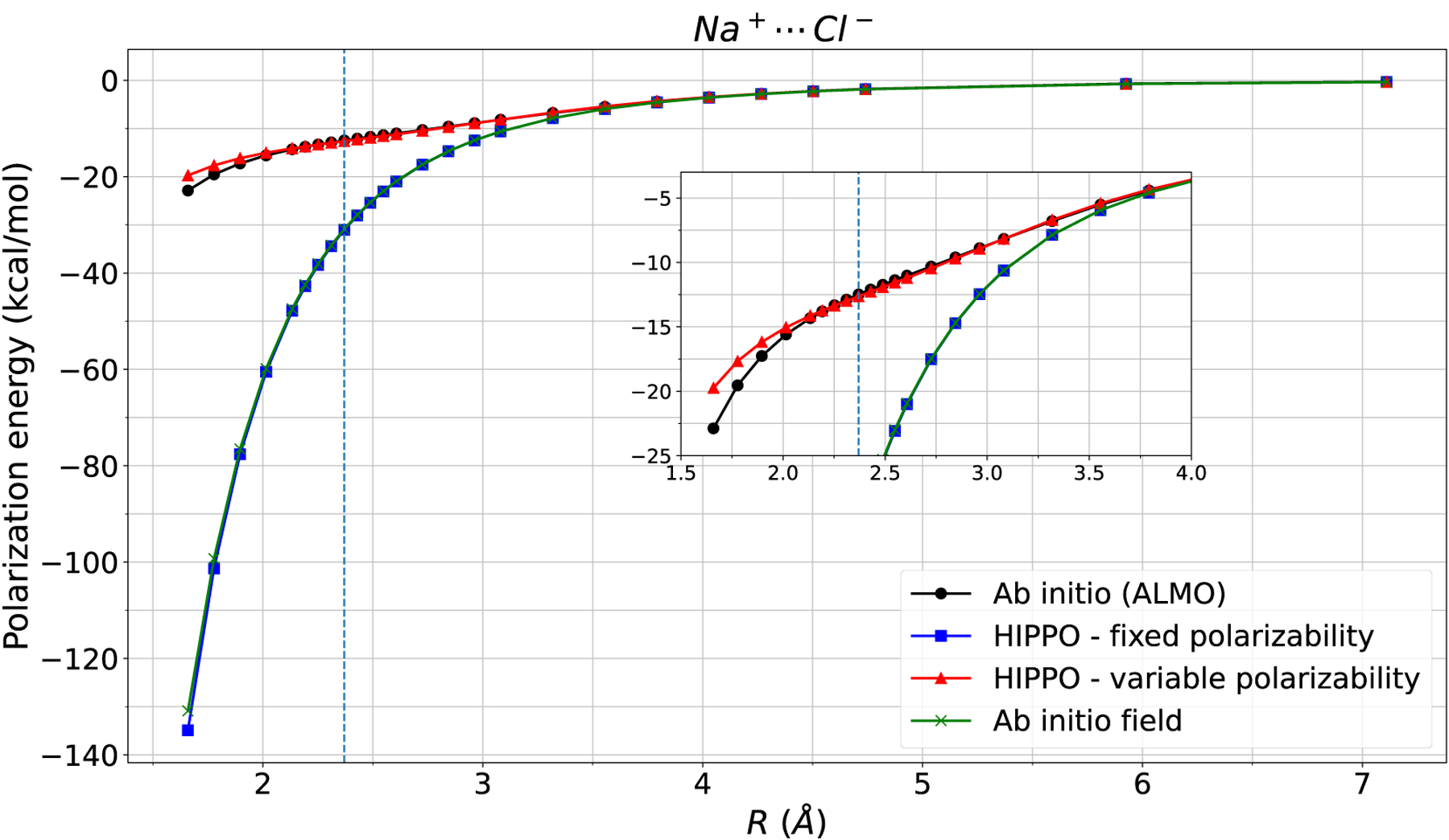
Polarization energy of the sodium chloride dimer is computed four different ways. The HIPPO variable polarizability model closely mirrors ALMO polarization energy, whereas the HIPPO fixed polarizability model matches the ab initio field polarization energy. The issue with over polarization in classical force fields lies in the polarizability, not the permanent electric field. The vertical line indicates equilibrium distance.

Next, the polarization energy of four ion dimers, Na-Cl, Na-Br, K-Cl, and K-Br are computed and displayed in Figure 4. Classical force fields struggle to fit ab initio polarization energy. To artificially dampen the polarization energy, ion polarizabilities are often decreased from its gas phase values. For example, the AMOEBA force field uses polarizability values of 0.12, 0.78, 4.0, 5.65 ų for Na⁺, K⁺, Cl⁻, and Br⁻, respectively, whereas its respective gas phase values are 0.157, 0.830, 5.482, and 7.268 ų. The most dramatic change is for chloride and bromide, where values are decreased by ~1.5 ų. These values are reasonable given that AMOEBA is mainly used for bulk phase simulations, and in bulk phase, the chloride polarizability decreases to ~3.5 ų and bromide to ~4.6 ų. 26, 55, 56 It is likely that AMOEBA has chosen polarizability values that are in between gas phase and bulk phase, in an attempt to fit both the gas phase and bulk phase polarization energy. With the variable polarizability model, however, this manual “tuning of parameters” is unnecessary for monatomic ions as the chemical environment damps the polarizability. Figure 4 shows good agreement between ALMO polarization energy and the variable polarizability model. This is a remarkable improvement over the fixed polarizability model. At equilibrium distance, the fixed polarizability model overestimates Na-Cl polarization energy by ~20kcal/mol. Similar trends are seen for other ion-ion dimers. However, Figure 4 shows that variable polarizability reproduces the ALMO polarization energy.

Figure 4: Ion-ion polarization energy.

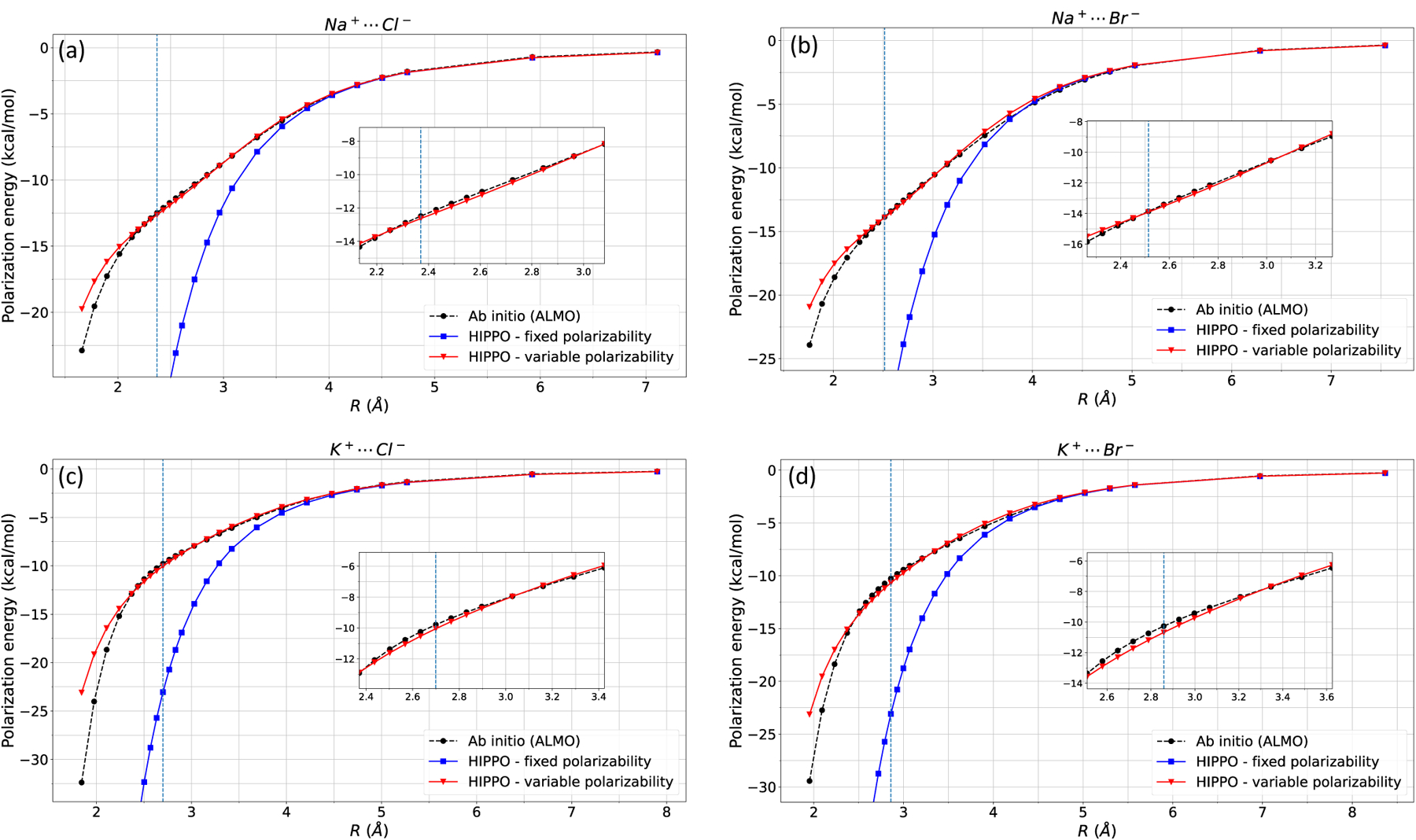
HIPPO fixed and variable polarizability models of a) Na-Cl, b) Na-Br, c) K-Cl, and d) K-Br are compared against ab initio (ALMO) polarization energy. The vertical line indicates equilibrium distance.

Ion-water interactions are crucial in modeling biomolecular systems as they determine many thermodynamic properties such as solvation free energy, diffusion coefficient, mean ionic activity coefficient, and radial distribution functions. The largest contribution to the many-body interaction energy is the two-body energy; therefore, it is very importance to get the correct two-body interaction energies. The three-body energy term has an important, yet smaller contribution to the many-body interaction energy, and we will show later that these terms are also in good agreement with ab initio calculations. Figure 5 shows the polarization energy of ion-water dimers. All four ion-water dimers (Na, Cl, K, and Br – water) dimers agree with the ab initio polarization energy. The HIPPO model with fixed polarizability shows a similar trend to Figure 3, where the polarization energy is too negative compared with ab initio values. The electrostatic and polarization parameters are printed Table 1.

Figure 5: Ion-water polarization energy.

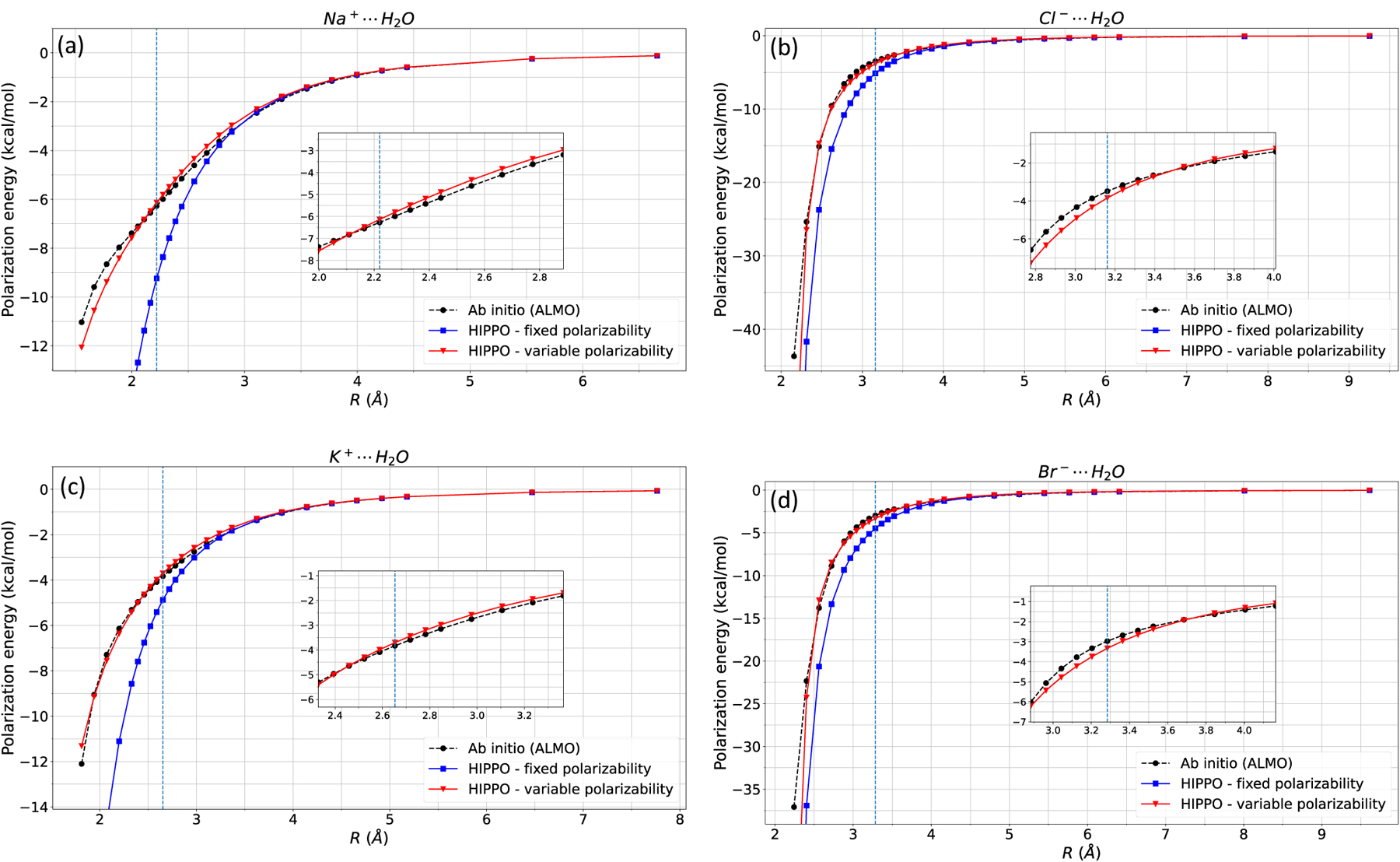
HIPPO fixed and variable polarizability models of a) Na-water, b) Cl-water, c) K-water, and d) Br-water are compared against ab initio (ALMO) polarization energy. The vertical line indicates equilibrium distance.

Table 1:

Electrostatics and polarization parameters.

	Charge Penetration		Polarization
Atom	Z	${\zeta }_{ele}({\AA }^{-1})$	$\mathit{\alpha }({\AA }^3)$	k	q	${\zeta }_{\mathit{\text{expol}}}({\AA }^{-1})$
O (water)	6.000	4.609	1.219	6.238	0.255	1.586
H (water)	1.000	4.637	0.143	9.273	0.001	5.685
Na+	4.090	5.346	0.157	5.738	12.965	9.151
K+	8.689	4.550	0.830	5.429	4.882	5.344
Cl−	9.937	3.404	5.482	2.211	1.129	1.178
Br−	12.129	3.223	7.268	2.354	1.128	1.114

Next, the repulsion, dispersion, and charge transfer parameters were fit to the corresponding ALMO interaction energies. Although a complete parameterization of monovalent ions is not the focus of this paper, we fit other energy components as a proof of concept that the total energy computed from this new polarization model is compatible with the previous developments of HIPPO. In Figure 6, the total interaction energy of ion-ion dimers is presented, and Figure 7 shows the total interaction energy of ion-water dimers.

Figure 6: Ion-ion total interaction energy.

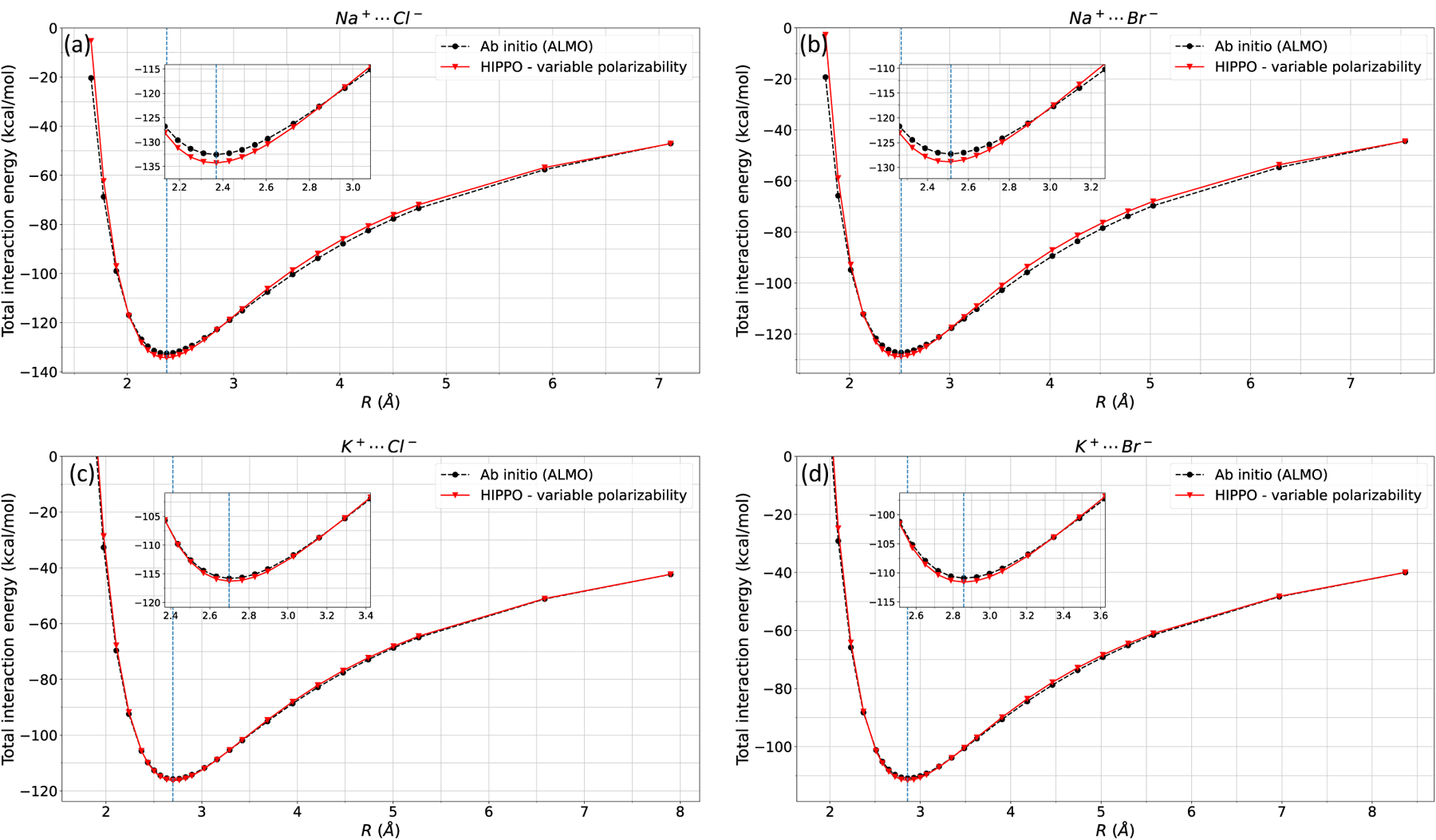
HIPPO total interaction energies of a) Na-Cl, b) Na-Br, c) K-Cl, and d) K-Br are compared against ab initio (ALMO) interaction energy.

Figure 7: Ion-water total interaction energy.

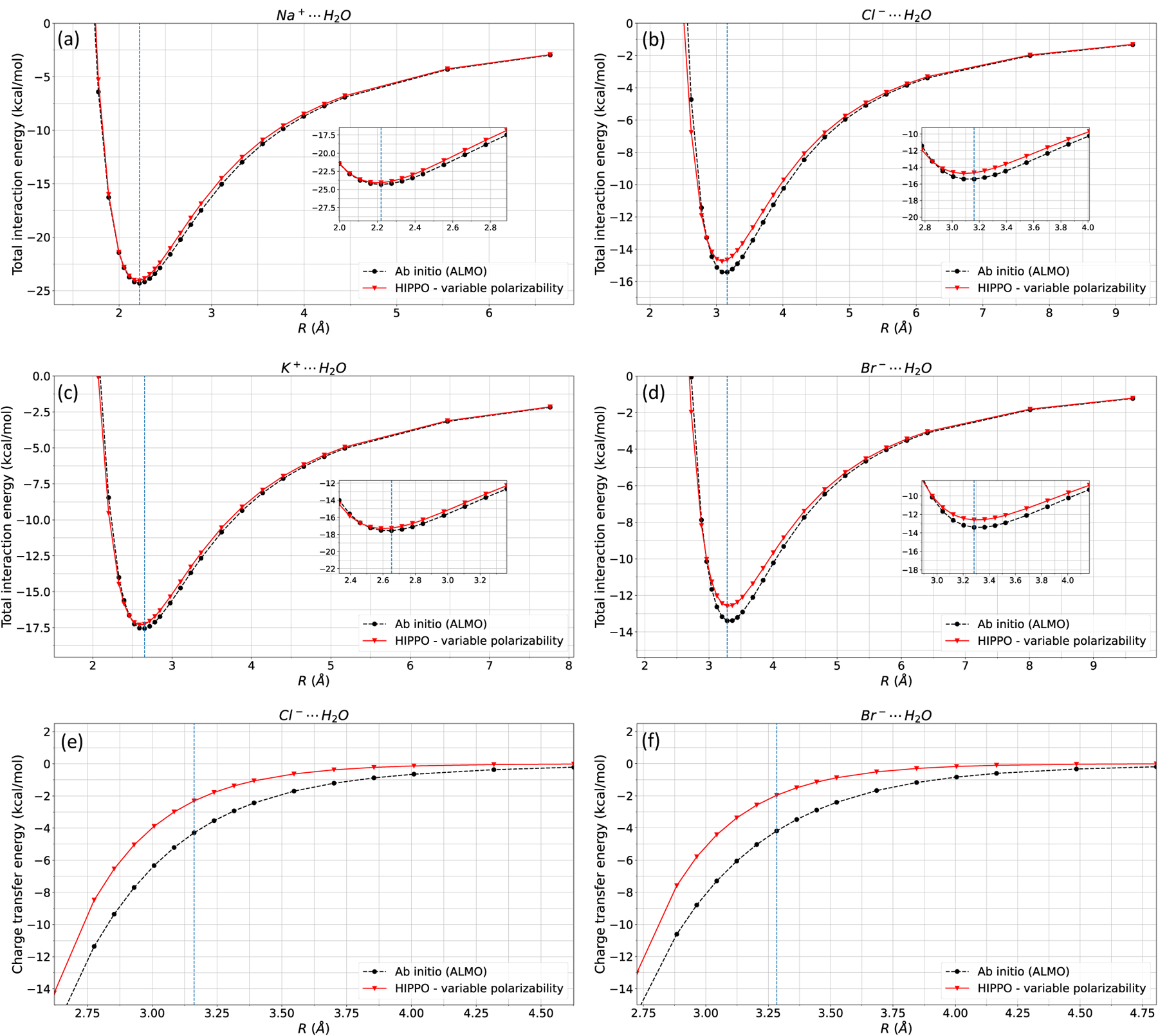
HIPPO total interaction energies of a) Na-water, b) Cl-water, c) K-water, and d) Br-water are compared against ab initio (ALMO) interaction energy. The interaction energies of Cl-water and Br-water are ~1 kcal/mol greater than that of ALMO, and the leading error is due to HIPPO underestimating charge transfer compared to ALMO. HIPPO charge transfer energies of e) Cl-water and f) Br-water is compared against ab initio (ALMO) charge transfer energy.

Ion-ion dimer interactions is a good “stress-test” to evaluate the robustness of a molecular dynamics force field. Interaction energies of the water dimer at equilibrium distance is of the order ~−5kcal/mol, whereas monatomic cation-anion dimer interaction at equilibrium distance is typically ~−120kcal/mol. Quantitative agreement of the ion-ion interaction energies suggests that the underlying theory is well-founded and physics-based. The four ion-ion interaction pairs are correct up to ~1kcal/mol at equilibrium distance, and more importantly reproduce the interaction energy curve along the full distance scans (Figure 6).

Ion-water dimer interaction energies are quite good, especially for the cation-water pairs (Figure 7 a, c). However, the anion-water HIPPO interaction energies (Figure 7 b, d) are off by ~1 kcal/mol. Upon further inspection, Figure 7e, f show that the leading error is from charge transfer. HIPPO charge transfer is not negative enough, leading to an increase in the total interaction energy. The error of the total interaction energy is not from the polarization model as Figure 5 shows good agreement between ALMO and HIPPO polarization energies. This indicates that the simple pairwise charge transfer function may need modifications to capture anion-water interaction energies.

A final test for the variable polarizability model is the three-body interaction energy. The three-body interaction energy for three molecules is computed as follows:

$$E_{3-\mathit{\text{ Body }}}=E_{123}-\left(E_{12}+E_{23}+E_{13}\right)+\left(E_1+E_2+E_3\right)$$

The three-body energy is the leading order energy correction after the two-body interaction energy. In HIPPO, three-body energy arises from polarization. In the final test of the variable polarizability model, we constructed three-ion configurations, either with 1 cation and 2 anions or 2 cations and 1 anion located at right angles of each other as indicated in Figure 1. One of the two ions is fixed in the equilibrium distance, and the third ion is scanned from the equilibrium distance to 3x the equilibrium distance. This stress case is a configuration that never occurs in bulk phase. In bulk phase, water molecules surround the ions and form a semi-structured shell around the ion. Although this configuration does not occur in simulations or experiments, it is a good system to test the underlying physics of the model. In the ab initio three-body calculations, the SCF-MI (Self-Consistent Field, Molecular Interactions) procedure⁵⁸ along with the wB97M-V functional (used in ALMO)⁴⁹ is used to remove three-body charge transfer effects. Three-body dispersion and repulsion contribute to the total three-body energies, although they are usually smaller than the three-body polarization term.

Figure 8 shows that HIPPO variable polarizability model outperforms both AMOEBA and HIPPO fixed polarizability models. Especially for the 1 cation 2 anion cases (Figure 8 a, c, e, g) HIPPO variable polarizability model displays remarkable improvement over the fixed polarizability and AMOEBA model. For 1 K⁺ and 2Cl⁻/Br⁻ systems, the HIPPO variable polarizability model is always within 1 kcal/mol of the ab initio data. For 1 Na⁺ and 2Cl⁻/Br⁻ systems, the error at equilibrium distance is reduced from ~20 kcal/mol to ~5 kcal/mol. The error is presumably from three-body repulsion, three-body dispersion, higher order polarization energy, or higher order variable polarizability. Decomposition of this error is difficult to compute (many body energy decomposition is an area of active research). However, this small difference may not be significant as these three ion configurations at a right angle is never observed in simulation or in experiments, and because it is still a tremendous improvement over the fixed polarizability model. Next, turning to the 2 cation and 1 anion cases, we observe that the three-body energies are within the desired chemical accuracy. The 2 Na⁺ and 1 Cl⁻/Br⁻ three body energies are within 1 kcal/mol from ab initio data along the distance scan, and the 2 K⁺ and 1Cl⁻/Br⁻ three body energies are within 1 kcal/mol up to ~3.5 Å. We have shown that the variable polarizability reproduces ab initio three-body even in artificial, extreme environments.

Figure 8: Ion-ion three-body energies.

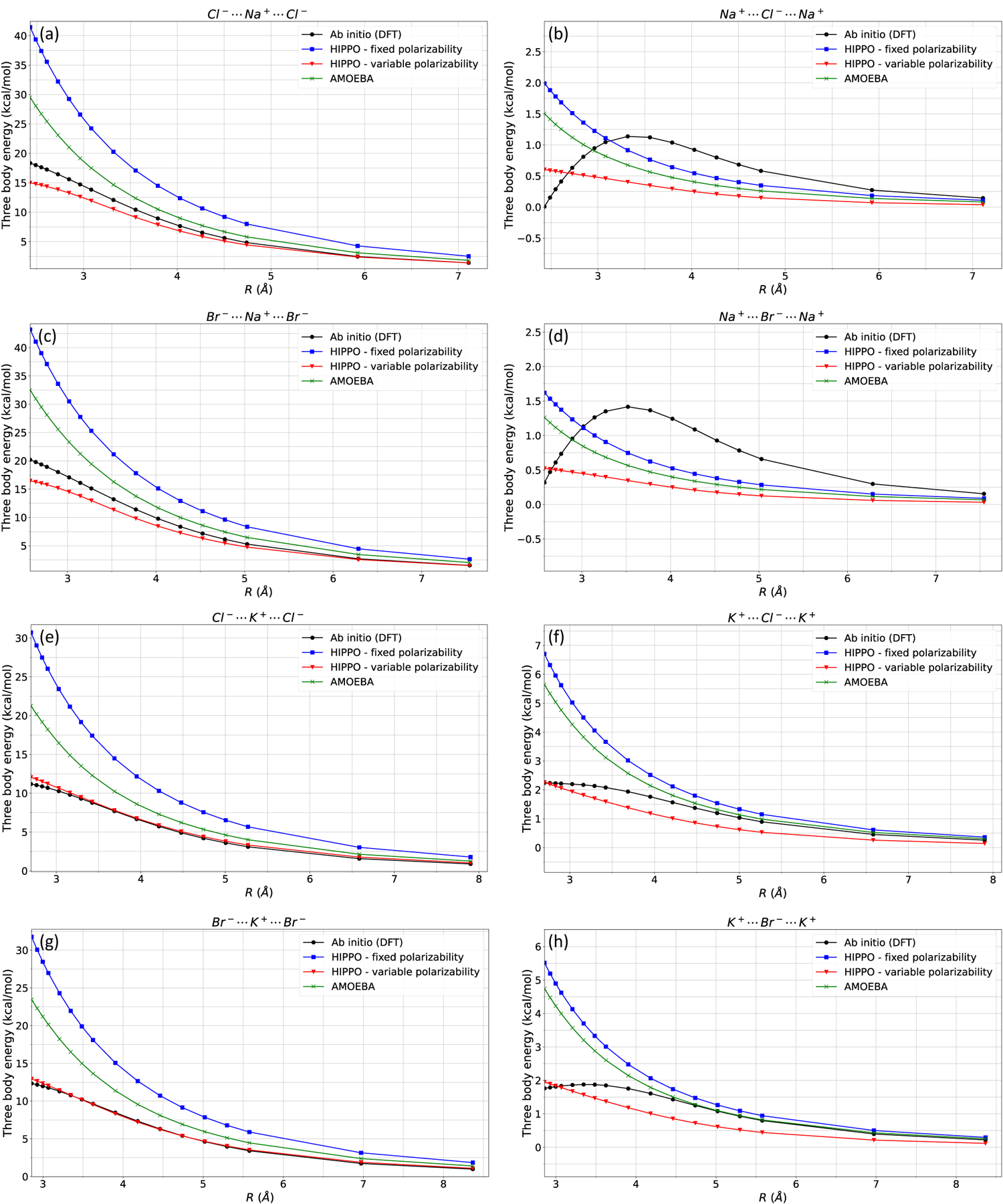
Ion-ion three-body energies are computed for a) Cl-Na-Cl, b) Na-Cl-Na, c) Br-Na-Br, d) Na-Br-Na, e) Cl-K-Cl, f) K-Cl-K, g) Br-K-Br, and h) K-Br-K trimers. HIPPO with variable polarizability is closer to the ab initio (DFT) values, compared with HIPPO with fixed polarizability and AMOEBA. Small differences between ab initio and HIPPO three-body energy may be from three-body dispersion or coupling of polarizability damping between different cartesian coordinates.

In Figure 9, the three-body interaction energies are computed for either 1 ion and 2 water or 2 ions and 1 water configurations. The 1 ion and 2 water systems have stable minima, and the energy minimized structures are used as the starting point of the energy scans, as shown in Figure 1. The 2 ion and 1 water systems do not display stable minima, and an artificial configuration is constructed. We are more concerned with the 1 ion and 2 water systems (as they have a stable minimum and occurs in simulation), but have included the 2 ion and 1 water system as a stress case. In almost all cases, the HIPPO variable polarizability model outperforms the fixed polarizability model and AMOEBA. Most of the three-body energies are within 1 kcal/mol, representing the desired chemical accuracy. Therefore, we show that the HIPPO variable polarizability model robustly reproduces the ab initio three-body interactions for three-ion and ion-water three-body configurations.

Figure 9: Ion-water three-body energies.

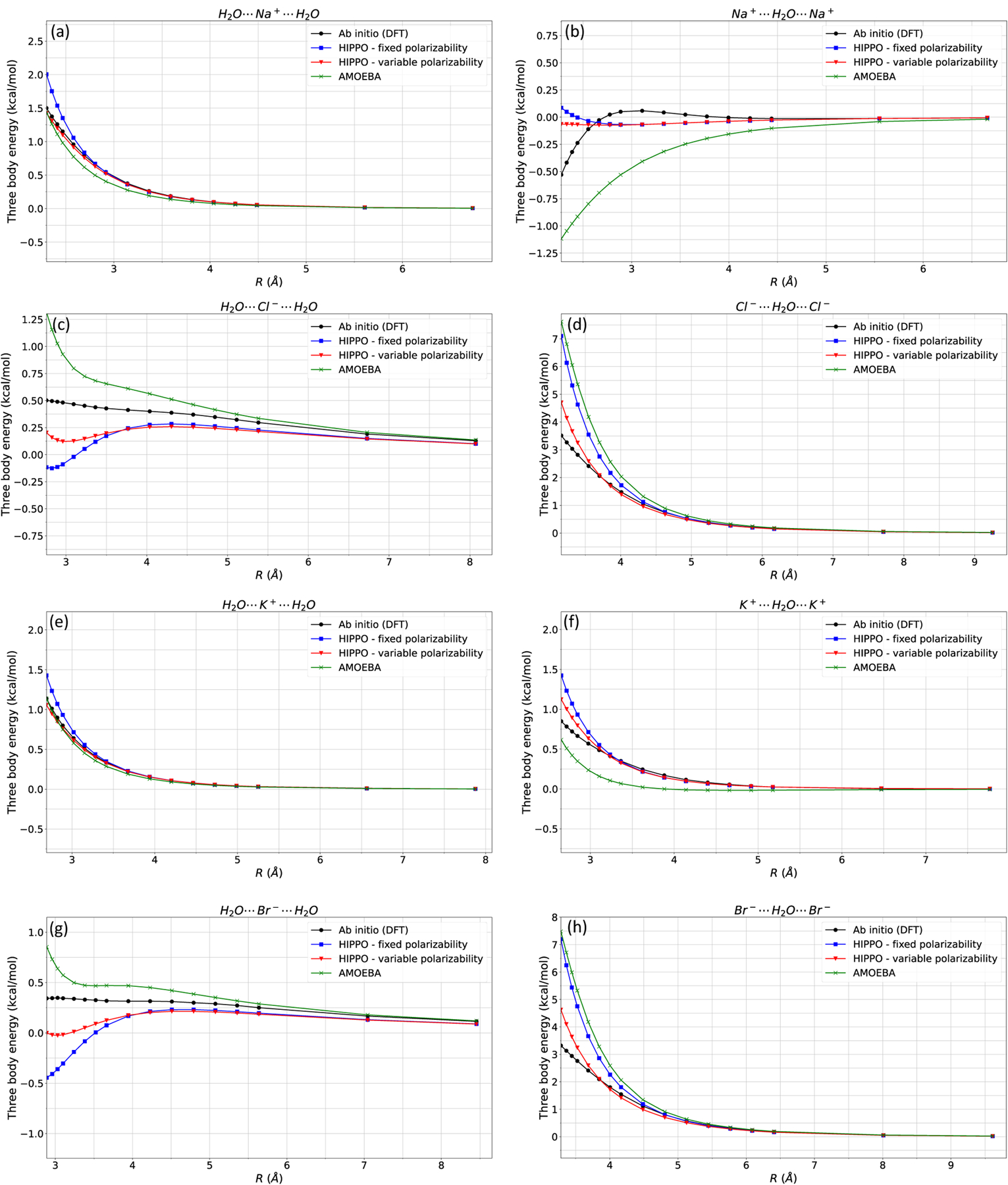
Ion-water three-body energies are computed for a) water-Na-water, b) Na-water-Na, c) water-Cl-water, d) Cl-water-Cl, e) water-K-water, f) K-water-K, g) water-Cl-water, and h) Cl-water-Cl. For almost all cases, HIPPO with variable polarizability is an improvement to the three-body energies. Most of the three-body interaction energies are within 1 kcal/mol, which is the desired chemical accuracy.

As a final test of the variable polarizability model, a cluster of 20 water molecules and one ion was simulated for 10 ns. One-hundred snapshots were taken at equal intervals, and the polarizability of the ion was computed. The polarizability of chloride went down from the gas phase value of 5.482 to 4.085 ų, and the polarizability of bromide went down from 7.268 to 5.371 ų. The polarizability of sodium changed from 0.157 to 0.105 ų, and potassium from 0.83 to 0.59 ų. These results are expected for anions; however, for cations, both computational and experimental studies suggest that polarizabilities are varied only slightly (resulting in slight enhancement or damping of polarizabilities) upon hydration.^26,27,29 In the discussions section, we will propose a method to turn off variable polarizability for certain atoms like cations, where the variable polarizability effects are smaller and perhaps more complex. A complete parameterization and analysis of bulk phase properties of ions solvated in water will be presented in the future, but we have shown that the variable polarizability model is able to respond to the chemical environment and decrease the gas phase polarizabilities. Although the chloride and bromide polarizabilities are still slightly larger than the DFT^26,27 derived bulk phase polarizabilities (3.5 and 4.6 ų, respectively), we are hopeful that a complete reparameterization including thermodynamic and bulk properties will lead to even closer agreement. Even so, by incorporating variable polarizability, we were able to bring down the polarizability of chloride and bromide by ~1.5 – 2.0 ų, which is a nontrivial improvement over current classical forcefields.

V. Discussion and Conclusions

The computational efficiency of a molecular dynamics simulation affords us the ability to study large scale chemical and biological systems that are found in nature. However, this efficiency does not necessarily demand that we abandon the quantum mechanical reality that is observed at short range. In particular, two important short-ranged effects for polarization are charge penetration and exchange polarization. In Figures 2 and 3, we have shown that inclusion of charge penetration reproduces the electrostatic energy and electric field created by the nuclear charge and distributed electrons. However, correcting for charge penetration alone does not result in accurate polarization energies. For a proper characterization of polarization energy, exchange polarization effects need to be included. The variable polarizability model described here captures this effect and leads to good agreement with two-body and three-body energies.

In our model, the polarizability is damped as follows: ${\mathit{\alpha }}^{-1}\to {\mathit{\alpha }}^{-1}\left(1+\mathit{k}{\mathit{S}}^2\right)$. The damping factor $\mathit{k}{\mathit{S}}^2$ is chosen on an empirical basis to reflect that polarization damping is a function of the proximity of neighboring atoms. Alternative expressions of the form ${\mathit{\alpha }}^{-1}(1+\mathit{F})$ may exist, where $\mathit{F}$ is a positive definite matrix. It is possible an expansion in $\mathit{S}$, such as $1+{\mathit{k}}_1\mathit{S}+{\mathit{k}}_2{\mathit{S}}^2+\cdots$ could also produce a viable model; however, this approach is not explored to keep the model simple and computationally efficient. In addition, this model allows one to choose the atoms that will feel exchange-polarization. By setting the $\mathit{k}$ constant to zero, the exchange-polarization may be turned off. This is useful for force field development as exchange-polarization effects may only be a small component of the total interaction energy for certain dimers. Also, this simple model neglects higher order exchange-polarization effects as computed from rigorous perturbation theory.^31,32 Experimental and computational studies also suggest that monatomic anions’ polarizability decreases upon hydration, but that the effect is much less pronounced for cations.^27,29 Under this scheme, one can choose to include variable polarizability for chloride but not for sodium ions.

Fortunately, we find the $\mathit{k}{\mathit{S}}^2$ damping model accomplishes the desired chemical accuracy needed for robust MD simulations. This damping scheme works well under the HIPPO model, where charge penetration effects are derived from a hydrogen-like potential. It is yet to be seen whether this scheme is effective with Thole damping (which uses Gaussian-like charge penetration damping) or Drude oscillators. In this HIPPO model, polarizability is allowed to vary depending on the intermolecular distance between two atoms. It accurately reproduces ab initio data and solves the over-polarization problem for ions. This is an exciting development, as ions have historically been difficult to simulate due to their strong electric fields, diffuse electron distributions, and strong intermolecular forces. As ions are a critical component on many molecular systems and simulations, incorporation of this model may better represent the energy potential surface and lead to a more transferable empirical potential compared to the current fixed polarizability models.

Appendix

Permanent Electric Field:

(Field at induced dipole $i$, due to permanent moments of atom $j$ using Stone’s notation, $\alpha ,\beta ,\gamma =x,y$, or $z)$

$$\begin{gathered} E_{i,\alpha }^{\mathit{\text{perm}}}=-{\nabla }_{\alpha }\left(T_{ij}\right)\cdot Z_j-{\nabla }_{\alpha }\left(T_{ij}^{\mathit{\text{damp}}}\right)\cdot q_j+{\nabla }_{\alpha \beta }\left(T_{ij}^{\mathit{\text{damp}}}\right)\cdot d_{j,\beta }-\frac{1}{3}{\nabla }_{\alpha \beta \gamma }\left(T_{ij}^{\mathit{\text{damp}}}\right)\cdot {\Theta }_{j,\beta \gamma } \\ {\nabla }_{\alpha }\left(T_{ij}\right)={\nabla }_{\alpha }\left(\frac{1}{R}\right)=-\frac{R_{\alpha }}{R^3} \\ {\nabla }_{\alpha }\left(T_{ij}^{\mathit{\text{damp}}}\right)={\nabla }_{\alpha }\left(f^{\mathit{\text{damp}}}\frac{1}{R}\right)=-f_3^{\mathit{\text{damp}}}\frac{R_{\alpha }}{R^3} \\ {\nabla }_{\alpha \beta }\left(T_{ij}^{\mathit{\text{damp}}}\right)={\nabla }_{\alpha \beta }\left(f^{\mathit{\text{damp}}}\frac{1}{R}\right)=f_5^{\mathit{\text{damp}}}\frac{3R_{\alpha }{R}_{\beta }}{R^5}-f_3^{\mathit{\text{damp}}}\frac{{\delta }_{\alpha \beta }}{R^3} \\ {\nabla }_{\alpha \beta \gamma }\left(T_{ij}^{\mathit{\text{damp}}}\right)={\nabla }_{\alpha \beta \gamma }\left(f^{\mathit{\text{damp}}}\frac{1}{R}\right)=-f_7^{\mathit{\text{damp}}}\frac{15R_{\alpha }{R}_{\beta }{R}_{\gamma }}{R^7}+f_5^{\mathit{\text{damp}}}\frac{3\left(R_{\alpha }{\delta }_{\beta \gamma }+R_{\beta }{\delta }_{\alpha \gamma }+R_{\gamma }{\delta }_{\alpha \beta }\right)}{R^5} \\ {f}_3^{\mathit{\text{damp}}}=1-\left(1+{\zeta }_{j}R+\frac{1}{2}{\left({\zeta }_{j}R\right)}^2\right)e^{-{\zeta }_{j}R} \\ {f}_5^{\mathit{\text{damp}}}=1-\left(1+{\zeta }_{j}R+\frac{1}{2}{\left({\zeta }_{j}R\right)}^2+\frac{1}{6}{\left({\zeta }_{j}R\right)}^3\right)e^{-{\zeta }_{j}R} \\ {f}_7^{\mathit{\text{damp}}}=1-\left(1+{\zeta }_{j}R+\frac{1}{2}{\left({\zeta }_{j}R\right)}^2+\frac{1}{6}{\left({\zeta }_{j}R\right)}^3+\frac{1}{30}{\left({\zeta }_{j}R\right)}^4\right)e^{-{\zeta }_{j}R} \end{gathered}$$

Induced Dipole Electric Field:

(Field at induced dipole $i$, due to induced dipole $j$ using Stone’s notation, $\alpha ,\beta =x,y$, or $z$)

$$E_{i,\alpha }^{\mathit{\text{induced }}}={\nabla }_{\alpha \beta }\left(T_{ij}^{\mathit{\text{overlap }}}\right)\cdot {\mu }_{j,\beta }$$

$${\nabla }_{\alpha \beta }\left(T_{ij}^{\mathit{\text{overlap }}}\right)={\nabla }_{\alpha \beta }\left(f^{\mathit{\text{overlap }}}\frac{1}{R}\right)=f_5^{\mathit{\text{overlap }}}\frac{3R_{\alpha }{R}_{\beta }}{R^5}-f_3^{\mathit{\text{overlap }}}\frac{{\delta }_{\alpha \beta }}{R^3}$$

$$f_3^{\mathit{\text{overlap}}}=\{\begin{array}{ll}1-\left(1+\zeta R+\frac{1}{2}{(\zeta R)}^2+\frac{7}{48}{(\zeta R)}^3+\frac{1}{48}{(\zeta R)}^4\right)e^{-\zeta R},\hfill & {\zeta }_i={\zeta }_j\hfill \\ 1-A^2\left(1+{\zeta }_{i}R+\frac{1}{2}{\left({\zeta }_{i}R\right)}^2\right)e^{-{\zeta }_{i}R}-B^2\left(1+{\zeta }_{j}R+\frac{1}{2}{\left({\zeta }_{j}R\right)}^2\right)e^{-{\zeta }_{j}R}-2A^{2}B\left(1+{\zeta }_{i}R\right)e^{-{\zeta }_{i}R}-2B^{2}A\left(1+{\zeta }_{j}R\right)e^{-{\zeta }_{j}R},\hfill & {\zeta }_i\ne {\zeta }_j\hfill \end{array}$$

$$f_5^{\mathit{\text{overlap}}}=\left\{\begin{array}{c}1-\left(1+\zeta R+\frac{1}{2}{(\zeta R)}^2+\frac{1}{6}{(\zeta R)}^3+\frac{1}{24}{(\zeta R)}^4+\frac{1}{144}{(\zeta R)}^4\right)e^{-\zeta R},{\zeta }_i={\zeta }_j\\ 1-A^2\left(1+{\zeta }_{i}R+\frac{1}{2}{\left({\zeta }_{i}R\right)}^2+\frac{1}{6}{\left({\zeta }_{i}R\right)}^2\right)e^{-{\zeta }_{i}R}-\\ B^2\left(1+{\zeta }_{j}R+\frac{1}{2}{\left({\zeta }_{j}R\right)}^2+\frac{1}{6}{\left({\zeta }_{j}R\right)}^2\right)e^{-{\zeta }_{j}R}-\\ 2A^{2}B\left(1+{\zeta }_{i}R+\frac{1}{3}{\left({\zeta }_{i}R\right)}^2\right)e^{-{\zeta }_{i}R}-\\ 2B^{2}A\left(1+{\zeta }_{j}R+\frac{1}{3}{\left({\zeta }_{j}R\right)}^2\right)e^{-{\zeta }_{j}R},{\zeta }_i\ne {\zeta }_j\end{array}\right.$$

$$B=\frac{{\zeta }_i^2}{{\zeta }_i^2-{\zeta }_j^2}\mathit{\text{and}}A=\frac{{\zeta }_j^2}{{\zeta }_j^2-{\zeta }_i^2}$$