A Bayesian fine-mapping model using a continuous global-local shrinkage prior with applications in prostate cancer analysis

Summary

The aim of fine mapping is to identify genetic variants causally contributing to complex traits or diseases. Existing fine-mapping methods employ Bayesian discrete mixture priors and depend on a pre-specified maximum number of causal variants, which may lead to sub-optimal solutions. In this work, we propose a Bayesian fine-mapping method called h2-D2, utilizing a continuous global-local shrinkage prior. We also present an approach to define credible sets of causal variants in continuous prior settings. Simulation studies demonstrate that h2-D2 outperforms current state-of-the-art fine-mapping methods such as SuSiE and FINEMAP in accurately identifying causal variants and estimating their effect sizes. We further applied h2-D2 to prostate cancer analysis and discovered some previously unknown causal variants. In addition, we inferred 369 target genes associated with the detected causal variants and several pathways that were significantly over-represented by these genes, shedding light on their potential roles in prostate cancer development and progression.

We develop a fine-mapping method, called h2-D2, utilizing a continuous global-local shrinkage prior, and propose an approach to define credible set of causal variants in this framework. Our proposed method outperforms the state-of-art fine-mapping methods based on discrete mixture priors.

Introduction

Genome-wide association studies (GWASs) have discovered numerous genetic variants associated with a wide range of complex traits and diseases.¹ However, pinpointing the specific variants that have causal effects on the traits is challenging due to the presence of high linkage disequilibrium (LD) among single-nucleotide polymorphisms (SNPs) and their small effect sizes.^2,3,4 The goal of statistical fine mapping is to identify the causal variants that have nonzero effects on the trait, which is essentially a statistical problem known as “variable selection.” Since it is difficult to distinguish a causal variant from other variants highly correlated with it without extra information, penalized regression methods sometimes fail to select the true causal variants.⁵ On the other hand, Bayesian methods are more appropriate for fine mapping by providing posterior “credible sets” (CSs).⁴ A level 1 – α CS is defined as a set of variants that contains at least one causal variant with a posterior probability of 1 – α or greater.^6,7 A CS may contain multiple highly correlated candidate causal variants for further functional validation.

To date, many Bayesian fine-mapping methods have been developed, including CAVIAR,² CAVIARBF,⁵ PAINTOR,³ JAM,⁸ DAP,⁹ FINEMAP,^10,11 and SuSiE.^6,12 All these methods are based on discrete mixture priors, specifying a prior probability for each variant being causal. If there are M SNPs in the region of interest, then the number of possible models is 2^M. To reduce computational cost, these methods need to set limits on the maximum number of causal variants. However, mis-specifying the number may lead to decrease in performance.¹² In addition, existing methods rely on exhaustive search, shotgun stochastic search, or stepwise selection to explore the space of causal configurations, which can be time consuming or lead to poor sub-optimal solutions.^6,12

In Bayesian analysis, there is another class of shrinkage priors termed “continuous global-local shrinkage priors.” Existing continuous priors have been shown to be efficient variable selection tools^{13,14,15,16,17,18,19,20} and have been successfully applied in genetic studies, including polygenic risk prediction.²¹ However, continuous shrinkage priors are hardly used in fine mapping. One shortcoming of continuous priors is that they require additional procedures in order to perform variable selection, as the posterior mean of regression coefficients is almost surely not sparse. Existing approaches include hard thresholding methods,^15,22 penalized credible regions,^23,24 and posterior variable selection summary.²⁵ Nonetheless, these approaches can produce only a single sparse model instead of several candidate models, and cannot generate credible sets similar to those obtained using discrete mixture priors.

In this paper, we introduce a Bayesian fine-mapping method based on a continuous global-local shrinkage prior, called the heritability-induced Dirichlet decomposition (h2-D2) prior, which is a variant of R2-D2 prior.²⁰ R2-D2 prior possesses both unbounded density around the origin and very heavy tails, thus enabling it to model the extremely sparse structure of the fine-mapping coefficients. Our proposed h2-D2 prior inherits the same desirable properties as R2-D2 and is adapted specifically to GWAS data. Without loss of generality, we will refer to our method, which represents the entire fine-mapping process, as h2-D2 throughout the manuscript.

Moreover, in order to address the limitations of continuous priors, inspired by the principles of frequentist hypothesis testing, we propose a statistic, termed “credible level,” which can be easily computed from posterior samples, to quantify how likely one or a set of SNPs have nonzero effects. We further define credible sets in the framework of continuous priors, offering a selection of candidate variants in the post-selection process.

Our simulation studies show that h2-D2 has better performance in identifying causal variants and accurately estimating effect sizes than current state-of-the-art fine-mapping methods such as SuSiE and FINEMAP. The CSs produced by h2-D2 exhibit superior power and achieve the target level of coverage when accurate linkage disequilibrium (LD) matrices are provided. Finally, we apply h2-D2 to a prostate cancer GWAS, identifying some causal signals that were not previously reported. The identified credible causal variants show significant enrichment in active gene regulatory regions and binding sites of specific transcription factors. In addition, we infer a total of 369 likely target genes associated with these credible causal variants. These genes are significantly over-represented in several pathways, providing valuable insights into the potential biological mechanisms underlying prostate cancer development and progression. We conclude with a discussion of future topics and further describe our software tool h2-D2 to implement the method for public use.

Material and methods

Overview of h2-D2

For a GWAS of a quantitative trait, consider a genomic region of interest containing M variants. The relationship between phenotypes and genotypes can be modeled by a multiple linear regression model:

$$y={\mathit{x}}^{\top }\mathit{\beta }+\epsilon \text{,}$$ (Equation 1)

where y is the phenotype value of an individual selected randomly from a population, $\mathit{x}\in {\mathbb{R}}^M$ is the genotype vector of the M variants for the individual, $\mathit{\beta }={\left({\beta }_1,\dots ,{\beta }_M\right)}^{\top }$ is an M-vector of effect sizes to be estimated, and ε denotes the error term. We assume all phenotype values have been standardized to ensure E(y) = 0 and Var(y) = 1. The genotypes are also standardized such that E(x) = 0 and Var(x) = R, where $\mathit{R}\in {\mathbb{R}}^{M\times M}$ is the LD matrix characterizing the correlations among the M genetic variants. Furthermore, we assume that the error term ε follows a normal distribution, $\epsilon \sim \mathrm{N}\left(0,{\sigma }_{\epsilon }^2\right)$.

We introduce a prior for β satisfying E(β) = 0 and $\text{Var}\left(\mathit{\beta }\right)=\mathbf{\Sigma }$, where $\mathbf{\Sigma }$ is an M × M diagonal matrix with diagonal elements ${\sigma }_1^2,\dots ,{\sigma }_M^2$. The narrow-sense heritability h² of the quantitative trait explained by the M SNPs can be expressed as

$$h^2=\frac{\text{Var}\left({\mathit{x}}^{\top }\mathit{\beta }\right)}{\text{Var}\left(y\right)}=\text{Var}\left({\mathit{x}}^{\top }\mathit{\beta }\right)={\mathrm{E}}_{\mathit{\beta }}\left[\text{Var}\left({\mathit{x}}^{\top }\mathit{\beta }\mid \mathit{\beta }\right)\right]+{\text{Var}}_{\mathit{\beta }}\left[\mathrm{E}\left({\mathit{x}}^{\top }\mathit{\beta }\mid \mathit{\beta }\right)\right]={\mathrm{E}}_{\mathit{\beta }}\left[\text{Var}\left({\mathit{x}}^{\top }\mathit{\beta }\mid \mathit{\beta }\right)\right]=\mathrm{E}\left[{\mathit{\beta }}^{\top }\text{Var}\left(\mathit{x}\right)\mathit{\beta }\right]=\mathrm{E}\left({\mathit{\beta }}^{\top }\mathit{R}\mathit{\beta }\right)=\text{tr}\left(\mathit{R}\mathrm{E}\left(\mathit{\beta }{\mathit{\beta }}^{\top }\right)\right)=\text{tr}\left(\mathit{R}\mathbf{\Sigma }\right)=\sum _{j=1}^M{\sigma }_j^2\le 1\text{,}$$ (Equation 2)

where the last inequality holds because $1=\text{Var}\left(y\right)=\text{Var}\left({\mathit{x}}^{\top }\mathit{\beta }\right)+\text{Var}\left(\epsilon \right)\ge \text{Var}\left({\mathit{x}}^{\top }\mathit{\beta }\right)$. Then ${\sigma }_j^2$ can be interpreted as the per-variant heritability of variant j.

To achieve an ideal prior that shrinks most elements of β toward zero while retaining some large coefficients, we impose a Dirichlet prior on the variance terms:

$$\left({\sigma }_1^2,\dots ,{\sigma }_M^2,1-h^2\right)\sim \text{Dir}\left(a_1,\dots ,a_M,b\right)\text{,}$$ (Equation 3)

where $a_1,\dots ,a_M\in \left(\mathrm{0,1}\right)$ and b > 0 are hyper-parameters. Additionally, since the double-exponential (or Laplace) distribution places more probability mass around zero and has heavier tails than the normal distribution,²⁰ we assign a double-exponential prior to each element of β:

$$\begin{array}{cc}{\beta }_j\mid {\sigma }_j^2\sim & \text{DE}\left(\sqrt{{\sigma }_j^2/2}\right),j=1,\dots ,M\text{,}\end{array}$$ (Equation 4)

where $\text{DE}\left(\delta \right)$ denotes a double-exponential distribution with mean 0 and variance $2{\delta }^2$.

As do many other fine-mapping methods, our proposed h2-D2 requires GWAS summary data only.²⁶ Assume the GWAS summary statistics $D={\left\{{\hat{\beta }}_j,{\hat{e}}_j\right\}}_{j=1}^M$ are computed from a cohort of N individuals, where ${\hat{\beta }}_j$ is the marginal effect size estimate of SNP j computed from standardized phenotypes and genotypes, while ${\hat{e}}_j$ is its standard error. Let $\hat{\mathit{\beta }}={\left({\hat{\beta }}_1,\dots ,{\hat{\beta }}_M\right)}^{\top }$, ${\hat{s}}_j={\left({\hat{e}}_j^2+N^{-1}{\hat{\beta }}_j^2\right)}^{1/2}$ for $j=1,\dots ,M$, and $\hat{\mathit{S}}=\text{diag}\left({\hat{s}}_1,\dots ,{\hat{s}}_M\right)$. The LD matrix is estimated from some reference panel as $\hat{\mathit{R}}$. The “Regression with Summary Statistics” likelihood is given by

$$\hat{\mathit{\beta }}\mid \mathit{\beta },\hat{\mathit{S}},\hat{\mathit{R}}\sim {\mathrm{N}}_M\left(\hat{\mathit{S}}\hat{\mathit{R}}{\hat{\mathit{S}}}^{-1}\mathit{\beta },\hat{\mathit{S}}\hat{\mathit{R}}\hat{\mathit{S}}\right)\text{,}$$ (Equation 5)

where ${\mathrm{N}}_k\left(\mathit{\mu },\mathbf{\Lambda }\right)$ denotes the k-variate normal distribution with mean $\mathit{\mu }$ and covariance matrix $\mathbf{\Lambda }$.

If the genotypes or phenotypes are not standardized, the standardized marginal effect size estimates can be recovered from the single-SNP association z-scores ${\hat{z}}_1,\dots ,{\hat{z}}_M$ and the sample size,¹² i.e.,

$${\hat{\beta }}_j=\frac{{\hat{z}}_j}{\sqrt{N+{\hat{z}}_j^2}},{\hat{e}}_j=\frac{1}{\sqrt{N+{\hat{z}}_j^2}}\text{.}$$ (Equation 6)

The h2-D2 prior can also be applied to binary traits by considering the observed-scale heritability (supplemental methods). A Markov Chain Monte Carlo (MCMC) algorithm that is compatible with both quantitative traits and binary traits is developed to obtain samples from the posterior distribution (supplemental methods).

Credible level and credible set

For the j^th SNP, consider the null hypothesis $H_{0j}:{\beta }_j=0$. In the frequentist framework, $H_{0j}$ can be rejected at the level of α if 0 is not contained in a confidence interval of ${\beta }_j$ at the level of $1-\alpha$. We migrate this approach to the Bayesian framework by replacing the confidence interval with the Bayesian credible interval. We propose the following statistic to evaluate how likely SNP j is causal:

$${\text{CL}}_j\triangleq \left|\widehat{\mathrm{Pr}}\left({\beta }_j>0\mid D\right)-\widehat{\mathrm{Pr}}\left({\beta }_j<0\mid D\right)\right|\in \left[\mathrm{0,1}\right]\text{,}$$ (Equation 7)

where the posterior probability $\widehat{\mathrm{Pr}}\left(·\mid D\right)$ is estimated from the MCMC samples. We term this statistic as the “credible level” of SNP j, since it can be interpreted as the maximum level such that the corresponding equal-tailed credible interval of β_j does not cover 0.

Next, we extend this concept to multiple SNPs and define credible sets (CSs) accordingly. Consider a set of SNPs $\mathcal{C}=\left\{j_1,\dots ,j_k\right\}$. Claiming that $\mathcal{C}$ is a level 1 – α CS is equivalent to rejecting the null hypothesis $H_{0\mathcal{C}}:{\mathit{\beta }}_{\mathcal{C}}\triangleq {\left({\beta }_{j_1},\dots ,{\beta }_{j_k}\right)}^{\top }=0$ at the significance level of α. If $H_{0\mathcal{C}}$ is true, then for any $\mathit{v}\in {\mathbb{R}}^k$, ${\mathit{v}}^{\top }{\mathit{\beta }}_{\mathcal{C}}=0$ is true. Therefore, we can construct a credible region for ${\mathit{\beta }}_{\mathcal{C}}$ based on ${\mathit{v}}^{\top }{\mathit{\beta }}_{\mathcal{C}}$. Theoretical studies have suggested that when studying the association between multiple SNPs and a single phenotype, testing the association between the phenotype and principal components of SNP genotypes with large eigenvalues are generally more powerful than the other tests.²⁷ In other words, constructing the credible region of ${\mathit{\beta }}_{\mathcal{C}}$ based on ${\mathit{u}}_1^{\top }{\mathit{\beta }}_{\mathcal{C}}$ and rejecting $H_{0\mathcal{C}}$ if 0 is not contained in the credible region leads to a high power, where ${\mathit{u}}_1$ is an eigenvector of the LD matrix of SNPs in $\mathcal{C}$ corresponding to its largest eigenvalue (supplemental methods). Therefore, we define the credible level of $\mathcal{C}$ as

$${\text{CL}}_{\mathcal{C}}\triangleq \left|\widehat{\mathrm{Pr}}\left({\mathit{u}}_1^{\top }{\mathit{\beta }}_{\mathcal{C}}>0\mid D\right)-\widehat{\mathrm{Pr}}\left({\mathit{u}}_1^{\top }{\mathit{\beta }}_{\mathcal{C}}<0\mid D\right)\right|\text{.}$$ (Equation 8)

If ${\text{CL}}_{\mathcal{C}}\ge 1-\alpha$, we can reject $H_{0\mathcal{C}}$ at the level of α and conclude that $\mathcal{C}$ is a level 1 – α credible set. A greedy algorithm is designed to search all CSs achieving a pre-specified level (supplemental methods).

Choice of hyper-parameters

In the Dirichlet prior (Equation 3), a smaller α_j leads to a higher concentration around 0 for β_j, while a larger b indicates a stronger global shrinkage. When incorporating external information, such as functional annotations, if the j^th SNP is more likely to be causal, a larger α_j can be set. By default, we suggest setting $a_1=\dots =a_M=a\in \left[\mathrm{0.001,0.01}\right]$ for general fine-mapping tasks. Setting α < 0.001 would make the MCMC chain converge slowly, while α > 0.01 can be considered if there are evidences that the region may harbor a large number of causal variants (e.g., more than 10).

As for the choice of b, if an in-sample or highly accurate LD matrix $\hat{\mathit{R}}$ is available, we recommend the estimation of the local heritability using some well-known estimation procedures, such as the HESS estimator,²⁸ which is defined as:

$$\widehat{h^2}=\frac{N{\hat{\mathit{\beta }}}^{\top }{\hat{\mathit{R}}}^{-1}\hat{\mathit{\beta }}-M}{N-M}\text{.}$$ (Equation 9)

Then, b can be chosen as follows:

$$b=\frac{\left(1-\widehat{h^2}\right){\sum }_{j=1}^M{a}_j}{\widehat{h^2}}\text{.}$$ (Equation 10)

However, if the accuracy of $\hat{\mathit{R}}$ is poor, the HESS estimator may exhibit a large bias. In this scenario, even if the true heritability is known, setting b according to (Equation 10) can lead to large effect size estimates for some non-causal variants in h2-D2. This is consistent with a recent finding that significant miscalibration due to external LD matrices can produce suspicious results in meta-analysis fine-mapping studies.²⁹ Therefore we suggest performing quality control to filter out outlier variants before fine mapping, and setting $b\in \left[{10}^4{\sum }_{j=1}^M{a}_j,2\times {10}^5{\sum }_{j=1}^M{a}_j\right]$ for GWAS fine-mapping tasks or setting $b\in \left[10{\sum }_{j=1}^M{a}_j,200{\sum }_{j=1}^M{a}_j\right]$ for expression quantitative trait loci (eQTL) fine-mapping tasks.

UK Biobank data preprocessing

We selected British individuals from the UK Biobank (UKBB) database based on specific criteria. The selection process involved the following steps. (1) Only individuals with available genotype data were included (data field 22005). (2) Individuals with inconsistent genetic sex (data field 22001) and self-reported sex (data field 31) were excluded. (3) We removed individuals that are recommended to be excluded from genomic analysis (data field 22010). (4) Outlier individuals for heterozygosity or missing rate were excluded (data field 22027). (5) Individuals with close familial relationships were removed to avoid any potential bias in the analysis (data field 22018). (6) We specifically chose individuals who self-identified as “White British” to ensure homogeneity in the population (data field 21000 is “1001”). After applying these filtering criteria, a total of 275,768 individuals were retained for further analysis.

Subsequently, we focused on variants that met the following criteria. (1) Only bi-allelic variants were considered to simplify the analysis. (2) Variants with a minor allele frequency (MAF) of at least 1% were included. (3) Variants with INFO score > 0.8 and Hardy-Weinberg equilibrium p value > 10⁻⁶ were included to ensure high-quality genotype data. The preprocessing of genotype data was conducted using PLINK 2.0 (v2.00a3.3LM).³⁰ The rsID of selected variants were labeled based on dbSNP database (build 151).

Partition LD blocks

We noticed that the LD blocks partitioned by LDetect based on 1000 Genome reference panel are not optimal for UKBB reference panel.³¹ We developed a method to divide the whole genome into nearly independent LD blocks, so as to improve computational efficiency and achieve accurate fine-mapping results.

For a given LD matrix $\hat{\mathit{R}}$ of M SNPs, we defined the optimal splitting as the solution to the following optimization problem:

$$\underset{k\in \left\{1,\dots ,M\right\}}{\mathrm{argmin}}\frac{{\sum }_{1\le j_1\le k,k<j_2\le M}{r}_{j_1{j}_2}^2}{k\left(M-k\right)}$$

i.e., minimizing the average squared correlation r² between two blocks. Our algorithm iteratively identifies optimal splitting points between consecutive LD blocks obtained from LDetect. If the loss in optimal splitting, defined as the difference in the values of objective function before and after the split, is smaller than 0.001 and the size of the split block is not smaller than 50, the split point is accepted. This process is performed recursively for each split block until no further split points satisfying the conditions can be found.

We used the R package “bigsnpr” to compute LD matrices.³² As a result, we divided the entire autosomal region (excluding the major histocompatibility complex [MHC] regions) into a total of 3,717 nearly independent LD blocks. We provide the scripts and the full list of LD blocks on our GitHub repository at https://github.com/xiangli428/PrCaFineMapping. This approach leads to improved efficiency and accuracy in fine-mapping analyses when using the UKBB reference panel.

1000 Genomes Project data preprocessing

We included 522 unrelated individuals with superpopulation code “EUR” from 1000 Genomes Project on GRCh38 in our analysis.^33,34 The coordinates of variants were converted from hg38 (GRCh38) to hg19 reference assembly using the UCSC Genome Browser LiftOver tool (https://genome.ucsc.edu/cgi-bin/hgLiftOver). Variants with a MAF of 0 within the Eurpoean population were removed. The genotype data preprocessing and computation of LD matrices were performed using PLINK (v1.90b6.26).³⁵

Simulations

We conducted simulation studies using UKBB imputed genotype data from 275,768 unrelated British individuals.³⁶ For the simulations, we selected 100 nearly independent LD blocks on chromosome 2 (Table S1) and included variants that were present in both UKBB reference panel and 1000 Genomes reference panel. We pruned SNPs such that the absolute correlation $\left|r\right|$ between any two SNPs was less than 0.99. Each block contained a varying number of SNPs, ranging from 288 to 1,122, and had a length between 0.25 and 2 Mb.

We designed four simulation scenarios with varying sample sizes, local heritabilities, and numbers of causal variants. For the first three scenarios, we used the genotypes of all 275,768 individuals and considered different combinations of local heritability and number of causal variants: (1) h² = 0.1%, n_causal = 5; (2) h² = 0.05%, n_causal = 5; and (3) h² = 0.1%, n_causal = 5. In the last scenario, we simulated eQTL studies, where the sample size was small (n = 1,000), but the effect sizes of causal SNPs were large (h² = 10%, n_causal = 5). Genotype values of each SNP were standardized. In each scenario, for each block, the causal variants were chosen randomly and the effect sizes of causal variants were sampled from a normal distribution with mean 0. The phenotype values were then computed according to the multiple regression model (Equation 1), where the error term $\mathit{\epsilon }$ were sampled from a multivariate normal distribution with mean 0 and covariance matrix ${\sigma }_{\epsilon }^2{\mathit{I}}_N$. ${\sigma }_{\epsilon }^2$ was chosen such that $\text{Var}\left({\mathit{x}}^{\top }\mathit{\beta }\right)/\left(\text{Var}\left({\mathit{x}}^{\top }\mathit{\beta }\right)+{\sigma }_{\epsilon }^2\right)$ equaled h² in each scenario. After standardizing the phenotype values and scaling the effect sizes of causal variants consistently, we computed summary statistics for each variant.

To assess the influence of LD matrix accuracy on the fine-mapping performance, we computed four LD matrices for each block. The first one was an in-sample LD matrix computed from all 275,768 UKBB individuals ($\hat{\mathit{R}}$). The second and the third were down-sample LD matrices, computed from randomly sampled 3,000 or 500 UKBB individuals, denoted by ${\hat{\mathit{R}}}_{\text{UKBB},3000}$ and ${\hat{\mathit{R}}}_{\text{UKBB},500}$, respectively. The fourth was an out-of-sample LD matrix computed from 522 unrelated European ancestry individuals using the genotype data from the 1000 Genomes Project on GRCh38, denoted by ${\hat{\mathit{R}}}_{1\text{KG}}$. When using mismatched LD matrices, we applied SLALOM to all pairs of SNPs with $\left|r\right|\ge 0.8$ and removed outlier non-causal variants with DENTIST-S statistics ≥ 40.²⁹

Compared methods

We performed a comprehensive comparison between h2-D2 and two state-of-the-art fine-mapping methods requiring only summary statistics, FINEMAP^10,11 and SuSiE-RSS.¹² FINEMAP utilizes a general discrete distribution as prior for the number of causal SNPs,

$$\mathrm{Pr}\left(\text{number}\text{of}\text{causal}\text{SNPs}\text{is}k\right)=p_k,k=1,\dots ,K\text{,}$$ (Equation 11)

where $K\ll M$ is the maximum number of causal variants, and uses a shotgun stochastic search algorithm to identify models with high posterior probabilities. SuSiE is a variable selection method that decomposes the effect size as the sum of single-effect vectors and imposes a multinomial prior distribution on each single-effect vector.⁶ SuSiE adopts an iterative Bayesian stepwise selection algorithm to optimize a variational approximation to the posterior distribution, as well as a refinement procedure to address the convergence problem of the algorithm.

As for the choices of hyper-parameters, for h2-D2, we set $a_1=\dots =a_M=a=0.005$. When using LD matrices $\hat{\mathit{R}}$ or ${\hat{\mathit{R}}}_{\text{UKBB},3000}$, we set b according to Equation 9 and Equation 10. When using ${\hat{\mathit{R}}}_{\text{UKBB},500}$ or ${\hat{\mathit{R}}}_{1\text{KG}}$, we set b = 2 × 10⁵Ma for scenarios 1–3 and 100Ma for scenario 4, respectively. We ran 11,000 iterations of MCMC and discarded the first 1,000 iterations. We used the potential scale reduction factor (PSRF) to monitor the convergence of MCMC algorithm (supplemental methods). If the PSRF of any β_j for $j\in \left\{1,\dots ,M\right\}$ is larger than 1.1, we discarded the first 5,000 iterations and ran further 5,000 iterations and repeated this process until convergence.

We ran SuSiE (0.12.35) with the number of single-effect vectors “L” specified as the true number of causal variants in each scenario (5 or 10). We set “estimate_residual_variance = TRUE” when using in-sample LD matrices or “estimate_residual_variance = FALSE” otherwise. In addition, we set “refine = TRUE” and “var_y = 1.” The marginal posterior mean of effect size of the j^th SNP was obtained by the following formula:

$${\overline{\beta }}_j=\sum _{l=1}^L{\alpha }_{lj}{\mu }_{lj}\text{,}$$ (Equation 12)

where α_lj is the inclusion probability of SNP j in the l^th single-effect, and μ_lj is the posterior mean of effect size of the j^th SNP conditional on inclusion in the l^th single-effect.

We used FINEMAP (v.1.4.1) in our simulations. We set the maximum number of causal variants as the true number of causal variants in each scenario, specified the prior standard deviations of effect sizes (–prior-std) as the true $\sqrt{h^2/n_{\text{causal}}}$ in each scenario, and used default settings for the prior probabilities for the number of causal variants. We used option “–std-effects” to output mean and standard deviation of the posterior effect size distribution for standardized dosages and obtained the marginal posterior mean of effect sizes from the “mean” column of the output file “dataset.snp.” We used default settings for all the other parameters.

Comparison of causal variant effect sizes and their posterior mean in simulation studies

In each simulation setting, we aggregated the results of 100 datasets. Since causal variants with small effect sizes are difficult to be identified by fine-mapping methods, we used the following piecewise linear model to assess the relationship between the true effect sizes (β) of causal SNPs and their posterior means ($\overline{\beta }$):

$$\overline{\beta }=\{\begin{array}{cc}k\left(\beta -{\beta }_0\right)& \text{for}\beta >{\beta }_0,\\ 0& \text{for}\left|\beta \right|\le {\beta }_0,\\ k\left(\beta +{\beta }_0\right)& \text{for}\beta <-{\beta }_0,\end{array}$$ (Equation 13)

where k and β₀ > 0 are the coefficients to be estimated. We used least square method to estimate these coefficients.

Prostate cancer GWAS data preprocessing

We applied h2-D2 to identify candidate causal variants of prostate cancer (PrCa) using GWAS summary data from a large meta-analysis involving affected individuals (n₁ = 79,148) and control subjects (n₀ = 61,106) of European ancestry.³⁷ We excluded the MHC region (chr6:25–33 M) from our analysis. The remaining autosomal regions were partitioned into 3,717 nonoverlapping regions with approximately independent LD. There are 126 risk regions out of 3,717 regions (i.e., contain at least one SNP with p < 5 × 10⁻⁸). 275,768 unrelated British individuals from UKBB were used as reference panel.

We filtered out SNPs that were duplicated, those that were not present in UKBB reference panel, those with an imputation r² < 0.3, those with a standard error of marginal effect size on the allelic scale <5 × 10⁻³ or >10⁻², those with a MAF < 0.01 in UKBB reference panel, or those with a logit(MAF) difference between UKBB reference panel and meta-analysis larger than 0.5. Since mismatched LD matrices were used, to avoid unreliable results, for each pair of SNPs with an absolute correlation $\left|r\right|\ge 0.5$, we checked if the pattern of LD and GWAS summary statistics is suspicious using DENTIST-S statistic.²⁹ If the DENTIST-S statistic was greater than or equal to 30, the less significant SNP would be removed. After these quality control steps, 6,446,747 common SNPs were retained in our analysis. Before fine-mapping, the variants were pruned such that all pairwise correlation $\left|r\right|<0.95$. A total of 1,342,199 tag SNPs were retained for fine mapping. We used h2-D2 with specific hyper-parameters ($a_1=\dots a_M=0.005$ and b = 2 × 10⁵) to fine map each region and identify 95% CSs. Each 95% CS includes a set of tag SNPs with a joint credible level ≥ 0.95, as well as the pruned SNPs that are in high LD with them.

Annotations of variants

The gene-based annotations of variants and their associated genes were extracted from the dbSNP database (build 151) with GRCh37.p13 as the reference assembly.³⁸ These annotations include: NSF (non-synonymous frameshift), NSM (non-synonymous missense), NSN (non-synonymous nonsense), SYN (synonymous), U3 (in 3′ UTR), U5 (in 5′ UTR), ASS (in acceptor splice site), DSS (in donor splice-site), INT (in intron), R3 (in 3′ gene region), and R5 (in 5′ gene region).

PrCa-specific cis- and trans-eQTL data were obtained from PancanQTL database.³⁹ cis-eQTLs from normal prostate tissues mapped in European-American subjects were obtained from GTEx V8 database.⁴⁰

DNaseI peaks, ChIP-seq peaks of histone marks, and transcription factor binding sites in prostate-derived cell lines were obtained from Cistrome database.⁴¹ Details of downloaded data are shown in Table S6. The peak coordinates were converted from hg38 to hg19 reference assembly using LiftOver. Variants located within these peaks were selected using BEDTools.

Enhancer-promoter loops identified from Hi-C data in RWPE1, C42B, and 22Rv1 cell lines were obtained from Rhie et al.⁴² Annotated H3K27ac HiChIP loops in LNCaP cell line were obtained from Giambartolomei et al.⁴³ Variants located within the identified enhancers were selected using BEDTools.

Pathway enrichment analysis

Potential target genes of credible causal variants (CCVs) were derived by integrating (1) associated genes of CCVs annotated in dbSNP database (build 151); (2) associated genes of eQTLs in CCVs in PancanQTL and GTEx V8 databases; and (3) genes whose promoters interact with enhancers covering CCVs in Hi-C or H3K27ac HiChIP data. Protein-coding genes were retained based on GENCODE v.42 annotations mapped to GRCh37 assembly.

Enrichment analyses for pathways from GO Biological Process⁴⁴ and WikiPathways⁴⁵ were carried out using GeneCodis 4 with “Universe scope = Annotated.”⁴⁶ To remove redundant pathways, we computed Dice coefficients for all pairs of pathways. If the Dice coefficient between two pathways is larger than 0.3, only the more significant one was retained.

Results

Simulation results

We conducted simulation studies to evaluate the performance of h2-D2 and compared it with other fine-mapping methods. In brief, we chose 100 regions on chromosome 2 (Table S1) and simulated quantitative traits for each region. We considered four scenarios with varying sample sizes, local heritabilities, and numbers of causal variants. To examine the influence of LD matrix accuracy on the fine-mapping performance, we computed four LD matrices from different reference panels with varying sample sizes for each region. Details are provided in material and methods.

We compared h2-D2 with two state-of-the-art fine-mapping methods, FINEMAP^10,11 and SuSiE-RSS.^6,12 On the SNP level, we evaluated the performance of variable selection using the area under the precision-recall curve (AUPRC), which was computed based on the credible level of each SNP for h2-D2 or the marginal posterior inclusion probability (PIP) of each SNP for SuSiE and FINEMAP. In addition, we assessed the accuracy of effect size estimation using the sum of squared error (SSE) of β based on its posterior mean, which was defined as

$$\parallel \overline{\mathit{\beta }}-\mathit{\beta }{\parallel }_2^2=\sum _{j=1}^M{\left({\overline{\beta }}_j-{\beta }_j\right)}^2\text{,}$$

where $\overline{\mathit{\beta }}={\left({\overline{\beta }}_1,\dots ,{\overline{\beta }}_M\right)}^{\top }$ is the marginal posterior mean of β. When using in-sample LD matrices, h2-D2 consistently outperformed SuSiE and FINEMAP in terms of both AUPRC and SSE across all scenarios (Figures 1A and 1B; Table S2). As expected, all methods exhibited degraded performance as the accuracy of the LD matrices decreased. In most cases, h2-D2 still demonstrated superior performance. Additionally, h2-D2 was better calibrated than SuSiE and FINEMAP, particularly when inaccurate LD matrices were used (Figure S1; Table S3). The performance of SuSiE was close to that of h2-D2. However, FINEMAP had significantly larger SSE and performed much worse in scenario 3 where the true number of causal variants was 10.

Figure 1.

Performance comparison of h2-D2, SuSiE and FINEMAP on simulated data

In (A)–(G), all values are the average ones across 100 datasets, with standard errors indicated by the error bars. Numerical results are available in Table S2.

(A) Area under the precision-recall curve (AUPRC) based on the credible level of each SNP for h2-D2 or the marginal posterior inclusion probability of each SNP for SuSiE and FINEMAP.

(B) Sum of squared error (SSE) of β based on its posterior mean, scaled by h² in each scenario.

(C) Number of detected 95% credible sets (CSs).

(D) Coverage of 95% CS (the proportion of CSs that capture at least one causal variant).

(E) Power of 95% CS (the proportion of causal variants captured by at least one CS).

(F) Size of 95% CS (the number of variants in each CS).

(G) Purity of 95% CS (the minimum absolute correlation among all pairs of SNPs in each CS).

(H) Runtime of the three methods against the number of variants in scenario 1. Each point represents a simulated dataset. For h2-D2, MCMC ran 10,000 iterations. For SuSiE, L = 5. For FINEMAP, K = 5 and the number of iterations is 100,000.

To gain further insights into the differences among the three methods, we compared the AUPRC for each simulated dataset between h2-D2 and the other two methods (Figure S2). While the AUPRC values were generally close for all three methods across most datasets, h2-D2 exhibited significantly better performance in certain datasets. By visualizing the fine-mapping results of these datasets, we noticed that in many cases if there was a non-causal SNP having moderate LD with one or more causal SNPs and having a stronger marginal association than causal SNPs, SuSiE and FINEMAP tended to select that non-causal SNP instead of the causal ones. Figure S3 provides two examples illustrating this issue. This phenomenon may be attributed to the stepwise selection nature of SuSiE and the shotgun stochastic search algorithm employed by FINEMAP. Once a marginally significant variant is included in the model, it is difficult for discrete mixture prior-based methods to remove it, i.e., the algorithms are more prone to be trapped into sub-optimal solutions. It appears that the refinement step of SuSiE cannot always alleviate this problem. On the other hand, continuous shrinkage prior-based methods allow for the continuous updating of coefficients, enabling smoother transitions among different local modes, and making the MCMC algorithm to explore the space of causal configurations more extensively.

We also compared differences among the three methods in effect size estimation. We grouped the variants into causal and non-causal categories and analyzed the prediction error for each group (material and methods, Figures S4 and S5). Although SuSiE and h2-D2 produced similar estimation of causal variant effect sizes, h2-D2 had smaller prediction errors for the non-causal variant effect sizes, suggesting that h2-D2 had a lower false discovery rate (FDR) than SuSiE. While FINEMAP demonstrated the lowest SSE for non-causal variant effect sizes, it grossly underestimated causal variant effect sizes, presumably from excessive shrinkage, resulting in larger SSE compared with SuSiE and h2-D2.

Next, we compared the level 95% CSs produced by the three methods. As shown in Figures 1C–1G and Table S2, when using $\hat{\mathit{R}}$ or ${\hat{\mathit{R}}}_{\text{UKBB},3000}$, the numbers of 95% CSs generated by the three methods were comparable, and CSs from h2-D2 exhibited higher coverage and greater power in most cases. When using ${\hat{\mathit{R}}}_{\text{UKBB},500}$ or ${\hat{\mathit{R}}}_{1\text{KG}}$, SuSiE and FINEMAP detected more CSs with higher power but lower coverage, while h2-D2 detected fewer CSs with lower power but higher coverage. These results suggested that the CSs from h2-D2 have a lower FDR even when low-accuracy LD matrices are used. Although the CSs based on continuous priors may not guarantee the frequentist coverage, we found that the coverage was generally higher or close to the target level of 0.95, except when using ${\hat{\mathit{R}}}_{1\text{KG}}$. In general, 95% CSs from h2-D2 had larger sizes and lower purities. We computed the coverage of CSs grouped by their sizes, suggesting that in most cases, CSs from h2-D2 have the highest coverage within the group, especially for 1-SNP and 2-SNP CSs (Figure S6; Table S4). Since SuSiE computes posterior mode and FINEMAP uses shotgun stochastic search to explore regions with high posterior probability density, these methods focus on some of the “best” combinations of variables, resulting in smaller CSs with higher FDR. In contrast, h2-D2 samples from the full posterior distribution, providing a more comprehensive representation of the uncertainty in the fine-mapping results.

Finally, we compared the runtime of the three methods (Figure 1H). The computational complexity of h2-D2 is proportional to M² (where M is the number of variants) and the number of MCMC iterations (n_MCMC), while the computational complexity of SuSiE is proportional to M² and the number of single effects L. When n_MCMC = 10,000 and L = 5, the runtime of h2-D2 were approximately three times as long as the runtime of SuSiE. The computational complexity of FINEMAP is primarily determined by the maximum number of causal variants and the number of iterations, so the runtime of FINEMAP didn’t significantly vary with the number of variants.

Fine-mapping causal variants of prostate cancer

We applied h2-D2 to identify candidate causal variants of prostate cancer (PrCa) using GWAS summary data from a large meta-analysis of European ancestry (material and methods).³⁷ Overall, we identified 160 CSs at 95% level (Table S5), containing 4,515 credible causal variants (362 tags). Among these CSs, 91 overlapped with the 106 CSs in autosomal risk loci reported by Dadaev et al.⁴⁷ and 86 overlapped with the CSs identified by Giambartolomei et al.⁴³ Out of the 3,717 regions analyzed, 93 regions contained a single CS, while 22 regions contained multiple CSs. There were 6 CSs detected within non-risk regions (i.e., regions with no variant that have a marginal p < 5 × 10⁻⁸). The region with the greatest number of CSs was chr8:127,708,268–128,658,961, where 15 CSs were detected. This finding is consistent with previous research that chr8q24 region harbors multiple loci associated with PrCa susceptibility.⁴⁸ The sizes of the CSs ranged from 1 to 282 variants, with a median size of 12 variants. There were 18 CSs containing only a single variant (Table 1), including some well-established causal variants of PrCa, such as rs77559646, which disrupts ANO7 mRNA splicing and protein expression,⁴⁹ and rs61752561, which affects glycosylation and function of prostate-specific antigen.⁵⁰

Table 1.

Single-SNP 95% credible sets of prostate cancer

Fine-mapping regiona	Variantb	rsIDc	AAFd	p valuee	CLf	Putative target gene(s)g	Association type(s)h
chr2:62,482,371–64,700,760	2_63301164_G_A	rs6545977	0.50	7.35 × 10−46	1	–	–
chr2:241,912,029–243,041,411	2_242135265_G_A	rs77559646	0.02	9.93 × 10−21	1	ANO7	NSMi, INTj
chr3:169,194,244–170,170,389	3_170083629_C_G	rs61436251	0.21	1.76 × 10−63	1	SKIL	INT
chr5:1,279,701–1,551,138	5_1288547_T_C	rs2853676	0.73	8.86 × 10−12	0.99	TERT	INT
chr5:1,551,930–2,131,681	5_1895829_C_T	rs12653946	0.42	9.58 × 10−22	0.99	IRX4	cis eQTL (GTEx)
chr6:159,951,830–161,847,113	6_160581374_A_G	rs651164	0.69	2.15 × 10−36	1	SOD2, ACAT2, TCP1, MRPL18	Enhancer (H3K27ac, HiChIP, LNCaP)
chr6:159,951,830–161,847,113	6_160581502_T_C	rs4646283	0.14	1.31 × 10−5	0.99	SOD2, ACAT2, TCP1, MRPL18	Enhancer (H3K27ac, HiChIP, LNCaP)
chr8:127,708,268–128,658,961	8_128108726_G_A	rs35365584	0.33	3.60 × 10−67	1	MYC	Enhancer (H3K27ac, HiChIP, LNCaP)
chr8:127,708,268–128,658,961	8_128540776_C_G	rs12549761	0.12	5.20 × 10−77	1	–	–
chr8:128,659,713–129,297,518	8_128665480_C_T	rs4385433	0.37	6.91 × 10−8	0.96	–	–
chr10:50,839,567–53,146,331	10_51549496_T_C	rs10993994	0.62	2.29 × 10−147	1	TIMM23B, MSMB, NCOA4	INT, R5k, cis eQTL (GTEx)
chr11:124,697,216–125,111,546	11_125054793_C_T	rs138466039	0.01	2.01 × 10−11	1	PKNOX2	INT, cis eQTL (GTEx)
chr12:12,101,106–12,922,339	12_12871099_T_G	rs2066827	0.24	2.31 × 10−9	1	CDKN1B	NSM,R3l
chr13:73,847,474–74,347,673	13_74084684_G_A	rs61957204	0.07	3.29 × 10−11	1	–	–
chr14:23,251,130–23,598,976	14_23305649_T_C	rs1004030	0.42	1.55 × 10−8	0.98	MMP14	R5
chr17:7,251,713–8,007,416	17_7571752_T_G	rs78378222	0.01	1.73 × 10−9	1	TP53	U3m
chr19:51,254,187–51,450,534	19_51361382_G_A	rs61752561	0.04	2.33 × 10−8	1	KLK3	NSM, INT
chr22:42,872,086–43,649,657	22_43500212_G_T	rs5759167	0.50	5.55 × 10−71	1	–	–

^aChromosome (chr) number and boundary of fine-mapping region (GRCh37/hg19).

^bVariant ID in the format {chr}_{pos}_{ref_seq}_{alt_seq}.

^cdbSNP (build 151, GRCh37/hg19) rsID.

^dAlternative allele frequency of controls in meta-analysis.

^eMeta-analysis p value.

^fh2-D2 credible level.

^gPutative target gene(s) of the variant.

^hAssociation type(s) between the variant and its putative target gene(s).

ⁱNon-synonymous missense.

^jIn, intron.

^kIn 5′ gene region.

^lIn 3′ gene region.

^mIn 3′ UTR.

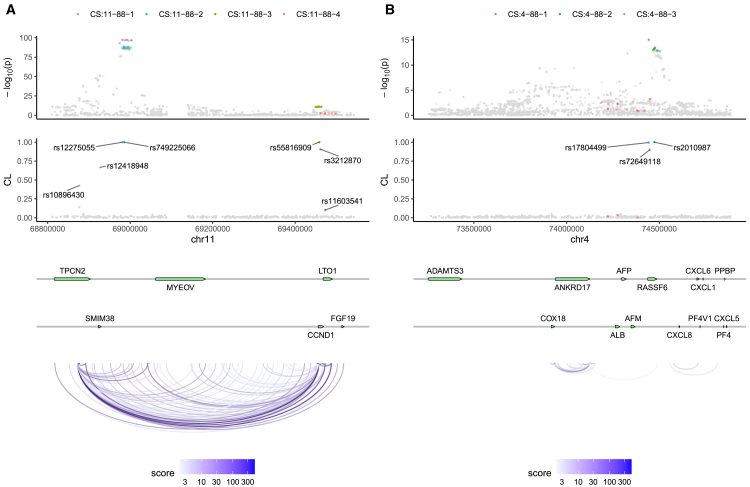
In our analysis, we identified some independent association signals that have not been previously reported. One such example is chr11:68,810,837–69,542,062, where four 95% CSs were detected (Figures 2A and S7A). CS:11-88-1 is represented by rs12275055 (p = 3.7 × 10⁻⁹⁸), which is known to have pleiotropic associations with multiple cancer types.⁵¹ This SNP acts as an eQTL in multiple tissues for TPCN2, which plays a role in autophagy progression and extracellular vesicle secretion in cancer cells.⁵² The location of CS:11-88-2 overlaps with CS:11-88-1. Hi-C data from the normal prostate cell line RWPE1 indicated that several SNPs within CS:11-88-2 are located in an enhancer region that looped to the promoter of the cell cycle-related gene CCND1.⁴² Furthermore, an interaction between the TPCN2 promoter and the CCND1 promoter was detected by H3K27ac HiChIP in the LNCaP prostate cancer cell line.⁴³ These findings suggested a possible mechanism involving a three-way interaction between an enhancer harboring the causal SNPs in CS:11-88-1 and CS:11-88-2, the TPCN2 promoter, and the CCND1 promoter. We also identified two other CSs, CS:11-88-3 and CS:11-88-4, near the gene CCND1. Within CS:11-88-3, 4 out of 17 variants are located in the 5′ flanking region of CCND1. In CS:11-88-4, the most likely causal variant is the lead SNP rs3212870 (p = 1.5 × 10⁻³), which is located intronic in CCND1. The associations between CS:11-88-4 and PrCa have not been previously reported because of the weak marginal associations, which can be explained by the strong opposite effects of CS:11-88-1 and CS:11-88-2 as well as the moderate LD between CS:11-88-4 and them (Figure S7A). Another interesting example is chr4:73,256,856–74,885,359 (Figures 2B and S7B), where we identified a CS, CS:4-88-3, insignificantly associated with PrCa (minimum p = 6.5 × 10⁻⁴). Our analysis suggested that this signal is masked by the other two signals in this region, CS:4-88-1 and CS:4-88-2. The lead SNP in CS:4-88-3, rs72649118, is a non-synonymous missense SNP of RASSF6, a member of the RASSF family of tumor suppressors.⁵³

Figure 2.

Fine-mapping results of two genomic regions in prostate cancer data analysis

chr11:6,881,0837–69,542,062 (A) and chr4:73,256,856–74,885,359 (B). The top panel depicts the marginal associations of variants (−log₁₀(p)) from the GWAS meta-analysis data. The semitransparent points represent pruned variants in fine mapping. The second panel illustrates the credible levels of tag SNPs computed by h2-D2. In the first two panels, each color represents a 95% credible set (CS). The CS is named in the format CS:{chromosome ID}-{region ID}-{index}. The third panel displays the positions of genes in the corresponding regions. The bottom panel demonstrates the H3K27ac HiChIP loops detected in the LNCaP prostate cancer cell line.⁴³

Functional enrichment of prostate cancer credible causal variants

We used the hypergeometric tests to investigate the enrichment of credible causal variants (CCVs) in specific genomic features, including prostate-specific DNaseI hypersensitivity sites, ChIP-seq peaks of transcription factors, and histone marks (material and methods). We observed significant enrichment of CCVs in active regulatory regions (defined by H3K27ac and H3K4me1 marks), active gene promoters (defined by H3K4me3 and H3K9ac marks), actively transcribed gene bodies (defined by H3K36me3 and H3K79me2 marks), and DNaseI hypersensitivity sites (Figure 3A; Table S6). CCVs were also significantly enriched in the binding sites of various transcription factors (Figure 3B; Table S6), including AR (androgen receptor), FOXA1, and NKX3.1.

Figure 3.

Functional enrichment of credible causal variants

(A and B) Enrichment of credible causal variants in prostate-specific (A) histone marks and DNaseI hypersensitivity sites (B) top 10 transcription factor binding sites. Hypergeometric test p values are adjusted using the Benjamini-Hochberg (BH) method.

(C) A linear regression model is fitted for the logarithm of per-SNP heritabilities of tag SNPs using the functional annotations of tag SNPs as predictors. Effect sizes and adjusted p values of significant functional annotations are shown. p values are adjusted using the BH method. Significance is defined as p_adj < 0.05.

To formally evaluate the relationship between the biological functions associated with SNPs and their contributions to the risk of PrCa, we fitted a linear model for the logarithm of per-SNP heritability (i.e., the posterior mean of squared effect size) of all 1,342,199 tag SNPs using the following functional annotations of SNPs as predictors: (1) 11 gene-based annotations extracted from the dbSNP database (build 151)³⁸; (2) cis- and trans-eQTLs within PrCa tissues from the TCGA database³⁹; (3) cis-eQTLs within normal prostate tissues from the GTEx v.8 database⁴⁰; (4) DNaseI hypersensitivity sites, ChIP-seq peaks of 48 transcription factors and 9 histone modifications from normal prostate or prostate cancer cell lines, obtained from the Cistrome Data Browser⁴¹; (5) enhancer elements identified by Hi-C data and H3K27ac ChIP-seq peaks in normal prostate (RWPE1) and prostate cancer (C42B and 22Rv1) cell lines⁴²; and (6) enhancer elements predicted by H3K27ac HiChIP in the prostate cancer cell line LNCaP.⁴³ In addition, log(f(1 – f)) and log(LD score) were included as covariates, where f is the minor allele frequency of SNP. This analysis revealed that cis-eQTL (TCGA) (p_adj = 1.3 × 10⁻¹³⁷), cis-eQTL (GTEx) (p_adj = 4.6 × 10⁻⁵⁴), and enhancer (H3K27ac HiChIP, LNCaP) (p_adj = 3.3 × 10⁻⁴⁷) were the most significant three annotations associated with per-SNP heritability (Figure 3C; Table S7). trans-eQTL (TCGA) (p_adj = 2.1 × 10⁻⁸) exhibited the largest effect size (0.36). Notably, HDAC1 (histone deacetylase 1) binding site was the only significant functional annotation with a negative effect on per-SNP heritability. These findings indicated that genetic variants influencing gene expression levels and enhancer activity play a crucial role in the development and progression of PrCa.

Putative target genes of prostate cancer credible causal variants

To identify potential target genes of CCVs, we integrated various sources of information, including gene-based annotations from the dbSNP database (build 151), eQTL data, and enhancer-promoter interaction data from Hi-C and HiChIP experiments (material and methods). As a result, we identified 369 protein-coding genes as potential target genes of CCVs across all 95% CSs (Figure 4A; Table S5).

Figure 4.

Putative target genes associated with credible causal variants

(A) Venn diagram showing the numbers of putative target genes inferred from different sources of information.

(B) Enrichment of putative target genes in pathways from Gene Ontology Biological Processes and WikiPathways. Hypergeometric test p values are adjusted using the BH method. Pathways with p_adj < 0.005 are shown.

We further conducted pathway enrichment analysis to gain insights into the biological functions and processes associated with these putative target genes. Our analysis revealed significant over-representation of these genes in 29 non-redundant pathways at an FDR of 0.05 (Figure 4B; Table S8). Notable enriched pathways included prostate gland development, DNA damage response (only ATM dependent), positive regulation of transcription by RNA polymerase II, and regulation of mitotic cell cycle. The enrichment of putative target genes in cellular response to BMP (bone morphogenetic protein) stimulus, collagen catabolic process, and definitive hemopoiesis pathways may be attributed to the involvement of these processes in PrCa bone metastasis.^54,55,56 Furthermore, putative target genes were also over-represented in toxin transport pathway. Although previous studies have reported associations between PrCa and several genes in toxin transport pathway, such as SLC22A1–A3,^57,58 the relationship between PrCa and this pathway is not well elucidated and needs further investigation.

Discussion

In this article, we present h2-D2, a fine-mapping model that utilizes a continuous global-local shrinkage prior. As an extension of R2-D2, h2-D2 is designed for GWAS data where the phenotype values are standardized. Unlike existing fine-mapping methods that rely on discrete mixture priors, h2-D2 does not impose a constraint on the maximum number of causal variants and allows for the exploration of a wider range of causal configurations. In addition, h2-D2 does not rely on assumptions regarding the distribution of causal variant effect sizes, and is compatible with infinitesimal effect assumption for non-causal variants, which has been adopted by some recent works in fine mapping.^59,60 These features ensure the applicability and flexibility of h2-D2 in various scenarios.

We develop an efficient MCMC algorithm for h2-D2 to sample from the posterior distribution. We utilize several strategies to accelerate the mixing of MCMC chains, allowing for a more extensive exploration of the model space. Simulation studies show that h2-D2 is less likely to get trapped into local optima and performs better in variable selection, effect size estimation, and calibration than discrete-mixture-prior-based methods including SuSiE and FINEMAP. This may be due to the property of continuous priors that the coefficients are updated continuously and the transitions among local modes can be smooth. Our results also highlight the importance of using accurate LD matrices derived from adequately large reference panels, which concurs with previous discoveries.^12,61

Another important contribution of our work is that we propose an inference approach to define credible sets in the framework of continuous priors, which addresses the limitation of continuous priors that do not yield selection results directly. Simulation studies show that the CSs produced by h2-D2 can achieve the target level of coverage, are well powered when using in-sample LD matrices, and exhibit an improved control of FDR when using mismatched LD matrices. These results suggest the robustness and effectiveness of our proposed approach. Theoretical properties of the credible level defined for multiple SNPs deserve further investigation. Additionally, we acknowledge that the greedy search algorithm used to identify credible sets may not always yield the optimal sets and may miss some sets (supplemental methods). Further refinement and improvement of the algorithm are needed to enhance its performance.

In the real data application on a prostate cancer GWAS, we identified several causal signals that have not been previously reported. Variants in 95% CSs are significantly over-represented in prostate-specific epigenetic marks associated with activation of gene transcription. Through integrating gene-based annotation of SNPs, eQTL, Hi-C, and HiChIP data in prostate cell lines, we identified 369 potential target genes of variants in 95% CSs. These genes are enriched in prostate development and cancer-related pathways.

As a future direction, fine-mapping resolutions may be improved by integrating functional annotations into the h2-D2 prior. Stratified LD score regression-based methods like PolyFun⁶² are well suited to be incorporated with h2-D2, since h2-D2 prior is imposed on the per-SNP heritability directly. Furthermore, h2-D2 can also be extended to multi-trait fine mapping. Given the widespread existence of pleiotropy, fine-mapping multiple traits simultaneously has the potential to enhance the power of identifying shared causal variants among traits.^63,64,65 Jointly analyzing multiple traits may provide valuable insights into the genetic architecture underlying complex diseases and traits and improve our understanding of the shared genetic basis between different phenotypes.

Data and code availability

The UK Biobank data were accessed under application number 28732. Prostate cancer summary data are available from the PRACTICAL Consortium (http://practical.icr.ac.uk/blog/?page_id=8164). Enhancer-promoter loops identified from Hi-C data in RWPE1, C42B, and 22Rv1 cell lines are available at https://static-content.springer.com/esm/art%3A10.1038%2Fs41467-019-12079-8/MediaObjects/41467_2019_12079_MOESM7_ESM.xlsx. Annotated H3K27ac HiChIP loops in LNCaP cell line are available at https://ars.els-cdn.com/content/image/1-s2.0-S0002929721004195-mmc3.csv. The software h2D2 is available at https://github.com/xiangli428/h2D2. Scripts and data related to PrCa fine-mapping analysis are available at https://github.com/xiangli428/PrCaFineMapping.

Published: January 2, 2024

Web resources

• 1000 Genomes Project on GRCh38, https://www.internationalgenome.org/

• BEDTools, https://bedtools.readthedocs.io/en/latest/

• bigsnpr, https://privefl.github.io/bigsnpr/

• Cistrome, http://cistrome.org/

• dbSNP (build 151) with GRCh37.p13 as reference assembly, https://ftp.ncbi.nih.gov/snp/organisms/human_9606_b151_GRCh37p13/

• FINEMAP, http://christianbenner.com/

• GeneCodis, https://genecodis.genyo.es/

• GTEx V8, https://gtexportal.org/home/

• LDetect, https://bitbucket.org/nygcresearch/ldetect/src/master/,

• PancanQTL, http://gong_lab.hzau.edu.cn/PancanQTL/

• Plink, https://zzz.bwh.harvard.edu/plink/

• Prostate cancer summary data, http://practical.icr.ac.uk/blog/?page_id=8164

• SuSiE, https://github.com/stephenslab/susieR

• UK Biobank, https://www.ukbiobank.ac.uk/

Supplemental information

Table S1. List of 100 blocks on chr2 selected for simulation studies

For each block, the 1-based start coordinate and end coordinate in GRCh37 are shown (both positions are inclusive).

Table S2. Numerical results of simulation studies

For each setting and each method, the average values and standard errors across 100 simulated datasets for all metrics are reported.

Table S3. Numerical results of calibration in simulation studies

For each setting and each method, the results of 100 simulated datasets are aggregated, and the SNPs are divided into 4 bins based on their CLs or PIPs. For each bin, we report the number of variants, the expected proportion of causal variants, the true proportion of causal variants as well as the lower bound and upper bound of its 95% Wilson score confidence interval.

Table S4. Numerical results of the coverage of 95% CSs grouped by the sizes of CSs in simulation studies

For each setting and each method, the 95% CSs of 100 simulated datasets are aggregated, and separated into groups according to their sizes. The number of CSs within each group and the number of CSs contain at least one causal variant within each group are shown.

Table S5. Full list of variants in 95% CSs identified by h2-D2 in prostate cancer fine-mapping analysis

For each variant, we report the information contained in meta-analysis summary data, h2-D2 fine-mapping summary statistics, as well as detailed annotations. In addition, if the variant is in a CS identified by Dadaev et al. or Giambartolomei et al. we reported the fine-mapping region.

Table S6. Enrichment of variants in 95% credible sets within DNaseI hypersensitive sites, ChIP-seq peaks of histone marks, and transcription factor binding sites

For each annotation, we report the name of factor, the GEO accession number, the ID in CistromeDB, the type of annoation (HM: histone modification, TF: transcription factor), the odds ratio, the P-value and the BH-adjusted P-value of hypergeometric test.

Table S7. Estimated regression coefficients of linear model fitting log β 2 of tag SNPs by all functional annotations

For each annotation, we report the name of annoation, the type of of annoation, the estimated regression coefficient as well as its standard error, t-value, P-value, and BH-adjusted P-value.

Table S8. Enrichment of putative target genes regulated by credible causal variants within pathways from GO Biological Process and WikiPathways

Redundant pathways were removed (material and methods). For each pathway, we report the database, description, ID, the number of putative target genes found in this pathway, the number of putative target genes contained in the database, the number of genes in this pathway, the number of genes in the database, P-value, BH-adjusted P-value, relative enrichment, odds ratio, and the names of putative target genes found in this pathway.