Thin-film transistor for temporal self-adaptive reservoir computing with closed-loop architecture

Abstract

Reservoir computing is a powerful neural network–based computing paradigm for spatiotemporal signal processing. Recently, physical reservoirs have been explored based on various electronic devices with outstanding efficiency. However, the inflexible temporal dynamics of these reservoirs have posed fundamental restrictions in processing spatiotemporal signals with various timescales. Here, we fabricated thin-film transistors with controllable temporal dynamics, which can be easily tuned with electrical operation signals and showed excellent cycle-to-cycle uniformity. Based on this, we constructed a temporal adaptive reservoir capable of extracting temporal information of multiple timescales, thereby achieving improved accuracy in the human-activity-recognition task. Moreover, by leveraging the former computing output to modify the hyperparameters, we constructed a closed-loop architecture that equips the reservoir computing system with temporal self-adaptability according to the current input. The adaptability is demonstrated by accurate real-time recognition of objects moving at diverse speed levels. This work provides an approach for reservoir computing systems to achieve real-time processing of spatiotemporal signals with compound temporal characteristics.

Recurrent neural network with self-adaptability is implemented in thin-film transistors for spatiotemporal signal processing.

INTRODUCTION

The neural network–based computing paradigm offers the possibility of processing information with extremely high energy efficiency and handling the avalanche of spatiotemporal data generated at an ever-increasing rate (1–4). Recently, recurrent neural network (RNN) has shown remarkable strength in dealing with spatiotemporal data (5, 6). Nonetheless, the complicated internal connections of the conventional RNN require massive memory for storage. Coupled with the vanishing and exploding gradient issues, the training and hardware implementation of RNN are complex and costly (7, 8).

As a variant of RNN, reservoir computing (RC) is proposed by replacing the complex recursive network with relatively fixed nonlinear reservoirs (9, 10). A typical RC system consists of reservoirs for mapping input into high-dimensional space and a readout network for analyzing the high-dimensional reservoir states. In general, only the readout network requires training, which can be accomplished with simple methods such as the back-propagation algorithm and linear regression. Therefore, the training cost is substantially reduced (11). Another crucial characteristic of reservoirs is the fading memory (FM), which means that the reservoir state is influenced by input from the recent past while independent of that from the far past (12–14). With this feature, RC can reveal the implicit correlation of temporal patterns. In recent years, RC has succeeded in a broad range of applications, such as temporal pattern classification and prediction (15–17). Various physical systems have been proposed for hardware implementation of the reservoir, including the coupled mechanical oscillator (18, 19) and photonic system (20, 21). However, these systems are still relatively restricted in processing speed, power efficiency, and scalability, and are mostly not compatible with the modern integrated circuit (22).

Benefitted by the theory developed for RC with a single nonlinear node (14, 23, 24), constructing RC systems with electronic devices, including memristor devices (25–29), ferroelectric devices (30–32), nanowire network (33–35), and spintronic oscillator (36–38), is successfully demonstrated with the advantages of small area, simple structure, and high power efficiency. The intrinsic nonlinearity and randomness of the device can be naturally used to promote the richness and separability of reservoir states and thus can further improve the system performance. By far, these hardware RC systems have shown strong capability in diverse temporal processing tasks, such as recognizing spoken digits (26, 31, 39) and medical signals (40, 41), as well as forecasting chaotic systems (42–44).

However, a fundamental problem still lies in the way of its further application. The temporal dynamics of the reservoir, as key hyperparameters, would notably affect the system performance in a highly task-specific manner (14, 41, 45, 46), which means that for the optimization of the system, deliberate adjustment of the reservoir is generally required. In contrast, the electronic devices implementing physical reservoirs are used as a “black box,” resulting in the characteristics of reservoirs being determined by the fabrication process, and therefore are normally not adaptive. This conflict has rendered most precedent systems only applicable for tasks with a timescale matching specific physical devices.

A compromising solution addressing this challenge is to rescale the recorded temporal data to adapt to the temporal dynamics of the hardware RC system (26). However, this will cost excessive latency and storage overhead and is especially not in favor of real-time processing. A superior solution would be the development of electronic devices capable of reservoir adaptation, which has been experimentally shown to be effective in extracting information from multiple temporal levels (41, 45). However, it still requires the knowledge of the optimal reservoir characteristics for specific tasks in advance, which places a severe obstacle in the actual applications because the timescale is usually an unknown and constantly varying quantity.

In this work, we fabricated an indium gallium zinc oxide (IGZO) thin-film transistor (TFT) with controllable temporal dynamics, which shows excellent cycle-to-cycle uniformity as well as the four-order-tunable timescale. On the basis of the device, we experimentally demonstrated a temporal adaptive reservoir where the operation voltage can easily adjust the hyperparameter timescale (τ). By matching the temporal dynamics and applying a multi-timescale strategy, this RC system outperforms its temporal invariant counterpart in classifying six human activities, improving the accuracy from 84.2 to 96.7%. Moreover, we proposed a closed-loop architecture that can dynamically adjust the reservoir hyperparameters by self-feedback to flexibly adapt the system to present input signals. We experimentally verified this design in a real-time motion classifying task containing vastly different speed conditions. This work shows a back-end-of-line (BEOL) compatible approach for implementing the temporally controllable hardware RC system based on a simple physical structure. It further presents a promising solution to self-adaptively optimize the hyperparameters in the RC systems toward a broad input spectrum.

RESULTS

Temporal adaptive RC

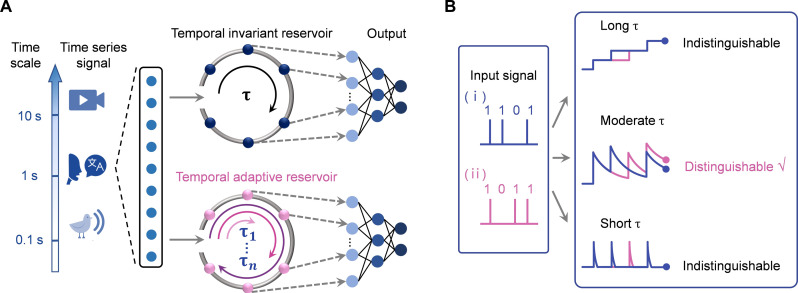
Figure 1A shows the structure of RC systems, which consists of multiple dynamical nodes implemented with single devices and a readout network. The physical device functions as the reservoir, wherein the current evolves under the joint effect of input stimulus and FM. Because the chronological information varies for different inputs, the current responses are also different. Thus, we can use the device conductance as the input of the readout network to classify the input temporal series.

Fig. 1. Temporal adaptive reservoir.

(A) Schematic of the concept of temporal adaptive reservoir. The recurrent structure of RC enables it to capture the temporal correlation in time series. Reservoir with variable temporal dynamics is more advantageous than temporal invariant reservoir, given that the input signals in practical scenarios usually have diverse timescales that may differ by several orders in length. (B) Temporal dynamics of the reservoir have a crucial influence on the separability of reservoir states. Either too long or too short reservoir temporal scale will lead to confusion of final states and, finally, the failure of subsequent neural networks. Moderate temporal scale is essential for optimizing the RC system.

However, the interval of the input stimulus should be comparable to the FM timescale (τ) of the physical devices. If τ is too long compared to the temporal scale of input data, the chronological relationship will be overwhelmed because input at any time point will impose nearly equal effects on the final output. On the other hand, if τ is too short for the input data, the effect of former input will decay too fast to couple with later input. We adopted an example to illustrate this point straightforwardly as shown in Fig. 1B, where the reservoir output will rise upon input spikes, and gradually decay because of the FM. This example shows that with either too long or too short τ, the reservoir states corresponding to input series “1101” and “1011” will be completely confused, resulting in failure in classification. Two distinguishable states are generated only with moderate τ (see fig. S3).

Considering that the input spatiotemporal data in practical applications may greatly differ in timescale, we propose a temporal adaptive reservoir as shown in Fig. 1A. This configuration has adjustable temporal dynamics and is optimizable toward specific input. In such a configuration, the devices used as reservoirs capable of controllable FM characteristics are of vital importance.

TFT device

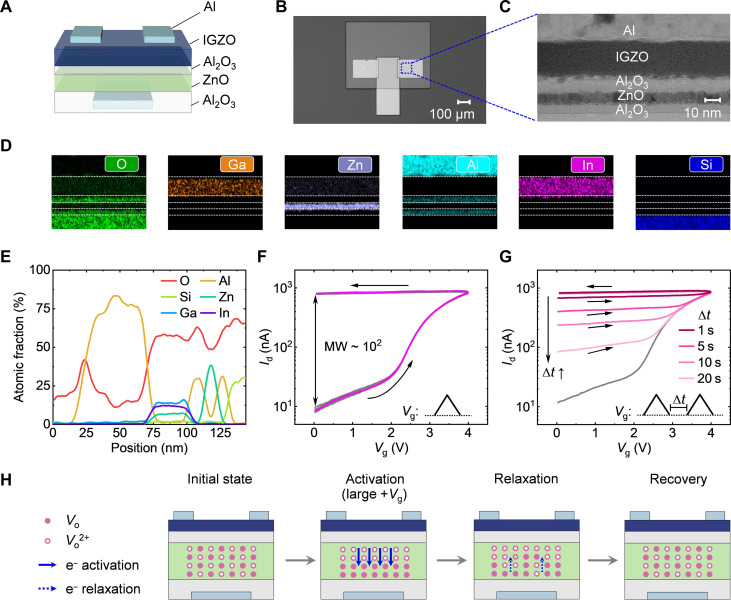
The structure of our proposed FM TFT is shown in Fig. 2A. Al is sputtered for gate/drain/source electrodes, while 30-nm IGZO is sputtered as the channel. With the aim of introducing memory characteristics to this device, we deposited 10-nm ZnO as an interlayer between the gate and channel and insulated it with two atomic layer deposition (ALD) Al₂O₃ layers. The thickness of both insulation layers is 6 nm. The device structure is then validated by morphology and elemental characterization. Figure 2B shows the optical microscope photo. Figure 2C shows the transmission electron microscope (TEM) photo of the intersection of the marked region in Fig. 2B in which clear and uniform edges are observed. We performed the energy-dispersive spectrum (EDS) mapping and EDS line scanning to characterize the elemental distribution, as shown in Fig. 2 (D and E).

Fig. 2. Structure and characterization of the FM TFT.

(A) Structure of the proposed FM TFT. The drain, source, and gate electrodes are composed of Al. IGZO is used as channel material. In addition, an interlayer of ZnO is deposited between the gate and the channel. The insulation layers are all composed of Al₂O₃. (B) Optical microscope photo of FM TFT. (C) Transmission electron microscope (TEM) photo of the intersection. (D) EDS mapping. (E) EDS line scanning result. (F) MW of 10 repeated DC sweep measurements. The gate voltage sweeps from 0 to 4 V and back to 0 V. The drain voltage keeps at 0.5 V. Obvious MW can be observed afterward. (G) FM effect. Two identical DC sweeps are consecutively applied to the gate electrode. The residual MW diminishes gradually as the time interval Δt increases, showing FM behavior. (H) Physical mechanism of the FM behavior. The change of drain current is caused by the redistribution of oxygen vacancies in ZnO.

We observed the expected memory characteristic through the DC measurement, as shown in Fig. 2F. We applied a double sweep voltage to the gate electrode that ramps from 0 to 4 V and then back to 0 V. During this period, the voltage of the drain electrode is kept as 0.5 V, while the source electrode is grounded. The source electrode is always kept at 0 V if not specified in the following measurements. The drain current (I_d) shows apparent counterclockwise hysteresis during the double sweep with a memory window (MW) of around 10². The results of 10 repeated measurements are plotted in a gray line, indicating a uniform memory characteristic. We also found the MW increasing as the sweep voltage rises (see fig. S4). It is notable that the memory is volatile. Repeating the double sweep after a time interval Δt (Fig. 2G), we show that as Δt increases, the residual MW gradually decreases before eventually returning to zero.

We speculate that the physical mechanism of FM behavior is the redistribution of electrons among the oxygen vacancies in the ZnO layer (Fig. 2H) (47–49). There exist many oxygen vacancies (V_o) in ZnO, which are electrically neutral and will become positively charged V_o²⁺ if not occupied by electrons, i.e., V_o → V_o²⁺+2e⁻. When applying positive gate voltage (V_g), electrons in V_o are activated away from the initial energy level. They are then swept toward the gate and retrapped by defect level, leaving more V_o²⁺ localized near the IGZO channel. Although the overall charge conservation still holds, charges closer to the channel will enforce a stronger electrostatic effect (note S1). Therefore, the IGZO bandgap is bent down by V_o²⁺, resulting in a higher drain current. After removing the positive gate voltage, the electrons undergo relaxation and gradually recover to the initial distribution, which is also reflected by the gradual decrease of drain current. This whole process is elaborated with the bandgap illustration in fig. S5. The charge accumulation analysis is shown in fig. S6.

Modulation of temporal dynamics characteristics

To explore the modulation method of the FM behavior, we measured and analyzed the responsive drain current with different input voltage pulses. Figure 3A illustrates the waveform of voltage for measurement. The voltage pulse is applied to the gate electrode. Three pulse parameters are extracted for investigation: pulse width, pulse amplitude (V_pulse), and base voltage (V_base). Meanwhile, a constant voltage is applied to the drain electrode. We show the response of the drain current to a single positive gate voltage pulse in Fig. 3B, in which an abrupt increment ΔI_d is aroused by the stimulus, followed by the gradual relaxation of I_d until it eventually restores to the initial state. We found that the FM behavior curve is well fitted by the stretched-exponential expression

$$I(t)=I_0+\mathrm{\Delta }{I}_{\mathrm{d}}\text{exp}[-{\left(\frac{t-t_0}{\mathrm{\tau }}\right)}^{\mathrm{\beta }}]$$ (1)

Fig. 3. Modulation of the FM behavior.

(A) Waveform schematic of the pulse for measurement. Square-wave voltage signal is applied to the gate electrode, while a constant voltage is applied to the drain electrode. Pulse width, V_pulse, and V_base are marked in the figure. For all the following experiments, the source voltage is 0 V. (B) Model and the experimental result of the FM behavior. The relaxation of drain current after a single pulse is well fitted by the stretched-exponential relaxation model. The increment of drain current ΔI_d and the relaxation time τ are extracted to describe FM characteristics. (C and D) FM behavior of various pulse widths (5 to 25 μs), with V_pulse = 4 V, V_base = 0 V, and drain voltage = 0.1 V. Pulse width shows facilitation effect on ΔI_d, while negligible influence on τ. (E and F) FM behavior of various V_pulse (3.5 to 4.5 V), with pulse width of 20 μs, V_base = 0 V, and drain voltage = 0.1 V. V_base also shows facilitation effect on ΔI_d, while negligible influence on τ. (G and H) FM behavior of various V_base (0 V to −2 V), with a pulse width of 20 μs, V_pulse = 4 V, and drain voltage = 0.1 V. V_pulse shows facilitation effect on both ΔI_d and τ, inducing a remarkable modulation range of the relaxation time τ.

This is a commonly used model for characterizing the relaxation mechanism in systems with randomly positioned traps (50), where an inhibitory temporal factor β∈(0,1) is introduced to modify the classic exponential decay relationship. β represents the physics image that the recombination rate continuously decreases with the depletion of remaining traps. The matching between the stretched-exponential model and our experimental result coincides with the aforementioned physical mechanisms.

In the following, we look into how the input pulse affects the magnitude of responsive current ΔI_d and the temporal characteristic constant τ. Figure 3C shows the current response to pulses with different widths (5 to 25 μs). Longer pulse width results in higher ΔI_d but almost unchanged τ, as shown in Fig. 3D. This is because the redistribution of electrons and the subsequent current increment are more prominent with longer activation time. Figure 3E shows the current response to pulses with different V_pulse (3.5 to 4.5 V). Similarly, higher V_pulse gives rise to higher ΔI_d and almost unchanged τ, as shown in Fig. 3F, because the activation rate is promoted under higher activation bias. In both cases, τ is almost unaffected, which is easily understood because the relaxation process is irrelevant to the activation condition. Inspired by this, we measured the responsive current under multiple V_base conditions (−2 to 0 V) as shown in Fig. 3 (G and H). Results show that not only ΔI_d increases with V_base but also τ is changed substantially. Specifically, τ gets smaller when V_base gets more negative. This is because more negative gate voltage will accelerate the recovery of the distribution of V_o²⁺ by lifting the bandgap of ZnO and eventually leading to faster relaxation. Repeated measurements with a broader variation range of V_base have shown a remarkable modulation range of τ (around 10⁴) with good uniformity (see fig. S7). Moreover, the broad applicability of this modulating method is confirmed in fig. S8, in which the relation of τ-V_base still holds in various pulse conditions. Last, we have examined the influence of V_base modulation on other device parameters. It is observed that the modulation has no clear effect on β (fig. S9). The impacts on initial current state and the activation process are also measured and analyzed in figs. S10 and S11. In conclusion, the temporal dynamics of this TFT device can be easily adjusted within a broad range, providing a feasible platform for hardware implementation of temporal adaptive RC.

Characteristics for RC

Enabled by the FM TFT, we constructed a hardware RC system. To verify its performance and reliability, we looked into the separability, cycle-to-cycle uniformity, and endurance. In this part, these three characteristics will be discussed respectively.

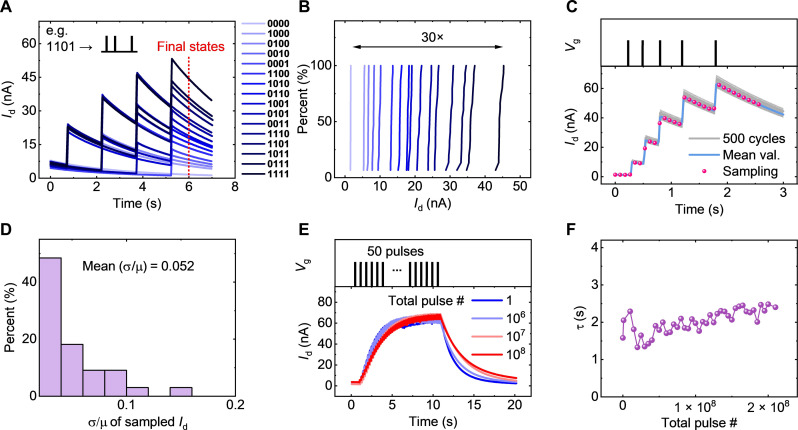
To verify the separability of reservoir states generated by FM TFT, we applied a series of 4-bit pulse sequences representing 16 different inputs (Fig. 4A). After the pulse sequence, we sampled the responsive current and took it as the reservoir state. It is observed that the 16 final states are distinguishable from each other. The excellent separability is more straightforwardly shown through the cumulative probability distribution in Fig. 4B, where no obvious overlap exists among the reservoir states by virtue of a relatively large output range of nearly 30 times.

Fig. 4. Characteristics of the hardware-implemented reservoir.

(A) Experimental readout current of FM TFT in response to 16 different pulse sequences. (B) Cumulative probability distribution of the final states in (C). Sixteen distinguishable drain current states are observed, with a large range of nearly 30 times. The time point of sampling final states is marked by the dashed line in (A). (C) Experimental cycle-to-cycle variation test of FM TFT. The same spike sequence is applied to gate electrode for 500 times. The readout current shows good uniformity. (D) Cycle-to-cycle variation level of readout current sampled from 30 uniformly distributed time points in (C). The deviation represented by σ/μ is calculated for each time point. The histogram shows that σ/μ of most time points is within 0.1, indicating good uniformity. (E) Experimental endurance test of FM TFT. The response of drain current to 50 consecutive pulses is used to represent the reservoir characteristics. As the number of total pulses increases to 10⁸, the curve of responsive current shows no obvious degradation. (F) Evolution of τ in the endurance test. The stability of τ is maintained during the 2 × 10⁸ positive pulses.

Cycle-to-cycle uniformity is another important figure of merit for hardware reservoirs because its variation is usually one of the main origins of errors in RC. We examined this characteristic by repeatedly applying a certain pulse sequence for 500 times and analyzing the variation, as shown in Fig. 4C. To ensure credibility and representativeness, the pulse sequence for the test was extracted from the experimental demonstration of human activity recognition (HAR), which will be introduced later. Results through 500 cycles have shown excellent uniformity of the responsive FM behavior, with almost identical τ and only slight variation in ΔI_d. For a more quantitative analysis, we took the uniformly sampled 30 current values as the reservoir output within each cycle—the same as the sampling method adopted in the HAR demonstration—and examined its uniformity. The variation of reservoir output throughout 500 cycles is shown in Fig. 4D, with a very small mean σ/μ of 0.052, indicating high cycle-to-cycle stability of the reservoir output. Our further simulation has shown that such cycle-to-cycle variation will only pose a negligible influence on the overall accuracy of the RC system (fig. S12). We have also measured multiple devices for the V_g-sweep behavior, the single-pulse response, and the modulation of FM behavior (figs. S13 to S15). The qualitatively identical activation behavior and relaxation behavior are observed for different devices. The applicability of the modulation scheme is also confirmed.

Moreover, to verify the endurance of the hardware reservoir, we applied positive pulse trains (width = 5 μs, V_pulse = 3.5 V, V_base = −0.2 V, V_d = 0.1 V) to the gate electrode and investigated the degradation of FM behavior. To emulate the real working process of the reservoir, we use the response of the drain current toward 50 consecutive pulses to characterize the FM behavior (Fig. 4E). During the application of 50 pulses, the drain current gradually rises until saturation and then drops after removing the pulses. As the total number of pulses accumulates to 10⁸, the responsive curve still exhibits normal FM behavior with only slight drifting, which means that the hardware reservoir has reliable endurance. We show in Fig. 4F that no noticeable degradation is observed for τ even when the total pulse number reaches 2 × 10⁸. Extra measurement is also conducted to investigate the gradual degradation process that occurs when pulse number keeps accumulating (fig. S16). It is notable that the excellent endurance of more than 10⁸ is advantageous for the hardware implementation of the RC system. The FM TFT implemented reservoir also has advantages in power efficiency due to the relatively low working current (see fig. S17).

Hardware implementation of temporal adaptive reservoir

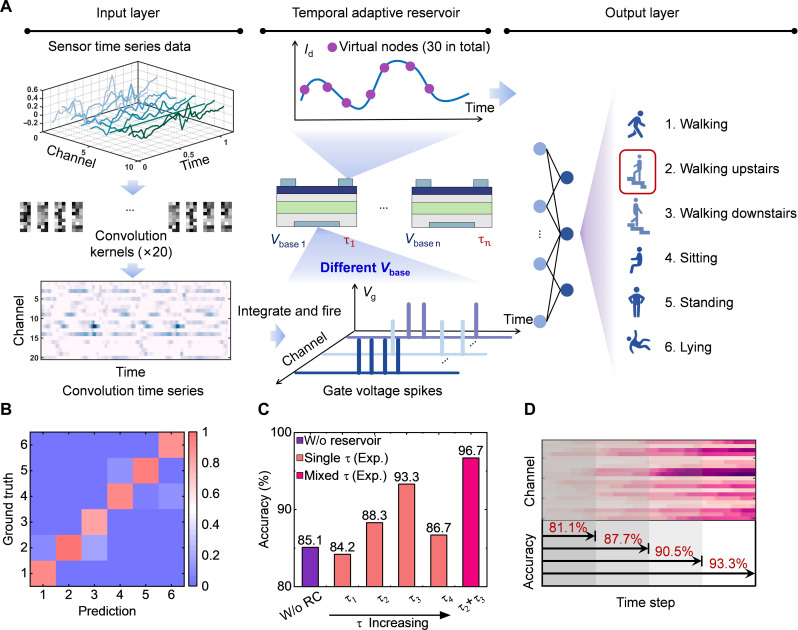
Here, we used the RC system constructed by FM TFT devices to experimentally demonstrate the temporal adaptive reservoir (Fig. 5A). To examine the performance, the system is applied for recognizing six human activities on the basis of the Human Activity Recognition Using Smartphones dataset (51). Details about the dataset are provided in Materials and Methods. First, the input spatiotemporal signal is fed into 20 random convolution kernels, generating a 20-channel outcome. The detailed configuration of the convolution kernels is shown in fig. S18. It is reported that completely random convolution ahead of RC can effectively promote accuracy although having a slight drop compared to the fully trained convolutional kernel (52). Then, we convert the convolution outcome into the pulse sequence with the integrate-and-fire principle, which will be inputted into the hardware reservoir. The hardware reservoir is implemented by FM TFT, where the gate voltage is the input and the drain current is the output. The “virtual node” method is adopted here, which refers to constructing the reservoir with the sequential output of a single physical nonlinear node (42). Here, we applied the 20-channel pulse sequence to the gate and uniformly sampled 30 output nodes from the responsive drain current for each channel. Notably, the reservoir is temporal adaptive as we can adjust the timescale τ by changing V_base of the input voltage sequence. Last, we combined the sampled current of all channels and transferred the reservoir output into a fully connected neural network (FCN) for classification. The FCN has 600 input nodes and 6 output nodes, with two hidden layers of 100 × 50. It uses tanh as the activation function and is trained with the back-propagation method based on the training dataset.

Fig. 5. Temporal adaptive reservoir based on FM TFT.

(A) Illustration of the hardware temporal adaptive reservoir implemented with FM TFT. The input time series are first fed into 20 random convolution kernels. The convolution output is then converted into pulse sequences following the integrate-and-fire method. While the pulse sequences are applied to the gate voltage of FM TFT, the drain current is sampled as virtual nodes, which are then fed into a 600 × 100 × 50 fully connected neural network for classification. This RC system can complete the recognition of six human activities (walking, walking upstairs, walking downstairs, sitting, standing, and lying). (B) Confusion matrix of experimental recognition outcome for τ₃ condition. (C) Comparison of experimental accuracy of different temporal characteristics. As τ increases (τ₁ = 0.38 s, τ₂ = 2.42 s, τ₃ = 5.20 s, and τ₄ = 7.51 s), the accuracy first rises and then falls. Mixed-τ system combining the output of τ₂ and τ₃ conditions shows a higher accuracy of 96.7% with the same reservoir size. (D) Experimental result of prediction functionality. Good recognition result is obtained even with incomplete input data.

In the experiment, four V_base conditions (V_base = −0.8, −0.6, −0.4, and −0.2 V) with varied reservoir temporal dynamics (from τ₁ to τ₄) are performed, respectively, with the intermediate outcome shown in fig. S19. The confusion matrix of the recognition result for τ₃ is depicted in Fig. 5B. After 200 training epochs, the six activities—walking, walking upstairs, walking downstairs, sitting, standing, laying—are correctly classified for most samples in the testing set, proving good capability of this RC system. The comparison of the performance of diverse temporal conditions can be seen in Fig. 5C. As τ increases from τ₁ to τ₄, the recognition accuracy first rises and then falls. The peak value of 93.3% is reached at τ₃ = 5.20 s @ V_base = −0.4 V, while the lowest value of 84.2% is reached at τ₁ = 0.38 s @ V_base = −0.8 V. The difference in accuracy originates from the fact that the temporal patterns in the HAR dataset have intrinsic timescales and can be classified with the optimal precision by reservoirs that have matched temporal dynamics. This result proves that the system performance can be optimized by adjusting τ to match the task. Furthermore, we performed a mixed-τ scheme with the experimental data of two out of the measured devices and proved its effectiveness. By constructing the reservoir states with channels selected half from the τ₂ condition and half from the τ₃ condition—the two better-performing cases, we obtained an even higher accuracy of 96.7% with an equal number of reservoir nodes. This improvement is attributed to the fact that the same reservoir can capture more features of diverse timescales by mixing different τ (53). Last, we found that acceptable recognition precision can be obtained even with incomplete input of the spatiotemporal data. We experimentally show this capability in Fig. 5D, where we input part of the HAR data (25, 50, and 75%) to the RC system. The system achieves >80% accuracy with only 25% data inputted, and it keeps rising as more portion is being fed with.

Closed-loop architecture for self-adaptive RC

Enabled by temporal adaptability, the scope of RC can be extended to temporal signals with remarkably different temporal dynamics. We conducted an experiment that identified the direction of objects moving at diverse speeds to verify this. We used a dataset developed by a recent work (54), which contains video clips of balls moving up, down, left, and right, with different moving speed levels included.

As for the processing flow of the RC system, we first down-sampled the image of each frame into 6 × 6 pixels. The images are then binarized by dividing from the median value. We constructed a pulse sequence for each pixel by connecting the adjacent frames, which will then be represented by the gate voltage and fed into the hardware reservoir as input (Fig. 6A). The method for measurement of reservoir states is the same as discussed in the HAR task. FCN with two hidden layers (300 × 100) and the back-propagation method is applied for readout. As indicated in the former part, because various speed conditions correspond to distinct timescales, the temporal dynamics that they need for the reservoir will also differ. To explore the optimal space of the temporal hyperparameter, we simulated the classifying process in various τ conditions. Expectedly, the result in Fig. 6B shows that shorter τ is required for classifying motion with faster speed, while longer τ is preferred for slower speed. The simulation result provides specific guidelines for setting the optimal τ according to a certain speed level.

Fig. 6. Closed-loop architecture for reservoir based on FM TFT.

(A) Input temporal signals of the real-time recognition task. The dataset is composed of video clips of ball moving up, down, left, and right, as well as empty scene (void). Video is first down-sampled to 6 × 6 pixels and then inputted to FM TFT in the form of voltage pulses. (B) The simulated recognition accuracy of various reservoir τ and object speed. It is indicated that accurate classification requires the matching between τ and the object. (C) Experimental result of real-time recognition in two speed conditions. τ is respectively chosen to match different timescales. High accuracy is achieved in both cases. (D) Schematic of the closed-loop structure for reservoir. The outcome of readout layer is used as feedback to adjust the hyperparameters of reservoir. (E) Correspondence relation of the feedback and output result. If the classification outcome shows that speed is too fast, V_base will be adjusted toward more negative to obtain shorter τ and vice versa. (F and G) Experimental demonstration of self-adaptive RC system with closed-loop structure. (F) Measured drain current. (G) Computing output of the RC system. Initially, the speed is 0.8 m/s and accurate real-time recognition is achieved. As the speed later increases to 8 m/s, a mismatch between τ and the speed is detected and then corrected by adjusting V_base from −0.5 to −1.5 V.

To verify that the temporal adaptive reservoir can fully process signals with diverse timescales, we experimentally applied the system to recognize objects at two notably different speeds: 40 and 0.04 m/s. Guided by the simulation outcome, we set τ = 0.014 s for the fast case and τ = 5.5 s for the slow case. The four moving directions are inputted sequentially in the order of up-down-left-right. Results in Fig. 6C show that accurate real-time classification is achieved for both speed levels.

Nevertheless, the optimization paradigm is strictly limited by far. The optimization of reservoir should be accomplished ahead of functioning, wherein the hyperparameters are adjusted to preferable values relying on the prior knowledge of the timescale of input signals and a look-up table of the optimal hyperparameter set. However, the last two requirements will be costly for real-time processing because the characteristics of input signals could be varying constantly, and the optimal choice of hyperparameter is usually unobtainable in advance. A more appealing solution is to let the RC system itself generate real-time instructions on the hyperparameter optimization.

On the basis of this idea, we designed a closed-loop architecture (Fig. 6D). The term “closed-loop” means using the output of the RC system as feedback to self-adaptively adjust the reservoir. To elucidate this architecture, we first clarify the mathematical form (14) of conventional RC as

$$\{\begin{array}{c}\mathbf{x}(n)=(1-\mathbf{\alpha })\odot \mathbf{x}(n-1)+\mathbf{\alpha }\odot f[\mathbf{x}(n-1),\mathbf{u}(n)]\hfill \\ \mathbf{y}(n)=\mathrm{\Psi }[\mathbf{x}(n)]\hfill \end{array}$$ (2)

where u (n) is the input at time step n, x (n) is the corresponding reservoir state, and y (n) is the computation output. α = [α₁, …, α_M] is the vector of leakage rate, where each element α_m = Δt/τ_m represents the leakage rate of the corresponding subreservoir, given the sampling interval of Δt. $\odot$ is the Hadamard product. f denotes the nonlinear transformation function, and Ψ denotes the readout layer. In contrast, the expression of the reservoir with the closed-loop structure is

$$\{\begin{array}{c}[{\mathbf{\alpha }}_n,f_n]=\mathcal{F}[\mathbf{y}(n-1)]\hfill \\ \mathbf{x}(n)=(1-{\mathbf{\alpha }}_n)\odot \mathbf{x}(n-1)+{\mathbf{\alpha }}_n\odot f_n[\mathbf{x}(n-1),\mathbf{u}(n)]\hfill \\ \mathbf{y}(n)=\mathrm{\Psi }[\mathbf{x}(n)]\hfill \end{array}$$ (3)

where $\mathcal{F}$ denotes the closed-loop feedback function. In the upgraded architecture, the hyperparameters in the reservoir (α and those implicitly contained in f) are no longer fixed. Instead, they are updated according to the latest historical computation outcome. Specifically, we reconstructed FCN as the readout layer to determine whether the temporal dynamics of the reservoir are matching with current input signals. The FCN was retrained with two more output labels: “speed too fast” and “speed too slow.” We set the correspondence between output and the closed-loop feedback as shown in Fig. 6E. When the RC system outputs speed too fast, meaning shorter τ is needed, V_base will be adjusted toward more negative, which will induce higher α_n in Eq. 3. When the RC system outputs speed too slow, V_base will be adjusted toward more positive. While if the correct moving direction is recognized or no moving object is detected at all, V_base will remain constant.

We experimentally demonstrated the closed-loop RC based on FM TFT. The RC system was used to perform the real-time recognition task at varying speeds. The speed has increased from 0.8 to 8 m/s in this experiment. In the first stage, V_base is set to be −0.5 V. In this condition, the temporal dynamics of the reservoir are well suitable for the object speed of 0.8 m/s. The RC system accurately classifies the moving direction. In the second stage, however, the object speed has then increased to 8 m/s and is thus too fast for present reservoir settings. Therefore, the RC system without the closed-loop architecture will no longer be able to correctly identify the moving direction (see fig. S20). In comparison, with the closed-loop architecture, the RC system can detect this mismatch as the recognition output being speed too fast. In the following third stage, the system reacts to the mismatch by adjusting the V_base level from −0.5 to −1.5 V. With the renewed temporal dynamics, the system restores its recognition accuracy at the speed of 8 m/s. So far, a complete real-time optimization process has been performed. The measured drain current is shown in Fig. 6F, and the comparison between the recognition outcome and the actual input is shown in Fig. 6G. The counterpart experiment in which the system reacts to speed too slow situation is also conducted as shown in fig. S21. The discrepancy of inference outcome at the beginning of each pattern transformation is because the input data used for calculation are from the near historical time steps. Last, we evaluated the extra cost of introducing the closed-loop architecture in fig. S22 and table S1, which show that only +0.31% energy consumption and +0.30% area overhead will be added to the FCN part. Thus far, we have verified the capability and efficiency of closed-loop architecture in optimizing the RC system for sophisticated temporal conditions.

DISCUSSION

In this work, we proposed a closed-loop architecture to address the limitation in self-adaptation of C, and experimentally performed real-time optimization in a hardware RC system. The demonstration is based on IGZO-channel TFT with ZnO interlayer. This device shows excellent cycle-to-cycle uniformity and endurance of 10⁸ and, the controllable FM characteristics. With this device, we constructed the temporal adaptive reservoir, where the temporal dynamics of the reservoir are changed by varying operation voltage. We proved its advantage over the trivial temporal invariant reservoir by applying this reservoir to a HAR task. We tested the reservoirs with various temporal constant τ and found that by choosing the optimal condition, accuracy is improved from 84.2 to 93.3%. On the basis of this, we applied a mixed-τ scheme to capture multi-timescale information and obtained a higher accuracy of 96.7%. Furthermore, we proposed a closed-loop architecture that can perform self-adaptive optimization of the reservoir hyperparameters. The closed-loop RC system is experimentally demonstrated in the task of real-time recognition of objects moving at speeds varying within a wide range. For example, the self-adaptive transition is performed as the moving speed changes from 0.8 to 8 m/s.

This work proves that the performance of hardware RC systems can be prominently improved by optimizing the hyperparameters. It also shows a method for the self-adaptive optimization of the RC system without additional external information. We mainly focused on the temporal characteristics of the reservoir by far, while precedent researches have also revealed the importance of other hyperparameters including the input gain, the scaling factor, and the feedback density (20, 21). Inspired by this, the effects of other hyperparameters remain to be elucidated in the context of closed-loop architecture. Future works may also involve more refined closed-loop architecture for more sophisticated scenarios. Besides, integrating the RC systems with closed-loop structures on chips will be a valuable and appealing topic.

MATERIALS AND METHODS

TFT fabrication

The Al gate electrode is deposited by RF sputtering on Si/SiO₂ (60 nm) substrate. Al₂O₃ (6 nm) is deposited by ALD at temperature of 100°C. ZnO (10 nm) is deposited by RF sputtering. After that, another 6-nm Al₂O₃ is deposited with the same condition. The IGZO channel is deposited by RF sputtering with pure Ar atmosphere at room temperature. Then, the Al drain/source is deposited by RF sputtering. The patterning method is lithography and lifting off. At last, the TFT goes through air atmosphere annealing at 200°C for 1 hour.

Characterization

The DC measurement is conducted with the source/measure unit (SMU) in B1500A semiconductor parameter analyzer (Keysight). For pulse characterization of FM, 81160A pulse generator and SMU are used. The TEM and EDS analysis are conducted in WinTech Nano in Suzhou, China.

HAR dataset

This dataset contains signals of six kinds of human activities recorded by Samsung smartphones, namely, walking, walking upstairs, walking downstairs, sitting, standing, and lying. Each sample contains nine-dimensional time series respectively collected by a three-axial gyroscope, a gravity accelerator, and a three-axial linear body accelerator. Each time series consists of 128 temporal steps, with the sampling frequency being 50 Hz. The duration of each sample is 2.56 s.

Measurement method for hardware reservoir

For the HAR demonstration, 81160A pulse generator and SMU are used. For the demonstration of real-time recognition of moving direction, the waveform generator/fast measurement unit in B1530 (Keysight) is used. The electrical signals are applied to and collected from the TFT device through probe. The readout current is normalized to [0,1] when feeding into the subsequent FCN.

In our demonstration, the input signals of different channels are sequentially applied to the same TFT device in consideration of operational simplicity. For practical application, different channels can be implemented with different physical devices for parallel processing. In this case, each device functions as a subreservoir. The influence of device-to-device variability would emerge when extending from single device to multiple devices. However, we estimate that this will not lead to performance degradation, as the quantitative difference in device characteristics will be learned by the subsequent FCN, let alone it has been reported (43) that for hardware RC based on multiple devices with characteristics that are quantitatively different but qualitatively identical, the device-to-device variability can actually promote the richness of reservoir states and therefore improve the capability of recognition.

Mathematical manifestation of reservoir states

The specific structure of reservoir states in the real-time processing demonstration is discussed as follows. We assume that the total number of applied reservoir channels is M (in this demonstration M = 36). For the channel m at time point n, we denote the input voltage as u_m,n, and the output drain current as x_m,n. In this way, the reservoir states and the corresponding input vector can be written as

$$\mathbf{x}(n)=\left[\begin{array}{c}{x}_{\mathit{1},n-S+\mathit{1}}\\ x_{\mathit{1},n-S+\mathit{2}}\\ ⋮\\ x_{\mathit{1},n}\\ ⋮\\ x_{M,n-S+\mathit{1}}\\ x_{M,n-S+\mathit{2}}\\ ⋮\\ x_{M,n}\end{array}\right]\mathbf{u}(n)=\left[\begin{array}{l}{u}_{\mathit{1},n-S+\mathit{1}}\\ u_{\mathit{1},n-S+\mathit{2}}\\ ⋮\\ u_{\mathit{1},n}\\ ⋮\\ u_{M,n-S+\mathit{1}}\\ u_{M,n-S+\mathit{2}}\\ ⋮\\ u_{M,n}\end{array}\right]$$ (4)

S denotes the length of total time steps that are included for reservoir processing in one single step, which in our experiment is set as S = 5.

Simulation method

To perform the simulation in Fig. 6B, we constructed a behavioral model of the device to characterize the responsive current to pulse stimulus. As suggested in Fig. 3B, this can be achieved by modeling the dependence of ΔI_d and τ on operation conditions. It is found that τ almost stays unchanged during various pulse conditions, while the magnitude of ΔI_d is greatly dependent on the I_d level. The specific relation and suspected mechanism are shown in note S1. Here, we applied a simple fitting function

$$\mathrm{\Delta }{I}_{\mathrm{d}}=\{\begin{array}{c}{a}_1{I}_{\mathrm{d}}^2+b_1{I}_{\mathrm{d}}+c_1,I_{\mathrm{d}}<I_{\mathrm{th}}\hfill \\ a_2{I}_{\mathrm{d}}^2+b_2{I}_{\mathrm{d}}+c_2,I_{\mathrm{d}}\ge I_{\mathrm{th}}\end{array}$$ (5)

where a₁, b₁, c₁, a₂, b₂, and c₂ are fitting coefficients that are decided by measured result. On the basis of this model, the simulated responsive current can well represent the experimental fact.

Supplementary Materials

This PDF file includes:

Note S1

Figs. S1 to S22

Table S1

References