Efficient designs and analysis of two-phase studies with longitudinal binary data

Abstract

Researchers interested in understanding the relationship between a readily available longitudinal binary outcome and a novel biomarker exposure can be confronted with ascertainment costs that limit sample size. In such settings, two-phase studies can be cost-effective solutions that allow researchers to target informative individuals for exposure ascertainment and increase estimation precision for time-varying and/or time-fixed exposure coefficients. In this paper, we introduce a novel class of residual-dependent sampling (RDS) designs that select informative individuals using data available on the longitudinal outcome and inexpensive covariates. Together with the RDS designs, we propose a semiparametric analysis approach that efficiently uses all data to estimate the parameters. We describe a numerically stable and computationally efficient EM algorithm to maximize the semiparametric likelihood. We examine the finite sample operating characteristics of the proposed approaches through extensive simulation studies, and compare the efficiency of our designs and analysis approach with existing ones. We illustrate the usefulness of the proposed RDS designs and analysis method in practice by studying the association between a genetic marker and poor lung function among patients enrolled in the Lung Health Study (Connett et al, 1993).

1. INTRODUCTION

The Lung Health Study (LHS) was a multicenter randomized clinical trial examining whether a smoking cessation intervention program combined with bronchodilators use can slow down lung function decline in patients with mild to moderate chronic obstructive pulmonary disease (Connett et al., 1993). Patients in the LHS were followed up for a total of five years and information on lung function was collected annually. As part of the study, genetic data were collected and two novel loci associated with accelerated lung function decline were identified (Hansel et al., 2013). While the LHS collected genetic data on a large percentage of participants, this is not always the case. In many clinical trials and/or cohort studies, blood samples are collected at recruitment and stored for later use. In this paper, we conceive of a scenario where information on lung function and baseline covariates are available for everyone in the LHS, but genetic data need to be collected from the analysis of the stored blood samples. In particular, we assume that, due to resource constraints, genetic information could only be collected on 600 subjects out of the 2,562 subjects in the LHS, and we aim to estimate the odds ratio of having poor lung function at the beginning and at the end of follow-up, as well as the potential differential rate of lung function decline between subjects with and without the T-allele at SNP rs10761570.

In settings like the LHS, where ascertainment costs limit the sample size, two-phase outcome-dependent sampling (ODS) designs, which use information available for all study subjects (phase 1) to target, for exposure ascertainment, individuals that are the most informative about the research question of interest (phase 2), can reduce costs and increase estimation precision compared to simple random sampling (SRS) designs (White, 1982). Classical two-phase ODS designs stratify subjects based on their outcome value and assign to each subject a sampling probability based on stratum membership, as exemplified by the case-control (Breslow, 1996) and extreme-tail sampling designs (Zhou et al., 2002; Lin et al., 2013) for cross-sectional binary and continuous outcomes, respectively. Regardless of the outcome, it has been shown that the efficiency of a two-phase ODS design can be enhanced when one further stratifies on inexpensive covariates (Breslow and Chatterjee, 1999).

With the exception of case-control designs, where Prentice and Pyke (1979) showed that valid inference can be obtained using standard logistic regression, analysis procedures that do not appropriately account for the biased phase 2 sampling design will generally lead to invalid results (Holt et al., 1980; Lin et al., 2013). Two broad classes of analysis methods that can properly account for the sampling design include: complete-case analysis methods that only include subjects selected in phase 2 with complete data on outcome, inexpensive covariates, and expensive exposure (Zhou et al., 2002; Schildcrout and Heagerty, 2008), and full-cohort analysis methods that combine complete data available for subjects selected in phase 2 with outcome and covariate data available from those not selected (Lawless et al., 1999; Tao et al., 2017). While complete-case analysis methods enjoy wider applicability because they only require data access for subjects selected in phase 2 along with knowledge of the study design, full-cohort analysis methods tend to be more efficient as additional information from subjects not selected in phase 2 are incorporated into the analysis.

Extensions of two-phase ODS studies to longitudinal binary outcomes have been discussed in the literature (Neuhaus and Jewell, 1990; Schildcrout and Heagerty, 2008). For instance, Neuhaus and Jewell (1990) suggested selecting clusters with probability depending on the number of events observed in the cluster and estimating cluster-varying covariates’ regression coefficients using conditional logistic regression. Schildcrout and Heagerty (2008, 2011) introduced the “none-some-all” (NSA) design, where subjects are divided into three strata based on whether they never experienced the outcome (the “none” stratum), experienced the outcome at some but not all time points (the “some” stratum), or always experienced the outcome (the “all” stratum). They demonstrated that appropriate designs should be chosen according to inferential targets. For instance, if interest lies in the estimation of time-varying exposure coefficients, sampling subjects from the “some” stratum only is the most efficient NSA design. However, if interest lies in the estimation of time-fixed exposure coefficients or a combination of time-fixed and time-varying exposure coefficients, then it is unclear what the optimal NSA design would be. To find the optimal NSA design in these situations, Tao et al. (2021) introduced the two-wave NSA design, a data adaptive sampling strategy that splits phase 2 sample selection into two waves and optimizes the sampling scheme in the second wave based on data collected in the first wave. This design could be computationally demanding because of its search for optimal phase 2 stratum sizes after the first wave. It would be practically appealing to develop an easy-to-implement, single-wave design that can incorporate information on available outcomes and covariates to boost estimation efficiency.

To conduct statistical inference under two-phase ODS with longitudinal binary data, Schildcrout and Heagerty (2008, 2011) proposed an ascertainment corrected maximum likelihood (ACML) estimator, a complete-case analysis method. The method is statistically valid but not efficient because phase 1 information available on subjects not selected in phase 2 is ignored in the analysis. Furthermore, the ACML algorithm must be tailored to each NSA design, which limits its applicability. To improve estimation efficiency over the ACML, Schildcrout et al. (2015, 2018) introduced a multiple imputation (MI) approach that exploits complete information on subjects selected in phase 2 along with partial information on the remaining subjects. This MI is a fully parametric approach. Thus, its validity hinges on the correct specification of the imputation model.

In this paper, we present an efficient sieve maximum likelihood estimator (SMLE) that extends the work of Tao et al. (2017) to accommodate longitudinal binary outcomes. It is a flexible full-cohort analysis method that can be used regardless of the two-phase ODS design. Like the MI, the SMLE models the conditional distribution of the expensive exposure given inexpensive covariates, but it does so nonparametrically and thus is robust to model misspecification. It possesses desirable statistical properties, including consistency, asymptotic normality, and asymptotic efficiency. In addition, we propose novel residual-dependent sampling (RDS) designs that utilize information on outcome and inexpensive covariates available on all study subjects in phase 1 to select informative individuals for expensive exposure ascertainment. We note that RDS designs have been shown to lead to efficiency gains over ODS designs in other settings, including generalized linear models for scalar response data (Tao et al., 2020) and linear mixed models for quantitative longitudinal data (Sun et al., 2017; Di Gravio et al., 2023).

The rest of the paper is organized as follows. In Section 2, we describe a marginalized model for longitudinal binary data to be used throughout the paper. In Section 3, we introduce a novel class of RDS designs. We describe the newly developed SMLE method in Section 4, and we explore operating characteristics of the proposed designs and inference procedures in Section 5. In Section 6, we demonstrate how the designs and inference procedures can be used in the LHS. Finally, we conclude the paper with a discussion in Section 7.

2. MARGINALIZED TRANSITION AND LATENT VARIABLE MODEL

Let N be the number of subjects in the phase 1 cohort, m_i be the number of observations for the ith subject (i = 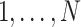), and p₁ and p₂ be the numbers of expensive exposures and inexpensive covariates, respectively. Let 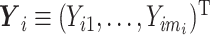be the m_i-vector of binary responses, 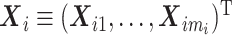be the m_i × p₁ matrix of expensive exposures, and be the m_i × p₂ matrix of inexpensive covariates for the ith subject, with 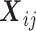and 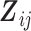being the p₁-vector of expensive exposures and p₂-vector of inexpensive covariates at the jth observation, respectively. The marginalized transition and latent variable (mTLV) model (Schildcrout and Heagerty, 2007) is defined by 2 equations:

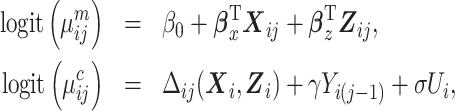(1)

where 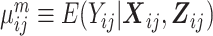is the marginal mean of the outcome Y_ij given covariates 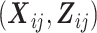, and 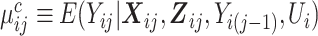is the conditional mean of the outcome Y_ij given covariates 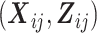, a transition term, Y_{i(j − 1)}, and a random intercept, U_i, assumed to follow a standard normal distribution. are regression coefficients in the marginal and conditional mean models. Note that the parameters of the conditional mean model, γ and σ, can depend on covariates . For ease of exposition, however, we assume that γ and σ are scalars throughout this paper.

The quantity 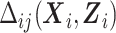in the conditional mean model is an implicit function of 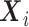and 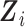that renders the marginal and conditional mean models coherent, that is, it is the value that implies the marginal mean is, in fact, a marginalization of the conditional mean over Y_{i(j − 1)} and U_i. Let 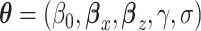, the density function corresponding to the ith subject can be expressed as

(2)

where ϕ(·) is the standard normal density function. When the expensive exposures are ascertained for all N subjects in the phase 1 cohort, inference on can be made by maximizing the log-likelihood 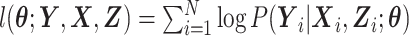using a Newton-Raphson algorithm.

Remark 1

The log-likelihood in (2) requires the calculation of for all subjects i at time j. This is done sequentially by solving, at each time j, the convolution equation relating the marginal and conditional means: . Since this equation has no closed-form solution, we solve it with the Newton-Raphson algorithm. Details are presented in Web Appendix A.

3. TWO-PHASE RDS DESIGNS

We introduce two-phase RDS designs that select informative individuals for expensive exposure ascertainment by exploiting the longitudinal binary outcome and inexpensive covariate data available for all subjects at phase 1. Specifically, we first build an mTLV model using phase 1 data only:

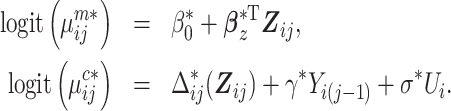(3)

Then, we use the coefficients estimated from equation (3) to compute the predicted outcome for every subject i at observation j and calculate the residual . We aim to select subjects that are informative about in phase 2 based on a subject-specific summary of 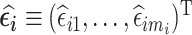. We call these sampling strategies RDS designs because 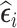are the residuals of the marginal mean component of an mTLV model.

Similar to the NSA design, the ideal RDS design will depend on the estimation target. We explore three RDS designs that are desirable for different inferential targets. The first two RDS designs aim to increase between-subject variability, and thus are expected to be efficient for estimation of time-fixed exposure coefficients: the first design, denoted by mR [n_2l , n_2h], selects for phase 2 exposure ascertainment the n_2l and n_2h individuals with the lowest and highest subject-specific mean of the residuals 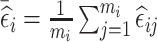; whereas, the second design, denoted by abs.mR [n₂], selects the n₂ individuals with the highest values of the absolute value of 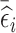. These two designs are different under most circumstances as the distribution of is usually not symmetric about zero. The third design aims to increase within-subject variability, and thus is expected to be efficient for estimation of time-varying exposure coefficients. The design selects for phase 2 exposure ascertainment the n₂ individuals with the highest subject-specific variance of residuals .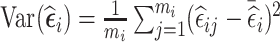

The three aforementioned RDS designs can be combined if researchers want to improve efficiency for estimation of time-fixed and time-varying exposure coefficients simultaneously. That is, one can select a portion of subjects in phase 2 based on 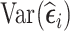, and select the remaining subjects based on 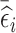. The proportion of subjects selected based on 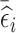or 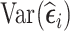can be chosen according to whether there is more interest on time-fixed or time-varying exposure coefficients, respectively.

Remark 2

The RDS designs make the implicit assumption that the coefficients associated with the expensive exposure are small. This assumption is not restrictive in that design efficiency matters the most when the expensive exposure effects are small, which is the case for most genetic studies. Even when the expensive exposure effect is large and thus model (3) is misspecified, we would still expect the RDS designs to target informative individuals for phase 2. Because model (3) is only used at the design stage to select phase 2 subjects and the eventual analysis model will incorporate , the misspecification of (3) will only impact the efficiency of the RDS design, not the validity of the downstream analysis.

4. THE SIEVE MAXIMUM LIKELIHOOD ESTIMATOR

Let S denote the sampling indicator, such that S_i = 1 if subject i was selected for phase 2 exposure ascertainment, and S_i = 0 otherwise. In any two-phase ODS design, being sampled for phase 2 depends on 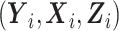only through the phase 1 data 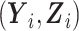; thus, information on the expensive exposure 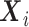is missing at random, and the observed data log-likelihood can be written as the sum of the contributions from subjects selected in phase 2 with data on and the remaining subjects with data on 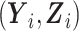without accounting for the distribution of S, that is,

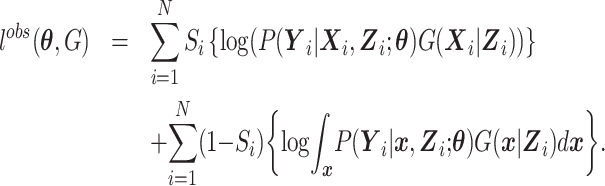(4)

Here, 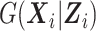is the conditional density of the expensive exposures 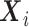given the set of inexpensive covariates , and the integral on the right-hand side of equation (4) is taken across all possible values of the expensive exposures.

Our primary interest is the estimation of 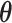in the mTLV model 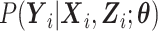. The conditional distribution is a nuisance parameter. To avoid additional assumptions beyond those made by the mTLV model, we estimate 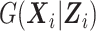using nonparametric maximum likelihood estimation. Let m denote the total number of distinct values of 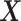observed in the phase 2 sample, with being the m observed distinct values. We estimate by a discrete probability function with point masses at 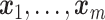. This estimation is feasible when contains categorical variables only. It becomes infeasible to estimate with its empirical distribution in the presence of continuous inexpensive covariates because, in that situation, only a small number of observations of 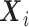would be associated with each level of .

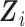To accommodate continuous 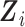, we approximate 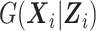using the method of sieves (Grenander, 1981). Specifically, we construct the approximating functions needed to estimate 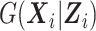using the B-spline basis as

(5)

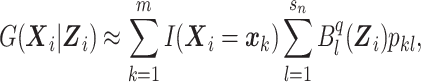(6)

where 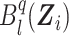is the lth B-spline function of degree q, s_n is the size of the B-spline basis, and p_kl is the coefficient associated with 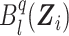at . Details on the computation of 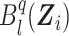can be found in Web Appendix B. We note that by the approximation theory of B-splines (Schumaker, 2007), both equation (5) and the logarithm of equation (6) converge to 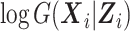as s_n increases. We use equation (5) for computational convenience. Given the approximations in equations (5) and (6), the observed data log likelihood becomes

(7)

The parameters 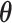and p_kl (k = 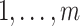; l = 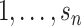) can be estimated by maximizing the log-likelihood (7) under the constraints 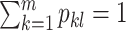and p_kl ≥ 0, ∀l, k. The constraints on p_kl are necessary as 1) the B-splines basis used to approximate 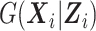are standardized such that 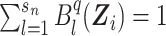, and 2) 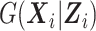is a conditional probability function.

Direct maximization of equation (7) is not straightforward as the second term describing the contribution of unsampled subjects is intractable. Following Tao et al. (2017), we define for the unsampled subjects a latent variable W ∈ {1/s_n, 2/s_n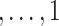} such that the second term on the right-hand side of (7) can be interpreted as the log-likelihood contribution from assuming that the complete data are comprised of 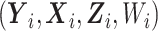, but only and 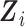are observed. To facilitate this interpretation, W_i needs to satisfy the constraints , , 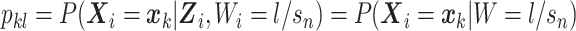and 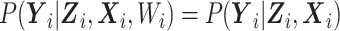. Then, we propose an EM algorithm to maximize the log-likelihood (7), where the complete-data log-likelihood is

(8)

Details of the EM algorithm are presented in Web Appendix B. It follows from Theorems S.1 and S.2 in Tao et al. (2017) that the resulting SMLE 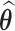at convergence is consistent, asymptotically normal, and asymptotically efficient.

To estimate the covariance matrix, 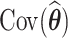, we use the profile likelihood method of Murphy and van der Vaart (2000) (see Web Appendix B). From the covariance matrix, one can extract estimated standard errors and compute confidence intervals based on the normal distribution.

Remark 3

According to Condition (C.5) in the Supplementary Material of Tao et al. (2017), the size of the B-spline basis used in equations (5) and (6) to approximate needs to grow exponentially with the number of continuous inexpensive covariates that are correlated with . When there are more than two continuous covariates, it will become impractical to estimate nonparametrically. In this situation, we recommend obtaining a lower-dimensional summary of , denoted by , and then construct B-spline approximations for rather than . One may construct by 1) incorporating prior knowledge and removing covariates in that are believed to be independent of , or 2) using dimension reduction techniques such as principal component analysis.

5. SIMULATION STUDIES

We evaluated the validity of the SMLE under different scenarios. In particular, we considered: 1) binary expensive exposure and inexpensive covariates, 2) continuous expensive exposure and inexpensive covariates, 3) small and large cluster sizes, and 4) mTLV models with a short-range dependence term (Y_{i(j − 1)}) and models with a short-range dependence term and a long-range dependence term (U_i). The results are presented in Web Appendix D. Overall, the SMLE performed well, providing virtually unbiased coefficient and standard error estimators and confidence intervals with appropriate coverage probabilities.

After evaluating the validity of the SMLE approach, we compared its efficiency to that of existing inference procedures. In particular, to study the potential efficiency gains due to including all available phases 1 and 2 data in the estimation procedure, we compared the SMLE with two complete-case approaches: standard maximum likelihood (ML) inference using the phase 2 sample only under the SRS design, and a conditional likelihood procedure, ACML, under the NSA design. Additionally, we compared the SMLE with the MI approach of Schildcrout et al. (2015), a full-likelihood procedure. Details on the ACML and MI procedures can be found in Web Appendix C. We generated data from the model:

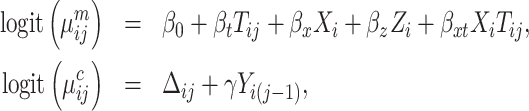(9)

where X_i denotes a binary expensive exposure to be measured in phase 2, Z_i denotes a binary inexpensive covariate available on every subject in phase 1, and T_ij ∈ {0, m_i − 1} denotes a time variable. We generated X_i and Z_i such that P(Z_i = 1) = 0.3 and logitP(X_i = 1|Z_i) = −2.2 + 2Z_i. The resulting prevalence of X_i was approximately 20%. We considered two scenarios with different record lengths. In the first scenario, we chose m_i randomly from 3 to 6, set the regression coefficients in equation (9) to (β₀, β_t, β_x, β_z, β_xt, γ) = (−2.95, 0.15, 0.25, 1.5, 0.15, 2), and generated data for 2,000 subjects, with an average of 1,320, 655, and 25 subjects in the “none” , “some” 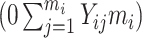, and “all” 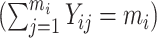strata, respectively. In the second scenario, we increased the cluster size so that each subject had 6 to 16 observations recorded between T_ij = 0 and T_ij = 5, set the regression coefficients in equation (9) to (β₀, β_t, β_x, β_z, β_xt, γ) = (−3, 0.15, 0.25, 1.5, 0.15, 2), and generated data for 2,000 subjects, with an average of 900 and 1,100 subjects in the “none” and “some” strata, respectively. In both scenarios, outcome prevalence was 14%.

Together with the analysis methods, we compared SRS, RDS, and NSA designs under the assumption that information on X_i could be collected for 500 of the 2,000 subjects with complete data on . Regardless of the cluster size, we selected 1) 500 subjects with an SRS design, 2) 500 subjects with the highest 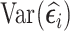(vR [500]), 3) 500 subjects with the highest absolute value of 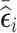(abs.mR [500]), 4) 250 subjects with the lowest value of 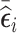and 250 subjects with the highest value of 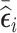(mR [250, 250]), and 5) 500 subjects from the “some” stratum (NSA [0, 500, 0]). Additionally, in the small cluster size scenario, we randomly selected 10, 480, and 10 subjects from the “none,” “some,” and “all” strata, respectively (NSA [10, 480, 10]); whereas, in the large cluster size scenario, we selected 50 and 450 subjects from the “none” and “some” strata, respectively (NSA [50, 450, 0]). The choice of NSA [10, 480, 10] and NSA [50, 450, 0] was informed by Schildcrout and Heagerty (2011), which showed that even a small number of subjects selected from the “none” and “all” strata can substantially improve the precision of estimating time-fixed covariates’ coefficients. We studied several NSA designs that sampled in phase 2, a majority of subjects from the “some” stratum and the reminder from the “none” and “all” strata. The results were similar to the settings presented here and are thus not shown. Additional RDS designs that combine sampling based on the residuals’ mean and variance are presented in Web Appendix D.

Figure 1 and Table 1 show the relative efficiency (RE) of the designs and inference procedures compared to SRS with the ML in the small cluster size scenario. Towards estimating (β₀, β_t, β_z), the SMLE was much more efficient than the ML and ACML because the SMLE incorporated information on (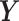, Z) for subjects not selected in phase 2. Towards estimating (β_x , β_xt), the SMLE was also more efficient than the ML and ACML. For instance, under the NSA [0, 500, 0] design, the SMLE improved estimation efficiency over the ACML by 13% (RE 3.03 vs 2.68) for β_xt. When fixing the inference procedure and comparing the RE between designs, we found that RDS designs tended to be more efficient than the SRS and NSA designs. In particular, using the SMLE, vR [500] was more efficient than NSA [0, 500, 0] towards estimating β_xt, with an 8% (RE 3.27 vs 3.03) efficiency gain. Similarly, abs.mR [500] and mR [250, 250] were more efficient than NSA [10, 480, 10] towards estimating β_x, with 40% (RE 2.55 vs 1.82) and 39% (RE 2.53 vs 1.82) efficiency gains, respectively. In addition, the abs.mR [500] and mR [250, 250] designs led to the highest efficiency gains towards estimating β_x + 5β_xt, the association between the expensive exposure and outcome at the end of follow-up. Compared to SRS with the SMLE, efficiency gains for abs.mR [500] and mR [250, 250] were 70% (RE 2.14 vs 1.26) and 68% (RE 2.12 vs 1.26), respectively (Figure 1).

FIGURE 1.

Efficiency of two-phase ODS designs and analysis procedures relative to SRS with the ML for β_x, β_xt, and β_x + 5β_xt.

TABLE 1.

Efficiency of different two-phase ODS designs and analysis procedures relative to SRS with the ML across 5,000 replicates for correlated X_i and Z_i and small cluster size.

Design + Method	β0	βx	βt	βz	βxt	γ
NSA [0, 500, 0] + ACML	0.73	1.24	2.69	0.69	2.68	1.02
NSA [10, 480, 10] + ACML	0.98	1.58	2.59	0.88	2.71	1.30
SRS [500] + SMLE	3.05	1.26	2.48	2.74	1.40	3.85
NSA [0, 500, 0] + SMLE	3.65	1.50	3.67	2.72	3.03	3.85
NSA [10, 480, 10] + SMLE	3.71	1.82	3.59	2.99	3.02	3.86
vR [500] + SMLE	3.57	1.27	3.68	2.47	3.27	3.77
mR [250, 250] + SMLE	3.58	2.53	3.07	3.41	2.17	4.01
abs.mR [500] + SMLE	3.57	2.59	3.10	3.43	2.20	4.01

Figure 1 and Table 2 show the RE of the designs and inference procedures compared to SRS with the ML in the large cluster size scenario. Towards estimating β_x and β_xt, the efficiency gains of the SMLE over the ACML and ML were higher than those observed in the small cluster size scenario. For instance, under the NSA [0, 500, 0] design, the SMLE improved estimation efficiency of β_xt over the ACML by 31% (RE 2.18 vs 1.67). For all other coefficients, results were similar to those observed in the small cluster size scenario. When fixing the inference procedure and comparing the RE among designs, it is interesting to note that towards estimating β_xt, vR [500] led to a 38% (RE 3.01 vs 2.18) efficiency gain when compared to NSA [0, 500, 0]. This is a higher efficiency gain than that in the small cluster size scenario. On the other hand, efficiency gains for β_x were similar to those observed in the small cluster size scenario. Towards estimating β_x + 5β_xt, RDS designs led to higher efficiency gains. Compared to SRS with the SMLE, efficiency gains for abs.mR [500], mR [250, 250], and vR [500] were 62% (RE 2.56 vs 1.58), 62% (RE 2.55 vs 1.58), and 58% (RE 2.49 vs 1.58), respectively (Figure 1). The similar efficiency gains among the three RDS designs might be explained by the relatively high correlation between 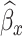and in the large cluster size scenario (Web Figures 1 and 2).

TABLE 2.

Efficiency of different two-phase ODS designs and analysis procedures relative to SRS with the ML across 5,000 replicates for correlated X_i and Z_i and large cluster size.

Design + Method	β0	βx	βt	βz	βxt	γ
NSA[0, 500, 0] + ACML	0.94	1.37	1.65	0.94	1.67	1.29
NSA[50, 450, 0] + ACML	1.14	1.36	1.53	1.04	1.58	1.35
SRS[500] + SMLE	2.90	1.38	2.64	2.74	1.58	3.72
NSA[0, 500, 0] + SMLE	3.26	1.75	3.11	2.96	2.18	3.73
NSA[50, 450, 0] + SMLE	3.19	1.70	3.00	2.94	2.05	3.76
vR[500] + SMLE	3.51	1.89	3.51	2.88	3.01	3.73
mR[250, 250] + SMLE	3.57	2.61	3.34	3.19	2.53	3.85
abs.mR[500] + SMLE	3.53	2.68	3.38	3.31	2.56	3.85

FIGURE 2.

Point estimates and 95% confidence intervals (CI) from the analysis of the LHS data. The left panel shows the difference in rate of lung function decline between those with and without the T-allele at SNP rs10761570. The middle and right panels show the differences in lung function between those with and without the T-allele at SNP rs10761570 at the first and last visits, respectively.

Finally, in Web Appendix E, we compared the efficiency of the SMLE and MI procedures for the small cluster size scenario. Since the MI approach of Schildcrout et al. (2015) is only applicable to NSA designs, we performed the comparisons under the NSA [10, 480, 10] design only. Towards estimating model coefficients, the SMLE was as efficient as the MI; that is, there was virtually no efficiency loss incurred by the nonparametric modeling of the nuisance parameter G.

6. THE LUNG HEALTH STUDY

We considered 2,562 participants in the LHS with at least two observations and implemented a series of two-phase designs to study genetic associations with poor lung function. We defined the time-varying binary (yes/no) outcome to be “yes” if forced expiratory volume (FEV₁) was less than 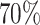and FEV₁ divided by forced vital capacity was less than 0.7 (Bhatt et al., 2013). This resulted in a 27 outcome prevalence and 1,570, 602, and 390 subjects in the “none,” “some,” and “all” strata, respectively. We studied the mTLV model in (1) where X_i is the indicator of the presence of the T-allele at SNP rs10761570, P (X_i = 1) = 0.19, and 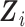includes study year, pack-years smoking, number of cigarettes smoked per day during the year before enrollment in the LHS, body mass index (BMI), sex, age, FEV₁ at baseline, and the interactions of study year with baseline X_i, age, sex, and FEV₁.

Our interests lie in the inference of the parameters corresponding to the difference in lung function between those with and without the T-allele at SNP rs10761570 at the first and last visit of the study and the difference in rate of lung function decline between those with and without the T-allele at SNP rs10761570. Even though the LHS provided complete genetic data, for illustration we considered a scenario where genetic information was not available and, due to budget constraints, could only be collected on 600 subjects. Specifically, we examined the following combinations of designs and inference approaches: 1) SRS + ML, 2) NSA [90, 420, 90] + ACML, 3) SRS + SMLE, (4) NSA [90, 420, 90] + SMLE, 5) abs.mR [600] + SMLE, 6) mR [300, 300] + SMLE, and 6) vR [600] + SMLE. When implementing the NSA design, we adopted a sampling scheme similar to that in the simulation study in the small cluster size scenario, where we selected approximately 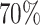of subjects from the “some” stratum and selected the remaining subjects in equal numbers from the “none” and “all” strata. When conducting the SRS and NSA [90, 420, 90] designs, we repeated the phase 2 sample selection 200 times and reported the average estimated coefficients and standard errors across those replicates. The abs.mR [600], mR [300, 300], and vR [600] designs are deterministic in nature and thus were carried out only once.

Because BMI, number of cigarettes smoked, pack-years, and baseline FEV₁, might be correlated with SNP rs10761570, it would be challenging to estimate nonparametrically due to the curse of dimensionality. To address this issue, we first performed a principal component analysis of these covariates, took the first principal component, denoted by 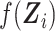, and then estimated using B-spline approximation with s_n = 10 and q = 1. Although not reported in the paper, analyses that treated all inexpensive covariates as independent of the SNP, and analyses that used different (s_n, q) yielded similar results. This is due to the fact that SNP rs10761570 is effectively unassociated with the inexpensive covariates. We note that Tao et al. (2017) observed in their simulation studies that the SMLE has virtually no efficiency loss when inexpensive covariates that are independent of expensive covariates are treated as if they were correlated with expensive covariates.

The results from the full-cohort and two-phase ODS designs are presented in Figure 2 and Web Table 5. In the full-cohort analysis, there was no evidence of an association between the presence of at least one copy of the T-allele at SNP rs10761570 and having poor lung function at the first and last visit. Estimated log-odds ratio were −0.285 (95 CI: −0.612, 0.041) at the first visit and −0.154 (95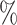 CI: −0.443, 0.136) at the last visit. The odds ratio estimates under the two-phase ODS designs were concordant to those of the full-cohort analysis.

We observed that uncertainty estimate patterns in the LHS analysis were consistent with those in the simulation studies. Compared to the ML and ACML, the SMLE increased the precision of the coefficients’ estimates. For instance, the standard error associated with the estimation of β_x was 0.429 in SRS + ML and 0.296 in SRS + SMLE. Regarding design efficiency, the NSA and RDS designs improved the precision of the target parameters relative to SRS. In particular, mR [300, 300] and abs.mR [600] led to the smallest standard errors for the coefficients associated with time-fixed covariates, whereas vR [600] led to the smallest standard errors for the coefficients associated with time-varying covariates. Note that since vR [600] sampled 600 out of the 602 subjects in the “some” stratum, we expect NSA [0, 600, 0] to be essentially identical to vR [600]. Efficiency gains of the NSA and RDS designs over the SRS design can also be observed at the end of the follow-up. The standard errors associated with the log-odds ratios of having at least 1 copy of the T-allele versus none at SNP rs10761570 at the end of follow-up were 0.378, 0.305, and 0.205 for SRS + SMLE, NSA [90, 420, 90] + SMLE, and mR [300, 300] + SMLE, respectively. For regression coefficients of the inexpensive covariates, two-phase ODS designs coupled with the SMLE yielded standard errors similar to those in the full-cohort analysis. This is expected because the SMLE uses all information about inexpensive covariates that is available in the full-cohort analysis.

7. DISCUSSION

We proposed novel RDS designs for practical settings where information on a longitudinal binary outcome and covariates are available on all members of a cohort, but additional data on expensive exposures need to be collected. Compared to the existing designs, the proposed RDS designs can improve efficiency of estimating regression coefficients. In particular, when interest lies in time-varying exposure coefficients, the vR [n₂] design could be used in lieu of the NSA [0, n₂, 0] design. The vR [n₂] design can be regarded as a “refinement” to the optimal NSA design for time-varying covariates when we do not have enough resources to sample everyone from the informative “some” stratum: in this situation, the optimal NSA design will randomly select n₂ subjects from the “some” stratum, while the proposed design will select subjects with the highest , most of whom belong to the “some” stratum. In our simulations, the vR [n₂] design led to the highest efficiency gain when we could only sample approximately 55% of the subjects in the “some” stratum.

When interest lies in time-fixed exposure coefficients, the mR [n_2l , n_2h] and abs.mR [n₂] designs are highly efficient. In our simulation studies and applications to the LHS data, the mR [n_2l, n_2h] and abs.mR [n₂] designs are more efficient than all of the NSA designs considered there. When interest lies in a combination of time-varying and time-fixed exposure coefficients, efficiency can be increased by combining vR [n₂] with either mR [n_2l, n_2h] or abs.mR [n₂], or, when the cluster size is large, by implementing an mR [n_2l, n_2h] or an abs.mR [n₂] design. We are not sure whether the RDS designs are more efficient than all NSA designs, as the optimal NSA design is unknown. While the two-wave NSA design of Tao et al. (2021) has the potential to identify the optimal NSA design in the second wave, it relies on accurate parameter estimation in the first wave, in which subjects are selected through some conventional, suboptimal design. Consequently, the overall design efficiency can be compromised when combining the two waves, especially when a large first wave is required to accurately estimate the model parameters. Thus, we believe that the proposed mR [n_2l, n_2h] and abs.mR [n₂] designs can be more attractive than the NSA designs. We note that RDS designs can only be conducted when both outcome and inexpensive covariates are available for analysis at the study planning stage, which is not always the case. When only outcome data are available at the study planning stage, NSA designs are recommended.

Together with the designs, we proposed an inference procedure that extends the work of Tao et al. (2017) to binary longitudinal data. The SMLE approach can handle continuous and binary expensive and inexpensive covariates and allows these covariates to be correlated with each other. It does not make any assumption on 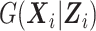and thus is more robust to model misspecification than the fully parametric MI approach of Schildcrout et al. (2015). Our simulation study comparing the SMLE and MI approaches when the imputation model in the MI was correctly specified showed that the nonparametric modeling of 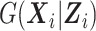in the SMLE did not incur efficiency loss. Furthermore, because the SMLE can use the data for inexpensive covariates from all study subjects, it is nearly as efficient as the full-cohort analysis irrespective of the study design when estimating inexpensive covariates’ effects.

Even though the SMLE does not make any assumption on 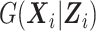, it requires the analyst to choose the size s_n and degree q of the B-spline basis used for the approximation of 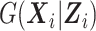. The choice of (s_n, q) depends on the number of subjects in the original cohort. Usually, s_n increases with larger phase 1 sample size, and q is less or equal to four, where q = 4 corresponds to cubic splines. In practice, the analyst could choose (s_n , q) in a data-adaptive manner using K-fold cross-validation: for a fixed (s_n, q), one evaluates the observed data log-likelihood (7) in the kth fold (k = 1K) using the estimates obtained in the other (K − 1) folds. The optimal (s_n, q) is the one that maximizes the average out-of-folds predicted log-likelihood. In our simulation studies and in the LHS example, the results were not sensitive to the choice of (s_n, q).

We have focused on designs and inference procedures for a longitudinal binary outcome with an mTLV model. Alternatively, one may use a conditionally specified generalized linear mixed model (GLMM) (Stiratelli et al., 1984; Breslow and Clayton, 1993). The advantages and disadvantages of the conditionally and marginally specified models have been widely debated in literature (Zeger et al., 1988; Neuhaus et al., 1991; Lindsey and Lambert, 1998). Extension of the SMLE approach to GLMMs would require us to estimate 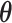in the EM algorithm using a weighted GLMM instead of a weighted mTLV model. RDS designs can also be extended to a GLMM framework by sampling based on the estimated random effects from a GLMM model relating the outcome to the inexpensive covariates. Future research include extending designs and inference procedures to ordinal longitudinal outcomes, and exploring the impact of model misspecification on the proposed inference procedures.

Supplementary Material

ujad010_Supplemental_Files

Web Appendices, Tables, and Figures referenced in Sections 5 and 6 are available with this paper at the Biometrics website on Oxford Academic. The designs and methods presented in the paper are implemented in the dames R package, which is freely available on GitHub at https://github.com/ChiaraDG/dames. The package vignette explains how to reproduce the simulation and LHS data analysis results presented in this paper. The R code used to conduct the analyses described in Section 5 is available with this paper at the Biometrics website on Oxford Academic.

FUNDING

This research was supported by the National Institute of Health grants R01HL094786 and R01AI131771 and the 2022 Biostatistics Faculty Development Award from the Department of Biostatistics at Vanderbilt University Medical Center.

CONFLICT OF INTEREST

None declared.

DATA AVAILABILITY

The Lung Health Study data used for the analyses in Section 6 were obtained from dbGaP at http://www.ncbi.nlm.nih.gov/sites/entrez?db=gap through dbGaP accession [phs000335.v3.p2].