ABSTRACT
A dynamic treatment regime (DTR) is a sequence of treatment decision rules that dictate individualized treatments based on evolving treatment and covariate history. It provides a vehicle for optimizing a clinical decision support system and fits well into the broader paradigm of personalized medicine. However, many real-world problems involve multiple competing priorities, and decision rules differ when trade-offs are present. Correspondingly, there may be more than one feasible decision that leads to empirically sufficient optimization. In this paper, we propose a concept of “tolerant regime,” which provides a set of individualized feasible decision rules under a prespecified tolerance rate. A multiobjective tree-based reinforcement learning (MOT-RL) method is developed to directly estimate the tolerant DTR (tDTR) that optimizes multiple objectives in a multistage multitreatment setting. At each stage, MOT-RL constructs an unsupervised decision tree by modeling the counterfactual mean outcome of each objective via semiparametric regression and maximizing a purity measure constructed by the scalarized augmented inverse probability weighted estimators (SAIPWE). The algorithm is implemented in a backward inductive manner through multiple decision stages, and it estimates the optimal DTR and tDTR depending on the decision-maker’s preferences. Multiobjective tree-based reinforcement learning is robust, efficient, easy-to-interpret, and flexible to different settings. We apply MOT-RL to evaluate 2-stage chemotherapy regimes that reduce disease burden and prolong survival for advanced prostate cancer patients using a dataset collected at MD Anderson Cancer Center.
Keywords: causal inference, decision tree, dynamic treatment regimes, multiobjective optimization, personalized medicine
1. INTRODUCTION
Personalized healthcare is an emerging field, tailoring treatment decisions to heterogeneous patient characteristics. It is especially useful in chronic disease management, which often requires a sequence of treatment decisions that adapt dynamically as the disease progresses. These sequential decision rules, one per stage of the disease progression, mapping patient-specific features to a recommended treatment, are referred to as dynamic treatment regimes (DTRs) or individualized treatment strategies (ITSs) (Murphy et al., 2001; Chakraborty and Murphy, 2014). These approaches not only individualize healthcare according to patient-synthesized information changes but also select optimal medical intervention dynamically over time (Murphy, 2003; Robins, 2004).
Various statistical methods have been developed to identify and evaluate optimal DTRs using observational data. For instance, parametric and semiparametric methods include marginal structural models with inverse probability weighting (Hernán et al., 2001; Murphy et al., 2001; Wang et al., 2012), G-estimation of structural nested mean models (Robins 1997, 2004), targeted maximum likelihood estimations (Van der Laan and Rubin 2006), and likelihood-based approaches (Thall et al., 2007). However, specifying assumptions for conditional models may hinder their practice in certain circumstances, and a moderate-to-large number of covariates makes working model specification challenging. To address these concerns, various nonparametric methods have been proposed; for example, Q-learning methods (Zhao et al., 2011; Moodie et al., 2013; Qian and Murphy, 2011), and Bayesian nonparametric model (Murray et al., 2018). Despite the excellent prediction accuracy and reduced risks of model misspecification, these data-driven methods may have higher computational cost and be difficult to interpret, obstructing their application (Rudin et al., 2022). This tension between interpretability and prediction performance has inspired a recent research stream of rule-based learning methods. To alleviate strict modeling assumptions and maintain interpretability, Laber and Zhao (2015) proposed a tree-based method for estimating optimal treatment regimes, while Tao et al. (2018) generalized the method using the doubly robust approach and developed a tree-based reinforcement learning (T-RL) that supports multistage decision-making.
Nevertheless, 2 questions often arise in clinical studies. First, there may exist some situations where several treatment options produce similar favorable results. Providing all such options allows practitioners to have more room to adapt their decisions to the patient’s implicit information. Suppose, for example, that two treatments have roughly equal effectiveness, but one is much more expensive than the other. This information will benefit the patient by avoiding overspending. In this situation, if a clinically effective threshold for an outcome is defined, multiple feasible decision rules can be offered. Second, the identification of the optimal DTR in most literature is often limited by optimizing only one target outcome among the population of interest. However, in many real-world decision-making problems, the multiplicity of criteria for judging the alternative is pervasive, and optimization results may vary for different objectives (Lizotte et al., 2012). One common example in medicine is the efficacy-toxicity conundrum. For instance, Yoon et al. (2021) employed the T-RL method to investigate DTRs to increase hand functions and reduce pain, respectively. Accordingly, the 2 decision trees are distinct due to the inherent trade-off between objectives. The other study that motivated this research is a clinical trial on advanced prostate cancer that was conducted at MD Anderson Cancer Center (Thall et al., 2000). In this trial, each patient underwent 1 or 2 chemotherapy regimens at 2 stages according to their response to the treatment. Several clinical outcomes were recorded, such as survival time, posttreatment toxicity level, and treatment efficacy. The trial’s principal investigators introduced a new metric, the “expert score,” to gauge the clinical desirability of both toxicity and efficacy outcomes combined. By viewing survival time as a long-term outcome of chemotherapy, the “expert score” can be considered an immediate treatment effect. Notably, a previous investigation by Wang et al. (2012) demonstrated a disparity in the optimal 2-stage regimen when considering survival versus the “expert score” as the primary objective. These two examples prompt a question on how to concurrently optimize multiple objectives while effectively reconciling competing clinical priorities.
This multiobjective optimization problem (MOP) is attracting growing interest from researchers in various disciplines. Multiobjective optimization problem is usually considered in situations where (1) a single objective cannot adequately capture the complexity of the problem or the diverse needs and preferences of patients and healthcare providers, (2) there are inherent trade-offs between objectives, or (3) multiple outcomes are considered equally important, and optimizing only one will result in suboptimal decisions regarding the other objectives. Techniques to solve MOPs can be broadly classified into 2 categories: Scalarization methods and Pareto methods (Gunantara, 2018). The former solve MOPs by translating them to mono-objective problems via scalarization functions; the latter, on the other hand, keep the elements of the objectives separated throughout the optimization process and utilizes Pareto dominance to distinguish the Pareto front (PF) as the solutions (Pareto and Bonnet, 1927). Many recent medical studies have focused on tackling MOP. For instance, Lizotte and Laber (2016) developed a multirewards linear fitted-Q iteration algorithm to provide a set of personalized solutions, Lobato et al. (2016) presented a multiobjective differential evolution algorithm to determine dose administration, and many studies estimated optimal treatments by employing various multiobjective evolutionary algorithms (MOEAs) (Luong et al., 2018; Ochoa et al., 2020). However, the Pareto-based MOEAs may be ineffective in solving MOP with more than 4 objectives (Li et al., 2015) and are limited by high computational cost (Bringmann and Friedrich, 2009). Alternatively, rule-based learning is more suitable for estimating DTRs given its parsimony, interpretability, and low cost. These features prompted us to develop a novel tree-based learning method to identify DTRs with multiple objectives.
In this paper, we present a concept of tolerant dynamic treatment regime (tDTR), which provides a set of feasible solutions at each stage. Moreover, we develop a multiobjective tree-based reinforcement learning (MOT-RL) method to directly estimate tDTRs in a multistage multitreatment setting. At each stage, the user provides a weight vector indicating preferences and a tolerance rate. Multiobjective tree-based reinforcement learning evaluates the tDTR tree by recursively partitioning the space to maximize a multiobjective purity measure, which is constructed by linearly scalarizing the estimated counterfactual mean of each outcome. Our method has several advantages: First, MOT-RL uses decision trees and thus is easy-to-use and highly interpretable. Moreover, it is capable of handling various types of covariates and is flexible to model personalized tDTR with multiple outcomes. Lastly, the robustness of the estimation is warranted by embedding a doubly robust augmented inverse probability weighted estimator ( ) in the decision tree algorithm.
) in the decision tree algorithm.
The remainder of this article is as follows: In Section 2, we formalize the problem of estimating the optimal DTR in a multistage multitreatment setting using the counterfactual framework and present the concept of tolerant regimes. Then, we utilize a linear scalarization function to derive a purity measure for multiobjective decision trees. Additionally, we present stopping rules for terminating tree growth to avoid over-fitting and developed the MOT-RL algorithm for multiple-stage settings in a backward inductive manner. Two scenarios are simulated in Section 3 to evaluate the performance of MOT-RL. Further, in Section 4, we illustrate our method with a case study to identify optimal tolerant 2-stage chemotherapy regimes for prostate cancer patients under different preferences in reducing disease burden and prolonging survival. We conclude in Section 5 with discussions and suggestions for future research.
2. MULTIOBJECTIVE TREE-BASED REINFORCEMENT LEARNING
2.1. Tolerant dynamic treatment regime
Consider a multistage decision problem with T decision stages and Kj (Kj ≥ 2) treatment options at the j th (j = 1, 2 T) stage. Data may come from either randomized trials or observational studies. At stage j, let Aj denote the treatment indicator with observed value
T) stage. Data may come from either randomized trials or observational studies. At stage j, let Aj denote the treatment indicator with observed value  . Let
. Let 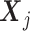 denote the patient characteristics prior to the treatment assignment Aj. Let Rj be the reward following Aj, which depends on the history
denote the patient characteristics prior to the treatment assignment Aj. Let Rj be the reward following Aj, which depends on the history 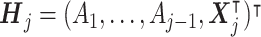 , and it is also a part of
, and it is also a part of 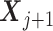 . The overall outcome of interest is Y = f(R1
. The overall outcome of interest is Y = f(R1 RT), where f(·) is a prespecified function. Assume Y is bounded and is preferable with a larger value. The observed data from n subjects are
RT), where f(·) is a prespecified function. Assume Y is bounded and is preferable with a larger value. The observed data from n subjects are 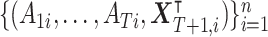 and are assumed to be independent and identically distributed. Without loss of generality, the outcome is considered to be standardized properly in the following, and the subject index i is suppressed when no confusion exists.
and are assumed to be independent and identically distributed. Without loss of generality, the outcome is considered to be standardized properly in the following, and the subject index i is suppressed when no confusion exists.
A DTR is a sequence of individualized treatment rules, 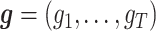 , where gj is a mapping from the domain of the history
, where gj is a mapping from the domain of the history  to the domain of the treatment assignment Aj, for j = 1, 2
to the domain of the treatment assignment Aj, for j = 1, 2 T, and A0 is set as Ø. To define and identify the optimal DTR, the counterfactual framework for causal inference is applied (Robins, 1986). At stage T, let Y*(A1
T, and A0 is set as Ø. To define and identify the optimal DTR, the counterfactual framework for causal inference is applied (Robins, 1986). At stage T, let Y*(A1 AT − 1, aT), simplified as Y*(aT), denote the counterfactual outcome for a patient treated with
AT − 1, aT), simplified as Y*(aT), denote the counterfactual outcome for a patient treated with  conditional on previous treatments (A1
conditional on previous treatments (A1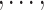 AT − 1); also, let Y*(gT) denote the counterfactual outcome under regime gT, where
AT − 1); also, let Y*(gT) denote the counterfactual outcome under regime gT, where
 |
(1) |
The performance of gT is measured by the counterfactual mean outcome E{Y*(gT)}, and the optimal regime is defined as
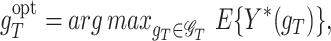 |
(2) |
where 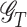 is a class of all possible regimes. The following 3 assumptions are made to connect the distribution of counterfactual outcomes with the one for observed data (Murphy et al., 2001; Robins and Hernán, 2008; Orellana et al., 2010).
is a class of all possible regimes. The following 3 assumptions are made to connect the distribution of counterfactual outcomes with the one for observed data (Murphy et al., 2001; Robins and Hernán, 2008; Orellana et al., 2010).
Assumptions 1
(Consistency): Assume the observed outcomes are identical with the counterfactual outcomes under the actual treatment assigned to the patient, that is,
This also implies there is no interference between subjects.
Assumptions 2
(No unmeasured confounding): Assume that treatment AT is randomly assigned depending only on
, that is,
.
Assumptions 3
(Positivity): Assume there exist constants c0 and c1 (0 < c0 < c1 < 1), such that the propensity score
with probability 1.
Under the above 3 assumptions, Tao and Wang (2017) derived that
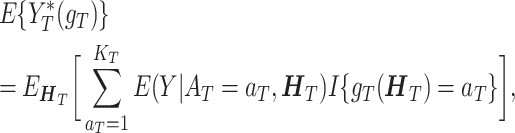 |
(3) |
where  denotes the expectation with respect to the marginal joint distribution of the observed data
denotes the expectation with respect to the marginal joint distribution of the observed data 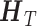 . We denote the conditional mean
. We denote the conditional mean  as
as 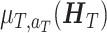 . The optimal regime at stage T is
. The optimal regime at stage T is
 |
(4) |
However, in many scenarios, there may exist a few comparable strategies. Rather than a single optimal regime, providing a set of viable solutions to decision-makers, such as clinicians and healthcare practitioners, would be a more practical and flexible approach. This motivates us to propose a concept of tolerant regimes as follows:
At stage T, for a tolerance rate δT, a regime is considered tolerant if its counterfactual mean outcome is within the upper δT proportion of the counterfactual mean outcome between the worst and the optimal regimes. The corresponding class of such regimes is named as a tolerant set, denoted as 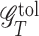 , where
, where
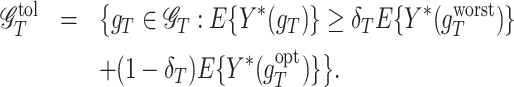 |
(5) |
At stage j ∈ {1 T − 1}, given a regime gj + 1 at the next stage, a stage-specific pseudo-outcome POj can be calculated using the observed data by backward induction (Bather, 2000), where
T − 1}, given a regime gj + 1 at the next stage, a stage-specific pseudo-outcome POj can be calculated using the observed data by backward induction (Bather, 2000), where  Following Murphy (2004) and Tao et al. (2018), to estimate
Following Murphy (2004) and Tao et al. (2018), to estimate  , we define a tolerant-specific pseudo-outcome
, we define a tolerant-specific pseudo-outcome 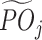 , which is the average of pseudo-outcome of all tolerant regimes in
, which is the average of pseudo-outcome of all tolerant regimes in  . The tolerant-specific pseudo-outcome at stage T is set as
. The tolerant-specific pseudo-outcome at stage T is set as 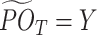 . By backward induction,
. By backward induction,  is defined in a recursive form as
is defined in a recursive form as
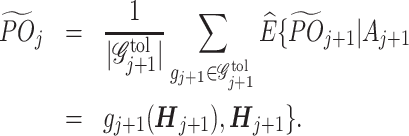 |
(6) |
Technically, one can also use the minimum, maximum, or quantile to define 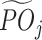 ; however, we use average in this paper because it is intuitive and utilizes information from all possible tolerant regimes. Similarly, the conditional mean
; however, we use average in this paper because it is intuitive and utilizes information from all possible tolerant regimes. Similarly, the conditional mean 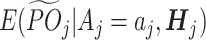 is denoted as
is denoted as  . Let
. Let  denote the counterfactual tolerant-specific pseudo-outcome for a patient with treatment aj at stage j.
denote the counterfactual tolerant-specific pseudo-outcome for a patient with treatment aj at stage j.  . The 3 assumptions mentioned above are modified as follows: (1) Consistency:
. The 3 assumptions mentioned above are modified as follows: (1) Consistency:  ; (2) No unmeasured confounding:
; (2) No unmeasured confounding: 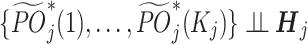 ; and (3) Positivity:
; and (3) Positivity: 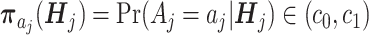 with probability 1, where 0 < c0 < c1 < 1. Based on these assumptions, the optimal treatment at stage j can be formulated as
with probability 1, where 0 < c0 < c1 < 1. Based on these assumptions, the optimal treatment at stage j can be formulated as
 |
(7) |
Consequently, the tolerant set at stage j under tolerance rate δj is
 |
(8) |
2.2. Multiobjective scalarization in tDTR
In MOPs, the value function, denoted as  is a vector-valued function that quantifies the multiple, often conflicting, objectives of the optimization problem. Each component of the value function represents an individual objective to be simultaneously optimized. We assume there are d ( ≥ 2) objectives. At stage j, the value function is a vector of counterfactual mean outcomes,
is a vector-valued function that quantifies the multiple, often conflicting, objectives of the optimization problem. Each component of the value function represents an individual objective to be simultaneously optimized. We assume there are d ( ≥ 2) objectives. At stage j, the value function is a vector of counterfactual mean outcomes, 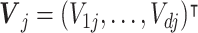 . Given a weight vector,
. Given a weight vector, 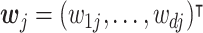 , where wij ≥ 0, ∀i ∈ {1
, where wij ≥ 0, ∀i ∈ {1 d}. We propose to solve the MOP by scalarization as:
d}. We propose to solve the MOP by scalarization as:
 |
(9) |
where ρ is the scalarization function. That is, an optimal treatment is the treatment from the tolerant set  that maximizes the scalarization function. Roijers and Whiteson (2017) summarized 3 critical factors that contribute to the optimal solution to the MOP: (i) whether single or multiple policies are required, (ii) the nature of the scalarization function, and (iii) whether policies are stochastic or deterministic. For (i), we allow the weight vector to be prespecified, which will yield a unique stationary optimal regime as desired. For (ii), Roijers and Whiteson (2017) summarized 2 types of scalarization functions: linear combinations of multiobjective rewards and monotonically increasing functions of rewards. The former is most commonly used, which computes the weighted sum of all objectives (Barrett and Narayanan, 2008; Natarajan and Tadepalli, 2005),
that maximizes the scalarization function. Roijers and Whiteson (2017) summarized 3 critical factors that contribute to the optimal solution to the MOP: (i) whether single or multiple policies are required, (ii) the nature of the scalarization function, and (iii) whether policies are stochastic or deterministic. For (i), we allow the weight vector to be prespecified, which will yield a unique stationary optimal regime as desired. For (ii), Roijers and Whiteson (2017) summarized 2 types of scalarization functions: linear combinations of multiobjective rewards and monotonically increasing functions of rewards. The former is most commonly used, which computes the weighted sum of all objectives (Barrett and Narayanan, 2008; Natarajan and Tadepalli, 2005),
 |
(10) |
where  is typically assumed for convenience. Given the fact that a linear scalarization guarantees a single deterministic policy, while the strictly monotonically increasing scalarization may produce a single nonstationary policy or a mixture policy of 2 or more deterministic policies, we employ single-policy linear scalarization in the following.
is typically assumed for convenience. Given the fact that a linear scalarization guarantees a single deterministic policy, while the strictly monotonically increasing scalarization may produce a single nonstationary policy or a mixture policy of 2 or more deterministic policies, we employ single-policy linear scalarization in the following.
2.3. Multiobjective purity measure for building tolerant trees
A classification and regression tree (CART) is a binary decision tree constructed by recursively splitting a parent node into 2 child nodes with a lowest misclassification rate, starting from the root node that contains all the learning samples. A well-defined measure for purity is crucial to the tree building. Commonly used impurity measures for traditional unsupervised CART include Gini index, least squares deviation, and information index for categorical outcomes. In contrast, a DTR problem estimates the nonobservable optimal treatment for a patient. Thus, we define a purity measure for DTR trees using the estimated counterfactual mean outcomes for all objectives, which can be inferred from the observed treatments and outcomes. Optimal splits are selected by maximizing the purity of the child nodes, which, in turn, maximizes the counterfactual mean within each partition, thereby achieving maximum purity throughout the tree. The robustness of the estimation is improved by employing an  for the counterfactual mean outcomes proposed by Tao and Wang (2017).
for the counterfactual mean outcomes proposed by Tao and Wang (2017).
At stage j (j = 1 T), the tolerant-specific pseudo-outcome of i th objective (i = 1
T), the tolerant-specific pseudo-outcome of i th objective (i = 1 d) is calculated by
d) is calculated by  ; let
; let 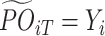 , the observed outcome for the i th objective at stage T. Given the estimated conditional mean
, the observed outcome for the i th objective at stage T. Given the estimated conditional mean  and the estimated propensity score
and the estimated propensity score  , the
, the 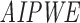 of
of  is
is
 |
(11) |
Property: The above  is a consistent estimator of
is a consistent estimator of 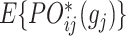 if either the propensity model of
if either the propensity model of  or the conditional mean model of
or the conditional mean model of  is correctly specified, and thus the method is doubly robust.
is correctly specified, and thus the method is doubly robust.
Let the value function for the i th objective be 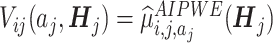 . With a weight
. With a weight 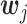 , we construct a scalarized-
, we construct a scalarized-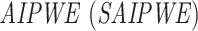 for counterfactual mean outcomes as
for counterfactual mean outcomes as
 |
(12) |
Given a partition γ and  , let
, let  denote the decision rule that assigns treatment aγ to subjects in γ and treatment
denote the decision rule that assigns treatment aγ to subjects in γ and treatment  to subjects in
to subjects in  at stage j (j = 1
at stage j (j = 1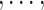 T), where
T), where 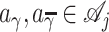 . The purity of such a node split is
. The purity of such a node split is
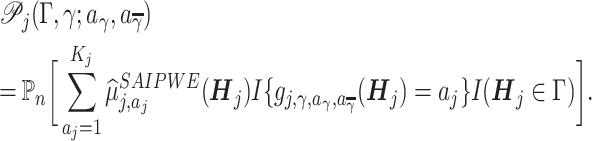 |
(13) |
The best treatment assignment for γ and  leads to a maximum purity of split, denoted as
leads to a maximum purity of split, denoted as  Moreover, if Γ does not split, all subjects in that node will be assigned with the same treatment
Moreover, if Γ does not split, all subjects in that node will be assigned with the same treatment 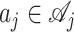 . The purity of such a node (leaf) is
. The purity of such a node (leaf) is
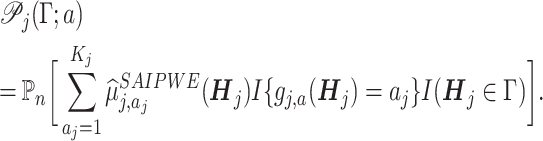 |
(14) |
Assigning a single best treatment leads to a maximum leaf purity  . Conversely, the worst treatment yields a minimum leaf purity
. Conversely, the worst treatment yields a minimum leaf purity  . We define the range of leaf purity as
. We define the range of leaf purity as 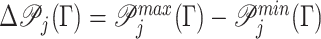 . For each leaf, a tolerant set is generated under a given tolerance rate, δj. A geometrical illustration for a bi-objective case is given in Figure 1, where the value functions
. For each leaf, a tolerant set is generated under a given tolerance rate, δj. A geometrical illustration for a bi-objective case is given in Figure 1, where the value functions  and
and 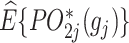 form a 2-dimensional coordinate, and the weight vector
form a 2-dimensional coordinate, and the weight vector  is drawn. Each of the 10 points represents a regime, forming the feasible space together. As shown in Figure 1A, the point with a projection onto the weight vector farthest from the origin represents the optimal regime. The nearest and the farthest projection yield
is drawn. Each of the 10 points represents a regime, forming the feasible space together. As shown in Figure 1A, the point with a projection onto the weight vector farthest from the origin represents the optimal regime. The nearest and the farthest projection yield  , and the tolerant regimes can be identified as points falling into the blue region in Figure 1B, which are marked by red crosses.
, and the tolerant regimes can be identified as points falling into the blue region in Figure 1B, which are marked by red crosses.
FIGURE 1.
A geometrical illustration of a bi-objective optimization problem at stage j. (A) The 2 axes represent the estimated counterfactual mean pseudo-outcome of the 2 objectives, respectively, denoted as 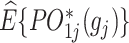 and
and 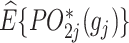 . Each point represents a decision rule at stage j, and together they constitute a feasible set. With a given weight vector
. Each point represents a decision rule at stage j, and together they constitute a feasible set. With a given weight vector 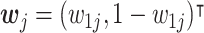 , the point with a projection onto the weight vector farthest from the origin is identified as the optimal regime.
, the point with a projection onto the weight vector farthest from the origin is identified as the optimal regime.  , the range of purity, is determined by the distance between the nearest and the farthest projections. (B) With a tolerance rate δj, the tolerant set at stage j can be identified as points falling into the upper δj percentage of
, the range of purity, is determined by the distance between the nearest and the farthest projections. (B) With a tolerance rate δj, the tolerant set at stage j can be identified as points falling into the upper δj percentage of  , which are marked by crosses.
, which are marked by crosses.
2.4. Recursive partitioning and multistage implementation
At each stage, the tDTR tree is grown through recursive partitioning. Each split depends on 1 covariate that supports personalized treatment assignment based on the value of this variable and improves the purity measure. This type of variable is known as a tailoring variable. For an ordinal or continuous covariate with C different values, there are C − 1 unique splits that indicate the cutoff value to separate node space Γ into child node γ and 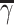 . For categorical covariate with L categories, there are 2L − 1 − 1 unique splits that indicate, which subset of the categories is included in the child node γ; the rest are assigned to node
. For categorical covariate with L categories, there are 2L − 1 − 1 unique splits that indicate, which subset of the categories is included in the child node γ; the rest are assigned to node 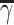 . Among all possible splits, the best split γopt is chosen by maximizing
. Among all possible splits, the best split γopt is chosen by maximizing 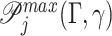 . To avoid over-fitting, 3 parameters are required adaptively based on the data. A positive number λ specifies the minimum improvement in the purity of splitting, an integer n0 specifies the minimal leaf size, and the other integer dmax specifies the maximum depth of the tree. These parameters jointly determine 4 Stopping Rules for terminating the tDTR tree growth, which are as follows:
. To avoid over-fitting, 3 parameters are required adaptively based on the data. A positive number λ specifies the minimum improvement in the purity of splitting, an integer n0 specifies the minimal leaf size, and the other integer dmax specifies the maximum depth of the tree. These parameters jointly determine 4 Stopping Rules for terminating the tDTR tree growth, which are as follows:
Rule 1. If the current node size is less than 2n0, then the node would not be split.
Rule 2. If all possible splits result in a child node size less than n0, then the node would not be split.
Rule 3. If the tree depth reaches dmax, then the tree would stop growing.
Rule 4. If
 , then the node would not be split.
, then the node would not be split.
The recursive partitioning starting from the root node is implemented by Algorithm 1.

The estimation proceeds from stage T and inducts backward to generate a tDTR tree for each of the prior stages. To increase robustness against model misspecification and reduce the accumulated bias from the conditional mean models (Huang et al., 2015), Tao et al. (2018) defined a modified version of the pseudo-outcome, named the cumulative pseudo-outcome (CPO). Instead of using only the model-based values under the future optimal regime, 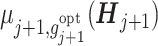 , the CPO combines the observed outcomes with the expected future loss due to suboptimal treatments. Nevertheless, the CPO is limited to addressing single objective problems and cannot handle tDTRs that involve multiple feasible regimes. Thus, we propose a cumulative tolerant-specific pseudo-outcome (CTPO) for each objective in a multiobjective tDTR, which represents a summation of the observed outcome and the expected future loss due to subtolerant treatments, denoted as
, the CPO combines the observed outcomes with the expected future loss due to suboptimal treatments. Nevertheless, the CPO is limited to addressing single objective problems and cannot handle tDTRs that involve multiple feasible regimes. Thus, we propose a cumulative tolerant-specific pseudo-outcome (CTPO) for each objective in a multiobjective tDTR, which represents a summation of the observed outcome and the expected future loss due to subtolerant treatments, denoted as  , where
, where
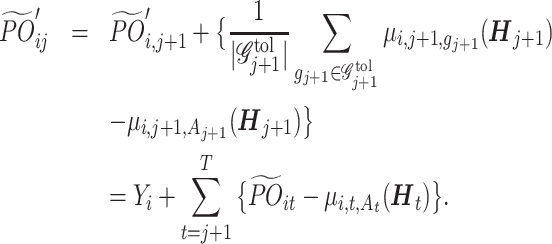 |
(15) |
Algorithm 2 describes the implementation of MOT-RL that inducts backward through the last stage to the initial stage.

3. SIMULATION STUDIES
Simulation studies are conducted on 2 scenarios to investigate the performance of our proposed method. We first consider a bi-objective scenario (d = 2) with 3 treatment options (K = 3), in which a single-stage and a 2-stage case are simulated. For each case, MOT-RL is applied to 4 tolerance rates ( ) and 21 weight vectors [(0, 1)⊺ to (1, 0)⊺ with 0.05 increments and reductions in the first and second weight, respectively]. In addition, a tri-objective scenario (d = 3) with 3 treatment options (K = 3) is also considered. In each simulation, 1000 replications are conducted on a training sample size of 500 or 1000 and a testing sample size of 1000. Under certain tolerance rates, the training data are used to estimate the tDTR tree and predict the tolerant treatments in the testing data. The percentage of subjects whose estimated tolerant set contains the true optimal treatment is evaluated and recorded as
) and 21 weight vectors [(0, 1)⊺ to (1, 0)⊺ with 0.05 increments and reductions in the first and second weight, respectively]. In addition, a tri-objective scenario (d = 3) with 3 treatment options (K = 3) is also considered. In each simulation, 1000 replications are conducted on a training sample size of 500 or 1000 and a testing sample size of 1000. Under certain tolerance rates, the training data are used to estimate the tDTR tree and predict the tolerant treatments in the testing data. The percentage of subjects whose estimated tolerant set contains the true optimal treatment is evaluated and recorded as  . Moreover, the counterfactual mean outcome for each objective in the testing population is estimated by the true outcome model and the estimated tolerant regime.
. Moreover, the counterfactual mean outcome for each objective in the testing population is estimated by the true outcome model and the estimated tolerant regime.
3.1. Scenario 1: bi-objective optimization
Six baseline covariates X1 X6 are considered, where the former 5 are generated from N(0, 1), and X6 is randomly sampled from “Yes” and “No”.
X6 are considered, where the former 5 are generated from N(0, 1), and X6 is randomly sampled from “Yes” and “No”.
(a) Single-stage case: The observed treatment A1 takes values in {0, 1, 2} and is generated from Multinomial(π10, π11, π12), where
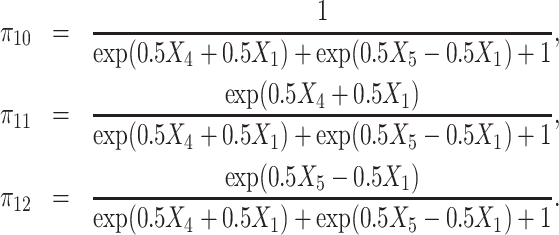 |
(16) |
A tree-structured true optimal regime is considered as
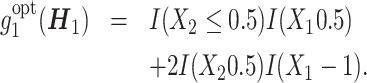 |
(17) |
Correspondingly, the 2 observed rewards at stage 1, R11 and R21, are generated as follows:
 |
(18) |
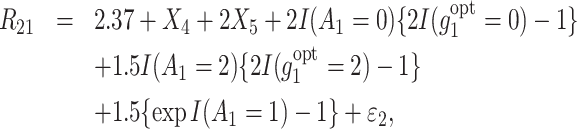 |
(19) |
where ε1, ε2 ∼ N(0, 1) or ε1, ε2 ∼ N(0, 5).
The first reward function, R11, equally penalizes all suboptimal treatments, and we assume that A1 = 1 leads to an adverse effect on R11. The second reward function, R21, is penalized with different losses depending on suboptimal treatments received. In contrast, we assume a positive effect on R21 when A1 = 1. As an analogy to cancer treatment, treatment option 1 has a higher efficacy (R21), but is less safe (R11) and causes greater toxicity compared to the other options. These 2 rewards are treated as the outcomes directly, where Y1 = R11 and Y2 = R21.
Table 1 summarizes the performance of the T-RL method by Tao et al. (2018) and MOT-RL under 5 different sets of weights. Consequently, while T-RL optimizes its target objective well, it leaves the other objective poorly optimized. Multiobjective tree-based reinforcement learning, however, simultaneously optimizes both objectives and achieves higher 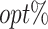 , especially when using equal weights. In addition, the
, especially when using equal weights. In addition, the 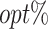 is greatly enhanced with a larger sample size, as expected.
is greatly enhanced with a larger sample size, as expected.
TABLE 1.
Simulation result for Scenario 1a with 1 stage and 3 treatment options (sample size N = 500 or 1000, 100 replications).
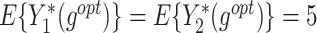
| |||||||
|---|---|---|---|---|---|---|---|
| Method | N = 500 | N = 1000 | |||||
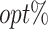
|
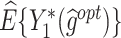
|
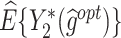
|
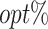
|
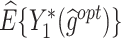
|
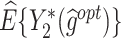
|
||
| T-RL | Y 1 as outcome | 77.32 (2.10) | 4.96 (0.11) | 3.36 (0.11) | 77.75 (2.15) | 4.97 (0.14) | 3.41 (0.10) |
| Y 2 as outcome | 21.21 (1.25) | -0.36 (0.06) | 4.94 (0.07) | 21.15 (0.89) | -0.36 (0.04) | 4.94 (0.08) | |
| MOT-RL: w = (0.3, 0.7) | |||||||
| 100% tolerant | 78.64 (18.21) | 3.49 (1.14) | 4.43 (0.19) | 81.24 (16.85) | 3.71 (1.06) | 4.41 (0.20) | |
| 90% tolerant | 78.72 (18.23) | 3.47 (1.12) | 4.44 (0.18) | 82.00 (16.53) | 3.72 (1.04) | 4.40 (0.19) | |
| 70% tolerant | 79.97 (18.01) | 3.25 (0.98) | 4.47 (0.14) | 82.81 (16.17) | 3.27 (0.84) | 4.50 (0.13) | |
| 50% tolerant | 80.53 (17.99) | 1.47 (0.56) | 4.64 (0.12) | 83.05 (15.88) | 1.45 (0.43) | 4.65 (0.10) | |
| MOT-RL: w = (0.4, 0.6) | |||||||
| 100% tolerant | 95.62 (5.37) | 4.61 (0.31) | 4.32 (0.10) | 97.65 (4.28) | 4.71 (0.25) | 4.34 (0.08) | |
| 90% tolerant | 95.68 (5.34) | 4.60 (0.32) | 4.32 (0.10) | 97.77 (4.19) | 4.72 (0.25) | 4.34 (0.08) | |
| 70% tolerant | 96.00 (5.09) | 4.58 (0.35) | 4.32 (0.12) | 97.82 (4.18) | 4.70 (0.25) | 4.34 (0.08) | |
| 50% tolerant | 96.46 (4.82) | 3.84 (0.43) | 4.43 (0.16) | 97.94 (4.18) | 3.85 (0.36) | 4.48 (0.09) | |
| MOT-RL: w = (0.5, 0.5) | |||||||
| 100% tolerant | 97.97 (1.98) | 4.74 (0.12) | 4.32 (0.09) | 98.81 (0.97) | 4.78 (0.09) | 4.33 (0.08) | |
| 90% tolerant | 97.97 (1.98) | 4.74 (0.12) | 4.32 (0.09) | 98.81 (0.97) | 4.78 (0.09) | 4.33 (0.08) | |
| 70% tolerant | 98.04 (1.91) | 4.75 (0.12) | 4.31 (0.09) | 98.81 (0.97) | 4.78 (0.09) | 4.34 (0.08) | |
| 50% tolerant | 98.17 (1.50) | 4.64 (0.30) | 4.32 (0.11) | 98.86 (0.86) | 4.76 (0.15) | 4.33 (0.09) | |
| MOT-RL: w = (0.6, 0.4) | |||||||
| 100% tolerant | 97.64 (3.49) | 4.76 (0.11) | 4.29 (0.16) | 98.40 (3.14) | 4.79 (0.09) | 4.31 (0.16) | |
| 90% tolerant | 97.64 (3.49) | 4.76 (0.11) | 4.28 (0.16) | 98.40 (3.14) | 4.79 (0.09) | 4.31 (0.16) | |
| 70% tolerant | 97.71 (3.45) | 4.76 (0.11) | 4.28 (0.16) | 98.40 (3.14) | 4.79 (0.09) | 4.31 (0.17) | |
| 50% tolerant | 97.73 (3.46) | 4.76 (0.11) | 4.25 (0.19) | 98.50 (3.12) | 4.79 (0.11) | 4.30 (0.18) | |
| MOT-RL: w = (0.7, 0.3) | |||||||
| 100% tolerant | 89.84 (9.96) | 4.84 (0.16) | 3.93 (0.46) | 92.01 (10.05) | 4.86 (0.12) | 4.02 (0.46) | |
| 90% tolerant | 90.07 (9.99) | 4.85 (0.15) | 3.93 (0.45) | 92.01 (10.05) | 4.86 (0.12) | 4.02 (0.46) | |
| 70% tolerant | 90.48 (9.93) | 4.85 (0.15) | 3.91 (0.44) | 92.46 (9.76) | 4.86 (0.11) | 4.01 (0.45) | |
| 50% tolerant | 90.95 (9.76) | 4.83 (0.15) | 3.88 (0.42) | 92.68 (9.63) | 4.86 (0.12) | 3.96 (0.44) | |
The 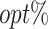 column indicates the empirical mean and standard error (SE) of the percentage of subjects whose estimated treatment set includes the actual optimal treatment. The
column indicates the empirical mean and standard error (SE) of the percentage of subjects whose estimated treatment set includes the actual optimal treatment. The  and
and  columns present the empirical mean and SE of the estimated counterfactual mean outcomes of the 2 objectives, determined by the observed outcomes and the estimated optimal (or tolerant) dynamic treatment regime (DTR). T-RL, tree-based reinforcement learning by Tao and Wang (2018); MOT-RL, multiobjective tree-based reinforcement learning.
columns present the empirical mean and SE of the estimated counterfactual mean outcomes of the 2 objectives, determined by the observed outcomes and the estimated optimal (or tolerant) dynamic treatment regime (DTR). T-RL, tree-based reinforcement learning by Tao and Wang (2018); MOT-RL, multiobjective tree-based reinforcement learning.
A convex shape is formed by the optimization results of all 21 weights, as shown in Figure 2A(i). The points in the upper left region are the feasible tDTRs for optimizing treatment efficacy, while those on the right-end are feasible tDTRs for optimizing safety. The tDTRs that balance and optimize the 2 objectives simultaneously can be identified as the points in the “elbow region,” which lead to higher values of  [Figure 2A(ii)].
[Figure 2A(ii)].
FIGURE 2.
Simulation results of multiobjective tree-based reinforcement learning (MOT-RL) for the 2 cases in Scenario 1. Each case is simulated with a 70% tolerance rate on 21 different weight vectors [(0, 1)⊺ to (1, 0)⊺ with 0.05 increments]. (A) Single-stage case: (i). The optimization results for all weights. Each point represents a tolerant dynamic treatment regime (tDTR) with a specific weight vector as marked below, and the coordinates of the point indicate the estimated counterfactual mean outcomes,  and
and  . The horizontal and vertical error bars indicate the estimated standard error (SE) for the optimized result of the first and second objectives, respectively. (ii) The percentage of subjects whose estimated treatment set includes the actual optimal treatment (
. The horizontal and vertical error bars indicate the estimated standard error (SE) for the optimized result of the first and second objectives, respectively. (ii) The percentage of subjects whose estimated treatment set includes the actual optimal treatment (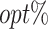 ) of all tDTRs. Each tDTR is represented by its weight on the first objective w1. The error bars indicate SE of
) of all tDTRs. Each tDTR is represented by its weight on the first objective w1. The error bars indicate SE of  . (B) 2-stage case: (i) The optimization results for all weights at stage 1.
. (B) 2-stage case: (i) The optimization results for all weights at stage 1. 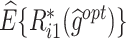 , the estimated counterfactual reward mean of the i th objective (i = 1, 2) at stage 1. (ii) The optimization results for all weights at stage 2.
, the estimated counterfactual reward mean of the i th objective (i = 1, 2) at stage 1. (ii) The optimization results for all weights at stage 2.  , the estimated counterfactual reward mean of the i th objective (i = 1, 2) at stage 2. (iii) The overall optimization results for all weights, defined as the summation of stage 1 and stage 2 results.
, the estimated counterfactual reward mean of the i th objective (i = 1, 2) at stage 2. (iii) The overall optimization results for all weights, defined as the summation of stage 1 and stage 2 results.
(b) 2-stage case: We further generate the second treatment stage data based on the above case (a). The observed treatment A2 takes values in {0, 1, 2} and is generated from Multinomial(π20, π21, π22), where
 |
(20) |
The stage 2 true optimal regime 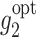 is
is
 |
(21) |
The 2 observed rewards R12 and R22 are generated as follows:
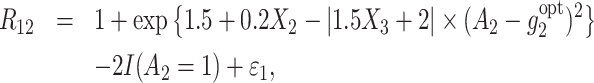 |
(22) |
 |
(23) |
where ε1, ε2 ∼ N(0, 1) or ε1, ε2 ∼ N(0, 5). The reward functions R12 and R22 are generated with similar penalty rules as in (a), and the 2 outcomes are the sum of immediate rewards for each objective at each stage, that is, Y1 = R11 + R12 and Y2 = R21 + R22.
Accordingly, the overall  of T-RL is low regardless of its target objective, while MOT-RL achieves a 90% of overall
of T-RL is low regardless of its target objective, while MOT-RL achieves a 90% of overall 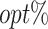 under the equal weight (Table 2). The optimization results at stage 1 and stage 2 are presented in Figure 2B(i) and (ii), respectively. A similar trade-off relationship is observed at stage 1, and the decisions in the “elbow region” balance between efficacy and safety. At stage 2, the decisions under roughly equal weights maximize both objectives. The summation of the 2 stages is also considered in Figure 2B(iii), and the most recommended tDTRs are those in the upper right region.
under the equal weight (Table 2). The optimization results at stage 1 and stage 2 are presented in Figure 2B(i) and (ii), respectively. A similar trade-off relationship is observed at stage 1, and the decisions in the “elbow region” balance between efficacy and safety. At stage 2, the decisions under roughly equal weights maximize both objectives. The summation of the 2 stages is also considered in Figure 2B(iii), and the most recommended tDTRs are those in the upper right region.
TABLE 2.
Simulation result for Scenario 1b with 2 stages and 3 treatment options (sample size N = 1000, 100 replications).
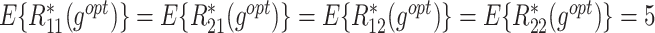 ;
; | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
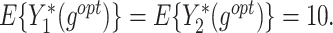
| ||||||||||
| Method | Stage 1 | Stage 2 | Overall | |||||||
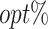
|
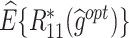
|
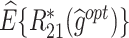
|
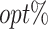
|
|
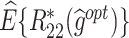
|
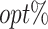
|

|
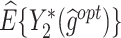
|
||
| T-RL | Y 1 as outcome | 77.75 (1.32) | 4.98 (0.07) | 3.35 (0.09) | 65.51 (5.20) | 4.31 (0.11) | 2.74 (0.28) | 43.89 (5.33) | 9.29 (0.14) | 6.09 (0.28) |
| Y 2 as outcome | 21.31 (1.19) | −0.36 (0.07) | 4.94 (0.07) | 77.36 (13.12) | 3.89 (1.06) | 4.20 (0.30) | 18.51 (6.74) | 3.53 (1.05) | 9.14 (0.30) | |
| MOT-RL: w = (0.3, 0.7) | ||||||||||
| 100% tolerant | 71.07 (12.41) | 3.11 (0.78) | 4.39 (0.20) | 96.02 (2.81) | 4.76 (0.16) | 4.58 (0.05) | 69.08 (12.04) | 7.87 (0.77) | 8.97 (0.21) | |
| 90% tolerant | 71.59 (12.46) | 3.12 (0.78) | 4.38 (0.20) | 96.16 (2.73) | 4.76 (0.16) | 4.58 (0.05) | 69.66 (12.11) | 7.88 (0.78) | 8.96 (0.21) | |
| 70% tolerant | 72.64 (12.19) | 3.10 (0.76) | 4.39 (0.20) | 96.38 (2.83) | 4.70 (0.17) | 4.58 (0.05) | 70.82 (11.94) | 7.80 (0.78) | 8.96 (0.20) | |
| 50% tolerant | 73.94 (12.01) | 2.94 (0.83) | 4.40 (0.23) | 96.62 (2.96) | 4.26 (0.28) | 4.51 (0.06) | 71.23 (11.89) | 7.19 (0.83) | 8.91 (0.24) | |
| MOT-RL: w = (0.4, 0.6) | ||||||||||
| 100% tolerant | 82.49 (12.28) | 3.78 (0.71) | 4.31 (0.23) | 96.08 (3.13) | 4.76 (0.19) | 4.58 (0.06) | 79.18 (12.36) | 8.54 (0.72) | 8.90 (0.24) | |
| 90% tolerant | 82.74 (12.30) | 3.79 (0.70) | 4.31 (0.24) | 96.08 (3.13) | 4.76 (0.19) | 4.58 (0.06) | 79.39 (12.36) | 8.55 (0.71) | 8.89 (0.24) | |
| 70% tolerant | 83.02 (12.57) | 3.82 (0.69) | 4.30 (0.23) | 96.18 (3.15) | 4.74 (0.19) | 4.58 (0.06) | 80.70 (12.69) | 8.55 (0.71) | 8.88 (0.24) | |
| 50% tolerant | 84.13 (12.27) | 3.76 (0.63) | 4.33 (0.25) | 96.52 (2.75) | 4.61 (0.24) | 4.55 (0.11) | 82.98 (12.45) | 8.37 (0.69) | 8.88 (0.28) | |
| MOT-RL: w = (0.5, 0.5) | ||||||||||
| 100% tolerant | 91.19 (9.96) | 4.35 (0.51) | 4.28 (0.23) | 95.99 (3.10) | 4.76 (0.18) | 4.58 (0.06) | 89.53 (10.49) | 9.10 (0.56) | 8.86 (0.23) | |
| 90% tolerant | 91.54 (9.94) | 4.36 (0.50) | 4.28 (0.24) | 95.99 (3.10) | 4.76 (0.18) | 4.58 (0.06) | 89.86 (10.52) | 9.12 (0.56) | 8.86 (0.24) | |
| 70% tolerant | 92.27 (9.89) | 4.37 (0.50) | 4.27 (0.24) | 95.99 (3.10) | 4.75 (0.19) | 4.58 (0.06) | 90.55 (10.57) | 9.12 (0.56) | 8.85 (0.24) | |
| 50% tolerant | 93.07 (9.58) | 4.27 (0.53) | 4.25 (0.29) | 96.30 (2.66) | 4.68 (0.21) | 4.56 (0.11) | 91.56 (10.05) | 8.96 (0.60) | 8.81 (0.31) | |
| MOT-RL: w = (0.6, 0.4) | ||||||||||
| 100% tolerant | 90.36 (10.73) | 4.72 (0.27) | 4.04 (0.45) | 95.68 (3.27) | 4.74 (0.19) | 4.58 (0.06) | 88.29 (11.35) | 9.46 (0.35) | 8.62 (0.46) | |
| 90% tolerant | 90.46 (10.70) | 4.73 (0.27) | 4.03 (0.47) | 95.68 (3.27) | 4.74 (0.19) | 4.58 (0.06) | 88.36 (11.32) | 9.47 (0.35) | 8.61 (0.48) | |
| 70% tolerant | 91.07 (10.54) | 4.74 (0.24) | 4.04 (0.46) | 95.84 (2.80) | 4.73 (0.21) | 4.57 (0.11) | 89.03 (10.95) | 9.47 (0.30) | 8.61 (0.47) | |
| 50% tolerant | 92.23 (9.98) | 4.68 (0.29) | 4.06 (0.44) | 96.17 (1.91) | 4.70 (0.23) | 4.55 (0.17) | 90.50 (10.12) | 9.38 (0.37) | 8.61 (0.46) | |
| MOT-RL: w = (0.7, 0.3) | ||||||||||
| 100% tolerant | 84.50 (10.11) | 4.88 (0.17) | 3.67 (0.46) | 95.04 (4.06) | 4.71 (0.22) | 4.56 (0.08) | 78.72 (10.65) | 9.59 (0.27) | 8.23 (0.47) | |
| 90% tolerant | 84.57 (10.15) | 4.89 (0.17) | 3.67 (0.47) | 95.08 (3.88) | 4.71 (0.22) | 4.56 (0.08) | 78.83 (10.53) | 9.59 (0.28) | 8.23 (0.48) | |
| 70% tolerant | 84.97 (10.11) | 4.88 (0.16) | 3.66 (0.47) | 95.37 (3.25) | 4.70 (0.24) | 4.55 (0.15) | 79.50 (10.42) | 9.58 (0.27) | 8.21 (0.50) | |
| 50% tolerant | 85.25 (10.02) | 4.87 (0.17) | 3.64 (0.45) | 95.83 (1.99) | 4.69 (0.26) | 4.52 (0.21) | 80.20 (10.36) | 9.55 (0.30) | 8.16 (0.49) | |
The 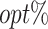 column indicates the empirical mean and standard error (SE) of the percentage of subjects whose estimated treatment set includes the actual optimal treatment, which is recorded for stage 1, stage 2, and both stage 1 and stage 2 (overall). The
column indicates the empirical mean and standard error (SE) of the percentage of subjects whose estimated treatment set includes the actual optimal treatment, which is recorded for stage 1, stage 2, and both stage 1 and stage 2 (overall). The  column presents the empirical mean and SE of the estimated counterfactual mean rewards of i th objective at stage j, Rij (i, j = 1, 2), which are obtained from true rewards and the estimated optimal (or tolerant) regime. The
column presents the empirical mean and SE of the estimated counterfactual mean rewards of i th objective at stage j, Rij (i, j = 1, 2), which are obtained from true rewards and the estimated optimal (or tolerant) regime. The  column presents the empirical mean and SE of the estimated counterfactual mean outcome of the ith objective.
column presents the empirical mean and SE of the estimated counterfactual mean outcome of the ith objective.
3.2. Scenario 2: tri-objective optimization
Ten baseline covariates X1 X10 are considered in this scenario. The former 9 are generated from N(0, 1), while X10 is randomly sampled from “Yes” and “No”. The observed treatment A takes values in {0, 1, 2} and is generated from Multinomial(π0, π1, π2), where
X10 are considered in this scenario. The former 9 are generated from N(0, 1), while X10 is randomly sampled from “Yes” and “No”. The observed treatment A takes values in {0, 1, 2} and is generated from Multinomial(π0, π1, π2), where
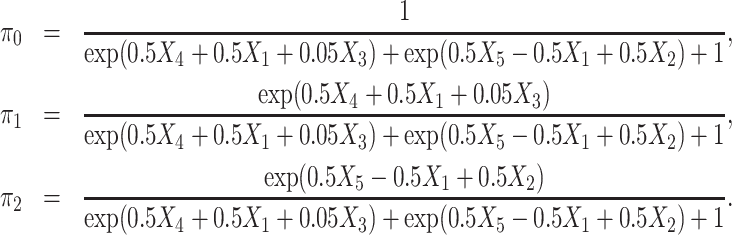 |
(24) |
A tree-structured underlying optimal regime is considered as
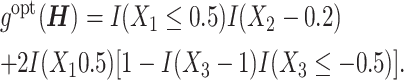 |
(25) |
Correspondingly, the 3 observed rewards, Y1, Y2, and Y3 are generated as follows:
 |
(26) |
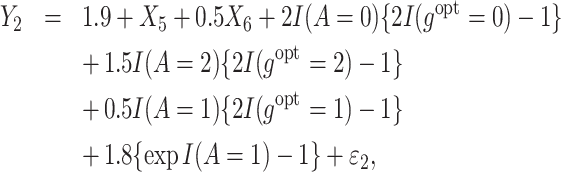 |
(27) |
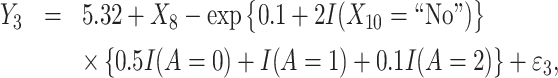 |
(28) |
where ε1, ε2, ε3 ∼ N(0, 1).
Similarly as in Scenario 1, treatment option 1 leads to a positive effect on efficacy (Y1, the higher the more effective) but a negative effect on safety (Y2, the higher the less toxic). Additionally, a third outcome is generated to represent the cost of treatment (Y3, a higher value indicates a lower cost). Thus, this simulation further mimics how to achieve the optimal cost-effective treatment strategies, while also balancing treatment efficacy and side effects. We assume X10 indicates whether the subject is insured. Regardless of the insurance status, the most expensive option is treatment 1, followed by treatment 0 and then treatment 2. Then, we employ MOT-RL to 231 distinct weights (0.05 difference in weight of any objective), and each optimization result is presented as a scatter point in the 3-dimensional space formed by the 3 estimated counterfactual mean outcomes [Figure 3A]. A convex surface is identified, on which we use a contour plot to demonstrate the sum of 3 estimated counterfactual mean outcomes. The darkest region is where the sum achieves the highest, and the corresponding tDTRs optimize both safety and efficacy, as well as remain cost-effective. Consequently, those decision rules achieve higher values of 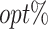 as shown in Figure 3B. We want to note that Figures 2 and 3 are only used for visualizing the comparison of different weights. For practitioners to use MOT-RL to generate multistage tolerance DTR trees, they only need to enter patient-level data (outcomes, covariates), weights, and tolerance rate.
as shown in Figure 3B. We want to note that Figures 2 and 3 are only used for visualizing the comparison of different weights. For practitioners to use MOT-RL to generate multistage tolerance DTR trees, they only need to enter patient-level data (outcomes, covariates), weights, and tolerance rate.
FIGURE 3.
Simulation results of multiobjective tree-based reinforcement learning (MOT-RL) on Scenario 2. (A) The optimization results of MOT-RL with a 70% tolerance rate on 231 different weight vectors (0.05 difference in weight of any objective). Each point represents a tolerant dynamic treatment regime (tDTR) with a specific weight vector. A contour plot is drawn on the fitted surface to display the summation of the 3 counterfactual mean outcomes. The red region indicates a higher sum, where the corresponding tDTRs more effectively balance the 3 competing objectives. (B) The percentage of subjects whose estimated treatment set includes the actual optimal treatment (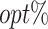 ) of all tDTRs. Each tDTR is represented by its weight on the first and second objectives, w1 and w2.
) of all tDTRs. Each tDTR is represented by its weight on the first and second objectives, w1 and w2.
In general, the speed of the algorithm is reasonably fast, despite computation time increases with the number of objectives.
4. APPLICATION TO ADVANCED PROSTATE CANCER DATA
The data are from a clinical trial conducted at MD Anderson Cancer Center from 1998 to 2006 (Thall et al., 2000). One hundred and fifty advanced prostate cancer patients were enrolled and received 2-4 courses of chemotherapy (hereafter, “chemo”) at baseline, week 8, and possibly week 16 and 24, depending on the per-course responses. At enrollment, patients were randomized to receive 1 of the 4 candidate chemos: cyclophosphamide, vincristine, and dexamethasone (CVD); ketoconazole, doxorubicin alternating with vinblastine, estramustine (KA/VE); paclitaxel, estramustine, and carboplatin (TEC); and paclitaxel, estramustine, and etoposide (TEE). During the trial, patients remained on the same regimen if showing a favorable response but otherwise were randomly assigned to 1 of the other 3 chemos. Patients’ characteristics were collected at the baseline and per-course variables were measured at the end of each course (see Web Appendix A for details). We use the subscript j = 0, 1, 2 to denote the stages of baseline, postfirst chemo, and postsecond chemo, respectively. Six subjects who quit the trial due to extreme progressive disease or toxicity were excluded, resulting in 144 patients enrolled (25% CVD, 24.3% KA/VE, 25.7% TEC, and 25% TEE for the initial treatment). Two subjects have missing stage 1 prostate-specific antigen (PSA) values, and the missing data are imputed by using IVEware (2002).
We apply MOR-TL to the above data to maximize 2 outcomes at stage j: (i) the “expert score” (a value between 0 and 1 indicating the clinical desirability of the toxicity and efficacy outcomes, defined by trial principal investigators), Y1j = ESj; (ii) the survival time of the patient, Y2j = STj. The chemo received at stage j is recorded as Aj, j = 1, 2. The covariate and treatment history at stage 2 is  . Linear regression models are fitted for
. Linear regression models are fitted for 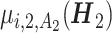 using Yi2, i = 1, 2, including interactions between A2 and all variables in
using Yi2, i = 1, 2, including interactions between A2 and all variables in 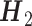 . The propensity score
. The propensity score 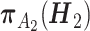 is derived by fitting a multinomial logistic regression model including the main effects of all variables in
is derived by fitting a multinomial logistic regression model including the main effects of all variables in 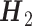 . We set the minimal node size n0 = 15, maximum tree depth dmax = 3, minimum purity improvement
. We set the minimal node size n0 = 15, maximum tree depth dmax = 3, minimum purity improvement  , and tolerance rate δ = 0.2. The stage 1 history matrix is
, and tolerance rate δ = 0.2. The stage 1 history matrix is  . Similar procedures are repeated except using the CTPOs as the outcomes, where
. Similar procedures are repeated except using the CTPOs as the outcomes, where 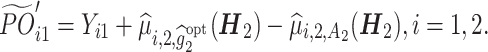
The 2-stage 80% tDTR trees for 5 different preferences are presented in Figure 4. First, when all weights are on the expert score to temporarily diminish disease burden, all patients are recommended to take TEE as the initial chemo. After that, 1 tailoring variable at stage 2 is identified as the postfirst chemo PSA [PSA1 median (range): 50.5 (0.2, 2379)]. Patients with PSA1 less than 146 ng/mL are encouraged to take CVD as the salvage chemo, and KA/VE otherwise. Conversely, when we regard prolonging survival as the only objective, the tailoring variables for stage 1 are hemoglobin level [Hgb, median (range): 13.2 (9.5, 15.7)] and months of receiving hormone therapy [TRx, median (range): 34.7 (5.9, 176.0)]. Patients with Hgb less than 12.9 g/dL are encouraged to take CVD as the initial chemo. Among patients with Hgb higher than this threshold, those with TRx greater than 49.8 months are recommended to take TEE as the initial chemo, otherwise, take KA/VE or TEC. All patients are recommended to take either CVD or TEC as the salvage chemo. The suggested regimes for these 2 mono-objective cases are consistent with previous studies by Wang et al. (2012), who indicated the best regime for all patients to optimize their expert score is (TEC, CVD) and to prolonging survival are (CVD, TEC) and (KA/VE, CVD). In addition, 3 intermediate weights, (0.2, 0.8)⊺, (0.5, 0.5)⊺, and (0.8, 0.2)⊺ are also considered. Taking the equal weight, for example, the tailoring variable for stage 1 is found to be the baseline PSA [PSA0, median (range): 45 (1, 1877)] with a cutoff at 33 ng/mL. Patients with PSA0 lower than this threshold are encouraged to take TEC as the initial chemo, and TEE otherwise. At stage 2, patients who took TEC at stage 1 are encouraged to take CVD. Among the rest of the patients, those with PSA1 higher than 125 ng/mL are encouraged to take KA/VE; otherwise, take either CVD or KA/VE. Unlike existing studies that gave a universal suggestion on treatment among all prostate cancer patients, our proposed method divides the population into subgroups to provide personalized treatment advice and is flexible to incorporate preferences on different clinical objectives.
FIGURE 4.
The estimated 80% tolerant dynamic treatment regime (tDTR) trees of the 2-stage chemotherapy for advanced prostate cancer patients with 5 different weights. Numbers in squares represent node numbers, and variables in circles represent tailoring variables. The splitting rule for a continuous tailoring variable is indicated by a cut-off value, whereas the splitting rule for a categorical tailoring variable is expressed as 2 subsets of all possible categories. Below each ending node (leaf) is the corresponding suggested treatment (set), where the optimal treatment is highlighted in bold, and a tolerant set is provided if there is more than 1 viable treatment within the 80% tolerance rate. PSA0, baseline prostate-specific antigen (PSA) level (ng/mL). PSA1, post stage 1 PSA level (ng/mL). A1, chemotherapy received at stage 1. TRx, time of receiving hormone therapy (mo). Hgb, hemoglobin level (g/dL). Age, patient’s age at enrollment.
5. DISCUSSION
In this paper, we propose the concept of a tolerant regime and present a general and explicit development of MOT-RL, a tree-based DTR learning approach. It is particularly effective for settings with multiple objectives and more than 1 stage, where trees are favored for interpretability and flexibility in treatment choice is preferred over strict maximization. One of the most notable features of MOT-RL is that it provides a platform to balance decision-makers’ preferences on multiple competing clinical priorities and identify the corresponding individualized treatment decision rules. This flexible design allows both practitioners and patients to get involved in tailoring personalized medical intervention, as well as presenting intermediate solutions that were not achievable by previous methods optimizing a single objective. In addition, introducing the concept of tolerant regimes provides decision-makers with optimal and practically comparable alternatives, thus eliminating obvious ineffective options while still allowing room for them to make personalized choices. Furthermore, the MOT-RL benefits from the easy-to-use and highly interpretable features of tree-based learning and is capable of handling various types of covariates without distributional assumptions. Last but not least, the proposed method has improved estimation robustness by embedding doubly robust  in the decision tree algorithm.
in the decision tree algorithm.
There are several extensions of our methods that may further facilitate and make positive impacts for providing evidence-based clinical decision tools. One possible extension of the MOT-RL is to generalize the linear scalarization in the purity measure to other monotonically increasing scalarizations (Roijers and Whiteson, 2017). However, the choice of scalarization function requires case-specific clinical knowledge, and more restrictions may be needed to generate a meaningful single deterministic policy serving as the optimal regime. Another potential topic that deserves future research is integrating Pareto-based multiobjective optimization methods into tree-based learning. Specifically, various MOEAs were developed to tackle optimization problems that have more than 4 objectives, such as Nondominated Sorting Genetic Algorithm version 2 (NSGA-II, Deb et al., 2002) and Multiobjective Evolutionary Algorithm based on Decomposition (MOEA/D, Zhang and Li, 2007). With these tools, there is no requirement to prespecify weight vectors for preferences. Instead, feasible decisions are determined by estimating the “dominant” options, namely, the PF. Nevertheless, the implementation of recursive partitioning when building the decision tree based on multidimensional outcomes remains challenging. A reasonable novel purity measure derived from higher dimensional outcomes in that case to support the binary split of the decision tree is of future research interest.
Supplementary Material
Web Appendices referenced in Section 4 and a zip file containing R code and example data are available with this paper at the Biometrics website on Oxford Academic. The R package MOTRL and more direction for application can be found in GitHub at https://github.com/Team-Wang-Lab/MOTRL.
Acknowledgement
The authors thank the Co-Editor, Associate Editor, and referees for providing invaluable insights and constructive feedback that improved the presentation of the paper.
Contributor Information
Yao Song, Department of Biostatistics, University of Michigan, Ann Arbor, MI 48105, United States.
Lu Wang, Department of Biostatistics, University of Michigan, Ann Arbor, MI 48105, United States.
FUNDING
This research is partially supported by the NIH Grants P50-DA-054039-02, P30-ES-017885-10-A1, R01-ES-033515-01, and CDC Grant R01-CE-003497-01.
CONFLICT OF INTEREST
None declared.
DATA AVAILABILITY
The data that support the findings in this paper are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.
References
- Barrett L., Narayanan S. (2008). Learning all optimal policies with multiple criteria. In Proceedings of the 25th International Conference on Machine Learning, 41–47. [Google Scholar]
- Bather J. (2000). Decision Theory: An Introduction to Dynamic Programming and Sequential Decisions. Chichester, NY: John Wiley & Sons, Inc [Google Scholar]
- Bringmann K., Friedrich T. (2009). Don’t be greedy when calculating hypervolume contributions. In Proceedings of the 10th ACM SIGEVO Workshop on Foundations of Genetic Algorithms, 103–112. [Google Scholar]
- Chakraborty B., Murphy S. A. (2014). Dynamic treatment regimes. Annual Review of Statistics and Its Application, 1, 447–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deb K., Pratap A., Agarwal S., Meyarivan T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6, 182–197. [Google Scholar]
- Gunantara N. (2018). A review of multi-objective optimization: methods and its applications. Cogent Engineering, 5, 1502242. [Google Scholar]
- Hernán M. A., Brumback B., Robins J. M. (2001). Marginal structural models to estimate the joint causal effect of nonrandomized treatments. Journal of the American Statistical Association, 96, 440–448. [Google Scholar]
- Huang X., Choi S., Wang L., Thall P. F. (2015). Optimization of multi-stage dynamic treatment regimes utilizing accumulated data. Statistics in Medicine, 34, 3424–3443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- IVEware (2002). IVEware: Imputation and Variance Estimation Software. Institute for Social Research, University of Michigan. Available from: https://src.isr.umich.edu/software/iveware/. [Accessed 14 September 2023]. [Google Scholar]
- Laber E. B., Zhao Y. Q. (2015). Tree-based methods for individualized treatment regimes. Biometrika, 102, 501–514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li B., Li J., Tang K., Yao X. (2015). Many-objective evolutionary algorithms. ACM Computing Surveys, 48, 1–35. [Google Scholar]
- Lizotte D. J., Bowling M., Murphy S. A. (2012). Linear fitted-Q iteration with multiple reward functions. Journal of Machine Learning Research, 13, 3253–3295. [PMC free article] [PubMed] [Google Scholar]
- Lizotte D. J., Laber E. B. (2016). Multi-objective Markov decision processes for data-driven decision support. Journal of Machine Learning Research, 17, 7378–7405. [PMC free article] [PubMed] [Google Scholar]
- Lobato F. S., Machado V. S., Steffen V. (2016). Determination of an optimal control strategy for drug administration in tumor treatment using multi-objective optimization differential evolution. Computer Methods and Programs in Biomedicine, 131, 51–61. [DOI] [PubMed] [Google Scholar]
- Luong N. H., Alderliesten T., Bel A., Niatsetski Y., Bosman P. A. (2018). Application and benchmarking of multi-objective evolutionary algorithms on high-dose-rate brachytherapy planning for prostate cancer treatment. Swarm and Evolutionary Computation, 40, 37–52. [Google Scholar]
- Moodie E. E., Dean N., Sun Y. R. (2013). Q-learning: flexible learning about useful utilities. Statistics in Biosciences, 6, 223–243. [Google Scholar]
- Murphy S. A. (2003). Optimal dynamic treatment regimes. Journal of the Royal Statistical Society: Series B Statistical Methodology, 65, 331–355. [Google Scholar]
- Murphy S. A. (2004). An experimental design for the development of adaptive treatment strategies. Statistics in Medicine, 24, 1455–1481. [DOI] [PubMed] [Google Scholar]
- Murphy S. A., van der Laan M. J., Robins J. M. (2001). Marginal mean models for dynamic regimes. Journal of the American Statistical Association, 96, 1410–1423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray T. A., Yuan Y., Thall P. F. (2018). A bayesian machine learning approach for optimizing dynamic treatment regimes. Journal of the American Statistical Association, 113, 1255–1267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Natarajan S., Tadepalli P. (2005). Dynamic preferences in multi-criteria reinforcement learning. In Proceedings of the 22nd International Conference on Machine Learning, 601–608. [Google Scholar]
- Ochoa G., Christie L. A., Brownlee A. E., Hoyle A. (2020). Multi-objective evolutionary design of antibiotic treatments. Artificial Intelligence in Medicine, 102, 101759. [DOI] [PubMed] [Google Scholar]
- Orellana L., Rotnitzky A., Robins J. M. (2010). Dynamic regime marginal structural mean models for estimation of optimal dynamic treatment regimes. The International Journal of Biostatistics, 6, 1–49. [PubMed] [Google Scholar]
- Pareto V., Bonnet A. (1927). Manuel d’économie politique. Traduit sur l’édition italienne par Alfred Bonnet. Paris: Marcel Giard. [Google Scholar]
- Qian M., Murphy S. A. (2011). Performance guarantees for individualized treatment rules. The Annals of Statistics, 39, 1180–1210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robins J. M. (1986). A new approach to causal inference in mortality studies with a sustained exposure period-application to control of the healthy worker survivor effect. Mathematical Modelling, 7, 1393–1512. [Google Scholar]
- Robins J. M. (1997). Causal inference from complex longitudinal data. In: Latent Variable Modeling and Applications to Causality. (ed. M. Berkane), 69–117. New York, NY: Springer. [Google Scholar]
- Robins J. M. (2004). Optimal structural nested models for optimal sequential decisions. In: Proceedings of the Second Seattle Symposium in Biostatistics, 189–326. New York, NY: Springer. [Google Scholar]
- Robins J. M., Hernán M. A. (2008). Estimation of the causal effects of time-varying exposures. In: Longitudinal Data Analysis. Boca Raton, FL: CRC Press. [Google Scholar]
- Roijers D. M., Whiteson S. (2017). Multi-Objective Decision Making, 9–17. San Rafael, CA: Morgan & Claypool. [Google Scholar]
- Rudin C., Chen C., Chen Z., Huang H., Semenova L., Zhong C. (2022). Interpretable machine learning: fundamental principles and 10 grand challenges. Statistics Surveys, 16, 1–85. [Google Scholar]
- Tao Y., Wang L. (2017). Adaptive contrast weighted learning for multi-stage multi-treatment decision-making. Biometrics, 73, 145–155. [DOI] [PubMed] [Google Scholar]
- Tao Y., Wang L., Almirall D. (2018). Tree-based reinforcement learning for estimating optimal dynamic treatment regimes. The Annals of Applied Statistics, 12, 1914–1938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thall P. F., Millikan R. E., Sung H. (2000). Evaluating multiple treatment courses in clinical trials. Statistics in Medicine, 19, 1011–1028. [DOI] [PubMed] [Google Scholar]
- Thall P. F., Wooten L. H., Logothetis C. J., Millikan R. E., Tannir N. M. (2007). Bayesian and frequentist two-stage treatment strategies based on sequential failure times subject to interval censoring. Statistics in Medicine, 26, 4687–4702. [DOI] [PubMed] [Google Scholar]
- Van der Laan M. J., Rubin D. (2006). Targeted maximum likelihood learning. The International Journal of Biostatistics, 2, 1–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L., Rotnitzky A., Lin X., Millikan R. E., Thall P. F. (2012). Evaluation of viable dynamic treatment regimes in a sequentially randomized trial of advanced prostate cancer. Journal of the American Statistical Association, 107, 493–508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoon A. P., Wang Y., Wang L., Chung K. C. (2021). What are the tradeoffs in outcomes after casting versus surgery for closed extraarticular distal radius fractures in older patients? A statistical learning model. Clinical Orthopaedics and Related Research, 479, 2691–2700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Q., Li H. (2007). MOEA/D: a multiobjective evolutionary algorithm based on decomposition. IEEE Transactions on Evolutionary Computation, 11, 712–731. [Google Scholar]
- Zhao Y., Zeng D., Socinski M. A., Kosorok M. R. (2011). Reinforcement learning strategies for clinical trials in nonsmall cell lung cancer. Biometrics, 67, 1422–1433. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Web Appendices referenced in Section 4 and a zip file containing R code and example data are available with this paper at the Biometrics website on Oxford Academic. The R package MOTRL and more direction for application can be found in GitHub at https://github.com/Team-Wang-Lab/MOTRL.
Data Availability Statement
The data that support the findings in this paper are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.






