Euclidean and Shape-Based Analysis of the Dynamic Mitral Annulus in Children Using a Novel Open-Source Framework

Abstract

Background

The dynamic shape of the normal adult mitral annulus has been shown to be important to mitral valve function. However, annular dynamics of the healthy mitral valve in children have yet to be explored. We sought to model and quantify the shape and major modes of variation of pediatric mitral valve annuli at four phases in the cardiac cycle using transthoracic echocardiograms.

Methods

The mitral valve annuli of 100 children and young adults with normal 3D echocardiograms were modeled in four different cardiac phases using the SlicerHeart extension for 3DSlicer. Annular metrics were quantified using SlicerHeart and optimal normalization to BSA was explored. Mean annular shapes and the principal components of variation were computed using custom code implemented in a new SlicerHeart module (Annulus Shape Analyzer). Shape was regressed over metrics of age and body surface area (BSA) and the mean shapes for five age-stratified groups were generated.

Results

The annular height to commissural width ratio (AHCWR) of the mitral valve (“saddle shape”) changed significantly through age for systolic phases (p<0.001) but within a narrow range (Medians 0.20–0.25). Annular metrics change statistically between the diastolic and systolic phases of the cardiac cycle. Visually, the annular shape was maintained with respect to age and BSA. Principal component analysis revealed that the pediatric mitral annulus primarily varies in size (Mode 1), AHCWR (Mode 2) and sphericity (Mode 3).

Conclusions

The saddle shaped mitral annulus is maintained throughout childhood but varies significantly throughout the cardiac cycle. The major modes of variation in the pediatric mitral annulus are due to size, AHCWR, and sphericity. The generation of age- and size-specific mitral annular shapes may inform the development of appropriately scaled absorbable or expandable mitral annuloplasty rings for children.

INTRODUCTION

Mitral annulus (MA) shape and dynamics have been shown to be critical to adult mitral valve function [1, 2]. Lower annular height to commissural width ratio (AHCWR) has been associated with greater leaflet stress, greater valve regurgitation, and chordal rupture [3–5]. Understanding of the importance of non-planar saddle shape of the normal adult mitral valve, and consequences of loss of that shape in the setting of pathology, has led to the development of non-planar annuloplasty rings which are now ubiquitously applied in adult mitral valve repair [6–11].

Mid-systolic mitral annular geometry has previously been explored in normal children and those with leaflet prolapse [12, 13]. While pediatric mitral valve dynamics have been explored in a small cohort[14], a larger analysis of how pediatric MA shape changes throughout the cardiac cycle has yet to be performed. Further, the actual dynamic shape of the pediatric annulus, as opposed to geometric metrics of shape (diameter, area), has not been described. Defining the actual shape may inform our understanding of normal pediatric annular biomechanics as well as the potential development of pediatric specific annuloplasty rings that are either absorbable, or built to accommodate growth [9, 15–19]. While such an analysis can partially be accomplished with traditional metrics using Euclidean geometry(e.g. diameter, area), shape analysis allows the creation of mean shapes, comparison of mean shapes across age, the assessment of the principal modes of variation, and regression of annular shape across continuous variables such as age or size [20–23].

As such, we sought to define the pediatric MA shape throughout the cardiac cycle and quantify how MA annular dynamics and shape vary with age and size (e.g. body surface area). In addition, we implement these capabilities into an open-source tool that can be applied to analyze the annular shape and dynamics, further understand differences between functional and dysfunctional valves, and inform annuloplasty design in pediatric patients.

METHODS

Subjects and Image Acquisition

We analyzed an existing dataset of 100 patients with structurally normal hearts for whom transthoracic three-dimensional echocardiography (3DE) had been collected for clinical studies [12]. All 3DE datasets were apical 4-chamber acquisitions. Functional or structural heart disease was suspected in these children but judged to be absent by the treating cardiologist. The original inclusion criteria for this existing cohort were as follows: (1) referral for clinical 3DE, (2) no history of congenital or acquired heart disease, (3) no more than trivial valvular regurgitation, (4) no structural defects (patient foramen ovale and trivial branch pulmonary artery stenosis permitted in infants), (5) left ventricle end-diastolic volume Z score >−2.5 and <+2.5, and (6) normal left-ventricle systolic function (ejection fraction >55%) on a complete two-dimensional (2D) and Color Doppler echocardiogram. The study was approved by the Committee on Clinical Investigation at Boston Children’s Hospital [12].

Annular Curve Modeling and Quantification

Annular modeling was performed analogous to our previous work by employing the mitral valve presets in the new SlicerHeart Valve Annulus Analysis module within 3DSlicer [22–24]. Four equally spaced phases in the cardiac cycle were modeled for the MA and aortic annulus (AA): end-diastole (ED), mid-systole (MS), end-systole (ES), and mid-diastole (MD). Euclidean annular metrics, described in Table 1 and Figure 1, were measured in each phase using the SlicerHeart Valve Quantification module [22–24].

Table 1.

Description of Annular Parameters

Variable	Description
BSA (m2)	Body surface area
Annular Circumference (mm)	Distance around annular circumference
Annular Height (mm)	Height of mitral annulus (lowest point to highest point)
A-P Diameter (mm)	Distance from anterior mitral annulus to posterior annulus
AL-PM Diameter (mm)	Distance from anterolateral annulus to posteromedial annulus
A-P Bending Angle (°)	Angle between distances from the center to points A and P respectively
AL-PM Bending Angle (°)	Angle between distances from the center to points AL and PM respectively
2D Annular Area (cm2/m2)	Area of surface enclosed by modeled 3D mitral annulus and projected onto annular least squares plane
3D Annular Area (cm2/m2)	Minimum area of manifold surface generated from and enclosed by modeled 3D mitral annulus
Annular Height to Width Ratio	Annular height / AL-PM diameter
Sphericity	A-P diameter / AL-PM diameter

Figure 1. Visualization of Mitral Annular Metrics.

A. Annular circumference; B. Annular height; C. 3D annular area; D. A-P Diameter; E. AL-PM diameter; F. Dynamic comparison of annular metrics through cardiac cycle. A-P = anterior-posterior, AL-PM = anterolateral-posteromedial.

Normalization and Statistical Analysis

The Kruskal-Wallis test was performed to assess changes in MA parameters across age groups. A Friedman test was performed, with a Nemenyi post-hoc analysis, on continuous variables across age groups to determine differences in annular metrics across the cardiac cycle.

Cardiac output is thought to be proportional to body surface area (BSA), and valve area is thought to be associated to BSA [17]. As such, annular metrics (e.g. diameter, circumference) would teleologically vary with the square root of BSA, as validated for the aortic valve using 2D-echocardiography [17]. In this study, annular area measurements were first normalized to BSA, and linear measurements were normalized to BSA^0.5 as previously described [17, 23]. To further investigate normalization methods, both variable-specific and type-optimized normalization were explored by finding the value of x that minimizes the slope of Variable/BSA^x vs. BSA for each metric and metric type. Additional details about this exploration are provided in Appendix A.

Shape Parametrization and Analysis

The Annulus Shape Analyzer module in Slicer Heart was created to extend previous shape methods and implement them in an open-source software [24]. This module facilitates Procrustes alignment (a method to optimally align shapes) [22, 23], calculation of population mean shape, principal component analysis (PCA), curve comparisons, and regression of mean shape with respect to demographic variables [24]. Procrustes alignment, mean shape model generation, and PCA (see Appendix B) were conducted analogously to our previous descriptions [22, 23]. In this study, we present PCA on 1) shape-aligned and 2) shape- and scale-aligned MA data. Finally, annular models were regressed over continuous demographic variables (i.e., age, height, BSA) to further explore how shape varies with respect to growth.

Physical Annulus Models

Annular models were 3D printed to demonstrate proof of concept for the “on demand” generation of size specific, absorbable, or expandable pediatric annuloplasty rings. The mean annular model for each age group was exported from 3DSlicer as a stereolithography file (.stl) and 3D printed with a radius of 0.60 mm on a material jetting printer (J750, Stratasys, Eden Prairie, MN) using polycarbonate material (VeroVivid, Stratasys, Eden Prairie, MN) [24].

RESULTS

The MA of 100 patients (44% female) with normal echocardiograms were successfully modeled in each cardiac phase (ED, MS, ES, and MD). Patient-age ranged from 1 day to 22 years (Median 9.92 IQR 5.99–14.7); BSA ranged from 0.17 to 2.18 m², and weight spanned 2.2 to 92.3 kg (Table 2).

Table 2.

Demographics

Variable	<1 y (n=8)	1–5 y (n=13)	>5–9 y (n=21)	>9–13 y (n=27)	>13 y (n=31)	All Ages (n=100)
Age at Analysis (y)	0.03 [0.02–0.2]	3.2 [3.1–4.5]	7.0 [6.2–7.7]	11.2 [9.7–11.6]	16.0 [15.0–17.0]	9.7 [5.4–14.7]
Female Gender n (%)	3 (38)	8 (62)	10 (48)	7 (26)	14 (45)	42 (42)
Height (cm)	51 [48–55]	99 [97–108]	122 [118–125]	143 [139–149]	169 [164–176]	140 [117–162]
Weight (kg)	3.4 [2.8–5.5]	15.7 [15.0–17.3]	23.6 [22.4–25.9]	37.2 [32.5–44.3]	60.0 [56.1–63.9]	32.5 [21.9–55.2]
BSA (m2)	0.22 [0.20–0.30]	0.68 [0.64–0.72]	0.91 [0.87–0.94]	1.22 [1.12–1.36]	1.69 [1.61–1.75]	1.1 [0.8–1.6]
Heart Rate (bpm)	132 [123–142]	94 [89–102]	79 [76–84]	75 [65–78]	64 [58–72]	76 [66–85]
Frame Rate (Hz)	26.0 [25.0–29.25]	31.0 [29.25–34.25]	33.0 [30.0–37.0]	34.0 [31.0–35.0]	29.0 [22.0–33.0]	31.0 [25.2–35.0]

Values listed are Median [IQR].

BSA = body surface area.

Exploration of BSA-Based Normalization in Mitral Annular Metrics

Plots of BSA-normalized annular circumference and area with respect to BSA are shown in Figure 2. Initially, annular area measurements were normalized to BSA, and linear measurements were normalized to BSA^0.5 as previously described (Figure 2 Left Panels) [17, 23]. However, with this normalization, a persistent negative trend was observed between annular metrics and these standard relationships to BSA. As such, we investigated optimal exponents for BSA normalization in our cohort as detailed in Appendix A. In this cohort, linear metrics (e.g. annular diameter) were optimally normalized to BSA^0.45, and area metrics were optimally normalized to BSA^0.86 (Figure 2 Right Panels).

Figure 2. Relationship of Mitral Annular Circumference and Annular Area to Body Surface Area (BSA).

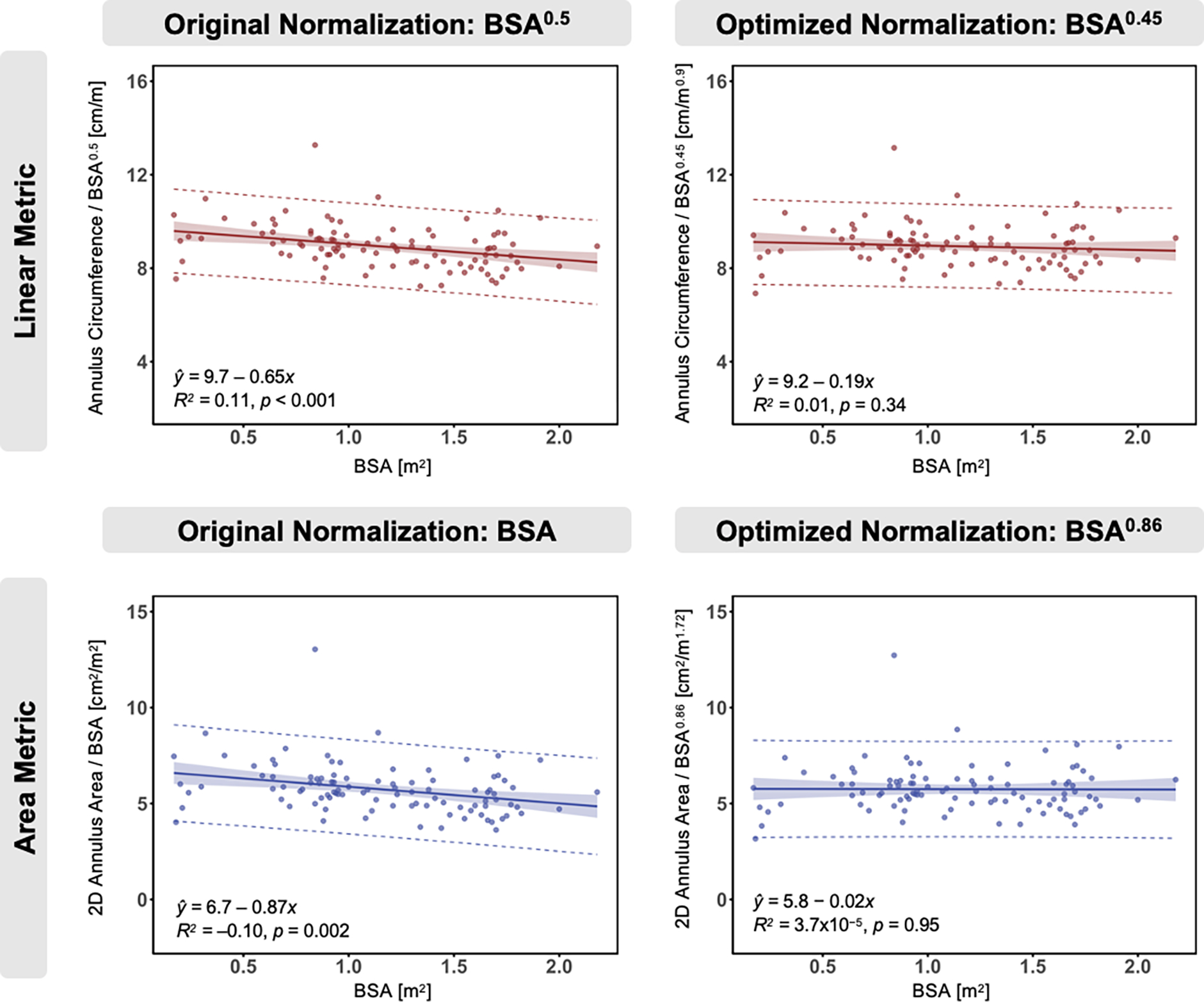
Original normalization (left) of linear metric to BSA^0.5 and area metric to BSA, and optimized normalization (right) of linear metric to BSA^0.45 and area metric to BSA^0.86. Optimized normalization was identified by finding the value of x that minimizes the average slope of Variable/BSA^x vs. BSA across variables of each type. All annular metrics in mid-systole. Solid line = best fit line, shaded area = 95% confidence limits, dashed line = 95% prediction limits. p-values computed via linear regression t-test.

Traditional Annular Modeling

Annular metrics varied significantly in an individual patient through the cardiac cycle as presented in Table 3. Specifically, adjusted p-values in Supplementary Table S1 demonstrated statistically significant changes are observed between MS and MD annular dimensions and ES and ED. Annular height increased in systolic phases, while A-P distance contracted in systole.

Table 3.

Non-Normalized Annular Dimensions Throughout Cardiac Cycle

Variable	ED	MS	ES	MD	Max Change (%)	p-value
Annular Height (cm)	0.61 [0.51–0.75]	0.64 [0.54–0.76]	0.62 [0.53–0.74]	0.55 [0.46–0.70]	24 [16–33]	<0.001
A-P Distance (cm)	2.4 [2.1–2.8]	2.6 [2.3–2.9]	2.7 [2.4–3.1]	2.5 [2.1–3.0]	14 [10–19]	<0.001
AL-PM Distance (cm)	3.1 [2.7–3.5]	3.1 [2.7–3.5]	3.1 [2.7–3.5]	3.2 [2.7–3.6]	8 [6–13]	<0.001
AHCWR	0.20 [0.18–0.24]	0.22 [0.20–0.25]	0.21 [0.18–0.24]	0.19 [0.17–0.21]	28 [16–40]	<0.001
Sphericity	0.78 [0.73–0.83]	0.86 [0.79–0.91]	0.88 [0.83–0.95]	0.80 [0.75–0.85]	16 [11–22]	<0.001

Values listed are Median [IQR].

ED = End-diastole, MS = Mid-Systole, ES = End-Systole, MD = Mid-Diastole.

A-P = anterior-posterior, AL-PM = anterolateral-posteromedial.

AHCWR = annular height to commissural width ratio

Sphericity = A-P distance/AL-PM distance.

Max Change = maximum value in cardiac cycle (MD or ED) minus minimum value in cardiac cycle (MS or ES).

MA median metrics across the five stratified age groups are shown in Table 4. The annular height to commissural width ratio (AHCWR) of the mitral valve (“saddle shape”) changed significantly through age for systolic phases (p<0.001) but within a narrow range (Medians 0.20–0.25). Annular sphericity (anterior-posterior diameter/anterior-lateral to posterior-medial diameter ratio), did not significantly change across age. The results for annular metrics normalized to optimized BSA-indexing exponents are presented in the Appendix A.

Table 4.

Non-Normalized Annular Dimensions by Age Group

Variable	<1 y (n=8)	1–5 y (n=13)	>5–9 y (n=21)	>9–13 y (n=27)	>13 y (n=31)	All Ages (n=100)	p-value
BSA (m2)	0.22 [0.2–0.3]	0.68 [0.64–0.72]	0.91 [0.87–0.94]	1.22 [1.12–1.36]	1.69 [1.61–1.75]	1.13 [0.86–1.58]	--
Annular Height (cm)
ED	0.33 [0.30–0.38]	0.53 [0.48–0.61]	0.52 [0.47–0.59]	0.62 [0.56–0.68]	0.78 [0.69–0.92]	0.61 [0.51–0.75]	<0.001
MS	0.37 [0.31–0.43]	0.57 [0.54–0.60]	0.60 [0.54–0.67]	0.64 [0.57–0.70]	0.84 [0.75–0.94]	0.64 [0.55–0.76]	<0.001
ES	0.33 [0.30–0.40]	0.53 [0.48–0.57]	0.59 [0.53–0.63]	0.61 [0.56–0.66]	0.83 [0.71–0.94]	0.62 [0.53–0.74]	<0.001
MD	0.32 [0.28–0.36]	0.48 [0.45–0.52]	0.52 [0.44–0.53]	0.62 [0.53–0.66]	0.72 [0.65–0.87]	0.55 [0.46–0.70]	<0.001
A-P Distance (cm)
ED	1.3 [1.2–1.5]	1.9 [1.7–2.1]	2.1 [2.0–2.3]	2.4 [2.3–2.6]	2.9 [2.6–3.1]	2.4 [2.1–2.8]	<0.001
MS	1.2 [1.2–1.5]	2.1 [2.0–2.4]	2.4 [2.3–2.5]	2.7 [2.5–2.9]	3.1 [2.8–3.4]	2.6 [2.3–2.9]	<0.001
ES	1.3 [1.2–1.5]	2.1 [2.1–2.3]	2.5 [2.4–2.6]	2.8 [2.5–2.9]	3.3 [3.0–3.5]	2.7 [2.4–3.1]	<0.001
MD	1.3 [1.2–1.5]	2.0 [1.8–2.1]	2.2 [2.1–2.4]	2.6 [2.4–2.8]	3.1 [2.9–3.3]	2.5 [2.1–3.0]	<0.001
AL-PM Distance (cm)
ED	1.5 [1.3–1.7]	2.5 [2.2–2.9]	2.8 [2.6–3.0]	3.2 [3.1–3.4]	3.7 [3.4–3.8]	3.1 [2.7–3.5]	<0.001
MS	1.4 [1.2–1.7]	2.6 [2.4–2.8]	2.8 [2.5–3.0]	3.2 [3.1–3.4]	3.5 [3.2–3.7]	3.1 [2.7–3.5]	<0.001
ES	1.4 [1.2–1.7]	2.5 [2.3–2.7]	2.8 [2.6–3.0]	3.2 [3.0–3.4]	3.6 [3.4–3.8]	3.1 [2.7–3.5]	<0.001
MD	1.5 [1.3–1.7]	2.5 [2.4–2.7]	2.9 [2.6–3.0]	3.4 [3.2–3.5]	3.7 [3.5–4.0]	3.2 [2.7–3.6]	<0.001
AHCWR
ED	0.22 [0.20–0.24]	0.21 [0.20–0.24]	0.19 [0.17–0.2]	0.20 [0.17–0.21]	0.23 [0.19–0.24]	0.20 [0.18–0.24]	0.009
MS	0.25 [0.23–0.28]	0.22 [0.20–0.25]	0.22 [0.20–0.23]	0.20 [0.18–0.22]	0.24 [0.21–0.27]	0.22 [0.20–0.25]	<0.001
ES	0.22 [0.21–0.27]	0.21 [0.19–0.23]	0.21 [0.19–0.23]	0.19 [0.17–0.21]	0.23 [0.20–0.26]	0.21 [0.18–0.24]	<0.001
MD	0.21 [0.19–0.23]	0.20 [0.17–0.21]	0.18 [0.16–0.19]	0.18 [0.16–0.19]	0.20 [0.18–0.23]	0.19 [0.17–0.21]	0.007
Sphericity
ED	0.86 [0.77–0.93]	0.77 [0.73–0.80]	0.77 [0.73–0.80]	0.78 [0.73–0.81]	0.8 [0.73–0.86]	0.78 [0.73–0.83]	0.23
MS	0.93 [0.91–0.98]	0.82 [0.79–0.89]	0.85 [0.80–0.90]	0.83 [0.79–0.88]	0.88 [0.82–0.93]	0.86 [0.79–0.91]	0.02
ES	0.92 [0.90–0.96]	0.86 [0.84–0.92]	0.91 [0.80–0.97]	0.86 [0.80–0.90]	0.88 [0.84–1.0]	0.88 [0.83–0.95]	0.11
MD	0.84 [0.80–0.95]	0.78 [0.73–0.82]	0.79 [0.73–0.84]	0.78 [0.75–0.84]	0.83 [0.79–0.87]	0.80 [0.75–0.85]	0.05

Values listed are Median [IQR].

ED = End-diastole, MS = Mid-Systole, ES = End-Systole, MD = Mid-Diastole.

BSA = body surface area, A-P = anterior-posterior, AL-PM = anterolateral-posteromedial, AHCWR = annular height to commissural width ratio, Sphericity = A-P distance/AL-PM distance.

Shape Analysis of Mitral Annuli

The mid-systolic mean annular shape and principal modes of shape variation in the entire cohort are shown for shape aligned and shape+scale aligned MA data in Figure 3. The greatest variations in pediatric MA shape are physical size, AHCWR, and sphericity as elaborated in Video 1. A comparison of the explained variance ratios between the two PCA analyses are shown in Figure 4. Size accounted for 87% of the total variation in MA shape. When scale (physical size) is removed to isolate changes in annular shape, 34% of MA shape variation is due to AHCWR, and 18% of MA shape variation is due to sphericity (Figure 4).

Figure 3. Shape and Principal Component Analysis (PCA) of Mitral Annuli.

A. Mean shape of mitral annulus; B. Variation observed from PCA of shape-aligned annuli – Mode 1: size, Mode 2: AHCWR, Mode 3: sphericity; C. Variation observed from PCA of shape- and scale-aligned annuli – Mode 1: AHCWR, Mode 2: sphericity, Mode 3: other variation. PCA curves show variation +/− two standard deviations. Analysis performed in mid-systole across all age cohorts (0–22 years).

Figure 4. Explained Variance Ratio from Principal Component Analysis (PCA).

A. Shape-aligned; B. Shape- and scale-aligned mitral annuli. In Shape-Aligned PCA, Mode 1 explains 87% of the variation that occurs in our mitral annulus dataset, Mode 2 explains 4.5% of the variation, and Mode 3 explains 2.5% of the total variation. In Shape- and Scale-Aligned PCA, Mode 1 explains 34% of the variation that occurs in mitral annulus shape, Mode 2 explains 18% of the variation, and Mode 3 explains 11% of the total variation. To ensure the mitral annulus data is being analyzed correctly, we perform a Procrustes shape alignment to conduct “Shape-Aligned” PCA. When size is removed as a variation factor in PCA, we assess a shape- and scale-aligned dataset.

The shape and size-aligned comparison of MA mean models within each age cohort again displays a qualitatively consistent saddle shape but does not significantly change in dimensions. The 3D-printed MA mean shape models in MS demonstrate similar dimensional characteristics with increasing size due to age in Figure 5. This is echoed when MA shape is regressed across BSA and age in Video 2.

Figure 5. 3D Printed Mean Mitral Annular Curves Across Age.

A. Lateral view; B. Atrial view. Quarter provides reference of scale.

Open-Source Software Tools

The described annular modeling functionality has been implemented in the Annular Shape Analyzer module and is available open source at www.github.com/SlicerHeart and implemented in the SlicerHeart Extension for 3D Slicer [24].

DISCUSSION

We present a detailed analysis of the dynamic MA in a cohort of 100 structurally normal children and young adults. Our primary finding is that while MA parameters vary throughout the cardiac cycle, the shape is largely maintained across age and BSA. Further, we found that the primary modes of variation in the pediatric mitral annulus are physical size, AHCWR, and sphericity. Finally, the models of this cohort, in concert with newly created shape analysis tools, enables the creation of age- and size-specific 3D annular curves that may eventually inform the design of patient-specific annuloplasty rings for children.

We had previously published the general relationship between 3D mid-systolic mitral annular metrics and BSA but did not explore determination of the optimal relationship to BSA[12]. Notably, most allometric studies for valve anatomy have been limited to animal samples [25, 26]. However, Sluysman et el. had performed this analysis for 2D measurements of aortic annuli and they determined that linear metrics are best indexed to BSA^0.5, and area metrics are best indexed to BSA when making allometric comparisons of heart anatomy across size[17, 26]. We initially normalized as per Sluysman et al. but found a resulting negative bias with this normalization. In further explorations we found linear metrics were optimally indexed to BSA^0.45, and area metrics were optimally indexed to BSA^0.86. To our knowledge, this is the first analysis of optimal normalization of 3D atrioventricular annular metrics in a pediatric population. This study also demonstrates how it may be difficult to observe changes in pediatric anatomic geometry without first establishing population-specific normalization indexes.

The pediatric mean MA shape varies throughout the cardiac cycle but closely follows the established paraboloid (“saddle shape”) as previously described for both the adult and pediatric MV. Specifically, the mid-systolic AHCWR median results for this dataset (0.22 IQR 0.20–0.25) came within a similar range to the adult mean results of AHCWR (0.22 ± 0.06) [20], however were slightly lower compared to our previous MA analysis using commercial software (0.24 IQR 0.22–0.28) [27]. Overall, MA dynamic shape in non-mid systolic phases paralleled previous studies of adult MA dynamics [1, 2, 28, 29]. In comparison, the adult normal MA undergoes contraction in AP diameter, with increase in annular height, at early systole [1, 28, 29]. These changes are through to aid coaptation between the anterior and posterior leaflet (decreased AP distance). Similarly, in our pediatric cohort we demonstrated decreasing values of AP diameter as the MV is about to close in ED, while annular height increases in systolic phases, generally consistent with prior work by Nii et al[14].

However, while simple Euclidean metrics (diameter, area) provide a concise and clinically familiar description of MA anatomy, shape analysis considers the complete morphology of an anatomic structure [21]. Shape analysis methods have previously supported characterization of the adult MV, complete atrioventricular canal, and the tricuspid valve in patients with hypoplastic left heart syndrome [20, 22, 23]. These methods further confirmed that the scaled pediatric MA shape is relatively preserved and invariant through childhood. Most changes in MA shape were attributed to scale(physical size), with only subtle variations influencing AHCWR, and sphericity, similar to previous analyses in normal adults [20]. AHCWR has been hypothesized to be important to reducing leaflet stress, and lower values are associated with clinically significant regurgitation [13, 22, 30]. Our findings of preservation of annular shape across a wide range of sizes of children and adults with normally functioning valves thus further supports the previously described importance of annular shape to MV function.

Clinical Implications

The established values for healthy MA shape through childhood and healthy MA dynamics in this study will allow comparison to dysfunctional valves and may help inform restoration of healthy MA shape with informed prediction of growth in childhood. Specifically, the Annulus Shape Analyzer module in combination with this open-data normal mitral cohort help facilitate patient-specific comparisons of dysfunctional annuli to normal pediatric annular shape and size. Further, regression across this population allows the creation of age-specific geometries with respect to patient demographics (e.g., BSA, age, or height) which could inform the design of annuloplasty rings for children.

Annuloplasty is a common form of valve repair in adults, and often employs an annuloplasty ring[31, 32]. However, the need for annular growth has traditionally restricted application of rings to older children to avoid developing elevated mitral inflow gradients with time[33–35]. Pediatric atrioventricular annuloplasty now offer a variety of options to help abate the effects of growth on the repair with suture based annuloplasty and the growing potential for the use of emerging absorbable or expandable annuloplasty rings [15, 36]. The 3D shapes and ability to regress across BSA thus creates the potential to generate size appropriate annular curves “on demand” to enable the generation of age- and size-specific annuloplasty devices [9, 15, 16]. MA shape for a given patient size may then act as a template for customized prosthetic design [37].

Limitations and Future Directions

This is a retrospective study. Acquisition of data was primarily conducted for left ventricular volume assessment and not specifically for MA analysis. 3DE acquisition focused on the MV would be expected to improve image quality, frame rates, and subsequent MA analysis. There may also be sample bias because of small sample numbers within the cohort and lack of patient cooperation from the younger children. Our analysis was semi-automatic; future application of automated annular tracking throughout the cardiac cycle may allow measurement of every frame of data and reduce interuser variability.

CONCLUSION

The MA saddle shape is largely maintained with growth throughout childhood but varies significantly throughout the cardiac cycle. The data and tools created by this work may inform the development of appropriately scaled mitral annuloplasty rings or expandable devices for children. However, further investigation of changes in MA dynamics with respect to mitral pathology and intervention in children is needed.

Supplementary Material

3

Video 1: Principal Component Analysis on Pediatric Normal Mitral Annuli Models

4

Video 2: Pediatric Mitral Annuli Shape Regression Over Age and Body Surface Area

Central Illustration. Framework for Euclidean Feature and Shape Characterization in Pediatric Mitral Annuli (MA).

Quantification of MA models allowed exploration of MA dynamics and allometric relations with respect to BSA. Shape Analysis was used calculate Mean Shape and Principal Component Analysis was applied to explore variations of the MA shape across the population. Finally, the MA models and MA analysis tool will facilitate future comparison of MA of dysfunctional valves to normal valves, and may inform design and selection of size-appropriate mitral annular rings. ED = end-diastole, MD = mid-diastole, MS = mid-systole, ES = end-systole. A-P Distance = Anterior-Posterior Distance. BSA = Body Surface Area.

Highlights.

• We modeled the dynamic mitral annular(MA) shape of a pediatric cohort.

• The dynamic MA shape varies throughout contraction but is maintained across age.

• The MA varies slightly in shape, but primarily in annular size across childhood.

• We provide a pediatric MA dataset and tools to enable future investigations

Abbreviations:

2D

Two – Dimensional

3DE

Three – Dimensional Echocardiography

AA

Aortic Annulus

A-P

Anterior-posterior

AL-PM

Anterolateral-posteromedial

AHCWR

Annular Height to Commissural Width Ratio

BSA

Body Surface Area

ED

End-diastolic

ES

End-systolic

IQR

Inter-quartile Range

MA

Mitral Annulus

MD

Mid-diastolic

MS

Mid-systolic

PCA

Principal Component Analysis