Three-Dimensional Super Resolution Ultrasound Imaging with a Multi-Frequency Hemispherical Phased Array

Abstract

Background:

High resolution imaging of the microvasculature plays an important role in both diagnostic and therapeutic applications in the brain. However, ultrasound pulse-echo sonography imaging the brain vasculatures has been limited to narrow acoustic windows and low frequencies due to the distortion of the skull bone, which sacrifices axial resolution since it is pulse length dependent.

Purpose:

To overcome the detect limit, a large aperture 256-module sparse hemispherical transmit/receive array was used to visualize the acoustic emissions of ultrasound-vaporized lipid-coated decafluorobutane nanodroplets flowing through tube phantoms and within rabbit cerebral vasculature in vivo via passive acoustic mapping and super resolution techniques.

Methods:

Nanodroplets were vaporized with 55 kHz burst-mode ultrasound (burst length = 145 μs, burst repetition frequency = 9–45 Hz, peak negative acoustic pressure = 0.10–0.22 MPa), which propagates through overlying tissues well without suffering from severe distortions. The resulting emissions were received at a higher frequency (612 kHz or 1224 kHz subarray) to improve the resulting spatial resolution during passive beamforming. Normal resolution three-dimensional images were formed using a delay, sum, and integrate beamforming algorithm, and super-resolved images were extracted via Gaussian fitting of the estimated point-spread-function to the normal resolution data.

Results:

With super resolution techniques, the mean lateral (axial) full-width-at-half-maximum image intensity was 16 ± 3 (32 ± 6) μm, and 7 ± 1 (15 ± 2) μm corresponding to ~1/67 of the normal resolution at 612 and 1224 kHz, respectively. The mean positional uncertainties were ~1/350 (lateral) and ~1/180 (axial) of the receive wavelength in water. In addition, a temporal correlation between nanodroplet vaporization and the transmit waveform shape was observed, which may provide the opportunity to enhance the signal-to-noise ratio in future studies.

Conclusions:

Here, we demonstrate the feasibility of vaporizing nanodroplets via low frequency ultrasound and simultaneously performing spatial mapping via passive beamforming at higher frequencies to improve the resulting spatial resolution of super resolution imaging techniques. This method may enable complete four-dimensional vascular mapping in organs where a hemispherical array could be positioned to surround the target, such as the brain, breast, or testicles.

I. INTRODUCTION

High resolution vascular imaging is desirable for both diagnostic and therapeutic applications in the brain ¹, ranging from diabetes ², to cerebral tumors ³, to neurodegenerative diseases such as Alzheimer’s disease (AD) and Parkinson’s disease (PD) ^4,5. Currently in clinical practice, several imaging modalities are employed to probe cerebral blood vasculature. For example, computed tomography angiography (CTA) offers an in-plane spatial resolution down to 0.2 mm with the development of ultra-high-resolution CT scanners ⁶, which enables visualization of lenticulostriate arteries ⁷, the proximal parts of intracortical arteries and veins between 0.15–0.75 mm ⁸ in patients. Magnetic resonance angiography (MRA) is able to detect vasculature of various sizes, down to a limit depending on the magnetic field strength ⁹. At standard field strengths (1.5 or 3.0 T), MRA can visualize only the larger intracranial arteries (resolution:0.78 × 0.78 × 1 mm³ or 0.39 × 0.39 × 0.5 mm³). Higher spatial resolution (e.g., 0.25 × 0.3 × 0.4 mm³) can be achieved at ultrahigh fields (e.g., 7 T ¹⁰), providing the capability to visualize intracranial perforating arteries branching off from the circle of Willis and their proximal branches. Compared to these two modalities, ultrasound imaging (USImg) is non-ionizing, more affordable and widely accessible, but is limited in resolution by diffraction to the scale of its wavelength. Clinically, pulse-echo USImg has been used to visualize cerebral vasculature, but its resolution is limited to detecting major blood vessels (~ 1 mm) due to the trade-off between the transmit frequency and the axial resolution, especially in transcranial applications ^11,12. Lower frequencies (e.g., sub-MHz frequency used in therapeutic ultrasound ^13,14) experience less attenuation and distortion induced by the presence of the human skull bone ¹⁵, however, they in turn increase the pulse length which sacrifices axial resolution.

The diffraction limit has previously been overcome through the development of super resolution (SR) techniques in optical microscopy. In other words, the signals coming from sources spaced closer than the classical diffraction limit (i.e., $\lambda /2$) can be separated via SR imaging. In 2006, the introduction of fluorescence photoactivated localization microscopy ¹⁶, photoactivated localization microscopy ¹⁷ and stochastic optical reconstruction microscopy ¹⁸ successfully improved the imaging resolution by at least an order of magnitude compared to traditional optical microscopy. Inspired by the field of optics, ultrasound localization microscopy (ULM) was proposed in 2010 ¹⁹ by Couture et al. and the feasibility of localizing microbubbles with SR was demonstrated in vitro with a one-dimensional (1D) imaging phased array ^20,21. In parallel, an alternative method which combined long ultrasound bursts from a hemispherical phased array with a sparse detector array to perform passive beam forming and SR technique was developed. It was used to image through an ex vivo human skull cap and was shown to achieve four-dimensional bubble mapping in tube phantoms ²², providing the lateral and axial intensity full-width at half-maximum (FWHM) of approximately 1/50 and 1/25, respectively, of the ultrasound wavelength at the received frequency (612 kHz) on average. Various data processing techniques have also been investigated to shorten the total acquisition time, which include a localization-based method via curve fitting and a deconvolution-based method adapted from Mukamel et al. ²³ to passive acoustic imaging, allowing SR imaging to be performed in larger and/or multiple excitation volumes ²⁴. In further studies it has been demonstrated that ULM with microbubbles is capable of imaging ear ²⁵ and cerebral microvasculature in mice ²⁶ and rats ²⁷, renal microvasculature in rats ^28,29 and mice ³⁰, lymph node vasculature in rabbits ³¹, vasa vasorum in a rabbit atherosclerosis model ³², as well as tumor angiogenesis in mice ³³ and rats ^34,35. On top of the applications in imaging the microvasculature network, ULM has also shown the capability to quantify functional hyperemia dynamically at microscopic scale with a 6.5-μm spatial and 1-s temporal resolution in deep rat brain regions ³⁶. In addition, the feasibility of three-dimensional (3D) SR approaches has been investigated to assess microvasculature volumetrically via the use of a hemispherical large aperture phased array ²², a linear probe mounted to a motorized precision motion stage ^31,34, a 1.5-dimensional array ³⁷, a pair of US transducers positioned at 90° ³⁸, a matrix array probe ^27,39, as well as a two-dimensional (2D) sparse array ⁴⁰. Specifically, 3D ULM of in vivo whole brain microvascular has been achieved on mice ⁴¹, chicken embryo ⁴², and rats ^27,42. With the improved resolution, a more precise description of the microvasculature has been provided to discriminate between ischemic and hemorrhagic stroke in early phase in rats’ brains ⁴³. In 2018, these techniques were employed with clinical scanners in patients for the first time to image breast tumor vasculature ⁴⁴ and lower limbs ⁴⁵. In 2021, Demené et al. successfully imaged deep cerebral vasculature and mapped blood flow in patients at a resolution of 25 μm with ultrafast ULM ⁴⁶. In 2023, ULM was performed on patients with Takayasu arteritis (TA) and demonstrated its capability to distinguish active TA from quiescent TA and show increased inflammatory activities from the number of tracked microbubbles and their path per second of acquisition ⁴⁷. These human applications have demonstrated the utility of using SR USImg techniques in diagnosing vascular abnormalities and understanding hemodynamics in a clinical setting.

In addition to tracking microbubbles flowing within vascular compartments using SR techniques, nanodroplets have recently gained attention in this setting as they can be selectively activated both spatially and temporally, have longer circulation times than microbubbles, and can extravasate from cancerous tissues offering contrast beyond the vasculature. Having been studied for both therapeutic and diagnostic applications in the past two decades ^48–53 (reviewed previously ⁵⁴), nanodroplets have been investigated in the context of SR imaging since 2016, either through acoustic ^55–58 or optical ^59–61 activation. It has been shown through acoustic wave sparsely activated localization microscopy (AWSALM) ⁵⁶ that nanodroplets can be switched on and off at the ultrasound pulse repetition frequency (PRF). Using nanodroplets in this way allows SR images to be obtained much faster due to signal accumulation at the rate of the PRF, and localizing the resultant microbubbles is less dependent on the concentration of the ultrasound contrast agent and the blood flow velocity ^56,57.

The goal of SR USImg is to spatially localize the microbubbles or vaporized nanodroplets. This can be performed using various approaches in the radio frequency (RF) domain or on beamformed images themselves. Different from active USImg in pulse-echo mode, passive acoustic mapping (PAM) can localize acoustic source fields without being limited to short transmit pulse lengths. Originally adopted from passive imaging with receiver arrays in geophysics applications ^62–65, PAM can spatially map cavitation activity over time during FUS applications ^66–74. A major advantage of PAM is that axial resolution is mainly determined by the receive frequency and phased array aperture ⁶³, and is independent of source emission duration ⁷¹. The use of PAM with large-aperture hemispherical phased arrays allows for 3D localization of the microbubble cavitation events as a function of time with high spatial and temporal resolution ^75,76 without mechanical translation or rotation of the device ^74,77–79. When further combined with SR processing techniques, the capability of imaging individual microbubbles through an ex vivo human skull cap has been demonstrated in a spiral tube phantom using a large-aperture hemispherical receive array ²², demonstrating immense potential for imaging deep-seated cerebral vascular structures. To further improve the resulting image resolution and spatial localization of cavitation events with this approach, transducer arrays with a finer point spread function (PSF), higher receive frequencies, enhanced receive sensitivity, and with an increased number of receivers are needed ⁷⁸.

In this study, we constructed a multi-frequency hemispherical array similar to those described previously ^74,80 but with an additional low frequency transmit array for nanodroplet activation. The advantage of low frequency excitation is that the transmit wave experiences minimal distortions even when transmitted through bone. In addition, low frequency excitation can offer a longer rarefactional or compressional regime to be superimposed with a short burst at higher frequency in a phase-dependent manner for the purpose of modulating nanodroplet vaporizations, similar to the ultrasonic exposure schemes used in the second order ultrasound field burst ^81–83 and radial modulation imaging ^84–87. Following construction, the array’s utility in the context of vasculature imaging via PAM and SR techniques was explored at receive frequencies of 612 kHz and 1224 kHz, to investigate the capability of mapping the vaporized lipid-coated decafluorobutane (DFB) nanodroplets flowing through tube phantoms, as well as rabbit cerebral vasculatures in vivo. The temporal correlation between nanodroplet vaporization and the transmit waveform shape was investigated. Finally, the effects of various parameters on the resulting SR images were explored.

II. METHODS

II.A. Phased Array Construction

The geometry of the in-house built phased array is similar to that described in previous studies ^74,80,88. In brief, the base frame of the array was a hemispherical dome with an aperture of 31.8 cm, which was formed by assembling four quadrants of plastic 3D printed shells (Accura ClearVue^™, Viper^™, si2SLA; 3D systems Inc., Rock Hill, SC, USA). 256 transducer modules were sparsely distributed on the inner surface of the hemispherical dome, whose locations [Figure 1(a)] were confirmed using acoustic triangulation as described in previous studies ^74,77,80. An illustration of the cross-sectional view of a single module is shown in Figure 1(b). Each module is composed of 4 cylindrical lead zirconate titanate (PZT)-4 elements (DeL Piezo Specialties, LLC, West Palm Beach, FL, USA) driven at their lateral mode resonant frequency of 55, 306, 612, and 1224 kHz, respectively. The element dimensions (Table 1) were chosen to provide a similar steering range and imaging volume across all driving frequencies by maintaining their dimensions relative to the acoustic wavelength ⁸⁰. An exterior concentric housing was placed around the module forming a flat surface together with the four concentric ring transducers. A thin layer of plastic film (Mylar^™; DuPont, Wilmington, DE, USA) was epoxied to the front surface, sealing the modules and providing air loading for the transducers. The signal and ground lines from coaxial cables were soldered to the inner and outer electrodes of each element, respectively. The 306, 612, and 1224 kHz elements were soldered to an adapter connected to a circuit board that enables switching and selection of the array's transmit and receive frequencies for a given sonication. Variable gain pre-amplifiers were implemented within the receive lines. Coaxial cables from 55 kHz elements were soldered to 64-channel edge cards (4 cards total), allowing them to be driven by a separate custom driving system built in-house.

Figure 1.

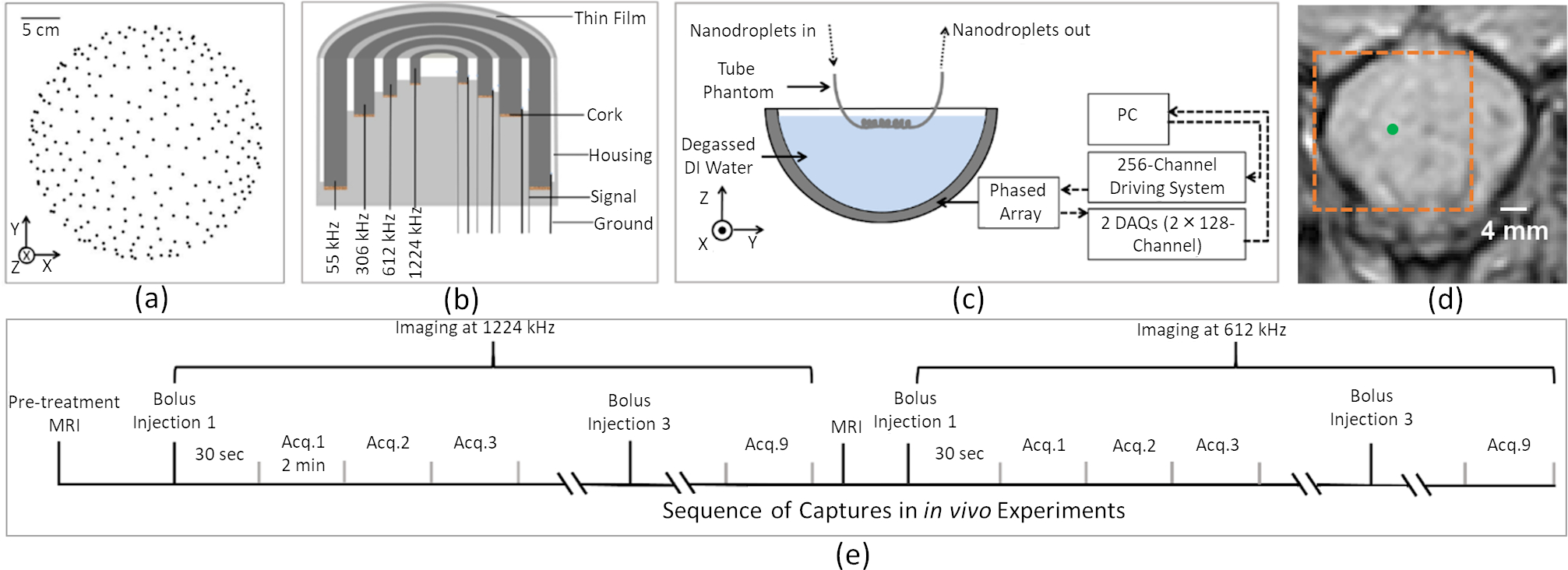
Clinical-scale prototype FUS brain system and experimental setup. (a) Transducer module layout (256 modules). (b) Module design schematic. (c) Illustration of experimental setup for benchtop measurements. (d) Target location (green dot) and reconstruction region (orange dash line) overlaid on a pre-treatment axial magnetic resonance (MR) image during in vivo experiments. (e) Timing diagram illustrating the sequence of captures during in vivo experiments

Table 1.

Transducer element dimensions at each operational frequency.

Frequency (kHz)	OD (mm)	ID (mm)	Height (mm)
55	15.3	11.0	30.0
306	10.0	7.00	6.00
612	5.00	3.50	3.00
1224	2.50	1.75	1.50

Following construction of the multi-frequency array, the element locations were confirmed via acoustic triangulation with the 612 kHz elements ⁷⁷, by inferring the time of flight from the received impulse signals excited from a fixed source emitter (PZT tube, 1 mm diameter, 5 mm length, 500 kHz center frequency in lateral mode) at various target locations in the field. In addition, with the source placed at the array’s geometric focus, the mean temporal-peak magnitude of the received RF data was compared to that obtained with the array used in O’Reilly and Hynynen ²² to quantitatively compare the difference in element sensitivities between the two 612 kHz receive arrays.

II.B. Benchtop Experiments

The benchtop experimental setup is illustrated in Figure 1(c). The device’s acoustic field distribution was characterized at each transmit frequency similar to the process described in ⁸⁰. The low (55 kHz) and high (306, 612, and 1224 kHz) frequency elements were driven with burst lengths of 300 μs and 150 μs at a burst repetition frequency of 50 Hz using two custom in-house built 256-channel driving systems, respectively. A calibrated fiber optic hydrophone (tapered fiber, active element diameter = 10 μm, Precision Acoustics, Dorset, UK) mounted on a three-axis positioning system (Superior Electric Motors, Inc., Bristol, CT, USA; Velmex, Inc., Bloomfield, NY, USA) was used to receive the transmitted signals from the high frequency elements. An in-house built hydrophone (PZT tube, 1 mm diameter, 5 mm length, 500 kHz center frequency in lateral mode) was used to receive the transmitted signal from the 55 kHz subarray, whose sensitivity was calibrated using a scanning vibrometer (PSV-400, Polytec Inc., Irvine, CA, USA) at 55 kHz ⁸⁹. Signals received by the hydrophones were captured by a digital oscilloscope (TDS 3012B, Tektronix, Richardson, TX, USA) and saved via an RS-232 serial connection to a central processing unit (CPU) for analysis. Electronic beam steering was performed at various distances along lateral and axial axes within the field for measurement of the spatial-peak-temporal-peak (SPTP) negative pressure at each transmit frequency, and the acoustic pressure field distributions were measured in both the lateral and axial planes (Figure 2).

Figure 2.

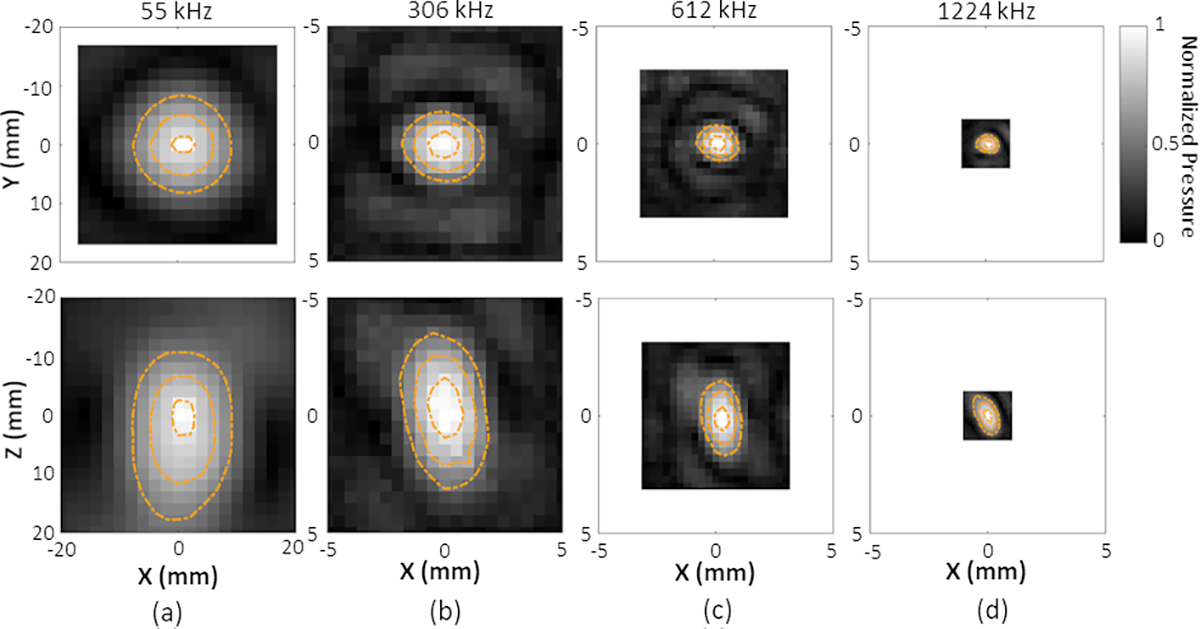
Lateral (upper row) and axial (bottom row) temporal-peak negative pressure field distributions generated at the array’s geometric focus for transmit frequencies of (a) 55 kHz, (b) 306 kHz, (c) 612 kHz, and (d) 1224 kHz. All plots are self-normalized to the SPTP negative pressure for a given frequency. Linear contours are displayed at 20% intervals from 50% to 90% of the SPTP pressure.

The phased array’s transmit steering capability at each transmit frequency is quantitatively evaluated in Figure 3. The SPTP negative pressure values at different target locations were normalized to the SPTP pressure achieved for each transmit frequency under a constant driving voltage. The error bars on the acoustic pressure data at high frequencies (306, 612, and 1224 kHz) and low frequency (55 kHz) are based on 13% and 1% uncertainties of the fiber-optic hydrophone and the in-house built hydrophone, respectively. 1D Gaussian fittings were applied to the acoustic pressure steering data (dashed lines). The effective steering range for each transmit frequency was obtained by calculating the range within which the SPTP negative pressure at the target is greater than or equal to 50% of the SPTP pressure at the geometric focus (Table 2) with error bars denoting 5% uncertainty from the 1D Gaussian fitting. The lateral and axial FWHM sizes of the acoustic pressure distributions were calculated via two dimensional (2D) Gaussian fitting and the focal spot sizes as a function of the target location for each transmit frequency (Figure 3).

Figure 3.

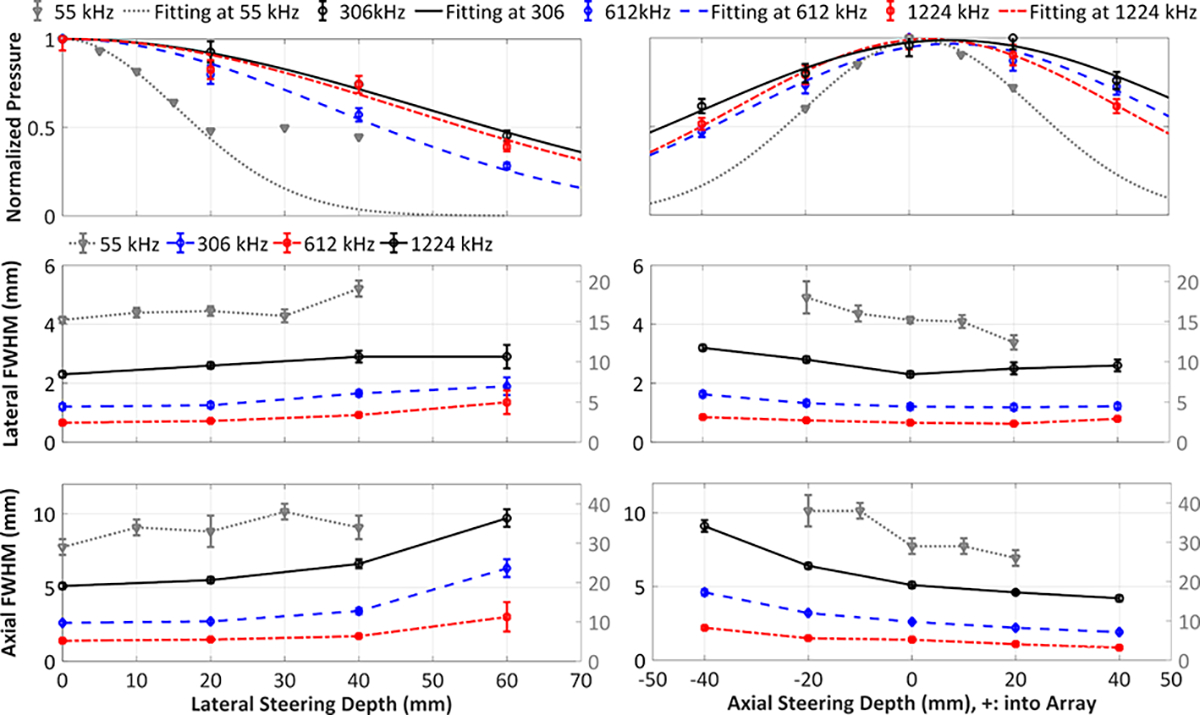
Acoustic characterization of the clinical-scale prototype FUS brain system at each transmit frequency (55 kHz (grey), 306 kHz (black), 612 kHz (blue), 1224 kHz (red)). SPTP negative pressure (top row) and transmit focal size (pressure-FWHM) in lateral (middle row) and axial (bottom row) directions obtained in water as a function of target location for beam steering along lateral (left column) and axial axes (right column). The focal size values for the 55 kHz transmit frequency are denoted by the right Y-axes.

Table 2.

Effective lateral and axial transmit steering ranges at each array driving frequency measured in water. Errors quoted are based on the 5% uncertainty in the 1D Gaussian fitting procedure.

Frequency (kHz)		55	306	612	1224
Steering Range (mm)	Lateral	37 ± 3	115 ± 4	86 ± 12	109 ± 13
	Axial	52 ± 4	111 ± 21	94 ± 18	88 ± 5

A spiral tube phantom was placed within the dome parallel to the X-axis. The phantom was made from polytetrafluoroethylene tubing (inner diameter = 1 mm, outer diameter = 1.2 mm, Cole-Parmer, Vernon Hills, IL, USA) following the methods described in ²². The fully relaxed tube phantom was in an irregular spiral shape with an approximate diameter of 4 mm and a pitch of 4–5 mm.

Lipid-coated DFB (C₄F₁₀, Synquest Labs, US) nanodroplets were fabricated following a modified condensation technique ⁹⁰, as described in ⁵³. The nanodroplets were formed by replacing the original gas core, octafluoropropane (C₃F₈), in Definity^™ microbubbles (Lantheus Medical Imaging, North Billerica, MA, USA) with C₄F₁₀, the latter of which has a higher boiling point. The resulting nanodroplet diameter after condensation and size exclusion was measured to be 210 ± 80 nm via dynamic light scattering (ZetaSizer, Malvern Panalytical, UK). The average stock concentration was 1.03 × 10¹¹ particles/mL (p/mL) measured at 1:10 dilution (NanoSight, Malvern Panalytical, UK) ⁵³.

The fabricated nanodroplet solution was further diluted in deionized water at a ratio between 1: 10⁵ and 1: 10³ by volume, corresponding to concentrations of approximately 1.03 × 10⁶ and 1.03 × 10⁸ p/mL. The ultrasound field was generated by driving the 55 kHz elements with a burst length of 145 μs using a custom 256-channel driving system (see Table 3 for additional sonication parameters). The threshold peak negative acoustic pressure to activate nanodroplets was determined by ramping up the driving system input voltage (step size = 0.01 MPa) until the received signals could be beamformed to produce a single localized source via PAM [peak side-lobe ratio (PSLR) ≤ −3 dB]. The corresponding pressure activation thresholds were measured as 0.180 MPa and 0.168 MPa for receive frequencies of 612 kHz and 1224 kHz, respectively. Receive data were acquired for 410 μs starting from the transmit burst trigger using either the 612 kHz or 1224 kHz array elements. The RF data were pre-amplified with a receive gain of 1.26 and recorded using two SonixDAQ receivers at a sampling rate of 10 MS/s. The phased array was electronically focused to evenly-spaced targets along the tube elongation direction (i.e., X-axis) in the coordinate system of the phased array (Table 3), covering the 20 mm length of the spiral phantom. The data captured from each target is referred to as one frame. The average steering speed between two successive targets was approximately 20 ms. The data captured once the array completed electronic steering through all targets within one trigger interval is referred to as one round. Each round was repeated every 2 seconds until the 1-GB buffers of the SonixDAQs were filled. To image the spiral tube phantom, a total of 3960 (9 frames/round × 110 rounds × 4 consecutive captures) and 4950 (45 frames/round × 22 rounds × 5 consecutive captures) frames were captured at 612 kHz and 1224 kHz, respectively.

Table 3.

Summary of the transmit, acquisition, and data processing parameters employed during benchtop and in vivo experiments.

Type	Pressure [Increment] (MPa)	Target [Spacing (mm)]	PRF (Hz)	Rx (kHz)	Injected Nanodroplet Concentration (p/mL)	Injection	Acquisition	PAM Voxel Size (mm)	SR Mesh Size (mm)
Imaging PSF	0.05 – 0.18, [0.01]	2×1/sec, [2]	0.5	612	107	gravity driven, 3.2mL/min	2fr×18rd× 14steps×1acq	0.25	N/A
				1224				0.125
Tube Phantom	0.19	9×1/sec, [2.5]		612	106		9fr×110rd×4acq	0.25	0.025
	0.17	9×5/sec, [2.5]		1224	108		45fr×22rd×5acq	0.125
In vivo	0.22	single	50	612	1011	0.4mL×3 boluses	50fr×67rd ×3acq/inj	0.25	0.025
				1224				0.125

^*Rx: receive; fr: frame, formed by beamforming RF data at one target; rd: round, formed by the number of frames within one trigger interval; acq: acquisition, stopping when the selected buffer sizes on SonixDAQs are filled; inj: injection.

II.C. In Vivo Experiments

One New Zealand White rabbit (male, 3.5 kg; Charles River, Saint-Constance, QC, Canada) was used to assess the feasibility of nanodroplet imaging via PAM and SR techniques with this device. The experimental protocol was similar to previous studies from our group ^91,92, and was approved by Sunnybrook Research Institute′s Animal Care Committee. The rabbit was first anesthetized via an intramuscular injection of a mixture of ketamine (50 mg/kg/h) and xylazine (5 mg/kg/h). The rabbit was then intubated, and anesthesia was maintained using 1–3% isofluorane and medical air (2 L/min). The hair on the rabbit′s head was removed using a razor and depilatory cream. The ear vein was catheterized using a 22G angiocatheter. The animal was placed supine on a platform and the head was acoustically coupled via ultrasound gel to a plastic membrane that was in contact with the water-filled array. The platform with the animal was moved between the array and a 3 T MR imaging scanner (Biograph mMR, Siemens Healthcare, Erlangen, Germany) for treatment planning and assessment of any induced bioeffects. A 3-plane localizer sequence [repetition time (TR): 8.6 ms; echo time (TE): 4 ms; number of averages: 2; echo train length: 1; matrix size: 512×512; FOV: 23×23 cm²; slice thickness: 3 mm] was performed before and after each USImg sequence at each receive frequency for both targeting [Figure 1(d)] and assessment of any changes in animal position. Subsequently, a T₂*-weighted sequence (TR: 3100 ms; TE: 82 ms; number of averages: 2; echo train length: 8; matrix size: 256×256; FOV: 10×10 cm²; slice thickness: 1.5 mm) was acquired to confirm the absence of red blood cell (RBC) extravasations caused by the sonications ⁹³. No RBC extravasations were observed at any target location during the in vivo experiment. Finally, a T₁-weighted sequence (TR: 500 ms; TE: 8.6 ms; number of averages: 3; echo train length: 4; matrix size: 256×256; FOV: 10×10 cm²; slice thickness: 1.5 mm) was acquired after intravenous injection of a gadolinium-based MRI contrast agent (0.1 ml/kg Gadovist^™; Bayer Inc., Toronto, ON, Canada) to detect changes in blood-brain barrier permeability. Two different receive frequencies were tested (Table 3) following a sequence demonstrated in Figure 1(e), both with transmit burst lengths of 200 μs per target at 0.22 MPa [mechanical index (MI) = 0.94]. Short burst length was chosen to be less than the average time of flight of a round trip between elements and selected target, in order to minimize the cross-talking between the transmit and receive channels and suppress the generation of bio-effects during USImg while maintaining a steady acoustic pressure field for nanodroplet vaporization. Prior to nanodroplet injection, baseline measurements were acquired for subtraction prior to beamforming. A bolus of lipid-coated C₄F₁₀ nanodroplets (10¹¹ p/mL, 0.4 mL) was delivered via a tail vein catheter 30 seconds before the start of sonication. Three consecutive data acquisitions (capture length = 250 μs, sampling rate = 10 MS/s, buffer size = 2 GB or 3350 captures) beginning 200 μs after the transmit trigger were performed for each injection for both receive frequencies (see Table 3 for additional information). The capture length was determined by the transmit burst length. The 200 μs-delayed on receive side would reduce the impact from the transmit waveform and lower the sample size per frame. Single target was used in in vivo experiment to save the phase loading time and thus maximize the PRF of the transmit burst on the in-house built driving system. Each capture was separated by approximately 2 min, to allow time to clear the buffers by downloading the data to a PC (Intel^® Core (TM) i5–3570 CPU @ 3.40 GHz, 24 GB RAM, NVIDIA GeForce GTX 1080 graphics processing unit), which will be used for data processing and beamforming offline.

II.D. Normal Resolution Image Processing

All data analysis was performed in MATLAB^™ (R2018b, Mathworks, Natick, MA, USA). RF data was reconstructed via PAM and normal resolution images of the tube phantom were compiled following the delay, sum, and integrate beamforming algorithm described in previous studies ^63,77,92. For both the tube phantom and in vivo experiments, baseline captures without the injection of nanodroplets were performed. The RF data acquired from baseline without nanodroplets present were subtracted from the RF data with nanodroplets present line-by-line prior to beamforming, in order to suppress reflections from stationary structures including tubing walls, water-air interface, and skull surface. Following subtraction, the RF data were digitally filtered using a fourth-order Butterworth band-pass filter with a 400 kHz bandwidth centered about the receive frequency. Following subtraction, the RF data were digitally filtered using a fourth-order Butterworth band-pass filter with a 400 kHz bandwidth centered about the receive frequency. The imaging PSF near the array’s geometric focus was estimated by imaging a diluted solution of nanodroplets (1.03 × 10⁷ p/mL) using both the 612 kHz and 1224 kHz receive subarrays (Figure 4). A pre-defined acoustic imaging FOV was chosen to cover all focal targets (20 × 10 × 10 mm³ and 20 × 8 × 6 mm³ with a voxel size of $\lambda /10$ for receive frequencies of 612 kHz and 1224 kHz, respectively). For each voxel at location $\mathit{r}$ within the FOV, the signals were first scaled and delayed as follows:

$$Q_n\left(\mathit{r},t\right)=\widehat{p_n}\left(t+\frac{‖{\mathit{r}}_n-\mathit{r}‖}{c}-s_n\right)·‖{\mathit{r}}_n-\mathit{r}‖,$$ (1)

where $\widehat{p_n}$ is the filtered time-dependent pressure captured by receiver $n$ at location ${\mathit{r}}_n$, $c$ is the speed of sound in water, $‖{\mathit{r}}_n-\mathit{r}‖$ is the distance between receiver $n$ and voxel location, $s_n$ is the skull delay correction term for receiver $n$. The intensity of each voxel was then calculated by integrating the modified signal over a time window [$t_0,t_0+T$] as follows, to reconstruct a source field intensity distribution for each frame:

$$I\left(\mathit{r}\right)=\frac{1}{T}{\int }_{t_0}^{t_0+T}\left[{\sum }_{n=1}^N{\sum }_{\begin{array}{c}m=1\\ n\ne m\end{array}}^N{Q}_n(\mathit{r};t)Q_m(\mathit{r};t)\right]dt,$$ (2)

where $N$ is the number of receive elements in the array. This reconstructed source field intensity distribution was normalized to the spatial-peak intensity within the 3D volume. Unlike the filtering method applied to a stack of resulting images using singular value decomposition (SVD) to reduce stationary signals and filter individual cavitation source signals by differentiating the spatiotemporal coherence from the tissue and blood motion ^46,94, subtraction of the baseline RF signals from the ones with nanodroplets present was performed in our study followed by the selection of good frames based on the side-lobe intensity level. Reconstructed frames whose first largest side-lobe level was less than −3 dB of the peak main lobe intensity were determined and will be denoted hereafter as the “one-source” set. Each of these self-normalized frames were stacked together and a maximum intensity projection (MIP) was carried out across all frames. During tube phantom imaging, there were 258 (3960) and 515 (4950) frames with a single distinct source (total number of frames) when receiving at 612 kHz and 1224 kHz, respectively. To further increase the number of frames kept and improve phantom visualization, frames whose second largest side-lobe level was less than −3 dB of the peak main lobe intensity were also determined, denoted hereafter as the “two-source” set, resulting in 522 and 1743 frames when receiving at 612 kHz and 1224 kHz, respectively. The two-source frame set was used to form all the normal resolution images provided in this study [Figure 5 & Figure 8(a,d)]. Similar image processing techniques were applied to obtain normal resolution images from the in vivo data. Normal resolution images were first reconstructed within the imaging FOV of 20 × 20 × 20 mm³ and 18 × 18 × 18 mm³ centered at the target location [7, 2, 8.5] mm (relative to the geometric focus of the phased array) with a voxel size of $\lambda$/10 at the receive frequency of 612 kHz and 1224 kHz, respectively. Out of 30150 total frames, 1184 (2136) and 89 (259) frames were identified in the one-source (two-source) set when receiving at 612 kHz and 1224 kHz, respectively.

Figure 4.

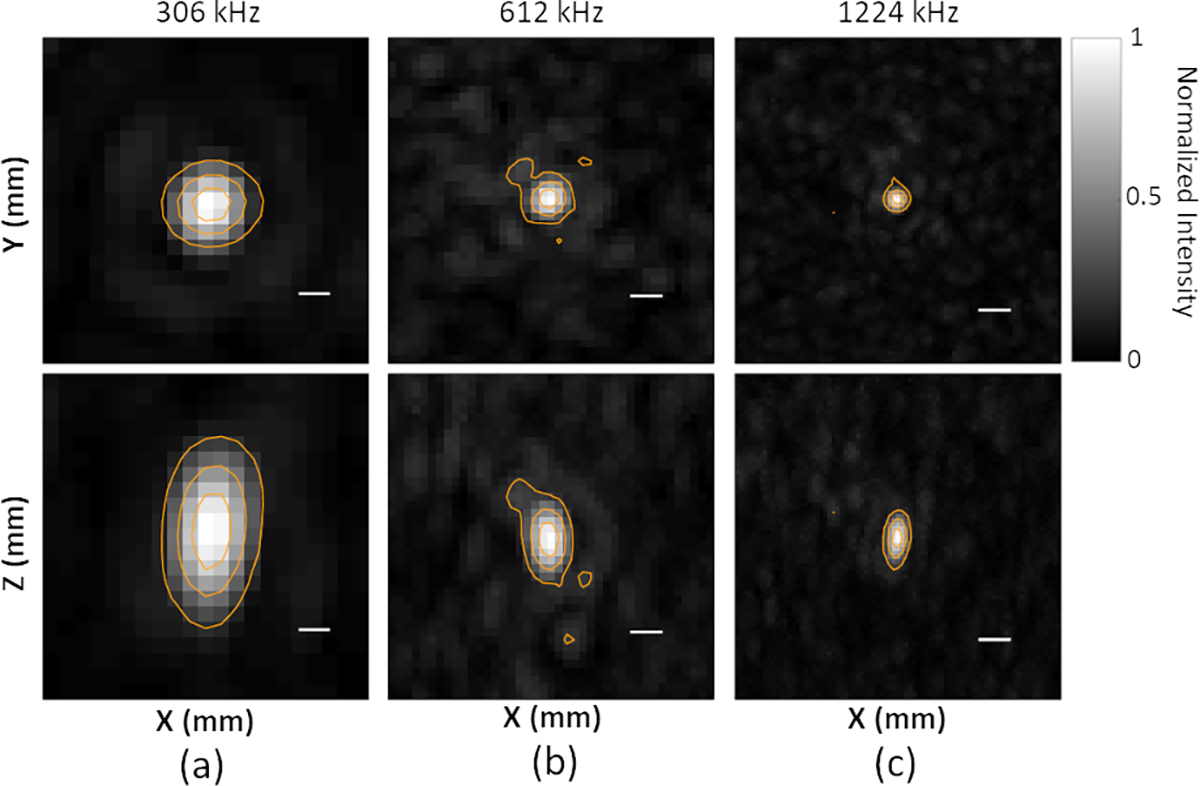
Imaging PSF for (a) 306 kHz, (b) 612 kHz, and (c) 1224 kHz receiver arrays. Scale bars indicate 1 mm. All plots are self-normalized to the spatial-peak source field intensity for a given frequency. Linear contours are displayed at 20% (−7 dB), 50% (−3 dB), and 80% (−1 dB) of the spatial-peak source field intensity.

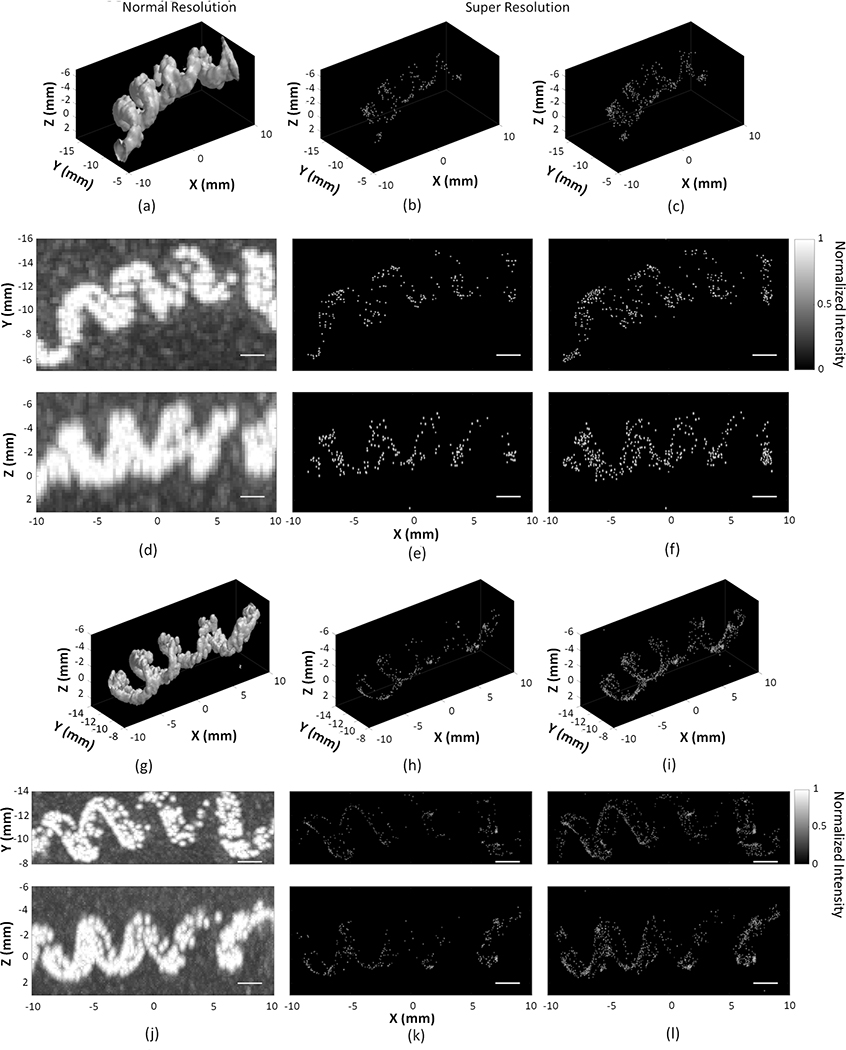
Figure 5.

Three-dimensional (3D) rendering of the maximum pixel projection image of vaporized nanodroplets flowing in the spiral tube phantom, with the −3 dB iso-surface shown at normal resolution using the two-source frame set at (a,g), super resolution (SR) using the one-source frame set (b,h), and two-source frame set (c,i). Corresponding normalized multi-frame maximum intensity projection images at normal resolution (d,j), SR using the one-source frame set (e,k), and two-source frame set (f,l), respectively. Receive frequencies are at 612 kHz (a-f) and 1224 kHz (g-l). Scale bars indicate 2 mm. To improve visibility, standard deviations in the three dimensions are shown as four times the uncertainties on the position estimate.

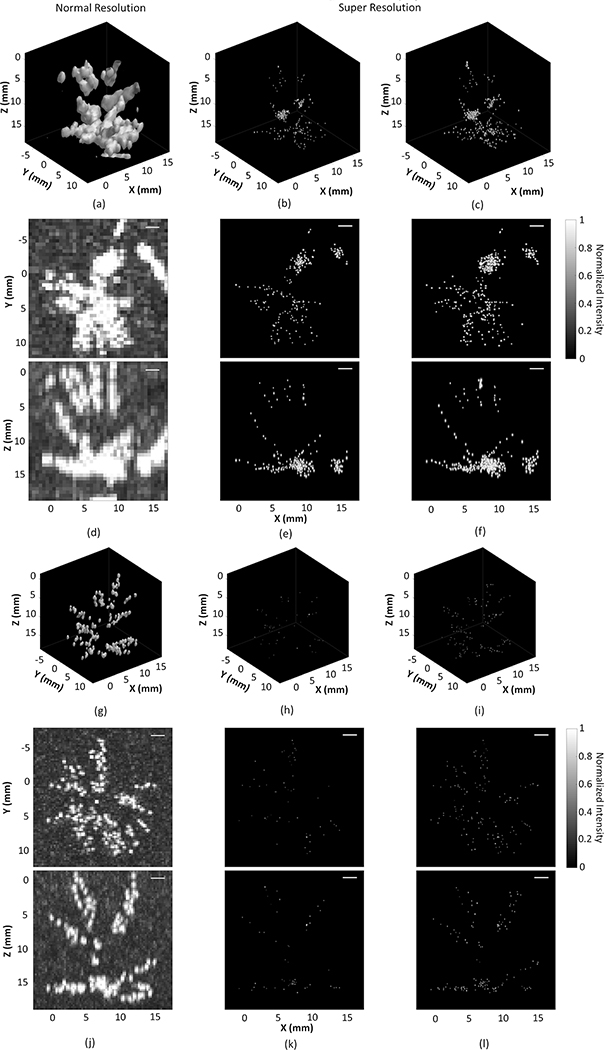
Figure 8.

Three-dimensional (3D) rendering of the maximum pixel projection image of vaporized nanodroplets flowing within rabbit cerebral vasculature, with the −3 dB iso-surface shown at normal resolution using the two-source frame set at (a,g), super resolution (SR) using the one-source frame set (b,h), and two-source frame set (c,i). Corresponding normalized multi-frame maximum intensity projection images at normal resolution (d,j), SR using the one-source frame set (e,k), and two-source frame set (f,l), respectively. Receive frequencies are at 612 kHz (a-f) and 1224 kHz (g-l). Scale bars indicate 2 mm. To improve visibility, standard deviations in the three dimensions are shown as four times the uncertainties on the position estimate.

II.E. Super Resolution Image Processing

SR image generation was based on the signal processing techniques described in ²². In brief, for each frame in the one-source frame set, a 3D Gaussian fitting was first performed over a volume of $\lambda \times \lambda \times 2\lambda$ centered on the voxel of maximum source field intensity using fixed standard deviation values calculated from the experimentally-determined imaging PSF. To visualize the associated SR images, 3D Gaussian distributions were plotted centered on the estimated source locations with standard deviation values equal to the positional uncertainties on the aforementioned fits (95% confidence intervals). Frames with uncertainty magnitudes greater than 1.5 times the interquartile range beyond the third quartile were discarded as outliers ²², resulting in the exclusion of 9/258 and 7/515 frames in the one-source frame set at 612 kHz and 1224 kHz, respectively. Two-source 3D Gaussian fitting was performed on the two-source frame set, resulting in the exclusion of 12/522 and 96/1743 frames at 612 kHz and 1224 kHz, respectively. The mean positional uncertainties obtained from the 3D Gaussian fitting procedure across all frames excluding outliers was calculated. The standard deviation associated with these data was also computed, distinct from the Gaussian fitting uncertainties described above, which potentially represents variation due to the vaporization of nanodroplets of different initial sizes, or the vaporization of multiple nanodroplets. The same image processing techniques were applied to obtain SR images from the in vivo data. 3D Gaussian fitting resulted in the exclusion of 12 / 1184 (142 / 2136) and 6 / 89 (9 / 259) frames at 612 kHz and 1224 kHz for the one-source (two-source) sets, respectively.

III. RESULTS

III.A. Transmit Array Characterization

The temporal-peak negative acoustic pressure field distributions generated at the geometric focus for each transmit frequency are displayed in Figure 2. Figure 3 quantifies the SPTP negative acoustic pressure and focal spot pressure-FWHM dimensions as a function of steering distance within the field along the lateral and axial axes for each transmit frequency. The corresponding effective steering ranges are estimated in Table 2. Specifically, the transmit frequency of 55 kHz used for nanodroplet vaporization provides a focal spot at the geometric focus with lateral and axial FWHM dimensions of 15.2 ± 0.4 mm and 29 ± 2 mm, respectively. No substantial change in the FWHM dimensions was observed within the effective lateral steering range of 37 ± 3 mm. When electronic beam steering was performed along the axial axis into the array (i.e., +Z direction), the mean lateral FWHM dimension decreased from 18 ± 2 mm at [0, 0, −20] mm to 12 ± 1 mm at [0, 0, 20] mm, whereas the axial FWHM dimension decreased from 38 ± 4 mm to 26 ± 2 mm.

III.B. Receive Array Characterization

Figure 4 shows PAM reconstructions of a representative nanodroplet vaporization event near the array’s geometric focus for receive frequencies of 612 and 1224 kHz. PSLR at all three receive frequencies remain below or equal to 20% of the maximum intensities of main lobe. Grating lobes won’t be formed in this sparse hemispherical array due to the random arrangement of modules which breaks the periodic element arrangement of the conventional imaging probes ⁹⁵. The lateral (axial) intensity-FWHM dimensions of the receiver array’s PSF are calculated as 1.95 ± 0.03 mm (3.78 ± 0.06 mm), 0.97 ± 0.03 mm (1.84 ± 0.05 mm), and 0.52 ± 0.01 mm (1.14 ± 0.02 mm) at 306 kHz, 612 kHz, and 1224 kHz, respectively. The corresponding fixed lateral (axial) standard deviations are 0.83 mm (1.61 mm), 0.42 mm (0.78 mm), and 0.22 mm (0.48 mm) along lateral direction at 306 kHz, 612 kHz, and 1224 kHz, respectively. These values were used during the 3D Gaussian fitting procedure ²² when generating SR images.

III.C. Imaging Spiral Tube Phantom

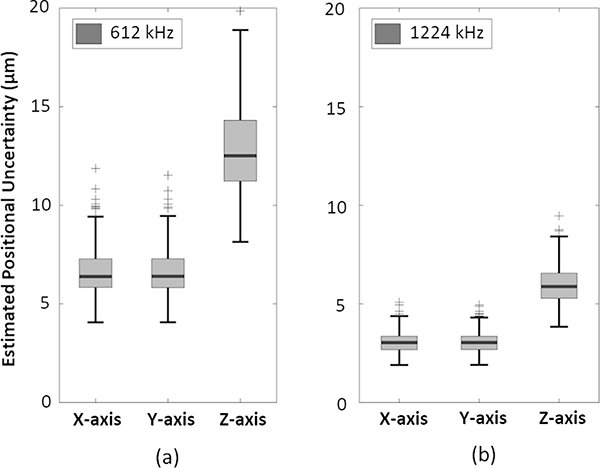
Figure 5 displays composite MIP images at both normal and SR for receive frequencies of 612 kHz and 1224 kHz. The tube phantom structure is clearly discernable at both receive frequencies. The spiral diameter is approximately 5 mm and 4 mm measured at 612 kHz and 1224 kHz, respectively, whereas the pitch is approximately 5 mm at both receive frequencies. Images captured at 1224 kHz demonstrate better spatial resolution than at 612 kHz. For the resulting SR images generated using the one-source frame set, the mean positional uncertainties along the lateral (axial) direction were 7 ± 1 μm (14 ± 2 μm) and 3 ± 1 μm (6 ± 1 μm), corresponding to a mean lateral (axial) intensity-FWHM of 16 ± 3 μm (32 ± 6 μm) and 7 ± 3 μm (15 ± 3 μm) at 612 kHz and 1224 kHz, respectively (Figure 6). The two-source frame set provided similar positional uncertainties at both receive frequencies. The lateral positional uncertainty is expected to be smaller than the axial one, which arises from the inherent characteristics of the PSF used in the 3D Gaussian fitting. This PSF displays a narrower lateral spread due to a tighter focusing in the lateral plane afforded by the hemispherical array geometry.

Figure 6.

Box and whisker plots of the estimated positional uncertainties along each Cartesian axis from the one-source frame set at receive frequencies of (a) 612 kHz, and (b) 1224 kHz from tube phantom imaging data. Crosses denote outliers (data points beyond the third quartile by more than 1.5 times the interquartile range).

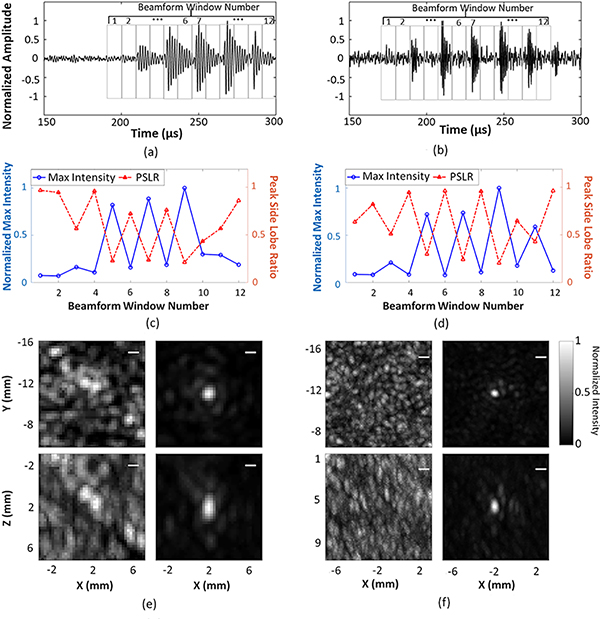
Figure 7 illustrates a temporal correlation between the beamformed RF waveform at the location of spatial-peak source field intensity, delayed-and-summed across all array channels, and nanodroplet vaporization for receive frequencies of 612 kHz and 1224 kHz, respectively. As can be seen in Figure 7(a,b), five distinct local maxima are present in the beamformed RF waveform, separated with a burst length corresponding to the transmit wave period. A beamforming window of 9 μs in duration, equivalent to one half a period at 55 kHz, was moved throughout the RF waveforms, and corresponding PAM images from each window were reconstructed at both receive frequencies. The normalized spatial-peak source field intensity and PSLR as a function of beamforming window is plotted in Figure 7(c,d). The spatial-peak source field intensity was higher, and the PSLR was below −3 dB within beamforming windows, indicating reconstruction of a single distinct source, which corresponds to local maxima in the RF waveforms. Example MIP images reconstructed for beamforming window numbers 4 and 5 are provided in Figure 7(e,f) at 612 kHz and 1224 kHz, respectively.

Figure 7.

Temporal correlation of the beamformed RF waveform and nanodroplet vaporization at receive frequencies of 612 kHz (left column) and 1224 kHz (right column), respectively. (a,b) Beamforming integration window (integration time = 9 μs) was moved through the RF waveform. (c,d) Normalized spatial-peak source field intensity and PSLR of the reconstructed images as a function of the beamforming window. (e,f) Examples of corresponding image reconstructions for beamforming window numbers 4 and 5. Scale bars indicate 1 mm. Videos of this temporal correlation at 612 kHz (Video1_TemporalCorrelation612kHz.avi) and 1224 kHz (Video2_TemporalCorrelation612kHz.avi) can be found in Supplementary Material.

III.D. Imaging Rabbit Cerebral Vasculature

Figure 8 displays composite MIP images of the rabbit cerebral vasculature at both normal and SR with different receive frequencies. The 612 kHz receiver array visualized a larger portion of vasculature close to the rabbit skull bone (approximately 15 mm from geometric focus into the array) than the 1224 kHz array, whereas the 1224 kHz receive array was able to show vessel branches in greater detail. It is important to note that the data for 612 kHz and 1224 kHz are from separate acquisitions. 3D Gaussian fitting to the two-source frame set revealed a larger portion of the cerebral vasculature (Figure 8(c,f)). For the resulting SR images with the two-source frame set, the mean positional uncertainties along the lateral (axial) direction were 9 ± 3 μm (19 ± 6 μm) and 3 ± 1 μm (7 ± 2 μm), corresponding to a mean lateral (axial) intensity-FWHM of 22 ± 6 μm (45 ± 13 μm) and 8 ± 2 μm (16 ± 4 μm) at 612 kHz and 1224 kHz, respectively (Figure 9). The one-source frame set provided similar positional uncertainties, which are 8 ± 3 μm (17 ± 5 μm) and 3 ± 1 μm (6 ± 2 μm) along the lateral (axial) direction at 612 kHz and 1224 kHz, respectively.

Figure 9.

Box and whisker plots of the estimated positional uncertainties along each Cartesian axis from the two-source frame set at receive frequencies of (a) 612 kHz, and (b) 1224 kHz from in vivo rabbit cerebrovascular imaging data. Crosses denote outliers (data points beyond the third quartile by more than 1.5 times the interquartile range).

IV. DISCUSSIONS

The large-aperture transmit/receive phased array employed in this study was capable of producing clear normal resolution images of a spiral tube phantom by activating nanodroplets and reconstructing the scattered signals via PAM. The phantom structure was discernible from these diffraction-limited images (Figure 5) at both receive frequencies investigated. The application of SR processing techniques substantially enhanced the resulting image resolution. Previously, a 128-disc element (diameter = 2.54 mm) receive array at 612 kHz was used to image a spiral tube phantom through an ex vivo human skull using 3D transcranial passive acoustic mapping and SR imaging techniques ²². In this study, the array's performance was improved by using PZT tube receivers with sensitivities approximately 6.8 times higher than the disc elements'. The current phased array at 612 kHz provided a finer point spread function size, with approximately 24% (27%) smaller lateral (axial) intensity FWHM and fixed standard deviation compared to the previous array ²². The mean estimated positional uncertainties (mean ± standard deviation) at 612 kHz were 7 ± 1 μm laterally and 14 ± 2 μm axially, about 65% finer. A temporal resolution five times higher at 50 volumes/s was achieved using the in-house built driving system, which may be further improved by considering the temporal correlation between the vaporization of nanodroplets and the rarefactional regime of the 55 kHz transmit waveform ⁷⁵. The data processing method remained similar. The frames with the intensity amplitude of the second largest side-lobe intensity less than −3 dB of the maximum intensity of the main lobe were taken into the Gaussian fitting process due to limited number of vaporized nanodroplets localized. Using commercial imaging probes, 3D ULM has been conducted to successfully image the whole brain microvasculature using ultrafast imaging technique. Demeulenaere et al. demonstrated the capability of performing 3D ultrafast ULM using a 32-by-32 matrix array probe at 7.81 MHz and a 1024-channel driving system, with an ultrafast Doppler imaging sequence to transcranially image the whole mouse brain (13×13×20 mm³). A spatial resolution of 20 μm and a temporal resolution of 750 volumes/s were achieved. Microbubble spatial density was measured to be in the range of 1900–14741 microbubbles/mm³. Brain microvascular vessels ranging from 20 to 200 μm in diameter could be identify on the microbubble density map ⁴¹. In another study performed by Lok et al., a 3D bipartite graph-based method with Kalman filtering-based tracking and adaptive interpolation was used to investigate the complex MB flow dynamics in an in vivo chicken embryo brain with intact skull. The same 2D matrix probe was used with power Doppler imaging sequence at a temporal resolution around 350 volumes/s. Four 256-channel sub-apertures were used for collecting the RF data sequentially during four transmissions and receptions to reduce the system complexity. The spatial resolution was around 52 μm, which could be achieved only when the proposed MB tracking and pairing methods were utilized ⁴². Although our approach currently falls short in measuring the microvascular size and providing blood velocity information compared to 3D ultrafast transcranial ULM, it shows promise for clinical transcranial FUS treatments. The hemispherical phased array operates at a lower frequency range, experiencing less skull-induced distortion and attenuation. Moreover, exact registration can be achieved between the sub-arrays used for imaging and treatment. This array also has the potential to image deep-seated region in brain tissue due to its wide beam steering range (Figure 3).

By using nanodroplets in combination with the low transmit frequency of 55 kHz, a temporal correlation between nanodroplet vaporization and the transmit waveform shape was observed. The switching-on and -off mechanism of nanodroplets due to the vaporization and re-condensation or disruption corresponding to the transmit waveform has been observed within the first five cycles using high-speed optical imaging ⁹⁶. Our hypothesis was that this temporal correlation could also be illustrated via PAM. At the threshold peak negative pressure, the nanodroplets remain inactivated or recondensed during the compressional phases of the transmit wave, while experiencing vaporization during the rarefactional phases, which could be observed via PAM with a beamforming window size tuned to half of the transmit period. This correlation is demonstrated in Figure 7 at both receive frequencies. Since every two adjacent local maxima in the beamformed RF waveform was one wavelength of the transmit frequency, it was correlated to the transmit pulsing scheme with 8 cycles at 55 kHz. Both the spatial-peak source field intensity and the PSLR change as a function of the beamforming windows. From windows 2 to 11, the peaks in the spatial-peak source field intensity and the valleys in the PSLR demonstrate good reconstructions (i.e., ‘one-source’), which can be linked to the vaporization of nanodroplets and thus the rarefactional phase of the transmit pulse. The correlation becomes more observable when the receive frequency was increased from 612 kHz to 1224 kHz. However, there was an exception at window 11 in Figure 7(c) when received at 612 kHz, where no obvious increase in intensity was seen, compared to that at window 10 (compressional phase). This was not expected since window 11 was correlated to the rarefactional phase of the transmit pulse, based on Figure 7(a). The decreased intensity may be due to the following factors: first, a lack of overlap of the transmit pulses from the transmit elements resulting in a decreased acoustic pressure; second, insufficient nanodroplet recondensation in the compressional phase (window 10) or fragmentation of the resulting microbubble in rarefactional phase (window 11), as seen in high-speed optical imaging after several cycles (Figure 6 in Wu et al. ⁹⁶).

During in vivo experiments, the small number of discrete nanodroplets detected limited visualization of the complete vascular network and precluded size estimation of the vessels and nanodroplet tracking, which may be due to insufficient nanodroplet vaporization efficiency. The vaporization efficiency of lipid coated C₄F₁₀ nanodroplets was reported previously as 0.3% at 750–900 kPa at 1.5 MHz in a 200 μm-diameter micro cellulose tube ⁹⁷. Based on the flow speed, tube diameter, nanodroplet concentration, and the number of images within the one-source frame set, the nanodroplet vaporization efficiency in our study was estimated to be 1 in 1 million (assuming all detected particles in the concentration measurement are activated nanodroplets rather than inert liposomes). This estimate requires further verification with tube phantom imaging with varying tube sizes and flow speeds, as well as supplemental imaging with other modalities including contrast-enhanced ultrasound (CEUS) imaging or high-speed optical imaging ⁹⁸ and measuring the proportion of nanodroplets and liposomes in the solution. Furthermore, a registration of conventional imaging probe ⁹⁶ or high-speed camera ⁹⁸ can be used to verify nanodroplet vaporization and estimate the sensitivity of this hemispherical phased array in imaging the vaporized nanodroplets in the future.

The use of low-frequency ultrasound will benefit transcranial applications since it experiences less distortion and attenuation when passing through skull bone ⁹⁹. As a result, better transcranial focusing can be achieved and skull-surface overheating can be suppressed. In addition, the relatively long rarefactional or compressional regimes offer the opportunities to be combined with high frequency short bursts. In the future, a second transmit burst at higher frequency of 306, 612, or 1224 kHz could be superimposed to the rarefaction region of the low transmit frequency, driven by a separate driving system, to further modulate nanodroplet vaporization. With the current scheme transmitting at 55 kHz, we predict that vaporization is mechanically driven (i.e., the prolonged exposure to negative pressure during the rarefactional cycle triggers the liquid to gas conversion). However, superimposing higher frequency transmit bursts may exploit additional vaporization mechanisms and increase vaporization efficiency, such as superharmonic focusing, which relies on the diffraction of high frequency waves inside the droplet ¹⁰⁰. Furthermore, higher frequency transmit bursts can enhance the scattered signals and may increase the number of vaporized nanodroplets being detected and thus shorten the total acquisition time. Besides, it can allow stable cavitation of the vaporized nanodroplets to be detected since the receive frequency can be tuned to the sub- or the second-harmonic frequency of the transmit frequency, instead of receiving the wideband inertial cavitation signals when the phased array is transmitting at 55 kHz. However, higher pressure may be needed to vaporize the nanodroplets with increased ultrasound frequency given the nanodroplet size (210 ± 80 nm) and the frequency range (between 306 kHz and 1224 kHz) ^96,101. The vaporization threshold pressure is expected to be increased with the presence of skull bone due to the increased insertion loss at higher transmit frequency ⁸⁰. Finally with the presence of human skull, aberration correction needs to be performed for the high frequency elements for both transmit and receive. Skull phase ¹⁰² and amplitude ^103,104 corrections can be estimated noninvasively with transcranial ultrasound propagation models using either analytical (e.g., ray tracing ¹⁰²) or numerical techniques (e.g., ray-acoustic model ^13,78, and full-wave model ^{103,105–107}) incorporated with the computerized tomography-derived skull density. Skull aberration correction can also be achieved with cavitation-based method ^22,108.

One limitation of performing sonication at low frequencies is the formation of standing waves inside the rabbit skull. This can expose the entire brain in small animal models to the acoustic field, increasing the risk of potential intracerebral hemorrhage. Moreover, under similar MI, simulations have indicated that low frequencies exhibit a narrower stable cavitation range and higher microbubble expansion ratio, and they have been shown to induce greater mechanical damage and tumor cell death compared to high frequencies ¹⁰⁹. To ensure the safety in our study, the maximum MI used was 0.94 during in vivo experiment, which was selected slightly higher than the threshold pressure to detect nanodroplet vaporization in benchtop measurements considering the reduced pressure due to the attenuation of rabbit skull, brain tissue, and beam steering. Several MRI sequences were consecutively performed after the USImg to further assess whether there were any induced bio-effects. No hypointense area was found on the T₂*-weighted MRI data acquired after the sequences of USImg [Figure S-3(b)], compared to the T₂*-weighted MRI data taken before sonication [Figure S-3(a)]. The absence of red blood cell (RBC) extravasations caused by the sonications was confirmed. In addition, no obvious change of the blood-brain barrier permeability was observed, indicated by the post-gadolinium T₁-weighted MRI data [Figure S-3(c)], similar to what has been observed in a nanodroplet-mediated drug delivery study ⁵³.

Other potential approaches to enhance nanodroplet vaporization efficiency include fabricating nanodroplets formed from a mixture of perfluorocarbons. For example, adjusting the volume mixing ratio between a second perfluorocarbon with a lower boiling point and the original one with higher boiling point (e.g., introducing DFB (C₄F₁₀) into perfluorohexane (C₆F₁₄) nanodroplets ¹¹⁰, or octafluoropropane (C₃F₈) into DFB (C₄F₁₀) nanodroplets ¹¹¹). Finally, the use of a supplemental imaging modality (e.g., CEUS, CTA or MRA) to delineate the rabbit’s cerebral vascular network would be beneficial during or after future in vivo experiments ^112,113, for comparison and quantification of the ultrasound images at both normal and SR.

The normal resolution MIP images obtained from vaporized nanodroplets at two distinct receive frequencies provided slightly different vessel structures in vivo (Figure 8). Several factors may have contributed to this difference. First, the attenuation coefficient of rabbit skull bone at 1224 kHz is higher than at 612 kHz ⁹⁹, resulting in lower RF signal amplitudes when receiving at 1224 kHz. Second, the 1224 kHz receive elements have lower sensitivity owing to their smaller surface area.

The estimated positional uncertainties observed in vivo [Figure 9(a)] were slightly increased compared to corresponding benchtop measurements [Figure 6(a)]. The increment is on average 2 μm (5 μm) along lateral (axial) direction at the receive frequency of 612 kHz, and only 1 μm along axial direction at 1224 kHz, which may have resulted from a combination of factors. First, spatially-coherent sources in vivo may have originated from multiple nanodroplets, given the nanodroplet concentration in the blood after the first injection (~1.8 × 10⁸ p/mL) and the time between two nanodroplet injections [~ 6.5 min, shown in Figure 1(e)] are shorter than the half-life of the nanodroplets in vivo (reported in a rodent model 8.4 ± 1.7 min ⁵³). The nanodroplet concentration in blood was calculated from 0.4 mL bolus injection of 10¹¹ p/mL nanodroplet solution into a 3.5 kg rabbit with a blood-volume of 64 mL/kg. Second, the relatively small cerebral vasculature structures and low flow velocities in rabbits may have resulted in repetitive vaporization/mapping of the same nanodroplet or microbubble subsets if the nanodroplets failed to recondense. The intensity of these nanodroplet subsets could dominate the reconstructed volume, even when the electronic beam was steered away, until the final collapse and dissolution of the microbubble occurs. Since the source field intensity was self-normalized within each frame, some images with PSLR values above −3 dB may have spatial coherence yet wouldn’t be retained. In other words, the criteria for one-source frame set selection may underestimate the total number of nanodroplet vaporization events. To attempt to mitigate this issue, the frame selection criteria for the generation of SR images was loosened so that frames with the second largest side-lobe intensity below −3 dB were included. As a result, 3D Gaussian fittings were applied to maximum two sources in a single frame in the two-source frame set, which resulted in a larger portion of the imaged object to be visible. However, the criteria to select the two-source frames still needs further investigation. Instead of selecting frames based on a sidelobe threshold of −3 dB within a single frame, a setting of global source field intensity threshold may be helpful so that frames with more than two distinct sources can be included, and more voxel locations can be resolved via SR. In addition, the corresponding waveforms of the beamformed RF data summed from all the receive channels could be studied to see if a correlation exists between the SPTP values of the waveform amplitudes and the absolute source field intensity with spatial coherence.

There are several limitations to our study. Although the large-aperture phased array presented here is clinical-scale, benchtop experiments with ex vivo human skull caps cannot be performed at present due to the limited acoustic power output available at the 55 kHz transmit frequency. In addition, we observed that vaporized nanodroplets tended to distribute close to the inner tube walls [Figure 5(c,f)], indicating that the flow rate may have been too high, resulting in a larger shear force applied on the resultant microbubbles than that from the acoustic radiation force. In this scenario, nanodroplets close to the central portion of the tube would not have sufficient time to be activated within the acoustic pressure field, assuming laminar flow within the tube phantom. In future benchtop experiments, various flow rates will be investigated through the use of an infusion pump. The third limitation of this study is the absence of motion correction during in vivo experiment. Due to the limited nanodroplet vaporization events, it is currently challenging to detect distinct vascular structure in each frame using PAM for a rigid registration. However, to mitigate this limitation, the head of the rabbit was fixed to the phased array with a bite bar and two ear bars during experiment. As mentioned in Methods II C, a 3-plane localizer sequence was performed before and after each USImg sequence at both 612 kHz and 1224 kHz receive frequencies for targeting and assessment of any changes in animal position. No obvious position changes were observed. In the future experiment, three narrow-band source emitters (piezo ceramic tube; 1mm diameter, 512kHz center frequency ⁸⁰) can be attached to the animal’s head, enabling source localization using PAM with the hemispherical array. For a clinical scenario, tracking human skull motion can be feasible once a high frequency diagnostic array ^88,114 is integrated into this hemispherical array and the speed of skull surface localization is improved. Finally, computational time is another limitation of the current work. At present, the processing time is not sufficient for SR imaging in real-time. It currently takes ~1–2 sec to process a single frame (81 × 81 × 81 voxels at 612 kHz and 145 × 145 × 145 voxels at 1224 kHz, integration time of 1500 temporal samples, 256 channels), and ~1–2 hours to process a 4 GB data capture via PAM (2 GB buffer size per SonixDAQ) to form MIP images at normal resolution. As for the computational time associated with SR processing, approximately 2.7 sec is required for 3D Gaussian fitting of a single ‘one-source’ frame (401 × 401 × 401voxels). The imaging frame rate could be improved if nanodroplet activation efficiency could be increased such that frames with multiple distinct sources within the imaging FOV could be achieved within a single capture. Since no extravasation of RBC or change of the BBB permeability has been observed in T₂*-weighted and T₁-weighted MRI (Figure S-3), utilizing the USImg sequence in conjunction with nanodroplets for SR on the hemispherical array, even if not in real-time, has the potential to be conducted both before and after transcranial FUS treatment. This approach allows for targeting and assessing the treatment’s effectiveness, potentially offering insights into vascular differences beyond the capabilities of current MR assessments.

V. CONCLUSIONS

The feasibility of mapping ultrasound-vaporized nanodroplets with PAM and SR imaging techniques was demonstrated using a large-aperture multi-frequency hemispherical phased array by imaging a tube phantom in vitro and rabbit cerebral vasculature in vivo. The improved receive element sensitivities and increased element count of the novel array design resulted in a reduction of the estimated localization uncertainties during benchtop experiments compared to previous measurements with a different device. A temporal correlation between nanodroplet vaporization and the rarefactional phase of the transmit waveform was observed, demonstrating the potential of using low-frequency ultrasound to modulate the nanodroplet vaporization process. In addition, the relatively long wavelength of 55 kHz provides opportunities to superimpose a second higher frequency wave to further modulate and detect nanodroplet vaporization or condensation to improve the image signal-to-noise ratio and spatial resolution, which will be investigated in the future. This study demonstrates the potential of using a clinical-scale hemispherical transmit/receive array to provide 3D SR images to map the vascular network pre- or post-focused ultrasound treatment with a mean intensity-FWHM dimension of approximately 1/67 of the normal, diffraction-limited resolution.