Abstract
There is an unmet need to classify cancer-promoting kinase mutations in a mechanistically cognizant way. The challenge is to understand how mutations stabilize different kinase configurations to alter function, and how this influences pathogenic potential of the kinase and its responses to therapeutic inhibitors. This goal is made more challenging by the complexity of the mutational landscape of diseases, and is further compounded by the conformational plasticity of each variant where multiple conformations coexist. We focus here on the human MEK1 kinase, a vital component of the RAS/MAPK pathway in which mutations cause cancers and developmental disorders called RASopathies. We sought to explore how these mutations alter the human MEK1 kinase at atomic resolution by utilizing enhanced sampling simulations and free energy calculations. We computationally mapped the different conformational stabilities of individual mutated systems by delineating the free energy landscapes, and showed how this relates directly to experimentally quantified developmental transformation potentials of the mutations. We conclude that mutations leverage variations in the hydrogen bonding network associated with the conformational plasticity to progressively stabilize the active-like conformational state of the kinase while destabilizing the inactive-like state. The mutations alter residue-level internal molecular correlations by differentially prioritizing different conformational states, delineating the various modes of MEK1 activation reminiscent of a gear-shifting mechanism. We define the molecular basis of conversion of this kinase from its inactive to its active state, connecting structure, dynamics, and function by delineating the energy landscape and conformational plasticity, thus augmenting our understanding of MEK1 regulation.
Introduction
Cells must receive and respond to signals in order to co-ordinate activities and to determine cell fate [1–3]. Signaling relies on various biomolecules to transfer information along the key biochemical pathways, and protein kinases play a crucial role by mediating phosphorylation of protein substrates to control their activity [4]. Errors in signaling due to aberrant kinase activity underlie many cancers [5]. Through research spanning decades, kinases have thus been identified as prime therapeutic targets for small molecule inhibitors that can correct aberrant signaling. Beyond the central roles that they play in signaling biology [6–8], kinases are rich targets because of the substantial role played by their structure and inherent conformational plasticity [9] combined with the conformational selectivity of inhibitors that can selectively bind to specific conformational states [6,10].
The canonical kinase domain (KD) can be subdivided into two lobes: the N-lobe and the C-lobe. ATP and most (ATP-competitive) inhibitors bind in the pocket between these lobes. Three switch-like structural distinguish the active/active-like and inactive/inactive-like configurations in protein kinases: unfolding of the activation loop (A-loop) from a partially helical (inactive) to an extended loop (active) structure; the presence (active) and absence (inactive) of a predicted salt bridge between a lysine side chain in strand β3 (K97 in MEK1) and a glutamate in the αC helix (E114 for MEK1); and the conformation of the so-called ‘DFG motif’, which adopts a ‘DFG-in’ conformation in the active state (with D208 of MEK1 projecting towards the ATP binding pocket and F209 facing outwards) versus the ‘DFG-out’ conformation in the inactive state.
Through improvement in gene sequencing technologies, numerous kinase mutations have been identified in patients’ tumors, leading to a burgeoning amount of data. For example, mutations observed in cancer patients number in the millions in the COSMIC database [11]. Mutations in protein kinases are well spread over the different subdomains [12], and may contribute in different ways to the oncogenic potential and/or inhibitor response in a way that demands that each must currently be studied individually. Hence, there is an unmet potential for computational techniques both to classify or cluster the mutations and to provide mechanistic insights into how they alter kinase conformation to alter the function — and how this relates to the oncogenic potential [13] as well as inhibitor response [14]. However, the complexity of the cancer mutational landscape frustrates the process of rational identification of drivers that potentiate an oncogenic/invasive phenotype [15]. Moreover, a large part of the human kinome remains unexplored and uncharacterized [16].
The inhibitors that bind to protein kinases are classified into various types based on their conformational selectivity [17]. Introducing a mutation may alter this selectivity and lead to altered drug sensitivity and thus treatment resistance. In general, the effects of each mutation are unknown unless probed individually.
In this study, we focus on the human MEK1 kinase, which is a vital component of the RAS/MAPK pathway. Mutations in the RAS/MAPK pathway are known to drive many cancers, and also cause several developmental disorders called RASopathies [18,19]. Our goal is to develop a metric to classify or cluster mutations in kinases based on an understanding of the central role of protein dynamics in determining kinase function [20,21], and computational work that has addressed protein dynamics more generally [22–27]. Specifically, we sought to explore molecular mechanisms (and effects of mutations) at atomic resolution in the human MEK1 kinase against the backdrop of experimental work on reporters of enzyme kinetics in the literature [28]. We utilized enhanced sampling simulations and free energy calculations to perform metadynamics simulations for an aggregate 8 μs per system for key mutated systems and found that computationally mapping the different conformational stabilities of each mutated system by delineating free energy landscapes related well to previously experimentally determined transformation potentials of the same mutations expressed in vivo in Drosophila melanogaster.
We conclude that mutations leverage conformational plasticity to progressively stabilize the active-like conformational state while destabilizing the inactive-like state, thereby driving kinase activation. Moreover, by differentially stabilizing different conformational states, the mutations alter residue-level internal molecular correlations by perturbing a hydrogen bonding network. We like the various modes of MEK1 activation to a gear-shifting mechanism in which mutations significantly perturb the correlations between the N-lobe and the C-lobe. At a more granular subdomain resolution, hydrogen bond (HB) distributions are essential contributors to the varied patterns of internal correlation.
Results
Conformational plasticity of MEK1 wild type revealed through free energy landscape from metadynamics simulations
Metadynamics simulations were performed for 8 μs total for wild type (WT) MEK1 (see Figure 1a). The resulting energy landscape represents metastable states in a two-dimensional projection of the two collective variables, with free energy values represented by colors in Figure 1a legend. The convergence of the free energy plot was tracked as outlined in Methods, and the results of the convergence analyses for WT MEK1 are provided in Supplementary Figure S1. On the landscape, certain zones of interest were identified that represent active, inactive, and several intermediate configurations. The zones depicted in Figure 1 as free energy contour maps are numbered and color coded in Supplementary Figure S2; moreover, the characteristics of each zone are elaborated in Supplementary Figures S2(f) and S3.
Figure 1.
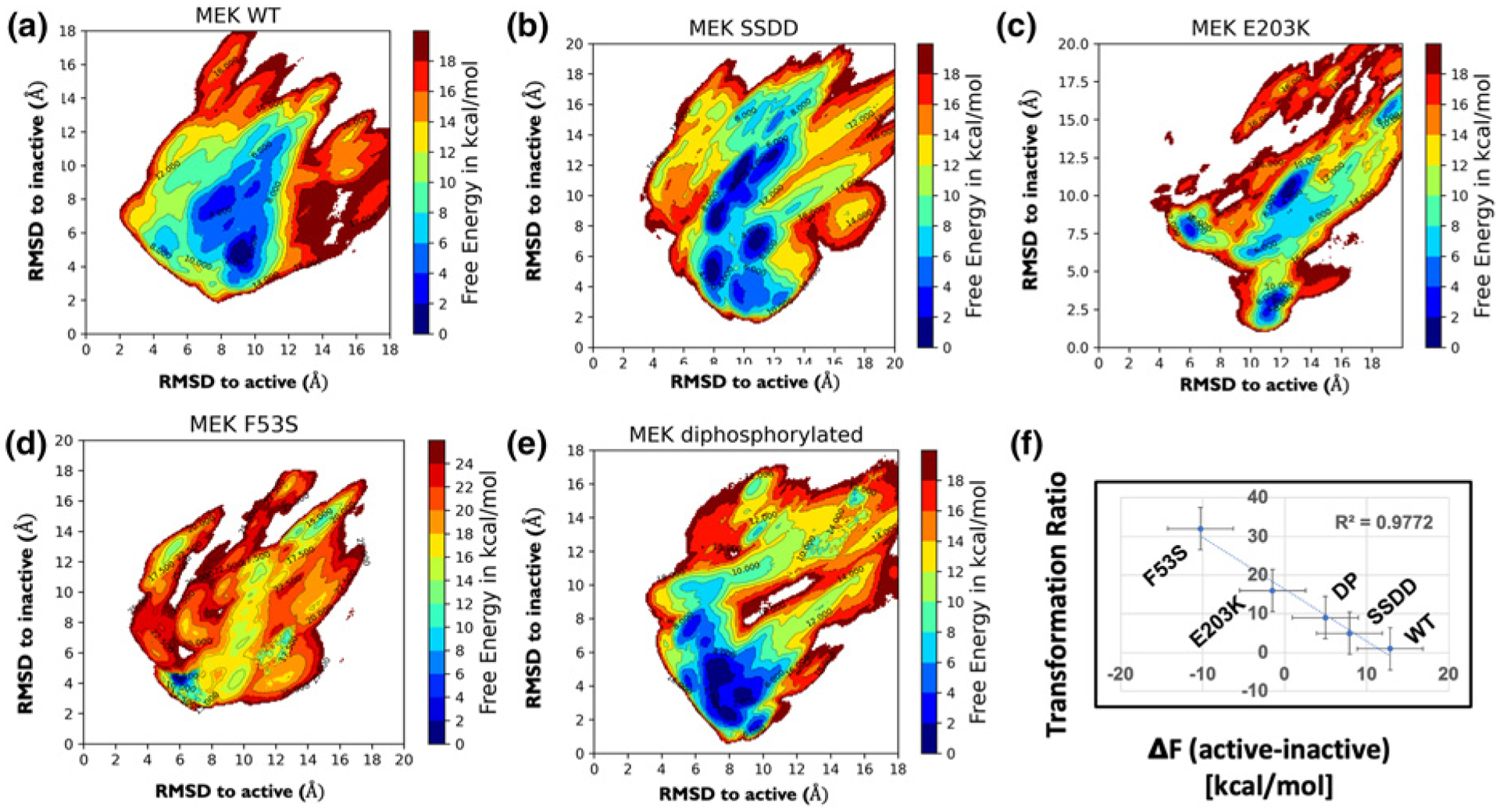
Free energy landscapes of MEK1 WT, SSDD, di-phosphorylated (DP), F53S, and E203K (a–e). A remarkable linear correlation is observed between the change in the free energies of active and inactive states and the transformational ability in a developmental assay (f). The transformation ratio is the ratio of cell proliferation after and before activation of MEK1, and corresponds to cell proliferation propensity in the active relative to inactive MEK1 systems.
The progression of the MEK1 WT system from inactive to active configuration was tracked by delineating the properties of each zone (state) using the three switch variables described earlier, defined based on the unfolding of the A-loop, the K/E salt bridge, and the DFG conformation (see Supplementary Figure S3). The DFG flip is quantified by measuring the dihedral angle formed by the four atoms: C(207 Cα)-C(207 Cβ)-D(208 Cα)-D(208 Cγ). In the active conformation, the D of the DFG motif (D208 for MEK) points towards the ATP binding pocket, and the F of the motif (F209 for MEK) flips outwards. This is the DFG-in conformation (e.g. in zones 3, 5–8 for WT in Supplementary Figure S3). In contrast, in the inactive conformation, the D of the DFG motif points away from the ATP, whereas the F is flipped ‘in’ (the DFG-out conformation (zone 1 for WT in Supplementary Figure S3)). The KE salt bridge is completely broken in all instances in zones 1 and 3 (inactive-like) for WT, while it is formed in the majority of instances (active-like) in zones 2, 7 (Supplementary Figure S3). Similarly, the A-loop is partially helical in zones 1 and 2 in WT while fully unraveled in zone 5, 6 (as quantified by the HB occupancy histogram of the A-loop. We adopt a set of three binary representations of these switch variables according to the convention KE salt bridge = 0/1; DFG flip = 0/1; A-loop conformation = 0/1, where 0 = inactive-like and 1 = active-like. Therefore, [0:0:0] is the most inactive-like conformation, and [1:1:1] is the most active-like conformation. Based on these metrics for the three switch variables (order parameters), zone 1 represents the inactive-like (and also thermodynamically the most stable) state for WT MEK1. Zone 7, by contrast, represents the most active-like state.
Based on the computed free energies, we infer that the WT MEK system disproportionately favors the inactive configuration (see Supplementary Figure S3 and Table 1 for free energies), and the system navigates to the active conformation through a series of conformational transitions involving different changes in the three switch variables (see Supplementary Figure S3). The free energy of the MEK WT configuration increases as the differential transition towards the active configuration occurs. The KE salt bridge is formed between K97 in strand β3 and E114 in the αC helix (defined as 3–4 Å separation). In the case of the WT system, this close approach has a significant free energy cost and is, therefore, inaccessible under normal conditions. We observed two distinct conformational states for the DFG-out state (zones 1, 2, 3), characteristic of inactive MEK. Flipping of the DFG motif to the DFG-in state was observed in zone 4 and the subsequent zones 5–8 stabilized the active DFG-in state. The smallest free energy difference between the DFG-out and DFG-in sustaining states is 1–3 kcal/mol (between zones 3 and 5).
Table 1.
Stability of active conformation in MEK1 variants reported through differences in computed free energies between states: active–inactive; active–stable; inactive–stable
| In order of least active to most active systems (reorder this) | Δ Free energy (kcal/mol) | Conformation most stabilized KE salt bridge: DFG flip: A-loop (Inactive = 0, Active = 1, anything intermediate = 0.5) |
||
|---|---|---|---|---|
| Active-inactive | Active-stable | Inactive-stable | ||
| WT | 12.85 | 12.85 | 0 | [0:0:0] |
| SSDD | 7.91 | 10.58 | 2.67 | [0:0.5:0] |
| DP MEK | 4.94 | 8.15 | 3.21 | [0:0:0.5] |
| F53S | 1.65 | 11.93 | 10.28 | [0.5:0.5:0.5] |
| −10.28 | 0 | 10.28 | (if the most stable zone is kinase active) | |
| E203K | 1.05 | 2.53 | 1.48 | [0.5:0.5:1] |
| −1.48 | 0 | 1.48 | (if the most stable zone is kinase active) | |
The third column lists the status of the [KE salt bridge: DFG flip: A-loop], each showing either Inactive = 0, Active = 1, or intermediate = 0.5 characteristics.
Conformational plasticity analysis of MEK1 variants suggests a gear-shift mechanism of MEK1 hyperactivation
The conformational plasticity of the mutated and post-translationally modified (phosphorylated) systems, SSDD, E203K, F53S, and di-phosphorylated MEK1, were investigated by carrying out an aggregate of 8 μs of metadynamics using a similar approach to that described for the WT MEK1 system. It is evident from the resulting free energy landscapes (Figure 1) that the alterations introduced significantly alter the free energy landscapes when compared with wild type. Both the number of zones and the free energies of the zones are different; see Figure 1 and note that the zones for each system are defined in Supplementary Figure S2.
The progression of the MEK1 variant systems (SSDD, E203K, F53S, and DP) from inactive to active configuration was again tracked by delineating the properties of each zone (state) using the switch variables used to describe WT MEK1 above; compare Supplementary Figures S4–S7 with Supplementary Figure S3. Each variant system displays similar conformational plasticity as seen in the WT system, with the characteristics of each zone (metastable state) delineated by the unfolding of the A-loop, the status of the K/E salt bridge, and the DFG conformation. The categorization of each zone in Supplementary Figures S4–S7 is provided using the [X:Y:Z] convention based on the values of the three switch variables (order parameters). As collectively observed in the conformational landscapes, all systems visit inactive-like zones (states), active-like zones, and intermediate zones. The cube plots in Figure 2 depict the possible distribution of 25 states based on the categorization provided by the switch variables and the populated states in each of the MEK1 systems; here, the numbers correspond to the zone numbers and the indices I, S, and A denote the inactive, stable, and active zones in each system. The cube plots enable a quick comparison of the zones across MEK1 systems.
Figure 2.

The categorization of each of the zones is provided using the [X = KE salt bridge:Y = DFG flip: Z = A-loop helicity] convention based on the values of the three switch variables. Cubes depict the full extent of 25 states possible from the combinations of switch variables and the states populated in each MEK1 system. The numbers in each cube correspond to the zone numbers in the free energy plot and the inactive, stable, and active zones are marked with I, S, A, respectively. The comparison of switch variables of the most stable conformational state/zone across the five MEK1 systems.
Computation of the free energy landscape enables us to ascribe relative stabilities (free energies) to each zone. A comparison of the most stable conformational state/zone across the five MEK1 systems is provided in Figure 2. An intriguing pattern emerges in which the most stable state displays a different transition as we move down the list of systems. For WT, each of the collective variables (K/E bridge, DFG motif and A-loop conformations) is inactive-like. The DFG motif is intermediate/mid for SSDD, F53S and E203K and the A-loop is unfolded or partially unfolded for F53S and E203K. Although all of the systems studied display a broken KE salt bridge, it is evident that the distances between the K and E residues favor lower values of the activating mutants F53S and E203K.
Table 1 summarizes the computed free energy difference between the active-like and the inactive-like conformations of MEK1 in order of decreasing difference between these values. The free energy difference between the inactive conformation and the most stable conformation increases progressively as one progresses down the table with the exception of E203K, and the free energy difference between the active conformation and the most stable conformation decreases (except for F53S). This trend implies a cascading gear-shift mechanism of activation in which each shift in one of the conformational switch variables stabilizes a different stable conformational state that is more activating than the previous. The E203K mutation enhances stability of the active conformation, whereas the F53S mutation decreases the stability of the inactive conformation. The F53S and E203K systems show higher degrees of the shift in stabilities noted above than the phospho-mimetic mutant SSDD and the post-translationally modified DP systems.
Interestingly, the most stable states for F53S and E203K display partially active characteristics, with several switch variables stabilized either in the active state or part way between active and inactive (see last column of Table 1). For this reason, if the stable state is also taken as the active state, we can rank the activity of MEK1 based on the free energy difference between the active and the inactive states for the MEK1 variants: WT < SSDD < DP < E203K < F53S. The corresponding free energy difference between active and stable states decreases in the order WT > SSDD > DP > E203K~F53S. The phospho-mimetic mutation SSDD, which is a proxy to mimic the phosphorylated environment in MEK, is seen to rank closer to the DP MEK1 system as expected. The F53S and E203K mutations are predicted to be the most activating mutations in the list. The free energy difference between active and inactive states decreases for all MEK1 variants compared with the WT, in agreement with experimental literature that reports these variants as activating [28]. Intriguingly the trend in the free energy differences reported here also closely tracks the experimental trend of the transforming ability of these MEK1 variants seen in D. melanogaster experiments performed in vivo [19,28]. Remarkably, there is a near linear correlation between the energy differences calculated here and the previously reported experimental data, as shown in Figure 1f.
Internal correlations at the slow conformational switching timescales may be responsible for the gear-shifting mechanism
Next, we asked whether the individual MEK1 variants differ in conformational plasticity and the nature of internal motions in the KD. By analyzing conformational fluctuations, we can infer a wealth of information beyond free energies to help delineate dynamic aspects of molecular mechanisms. To this end, we computed Boltzmann weighted dynamical correlations (BW-DCs), which serve as extensions to the more traditional covariance analysis and extend the time domain to the experimentally relevant timescales of conformational transitions. Figure 3a–e maps the Boltzmann weighted normalized residue-level correlations for the different MEK1 variants, and the fingerprint of subdomain level motions are discernably different between the individual MEK1 systems. A direct way of quantifying the similarities and differences in residue-level correlations across systems is to perform a hierarchical clustering analysis based on the pairwise squared distance between the Boltzmann weighted correlation matrices, see Figure 3f.
Figure 3.
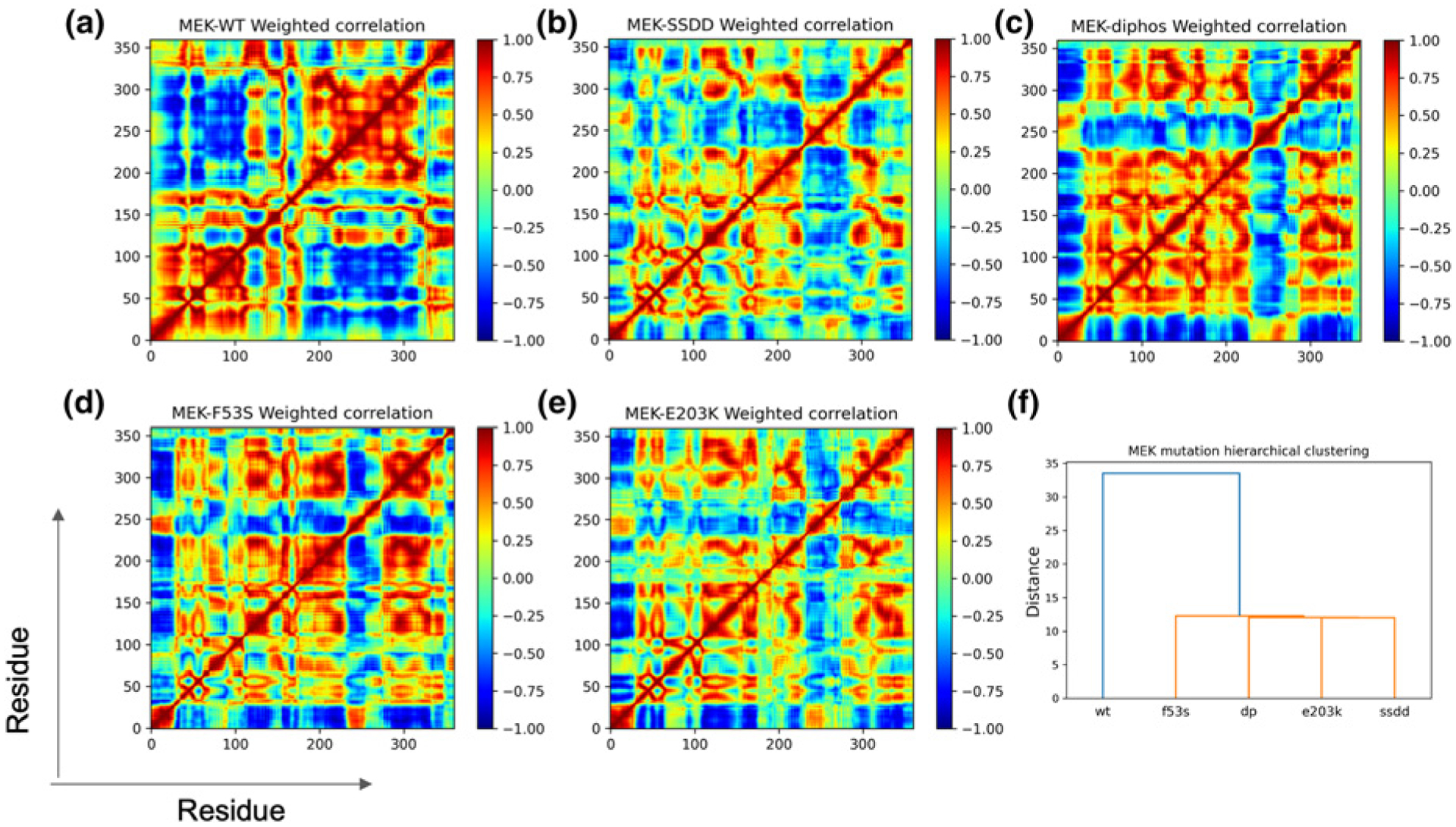
Boltzmann weighted residue-residue dynamical correlation (BW-DC) matrix for MEK1 variants (a–e). Hierarchical cluster using mean-squared distance between correlation matrices as a distance metric (f).
Based on the internal correlations and the computed tree, we can classify the different MEK1 variants into distinct classes, showing that the WT is distinct from the activating MEK1 variants. Moreover, the individual activated MEK1 variants differ substantially from one another in the patterns of residue-level correlations. The most striking features in WT are co-ordinated strongly positive correlations within the N-lobe (residues 1–144) and the C-lobe (residues 149–367) plus the substantial anti-correlation between the C-lobe and the N-lobe [9]. These features are clearly compromised in all of the MEK1 variants. In the DP and F53S MEK1 systems, the sub-block of N-lobe correlations shift and extend to part of the C-lobe, including the C-lobe elements αD (149–159), αE (162–185), the catalytic loop (186–194), β7 (196–198), β8 (204–206), and the A-loop (208–233). The sub-block of C-lobe correlations also shrinks to include just αG (309–319), αH (331–342), and αI (351–367) — even though the correlations themselves appear to maintain correlation intensity. The SSDD and E203K systems show fingerprints similar to those of DP and F53S MEK1, but with the strengths of the correlation intensities diminished. One notable differentiator between the highly activating variants (DP, E203K, F53S) and the weakly (or non) activating variants (SSDD and WT) is an enhanced correlation between the Nα subdomain and other subdomains in the highly activated variants that are absent from the weakly activating ones. This feature highlights the importance of Nα and its interactions in the activation mechanism, a property that has been confirmed by previous structural studies in the context of some activating MEK1 mutants such as C121S [29].
To translate the patterns of the Boltzmann weighted correlation matrices of Figure 3 into more readily interpretable observations, we used coarse-grained correlation matrices to record averaged correlations between secondary structure elements and kinase subdomains as a 18 × 18 matrix (Figure 4); for reference, the 18 elements are described in Table 2. Among the lower sub-block (Nα-β5), where the patterns of correlations are most diverse across the MEK1 systems, we find that the regions β1, P-loop (PL), β2, β3, β4, are strongly correlated in both the WT and mutated systems. However, in comparison with WT, the αC helix correlations are lost in the mutant systems, suggesting a relatively free motion and a lower energetic barrier for the αC helix to move ‘in’ and ‘out’. Overall several other subdomain correlations are also significantly weaker in magnitude (and opposite in sign) in the mutated variants than in WT (e.g. αG-β4, β8-β2), consistent with the significant stabilization (lowering of the free energies) of the active-like states in the mutants. The comparison of the coarse-grained correlations between subdomains is easily visualized in the chord plots in Figure 4, which show connections between the elements when the average correlation/anti-correlation exceeds a magnitude of 0.7. The variation in the subdomain-level average correlations depicted in the chord plots is akin to differences in the engagement of gears and crankshafts that can be thought of as driving activation of the various MEK1 systems. Based on the chord plots, we conclude that compared with WT, the SSDD variant weakens the magnitudes of positive correlations within the N- and C-lobes as well as negative correlations between the lobes. The DP system instead strengthens positive correlations across the KD and diminishes negative correlations. The F53S and E203K variants both display weakened correlations overall compared with WT and DP, but show different patterns. The F53S variant shows strengthened correlations between the β-strands, whereas the E203K variant enhances the correlations involving the α helices. These differences present a striking correlation with the different modes of stabilization, namely E203K stabilizes the active-like and inactive-like conformational states, whereas the F53S mutation primarily destabilizes the inactive-like conformational state. The enhanced correlations between Nα and other subdomains that are seen only in highly activating variants (DP, E203K, F53S) are also clearly evident from the chord plots in Figure 4.
Figure 4.
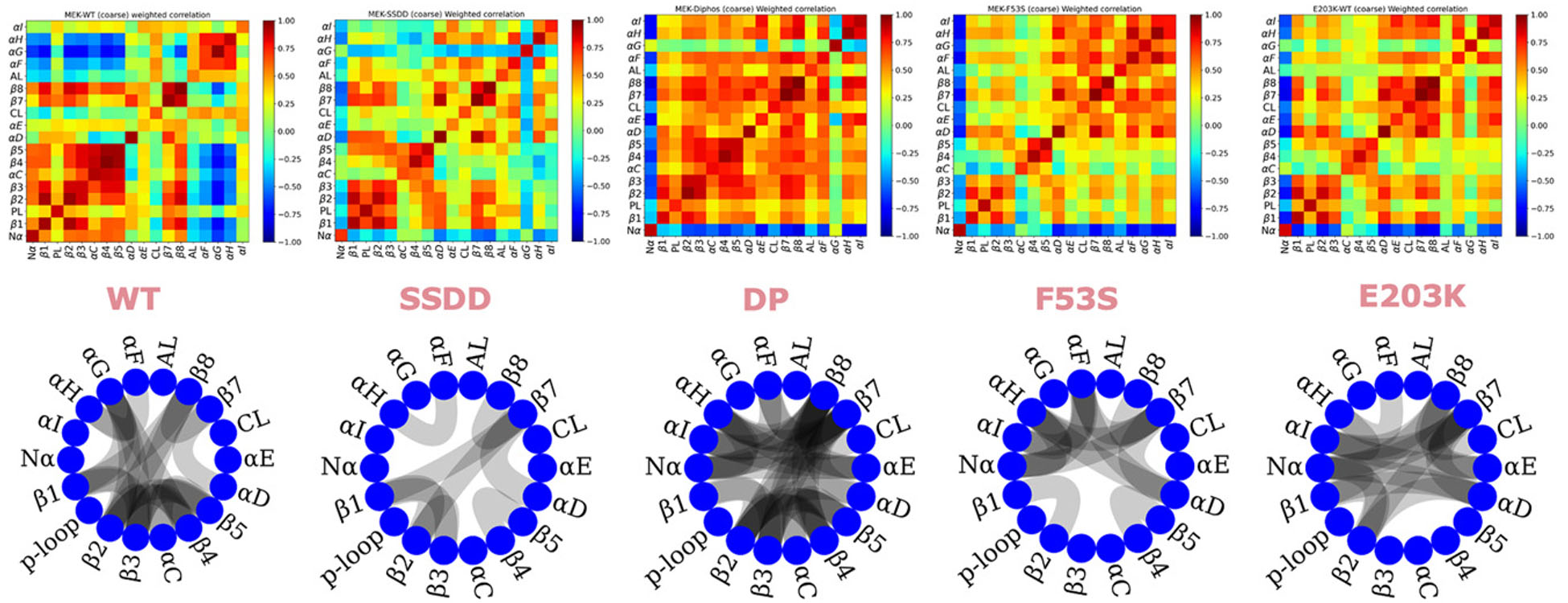
18 × 18 Coarse-grained correlation matrices as well as internal correlations of kinase subdomains in MEK1 from coarse-grained BW-DC matrices (top) depicted as a chord plot generated with a threshold of 0.7 (bottom).
Table 2.
Definitions of subdomains in MEK1
| CG subdomain | Sequence | CG subdomain | Sequence |
|---|---|---|---|
| 1: N terminal helix (Nα) | 43–60 | 10: αE | 162–185 |
| 2: β1 | 68–74 | 11: Catalytic loop | 186–194 |
| 3: P-loop | 75–81 | 12: β7 | 196–198 |
| 4: β2 | 82–87 | 13: β8 | 204–206 |
| 5: β3 | 92–100 | 14: A-loop | 208–233 |
| 6: αC | 107–125 | 15: αF | 242–259 |
| 7: β4 | 129–134 | 16: αG | 309–319 |
| 8: β5 | 138–144 | 17: αH | 331 −342 |
| 9: αD | 149–159 | 18: αI | 351–367 |
Implications for solvent accessibility, hydrogen bonding, and hydrogen-deuterium exchange propensity
Altered internal correlations will necessarily also change HB occupancy and solvent accessible surface area, which should, therefore, differ across the MEK1 variants. HB networks and solvent accessibility are two of the most prominent molecular-level properties impacted by internal protein motion, and can connect the dynamics observed in biomolecular simulations with experimental observations of hydrogen–deuterium exchange (HDX), for example. Although it is traditionally routine to analyze molecular dynamics (MD) trajectories to compute these two properties, the timescale accessed in the simulations usually severely limits the value of the analysis. Since our study provided access to protein configurations and the associated free energy landscapes, we are able to compute Boltzmann weighted hydrogen bond (BW-HB) occupancies and Boltzmann weighted solvent accessibilities (BW-SASA), and have done so for three MEK1 systems (WT, the moderately activating SSDD, and the hyperactivating E203K variant) as shown in Supplementary Figure S8.
As expected, the A-loop in WT MEK1 (which is partially helical) has higher HB occupancy, and this is partly retained in the SSDD system. However, the E203K system has significantly lower HB occupancy, consistent with the extended (active-like) conformation of the A-loop being the more stable state. This trend for the A-loop is also evident by examining the HB occupancy of the stable zone in Figure 2 across the different MEK1 systems.
There is elevated solvent accessibility for the residues of the A-loop in the MEK1 WT system when compared with the two variants. The HB occupancy of the αC helix in the WT system is higher than that of SSDD and E203K, reflecting the in/out motion of the αC helix that accounts for some of the conformational plasticity. We also observe that the P-loop solvent accessibility is significantly higher for E203K than for WT or SSDD. In comparison, the catalytic loop has lower HB occupancy and solvent accessibility across all systems. The HB occupancy and solvent accessibility for β-strand regions do not vary significantly across the systems. The above observations suggest that although E203K and SSDD are both activating mutations, they may utilize different activation modes. Namely, E203K shows a reduced HB network and altered solvent accessibility around the A-loop, whereas SSDD utilizes differences in solvent accessibility of a few crucial residues of the A-loop.
Since our results integrate conformational plasticity, dynamics, and function (activation), we sought to compare the inferences of our computational results with experimentally determined HDX. The rate of exchange of backbone amide hydrogens with solvent occurs on two timescales: one in which the rate of unfolding/folding is limiting and one limited by the rate of intrinsic hydrogen exchange itself. If the rate of intrinsic hydrogen exchange is greater than the rate of unfolding/folding, the kinetics are classified as EX1. Conversely, EX2 kinetics apply if the rate of folding/unfolding is greater than the rate of hydrogen exchange. The mass spectrometry-based HDX experiments reported for MEK [30] described specific regions to have mixed EX1/EX2 kinetics while the rest were described to follow EX2 kinetics.
We reasoned that a proxy for the rate of intrinsic hydrogen exchange available from our computations is ; i.e. exchange rate should also depend on the HB occupancy, i.e. the higher the HB occupancy (protection), the lower the exchange rate. Analogously, a proxy for the rate of local folding/unfolding is the associated fluctuations in BW-SASA, which accompanies the conformational fluctuations; more specifically, we computed the coefficient of variation (or the ratio of standard deviation to the mean:) in the BW-SASA. Our reasoning for these proxies is premised on the BW-HB and BW-SASA sufficiently capturing long-timescale conformational fluctuations, which traditional MD simulations typically run for microseconds do not capture. To distinguish between EX1 and EX2, we compute the ratio as a proxy for the ratio of the rate of folding/unfolding to that of intrinsic exchange. We depict the ratio of the coefficient of variation in BW-SASA and for MEK1 WT and two of the MEK1 variants (SSDD and E203K) in Supplementary Figure S8. If this computed ratio is high, we predict that the exchange will be in EX2 mode, where the rate of conformational fluctuations exceeds that of the backbone hydrogen exchange. In contrast, a low value of the ratio is indicative of a mixed EX1/EX2 mode of exchange kinetics (see Supplementary Figure S8c,f,i) in which the rate of conformational changes is lower than that of exchange. For WT, for which HDX experimental data are available, an average value of the ratio we are calculating over the residues spanned by the peptides defined in the HDX experiments [30] is plotted as a bar at that value. It is evident that the peptides colored in red have a lower ratio (mixed EX1/EX2), and many of the green peptides show a higher ratio (EX2), which is correctly predicted. We note that our method does incorrectly resolve a few peptides colored in green (experimentally classified as EX2) but show a low computed ratio: this could be attributed to unfolding coupled to solvent fluctuations, which are not currently sampled in our calculations and will be the subject of a future study. While the comparisons between experiments and simulations are made for MEK1 WT, we have computed the same ratio for SSDD and E203K variants (see Supplementary Figure S8), for which we do not have experimental HDX data. Nevertheless, we note that the peptides around residue number 200 (marked by a black circle), which undergo a significant change in the ratio, also correspond to the location of the SSDD mutations, S218D, and S222D; intriguingly, we observe a similar trend for E203K, which is also close to this location.
Discussion and conclusion
Allostery and multiple states cause a combinatorically large set of possibilities for drug and ATP-bound states, and different inhibitors can sensitize different states based on context. It is well appreciated that multiple conformational states mediate the inactive-to-active transitions in kinases [7], shedding light on the conformational plasticity of these enzymes. Here we show that numerous states further exemplify the complexity even for the monomer kinase in its activation, and that individual mutations differentially stabilize these states.
We find that the MEK1 variants display widely differing distributions of metastable states with different relative thermodynamic stabilities. By comparing the relative stabilities of the active-like and inactive-like states in reference to the most stable conformational state, we conclude that activating mutations leverage the conformational plasticity of the KD, preferring intermediate conformations while either destabilizing the inactive-like conformational state or stabilizing the active-conformational state to promote activation. We observed a progressive and step-wise activation mode for MEK1 in our simulations, reminiscent of a gear-shifting mechanism, for activation both by post-translational modification (DP and SSDD) and by mutation (F53S and E203K). WT MEK1 favors stabilization of the inactive kinase configuration, E203K favors the active state the most, and our computed free energy differences correctly rank the MEK1 variant systems according to their transformational ability in experimental studies. Most kinases are known to have allosteric mode for activation and the role of N and C terminal in such positive and negative regulation are well known. Our results focus on just the KD in the absence of the additional allosteric interactions from subdomains outside the kinase, and the gear-shifting mechanism points to a core machinery that regulates conformational plasticity.
We report new analysis methodologies to map the free energy landscape of the conformational plasticity on to long-timescale protein dynamical correlation in MEK1 kinase variants by connecting the underlying conformational plasticity that emerges from the metastable states or zones of the free energy landscape with internal residue-level Boltzmann weighted molecular correlations. We conclude that mutations leverage conformational plasticity to alter residue-level internal molecular correlations, delineating the various modes of MEK1 activation involved in the gear-shifting mechanism. The mutations significantly perturb correlations between the N-lobe and the C-lobe at the full kinase system resolution. At a more granular subdomain resolution, HB distributions are essential contributors to the altered patterns of internal correlation. The tree based on hierarchical clustering projects these correlation differences into one dimension based on the squared-difference metric. This clustering places the WT kinase in a distinct class from the activating MEK1 variants. Based on the ensemble weighted dynamical correlations, we also observed that the activating mutations disrupt correlations between the C- and N- lobes, and the two most activating mutations (E203K and F53S) lead to different patterns of subdomain level correlations, with the former coordinating the α helices and the latter coordinating the β strands. Intriguingly the three most activating variants, DP, E023K, and F53S each show enhanced correlations between the Nα subdomain and other subdomains, a feature that is absent from WT and the mildly activating SSDD variant.
We also observe that the activating mutations increase the flexibility of the A-loop, P-loop, as recorded by the increase in root-mean-squared deviations (RMSDs) associated with these regions (see Supplementary Figure S9a). This pattern of altered flexibility has been reported in other kinase systems, where it was also shown to be correlated with an altered HB network [13]. We show in Figure 2 and Supplementary Figures S3–S7 that the HB network surrounding the A-loop is perturbed significantly across the zones and across the systems. Hence, we were curious if we could infer this from standard unbiased MD simulations (see Supplementary Methods). Indeed, we observe this to be the case for MEK1, where activating mutations disrupt the HB network between the αC helix and the A-loop of MEK1 (Supplementary Figure S9b); see also Methods for how the persistence in HB is computed. For comparison, we note that the neutral (non-activating) mutation, E203Q, does not conform to this pattern. Intriguingly, we further investigated whether this trend holds for 21 known activating mutations of MEK1 as reported in Supplementary Figure S9c (all except P124S, C121S, E203V, A257V, L235H), there was a persistent disruption of one or more HBs in the inactive state.
We note that this signature of destabilizing the inactive-like conformation by perturbing the HB network in the αC helix and the A-loop is shared across other kinase systems and appears to account for the mechanism in 60% of kinase mutations observed in ALK, BRAF, HER2, and EGFR in cancers [12,13]. The exceptions noted above for MEK1 could represent activation through other mechanisms or could represent a false negative (likely due to insufficient sampling of HB statistics in 1 μs MD simulations). In addition, we note that the linear trend between enzyme activity and cell transformation index has also been observed in ALK-driven cancers [13], consistent with our similar findings for MEK1. In furthering this observation of the linear correlation in MEK1-driven transformation we conclude that the activating MEK1 variants utilize conformational plasticity to stabilize the active-like conformation through a perturbation of the HB network, which explains why the persistence of HB is a good indicator of kinase activation, especially given the important rearrangement surrounding the 310helix in the A-loop during activation.
A direct comparison between the conformational plasticity revealed by our computations and experiment could be made if protection factors per residue were available from HDX experiments. Nevertheless, our approach in utilizing the Boltzmann weighted HB and SASA obtained from the free energy landscape paves a concrete path forward to compare conformational fluctuations at long-time scales, thereby encapsulating the conformational plasticity that is not captured through conventional MD. This ensemble weighting approach enables the classification of MEK1 variants based on long-timescale dynamical fluctuations informed by molecular mechanisms, including allosteric mechanisms that are at play. Specifically, utilizing data from the free energy landscape obtained through enhanced sampling, we have defined and computed a new metric based on Boltzmann weighted averaging of solvent accessibility and hydrogen bonding and the associated fluctuations to correlate to HDX kinetics regimes in experiments.
Mutations cause aberration and induce drug sensitivity and resistance through altered ATP binding affinity, drug binding affinity, and kinase activation [12]. We note that our attempts at docking ATP to multiple zones of the WT, SSDD, and E203K systems revealed that the zones do not for the most part preferentially exclude ATP binding and can accommodate the favorable interactions with ATP in several (but not all) of the zones; see details of the docking protocol in Methods and the summary of data in Supplementary Figure S10 and Table S1. Notably, several of the ATP-bound conformations also produce reactant competent geometries of the active site upon substrate binding, see Supplementary Figure S11 and Table S2. This insight can be utilized in allosteric modulation, drug design, and understanding the molecular mechanisms of drug efficacy in cancer and Rasopathies [31]. Indeed, in a recent report, Khan et Al. solved several crystal structures of MEK bound to various MEK inhibitors, observing unexpected modes of drug binding directly attributed to the conformational plasticity of the kinase. They showed that these new binding modes have direct implications for the design of next-generation drugs that target the RAS pathway [32]. It would also be interesting to extend our work to include MEK1 in complex with BRAF and KSR to investigate the activation mechanisms in the context of MEK1 heterodimers.
MAP kinase-1 (MEK1) phosphorylates and activates the MAP kinases, ERK1 and ERK2, in the MAP kinase cascade, a signaling pathway that regulates mammalian cell growth and differentiation. Several inhibitors of MEK1 have been identified as therapeutics for cancer or common Mendelian diseases referred to as RASopathies [33,34]. The high frequency of gain-of -function mutations in the RAS–MAPK pathway across cancers has prompted the development of inhibitors. However, most drugs have been limited due to poor efficacy, toxicity, or resistance [35]. The escape mechanisms to current MAPK inhibitors, which often occur through re-activation of the pathway [36–38], reveal clear limitations in currently available drugs. They also suggest that more effective strategies to target the MAPK cascade may still achieve therapeutic responses in a broader range of cancer patients. Mutations in MEK1/2 have been described as a resistance mechanism to BRAF/MEK inhibitor treatment. Therefore, the main contribution of the current work is defining the molecular basis of conversion of this kinase from its inactive to its active state, connecting structure, dynamics, and function through delineating the energy landscape and conformational plasticity essential in understanding the regulation of MEK1.
Materials and methods
Structural modeling of MEK1 variants
All structures and homology models were constructed using MODELLER [39]. The inactive WT MEK KD structure (residues 34–393) was prepared by filling in missing residues in the crystal structure of MEK1 in an inactive conformation (PDB: 3EQD) [40]. The homology model of active MEK KD was generated with MODELLER, using the active human MST3 kinase KD structure (PDB: 3A7F) [41] as the primary template. The human MST3 kinase shows the highest sequence similarity to MEK1 among the serine threonine kinases for which a canonical active structure is available in the PDB. The MEK1 variant structures were generated by using MODELLER to introduce the relevant point mutations and CHARMM-GUI [42] to phosphorylate residues to mimic MEK1 regulation. The variants included the phosphor-mimetic SSDD double mutant, E203K and F53S single mutants, and the DP MEK1 system. We utilized modeller instead of Alphafold2 because the structure of human MEK1 from Alphafold2 results in a model for the inactive conformation for which there is already a crystal structure. All structures were initially modeled without a bound substrate; however, in in further analysis, we investigated structures bound to ATP and substrate as noted in sections below.
Molecular dynamics
Simulations were run using GROMACS 2018 [43] with the Charmm27 force field [44] using TIP3P [45] explicit solvent in a periodic water box with at least 12 Å between the protein and box edge. An ionic concentration corresponding to 0.15 M NaCl was used, and the final charge of the whole system was zero. Energy minimization was carried out using the steepest descent. The system was equilibrated first at constant volume and temperature using the Berendsen thermostat [46] before ‘production’ MD simulations were carried out at constant pressure using the Parrinello–Rahman barostat [47]. Equilibration and production MD runs were carried out at a constant temperature with the linear center of mass motion removal. LINCS [48] was used to constrain all bonds during equilibration, and HBs were constrained during production MD. A time-step of 2 fs was used in the integration. The particle mesh Ewald method [49] was used to account for long-range electrostatics interactions. Unbiased simulations were run for 1 μs before they were subjected to metadynamics. All the input scripts are available on GitHub [50].
Metadynamics and collective variables
GROMACS 2018.6 was patched to PLUMED 2.3.5 [51] to enable enhanced sampling to be performed using metadynamics. The well-tempered metadynamics or WTMD [52] method was adopted to sample the large-scale configurational space between the inactive and the active configurations of MEK. The collective variables are geometry-based, i.e. RMSD from the active structure and RMSD from the inactive structure. In computing the RMSD, only the αC helix and the A-loop residues are considered; i.e. the structures are aligned taking all residues except the αC helix and the A-loop into consideration, and the RMSD is then calculated. These collective variables are effective in capturing all the three transitional switches mentioned above, i.e. β3K/αC E salt bridge (intact in active state, absent from inactive state); DFG (in — active, out — inactive); and the A-loop (extended loop in active state, partially helical in inactive state), as these are all connected to the motion in the αC helix and the A-loop. We note that while we have relied on HB analysis for determining the partial folding of the A-loop, a comparison to the secondary structure classification database using the DSSPs (define secondary structure of proteins) analysis provided similar conclusions, as noted in Supplementary Figure S12. We also note that other choices of switch variables including the C- and R-spine could be used, but are already considered within the variables used in this work as discussed in the literature [53,54].
Metadynamics involves adding an external history-dependent Gaussian potential for the system to be able to cross the barrier given by
| (1) |
The metadynamics are run in parallel using 10 walkers, i.e. 10 parallel simulations that sample the configurational space simultaneously and are collectively informed about the deposited Gaussian potentials on the CV grid space through the file sharing system of PLUMED. The well-tempered metadynamics uses decaying Gaussian height to ensure smoother convergence.
| (2) |
In the large time limit, the free energy for the CV space is given by
| (3) |
In the PLUMED script, we set the energy in kcal/mol and length in Å. The parameters used in this study to perform WTMD are as follows: bias factor , height = 0.6, and pace = 500. The PLUMED script is available on GitHub [50].
Since we carry out the metadynamics under constant volume, we compute the Helmholtz free energy . Convergence of the free energy landscape in metadynamics was ensured by computing the free energies of specific states (zones) and requiring that these zones of interest in the free energy landscape of each system converged to within 1 kcal/mol over a 1 μs extension of the metadynamics simulations. The evolution of the free energy of the zones or states was tracked according to:
| (4) |
Here, is the free energy of the state, is the free energy value at that collective variable co-ordinates , obtained directly from the free energy landscape.
Metadynamics simulations were performed on a Linux-based high-performance computing cluster called ‘rusty’ at the Flatiron Institute, NY, requiring a total of 710.6k CPU hours.
Choice of collective variables
The basic fundamental function of any enhanced sampling method (ESM) is to address the bottleneck of MD simulations regarding the high-energy barriers that hinder the system from accessing the configurations in multiple minima, thereby making it a rare event [55]. The procedure is to accelerate thermodynamics calculations by modifying the potential energy surface by adding a bias potential to the Hamiltonian of the system and thereby reducing the energy barrier for the transition. These bias potentials may or may not be given certain predefined essential co-ordinates or vectors before depositing them on the high-dimensional complex landscape of the system, known as collective variables. ESMs are, therefore, broadly classified into two categories based on their working strategy: collective variable-based methods (CVMs) and collective variable-free methods (CVFMs). Examples of CVM methods include Umbrella Sampling [56] implemented along with the weighted histogram analysis method (WHAM) [57], Metadynamics [58], and Temperature Accelerated Molecular Dynamics [59]. Examples of CVFMs include parallel tempering [60] or replica exchange MD [61], and BOLAS [62]. Recently, the Parrinello group introduced a new class of collective variable-based ESMs called ‘On the fly Probability Enhanced Sampling’ (OPES) simulation, that work towards unifying the CVM and CVFM ESMs [63]. The OPES method aims to modify the physical distribution of CVs by iteratively adding the bias potentials to reach the target probability distribution in configuration space that is explicitly or implicitly sampled by any CV or CV-free ESMs. The OPES method has been used to sample any expanded ensembles including multicanonical [63] and multithermal-multibaric ensemble [64], which are usually sampled via CVM approaches such as replica exchange.
Machine-learning (ML) enabled collective variable identification and ML-enabled enhanced sampling is an emerging area to explore free energy landscapes, some of which are described in a perspective article summarizing ML-based ideas that are solving both of these limitations, with a focus on their key theoretical underpinnings and remaining challenges [65].
In the current work, we chose to pursue a CVM route, using prescribed CVs based on RMSDs and the method of metadynamics primarily because our end anchor states (inactive and active confirmations) are well defined and the CVs chosen to meet the important criteria of both distinctly separating the two anchor states and correctly capturing the experimentally recognized transitions in the various conserved subdomains. Moreover, since our focus is on the thermodynamic stabilities of metastable states rather than transition pathways, our approach enables a straightforward quantification of the free energy landscape that is experimentally tractable, as we show later by correlating our results with HDX experiments. We note that we do not make any claims of transition pathways [66,67] or transition states in this study as they are beyond the scope of our objectives — although these are nevertheless worth exploring separately in future studies.
Data analysis
Trajectory analyses were performed, unless otherwise noted, on the whole trajectory using the MDAnalysis package [68] in Python. In aggregate, 8 μs simulations for five systems totaling 40 μs of enhanced sampling simulations generated an extensive dataset for analyses, and we implemented parallel computing in Python using the package mpi4py [69] to obtain Boltzmann weighted average quantities such as the BW-DC matrices, solvent accessible surface area (BW-SASA), and hydrogen bond (BW-HB) occupancies. Python scripts that implement these analyses using parallel Python libraries are available on GitHub [50].
BW-DC
The normalized covariance matrix gives the traditional residue-level dynamical correlation. We propose a modified BW-DC given by
| (5) |
here, , where is co-ordinate of residue in frame ; and is the mean location of residue over total frames. The computation of is also Boltzmann weighted, wherein:
| (6) |
Here, is the total number of frames, and is the free energy mapped to the configuration in frame . Each conformation visited in the metadynamics is mapped to a probability given by .
Hierarchical clustering
Under the assumption of equal weight for all residues, we compute the element-wise square difference between the matrices of the BW-DC of all pairs of the MEK1 systems to perform hierarchical clustering of the mutants.
Coarse-grained BW-DC
To obtain correlations at the subdomains or secondary structure level and ascribe a broad mechanism, we coarse-grained the residue-level BW-DC matrix to their secondary structure [70] as follows. The following residue number ranges were assigned to each of the 18 subdomains (see Table 2). The NxN BW-DC matrix was reduced to a 18 × 18 coarse-grained matrix by averaging the correlation coefficients in each sub-block.
BW-SASA
Boltzmann weighted solvent accessible surface area is computed as
| (7) |
Here, is the solvent accessible surface area of residue in frame is the total number of frames in the trajectory; is the free energy of the frame of the trajectory; and is the Boltzmann weighted SASA of residue . The variance of BW-SASA is computed as
| (8) |
| (9) |
BW-HB
The BW-HB is computed as
| (10) |
Here, is Boltzmann weighted H-bond occupancy of residue .
Chord plots
The chord plots (graphs with nodes and edges) were derived from the coarse-grained 18 by 18 matrices and made using the Python package nxviz [71], where the nodes represent the secondary structure domain, and the edges represent the correlation value above a chosen cutoff value of 0.7.
Analysis of persistence of hydrogen bonding occupancy
Step 1. For hydrogen bonding (HB) occupancy of WT and mutated MEK1, we first calculated the average number of HBs formed by each residue from both the αC helix domain (residues 105–123) and A-loop (residues 206–229) from the last 50 ns of MD simulation trajectories using MDAnalysis version 0.20.1 [72]; note that the HB is considered to be formed if: (1). The distance between hydrogen acceptor and hydrogen donor is less than 0.32 nm and (2). The donor-hydrogen-acceptor angle is larger than 150°. In addition, the is excluded if a salt bridge is formed between the -donor and -acceptor. Note that each amino acid is considered to have a maximum of three possible HBs: a backbone donor, a backbone acceptor, and the side chain (if possible). Some residues such as Arg or Asp can have more than one side chain HBs in a single frame, in which case those excess side chain HBs are excluded.
Step 2. Calculate the HB occupancy difference between the mutant and WT MEK1 protein as for each residue within the two domains. If the condition is satisfied, will be added to the accumulated occupancy, as is plotted in Supplementary Figure S9c.
Molecular docking
In a previous study it was reported that specific inhibitors can bind their target proteins in multiple conformational states of the protein [73]. Schrodinger’s (v. 2019.4) Glide software [74,75] was used to perform induced fit docking of ATP to MEK structures extracted from the zones of the metadynamics simulations [76,77]. First, the ATP ligand was prepared by adding missing atoms, assigning charges, and optimizing the geometry using the ‘Ligand Preparation Wizard’ tool. Next, the MEK kinase structure was prepared by adding missing atoms, assigning charges, optimizing the hydrogen bonding network, and performing restrained minimization using the ‘Protein Preparation Wizard’ tool. The kinase structure was then aligned to a known crystal structure of MEK (PDB: 3EQD) [40], which has water molecules, ATP-γS, and Mg2+ ions in the active site. The water molecules, Mg2+ ions, and ATP-γS are now effectively aligned to the binding site of the KD structure. The Mg2+ ions and water molecules are important as they co-ordinate key interactions between ATP and the MEK binding site residues. The centroid of ATP-γS is used as the center of the box for the docking protocol, as this provides the best estimate of the centroid of the binding site. Next, the Standard Induced Fit Docking protocol was followed, using the OPLS3e force field [78] and Standard Precision (all other settings are default), to dock ATP to the MEK kinase structure. The poses output by the docking algorithm are scored using the GlideScore function, which calculates a predicted binding affinity. The top-ranked poses are further filtered by assessing for biological validity. A pose is considered reaction competent if it meets the following criteria: (1). The DFG motif of MEK is in the ‘in’ conformation (D in) and the carboxyl group of MEK is positioned such that it is close to coordinating Mg2+; (2). The adenine region of ATP forms at least two HBs with residues in the hydrophobic pocket of MEK and the ribose group of ATP is positioned properly away from the hydrophobic region; and (3). The Mg2+ in the active site co-ordinates with the oxygens from two of the phosphate groups of ATP. All the input scripts are available on GitHub [50].
Peptide substrate was docked to reaction competent MEK1 + ATP + Mg2+ complexes to model the transition states of target residue phosphorylation. The peptide substrate was modeled from the sequence 181FLTEYVA187 in the A-loop of ERK1 (PDB: 5UMO). The rigid-receptor Glide docking protocol was used for peptide docking with the box center defined in the proximity of the γ-phosphate and other settings kept as default. Resulting peptide poses were assessed based on biological validity. Peptide poses were marked valid if the hydroxyl group on either the peptide tyrosine or threonine was oriented towards the γ-phosphate by following the metrics described in a previous study [79].
Supplementary Material
Significance statement.
Every cancer patient will have their genome sequenced; already true for many cancers. What does an oncologist do with this information, and how can they personalize therapy based on the knowledge of mutations? Classifying driver mutations from passengers in kinases, among the most common drug targets, is a grand challenge best addressed through interpretable prediction algorithms. Moreover, we need to know the molecular mechanisms associated with disease-driving mutants to design rational therapies or overcome resistance. Computational tools that are accurate enough for reliable predictions and fast enough to be deployed in real-time can significantly aid in clinical decision making and optimization of therapy, thus advancing the goal of personalized medicine.
Acknowledgements
We are thankful for the helpful discussions with Stanislav Shvartsman, Mark Lemmon, Boris Kholodenko, Oleksii Rukhlenko, William Hlavacek, and Marcus Bosenburg. Computational resources are made partly available through the high-performance cluster ‘rusty’ of the Flatiron Institute, NY, and by XSEDE (Access) under grant MCB200101.
Funding
We also acknowledge support in part from NIH grants CA227550, CA244660, and CA250044.
Abbreviations
- BW-DC
Boltzmann weighted dynamical correlation
- BW-HB
Boltzmann weighted hydrogen bond
- BW-SASA
Boltzmann weighted solvent accessible surface area
- CVFMs
collective variable-free methods
- CVMs
collective variable-based methods
- DP
di-phosphorylated
- ESM
enhanced sampling method
- HB
hydrogen bond
- HDX
hydrogen-deuterium exchange
- KD
kinase domain
- MD
molecular dynamics
- MEK1
MAP kinase-1
- ML
machine-learning
- OPES
on-the-fly probability enhanced sampling method
- RMSD
root-mean-squared deviation
- WHAM
weighted histogram analysis method
Footnotes
Competing Interests
The authors declare that there are no competing interests associated with the manuscript.
CRediT Author Contribution
Ravi Radhakrishnan: Conceptualization, Resources, Formal analysis, Supervision, Funding acquisition, Validation, Investigation, Visualization, Methodology, Writing — original draft, Project administration, Writing — review and editing. Keshav Patil: Conceptualization, Formal analysis, Validation, Investigation, Visualization, Methodology, Writing — original draft, Writing — review and editing. Yiming Wang: Investigation, Writing — review and editing. Zhangtao Chen: Investigation, Writing — review and editing. Krishna Suresh: Investigation, Visualization, Writing — review and editing.
Ethics Statement
This work did not involve any human subjects or animal studies research.
Data Availability
All the input scripts and key structure files are available on GitHub [50]. Supplementary Figures S1, S12 and Tables S1, S2 are provided with this manuscript. Upon submission, authors agree to make any additional materials, data, code, and associated protocols available upon request.
References
- 1.Ryu H, Chung M, Dobrzyński M, Fey D, Blum Y, Lee S et al. (2015) Frequency modulation of ERK activation dynamics rewires cell fate. Mol. Syst. Biol 11, 838 10.15252/msb.20156458 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Frum T and Ralston A (2015) Cell signaling and transcription factors regulating cell fate during formation of the mouse blastocyst. Trends Genet. 31, 402–410 10.1016/j.tig.2015.04.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Perrimon N, Pitsouli C and Shilo B-Z (2012) Signaling mechanisms controlling cell fate and embryonic patterning. Cold Spring Harb. Perspect. Biol 4, a005975 10.1101/cshperspect.a005975 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ardito F, Giuliani M, Perrone D, Troiano G and Lo Muzio L (2017) The crucial role of protein phosphorylation in cell signaling and its use as targeted therapy (Review). Int. J. Mol. Med 40, 271–280 10.3892/ijmm.2017.3036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lemmon MA and Schlessinger J (2010) Cell signaling by receptor tyrosine kinases. Cell 141, 1117–1134 10.1016/j.cell.2010.06.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tong M and Seeliger MA (2015) Targeting conformational plasticity of protein kinases. ACS Chem. Biol 10, 190–200 10.1021/cb500870a [DOI] [PubMed] [Google Scholar]
- 7.Xie T, Saleh T, Rossi P and Kalodimos CG (2020) Conformational states dynamically populated by a kinase determine its function. Science 370, eabc2754 10.1126/science.abc2754 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jacobs MD, Caron PR and Hare BJ (2008) Classifying protein kinase structures guides use of ligand-selectivity profiles to predict inactive conformations: structure of lck/imatinib complex. Proteins: Struct. Funct. Bioinform 70, 1451–1460 10.1002/prot.21633 [DOI] [PubMed] [Google Scholar]
- 9.Huse M and Kuriyan J (2002) The conformational plasticity of protein kinases. Cell 109, 275–282 10.1016/S0092-8674(02)00741-9 [DOI] [PubMed] [Google Scholar]
- 10.Plattner N and Noé F (2015) Protein conformational plasticity and complex ligand-binding kinetics explored by atomistic simulations and Markov models. Nat. Commun 6, 7653 10.1038/ncomms8653 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tate JG, Bamford S, Jubb HC, Sondka Z, Beare DM, Bindal N et al. (2018) COSMIC: the catalogue of somatic mutations in cancer. Nucleic Acids Res. 47, D941–D947 10.1093/nar/gky1015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jordan EJ, Patil K, Suresh K, Park JH, Mosse YP, Lemmon MA et al. (2019) Computational algorithms for in silico profiling of activating mutations in cancer. Cell. Mol. Life Sci 76, 2663–2679 10.1007/s00018-019-03097-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Patil K, Jordan EJ, Park JH, Suresh K, Smith CM, Lemmon AA et al. (2021) Computational studies of anaplastic lymphoma kinase mutations reveal common mechanisms of oncogenic activation. Proc. Natl Acad. Sci. U.S.A 118, e2019132118 10.1073/pnas.2019132118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hu R, Xu H, Jia P and Zhao Z (2020) KinaseMD: kinase mutations and drug response database. Nucleic Acids Res. 49, D552–D561 10.1093/nar/gkaa945 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Vogelstein B, Papadopoulos N, Velculescu VE, Zhou S, Diaz LA and Kinzler KW (2013) Cancer genome landscapes. Science 339, 1546–1558 10.1126/science.1235122 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fedorov O, Marsden B, Pogacic V, Rellos P, Müller S, Bullock AN et al. (2007) A systematic interaction map of validated kinase inhibitors with Ser/Thr kinases. Proc. Natl Acad. Sci. U.S.A 104, 20523–20528 10.1073/pnas.0708800104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lake EW, Muretta JM, Thompson AR, Rasmussen DM, Majumdar A, Faber EB et al. (2018) Quantitative conformational profiling of kinase inhibitors reveals origins of selectivity for Aurora kinase activation states. Proc. Natl Acad. Sci. U.S.A 115, E11894–E11903 10.1073/pnas.1811158115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rauen KA (2013) The RASopathies. Annu. Rev. Genom. Hum. Genet 14, 355–369 10.1146/annurev-genom-091212-153523 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jindal GA, Goyal Y, Yamaya K, Futran AS, Kountouridis I, Balgobin CA et al. (2017) In vivo severity ranking of Ras pathway mutations associated with developmental disorders. Proc. Natl Acad. Sci. U.S.A 114, 510–515 10.1073/pnas.1615651114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tokuriki N and Tawfik DS (2009) Protein dynamism and evolvability. Science 324, 203–207 10.1126/science.1169375 [DOI] [PubMed] [Google Scholar]
- 21.Smock RG and Gierasch LM (2009) Sending signals dynamically. Science 324, 198–203 10.1126/science.1169377 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Scheraga HA, Khalili M and Liwo A (2007) Protein-folding dynamics: overview of molecular simulation techniques. Annu. Rev. Phys. Chem 58, 57–83 10.1146/annurev.physchem.58.032806.104614 [DOI] [PubMed] [Google Scholar]
- 23.Pantsar T, Rissanen S, Dauch D, Laitinen T, Vattulainen I and Poso A (2018) Assessment of mutation probabilities of KRAS G12 missense mutants and their long-timescale dynamics by atomistic molecular simulations and Markov state modeling. PLOS Comput. Biol 14, e1006458 10.1371/journal.pcbi.1006458 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dodson GG, Lane DP and Verma CS (2008) Molecular simulations of protein dynamics: new windows on mechanisms in biology. EMBO Rep. 9, 144–150 10.1038/sj.embor.7401160 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Rodrigues CH, Pires DE and Ascher DB (2018) Dynamut: predicting the impact of mutations on protein conformation, flexibility and stability. Nucleic Acids Res. 46, W350–W355 10.1093/nar/gky300 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sultan MM, Wayment-Steele HK and Pande VS (2018) Transferable neural networks for enhanced sampling of protein dynamics. J. Chem. Theory Comput 14, 1887–1894 10.1021/acs.jctc.8b00025 [DOI] [PubMed] [Google Scholar]
- 27.Ma H, Zhou Q, Wu M, Zhang M, Yao B, Gao T et al. (2018) Tailoring the oxygenated groups of graphene hydrogels for high-performance supercapacitors with large areal mass loadings. J. Mater. Chem. A 6, 6587–6594 10.1039/C7TA10843E [DOI] [Google Scholar]
- 28.Patel AL, Yeung E, McGuire SE, Wu AY, Toettcher JE, Burdine RD et al. (2019) Optimizing photoswitchable MEK. Proc. Natl Acad. Sci. U.S. A 116, 25756–25763 10.1073/pnas.1912320116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kubota Y, Fujioka Y, Patil A, Takagi Y, Matsubara D, Iijima M et al. (2022) Qualitative differences in disease-associated MEK mutants reveal molecular signatures and aberrant signaling-crosstalk in cancer. Nat. Commun 13, 4063 10.1038/s41467-022-31690-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yun WM, Kim K, Park YJ and Chung YK (2021) Conformational dynamics analysis of MEK1 using hydrogen/deuterium exchange mass spectrometry. Protein Pept. Lett 28, 481–488 10.2174/0929866527666201103152534 [DOI] [PubMed] [Google Scholar]
- 31.Yaeger R and Corcoran RB (2019) Targeting alterations in the RAF-MEK pathway. Cancer Discov. 9, 329–341 10.1158/2159-8290.CD-18-1321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Khan ZM, Real AM, Marsiglia WM, Chow A, Duffy ME, Yerabolu JR et al. (2020) Structural basis for the action of the drug trametinib at KSR-bound MEK. Nature 588, 509–514 10.1038/s41586-020-2760-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhao Y and Adjei AA (2014) The clinical development of MEK inhibitors. Nat. Rev. Clin. Oncol 11, 385–400 10.1038/nrclinonc.2014.83 [DOI] [PubMed] [Google Scholar]
- 34.Simanshu DK, Nissley DV and McCormick F (2017) RAS proteins and their regulators in human disease. Cell 170, 17–33 10.1016/j.cell.2017.06.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Samatar AA and Poulikakos PI (2014) Targeting RAS-ERK signalling in cancer: promises and challenges. Nat. Rev. Drug Discov 13, 928–942 10.1038/nrd4281 [DOI] [PubMed] [Google Scholar]
- 36.Emery CM, Vijayendran KG, Zipser MC, Sawyer AM, Niu L, Kim JJ et al. (2009) MEK1 mutations confer resistance to MEK and B-RAF inhibition. Proc. Natl Acad. Sci. U.S.A 106, 20411–20416 10.1073/pnas.0905833106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wagle N, Van Allen EM, Treacy DJ, Frederick DT, Cooper ZA, Taylor-Weiner A et al. (2014) MAP kinase pathway alterations in BRAF-mutant melanoma patients with acquired resistance to combined RAF/MEK inhibition. Cancer Discov. 4, 61–68 10.1158/2159-8290.CD-13-0631 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lu H, Liu S, Zhang G, Bin W, Zhu Y, Frederick DT et al. (2017) PAK signalling drives acquired drug resistance to MAPK inhibitors in BRAF-mutant melanomas. Nature 550, 133–136 10.1038/nature24040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Šali A and Blundell TL (1993) Comparative protein modelling by satisfaction of spatial restraints. J. Mol. Biol 234, 779–815 10.1006/jmbi.1993.1626 [DOI] [PubMed] [Google Scholar]
- 40.Fischmann TO, Smith CK, Mayhood TW, Myers JE Jr, Reichert P, Mannarino A et al. (2009) Crystal structures of MEK1 binary and ternary complexes with nucleotides and inhibitors. Biochemistry 48, 2661–2674 10.1021/bi801898e [DOI] [PubMed] [Google Scholar]
- 41.Ko TP, Jeng WY, Liu CI, Lai MD, Wu CL, Chang WJ et al. (2010) Structures of human MST3 kinase in complex with adenine, ADP and Mn2+. Acta Crystallogr. D 66, 145–154 10.1107/S0907444909047507 [DOI] [PubMed] [Google Scholar]
- 42.Jo S, Kim T, Iyer VG and Im W (2008) CHARMM-GUI: a web-based graphical user interface for CHARMM. J. Comput. Chem 29, 1859–1865 10.1002/jcc.20945 [DOI] [PubMed] [Google Scholar]
- 43.Berendsen HJC, van der Spoel D and van Drunen R (1995) GROMACS: a message-passing parallel molecular dynamics implementation. Comput. Phys. Commun 91, 43–56 10.1016/0010-4655(95)00042-E [DOI] [Google Scholar]
- 44.Bjelkmar P, Larsson P, Cuendet MA, Hess B and Lindahl E (2010) Implementation of the CHARMM force field in GROMACS: analysis of protein stability effects from correction maps, virtual interaction sites, and water models. J. Chem. Theory Comput 6, 459–466 10.1021/ct900549r [DOI] [PubMed] [Google Scholar]
- 45.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW and Klein ML (1983) Comparison of simple potential functions for simulating liquid water. J. Chem. Phys 79, 926–935 10.1063/1.445869 [DOI] [Google Scholar]
- 46.Berendsen HJC, Postma JPM, Gunsteren WFV, DiNola A and Haak JR (1984) Molecular dynamics with coupling to an external bath. J. Chem. Phys 81, 3684–3690 10.1063/1.448118 [DOI] [Google Scholar]
- 47.Parrinello M and Rahman A (1981) Polymorphic transitions in single crystals: a new molecular dynamics method. J. Appl. Phys 52, 7182–7190 10.1063/1.328693 [DOI] [Google Scholar]
- 48.Hess B, Bekker H, Berendsen HJC and Fraaije JGEM (1997) LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem 18 1463–1472 [DOI] [Google Scholar]
- 49.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H and Pedersen LG (1995) A smooth particle mesh Ewald method. J. Chem. Phys 103, 8577–8593 10.1063/1.470117 [DOI] [Google Scholar]
- 50.Patil K (2019) Github repository. https://github.com/KesPatil/MEK_kinase/tree/main/
- 51.Bonomi M, Branduardi D, Bussi G, Camilloni C, Provasi D, Raiteri P et al. (2009) PLUMED: a portable plugin for free-energy calculations with molecular dynamics. Comput. Phys. Commun 180, 1961–1972 10.1016/j.cpc.2009.05.011 [DOI] [Google Scholar]
- 52.Barducci A, Bussi G and Parrinello M (2008) Well-tempered metadynamics: a smoothly converging and tunable free-energy method. Phys. Rev. Lett 100, 020603 10.1103/PhysRevLett.100.020603 [DOI] [PubMed] [Google Scholar]
- 53.Shih AJ, Telesco SE, Choi SH, Lemmon MA and Radhakrishnan R (2011) Molecular dynamics analysis of conserved hydrophobic and hydrophilic bond-interaction networks in ErbB family kinases. Biochem. J 436, 241–251 10.1042/BJ20101791 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Meharena HS, Chang P, Keshwani MM, Oruganty K, Nene AK, Kannan N et al. (2013) Deciphering the structural basis of eukaryotic protein kinase regulation. PLoS. Biol 11, e1001680 10.1371/journal.pbio.1001680 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hartmann C, Banisch R, Sarich M, Badowski T and Schütte C (2014) Characterization of rare events in molecular dynamics. Entropy 16 350–376 10.3390/e16010350 [DOI] [Google Scholar]
- 56.Kästner J (2011) Umbrella sampling. WIREs Comput. Mol. Sci 1, 932–942 10.1002/wcms.66 [DOI] [Google Scholar]
- 57.Roux B (1995) The calculation of the potential of mean force using computer simulations. Comput. Phys. Commun 91, 275–282 [DOI] [Google Scholar]
- 58.Barducci A, Bonomi M and Parrinello M (2011) Metadynamics. WIREs Comput. Mol. Sci 1, 826–843 10.1002/wcms.31 [DOI] [Google Scholar]
- 59.Abrams CF and Vanden-Eijnden E (2010) Large-scale conformational sampling of proteins using temperature-accelerated molecular dynamics. Proc. Natl Acad. Sci. U.S.A 107, 4961–4966 10.1073/pnas.0914540107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Earl DJ and Deem MW (2005) Parallel tempering: theory, applications, and new perspectives. Phys. Chem. Chem. Phys 7, 3910–3916 10.1039/b509983h [DOI] [PubMed] [Google Scholar]
- 61.Sugita Y and Okamoto Y (1999) Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett 314, 141–151 10.1016/S0009-2614(99)01123-9 [DOI] [Google Scholar]
- 62.Radhakrishnan R and Schlick T (2004) Biomolecular free energy profiles by a shooting/umbrella sampling protocol, “BOLAS”. J. Chem. Phys 121 2436–2444 10.1063/1.1766014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Invernizzi M, Piaggi PM and Parrinello M (2020) Unified approach to enhanced sampling. Phys. Rev X 10, 041034 10.1103/PhysRevX.10.041034 [DOI] [Google Scholar]
- 64.Piaggi PM and Parrinello M (2019) Multithermal-multibaric molecular simulations from a variational principle. Phys. Rev. Lett 122, 050601 10.1103/PhysRevLett.122.050601 [DOI] [PubMed] [Google Scholar]
- 65.Wang Y, Lamim Ribeiro JM and Tiwary P (2020) Machine learning approaches for analyzing and enhancing molecular dynamics simulations. Curr. Opin. Struct. Biol 61, 139–145 10.1016/j.sbi.2019.12.016 [DOI] [PubMed] [Google Scholar]
- 66.Dellago C, Bolhuis PG and Geissler PL (2002) Transition path sampling. Adv. Chem. Phys 123, 1–81 10.1002/0471231509.ch1 [DOI] [PubMed] [Google Scholar]
- 67.Weinan E, Ren WQ and Vanden-Eijnden E (2005) Transition pathways in complex systems: reaction coordinates, isocommittor surfaces, and transition tubes. Chem. Phys. Lett 413, 242–247 10.1016/j.cplett.2005.07.084 [DOI] [Google Scholar]
- 68.Gowers RJ, Linke M, Barnoud J, Reddy TJE, Melo MN, Seyler SL et al. (2019) MDAnalysis: a python package for the rapid analysis of molecular dynamics simulations. In Conference: Proc. of the 15th Python in Science Conf. 98,105. (SCIPY 2016) United States. 10.25080/Majora-629e541a-00e [DOI] [Google Scholar]
- 69.Dalcín L, Paz R and Storti M (2005) MPI for python. J. Parallel Distrib. Comput 65, 1108–1115 10.1016/j.jpdc.2005.03.010 [DOI] [Google Scholar]
- 70.Mansour SJ, Candia JM, Matsuura JE, Manning MC and Ahn NG (1996) Interdependent domains controlling the enzymatic activity of mitogen-activated protein kinase kinase 1. Biochemistry 35, 15529–15536 10.1021/bi961854s [DOI] [PubMed] [Google Scholar]
- 71.Hagberg AA, Schult DA and Swart PJ (2008) Exploring Network Structure, Dynamics, and Function using NetworkX. In Proceedings of the 7th Python in Science Conference (Varoquaux G, Vaught T and Millman J, eds), pp. 11–15, Pasadena, CA, https://www.osti.gov/servlets/purl/960616. [Google Scholar]
- 72.Michaud-Agrawal N, Denning EJ, Woolf TB and Beckstein O (2011) MDAnalysis: a toolkit for the analysis of molecular dynamics simulations. J. Comput. Chem 32, 2319–2327 10.1002/jcc.21787 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Park JH, Liu Y, Lemmon MA and Radhakrishnan R (2012) Erlotinib binds both inactive and active conformations of the EGFR tyrosine kinase domain. Biochem. J 448, 417–423 10.1042/BJ20121513 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Friesner RA, Murphy RB, Repasky MP, Frye LL, Greenwood JR, Halgren TA et al. (2006) Extra precision glide: docking and scoring incorporating a model of hydrophobic enclosure for protein-ligand complexes. J. Med. Chem 49, 6177–6196 10.1021/jm051256o [DOI] [PubMed] [Google Scholar]
- 75.Friesner RA, Banks JL, Murphy RB, Halgren TA, Klicic JJ, Mainz DT et al. (2004) Glide: a new approach for rapid, accurate docking and scoring. 1. Method and assessment of docking accuracy. J. Med. Chem 47, 1739–1749 10.1021/jm0306430 [DOI] [PubMed] [Google Scholar]
- 76.Sherman W, Day T, Jacobson MP, Friesner RA and Farid R (2006) Novel procedure for modeling ligand/receptor induced fit effects. J. Med. Chem 49, 534–553 10.1021/jm050540c [DOI] [PubMed] [Google Scholar]
- 77.Sherman W, Beard HS and Farid R (2006) Use of an induced fit receptor structure in virtual screening. Chem. Biol. Drug Des 67, 83–84 10.1111/j.1747-0285.2005.00327.x [DOI] [PubMed] [Google Scholar]
- 78.Harder E, Damm W, Maple J, Wu C, Reboul M, Xiang JY et al. (2016) OPLS3: a force field providing broad coverage of drug-like small molecules and proteins. J. Chem. Theory Comput 12, 281–296 10.1021/acs.jctc.5b00864 [DOI] [PubMed] [Google Scholar]
- 79.Liu Y and Radhakrishnan R (2014) Computational delineation of tyrosyl-substrate recognition and catalytic landscapes by the epidermal growth factor receptor tyrosine kinase domain. Mol. Biosyst 10, 1890–1904 10.1039/C3MB70620F [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All the input scripts and key structure files are available on GitHub [50]. Supplementary Figures S1, S12 and Tables S1, S2 are provided with this manuscript. Upon submission, authors agree to make any additional materials, data, code, and associated protocols available upon request.


