Significance
Synaptic plasticity underlies learning in neuronal systems. Spike timing–dependent plasticity (STDP), on time scales of tens of ms, is well studied experimentally. However, reconciling STDP with “one-shot learning” (i.e., formation of rodent hippocampal place cells) has been challenging. Recently, behavioral time scale synaptic plasticity (BTSP), over longer time scales of seconds, has been observed experimentally, and provides an attractive alternative to STDP. Here, a computational model of the biochemical reactions within a spine head of the synapse is developed and shown to capture realistic responses to both STDP and BTSP stimulation protocols. Mechanisms by which the model responds faithfully over such disparate time scales are identified, including a “priming mechanism” that enhances BTSP.
Keywords: synaptic plasticity, long-term potentiation, long-term depression, STDP, BTSP
Abstract
Synaptic plasticity [long-term potentiation/depression (LTP/D)], is a cellular mechanism underlying learning. Two distinct types of early LTP/D (E-LTP/D), acting on very different time scales, have been observed experimentally—spike timing dependent plasticity (STDP), on time scales of tens of ms; and behavioral time scale synaptic plasticity (BTSP), on time scales of seconds. BTSP is a candidate for a mechanism underlying rapid learning of spatial location by place cells. Here, a computational model of the induction of E-LTP/D at a spine head of a synapse of a hippocampal pyramidal neuron is developed. The single-compartment model represents two interacting biochemical pathways for the activation (phosphorylation) of the kinase (CaMKII) with a phosphatase, with ion inflow through channels (NMDAR, CaV1,Na). The biochemical reactions are represented by a deterministic system of differential equations, with a detailed description of the activation of CaMKII that includes the opening of the compact state of CaMKII. This single model captures realistic responses (temporal profiles with the differing timescales) of STDP and BTSP and their asymmetries. The simulations distinguish several mechanisms underlying STDP vs. BTSP, including i) the flow of through NMDAR vs. CaV1 channels, and ii) the origin of several time scales in the activation of CaMKII. The model also realizes a priming mechanism for E-LTP that is induced by flow through CaV1.3 channels. Once in the spine head, this small additional opens the compact state of CaMKII, placing CaMKII ready for subsequent induction of LTP.
Synaptic plasticity is an essential mechanism that underlies learning and memory. At present, however, synaptic plasticity, with its many diverse forms, is far from thoroughly understood. Experimental studies have shown that electrical or spiking stimuli can lead to a strengthening or weakening of synapses lasting for hours, days to years—termed long-term potentiation/depression (LTP/LTD) (1, 2). STDP (spike timing dependent plasticity) is a form of synaptic plasticity (3–5), which is induced by a standard stimulus protocol of many repetitive pairs of pre-synaptic and post-synaptic spikes, with a short time interval of tens of milliseconds separating the pre-post members of each pair. STDP is Hebbian, with LTP (LTD) occurring when the pre-synaptic spike precedes (follows) the post-synaptic spike of each pair (6). While STDP is a beautiful realization of Hebbian learning, there are probably other mechanisms of synaptic plasticity that underlie other types of learning. For example, rodent hippocampal CA1 place cells learn location with remarkable ease, after the rodent makes only one (or a few) passes across the specific location. The time scales and “one-shot” nature of learning are difficult to reconcile with the properties of STDP (7–9). Recently, a very different form of synaptic plasticity, BTSP (behavioral time scale synaptic plasticity), has been observed to emerge from a different stimulus protocol (10). This BTSP form of LTP seems more likely to underlie such one-shot learning, with its characteristics very different from those of STDP. BTSP operates over much slower time scales (seconds, rather than tens of milliseconds) and is not Hebbian (with LTP occurring whether or not the pre-synaptic excitation occurs before or after the post-synaptic excitation).
Experimental studies have identified two elements as vital for LTP/D. First, the intracellular calcium influx through NMDAR and CaV channels has been shown to be necessary and sufficient for LTP/LTD (11–14). Second, two proteins (CaMKII and a Phosphatase) that are activated by the calcium influx are known to modify the synaptic efficacy. The activation (phosphorylation) of the kinase CaMKII is initiated by the calcium–CaM complex and sustained by the autophosphorylation of CaMKII. This active state of CaMKII then triggers a conformational change of the AMPARs, leading to a strengthening of synaptic transmission (15–18). Similarly, the phosphatase (PP), which catalyzes dephosphorylation, has also been shown to be necessary for the induction of LTD (19–21). In addition, Tsien et al. have argued from existing experimental results (22–26) to propose a priming mechanism that could enhance one-shot learning (27). This priming mechanism is induced by a small steady depolarization that causes a small amount of calcium to flow through CaV1.3 channels into the spine head, where it would induce a transient activation of CaMKII, placing the synapse ready for a stronger one-shot signal to induce LTP.
Our work began from some questions: Can a single computational model of the biochemical reactions within the spine head at a synapse realize both STDP and BTSP when stimulated by the STDP or BTSP protocols, respectively? If so, what are the mechanisms by which this single model realizes the very different characteristics of STDP vs. BTSP (vastly different time scales and Hebbian nature)? In addition, can a priming mechanism involving calcium channels (CaV channels) (27) be realized in the same model; and, if so, what are the characteristics of the model’s priming mechanism and how does it relate to BTSP and one-shot learning?
In this paper, we construct a realistic biological model of the post-synaptic biochemical reactions at a single synapse during E-LTP. We start from Graupner and Brunel’s detailed model of the biochemical reactions of the activation of CaMKII (28), which successfully reproduces the response to a STDP protocol with a bistable single-compartment system of ordinary differential equations (ODEs). Starting from this model, we enhance it with the addition of the compact state of CaMKII, and we also remove the traditional phosphatase I1-PP1 signaling pathway which does not apply to CA1 pyramidal neurons (29–33) and substitute instead a phenomenological representation (34). The resulting model is tri-stable with three coexisting stable steady states of kinase and PP activity directly related to the synapse’s basal, LTP & LTD states. Under stimulation, the system makes transitions from the basal state to either of the LTP/D states—corresponding to the occurrence of LTP/D. In reality, these states of CaMKII and PP activity are likely at best meta-stable, becoming unstable over longer time scales by mechanisms not modeled here (35).
The paper is organized as follows: After presenting the model, we then validate that it has a realistic response to both a prescribed calcium stimulus and a STDP signaling protocol, and that it captures the distinct behavior of LTP/LTD and the short timescales associated with the STDP protocol. We then establish that a priming picture can be realized in the model, through a mild depolarization that opens CaV1 channels to a inflow that primes the activation of CaMKII. This establishes the importance of CaV1-CaMKII signaling in the model and, thus, its possible importance for one-shot learning. Next, we establish that the model exhibits a realistic response to the BTSP protocol (the same model, with no changes in parameter values), demonstrating the model’s ability to reproduce the long timescales and the non-Hebbian nature of the BTSP. We then analyze the timescale of CaMKII activity within the model and identify a central role of CaMKII in integrating the information of the BTSP pre-synaptic and post-synaptic stimuli spaced several seconds apart, thus, showing how BTSP can share a similar seconds-long timescale with CaMKII activity. Finally, we explore how priming could i) enhance CaMKII’s role as an information integrator and ii) extend the timescale of BTSP.
Results
Qualitative Description of the Model.
We have developed and implemented a detailed computational model of the biochemical reactions responsible for E-LTP/D for synapses of CA1 pyramidal cells in the rodent hippocampus. The reaction scheme is illustrated in Fig. 1A, and the model is summarized in Materials and Methods, with a complete description in SI Appendix. Presynaptic spikes and postsynaptic spikes and plateau potentials open ion channels (NMDAR, CaV), allowing ions to flow into the spine head. The increasing calcium concentration will activate the kinase CaMKII and a generic PP, which will continue to activate themselves through autocatalytic reactions, while the two will inhibit each other through phosphorylation and dephosphorylation. The model is a single-compartment model of the post-synaptic density (PSD), containing well-mixed ions, CaM, CaMKII, and PP. We begin from the detailed CaMKII model (28) with several enhancements—including making more of the reactions reversible and adding the important compact state of CaMKII, with transitions between this compact state and an open inactive state that is capable of being activated. The resulting model of the CaMKII-PP dynamical system exhibits tri-stability, with basal, LTP, and LTD states.
Fig. 1.
Calcium-induced synaptic plasticity: A model of CaMKII and PP interaction. (A) Chemical reaction scheme of the model. Calcium flows into the spine head through NMDAR and VGCC and activates CaMKII (after binding with CaM to form the calcium–CaM complex) and PP. Active CaMKII and PP mutually inhibit through phosphorylation and dephosphorylation. (B) pCaMKII (phosphorylated CaMKII) and active PP level during a calcium pulse stimulus. The Top graphs show the phosphorylated CaMKII (blue traces) and active PP (red traces) concentrations, with the calcium concentration is given at the Bottom (black traces). Left panel, CaMKII and PP are weakly activated during a weak pulse (0.02 M, 5 s) and return to the basal state when is removed. Middle panel, PP is activated by a slightly stronger stimulus with the same duration (0.1 M, 5 s) and stays active, leading to LTD. Right panel, During high level stimulus (0.3 M, 2 s), both CaMKII and PP are active while the kinase activity is dominant after the stimulus. (C) Dependence of the sign of synaptic modification on level and duration during a pulse (Note that for any fixed duration, the results are similar to the BCM rule). 1. A is adapted and redrawn from (16, 34).
Tri-stability of Synaptic Efficacy.
It is well known that intracellular calcium dynamics can induce both LTP and LTD states (12–14). Moderate, long-lasting calcium leads to LTD, while a large calcium inflow of short duration will trigger LTP (36, 37). To study this in the model, we begin with a prescribed calcium inflow (Fig. 1B). Initialized in the basal state (of low CaMKII and PP activities), a large calcium pulse (M, for 2 s) will place the system within the basin of attraction of the LTP state (of high CaMKII phosphorylation and low PP activity). In contrast, again beginning from the basal state, a longer calcium stimulus of moderate strength (M, for 5 s) places the system within the basin of attraction of the LTD state (of low CaMKII phosphorylation and high PP activity). As a comparison, after a weak calcium stimulus (M, for 5 s) on the basal state, the system will return to the basal state, showing the basal state is stable under perturbations. The LTP and LTD states are also stable under similar perturbation experiments (SI Appendix, Fig. S9).
To further study how the magnitudes and durations of the calcium dynamics determine the steady states, we simulate the system with different calcium pulse profiles. The results are summarized in the phase diagram of Fig. 1C. In this figure, the system always starts from the basal state, similar to the above simulations. A mild stimulus, either of small magnitude or short duration, will be unable to push the system outside of the basin of attraction of the basal state. However, a stimulus with a moderate magnitude between 0.075 and 0.125 M will induce the system to an LTD state when it is of sufficient duration (larger than 1 s). A strong stimulus with a magnitude larger than 0.2 M will lead to LTP. It is noteworthy in the phase diagram that a more extended time window is required for LTD to happen, which is consistent with experimental observations (36, 37). We also observe an intermediate region in Fig. 1C for the basal state between LTD and LTP (when the stimulus magnitude is around 0.15 M). This intermediate region is similar to that observed in the phenomenological model of (34, Fig. 2D), where the authors note a similarity with the switch from depression to potentiation in the BCM rule (38). The phase diagram of Fig. 1C is a useful guide to the mechanisms underlying transitions to LTD.
Fig. 2.
Synaptic modification in response to STDP protocols. (A) Calcium dynamics during a pair of a pre-synaptic and a post-synaptic spikes at different timing differences . The time course of the intracellular calcium concentration is generated by the model in response to a pre-synaptic spike at ms and a post-synaptic spike at ms. The values are noted in the legend. (B) Temporal evolution of calcium, PP1 activity, and phosphorylated CaMKII activity level during STDP stimulation protocols with ms (Left panel) and ms (Right panel). 60 pairs of pre-synaptic and post-synaptic spikes in 1 Hz evoke LTP at ms but lead to LTD at ms. (C) Synaptic modifications in response to STDP protocols. In the deterministic (black curve) setting, STDP protocols with between and ms evoke LTP, and between and ms evoke LTD. In the stochastic setting (red curve), STDP protocols with between and ms evoke LTP, and between and ms evoke LTD.
It is known experimentally that both LTP and LTD can be reversed with appropriate stimuli, which is termed depotentiation and dedepression, respectively (39, 40). We conduct simulations of this phenomena similar to those in (34) and present the results in SI Appendix, Fig. S5B (SI Appendix). A moderate pulse stimulus (0.08 M, 10 s) reverses LTP, moving it back to the basal state, while a substantial calcium influx (0.35 M, 3 s) can reverse the LTD to the basal state.
STDP Simulations.
We have just described the responses of the model to prescribed calcium inflow. However, in experiments calcium inflow is not directly prescribed; rather, the experiment controls synaptic events (pre-synaptic and post-synaptic spike trains and dendritic plateau potentials) through current injection, which in turn leads to calcium inflow through NMDAR and CaV channels. Following (28), we simulate the calcium inflow that results from these prescribed synaptic events, as described in detail in Materials and Methods and SI Appendix.
LTP induced by STDP has been observed in many experiments [see, for e.g., (3, 4, 5)], with the traditional signaling protocol of (5). Pairs of pre-synaptic and post-synaptic spikes are evoked repetitively with controlled timing differences between the two spikes. The synapse is strengthened when the pre-synaptic spikes precede the post-synaptic ones, while it is weakened if the post-synaptic neuron spikes earlier, all within 50 to 100 ms. This causality property makes STDP a natural candidate for Hebbian learning (41, 42).
We use a standard STDP protocol containing 60 repetitive pairs of pre-synaptic and post-synaptic spikes, with a frequency of 1 Hz (5). The calcium dynamics evoked by one pair of spikes is shown in Fig. 2A. When the pre-synaptic spike slightly precedes the post-synaptic spike, a large calcium influx results, as the magnesium block of the NMDAR channels is removed by the membrane depolarization through back-propagating action potential of the post-synaptic neuron. When the pre-synaptic spike is slightly after the post-synaptic spike, the removal of the magnesium block is not complete, resulting in a relatively moderate increase in calcium concentration. When the two spikes occur with a time difference longer than 100 ms, either positive or negative, the relatively weak total calcium inflow is almost a linear summation.
In Fig. 2B, we show the response of the CaMKII and PP interacting systems to this STDP signaling protocol. For a small negative timing difference t 20 ms (t pre-synaptic spike time minus post-synaptic spike time, within one pair), a large calcium influx will activate CaMKII significantly, and the activation is accumulated steadily during each pair of spikes. In contrast, PP is activated during spikes but quickly drops back to the resting concentration when the stimulus is off, and no cumulative effect can be observed. That leads to a significant amount of activated CaMKII with no change for PP, leading to the steady state in which CaMKII dominates. For extensive negative t (100 ms), both CaMKII and PP show the increase-and-decay behavior, and neither can be accumulated during the presentation of multiple pairs (SI Appendix, Fig. S6).
Similar behavior can be found for positive t, as also presented in Fig. 2B. For small positive t (40 ms), the long, moderate calcium influx will activate PP, and the activation is accumulated during each pair of stimuli. At the same time, it will only induce a moderate activation of CaMKII, further restricted by the significant inhibition by active PP, which places the system in the attractor basin of the LTD state. For large positive t (100 ms), although both CaMKII and PP accumulate slightly, the accumulation does not lead the system to either LTP or LTD state (SI Appendix, Fig. S6). Thus, the different calcium inflow profiles lead to the particular activity of CaMKII and PP, which finally leads to the asymmetric STDP.
The system’s response under the STDP protocol for a broader range of the timing difference t is shown in Fig. 2C. We notice that LTP occurs for a short interval of negative t, while LTD is induced for a somewhat longer interval of positive t, both in tens of milliseconds. The system will return to the original steady state for timing differences beyond that range. Besides, between the LTP interval and LTD interval, there is an intermediate area near ms where no learning happens, which is also seen in other simulation studies (28, 43).
The stochastic opening of ion channels, a primary contributor to the noise of calcium dynamics, will smooth these deterministic results. To represent this stochastic effect, we include two sources of noise following (28): i) random maximum conductance of NMDAR at each presynaptic spike and ii) random maximum conductance of the CaV channels at each postsynaptic spike. Similar to the deterministic case, the average of the number of AMPARs is used as the indicator of synaptic efficacy, also related to the transition probability from the basal state to the LTP or LTD state. The smoothed results are also shown in Fig. 2C. The synaptic efficacy is approximately an exponentially decaying function of the timing difference t for both positive and negative intervals. The result is consistent with experimental observations and previous numerical simulations, in particular, the asymmetric behavior of LTP/LTD and the short-range learning window over several tens of milliseconds.
Voltage-Dependent Learning.
Experiments have shown that place cells can be firmly induced in vivo by the injection of a small direct-current (DC) stimulus, which increases the baseline membrane potential by only a few millivolts (25). This induction is mainly reversible, and has been shown to result from the voltage dependency of peri-somatic channels (44). Here, we investigate the model’s LTP dependence on the baseline membrane potential, which could be related to the small residual irreversible components observed by Lee et al. (25). It is not clear how the place cell is induced in vivo; thus, there are possibly several different experimental protocols that can lead to induction. Here, we borrow from an in vitro protocol used in (10) in a study of the production of LTP and the formation of place cells. Our stimulus protocol consists in a plateau potential which can be induced by sodium current injection or occur naturally (10), following three pre-synaptic spikes [versus ten in (10)], together with a small DC mimicking the mild depolarization used in (25).
The calcium dynamics under our protocol (with and without DC injection) is shown in Fig. 3A. Given that the timing difference between the pre-synaptic spikes and plateau potential is large enough (500 ms), the calcium dynamics is a superimposition of the two stimuli with no overlapping effects. The DC injection increases the resting membrane potential, which increases the baseline calcium concentration by 5% (from 0.1 to 0.105 M) through the opening of CaV1.3 channels. In addition, it also slightly releases the magnesium block of the NMDA channels, allowing a significant calcium influx during a pre-synaptic spike train.
Fig. 3.
Synaptic modification in response to voltage-dependent learning. (A) Calcium dynamics during the combination of a plateau potential and pre-synaptic spike trains, with and without DC stimulus. The time course of the intracellular calcium concentration is generated by the model in response to three pre-synaptic spikes starting at s in 10 Hz and a 300-ms plateau potential initiating at s. The 90 pA DC increases the baseline calcium concentration from M to 0.105 M. (B) Temporal evolution of calcium, PP1, and phosphorylated CaMKII activity level during voltage-dependent one-shot learning. The Left panel shows the results without DC, and the Right panel shows the results with DC. No LTP is induced without DC, while a sustained 90-pA current injection is enough to switch the response to CaMKII domination (LTP). (C) Synaptic modifications in response to voltage-dependent one-shot learning with varying amounts of DC injection. A sharp transition to learning occurs at 85 pA in the deterministic setting (black curve), and a similar transition is observed in the range of 70 to 130 pA for the stochastic setting (with the half height of the transition at 100 pA).
The results with and without DC are shown in Fig. 3B. For the case without DC, we see mild increases of CaMKII and PP during the two stimuli, with PP slightly dominating the competition. The system rapidly decays back to the basal state. For the case with DC, a larger amount of CaMKII is activated during the pre-synaptic spikes, and CaMKII is further activated by the persistent, significant calcium influx induced by the plateau potential. The phosphorylated CaMKII dominates after the stimulus and dramatically inhibits the activity of PP, which finally leads to LTP. The above results show how an increase in the membrane potential by several millivolts could switch the system from no learning to learning. It is worth emphasizing that during this shallow voltage range, the voltage dependency of NMDAR channels is mild; in contrast, CaV channels (especially CaV1.3) have a much steeper voltage dependency [SI Appendix, Fig. S8A]. As a result, the CaV channels contribute most to the changes in calcium dynamics caused by DC injection when there are no pre-synaptic spikes [SI Appendix, Fig. S8B].
Next, we investigate how the amplitude of the DC injection will influence learning, by injecting DCs of different magnitudes [Fig. 3C]. In all cases, the system terminates in either the basal or the LTP state, with no LTD state observed. In this deterministic setting, the transition from basal to LTP is sharp at DC = 85 pA, corresponding to a baseline membrane potential of 62.5 mV. When the calcium inflow is stochastic, this sharp transition is smoothed (Fig. 3C). It remains steep, however, with a transition from no learning to complete learning over the interval (70pA, 130pA), which corresponds to an interval of membrane potential only 5mV wide (65mV, 70mV), as reported in (25). (See also SI Appendix, Fig. S7.)
Essence of Priming.
Recently, a priming mechanism has been proposed by the Tsien Lab (27) for a possible role to enhance one-shot learning of CA3 to CA1 synapses of place cells in the rat hippocampus, based on a detailed inspection of experimental results about CaMKII activity. This priming picture can be described as follows: The synapse can get primed by mild depolarization and eventually become potentiated if a plateau potential follows within a few seconds. This primed state itself is not stable, as the synapse can return to its original, nonprimed state after the mild depolarization is turned off. An intermediate, partially active state of CaMKII serves as a priming for the following stimulus. The mild depolarization required for priming lies in a voltage range where voltage-dependent CaV channels (CaV1.3) show steep dependency, indicating a possible important role for CaV channels in hippocampal place field formation.
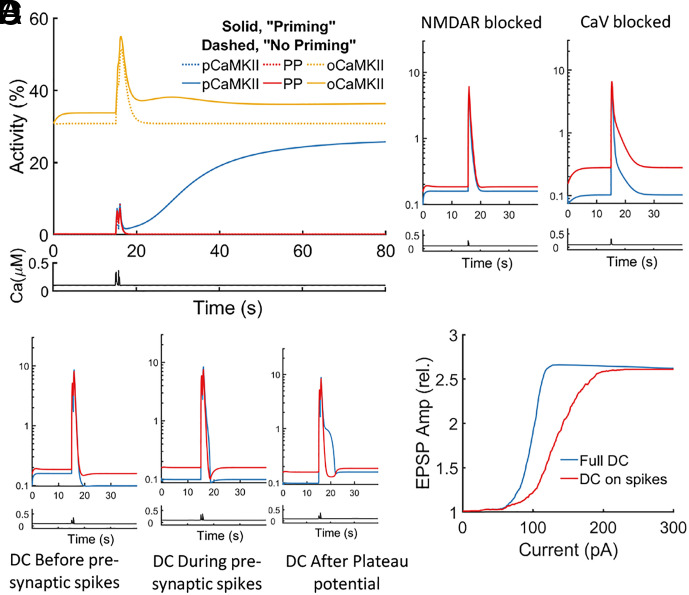
As shown in the previous section, DC injection can influence learning. Here, we make a direct detailed comparison of the dynamics with and without DC [Fig. 4A]. Before the onset of pre-synaptic spikes, the most observable difference is the increase of oCaMKII (open but unphosphorylated CaMKII) caused by the application of DC. The more open CaMKII, combined with the greater calcium influx during pre-synaptic spikes, prepares the system [more oCaMKII and pCaMKII (phosphorylated CaMKII)] before the onset of plateau potential—making it easier for the plateau potential to induce LTP, which is exactly the meaning of priming. In addition, this priming preparation is a transient activity of CaMKII, which can be reversed when no following stimulus is presented and DC is removed—also consistent with the meaning of priming.
Fig. 4.
Priming and the role of NMDAR and CaV channels. (A) Comparison of time courses of calcium, PP1, phosphorylated, and open CaMKII activity level during the one-shot learning protocol, with and without DC (priming). The intracellular calcium increases by 5% with DC, raising open CaMKII by 10% (same data as in Fig. 3B, different scales). (B) Temporal evolution of calcium, PP1, and phosphorylated CaMKII activity level during the one-shot learning protocol, with NMDAR or CaV channels blocked. Blocking NMDAR channels (Left panel) or CaV channels (Right panel) abolishes LTP. (C) Temporal evolution of calcium, PP1, and phosphorylated CaMKII activity level during the one-shot learning protocol, with transient DC. Left panel, Activities with DC only before pre-synaptic spike trains. Middle panel, Activities with DC only during pre-synaptic spike trains. Right panel, Activities with DC only after plateau potential. None of the three stimuli is enough to induce LTP. (D) Synaptic modifications in response to voltage-dependent one-shot learning with varying amounts of DC injection in the stochastic setting. The blue curve shows the results with DC throughout the experiment (same data as Fig. 3C), and the red curve shows the results with DC applied only during pre-synaptic spike trains. Transitions are observed at both curves, but a higher range of DC (90 to 210 pA, half height at 150 pA) is required for the transition to happen with depolarization only on pre-synaptic spikes compared with complete DC (transition occurs at 70 to 130 pA, half height at 100 pA).
Next, we separately block NMDAR and CaV channels to investigate their roles in LTP. Blocking NMDAR channels prevents Ca2+ inflow during presynaptic spiking, whereas blocking CaV channels prevents Ca2+ inflow during the postsynaptic plateau. Each block prevents LTP [Fig. 4B], consistent with experimental results (10). Next, we turn to the roles of NMDAR and CaV channels in priming induced by a steady mild depolarization. CaV channels play an essential role, as they are the only channels influenced by the steady mild depolarization before presynaptic spikes and after the plateau [SI Appendix, Fig. S8B]. There are three stages in priming (before and during presynaptic spikes, and after the plateau). These three stages must work together, as mild steady depolarization in any of the three does not result in LTP [Fig. 4C]. Finally, we note that depolarization can increase the baseline calcium concentration in two ways—i) through CaV channels and ii) through NMDAR channels (at larger depolarization through presynaptic spiking). Fig. 4D shows that although it is possible to induce LTP with depolarization only during presynaptic spikes, a larger depolarization is required. Thus, if there is no increase in baseline calcium during the priming stage, a stronger stimulus is needed to induce LTP, either by a prolonged plateau potential or by larger calcium inflow through NMDAR channels.
BTSP Protocol Reproduced.
BTSP is a recently observed plateau-potential induced plasticity rule in CA1 pyramidal neurons (10, 45), with characteristics that make it a likely candidate for the synaptic plasticity underlying types of one-shot learning. Unlike classical Hebbian learning, the synapse will be potentiated if the corresponding pre-synaptic neuron fires seconds before or after the plateau potential, and over a much longer time separation than STDP. BTSP does not require tens of presentations of stimulus pairs to induce LTP; rather, in BTSP five or fewer repetitive stimulus pairs will induce LTP. These two features (longer time duration and much fewer repetitions) make BTSP a good candidate for the underlying mechanism for the emergence of place cells in hippocampal area CA1.
Here, we describe the model’s response to a BTSP stimulus protocol. We use a stimulus protocol that is similar to in vitro experiments (10)—a combination of 10 pre-synaptic spikes at 10 Hz, together with a 300 ms plateau potential generated by sodium current injection, separated by fixed timing differences spanning from 6,000 to 6,000 ms. Slightly different from the experiment, a small DC (42 pA) is applied constantly throughout the simulation; thus, raising the model’s resting membrane potential to mV. The calcium dynamics under this protocol are shown in Fig. 5A. Here, we use only two pairs of stimuli with a 15-s interval, as it is reported in (10) that one or two pairs can already induce LTP. As shown in Fig. 5A, when the absolute timing difference t is smaller than 1,000 ms, there will be an overlap between the pre-synaptic spike train and the plateau potential, which leads to a large calcium influx through the NMDAR channel. However, beyond that time duration, the nonlinear effect is not observed, and the calcium dynamics is only a superposition of the calcium responses to the two separated synaptic events.
Fig. 5.
Synaptic modification in response to BTSP protocols. (A) Calcium dynamics during a pair of pre-synaptic spike trains and a plateau potential at different timing differences (corresponding voltage dynamics shown in SI Appendix, Fig. S11). Shown is the time course of intracellular calcium concentration in response to ten pre-synaptic spikes at a frequency of 10 Hz, centered at 0 s, and a 300-ms plateau potential beginning at ms, with a sustained depolarization by 42-pA DC injection. The specific values of are noted in the legend. (B) Temporal evolution of calcium, PP1 activity, and phosphorylated CaMKII activity level during BTSP stimulation protocols with 1,500 ms (Left panel) and 2,500 ms (Right panel). Two pairs of pre-synaptic spike trains and a plateau potential (15 s interval) evoke LTP at 1,500 ms but have no effect at 2,500 ms. (C) Synaptic modifications in response to BTSP protocols. In the deterministic (black curve) setting, BTSP protocols with between 2,400 and 1,950 ms evoke LTP, and beyond that leads to no learning. In the stochastic setting (red curve), BTSP protocols with between 4,500 and 4,000 ms evoke LTP, and beyond that leads to almost no change.
Fig. 5B and SI Appendix, Fig. S1A present the model dynamics of CaMKII and PP under different t, the timing difference between the pre-synaptic spike trains and the post-synaptic plateau potential. For a small t (100 ms) within the overlapping interval, the large calcium influx leads to a dramatic increase of active or phosphorylated CaMKII (pCaMKII) which eventually causes LTP. The responses change as t is increased in magnitude (SI Appendix, Fig. S1A). For t 1,500 ms, one pair of the stimulus leads to a relatively minor increase of pCaMKII, but still greater than PP. A significant proportion of phosphorylated CaMKII is retained until the onset of the next pair of stimuli, when it gets amplified and dominates, producing LTP. However, if the t is even larger (2,500 ms), a single stimulus will lead to only a mild increase of CaMKII activity, which will completely diminish during the period between the two pairs of stimuli, resulting in no change in synapse efficacy. Results for positive t are similar (SI Appendix, Fig. S1A) and share the same dependency on the timing differences. However, in this case of positive t, the range of t which can induce LTP is smaller than it is for negative t, an asymmetry that we will discuss below.
Fig. 5C shows BTSP for a wide range of t. In particular, we note that even if the two signals are separated by several seconds, the synapse will still be steadily potentiated—a long timescale consistent with experiments. The model’s BTSP results when the calcium inflow is stochastic are also presented. In this case, the timescales remain several seconds, as does the asymmetry in t, with the time range for potentiation longer for than for , exactly as reported in (10). Finally, we emphasize the role in the model of the small DC that increases the baseline membrane potential: Without it, the CaMKII in the model still gets potentiated, however, with LTP only occurring for shorter t than with the DC [SI Appendix, Fig. S1B]. The small DC makes it easier for the model to perform consistently with experimental observations. We note that Milstein et al. (46) observe that increasing membrane excitability helps the expansion of the timescale of BTSP, consistent with the model’s performance.
Mechanism Underlying Long Timescale of BTSP.
BTSP has a seconds-long timing difference between pre-synaptic and post-synaptic events, several tens times larger than the 100 ms timescale of STDP. It is well known that the calcium dynamics inside the synapse decays very rapidly due to the fast diffusion of calcium ions. In addition, our simulation results indicate that the NMDAR channels, which play the role of coincidence detectors in STDP, cannot detect pre-synaptic signal and post-synaptic signals together if their timing difference exceeds 100 ms, which is consistent with experimental measurements of the timescale of NMDAR activity (47). These two properties suggest that neither calcium dynamics nor NMDAR channels are suitable candidates to capture the BTSP timing difference between pre-synaptic spikes and plateau potential.
To identify the origin of the model’s seconds-long BTSP timescale, we first trace the activities of CaMKII and PP, and the relationship of these activities to the stimulus. The typical decays of open but unphosphorylated CaMKII, phosphorylated CaMKII, and active PP after pre-synaptic spike trains are presented in Fig. 6A. As the system is not perturbed outside of the basal state’s basin of attraction, all three decay exponentially back to the resting concentration. Fig. 6A shows that the decay of oCaMKII is much slower than the decays of pCaMKII and PP. The decay of oCaMKII mainly depends on the rates of docking and undocking of CaMKII subunits, while the decay of pCaMKII and PP is due to their mutual inhibition, which can be quite rapid when both are highly active. Although we have shown in the previous sections that the activity of oCaMKII increases during the DC injection, the exact role of oCaMKII in priming is still unclear. We perform a perturbation experiment to analyze this. Specifically, we increase the initial amount of oCaMKII while conserving the total concentration (= oCaMKII + cCaMKII), where cCaMKII denotes the concentration of CaMKII that is neither open nor phosphorylated, in order to study how the magnitude of the concentration of oCaMKII modulates the response of the whole system to the same stimulus. In the set-up of the computational model, a single plateau potential (of the particular amplitude and duration as used in the protocol) cannot induce the system to enter an LTP state. However, as shown in Fig. 6B, Left, the plateau potential combined with a perturbation that increases the initial concentration of oCaMKII by M (about 12%) is enough to induce LTP, confirming a critical role of oCaMKII in our model. Moreover, as also presented in Fig. 6 B, Right, we can delay the onset of the plateau potential (for example, with a delay of 2.4 s), and LTP will still be induced—provided oCaMKII is initially increased by 100%. The required increase of oCaMKII and the duration of 2.4 s is consistent with BTSP, which suggests possible roles of both the priming of oCaMKII and the timescale of this activity in determining the timescale of BTSP.
Fig. 6.
Mechanism underlying long timescale. (A) Estimating timescales of open CaMKII, phosphorylated CaMKII, and PP activity. The decay dynamics of open CaMKII (Left panel), phosphorylated CaMKII and PP (Right panel) after ten 10 Hz pre-synaptic spikes starting at 0 s are shown. All the decay dynamics can be fitted well with an exponential decay (dashed line), with time constants noted in the legends. (B) Temporal evolution of PP1, phosphorylated and open CaMKII activity level in response to a plateau potential with a perturbation on open CaMKII activity. The plateau potential is initiated by a 5,000 pA current injection, lasting for 300 ms, starting at s (Left panel) or s (Right panel), accompanied by a sustained 42-pA depolarization. A perturbation that increases oCaMKII by M (12%) at the beginning of plateau potential (Left panel) or increases oCaMKII by M (100%) 2.4 s before plateau potential (Right panel) evokes LTP (as shown in the Insets). Neither scenario evokes LTP when the perturbation is not presented. (C) Temporal evolution of PP1, phosphorylated and open CaMKII activity level in response to a plateau potential with a perturbation on phosphorylated CaMKII activity. The plateau potential is initiated by a 5,000 pA current injection, lasting for 300 ms, starting at s (Left panel) or s (Right panel). A perturbation that increases pCaMKII by M at the beginning of plateau potential (Left panel) or increases pCaMKII by M 1.5 s before plateau potential (Right panel) evokes LTP (as shown in the Insets). Neither scenario evokes LTP when the perturbation is not presented.
Thus, in the model, oCaMKII plays a vital role in priming; however, pCaMKII could also contribute to priming. Hence, we repeat the perturbation experiment instantaneously increasing pCaMKII (instead of oCaMKII). Fig. 6C shows that the immediate increase of pCaMKII also amplifies the system’s response to the plateau potential and results in LTP, as is consistent with expectation. Since pCaMKII decays faster than oCaMKII, a shorter delay of the plateau potential (1.5 s) is demanded for LTP to follow an instantaneous increase in pCaMKII than to follow an instantaneous increase in oCaMKII (2.5 s). We note that this shorter delay is required, even though some of the increased pCaMKII decays into the slower decaying oCaMKII.
Discussion
We have developed and implemented a detailed computational model of the biochemical reactions responsible for E-LTP/D for synapses of CA1 pyramidal neurons in the hippocampus. The model is a single-compartment model of the PSD of the spine head, containing well-mixed ions, CaM, CaMKII, and PP. The biochemical reactions of the two interacting pathways [the kinase CaMKII pathway and a phenomenological phosphatase PP pathway] are described by a deterministic system of ODEs. The ion inflow (including ) is described by ion channels—NMDAR, CaV1, and Na channels. The dynamics is tri-stable, with three stable fixed points that represent the basal, LTP, and LTD states, together with the transient dynamics that describes the phosphorylation of CaMKII (that we identify with the formation of E-LTP), and the dephosphorylation of PP (that we identify with the formation of E-LTD). As in in-vitro experiments, LTP/D can be induced by distinct signaling protocols, with STDP induced by many repetitions of pre-post synaptic spike pairs and BTSP induced by a few pre-synaptic spikes followed or preceded by a plateau potential.
Our model realizes both STDP and BTSP in one model of the biochemistry in the PSD, with one identical set of parameter values. The model captures realistic responses to each signaling protocol (temporal profiles of the transient approaches to E-LTP, with proper timescales and Hebbian nature): For STDP, a causal (asymmetric) Hebbian temporal profile, with inter-spike time separation within each pair of tens of ms; for BTSP, a non-Hebbian temporal profile, with transient time scales of several seconds. Moreover, analysis of simulations identifies, within the model, differing primary mechanisms underlying STDP and BTSP: the flow through NMDAR channels sets the millisecond time scale and the causal Hebbian properties of STDP; CaMKII activity sets the slower time scales and noncausal nature of BTSP. In addition, the model supports a priming mechanism that is induced by a small depolarization sufficient to open CaV1.3 channels for ion flow into the spine head. Once in the PSD, this opens the closed compact state of CaMKII, placing CaMKII ready for activation (phosphorylation), triggering the induction of LTP, as well making it easier to realize BTSP. Thus, the model confirms expectations that NMDAR is responsible for the time scales of Hebbian plasticity of STDP and that flow through CaV1 channels could enable a priming mechanism. In addition, the model clearly identifies the interaction of the timescales of the activation of CaMKII with those of the signaling protocols that result in STDP, BTSP, and priming.
Currently, it is not clear experimentally whether co-existing stable fixed points represent either early LTP or the fully phosphorylated state of active CaMKII. In the case of early LTP, the existence of bistable synapses is supported by experimental work showing an all-or-nothing transition of synaptic efficacy (48, 49); however, other experimental studies suggest synapses with a more graded degree of potentiation (50, 51). It also remains unclear experimentally whether stable E-LTP can be achieved by the biochemical activity of CaMKII and PP. Although many modeling simulations observe and implement steady states of the CaMKII & PP system (52–55), newer findings show that the stable plasticity does not have to rely on the stability of the fully activated state of CaMKII (35, 56, 57). Here, we focus on modeling the induction of early LTP/D, over the first several minutes. Active CaMKII could be, and likely is, unstable over longer timescales (hours to days) due to succeeding reactions that are not included in our current model. We view the tri-stable fixed points in our model as representing states that are at best meta-stable, but with sufficient lifetimes to organize the transient dynamics of early LTP/D.
Most previous models of STDP [and all models of BTSP] are phenomenological descriptions of the strengthening/weakening of synapses, including the STDP work (58, 59, 60) [and the BTSP work (61, 62)]. Notable exceptions are the works of (28, 57), which model in some detail the biochemical reactions of CaMKII. Our model of the biochemistry in the PSD begins from the detailed model of the activation of CaMKII of (28) but with several enhancements: First, to model the binding and disassociation of molecules and how they influence phosphorylation and dephosphorylation, we replace Michaelis–Menten schemes (quasi-steady-state) with quasi-equilibrium representations, which are a more fundamental description of the catalytic reactions. Second and most importantly, our representation of the activity states of CaMKII includes the compact state of CaMKII, together with the transition between this compact state and an open but inactive state of CaMKII that is later activated. The presence of the compact state has been well established experimentally (16, 63, 64) and it plays an important role in the model, where inducing a transition from compact to open increases the sensitivity of CaMKII to mild stimuli, and thus strengthens its role as an information integrator, on which we will elaborate below. Third, the model describes the kinase CaMKII pathway interacting with a phosphatase PP pathway, in which the bio-chemical reactions of the CaMKII pathway are described in detail as in (28), while the PP pathway is treated as a generic phosphatase pathway. Details of the particular phosphatases relevant for CA1 pyramidal neurons are still being studied experimentally and seem to us somewhat open. For example, the commonly studied phosphatase inhibitor-1 (I-1) has been shown to have no effect on the PP1-mediated regulation of NMDAR-dependent synaptic plasticity in CA1 pyramidal neurons (29–33). Thus, we decided to represent the phosphatase pathway rather generically, adapting a phenomenological representation from Pi and Lisman (34). Our model of the two interacting pathways retains the tri-stability of the fully phenomenological model of Pi and Lisman—creating a straightforward representation of the synapse’s basal, LTP, and LTD states without ambiguity, and allowing a clear distinction between depression (transition from basal to LTD) and depotentiation (transition from LTP to basal).
Most models of LTP/D in response to the STDP signaling protocol show on the LTP side (negative ) a re-emergence of a “second window” of LTD as the timing difference becomes more negative. This seems reasonable since moderate calcium inflow is known to produce LTD while larger calcium inflow produces LTP; however, this re-emergence is not observed experimentally. Similar effects would be expected when modeling other signaling protocols such as priming and BTSP. Our model does not show a second LTD window for the STDP protocol, nor does extraneous LTD appear under the priming and BTSP protocols. These characteristics arise from the model’s particular responses to the magnitude and duration of the calcium inflow profiles. A revisit to the phase diagram in Fig. 1C reveals two distinct scenarios underlying this absence: i) a brief stimulus ( s) with increased magnitude solely initiates a basal-to-LTP transition, avoiding the LTD region; ii) comparatively, a strong stimulus (M) with decreasing duration exclusively reverts the LTP state back to basal, once again eluding LTD. As shown in detail in SI Appendix, these transitions within our model, devoid of traversals of the LTD region, explain the omitted second LTD window in the STDP protocol, as well as the omission of possible extraneous LTD regions under priming and BTSP protocols. Our work emphasizes a characteristic of our model that is related to tri-stability with a natural basal steady state, offering a more robust and intrinsic resolution to this issue than the delicate balance required for previous models (65).
Fig. 1C also explains the incapability of a single plateau potential to induce BTSP due to its limited calcium influx duration through CaV channels in the absence of pre-synaptic spikes activating NDMAR channels. Given the limited density of CaV channels in the PSD, and their calcium-induced inactivation during depolarization, the total calcium influx is restricted within reasonable ranges of the plateau potential’s strength or duration. This aligns with the idea that a pre-synaptic signal, serving as a synaptic “tag,” is necessary for BTSP.
It is widely known that CaMKII plays essential roles in synaptic plasticity, especially in early LTP & LTD. For example, experiments show that active CaMKII binds to the NMDAR and AMPAR channels, where it leads to a strengthening of the synapse (16, 17). In addition, there is experimental evidence that CaMKII can act as a frequency decoder in synaptic plasticity (66, 67). Recent experiments also suggest the critical involvement of CaMKII in BTSP (68). Our model highlights the potential importance of the seconds-long time scale of the transient activation of CaMKII. As shown in Fig. 6, during this time, CaMKII can be partially activated through a weak stimulus, including pre-synaptic spikes and DC, making LTP easier to be induced by more potent stimuli which follows [for example, the plateau potential as in (10)] [Fig. 6]. This transient activity can sustain for seconds and be further prolonged through phosphorylation of CaMKII, consistent with experimental findings (35, 56). The similarity between the timescale of CaMKII and the timescale of BTSP is intriguing: In the model’s description of BTSP, the activity of CaMKII successfully integrates information of pre-synaptic spikes and the plateau potential, spaced seconds apart. Moreover, again in the model, the time scales of active CaMKII play a vital role in STDP: With a seconds-long duration of activity, CaMKII is retained during the 1-s intervals between the spike pairs (STDP utilizes a 1-Hz stimulus protocol) and accumulates within the large number of repetitions. In summary, the seconds-long time scale of the transient activation of CaMKII allows it to function as an information integrator, both sensitively and stably, making it suitable for different signaling patterns. In other words, the transient activation of CaMKII could operate as an eligibility trace for learning (46, 69, 70).
Our model also realizes a proposed theory of priming (27) in which CaMKII is mildly activated, making it easier for a strong stimulus to induce LTP. In the model, priming is activated by a small DC that selectively opens CaV1.3 channels, allowing for mild inflow which triggers the partial activation of CaMKII. The selectivity for CaV1.3 is thought to occur because, in the voltage range of the mild depolarization, CaV1.3 has a much steeper voltage dependence than CaV1.2 or NMDAR (27). With the model, we investigate the potential role of CaV1.3 channels in priming: First, we measure an enhanced calcium inflow through CaV1 channels (primarily CaV1.3) opened by the mild depolarization. This increases the baseline calcium concentration, which in turn enhances CaMKII activity. During priming, CaV1.3 channels primarily contribute to the mild increase in calcium concentration, even though they constitute only a small portion (around ) of the CaV1 channels in the spine head (71, 72). We further highlight the role of CaV1.3 channels within the model by showing that the deactivation of CaV1.3 abolishes priming and obstructs learning [Fig. 4 and SI Appendix, Fig. S8C]. As demonstrated in Fig. 4D, a depolarization of adequate amplitude targeting only NMDAR can also facilitate the initiation of LTP. This suggests an alternative signaling pathway for LTP, distinct from the mild depolarization that opens CaV channels and primes CaMKII. Note that such necessarily substantial depolarizations could occur during unitary synaptic events in the dendritic spines, causing high peak voltages due to the large spine neck resistance (73, 74).
The model also shows the potential role of priming in behavioral plasticity (like BTSP). In the model, priming through DC injections extends the timescale of BTSP [SI Appendix, Fig. S1B], consistent with experimental findings that increasing baseline membrane potential will increase the timescale of BTSP (46). Analysis [Fig. 4] shows that priming increases the concentration of open CaMKII and slows its decay, which further prolongs CaMKII activity as an information integrator. In reality, this priming could arise from several possible sources—for example, a small DC injection or a transient ramp-like depolarization of place cells. Priming through ramp-like depolarization could explain the irreversible components in experiments of (25). Alternatively, a depolarizing current from other afferent neurons could function as a signal modulating the plasticity, providing a possible explanation for the differences in mouse learning across familiar and novel settings (75). In any event, the model predicts that weak priming will lead to an LTP that can easily be reversed, and stronger priming will result in a more robust LTP.
In the deterministic model, transitions between the three fixed points (basal, LTP, LTD) are abrupt, while in reality, the strengths of LTD and LTP are graded. To capture graded behavior, we introduced a phenomenological noise term that perturbs the ion flow through the channels, in a manner similar to previous work (59, 65, 76). As shown in Results [Figs. 2, 3, and 5], in this stochastic setting, the properties of these transients are graded, with the transition probabilities between different states of CaMKII encoding changes in synaptic efficacy during different stimuli. In future work, this phenomenological noise should be replaced by a more detailed stochastic description of the biochemical reactions within the very small spine head. In this more realistic setting, stochasticity will arise from stochastic inflow through the ion channels, as well as from the small number of ions and proteins present in the spine head.
Our model can be generalized in several directions. In addition to discreteness effects with stochastic representations, the effects of the nonuniformity of calcium concentration throughout the spine head must be captured. For example, there is a much higher calcium concentration near the mouths of the channels, a spatial region of the spine head termed the calcium nanodomain, (77, 78) that leads to a spatially local calcium dynamics (79). Also, CICR (calcium-induced calcium release) from internal storage could play an important role in plasticity for neurons with spine apparatus (80, 81). A particularly important possibility for CICR in BTSP arises from recent work in Yasuda’s Lab (82), in which the authors use an improved CaMKII sensor to measure the presence of active CaMKII in a dendritic spine responding to a BTSP stimulus protocol. They report no detection of active CaMKII in the induction stage, but only later in the dendrite. One possible explanation (82) is that there is not enough Ca2+ entering the PSD to trigger the activation of CaMKII; rather, the calcium activates a delayed CICR release through IP3s, which then triggers the activation of CaMKII. Describing such spatially inhomogeneous effects will require a spatially extended description of the spine head, including at least a multi-compartment representation approximating calcium diffusion. In addition, CaMKII and PP are known to be localized in the PSD (20, 83) and interact with ion channels (NMDAR, AMPAR, CaV) through conformational changes there (26, 84–89). The conformational signaling and localization will also require a compartmental model distinguishing PSD and the rest of the spine head. A more realistic description of the LTD pathway is also needed. Given the diversity of experimental results, several pathways may be involved in the induction of LTD (21, 90); a more detailed model of calcium-inducing LTD must await further experimental studies.
An extension beyond a single synapse to multiple synapses and multiple neurons will be needed to model fully the emergence of place cells. Recently BTSP has been shown to be reversible (46), with initially weak synapses strengthened while initially strong synapses weakened by the same BTSP protocol. Our model in its present form does not capture this form of reversibility because the stability or instability of the LTP state does not depend upon the initial synaptic strength. Currently unspecified mechanisms would have to be added to the model to incorporate this dependence. Possible mechanisms for future investigation include multi-synaptic interactions, phosphorylation at additional specific sites of CaMKII such as Thr-305(6) (91), and downstream processes for AMPAR strengthening.
Materials and Methods
We utilize a single-compartmental, deterministic representation by a system of ODEs to model the biochemical reactions of early LTP/D at the PSD region of a single synapse onto a post-synaptic dendritic spine. Synaptic events will depolarize the membrane and open the relevant ion channels, allowing calcium ions to flow into the spine head. The increasing calcium concentration will activate CaMKII and phosphatase, which will further activate themselves through autocatalytic reactions, while the two will inhibit each other through phosphorylation and dephosphorylation. This sequence of chemical reactions culminates in a strengthening (weakening) of the synaptic strength known as LTP (LTD). The general reaction scheme is illustrated in Fig. 1A.
We describe the model in two parts: i) the dynamics of membrane potential and intracellular calcium concentration, including the dynamics of ion channels; ii) the biochemical reactions composed of two interacting pathways—one “UP” pathway that strengthens the synapses through a kinase called CaMKII, and one “DOWN” pathway that weakens the synapses through a phosphatase (phenomenologically described), combined with a “read-out” mechanism of LTP and LTD from the activity of CaMKII and phosphatase. A complete and detailed description of the model and its parameters is provided in SI Appendix.
Membrane Potential and Calcium Signaling.
To model the chemical system under different stimulus protocols, we need to investigate how the synaptic events induce calcium concentration changes in the spine head. To describe the dynamics of the membrane potential, we follow Graupner and Brunel (28) and embed the spine head in the whole cell.
Membrane potential.
We use a Hodgkin–Huxley formalism model to describe the membrane potential with the following equation:
| [1] |
where is the membrane capacitance, and are the ion currents from different sources. (Eq. 1) describes the voltage V as an iso-potential for the whole cell, including both the soma and the dendrite. Accordingly, capacitance, leakage conductance, and the conductance of sodium and potassium channels are all selected with respect to a surface area of 10,000 m2 (roughly the surface area of a pyramidal neuron), ensuring the generation of a realistic action potential. Moreover, the AMPAR channel conductance is scaled up by tenfold compared to its typical value on one single spine head, resulting in the generation of an EPSP around 1 mV—a value consistent with experimental observations at the soma. The NMDAR and calcium channels represent ion flow into the spine head. We keep these two conductances normalized to a single spine head (no scaling up), to produce reasonable calcium dynamics within the spine head. In the single-compartment iso-potential model, there is no distinction between the voltage at the spine head and that at the soma; thus, in our model, the NMDAR and CaV synaptic input at the spine head only contribute negligibly to EPSPs at the spine head.
Voltage-dependent calcium channels.
Voltage-gated calcium channels (VGCC) (CaV1.2, CaV1.3) potentially play an important role in the mechanisms underlying LTP/LTD. A model beyond a Hodgkin–Huxley representation is required as these channel types show calcium-induced inactivation. Thus, we take a Markovian model of CaV channels in the rabbit heart cell (92) and adapt it to CaV1.2, CaV1.3 channels in the spine setting (93, 94).
Calcium signaling in a dendritic Spine.
Calcium concentration change in the PSD is modeled in a single compartment uniformly in space, similar to (28). Two main sources of calcium inflow into the PSD are calcium influx through NMDAR and VGCC. The calcium concentration follows the differential equation:
| [2] |
where is the factor converting the calcium current to calcium concentration change per unit time and are the fast buffering factors of calcium influx through NMDAR and CaV channels, respectively. The extrusion, diffusion, and slow buffering of calcium are not modeled explicitly, but described by a leak term with single exponential decay to the resting calcium concentration with the time constant equal to 12 ms.
Calcium trace with noise.
The stochastic simulations are performed by adding noise to the calcium dynamics during the synaptic events, through the stochastic opening and closing of ion channels. To represent this stochastic effect, we include two sources of noise following (28): i) random maximum conductance of NMDAR at each presynaptic spike and ii) random maximum conductance of the CaV channels at each postsynaptic spike and plateau potential. During each synaptic event, the channel conductance is drawn from a Gaussian distribution with a given mean and variance, chosen so that the stochastic system can reproduce smooth results, consistent with experiments.
Experimental stimulus protocols.
Prescriptions of presynaptic and postsynaptic spikes and postsynaptic plateau potentials are required to simulate the system under different experimental protocols. Instead of modeling spiking as in vivo, we initiate the system with prescribed presynaptic and postsynaptic spike trains (and plateau potentials).
In our model, we do not detail the presynaptic spiking, the release of neurotransmitters at the presynaptic side, the diffusion of transmitters into the synaptic cleft, or their capture by glutamate receptors. Consequently, synaptic failure is not considered. Instead, we only describe the binding of neurotransmitters to AMPARs and NMDARs. After each presynaptic spike, each AMPAR and NMDAR will bind to one neurotransmitter immediately, initiating channel activation (shown in SI Appendix). For the postsynaptic spikes, we generate an artificial action potential by applying a 1 ms pulse current of 3,000pA, which causes a spike approximately 2 ms after the current injection. Similarly, the postsynaptic plateau potential is induced by a sustained current of 4,000 pA (3,000 pA for the stochastic scenarios), typically lasting for 300 ms.
Biochemical Reactions in a Single Chamber.
The model of biochemical reactions is based on a model of early LTP/D (28) as a bistable system of ODEs, with both UP and DOWN pathways. The model describes the calcium-induced activation of both the kinase (CaMKII) and the phosphatase and the mutual inhibition between the two, with detailed reaction scheme illustrated in Fig. 1 and SI Appendix, Fig. S4 (SI Appendix). Starting from the model in (28), we replace several components in the UP kinase pathway with a more realistic and precise description (adding a compact state of CaMKII (63) and using quasi-equilibrium instead of a Michaelis–Menten scheme). We remove the traditional I1-PP1 signaling for the DOWN phosphatase pathway as it is reported not to be observed in CA1 pyramidal neurons (29–33) and substitute with a phenomenological representation (34). This resulting model is tri-stable with three coexisting stable steady states, directly related to the synapse’s basal, LTP, and LTD states.
Binding and disassociation in fast equilibrium.
The inflowing calcium will bind with calmodulin (CaM), and the calcium–CaM complex can further bind to CaMKII and trigger its activation. At the same time, the phosphorylation of CaMKII requires the binding of ATP and the dephosphorylation of CaMKII requires the binding of phosphatase. We introduce a fast-equilibrium assumption to describe the binding and disassociation between molecules. Specifically, we assume that for the binding of molecular X with Y,
| [3] |
holds for all time, where are the concentration of free , free and complex, respectively, and is a dissociation constant independent of time.
CaM is a calcium-binding messenger protein with two lobes (the N- and C-domains), and each lobe can bind to at most two calcium ions. The resulting calcium–CaM complex can further bind to CaMKII and trigger its activation. For simplicity, we consider only the number of calcium ions bound to calmodulin without distinguishing between states with different binding sites but the same number of calcium ions bound. This simplification leads to five states of CaM (from zero to four ions bound), similarly to (28). Fast-equilibrium is used to model the binding and disassociation of calcium ions, leading to four algebraic equations (shown in SI Appendix).
CaMKII is a dodecameric holoenzyme composed of two stacked hexameric rings formed by six functionally coupled subunits (95). Each subunit provides multiple binding sites for different molecules, and the binding can promote the phosphorylation or dephosphorylation of each subunit, as illustrated in SI Appendix, Fig. S4A. In our model, we also assume that the binding and dissociation of molecules (calcium–CaM complex, phosphatase, ATP, ADP) with CaMKII is in fast equilibrium, similar to calcium binding to calmodulin (detailed equations presented in SI Appendix). The fast-equilibrium assumption, combined with the description of how the binding catalyzes reactions (discussed in the next section), provides an alternative model to describe the catalyzation of phosphorylation and dephosphorylation of CaMKII subunits instead of the Michaelis–Menten scheme used in (28).
Phosphorylation and dephosphorylation of CaMKII.
The binding of the calcium–CaM complex will initiate the phosphorylation at threonine-286 (Thr-286) in the regulatory domain of CaMKII, which disrupts the binding of the regulatory domain to the kinase domain (95). After being phosphorylated, CaMKII subunits can stimulate the phosphorylation of the neighboring subunits, prolonging the activation after the calcium stimulus (96). In our model, CaMKII activity serves as an indicator of potentiation. It is treated in some detail, but with some aspects not considered for simplicity, such as different isoforms of CaMKII subunits or the phosphorylation at Thr-305 and 306.
In modeling the phosphorylation and dephosphorylation of CaMKII, we closely follow Graupner and Brunel (28). Since little is known about how the two rings of the CaMKII interact and how that affects phosphorylation (97), we suppose the two are independent of each other and model only one six-subunit ring. Each CaMKII kinase is treated as a six-subunit ring in which each subunit can be phosphorylated or unphosphorylated independently. This results in a total of 14 states under rotation invariance, as shown in SI Appendix, Fig. S4C. The transition between these different states is through the phosphorylation and dephosphorylation of subunits, which can be divided into two categories (illustrated in SI Appendix, Fig. S4 A and B): i) the spontaneous phosphorylation and dephosphorylation of one subunit and ii) the neighboring phosphorylation of CaMKII (and its reverse reaction). We present the detailed equations and parameters in SI Appendix.
Docking and undocking of CaMKII.
The presence of the compact state of CaMKII has been well established experimentally (16, 63, 64, 98). Compact CaMKII can be bound to actin filaments in the spine head and dendritic shaft, where the compact state’s release from the actin is triggered by calcium–calmodulin binding (26). In our model, we include this compact state as an additional state of CaMKII. Compact CaMKII can become open (“undocking”) with a calcium-dependent rate, and the open CaMKII can return to the compact state (“docking”) when it has no phosphorylated subunits and is not bound to calmodulin or phosphatase [SI Appendix, Fig. S4D].
The transition between the compact state and open state is given by
| [4] |
| [5] |
where and are the concentration of the CaMKII in the compact state and the open state with no phosphorylated subunits, respectively, and is the probability that one unphosphorylated subunit is not bound to calmodulin or phosphatase.
Phenomenological phosphatase dynamics.
Details of the particular phosphatases relevant for CA1 pyramidal neurons are still being studied experimentally (21), and seems to us somewhat open. Thus, we decided to represent the phosphatase pathway rather generically, adapting a phenomenological representation from Pi and Lisman (34):
| [6] |
with and
| [7] |
and are the concentrations of active (dephosphorylated) and inactive (phosphorylated) phosphatase, respectively and is the baseline dephosphorylation activity rate. describes the calcium-dependent rate of dephosphorylation with a lower activation threshold (compared with CaMKII).
LTP, LTD, and synaptic efficacy.
In the model, LTP is represented by the dominance of the concentration of active CaMKII over active PP, and LTD by the dominance of the concentration of active PP over CaMKII. As an indicator of the resulting synaptic efficacy, we adopt a heuristic “read-out” representation [taken from (34)] of the ratio of the number of AMPA receptors on the spine head before and after induction:
| [8] |
where is the number of AMPA receptors on the membrane, and is the number of total available AMPA receptors. In this heuristic representation of AMPA trafficking, () is the rate AMPA is inserted into (removed from) the membrane, represented by a linear functions -pagination . We emphasize that (Eq. 8) operates on a much slower time scale than the activation of CaMKII and PP; thus, (Eq. 8) does not couple back to the dynamics of the CaMKII and PP, but is just a read-out from the concentrations of active CaMKII and PP, which provides an indication of synaptic efficacy.
Supplementary Material
Appendix 01 (PDF)
Acknowledgments
We gratefully acknowledge Richard Tsien for discussions generally about hippocampal synaptic plasticity at the molecular-cellular level and in particular about a possible role of CaV channels in a priming mechanism for long term potentiation.
Author contributions
G.L., D.W.M., and C.S.P. designed research; performed research; contributed new reagents/analytic tools; analyzed data; and wrote the paper.
Competing interests
The authors declare no competing interest.
Footnotes
Reviewers: N.B., Duke University; M.G., University of Paris Descartes; and A.D.M., Rutgers University.
Contributor Information
Guanchun Li, Email: guanchun.li@nyu.edu.
David W. McLaughlin, Email: david.mclaughlin@nyu.edu.
Data, Materials, and Software Availability
The source codes for the computer model can be found on GitHub (99).
Supporting Information
References
- 1.Bliss T. V., Lømo T., Long-lasting potentiation of synaptic transmission in the dentate area of the anaesthetized rabbit following stimulation of the perforant path. J. Physiol. 232, 331–356 (1973). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Dudek S. M., Bear M. F., Homosynaptic long-term depression in area CA1 of hippocampus and effects of N-methyl-D-aspartate receptor blockade. Proc. Natl. Acad. Sci. U.S.A. 89, 4363–4367 (1992). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Markram H., Lübke J., Frotscher M., Sakmann B., Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275, 213–215 (1997). [DOI] [PubMed] [Google Scholar]
- 4.Magee J. C., Johnston D., A synaptically controlled, associative signal for Hebbian plasticity in hippocampal neurons. Science 275, 209–213 (1997). [DOI] [PubMed] [Google Scholar]
- 5.Bi G., Poo M., Synaptic modifications in cultured hippocampal neurons: Dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hebb D. O., The Organization of Behavior: A Neuropsychological Theory (Psychology Press, 2005). [Google Scholar]
- 7.Blum K. I., Abbott L. F., A model of spatial map formation in the hippocampus of the rat. Neural Comput. 8, 85–93 (1996). [DOI] [PubMed] [Google Scholar]
- 8.Izhikevich E. M., Solving the distal reward problem through linkage of STDP and dopamine signaling. Cereb. Cort. 17, 2443–2452 (2007). [DOI] [PubMed] [Google Scholar]
- 9.Cassenaer S., Laurent G., Conditional modulation of spike-timing-dependent plasticity for olfactory learning. Nature 482, 47–52 (2012). [DOI] [PubMed] [Google Scholar]
- 10.Bittner K. C., Milstein A. D., Grienberger C., Romani S., Magee J. C., Behavioral time scale synaptic plasticity underlies CA1 place fields. Science 357, 1033–1036 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Malenka R. C., Kauer J. A., Zucker R. S., Nicoll R. A., Postsynaptic calcium is sufficient for potentiation of hippocampal synaptic transmission. Science 242, 81–84 (1988). [DOI] [PubMed] [Google Scholar]
- 12.J. A. Cummings, R. M. Mulkey, R. A. Nicoll, R. C. Malenka, Ca2+ signaling requirements for long-term depression in the hippocampus. Neuron 16, 825–833 (1996). [DOI] [PubMed]
- 13.D. Neveu, R. S. Zucker, Postsynaptic levels of [Ca2+] i needed to trigger LTD and LTP. Neuron 16, 619–629 (1996). [DOI] [PubMed]
- 14.Inglebert Y., Aljadeff J., Brunel N., Debanne D., Synaptic plasticity rules with physiological calcium levels. Proc. Natl. Acad. Sci. U.S.A. 117, 33639–33648 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Colbran R. J., Brown A. M., Calcium/calmodulin-dependent protein kinase II and synaptic plasticity. Curr. Opin. Neurobiol. 14, 318–327 (2004). [DOI] [PubMed] [Google Scholar]
- 16.Lisman J., Yasuda R., Raghavachari S., Mechanisms of CaMKII action in long-term potentiation. Nat. Rev. Neurosci. 13, 169–182 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Herring B. E., Nicoll R. A., Long-term potentiation: From CaMKII to AMPA receptor trafficking. Annu. Rev. Physiol. 78, 351–365 (2016). [DOI] [PubMed] [Google Scholar]
- 18.Nicoll R. A., Schulman H., Synaptic memory and CaMKII: A review (Physiol, Rev, 2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Munton R. P., Vizi S., Mansuy I. M., The role of protein phosphatase-1 in the modulation of synaptic and structural plasticity. FEBS Lett. 567, 121–128 (2004). [DOI] [PubMed] [Google Scholar]
- 20.Colbran R. J., Protein phosphatases and calcium/calmodulin-dependent protein kinase II-dependent synaptic plasticity. J. Neurosci. 24, 8404–8409 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Foley K., McKee C., Nairn A. C., Xia H., Regulation of synaptic transmission and plasticity by protein phosphatase 1. J. Neurosci. 41, 3040–3050 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Borroni A. M., Fichtenholtz H., Woodside B. L., Teyler T. J., Role of voltage-dependent calcium channel long-term potentiation (LTP) and NMDA LTP in spatial memory. J. Neurosci. 20, 9272–9276 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Woodside B., Borroni A., Hammonds M., Teyler T., NMDA receptors and voltage-dependent calcium channels mediate different aspects of acquisition and retention of a spatial memory task. Neurobiol. Learn. Memory 81, 105–114 (2004). [DOI] [PubMed] [Google Scholar]
- 24.Moosmang S., et al. , Role of hippocampal Cav1. 2 Ca2+ channels in NMDA receptor-independent synaptic plasticity and spatial memory. J. Neurosci. 25, 9883–9892 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lee D., Lin B. J., Lee A. K., Hippocampal place fields emerge upon single-cell manipulation of excitability during behavior. Science 337, 849–853 (2012). [DOI] [PubMed] [Google Scholar]
- 26.Li B., Tadross M. R., Tsien R. W., Sequential ionic and conformational signaling by calcium channels drives neuronal gene expression. Science 351, 863–867 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ma H., et al. , Excitation-transcription coupling, neuronal gene expression and synaptic plasticity. Nat. Rev. Neurosci. 24, 672–692 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Graupner M., Brunel N., STDP in a bistable synapse model based on CaMKII and associated signaling pathways. PLoS Comput. Biol. 3, e221. (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Allen P. B., et al. , Protein phosphatase-1 regulation in the induction of long-term potentiation: Heterogeneous molecular mechanisms. J. Neurosci. 20, 3537–3543 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bibb J. A., et al. , Phosphorylation of protein phosphatase inhibitor-1 by Cdk5. J. Biol. Chem. 276, 14490–14497 (2001). [DOI] [PubMed] [Google Scholar]
- 31.Cohen P. T., Protein phosphatase 1-targeted in many directions. J. Cell Sci. 115, 241–256 (2002). [DOI] [PubMed] [Google Scholar]
- 32.Feng J., et al. , Spinophilin regulates the formation and function of dendritic spines. Proc. Natl. Acad. Sci. U.S.A. 97, 9287–9292 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kennedy M. B., Synaptic signaling in learning and memory. Cold Spring Harb. Persp. Biol. 8, a016824 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Pi H. J., Lisman J. E., Coupled phosphatase and kinase switches produce the tristability required for long-term potentiation and long-term depression. J. Neurosci. 28, 13132–13138 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.J. Y. Chang, Y. Nakahata, Y. Hayano, R. Yasuda, Mechanisms of Ca2+/calmodulin-dependent kinase II activation in single dendritic spines. Nat. Commun. 10, 1–12 (2019). [DOI] [PMC free article] [PubMed]
- 36.S. N. Yang, Y. G. Tang, R. S. Zucker, Selective induction of LTP and ltd by postsynaptic [Ca2+]i elevation. J. Neurophysiol. 81, 781–787 (1999). [DOI] [PubMed]
- 37.Mizuno T., Kanazawa I., Sakurai M., Differential induction of LTP and LTD is not determined solely by instantaneous calcium concentration: An essential involvement of a temporal factor. Euro. J. Neurosci. 14, 701–708 (2001). [DOI] [PubMed] [Google Scholar]
- 38.Bienenstock E. L., Cooper L. N., Munro P. W., Theory for the development of neuron selectivity: Orientation specificity and binocular interaction in visual cortex. J. Neurosci. 2, 32–48 (1982). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Muller D., Hefft S., Figurov A., Heterosynaptic interactions between up and LTD in CA1 hippocampal slices. Neuron 14, 599–605 (1995). [DOI] [PubMed] [Google Scholar]
- 40.Huang C. C., Liang Y. C., Hsu K. S., Characterization of the mechanism underlying the reversal of long term potentiation by low frequency stimulation at hippocampal CA1 synapses* 210. J. Biol. Chem. 276, 48108–48117 (2001). [DOI] [PubMed] [Google Scholar]
- 41.Song S., Miller K. D., Abbott L. F., Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 3, 919–926 (2000). [DOI] [PubMed] [Google Scholar]
- 42.Abbott L. F., Nelson S. B., Synaptic plasticity: Taming the beast. Nat. Neurosci. 3, 1178–1183 (2000). [DOI] [PubMed] [Google Scholar]
- 43.K. D. Carlson, N. Giordano, Interplay of the magnitude and time-course of postsynaptic Ca2+ concentration in producing spike timing-dependent plasticity J. Comput. Neurosci. 30, 747–758 (2011). [DOI] [PubMed]
- 44.Hsu C. L., Zhao X., Milstein A. D., Spruston N., Persistent sodium current mediates the steep voltage dependence of spatial coding in hippocampal pyramidal neurons. Neuron 99, 147–162 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bittner K. C., et al. , Conjunctive input processing drives feature selectivity in hippocampal CA1 neurons. Nat. Neurosci. 18, 1133–1142 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Milstein A. D., et al. , Bidirectional synaptic plasticity rapidly modifies hippocampal representations. Elife 10 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Lester R. A., Clements J. D., Westbrook G. L., Jahr C. E., Channel kinetics determine the time course of NMDA receptor-mediated synaptic currents. Nature 346, 565–567 (1990). [DOI] [PubMed] [Google Scholar]
- 48.Petersen C. C., Malenka R. C., Nicoll R. A., Hopfield J. J., All-or-none potentiation at CA3-CA1 synapses. Proc. Natl. Acad. Sci. U.S.A. 95, 4732–4737 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.O’Connor D. H., Wittenberg G. M., Wang S. S. H., Graded bidirectional synaptic plasticity is composed of switch-like unitary events. Proc. Natl. Acad. Sci. U.S.A. 102, 9679–9684 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.K. K. Liu, M. F. Hagan, J. E. Lisman, Gradation (approx., 10 size states) of synaptic strength by quantal addition of structural modules. Philos. Trans. R. Soc. B: Biol. Sci. 372, 20160328 (2017). [DOI] [PMC free article] [PubMed]
- 51.Mel B. W., Schiller J., Poirazi P., Synaptic plasticity in dendrites: Complications and coping strategies. Curr. Opin. Neurobiol. 43, 177–186 (2017). [DOI] [PubMed] [Google Scholar]
- 52.Lisman J., A mechanism for the Hebb and the anti-Hebb processes underlying learning and memory. Proc. Natl. Acad. Sci. U.S.A. 86, 9574–9578 (1989). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.A. M. Zhabotinsky, Bistability in the Ca2+/calmodulin-dependent protein kinase-phosphatase system. J. Biophys. 79, 2211–2221 (2000). [DOI] [PMC free article] [PubMed]
- 54.Hayer A., Bhalla U. S., Molecular switches at the synapse emerge from receptor and kinase traffic. PLoS Comput. Biol. 1, e20 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Miller P., Zhabotinsky A. M., Lisman J. E., Wang X. J., The stability of a stochastic CaMKII switch: Dependence on the number of enzyme molecules and protein turnover. PLoS Biol. 3, e107 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Chang J. Y., et al. , CaMKII autophosphorylation is necessary for optimal integration of Ca2+ signals during LTP induction, but not maintenance. Neuron 94, 800–808 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Pharris M. C., et al. , A multi-state model of the CaMKII dodecamer suggests a role for calmodulin in maintenance of autophosphorylation. PLoS Comput. Biol. 15, e1006941. (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Shouval H. Z., Bear M. F., Cooper L. N., A unified model of NMDA receptor-dependent bidirectional synaptic plasticity. Proc. Natl. Acad. Sci. U.S.A. 99, 10831–10836 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Shouval H. Z., Kalantzis G., Stochastic properties of synaptic transmission affect the shape of spike time-dependent plasticity curves. J. Neurophysiol. 93, 1069–1073 (2005). [DOI] [PubMed] [Google Scholar]
- 60.Clopath C., Büsing L., Vasilaki E., Gerstner W., Connectivity reflects coding: A model of voltage-based STDP with homeostasis. Nat. Neurosci. 13, 344–352 (2010). [DOI] [PubMed] [Google Scholar]
- 61.Cone I., Shouval H. Z., Learning precise spatiotemporal sequences via biophysically realistic learning rules in a modular, spiking network. Elife 10, e63751 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.T. Moldwin, L. S. Azran, I. Segev, A generalized framework for the calcium control hypothesis describes weight-dependent synaptic changes in behavioral time scale plasticity. bioRxiv (2023). https://www.biorxiv.org/content/10.1101/2023.07.13.548837v3 (Accessed 16 July 2023).
- 63.Chao L. H., et al. , A mechanism for tunable autoinhibition in the structure of a human Ca2+/calmodulin-dependent kinase II holoenzyme. Cell 146, 732–745 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Myers J. B., et al. , The CaMKII holoenzyme structure in activation-competent conformations. Nat. Commun. 8, 1–15 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Graupner M., Brunel N., Calcium-based plasticity model explains sensitivity of synaptic changes to spike pattern, rate, and dendritic location. Proc. Natl. Acad. Sci. U.S.A. 109, 3991–3996 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Mayford M., Wang J., Kandel E. R., O’Dell T. J., CaMKII regulates the frequency-response function of hippocampal synapses for the production of both LTD and LTP. Cell 81, 891–904 (1995). [DOI] [PubMed] [Google Scholar]
- 67.De Koninck P., Schulman H., Sensitivity of CaM kinase II to the frequency of Ca2+ oscillations Science 279, 227–230 (1998). [DOI] [PubMed] [Google Scholar]
- 68.Xiao K., Li Y., Chitwood R. A., Magee J. C., A critical role for CaMKII in behavioral timescale synaptic plasticity in hippocampal CA1 pyramidal neurons. Sci. Adv. 9, eadi3088 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Gerstner W., Lehmann M., Liakoni V., Corneil D., Brea J., Eligibility traces and plasticity on behavioral time scales: Experimental support of neohebbian three-factor learning rules. Front. Neural Circuit. 12, 53 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Magee J. C., Grienberger C., Synaptic plasticity forms and functions. Annu. Rev. Neurosci. 43, 95–117 (2020). [DOI] [PubMed] [Google Scholar]
- 71.Hell J. W., et al. , Identification and differential subcellular localization of the neuronal class C and class D L-type calcium channel alpha 1 subunits. J. Cell Biol. 123, 949–962 (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Xu W., Lipscombe D., Neuronal CaV1. 31 l-type channels activate at relatively hyperpolarized membrane potentials and are incompletely inhibited by dihydropyridines. J. Neurosci. 21, 5944–5951 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Harnett M. T., Makara J. K., Spruston N., Kath W. L., Magee J. C., Synaptic amplification by dendritic spines enhances input cooperativity. Nature 491, 599–602 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Beaulieu-Laroche L., Harnett M. T., Dendritic spines prevent synaptic voltage clamp. Neuron 97, 75–82 (2018). [DOI] [PubMed] [Google Scholar]
- 75.Zhao X., Hsu C. L., Spruston N., Rapid synaptic plasticity contributes to a learned conjunctive code of position and choice-related information in the hippocampus. Neuron 110, 96–108 (2022). [DOI] [PubMed] [Google Scholar]
- 76.Goldwyn J. H., Shea-Brown E., The what and where of adding channel noise to the Hodgkin-Huxley equations. PLoS Comput. Biol. 7, e1002247 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Chad J., Eckert R., Calcium domains associated with individual channels can account for anomalous voltage relations of Ca-dependent responses. Biophys. J. 45, 993–999 (1984). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Simon S. M., Llinás R. R., Compartmentalization of the submembrane calcium activity during calcium influx and its significance in transmitter release. Biophys. J. 48, 485–498 (1985). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Tadross M. R., Tsien R. W., Yue D. T., Ca2+ channel nanodomains boost local Ca2+ amplitude Proc. Natl. Acad. Sci. U.S.A. 110, 15794–15799 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.O’Hare J. K., et al. , Compartment-specific tuning of dendritic feature selectivity by intracellular Ca2+ release. Science 375, eabm1670 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Rosado J., et al. , Calcium modeling of spine apparatus-containing human dendritic spines demonstrates an “all-or-nothing’’ communication switch between the spine head and dendrite. PLoS Comput. Biol. 18, e1010069 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.A. Jain et al., Dendritic, delayed and stochastic CaMKII activation underlies behavioral time scale plasticity in CA1 synapses. bioRxiv [Preprint] (2023). https://www.biorxiv.org/content/10.1101/2023.08.01.549180v1 (Accessed 1 August 2023).
- 83.S. Strack, M. A. Barban, B. E. Wadzinski, R. J. Colbran, Differential inactivation of postsynaptic density-associated and soluble Ca2+/calmodulin-dependent protein kinase II by protein phosphatases 1 and 2A. J. Neurochem. 68, 2119–2128 (1997). [DOI] [PubMed]
- 84.Bayer K., et al. , Interaction with the NMDA receptor locks CaMKII in an active conformation. Nature 411, 801–805 (2001). [DOI] [PubMed] [Google Scholar]
- 85.Chan S. F., Sucher N. J., An NMDA receptor signaling complex with protein phosphatase 2A. J. Neurosci. 21, 7985–7992 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Hudmon A., et al. , CaMKII tethers to L-type Ca2+ channels, establishing a local and dedicated integrator of Ca2+ signals for facilitation. J. Cell Biol. 171, 537–547 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Aow J., Dore K., Malinow R., Conformational signaling required for synaptic plasticity by the NMDA receptor complex. Proc. Natl. Acad. Sci. U.S.A. 112, 14711–14716 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Tullis J. E., et al. , LTP induction by structural rather than enzymatic functions of CaMKII. Nature 1–8 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.X. Chen et al., CaMKII autophosphorylation but not downstream kinase activity is required for synaptic memory. bioRxiv [Preprint] (2023). https://www.biorxiv.org/content/10.1101/2023.08.25.554912v1 (Accessed 25 August 2023).
- 90.Hou H., et al. , Synaptic NMDA receptor stimulation activates PP1 by inhibiting its phosphorylation by Cdk5. J. Cell Biol. 203, 521–535 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Cook S. G., Buonarati O. R., Coultrap S. J., Bayer K. U., CaMKII holoenzyme mechanisms that govern the LTP versus LTD decision. Sci. Adv. 7, eabe2300 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Mahajan A., et al. , A rabbit ventricular action potential model replicating cardiac dynamics at rapid heart rates. Biophys. J. 94, 392–410 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Lipscombe D., Helton T. D., Xu W., L-type calcium channels: The low down. J. Neurophysiol. 92, 2633–2641 (2004). [DOI] [PubMed] [Google Scholar]
- 94.Helton T. D., Xu W., Lipscombe D., Neuronal L-type calcium channels open quickly and are inhibited slowly. J. Neurosci. 25, 10247–10251 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Lisman J., Schulman H., Cline H., The molecular basis of CaMKII function in synaptic and behavioural memory. Nat. Rev. Neurosci. 3, 175–190 (2002). [DOI] [PubMed] [Google Scholar]
- 96.Hanson P. I., Meyer T., Stryer L., Schulman H., Dual role of calmodulin in autophosphorylation of multifunctional CaM kinase may underlie decoding of calcium signals. Neuron 12, 943–956 (1994). [DOI] [PubMed] [Google Scholar]
- 97.J. M. Bradshaw, A. Hudmon, H. Schulman, Chemical quenched flow kinetic studies indicate an intraholoenzyme autophosphorylation mechanism for Ca2+/calmodulin-dependent protein kinase II. J. Biol. Chem. 277, 20991–20998 (2002). [DOI] [PubMed]
- 98.M. M. Stratton, L. H. Chao, H. Schulman, J. Kuriyan, Structural studies on the regulation of Ca2+/calmodulin dependent protein kinase II. Curr. Opin. Struct. Biol. 23, 292–301 (2013). [DOI] [PMC free article] [PubMed]
- 99.G. Li, “Biochemical Model LTP-LTD”. GitHub. https://github.com/GuanchunLi/Biochemical-Model-LTP-LTD/. Deposited 14 January 2024.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Data Availability Statement
The source codes for the computer model can be found on GitHub (99).