Archimedean Heronian mean operators based on complex intuitionistic fuzzy sets and their applications in decision-making problems

Abstract

In this article, we derive the Archimedean aggregation operators for complex intuitionistic fuzzy sets, for this, first, we evaluate some Archimedean operational laws based on complex intuitionistic fuzzy values and then we discuss their special cases because the Archimedean norms are the general form of all existing norms, for instance, algebraic, Einstein, Hamacher, and Frank operational laws. Furthermore, we present the complex intuitionistic fuzzy Archimedean Heronian aggregation operator and complex intuitionistic fuzzy weighted Archimedean Heronian aggregation operator. Several special cases and the basic properties of the above-proposed operators are also diagnosed, because proposing the Heronian mean operators based on Archimedean norms are very challenging and complicated tasks, because of their features and structure. Additionally, a decision-making process is developed under the identified operators by using complex intuitionistic fuzzy information. Finally, we illustrate several examples to show the multi-attribute decision-making technique is more flexible than the prevailing works with the help of sensitive analysis between explored and certain prevailing works.

1. Introduction

The decision-making procedure is a technique that contains a lot of types, for instance, MADM technique, MAGDM technique, MCDM technique, and many others, which are used for addressing the best optimal among the collection of finite decisions. In some cases, experts have lost a lot of data, if they use the classical information for evaluating the MADM procedure because in the case of classical set theory, experts have only two opinions like zero or one. Zadeh [1] extended the range of the classical set and derived the FS. The range of FS is unit interval instead of {0,1} and because of this reason, experts have a lot of space for taking their decision. Adjust the grade of falsity is a very challenging task for scholars, because in many cases the falsity grade played an important role, especially during the elections, For handling such kind of problems, Atanassov [2] computed the IFS with a well-known rule: $0\le {\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{TD}}\left({\mathcal{x}}_{EL}\right)+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{FD}}\left({\mathcal{x}}_{EL}\right)\le 1$, where ${\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{FD}}\left({\mathcal{x}}_{EL}\right)$ and ${\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{TD}}\left({\mathcal{x}}_{EL}\right)$ represents the TD and FD. Some extensions and implementations of IFS are as follows: IVIFSs [3], Dombi aggregation operators for IFSs [4], entropy measures for IVIFSs [5], Bipolar soft sets [6], failure mode and effects analysis [7], improved TODIM processes [8], operational laws for IFSs [9], aggregation and infinite chains for IFSs [10], parameterized IVIFSs [11], telecom services providers under the IFSs [12], MABAC method for IFSs [13], and distance measures for IVIFSs [14].

The TD in FS theory is computed in the form of a simple function that can easily deal with one-dimensional information, but in our daily life problems, experts have faced a lot of problems that are present in the shape of two-dimensional information. For managing such kinds of problems, we needed to find a structure that has computed in the shape of a complex number, where the complex number can easily depict the two-dimensional problem. Therefore, we found a novel concept of complex FS (CFS), which was invented by Ramot et al. [15]. The TD in CFS is arranged in the shape of polar coordinates. Furthermore, operation properties for CFS were explored by Zhang et al. [16], complex fuzzy logic was explored by Ramot et al. [17], systematic view of CFS was presented by Yazdanbakhsh and Disk [18], neuro-fuzzy architecture for CFSs was developed by Chan et al. [19], complex neuro-fuzzy ARIMA forecasting was initiated by Li and Chiang [20], Distance measures for CFS was proposed by Hu et al. [21], periodic factor based on CFS was investigated by Ma et al. [22], linguistic variable for CFS was explored by Alkouri and Salleh [23], cross-entropy measures for CFSs was developed by Liu et al. [24], and distance measures for interval-valued CFSs were presented Dai et al. [25]. But sometimes the principle of CFS is enabled to describe the ambiguity and inconsistency in genuine life dilemmas. For this, the principle of complex IFS (CIFS) was initiated by Alkouri and Salleh [26] by putting the FD ${\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{CI}}\left({\mathcal{x}}_{EL}\right)={\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}\left({\mathcal{x}}_{EL}\right)e^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\left({\mathcal{x}}_{EL}\right)\right)}$ in the region of CFSs, which covers only the TD ${\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{CI}}\left({\mathcal{x}}_{EL}\right)={\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}\left({\mathcal{x}}_{EL}\right)e^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\left({\mathcal{x}}_{EL}\right)\right)}$ with some well-known rules: $0\le {\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}\left({\mathcal{x}}_{EL}\right)+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}\left({\mathcal{x}}_{EL}\right)\le 1$ and $0\le {\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\left({\mathcal{x}}_{EL}\right)+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\left({\mathcal{x}}_{EL}\right)\le 1$. CFSs are the specific part of the CIFSs, and numerous individuals have employed them in distinct regions. For illustration, information measures [27], robust correlation coefficient [28], generalized geometric aggregation operators [29], robust averaging/geometric aggregation operators [30], aggregation operators for generalized CIFSs [31], power aggregation operators [32], preference relation for CIFSs [33], and complex intuitionistic fuzzy soft sets [34].

The fundamental theory of Archimedean norms for IFS was proposed by Xia et al. [35], with the help of Archimedean norms, we can easily derive any kind of operators and their special cases. Furthermore, Luo et al. [36] initiated the exponential laws for IFS. Garg and Rani [37] elaborated on the generalized Bonferroni mean operators for IFSs. Moreover, Yu [38] initiated interval-valued multiplicative IFS based on Archimedean TN and TCN. Ma and Yang [39] presented the weighted mean operators using the Archimedean TN and TCN for IFSs. Liu et al. [40] derived the Quasi-OWA operators. Liu and Chen [41] proposed to the HM operators. Seikh and Mandal [42] evaluated the Frank operators for q-rung orthopair fuzzy sets and their application in decision-making. Recently, Seikh and Mandal [43] evaluated the Frank operators for picture fuzzy sets and their application in decision-making problems. After a brief discussion, we noticed that all experts have the following major issues, such as:

• 1)How do we evaluate generalized operational laws for all t-norms and t-conorms?
• 2)How do we propose generalized aggregation operators for CIFSs?
• 3)How do we rank all the alternatives for evaluating the best optimal between a finite number of alternatives?

For dealing with the above three queries, we needed to develop the Archimedean Heronian mean operators for CIFSs because, with the help of these investigations, we can easily derive any kind of operators. It is clear that many scholars have invented the Heronian mean operators for FSs, and IFSs, but no one can derive it for CIFSs. Furthermore, the Archimedean operational laws for IFS have been proposed, but no one can derive them for CIFSs. Combining the Archimedean operational laws and Heronian mean operators with CIFS is very awkward and complicated because no one can derive it after the investigation of CIFS in 2012 up to yet. The proposed techniques are very reliable and dominant because of their structure, where many advantages follow, for instance, Archimedean aggregation operators, Heronian mean operators, Aggregation operators, Einstein aggregation operators, Hamacher aggregation operators, Frank aggregation operators, Heronian Aggregation operators, Einstein Heronian aggregation operators, Hamacher Heronian aggregation operators, and Frank Heronian aggregation operators for FSs, IFSs, CFSs, and CIFSs are exceptional cases of the derived work. Similarly, we have a lot of possibilities to derive different types of operators from the invented Archimedean Heronian mean operators based on CIFSs. Based on the above advantages, the major contributions of the derived operators are listed below:

• 1)To propose the Archimedean operational laws based on CIF values.
• 2)To derive the algebraic operational laws, Einstein operational laws, Hamacher operational laws, and Frank operational laws from the Archimedean operational laws by using different values of the functions in Archimedean operational laws.
• 3)To evaluate the CIFAHA operator and CIFWAHA operator. Several special cases and the basic properties of the above-proposed operators are also diagnosed.
• 4)To illustrate the MADM process is developed under the identified operators by using CIF information.
• 5)To discover several examples to show the MADM technique is massively more flexible than the prevailing works with the help of sensitive analysis between explored and certain prevailing works. The major findings of the proposed theory are stated in Fig. 1.

Fig. 1.

Representation of the summery of the proposed approaches.

The major objective of this analysis is reviewed in the subsequent approaches: In section 2, we revised the prevailing principles of CIFSs and their algebraic laws. Moreover, the principle of HM operator, algebraic, Einstein, Hamacher, frank operational laws, and the generalized form of TN and TCN are also revised in this study. In section 3, we elaborated on the algebraic, Einstein, Hamacher, and Frank rules for the CIF setting. Numerous specific cases of the presented rules are also illustrated with the help of parameters. In section 4, we initiated the CIFAHA operator and the CIFWAHA operator. Several important properties and their related results are also diagnosed. In section 5, we developed a MADM process under the identified operators by using CIF information. We illustrated several examples to show the MADM technique is massive flexible than the prevailing works with the help of sensitive analysis between explored and certain prevailing works. In section 6, we employed the assumption of this analysis.

2. Preliminaries

In this analysis, we revised the prevailing principles of CIFSs and their algebraic laws. Moreover, the principle of HM operator, algebraic, Einstein, Hamacher, frank operational laws, and the generalized form of TN and TCN are also revised in this study. The term ${\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{CI}}\left({\mathcal{x}}_{EL}\right)={\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}\left({\mathcal{x}}_{EL}\right)e^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\left({\mathcal{x}}_{EL}\right)\right)}$ and ${\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{CI}}\left({\mathcal{x}}_{EL}\right)={\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}\left({\mathcal{x}}_{EL}\right)e^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\left({\mathcal{x}}_{EL}\right)\right)}$, stated the TD and FD and the universal were invented by ${\mathfrak{X}}_u$.

Definition 1

[26] An CIFS ${\stackrel{═}{\mathfrak{k}\xi }}_{CI}$ is invented by:

$${\stackrel{═}{\mathfrak{k}\xi }}_{CI}=\left\{\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{CI}}\left({\mathcal{x}}_{EL}\right),{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{CI}}\left({\mathcal{x}}_{EL}\right)\right):{\mathcal{x}}_{EL}\in {\mathfrak{X}}_u\right\}$$ (1)

where ${\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{CI}}\left({\mathcal{x}}_{EL}\right)={\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}\left({\mathcal{x}}_{EL}\right)e^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\left({\mathcal{x}}_{EL}\right)\right)}$ and ${\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{CI}}\left({\mathcal{x}}_{EL}\right)={\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}\left({\mathcal{x}}_{EL}\right)e^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\left({\mathcal{x}}_{EL}\right)\right)}$, with $0\le {\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}\left({\mathcal{x}}_{EL}\right)+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}\left({\mathcal{x}}_{EL}\right)\le 1$ and $0\le {\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\left({\mathcal{x}}_{EL}\right)+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\left({\mathcal{x}}_{EL}\right)\le 1$. The structure ${\mathbb{R}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{CI}}={\mathbb{R}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}\left({\mathcal{x}}_{EL}\right)e^{i2\pi \left({\mathbb{R}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\left({\mathcal{x}}_{EL}\right)\right)}=\left(1-\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}\left({\mathcal{x}}_{EL}\right)+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}\left({\mathcal{x}}_{EL}\right)\right)\right)e^{i2\pi \left(1-\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\left({\mathcal{x}}_{EL}\right)+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\left({\mathcal{x}}_{EL}\right)\right)\right)}$, conveyed the neutral grade. The CIFNs are mentioned by: ${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)}\right),\theta =1,2,\dots ,\mathfrak{L}$.

Definition 2

[28] Choose any two CIFNs ${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}\right)$ and ${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)}\right)$, then

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\oplus {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}=\left(\begin{array}{c}\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}+{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\right)e^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}+{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)},\\ {\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)}\end{array}\right)$$ (2)

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\otimes {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}=\left(\begin{array}{c}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)},\\ \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\right)e^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)}\end{array}\right)$$ (3)

$$\stackrel{═}{{\gamma }_{SC}}{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}=\left(1-{\left(1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}{e}^{i2\pi \left(1-{\left(1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}^{\stackrel{═}{{\gamma }_{SC}}}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}^{\stackrel{═}{{\gamma }_{SC}}}\right)}\right),\stackrel{═}{{\gamma }_{SC}}>0$$ (4)

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}^{\stackrel{═}{{\gamma }_{SC}}}=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}^{\stackrel{═}{{\gamma }_{SC}}}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}^{\stackrel{═}{{\gamma }_{SC}}}\right)},1-{\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}{e}^{i2\pi \left(1-{\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}\right)}\right),\stackrel{═}{{\gamma }_{SC}}>0$$ (5)

For more simplification, we justify the data in Def. (2) with the help of some suitable examples, for this we consider any two CIFNs, such as ${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}=\left(0.5e^{i2\pi \left(0.6\right)},0.3e^{i2\pi \left(0.2\right)}\right)$ and ${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}=\left(0.7e^{i2\pi \left(0.8\right)},0.2e^{i2\pi \left(0.1\right)}\right)$ with $\stackrel{═}{{\gamma }_{SC}}=2$, then

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\oplus {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}=\left(\begin{array}{c}\left(0.5+0.7-0.5*0.7\right)e^{i2\pi \left(0.6+0.8-0.6*0.8\right)},\\ \left(0.3*0.2\right)e^{i2\pi \left(0.2*0.1\right)}\end{array}\right)=\left(\begin{array}{c}\left(1.2-0.35\right)e^{i2\pi \left(1.4-0.48\right)},\\ \left(0.06\right)e^{i2\pi \left(0.02\right)}\end{array}\right)=\left(\left(0.85\right)e^{i2\pi \left(0.92\right)},\left(0.06\right)e^{i2\pi \left(0.02\right)}\right)\text{.}$$

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\otimes {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}=\left(\begin{array}{c}\left(0.5*0.7\right)e^{i2\pi \left(0.6*0.8\right)},\\ \left(0.3+0.2-0.3*0.2\right)e^{i2\pi \left(0.2+0.1-0.2*0.1\right)}\end{array}\right)=\left(\begin{array}{c}\left(0.35\right)e^{i2\pi \left(0.48\right)},\\ \left(0.5-0.06\right)e^{i2\pi \left(0.3-0.02\right)}\end{array}\right)=\left(\left(0.35\right)e^{i2\pi \left(0.48\right)},\left(0.44\right)e^{i2\pi \left(0.28\right)}\right)\text{.}$$

$$2*{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}=\left(1-{\left(1-0.5\right)}^2{e}^{i2\pi \left(1-{\left(1-0.6\right)}^2\right)},{\left(0.3\right)}^2{e}^{i2\pi {\left(0.2\right)}^2}\right)=\left(1-{\left(0.5\right)}^2{e}^{i2\pi \left(1-{\left(0.4\right)}^2\right)},\left(0.09\right)e^{i2\pi \left(0.04\right)}\right)=\left(\left(1-0.25\right)e^{i2\pi \left(1-0.16\right)},\left(0.09\right)e^{i2\pi \left(0.04\right)}\right)=\left(\left(0.75\right)e^{i2\pi \left(0.84\right)},\left(0.09\right)e^{i2\pi \left(0.04\right)}\right)\text{.}$$

$${\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\right)}^2=\left({\left(0.5\right)}^2{e}^{i2\pi {\left(0.6\right)}^2},1-{\left(1-0.3\right)}^2{e}^{i2\pi \left(1-{\left(1-0.2\right)}^2\right)}\right)=\left(\left(0.25\right)e^{i2\pi \left(0.36\right)},1-{\left(0.7\right)}^2{e}^{i2\pi \left(1-{\left(0.8\right)}^2\right)}\right)=\left(\left(0.25\right)e^{i2\pi \left(0.36\right)},\left(1-0.49\right)e^{i2\pi \left(1-0.64\right)}\right)=\left(\left(0.25\right)e^{i2\pi \left(0.36\right)},\left(0.51\right)e^{i2\pi \left(0.36\right)}\right)\text{.}$$

Definition 3

[29] Choose any CIFN ${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}\right)$, then the score value (SV) is invented by:

$$\stackrel{═}{{\mathfrak{S}}_{SV}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\right)=\frac{1}{2}\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}+{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)$$ (6)

where $\stackrel{═}{{\mathfrak{S}}_{SV}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\right)\in \left[-1,1\right]$.

Definition 4

[30] Choose any CIFN ${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}\right)$, then the accuracy value (AV) is invented by:

$$\stackrel{═}{{\mathfrak{R}}_{AV}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\right)=\frac{1}{2}\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}+{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)$$ (7)

where $\stackrel{═}{{\mathfrak{R}}_{AV}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\right)\in \left[0,1\right]$.

Keeping in mind Eqs. (1), (2), (3), (4), (5), we have the following notions.

Definition 5

[30] Choose any two CIFNs ${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}\right)$ and ${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)}\right)$, then by using Eq. (6) and Eq. (7), we initiate

• 1.$⟹\stackrel{═}{{\mathfrak{S}}_{SV}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\right)>\stackrel{═}{{\mathfrak{S}}_{SV}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}\right)⟹{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}$;
• 2.$⟹\stackrel{═}{{\mathfrak{S}}_{SV}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\right)<\stackrel{═}{{\mathfrak{S}}_{SV}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}\right)⟹{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}<{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}$;
• 3.
  $⟹\stackrel{═}{{\mathfrak{S}}_{SV}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\right)=\stackrel{═}{{\mathfrak{S}}_{SV}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}\right)⟹$.

  • i)
    $⟹\stackrel{═}{{\mathfrak{R}}_{AV}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\right)>\stackrel{═}{{\mathfrak{R}}_{AV}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}\right)⟹{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}$;
  • ii)
    $⟹\stackrel{═}{{\mathfrak{R}}_{AV}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\right)<\stackrel{═}{{\mathfrak{R}}_{AV}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}\right)⟹{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}<{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}$;
  • iii)
    $⟹\stackrel{═}{{\mathfrak{R}}_{AV}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\right)=\stackrel{═}{{\mathfrak{R}}_{AV}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}\right)⟹{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}={\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}$.

Definition 6

[40] Choose any group of integers (+ve) ${\stackrel{═}{\mathfrak{k}\xi }}_{PI-\theta },\theta =1,2,\dots ,\mathfrak{L}$, thus

$$H{M}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{PI-1},{\stackrel{═}{\mathfrak{k}\xi }}_{PI-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{PI-\mathfrak{L}}\right)={\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=1}^{\mathfrak{L}}{\stackrel{═}{\mathfrak{k}\xi }}_{PI-\theta }^{\stackrel{═}{\mathcal{f}}}{\stackrel{═}{\mathfrak{k}\xi }}_{PI-k}^{\stackrel{═}{\mathcal{g}}}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}$$ (8)

Eq. (8) represents the HM operator, where $\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}\ge 0$. Furthermore, various valuable and well-known norms are stated below:

• 1.Algebraic norms [41]:

$$\overbrace{{\mathbb{T}}_{TN}}\left({\mathcal{x}}_{EL},{\mathcal{y}}_{EL}\right)={\mathcal{x}}_{EL}{\mathcal{y}}_{EL}⟶\mathrm{t}-\text{norm}\left(\text{additive}\text{generator}\right):\overbrace{\eta }\left(\stackrel{\dots }{\mathcal{t}}\right)=-\ln \left(\stackrel{\dots }{\mathcal{t}}\right)$$ (9)

$$\overbrace{{\mathbb{S}}_{TN}}\left({\mathcal{x}}_{EL},{\mathcal{y}}_{EL}\right)={\mathcal{x}}_{EL}+{\mathcal{y}}_{EL}-{\mathcal{x}}_{EL}{\mathcal{y}}_{EL}⟶\mathrm{t}-\text{conorm}\left(\text{additive}\text{generator}\right):\overbrace{\mathfrak{V}}\left(\stackrel{\dots }{\mathcal{t}}\right)=-\ln \left(1-\stackrel{\dots }{\mathcal{t}}\right)$$ (10)

• 2.Einstein norms [41]:

$$\overbrace{{\mathbb{T}}_{TN}}\left({\mathcal{x}}_{EL},{\mathcal{y}}_{EL}\right)=\frac{{\mathcal{x}}_{EL}{\mathcal{y}}_{EL}}{1+\left(1-{\mathcal{x}}_{EL}\right)\left(1-{\mathcal{y}}_{EL}\right)}⟶\mathrm{t}-\text{norm}\left(\text{additive}\text{generator}\right):\overbrace{\eta }\left(\stackrel{\dots }{\mathcal{t}}\right)=\ln \left(\frac{2-\stackrel{\dots }{\mathcal{t}}}{\stackrel{\dots }{\mathcal{t}}}\right)$$ (11)

$$\overbrace{{\mathbb{S}}_{TN}}\left({\mathcal{x}}_{EL},{\mathcal{y}}_{EL}\right)=\frac{{\mathcal{x}}_{EL}+{\mathcal{y}}_{EL}}{1+{\mathcal{x}}_{EL}{\mathcal{y}}_{EL}}⟶\mathrm{t}-\text{conorm}\left(\text{additive}\text{generator}\right):\overbrace{\mathfrak{V}}\left(\stackrel{\dots }{\mathcal{t}}\right)=\ln \left(\frac{1+\stackrel{\dots }{\mathcal{t}}}{1-\stackrel{\dots }{\mathcal{t}}}\right)$$ (12)

• 3.Hamacher norms [41]:

$$\overbrace{{\mathbb{T}}_{TN}}\left({\mathcal{x}}_{EL},{\mathcal{y}}_{EL}\right)=\frac{{\mathcal{x}}_{EL}{\mathcal{y}}_{EL}}{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right)\left({\mathcal{x}}_{EL}+{\mathcal{y}}_{EL}-{\mathcal{x}}_{EL}{\mathcal{y}}_{EL}\right)}⟶\mathrm{t}-\text{norm}\left(\text{additive}\text{generator}\right):\overbrace{\eta }\left(\stackrel{\dots }{\mathcal{t}}\right)=\ln \left(\frac{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right)\stackrel{\dots }{\mathcal{t}}}{\stackrel{\dots }{\mathcal{t}}}\right)$$ (13)

$$\overbrace{{\mathbb{S}}_{TN}}\left({\mathcal{x}}_{EL},{\mathcal{y}}_{EL}\right)=\frac{{\mathcal{x}}_{EL}+{\mathcal{y}}_{EL}-{\mathcal{x}}_{EL}{\mathcal{y}}_{EL}-\left(1-\widehat{{\delta }_{SC}}\right){\mathcal{x}}_{EL}{\mathcal{y}}_{EL}}{1-\left(1-\widehat{{\delta }_{SC}}\right){\mathcal{x}}_{EL}{\mathcal{y}}_{EL}}⟶\mathrm{t}-\text{conorm}\left(\text{additive}\text{generator}\right):\overbrace{\mathfrak{V}}\left(\stackrel{\dots }{\mathcal{t}}\right)=\ln \left(\frac{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right)\left(1-\stackrel{\dots }{\mathcal{t}}\right)}{1-\stackrel{\dots }{\mathcal{t}}}\right)$$ (14)

• 4.Frank norms [41]:

$$\overbrace{{\mathbb{T}}_{TN}}\left({\mathcal{x}}_{EL},{\mathcal{y}}_{EL}\right)={\log }_{\widehat{{\delta }_{SC}}}\left(1+\frac{\left({\widehat{{\delta }_{SC}}}^{{\mathcal{x}}_{EL}}-1\right)\left({\widehat{{\delta }_{SC}}}^{{\mathcal{y}}_{EL}}-1\right)}{\left(\widehat{{\delta }_{SC}}-1\right)}\right)⟶\mathrm{t}-\text{norm}\left(\text{additive}\text{generator}\right):\text{If}\widehat{{\delta }_{SC}}=1,\text{then}\overbrace{\eta }\left(\stackrel{\dots }{\mathcal{t}}\right)=-\ln \left(\stackrel{\dots }{\mathcal{t}}\right),\text{if}\widehat{{\delta }_{SC}}\ne 1,\text{then}\overbrace{\eta }\left(\stackrel{\dots }{\mathcal{t}}\right)=-\ln \left(\frac{\widehat{{\delta }_{SC}}-1}{{\widehat{{\delta }_{SC}}}^{\stackrel{\dots }{\mathcal{t}}}-1}\right)$$ (15)

$$\overbrace{{\mathbb{S}}_{TN}}\left({\mathcal{x}}_{EL},{\mathcal{y}}_{EL}\right)=1-{\log }_{\widehat{{\delta }_{SC}}}\left(1+\frac{\left({\widehat{{\delta }_{SC}}}^{{1-\mathcal{x}}_{EL}}-1\right)\left({\widehat{{\delta }_{SC}}}^{1-{\mathcal{y}}_{EL}}-1\right)}{\left(\widehat{{\delta }_{SC}}-1\right)}\right)⟶\mathrm{t}-\text{conorm}\left(\text{additive}\text{generator}\right):\text{If}\widehat{{\delta }_{SC}}=1,\text{then}\overbrace{\mathfrak{V}}\left(\stackrel{\dots }{\mathcal{t}}\right)=-\ln \left(1-\stackrel{\dots }{\mathcal{t}}\right),\text{if}\widehat{{\delta }_{SC}}\ne 1,\text{then}\overbrace{\mathfrak{V}}\left(\stackrel{\dots }{\mathcal{t}}\right)=-\ln \left(\frac{\widehat{{\delta }_{SC}}-1}{{\widehat{{\delta }_{SC}}}^{1-\stackrel{\dots }{\mathcal{t}}}-1}\right)$$ (16)

The modified and general form of TN and TCN is listed below in Eq. (17) and Eq. (18):

$$\overbrace{{\mathbb{T}}_{TN}}\left({\mathcal{x}}_{EL},{\mathcal{y}}_{EL}\right)=\overbrace{{\eta }^{-1}}\left(\overbrace{\eta }\left({\mathcal{x}}_{EL}\right)+\overbrace{\eta }\left({\mathcal{y}}_{EL}\right)\right)$$ (17)

$$\overbrace{{\mathbb{S}}_{TN}}\left({\mathcal{x}}_{EL},{\mathcal{y}}_{EL}\right)=\overbrace{{\mathfrak{V}}^{-1}}\left(\overbrace{\mathfrak{V}}\left({\mathcal{x}}_{EL}\right)+\overbrace{\mathfrak{V}}\left({\mathcal{y}}_{EL}\right)\right)$$ (18)

where $\overbrace{\mathfrak{V}}\left(\stackrel{\dots }{\mathcal{t}}\right)=\overbrace{\eta }\left(1-\stackrel{\dots }{\mathcal{t}}\right)$.

3. Archimedean operational laws for CIFSs

In this section, we discover the well-known and famous theory of algebraic, Einstein, Hamacher, and Frank's rules for CIF information. These operations play an essential role in the construction of any kind of aggregation operator.

Definition 7

Choose any two CIFNs ${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}\right)$ and ${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)}\right)$, then

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\oplus {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}=\left(\overbrace{{\mathbb{S}}_{TN}}\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}},{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\right)e^{i2\pi \left(\overbrace{{\mathbb{S}}_{TN}}\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}},{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)\right)},\overbrace{{\mathbb{T}}_{TN}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\right)e^{i2\pi \left(\overbrace{{\mathbb{T}}_{TN}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)\right)}\right)$$

$$=\left(\begin{array}{c}\overbrace{{\mathfrak{V}}^{-1}}\left(\overbrace{\mathfrak{V}}\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)+\overbrace{\mathfrak{V}}\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\right)\right)e^{i2\pi \left(\overbrace{{\mathfrak{V}}^{-1}}\left(\overbrace{\mathfrak{V}}\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)+\overbrace{\mathfrak{V}}\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)\right)\right)},\\ \overbrace{{\eta }^{-1}}\left(\overbrace{\eta }\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)+\overbrace{\eta }\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\right)\right)e^{i2\pi \left(\overbrace{{\eta }^{-1}}\left(\overbrace{\eta }\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)+\overbrace{\eta }\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)\right)\right)}\end{array}\right)$$ (19)

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\otimes {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}=\left(\overbrace{{\mathbb{T}}_{TN}}\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}},{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\right)e^{i2\pi \left(\overbrace{{\mathbb{T}}_{TN}}\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}},{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)\right)},\overbrace{{\mathbb{S}}_{TN}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\right)e^{i2\pi \left(\overbrace{{\mathbb{S}}_{TN}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)\right)}\right)$$

$$=\left(\begin{array}{c}\overbrace{{\eta }^{-1}}\left(\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)+\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\right)\right)e^{i2\pi \left(\overbrace{{\eta }^{-1}}\left(\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)+\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)\right)\right)},\\ \overbrace{{\mathfrak{V}}^{-1}}\left(\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)+\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\right)\right)e^{i2\pi \left(\overbrace{{\mathfrak{V}}^{-1}}\left(\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)+\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)\right)\right)}\end{array}\right)$$ (20)

$$\stackrel{═}{{\gamma }_{SC}}{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}=\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{{\gamma }_{SC}}\overbrace{\mathfrak{V}}\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)\right)e^{i2\pi \left(\overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{{\gamma }_{SC}}\overbrace{\mathfrak{V}}\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)\right)\right)},\overbrace{{\eta }^{-1}}\left(\stackrel{═}{{\gamma }_{SC}}\overbrace{\eta }\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)\right)e^{i2\pi \left(\overbrace{{\eta }^{-1}}\left(\stackrel{═}{{\gamma }_{SC}}\overbrace{\eta }\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)\right)\right)}\right)$$ (21)

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}^{\stackrel{═}{{\gamma }_{SC}}}=\left(\overbrace{{\eta }^{-1}}\left(\stackrel{═}{{\gamma }_{SC}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)\right)e^{i2\pi \left(\overbrace{{\eta }^{-1}}\left(\stackrel{═}{{\gamma }_{SC}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)\right)\right)},\overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{{\gamma }_{SC}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)\right)e^{i2\pi \left(\overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{{\gamma }_{SC}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)\right)\right)}\right)$$ (22)

To select the data in Eq. (9) and Eq. (10), then the data in Eq. (19) to Eq. (22) will be transformed to Eq. (2) to Eq. (5), called algebraic laws, further, to select the data in Eq. (11) and Eq. (12), then the data in Eq. (19) to Eq. (22) will be transformed to Eq. (23) to Eq. (26), called Einstein laws, such as

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\oplus {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}=\left(\begin{array}{c}\frac{\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}+{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\right)}{1+{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}}{e}^{i2\pi \left(\frac{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}+{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}}{1+{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}}\right)},\\ \frac{{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}}{1+\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\right)}{e}^{i2\pi \left(\frac{{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}}{1+\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)}\right)}\end{array}\right)$$ (23)

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\otimes {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}=\left(\begin{array}{c}\frac{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}}{1+\left(1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)\left(1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\right)}{e}^{i2\pi \left(\frac{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}}{1+\left(1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)\left(1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)}\right)},\\ \frac{\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\right)}{1+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}}{e}^{i2\pi \left(\frac{{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}}{1+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}}\right)}\end{array}\right)$$ (24)

$$\stackrel{═}{{\gamma }_{SC}}{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}=\left(\begin{array}{c}\frac{{\left(1+{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}-{\left(1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(1+{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}+{\left(1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{e}^{i2\pi \left(\frac{{\left(1+{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}-{\left(1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(1+{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}+{\left(1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}}\right)},\\ \frac{2{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(2-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}^{\stackrel{═}{{\gamma }_{SC}}}}{e}^{i2\pi \left(\frac{2{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(2-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}^{\stackrel{═}{{\gamma }_{SC}}}}\right)}\end{array}\right),\stackrel{═}{{\gamma }_{SC}}>0$$ (25)

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}^{\stackrel{═}{{\gamma }_{SC}}}=\left(\begin{array}{c}\frac{2{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(2-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}+{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}^{\stackrel{═}{{\gamma }_{SC}}}}{e}^{i2\pi \left(\frac{2{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(2-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}+{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}^{\stackrel{═}{{\gamma }_{SC}}}}\right)},\\ \frac{{\left(1+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}-{\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(1+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}+{\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{e}^{i2\pi \left(\frac{{\left(1+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}-{\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(1+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}+{\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}}\right)}\end{array}\right),\stackrel{═}{{\gamma }_{SC}}>0$$ (26)

To select the data in Eq. (11) and Eq. (12), then the data in Eq. (19) to Eq. (22) will be transformed to Eq. (27) to Eq. (30), called Hamacher laws, such as

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\oplus {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}=\left(\begin{array}{c}\frac{\left(\begin{array}{c}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}+{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\\ -\left(1-\widehat{{\delta }_{SC}}\right){\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\end{array}\right)}{1-\left(1-\widehat{{\delta }_{SC}}\right){\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}}{e}^{i2\pi \left(\frac{\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}+{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}-\left(1-\widehat{{\delta }_{SC}}\right){\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)}{1-\left(1-\widehat{{\delta }_{SC}}\right){\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}}\right)},\\ \frac{{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}}{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right)\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\right)}{e}^{i2\pi \left(\frac{{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}}{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right)\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)}\right)}\end{array}\right)$$ (27)

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\otimes {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}=\left(\begin{array}{c}\frac{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}}{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right)\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}+{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\right)}{e}^{i2\pi \left(\frac{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}}{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right)\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}+{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)}\right)},\\ \frac{\left(\begin{array}{c}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\\ -\left(1-\widehat{{\delta }_{SC}}\right){\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}\end{array}\right)}{1-\left(1-\widehat{{\delta }_{SC}}\right){\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-2}}}{e}^{i2\pi \left(\frac{\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}-\left(1-\widehat{{\delta }_{SC}}\right){\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}\right)}{1-\left(1-\widehat{{\delta }_{SC}}\right){\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-2}}}\right)}\end{array}\right)$$ (28)

$$\stackrel{═}{{\gamma }_{SC}}{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}=\left(\begin{array}{c}\frac{{\left(1+\left(\widehat{{\delta }_{SC}}-1\right){\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}-{\left(1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(1+\left(\widehat{{\delta }_{SC}}-1\right){\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}+\left(\widehat{{\delta }_{SC}}-1\right){\left(1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{e}^{i2\pi \left(\frac{{\left(1+\left(\widehat{{\delta }_{SC}}-1\right){\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}-{\left(1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(1+\left(\widehat{{\delta }_{SC}}-1\right){\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}+\left(\widehat{{\delta }_{SC}}-1\right){\left(1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}}\right)},\\ \frac{2{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(1+\left(\widehat{{\delta }_{SC}}-1\right)\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)\right)}^{\stackrel{═}{{\gamma }_{SC}}}+\left(\widehat{{\delta }_{SC}}-1\right){\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}^{\stackrel{═}{{\gamma }_{SC}}}}{e}^{i2\pi \left(\frac{2{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(1+\left(\widehat{{\delta }_{SC}}-1\right)\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)\right)}^{\stackrel{═}{{\gamma }_{SC}}}+\left(\widehat{{\delta }_{SC}}-1\right){\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}^{\stackrel{═}{{\gamma }_{SC}}}}\right)}\end{array}\right),\stackrel{═}{{\gamma }_{SC}}>0$$ (29)

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}^{\stackrel{═}{{\gamma }_{SC}}}=\left(\begin{array}{c}\frac{2{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(1+\left(\widehat{{\delta }_{SC}}-1\right)\left(1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)\right)}^{\stackrel{═}{{\gamma }_{SC}}}+\left(\widehat{{\delta }_{SC}}-1\right){\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}^{\stackrel{═}{{\gamma }_{SC}}}}{e}^{i2\pi \left(\frac{2{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(1+\left(\widehat{{\delta }_{SC}}-1\right)\left(1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)\right)}^{\stackrel{═}{{\gamma }_{SC}}}+\left(\widehat{{\delta }_{SC}}-1\right){\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}^{\stackrel{═}{{\gamma }_{SC}}}}\right)},\\ \frac{{\left(1+\left(\widehat{{\delta }_{SC}}-1\right){\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}-{\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(1+\left(\widehat{{\delta }_{SC}}-1\right){\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}+\left(\widehat{{\delta }_{SC}}-1\right){\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{e}^{i2\pi \left(\frac{{\left(1+\left(\widehat{{\delta }_{SC}}-1\right){\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}-{\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(1+\left(\widehat{{\delta }_{SC}}-1\right){\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}+\left(\widehat{{\delta }_{SC}}-1\right){\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}\right)}^{\stackrel{═}{{\gamma }_{SC}}}}\right)}\end{array}\right),\stackrel{═}{{\gamma }_{SC}}>0$$ (30)

To choose the value of $\widehat{{\delta }_{SC}}=1$ in Eq. (27) to Eq. (30), we will get the data in Eq. (2) to Eq. (5), when we select the value of $\widehat{{\delta }_{SC}}=2$ in Eq. (27) to Eq. (30), thus we will derive the data in Eq. (23) to Eq. (26). To consider the data in Eq. (13) and Eq. (14), then the data in Eq. (19) to Eq. (22) will be transformed to Eq. (31) to Eq. (34), called Frank laws, such as

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\oplus {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}=\left(\begin{array}{c}1-{\log }_{\widehat{{\delta }_{SC}}}\left(1+\frac{\prod _{\theta =1}^2\left({\widehat{{\delta }_{SC}}}^{1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}-1\right)}{\widehat{{\delta }_{SC}}-1}\right)e^{i2\pi \left(1-{\log }_{\widehat{{\delta }_{SC}}}\left(1+\frac{\prod _{\theta =1}^2\left({\widehat{{\delta }_{SC}}}^{1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}-1\right)}{\widehat{{\delta }_{SC}}-1}\right)\right)},\\ {\log }_{\widehat{{\delta }_{SC}}}\left(1+\frac{\prod _{\theta =1}^2\left({\widehat{{\delta }_{SC}}}^{{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}-1\right)}{\widehat{{\delta }_{SC}}-1}\right)e^{i2\pi \left({\log }_{\widehat{{\delta }_{SC}}}\left(1+\frac{\prod _{\theta =1}^2\left({\widehat{{\delta }_{SC}}}^{{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}-1\right)}{\widehat{{\delta }_{SC}}-1}\right)\right)}\end{array}\right)$$ (31)

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}\otimes {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}=\left(\begin{array}{c}{\log }_{\widehat{{\delta }_{SC}}}\left(1+\frac{\prod _{\theta =1}^2\left({\widehat{{\delta }_{SC}}}^{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}-1\right)}{\widehat{{\delta }_{SC}}-1}\right)e^{i2\pi \left({\log }_{\widehat{{\delta }_{SC}}}\left(1+\frac{\prod _{\theta =1}^2\left({\widehat{{\delta }_{SC}}}^{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}-1\right)}{\widehat{{\delta }_{SC}}-1}\right)\right)},\\ 1-{\log }_{\widehat{{\delta }_{SC}}}\left(1+\frac{\prod _{\theta =1}^2\left({\widehat{{\delta }_{SC}}}^{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}-1\right)}{\widehat{{\delta }_{SC}}-1}\right)e^{i2\pi \left(1-{\log }_{\widehat{{\delta }_{SC}}}\left(1+\frac{\prod _{\theta =1}^2\left({\widehat{{\delta }_{SC}}}^{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}-1\right)}{\widehat{{\delta }_{SC}}-1}\right)\right)}\end{array}\right)$$ (32)

$$\stackrel{═}{{\gamma }_{SC}}{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}=\left(\begin{array}{c}1-{\log }_{\widehat{{\delta }_{SC}}}\left(1+\frac{{\left({\widehat{{\delta }_{SC}}}^{1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}}-1\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(\widehat{{\delta }_{SC}}-1\right)}^{\stackrel{═}{{\gamma }_{SC}}-1}}\right)e^{i2\pi \left(1-{\log }_{\widehat{{\delta }_{SC}}}\left(1+\frac{{\left({\widehat{{\delta }_{SC}}}^{1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}}-1\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(\widehat{{\delta }_{SC}}-1\right)}^{\stackrel{═}{{\gamma }_{SC}}-1}}\right)\right)},\\ {\log }_{\widehat{{\delta }_{SC}}}\left(1+\frac{{\left({\widehat{{\delta }_{SC}}}^{{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}}-1\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(\widehat{{\delta }_{SC}}-1\right)}^{\stackrel{═}{{\gamma }_{SC}}-1}}\right)e^{i2\pi \left({\log }_{\widehat{{\delta }_{SC}}}\left(1+\frac{{\left({\widehat{{\delta }_{SC}}}^{{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}}-1\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(\widehat{{\delta }_{SC}}-1\right)}^{\stackrel{═}{{\gamma }_{SC}}-1}}\right)\right)}\end{array}\right),\stackrel{═}{{\gamma }_{SC}}>0$$ (33)

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}^{\stackrel{═}{{\gamma }_{SC}}}=\left(\begin{array}{c}{\log }_{\widehat{{\delta }_{SC}}}\left(1+\frac{{\left({\widehat{{\delta }_{SC}}}^{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}}-1\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(\widehat{{\delta }_{SC}}-1\right)}^{\stackrel{═}{{\gamma }_{SC}}-1}}\right)e^{i2\pi \left({\log }_{\widehat{{\delta }_{SC}}}\left(1+\frac{{\left({\widehat{{\delta }_{SC}}}^{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}}-1\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(\widehat{{\delta }_{SC}}-1\right)}^{\stackrel{═}{{\gamma }_{SC}}-1}}\right)\right)},\\ 1-{\log }_{\widehat{{\delta }_{SC}}}\left(1+\frac{{\left({\widehat{{\delta }_{SC}}}^{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-1}}}-1\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(\widehat{{\delta }_{SC}}-1\right)}^{\stackrel{═}{{\gamma }_{SC}}-1}}\right)e^{i2\pi \left(1-{\log }_{\widehat{{\delta }_{SC}}}\left(1+\frac{{\left({\widehat{{\delta }_{SC}}}^{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-1}}}-1\right)}^{\stackrel{═}{{\gamma }_{SC}}}}{{\left(\widehat{{\delta }_{SC}}-1\right)}^{\stackrel{═}{{\gamma }_{SC}}-1}}\right)\right)}\end{array}\right),\stackrel{═}{{\gamma }_{SC}}>0$$ (34)

4. Proposed archimedean operators for CIFSs

In this section, we discovered the CIFAHA operator, CIFWAHA operator, and their special cases with the help of some conditions. Several important properties and their related results are also diagnosed.

Definition 8

Choose any group of CIFNs ${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)}\right),\theta =1,2,\dots ,\mathfrak{L}$, then the CIFAHA operator is invented by:

$$CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)={\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=1}^{\mathfrak{L}}{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }^{\stackrel{═}{\mathcal{f}}}\otimes {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-k}^{\stackrel{═}{\mathcal{g}}}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}$$ (35)

where $\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}\ge 0$.

Theorem 1

Choose any group of CIFNs${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)}\right),\theta =1,2,\dots ,\mathfrak{L}$, then by using Eq. (35), we initiate

$$CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)=\left(\begin{array}{c}\overbrace{{\eta }^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)\right)\right)\right)\right)\\ e^{i2\pi \left(\overbrace{{\eta }^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)\right)\right)\right)\right)\right)\right)},\\ \overbrace{{\mathfrak{V}}^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\eta }\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)\right)\right)\right)\right)\\ e^{i2\pi \left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\eta }\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)\right)\right)\right)\right)\right)\right)}\end{array}\right)$$ (36)

Proof: Consider

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }^{\stackrel{═}{\mathcal{f}}}=\left(\overbrace{{\eta }^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)\right)e^{i2\pi \left(\overbrace{{\eta }^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)\right)\right)},\overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)\right)e^{i2\pi \left(\overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)\right)\right)}\right)$$

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-k}^{\stackrel{═}{\mathcal{g}}}=\left(\overbrace{{\eta }^{-1}}\left(\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)e^{i2\pi \left(\overbrace{{\eta }^{-1}}\left(\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)\right)\right)},\overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)e^{i2\pi \left(\overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)\right)\right)}\right)$$

then,

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }^{\stackrel{═}{\mathcal{f}}}\otimes {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-k}^{\stackrel{═}{\mathcal{g}}}=\left(\overbrace{{\eta }^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)\right)e^{i2\pi \left(\overbrace{{\eta }^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)\right)\right)},\overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)\right)e^{i2\pi \left(\overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)\right)\right)}\right)\otimes \left(\overbrace{{\eta }^{-1}}\left(\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)e^{i2\pi \left(\overbrace{{\eta }^{-1}}\left(\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)\right)\right)},\overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)e^{i2\pi \left(\overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)\right)\right)}\right)$$

$$=\left(\begin{array}{c}\overbrace{{\eta }^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)e^{i2\pi \left(\overbrace{{\eta }^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)\right)\right)},\\ \overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)e^{i2\pi \left(\overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)\right)\right)}\end{array}\right)$$

and,

$$\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=1}^{\mathfrak{L}}{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }^{\stackrel{═}{\mathcal{f}}}\otimes {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-k}^{\stackrel{═}{\mathcal{g}}}=\left(\begin{array}{c}\overbrace{{\mathfrak{V}}^{-1}}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)\right)\right)\\ e^{i2\pi \left(\overbrace{{\mathfrak{V}}^{-1}}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)\right)\right)\right)\right)},\\ \overbrace{{\eta }^{-1}}\left(\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)\right)\right)\right)\\ e^{i2\pi \left(\overbrace{{\eta }^{-1}}\left(\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)\right)\right)\right)\right)\right)}\end{array}\right)$$

$$\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=1}^{\mathfrak{L}}{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }^{\stackrel{═}{\mathcal{f}}}\otimes {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-k}^{\stackrel{═}{\mathcal{g}}}=\left(\begin{array}{c}\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)\right)\right)\right)\\ e^{i2\pi \left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)\right)\right)\right)\right)\right)},\\ \overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)\right)\right)\right)\\ e^{i2\pi \left(\overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)\right)\right)\right)\right)\right)}\end{array}\right)$$

$$CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)={\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=1}^{\mathfrak{L}}{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }^{\stackrel{═}{\mathcal{f}}}\otimes {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-k}^{\stackrel{═}{\mathcal{g}}}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}=\left(\begin{array}{c}\overbrace{{\eta }^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)\right)\right)\right)\right)\\ e^{i2\pi \left(\overbrace{{\eta }^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)\right)\right)\right)\right)\right)\right)},\\ \overbrace{{\mathfrak{V}}^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\eta }\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)\right)\right)\right)\right)\\ e^{i2\pi \left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\eta }\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)\right)\right)\right)\right)\right)\right)}\end{array}\right)\text{.}$$

Under Eq. (35) and Eq. (36), we employed some properties like idempotency, monotonicity, and boundedness.

Property 1

Choose any group of CIFNs${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)}\right),\theta =1,2,\dots ,\mathfrak{L}$. If${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }={\stackrel{═}{\mathfrak{k}\xi }}_{CIN}=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\right)}\right)$, then

$$CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)={\stackrel{═}{\mathfrak{k}\xi }}_{CIN}$$ (37)

Proof: By hypothesis ${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }={\stackrel{═}{\mathfrak{k}\xi }}_{CIN}=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\right)}\right)$, then

$$CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)={\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=1}^{\mathfrak{L}}{\stackrel{═}{\mathfrak{k}\xi }}_{CIN}^{\stackrel{═}{\mathcal{f}}}\otimes {\stackrel{═}{\mathfrak{k}\xi }}_{CIN}^{\stackrel{═}{\mathcal{g}}}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}$$

$$={\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=1}^{\mathfrak{L}}{\stackrel{═}{\mathfrak{k}\xi }}_{CIN}^{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}={\left(\frac{2}{1\left(1+1\right)}\sum _{\theta =1}^1\sum _{k=1}^1{\stackrel{═}{\mathfrak{k}\xi }}_{CIN}^{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}$$

$={\left(\frac{2}{2}{\stackrel{═}{\mathfrak{k}\xi }}_{CIN}^{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}={\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN}^{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}={\stackrel{═}{\mathfrak{k}\xi }}_{CIN}\text{.}$ This proves Eq. (37).

Property 2

Choose any group of CIFNs${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)}\right),\theta =1,2,\dots ,\mathfrak{L}$. If${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }\le {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }^{*}$, then

$$CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)\le CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}^{*},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}^{*},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}^{*}\right)$$ (38)

Proof: By hypothesis, we know that if ${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }\le {\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }^{*}$ that's mean ${\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\le {\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}^{*},{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\le {\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}^{*}$ and ${\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\ge {\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}^{*},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\ge {\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}^{*}$, then

$$\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\le \stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}^{*}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}^{*}\right)$$

thus,

$$\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)\le \sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}^{*}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}^{*}\right)\right)$$

then,

$$\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)\right)\le \frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}^{*}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}^{*}\right)\right)\right)$$

thus,

$$\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)\right)\right)\le \overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}^{*}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}^{*}\right)\right)\right)\right)$$

therefore,

$$\overbrace{{\eta }^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)\right)\right)\right)\right)\le \overbrace{{\eta }^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}^{*}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}^{*}\right)\right)\right)\right)\right)\right)$$

Similarly, we investigate for an unreal term, such that

$$\overbrace{{\eta }^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)\right)\right)\right)\right)\right)\le \overbrace{{\eta }^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}^{*}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}^{*}\right)\right)\right)\right)\right)\right)$$

Moreover, for real and unreal terms of FD, we have

$$\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\eta }\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)\right)\right)\right)\right)\ge \overbrace{{\mathfrak{V}}^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\eta }\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}^{*}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}^{*}\right)\right)\right)\right)\right)\right)$$

and,

$$\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\eta }\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)\right)\right)\right)\right)\right)\ge \overbrace{{\mathfrak{V}}^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\eta }\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}^{*}\right)+\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}^{*}\right)\right)\right)\right)\right)\right)$$

By using Eq. (6), we easily get the terms.

$CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)\le CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}^{*},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}^{*},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}^{*}\right)\text{.}$ This proves Eq. (38).

Property 3

Choose any group of CIFNs${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)}\right),\theta =1,2,\dots ,\mathfrak{L}$. If${\stackrel{═}{\mathfrak{k}\xi }}_{CIN}^{-}=\left(\underset{\theta }{\min }{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left(\underset{\theta }{\min }{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)},\underset{\theta }{\max }{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left(\underset{\theta }{\max }{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)}\right)$and${\stackrel{═}{\mathfrak{k}\xi }}_{CIN}^{+}=\left(\underset{\theta }{\max }{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left(\underset{\theta }{\max }{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)},\underset{\theta }{\min }{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left(\underset{\theta }{\min }{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)}\right)$, then

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN}^{-}\le CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)\le {\stackrel{═}{\mathfrak{k}\xi }}_{CIN}^{+}$$ (39)

Proof: To prove Eq. (39), we proceed as follows:

By hypothesis ${\stackrel{═}{\mathfrak{k}\xi }}_{CIN}^{-}=\left(\underset{\theta }{\min }{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left(\underset{\theta }{\min }{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)},\underset{\theta }{\max }{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left(\underset{\theta }{\max }{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)}\right)$ and ${\stackrel{═}{\mathfrak{k}\xi }}_{CIN}^{+}=\left(\underset{\theta }{\max }{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left(\underset{\theta }{\max }{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)},\underset{\theta }{\min }{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left(\underset{\theta }{\min }{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)}\right)$, then by using Property 2, we initiate

$$CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}^{-},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}^{-},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}^{-}\right)\le CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)\le CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}^{+},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}^{+},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}^{+}\right)$$

where $CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}^{-},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}^{-},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}^{-}\right)={\stackrel{═}{\mathfrak{k}\xi }}_{CIN}^{-}$ and $CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1}^{+},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2}^{+},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}^{+}\right)={\stackrel{═}{\mathfrak{k}\xi }}_{CIN}^{+}$, then

$${\stackrel{═}{\mathfrak{k}\xi }}_{CIN}^{-}\le CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)\le {\stackrel{═}{\mathfrak{k}\xi }}_{CIN}^{+}\text{.}$$

Where various realistic cases are stated below:

• 1.For $\stackrel{═}{\mathcal{g}}=0$, Eq. (36) will be transformed to

$$CIFAH{A}^{\stackrel{═}{\mathcal{f}},0}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)=\left(\begin{array}{c}\overbrace{{\eta }^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\left(\mathfrak{L}+1-\theta \right)\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)\right)\right)\right)\right)\right)\\ e^{i2\pi \left(\overbrace{{\eta }^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\left(\mathfrak{L}+1-\theta \right)\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)\right)\right)\right)\right)\right)\right)},\\ \overbrace{{\mathfrak{V}}^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\left(\mathfrak{L}+1-\theta \right)\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)\right)\right)\right)\right)\right)\\ e^{i2\pi \left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\left(\mathfrak{L}+1-\theta \right)\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)\right)\right)\right)\right)\right)\right)}\end{array}\right)$$ (40)

Signified as a CIF generalized heavy-weighted averaging operator (CIFGHWAO).

• 2.For $\stackrel{═}{\mathcal{f}}=1$, and $\stackrel{═}{\mathcal{g}}=0$, Eq. (36) will be transformed to

$$CIFAH{A}^{1,0}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)=\left(\begin{array}{c}\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\left(\mathfrak{L}+1-\theta \right)\overbrace{\mathfrak{V}}\left(\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)\right)\right)\right)\\ e^{i2\pi \left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\left(\mathfrak{L}+1-\theta \right)\overbrace{\mathfrak{V}}\left(\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)\right)\right)\right)\right)},\\ \overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\left(\mathfrak{L}+1-\theta \right)\overbrace{\eta }\left(\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)\right)\right)\right)\\ e^{i2\pi \left(\overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\left(\mathfrak{L}+1-\theta \right)\overbrace{\eta }\left(\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)\right)\right)\right)\right)}\end{array}\right)$$ (41)

Signified as a CIF heavy-weighted averaging operator (CIFHWAO).

• 3.For $\stackrel{═}{\mathcal{f}}=0$, Eq. (36) will be transformed to

$$CIFAH{A}^{0,\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)=\left(\begin{array}{c}\overbrace{{\eta }^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{g}}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\overbrace{i\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)\right)\right)\right)\right)\right)\\ e^{i2\pi \left(\overbrace{{\eta }^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{g}}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}i\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)\right)\right)\right)\right)\right)\right)},\\ \overbrace{{\mathfrak{V}}^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{g}}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}i\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)\right)\right)\right)\right)\right)\\ e^{i2\pi \left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{g}}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}i\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)\right)\right)\right)\right)\right)\right)}\end{array}\right)$$ (42)

Signified as a CIFGHWAO.

• 4.For $\stackrel{═}{\mathcal{f}}=0$ and $\stackrel{═}{\mathcal{g}}=1$, Eq. (36) will be transformed to

$$CIFAH{A}^{0,1}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)=\left(\begin{array}{c}\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\overbrace{i\mathfrak{V}}\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)\right)\right)\\ e^{i2\pi \left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\overbrace{i\mathfrak{V}}\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)\right)\right)\right)},\\ \overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\overbrace{i\eta }\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)\right)\right)\\ e^{i2\pi \left(\overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\overbrace{i\eta }\left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)\right)\right)\right)}\end{array}\right)$$ (43)

• 5.By using Eq. (9) and Eq. (10), Eq. (36) will be transformed to

$$CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)=\left(\begin{array}{c}{\left(1-{\left(\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}\left(1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}^{\stackrel{═}{\mathcal{f}}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}^{\stackrel{═}{\mathcal{g}}}\right)\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}{e}^{i2\pi \left({\left(1-{\left(\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}\left(1-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}^{\stackrel{═}{\mathcal{f}}}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}^{\stackrel{═}{\mathcal{g}}}\right)\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}\right)},\\ 1-{\left(1-{\left(\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}\left(1-{\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)}^{\stackrel{═}{\mathcal{g}}}\right)\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}\\ e^{i2\pi \left(1-{\left(1-{\left(\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}\left(1-{\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)}^{\stackrel{═}{\mathcal{g}}}\right)\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}\right)}\end{array}\right)$$ (44)

Signified as a CIFHM operator.

• 6.By using Eq. (11) and Eq. (12), Eq. (36) will be transformed to

$$CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)=\left(\begin{array}{c}\frac{2{\left(z_R^{\prime }+z_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}{{\left(z_R^{\prime }+3z_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}+{\left(z_R^{\prime }+z_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}{e}^{i2\pi \left(\frac{2{\left(z_I^{\prime }+z_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}{{\left(z_I^{\prime }+3z_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}+{\left(z_I^{\prime }+z_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}\right)},\\ \frac{{\left(y_R^{\prime }+3y_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}-{\left(y_R^{\prime }-y_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}{{\left(y_R^{\prime }+3y_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}+{\left(y_R^{\prime }-y_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}{e}^{i2\pi \left(\frac{{\left(y_I^{\prime }+3y_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}-{\left(y_I^{\prime }-y_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}{{\left(y_I^{\prime }+3y_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}+{\left(y_I^{\prime }-y_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}\right)}\end{array}\right)$$ (45)

Where $\begin{array}{l}{z}_R^{\prime }=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(\left({\left(\frac{2-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{2-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}}{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}}\right)}^{\stackrel{═}{\mathcal{g}}}\right)+3\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}},\\ z_R^{″}=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(\left({\left(\frac{2-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{2-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}}{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}}\right)}^{\stackrel{═}{\mathcal{g}}}\right)-1\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}},\\ y_R^{\prime }=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(\left({\left(\frac{1+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{1+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}}{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}}\right)}^{\stackrel{═}{\mathcal{g}}}\right)+3\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}},\\ y_R^{″}=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(\left({\left(\frac{1+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{1+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}}{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}}\right)}^{\stackrel{═}{\mathcal{g}}}\right)-1\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}}\end{array}$ and $\begin{array}{l}{z}_I^{\prime }=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(\left({\left(\frac{2-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{2-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}}{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}}\right)}^{\stackrel{═}{\mathcal{g}}}\right)+3\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}},\\ z_I^{″}=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(\left({\left(\frac{2-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{2-{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}}{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}}\right)}^{\stackrel{═}{\mathcal{g}}}\right)-1\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}},\\ y_I^{\prime }=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(\left({\left(\frac{1+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{1+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}}{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}}\right)}^{\stackrel{═}{\mathcal{g}}}\right)+3\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}},\\ y_I^{″}=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(\left({\left(\frac{1+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{1+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}}{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}}\right)}^{\stackrel{═}{\mathcal{g}}}\right)-1\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}}\end{array}$.

Signified as a CIF Einstein HM operator.

• 7.By using Eq. (13) and Eq. (14), Eq. (36) will be transformed to

$$CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)=\left(\begin{array}{c}\frac{\widehat{{\delta }_{SC}}{\left(z_R^{\prime }-z_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}{{\left(z_R^{\prime }+\left({\widehat{{\delta }_{SC}}}^2-1\right)z_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}+\left(\widehat{{\delta }_{SC}}-1\right){\left(z_R^{\prime }-z_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}{e}^{i2\pi \left(\frac{\widehat{{\delta }_{SC}}{\left(z_I^{\prime }-z_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}{{\left(z_I^{\prime }+\left({\widehat{{\delta }_{SC}}}^2-1\right)z_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}+\left(\widehat{{\delta }_{SC}}-1\right){\left(z_I^{\prime }-z_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}\right)},\\ \frac{{\left(y_R^{\prime }+3y_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}-{\left(y_R^{\prime }-y_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}{{\left(y_R^{\prime }+3y_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}+{\left(y_R^{\prime }-y_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}{e}^{i2\pi \left(\frac{{\left(y_I^{\prime }+3y_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}-{\left(y_I^{\prime }-y_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}{{\left(y_I^{\prime }+3y_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}+{\left(y_I^{\prime }-y_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}\right)}\end{array}\right)$$ (46)

Where

$$z_R^{\prime }=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(\left({\left(\frac{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right){\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right){\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}}{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}}\right)}^{\stackrel{═}{\mathcal{g}}}\right)+{\widehat{{\delta }_{SC}}}^2-1\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}},z_R^{″}=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(\left({\left(\frac{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right){\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right){\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}}{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}}\right)}^{\stackrel{═}{\mathcal{g}}}\right)-1\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}},y_R^{\prime }=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(\left({\left(\frac{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right)\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)}{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right)\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)}{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}}\right)}^{\stackrel{═}{\mathcal{g}}}\right)+{\widehat{{\delta }_{SC}}}^2-1\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}},y_R^{″}=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(\left({\left(\frac{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right)\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)}{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right)\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)}{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}}\right)}^{\stackrel{═}{\mathcal{g}}}\right)-1\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}}$$

and

$$z_I^{\prime }=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(\left({\left(\frac{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right){\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right){\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}}{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}}\right)}^{\stackrel{═}{\mathcal{g}}}\right)+{\widehat{{\delta }_{SC}}}^2-1\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}},z_I^{″}=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(\left({\left(\frac{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right){\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right){\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}}{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}}\right)}^{\stackrel{═}{\mathcal{g}}}\right)-1\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}},y_I^{\prime }=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(\left({\left(\frac{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right)\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)}{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right)\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)}{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}}\right)}^{\stackrel{═}{\mathcal{g}}}\right)+{\widehat{{\delta }_{SC}}}^2-1\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}},y_I^{″}=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(\left({\left(\frac{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right)\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)}{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{\widehat{{\delta }_{SC}}+\left(1-\widehat{{\delta }_{SC}}\right)\left(1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)}{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}}\right)}^{\stackrel{═}{\mathcal{g}}}\right)-1\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}}.$$

Signified as a CIF Hamacher HM operator.

• 8.By using Eq. (15) and Eq. (16), Eq. (36) is changed to

$$CIFAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)=\left(\begin{array}{c}{\log }_{\widehat{{\delta }_{SC}}}\left(\frac{{\left(z_R^{\prime }+\left(\widehat{{\delta }_{SC}}-1\right)z_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}+\left(\widehat{{\delta }_{SC}}-1\right){\left(z_R^{\prime }-z_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}{{\left(z_R^{\prime }+\left(\widehat{{\delta }_{SC}}-1\right)z_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}\right)\\ e^{i2\pi \left({\log }_{\widehat{{\delta }_{SC}}}\left(\frac{{\left(z_I^{\prime }+\left(\widehat{{\delta }_{SC}}-1\right)z_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}+\left(\widehat{{\delta }_{SC}}-1\right){\left(z_I^{\prime }-z_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}{{\left(z_I^{\prime }+\left(\widehat{{\delta }_{SC}}-1\right)z_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}\right)\right)},\\ {\log }_{\widehat{{\delta }_{SC}}}\left(\frac{\widehat{{\delta }_{SC}}{\left(y_R^{\prime }+\left(\widehat{{\delta }_{SC}}-1\right)y_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}{{\left(y_R^{\prime }+\left(\widehat{{\delta }_{SC}}-1\right)y_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}+\left(\widehat{{\delta }_{SC}}-1\right){\left(y_R^{\prime }-y_R^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}\right)\\ e^{i2\pi \left({\log }_{\widehat{{\delta }_{SC}}}\left(\frac{\widehat{{\delta }_{SC}}{\left(y_I^{\prime }+\left(\widehat{{\delta }_{SC}}-1\right)y_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}{{\left(y_I^{\prime }+\left(\widehat{{\delta }_{SC}}-1\right)y_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}+\left(\widehat{{\delta }_{SC}}-1\right){\left(y_I^{\prime }-y_I^{″}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}}\right)\right)}\end{array}\right)$$ (47)

Where

$$z_R^{\prime }=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(1+\left(\widehat{{\delta }_{SC}}-1\right)\left({\left(\frac{{\widehat{{\delta }_{SC}}}^{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}-1}{\widehat{{\delta }_{SC}}-1}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{{\widehat{{\delta }_{SC}}}^{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}}-1}{\widehat{{\delta }_{SC}}-1}\right)}^{\stackrel{═}{\mathcal{g}}}\right)\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}},z_R^{″}=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(1-\left({\left(\frac{{\widehat{{\delta }_{SC}}}^{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}-1}{\widehat{{\delta }_{SC}}-1}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{{\widehat{{\delta }_{SC}}}^{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}}-1}{\widehat{{\delta }_{SC}}-1}\right)}^{\stackrel{═}{\mathcal{g}}}\right)\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}},y_R^{\prime }=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(1+\left(\widehat{{\delta }_{SC}}-1\right)\left({\left(\frac{{\widehat{{\delta }_{SC}}}^{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}-1}{\widehat{{\delta }_{SC}}-1}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{{\widehat{{\delta }_{SC}}}^{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}}-1}{\widehat{{\delta }_{SC}}-1}\right)}^{\stackrel{═}{\mathcal{g}}}\right)\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}},y_R^{″}=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(1+\left(\widehat{{\delta }_{SC}}-1\right)\left({\left(\frac{{\widehat{{\delta }_{SC}}}^{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}}-1}{\widehat{{\delta }_{SC}}-1}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{{\widehat{{\delta }_{SC}}}^{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}}-1}{\widehat{{\delta }_{SC}}-1}\right)}^{\stackrel{═}{\mathcal{g}}}\right)\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}}$$

and

$$z_I^{\prime }=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(1+\left(\widehat{{\delta }_{SC}}-1\right)\left({\left(\frac{{\widehat{{\delta }_{SC}}}^{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}-1}{\widehat{{\delta }_{SC}}-1}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{{\widehat{{\delta }_{SC}}}^{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}}-1}{\widehat{{\delta }_{SC}}-1}\right)}^{\stackrel{═}{\mathcal{g}}}\right)\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}},z_I^{″}=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(1-\left({\left(\frac{{\widehat{{\delta }_{SC}}}^{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}-1}{\widehat{{\delta }_{SC}}-1}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{{\widehat{{\delta }_{SC}}}^{{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}}-1}{\widehat{{\delta }_{SC}}-1}\right)}^{\stackrel{═}{\mathcal{g}}}\right)\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}},y_I^{\prime }=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(1+\left(\widehat{{\delta }_{SC}}-1\right)\left({\left(\frac{{\widehat{{\delta }_{SC}}}^{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}-1}{\widehat{{\delta }_{SC}}-1}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{{\widehat{{\delta }_{SC}}}^{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}}-1}{\widehat{{\delta }_{SC}}-1}\right)}^{\stackrel{═}{\mathcal{g}}}\right)\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}},y_I^{″}=\prod _{\theta =1}^{\mathfrak{L}}\prod _{k=\theta }^{\mathfrak{L}}{\left(1+\left(\widehat{{\delta }_{SC}}-1\right)\left({\left(\frac{{\widehat{{\delta }_{SC}}}^{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}}-1}{\widehat{{\delta }_{SC}}-1}\right)}^{\stackrel{═}{\mathcal{f}}}{\left(\frac{{\widehat{{\delta }_{SC}}}^{1-{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}}-1}{\widehat{{\delta }_{SC}}-1}\right)}^{\stackrel{═}{\mathcal{g}}}\right)\right)}^{\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}}.$$

Signified as a CIF Frank HM operator.

Definition 9

Choose any group of CIFNs ${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)}\right),\theta =1,2,\dots ,\mathfrak{L}$, then the CIFWAHA operator is invented by:

$$CIFWAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)={\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=1}^{\mathfrak{L}}{\left(\mathfrak{L}\stackrel{═}{{\omega }_{\theta }}{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }\right)}^{\stackrel{═}{\mathcal{f}}}\otimes {\left(\mathfrak{L}\stackrel{═}{{\omega }_k}{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-k}\right)}^{\stackrel{═}{\mathcal{g}}}\right)}^{\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}}$$ (48)

Observed that $\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}\ge 0$, with $\stackrel{═}{\omega }={\left({\stackrel{═}{\omega }}_1,{\stackrel{═}{\omega }}_2,\dots ,{\stackrel{═}{\omega }}_{\mathfrak{L}}\right)}^T\text{,}$ $\sum _{\theta =1}^{\mathfrak{L}}\stackrel{═}{{\omega }_{\theta }}=1$, called weight vectors

Theorem 2

Choose any group of CIFNs${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta }=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)}\right),\theta =1,2,\dots ,\mathfrak{L}$, then by using Eq. (48), we initiate

$$CIFWAH{A}^{\stackrel{═}{\mathcal{f}},\stackrel{═}{\mathcal{g}}}\left({\stackrel{═}{\mathfrak{k}\xi }}_{CIN-1},{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\mathfrak{L}}\right)=\left(\begin{array}{c}\overbrace{{\eta }^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\begin{array}{c}\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\mathfrak{L}\stackrel{═}{{\omega }_{\theta }}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)\right)+\\ \stackrel{═}{\mathcal{g}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\mathfrak{L}\stackrel{═}{{\omega }_k}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)\end{array}\right)\right)\right)\right)\right)\right)\\ e^{i2\pi \left(\overbrace{{\eta }^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\mathfrak{L}\stackrel{═}{{\omega }_{\theta }}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)\right)+\stackrel{═}{\mathcal{g}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\mathfrak{L}\stackrel{═}{{\omega }_k}{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)\right)\right)\right)\right)\right)\right)\right)\right)},\\ \overbrace{{\mathfrak{V}}^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\begin{array}{c}\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\mathfrak{L}\stackrel{═}{{\omega }_{\theta }}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta }}\right)\right)+\\ \stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\mathfrak{L}\stackrel{═}{{\omega }_k}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-k}}\right)\right)\end{array}\right)\right)\right)\right)\right)\right)\\ e^{i2\pi \left(\overbrace{{\mathfrak{V}}^{-1}}\left(\frac{1}{\stackrel{═}{\mathcal{f}}+\stackrel{═}{\mathcal{g}}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\frac{2}{\mathfrak{L}\left(\mathfrak{L}+1\right)}\left(\sum _{\theta =1}^{\mathfrak{L}}\sum _{k=\theta }^{\mathfrak{L}}\overbrace{\eta }\left(\overbrace{{\mathfrak{V}}^{-1}}\left(\stackrel{═}{\mathcal{f}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\mathfrak{L}\stackrel{═}{{\omega }_{\theta }}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta }}\right)\right)+\stackrel{═}{\mathcal{g}}\overbrace{\mathfrak{V}}\left(\overbrace{{\eta }^{-1}}\left(\mathfrak{L}\stackrel{═}{{\omega }_k}{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-k}}\right)\right)\right)\right)\right)\right)\right)\right)\right)}\end{array}\right)$$ (49)

Proof: Skipped.

5. Decision-making procedure for derived operators

In this section, we concentrate on evaluating the MADM procedure in the presence of the invented operators for CIFSs. For this, we used the special cases of the proposed operators and tried to evaluate their decision matrix to enhance the stability and worth of the invented operators.

5.1. The procedure of the MADM technique

Consider the finite collection of alternatives ${\stackrel{═}{\mathfrak{k}\xi }}_{AL}=\left\{{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1},{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{AL-m}\right\}$ and $\mathfrak{L}$ number of attributes ${\stackrel{═}{\mathfrak{k}\xi }}_{AT}=\left\{{\stackrel{═}{\mathfrak{k}\xi }}_{AT-1},{\stackrel{═}{\mathfrak{k}\xi }}_{AT-2},\dots ,{\stackrel{═}{\mathfrak{k}\xi }}_{AT-\mathfrak{L}}\right\}$ with weight vector $\stackrel{═}{\omega }={\left({\stackrel{═}{\omega }}_1,{\stackrel{═}{\omega }}_2,\dots ,{\stackrel{═}{\omega }}_{\mathfrak{L}}\right)}^T$ with a rule $\sum _{\theta =1}^{\mathfrak{L}}\stackrel{═}{{\omega }_{\theta }}=1$. For the above information, we compute the matrix by including their values in the shape of CIFNs, such as ${\stackrel{═}{\mathfrak{k}\xi }}_{CIN-\theta k}=\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta k}}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta k}}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta k}}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta k}}\right)}\right),\theta =1,2,\dots ,\mathfrak{L},k=1,2,\dots ,m$, where ${\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{CI}}\left({\mathcal{x}}_{EL}\right)={\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}\left({\mathcal{x}}_{EL}\right)e^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\left({\mathcal{x}}_{EL}\right)\right)}$ and ${\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{CI}}\left({\mathcal{x}}_{EL}\right)={\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}\left({\mathcal{x}}_{EL}\right)e^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\left({\mathcal{x}}_{EL}\right)\right)}$, with $0\le {\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}\left({\mathcal{x}}_{EL}\right)+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_R}\left({\mathcal{x}}_{EL}\right)\le 1$ and $0\le {\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\left({\mathcal{x}}_{EL}\right)+{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_I}\left({\mathcal{x}}_{EL}\right)\le 1$. For simplification of some numerical examples, we evaluate the procedure of decision-making techniques, such as

Stage 1: To select the CIFNs, we construct the matrix, if the matrix covers the cost type of data, then we normalize the matrix, such as

$$\stackrel{═}{{\mathbb{D}}_{DM}}=\{\begin{array}{cc}\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta k}}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta k}}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta k}}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta k}}\right)}\right)& forbenefittypesdata\\ \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta k}}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta k}}\right)},{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta k}}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta k}}\right)}\right)& forcosttypesdata\end{array}$$

But in the case of benefit types of data, we are not required to normalize the data.

Stage 2: We aggregate the information in the matrix.

Stage 3: Derive or discover the score value (SV) of the above aggregated information.

Stage 4: For discovering the most preferable decision, based on the score values, we rank alternatives. The graphical representation of the proposed decision-making procedure is listed in Fig. 2.

Fig. 2.

Geometrical representation of the proposed decision-making procedure.

Finally, we analyze some examples based on the invented theory for evaluating the consistency and validity of the proposed operators as well as the decision-making procedure.

5.2. Analysis of best madia communications

Media communication covers numerous techniques and technologies for transmitting or showing information, data, material, or messages with the help of different sources like the internet, mobile phones, television, and different channels. All these channels are categorized into different kinds based on the medium or platform exploited for communications. The major influence of this application is to find the best kind of media communications among the five best, such as:

• 1)Print Media “${\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}$”.
• 2)Broadcast Media “${\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}$”.
• 3)Digital Media “${\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$”.
• 4)Social Media “${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}$”.
• 5)Telecommunications “${\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}$”.

To address the best one, we use some features as an attribute's values, such as ${\stackrel{═}{\mathfrak{k}\xi }}_{AT-1}$: Growing analysis, ${\stackrel{═}{\mathfrak{k}\xi }}_{AT-2}$: Community-governmental impact, ${\stackrel{═}{\mathfrak{k}\xi }}_{AT-3}$: Ecological impact, and ${\stackrel{═}{\mathfrak{k}\xi }}_{AT-4}$: others. To achieve our target, we consider the weight vectors, such as $0.3,0.3,0.3\text{,}$ and $0.1$. For simplification of some numerical examples, we evaluate the procedure of decision-making techniques, such as

Stage 1: To select the CIFNs, we construct the matrix, see Tables 1 and If the matrix covers the cost type of data, then we normalize the matrix, such as

$$\stackrel{═}{{\mathbb{D}}_{DM}}=\{\begin{array}{cc}\left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta k}}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta k}}\right)},{\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta k}}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta k}}\right)}\right)& forbenefittypesdata\\ \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta k}}{e}^{i2\pi \left({\mathfrak{N}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta k}}\right)},{\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{R-\theta k}}{e}^{i2\pi \left({\mathfrak{M}}_{{\stackrel{═}{\mathfrak{k}\xi }}_{I-\theta k}}\right)}\right)& forcosttypesdata\end{array}$$

Table 1.

The original matrix is given by the decision-maker.

	${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{T}-\mathbf{1}}$	${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{T}-\mathbf{2}}$
${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{L}-\mathbf{1}}$	$\left(0.7e^{i2\pi \left(0.8\right)},0.2e^{i2\pi \left(0.1\right)}\right)$	$\left(0.71e^{i2\pi \left(0.81\right)},0.21e^{i2\pi \left(0.11\right)}\right)$
${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{L}-\mathbf{2}}$	$\left(0.8e^{i2\pi \left(0.5\right)},0.1e^{i2\pi \left(0.3\right)}\right)$	$\left(0.81e^{i2\pi \left(0.51\right)},0.11e^{i2\pi \left(0.31\right)}\right)$
${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{L}-\mathbf{3}}$	$\left(0.5e^{i2\pi \left(0.4\right)},0.3e^{i2\pi \left(0.4\right)}\right)$	$\left(0.51e^{i2\pi \left(0.41\right)},0.31e^{i2\pi \left(0.41\right)}\right)$
${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{L}-\mathbf{4}}$	$\left(0.8e^{i2\pi \left(0.8\right)},0.1e^{i2\pi \left(0.1\right)}\right)$	$\left(0.81e^{i2\pi \left(0.81\right)},0.11e^{i2\pi \left(0.11\right)}\right)$
${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{L}-\mathbf{5}}$	$\left(0.6e^{i2\pi \left(0.7\right)},0.1e^{i2\pi \left(0.2\right)}\right)$	$\left(0.61e^{i2\pi \left(0.71\right)},0.11e^{i2\pi \left(0.21\right)}\right)$
	${\stackrel{═}{\mathfrak{k}\xi }}_{AT-3}$	${\stackrel{═}{\mathfrak{k}\xi }}_{AT-4}$
${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{L}-\mathbf{1}}$	$\left(0.72e^{i2\pi \left(0.82\right)},0.22e^{i2\pi \left(0.12\right)}\right)$	$\left(0.73e^{i2\pi \left(0.83\right)},0.23e^{i2\pi \left(0.13\right)}\right)$
${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{L}-\mathbf{2}}$	$\left(0.82e^{i2\pi \left(0.52\right)},0.12e^{i2\pi \left(0.32\right)}\right)$	$\left(0.83e^{i2\pi \left(0.53\right)},0.13e^{i2\pi \left(0.33\right)}\right)$
${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{L}-\mathbf{3}}$	$\left(0.52e^{i2\pi \left(0.42\right)},0.32e^{i2\pi \left(0.42\right)}\right)$	$\left(0.53e^{i2\pi \left(0.43\right)},0.33e^{i2\pi \left(0.43\right)}\right)$
${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{L}-\mathbf{4}}$	$\left(0.82e^{i2\pi \left(0.82\right)},0.12e^{i2\pi \left(0.12\right)}\right)$	$\left(0.83e^{i2\pi \left(0.83\right)},0.13e^{i2\pi \left(0.13\right)}\right)$
${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{L}-\mathbf{5}}$	$\left(0.62e^{i2\pi \left(0.72\right)},0.12e^{i2\pi \left(0.22\right)}\right)$	$\left(0.63e^{i2\pi \left(0.73\right)},0.13e^{i2\pi \left(0.23\right)}\right)$

But in the case of benefit types of data, we are not required to normalize the data. Anyhow the data in Table 1 is not required to be normalized.

Stage 2: To consider the data in Eq. (36) for $\stackrel{═}{\mathcal{f}}=\stackrel{═}{\mathcal{g}}=1$, the aggregation values are listed below:

$${\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}=\left(0.5909e^{i2\pi \left(0.6932\right)},0.3388e^{i2\pi \left(0.2249\right)}\right),{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}=\left(0.6932e^{i2\pi \left(0.4109\right)},0.2249e^{i2\pi \left(0.4377\right)}\right),{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}=\left(0.4109e^{i2\pi \left(0.3274\right)},0.4377e^{i2\pi \left(0.5286\right)}\right),{\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}=\left(0.6932e^{i2\pi \left(0.6932\right)},0.2249e^{i2\pi \left(0.2249\right)}\right),{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}=\left(0.4981e^{i2\pi \left(0.5909\right)},0.2249e^{i2\pi \left(0.3388\right)}\right)$$

Stage 3: For ranking values, we expose the score values, such as

$${\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}=0.3602,{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}=0.2207,{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}=-0.114,{\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}=0.4683,{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}=0.2626$$

Stage 4: The ranking information is listed below:

$${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$$

Seen that ${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}$ is the best one. Further, to eliminate the phase term from the data in Table 1, we obtained the simple IFS, see Table 2.

Table 2.

The original matrix is given by the decision-maker.

	${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{T}-\mathbf{1}}$	${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{T}-\mathbf{2}}$	${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{T}-\mathbf{3}}$	${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{T}-\mathbf{4}}$
${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{L}-\mathbf{1}}$	$\left(0.7,0.2\right)$	$\left(0.71,0.21\right)$	$\left(0.72,0.22\right)$	$\left(0.73,0.23\right)$
${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{L}-\mathbf{2}}$	$\left(0.8,0.1\right)$	$\left(0.81,0.11\right)$	$\left(0.82,0.12\right)$	$\left(0.83,0.13\right)$
${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{L}-\mathbf{3}}$	$\left(0.5,0.3\right)$	$\left(0.51,0.31\right)$	$\left(0.52,0.32\right)$	$\left(0.53,0.33\right)$
${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{L}-\mathbf{4}}$	$\left(0.8,0.1\right)$	$\left(0.81,0.11\right)$	$\left(0.82,0.12\right)$	$\left(0.83,0.13\right)$
${\stackrel{═}{\mathfrak{k}\mathit{\xi }}}_{\mathit{A}\mathit{L}-\mathbf{5}}$	$\left(0.6,0.1\right)$	$\left(0.61,0.11\right)$	$\left(0.62,0.12\right)$	$\left(0.63,0.13\right)$

To consider the data in Eq. (36) for $\stackrel{═}{\mathcal{f}}=\stackrel{═}{\mathcal{g}}=1$, the aggregated values are listed below:

$${\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}=\left(0.5909,0.3388\right),{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}=\left(0.6932,0.2249\right),{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}=\left(0.4109,0.4377\right),{\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}=\left(0.6932,0.2249\right),{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}=\left(0.4981,0.2249\right)$$

For ranking values, we expose the score values, such as

$${\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}=0.1261,{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}=0.2341,{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}=-0.013,{\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}=0.2341,{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}=0.1366$$

The ranking information is listed below:

$${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$$

Seen that ${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}$ is the best one. Moreover, we derive the comparison between proposed and existing operators to improve the worth of the derived theory.

5.3. Sensitive analysis

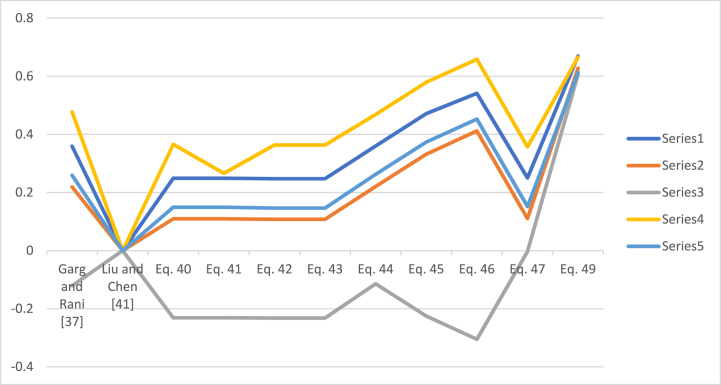
In this section, we compare the discovered operators with some prevailing operators based on the data in Table 1 with phase term and without phase term. For comparing the invented techniques with existing techniques, we consider some valuable and dominant techniques to improve the worth of the invented theory. For this, we consider the following existing techniques, such as Garg and Rani [37] elaborated generalized Bonferroni mean operators for CIFSs, Liu, and Chen [41] initiated the HM operators for IFSs, and proposed works based on CIFSs. To consider the data in Table 1, the comparative analysis is listed in Table 3.

Table 3.

Sensitive analysis (Table 1).

Methods	Score Values	Ranking Values
Garg and Rani [37]	$0.3593,0.2195,-0.121,0.4769,0.2593$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
Liu and Chen [41]	$CannotbeCalculated$	$CannotbeCalculated$
Eq. (40)	$0.2492,0.1094,-0.231,0.3658,0.1492$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
Eq. (41)	$0.2492,0.1094,-0.231,0.3658,0.1492$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
Eq. (42)	$0.2475,0.1077,-0.232,0.3635,0.1465$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
Eq. (43)	$0.2475,0.1077,-0.232,0.3635,0.1465$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
Eq. (44)	$0.3602,0.2207,-0.114,0.4683,0.2626$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
Eq. (45)	$0.4713,0.3318,-0.225,0.5794,0.3737$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
Eq. (46)	$0.5413,0.4118,-0.3051,0.6584,0.4527$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
Eq. (47)	$0.2501,0.1106,-0.003,0.3572,0.1515$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
Eq. (49)	$0.6695,0.6273,0.6061,0.6654,0.6128$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$

Seen that ${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}$ is the best one according to some operators and see that ${\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}$ is the best one according to some operators. The geometrical interpretation of the data in Table 3 is listed in Fig. 3.

Fig. 3.

Geometrical representation of the data in Table 3.

Furthermore, we state the influence of the parameters $\stackrel{═}{\mathcal{f}}$ and $\stackrel{═}{\mathcal{g}}$. For this, first, we fixed the value of $\stackrel{═}{\mathcal{f}}=1$, then for different values of $\stackrel{═}{\mathcal{g}}$, the ranking values are stated in Table 4.

Table 4.

Influence of the parameter $\stackrel{═}{\mathcal{g}}$, if $\stackrel{═}{\mathcal{f}}=1$, (Table 1).

Parameter	Score Values	Ranking Values
$\stackrel{═}{\mathcal{g}}=\mathbf{1}$	$0.3602,0.2207,-0.114,0.4683,0.1641$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{g}}=\mathbf{2}$	$0.414,0.2744,-0.0585,0.5181,0.2694$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{g}}=\mathbf{3}$	$0.447,0.307,-0.0255,0.5489,0.3216$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{g}}=\mathbf{5}$	$0.4867,0.3456,0.0123,0.5862,0.3763$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{g}}=\mathbf{7}$	$0.5102,0.3679,0.0331,0.6086,0.4055$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{g}}=\mathbf{9}$	$0.5258,0.3826,0.0463,0.6238,0.4238$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{g}}=\mathbf{10}$	$0.5318,0.3882,0.0513,0.6297,0.4306$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$

We fixed the value of $\stackrel{═}{\mathcal{f}}=1$, then the influence of the $\stackrel{═}{\mathcal{g}}$, stated in Table 5.

Table 5.

Influence of the parameter $\stackrel{═}{\mathcal{g}}$ if $\stackrel{═}{\mathcal{f}}=1$, (Table 1).

Parameter	Score Values	Ranking Values
$\stackrel{═}{\mathcal{g}}=\mathbf{1}$	$0.1261,0.234,-0.0134,0.2341,0.0892$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{g}}=\mathbf{2}$	$01549,0.2591,0.0153,0.2591,0.1396$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{g}}=\mathbf{3}$	$0.1726,0.2745,0.0326,0.2745,0.1645$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{g}}=\mathbf{5}$	$0.1936,0.2931,0.0525,0.2931,0.1905$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{g}}=\mathbf{7}$	$0.2058,0.3043,0.0636,0.3043,0.2043$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{g}}=\mathbf{9}$	$0.2139,0.3119,0.0707,0.3119,0.213$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{g}}=\mathbf{10}$	$0.2170,0.3148,0.0734,0.3148,0.2162$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$

We fixed the value of $\stackrel{═}{\mathcal{g}}=1$, then the influence of the $\stackrel{═}{\mathcal{f}}$, stated in Table 6.

Table 6.

Influence of the parameter $\stackrel{═}{\mathcal{f}}$ if $\stackrel{═}{\mathcal{g}}=1$, (Table 1).

Parameter	Score Values	Ranking Values
$\stackrel{═}{\mathcal{f}}=\mathbf{1}$	$0.3602,0.2207,-0.114,0.4683,0.1641$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{f}}=\mathbf{2}$	$0.4143,0.2747,-0.0583,0.5186,0.3181$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{f}}=\mathbf{3}$	$0.4476,0.3076,-0.0252,0.5496,0.3519$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{f}}=\mathbf{5}$	$0.4874,0.3463,0.0127,0.5871,0.3920$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{f}}=\mathbf{7}$	$0.5109,0.3687,0.0338,0.6096,0.4153$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{f}}=\mathbf{9}$	$0.5267,0.3835,0.0472,0.6248,0.4307$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{f}}=\mathbf{10}$	$0.5328,0.3892,0.0523,0.6307,0.4366$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$

We fixed the value of $\stackrel{═}{\mathcal{g}}=1$, then the influence of the $\stackrel{═}{\mathcal{f}}$, stated in Table 7.

Table 7.

Influence of the parameter $\stackrel{═}{\mathcal{f}}$ if $\stackrel{═}{\mathcal{g}}=1$, (Table 1).

Parameter	Score Values	Ranking Values
$\stackrel{═}{\mathcal{f}}=\mathbf{1}$	$0.1261,0.2341,-0.0134,0.2341,0.0892$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{f}}=\mathbf{2}$	$0.1550,0.2593,0.0154,0.2593,0.1631$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{f}}=\mathbf{3}$	$0.1727,0.2748,0.0327,0.2748,0.1791$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{f}}=\mathbf{5}$	$0.1938,0.2936,0.0527,0.2936,0.1981$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{f}}=\mathbf{7}$	$0.2062,0.3048,0.0639,0.3048,0.2092$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{f}}=\mathbf{9}$	$0.2143,0.3124,0.0711,0.3124,0.2164$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$
$\stackrel{═}{\mathcal{f}}=\mathbf{10}$	$0.2174,0.3154,0.0738,0.3154,0.2192$	${\stackrel{═}{\mathfrak{k}\xi }}_{AL-4}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-2}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-1}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-5}>{\stackrel{═}{\mathfrak{k}\xi }}_{AL-3}$

In the above investigation, we observed that for every value of parameters, we derive the same ranking results. The benefit of the proposed theory is that, with the help of proposed operators we can derive the ranking values of the many operators like algebraic, Einstein, Hamacher, and frank aggregation operators. Hence, the derived operator is more flexible and more dominant compared to other existing techniques.

6. Conclusion

Archimedean aggregation operators and Heronian mean operators are two different types of operators used for aggregating the collection of information into a singleton set. Keeping the advantages of the above operators, the major contributions of the derived operators are listed below:

• 1.We proposed the Archimedean operational laws based on CIF values.
• 2.We derived the algebraic operational laws, Einstein operational laws, Hamacher operational laws, and Frank operational laws from the Archimedean operational laws by using different values of the functions in Archimedean operational laws.
• 3.We evaluated the CIFAHA operator and CIFWAHA operator. Several special cases and the basic properties of the above-proposed operators are also diagnosed.
• 4.We illustrated the MADM process developed under the identified operators by using CIF information.
• 5.We discovered several examples to show the MADM technique is massively more flexible than the prevailing works with the help of sensitive analysis between explored and certain prevailing works.

6.1. Limitations of the proposed works

The proposed Archimedean Heronian mean operators based on CIFS are very flexible and dominant because of their structure and features, but in complicated situations, these ideas have not worked properly, for instance, if we are faced the information in the shape of yes, abstinence, no, and refusal, then the proposed operators based on CIFS have been failed. For this, we are required to compute these operators based on complex T-spherical fuzzy sets and their extensions.

6.2. Future direction

In the upcoming time, the proposed operators based on CIFS will receive a lot of attraction because, with the help of these operators, we can easily depict unreliable and vague information. Further, these operators will be utilized in the circumstances of complex Pythagorean fuzzy sets and their extensions. With the help of the proposed work, we can easily evaluate the problem of machine learning, medical diagnosis, artificial intelligence, neural networks, and many others if someone provides practical data. Moreover, we will employ the principle of complex fuzzy sets [[44], [45], [46]] quasirung orthopair fuzzy sets [47,48], complex q-rung orthopair fuzzy sets [[49], [50], [51]], complex spherical and T-spherical fuzzy sets [52,53], T-spherical fuzzy sets [[54], [55], [56]], and linear Diophantine fuzzy sets [[57], [58], [59], [60], [61]] in the environment of medical diagnosis, pattern recognition, manufacturing science, and computer science to grow the excellence of the explore mechanisms.

Ethics declaration statement

The authors state that this is their original work, and it is neither submitted nor under consideration in any other journal simultaneously.

Data availability

The authors agree that the data used in this manuscript is available to everyone and anyone can use this data by just citing this article.

CRediT authorship contribution statement

Zeeshan Ali: Writing – review & editing, Writing – original draft, Resources, Methodology, Investigation, Formal analysis, Conceptualization. Walid Emam: Resources, Methodology, Investigation, Funding acquisition, Formal analysis. Tahir Mahmood: Writing – review & editing, Validation, Supervision, Project administration, Investigation, Formal analysis, Conceptualization. Haolun Wang: Validation, Resources, Methodology, Investigation, Formal analysis.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.