Semi-supervised ROC analysis for reliable and streamlined evaluation of phenotyping algorithms

Abstract

Objective

High-throughput phenotyping will accelerate the use of electronic health records (EHRs) for translational research. A critical roadblock is the extensive medical supervision required for phenotyping algorithm (PA) estimation and evaluation. To address this challenge, numerous weakly-supervised learning methods have been proposed. However, there is a paucity of methods for reliably evaluating the predictive performance of PAs when a very small proportion of the data is labeled. To fill this gap, we introduce a semi-supervised approach (ssROC) for estimation of the receiver operating characteristic (ROC) parameters of PAs (eg, sensitivity, specificity).

Materials and Methods

ssROC uses a small labeled dataset to nonparametrically impute missing labels. The imputations are then used for ROC parameter estimation to yield more precise estimates of PA performance relative to classical supervised ROC analysis (supROC) using only labeled data. We evaluated ssROC with synthetic, semi-synthetic, and EHR data from Mass General Brigham (MGB).

Results

ssROC produced ROC parameter estimates with minimal bias and significantly lower variance than supROC in the simulated and semi-synthetic data. For the 5 PAs from MGB, the estimates from ssROC are 30% to 60% less variable than supROC on average.

Discussion

ssROC enables precise evaluation of PA performance without demanding large volumes of labeled data. ssROC is also easily implementable in open-source R software.

Conclusion

When used in conjunction with weakly-supervised PAs, ssROC facilitates the reliable and streamlined phenotyping necessary for EHR-based research.

Background and significance

Electronic health records (EHRs) are a vital source of data for clinical and translational research.¹ Vast amounts of EHR data have been tapped for real-time studies of infectious diseases, development of clinical decision support tools, and genetic studies at unprecedented scale.^2–10 This myriad of opportunities rests on the ability to accurately and rapidly extract a wide variety of patient phenotypes (eg, diseases) to identify and characterize populations of interest. However, precise and readily available phenotype information is rarely available in patient records and presents a major barrier to EHR-based research.^11,12

In practice, phenotypes are extracted from patient records with either rule-based or machine learning (ML)-based phenotyping algorithms (PAs) derived from codified and natural language processing (NLP)-derived features.^13,14 While PAs can characterize clinical conditions with high accuracy, they traditionally require a substantial amount of medical supervision that limits the automated power of EHR-based studies.¹⁵ Several research networks have spent considerable effort developing PAs, including i2b2 (Informatics for Integrating Biology & the Bedside), the eMERGE (Electronic Medical Records and Genomics) Network, and the OHDSI (Observational Health Data Sciences and Informatics) program that released APHRODITE (Automated PHenotype Routine for Observational Definition, Identification, Training, and Evaluation).¹⁶

Typically, PA development consists of 2 key steps: (i) algorithm estimation and (ii) algorithm evaluation. Algorithm estimation determines the appropriate aggregation of features extracted from patient records to determine phenotype status. For a rule-based approach, domain experts assemble a comprehensive set of features and corresponding logic to assign patient phenotypes.^12,13 As this manual assembly is highly laborious, significant effort has been made to automate algorithm estimation with ML. Numerous studies have demonstrated success with PAs derived from standard supervised learning methods such as penalized regression, random forest, and deep neural networks.^17–24 The scalability of a supervised approach, however, is limited by the substantial number of gold-standard labels required for model training. Gold-standard labels, which require time-consuming manual medical chart review, are infeasible to obtain for a large volume of records.^25,26

In response, semi-supervised (SS) and weakly-supervised methods for PA estimation that substantially decrease or eliminate the need for gold-standard labeled data have been proposed. Among SS methods, self-training and surrogate-assisted SS learning are common.^27–29 For example, Zhang et al¹⁵ introduced PheCAP, a common pipeline for SS learning that utilizes silver-standard labels for feature selection prior to supervised model training to decrease the labeling demand. Unlike gold-standard labels, silver-standard labels can be automatically extracted from patient records (eg, ICD codes or free-text mentions of the phenotype) and serve as proxies for the gold-standard label.^30,31 PheCAP was based on the pioneering work of Agarwal et al³² and Banda et al,³³ which introduced weakly-supervised PAs trained entirely on silver-standard labels. These methods completely eliminate the need for chart review for algorithm estimation and are the basis of the APHRODITE framework. Moreover, this work prompted numerous developments in weakly-supervised PAs, including methods based on non-negative matrix/tensor factorization, parametric mixture modeling, and deep learning, which are quickly becoming the new standard in the PA literature.^14,29

In contrast to the success in automating PA estimation, there has been little focus on the algorithm evaluation step. Algorithm evaluation assesses the predictive performance of a PA, typically through the estimation of the receiver operating characteristic (ROC) parameters such as sensitivity and specificity. At a high-level, the ROC parameters measure how well a PA discriminates between phenotype cases and controls relative to the gold-standard. As phenotypes are the foundation of EHR-based studies, it is critical to reliably evaluate the ROC parameters to provide researchers with a sense of trust in using a PA.^34–36 However, complete PA evaluation is performed far too infrequently due to the burden of chart review.^14,25,37

To address this challenge, Gronsbell and Cai³⁸ proposed the first semi-supervised method for ROC parameter estimation. This method assumes that the predictive model is derived from a penalized logistic regression model and was only validated on 2 PAs with relatively large labeled data sets (455 and 500 labels). Swerdel et al²⁵ later introduced PheValuator, and its recent successor PheValuator 2.0, to efficiently evaluate rule-based algorithms using “probabilistic gold-standard” labels generated from diagnostic predictive models rather than chart review.³⁷ Although the authors provided a comprehensive evaluation for numerous rule-based PAs, PheValuator can lead to biased ROC analysis, and hence a distorted understanding of the performance of a PA, when the diagnostic predictive model is not correctly specified.^39–41 PheValuator can also only be applied to rule-based PAs.

To fill this gap in the PA literature, we introduce a SS approach to precisely estimate the ROC parameters of PAs, which we call “ssROC”. The key difference between ssROC and classical ROC analysis (supROC) using only labeled data is that ssROC imputes missing gold-standard labels in order to leverage large volumes of unlabeled data (ie, records without gold-standard labels). By doing so, ssROC yields less variable estimates than supROC to enable reliable PA evaluation with fewer gold-standard labels. Moreover, ssROC imputes the missing labels with a nonparametric calibration of the predictions from the PA to ensure that the resulting estimates of the ROC parameters are unbiased regardless of the adequacy of PA.

Objective

The primary objectives of this work are to:

1. Extend the proposal of Gronsbell and Cai³⁸ to a wider class of weakly-supervised PAs that are common in the PA literature, including a theoretical analysis and development of a statistical inference procedure that performs well in finite-samples.

2. Provide an in-depth real data analysis of PAs for 5 phenotypes from Mass General Brigham (MGB) and extensive studies of synthetic and semi-synthetic data to illustrate the practical utility of ssROC.

3. Release an implementation of ssROC in open-source R software to encourage the use of our method by the informatics community.

Through our analyses of simulated, semi-synthetic, and real data, we observe substantial gains in estimation precision from ssROC relative to supROC. In the analysis of the 5 PAs from MGB, the estimates from ssROC are approximately 30% to 60% less variable than supROC on average. Our results suggest that, when used together with weakly-supervised PAs, ssROC can facilitate the reliable and streamlined PA development that is necessary for EHR-based research.

Materials and methods

Overview of ssROC

We focus on evaluating a classification rule derived from a PA with ROC analysis. ROC analysis assesses the agreement between the gold-standard label for a binary phenotype (eg, disease case/control), Y, and a PA score, S, indicating a patient’s likelihood of having the underlying phenotype (eg, the predicted probability of being a case). Y is typically obtained from chart review and S can be derived from various phenotyping methods. We focus on scores derived from parametric models fit with a weakly-supervised approach due to their ability to automate PA estimation and increasing popularity in the informatics literature.^{14,32,42–44} For ease of notation, we suppress the dependence of S on the estimated model parameter and provide more details on the PA in Section S3.

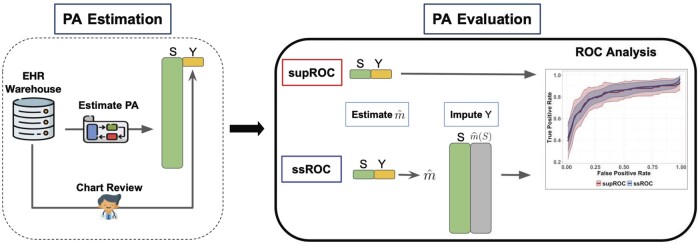
In classical supROC analysis, the data are assumed to contain information on both Y and S for all observations. However, in the phenotyping setting, Y is typically only available for a very small subset of patients due to the laborious nature of chart review. This gives rise to the semi-supervised setting in which a small labeled dataset is accompanied by a much larger unlabeled dataset. To leverage all of the available data and facilitate more reliable (ie, lower variance) evaluation of PAs, ssROC imputes the missing Y with a nonparametric recalibration of S, denoted as $\widehat{m}(S)$, to make use of the unlabeled data. An overview of ssROC is provided in Figure 1.

Figure 1.

Overview of PA estimation and evaluation. The phenotyping algorithm (PA) is first estimated to obtain the scores (S). Patient charts from the electronic health record (EHR) warehouse are reviewed to obtain the gold-standard label (Y) for PA evaluation. In classical supervised ROC analysis (supROC), only the labeled data from chart review is used to evaluate the PA’s performance. Semi-supervised ROC analysis (ssROC) uses the labeled data to impute the missing Y as $\widehat{m}(S)$ so that the unlabeled data can be utilized for estimation to yield more precise estimates of the ROC parameters.

Data structure and notation

More concretely, the available data in the SS setting consists of a small labeled dataset

$$\mathcal{L}=\left\{(Y_i,S_i)|i=1,\dots ,n\right\}$$

and an unlabeled dataset

$$\mathcal{U}=\left\{S_i|i=n+1,\dots ,n+N\right\}.$$

In the classical setting, it is assumed that (i) $\mathcal{U}$ is a much larger than $\mathcal{L}$ so that $n\ll N$ and (ii) the observations in $\mathcal{L}$ are randomly selected from the underlying pool of data. Throughout our discussion, we suppose that a higher value of S is more indicative of the phenotype. An observation is deemed to have the phenotype if $S>c$, where c is the threshold for classification.

ROC analysis

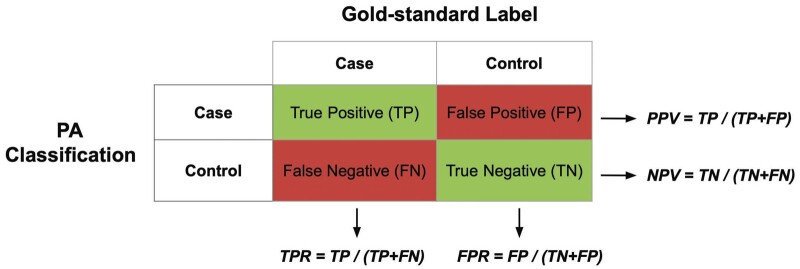
More formally, ROC analysis evaluates a PA with the true positive rate (TPR), false positive rate (FPR), positive predictive value (PPV), and negative predictive value (NPV). In diagnostic testing, the TPR is referred to as sensitivity, while the FPR is 1 minus the specificity.⁴⁵ For a given classification threshold, one may evaluate the ROC parameters by enumerating the correct and incorrect classifications. This information can be summarized in a confusion matrix as shown in Figure 2.

Figure 2.

Confusion matrix. The algorithm score from the phenotyping algorithm (PA) is used to determine phenotype case/control status based on the classification threshold. The ROC parameters are evaluated by enumerating the number of correct and incorrect classifications relative to the gold-standard label.

In practice, it is the task of the researcher to estimate an appropriate threshold for classification. This is commonly done by summarizing the trade-off between the TPR and FPR, defined respectively as

$$\text{TPR}(c)=P(S>c\hspace{0.17em}|\hspace{0.17em}Y=1) \text{and FPR}(c)=P(S>c\hspace{0.17em}|\hspace{0.17em}Y=0).$$

The ROC curve, $\text{ROC}(u)=\text{TPR}[{\text{FPR}}^{-1}(u)]$, summarizes the TPR and FPR across all possible choices of the threshold. In the context of PAs, c is often chosen to achieve a low FPR.²² An overall summary measure of the discriminative power of S in classifying Y is captured by the area under the ROC curve (AUC),

$$\text{AUC}={\int }_0^1\text{ROC}(u)du.$$

The AUC is equivalent to the probability that a phenotype case has a higher value of S than a phenotype control.⁴⁶ For a given threshold, the predictive performance of the classification rule derived from the PA is assessed with the PPV and NPV, defined respectively as

$$\begin{array}{c}\text{PPV}(c)=P(Y=1\hspace{0.17em}|\hspace{0.17em}S>c),\hspace{1em}\text{and}\\ \text{NPV}(c)=P(Y=0\hspace{0.17em}|\hspace{0.17em}S<c).\hfill \end{array}$$

Supervised ROC analysis

With only labeled data, one may obtain supervised estimators of the ROC parameters (supROC) with their empirical counterparts. For example, the TPR and FPR can be estimated as

$$\begin{array}{c}{\widehat{\text{TPR}}}_{\mathit{sup}}(c)=\frac{{\sum }_{i=1}^n{Y}_{i}I(S_i>c)}{{\sum }_{i=1}^n{Y}_i} \text{and}\\ {\widehat{\text{FPR}}}_{\mathit{sup}}(c)=\frac{{\sum }_{i=1}^n(1-Y_i)I(S_i>c)}{{\sum }_{i=1}^n(1-Y_i)}.\end{array}$$

The remaining parameters are estimated in a similar fashion. Variance estimates can be obtained from a resampling procedure, such as bootstrap or perturbation resampling.⁴⁷

ssROC: semi-supervised ROC analysis

Unlike its supervised counterpart that relies on only the labeled data, ssROC contains 2 steps of estimation to make use of the unlabeled data and provide a more reliable understanding of PA performance. In the first step, the missing labels are imputed by recalibrating the PA scores using a model trained with the labeled data. In the second step, the imputations are used in lieu of the gold-standard labels to evaluate the ROC parameters based on the PA scores in the unlabeled data in an analogous manner to supROC. Below we provide an overview of these 2 steps using the TPR as an example.

Step 1. Recalibrate the PA scores by fitting the model $m(S)=P(Y=1|S)$ with the labeled data. Obtain the imputations, $\{\widehat{m}(S_i)|i=n+1,\dots ,n+N\}$, for the unlabeled data based on the fitted model.

Step 2. Use the imputations to estimate the TPR with the unlabeled data as

$$\widetilde{\text{TP}}{\text{R}}_{\mathit{ssROC}}(c)=\frac{{\sum }_{i=n+1}^{n+N}\widehat{m}(S_i)I(S_i>c)}{{\sum }_{i=n+1}^{n+N}\widehat{m}(S_i)}.$$

The purpose of the first step is to ensure that the imputations do not introduce bias into the ROC parameter estimates. For example, utilizing the PA scores directly for imputation can distort the ROC parameter estimates due to potential inaccuracies of S in predicting Y. We propose to use a kernel regression model to nonparametrically impute the missing labels to prevent biasing the ssROC estimates.⁴⁰ Technical detail related to fitting the kernel regression model is provided in Section S1. In contrast, the purpose of the second step is to harness the large unlabeled dataset to produce estimates with lower variance than supROC. Similar to supROC, we propose a perturbation resampling procedure for variance estimation and detail 2 commonly used confidence intervals (CIs) based on the procedure in Section S2. In Section S3, we also provide a theoretical justification for the improved precision of ssROC relative to supROC for a wide range of weakly-supervised PAs.

Data and metrics for evaluation

We assessed the performance of ssROC using simulated, semi-synthetic, and real-world EHR data from MGB. All analyses used the R software package, ssROC, available at https://github.com/jlgrons/ssROC.

Simulation study

Our simulations cover PAs with high and low accuracy and varying degrees of calibration. For each accuracy setting, we simulated PA scores that (i) were perfectly calibrated, (ii) overestimated the probability of Y, and (iii) underestimated the probability of Y.⁴⁰ In all settings, Y was generated from a Bernoulli distribution with a prevalence of 0.3. To generate S, we first generated a random variable Z from a normal mixture model with $Z|Y=y\sim N({\alpha }_y,{\sigma }^2)$ and an independent noise variable from a Bernoulli mixture model with $ϵ|Y=y\sim \text{Bern}(p_y)$ for $y=0,1$. The PA score was obtained as

$$S=\{\begin{array}{cc}\text{expit}({\gamma }_0\hspace{0.17em}+\hspace{0.17em}{\gamma }_{1}Z)\hfill & \text{for perfect calibration}\hfill \\ \text{expit}(Z\hspace{0.17em}+\hspace{0.17em}ϵ)\hfill & \text{otherwise}\hfill \end{array}.$$ (1)

where ${\gamma }_0=({\alpha }_1^2\hspace{0.17em}-\hspace{0.17em}{\alpha }_0^2)/2{\sigma }^2+\text{log}\hspace{0.17em}\left[(1\hspace{0.17em}-\hspace{0.17em}\mu )/\mu )\right]$, ${\gamma }_1=({\alpha }_1\hspace{0.17em}-\hspace{0.17em}{\alpha }_0)/{\sigma }^2$, $\mu =P(Y=1)$, and $\text{expit}(x)=\frac{1}{1+e^{-x}}$. The values of ${\gamma }_0$ and ${\gamma }_1$ ensure that $S=P(Y=1|Z)$ for perfect calibration. Six simulation settings were obtained by varying $({\alpha }_0,{\alpha }_1,\sigma ,p_0,p_1)$, shown in Table 1. We also considered the extreme setting when S is independent of Y by permuting S generated from the model with high accuracy and perfect calibration. The calibration curves for each setting are presented in Figure S2. Across all settings, N = 10 000, $n=$ 75, 150, 250 and 500, and results are summarized across 5000 simulated datasets.

Table 1.

Parameter configurations for the 6 simulation studies.

	High PA accuracy	Low PA accuracy
Perfectly calibrated PA	(−0.5, 0.5, 0.5)	(−0.25, 0.25, 0.5)
Overestimated PA	(1, 2.3, 0.5, 0.3, 0.3)	(0.5, 1.2, 0.5, 0.5, 0.5)
Underestimated PA	(−2.6, −1.5, 0.5, 0.1, 0.1)	(−2.5, −1.5, 1, 0.3, 0.3)

The simulation settings were derived by varying the parameters $({\alpha }_0,{\alpha }_1,\sigma ,p_0,p_1)$ in Model 1.

Abbreviation: PA, phenotyping algorithm.

Semi-synthetic data analysis

To better reflect the complexity of PAs in real data, we generated semi-synthetic data for phenotyping depression with the MIMIC-III clinical database. MIMIC-III contains structured and unstructured EHR data from patients in the critical care units of the Beth Israel Deaconess Medical Center between 2001 and 2012.^21,48 As depression status is unavailable in patient records, it was simulated for all observations using a logistic regression model. That is, $Y\sim \text{Bern}[\text{expit}({\mathit{\beta }}^T\mathbf{X})]$ where

$$\mathit{\beta }=({\beta }_0,{\beta }_1,{\beta }_2,{\beta }_3),\mathbf{X}={(1,\hspace{0.17em}\text{log}(X_{\mathit{NLP}}+X_{\mathit{ICD}}+1),X_{\mathit{age}},\hspace{0.17em}\text{log}(X_{HU}+1\left)\right)}^T$$

$X_{\mathit{NLP}}$ is the number of depression related clinical concepts, $X_{\mathit{ICD}}$ is the number of depression related ICD-9 codes, $X_{\mathit{age}}$ is age at admission, and $X_{HU}$ is a measure of healthcare utilization based on the total number of evaluation and management Current Procedural Terminology (CPT) codes and the length of stay. The list of depression-related ICD-9 codes and clinical concepts are presented in Section S6.

Given the PA score is obtained from complex EHR data, we focus on simulating the phenotype to achieve high and low PA accuracy and present the calibration in Figure S4. We set $\mathit{\beta }=(1,4,0.05,-3)$ and $\mathit{\beta }=(1,1,0.01,-1)$ and to mimic a PA with high and low accuracy (AUC  =  90.1 and 72.6, respectively). The prevalence of Y in both settings was approximately 0.3. For both settings, the unlabeled set consisted of one visit from N = 32 172 unique patients and $n=$ 75, 150, 250, and 500 visits were randomly sampled 5000 times to generate labeled datasets of various sizes. We obtained the PA for depression by fitting PheNorm without the random corruption denoising step. PheNorm is a weakly-supervised method based on normalizing silver-standard labels with respect to patient healthcare utilization using a normal mixture model.⁴³ PheNorm is also used in our real-data analysis and described in detail in Section S4. $X_{\mathit{NLP}}$ and $X_{\mathit{ICD}}$ were used as silver-standard labels to fit PheNorm with $X_{HU}$ as the measure of healthcare utilization.

Real-world EHR data application

We further validated ssROC using EHR data from MGB, a Boston-based healthcare system anchored by 2 tertiary care centers, Brigham and Women’s Hospital and Massachusetts General Hospital. We evaluated PAs for 5 phenotypes, including cerebral aneurysm (CA), congestive heart failure (CHF), Parkinson’s disease (PD), systemic sclerosis (SS), and type 1 diabetes (T1DM). The data are from the Research Patient Data Registry which stores data on over 1 billion visits containing diagnoses, medications, procedures, laboratory information, and clinical notes from 1991 to 2017.

The full data for each phenotype consisted of patient records with at least one phenotype-related PheCode in their record.⁴⁹ A subset of patients was randomly sampled from the full data and sent for chart review. For each phenotype, the PA was obtained by fitting PheNorm without denoising using the total number of (i) phenotype-related PheCodes and (ii) positive mentions of the phenotype-related clinical concepts as the silver-standard labels and the number of notes in a patient’s EHR as the measure of healthcare utilization. The phenotypes represent different levels of PA accuracy, labeled and unlabeled dataset sizes, and prevalence (P). A summary of the 5 phenotypes is presented in Table 2.

Table 2.

Summary of the MGB phenotypes.

Phenotype	n	N	P	PheCode	CUI
Cerebral aneurysm (CA)	134	18 679	.68	433.5	C0917996
Congestive heart failure (CHF)	140	155 112	.18	428	C0018801
Parkinson’s disease (PD)	97	17 752	.62	332	C0030567
Systemic sclerosis (SS)	189	4272	.43	709.3	C0036421
Type 1 diabetes (T1DM)	121	46 013	.17	250.1	C0011854

The labeled dataset size ($n)$, the unlabeled dataset size (N), and the prevalence (P) of the 5 phenotypes as well as the main PheCode and concept unique identifier (CUI) used to train PheNorm. The underlying full data for each phenotype included all participants who passed the filter of $\ge 1$ PheCode for the phenotype of interest.

Benchmark method and reported metrics

We compared the PA evaluation results from ssROC and the benchmark, supROC, using the simulated, semi-synthetic, and real EHR data. We transformed the PA scores by their respective empirical cumulative distribution functions prior to ROC analysis. This transformation improves the performance of the imputation step, particularly when the distribution of S is skewed.⁵⁰ For the kernel regression, we used a Gaussian kernel with bandwidth determined by the standard deviation of the transformed PA scores divided by $n^{0.45}$.⁵¹ Additional detail related to the imputation step is provided in Section S1. We obtained variance estimates for the ROC parameters using perturbation resampling with 500 replications and weights from a scaled beta distribution, $4\cdot \text{Beta}(1/2,3/2)$, to improve finite-sample performance.⁵² We focused on logit-based CIs, described in Section S2.2, due to their improved coverage relative to standard Wald intervals.⁵³

We assessed percent bias for both supROC and ssROC by computing the mean of [(point estimate−ground truth)/(ground truth)×100%] across the replicated datasets. The ground truth values of the ROC parameters for the simulated and semi-synthetic data are provided in Tables S1 and S6. The empirical standard error (ESE) was computed as the standard deviation of the estimates from these datasets. The asymptotic standard error (ASE) was computed as the mean of the standard error estimates derived from the perturbation resampling procedure across the replicated datasets. Using mean squared error (MSE) as an aggregate measure of bias and variance, we evaluated the relative efficiency (RE) as the ratio of the MSE of supROC to the MSE of ssROC. The performance of our resampling procedure was assessed with the coverage probability (CP) of the 95% CIs for both estimation procedures. In the real data analysis, we present point estimates from both supROC and ssROC and the RE defined as the ratio of the variance of supROC to ssROC. We evaluated the performance of the PAs at an FPR of 10% and report the results for the AUC, classification threshold (Threshold), TPR, PPV, and NPV for all analyses.

Results

Simulation study

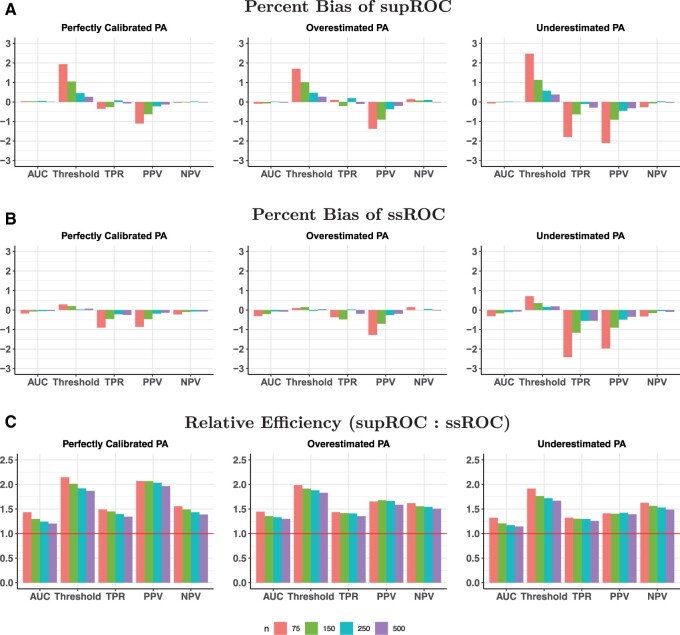
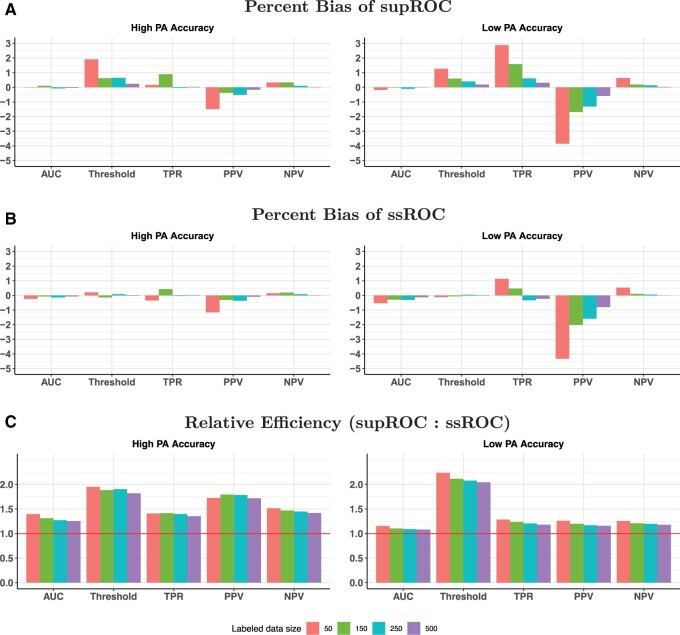
Figures 3 and 4 show the percent bias and RE in the high and low accuracy settings, respectively. Both ssROC and supROC generally exhibit low bias across all settings and ssROC often has lower bias than supROC. Additionally, ssROC has lower variance than supROC in all settings, as indicated by REs that consistently exceed 1. In the high accuracy setting, the median REs across all calibration patterns and labeled sizes is between 1.3 (AUC) and 1.9 (Threshold). For the low accuracy setting, the median REs range from 1.1 (AUC) to 1.6 (Threshold). Practically, these results imply that ssROC is more precise for a fixed amount of labeled than supROC. Alternatively, this reduction in variance can also be interpreted as a reduction in sample size required for ssROC to achieve the same variance as supROC. For example, the RE for PPV with $n=250$ under the setting of high PA accuracy and perfect calibration is 2, which suggests that ssROC can achieve the same variance as supROC with half the amount of labeled data.

Figure 3.

Percent bias and relative efficiency (RE) for high phenotyping algorithm (PA) accuracy settings at a false positive rate (FPR) of 10%. RE is defined as the mean squared error of supROC compared to the mean squared error of ssROC. For all scenarios, the size of the unlabeled was N=10 000.

Figure 4.

Percent bias and relative efficiency (RE) for low phenotyping algorithm (PA) accuracy settings at a false positive rate (FPR) of 10%. RE is defined as the mean squared error of supROC compared to the mean squared error of ssROC. For all scenarios, the size of the unlabeled was N=10 000.

When S is independent of Y, Figure S3 shows that ssROC has negligible bias, yields precision similar to supROC for the ROC parameters, and has improved precision for the threshold. These empirical findings demonstrate the robustness of ssROC to a wide range of PA scores and are further supported by our theoretical analysis in Section S3. Specifically, our analysis verifies that ssROC is guaranteed to perform on par supROC for the ROC parameters and yield more precise estimation for the Threshold when S is independent of Y.

The ESE, ASE, and CP for the 95% CIs of both supROC and ssROC are presented in Tables S2 and S3. The proposed logit-based CI consistently achieves reasonable coverage for both methods. The estimated variance for ssROC is also generally more accurate than that from supROC. Additionally, our results underscore the advantages of employing the logit-based interval over the standard Wald interval, particularly when n is small and/or the point estimate is near the boundary.

Semi-synthetic data analysis

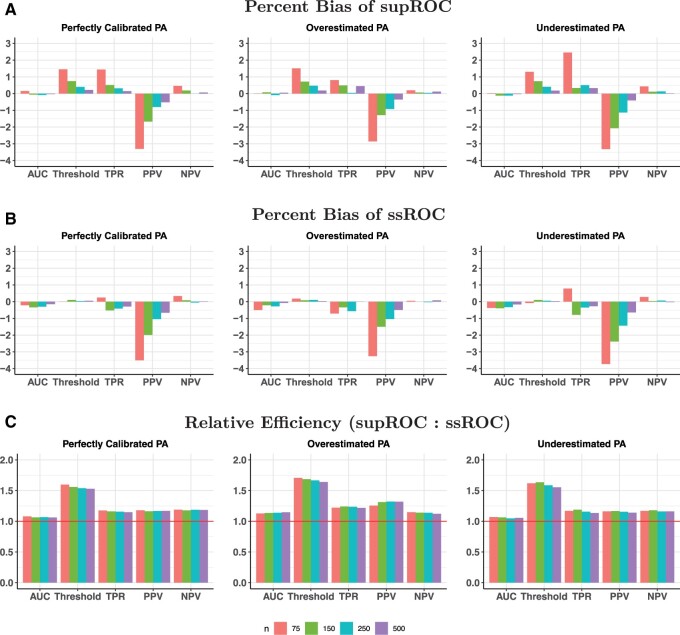
The findings from the semi-synthetic EHR data analysis align closely with the results of our simulations, further demonstrating the robustness of ssROC to the PA score. Generally, ssROC has smaller bias than supROC and both methods have small bias across all settings as highlighted in Figure 5A and B. ssROC again demonstrates improved precision relative to supROC. The median RE across labeled data sizes in the setting with high PA accuracy is between 1.3 (AUC) and 1.9 (Threshold) and between 1.1 (AUC) and 2.1 (Threshold) for the low accuracy setting. Additionally, Tables S7 and S8 show that the logit-based CIs for both methods yield reasonable coverage.

Figure 5.

Percent bias and relative efficiency (RE) for the semi-synthetic data analysis at a false positive rate (FPR) of 10%. RE is defined as the mean squared error of supROC compared to the mean squared error of ssROC. For both settings, the size of total data was 32 172.

Analysis of 5 PAs from MGB

Table 3 presents the point estimates for the 5 phenotypes from MGB, ordered by the AUC estimates from ssROC, at a FPR of 10%. As our primary focus is to compare ssROC with supROC, a single FPR was chosen for consistency across the phenotypes. However, this does lead to low TPRs for some phenotypes, such as CHF. Generally, the point estimates from ssROC are similar to those from supROC. There are some differences in the Threshold estimates for CA and SS, which leads to some discrepancies in the other estimates. As supROC is only evaluated at the unique PA scores in the labeled dataset, the Threshold estimate can be unstable at some FPRs. In contrast, ssROC is evaluated across a broader range of PA scores in the unlabeled dataset and results in more stable estimation.

Table 3.

Point estimates for the 5 phenotypes from MGB at a FPR of 10%.

Phenotype	Method	AUC	Threshold	TPR	PPV	NPV
CA	ssROC	81.3	64.0	51.0	89.8	51.5
	supROC	80.4	73.7	35.2	87.4	40.1
CHF	ssROC	83.2	84.9	42.0	44.1	89.2
	supROC	79.3	86.1	36.0	43.9	86.6
PD	ssROC	85.9	75.3	49.1	74.1	75.2
	supROC	81.6	80.1	34.1	72.4	64.1
SS	ssROC	89.4	59.8	60.6	89.9	60.7
	supROC	87.5	64.6	52.3	89.7	53.2
T1DM	ssROC	90.5	80.4	68.8	57.3	93.7
	supROC	91.5	80.1	75.0	59.8	94.8

Abbreviations: CA, cerebral aneurysm; CHF, congestive heart failure; FPR, false positive rate; MGB, Mass General Brigham; NPV, negative predictive value; PD, Parkinson’s disease; PPV, positive predictive value; SS, systemic sclerosis; ssROC, semi-supervised receiver operating characteristic analysis; supROC, supervised receiver operating characteristic analysis; T1DM, type 1 diabetes; TPR, true positive rate.

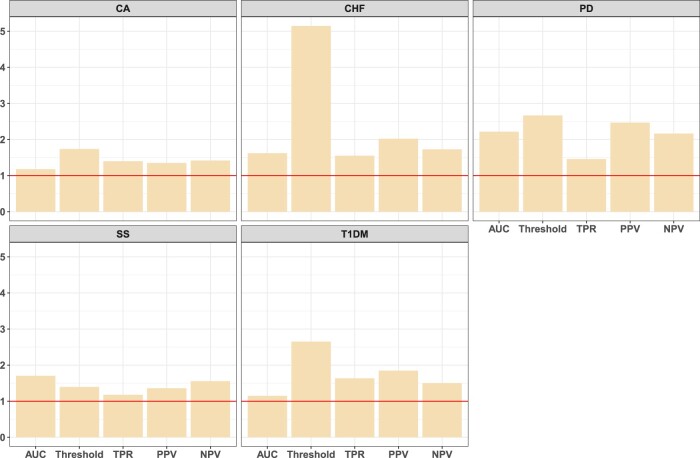
Figure 6 shows the RE of supROC to ssROC across the 5 phenotypes at a FPR of 10%. The median RE gain across phenotypes ranges from approximately 1.5 (AUC, TPR) to 2.7 (Threshold), implying that the estimates from ssROC are approximately 30%-60% less variable than supROC on average. It is worth noting the RE for the Threshold estimate for CHF is quite high. Figure S5 illustrates that this behavior can be explained by the empirical distribution of the resampled estimates. The distribution of the estimates from supROC are multimodal, while those from ssROC are approximately normal as expected. This behavior further emphasizes the stability of ssROC relative to supROC in real data.

Figure 6.

Relative efficiency (RE) for the 5 phenotypes from Mass General Brigham (MGB) at an false positive rate (FPR) of 10%. RE is defined as the ratio of the variance of supROC to that of ssROC.

Consistent with our simulation and theoretical results, we also observe that RE is linked to PA accuracy. For example, a phenotype with high PA accuracy, such as T1DM, exhibits a higher RE compared to CA, which has the lowest PA accuracy. Overall, these findings underscore the advantages of our proposed ssROC method compared to supROC in yielding more precise ROC analysis.

Discussion

Although high-throughput phenotyping is the backbone of EHR-based research, there is a paucity of methods for reliably evaluating the predictive performance of a PA with limited labeled data. The proposed ssROC method fills this gap. ssROC is a simple 2-step estimation procedure that leverages large volumes of unlabeled data by imputing missing gold-standard labels with a nonparametric recalibration of a PA score. Unlike existing procedures for PA evaluation in the informatics literature, ssROC eliminates the requirement that the PA be correctly specified to yield unbiased estimation of the ROC parameters and may be utilized for ML-based PAs.^25,37 While we focus specifically on weakly-supervised PAs in our theoretical analysis and data examples given their increasing popularity and ability to automate PA estimation, ssROC can also be used to evaluate rule-based or other ML-based PAs. Moreover, by harnessing unlabeled data, ssROC yields substantially less variable estimates than supROC in simulated, semi-synthetic, and real data. Practically, this translates into a significant reduction in the amount of chart review required to obtain a precise understanding of PA performance.

Although our work is a first step toward streamlining PA evaluation, there are several avenues that warrant future research. First, ssROC assumes that the labeled examples are randomly sampled from the underlying full data. In situations where the goal is to phenotype multiple conditions or comorbidities, more effective sampling strategies such as stratified random sampling have the potential to further enhance the efficiency of ssROC.⁵⁴ However, due to the large discrepancy in size of the labeled and unlabeled data, developing procedures to accommodate non-random sampling is nontrivial.⁵⁵ Second, the nonparametric recalibration step demands a sufficient amount of labeled data for the kernel regression to be well estimated. While our extensive simulation studies across a wide variety of PAs and sample sizes illustrate the robustness of ssROC, our future work will develop a parametric recalibration procedure that accommodates smaller labeled data sizes. Third, ssROC can also be extended for model comparisons and evaluation of fairness metrics, which are urgently needed given the increasing recognition of unfairness in informatics applications. The calibration step would need to be augmented in both settings to utilize additional information in multiple PA scores or protected attributes, respectively. This augmentation could potentially lead to a more efficient procedure as ssROC only uses information from one PA score for imputation. Lastly, our results demonstrate the ability of ssROC to provide accurate ROC evaluation for 5 phenotypes with variable prevalence, labeled and unlabeled dataset sizes, and PA accuracy within one health system. Further work is needed to understand the performance of our method across a diverse range of phenotypes and to extend our approach to accommodate federated analyses across multiple healthcare systems.

Conclusion

In this article, we introduced a semi-supervised approach, ssROC, that leverages a large volume of unlabeled data together with a small subset of gold-standard labeled data to precisely estimate the ROC parameters of PAs. PA development involves 2 key steps: (i) algorithm estimation and (ii) algorithm evaluation. While a considerable amount of effort has been placed on algorithm estimation, ssROC fills the current gap in robust and efficient methodology for predictive performance evaluation. Additionally, ssROC is simple to implement and is available in open-source R software to encourage use in practice. When used in conjunction with weakly-supervised PAs, ssROC demonstrates the potential to facilitate the reliable and streamlined phenotyping that is necessary for a wide variety of translational EHR applications.

Author contributions

Je.G. conceived and designed the study. Ji.G. conducted simulation and semi-synthetic data analyses. C.B. and C.H. conducted real data analyses. Je.G., Ji.G., C.B., P.V., and K.Z. analyzed and interpreted the results. Je.G. and Ji.G. drafted and revised the manuscript. All authors reviewed and approved the final manuscript.

Supplementary material

Supplementary material is available at Journal of the American Medical Informatics Association online.

Funding

The project was supported by the Natural Sciences and Engineering Research Council of Canada grant (RGPIN-2021-03734), the University of Toronto Connaught New Researcher Award, and the University of Toronto Seed Funding for Methodologists Grant (to Je.G.).

Conflict of interest

The authors have no conflicts of interest to declare.

Data availability

Our proposed method is implemented as an R software package, ssROC, which is available at https://github.com/jlgrons/ssROC.