Abstract
Objective
This study explores the feasibility of using machine learning to predict accurate versus inaccurate diagnoses made by pathologists based on their spatiotemporal viewing behavior when evaluating digital breast biopsy images.
Materials and Methods
The study gathered data from 140 pathologists of varying experience levels who each reviewed a set of 14 digital whole slide images of breast biopsy tissue. Pathologists’ viewing behavior, including zooming and panning actions, was recorded during image evaluation. A total of 30 features were extracted from the viewing behavior data, and 4 machine learning algorithms were used to build classifiers for predicting diagnostic accuracy.
Results
The Random Forest classifier demonstrated the best overall performance, achieving a test accuracy of 0.81 and area under the receiver-operator characteristic curve of 0.86. Features related to attention distribution and focus on critical regions of interest were found to be important predictors of diagnostic accuracy. Further including case-level and pathologist-level information incrementally improved classifier performance.
Discussion
Results suggest that pathologists’ viewing behavior during digital image evaluation can be leveraged to predict diagnostic accuracy, affording automated feedback and decision support systems based on viewing behavior to aid in training and, ultimately, clinical practice. They also carry implications for basic research examining the interplay between perception, thought, and action in diagnostic decision-making.
Conclusion
The classifiers developed herein have potential applications in training and clinical settings to provide timely feedback and support to pathologists during diagnostic decision-making. Further research could explore the generalizability of these findings to other medical domains and varied levels of expertise.
Keywords: breast pathology, medical education, medical residency training, machine learning, diagnostic decision-making, medical image interpretation, diagnostic accuracy
Background and significance
Over 1 million breast biopsies are estimated to occur annually in the United States and are interpreted and diagnosed by pathologists.1–3 Accurate pathological diagnosis of biopsy tissue is the linchpin for appropriate patient care, yet the perceptual and cognitive mechanisms responsible for reaching a successful diagnosis remain somewhat elusive.4–7 When pathologists inspect biopsy tissue, they dynamically allocate their visual attention to different regions of the tissue, increasing magnification to afford perception of cellular histopathological features and panning to different image regions.6,8–11 During this process, pathologists accumulate evidence to test emerging diagnostic hypotheses that will ultimately form the basis for a diagnostic decision.12–14 The visual interpretive behavior that pathologists exhibit during the evaluation of biopsy tissue may potentially predict whether they arrive at an accurate diagnosis.9–11,15 The present study used machine learning to explore this possibility, testing whether classifiers could be trained to distinguish accurate versus inaccurate pathologist diagnoses based only on information about the spatiotemporal dynamics of pathologist viewing behavior. If so, behaviors associated with diagnostic accuracy could be reinforced during residency training programs, form the basis for advanced competency assessments, or be used to adaptively trigger decision support tools (such as computer-aided diagnosis).
The advent of digital whole slide imaging in pathology has made it possible to record how pathologists interact with digitized biopsy images on their computer screens, including their zooming (magnification) and panning behavior as they evaluate each case. This was not feasible with traditional glass slides viewed with a microscope. These novel data recordings can be processed and analyzed to extract data features that quantify spatiotemporal dynamics of pathologists’ interpretive behavior. Critically, these features can be used as independent variables to train machine learning classifiers to distinguish accurate versus inaccurate diagnostic interpretations. To our knowledge, only one study has previously examined this possibility.16 In that study, radiology residents reviewed mammograms while wearing a head-mounted eye-tracking device, and 3 features derived from eye movement data were used to train a series of machine learning classifiers that also considered case-level characteristics and radiologist opinions. The models achieved high sensitivity to detect an accurate diagnosis (97.3%) but relatively low specificity (59%) overall. The authors discuss several reasons why the model’s specificity was low, including the small sample size (N = 20), small number of errors made by radiologists on their task, and a need for more features that characterize each physician’s unique behavior. The present study expands upon prior research to reveal viewing behaviors indicative of diagnostic accuracy in a relatively large sample of pathologists.
Objective
Herein, we collected a large dataset from 140 pathologists with varied experience levels; in general, larger sample sizes provide higher power to recognize patterns in data, particularly as the number of features increases.17 Furthermore, we used a set of test cases that has been extensively validated, including establishing consensus reference diagnoses, consensus regions of critical diagnostic importance, and normative accuracy data that shows high variability across pathologists.18–20 Rather than relying on expensive and time-consuming eye-tracking devices that are difficult to transport and use, we focused our analysis on data from viewing logs that are relatively unobtrusive and easy to implement in digital slide viewing software. Finally, we used both a diverse set of features calculated from viewing behavior and trained a diverse set of machine learning algorithms to compare classification performance among several machine learning algorithms including decision trees, random forest (RF), neural networks, and support vector machines (SVM). These models were trained with varying feature sets to help understand the generality of our findings to alternate contexts, cases, and pathologist expertise levels.
Materials and methods
For this analysis, we leveraged data from an ongoing study examining medical decision-making and diagnostic behavior in attending pathologists and residents training in pathology.
Participants
Data were collected from 140 (N = 140) participants at 9 different major university medical centers across the United States. Participants varied in experience, with 22 attending pathologists and 118 residents at varied levels of postgraduate training. Specifically, there were 25 first-year residents, 34 second-year residents, 25 third-year residents, and 14 fourth-year residents. All methods were carried out in accordance with the Declaration of Helsinki. Written informed consent was obtained in accordance with Institutional Review Board approvals granted by the University of California Los Angeles.
Test cases and critical regions of interest
We selected 32 cases from a standardized test set of 240 hematoxylin and eosin-stained digital whole slide images (WSI),18,19 each scanned at 40× objective using an iScan Coreo Au scanner. In our prior research, a consensus panel of 3 expert fellowship-trained breast pathologists reached agreement (using a modified Delphi technique) on a single consensus reference diagnosis for each case. In addition to agreeing upon a diagnosis, the panel also identified a single slide that provided all necessary and sufficient histopathological details to afford a successful diagnosis of a case, and identified one or more consensus regions of interest (cROIs) that best represented the most advanced diagnosis for the case. While these cROIs are never displayed to participants in our research, they form an important foundation for data analysis.
Cases varied in consensus diagnostic category, with 2 benign cases, 4 atypia cases, 4 low-grade ductal carcinoma in situ cases (lg-DCIS), 2 high-grade ductal carcinoma in situ cases (hg-DCIS), and 2 invasive cases. In the present research, diagnostic accuracy was operationalized as congruence (accurate) or incongruence (inaccurate) with the expert consensus diagnosis. Please refer to our prior research for details on the methodology used to identify a consensus diagnosis and region(s) of interest for each case,18,19 or for details on how cases were parsed into low- versus high-grade DCIS.21
Design and procedures
Participating pathologists independently reviewed a single set of 14 digital WSI of breast biopsy tissue derived from a larger test set of 32 cases, with each image representing a single case. During a data collection session, an experimenter guided participants through the review of 14 cases, one at a time. After each case, the pathologist arrived at a diagnostic decision and recorded it on a histology form. A practice case was used to familiarize participants with the custom WSI review interface, including zooming and panning, and our histology form. Case review was done on a 24″ Dell liquid crystal display (LCD) monitor at 1920 × 1080 resolution, attached to a Dell Precision workstation laptop.
While participants reviewed each case, our custom WSI review interface (built using HD View SL, Microsoft’s open-source Silverlight gigapixel image viewer; Microsoft, Inc., Redmond, WA, United States) continuously logged participant zooming and panning behavior (at ∼10 Hz) and saved it to a local SQL database. These files comprehensively represented case review behavior including zoom level and the location and size of the viewing area over time; each file represents a series of what we call viewing epochs, with each epoch describing a given zoom level, viewport size (ie, the dimensions of the viewable image region), and viewport location (ie, the location of the viewable image region’s origin within the global image coordinate system) at a point in time.
The histology form included a categorical diagnosis, identification of histologic types (ie, ductal, lobular), histopathological features (eg, necrosis, nuclear grading, tubule formation, mitotic activity), and a rating of case difficulty and confidence in their diagnosis. After reviewing a series of 14 cases, the participants were offered a gift card ($50USD). For resident pathologists, the experimenter returned on an annual basis to collect additional data; 50 of the 140 pathologists returned for a second visit, and 13 returned for a third visit.
Data processing and feature extraction
Data were processed using the Python programming language (v3.11.2), including the numpy,22 scipy,23 pandas,24 sklearn,25 imblearn,26 and matplotlib27 packages. Our objective was to quantify a comprehensive set of features that characterize temporal and spatial aspects of viewing behavior; these were largely motivated by features previously identified as correlated with diagnostic accuracy in extant research.6,28
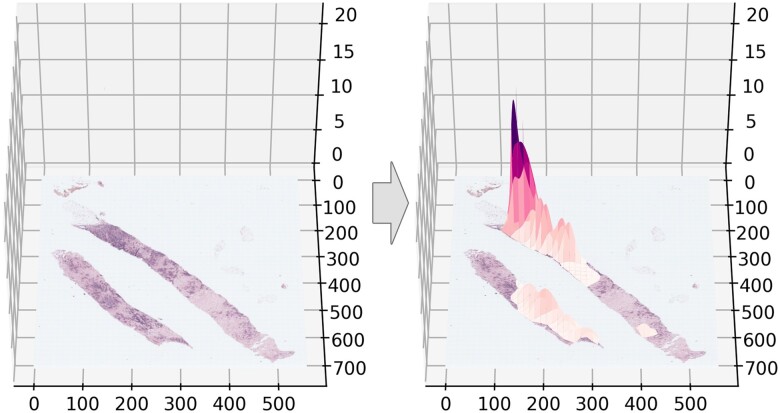
Using a feature engineering approach, we calculated 30 features. Some features were calculated using viewport data, including total viewing duration and proportion of viewing time spent at various zoom levels, whereas other features were derived from the distribution of attention over each case. To quantify the distribution of attention over each case, we plotted multivariate Gaussians to represent each viewing epoch, similar to eye-tracking data analysis methods that use fixation density maps derived from convolving eye fixation points with Gaussian filters centered upon each fixation point.29,30 This method assumes that visual attention is approximately normally distributed around a viewing centroid and that the higher the zoom and longer the duration of region viewing, the more evidence we have that visual attention is focused on that region. Each multivariate (x, y, z) Gaussian was overlaid onto the image at the centroid of each viewing epoch, with x and y dimensions matching the dimensions of the viewport size, and z (height) matching the duration (in seconds) of the viewing epoch. The series of Gaussians was convolved to represent a participant’s full probability distribution of attention over the image (Figure 1).
Figure 1.
A representative breast core biopsy case image (left) with an example multivariate Gaussian map overlaid (right). The x and y axes indicate the pixel coordinate space, and the z axis indicates the standardized height of the Gaussian map.
Each multivariate Gaussian map was printed to a table and standardized, resulting in a total of 3017 tables. Each table represented a single participant’s viewing behavior for a single case, matching the overall XY dimensions of the original image and divided into 80 × 80-pixel cells (ie, a 5 × 5 pixel region of an ×2.5 image scaled up 16× to 80 × 80 pixel region at 40×). Within each cell was a single value representing the height of the convolved multivariate Gaussians overlaid onto the image. Because background (white space) was not informative to image interpretation, we zeroed all table cells that contained no tissue by using established image foreground/background segmentation algorithms.31,32
We then used raw data and the resulting Gaussian tables to extract a set of 30 features detailed in Table 1. Note that all features were related to spatiotemporal characteristics of viewing behavior; no information regarding case consensus reference diagnostic category or pathologist characteristics were included in our primary analyses. This decision was made to increase the chances that our results might generalize to other cases and pathologists.
Table 1.
The 30 derived features and their respective descriptions, units, and descriptive statistics (mean, standard deviation).
| Feature | Description | Units | Mean (SD) for Accurate | Mean (SD) for Inaccurate | Mean (SD) |
|---|---|---|---|---|---|
| Temporal features | |||||
| Viewing duration | The amount of time, in seconds, that the participant spent reviewing the case. | Seconds | 98.27 (52.0) | 101.69 (57.02) | 100.25 (54.9) |
| Time to first zoom | The amount of time, in seconds, until the participant made their first zoom over 1×. | Seconds | 5.97 (3.11) | 5.09 (3.66) | 5.92 (3.44) |
| Time per zoom quartile (Q1) | The amount of time that the participant spent in the first zoom quartile. Zoom quartile was used for data reduction purposes, reducing the possible number of zoom levels from 60 to 4; for standardization purposes, the quartile calculation used data from all participants and cases (Q1: 1-2, Q2: 3-6, Q3: 7-11, Q4: 12-60). | Seconds | 22.69 (16.33) | 23.26 (16.90) | 23.02 (16.67) |
| Time per zoom quartile (Q2) | The amount of time that the participant spent in the second zoom quartile. | Seconds | 28.14 (20.57) | 30.04 (22.33) | 29.24 (21.62) |
| Time per zoom quartile (Q3) | The amount of time that the participant spent in the third zoom quartile. | Seconds | 18.57 (16.34) | 20.45 (17.0) | 19.66 (16.75) |
| Time per zoom quartile (Q4) | The amount of time that the participant spent in the fourth zoom quartile. | Seconds | 28.87 (32.54) | 27.93 (29.30) | 28.33 (30.71) |
| Proportion time per zoom quartile (Q1) | The proportion of time in the first zoom quartile relative to viewing duration. | Proportion | 0.26 (0.17) | 0.26 (0.17) | 0.26 (0.17) |
| Proportion time per zoom quartile (Q2) | The proportion of time in the second zoom quartile relative to viewing duration. | Proportion | 0.30 (0.16) | 0.30 (0.15) | 0.30 (0.15) |
| Proportion time per zoom quartile (Q3) | The proportion of time in the third zoom quartile relative to viewing duration. | Proportion | 0.19 (0.12) | 0.20 (0.12) | 0.19 (0.12) |
| Proportion time per zoom quartile (Q4) | The proportion of time in the fourth zoom quartile relative to viewing duration. | Proportion | 0.26 (0.20) | 0.24 (0.19) | 0.25 (0.19) |
| Time to first cROI view | The amount of time, in seconds, until the cROI first occupied >50% of the viewport area. The >50% threshold was chosen because it ensures the likelihood that attention was on the cROI is greater than chance. | Seconds | 50.83 (49.55) | 41.97 (47.87) | 45.71 (48.77) |
| cROI-related features | |||||
| Proportion of time on first cROI view | The proportion of total review time when the cROI occupied >50% of the viewport area. | Proportion | 0.26 (0.31) | 0.18 (0.22) | 0.22 (0.26) |
| Zoom level on first cROI view | The zoom level when the cROI first occupied >50% of the viewport area. | Zoom Level | 7.13 (4.41) | 8.32 (4.76) | 7.82 (4.65) |
| Proportion of viewport occupied by cROI on first cROI view | The proportion of the viewport that is occupied by the cROI when the cROI first occupied >50% of the viewport area. If the cROI never occupies >50% of viewport, 0 is entered. | Proportion | 0.48 (0.32) | 0.46 (0.29) | 0.47 (0.30) |
| Proportion of cROI visible in viewport on first cROI view | The proportion of the cROI that is viewable within the viewport when the cROI first occupies >50% of the viewport area. If the cROI never occupies >50% of viewport, 0 is used. | Proportion | 0.42 (0.34) | 0.47 (0.35) | 0.45 (0.35) |
| Proportion of time on cROI(s) | The cumulative amount of time spent viewing cROI(s), relative to viewing duration. | Proportion | 0.39 (0.37) | 0.24 (0.25) | 0.30 (0.31) |
| Proportion of attention to cROI | The sum of Gaussian table values for the cROI area(s) relative to the sum of Gaussian table values. | Proportion | 0.56 (0.41) | 0.42 (0.34) | 0.48 (0.38) |
| Peak-related features | |||||
| Peak count | The total number of peaks in the Gaussian table identified using local maxima. | Frequency | 1895.91 (1289.17) | 1738.99 (1138.95) | 1805.3 (1207) |
| Peak height mean | The mean height of each peak in the Gaussian table. | z Heightstd | 0.29 (0.47) | 0.20 (0.28) | 0.24 (0.37) |
| Peak height SD | The standard deviation of peak heights in the Gaussian table. | z Heightstd | 2.88 (1.81) | 2.73 (1.56) | 2.79 (1.67) |
| Peak height entropy | The entropy of peak heights in the Gaussian table. | Natsstd | 3.90 (1.48) | 3.69 (1.39) | 3.78 (1.43) |
| Peak height max | The maximum peak height in the Gaussian table. | z Heightstd | 74.54 (50.01) | 71.29 (46.97) | 72.66 (48.30) |
| Peak pairwise distance mean | The mean pairwise Euclidean distance between peaks in the Gaussian table. | Pixels | 458.11 (136.41) | 487.05 (156.84) | 474.82 (149.2) |
| Peak pairwise distance SD | The standard deviation of pairwise Euclidean distance between peaks in the Gaussian table. | Pixels | 254.27 (74.05) | 275.64 (94.02) | 266.61 (86.78) |
| Peak pairwise distance max | The maximum pairwise Euclidean distance between peaks in the Gaussian table. | Pixels | 1301.17 (397.24) | 1285.82 (409.79) | 1292.31 (404.5) |
| Peak positional entropy | The entropy of peak locations in x, y coordinate space in the Gaussian table. | Natsstd | 13.39 (2.22) | 13.38 (1.90) | 13.38 (2.04) |
| Cluster-related features | |||||
| Cluster count | The optimal number of clusters included in a k-means cluster analysis of 3D point cloud data derived from the Gaussian table. | Frequency | 3.96 (0.73) | 3.78 (0.84) | 3.86 (0.79) |
| Cluster max height mean | The mean of the maximum heights of each cluster identified in the cluster count process. | z Heightstd | 29.47 (18.04) | 29.61 (18.30) | 29.55 (18.19) |
| Cluster max height SD | The standard deviation of the maximum heights of each cluster identified in the cluster count process. | z Heightstd | 34.14 (25.58) | 32.94 (24.03) | 33.45 (24.7) |
| Cluster max height entropy | The entropy of the maximum heights of each cluster identified in the cluster count process. | Natsstd | 0.81 (0.36) | 0.77 (0.35) | 0.78 (0.36) |
Descriptives are also provided separately for accurate and inaccurate interpretations. Subscript std indicates standardized data.
For features relying upon peak identification, we leveraged the multidimensional image processing package (scipy.ndimage) and methods for calculating multidimensional maximum filters (maximum_filter).23 For features relying upon clustering, we leveraged the Scikit-learn and k-means clustering packages (sklearn.cluster.KMeans) along with a knee-point detection algorithm (kneed) for identifying the optimal number of clusters characterizing each Gaussian table.33,34 All 30 features were printed to a single array alongside diagnostic accuracy relative to the consensus diagnosis (binary, 1 = accurate, 0 = inaccurate); for the purposes of binary classification, the final dataset was moderately imbalanced, with 1742 inaccurate and 1275 accurate exemplars.
Machine learning
We used 4 methods to develop initial classifiers, and then selected the method with the best overall performance for further optimization:
Decision Trees (DT): These nonparametric supervised learning models logically test attributes against a threshold value to repeatedly divide instances into separate classes in a piecewise constant approximation, forming a structure resembling a tree.35 DTs are popular due to their relative intuitiveness, making processes and outputs relatively comprehensible. Herein, we applied the Classification and Regression Trees (CART) algorithm (DecisionTreeClassifier), implemented in scikit-learn 1.2.2.25
Random Forests: These classifiers are extensions of decision trees, fitting decision tree classifiers on many sub-samples of the entire dataset; it then relies on the averaged prediction of each classifier for the ensemble prediction. RF approaches are powerful complements to traditional decision trees, especially with large datasets, however, they can be slow to train and more difficult to interpret.36,37 Herein, we applied the RandomForestClassifier algorithm, a perturb-and-combine technique, implemented in scikit-learn 1.2.2.25
Artificial Neural Networks (ANN): These algorithms train on a dataset (using backpropagation) to learn one or more non-linear layers (hidden layers) that reside between the inputs and output.38 ANN models are very popular but they are also relatively difficult to interpret and are can be more sensitive than other algorithms to the presence of noise in training data.39 Herein, we applied the multilayer perceptron (MLP) algorithm (MLPClassifier), implemented in scikit-learn 1.2.2.
Support Vector Machines: These supervised learning algorithms are kernel-based approaches that are intended to increase generalization (through the reduction of overfitting) and discriminative power, primarily for binary classification problems.40 While SVM is considered one of the most powerful classification algorithms available, it can be very computationally burdensome and sensitive to imbalanced datasets. Herein, we applied the SVC algorithm in scikit-learn 1.2.2.25
All models were built using a stratified 70:30 train:test split. Our baseline models were trained using unbalanced classes and did not include hyperparameter tuning or cross-validation. The model with the best test performance (as measured by test AUC, area under the receiver-operator characteristic [ROC] curve; see Table 2) was selected for further optimization through hyperparameter tuning and cross-validation approaches.
Table 2.
Model performance for the 4 model types (DT, RF, ANN, and SVM), at baseline.
| Model | Version | Train accuracy | Test accuracy | Test precision | Test recall | Test F1 | Test AUC |
|---|---|---|---|---|---|---|---|
| DT | Baseline | 1.0 | 0.75 | 0.70 | 0.73 | 0.71 | 0.749 |
| RF | Baseline | 1.0 | 0.81 | 0.85 | 0.67 | 0.75 | 0.865 |
| ANN | Baseline | 0.75 | 0.76 | 0.71 | 0.74 | 0.72 | 0.832 |
| SVM | Baseline | 0.67 | 0.66 | 0.69 | 0.37 | 0.48 | 0.735 |
Accuracy = (TP + TN)/(All cases); Precision = TP/(TP + FP); Recall = TP/(TP + FN); F1 = 2*((precision*recall)/(precision + recall)).
Abbreviations: ANN = artificial neural networks; DT = decision trees; FN = false negative; FP = false positive; RF = random forest; SVM = support vector machines; TN = true negative; TP = true positive.
We then built separate models using undersampled and oversampled data. Oversampling and undersampling balances the representation of data in each class. There are several methods for balancing classes; herein, we used oversampling to randomly reproduce examples from the minority class, and undersampling to randomly remove data from the majority class. We report both approaches.
To optimize our selected model, we used hyperparameter tuning and k-folds cross-validation procedures applied to the training set from the original 70:30 train:test split. We focused on the following 5 parameters: number of estimators, maximum features, maximum depth, minimum samples until a split, and minimum samples until a leaf node is formed. For each of the 5 parameters, we tested how variation in levels of the parameter (eg, for maximum depth, levels 1-30) affected training and testing AUCs, seeking to maximize test AUC. This process was repeated with successively granular (eg, for maximum depth, levels 5-10) approximations of the optimal value for each parameter, lessening computational power associated with a full search. The downselected set of parameter levels was moved forward to grid search (using the sklearn GridSearchCV function), which implements k-fold cross validation and evaluates all possible combinations of parameters to find the combination that maximizes AUC. The k-folds cross-validation process involves randomly dividing the training data into k non-overlapping approximately equal sets (aka folds). The model is then trained k times for which k-1 folds are used to train the model while the remaining fold is used to validate the model. At each iteration the model’s performance on the validation set is evaluated using AUC score. Once all k iterations are completed, the AUC results are averaged across the k folds to ascertain the performance of the model and compare different hyperparameter settings. The best performing model is then evaluated by inputting the testing set from the original 70:30 train:test split. This process supports model selection and hyperparameter tuning and tests how well the model will generalize to new, unseen data.41
Because computing features related to cROIs requires each case to have undergone a consensus process to identify cROI locations, we also repeated all the above analyses after removing the 7 features that quantify attention towards the cROI. If the performance of the classifiers is similar to those built while including features related to the cROI, then that suggests our models may generalize favorably to novel cases that have not undergone analysis by a consensus panel. The results of these analyses are summarized herein but more thoroughly detailed in Supplementary Information.
Finally, we conducted exploratory analyses that included 3 additional features: standardized case difficulty level, case consensus diagnostic category, and the experience level of participating pathologists (resident versus attending physician). The goal of these exploratory analyses was to understand whether having additional case-level and pathologist-level information available to the classifier would improve performance.
Results
The overall performance of the 4 baseline models, including accuracy, precision (sensitivity), recall (positive predictive value), F1, and AUC, is detailed in Table 2. The overall best-performing model was RF, with the highest AUC, test accuracy, precision, and F1.
Results from models developed on oversampled and undersampled datasets are detailed in Table 3. Because oversampling did not consistently improve RF model performance relative to undersampling, and it can increase the odds of overfitting the model to training data and increase computational cost,42,43 we continued with only undersampled data.
Table 3.
Model performance for the 4 model types (DT, RF, ANN, and SVM), with the 2 sampling versions (undersampled, oversampled).
| Model | Version | Train accuracy | Test accuracy | Test precision | Test recall | Test F1 | Test AUC |
|---|---|---|---|---|---|---|---|
| DT | Undersampled | 1.0 | 0.74 | 0.68 | 0.75 | 0.71 | 0.837 |
| DT | Oversampled | 1.0 | 0.73 | 0.66 | 0.71 | 0.69 | 0.760 |
| RF | Undersampled | 1.0 | 0.80 | 0.78 | 0.74 | 0.76 | 0.868 |
| RF | Optimized | 1.0 | 0.81 | 0.80 | 0.74 | 0.76 | 0.863 |
| RF | Oversampled | 1.0 | 0.81 | 0.82 | 0.70 | 0.75 | 0.866 |
| ANN | Undersampled | 0.77 | 0.76 | 0.71 | 0.73 | 0.72 | 0.830 |
| ANN | Oversampled | 0.66 | 0.61 | 0.52 | 0.96 | 0.68 | 0.842 |
| SVM | Undersampled | 0.70 | 0.68 | 0.59 | 0.84 | 0.69 | 0.724 |
| SVM | Oversampled | 0.71 | 0.69 | 0.60 | 0.83 | 0.69 | 0.754 |
Final optimized RF model outcomes are provided.
Abbreviations: ANN: artificial neural networks; DT: decision trees; RF: random forest; SVM: support vector machines.
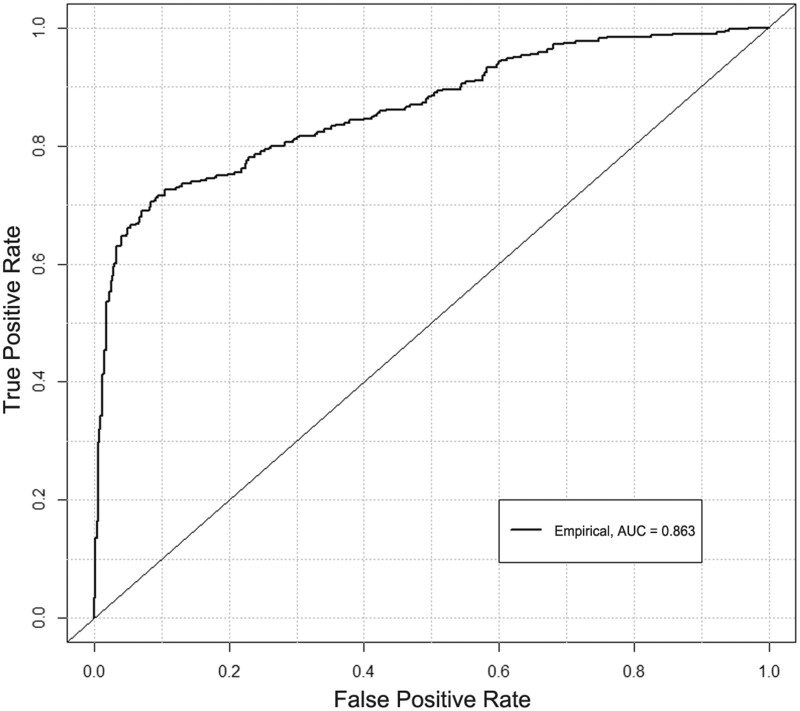
After optimization, the final RF model produced marginally higher overall test performance (Table 3). Specifically, while most measures of performance (ie, train accuracy, recall, F1, and AUC) remained similar to the unoptimized undersampled RF model, there was some improvement of test accuracy and precision. Note that the optimized model’s data correspond to an overall sensitivity of 0.74 and specificity of 0.86. The confusion matrix of the optimized model is detailed in Table 4, and the ROC curve is depicted in Figure 2.
Table 4.
Confusion matrix for testing data detailing classifier case counts for the 2 predicted labels and 2 true labels (0 = inaccurate, 1 = accurate), for the final optimized RF model.
| Predicted labels |
|||
|---|---|---|---|
| 0 | 1 | ||
| True labels | 0 | True negative: 452 | False positive: 71 |
| 1 | False negative: 101 | True positive: 282 | |
Figure 2.
A receiver-operating characteristic curve for the final optimized RF model, with an empirical fit. Also plotted is the notional performance of a random (diagonal) classifier.
Overall, these results suggest that we can successfully predict with moderate accuracy whether a pathologist will accurately or inaccurately diagnose a case based on only their viewing behavior. This model could be used in future training contexts to automatically monitor viewing behavior, proactively guide attention to relevant features, or provide decision supports to help pathologists successfully recognize perceived histopathological features and link them to correct diagnostic categories.6,44
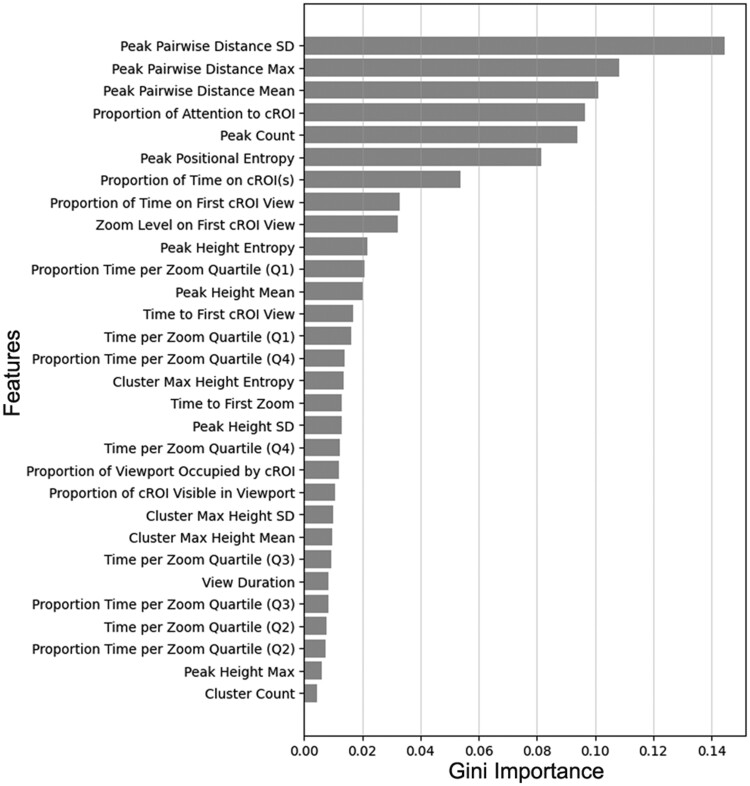
From the optimized RF model, we derived a feature importance list, calculated using Gini importance; higher Gini importance values (quantified as mean decrease in impurity) indicate that the feature plays a more significant role in the prediction process.25,36,37 The ranked feature importance for all 30 features is depicted in Figure 3. Features related to peak characteristics (especially relative to one another) tended to have higher Gini importance values. In other words, when building a classifier to predict diagnostic accuracy based on viewing behavior, the most important features of viewing behavior tend to be those quantifying the distance between regions receiving disproportionate levels of attention.
Figure 3.
The 30 features ranked in descending order of feature importance, for the final optimized RF model.
Results from our follow-up analyses omitting features related to cROIs can be found in the Supplementary Information. In summary, the optimized models performed very similarly to those detailed in Table 3, with the optimized RF model achieving an identical test AUC of 0.863. This is an important result because it suggests that our model could maintain its performance levels when generalized to cases that have not undergone analysis by a consensus panel and thus do not include identified cROIs.
The final exploratory analyses were conducted in 2 phases. First, we tested whether including case-level information (ie, case difficulty ratings and consensus diagnostic category: benign, atypia, lg-DCIS, hg-DCIS, invasive) would improve classifier performance. Following optimization, we were able to achieve test accuracy of 0.83 with an AUC of 0.88; the Precision was 0.88, Recall was 0.70, and F1 was 0.78. Second, we additionally included pathologist-level (ie, experience level: resident, attending) information. Following optimization, we were able to achieve test accuracy of 0.84 with an AUC of 0.88; the Precision was 0.90, Recall was 0.70, and F1 was 0.79. Thus, inclusion of case- and pathologist-level features provided some marginal (3.7%, 2.3%) improvement to classifier test accuracy and AUC, respectively. Overall, given the marginal increase in performance, this result indicates limited value to including additional case- and pathologist-level information in the model, and suggests potentially high generalizability of our results to other cohorts of pathologists and to cases with heterogeneous difficulty.
Discussion
Achieving accurate histopathological diagnoses is a challenging task involving a complex and dynamic interplay between perceived features of the tissue, specialized knowledge, and cognitive processing. Behavior, in this case zooming and panning, is a result of and contributor to those processes, and can give cognitive scientists a window into the mind.45–52 Specifically, we believe that pathologists’ dynamic viewing behavior can provide insights into the interpretive process as it unfolds, providing a glimpse into feature detection, recognition, and decision-making. If so, viewing behavior might prove valuable for the automated prediction of whether a pathologist is likely to arrive at an accurate or inaccurate diagnosis, motivating automated feedback and decision support systems for use in training and possibly clinical practice. The present study examined this possibility by building a series of machine learning classifiers that leveraged diverse features calculated from pathologists’ viewing behavior data.
In this analysis, we identified a series of 30 features that characterized the spatiotemporal distribution of pathologists’ viewing behavior over the digital biopsy images. This included information about viewing duration, zoom behavior, focused versus distributed attention, clusters of regional viewing, and attention toward critical image regions (ie, the cROIs). These features were used to train a series of classifiers including decision trees, RF, ANN, and SVM, with the critical dependent variable being the diagnostic accuracy of 140 participating pathologists. Through the process of balancing our datasets and optimizing the RF classifier, we were able to achieve surprisingly high performance relative to prior research examining the classification of mental states, learning, and task accuracy from human viewing behavior.50–55 Specifically, the optimized model achieved test accuracy of 0.81 and an AUC of 0.863, with high precision, recall, and F1.
Theories of visual search in diagnostic decision-making suggest that goal-driven (rather than stimulus-driven) eye movements are more strongly associated with clinician experience and diagnostic accuracy.6,15,56 In our assessment of feature importance, we found evidence supporting this assumption: the distribution of viewing peaks and attention to cROIs were critically important features. Based on the descriptive statistics (Table 1) comparing feature means in accurate versus inaccurate classes, accurate diagnoses tended to show a higher proportion of attention toward the cROI relative to non-cROI regions of the image. In other words, rather than distributing attention relatively evenly across the tissue space, more accurate diagnoses tend to be associated with more focused attention on critical image regions,6,11 and our RF classifier was able to leverage these patterns (alongside other features) to dissociate accurate versus inaccurate diagnoses. Perhaps more compelling, however, were the results found when excluding features related to cROIs entirely from our analysis; specifically, the model was able to maintain its performance levels without relying on cROI-related features (see Supplemental Information). This is a compelling result because it suggests our results may generalize to cases that have not been evaluated by an expert consensus panel. Indeed, one potential barrier facing the eventual implementation of our models in training contexts is the resource-intensive process of gathering experts to identify ROIs that can be used to calculate features. Our results suggest that this might not be necessary, with the models achieving identical overall performance (AUC) when relying primarily on features related to the distribution of focal attention over the entire image (ie, not just on the cROI).
The notion that pathologist viewing behavior reflects mental states and may predict diagnostic outcomes is grounded in theories of perception-action coupling and embodied cognition.45,57 In these theories, perception, thought, and action are reciprocally and inextricably bound as people interact with and understand the world around them. To guide movement in effective ways, we are continually gathering and processing information that shapes our understanding and motivates action; likewise, to effectively gather and process information we must move through our world in ways that facilitate those processes. This is generally considered a perception-action coupling cycle, which we believe can effectively characterize the way pathologists interact with microscopes and digital image viewers when interpreting biopsies. For example, pathologists change magnification (zoom) and pan to regions of visual salience, accumulate information, then change magnification again and pan to a new region that helps supplement, clarify, or refute emerging hypotheses.6,9,58 In this manner, patterns of visual behavior have shaped the pathologist’s thought process, and their thought processes have shaped their visual behavior; the result of this process is a full interpretation of the inspected tissue and a diagnostic decision. In support of this notion, several patterns of viewing behavior have been associated with diagnostic accuracy. For example, when pathologists view digital WSI of breast biopsies, the extent to which they find and focus visual attention on critical diagnostic regions (ie, consensus regions of interest) is positively associated with diagnostic accuracy.11 Similar results have been found with radiologists examining chest radiographs.59,60 Furthermore, we have found that visually scanning a whole slide image at a fixed plane of depth, rather than repeatedly zooming into regions, is positively associated with diagnostic accuracy.9 This result contrasts what has been found in radiology, wherein moving through images in depth (rather than scanning at a fixed depth) is positively associated with diagnostic accuracy.61 In both of these cases, the spatiotemporal patterns of interpretive behavior, including zooming and panning behavior, are associated with whether pathologists successfully reach an accurate diagnosis.28
Complementing our main analyses, we also conducted 2 exploratory analyses asking whether including case- or pathologist-level features could improve classifier performance. In the first analysis, we showed that including information regarding the case diagnostic category and normative difficulty ratings improved classifier performance by ∼4%. This was an interesting finding from a pedagogical perspective: if standardized cases are systematically presented to trainees, and diagnostic category and difficulty ratings exist for the cases, the algorithm is slightly more accurate at classifying whether viewing behavior is associated with an accurate or inaccurate diagnosis. In a training context, this could provide mentors with opportunities to provide in-the-moment feedback, trigger automated feedback, or prompt decision support systems that help direct attention to critical features, help students describe those features,44 and/or help map features to diagnostic categories. In the second analysis, we showed that additionally including information regarding the experience level of pathologists further improved classifier performance by about 2%. While not necessarily of value in pedagogical contexts, if the model is aware of pathologist-level experience levels, this could improve classifier performance in clinical contexts. While we do not believe our models are ready for application in a clinical decision support tool, we do believe they provide a compelling first demonstration that monitoring viewing behavior may prove valuable for predicting diagnostic outcomes and guiding performance training contexts. Continuing research will examine the potential utility of such tools for guiding visual attention and supporting the development diagnostic proficiency.
Strengths of our study include a larger sample size and more features than other studies in pathology or radiology, and an examination of more classification algorithms than any other study on this topic. Additional strengths include the examination of a medical diagnostic task of high clinical relevance and importance, and the analysis of diagnostic accuracy against case consensus reference diagnoses defined through comprehensive Delphi techniques.20 However, while the present results are found in the domain of breast pathology, we recognize that they may not generalize to other areas of pathology or medicine, such as dermatopathology or radiology. It is also possible that viewing behaviors observed in a research setting may differ from those observed during routine clinical case inspection, that experts’ viewing behaviors may differ considerably from residents’ viewing behavior, and that training expert viewing behavior may not confer accuracy advantages.6,62 Furthermore, whereas the current study relied upon pathologists reviewing a single slide that was wholly representative of the specimen, in practice pathologists have access to multiple slides representing individual tissue cross sections. While our expert consensus panel ensured that the case’s necessary histopathological information was always included on the single slide, our results may differ when pathologists have the opportunity to review multiple digital slides for a single case. Together, these questions provide compelling directions for future research.
Conclusion
In conclusion, we provide evidence that visual behavior assessed as pathologists review digital WSI can be used to successfully train classifiers to distinguish when the pathologists will provide an accurate versus inaccurate diagnosis. We take these results to suggest that monitoring viewing behavior in the absence of high-fidelity eye tracking can provide sufficient sensitivity to detect and leverage patterns of viewing behavior indicative of eventual diagnostic successes and failures. Classification algorithms developed for this purpose may hold potential in postgraduate training and clinical contexts, providing physicians with timely feedback and support during diagnostic decision-making.
Supplementary Material
Acknowledgements
We wish to thank Ventana Medical Systems, Inc., a member of the Roche Group, for use of iScan Coreo Au whole slide imaging system, and HD View SL for the source code used to build our digital viewer. We also wish to thank the staff, faculty, and trainees at the various pathology training programs across the United States for their participation and assistance in this study.
Contributor Information
Tad T Brunyé, Center for Applied Brain and Cognitive Sciences, Tufts University, Medford, MA 02155, United States; Department of Psychology, Tufts University, Medford, MA 02155, United States.
Kelsey Booth, Center for Applied Brain and Cognitive Sciences, Tufts University, Medford, MA 02155, United States.
Dalit Hendel, Center for Applied Brain and Cognitive Sciences, Tufts University, Medford, MA 02155, United States.
Kathleen F Kerr, Department of Biostatistics, University of Washington, Seattle, WA 98105, United States.
Hannah Shucard, Department of Biostatistics, University of Washington, Seattle, WA 98105, United States.
Donald L Weaver, Department of Pathology and Laboratory Medicine, Larner College of Medicine, University of Vermont and Vermont Cancer Center, Burlington, VT 05405, United States.
Joann G Elmore, Department of Medicine, David Geffen School of Medicine, University of California, Los Angeles, Los Angeles, CA 90095, United States.
Author contributions
J.G.E., D.L.W., T.T.B., and K.F.K. conceived and designed this study. T.T.B. collected the data. H.S. managed pathologist recruitment and scheduling, and provided feedback and suggestions on manuscript drafts. K.B. and D.H. processed the data and built the machine learning models, and T.T.B. drafted the manuscript. All authors reviewed the final manuscript and provided feedback and suggestions.
Supplementary material
Supplementary material is available at Journal of the American Medical Informatics Association online.
Funding
Research reported in this publication was supported by the National Cancer Institute of the National Institutes of Health under award numbers R01 CA225585, R01 CA172343, and R01 CA140560. The content is solely the responsibility of the authors and does not necessarily represent the views of the National Cancer Institute or the National Institutes of Health. Researchers are independent from funders, and the funding agency played no role in study design, conduct, analysis, or interpretation.
Conflict of interest
None declared.
Ethics approval and consent to participate
All methods were carried out in accordance with the Declaration of Helsinki. Participants provided written informed consent in accordance with Institutional Review Board approvals granted by the University of California Los Angeles.
Data availability
Due to the highly specialized nature of participant expertise and therefore increasing risk of identifiable data, we have decided not to make our data available in a repository. In the interest of minimizing the risk of participant identification, we will distribute study data on a case-by-case basis. Interested parties may contact Hannah Shucard at the University of Washington with data requests: hshucard@uw.edu.
References
- 1. Hubbard RA, Kerlikowske K, Flowers CI, et al. Cumulative probability of false-positive recall or biopsy recommendation after 10 years of screening mammography: a cohort study. Ann Intern Med. 2011;155(8):481-492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Elmore JG, Barton MB, Moceri VM, et al. Ten-year risk of false positive screening mammograms and clinical breast examinations. N Engl J Med. 1998;338(16):1089-1096. [DOI] [PubMed] [Google Scholar]
- 3. Dahabreh IJ, Wieland LS, Adam GP, et al. Core Needle and Open Surgical Biopsy for Diagnosis of Breast Lesions: An Update to the 2009 Report. Agency for Healthcare Research and Quality (US); 2014. Accessed May 5, 2023. https://www.ncbi.nlm.nih.gov/books/NBK246881/ [PubMed]
- 4. Lakhani SR, Ashworth A.. Microarray and histopathological analysis of tumours: the future and the past? Nat Rev Cancer. 2001;1(2):151-157. 10.1038/35101087 [DOI] [PubMed] [Google Scholar]
- 5. Jones C, Du M-Q, Lakhani SR, et al. Molecular and pathological characterization of human tumors. In: Bronchud MH, Foote M, Giaccone G., eds. Principles of Molecular Oncology. Totowa, NJ: Humana Press; 2004:215-232. 10.1007/978-1-59259-664-5_6 [DOI] [Google Scholar]
- 6. Brunyé TT, Drew T, Weaver DL, et al. A review of eye tracking for understanding and improving diagnostic interpretation. Cogn Res Princ Implic. 2019;4(7):1-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Krupinski EA. Current perspectives in medical image perception. Atten Percept Psychophys. 2010;72(5):1205-1217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Krupinski EA, Tillack AA, Richter L, et al. Eye-movement study and human performance using telepathology virtual slides. Implications for medical education and differences with experience. Hum Pathol. 2006;37(12):1543-1556. [DOI] [PubMed] [Google Scholar]
- 9. Drew T, Lavelle M, Kerr KF, et al. More scanning, but not zooming, is associated with diagnostic accuracy in evaluating digital breast pathology slides. J Vis. 2021;21(11):7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Crowley RS, Naus GJ, Stewart IJ, et al. Development of visual diagnostic expertise in pathology—an information-processing study. J Am Med Inform Assoc. 2003;10(1):39-51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Brunyé TT, Mercan E, Weaver DLDL, et al. Accuracy is in the eyes of the pathologist: The visual interpretive process and diagnostic accuracy with digital whole slide images. J Biomed Inform. 2017;66:171-179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Elstein AS, Schwartz A.. Clinical problem solving and diagnostic decision making: selective review of the cognitive literature. Br Med J. 2002;324(7339):729-732. 10.1136/bmj.324.7339.729 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Patel VL, Kaufman DR, Arocha JF.. Emerging paradigms of cognition in medical decision-making. J Biomed Inform. 2002;35(1):52-75. [DOI] [PubMed] [Google Scholar]
- 14. Sox HC, Blatt MA, Higgins MC, et al. Medical Decision Making. Boston, MA: Butterworths; 1988. 10.1002/9781118341544 [DOI] [Google Scholar]
- 15. Brunyé TT, Carney PA, Allison KH, et al. Eye movements as an index of pathologist visual expertise: a pilot study. PLoS One. 2014;9(8):e103447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Tourassi G, Voisin S, Paquit V, et al. Investigating the link between radiologists’ gaze, diagnostic decision, and image content. J Am Med Inform Assoc. 2013;20(6):1067-1075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Raudys SJ, Jain AK.. Small sample size effects in statistical pattern recognition: recommendations for practitioners. IEEE Trans Pattern Anal Machine Intell. 1991;13(3):252-264. [Google Scholar]
- 18. Oster N, Carney PA, Allison KH, et al. Development of a diagnostic test set to assess agreement in breast pathology: practical application of the Guidelines for Reporting Reliability and Agreement Studies (GRRAS). BMS Womens Health. 2013;13(3):1-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Elmore JG, Longton GM, Carney PA, et al. Diagnostic concordance among pathologists interpreting breast biopsy specimens. JAMA. 2015;313(11):1122-1132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Allison KH, Reisch LM, Carney PA, et al. Understanding diagnostic variability in breast pathology: lessons learned from an expert consensus review panel. Histopathology. 2014;65(2):240-251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Onega T, Weaver DL, Frederick PD, et al. The diagnostic challenge of low-grade ductal carcinoma in situ. Eur J Cancer. 2017;80:39-47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Harris CR, Millman KJ, van der Walt SJ, et al. Array programming with NumPy. Nature. 2020;585(7825):357-362. 10.1038/s41586-020-2649-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Virtanen P, Gommers R, Oliphant TE, et al. ; SciPy 1.0 Contributors. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat Methods. 2020;17(3):261-272. 10.1038/s41592-019-0686-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. McKinney W. Data structures for statistical computing in Python. In: Proceedings of the 9th Python in Science Conference. Austin, TX; 2010:56-61. https://conference.scipy.org/proceedings/scipy2010/pdfs/mckinney.pdf
- 25. Pedregosa F, Varoquaux G, Gramfort A, et al. Scikit-learn: machine learning in Python. J Mach Learn Res. 2011;12:2825-2830. [Google Scholar]
- 26. Lemaître G, Nogueira F, Aridas CK.. Imbalanced-learn: a python toolbox to tackle the curse of imbalanced datasets in machine learning. J Mach Learn Res. 2017;18:559-563. [Google Scholar]
- 27. Hunter JD. Matplotlib: a 2D graphics environment. Comput Sci Eng. 2007;9(3):90-95. [Google Scholar]
- 28. Ghezloo F, Wang P-C, Kerr KF, et al. An analysis of pathologists’ viewing processes as they diagnose whole slide digital images. J Pathol Inform. 2022;13(100104):1-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Nemoto H, Hanhart P, Korshunov P, et al. Ultra-eye: UHD and HD images eye tracking dataset. In: 2014 Sixth International Workshop on Quality of Multimedia Experience (QoMEX). Singpore: IEEE; 2014. 10.1109/QoMEX.2014.6982284 [DOI]
- 30. Wang K, Wang S, Ji Q. Deep eye fixation map learning for calibration-free eye gaze tracking. In: Proceedings of the Ninth Biennial ACM Symposium on Eye Tracking Research & Applications. New York, NY, USA: Association for Computing Machinery; 2016:47-55. 10.1145/2857491.2857515 [DOI]
- 31. Otsu N. A threshold selection method from gray-level histograms. IEEE Trans Syst Man Cybern. 1979;9(1):62-66. [Google Scholar]
- 32. Wu W, Mehta S, Nofallah S, et al. Scale-aware transformers for diagnosing melanocytic lesions. IEEE Access. 2021;9:163526-163541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Satopaa V, Albrecht J, Irwin D, et al. Finding a “Kneedle” in a haystack: detecting knee points in system behavior. In: 31st International Conference on Distributed Computing Systems Workshops, Minneapolis, MA, USA. IEEE; 2011:166-71. 10.1109/ICDCSW.2011.20 [DOI]
- 34. Arvai K. kneed. 2020. Accessed June 14, 2023. https://kneed.readthedocs.io/en/stable/
- 35. Kotsiantis SB. Decision trees: a recent overview. Artif Intell Rev. 2013;39(4):261-283. [Google Scholar]
- 36. Parmar A, Katariya R, Patel V.. A review on random forest: an ensemble classifier. In: Hemanth J, Fernando X, Lafata P, et al. , eds. International Conference on Intelligent Data Communication Technologies and Internet of Things (ICICI) 2018. Cham: Springer International Publishing; 2019:758-63. 10.1007/978-3-030-03146-6_86 [DOI] [Google Scholar]
- 37. Boulesteix A-L, Janitza S, Kruppa J, et al. Overview of random forest methodology and practical guidance with emphasis on computational biology and bioinformatics. WIREs Data Min Knowl. 2012;2(6):493-507. [Google Scholar]
- 38. Lippmann R. An introduction to computing with neural nets. IEEE ASSP Mag. 1987;4(2):4-22. [Google Scholar]
- 39. Dreiseitl S, Ohno-Machado L.. Logistic regression and artificial neural network classification models: a methodology review. J Biomed Inform. 2002;35(5-6):352-359. [DOI] [PubMed] [Google Scholar]
- 40. Cervantes J, Garcia-Lamont F, Rodríguez-Mazahua L, et al. A comprehensive survey on support vector machine classification: applications, challenges and trends. Neurocomputing. 2020;408:189-215. [Google Scholar]
- 41. Hastie T, Tibshirani R, Friedman J.. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2nd ed. Springer Publishing Company; 2009. [Google Scholar]
- 42. Thabtah F, Hammoud S, Kamalov F, et al. Data imbalance in classification: experimental evaluation. Inf Sci. 2020;513:429-441. [Google Scholar]
- 43. Kotsiantis S, Kanellopoulos D, Pintelas P.. Handling imbalanced datasets: a review. GESTS Int Trans Comput Sci Eng. 2006;30:25-36. [Google Scholar]
- 44. Brunyé TT, Balla A, Drew T, et al. From image to diagnosis: characterizing sources of error in histopathologic interpretation. Mod Pathol. 2023;36(7):100162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Warren WH. The perception-action coupling. In: Bloch H, Bertenthal BI, eds. Sensory-Motor Organizations and Development in Infancy and Early Childhood. Dordrecht: Kluwer; 1990:23-37. Accessed May 9, 2023. https://link.springer.com/chapter/10.1007/978-94-009-2071-2_2 [Google Scholar]
- 46. Spivey MJ, Dale R.. Continuous dynamics in real-time cognition. Curr Dir Psychol Sci. 2006;15(5):207-211. [Google Scholar]
- 47. Spivey M. The Continuity of Mind. Oxford University Press; 2008. [Google Scholar]
- 48. Song J-H, Nakayama K.. Target selection in visual search as revealed by movement trajectories. Vision Res. 2008;48(7):853-861. [DOI] [PubMed] [Google Scholar]
- 49. Freeman JB, Ambady N.. Motions of the hand expose the partial and parallel activation of stereotypes. Psychol Sci. 2009;20(10):1183-1188. [DOI] [PubMed] [Google Scholar]
- 50. Borji A, Itti L.. Defending Yarbus: eye movements reveal observers’ task. J Vis. 2014;14(3):29. [DOI] [PubMed] [Google Scholar]
- 51. Henderson JM, Shinkareva SV, Wang J, et al. Predicting cognitive state from eye movements. PLoS One. 2013;8(5):e64937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Kardan O, Berman MG, Yourganov G, et al. Classifying mental states from eye movements during scene viewing. J Exp Psychol Hum Percept Perform. 2015;41(6):1502-1514. [DOI] [PubMed] [Google Scholar]
- 53. Greene MR, Liu T, Wolfe JM.. Reconsidering Yarbus: a failure to predict observers’ task from eye movement patterns. Vision Res. 2012;62:1-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Lemay DJ, Doleck T.. Grade prediction of weekly assignments in MOOCS: mining video-viewing behavior. Educ Inf Technol. 2020;25(2):1333-1342. [Google Scholar]
- 55. Aouifi HE, Hajji ME, Es-Saady Y, et al. Predicting learner’s performance through video viewing behavior analysis using graph convolutional networks. In: 2020 Fourth International Conference On Intelligent Computing in Data Sciences (ICDS), Fez, Morocco. IEEE; 2020:1-6. 10.1109/ICDS50568.2020.9268730 [DOI]
- 56. Al-Moteri MO, Symmons M, Plummer V, et al. Eye tracking to investigate cue processing in medical decision-making: a scoping review. Comput Hum Behav. 2017;66:52-66. [Google Scholar]
- 57. Wilson M. Six views of embodied cognition. Psychon Bull Rev. 2002;9(4):625-636. [DOI] [PubMed] [Google Scholar]
- 58. Brunyé TT, Drew T, Kerr KF, et al. Zoom behavior during visual search modulates pupil diameter and reflects adaptive control states. PLoS One. 2023;18(3):e0282616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Carmody DP, Nodine CF, Kundel HL.. An analysis of perceptual and cognitive factors in radiographic interpretation. Perception. 1980;9(3):339-344. [DOI] [PubMed] [Google Scholar]
- 60. Kundel HL, Nodine CF.. Studies of eye movements and visual search in radiology. In: Senders JW, Fisher DF, Monty RA, eds. Eye Movements and the Higher Psychological Processes. Hillsdale, NJ: Lawrence Erlbaum Associates; 1978:317-27. [Google Scholar]
- 61. Drew T, Vo ML-H, Olwal A, et al. Scanners and drillers: characterizing expert visual search through volumetric images. J Vis. 2013;13(10):1-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Gegenfurtner A, Lehtinen E, Jarodzka H, et al. Effects of eye movement modeling examples on adaptive expertise in medical image diagnosis. Comput Educ. 2017;113:212-225. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Due to the highly specialized nature of participant expertise and therefore increasing risk of identifiable data, we have decided not to make our data available in a repository. In the interest of minimizing the risk of participant identification, we will distribute study data on a case-by-case basis. Interested parties may contact Hannah Shucard at the University of Washington with data requests: hshucard@uw.edu.