A Fully Differentiable Framework for 2D/3D Registration and the Projective Spatial Transformers

Abstract

Image-based 2D/3D registration is a critical technique for fluoroscopic guided surgical interventions. Conventional intensity-based 2D/3D registration approaches suffer from a limited capture range due to the presence of local minima in hand-crafted image similarity functions. In this work, we aim to extend the 2D/3D registration capture range with a fully differentiable deep network framework that learns to approximate a convex-shape similarity function. The network uses a novel Projective Spatial Transformer (ProST) module that has unique differentiability with respect to 3D pose parameters, and is trained using an innovative double backward gradient-driven loss function. We compare the most popular learning-based pose regression methods in the literature and use the well-established CMAES intensity-based registration as a benchmark. We report registration pose error, target registration error (TRE) and success rate (SR) with a threshold of 10 mm for mean TRE. For the pelvis anatomy, the median TRE of ProST followed by CMAES is 4.4 mm with a SR of 65.6% in simulation, and 2.2 mm with a SR of 73.2% in real data. The CMAES SRs without using ProST registration are 28.5% and 36.0% in simulation and real data, respectively. Our results suggest that the proposed ProST network learns a practical similarity function, which vastly extends the capture range of conventional intensity-based 2D/3D registration. We believe that the unique differentiable property of ProST has the potential to benefit related 3D medical imaging research applications. The source code is available at https://github.com/gaocong13/Projective-Spatial-Transformers.

I. Introduction

The development of image-based navigation solutions for minimally-invasive surgeries has been motivated by advances in interventional imaging, including the increased availability of C-arm X-ray imaging systems and recent developments in artificial intelligence techniques [1]. X-ray image-based navigation estimates the 3D pose of the surgical tool to the patient anatomy from 2D X-ray images, which has been studied for orthopedic applications, including periacetabular osteotomy [2], pelvic fracture fixation [3], femoroplasty [4], neuroelectrode placement [5], and spinal needle injection [6]. The pose estimation accuracy is critical for guiding the surgical tool to the planned target position.

Image-based 2D/3D registration is a key element of image-guided navigation solutions. Rigid 2D/3D registration computes the pose geometry of 3D objects from intra-operative 2D images, which is essential to estimate the tool-to-tissue spatial relationship. Specifically, it uses an objective similarity function to compute the difference between a target 2D image (such as an X-ray) and a synthesized 2D image derived from the 3D object. In X-ray imaging, such radiographic image synthesis from CT scans is called Digitally Reconstructed Radiography (DRR). Conventional image intensity-based 2D/3D registration methods use hand-crafted image similarity functions to perform iterative pose optimization, such as mutual information (MI) [7] or patch-based gradient normalized cross correlation (P-Grad-NCC) [8]. One challenge of such approaches is that the capture range is very limited due to the presence of local minima of hand-crafted loss functions. Thus, the initial object pose needs to be close enough to the ground truth pose to achieve the global optimum during registration.

Feature-based 2D/3D registration methods are an alternative to intensity-based approaches, where analytical pose solutions are computed from corresponding 2D and 3D geometric features. Researchers have investigated dominant features in the object projection image for pose recovery. Such examples include SIFT features for femur [9], Generalized Hough Transform (GHT) for spine vertebrae [10], learning-based shape encodings for metal implants [11], etc. In recent years, pose estimation using corresponding 2D and 3D anatomical landmarks has become popular. Researchers have proposed deep learning models that automatically detect 2D landmarks to solve the PnP problem [12] for pose estimation [13], [14], [15], [16], [17]. However, these features and anatomical landmarks are specific to every object and must be selected with domain knowledge and such that they are clearly visible in the target images.

Direct pose regression from image observations has gained interest in literature. Miao et al. were the first who employed CNN regressors to directly estimate the pose parameters [18]. As the idea was straightforward and the results were encouraging, a great amount of work followed this direction. For example, Li et al. proposed DeepIM, which performs iterative pose updates using learned gradient predictions [19]. Gu et al. designed an iterative scheme for X-ray registration by predicting Riemannian pose gradients [20]. Jaganathan et al. also learned pose updates through integrating Point-to-Plane Correspondences [21]. Several researchers formulated such learning-based 2D/3D registration with reinforcement learning paradigms [22], [23], [24], but they still perform pose regression at each iteration. Although the architectures varied, all the above methods aim to directly fit a mapping function from 2D image observations to 3D pose or pose updates, taking deep networks as powerful encoders. However, mathematically, such mapping is a highly complex and illposed problem in transmission X-ray imaging. Thus, these approaches by design are prone to yield strong overfitting in the training domain. The pose predictions can change dramatically even if only tiny changes of the input image appearance exist, because the learned mapping is unconstrained.

A more desirable solution than learning a mapping function is learning a practical “similarity function”, for example a convex function, for iterative registration. This is because 1) the problem complexity of fitting the neural network to a target function shape is lower than mapping to precise pose values, and 2) the iterative optimization is more likely to converge to the global optimum than unconstrained prediction mapping. However, such an approach requires computing differentiable gradient of the similarity function with respect to the 3D pose parameters for end-to-end network training and iterative registration updates. Unfortunately, this differentiable gradient computation for DRR projection with respect to both, the input data as well as the pose parameters, has not yet been explored. We first provide the mathematical problem formulation of 2D/3D registration and then describe the challenges of analytical gradient computation in the next paragraphs.

The problem of rigid 2D/3D registration can be formulated as follows: Given a 3D volumetric object $V$, six degrees of freedom (DoF) object pose parameter $\theta \in \text{SE}\left(3\right)$, a 2D target image $I_t$, a DRR projection operator $𝓟$, the objective is to search for the optimal pose parameter $\theta$ so that the image produced by $𝓟(V,\theta )$ best matches $I_t$. Mathematically, the mapping from a volumetric 3D object $V$ to a DRR image $I_m$ can be modeled as $I_m=A(\theta )V$, where $A(\theta )$ is the system matrix that depends on pose parameter $\theta \in \text{SE}\left(3\right)$. In conventional intensity-based 2D/3D registration, we seek to retrieve the pose parameter $\theta$ such that the moving image $I_m$ simulated from $V$ is as similar as possible to the target image $I_t$:

$$\underset{\theta \in \text{SE}(3)}{\max }\mathcal{S}\left(I_t,I_m\right)=\underset{\theta \in \text{SE}(3)}{\max }\mathcal{S}\left(I_t,A(\theta )V\right),$$ (1)

where $\mathcal{S}$ is the similarity objective function, such as P-Grad-NCC or MI. Gradient-descent-based optimization methods require the gradient $\frac{\partial \mathcal{S}}{\partial \theta }=\frac{\partial \mathcal{S}}{\partial A(\theta )}\frac{\partial A(\theta )}{\partial \theta }$ at every iteration. Although the mapping was constructed to be differentiable, analytic gradient computation is still impossible due to the excessively large memory footprint of $A\left(\theta \right)$ for all practical problem sizes¹. Thus, traditional stochastic optimization strategies are numeric-based methods without derivatives, such as Covariance Matrix Adaptation Evolution Strategy (CMAES) [26] or BOBYQA [27]. Due to such challenges, the similarity functions, including both hand-crafted and learning-based designs, are limited to be computed only on the 2D image domain by generating DRR image at every iteration.

Spatial Transformer Network (STN) [28] has been applied to 3D registration problems to estimate deformation field [29], [30]. In this work, we propose an analytically differentiable DRR renderer, which we call it Projective Spatial Transformer (ProST) module. It follows the terminology of STNs and extends their capabilities to spatial transformations in projective X-ray transmission imaging. We then present a fully differentiable framework using ProST, which learns a similarity function of convex shape for 2D/3D registration.

This paper is a journal extension of a previous conference paper publication [31]. The main contribution of the previous conference publication is introducing the ProST module, and demonstrating an example use case on 2D/3D registration with an end-to-end deep learning module. The contribution of this journal paper extends the previous work from the following perspectives:

• Re-designed 2D/3D registration network architecture with a cross vision transformer-based 2D encoder and training loss. Domain randomization was applied during training time.

• Demonstrated the superiority of the novel double backward gradient loss design and 3D feature learning with intensive controlled experiments. Quantitative performance was reported on variants of the ProST architecture and representative learning-based 2D/3D registration methods in the literature, using the conventional CMAES registration methods as a benchmark.

• Demonstrated the model’s generalization ability on large scale real pelvic X-ray images, including challenging image cases with surgical tool overlay and a different spine anatomy.

II. Methodology

A. Projective Spatial Transformer (ProST)

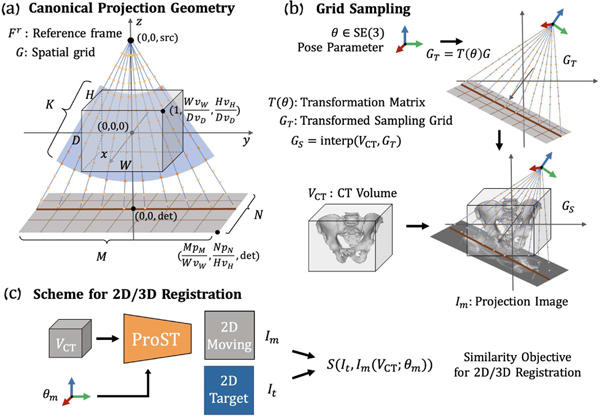
The proposed ProST module is presented in Fig. 1. ProST takes a CT volume $V_{\text{CT}}$ and its pose parameter $\theta$ as input and produces a DRR image $I_m$ using a spatial sampling grid $G$. In this section, we introduce its geometric design and its use for 2D/3D registration.

Fig. 1.

(a) Canonical projection geometry and a slice of cone-beam grid points are presented with key annotations. The blue fan covers the control points which are used for CT intensity interpolation. (b) Illustration of grid sampling transformer and projection. (c) Scheme of applying ProST to 2D/3D registration.

1). Canonical projection geometry:

Given a CT volume $V_{\text{CT}}\in {ℝ}^{D\times W\times H}$ with voxel size $\left(v_D,v_W,v_H\right)$, we define a reference frame $F^r$ with the origin at the center of $V_{\text{CT}}$. We use the volume depth $\left(D{v}_D\right)$ to normalize coordinates in the canonical geometry. The volume corner point coordinate $\left(D{v}_D/2,W{v}_W/2,H{v}_H/2\right)$ is transformed as $\left(1,\frac{W{v}_W}{D{v}_D},\frac{H{v}_H}{D{v}_D}\right)$ after normalization. Given an X-ray projection camera intrinsic matrix $\mathcal{K}\in {ℝ}^{3\times 3}$, we denote the associated source point as (0, 0, src) in $F^r$. The spatial grid $G$ of control points, shown in Fig. 1(a), lies on $M\times N$ rays originating from this source. Because the control points in regions where no CT voxels exist will not contribute to the line integral, we cut the grid point cloud to a cone-shaped structure that covers the exact volume space for memory concern (Fig. 1(a) blue fan). Thus, each ray has $K$ control points uniformly spaced within the volume $V$, so that the matrix $G\in {ℝ}^{4\times (M\times N\times K)}$ of control points is well-defined, where each column is a control point in homogeneous coordinates. These rays describe a cone-beam geometry which intersects with the detection plane, centered on (0, 0, det) and perpendicular to the $z$ axis with pixel size $\left(p_M,p_N\right)$, as determined by $\mathcal{K}$. The X-ray source (0, 0, src) and center of detector (0, 0, det) coordinates are all applied with the normalization factor $D{v}_D$. The upper-right corner of the detection plane is at $\left(\frac{M{p}_M}{W{v}_W},\frac{N{p}_N}{H{v}_H},\text{det}\right)$.

2). Grid sampling transformer:

ProST extends the canonical projection geometry by learning a transformation of the control points $G$ . Given a 6 DoF rigid pose parameter $\theta \in \text{SE}\left(3\right)$, we obtain a transformed set of control points via the affine transformation matrix $T\left(\theta \right)$ :

$$G_T=T(\theta )G,$$ (2)

as well as source point $T(\theta )\cdot (0,0,\text{src},1)$ and center of detection plane $T(\theta )\cdot (0,0,\det ,1)$. Since these control points lie within the volume $V$ but in between voxels, we perform differentiable linear interpolation of $V$ at the control points $G_T$, producing sampled control point values $G_S$:

$$G_S=\text{interp}\left(V,G_T\right)\text{,}$$ (3)

where $G_S\in {ℝ}^{M\times N\times K}$. Finally, we obtain a 2D image $I_m\in {ℝ}^{M\times N}$ by integrating along each ray. This is accomplished by “collapsing” the $k$ dimension of $G_S$:

$$I^{(m,n)}={\displaystyle \sum }_{k=1}^K{G}_S^{(m,n,k)}$$ (4)

Of note, the integrating operation (Eqn. 4) can be achieved as a single-step time-efficient matrix summation operation. The process above takes advantage of the spatial transformer grid $(G)$, which reduces the projection operation to a series of linear transformations. The intermediate variables are reasonably sized for modern computational graphics cards, and thus can be loaded as a tensor variable. This projection layer enables analytical gradient flow of DRR generation from the projection domain back to the 3D domain. Fig. 1 (c) shows how this scheme is applied to 2D/3D registration. By integrating deep convolutional layers, we show that ProST makes the deep neural network feasible to approximate a convex image similarity function in a data-driven manner.

B. Approximating Convex Image Similarity

Geodesic loss, $L_{\text{geo}}$, which is the square of the geodesic distance in SE(3), has been studied for registration problems due to its convexity with respect to pose transformations [32] [33]. Using ProST, we propose an end-to-end DeepNet architecture that learns to approximate the convex shape of $L_{\text{geo}}$, aiming at extending the capture range of 2D/3D registration. Given a sampling pose ${\theta }_m$ and a target pose ${\theta }_t$, we took the implementation of geomstats [34] to calculate the geodesic distance, $L_{\text{geo}}\left({\theta }_m,{\theta }_t\right)$, and the geodesic gradient, $\frac{\partial L_{\text{geo}}\left({\theta }_m,{\theta }_t\right)}{\partial {\theta }_m}$. We used the left canonical metric in the Euclidean group.

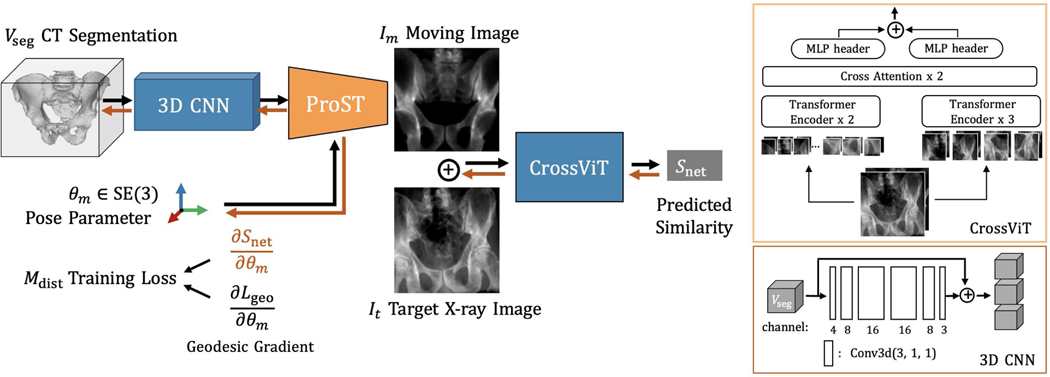
Fig. 2 shows the proposed DeepNet framework. The input includes a 3D segmentation volume: $V_{\text{seg}}$, a pose parameter ${\theta }_m\in SE\left(3\right)$ and a target image: $I_t$, which implies a target pose ${\theta }_t$. 3D to 2D projections are performed using the ProST projection module in orange. The learnable network parameters are colored in blue, with detailed structures on the right side. The 3D CNN is a skip connection from the input volume to multi-channel expansion just to learn the residual. The projected moving image $I_m$ and the target image $I_t$ are concatenated and then pass through a cross vision transformer (CrossViT) encoder. CrossViT is an advanced version of the standard vision transformer, which learns multi-scale feature representations by combining image patches of different sizes [35]. The final output is the network predicted similarity, $S_{\text{net}}$. In the following sections, we will then explain the network training techniques and their application to 2D/3D registration.

Fig. 2.

ProST DeepNet framework for 2D/3D registration. A pelvis segmentation ${\mathit{V}}_{\text{seg}}$ is illustrated as 3D input. The rigid pose parameter ${\mathit{\theta }}_m$ is shown using RGB cross arrows. An example target X-ray image ${\mathit{I}}_t$ and moving image ${\mathit{I}}_m$ generated from ProST are presented. Forward pass follows the black arrows. Backward pass follows orange arrows, where the gradient $\frac{\partial S_{\text{net}}}{\partial {\theta }_m}$ is computed. Detailed structures of CrossViT and 3D CNN are illustrated in blocks on the right.

C. Double Backward Training Loss

Since the target is to make $S_{\text{net}}$ similar to $L_{\text{geo}}$, a straightforward solution is defining it as a regression task, for example, using mean squared error, MSE $\left(S_{\text{net}},L_{\text{geo}}\right)$, as training loss. However, learning a 6 DoF convex loss landscape from image appearance is particularly challenging because of differences in absolute loss scales. In reality, the scale values do not contribute to the iterative optimization, but the shape of loss matters. Thus, we downgrade the task to focus on learning the convex shape, which essentially refers to learning the second-order gradients.

Specifically, the goal is to make the gradient of our network similarity function with respect to pose parameters, $\frac{\partial S_{\text{net}}}{\partial {\theta }_m}$, close to the geodesic gradient $\frac{\partial L_{\text{geo}}}{\partial {\theta }_m}$. The black arrows in Fig. 2 show the forward pass in a single iteration. The network output can be mathematically formulated as $S_{\text{net}}\left(\varphi ;V_{\text{seg}},{\theta }_m,I_t\right)$, where $\varphi$ are the network parameters. The gradients, $\frac{\partial S_{\text{net}}}{\partial {\theta }_m}$ and $\frac{\partial S_{\text{net}}}{\partial \varphi }$, are computed by applying back-propagation, illustrated with orange arrows in Fig. 2. Of note, we do not update network parameters $\varphi$ during this back-propagation. The network training loss is designed by calculating a distance measure, $M_{\text{dist}}\left(\frac{\partial S_{\text{net}}}{\partial \theta },\frac{\partial L_{\text{geo}}}{\partial \theta }\right)$, of the network pose gradient $\frac{\partial S_{\text{net}}}{\partial {\theta }_m}$ and geodesic gradient $\frac{\partial L_{\text{geo}}}{\partial {\theta }_m}$. Since the gradients are also 6 DoF, we again use the geodesic distance $L_{\text{geo}}$ as this distance measurement metric $M_{\text{dist}}$, which is the true network loss function during training.

We then perform a second forward pass, or “double backward” pass, to get $\frac{\partial M_{\text{dist}}}{\partial \varphi }$ for updating network parameters $\varphi$. To this end, we formulate the network training as the following optimization problem

$$\underset{\varphi }{\min }{M}_{\text{dist}}\left(\frac{\partial S_{\text{net}}\left(\varphi ;V_{\text{seg}},{\theta }_m,I_t\right)}{\partial {\theta }_m},\frac{\partial L_{\text{geo}}\left({\theta }_m,{\theta }_t\right)}{\partial {\theta }_m}\right).$$ (5)

Due to the unique goal of shaping the network function landscape to be convex, our double backward training design uses the gradient of geodesic distance to drive the entire network training. This is feasible only because ProST makes the network end-to-end differentiable with respect to the pose parameter ${\theta }_m$ and 3D volume. We will demonstrate the advantage of this training loss design in ablation studies (Section III-B).

D. Domain Randomization

Target images during training were generated using a physically-realistic X-ray simulation framework – DeepDRR [36], which is shown to be effective on learning-based X-ray imaging tasks compared to naive DRR [37], [38]. We applied domain randomization on DeepDRR target images to improve the generalization ability on unseen real data. Domain randomization is a domain generalization technique that introduces drastic changes in the training image appearances, which forces the network to learn domain-invariant features between training and target domains [39]. During each training iteration, we applied the following domain randomization methods sequentially each with a probability of 50% on the target image $I_t$:

• Inverting: $max\left(I_t\right)-I_t$ all image pixels were subtracted from the maximum intensity value;

• Gaussian noise injection: $I_t+N(0,\sigma )$, where $\sigma$ was uniformly chosen from the interval (0.005, 0.1) multiplied by the image intensity range.

• Gamma transform: $norm{\left(I_t\right)}^{\gamma }$, where $I_t$ was normalized by its maximum and minimum values, and $\gamma$ was uniformly selected from the interval (0.7, 1.3)

• Box corruption: a random number of box regions of $I_t$ were corrupted with large noise.

E. Application to 2D/3D Registration

When the trained network is applied to registration, the network parameters $\varphi$ are fixed, and the well-trained network including the ProST module is treated as a similarity objective function. Because the pose gradients $\frac{\partial S_{\text{net}}}{\partial {\theta }_m}$ are differentiable, the iterative registration optimization can be performed analytically using gradient-based methods such as stochastic gradient descent (SGD) rather than numerically sampling. Following the math descriptions of ProST in Section II-A and Fig. 1 and 2, the analytical gradient can be computed following:

$$\frac{\partial S_{\text{net}}}{\partial {\theta }_m}=\frac{\partial S_{\text{net}}}{\partial I_m}\frac{\partial I_m}{\partial G_S}\frac{\partial G_S}{\partial G_T}\frac{\partial G_T}{\partial T\left({\theta }_m\right)}\frac{\partial T\left({\theta }_m\right)}{\partial {\theta }_m}.$$ (6)

The whole framework is implemented in PyTorch, and the ProST operator is embeded as a PyTorch layer with tensor variables. With the help of the PyTorch autograd function, the 2D/3D registration is performed using PyTorch built-in optimizers and learning rate schedulers.

In the next section, we present our efforts in demonstrating its use case of extending the registration capture range with controlled comparison experiments.

III. Experiments

We performed intensive controlled studies of single-view 2D/3D registration on simulated and real X-ray images to evaluate our approach. We selected the state-of-the-art image intensity-based 2D/3D registration method as benchmark ², which uses Patch-based Gradient Normalized Cross Correlation (P-Grad-NCC) [8] score as the similarity metric and “Covariance Matrix Adaptation: Evolutionary Search” (CMAES) [40] as the optimization strategy. Due to its well-known robustness to local minima, the CMAES benchmark method for pose estimation of bone anatomy and surgical devices has been tested to meet clinical requirements in various orthopedic applications, including osteotomy [2], [13], femoroplasty [41], [4], core decompression of the hip [42], and transforaminal lumbar epidural injections [43], etc. Our experiments aim at demonstrating a substantially increased capture range of 2D/3D registration when CMAES is preceded by our ProST network. The initial pose geometry of the registration object was randomly sampled in a wide range. We compared the registration performance of running CMAES from initial poses against running CMAES from ProST-based pose estimations in all precisely controlled comparison studies.

We introduce our experiment design as follows: In Section III-A, we describe the general environment setup, dataset, and processing details. In Section III-B, we present the comparison studies, which include 1) architecture ablation and comparison: variations of ProST architecture and two representative learning-based registration methods in the literature, namely DeepIM [19] and DMW [20]; 2) image with overlays; 3) anatomy comparison: pelvis and spine. In Section III-C, we describe the initial pose sampling strategies and network training hyper-parameters, which were precisely controlled overall ablation experiments. In Section III-D, we present the evaluation metrics of the registration performance.

A. Experiment Environment and Dataset

Our X-ray simulation environment approximates a Siemens CIOS Fusion C-arm, which has image dimensions of 1536 × 1536, isotropic pixel spacing of 0.194 mm/pixel, and a source-to-detector distance of 1020 mm. The images were downsampled to have dimensions of 128 × 128 with a pixel spacing of 2.176 mm/pixel. The source to iso-center distance is 800 mm.

1). Simulation Study:

We selected twenty high-quality CT scans from the New Mexico Decedent Image Database (NMDID) [44] for training and simulation study. The CT scans were manually cropped to focus on the hip region and resampled to preserve an isotropic cubic shape of 128 voxels in each dimension. The pelvis anatomy was automatically segmented using the algorithm described in [45]. A separate set of twenty CT scans of the spine anatomy were selected from the same NMDID. The spine vertebrae were segmented using a coarse-to-fine vertebrae localization and segmentation method [46]. We utilized K-fold cross-validation to improve the representation of the sample population. The simulation testing dataset consists of twenty distinct patient scans, and we divided the CT scans into four folds, with each fold containing five CT scans. In each fold training/testing, we employed fourteen CT scans for training, one CT scan for validation, and the remaining five CT scans for testing. The simulation performance is reported as the average measure across the 4-fold testing. This 4-fold cross-validation scheme was applied to both the pelvis and spine anatomies.

2). Real Data Study:

In testing on real X-ray data, we trained each comparison method model using the full nineteen NMDID CT scans and one CT for validation. Our real hip X-ray data were selected from the cadaveric X-rays released by Grupp et al. [13]. Groundtruth poses of the pelvis were estimated using the comprehensive image intensity-based 2D/3D registration pipeline described in [13]. The coordinate frames of DeepDRR and xReg were calibrated to the ProST geometry convention as introduced in Section II-A.1.

B. Comparison Study Design

1). Architecture Ablation:

We conducted ablation studies on variations of the ProST registration architectures to demonstrate the effects of each key component design:

• Baseline: Baseline ProST network using all techniques introduced in Section. II.

• Full CT: The input 3D volume uses the full CT data instead of segmented volume. The architecture and training strategies stay the same.

• No DR: The architecture is the same as a baseline but domain randomization (DR) was removed during training time.

• No 3D Net: The 3D CNN part (Fig. 2) was removed. The goal is to compare the effect of 3D learnable parameters in approximating the desired convex similarity function.

• MSE Loss: To show the importance of gradient-driven double backward training loss design, we performed a comparison experiment using MSE $\left(S_{\text{net}},L_{\text{geo}}\right)$ to train the network. The other training settings were kept the same as baseline.

We also included comparisons with the other representative learning-based 2D/3D registration architectures in the literature:

• MICCAI: This is the conference published version of the ProST registration network at MICCAI 2020 [31]. The architecture and training loss was kept the same, while domain randomization was applied and training/testing data was set in line with the controlled experiments in this work.

• DeepIM: DeepIM is a popular deep iterative matching network for 6 DoF object pose estimation, which predicts direct pose updates by learning from the optical flow between moving and target images [19]. DeepIM was shown to achieve state-of-the-art results on benchmark computer vision datasets.

• DMW: DMW is also proposed to extend the capture range of 2D/3D registration by regressing pose updates from moving and target images [20]. It uses a sequence of DenseNet [47] blocks as the backbone and learns to predict direct geodesic gradients of the two relative poses. DMW was tested to be effective in recovering large pose initialization errors on pelvis X-rays.

DeepIM and DMW were selected as representatives of direct pose regression methods from 2D images in literature. Target and moving image pairs of these two comparison studies were generated using DeepDRR from the same CT data and pose distributions as ProST baseline training. Of note, except for No DR, domain randomization was consistently applied in all the other experiments.

2). Image with Overlays:

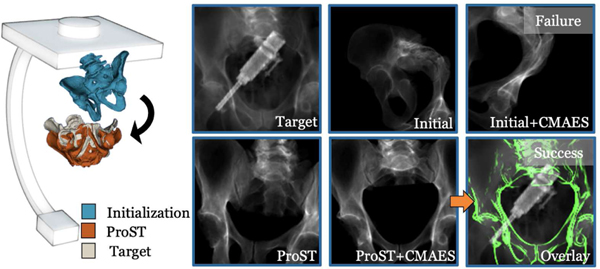
We simulated the challenging intraoperative imaging condition with the surgical tool in the C-arm capture range as overlays. The surgical tool was chosen an integrated drilling and injection device, which was custom-designed for the application of femoroplasty [4]. CT scans of the injection device were taken. For experiments on images with tool overlay, we randomly sampled the pose of the injection device and generated DRR from the CT. The tool DRR was overlayed on the original bone image as the target image. The testing network is the same trained baseline ProST model. We present an example target X-ray image with tool overlay in Fig. 3.

Fig. 3.

Illustration of an example iterative 2D/3D registration of the pelvis. The target image is a real pelvis X-ray image with tool overlay. Renderings of the initialization, ProST network registration estimation, and ground truth pose of the pelvis are illustrated on the left. The black arrow shows the difference between initialization and ProST registration poses. The target image, initial projection image, and the failed CMAES registration image from the initial are shown in the first row. The ProST registration image, successful CMAES registration image from ProST estimation, and an overlay image with DRR-derived edge in green are shown in the second row.

3). Anatomy:

We trained and tested the baseline model on the spine anatomy to demonstrate the generalization ability of ProST. Due to the scarcity of paired spine CT and X-ray images, we only tested the performance on the spine in simulation.

C. Pose Sampling Strategies and Training Parameters

We performed precisely controlled experimental training to benchmark the performance. All experiments were fed with training data from the same distribution and applied the same training strategies. The canonical geometry is the Anterior-Posterior (AP) view, which is the most common case in clinical use. Target training images $(I_t)$ were generated using DeepDRR, following a uniformly sampled pose geometry with the random translation of (−25, 25) mm and rotation of (−15, 15) degrees in all three axes. Moving training image $(I_m)$ poses were randomly sampled following Gaussian distributions with translation in mm of N(0, 25) for in-plane (X and Y) direction and N(0, 60) for depth (Z) direction, with rotation in degrees of N(0, 25) for all three axes. During testing in simulation, we followed the same training target image pose distribution to generate testing target images. We sampled an exhaustive initialization pose space following uniformly sampled translation of (−200, 200) mm for in-plane direction and (−300, 300) mm for depth direction, uniformly sampled rotation of (−50, 50) degrees. The pose sampling was done by a random generator and the same strategy was applied in real X-ray image testing.

During each training epoch, one CT was randomly selected, and target and moving image pairs were randomly generated following the distributions described above. 50 iterations were trained for every epoch. The ProST network architecture was trained using an SGD optimizer with a cyclic learning rate between 10e-6 and 10e-4 every 100 steps [48] and a momentum of 0.9. The batch size was chosen as 4 and we trained 300 epochs until full convergence. The training process took 15k different image pairs as input, which covers the sampling geometry and avoids overfitting. Following their original training strategies, DeepIM and DMW were trained using Adam optimizer with a learning rate schedule that starts from 1e-4 and decreases by 10% every 20 epochs as well as a momentum of 0.8. The batch size was chosen as 16 and the networks were trained for 150 epochs until full convergence.

D. Registration Testing and Evaluation Metrics

We performed learning-based and conventional CMAES iterative 2D/3D registration testing using randomly sampled target images and initial poses for all experiments on simulation and real X-ray data, separately. For ProST architecture variants including the MICCAI architecture, we used an SGD optimizer to optimize over the 6 DoF pose parameter (${\theta }_m$) iteratively until convergence up to a fixed number of steps with a learning rate of 0.1, which decays by a factor of 0.5 for every 15 steps. Because DeepIM and DMW do not learn a similarity score, poses were updated using direct network predictions by generating a DRR image and retrieving the network inference results at each iteration. The registration was considered to be converged if the predicted gradient magnitude went below a pre-defined threshold.

In simulation testing, we used the testing NMDID CT scans in each fold to simulate target images and the corresponding bone segmentations to perform registration. The testing data cover the full twenty CT scans. 50 images and poses per CT scan were randomly sampled following the distribution described in Section III-C, resulting in 1,000 testing cases. In real pelvic X-ray data testing, we manually selected 100 standard AP view images and 100 challenging view images. The challenging views include images with only partial pelvis visible or drastic orientations, which fall outside of the training target image distribution. Five registrations were performed on each image with the initial pose sampled from the same distribution as in simulation, resulting in 500 registrations for standard and challenging views, respectively.

For each testing, the CMAES registrations were performed from both the initial pose and the network estimated pose to compare the capture range. The CMAES optimizer was set with a pose sampling population size of 300 in each iteration, and sigmas of 45 degrees and 200 mm for rotation and translation, respectively, which was sufficient to cover the testing pose sampling space.

We report the following error metrics for evaluation:

• Registration Pose Error: A residual pose transformation was computed using the estimated $({\theta }_{\text{est}})$ and groundtruth $({\theta }_{\text{gt}})$ pose parameters:

  $$\delta T\left({\theta }_{\text{gt}},{\theta }_{\text{est}}\right)=T\left({\theta }_{\text{gt}}\right)T{\left({\theta }_{\text{est}}\right)}^{-1}$$ (7)

  We report the magnitude of translation and rotation errors in mean and median after decoupling $\delta T\left({\theta }_{\text{gt}},{\theta }_{\text{est}}\right)$ into each DoF.
• Target Registration Error (TRE): TRE is computed by calculating the average point to point distance of the bone segmentation $(P_{\text{seg}})$:

  $$\text{TRE}=mean\left(\parallel P_{\text{seg}}\cdot T\left({\theta }_{\text{gt}}\right)-P_{\text{seg}}\cdot T\left({\theta }_{\text{est}}\right){\parallel }_2\right)$$ (8)

  $P_{\text{seg}}$ refers to all coordinate points within the bone segmentation.

• Success Rate (SR): We define a threshold for successful registrations with TRE less than 10 mm. The success rate is computed as a percentage of the number of successful testings over all testings. The success rate is computed only for the CMAES registrations.

IV. Results

Qualitative results of the iterative 2D/3D registration process are shown in Fig. 3. We present an example registration using a real pelvis X-ray image with surgical tool overlay as target. The CMAES registrations from initialization failed at local minima. The 3D pose rendering shows that the object poses were much closer to ground truth after ProST registration, which then successfully converged to the global optimum using CMAES.

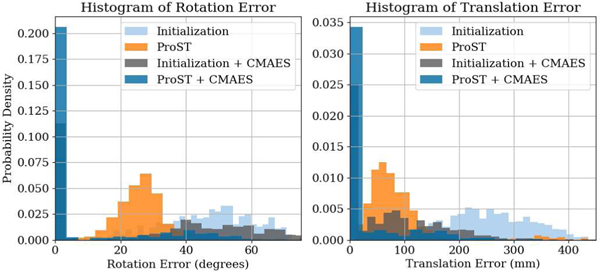
Numeric results of registration pose errors are presented in Table. I. Because our experiments were initialized with fairly large offsets, the mean errors were heavily biased by the large-scale outliers, which do not represent the actual distribution. Thus, we choose to only report errors at several percentiles. The CMAES from initialization achieved a median error of 22.4 degrees, 82.3 mm in simulation, and 57.9 degrees, 134.5 mm in real data, in rotation and translation, respectively. The ProST baseline model followed by CMAES performed the best across all the ablation studies, which achieved a median error of 0.26 degrees, 4.0 mm in simulation, and 13.6 degrees, 20.0 mm in real data, in rotation and translation, respectively. In Table. II, we report the TRE and success rate. Using our ProST baseline model, the CMAES registration success rate improved from 28.5% to 65.6% in simulation and 36.0% to 73.2% in real data. In Fig. 4, we plot the histograms of rotation and translation errors for the baseline model on real pelvis X-ray images. We clearly observe that ProST shifted the error distribution from initialization closer to zero, which resulted in a much higher success rate for CMAES, compared to CMAES from initialization.

TABLE I.

Registration Pose Error of Pelvis

	Simulation Study				Standard AP View Real X-ray
	Rotation Error (degrees)		Translation Error (mm)		Rotation Error (degrees)		Translation Error (mm)
	Mean	Median	Mean	Median	Mean	Median	Mean	Median
Initialization	49.5 ± 15.9	49.9	255.5 ± 99.6	251.6	47.6±15.1	48.6	246.5±82.6	246.9
+ CMAES	41.8 ± 34.5	22.4	120.8 ± 125.4	82.3	35.5±31.1	39.7	78.9±84.4	62.2
ProST Baseline	30.4 ± 27.4	22.4	122.2 ± 117.8	82.3	31.6±24.2	26.8	86.3±66.6	71.5
+ CMAES	22.0 ± 36.2	0.26	66.18 ± 105.3	4.0	13.9 ± 30.5	0.5	33.9 ± 70.1	1.7

In each block, we present the initialization or network estimated registration results, and the followed CMAES registration results.

TABLE II.

Target Registration Error (TRE) and Success Rate of Pelvis

	Simulation Study			Standard AP View Real X-ray
	TRE (mm)		SR (%)	TRE (mm)		SR (%)
	Mean	Median		Mean	Median
Initialization	267.4 ± 104.0	256.7		261.6 ± 90.7	255.3
+ CMAES	124.4 ± 124.8	101.7	28.5	113.1 ± 107.6	106.3	36.0
ProST Baseline	126.9 ± 124.6	84.3		107.4 ± 64.3	96.1
+ CMAES	58.2 ± 95.5	4.4	65.6	45.0 ± 88.1	2.2	73.2
ProST Tool Overlay	127.7 ± 113.9	91.5		107.5 ± 64.6	96.5
+ CMAES	79.8 ± 115.1	5.0	58.1	82.0 ± 99.3	24.1	48.4
ProST Full CT	244.7 ± 125.7	240.9		145.1 ± 89.9	120.9
CMAES	99.5 ± 110.9	62.0	45.4	76.6 ± 112.1	2.0	59.4
ProST No DR	122.4 ± 106.0	83.9		108.3 ± 66.5	96.5
+ CMAES	63.3 ± 101.1	4.3	65.4	51.9 ± 94.8	2.1	71.4
ProST No 3D Net	176.1 ± 134.2	131.7		172.4 ± 109.0	128.1
+ CMAES	94.9 ± 119.2	29.1	48.3	92.8 ± 116.3	23.1	49.2
ProST MSE Loss	268.3 ± 116.3	268.1		265.4 ± 112.4	260.5
+ CMAES	134.8 ± 131.8	109.7	27.9	126.3 ± 108.8	120.3	28.8
MICCAI	214.5 ± 118.1	193.2		246.1 ± 104.5	236.6
+ CMAES	97.2 ± 117.4	55.9	45.0	86.5 ± 110.5	2.9	51.2
DeepIM	150.0 ± 153.1	75.5		250.6 ± 125.6	226.4
+ CMAES	86.0 ± 126.3	4.7	59.6	113.7 ± 117.1	99.7	41.2
DeepIM Tool Overlay	158.1 ± 150.5	90.5		261.8 ± 129.7	236.9
+ CMAES	113.3 ± 139.7	43.2	57.6	145.6 ± 117.2	142.1	23.8
DMW	256.23 ± 92.49	247.88		285.1 ± 134.9	266.0
+ CMAES	128.87 ± 123.17	109.70	27.0	110.9 ± 109.4	94.4	38.4
DMW Tool Overlay	257.4 ± 94.9	248.2		287.9 ± 137.1	267.4
+ CMAES	136.9 ± 115.6	122.0	18.2	136.2 ± 110.1	133.3	24.8

Note: SR refers to Success Rate. The highest success rate is bolded.

Fig. 4.

Histogram of registration pose errors in translation and rotation for pelvis standard AP view real X-ray study from ProST baseline model registrations.

The results of our comparison experiments all performed worse than the baseline model. We present the results using ProST baseline model on the spine anatomy in Table. III. The success rate was 39.4%, compared to 23.3% using CMAES from initialization. We present discussions and analysis of the results in greater details in the next Section V.

TABLE III.

Target Registration Error (TRE) and Success Rate of Spine

	TRE (mm)		SR (%)
	Mean	Median
Initialization	267.3 ± 106.0	257.2
+ CMAES	148.5 ± 155.4	101.6	23.3
ProST Baseline	156.5 ± 121.9	126.7
+ CMAES	94.5 ± 135.9	43.2	39.4

Note: Table structure follows Table. I. The highest success rate is bolded.

V. Discussion

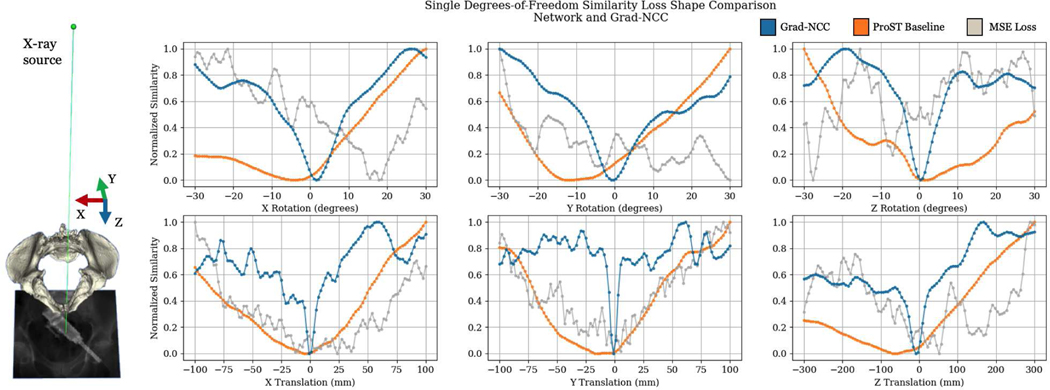
Our results suggest that ProST vastly increases the capture range of conventional CMAES intensity-based 2D/3D registration. This improvement is because the network similarity function has much fewer local minima than the hand-crafted image similarity functions, such as Grad-NCC. To our knowledge, this is the first time that the similarity function of X-ray image 2D/3D registration is learned to a target convex shape in an end-to-end fashion. Such breakthrough comes from the unique property of ProST: enabling differentiable gradient flow from the 2D domain to 3D, especially to the 3D pose parameters. We present a qualitative comparison of the network and Grad-NCC similarity function landscapes in Fig. 5. Since the similarity function is high dimensional with respect to the 6 DoF pose parameter, we plot each DoF individually by fixing the other DoF parameters as zeros. The similarity plots in Fig. 5 show that the network similarity is smoother and contains fewer local minima, especially in translations. Of note, we do not measure the convexity of the network similarity function. The plots in Fig. 5 serves as an example and the convexity is related to the specific testing image.

Fig. 5.

Single degree of freedom similarity loss shape comparison between network similarity and gradient normalized cross correlation (Grad-NCC). An example of projection geometry with axis directions is illustrated on the left.

In our comparison study involving images with surgical tool overlays, we found that the performance of the ProST network prediction remained consistent. The median TRE values for real images with and without tool overlays were 96.1 mm and 96.5 mm, respectively. However, the success rates decreased after performing the CMAES registration, with success rates of 73.2% and 48.4% observed for images with and without tool overlays, respectively. This decline can be attributed to the obstruction of local anatomical features, which are vital for intensity-based 2D/3D registration using the hand-crafted patch-based gradient normalized cross-correlation as the similarity function. On the other hand, the network’s similarity computation relies on global image information, enabling it to be more resilient to local feature changes. We want to emphasize we did not retrain the network for testing on images with tool overlays, and the network model is trained on purely simulation dataset, but generalizes well on unseen real cadaveric images, indicating its superior generalization ability.

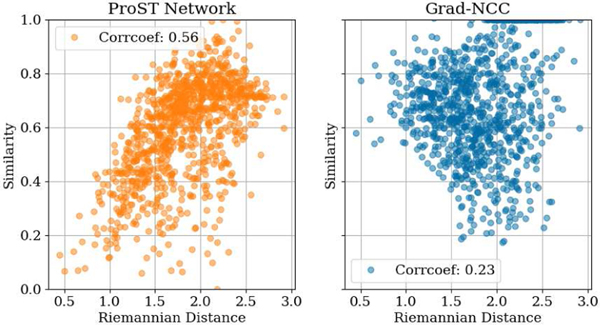
By learning a convex shape image similarity, the network similarity function has a higher correlation with respect to the 3D pose difference than the hand-crafted similarities. In Fig. 6, we present a correlation plot of the similarity values with respect to riemannian distances, indicating the 3D pose differences. The correlation coefficient is 0.56 for the network and 0.23 for Grad-NCC. Although the coefficient is still moderate, the comparison suggests that our learned similarity has the potential to be used as an indicator of registration uncertainty. Our future work will include studies using ProST to estimate the probability of registration uncertainty and its relationship to visualization paradigms [49], [50].

Fig. 6.

Correlation plot of similarity and pose Riemannian distance.

The current learning-based iterative 2D/3D registration methods in literature aim at predicting a pose update from 2D image observations by either framing it as a reinforcement learning task or direct gradient update regression. We included two representative methods in our comparison experiments, namely DeepIM [19] and DMW [20]. Such methods have the following limitations: 1) Since the registration does not optimize a cost function, but the iterative pose prediction is extracted from 2D images, there is no guarantee for convergence to global or local minima. The prediction can change drastically if the input image’s appearance alters by a small change. 2) Learning from only a 2D domain without 3D parameters limits the network ability, likely to overfit the training domain. 3) Pose regression-based 2D/3D registration approaches are performed with respect to a canonical coordinate system derived from an implicit atlas, which is challenging to be precisely defined. Our ProST registration method follows the same iterative optimization design as the intensity-based registration methods. The only difference is that we take advantage of the great expressivity of the deep network to learn a set of more complicated filters than the conventional hand-crafted ones. By leveraging the 3D image, we eliminate the need for the canonical frame. This design potentially makes generalization easier because the mapping that our method needs to learn is simple. In our comparison experiments, the success rates of ProST baseline model in simulation and real are 65.6% and 73.2%, respectively. DeepIM performs comparable to the baseline model in simulation with a success rate of 59.6%, but the performance drops substantially on real X-ray data with a success rate of 41.2%. When testing on images with tool overlays, the success rate of DeepIM was only 23.8%, which suggests the poor generalization ability of such methods.

We performed a controlled ablation study to demonstrate the importance of 3D parameters in the architecture by removing the 3D CNN part and keeping the other training/testing settings the same. The results are worse than the baseline in Table. I and II) for both the network and the following CMAES estimations. Although it is difficult to interpret the meaning of 3D features, the results suggest that the 3D network component makes learning easier for this task. We also performed a comparison study for using the full CT volume as input, and its performance is worse than using the segmented bone volume as input with real data success rate of 59.4%. We attribute the reason to be that the bone is a rigid object with higher attenuation than soft tissue, which is better for feature extraction.

Our architecture was trained with the novel double backward gradient loss. Our ablation experiment using MSE loss regression performs much worse than the baseline model, with success rates of 27.9% in simulation and 28.8% in real data, suggesting that the network failed to learn meaningful mappings in this regression task. The double backward gradient loss design is a more effective way to learn the shape of target loss. Of note, we did not optimize the hyper parameters but we controlled the training settings to be the same for comparison. Considering the obviously big differences in the comparison study results, we believe the effect of hyper parameters is minor. We performed an ablation study to show the effect of domain randomization (DR). The No DR results are slightly worse than the baseline model, with success rates of 65.4% in simulation and 71.4% in real. In future studies, we will explore advanced data augmentation strategies to enhance the model’s generalization capabilities. In this work, we used the advanced CrossViT as a 2D image encoder. The multi-scale patch-based feature extraction design learns more robust features than the ResNet block encoders used in the MICCAI published version [31]. Our comparison experiment of MICCAI architecture achieves success rates of 45.0% in simulation and 51.2% in real data, which are both worse than the CrossViT baseline model.

Single-view 2D/3D registration by nature has its ambiguity in depth translation and out-of-plane rotations. This is because the appearance of the projection changes much less when the object translates along the depth Z direction than in-plane translations. It is particularly challenging for the network to detect minor differences from the target image using an encoder architecture compared to hand-crafted image similarities. This ambiguity can be observed in the similarity loss shape plot in Fig. 5, where the network similarity presents flattened bottoms while Grad-NCC has a sharp curve around global minima. ProST network registration is particularly effective when the object is far away, but its accuracy is limited by this ambiguity when the pose is close to the target. Our experimental findings indicate that the registration ambiguity introduced by the network is largely rectified through the subsequent CMAES intensity-based registration process. Consequently, the flattened bottom of the similarity curve is closer to the ground truth pose than the initially far-off initialization. This suggests that the combination of the ProST learning-based registration and the CMAES registration effectively corrects the inherent ambiguity and facilitates accurate pose estimation.

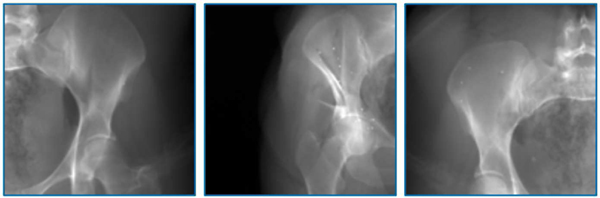
We tested the network models on real pelvis X-rays of challenging views. Three examples of challenging view X-ray images are shown in Fig. 7. The pelvis in these types of images is only partially visible. Thus the present features are very different from the AP view images during training. Numeric registration results are present in Table. IV. They are all deteriorated from the standard view image results with the highest success rate of 45.8%, corresponding to the ProST baseline model. This result suggests that the network similarity function does not generalize well on such challenging cases. Future work will include learning features that are more robust to challenging views.

Fig. 7.

Examples of challenging view pelvis X-rays.

TABLE IV.

Target Registration Error (TRE) and Success Rate of Pelvis

	Challenging View Real X-ray
	TRE (mm)		SR (%)
	Mean	Median
Initialization	268.0 ± 100.6	263.1
CMAES	149.9 ± 111.2	149.0	21.2
ProST Baseline	141.7 ± 83.2	119.1
CMAES	104.0 ± 113.6	65.0	45.8
ProST Tool Overlay	142.0 ± 86.2	117.8
CMAES	158.4 ± 115.5	158.8	18.2
DeepIM	258.9 ± 126.4	247.8
CMAES	159.8 ± 126.8	153.3	25.4
DMW	295.3 ± 134.1	278.9
CMAES	147.5 ± 113.3	149.4	25.0

Note: SR refers to Success Rate. The highest success rate is bolded.

We are aware that there are popular feature-based 2D/3D registration methods, such as solving a PnP problem using corresponding anatomical landmarks [13], [16], [17], which may be complementary to the intensity-based registration methods. However, these methods need to define meaningful landmark features manually and do not learn registration in an end-to-end fashion. Our method, however, learns the similarity function in a purely data-driven manner. We demonstrate our method using the spine as alternative anatomy. Pose estimation of the spine is more difficult than the pelvis because the spine is symmetric and the vertebrae are smaller. The success rate of ProST registration improves from 23.3% to 39.4%, suggesting its generalization ability on different anatomies.

Our results presented using registration pose error, TRE, and success rate are general measures to report the 2D/3D registration performance, which are commonly used in the literature [51], [18], [24]. This work does not tie to a specific clinical application, and thus we do not compare it against specific clinical requirements.

In our experiments, the CT data were downsampled to a cubic volumetric size of 128 voxels in each dimension, and the projection images were of size 128×128, which consumes about 15 GB of GPU memory in pipeline training. Although the design grid sampler in ProST eases the excessive use of memory computation, filling in an actual full-size CT data into a modern graphic card’s memory is still challenging. Such downsampling dropped information from the original data and limited the registration accuracy. Our future work includes improving the architecture design to fit data with higher resolution. This work does not compare choices of 3D CNN architectures, because the 3D gradient flow makes the network optimization complicated, and the memory limitation restricts the choice of advanced networks. Future work will focus on optimizing ProST module’s memory usage and evaluating the performance on higher resolution images, different 3D network architectures. The ProST network registration takes about 10 seconds, and the following CMAES intensity-based registration takes around 5 seconds, resulting in the full registration workflow runtime to be about 15 seconds. As a comparison, the average runtime of a conventional 2D/3D registration algorithm using landmark-based initialization is 7 seconds [13]. Our ProST workflow runtime takes additional eight seconds because: 1) the iterative optimization requires multiple passes through the neural network; and 2) our differentiable pipeline is a novel approach to 2D/3D registration requiring custom deep learning modules (such as the projective spatial transformer block), that have not yet benefited from considerable computational optimization, making them less efficient compared to standard feed-forward CNNs. Future work will consider speedup the workflow. This work only concerns rigid registrations because the sampling grid design is rigid and fixed. Our differentiable ProST module explicitly allows for making the geometry parameters learnable. Future work will include investigations on nonlinear registrations, such as deformable 2D/3D registrations.

VI. Conclusion

In this work, we present a fully differentiable 2D/3D registration framework, which learns a convex shape similarity function using a novel projective spatial transformer module. We performed controlled studies with intensive comparison experiments on simulation and real X-ray images. Our results suggest that the proposed registration method largely extends the convention intensity-based registration capture range and performs more robustly than the other learning-based pose regression methods in the literature. We believe that ProST has the potential to benefit learning-based 3D medical imaging research applications.