Skip to main content
PMC home page
Genome Research logoLink to Genome Research
letter
. 2005 May;15(5):665–673. doi: 10.1101/gr.3128605

Evolution of base-substitution gradients in primate mitochondrial genomes

Sameer Z Raina 1, Jeremiah J Faith 1,4, Todd R Disotell 2, Hervé Seligmann 1, Caro-Beth Stewart 3, David D Pollock 1,5
PMCID: PMC1088294  PMID: 15867428

Abstract

Inferences of phylogenies and dates of divergence rely on accurate modeling of evolutionary processes; they may be confounded by variation in substitution rates among sites and changes in evolutionary processes over time. In vertebrate mitochondrial genomes, substitution rates are affected by a gradient along the genome of the time spent being single-stranded during replication, and different types of substitutions respond differently to this gradient. The gradient is controlled by biological factors including the rate of replication and functionality of repair mechanisms; little is known, however, about the consistency of the gradient over evolutionary time, or about how evolution of this gradient might affect phylogenetic analysis. Here, we evaluate the evolution of response to this gradient in complete primate mitochondrial genomes, focusing particularly on A⇒G substitutions, which increase linearly with the gradient. We developed a methodology to evaluate the posterior probability densities of the response parameter space, and used likelihood ratio tests and mixture models with different numbers of classes to determine whether groups of genomes have evolved in a similar fashion. Substitution gradients usually evolve slowly in primates, but there have been at least two large evolutionary jumps: on the lineage leading to the great apes, and a convergent change on the lineage leading to baboons (Papio). There have also been possible convergences at deeper taxonomic levels, and different types of substitutions appear to evolve independently. The placements of the tarsier and the tree shrew within and in relation to primates may be incorrect because of convergence in these factors.

Nucleotide frequencies in mitochondrial DNA vary considerably across mammalian lineages (Honeycutt et al. 1995; Gissi et al. 2000). This creates considerable difficulties for phylogenetic inference, including biased attraction of branches leading to species with similar frequencies (Van Den Bussche et al. 1998; Reyes et al. 2000; Wiens and Hollingsworth 2000). Rates of evolution also vary (Honeycutt et al. 1995; Gissi et al. 2000), but it is unclear how rates and nucleotide frequencies are related; few studies have gone into these processes in detail. In reconstruction of deep primate phylogeny, variation in frequencies and rates is believed to cause consistent biases (Felsenstein 1978, 2001; Lockhart et al. 1992; Graybeal 1993; Meyer 1994; Yoder et al. 1996), but the reasons are unclear (Philippe and Laurent 1998) and it is uncertain how it should be taken into account. The underlying evolutionary mechanism has presumably changed, but how? One important factor, only recently clarified, is that different mutation types respond differently to a gradient of single-strandedness that is generated during mitochondrial replication (Faith and Pollock 2003). Thus, it is insufficient to assume that relationships among substitution types are constant across sites or across evolutionary time, and targeted methods are needed to evaluate the response to single-strandedness in individual genomes.

It is known (Clayton 1991, 2000; Tanaka and Ozawa 1994; Reyes et al. 1998; Faith and Pollock 2003) that the asymmetric nature of mitochondrial DNA replication leads to a gradient in duration of single-strandedness, DssH, and a gradient in susceptibility to mutation (for review, see Faith and Pollock 2003). The proportional time that a site spends single-stranded can be predicted (see Methods). Although there is some controversy over this mechanism of replication (Holt et al. 2000; Yang et al. 2002; Bowmaker et al. 2003; Holt and Jacobs 2003), a preponderance of biochemical evidence (Bogenhagen and Clayton 2003a,b) and all evolutionary analyses (Faith and Pollock 2003) support the “classic” model.

The single-stranded state is particularly prone to deaminations, especially deaminations of cytosine (C) and adenine (A), which cause transitions to thymine (T) and guanine (G) on the heavy strand (Asakawa et al. 1991; Tanaka and Ozawa 1994; Reyes et al. 1998). Since transition rates are much greater than transversion rates, these excess transitions lead to higher G/A and T/C ratios than in their absence. Frederico found that C is very unstable (Frederico et al. 1990, 1993), and the T/C ratio (or conversely, the A/G ratio on the light strand) increases quickly with increasing DssH, apparently saturating at low values of DssH (Faith and Pollock 2003). The deamination of A⇒hypoxanthine (which is replaced by G) is a slower process (Tarr and Comer 1964; Parham et al. 1966; Krasuski et al. 1997), and the gradient in DssH causes differences among genes in the rate of A⇒hypoxanthine deaminations on the heavy strand. This results in differences in the C/T ratio along the light strand (Limaiem and Henaut 1984; Delorme and Henaut 1991) and in differences in compositional bias, particularly at third codon positions and noncoding sites (Jermiin et al. 1994, 1995; Tanaka and Ozawa 1994; Reyes et al. 1998).

Although skew is a sensitive means of detecting differences among genes, the two standard skew measures (Perna and Kocher 1995) blend the effects of the two major single-stranded transitions. Faith and Pollock (2003), using maximum likelihood (ML) analyses of 45 vertebrates, found strong evidence that A⇒G substitution rates increase linearly with DssH, while other substitutions do not. C⇒T substitutions are more prevalent, but are uniformly high along the genome and thus contribute little to differences in nucleotide content along the genome. Although it has been traditional (Limaiem and Henaut 1984; Tanaka and Ozawa 1994; Reyes et al. 1998; Faith and Pollock 2003) to refer to substitutions and base frequencies with respect to the light strand, here we will refer to them based on the complementary heavy strand as in Krishnan et al. (2004b). Since the excess mutations occur on the heavy strand, this reduces the potential for confusion in the results and discussion, but differentiates our discussion from that in other papers.

Our current understanding of the evolutionary processes leading to mutational asymmetry in mitochondria suggests a means to better understand it. The slope of the G/A gradient is presumably an inverse function of the rate of replication and therefore inversely proportional to the efficiency of polymerase-γ (the replicating enzyme in vertebrate mitochondria). The intercept of the gradient is presumably a function of the G/A ratio in the absence of single-strandedness and the rate at which light-strand synthesis is initiated (which, in turn, might be affected by both the shape of the origin of replication and the binding abilities of the polymerase-γ accessory subunit). For other substitution types, particularly C⇒T, repair mechanisms (Meyer 1994) may alter the slope and intercept, and probably the linearity of response; when functioning efficiently they may completely eliminate any detectable response to single-strandedness.

We present here a study of the variation in nucleotide ratio gradients among primates and two outgroups. The primates, with 16 complete mitochondrial genomes, are the most densely sampled vertebrate order, and generally have an increased rate of evolution relative to other mammals (Gissi et al. 2000). We focused on the heavy-strand G/A gradient at third codon positions, since there is a strong expectation that it will increase linearly with DssH. We also report on the heavy-strand C/T and pyrimidine/purine [Y/R = (C+T)/(A+G)] ratios, and on G/A gradients at the first and second codon positions. We developed likelihood-based methods to evaluate the response to single-strandedness. A joint Bayesian and ML approach was used to evaluate the among-species differences in response to DssH, and both mixture model and hierarchical clustering methodologies were used to evaluate whether different species evolved in similar fashions. With these tools, we were able to detect and explain divergence and convergence of base frequencies among primates, and thus were able to provide a causal explanation for possible phylogenetic reconstruction bias in parts of the tree. To maintain the clarity of the results narrative, we have placed a great deal of the raw results from the likelihood analysis in Supplemental data tables, and reserve the figures and tables presented in the main paper for critical interpretive information.

Results

Evolution of G/A gradients

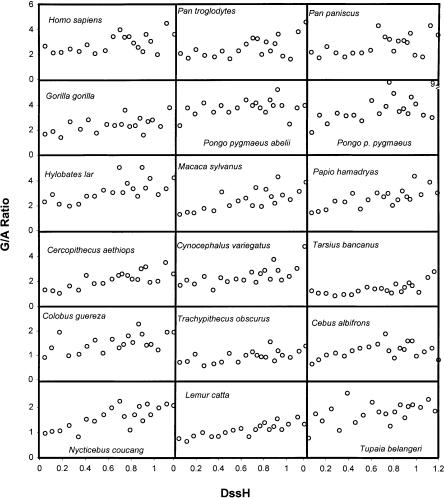
Our expectation, based on a joint analysis of complete vertebrate genomes (Faith and Pollock 2003), was that synonymous sites in individual primate genomes would have a linear relationship between the heavy-strand G/A ratio and the time spent single-stranded. Markov chain Monte Carlo (MCMC) runs on individual genomes showed significantly positive slopes in all cases (Fig. 1; Table 1). There was considerable variation among genomes in both slope and intercept, and values for many pairs of species were apparently different in that they lay outside their respective 95% credible intervals (Table 1). Comparisons of null models with one response curve per pair of genomes to models with independent response curves for each genome in a pair showed that, based on the 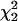Inline graphic distribution, most pairs of genomes have significantly different responses to time spent single-stranded (Supplemental Table A). To obtain a better idea of the meaning of this variation, we clustered species based on their G/A ratio responses using both a hierarchical clustering approach and a mixture model analysis with between two and eight mixture models. It is useful to compare and combine the two approaches, since hierarchical clustering may be order-dependent, while significance levels for the mixture models have uncertain validity (McLachlan and Peel 2000).

Figure 1.

Figure 1.

Open in a new tab

G/A ratios for complete primate mitochondrial genomes and two near outgroups. Third codon positions containing G/A were grouped into 20 equal-size bins for each genome, and the ratio of G/A in each bin is graphed versus the average DssH for that bin.

Table 1.

Maximum likelihood values and 95% CI for slopes and intercepts of G/A gradients in primates and two outgroups

Species Max like Slope Intercept
Homo sapiens -1275.61 0.860 (0.228, 1.561) 2.204 (1.768, 2.710)
Pan troglodytes -1339.08 0.925 (0.363, 1.490) 1.761 (1.403, 2.176)
Pan paniscus -1335.41 1.061 (0.491, 1.645) 1.686 (1.326, 2.126)
Gorilla gorilla -1332.45 1.187 (0.578, 1.794) 1.622 (1.266, 2.056)
Pongo pygmaeus abelii -1169.74 0.661 (0.110, 1.740) 3.096 (2.443, 3.636)
Pongo p. pygmaeus -1189.91 1.541 (0.502, 2.543) 2.417 (1.853, 3.155)
Hylobates lar -1214.29 1.544 (0.735, 2.331) 2.077 (1.643, 2.623)
Macaca sylvanus -1297.84 1.729 (1.216, 2.319) 1.197 (0.906, 1.531)
Papio hamadryas -1284.19 1.586 (0.962, 2.179) 1.451 (1.134, 1.832)
Cercopithecus aethiops -1353.94 1.494 (1.039, 2.018) 1.087 (0.830, 1.384)
Colobus guereza -1425.30 0.525 (0.195, 0.904) 1.104 (0.893, 1.351)
Trachypithecus obscurus -1469.87 0.415 (0.190, 0.630) 0.695 (0.567, 0.847)
Cebus albifrons -1405.69 0.344 (0.091, 0.642) 0.947 (0.743, 1.144)
Nycticebus coucang -1335.30 0.965 (0.609, 1.329) 0.906 (0.709, 1.147)
Lemur catta -1408.20 0.607 (0.359, 0.883) 0.688 (0.536, 0.870)
Tarsius bancanus -1422.08 0.708 (0.420, 0.994) 0.844 (0.673, 1.048)
Tupaia belangeri -1263.74 0.694 (0.303, 1.122) 1.258 (1.006, 1.557)
Cynocephalus variegatus -1269.62 1.132 (0.582, 1.658) 1.553 (1.224, 1.955)
Open in a new tab

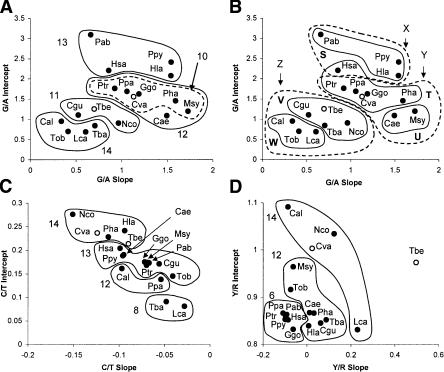
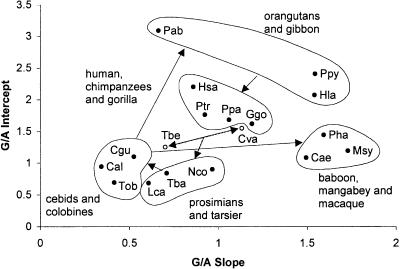
In the hierarchical clustering (Fig. 2A; Table 2), merging of the species into one large set of species (Group 10) and five species pairs (Groups 5–9) was not rejected at the 0.05% significance level (for further details, see Supplemental Discussion of Results). Species in these groups were sometimes but not always closely related to one another. At moderately large cost (δlnL < 10.0), these groups could be merged to form four new groups (Groups 11–14). The next two mergers were more incredible (45 > δlnL > 60), while all primates and outgroups could only be merged together as one group at an extremely unbelievable cost of δlnL = 497. Other interesting points are that the intercept tended to matter more in clustering than the slope, and as expected, clusters were more easily joined when a slightly smaller intercept was balanced with a slightly bigger slope.

Figure 2.

Figure 2.

Open in a new tab

Graph of MLE slopes versus MLE intercepts along with major clusters in ratio cluster analyses. We performed mixture (A) and hierarchical analyses (B) of G/A ratios, and hierarchical analyses of (C) C/T and (D) Y/R ratios. Groups are labeled by their order of clustering.

Table 2.

Summary of hierarchical clustering results for G/A gradients

Group Members
G/A
    Likely clusters (δLnL < 3.0)
        5 Orangutans (Ppy, Pab)
        6 Colubine and loris (Cgu, Nco)
        7 Human and gibbon (Hsa, Hla)
        8 Langur and lemur (Tob, Lca)
        9 Capuchin and tarsier (Cal, Tba)
        10 Flying lemur (Cva; outgroup), chimpanzees and gorilla (Ptr, Ppa, Ggo; great apes), baboon and macaque (Pha, Msy; Old World monkeys)
    Unclustered species
        Vervet monkey (Cae), tree shrew (Tbe)
    More unlikely clusters (3.0 < δLnL < 10.0)
        11 Tbe and Group 6
        12 Cae and Group 10
        13 Group 5 and Group 7
        14 Group 8 and Group 9
    Incredible clusters (δLnL > 10.0)
        15 Group 11 and Group 14
        16 Group 12 and Group 13
Open in a new tab

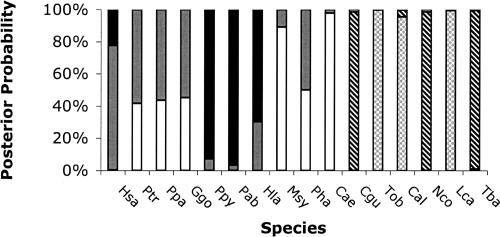
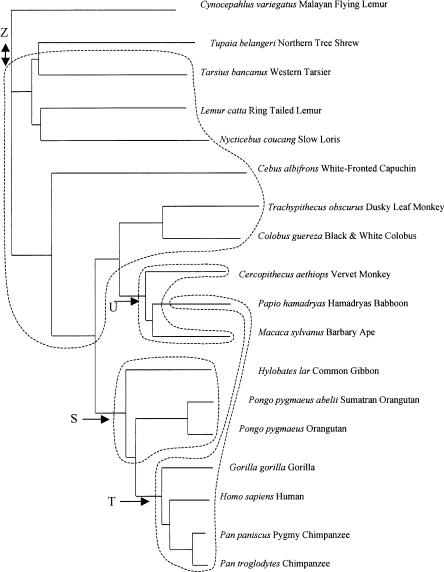
In mixture model analyses, all species were evaluated simultaneously (the outgroups were excluded), and the best set of models was determined (Supplemental Table C). In these analyses, the posterior probability that data from each species were generated by each model can be calculated (equation 5). According to this criterion, species were mostly associated with a particular model, although there was some variance in the posterior for the five and six model cases (data not shown). Clustering in the mixture models is obviously related to the results from the hierarchical analysis, but owing to the nonhierarchical nature of the mixture analysis, switches in alliances among groups can occur for different numbers of clusters (for more details, see Supplemental Discussion of Results). The mixture analysis shows that different species often share posterior allegiances between models, particularly when the ML slope and intercept values of the species are adjacent to one another (Fig. 3). If the mixture clusters are mapped onto a phylogenetic tree (Fig. 4), it is clear that the baboons, and to some extent all of the Old World monkeys, have converged to a similar response curve as the hominoids.

Figure 3.

Figure 3.

Open in a new tab

Posterior probabilities for each species to belong to each model for the five-model mixture. The posterior probabilities are averaged across 10 independent chains. The models in descending order of magnitude of intercept are black (Group S), gray (Group T), white (Group U), diagonal lines (Group V), and gray hatch (Group W). Group identifications are the same as in Figure 2B.

Figure 4.

Figure 4.

Open in a new tab

G/A mixture model groups mapped onto a phylogenetic tree of the primate species used in this study. This is the primate phylogeny most compatible with the mitochondrial sequences, but is probably inaccurate in some topological details (see Methods). Arrows indicate possible locations of large changes in the response curve, and are labeled to match the mixture model clusters in Figure 2B. A double-headed arrow is used between the flying lemur and the rest of the species to indicate the slight ambiguity in its outgroup status, as discussed in the text. Clusters shown are for the model with five clusters, except that clusters V and W have similar slopes and intercepts, and are grouped into cluster Z as in the three-cluster analysis.

An interpretation of the evolution of the G/A response curves can now be made (Fig. 5). The three deepest diverging primates, Lemur, Nycticebus, and Tarsius (strepsirrhines and tarsier), have similar slopes and intercepts, with some variation. In the transition to the anthropoid primates (including cebids and colobines), intercepts remained similar, but the slopes notably decreased. In apparently convergent events, the Old World monkeys (baboon, vervet, and macaque) increased their slopes and intercepts, as did the lesser and great apes. The hominoids are tightly clustered in intercepts (with the exception of Homo), and fairly clustered in slopes, but the orangutans and gibbon have the highest intercepts among the primates, and their slopes cover the extremes of the range among greater and lesser apes. Interestingly, the outgroup Cynocephalus is very similar to the gorilla, while the other outgroup, Tupaia, is closest to Tarsier.

Figure 5.

Figure 5.

Open in a new tab

Graph of MLE slopes versus MLE intercepts along with major groups showing a summary interpretation of G/A evolution. Arrows indicate possible changes in response curves, and are discussed in the text.

Evolution of C/T and Y/R gradients

Although the C/T ratio did not show a clear slope in our earlier study (Faith and Pollock 2003), we performed individual and hierarchical analyses on the C/T ratio response to single-strandedness to determine if there was any variation in the level of asymmetry or the existence of a slope among the primates (Supplemental Tables D and E). We also performed these analyses on the Y/R ratio at 4× redundant third codon positions to see if there was detectable variation in slopes and intercepts for transversions (Supplemental Tables F and G). As in the G/A analysis, various clusters were significant at different significance levels, although in the C/T analysis, there were only three discrete clusters that were not rejected at the 0.05% significance level (Table 3). Results with the C/T ratio are tentative because of the nonlinear response, and indeed, there is considerable complexity in the evolution of this response curve (Krishnan et al. 2004c).

Table 3.

Summary of hierarchical clustering results for C/T and Y/R gradients

Group Members
C/T
    Likely clusters (δLnL < 3.0)
        8 Lemur (Lca) and tarsier (Tba)
        12 Pygmy chimpanzee (Ppa) and capuchin (Cal)
        13 Human (Hsa), orangutans (Ppy, Pab), chimpanzee (Ptr), gorilla (Ggo), vervet monkey (Cae), macaque (Msy), colubine(Cgu), langur (Tob)
        14 Baboon (Pha), flying lemur and tree shrew (Cva, Tbe; outgroups), gibbon (Hla), loris (Nco)
    More unlikely clusters (3.0 < δLnL < 10.0)
        15 Group 12 and Group 13
    Incredible clusters (δLnL > 10.0)
        16 Group 14 and Group 15
Y/R
    Likely clusters (δLnL < 3.0)
        6 Human (Hsa), chimpanzees and gorilla (Prt, Ppa, Ggo; great apes), orangutans (Ppy, Pab)
        12 Gibbon (Hla), langur (Tob), baboon (Pha), colubine (Cgu), vervet monkey (Cae), tarsier (Tba), macaque (Msy)
        14 Loris and lemur (Nco, Lca; prosimians), capuchin (Cal), flying lemur (Cva; outgroup)
    Unclustered species
        Tree shrew (Tbe)
    Incredible clusters (δLnL > 10.0)
        15 Group 6 and Group 12
        16 Tbe and Group 14
Open in a new tab

In the Y/R ratio analysis, Tupaia was the only organism with a significant slope (Fig. 2D; Table 3; Supplemental Table F). Tupaia had an even ratio of pyrimidines to purines at zero DssH, but had a positively increasing bias toward pyrimidines with increasing DssH, and did not group with the likely clusters. The generally flat slopes in the primates provided little evidence for excess transversion mutations in response to single-strandedness, although the significant slope in Tupaia is preliminary evidence that such a response can exist in some organisms (and is perhaps usually controlled by efficient repair mechanisms). Interestingly, Tarsius did not group with the strepsirrhines and outgroups based on the Y/R ratio, while the deepest-branching New World monkey, Cebus, did, although the differences between the tarsier and Lemur were not large (Supplemental Tables F and G).

The bias toward purines in the apes and most monkeys indicates a derived trend. Although such a bias cannot occur in a perfectly symmetric mutation model (where the mutation processes are equivalent on both strands), the strong and consistent transition bias against C (described above) could conceivably create a transversion bias through secondary effects without any alteration in transversion rates. The pattern of species with this bias did not match the pattern of species differences in the C/T bias, however; thus, it seems probable that there may have been a derived change in the rates of at least one type of transversion. It is also possible that these differences could be due to derived changes in the degree of codon bias or some other form of selection on synonymous sites, although it seems implausible that such selective alternatives could explain the positive slope in Tupaia.

Correlation of first, second, and third codon positions, and comparison of phylogenetic trees

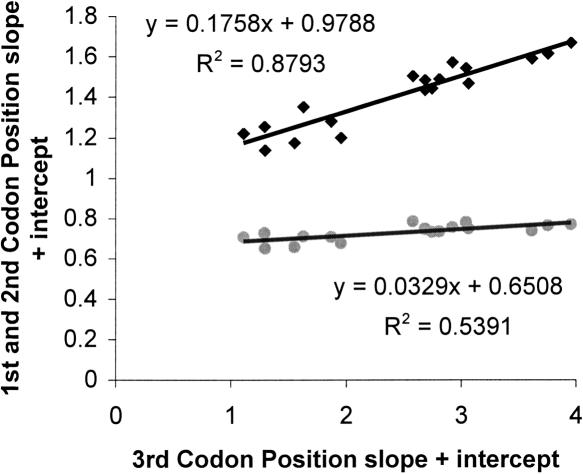
Evolutionary changes in the number of deaminations in the single-stranded state may also affect first and second codon positions, but because many more changes at first codon positions and all changes at second codon positions are nonsynonymous, they are constrained by selection at the amino acid level. At first codon positions, nine out of 18 slopes are significantly greater than zero, while for second codon positions no individual slopes are significant. Nevertheless, linear regressions of the G/A ratio slope plus intercept of both first and second codon positions on third codon positions (Fig. 6) are extremely significant (both probabilities are <0.001). Although the regression slopes are much less than one, particularly for the slow-evolving second codon positions, this result indicates, not surprisingly (Thomas and Wilson 1991; Kondo et al. 1993), that nucleotide biases in mutation rates also affect amino acid substitution rates, presumably mostly for neutral or nearly neutral substitutions.

Figure 6.

Figure 6.

Open in a new tab

Regression of slope plus intercept for different codon positions. The MLE estimators of slope plus intercept response curves for each species in the analysis for first codon positions (diamonds) and second codon positions (circles) versus third codon positions. The regression line is shown, and the slope, intercept, and R2 values are shown adjacent to each line.

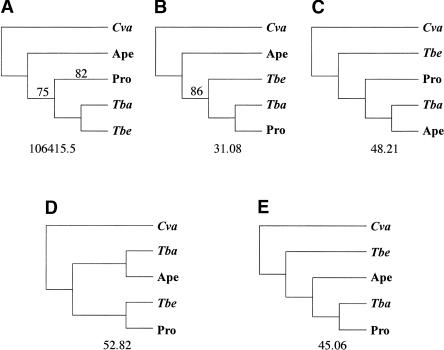
Evolutionary changes in biases in nucleotide and amino acid composition may affect phylogenetic reconstruction with mitochondrial data (Felsenstein 1978, 2001; Lockhart et al. 1992; Graybeal 1993; Meyer 1994; Yoder et al. 1996). The nucleotide data strongly support a tree (Fig. 7A) that is not consistent with most current views of primate phylogeny (Fig. 7C), although read Arnason and colleagues for an alternative viewpoint (Arnason et al. 2002). The amino acid data support a tree (Fig. 7B) that is only slightly improved relative to morphological expectations (Fig. 7C), and that is also the second-best tree in terms of DNA-based likelihood scores. Support for the favored tree is good, both in terms of relative likelihood scores compared to the expected tree and alternative intermediates (Fig. 7), and in terms of neighbor-joining bootstrap and Bayesian posterior probability support for branches.

Figure 7.

Figure 7.

Open in a new tab

Comparison of the most likely trees relating the deeply diverging primate groups and outgroups. Bootstrap values for the DNA-based NJ analysis are shown on (A) when <100%. Posterior probabilities for the nucleotide Bayesian analysis were 100%, and the one branch <100% in the amino acid analysis is shown in (B). The likelihood is shown for (A), the most likely topology under the DNA-based analysis, and differences from the most likely tree are shown underneath topologies (B–E).

Discussion

The results of this study provide details on the evolution of the response of various substitutions to the gradient of single-strandedness encountered during mitochondrial replication. For simplicity, we refer to evolution of this response as “gradient evolution” and the combined slope and intercept as the “response curve.” Gradient evolution was mostly phylogenetically consistent, but there are clear instances of convergent changes in the response curve. Since changes in equilibrium base frequencies are the necessary outcome of evolution of the mutation spectrum, and because evolution of base frequencies can dramatically mislead phylogenetic analyses (Felsenstein 1978, 2001; Lockhart et al. 1992; Graybeal 1993; Meyer 1994; Yoder et al. 1996), this result may explain some difficulties in primate phylogenies determined by mitochondrial analysis. In particular, the two supposed nonprimate outgroups, the tree shrew (Tupaia) and the flying lemur (Cynocephalus), do not cluster; this means either that physiological and nuclear evidence (Disotell 2003), including repetitive elements (Schmitz et al. 2002b), is wrong, that mitochondria have a dramatically different phylogeny (Arnason et al. 2002) from nuclear genes, or that the inferred mitochondrial tree is an artifact of mutational convergence in mitochondria. Recent evidence indicates that repetitive elements in the primates are extremely good markers with almost no phylogenetic contradictions (Salem et al. 2003; Ray et al. 2004). Furthermore, the controversial placement (Schmitz et al. 2001; Yoder 2003) of the tarsier as sister group to the strepsirrhines rather than to the anthropoid primates (if the flying lemur is used as an outgroup, or as the sister group to all other primates if the tree shrew and other mammals are used as an outgroup) (Arnason et al. 2002) may well also be an artifact of mutational convergence.

By placing these mutational convergences in the context of response to structural aspects of the replication system, we are able to provide considerable explanatory power to what is otherwise a confusing mixture of outcomes of these processes (i.e., the average nucleotide frequencies reached at dynamic equilibrium). The response curves for different mutation types that occur in the single-stranded state are controlled by at least three biological factors, including the rate of replication (presumably controlled by the functionality of polymerase-γ), the rate of initiation of light-strand synthesis, and the existence and activity of specific repair or protection mechanisms. Differences in protection and repair almost certainly underlie the differences between C⇒T and A⇒G substitutions, and repair seems necessitated by the high rate of C⇒T mutations that would otherwise occur at functional sites. In cases in which the polymerase is apparently highly efficient (e.g., the prosimians), repair may be less critical than in the case of, for example, humans, where the A⇒G response slope is steep, and polymerase is presumably less efficient. We do not, however, find any clear associations of low A⇒G slopes with details of the C⇒T response curve. It would be interesting to know whether rates of polymerization in various species are accurately predicted by the A⇒G slope.

The tools we have presented here are useful for comparative analysis and documenting the extent and range of evolution of mutational responses. The earlier observation of an average linear response of A⇒G substitutions in the vertebrates was based on a gene-by-gene analysis using phylogeny-based ML techniques (Faith and Pollock 2003), but our ability to assess the strength of the response in individual genomes with our likelihood approaches is surprisingly good. Based on our current analysis, incorporation of a gradient evolution model directly into phylogeny-based likelihood analysis, which could include allowing for changes in the strength of response along the phylogeny, will be necessary to obtain accurate estimates and variances for topology and divergence times. Although this entails considerable challenges, since the mutation process is different at every site in the genome, the expected power and accuracy of such a method are much greater than for existing methods. The consistency of the change in response to the gradient of single-strandedness may potentially allow the development of what would be a unique mixture of nonstationary models with differences in the substitution process at every site in a genome.

The existence of these substitution gradients along the genome that vary with substitution type and over time helps make a strong argument for dense taxonomic sampling, that is, “genomic biodiversity” (Pollock et al. 2000), even stronger. Higher-density sampling allows for more accurate prediction of site-specific rates in complex models, and more accurate prediction of site-specific differences can be extremely beneficial to phylogenetic reconstruction using likelihood-based techniques (Pollock and Bruno 2000). If the taxa sampled are closely related, a more accurate description of the mutation process should be obtained (Bielawski and Gold 2002). Furthermore, increased taxonomic sampling would allow more precise delineation of evolution of the gradient. We have developed a phylogeny-based Bayesian analysis to more precisely model the evolution of these gradients (Krishnan et al. 2004a,c), and greater amounts of taxon sampling will allow better direct inference of ancestral gradients, as well as better descriptions of the response curves for other substitutions besides A⇒G, which are clearly nonlinear (Faith and Pollock 2003).

Other potentially important effects of these gradients, and the evolution of these gradients, that should be considered are what kind of effect they have had on amino acid substitutions, whether they can be incorporated into codon-based models, and whether they substantially affect our ability to detect selection and adaptation in mitochondria using synonymous versus nonsynonymous substitution ratios. They may also affect how synonymous and nonsynonymous ratios are used in population genetics to understand how selection affects polymorphism levels.

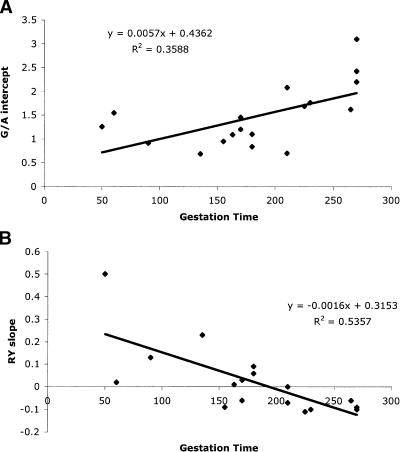
Since mitochondria are so closely tied to metabolism and energy consumption, it is relevant to consider whether the observed evolutionary changes might be tied to concurrent changes in physiology. The G/A response intercept has a significant positive slope when regressed against gestation time (Fig. 8A) (P < 0.01), and the R/Y response slope versus gestation time is significantly negative (Fig. 8B) (P < 0.01). In both of these cases, there are weaker relationships with other physiological factors that are themselves highly correlated with gestation time, including brain weight, longevity, and body mass at birth. The reasons for these relationships, although interesting, remain highly speculative. To accurately dissect causal factors and determine statistical significance will require higher-density sampling within primates and among other vertebrates and more examples of large-scale changes in gradient response curves, and more examples of large changes in brain weight, longevity, body mass at birth, and/or gestation time.

Figure 8.

Figure 8.

Open in a new tab

Linear regression of (A) G/A intercept and (B) R/Y slope versus gestation time. The slope, intercept, and R2 values are shown next to the regression lines.

Methods

Analysis of single genomes

All complete primate mitochondrial genomes available at the time this study was initiated were used (Table 4). As outgroups, we included the complete genomes of the flying lemur and the tree shrew. For all genomes, individual protein-coding genes were extracted and concatenated, and codon positions were determined automatically using C programs or Perl scripts. The relative duration of time spent single-stranded at any position in the mitochondrial genome can be predicted based on the standard model of replication and the relative locations of the heavy-strand replication (OH) and the origin of light-strand replication (OL) (see above and Faith and Pollock 2003). A normalized measure of the estimated time spent single-stranded, DssH (Tanaka and Ozawa 1994), is given in units of the (unknown) time it takes the polymerase to travel once around the genome.

Table 4.

Common names, scientific names, abbreviations used in figures, and accession numbers for sequences used

Common name Species Abb. Accession
Human Homo sapiens Hsa NC_001807a
Chimpanzee Pan troglodytes Ptr NC_001643b
Pygmy chimpanzee Pan paniscus Ppa NC_001644b
Gorilla Gorilla gorilla Ggo NC_001645b
Sumatran orangutan Pongo pygmaeus abelii Pab NC_002083c
Orangutan Pongo p. pygmaeus Ppy NC_001646b
Common gibbon Hylobates lar Hla NC_002082d
Barbary ape Macaca sylvanus Msy NC_002764e
Hamadryas baboon Papio hamadryas Pha NC_001992f
Vervet monkey Cercopithecus aethiops Cae AY863426g
Black & white colobus Colobus guereza Cgu AY863427g
Brown-ridged langur Trachypithecus obscurus Tob AY863425g
White-fronted capuchin Cebus albifrons Cal NC_002763e
Slow loris Nycticebus coucang Nco NC_002765e
Ring-tailed lemur Lemur catta Lca NC_004025h
Western tarsier Tarsius bancamus Tba NC_002811i
Northern tree shrew Tupaia belangeri Tbe NC_002521j
Malayan flying lemur Cynocephalus variegatus Cva NC_004031h
Open in a new tab

Likelihoods of slopes and intercepts in the mutational response to single-strandedness for individual species were calculated as follows: based on a model (M) and set of parameters (θ), the likelihood of a particular genome was calculated by multiplying across sites, i, in a sequence from species m, (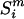Inline graphic), of length N,

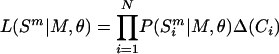graphic file with name M3.gif (1)

where Δ(Ci) is a δ function equal to zero or one depending on whether the site was in the class of interest (e.g., third codon positions of 4× redundant codons). For simplicity and clarity, the M will henceforth be dropped from equations and considered implicit, as will the Δ(Ci). Synonymous third codon positions were used to obtain sites that were least likely to have been affected by selection, although first and second codon positions were also analyzed for comparison. Frequency ratios arising from each pair of reciprocal transitions (G⇔A and T⇔C) were analyzed separately, as was the ratio arising from transversions between nucleotide classes (Y⇔R) for 4× redundant third codon positions.

Since G/A ratios are thought to increase linearly with DssH, it is reasonable, particularly for the G/A ratio, to build a simple linear model of increase in these ratios, and determine what plausible values are for the slope (ς) and intercept (ι). Thus, if 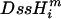Inline graphic is the calculated DssH value at site i for sequence m, and θ is the vector of unknown parameters in the model, then

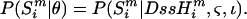graphic file with name M5.gif (2)

For an example using the G/A ratio, 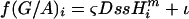Inline graphic, P(G)i = f(G/A)i/[1 + f(G/A)i], and P(A)i =1 – P(G)i. For each individual genome, a Markov chain was run using the Metropolis-Hastings Monte Carlo algorithm to sample the posterior probability space (Metropolis et al. 1953; Hastings 1970),

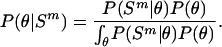graphic file with name M7.gif (3)

The prior probabilities, P(θ), were assumed to be flat, uninformative priors, with ς ranging from –∞ to ∞, and ι ranging from 0 to ∞. Proposals for ς and ι where f(G/A) < 0 for some 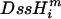Inline graphic were excluded. Parameter proposals in the Markov chain were distributed uniformly (∼U[–δ, +δ]) about the current state, with the magnitude of δ equal to 0.3 for both ς and ι; values of δ were chosen so that between 30% and 80% of the proposals were accepted. The 95% credibility interval was obtained by excluding the 2.5% most extreme values on either side of the mean, and the maximum for the run was taken as an estimate of the ML value. The chain was run for 100,000 generations, where the first 1000 generations were removed as burn-in. The rest of the generations were sampled at every 100-th spot in the chain. All chains were run 10 times with different seed values to detect any differences in ML values or distributions across runs. All likelihood values were stored and reported as natural logarithms.

Analysis of multiple genomes

To determine the similarity of genomes in their evolutionary patterns, Markov chains were also run over multiple genomes simultaneously in hierarchical and mixture model clustering schemes. In the hierarchical clustering scheme, single sets of ML estimators (MLEs) of slope and intercept for a group of genomes were determined jointly. The process began with the testing of all pairs of genomes, and the difference in log likelihoods (or log of the likelihood ratio) (δlnL) between the combined and separate calculations was found. The sequences forming a union with the smallest δlnL were then combined into one set. In subsequent stages, likelihoods and MLEs were calculated for the unions of all new pairs or sets, and again sequences from the union with the smallest δlnL were combined into a single set for the next stage. Thus, the species or groups of species were made to cluster in a hierarchical fashion until only one set existed. Since twice the δlnL for combining sets can be approximated as a χ2 distribution with two degrees of freedom, 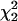Inline graphic (Rice 1995), we used the log likelihood differences as a measure of confidence in the formation of clusters.

In another clustering scheme, a Markov chain was run on third codon positions in the complete primate data set using a series of mixture models (the outgroups were not included in this scheme). In any one implementation of this method, a predetermined number of models (K) were allowed to exist, with the constraint that the models were ordered by strength of intercept to avoid problems of identifiability. The mixture density for a genome can be written as,

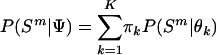graphic file with name M10.gif (4)

where Ψ is the vector containing all the unknown parameters in the mixture model, that is, all π k and θk, and the different models were given even and constant mixing proportions, π k =1/K. The δ value for updating both the ς and ι parameters was 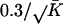Inline graphic, and overall likelihoods were calculated by multiplying the likelihoods for each genome. At any time point (i.e., for any set of parameters, θ) it is possible to calculate the posterior probability that a particular model applies to a particular species

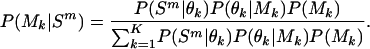graphic file with name M12.gif (5)

Mixture models were run with two to eight mixed models. The log likelihoods for these models are presented, but δlnLs for mixture models are not necessarily distributed as χ2 (McLachlan and Peel 2000), and determining the appropriate number of mixture models is one of the more difficult problems in statistics. The improvement in δlnL going from six to seven models was slight (only 4.12), and with seven models sequences had mixed affiliation among models. Accordingly, we limit results to six mixed models.

Phylogenetic analysis

Phylogenetic trees were obtained using the combined sequences of all 12 proteins coded on the light strand. A neighbor-joining tree was obtained from DNA sequences using the general time-reversible (GTR) model in Paup* (Swofford 2000). ML DNA and amino acids were found using GTR models in MrBayes (Huelsenbeck and Ronquist 2001). The topologies are similar and largely uncontroversial except for the deeper nodes (Schmitz et al. 2002b; Yoder 2003). To obtain comparative likelihood values, we also ran an ML analysis (based on DNA sequences and the GTR model) using the lscore function in Paup*. We also evaluated topologies intermediate between these and an alternative estimate of the “true” phylogeny (Schmitz et al. 2002b; Yoder 2003).

Acknowledgments

We thank Judith Beekman for comments on the manuscript. This work was supported by grants from the National Institutes of Health (GM065612-01 and GM065580-01), and the State of Louisiana Board of Regents [Research Competitiveness Subprogram LEQSF (2001-04)-RD-A-08 and the Millennium Research Program's Biological Computation and Visualization Center] and Governor's Biotechnology Initiative.

[Supplemental material is available online at www.genome.org.]

Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.3128605.

References

  1. Arnason, U., Gullberg, A., and Xu, X.F. 1996. A complete mitochondrial DNA molecule of the white-handed gibbon, Hylobates lar, and comparison among individual mitochondrial genes of all hominoid genera. Hereditas 124: 185–189. [Google Scholar]
  2. Arnason, U., Gullberg, A., and Janke, A. 1998. Molecular timing of primate divergences as estimated by two nonprimate calibration points. J. Mol. Evol. 47: 718–727. [DOI] [PubMed] [Google Scholar]
  3. Arnason, U., Gullberg, A., Burguete, A.S., and Janke, A. 2000. Molecular estimates of primate divergences and new hypotheses for primate dispersal and the origin of modern humans. Hereditas 133: 217–228. [DOI] [PubMed] [Google Scholar]
  4. Arnason, U., Adegoke, J.A., Bodin, K., Born, E.W., Esa, Y.B., Gullberg, A., Nilsson, M., Short, R.V., Xu, X., and Janke, A. 2002. Mammalian mitogenomic relationships and the root of the eutherian tree. Proc. Natl. Acad. Sci. 99: 8151–8156. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Asakawa, S., Kumazawa, Y., Araki, T., Himeno, H., Miura, K., and Watanabe, K. 1991. Strand-specific nucleotide composition bias in echinoderm and vertebrate mitochondrial genomes. J. Mol. Evol. 32: 511–520. [DOI] [PubMed] [Google Scholar]
  6. Bielawski, J.P. and Gold, J.R. 2002. Mutation patterns of mitochondrial H- and L-strand DNA in closely related Cyprinid fishes. Genetics 161: 1589–1597. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bogenhagen, D.F. and Clayton, D.A. 2003a. The mitochondrial DNA replication bubble has not burst. Trends Biochem. Sci. 28: 357–360. [DOI] [PubMed] [Google Scholar]
  8. Bogenhagen, D.F. and Clayton, D.A. 2003b. Concluding remarks: The mitochondrial DNA replication bubble has not burst. Trends Biochem. Sci. 28: 404–405. [DOI] [PubMed] [Google Scholar]
  9. Bowmaker, M., Yang, M.Y., Yasukawa, T., Reyes, A., Jacobs, H.T., Huberman, J.A., and Holt, I.J. 2003. Mammalian mitochondrial DNA replicates bidirectionally from an initiation zone. J. Biol. Chem. 278: 50961–50969. [DOI] [PubMed] [Google Scholar]
  10. Clayton, D.A. 1991. Replication and transcription of vertebrate mitochondrial DNA. Annu. Rev. Cell Biol. 7: 453–478. [DOI] [PubMed] [Google Scholar]
  11. Clayton, D.A. 2000. Transcription and replication of mitochondrial DNA. Hum. Reprod. 15 Suppl 2: 11–17. [DOI] [PubMed] [Google Scholar]
  12. Delorme, M.O. and Henaut, A. 1991. Codon usage is imposed by the gene location in the transcription unit. Curr. Genet. 20: 353–358. [DOI] [PubMed] [Google Scholar]
  13. Disotell, T.R. 2003. Primates: Phylogenetics. Encyclopedia of the human genome. Nature Publishing Group, London.
  14. Faith, J.J. and Pollock, D.D. 2003. Likelihood analysis of asymmetrical mutation bias gradients in vertebrate mitochondrial genomes. Genetics 165: 735–745. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Felsenstein, J. 1978. Cases in which parsimony or compatibility methods will be positively misleading. Syst. Zool. 27: 401–410. [Google Scholar]
  16. Felsenstein, J. 2001. Taking variation of evolutionary rates between sites into account in inferring phylogenies. J. Mol. Evol. 53: 447–455. [DOI] [PubMed] [Google Scholar]
  17. Frederico, L.A., Kunkel, T.A., and Shaw, B.R. 1990. A sensitive genetic assay for the detection of cytosine deamination: Determination of rate constants and the activation energy. Biochemistry 29: 2532–2537. [DOI] [PubMed] [Google Scholar]
  18. Frederico, L.A., Kunkel, T.A., and Shaw, B.R. 1993. Cytosine deamination in mismatched base pairs. Biochemistry 32: 6523–6530. [DOI] [PubMed] [Google Scholar]
  19. Gissi, C., Reyes, A., Pesole, G., and Saccone, C. 2000. Lineage-specific evolutionary rate in mammalian mtDNA. Mol. Biol. Evol. 17: 1022–1031. [DOI] [PubMed] [Google Scholar]
  20. Graybeal, A. 1993. The phylogenetic utility of cytochrome b: Lessons from bufonid frogs. Mol. Phylogenet. Evol. 2: 256–269. [DOI] [PubMed] [Google Scholar]
  21. Hastings, W.K. 1970. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 57: 97–109. [Google Scholar]
  22. Holt, I.J. and Jacobs, H.T. 2003. Response: The mitochondrial DNA replication bubble has not burst. Trends Biochem. Sci. 28: 355–356. [DOI] [PubMed] [Google Scholar]
  23. Holt, I.J., Lorimer, H.E., and Jacobs, H.T. 2000. Coupled leading- and lagging-strand synthesis of mammalian mitochondrial DNA. Cell 100: 515–524. [DOI] [PubMed] [Google Scholar]
  24. Honeycutt, R.L., Nedbal, M.A., Adkins, R.M., and Janecek, L.L. 1995. Mammalian mitochondrial DNA evolution: A comparison of the cytochrome b and cytochrome c oxidase II genes. J. Mol. Evol. 40: 260–272. [DOI] [PubMed] [Google Scholar]
  25. Horai, S., Hayasaka, K., Kondo, R., Tsugane, K., and Takahata, N. 1995. Recent African origin of modern humans revealed by complete sequences of hominoid mitochondrial DNAs. Proc. Natl. Acad. Sci. 92: 532–536. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Huelsenbeck, J.P. and Ronquist, F. 2001. MRBAYES: Bayesian inference of phylogenetic trees. Bioinformatics 17: 754–755. [DOI] [PubMed] [Google Scholar]
  27. Ingman, M., Kaessmann, H., Paabo, S., and Gyllensten, U. 2000. Mitochondrial genome variation and the origin of modern humans. Nature 408: 708–713. [DOI] [PubMed] [Google Scholar]
  28. Jermiin, L.S., Graur, D., Lowe, R.M., and Crozier, R.H. 1994. Analysis of directional mutation pressure and nucleotide content in mitochondrial cytochrome b genes. J. Mol. Evol. 39: 160–173. [DOI] [PubMed] [Google Scholar]
  29. Jermiin, L.S., Graur, D., and Crozier, R.H. 1995. Evidence from analyses of intergenic regions for strand-specific directional mutation pressure in metazoan mitochondrial-DNA. Mol. Biol. Evol. 12: 558–563. [Google Scholar]
  30. Kondo, R., Horai, S., Satta, Y., and Takahata, N. 1993. Evolution of hominoid mitochondrial DNA with special reference to the silent substitution rate over the genome. J. Mol. Evol. 36: 517–531. [DOI] [PubMed] [Google Scholar]
  31. Krasuski, A., Galinski, J., Smolenski, R.T., and Marlewski, M. 1997. Deamination of adenine and adenosine in staphylococci. Med. Dosw. Mikrobiol. 49: 113–122. [PubMed] [Google Scholar]
  32. Krishnan, N.M., Seligmann, H., Stewart, C.B., De Koning, A.P., and Pollock, D.D. 2004a. Ancestral sequence reconstruction in primate mitochondrial DNA: Compositional bias and effect on functional inference. Mol. Biol. Evol. 21: 1871–1883. [DOI] [PubMed] [Google Scholar]
  33. Krishnan, N.M., Seligmann, H., Raina, S.Z., and Pollock, D.D. 2004b. Detecting gradients of asymmetry in site-specific substitutions in mitochondrial genomes. DNA Cell Biol. 23: 707–714. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Krishnan, N.M., Raina, S.Z., and Pollock, D.D. 2004c. Analysis of among-site variation in substitution patterns. Biol. Proced. Online 6: 180–188. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Limaiem, J. and Henaut, A. 1984. Fluctuation of the incidence of the 4 bases along the mitochondrial genome of mammals using correspondence factorial analysis. C R Acad. Sci. III 298: 279–286. [PubMed] [Google Scholar]
  36. Lockhart, P.J., Howe, C.J., Bryant, D.A., Beanland, T.J., and Larkum, A.W. 1992. Substitutional bias confounds inference of cyanelle origins from sequence data. J. Mol. Evol. 34: 153–162. [DOI] [PubMed] [Google Scholar]
  37. McLachlan, G. and Peel, D. 2000. Finite mixture models. Wiley–Interscience, New York.
  38. Metropolis, N., Rosenbluth, A.W., Rosenbluth, M.N., Teller, A.H., and Teller, E. 1953. Equations of state calculations by fast computating machines. J. Chem. Phys. 21: 1087–1092. [Google Scholar]
  39. Meyer, A. 1994. Shortcomings of the cytochrome-B gene as a molecular marker. Trends Ecol. Evol. 9: 278–280. [DOI] [PubMed] [Google Scholar]
  40. Parham, J.C., Fissekis, J., and Brown, G.B. 1966. Purine-N-oxides. 18. Deamination of adenine-N-oxide derivatives. J. Org. Chem. 31: 966–968. [DOI] [PubMed] [Google Scholar]
  41. Perna, N.T. and Kocher, T.D. 1995. Patterns of nucleotide composition at fourfold degenerate sites of animal mitochondrial genomes. J. Mol. Evol. 41: 353–358. [DOI] [PubMed] [Google Scholar]
  42. Philippe, H. and Laurent, J. 1998. How good are deep phylogenetic trees? Curr. Opin. Genet. Dev. 8: 616–623. [DOI] [PubMed] [Google Scholar]
  43. Pollock, D.D. and Bruno, W.J. 2000. Assessing an unknown evolutionary process: Effect of increasing site-specific knowledge through taxon addition. Mol. Biol. Evol. 17: 1854–1858. [DOI] [PubMed] [Google Scholar]
  44. Pollock, D.D., Eisen, J.A., Doggett, N.A., and Cummings, M.P. 2000. A case for evolutionary genomics and the comprehensive examination of sequence biodiversity. Mol. Biol. Evol. 17: 1776–1788. [DOI] [PubMed] [Google Scholar]
  45. Raaum, R.L., Sterner, K.N., Noviello, C.M., Stewart, C.-B., and Disotell, T.R. 2005. Catarrhine primate divergence dates estimated from complete mitochondrial genomes: Concordance with fossil and nuclear DNA evidence. J. Hum. Evol. (in press). [DOI] [PubMed]
  46. Ray, D.A., Xing, J., Hedges, D.J., Hall, M.A., Laborde, M.E., Anders, B.A., White, B.R., Stoilova, N., Fowlkes, J.D., Landry, K.E., et al. 2004. Alu insertion loci and platyrrhine primate phylogeny. Mol. Biol. Evol. (in press). [DOI] [PubMed]
  47. Reyes, A., Gissi, C., Pesole, G., and Saccone, C. 1998. Asymmetrical directional mutation pressure in the mitochondrial genome of mammals. Mol. Biol. Evol. 15: 957–966. [DOI] [PubMed] [Google Scholar]
  48. Reyes, A., Pesole, G., and Saccone, C. 2000. Long-branch attraction phenomenon and the impact of among-site rate variation on rodent phylogeny. Gene 259: 177–187. [DOI] [PubMed] [Google Scholar]
  49. Rice, J.A. 1995. Mathematical statistics and data analysis. Duxbury Press, Belmont, CA.
  50. Salem, A.H., Ray, D.A., Xing, J., Callinan, P.A., Myers, J.S., Hedges, D.J., Garber, R.K., Witherspoon, D.J., Jorde, L.B., and Batzer, M.A. 2003. Alu elements and hominid phylogenetics. Proc. Natl. Acad. Sci. 100: 12787–12791. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Schmitz, J., Ohme, M., and Zischler, H. 2000. The complete mitochondrial genome of Tupaia belangeri and the phylogenetic affiliation of Scandentia to other eutherian orders. Mol. Biol. Evol. 17: 1334–1343. [DOI] [PubMed] [Google Scholar]
  52. Schmitz, J., Ohme, M., and Zischler, H. 2001. SINE insertions in cladistic analyses and the phylogenetic affiliations of Tarsius bancanus to other primates. Genetics 157: 777–784. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Schmitz, J., Ohme, M., and Zischler, H. 2002a. The complete mitochondrial sequence of Tarsius bancanus: Evidence for an extensive nucleotide compositional plasticity of primate mitochondrial DNA. Mol. Biol. Evol. 19: 544–553. [DOI] [PubMed] [Google Scholar]
  54. Schmitz, J., Ohme, M., Suryobroto, B., and Zischler, H. 2002b. The colugo (Cynocephalus variegatus, Dermoptera): The primates' gliding sister? Mol. Biol. Evol. 19: 2308–2312. [DOI] [PubMed] [Google Scholar]
  55. Swofford, D.L. 2000. Phylogenetic analysis using parsimony (*and other methods). Sinauer Associates, Sunderland, MA.
  56. Tanaka, M. and Ozawa, T. 1994. Strand asymmetry in human mitochondrial DNA mutations. Genomics 22: 327–335. [DOI] [PubMed] [Google Scholar]
  57. Tarr, H.L. and Comer, A.G. 1964. Deamination of adenine and related compounds and formation of deoxyadenosine and deoxyinosine by lingcod muscle enzymes. Can. J. Biochem. Physiol. 42: 1527–1533. [DOI] [PubMed] [Google Scholar]
  58. Thomas, W.K. and Wilson, A.C. 1991. Mode and tempo of molecular evolution in the nematode Caenorhabditis: Cytochrome oxidase II and calmodulin sequences. Genetics 128: 269–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Van Den Bussche, R.A., Baker, R.J., Huelsenbeck, J.P., and Hillis, D.M. 1998. Base compositional bias and phylogenetic analyses: a test of the “flying DNA” hypothesis. Mol. Phylogenet. Evol. 10: 408–416. [DOI] [PubMed] [Google Scholar]
  60. Wiens, J.J. and Hollingsworth, B.D. 2000. War of the Iguanas: Conflicting molecular and morphological phylogenies and long-branch attraction in iguanid lizards. Syst. Biol. 49: 143–159. [DOI] [PubMed] [Google Scholar]
  61. Xu, X. and Arnason, U. 1996. The mitochondrial DNA molecule of Sumatran orangutan and a molecular proposal for two (Bornean and Sumatran) species of orangutan. J. Mol. Evol. 43: 431–437. [DOI] [PubMed] [Google Scholar]
  62. Yang, M.Y., Bowmaker, M., Reyes, A., Vergani, L., Angeli, P., Gringeri, E., Jacobs, H.T., and Holt, I.J. 2002. Biased incorporation of ribonucleotides on the mitochondrial L-strand accounts for apparent strand-asymmetric DNA replication. Cell 111: 495–505. [DOI] [PubMed] [Google Scholar]
  63. Yoder, A.D. 2003. The phylogenetic position of genus Tarsius: Whose side are you on? In Tarsiers: Past, present, and future (eds. P.C. Wright et al.), pp. 161–175. Rutgers University Press, Piscataway, NJ.
  64. Yoder, A.D., Vilgalys, R., and Ruvolo, M. 1996. Molecular evolutionary dynamics of cytochrome b in strepsirrhine primates: The phylogenetic significance of third-position transversions. Mol. Biol. Evol. 13: 1339–1350. [DOI] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES