ABSTRACT
In clinical studies of chronic diseases, the effectiveness of an intervention is often assessed using “high cost” outcomes that require long-term patient follow-up and/or are invasive to obtain. While much progress has been made in the development of statistical methods to identify surrogate markers, that is, measurements that could replace such costly outcomes, they are generally not applicable to studies with a small sample size. These methods either rely on nonparametric smoothing which requires a relatively large sample size or rely on strict model assumptions that are unlikely to hold in practice and empirically difficult to verify with a small sample size. In this paper, we develop a novel rank-based nonparametric approach to evaluate a surrogate marker in a small sample size setting. The method developed in this paper is motivated by a small study of children with nonalcoholic fatty liver disease (NAFLD), a diagnosis for a range of liver conditions in individuals without significant history of alcohol intake. Specifically, we examine whether change in alanine aminotransferase (ALT; measured in blood) is a surrogate marker for change in NAFLD activity score (obtained by biopsy) in a trial, which compared Vitamin E (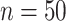 ) versus placebo (
) versus placebo (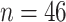 ) among children with NAFLD.
) among children with NAFLD.
Keywords: randomized clinical trial, rank test, small sample size, surrogate marker evaluation
1. INTRODUCTION
The health and economic burden from chronic diseases highlight the importance of identifying effective strategies for the prevention, treatment, and management of disease. Studies aimed at evaluating the effectiveness of such strategies often focus on outcomes that either require long-term follow-up of patients for example, time to dementia onset, or are invasive for example, derived from a biopsy (Lindström et al., 2006; Li et al., 2008). The identification and use of surrogate markers in such studies have the potential to improve our ability to make decisions about the effect of a treatment or intervention. When the surrogate marker can be obtained earlier than the occurrence of the clinical event of interest, such as dementia onset, use of the surrogate to test for a treatment effect would allow researchers to make conclusions regarding the treatment effect with less required follow-up time (Wittes et al., 1989; Parast et al., 2019; Wang et al., 2021). When the surrogate marker is a measurement that is less invasive or can be obtained with less cost or less burden, use of the surrogate has the potential to increase study compliance and participation, reduce patient burden, and/or decrease trial costs.
Over the past 4 decades, an incredible amount of progress has been made in the development of statistical methods to identify surrogate markers. In Prentice’s seminal paper on surrogate markers, he proposed a definition for a valid surrogate marker, which required that a test for a treatment effect on the surrogate marker also be a valid test for treatment effect on the primary outcome of interest (Prentice, 1989). This definition led to statistical methods that were developed to identify useful surrogate markers as those that “capture” a large proportion of the treatment effect on the primary outcome (Freedman et al., 1992; Wang and Taylor, 2002; Parast et al., 2016). While this proportion is commonly used in practice given its ease of interpretation, several other rigorous quantities have also been developed to assess the value of a surrogate marker, including the relative effect (RE) and adjusted association in the meta-analytic framework, and average causal necessity, average causal sufficiency, and the causal effect predictiveness surface in a principal stratification framework; see Elliott (2023) for a recent review.
Though many robust and rigorous methods are available to evaluate a surrogate marker, available methods are generally not able to handle small sample size studies. For example, while previously proposed nonparametric methods are ideal in that they require no restrictive model specification, the tradeoff is that a relatively large sample size is needed to apply these methods because they rely on, for example, kernel smoothing, which is known to perform poorly when the sample size is small due to slower convergence of estimates (Rosenblatt, 1969; Fan and Gijbels, 1992; Dabrowska, 1987). The alternative methods that do not use kernel smoothing require specification of various models that are unlikely to hold in practice and the adequacy of these models cannot be rigorously assessed when the sample size is small (Parast et al., 2016; Conlon et al., 2014). To our knowledge, there is currently no robust method to evaluate a surrogate marker, when the sample size is small. Furthermore, it is often the case that it is exactly these small studies where one is trying to identify a surrogate, for example, in small clinical trials of rare diseases, trials where a large sample is infeasible or unethical, and/or trials in a pediatric population with chronic disease (Dunoyer, 2011; Miyamoto and Kakkis, 2011).
Motivated by this open problem, we develop a novel nonparametric rank-based approach to evaluate a surrogate marker in a small sample setting. Specifically, we were motivated by a small study of children with nonalcoholic fatty liver disease (NAFLD), which is the most common cause of chronic liver disease in children in the US and ultimately results in advanced fibrosis, cirrhosis, and hepatocellular carcinoma (Nobili et al., 2019). This study, the Treatment of Nonalcoholic Fatty Liver Disease in Children (TONIC) trial, randomized children with NAFLD to Vitamin E, metformin, or placebo, and followed patients for 96 weeks. While the primary outcome in the study was sustained reduction in alanine aminotransferase (ALT; measured in blood), the study team states in Lavine et al. (2011) that in fact, “improvement in histology is a more desirable primary outcome measure than improvement in ALT” but they note that due to the lack of prior histology-based NAFLD trials in children, they could not calculate needed sample size for the trial using histology as the primary outcome. Therefore, they used ALT as a surrogate for histology, though they also measured histology, quantified via the NAFLD activity score, as a secondary outcome. Trial results showed no significant treatment effect of Vitamin E ( ) compared to placebo (
) compared to placebo (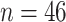 ) on sustained reduction in ALT, but did show a significant treatment effect on the change in NAFLD activity score (Lavine et al., 2011). This trial highlighted the need to rigorously question whether perhaps ALT is in fact not a sufficient surrogate marker for the NAFLD activity score to better inform future trial design.
) on sustained reduction in ALT, but did show a significant treatment effect on the change in NAFLD activity score (Lavine et al., 2011). This trial highlighted the need to rigorously question whether perhaps ALT is in fact not a sufficient surrogate marker for the NAFLD activity score to better inform future trial design.
The remainder of the article is organized as follows: Section 2 describes our proposed testing approach, including estimation and inference as well as implications for study design. Section 3 presents our simulation study, investigating the finite sample properties of our methods and compares to existing methods. Section 4 investigates ALT as a surrogate in the pediatric trial, and Section 5 offers concluding remarks.
2. METHODS
2.1. Notation and testing procedure
Let 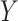 denote the primary outcome,
denote the primary outcome, 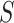 denote the surrogate marker, and
denote the surrogate marker, and 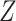 denote the treatment indicator, where treatment is randomized and
denote the treatment indicator, where treatment is randomized and 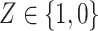 (eg, treatment versus control). We use potential outcomes notation, where each person has a set of potential outcomes
(eg, treatment versus control). We use potential outcomes notation, where each person has a set of potential outcomes 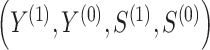 where
where  and
and 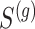 are the outcome and surrogate value when
are the outcome and surrogate value when  , respectively. The observed data consists of
, respectively. The observed data consists of 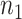 independently identically distributed (i.i.d) copies of
independently identically distributed (i.i.d) copies of 
 from the
from the 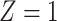 group, and
group, and  i.i.d copies of
i.i.d copies of 
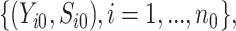 from the
from the  group. Our general setting is illustrated in Figure 1, where there exists a prior study, Study A, where the surrogate marker and primary outcome have both been measured. Our aim is to use Study A to evaluate
group. Our general setting is illustrated in Figure 1, where there exists a prior study, Study A, where the surrogate marker and primary outcome have both been measured. Our aim is to use Study A to evaluate 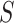 as a surrogate marker for
as a surrogate marker for 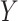 , the primary outcome. The ultimate goal is to be able to then conduct a future Study B where we only measure the surrogate marker, and test for a treatment effect using the surrogate marker. In this paper, we focus on a setting where the sample size is small such that the nonparametric approach of Parast et al. (2016), which utilizes kernel smoothing, to evaluate the surrogacy of
, the primary outcome. The ultimate goal is to be able to then conduct a future Study B where we only measure the surrogate marker, and test for a treatment effect using the surrogate marker. In this paper, we focus on a setting where the sample size is small such that the nonparametric approach of Parast et al. (2016), which utilizes kernel smoothing, to evaluate the surrogacy of 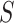 in Study A is not feasible, for example,
in Study A is not feasible, for example, 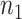 and
and 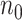 are
are  50. To evaluate
50. To evaluate 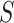 as a surrogate for
as a surrogate for 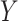 in Study A, we consider a test for a treatment effect based on
in Study A, we consider a test for a treatment effect based on 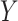 versus a test for a treatment effect based on
versus a test for a treatment effect based on 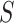 . Let
. Let  and
and 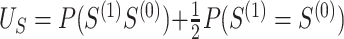 , and
, and
FIGURE 1.
General setting: Study A and Study B.
 |
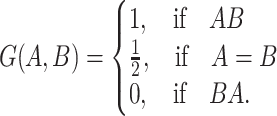 |
Note that 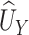 is the Mann-Whitney U-statistic examining the difference in
is the Mann-Whitney U-statistic examining the difference in 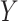 between the 2 treatment groups and similarly for
between the 2 treatment groups and similarly for  , and
, and  and
and 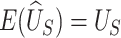 (Mann and Whitney, 1947). Consider the null hypothesis,
(Mann and Whitney, 1947). Consider the null hypothesis,
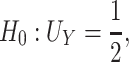 |
that is, there is no treatment effect on 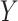 . To test
. To test 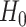 using the surrogate, we focus instead on testing
using the surrogate, we focus instead on testing
 |
that is, there is no treatment effect on 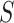 . Note that
. Note that 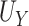 is equivalent to the area under the receiver operating characteristic curve considering
is equivalent to the area under the receiver operating characteristic curve considering  as a “predictor” of the treatment group assignment
as a “predictor” of the treatment group assignment  and similarly for
and similarly for 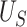 (Hanley and McNeil, 1982). In the following, we discuss our approach throughout in the context of U-statistics. We show in Web Appendix A that under these conditions.
(Hanley and McNeil, 1982). In the following, we discuss our approach throughout in the context of U-statistics. We show in Web Appendix A that under these conditions.
 is monotone increasing in
is monotone increasing in 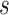 for any
for any  for
for 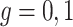
 for all
for all 
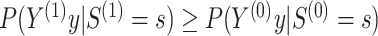 for all
for all 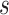 ,
,
the following holds:
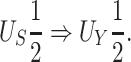 |
(1) |
Conditions (C1)-(C3) and result (1) are important as they ensure protection from a surrogate paradox situation (VanderWeele, 2013), where the treatment has a positive effect on the surrogate, the surrogate and the primary outcome are positively associated, but the treatment has a negative effect on the primary outcome. We discuss these conditions further in Web Appendix A. Note that we do not claim that 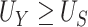 as it is possible that
as it is possible that 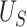 is substantially higher than
is substantially higher than 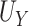 .
.
As noted above, the ultimate goal in our setting is to potentially use  as a replacement of
as a replacement of 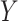 in the future Study B. That is, we want to make inference about the treatment effect on
in the future Study B. That is, we want to make inference about the treatment effect on 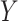 , quantified via
, quantified via  , using only
, using only  . Motivated by this, we propose to measure the strength of the surrogate via the simple difference between
. Motivated by this, we propose to measure the strength of the surrogate via the simple difference between 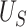 and
and 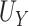 :
:
 |
and investigate whether 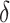 is bounded by a specified upper bound,
is bounded by a specified upper bound,  . To make a decision regarding utility of the surrogate marker, we focus on the following noninferiority test:
. To make a decision regarding utility of the surrogate marker, we focus on the following noninferiority test:
 |
(2) |
where 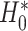 reflects a poor surrogate (inferior) and
reflects a poor surrogate (inferior) and 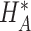 reflects a valid surrogate (noninferior) (Patterson and Jones, 2017). That is, we hope that
reflects a valid surrogate (noninferior) (Patterson and Jones, 2017). That is, we hope that 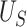 is “close enough” to
is “close enough” to 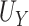 (or larger than
(or larger than 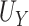 ) such that we can be reasonably confident that, in a future study, (1) if we reject
) such that we can be reasonably confident that, in a future study, (1) if we reject  based on
based on 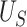 , this would reflect evidence of a treatment effect on
, this would reflect evidence of a treatment effect on  , or (2) if we do not reject
, or (2) if we do not reject  based on
based on 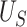 , this would imply that there is no or little treatment effect on
, this would imply that there is no or little treatment effect on 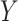 . In Section 2.2, we discuss selection of
. In Section 2.2, we discuss selection of 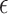 . Now, we focus on conducting the noninferiority test with a given
. Now, we focus on conducting the noninferiority test with a given 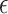 .
.
Using data from Study A, 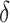 and
and 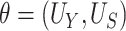 can be estimated by
can be estimated by 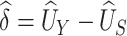 and
and 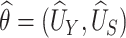 , respectively. Based on the theory for U-statistics, the null variance of
, respectively. Based on the theory for U-statistics, the null variance of  can be obtained as
can be obtained as  , and similarly for
, and similarly for  (Mann and Whitney, 1947). To obtain a confidence interval for
(Mann and Whitney, 1947). To obtain a confidence interval for 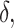 we use the variance derivations of DeLong et al. (1988) which can be used for any linear combination of U-statistics. Specifically, DeLong et al. (1988) shows that for any contrast
we use the variance derivations of DeLong et al. (1988) which can be used for any linear combination of U-statistics. Specifically, DeLong et al. (1988) shows that for any contrast 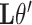 where
where 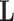 is a vector of coefficients,
is a vector of coefficients,
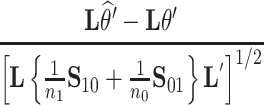 |
(3) |
has a standard normal distribution, where 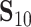 and
and 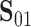 are provided in Web Appendix A. Thus, we obtain a
are provided in Web Appendix A. Thus, we obtain a 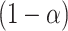 100% one sided confidence interval for
100% one sided confidence interval for 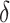 as
as  where
where 
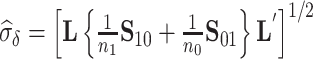 , the estimated SE of
, the estimated SE of 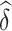 . We then have a formal testing procedure for testing (2) as follows:
. We then have a formal testing procedure for testing (2) as follows:
Calculate
 based on the observed data.
based on the observed data.Obtain a
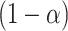 100% one-sided confidence interval as described above.
100% one-sided confidence interval as described above.Conclude that
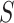 is a valid surrogate if the upper bound of the confidence interval is
is a valid surrogate if the upper bound of the confidence interval is  .
.
Note that we avoid referring to rejecting or failing to reject 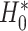 ; instead, we refer to the upper bound of the confidence interval and the implied conclusion regarding surrogacy. In addition, when the upper bound of the confidence interval is
; instead, we refer to the upper bound of the confidence interval and the implied conclusion regarding surrogacy. In addition, when the upper bound of the confidence interval is 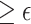 , it is not necessarily the case that one should state
, it is not necessarily the case that one should state  is not a valid surrogate marker; rather, we do not have sufficient evidence using this nonparametric approach that
is not a valid surrogate marker; rather, we do not have sufficient evidence using this nonparametric approach that 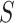 is a valid surrogate marker. In Section 3, we examine the finite sample performance of this proposed testing procedure, specifically its power and type 1 error, and compare to existing approaches. In Section 4, we use this approach to analyze the pediatric trial data.
is a valid surrogate marker. In Section 3, we examine the finite sample performance of this proposed testing procedure, specifically its power and type 1 error, and compare to existing approaches. In Section 4, we use this approach to analyze the pediatric trial data.
Remark. Our approach is similar in spirit to the RE proposed by Buyse and Molenberghs (1998), where RE is the ratio of the effect of the treatment on 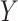 relative to the effect of treatment on
relative to the effect of treatment on 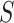 , estimated parametrically in the case of normally distributed
, estimated parametrically in the case of normally distributed 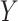 and
and  . When this ratio is equal to 1,
. When this ratio is equal to 1, 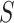 is said to be a perfect surrogate. Intuitively, this is similar to our motivation for
is said to be a perfect surrogate. Intuitively, this is similar to our motivation for 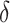 such that we expect
such that we expect 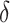 to be 0 when
to be 0 when  is a perfect surrogate for
is a perfect surrogate for  . Both are motivated by the ultimate goal of surrogate marker use in future studies which is to be able to make inference about the effect of treatment on
. Both are motivated by the ultimate goal of surrogate marker use in future studies which is to be able to make inference about the effect of treatment on 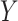 based on the treatment effect on
based on the treatment effect on 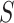 . However, both are also subject to limitations described in Molenberghs et al. (2002), namely that when these quantities are calculated in a single trial, strong assumptions are needed to conclude that any indication of surrogacy is relevant to future studies; we discuss this further in Section 5.
. However, both are also subject to limitations described in Molenberghs et al. (2002), namely that when these quantities are calculated in a single trial, strong assumptions are needed to conclude that any indication of surrogacy is relevant to future studies; we discuss this further in Section 5.
2.2. Selection of 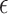
Choice of 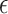 will likely depend on a number of factors including cost of primary outcome measurement, cost of surrogate marker measurement, cost of individual recruitment, potential follow-up time reduction if the surrogate is measured before the primary outcome, and information that might be available from previous studies. Certainly, one could consider a prespecified
will likely depend on a number of factors including cost of primary outcome measurement, cost of surrogate marker measurement, cost of individual recruitment, potential follow-up time reduction if the surrogate is measured before the primary outcome, and information that might be available from previous studies. Certainly, one could consider a prespecified 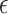 value such as 0.10; admittedly, there is no obvious single choice for
value such as 0.10; admittedly, there is no obvious single choice for 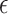 . Here, we propose an approach to select
. Here, we propose an approach to select  that may be useful if one is willing to select a data-driven and sample size-dependent
that may be useful if one is willing to select a data-driven and sample size-dependent 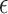 . We argue that it is reasonable to select
. We argue that it is reasonable to select 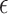 according to the ability to detect the treatment effect on the primary outcome via the surrogate marker (observed or hypothesized). Specifically, we want an approach that ensures the power of a test based on
according to the ability to detect the treatment effect on the primary outcome via the surrogate marker (observed or hypothesized). Specifically, we want an approach that ensures the power of a test based on 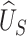 , since such a test is what would potentially be used to test for a treatment effect in a future study. Let’s say we want
, since such a test is what would potentially be used to test for a treatment effect in a future study. Let’s say we want 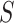 to be such that we would have
to be such that we would have 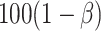 % power to detect a treatment effect on
% power to detect a treatment effect on 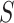 . Thus, we are only willing to deem a surrogate as adequate if it provides this level of power. Motivated by this, let’s first determine the value
. Thus, we are only willing to deem a surrogate as adequate if it provides this level of power. Motivated by this, let’s first determine the value  such that
such that
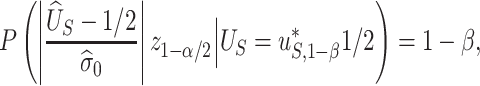 |
where 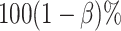 is the desired powered for a test for a treatment effect on
is the desired powered for a test for a treatment effect on 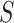 , if
, if 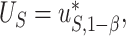 and
and  denotes the null variance of
denotes the null variance of  and
and  that is,
that is, 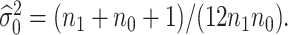 The power takes this form because one would reject the null hypothesis
The power takes this form because one would reject the null hypothesis 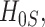 if
if  . It can be shown that:
. It can be shown that: 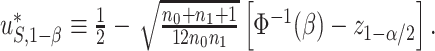 Therefore,
Therefore,  is the minimum value of
is the minimum value of 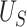 such that we would have
such that we would have  % power to detect a treatment effect on
% power to detect a treatment effect on 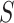 . Now, we define
. Now, we define  where
where 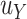 is the hypothesized treatment effect on the primary outcome, which we may be able to approximate by its empirical counterpart,
is the hypothesized treatment effect on the primary outcome, which we may be able to approximate by its empirical counterpart, 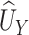 , in preliminary data. That is, we are willing to take
, in preliminary data. That is, we are willing to take  as a substitute for
as a substitute for 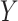 if
if  is at most
is at most 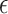 -distance away from
-distance away from 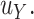 In summary,
In summary,  would depend on the hypothesized treatment effect on
would depend on the hypothesized treatment effect on  , and the desired power of the test based on
, and the desired power of the test based on 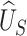 . The latter, in turn, depends on the sample size and significance level of the test.
. The latter, in turn, depends on the sample size and significance level of the test.
We illustrate the selection of  in Figure 2. The black line in this figure shows the recommended
in Figure 2. The black line in this figure shows the recommended  to use based on the proposed calculations at various sample sizes, assuming the desired power of the test based on
to use based on the proposed calculations at various sample sizes, assuming the desired power of the test based on 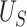 is.70 and
is.70 and 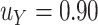 . For example, under these assumptions, if the total sample size is 40, then the recommended
. For example, under these assumptions, if the total sample size is 40, then the recommended  to use is 0.17. The gray line shows parallel calculations except assuming
to use is 0.17. The gray line shows parallel calculations except assuming 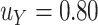 ; here, if the total sample size is 40, then the recommended
; here, if the total sample size is 40, then the recommended  value is 0.07. In Web Appendix B, we provide additional figures to illustrate selection of
value is 0.07. In Web Appendix B, we provide additional figures to illustrate selection of 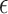 . In practice, such figures can help one understand what value of
. In practice, such figures can help one understand what value of  would be reasonable given their study specifics. While we focus on evaluating the surrogate in our current study, Study A, the fact that
would be reasonable given their study specifics. While we focus on evaluating the surrogate in our current study, Study A, the fact that  is defined as a function of the sample size means that one could calculate
is defined as a function of the sample size means that one could calculate 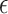 based on the intended sample size and hypothesized
based on the intended sample size and hypothesized 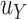 in the future study.
in the future study.
FIGURE 2.
Illustration of  selection as a function of the total sample size: the black line shows the recommended
selection as a function of the total sample size: the black line shows the recommended 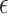 based on the proposed calculations at various sample sizes, assuming the desired power of
based on the proposed calculations at various sample sizes, assuming the desired power of  is 0.70 and assuming
is 0.70 and assuming 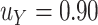 ; the gray line shows the recommended
; the gray line shows the recommended  based on the proposed calculations at various sample sizes, assuming the desired power for
based on the proposed calculations at various sample sizes, assuming the desired power for 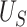 is 0.70 and assuming
is 0.70 and assuming 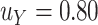 (
(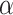 -level = 0.05).
-level = 0.05).
2.3. Power to identify a surrogate marker
In this section, we develop an approach to examine the power to identify a valid surrogate marker given a specified design. Specifically, we consider the case where the planned sample size for Study A is fixed (eg, due to budget) and known to be small (eg, 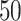 in each group). We aim to estimate the power of Study A in determining whether
in each group). We aim to estimate the power of Study A in determining whether 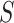 is a valid surrogate marker for
is a valid surrogate marker for 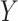 (ie, the upper bound of the confidence interval,
(ie, the upper bound of the confidence interval, 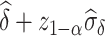 , is less than
, is less than 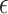 ) under some fixed alternative where
) under some fixed alternative where 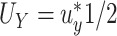 and
and 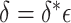 . At a fixed sample size
. At a fixed sample size  , where we assume without loss of generality that
, where we assume without loss of generality that 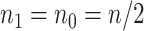 , the power at a type 1 error level
, the power at a type 1 error level  , defined as
, defined as 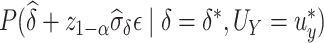 , can be expressed as
, can be expressed as
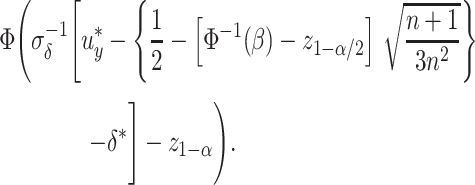 |
(4) |
However, this power depends on  the SD of
the SD of 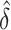 , which depends on the unknown correlation between
, which depends on the unknown correlation between 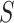 and
and  . If preliminary information about the joint distribution
. If preliminary information about the joint distribution 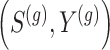 is available, then one could estimate
is available, then one could estimate  accordingly. When no such information is available, we show in Web Appendix C that one may approximate
accordingly. When no such information is available, we show in Web Appendix C that one may approximate 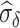 by
by  when
when 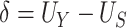 is not substantially far from zero, where
is not substantially far from zero, where  is the assumed Spearman’s rank correlation coefficient between
is the assumed Spearman’s rank correlation coefficient between  and
and 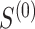 . Based on this approximation, we may estimate (4) by
. Based on this approximation, we may estimate (4) by
 |
(5) |
We can use (5) to examine the expected power at a fixed 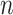 with various hypothesized values of
with various hypothesized values of 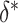 and
and  , with a specified value for either
, with a specified value for either 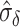 or
or 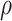 . For example, Figure 3 shows the expected power as a function of
. For example, Figure 3 shows the expected power as a function of 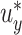 with
with  for various fixed alternatives
for various fixed alternatives  with
with  . In Section 3, we examine the empirical performance of this estimated power.
. In Section 3, we examine the empirical performance of this estimated power.
FIGURE 3.
Estimated power to identify a surrogate marker for various fixed alternatives 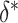 , as a function of
, as a function of 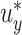 with
with  and
and 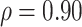 (
(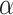 -level = 0.05).
-level = 0.05).
3. SIMULATION STUDY
3.1. Simulation goals and setup
The goals of this simulation study were to (1) examine the finite sample performance of our testing procedure with respect to power and Type 1 error across a variety of settings; (2) compare our approach to existing approaches (details provided below), which admittedly were not developed for the small sample size setting; (3) compare empirical power versus estimated power calculated as proposed in Section 2.3. Details regarding data generation are included in Web Appendix D. Briefly, Setting 1 was generated such that  was a useless surrogate and thus, allowed us to examine Type 1 error. In this setting,
was a useless surrogate and thus, allowed us to examine Type 1 error. In this setting, 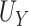 = 0.793,
= 0.793, 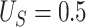 and
and 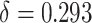 ; the true proportion of treatment effect on the primary outcome explained by the treatment effect on the surrogate (PTE), as defined in Parast et al. (2016), was 0. In Setting 2, we purposefully made
; the true proportion of treatment effect on the primary outcome explained by the treatment effect on the surrogate (PTE), as defined in Parast et al. (2016), was 0. In Setting 2, we purposefully made  an almost perfect surrogate to examine testing in such a setting. Here,
an almost perfect surrogate to examine testing in such a setting. Here, 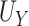 = 0.926,
= 0.926,  ,
,  , and the true PTE was 0.97. In Setting 3, we purposefully generated
, and the true PTE was 0.97. In Setting 3, we purposefully generated  such that it was not useless nor perfect, but rather, in between. Here,
such that it was not useless nor perfect, but rather, in between. Here, 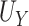 = 0.906,
= 0.906, 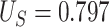 ,
, 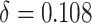 , and the true PTE was 0.57. In Settings 1-3, we simulated from nicely behaved normal distributions. In Setting 4, we purposefully generated data that were more complex to purposefully demonstrate the reasonable performance of our proposed approach and the poor performance of the existing model-based approaches. Here,
, and the true PTE was 0.57. In Settings 1-3, we simulated from nicely behaved normal distributions. In Setting 4, we purposefully generated data that were more complex to purposefully demonstrate the reasonable performance of our proposed approach and the poor performance of the existing model-based approaches. Here, 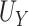 = 0.938,
= 0.938,  ,
,  , and the true PTE was 0.68. All simulations were summarized over 1000 replications with
, and the true PTE was 0.68. All simulations were summarized over 1000 replications with  and
and 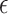 selection was based on a desired power of 0.80.
selection was based on a desired power of 0.80.
3.2. Simulation results
In each setting, we examined estimation of 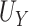 ,
,  , and
, and 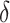 , where
, where 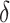 was our primary focus, in terms of bias, and SE estimation (empirical versus average of the estimated SE). In addition, we examined the empirical power (Type 1 error for Setting 1) as the proportion of simulations where the upper bound of the confidence interval for
was our primary focus, in terms of bias, and SE estimation (empirical versus average of the estimated SE). In addition, we examined the empirical power (Type 1 error for Setting 1) as the proportion of simulations where the upper bound of the confidence interval for 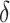 was less than
was less than 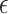 . Table 1 shows the simulation results for our proposed approach across all settings. These results show reasonably good performance of our estimation procedure for
. Table 1 shows the simulation results for our proposed approach across all settings. These results show reasonably good performance of our estimation procedure for  with minimal bias, and average SE (ASE) estimates close to the empirical SE (ESE). Estimation of
with minimal bias, and average SE (ASE) estimates close to the empirical SE (ESE). Estimation of 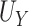 and
and  show minimal bias and similarly good SE estimation. The constructed confidence intervals show slight over-coverage for the true
show minimal bias and similarly good SE estimation. The constructed confidence intervals show slight over-coverage for the true 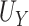 and
and 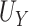 in all settings, and under-coverage for
in all settings, and under-coverage for 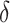 in Settings 3 and 4. This information regarding coverage for
in Settings 3 and 4. This information regarding coverage for 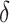 may be particularly useful if one is considering an alternative choice for
may be particularly useful if one is considering an alternative choice for 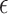 ; we discuss this further in Section 5. Testing results show that the test is conservative, which was expected given this is a nonparametric test for a small sample size setting. In Setting, 1 where the surrogate was useless, the upper bound of the confidence interval for
; we discuss this further in Section 5. Testing results show that the test is conservative, which was expected given this is a nonparametric test for a small sample size setting. In Setting, 1 where the surrogate was useless, the upper bound of the confidence interval for  was greater than
was greater than  for all simulation iterations that is, Type 1 error of 0. In Setting 2, where the surrogate was almost perfect, the power was 1 that is, the upper bound of the confidence interval for
for all simulation iterations that is, Type 1 error of 0. In Setting 2, where the surrogate was almost perfect, the power was 1 that is, the upper bound of the confidence interval for 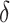 was less than
was less than  for all simulation iterations. For Settings 3 and 4, where the surrogate was neither perfect nor useless, power was 0.525 and 0.688, respectively.
for all simulation iterations. For Settings 3 and 4, where the surrogate was neither perfect nor useless, power was 0.525 and 0.688, respectively.
TABLE 1.
Simulation results for all settings using the proposed testing procedure for estimation of 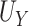 ,
, 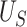 , and
, and 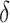 in terms of bias, ESE, ASE, and coverage of the 95% confidence intervals, and the empirical Type 1 error/Power testing
in terms of bias, ESE, ASE, and coverage of the 95% confidence intervals, and the empirical Type 1 error/Power testing 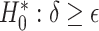 , with
, with 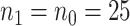 .
.
| Setting 1 (null) | |||
|---|---|---|---|
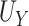
|
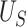
|
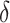
|
|
| Truth | 0.793 | 0.500 | 0.293 |
| Estimate | 0.791 | 0.503 | 0.289 |
| Bias | 0.002 | -0.003 | 0.004 |
| ESE | 0.063 | 0.084 | 0.101 |
| ASE | 0.064 | 0.083 | 0.105 |
| Coverage | 0.978 | 0.940 | 0.953 |
Testing  , Type 1 error , Type 1 error
| |||
| Setting 2 | |||
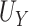
|

|
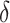
|
|
| Truth | 0.926 | 0.922 | 0.004 |
| Estimate | 0.924 | 0.920 | 0.003 |
| Bias | 0.002 | 0.002 | 0.000 |
| ESE | 0.036 | 0.037 | 0.010 |
| ASE | 0.036 | 0.037 | 0.011 |
| Coverage | 0.989 | 0.988 | 0.954 |
Testing 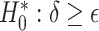 , Power , Power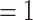
| |||
| Setting 3 | |||
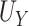
|
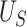
|
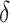
|
|
| Truth | 0.906 | 0.797 | 0.108 |
| Estimate | 0.904 | 0.794 | 0.110 |
| Bias | 0.002 | 0.003 | -0.002 |
| ESE | 0.042 | 0.063 | 0.035 |
| ASE | 0.041 | 0.063 | 0.037 |
| Coverage | 0.985 | 0.972 | 0.931 |
Testing 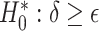 , Power , Power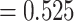
| |||
| Setting 4 | |||
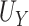
|
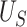
|

|
|
| Truth | 0.938 | 0.831 | 0.107 |
| Estimate | 0.936 | 0.828 | 0.108 |
| Bias | 0.002 | 0.003 | -0.001 |
| ESE | 0.037 | 0.057 | 0.039 |
| ASE | 0.036 | 0.058 | 0.040 |
| Coverage | 0.992 | 0.977 | 0.886 |
Testing 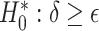 , Power , Power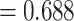
| |||
In Table 2, we compare the estimated power obtained using (5) to the empirical power for Settings 2-4, where we calculate the estimated power 3 different ways: (1) using 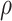 =
= 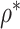 , which is the true rank correlation between
, which is the true rank correlation between  and
and 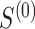 , (2) assuming
, (2) assuming 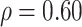 , and (3) assuming
, and (3) assuming 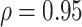 . The true correlations in Settings 2, 3, and 4 were 0.98, 0.91, and 0.82, respectively meaning that when we calculate estimated power assuming
. The true correlations in Settings 2, 3, and 4 were 0.98, 0.91, and 0.82, respectively meaning that when we calculate estimated power assuming 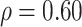 , we are under-estimating the correlation, and when we assume
, we are under-estimating the correlation, and when we assume 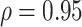 , we are under-estimating the correlation for Setting 2, but over-estimating the correlation for Settings 3 and 4. Results show that the estimated power using the true rank correlation is reasonably close to the empirical power from the simulation study. As expected, the estimated power under-estimates the empirical power when the assumed correlation is lower than the true correlation, and over-estimates the empirical power when the assumed correlation is higher than the true correlation. Simulation results showing the performance of existing approaches in Settings 1-4 are provided in Web Appendix D. Overall, our simulation study demonstrates the good finite sample performance of our proposed testing procedure in a small sample setting. Fully reproducible simulation code is publicly available in the SurrogateRank Repository (2023).
, we are under-estimating the correlation for Setting 2, but over-estimating the correlation for Settings 3 and 4. Results show that the estimated power using the true rank correlation is reasonably close to the empirical power from the simulation study. As expected, the estimated power under-estimates the empirical power when the assumed correlation is lower than the true correlation, and over-estimates the empirical power when the assumed correlation is higher than the true correlation. Simulation results showing the performance of existing approaches in Settings 1-4 are provided in Web Appendix D. Overall, our simulation study demonstrates the good finite sample performance of our proposed testing procedure in a small sample setting. Fully reproducible simulation code is publicly available in the SurrogateRank Repository (2023).
TABLE 2.
Empirical (Emp) power versus Estimated (Est) power in Settings 2-4 where estimated power is calculated in 3 different ways: (1) using 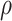 =
=  which is the true rank correlation between
which is the true rank correlation between 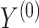 and
and 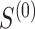 , (2) assuming
, (2) assuming  , and (3) assuming
, and (3) assuming 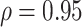 .
.
| Emp power | Est power, 
|
Est power, 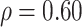
|
Est power, 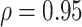
|
|
|---|---|---|---|---|
| Setting 2 | 1 | 1 | 0.835 | 1 |
| Setting 3 | 0.525 | 0.592 | 0.231 | 0.823 |
| Setting 4 | 0.688 | 0.658 | 0.393 | 0.987 |
4. DATA APPLICATION
We use our proposed method to investigate whether change in ALT from baseline to 96 weeks is a surrogate for change in NAFLD activity score in the TONIC trial described above. The NAFLD score combines information on steatosis (build up of fat in the liver), hepatocyte ballooning (form of liver cell degeneration associated with cell swelling and enlargement), and lobular inflammation (2 or more inflammatory cells within the lobule), such that higher numbers indicate worse liver function. ALT is an enzyme concentrated primarily in the liver, which increases when there is liver damage. Using our proposed method, 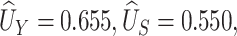 and
and 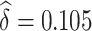 , and the 95% confidence interval was
, and the 95% confidence interval was  . Assuming a desired power of 0.70,
. Assuming a desired power of 0.70, 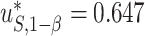 resulting in
resulting in 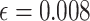 . Since the upper bound of the confidence interval for
. Since the upper bound of the confidence interval for 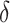 is above
is above  , we would conclude that there is not sufficient evidence to support change in ALT as a surrogate marker for change in NAFLD activity score.
, we would conclude that there is not sufficient evidence to support change in ALT as a surrogate marker for change in NAFLD activity score.
For comparison, we also calculated the proportion of treatment effect explained using the Freedman approach (Freedman et al., 1992), the more flexible but still model-based approach of Wang and Taylor (2002), the nonparametric kernel-based approach of Parast et al. (2016), and the nonparametric optimal transformation approach of Wang et al. (2020); point estimates and 95% confidence intervals were 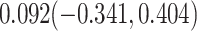 ,
, 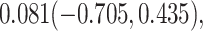 and
and 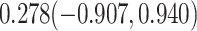 , and
, and  , respectively. All comparison approaches provide confidence intervals with a negative lower bound, with an especially wide confidence interval for the nonparametric kernel-based approach. Additional analytic results are provided in Web Appendix D.
, respectively. All comparison approaches provide confidence intervals with a negative lower bound, with an especially wide confidence interval for the nonparametric kernel-based approach. Additional analytic results are provided in Web Appendix D.
This illustration highlights the need for our proposed approach when the sample size is small. The available methods, first, are not meant to be used in a small sample setting and second, produce results that are difficult to interpret, with negative lower bounds and wide confidence intervals. In contrast, our approach offers unique insight into the use of ALT as a surrogate and specifically, provides evidence suggesting that ALT not be used as a surrogate in future studies in this population. While we do not provide a single number quantification of the strength of the surrogate like the proportion of treatment effect explained measure, this method does provide reasonable and actionable information about the strength of the surrogate that can be used to make decisions about future use of the surrogate.
5. DISCUSSION
Surrogate markers, used appropriately, can bring substantial savings in terms of time and cost in conducting randomized clinical trials. However, available methods to evaluate surrogate markers require either a large sample size or restrictive parametric assumptions, with no robust methods available for studies with a small sample size. This paper develops a statistical methodology to bridge this gap. We proposed a nonparametric rank-based approach to evaluate a surrogate marker in a small sample size setting, developed estimation and inference procedures, proposed an approach to examine power, and demonstrated good finite sample performance in a simulation study. Our method was motivated by a small clinical trial among children with NAFLD; we used our approach to determine whether change in ALT as a surrogate marker for change in NAFLD activity score. Our results led to the conclusion that there is not sufficient evidence to support change in ALT as a surrogate marker for change in NAFLD activity score, while results from available methods provided numerical results that were difficult to interpret. An R package implementing the methods proposed here, named SurrogateRank, is available in the SurrogateRank Repository (2023).
Our choice to focus on the Mann-Whitney rank-based U-statistic to quantify the treatment effect on the primary outcome and surrogate marker has 3 advantages. First, our proposed testing procedure is nonparametric and yields robust inference results in a small sample setting, where complex model checking is nearly impossible. Second, our approach is “scale-free” since the use of ranks puts 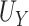 and
and 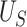 on the same scale even when
on the same scale even when  and
and 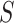 are not, which is usually the case in practice. This makes our approach invariant to transformations of
are not, which is usually the case in practice. This makes our approach invariant to transformations of 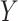 or
or 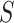 , which is a particularly important quality that is absent in available methods. For example, in the TONIC trial application, the nonparametric kernel-based approach of Parast et al. (2016) resulted in an estimate of the proportion of treatment effect explained equal to 0.278; if we instead use the outcome as
, which is a particularly important quality that is absent in available methods. For example, in the TONIC trial application, the nonparametric kernel-based approach of Parast et al. (2016) resulted in an estimate of the proportion of treatment effect explained equal to 0.278; if we instead use the outcome as  , this estimate is now 0.482, nearly twice as large. Third, our approach focuses on comparing the entire distribution of the 2 groups with respect to the primary outcome and surrogate marker, while available nonparametric focus instead on the mean; this is particularly advantageous when the distribution of the data is such that the mean fails to be a good summary of the outcome. These advantages highlight the utility of our approach, not just for small samples but also for large samples. Here, we focus on the small sample size problem, but there is nothing about our method that precludes it from being useful in a large sample size.
, this estimate is now 0.482, nearly twice as large. Third, our approach focuses on comparing the entire distribution of the 2 groups with respect to the primary outcome and surrogate marker, while available nonparametric focus instead on the mean; this is particularly advantageous when the distribution of the data is such that the mean fails to be a good summary of the outcome. These advantages highlight the utility of our approach, not just for small samples but also for large samples. Here, we focus on the small sample size problem, but there is nothing about our method that precludes it from being useful in a large sample size.
While these advantages of our proposed approach are not solely applicable to a small sample setting, methods to evaluate surrogate markers in a small sample setting are incredibly crucial. In a world where big data problems are ubiquitous, it is often forgotten that small data problems have not all been solved. Of course, this is a very difficult problem. It would be unsurprising for a reader to be skeptical of any attempt to validate a surrogate marker in a small single trial. However, this does not change the fact that there is a huge demand for surrogates and this demand is especially zealous in settings with small sample sizes. For clinical studies of rare diseases and/or disease in a pediatric setting, the studies are traditionally small and these are exactly the types of studies in which we are often desperate for a surrogate so that we can make conclusions about treatments sooner. Our pediatric NAFLD application is 1 example of such a study; another example is a currently recruiting clinical trial (ClinicalTrials.gov Identifier: NCT05067621), which is aiming to enroll 60 total participants aged 10-21 with the goal of providing mechanistic insights in support of Semaglutide therapy (glucagon-like peptide-1 receptor agonist, which increases insulin secretion) for prediabetes, new-onset type 2 diabetes, and nonalcoholic fatty liver disease in youth. In this planned study, participants will be randomized to semegalutide or placebo; the primary outcomes are change in oral disposition index and change in protein density fat fraction, and there are multiple surrogate markers of interest, including change in oral glucose tolerance test-derived biomarkers, glucose peak, glucagon levels, and incretin effect (NIH, 2022; Le Garf et al., 2021). It is warranted to harbor skepticism here, but important nonetheless to pursue the development of statistical methods that attempt to provide tools that are truly needed.
As mentioned above, the ultimate goal in the identification of a surrogate marker is to then use the surrogate marker to test for a treatment effect in a future study. In general, when we evaluate a surrogate in one study and then claim to be able to use it in a future study, we are making assumptions about the “transportability” of surrogate information from one study to another. In this paper, we focused solely on evaluating a surrogate in a single study, Study A. However, implicit in our framework, is an assumption about the transportability of  to a future study i.e., that
to a future study i.e., that 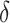 would remain the same in the future study. Whether such a transportability assumption holds depends on a number of factors, such as whether the patient population is different in the future study, whether there is heterogeneity in the utility of the surrogate, and to what extent conditions (C1)-(C3) hold in both studies. Informally, one needs to ask whether it is reasonable to assume that
would remain the same in the future study. Whether such a transportability assumption holds depends on a number of factors, such as whether the patient population is different in the future study, whether there is heterogeneity in the utility of the surrogate, and to what extent conditions (C1)-(C3) hold in both studies. Informally, one needs to ask whether it is reasonable to assume that 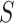 and
and 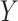 will behave in the same way, as captured by
will behave in the same way, as captured by 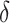 , in the future study. In a setting with multiple trials, one may consider a meta-analytic extension of our approach to investigate transportability; we discuss this further in Web Appendix E. Previous work has offered formal conditions for transportability of a surrogate marker to a future study via selection diagrams and do-calculus (Pearl and Bareinboim, 2011; Tikka and Karvanen, 2019; Bareinboim and Pearl, 2013). However, to our knowledge, there does not seem to be an existing framework to empirically investigate the plausibility of transportability in a surrogate marker setting, especially within a single study. Though beyond the scope of this paper, further work on transportability is an important area of future work.
, in the future study. In a setting with multiple trials, one may consider a meta-analytic extension of our approach to investigate transportability; we discuss this further in Web Appendix E. Previous work has offered formal conditions for transportability of a surrogate marker to a future study via selection diagrams and do-calculus (Pearl and Bareinboim, 2011; Tikka and Karvanen, 2019; Bareinboim and Pearl, 2013). However, to our knowledge, there does not seem to be an existing framework to empirically investigate the plausibility of transportability in a surrogate marker setting, especially within a single study. Though beyond the scope of this paper, further work on transportability is an important area of future work.
Our approach has some limitations. First, our testing procedure is conservative and may have low-to-moderate power in certain settings. However, given that the implication of our testing results may lead to use of the surrogate marker to test for a treatment effect in a future study, we believe conservative power may be desirable. Power gains may be achievable if one had multiple small studies available by considering a meta-analytic approach (see Web Appendix E). Second, while we propose an intuitive approach to select  , this approach may be inappropriate or undesirable in certain settings. For example, if one does not want
, this approach may be inappropriate or undesirable in certain settings. For example, if one does not want 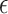 to depend on the sample size, does not agree with the concept of the bar for surrogacy depending on the sample size (note that higher sample sizes will result in a larger
to depend on the sample size, does not agree with the concept of the bar for surrogacy depending on the sample size (note that higher sample sizes will result in a larger  in the current proposal), or does not want
in the current proposal), or does not want 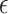 to depend on the observed
to depend on the observed 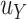 in the current study, an alternative approach will be needed. Lastly, the proposed approach is designed to accommodate outcomes and surrogates that are either continuous or on an ordinal scale with fine levels. Extending our approach to settings with outcomes or surrogates that are binary, counts, and/or censored time-to-event outcomes would not be trivial; at a minimum, one would need to consider identifying an appropriate validation criterion in these settings (Deltuvaite-Thomas et al., 2023). Further research on this topic is warranted.
in the current study, an alternative approach will be needed. Lastly, the proposed approach is designed to accommodate outcomes and surrogates that are either continuous or on an ordinal scale with fine levels. Extending our approach to settings with outcomes or surrogates that are binary, counts, and/or censored time-to-event outcomes would not be trivial; at a minimum, one would need to consider identifying an appropriate validation criterion in these settings (Deltuvaite-Thomas et al., 2023). Further research on this topic is warranted.
Supplementary Material
Web Appendices referenced in Sections 2, 3, 4, and 5, and a zip file containing code to replicate all results are available with this paper at the Biometrics website on Oxford Academic.
Acknowledgement
The TONIC study was supported by the National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK). The data were supplied by the NIDDK Central Repository. This manuscript was not prepared under the auspices of the TONIC study contributors and does not represent analyses or conclusions of the TONIC study contributors, the NIDDK Central Repository, or the NIH.
Contributor Information
Layla Parast, Department of Statistics and Data Science, University of Texas at Austin, Austin, TX 78712, United States.
Tianxi Cai, Department of Biostatistics, Harvard University, Boston, MA 02115, United States.
Lu Tian, Department of Biomedical Data Science, Stanford University, Stanford, CA 94305, United States.
FUNDING
This work was supported by NIDDK grant R01DK118354.
CONFLICT OF INTEREST
None declared.
DATA AVAILABILITY
The data from the Treatment of Nonalcoholic Fatty Liver Disease in Children (TONIC) study used in this paper are publicly available upon request from the National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK) Data Repository and completion of a data use agreement: https://repository.niddk.nih.gov/studies/tonic/.
References
- Bareinboim E., Pearl J. (2013). A general algorithm for deciding transportability of experimental results. Journal of Causal Inference, 1, 107–134. [Google Scholar]
- Buyse M., Molenberghs G. (1998). Criteria for the validation of surrogate endpoints in randomized experiments. Biometrics, 54, 1014–1029. [PubMed] [Google Scholar]
- Conlon A. S., Taylor J. M., Elliott M. R. (2014). Surrogacy assessment using principal stratification when surrogate and outcome measures are multivariate normal. Biostatistics, 15, 266–283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dabrowska D. M. (1987). Non-parametric regression with censored survival time data. Scandinavian Journal of Statistics, 14, 181–197. [Google Scholar]
- DeLong E. R., DeLong D. M., Clarke-Pearson D. L. (1988). Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics, 44, 837–845. [PubMed] [Google Scholar]
- Deltuvaite-Thomas V., Verbeeck J., Burzykowski T., Buyse M., Tournigand C., Molenberghs G., et al. (2023). Generalized pairwise comparisons for censored data: An overview. Biometrical Journal, 65, e2100354. [DOI] [PubMed] [Google Scholar]
- Dunoyer M. (2011). Accelerating access to treatments for rare diseases. Nature Reviews Drug Discovery, 10, 475–476. [DOI] [PubMed] [Google Scholar]
- Elliott M. R. (2023). Surrogate endpoints in clinical trials. Annual Review of Statistics and its Application, 10, 75–96. [Google Scholar]
- Fan J., Gijbels I. (1992). Variable bandwidth and local linear regression smoothers. The Annals of Statistics, 20, 2008–2036. [Google Scholar]
- Freedman L. S., Graubard B. I., Schatzkin A. (1992). Statistical validation of intermediate endpoints for chronic diseases. Statistics in Medicine, 11, 167–178. [DOI] [PubMed] [Google Scholar]
- Hanley J. A., McNeil B. J. (1982). The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology, 143, 29–36. [DOI] [PubMed] [Google Scholar]
- Lavine J. E., Schwimmer J. B., Van Natta M. L., Molleston J. P., Murray K. F., Rosenthal P., et al. (2011). Effect of vitamin e or metformin for treatment of nonalcoholic fatty liver disease in children and adolescents: the tonic randomized controlled trial. JAMA, 305, 1659–1668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Garf S., Nègre V., Anty R., Gual P. (2021). Metabolic fatty liver disease in children: A growing public health problem. Biomedicines, 9, 1915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G., Zhang P., Wang J., Gregg E. W., Yang W., Gong Q., et al. (2008). The long-term effect of lifestyle interventions to prevent diabetes in the china da qing diabetes prevention study: a 20-year follow-up study. The Lancet, 371, 1783–1789. [DOI] [PubMed] [Google Scholar]
- Lindström J., Ilanne-Parikka P., Peltonen M., Aunola S., Eriksson J. G., Hemiö K., et al. (2006). Sustained reduction in the incidence of type 2 diabetes by lifestyle intervention: follow-up of the finnish diabetes prevention study. The Lancet, 368, 1673–1679. [DOI] [PubMed] [Google Scholar]
- Mann H. B., Whitney D. R. (1947). On a test of whether one of two random variables is stochastically larger than the other. The Annals of Mathematical Statistics, 18, 50–60. [Google Scholar]
- Miyamoto B. E., Kakkis E. D. (2011). The potential investment impact of improved access to accelerated approval on the development of treatments for low prevalence rare diseases. Orphanet Journal of Rare Diseases, 6, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molenberghs G., Buyse M., Geys H., Renard D., Burzykowski T., Alonso A. (2002). Statistical challenges in the evaluation of surrogate endpoints in randomized trials. Controlled Clinical Trials, 23, 607–625. [DOI] [PubMed] [Google Scholar]
- NIH (2022). US National Library of Medicine: ClinicalTrials.gov: Semaglutide effects in obese youth with prediabetes/new onset type 2 diabetes and non-alcoholic fatty liver disease. https://clinicaltrials.gov/ct2/show/NCT05067621 [Accessed 15 November 2023].
- Nobili V., Alisi A., Valenti L., Miele L., Feldstein A. E., Alkhouri N. (2019). Nafld in children: new genes, new diagnostic modalities and new drugs. Nature Reviews Gastroenterology and Hepatology, 16, 517–530. [DOI] [PubMed] [Google Scholar]
- Parast L., Cai T., Tian L. (2019). Using a surrogate marker for early testing of a treatment effect. Biometrics, 75, 1253–1263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parast L., McDermott M. M., Tian L. (2016). Robust estimation of the proportion of treatment effect explained by surrogate marker information. Statistics in Medicine, 35, 1637–1653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson S. D., Jones B. (2017). Bioequivalence and Statistics in Clinical Pharmacology, New York: CRC Press. [Google Scholar]
- Pearl J., Bareinboim E. (2011). Transportability across studies: A formal approach. Technical report.
- Prentice R. L. (1989). Surrogate endpoints in clinical trials: definition and operational criteria. Statistics in Medicine, 8, 431–440. [DOI] [PubMed] [Google Scholar]
- Rosenblatt M. (1969). Conditional probability density and regression estimators. Multivariate Analysis II, 25, 31. [Google Scholar]
- SurrogateRank Repository (2023). The SurrogateRank package and repository. https://github.com/laylaparast/SurrogateRank/ [Accessed 15 November 2023].
- Tikka S., Karvanen J. (2019). Surrogate outcomes and transportability. International Journal of Approximate Reasoning, 108, 21–37. [Google Scholar]
- VanderWeele T. J. (2013). Surrogate measures and consistent surrogates. Biometrics, 69, 561–565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X., Cai T., Tian L., Bourgeois F., Parast L. (2021). Quantifying the feasibility of shortening clinical trial duration using surrogate markers. Statistics in Medicine, 40, 6321–6343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X., Parast L., Tian L., Cai T. (2020). Model-free approach to quantifying the proportion of treatment effect explained by a surrogate marker. Biometrika, 107, 107–122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y., Taylor J. M. (2002). A measure of the proportion of treatment effect explained by a surrogate marker. Biometrics, 58, 803–812. [DOI] [PubMed] [Google Scholar]
- Wittes J., Lakatos E., Probstfield J. (1989). Surrogate endpoints in clinical trials: cardiovascular diseases. Statistics in Medicine, 8, 415–425. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Web Appendices referenced in Sections 2, 3, 4, and 5, and a zip file containing code to replicate all results are available with this paper at the Biometrics website on Oxford Academic.
Data Availability Statement
The data from the Treatment of Nonalcoholic Fatty Liver Disease in Children (TONIC) study used in this paper are publicly available upon request from the National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK) Data Repository and completion of a data use agreement: https://repository.niddk.nih.gov/studies/tonic/.





