Dynamic network of intermolecular interactions in metal-organic frameworks functionalized by molecular machines

Abstract

Molecular machines enable external control of structural and dynamic phenomena at the atomic level. To efficiently transfer their tunable properties into designated functionalities, a detailed understanding of the impact of molecular embedding is needed. In particular, a comprehensive insight is fundamental to design hierarchical multifunctional systems that are inspired by biological cells. Here, we applied an on-the-fly trained force field to perform atomistic simulations of a systematically modified rotaxane functionalized metal-organic framework. Our atomistic studies reveal a symmetric and asymmetric interplay of the mechanically bonded rings (MBRs) within the framework depending on the local environment. As a result, their translational motion is modulated ranging from fast oscillatory behavior to cooperative and potentially directed shuttling. The derived picture of competitive interactions, which influence the operation mechanism of the MBRs embedded in these soft porous materials, promotes the development of responsive functional materials, which is a key step toward intelligent matter.

Competitive intermolecular interactions govern the operation mechanism of molecular shuttles in soft porous materials.

INTRODUCTION

Molecular machines and switching units are at the core of a large number of processes in nature including muscle contraction (1, 2), peptide synthesis (3–6), or the inter- and intracellular transport of small molecules (7, 8). Both their well-defined and often externally addressable dynamics and their molecular embedding are fundamental to obtain designed functionalities. The former gives access to precisely control properties at the molecular level, and the latter is crucial to transmit these features over several length and time scales. Inspired by living cells, where multiple nanoscale machines interplay and work together to perform specific and comprehensive tasks, the implementation of molecular machines into artificial and hierarchical architectures has become a major task due to the potential to achieve emergent functionality by molecular cooperativity. In recent years, several theoretical and experimental studies on the incorporation of molecular machines into well-defined molecular interfaces have been reported (9–21). Corresponding intelligent materials, which could act as a response to external physical and chemical stimuli, offer a substantial impact for applications ranging from medicine (19, 22) over chemistry (23) to environmental technologies (22, 24).

In this context, molecular machines constructed by mechanical bonds are promising candidates to control translational and rotational dynamics at the molecular level. The entanglement in these mechanically interlocked molecules (MIMs) restricts the configurational phase space and thus funnels the motion along specific pathways and enables to tailor molecular phenomena (25–33). However, to translate their tunable properties into designed functionalities, the arrangement, orientation, and interfacing of these units are crucial. Thus, the interplay of these units and their interaction with the local environment has to be understood at the atomic scale. Metal-organic frameworks (MOFs), which are built up by organic and inorganic building units, provide a highly modular scaffold to immobilize and orientate MIMs. On the basis of the nearly infinite number of structural and topological different networks (34–40), both the molecular environments and the arrangement of the molecular machines can be tailored almost arbitrary. Although only a small number of MOFs have been functionalized so far by molecular machine units (41–49), these pioneering studies already prove that the dynamics of the molecular machine units, such as molecular shuttling or rotational motion can be preserved in solid state due to the open structure. These studies further highlight that the switching between different states of the embedded molecular machine units may also affect the overall MOF structure and the intermolecular interaction within corresponding host-guest systems. Despite these promising results, which provide global information (such as if translational motion occurs after embedding in the MOF) and the advances in synthesizing these hierarchical structures, a fundamental understanding on how the embedded MIMs operate within the MOF matrix is still missing. In particular, the question if the network topology enables to modulate the motion of the embedded MIMs by defining the relative arrangement of the units and thus the intermolecular cooperativity (16) is so far unsolved. An atomistic picture of the coupled dynamics of the embedded rings would enable to decipher the role of the topology of the MOF to tailor the intermolecular interaction and thus to reveal its importance to design and synthesize corresponding functionalized MOFs with designated functionality.

Here, we report an atomistic investigation to derive such structure-function relationships by characterizing the coupled motion of the embedded MIMs and quantifying the intermolecular interactions. We provide a mechanistic insight into the impact of both the embedding of these building units in these architectures and their interaction within the scaffold on the dynamics of individual MIMs. Moreover, given the structural constraints by the network topology, we further focus on understanding how the number of neighboring MIMs affects the interactions between the embedded units and thus the translational and rotational motion of the MIMs. These investigations on systematic variations of adjacent organic units, which feature a MBR or not, will contribute to introduce rotaxane functionalized MOFs into the field of multivariate MOFs (50–58). In the latter case, highly complex and heterogeneous molecular architectures may be synthesized, where different units are incorporated in one MOF. The controlled diversity can be exploited to obtain sequential properties and functional materials with synergism. In this regard, we analyzed the structural and dynamic properties of the rotaxane units by systematically changing the periodic matrix.

For our systematic investigations, we considered a MOF functionalized with rotaxane-entities, which has been recently synthesized by the Loeb group and is labeled as UWDM-4 (University of Windsor Dynamic Material) (41, 44, 45). To study cooperative effects due to the motion of adjacent rotaxane units in the periodic framework, we followed the translational and rotational motion of the mechanically bonded rings (MBRs) within the periodic system at the atomic scale by performing molecular dynamic (MD) simulations. By capturing the structural evolution of multiple MBRs within the MOFs with high temporal and spatial resolution, we deciphered the impact of different local environments on the interplay of the embedded rotaxane molecules and their resulting cooperative functionalities. Our investigations reveal that the translation of the MBRs is substantially changed by the translational motion of neighboring MBRs. However, in contrast to this, the rotational dynamics is unaffected. The relative positions of the embedded MBRs and the neighboring rings introduced an element of asymmetry along the energy landscape of the shuttling motion. Thus, by providing an atomistic picture of the hierarchical MOF systems, cooperative effects are demonstrated. Moreover, the importance of static and dynamic asymmetries for promoting and obtaining directed and cooperative motion within a machine functionalized MOF is uncovered.

RESULTS

Structural properties of the embedded MBRs

To reveal the operation mechanism of the embedded MBRs, we performed MD simulations at different temperatures (300, 350, 400, 450, and 450 K) of a rotaxane functionalized MOF. The MOF topology is based on two interpenetrated cubic networks, similar to the IRMOF-5 (isorectecular MOF-5) structure (59), but is, in addition, interlinked by organic groups. These molecular crossbars can act as the axis for the MBRs to form embedded rotaxane type motifs. The organic linker connecting four inorganic corners is shown in Fig. 1A. Our atomistic investigations are conducted by applying ab initio parametrized interatomic potentials. We combined our on-the-fly trained potentials, which we benchmarked to describe equilibrium and out-of-equilibrium properties of the MBRs (60), with force fields, which we developed and validated with respect to quantum mechanical calculations, to accurately describe MOFs based on the Zn4O cluster (see Materials and Methods for more computational details and figs. S1 and S2) (13, 14).

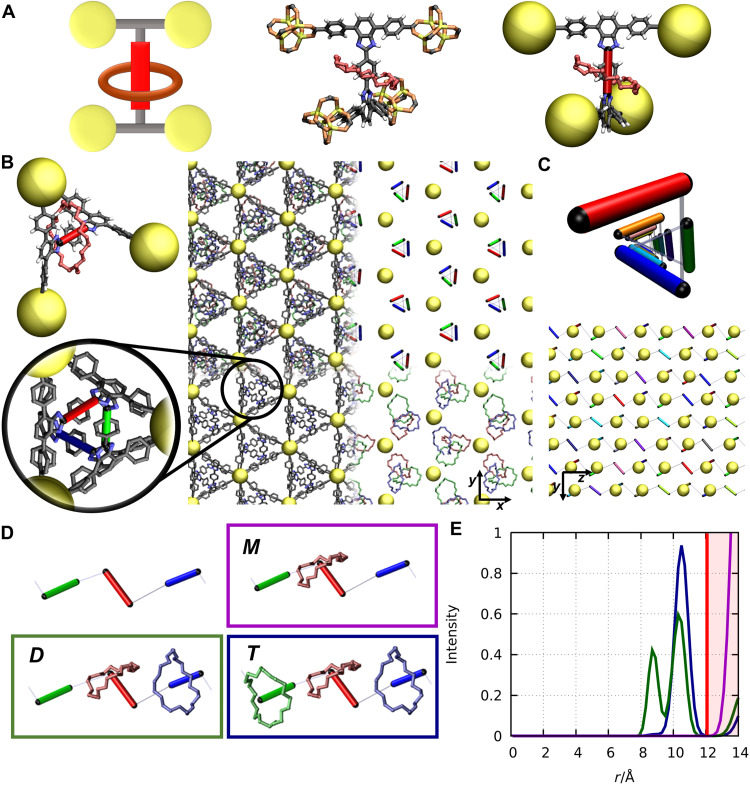
Fig. 1. Molecular structure of the rotaxane functionalized MOF.

(A) Representation of one organic linker connecting four inorganic Zn₄O corners. The left image sketches the structure of the building block, the center image shows an atomistic picture of the building block in ball-and-stick representation, and the right image shows a simplification of the atomistic picture. The inorganic corners are visualized by big yellow balls and the molecular crossbar (rotaxane axle) is simplified by a red stick. (B) Visualization of the pore structure from the z direction (top view). The image in the top left corner shows the orientation of the building block from the z direction. The picture at the right side shows the pore structure of the periodically assembled MOF structure. For clarity, different parts of the MOF are omitted, highlighting the arrangement of the crossbars (right top excerpt, simplified by a colored stick representation), the organic linkers (bottom left excerpt), and the rings (bottom right excerpt). The zoom-in view illustrates the relative arrangement of three linkers within a pore. (C) Illustration of the arrangement of the crossbars in the z direction. Top image shows a perspective view on the molecular helix, formed by the crossbars within a pore. Bottom image shows the chain-like arrangement along the z direction. The thin gray connection between the crossbars (colored sticks) is only a guide to the eye emphasizing the chain structure. (D) Differentiation of ring arrangements into three cases, each with different local environments. (E) Radial distribution function (RDF) measuring the relative distance between the rings for all three cases (M, violet graph; D, green graph; T, dark blue graph). The red line marks the distance to an adjacent one-dimensional chain.

To understand the interplay of the embedded MBRs, a detailed insight into the structural properties is crucial. In line with the experimental crystal structure (44), the optimized geometry of the rotaxane functionalized MOF exhibits an alternating arrangement of small and large pores along the xy plane (Fig. 1B). The embedded rotaxane units form helical arrangements along the z axis, which are separated by the large pores (Fig. 1, B and C). Because of this hierarchical arrangement, each MBR within the MOF can primarily interact along the one-dimensional chain with two neighboring units. To decipher cooperative effects based on the molecular embedding and inspired by the concept of sequence-dependent materials (61), we analyzed the structural and dynamics properties of the rotaxane units by systematically changing the periodic matrix. We distinguish three cases, which are defined by the local concentration of MBRs (Fig. 1D). The first case (T) represents the systems with each MBRs having two adjacent units. On the basis of this parent structure, vacant sites are created by removing every third MBR. In this structure, which represents case D, every MBR is surrounded by only one adjacent unit. In the third case (M), the density is further decrease, resulting in a MOF structure with MBRs without any adjacent ring. On the basis of atomistic simulations for each case, radial distribution functions (RDFs) with respect to the center of mass of the MBR were calculated to reveal the relative location of the rings depending on the vacancy site along the helical structure. The RDF for case T reveals one peak at around 10.2 Å (blue curve in Fig. 1E), which indicates that, in average, the MBRs preserve their relative arrangement with respect to the neighboring rings in the framework. In contrast to this, the MBRs in case D exhibit two well-defined relative arrangements. One peak is located at a distance of around 10.1 Å, similar to the systems in case T. However, although the local density is decreased, an additional peak at a closer distance (around 8.5 Å, green curve in Fig. 1E) is observed. Thus, the equilibrium position of the MBRs is influenced by the interaction between the rings, which is modulated by the local environment. In case M, the peak at around 14.0 Å in the RDF confirms the large distance between the MBRs, which results in negligible nonbonding interaction between rings.

Dynamics of the embedded MBRs

On the basis of this structural analysis, the translational and rotational dynamics of the MBRs within the MOFs were studied by calculating the rate constants for the shuttling and the rotation of the rings with respect to the axis (Fig. 2A; for computational details, see the “Calculation of the rotation and shuttling rates” section and figs. S3 and S4). By changing the embedding within the matrix, the rotation rate is almost unaffected (Fig. 2A).

Fig. 2. Dynamic features of the MBRs as a functional of molecular environment and temperature.

(A) Relative shuttling and rotation rates derived from the MD simulations at 400 K for the different cases, calculated with respect to case T. The error bars of the rotation events, created by counting errors, are partly negligible small and thus not visible. (B) Temperature dependency of the shuttling rates for case T (dark blue), D (dark-green), and M (violet). (C) Eyring plot for all three cases M, D, and T, based on the data shown in (B). The plots are based on the data presented in tables S1 and S2.

In contrast to this, the translational mobility of the MBRs is notably modulated depending on the local structure. Going from case T to case D, the shuttling rate increases, whereas, comparing case D and case M, a decrease is observed. A simple steric explanation can be excluded, because, in case M, the lowest density and, in case D, the highest density of MBRs are present, respectively. Moreover, this behavior is present for a temperature range between T = 300 to 500 K (Fig. 2B). The MD simulations at different temperatures enabled us to compute the activation energy for each case (Fig. 2C). In line with the calculated rate constants, the MBRs with one adjacent vacancy position (case D) show the lowest barrier for the translational dynamics [ΔE_A(D) = (4.4 ± 0.3) kcal/mol] compared to the MBRs in the fully occupied systems [ΔE_A(T) = (7.4 ± 0.9) kcal/mol] and the “diluted” matrix [ΔE_A(M) = (12.0 ± 1.3) kcal/mol]. These calculated results are in good agreement with reported experimentally measured and calculated results on the UWDM-4 and the individual rotaxane molecule in solution (44, 62). In the current study, we focused on the shuttling rate due to the embedding in the MOF. The small differences (underestimations) with respect to the measured data might thus be due to the absence of a solvation environment in the atomistic simulations, which is in line with experimental observations (63).

Molecular mechanism of the cooperative shuttling dynamics of the embedded MBRs

To understand the impact of molecular embedding on the translational dynamics of the MBRs, the shuttling events were investigated at the molecular level by analyzing the trajectories obtained by MD simulations in more detail. This molecular insight enabled us to characterize the translational motion for each case. As we will discuss below, not only the shuttling rate is changed by the different embeddings but also the type of motion is different.

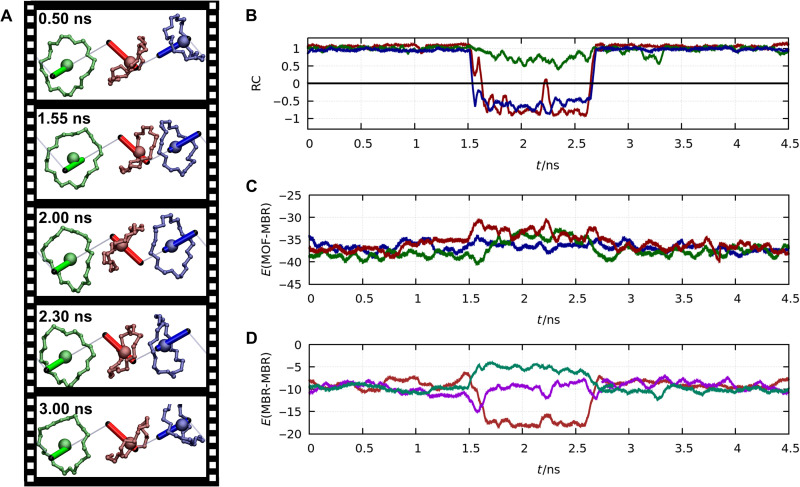
First, case M is discussed. In this case, each MBR has two adjacent vacancy sites and thus although embedded within the MOF backbone does not interact with other rings (see Fig. 3). In Fig. 3A, representative snapshots along the shuttling process are shown, illustrating the ring unit before and after the shuttling process. The stationary positions of the MBRs along the axis define the reaction coordinate RC = 1 and RC = −1, respectively (see fig. S5). Because no MBR is located at the neighboring crossbars, the local environment in both states is equal. This symmetry is confirmed considering the energetics along the shuttling path. The interaction energies between the framework and the MBR (see Fig. 3C) do not alter despite the detected shuttling process.

Fig. 3. Atomistic insights into the shuttling dynamic in case M.

(A) Representative snapshots extracted from a trajectory at 400 K showing the two stationary points of the translational motion. Only the molecular crossbars (represented by colored sticks) and the MBRs are visualized. The gray lines connecting the crossbars are shown as guide to the eye emphasizing the chain structure. (B) The position of the MBR along the crossbar is measured during the MD simulation. The y axis shows the reaction coordinate (RC), defined by the relative position of the MBR with respect to the center of mass of the axle. The stationary points are labeled with the value 1 and −1, respectively. The x axis measures the simulation time. (C) Plot of the interaction energy between the MBR and the MOF (y axis) during the MD simulation (the x axis shows the simulated time scale). The energy is given in units of kcal/mol. The data shown in (B) and (C) are averaged in a time window of 50 ps.

Next, we considered case T, in which each crossbar of the MOF is occupied by an MBR. Following the shuttling dynamics stepwise, the MBRs predominately arrange in a configuration, where they are apart (see, for example, Fig. 4A, at 0.5 ns, or fig. S6A, top). This relative arrangement of the MBR is in agreement with the calculated RDF (Fig. 1E). Starting from this state, the translational motion is initiated by the displacement of one ring (T_A; see Fig. 4B, at 1.5 ns). As a result, two MBRs (T_A and T_B) are into close contact, which increases the local density at this point along the one-dimensional chain in the framework (Fig. 4A, at 1.55 ns, and fig. S6A, bottom). Simultaneously, the local density around the origin position of T_A decreases due to the absence of the ring. This translational motion leads to an increase in attractive interaction energy between the MBRs (T_A and T_B) in close contact (Fig. 4D, violet graph at 1.55 ns), whereas the attractive interaction energy between the MBRs, which are now further apart (T_A and T_B), decreases (turquoise graph; Fig. 4D, at 1.55 ns). At the same time, analyzing the interaction between the MBRs and the framework (Fig. 4C) shows that, because of the displacement, the MBRs leave their energetically preferred position with respect to the axis (Fig. 4B, around 1.55 ns) and thus the attractive interaction energy with the framework decreases on average (Fig. 4C, around 1.55 ns). Consequently, in this configuration, the two rings in close contact T_A and T_B are in an energetically frustrated state, because the MOF-ring interaction creates a resulting force acting on the rings. To overcome this, one of these rings shuttles to reestablish the state, in which all MBRs are again apart from each other. If T_A moves, then the initial configuration would be obtained. Shuttling of T_B, on the other hand, results in a configuration, in which T_B and T_C are in close vicinity to each other (see Fig. 4A, at 2 ns, and Fig. 4B, from around 1.6 ns to around 2.2 ns). Although the respective pairwise interaction energy increases (see Fig. 4D, brown curve around 1.6 ns to around 2.2 ns), the two MBRs have again to leave their energetically preferred position with respect to the axle (see red and green curves in Fig. 4B, around 2 ns). This creates again an energetically frustrated arrangement, which can be resolved by the translation of T_B back to its initial position (see Fig. 4, at 2.3 ns). By subsequently shuttling of T_A, all MBRs are in the “far state” and the energetically preferred overall arrangement is retrieved (see Fig. 4, after 3 ns).

Fig. 4. Atomistic insights into the shuttling dynamic in case T.

(A) Representative snapshots extracted from a trajectory at 400 K. Only the molecular crossbars (represented by colored sticks) and the MBRs (colors are adapted to the crossbars) are visualized. The gray lines connecting the crossbars are shown as guide to the eye, emphasizing the chain structure. The blue colored MBR is labeled as T_A, the red unit as T_B, and the green unit as T_C. (B) The position of the MBR along the crossbar is measured during the MD simulation. The y axis shows the RC, defined by the relative position of the MBR with respect to the center of mass of the axle. The stationary points at the respective crossbar are labeled with the value 1 and −1, respectively. The x axis measures the simulation time. The colors of the graphs are adapted to (A). (C) Plot of the interaction energy between the MBR and the MOF (y axis) during the MD simulation (the x axis shows the simulated time scale). The colors are adapted to (A). (D) Measurement of the MBR-MBR interactions during the MD simulations. The violet plot indicates the MBR-MBR interaction between T_A and T_B, the turquoise plot indicates the interaction between T_A and T_C, and the brown plot corresponds to T_B and T_C. The energies are given in units of kcal/mol. The data shown in (B) to (D) are averaged in a time window of 50 ps.

The analysis of the shuttling events of the MBR with one neighboring ring unit and one adjacent vacancy site (case D) highlights the dynamic coupling of the local environment and the translational motion, which leads to the highest mobility compared to the other cases. The atomistic insight provided by the MD simulations enabled us to decipher the primary arrangement as indicated by the RDF (Fig. 1E). The second peak of the RDF at 10.1 Å can be assigned to a configuration, in which the MBRs are located in a far state (see Fig. 5, at 0.5 ns, and fig. S6B, top). The shuttling of one of the MBRs leads to an increase of the interaction between the rings due to the closer contact (see Fig. 5D, around 1 ns). This increase in the MBR-MBR interaction energy competes with the interaction energy between the MBRs and the MOF, which decreases at the same time (see Fig. 5C, around 1 ns). The relative position of the MBRs in the final stationary configuration (see Fig. 5A, at 1.5 ns, and Fig. 5B, at around 1.2 to 2.2 ns) can be associated with the first peak in the RDF (see Fig. 1E). The competition between the MBR-MBR and the MOF-MBR interaction results, similar to case T, in an energetically higher state. However, in contrast to case T, this configuration is substantially higher populated as evident by presences of the peak in the RDF, which gives an average picture of the structural properties. This metastable state, which is a result of the competing energy contributions and the asymmetric energy profile along the translation coordinate, promotes the shuttling dynamics of the MBRs. From this meta-stable state, one of the MBRs can translate to reach its initial position, in which an energetically more favorable arrangement with respect to the framework is obtained, but, at the same time, the attractive interaction energy between the rings is reduced (see Fig. 5D, around 2.5 ns).

Fig. 5. Atomistic insights into the shuttling dynamic in case D.

(A) Representative snapshots extracted from a trajectory at 400 K. Only the molecular crossbars (represented by colored sticks) and the MBRs (colors are adapted to the crossbars) are visualized. The gray lines connecting the crossbars are shown as guide to the eye emphasizing the chain structure. (B) The position of the MBR along the crossbar is measured during the MD simulation. The y axis shows the RC, defined by the relative position of the MBR with respect to the center of mass of the axle. The stationary points at the respective crossbar are labeled with the value 1 and −1 respectively. The x axis measures the simulation time. The colors of the graphs are adapted to (A). (C) Plot of the interaction energy between the MBR and the MOF (y axis) during the MD simulation (the x axis shows the simulated time scale). The colors are adapted to (A). (D) Measurement of the MBR-MBR interactions during the MD simulations. The energies are given in units of kcal/mol. The data shown in (B) to (D) are averaged in a time window of 50 ps.

DISCUSSION

On the basis of the atomistic investigations, a comprehensive picture of the molecular mechanism behind the dynamics within the rotaxane functionalized MOF can be derived, which reveals the importance of molecular embedding of the MBRs to achieve cooperative behavior within these architectures.

Incorporating MBRs within the backbone of the MOF, which are each separated by nonfunctionalized crossbars, prohibits substantial nonbonding interaction between the units. The energy landscape along the reaction coordinate is, in case M, symmetric because both resting states are energetically equal along the shuttling process. Moreover, because of the absence of neighboring MBRs, the energy profile of each shuttling process is not influenced by the position of the other MBRs within the MOF (see Fig. 6A). Thus, despite the immobilization, the intrinsic translational motion of the MBRs is not affected by the embedding (see fig. S7).

Fig. 6. Operating mechanism behind the molecular shuttling within rotaxane functionalized MOFs.

Illustration of the relevant MBR configurations for all three cases and how the potentials are affected by a shuttling process. The top images in each frame show an atomistic picture of the different relative configurations of the MBRs. The crossbars in the atomistic pictures are visualized by colored sticks. The MBR colors are adapted. The center of mass of the MBRs is shown by colored balls. The thin gray lines give a guide to the eye, highlighting the chain structure of the crossbars. The images in the middle sketch the energy potentials. The colored circles indicate the MBR position. The dashed arrows indicate a possible shuttling process, and the colored arrows indicate the change of the energy potentials due to the proposed shuttling event. The bottom images show the conditional probability distributions of the MBRs: case M: P(RC_r); case D: (A) P(RC_r|, RC_b > 0) and P(RC_b| RC_r > 0), and (B) P(RC_r| RC_b < 0) and P(RC_b |RC_r > 0); case T: (A) P(RC_g| RC_r > 0, RC_b > 0), P(RC_r| RC_g > 0, RC_b > 0), and P(RC_b| RC_g > 0, RC_r > 0), and (B) P(RC_g| RC_r < 0, RC_b > 0), P(RC_r| RC_g > 0, RC_b > 0), and P(RC_b| RC_g > 0, RC_r < 0). To compute the distributions, all 10 trajectories at 400 K are considered. Note that the data of all cases are symmetrized. Further data are given in figs. S8 and S9.

However, the operation mechanism changes notably if at least two MBRs are in close vicinity. As shown by the atomistic simulations, the embedding of the MBRs leads to a competition between the intermolecular interaction of neighboring MBRs and the interaction between the MBRs and the MOF. This is also highlighted in fig. S7 by measuring the displacement of the MBRs with respect to the different MBR-MBR configurations for all three cases. Focusing on case D, the energy landscape describing the shuttling of both neighboring MBRs becomes asymmetric (see Fig. 6 and fig. S7). Because of the competing interaction, one of the resting states is energetically metastable. In case D, at least one MBR is populating, due to the embedding within the network topology, this energetically higher configuration. The relaxation from this state is connected to a shuttling process, which, in turn, affects the MBR-MBR interaction. As a result, the underlying energy profiles are modulated (see light blue and pink arrows in Fig. 6B), leading to a state, in which both MBRs populate the energetically metastable configuration. Subsequently, one of the MBRs moves and reestablishes a state, in which only one MBR is populating the energetically higher state. The coupling of the shuttling process due to the embedding promotes the interconversion between these two energetically degenerated configurations. The driving force for the high shuttling rate is therefore an oscillatory behavior. Each of the MBRs aims to reach an energetically lower configuration, respectively. However, the embedding and the coupling between the MBRs enables only one of the MBRs at a time to populate this configuration.

The translational motion changes, if the one-dimensional chain of the crossbars within the framework is fully functionalized by MBRs. In equilibrium, the MBRs are arranged with maximum distance from each other, indicating that, because of the competition between the nonbonding interactions (MBR-MBR and MBR-MOF), the two resting states along the axis are energetically not equal (see Fig. 6C and fig. S7). In contrast to case D, each MBR within the MOF can populate the energetically lower configuration, which rationalized the lower shuttling dynamics in this case compared to the system with one vacancy site. By thermal activation, this equilibrium configuration can be disturbed if one of the MBRs shuttles. As shown by the analysis of the MD simulations, the translated MBR now populates an energetically higher configuration. However, because of the coupling of different intermolecular interactions, this shuttling process perturbs the energy landscape of both adjacent MBRs and thus their dynamics. Depending on the direction of the shuttling, the motion of the neighboring units is promoted, if the MBR moves closer, or suppress, if the MBR moves further apart. Consequently, this network of intermolecular interaction causes the system either to reestablish the initial state (additional exemplary sequence is shown in fig. S10) or to subsequently shuttle all MBRs to perform an overall concerted motion. Moreover, the dynamic asymmetry enables to observe directed and collective motion along the one-dimensional chain within the MOF (see Fig. 6C). In contrast to case D where the oscillation between energetically frustrated states leads to high shuttling rate, the symmetric nature of the intermolecular interaction in equilibrium decreases the translational rate. However, the intermolecular interaction between the MBRs leads to a lower activation energy compared to case M (Fig. 2). The latter emphasizes the role of nonbonding interactions within the matrix to promote the shuttling process.

More generally, our results obtained from the atomistic simulations highlight the importance to go beyond a purely static picture, in which only steric parameters are considered. In particular, the molecular mechanism (e.g., random or directed motion), which is crucial to rationally develop functional materials, can only be elucidated by providing a comprehensive insight into the dynamic network of intermolecular interaction within these hierarchical machineries.

MATERIALS AND METHODS

Computational details

The molecular mechanical calculations are performed using a locally modified version of the Tinker code (64). To describe the rotaxane functionalized system, ab initio parametrized force fields are applied. For the organic linkers, our recently on-the-fly trained rotaxane force field, which is validated in and out of the thermal equilibrium, is used (60). The inorganic corners are accurately described by a force field that is derived and validated with respect to quantum mechanical reference data and frequently used to describe Zn4O clusters (13, 14). To ensure charge neutrality by combining both force fields, the atomistic charges at the connection points are locally and manually adapted (fig. S1, the charge of the red marked C atom is changed to 0.14142 e).

To consider the periodicity of the system, a unit cell with cell parameters of a = 33.08 Å, b = 33.35 Å, and c = 28.76 Å and corresponding angles of α = 89.42°, β = 89.95°, and γ = 119.86° containing nine organic linkers and six inorganic corners is used (fig. S2). These parameters are determined by geometry optimization including a relaxation of the applied unit cell. The MD simulations are performed at 300, 350, 400, 450, and 500 K. At each temperature and for each case (T, D, and M), 10 independent simulations in the microcanonical ensemble (NVE) are performed. In a first step, to create uncorrelated initial geometries and velocities, one MD simulation at 500 K in the canonical ensemble (NVT), with a total runtime of 1 ns, is conducted. From this trajectory, 10 geometries are extracted. On the basis of these geometries, subsequent MD simulations in the canonical ensemble are performed. At each desired temperature (300, 350, 400, 450, and 500 K), 10 independent runs over 5 ns are carried out to equilibrate the system and create initial velocities for the NVE simulations. For the NVT simulations, the Nosé-Hoover thermostat is used (65). The final NVE simulations are performed over at least 5 ns, and their trajectories are used for the analysis of the structural and dynamic properties of the dynamic rotaxane functionalized MOF matrix (for details to the run times, see table S1).

The time propagation is predicted with time steps of 1.0 fs by using the Beeman algorithm (66). The charge-charge interactions are considered by the default smooth particle mesh Ewald approach (67) as provided by the Tinker code. Moreover, a van der Waals cutoff of 12 Å is used. Geometry optimizations are performed with a convergence criterion of 0.01 kcal/mol Å.

Calculation of the rotation and shuttling rates

The shuttling and rotation rates are measured by calculating the first derivation of the functions RC(t) and Ɵ(t). RC describes the reaction coordinate of the MBR with respect to the axle (see fig. S3A), and Ɵ describes the average change in the rotation angle of the MBR during the simulations (see fig. S4A). After deviation, the number of notable peaks is counted. For the translational motion, two stationary states along the dumbbell are available, which can easily be seen in the stepwise RC function (see fig. S3B). A peak in the deviation function is assessed as notable by a peak width of 0.03 ns and a height of 40 Å/ns. Figure S4B shows a shuttling process and the corresponding time derivation function of the RC. On the basis of the number of peaks detected as notable, the shuttling rate k is calculated. The SD Δk is calculated according to $\mathrm{\Delta }k=\mathrm{\Delta }Z/t=k/\sqrt{Z}$, where Z gives the number of events and $\mathrm{\Delta }Z=\sqrt{Z}$ is the corresponding SD. The relative counting errors (σ_rel = ΔZ/Z) are presented in Fig. 2 and tables S1 and S2.

To calculate the rotation angle, four characteristic vectors pointing from one O atom of the macrocycle to the O atom at the opposite side of the MBR are defined (see gray sticks in fig. S4A). The rotation angle Ɵ is defined as the average change of these connection vectors with respect to the connection vectors at the first frame of each trajectory (visualized by the thin black sticks in fig. S4A). The peaks in the time derivation function of Ɵ(t) (see fig. S4B) give insights into rotation processes, and notable peaks are again counted for determining the rotation rate. Only peaks in the time derivation function with a width of 0.01 ns and a height of 250°/ns are considered. Note that because of the high flexibility, the measurement of rotational processes is much more error-prone than the well-defined shuttling processes. With the increasing temperature, the detection of substantial rotation processes becomes even more difficult. The calculated rates have only a descriptive significance.

Supplementary Materials

This PDF file includes:

Figs. S1 to S10

Tables S1 and S2