Solving the protein sequence metric problem

Abstract

Biological sequences are composed of long strings of alphabetic letters rather than arrays of numerical values. Lack of a natural underlying metric for comparing such alphabetic data significantly inhibits sophisticated statistical analyses of sequences, modeling structural and functional aspects of proteins, and related problems. Herein, we use multivariate statistical analyses on almost 500 amino acid attributes to produce a small set of highly interpretable numeric patterns of amino acid variability. These high-dimensional attribute data are summarized by five multidimensional patterns of attribute covariation that reflect polarity, secondary structure, molecular volume, codon diversity, and electrostatic charge. Numerical scores for each amino acid then transform amino acid sequences for statistical analyses. Relationships between transformed data and amino acid substitution matrices show significant associations for polarity and codon diversity scores. Transformed alphabetic data are used in analysis of variance and discriminant analysis to study DNA binding in the basic helix-loop-helix proteins. The transformed scores offer a general solution for analyzing a wide variety of sequence analysis problems.

A major obstacle to rigorous statistical analyses of biological sequence data is the so-called “sequence metric problem,” i.e., use of alphabetic letter codes to characterize sequence elements. Letter codes lack a natural underlying metric for comparison. For example, the amino acid leucine (L) is more similar in its physiochemical properties to valine (V) than leucine is to alanine (A). However, the alphabetic “distance” between these letters in the alphabet does not reflect these relationships. Using single letters as nominal variables in sequence analyses results in a significant loss of resolution and information about physiochemical properties of amino acids when compared to interval variables.

Previous authors circumvented sequence metric problems in different ways. Some generated ad hoc quantitative indices to summarize amino acid variability (1, 2). However, ad hoc indices generally summarize only part of the total variability in amino acid attributes. If a numerical index approach is to be effective, indices must (i) represent the proximate causes of amino acid variability; (ii) reflect interpretable partitions of total amino acid variation; and (iii) resolve intercorrelations among relevant amino attributes.

More recently, researchers accepted the alphabetic character of these data and used information theory, e.g., entropy and mutual information, to describe variability and covariability among amino acid sites (3-10). Several authors (3, 4) carried out multivariate analyses on mutual information matrices to better understand the dimensionality and patterns that underlie multidimensional sequence data. The information theoretic approach to alphabetic data are a significant improvement over ad hoc indices; however, it still has serious shortcomings. For example, it is difficult to describe inverse (negative) relationships among sequence sites, such as those found with compensatory variation associated with amino acid charge or size (5, 6). Furthermore, this approach provides little information about the underlying causal complexity of observed intersite covariation.

Herein, we describe multivariate statistical analyses of a large number of amino acid attributes to resolve this sequence metric problem. Factor analysis is used to derive a small set of numerical values that summarize large and interpretable components of amino acid variation. This approach has many positive features and greatly facilitates statistical analysis of sequence data. Numerical scores produced in this way are of general utility and can be used in many types of analysis without modification. Our goals are to elucidate latent structure of multidimensional amino acid attribute data, describe the major patterns of interpretable covariation among these attributes, and explore some underlying causal components of multivariate attribute variation. Our approach facilitates (i) understanding dimensionality of multivariate sequence information; (ii) elucidation of multidimensional patterns of correlated amino acid attribute variation; (iii) understanding interrelationships between sequence, structural, and functional variation; (iv) standardization of data input for many different types of analyses; (v) decomposing sequence variation into its underlying evolutionary, structural, and functional components; and (vi) modeling dynamics of protein variability.

Materials and Methods

An amino acid index is a set of 20 numerical values representing different physiochemical and biological properties. The data analyzed here were obtained from an on-line database (AA-Index) containing 494 such amino acid indices (www.genome.ad.jp/dbget/aaindex.html). These indices include general attributes, such as molecular volume or size, hydrophobicity, and charge, as well as more specific measures, such as the amount of nonbonded energy per atom or side chain orientation angle.

Factor analysis was used to produce a subset of numerical descriptors that would summarize the entire constellation of amino acid physiochemical properties. A powerful exploratory statistical procedure, factor analysis simplifies high-dimensional data by generating a smaller number of “factors” that describe the structure of highly correlated variables (11-13). The resultant factors are linear functions of the original data, fewer in number than the original, and reflect clusters of covarying traits that describe the underlying or “latent structure” of the variables. Factor analysis models assume that observation i denoted x_i ∈ R^p, can be decomposed into 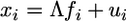, where 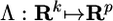is linear, and f_i ∼ N_k(0, I_k), u_i ∼ N_p(0, ψ), where ψ is diagonal, all f_i and u_j are independent, and k < p. The new set of inferred variables f_i are called common or latent factors, whereas u_j are called unique factors. Factor analysis differs from principal components analysis in that the latter does not distinguish between common and unique variance; with principal components, all u_i = 0.

The Λ matrix contains the factor coefficients λ_jk, which give the contribution of trait j to common factor k. The factor coefficient is a regression coefficient quantifying the relationship between the trait and the common factor. The communality 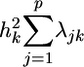is the proportion of the variation in the trait accounted for by the common factors. The uniqueness 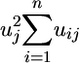is the portion of variability in the trait not accounted for by the common factors. Factors are rotated to simple structure to improve their interpretation. Such rotations maximize the number of -1, 0, and +1 factor coefficients and ensure that traits with high coefficients occur on only one or a few factors. Rotation methods include orthogonal and oblique solutions. The promax algorithm for oblique simple structure rotation is used here (11). Factor analysis produces a new set of synthetic traits called factor scores that are linear combinations of the original variables. These scores are the multivariate analog of univariate attribute amino acid indices, and they position each amino acid in a multivariate spectrum of attribute variability. Factor scores are then used to transform each alphabetic letter in aligned protein sequences to biologically meaningful numerical values. These numerically transformed sequences are then used to statistically evaluate hypotheses about evolution and structure of groups of proteins. These numerical transformations of amino acids are general and can be used in a broad range of analyses.

To understand the latent structure of sequence variation, amino acid variability can be partitioned into underlying causal components (6, 14) such that V_total = V_phylogeny + V_structure + V_function + V_interaction + V_stochastic. The model includes constraints on amino acid variability due to evolutionary history, structural and functional constraints, and random events not explained by the other main effects. The interaction component is necessary to account for possible nonlinearity. Herein, we examine the relationship between pairwise distances among amino acids based on the factor scores versus amino acid substitution matrices. This examination is done to explore the relative magnitude of structural versus phylogenetic components of protein variability. Substitution matrices estimate the rate amino acids changes over evolutionary time. Hence, relationships between patterns in amino acid variability versus changes in substitution matrix elements provide information about the underlying causes of sequence variability. Numerous amino acid substitution matrices exist; the six used here are JTT (15), Gonnet (16), WAG (17), and three different BloSum (18) matrices covering a range of evolutionary divergence. The Markov transition matrix P for each substitution matrix was computed from the log-odds scoring matrix and equilibrium amino acid probabilities, logarithmically transformed to a rate matrix, Q, then further reduced to the frequency-independent amino acid interconversion rate, S, normalized such that (-1/20)∑S_ii = 1 (19). The 190 elements of each substitution matrix were then compared with elements of five distance matrices generated from the five sets of factor scores. The extent of association between elements was determined by a product-moment correlation coefficient. A significant correlation indicates that variation in that particular attribute dimension is evolutionary in nature.

Results and Discussion

Attribute Selection. Factor analysis on the 494 attributes show that these data were highly redundant. A subset of 54 interpretable amino acid attributes was selected based on relative magnitude of factor coefficients, statistical distributional properties, relative ease of interpretation, and perceived structural importance. Factor analysis of these 54 amino acid attributes gave five “clusters,” or patterns of highly intercorrelated physiochemical variables (Table 1), a reduction in dimensionality of two orders of magnitude from the original 494 attributes. Table 5, which is published as supporting information on the PNAS web site, lists the subsets of amino acid attributes that exhibit very large coefficients for the five factors.

Table 1. The promax rotated factor pattern matrix for the 54 amino acid attribute analysis.

Amino acid attribute	F I	F II	F III	F IV	F V	Com.
Average nonbonded energy per atom	1.028	0.074	0.152	0.047	−0.079	0.982
Percentage of exposed residues	1.024	0.016	0.194	0.095	0.025	0.965
Average accessible surface area	1.005	−0.034	0.159	0.059	0.153	0.994
Residue accessible surface area in folded protein	0.950	0.098	0.178	0.039	0.237	0.961
No. of hydrogen bond donors	0.809	0.021	0.122	0.021	0.357	0.808
Polarity	0.790	−0.044	−0.388	0.027	−0.092	0.956
Hydrophilicity value	0.779	−0.153	−0.333	0.213	0.023	0.862
Polar requirement	0.775	−0.128	−0.335	−0.020	−0.245	0.939
Long range nonbonded energy per atom	0.725	−0.024	−0.394	0.189	−0.104	0.905
Negative charge	0.451	−0.218	−0.024	−0.052	−0.714	0.737
Positive charge	0.442	−0.246	−0.225	−0.085	0.708	0.730
Size	0.440	−0.112	0.811	−0.144	0.108	0.915
Normalized relative frequency of bend	0.435	0.674	−0.225	0.082	−0.118	0.912
Normalized frequency of β-turn	0.416	0.648	−0.346	−0.019	−0.079	0.969
Molecular weight	0.363	−0.091	0.657	−0.504	−0.047	0.923
Relative mutability	0.337	−0.172	−0.183	0.297	−0.296	0.416
Normalized frequency of coil	0.271	0.863	0.028	0.123	0.073	0.860
Average volume of buried residue	0.269	−0.153	0.766	−0.340	0.016	0.928
Conformational parameter of β-turn	0.243	0.693	−0.185	−0.439	0.078	0.837
Residue volume	0.225	−0.172	0.794	−0.292	0.036	0.946
Isoelectric point	0.224	−0.060	−0.049	0.163	0.967	0.955
Optimized propensity to form reverse turn	0.224	−0.005	−0.433	0.319	−0.194	0.563
Chou-Fasman parameter of coil conformation	0.201	0.780	−0.338	−0.052	0.048	0.948
Information measure for loop	0.196	0.786	−0.193	−0.335	0.181	0.908
Free energy in β-strand region	0.189	0.447	−0.125	0.127	−0.150	0.369
Side chain volume	0.181	−0.201	0.754	−0.299	0.088	0.948
Amino acid composition of total proteins	0.155	−0.163	−0.042	0.963	0.040	0.931
Average relative probability of helix	0.150	−1.004	−0.163	−0.068	−0.040	0.977
α-Helix indices	0.136	−0.939	−0.183	−0.219	0.014	0.893
Relative frequency of occurrence	0.111	−0.122	−0.079	0.931	−0.005	0.897
Helix-coil equilibrium constant	0.106	−0.724	0.368	−0.112	0.053	0.854
Amino acid composition	0.101	−0.024	−0.245	0.852	0.048	0.873
No. of codon(s)	0.079	0.133	0.087	0.867	0.294	0.778
Net charge	0.078	0.041	−0.004	0.147	0.967	0.932
Normalized frequency of turn	0.075	0.831	−0.088	−0.393	−0.051	0.859
Relative frequency in α-helix	0.061	−0.987	−0.270	−0.215	0.024	0.945
Average nonbonded energy per residue	0.042	0.376	0.001	−0.507	−0.295	0.428
Bulkiness	−0.036	−0.105	0.988	0.059	−0.244	0.897
Normalized relative frequency of coil	−0.047	0.353	−0.582	−0.082	0.135	0.494
Refractivity	−0.049	−0.061	0.471	−0.621	0.095	0.854
Normalized frequency of left-handed α-helix	−0.079	0.366	−0.641	−0.075	0.273	0.558
Heat capacity	−0.163	−0.366	0.152	−0.656	0.006	0.721
Free energy in α-helical region	−0.178	0.858	−0.002	−0.096	−0.101	0.750
Hydrophobicity factor	−0.224	0.200	0.833	−0.008	−0.098	0.728
Normalized frequency of extended structure	−0.390	0.335	0.706	0.152	0.054	0.779
Normalized frequency of β-sheet, unweighted	−0.460	0.108	0.611	0.121	0.040	0.711
Normalized frequency of β-sheet	−0.506	0.021	0.580	0.021	0.110	0.795
Information measure for pleated-sheet	−0.522	−0.132	0.438	0.069	0.179	0.724
Hydropathy index	−0.856	−0.171	0.131	0.221	−0.028	0.950
Eisenberg hydrophobic index	−0.864	0.008	0.175	0.004	−0.268	0.911
Average side chain orientation angle	−0.896	−0.160	0.000	−0.113	0.187	0.858
Average interactions per side chain atom	−0.928	−0.127	−0.141	0.062	0.135	0.842
Transfer free energy	−1.003	−0.027	−0.116	−0.114	−0.137	0.982
Percentage of buried residues	−1.017	−0.125	−0.169	−0.074	0.044	0.967

Magnitudes of the factor coefficients are the correlation of that attribute to the factor (F). Attributes with communality (Com.) estimates of <0.8 are shown in bold. Physiochemical interpretation of each factor is given in the text.

Factor I is bipolar (large positive and negative factor coefficients) and reflects simultaneous covariation in portion of exposed residues versus buried residues, nonbonded energy versus free energy, number of hydrogen bond donors, polarity versus nonpolarity, and hydrophobicity versus hydrophilicity (Table 1). The variable with the largest positive value was average nonbonded energy per atom computed as an average of pairwise interactions between constituent atoms (20). Another energy variable with a large negative coefficient is transfer free energy, which represents the partition coefficient of a particular amino acid between buried and accessible molar fractions (21). For simplicity, we designate Factor I as a polarity index. Table 5 shows those attributes from the original database with high pairwise product moment correlation coefficients (>0.85) with Factor I.

Factor II is a secondary structure factor. There is an inverse relationship of relative propensity for various amino acids in various secondary structural configurations, such as a coil, a turn, or a bend versus the frequency in an α-helix.

Factor III relates to molecular size or volume with high factor coefficients for bulkiness, residue volume, average volume of a buried residue, side chain volume, and molecular weight. A large negative factor coefficient occurs for normalized frequency of a left-handed α-helix.

Factor IV reflects relative amino acid composition in various proteins, number of codons coding for an amino acid, and amino acid composition. These attributes vary inversely with refractivity (22) and heat capacity (23).

Factor V refers to electrostatic charge with high coefficients on isoelectric point and net charge. As expected, there is an inverse relationship between positive and negative charge.

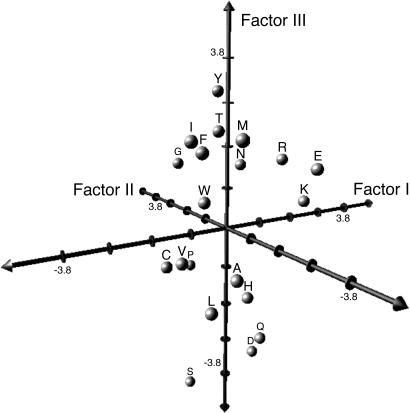
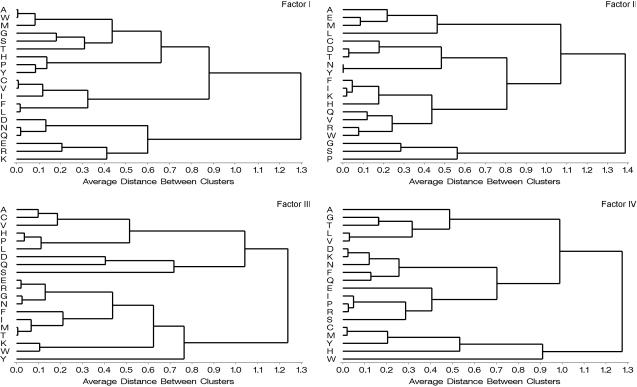
Factor Scores. The predicted value for each amino acid on each factor (factor score) can be substituted for alphabetic letter codes in sequence analyses (Table 2). Thus, each amino acid letter code can be translated into five highly interpretable numerical variables. Databases of aligned sequences are converted to five separate matrices of numerical values to facilitate statistical analyses of homologous amino acids (aligned sites) that can be analyzed individually or simultaneously. Conventional statistical analyses are now possible on these transformed sequence data. A three-dimensional projection of scores for Factors I-III clarifies the relationships among the 20 amino acids (Fig. 1). Conventionally, amino acid attributes are classified into functional groups. However, because of the diversity of amino acid attributes in the original database, other interpretations may exist about patterns of physiochemical variation. So the unweighted pair group method with arithmatic mean cluster analyses are shown to clarify multidimensional relationships among amino acids based on these independent sets of factor scores (Fig. 2).

Table 2. Five factor solution scores for the 54 selected amino acid attributes.

Amino acid	Factor I	Factor II	Factor III	Factor IV	Factor V
A	−0.591	−1.302	−0.733	1.570	−0.146
C	−1.343	0.465	−0.862	−1.020	−0.255
D	1.050	0.302	−3.656	−0.259	−3.242
E	1.357	−1.453	1.477	0.113	−0.837
F	−1.006	−0.590	1.891	−0.397	0.412
G	−0.384	1.652	1.330	1.045	2.064
H	0.336	−0.417	−1.673	−1.474	−0.078
I	−1.239	−0.547	2.131	0.393	0.816
K	1.831	−0.561	0.533	−0.277	1.648
L	−1.019	−0.987	−1.505	1.266	−0.912
M	−0.663	−1.524	2.219	−1.005	1.212
N	0.945	0.828	1.299	−0.169	0.933
P	0.189	2.081	−1.628	0.421	−1.392
Q	0.931	−0.179	−3.005	−0.503	−1.853
R	1.538	−0.055	1.502	0.440	2.897
S	−0.228	1.399	−4.760	0.670	−2.647
T	−0.032	0.326	2.213	0.908	1.313
V	−1.337	−0.279	−0.544	1.242	−1.262
W	−0.595	0.009	0.672	−2.128	−0.184
Y	0.260	0.830	3.097	−0.838	1.512

Fig. 1.

Plot of scores on Factors I-III for 20 amino acids.

Fig. 2.

Unweighted pair group method with arithmatic mean cluster analysis of distances computed from the scores from Factors I-IV. Factor V was omitted to conserve space.

Communality values, the sum of the squared factor coefficients for each physiochemical attribute, reflect the portion of the common variation in a trait explained by the five factors. Many of the traits expressed high communality values (>0.9), suggesting that they have high factor coefficients on at least one factor and that the five-factor model is sufficient (Table 1). However, some of the 54 attributes, like relative mutability (24), do not fit this model very well and have a large unique component of their variability. No attempt was made to deliberately seek out physicochemical variables that do not fit this statistical model. Clearly, there may be others among the 494 variables in the on-line database with significantly high unique fractions of their variability. Such variables should be analyzed by other methods.

To explore the effect of factor rotation, an orthogonal varimax rotation was compared with the nonorthogonal promax solution by computing pairwise product-moment correlation coefficients for the factor pattern coefficients (n = 54 per factor). Correlation coefficients ranged from 0.99 between varimax (Factor I) and promax (Factor I) to 0.96 between varimax (Factor V) and promax (Factor V). The correlation among factor scores ranged from 0.99 between varimax and promax (Factor III) to 0.95 between varimax and promax (Factor IV). Thus, whether one uses an orthogonal or nonorthogonal rotation has little effect on the interpretation of patterns of coefficients.

Interfactor Correlations. Is there significant correlation among factors? Such relationships can be estimated by the eigenvector correlations or through computation of correlation coefficients between scores from each factor. Factors III and V exhibit significant intercorrelation (r = 0.43), i.e., there is a higher-order relationship between molecular size and charge in these analyses. Furthermore, correlations between factor scores suggest a significant correlation (r = 0.64, P < 0.001) between Factors III and V.

Phylogenetic Versus Structural Variation. Can we partition variability in these five multivariate patterns of physiochemical attributes into underlying causal components? This question is explored through relationships between factor scores and substitution matrices. Six different substitution matrices based on different models of evolutionary change and degrees of evolutionary relationship are examined, including JTT, Gonnet, WAG, and three versions of BloSum. Factor scores from Table 2 were used to create separate distance matrices for polarity, propensity for secondary structure, molecular size, codon diversity, and charge among the 20 amino acids. These five matrices were compared element by element to JTT, WAG, and the BloSum30/60/90 substitution matrices. A product-moment correlation was also computed to assess the strength of relationship. Significant correlation between factor scores and elements of a substitution matrix suggests that factor score patterns contain a significant evolutionary (phylogenetic) component.

Table 3 shows the correlation between the five factor scores and the substitution matrix values. Correcting for multiple tests, there is a significant correlation between Factor I scores and all substitution matrices. Thus, a strong evolutionary basis exists for a complex pattern of covariation involving the extent of amino acid accessibility, polarity, hydrophobicity, and related attributes. These relationships have been substantiated in various experimental and analytical analyses. Atchley et al. (6) described in considerable detail patterns of variability in buried hydrophobic versus accessible hydrophilic sites in the dimerization domain of basic helix-loop-helix (bHLH) proteins. These observed patterns were related to natural selection, evolutionary change, and phylogenetic divergence.

Table 3. Product-moment correlation coefficients for the factor scores versus several substitution matrices.

r	WAG	JTT	Gonnet	BloSum30	BloSum60	BloSum90
F I	−0.41	−0.40	−0.32	−0.26	−0.26	−0.30
F II	−0.08	−0.05	−0.04	0.03	0.03	0.00
F III	0.04	0.04	0.05	0.05	0.05	0.03
F IV	−0.08	−0.12	−0.24	−0.28	−0.26	−0.23
F V	0.02	0.05	0.08	0.13	0.17	0.12

Elements shown include correlation coefficients and statistical significance. The sample size was 190, and |r| ≥ 0.212 is significant with a familywise error of P ≤ 0.05. F, Factor.

Factor IV, which reflects codon and amino acid diversity, exhibits a weaker but still highly significant correlation between physiochemical attributes and evolutionary change in patterns of substitution. Significant correlations are noted with Gonnet and the three BloSum matrices.

The remaining three factors indicate no significant association between physiochemical attribute variation and evolutionary patterns of amino acid substitution. Thus, variation in propensity to form various secondary structural configurations (Factor II), molecular size (Factor III), and charge (Factor V) cannot be ascribed to evolutionary divergence but rather to nonevolutionary changes in structure and function.

Applications of Factor Scores to Sequence Analysis. Let us explore DNA binding patterns in the bHLH proteins as an example of how factor scores of amino acid attributes can be used in sequence analyses. bHLH proteins bind DNA through a hexanucleotide E-box (CANNTG). There are five groups of bHLH proteins distinguished by the interactions among 13 amino acids in the basic DNA-binding region. These five DNA-binding groups and the included proteins have been discussed in detail (5, 6, 25-27). Here, we analyze some physiochemical aspects of amino acid variation in the DNA-binding region of 196 bHLH sequences from widely divergent proteins in a large number of organisms. The number of sequences in these groups, Groups A, B, C, D, and E, are 83, 72, 16, 9, and 16, respectively. It is well documented that the relative amino acid composition at sites 5, 8, 9, and 13 define these five binding groups (25). However, structural and functional aspects of these and other sites in the DNA-binding region are not well understood.

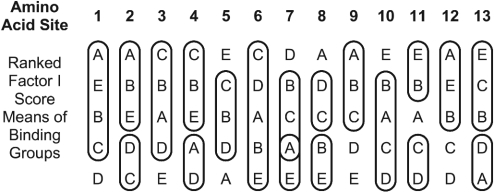
A series of univariate analyses of variance was carried out on the Factor I scores for the 13 amino acid sites in the basic region. Highly significant differences among these five groups exist for 12 of the 13 amino acid sites (Fig. 3). Only site 6 does not exhibit significant differences between the five binding groups. The factor score means for Factor I in each of the five binding groups are ranked. Means that do not differ significantly in a Bonferroni-corrected test are circled in Fig. 3. Such results can help answer important questions about biological sequences, e.g., physiochemical aspects of DNA binding, evolutionary consequences of amino acid composition at certain sites at nodes in a phylogenetic tree, and the basis for amino acid changes in multiple sequence alignments.

Fig. 3.

Analysis of variance of Factor I scores for amino acid sites 1-13 for five DNA-binding groups in the bHLH of proteins. Circled values do not differ significantly.

A multigroup discriminant analysis (canonical variate analysis) (11) of these five binding groups was carried out by using the Factor I-transformed sequence data for amino acid sites 1-13 (Table 4). Discriminant analysis finds an optimal subset of variables that maximize separation of a priori defined groups (i.e., the DNA-binding groups). Discriminant analysis explores the question “What combination of amino acid sites within the DNA-binding region best discriminate these five groups of proteins based on traits reflecting polarity, hydrophobicity, and accessibility?” Table 4 gives the first two discriminant function vectors and accounts for 91% of the total variance. Vector 1 has large coefficients on amino acid sites 5, 8, and 13, with an inverse relationship between site 8 versus 5 and 13. Consideration of the group means shows that this vector discriminates Group A from Groups B and E. Group A binds to an CAGCTG E-box and always has an R or K residue in amino acid site 8. Groups B and E bind to a CACGNG E-box and have H, R, or K residues at site 5 and R at site 13. This relationship explains the large discriminant function coefficients for these sites and that site 8 varies inversely from sites 5 and 13. Vector 2 distinguishes Groups C and D and has large coefficients on sites 9, 10, and 12. bHLH proteins that directly bind DNA always have an E residue at site 9, whereas non-DNA-binding proteins lack the E. Proteins in Groups C and D do not directly bind DNA. These simple analyses focusing only on Factor I data suggest that this overall approach can be very powerful for understanding important aspects of sequence variability.

Table 4. Discriminant function analyses (DF I and DF II) of 13 amino acid sites (Sn) in the basic region of bHLH proteins for five DNA-binding groups.

Site	DF I	DF II
S1	0.087	−0.051
S2	0.034	0.273
S3	−0.134	−0.060
S4	−0.206	−0.029
S5	−0.543	0.267
S6	0.315	0.012
S7	0.112	−0.215
S8	0.734	0.127
S9	0.187	0.757
S10	0.042	0.588
S11	−0.220	0.231
S12	0.157	0.496
S13	−0.691	0.024
Var., %	64.6	26.3
Means
Group A	4.318	0.758
Group B	−3.455	0.599
Group C	−2.490	−2.841
Group D	0.956	−10.108
Group E	−4.899	1.898

The data are the Factor I scores substituted for the alphabetic letters in the aligned sequences. The group means of discriminant functions I and II are given at the bottom of the table. Var., variation.

Conclusions

These results provide a method to quantify alphabetic information inherent to biological sequences. This approach produces five multidimensional patterns that summarize a large portion of the known variability among amino acids. These index or factor scores can be used to transform alphabetic letter codes for amino acids to five numerical values that are highly interpretable and that explain much of the information in the literature on amino acid attributes. The set of numerical scores provided here can be used in a wide variety of other types of analyses directed toward understanding the evolutionary, structural, and functional aspects of protein variability.