Conflicting Interfacial Electrostatic Interactions as a Design Principle to Modulate Long-Range Interdomain Communication

Abstract

The extent and molecular basis of interdomain communication in multidomain proteins, central to understanding allostery and function, is an open question. One simple evolutionary strategy could involve the selection of either conflicting or favorable electrostatic interactions across the interface of two closely spaced domains to tune the magnitude of interdomain connectivity. Here, we study a bilobed domain FF34 from the eukaryotic p190A RhoGAP protein to explore one such design principle that mediates interdomain communication. We find that while the individual structural units in wild-type FF34 are marginally coupled, they exhibit distinct intrinsic stabilities and low cooperativity, manifesting as slow folding. The FF3-FF4 interface harbors a frustrated network of highly conserved electrostatic interactions—a charge troika—that promotes the population of multiple, decoupled, and non-native structural modes on a rugged native landscape. Perturbing this network via a charge-reversal mutation not only enhances stability and cooperativity but also dampens the fluctuations globally and speeds up the folding rate by at least an order of magnitude. Our work highlights how a conserved but nonoptimal network of interfacial electrostatic interactions shapes the native ensemble of a bilobed protein, a feature that could be exploited in designing molecular systems with long-range connectivity and enhanced cooperativity.

Introduction

Multidomain proteins are one of the primary functional units in cellular systems.^1,2 Functionally, the presence of multiple domains enables compartmentalization of activity, with specific environmental cues enabling or eliminating interdomain communication. Structurally, these subdomains are connected by disordered or flexible regions, stretches of α-helices or β-strands depending on the protein family.³ They have also served as excellent model systems to study complex protein folding phenomena.⁴⁻⁹ Bilobed or two-domain systems are a subset of multidomain proteins that harbor two subdomains either in a standalone fashion or as a part of the larger multidomain protein. A classic case of the former is calmodulin, whose two subdomains are connected by a disordered linker region in the apo-form, which adopts a compact conformation; binding to Ca²⁺ promotes a conformational transition pushing the domains apart.^10,11 Kinases are another class of bilobed systems with distinct subfunctionalities associated with the N- and C-terminal lobes and implicated in an array of cellular activities.¹² Examples of the latter class are the effector binding domains (EBDs) of many prokaryotic transcription activators and repressors,^13,14 with the interface of the subdomains that constitute the EBDs binding to effector molecules, thus regulating function via allosteric modulation of DNA binding.

Bilobed proteins are characterized by their modularity, a key feature of protein evolution, allowing proteins to acquire new functions through gene duplication and divergence.¹⁵ Functional divergence is achieved in a bilobed system AB through mutations in either of the subdomains (A or B), or at the interface between A and B. Interfaces serve as “conduits” conveying not only the conformational status but also the binding status of one domain to the other. Thus, mutations at the interface can modulate the extent to which the subdomains communicate with each other. In addition, since interfaces connect two regions far in sequence, they could control the cooperativity of protein unfolding, a facet that could, in turn, determine the extent and nature of conformational heterogeneity in the native ensemble. It has also been predicted that the N-terminal domains of two-domain proteins fold faster than the C-terminal domains to prevent non-native interdomain interactions that could lead to aggregation and hence loss of function.¹⁶

Spatially close domains in the form of bilobed or even trilobed proteins are often encountered in the tandem repeats of FF domains in eukaryotes.^17,18 FF domains are 60–70 residue α-helical systems connected to the subsequent repeat domain via helices. The p190 RhoGTPase Activating Proteins (RhoGAPs) are the only known cytoplasmic proteins that harbor these tandem FF repeats along with an N-terminal GTP Binding Domain (GBD), two pseudo-GTPase domains followed by a C-terminal domain with GAP activity (Figure 1A).¹⁹ The p190A RhoGAP FF domains are known to bind various proteins either individually or as tandem repeats, with reports suggesting the presence of interdomain communication and, subsequently, complex disruption upon phosphorylation for the latter mode of binding.²⁰⁻²³ While the structure is available for FF1,¹⁹ only the AlphaFold2-predicted^24,25 structure of the other domains is available (Figures 1A and S1A). Despite the high structural similarity of the individual domains, differences in features such as sequence, electrostatic frustration, and coupling within and across domains exist, which could influence binding mechanisms and contribute to functional divergence in FF1–4. Among the tandem repeats, the FF3 and FF4, hereafter referred to as FF34, are spatially proximal and dumbbell-shaped with only a single intervening residue. Hence, FF34 acts as a bilobed system, with individual units behaving as a subdomain or a lobe.

Figure 1.

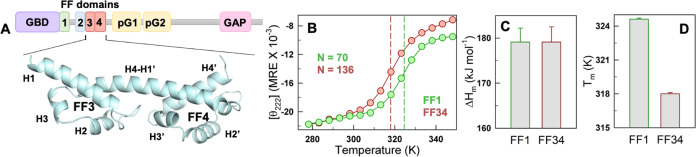
Bilobed FF34 displays marginal stability and cooperativity. (A) The domain architecture of p190A RhoGAP. The AlphaFold2-predicted model of FF34 displays a bilobed structure with FF3 and FF4 constituting the individual lobes. The individual helices are labeled. The long H4–H1′ helix forms a contiguous structure that connects H4 in FF3 to H1′ in FF4. (B) Thermal denaturation curves of FF34 (red) and FF1 (green) from far-UV CD experiment monitored at 222 nm and reported in mean residue ellipticity units of deg cm² dmol^–1. The dashed lines represent the melting temperature obtained from two-state fits. (C, D) Comparison of the unfolding enthalpies at the midpoint (C), and the melting temperatures (D). The FF34 tandem repeat displays lower melting temperature and similar cooperativity to that of FF1, despite being longer.

Here, employing the FF34 as a model bilobed protein, we ask what features determine the stability of one subdomain over the other, the precise nature of the unfolding mechanism, the degree of coupling between the subdomains, and the extent of heterogeneity in the native ensemble. Through structural analysis and a serendipitous mutation at the FF34 domain interface, we showcase the presence of a conserved charge troika that determines multiple local and global conformational traits of the native protein. Our work that employs a collection of ensemble spectroscopic experiments, calorimetry, statistical modeling, simulations, and sequence-structure analysis paves the way for identifying similar design principles that determine interdomain communication and cooperativity, the means to engineer them, with implications in allostery and protein design.

Methods

Purification of Human p190A RhoGAP FF34 and K113E Mutant

The gene of interest is FF34 (Protein sequence: MRNERKRVEMRRAFKENLETSPFITPGKPWEEARSFIMNEDFYQWLE ESVYMDIYGKHQKQIIDKAKEEFQELLLEYSELFYELELDAKPSKEKMGVIQDVLGEEQRFKALQKLQAERDALILKHIHFVYHPTKET, Uniprot id: Q9NRY4), was cloned into the pTXB1 vector (IMPACT Kit) with a C-terminal intein tag. The site-directed mutagenesis protocol (New England Biolabs, Inc.) was followed to generate the K113E mutant of FF34 using the primers designed according to the NEBaseChanger tool and Q5 Hot Start High-Fidelity 2X Master Mix.

The plasmid was transformed into Escherichia coli BL21(DE3) cells, and a single transformed colony was inoculated in 2 L of Luria–Bertani (LB) broth containing 0.005% ampicillin and grown at 37 °C and 180 rpm. The overexpression of the recombinant protein was induced at an optical density of ∼1 at 600 nm using 0.5 mM IPTG, post which the cells were grown at 16 °C for 18 h. The cells were harvested and lysed in 20 mM Tris, 0.5 M NaCl, 1 mM EDTA buffer, pH 8.5, in the presence of 1 mM PMSF using a Qsonica sonicator. The lysate was centrifuged at 10,500 rpm for 60 min, and the supernatant was loaded (0.5–1 mL/min) onto an affinity chromatography column with chitin resin (New England Biolabs, Inc.) previously equilibrated with the lysis buffer. Post washing, the intein tag was cleaved by incubating the column in lysis buffer in the presence of 75 mM β-mercaptoethanol for 20 h. The tagless protein of interest was eluted in 10 mL of buffer and passed through another freshly equilibrated chitin resin column to remove the traces of fusion protein and the intein tag. The flow-through containing the protein of interest was collected and passed through a Superdex 75pg size exclusion chromatography (SEC) column (GE Healthcare HiLoad 26/600), and the protein was eluted in 15 mM sodium phosphate buffer, pH 8, with an effective ionic strength of 150 mM. The purity of the eluted protein was identified to be >95% from an analysis of the coomassie-stained SDS-PAGE gel with the ImageJ software²⁶ (background correction was performed using the “Rolling Ball Background Subtraction” tool with a default rolling ball radius of 50 pixels). The pure protein fractions were stored at 4 °C for experiments.

The protein samples and freshly degassed buffer were filtered by using a 0.22 μm filter prior to experiments. The protein concentration was estimated with a UV–visible spectrophotometer (Jasco, Inc.) using an extinction coefficient of 19940 M^–1 cm^–1 at 280 nm for both constructs. All experiments were performed in 15 mM sodium phosphate buffer, pH 8, with an effective ionic strength of 150 mM.

Circular Dichroism (CD) and Fluorescence Spectroscopy

The CD-monitored thermal melts were acquired at protein concentrations of ∼10 μM to prevent precipitation at higher temperatures. The far-UV CD spectra were recorded as a function of temperature in a Jasco J-815 spectropolarimeter, whereas the near-UV CD signal was recorded at three wavelengths (268, 278, and 290 nm) in a ChirascanPlus q-CD instrument (Applied Photophysics). The protein samples were equilibrated at each temperature for 2 min before data collection. The thermal unfolding curves with a single transition were fit to a chemical two-state model with free-floating baselines to estimate the unfolding enthalpy (a measure of cooperativity) and melting temperature. For the chemical denaturation experiments using far-UV CD, the spectra were collected at three temperatures— 286, 298, and 310 K—in the presence of urea ranging from 0 to 6 M. The protein was incubated at room temperature in the presence of urea for 1 h prior to spectral acquisition. A ∼10 μM protein concentration was employed for fluorescence thermal melts. The protein solution was excited at 274 and 295 nm, and emission spectra were collected in the range between 280/300 and 550 nm. The data from the former were used for Tyr-Trp FRET analysis using singular value decomposition (SVD) to mathematically deconvolute and identify the significant spectral components and their relative amplitudes. Chemical denaturation experiments were done in denaturant concentrations and temperatures similar to those of far-UV CD experiments, with the excitation wavelength set to 280 nm.

Differential Scanning Calorimetry

Calorimetric measurements were performed at a single concentration of ∼44 μM for the WT in a VP-DSC microcalorimeter (Malvern 187 MicroCal VP, NL) at various scan rates (2, 2.5, 3, and 3.5 K min^–1), to avoid precipitation. Scan rates below 2 K min^–1 resulted in protein precipitation in the calorimetric cell. The resultant thermograms were averaged to obtain the heat capacity profile of the WT. The thermograms of the mutant were obtained at various concentrations at a fixed and standard scan rate of 1.5 K min^–1, as the mutant is well behaved in solution, to estimate absolute heat capacities.²⁷ Buffer-buffer baselines were collected before and after protein scans, and all samples were degassed at room temperature for 10 min prior to loading.

Stopped Flow Kinetics

The unfolding traces of FF34 WT and the mutant were obtained at 286 K by exciting the protein at 280 nm and using a 295 nm cutoff filter in a Chirascan SF3 Stopped Flow instrument (Applied Photophysics). The protein was rapidly mixed with buffer containing urea in the instrument to a final urea concentration ranging from 0.75 to 6 M and a protein concentration of ∼10 μM. Five traces, each with 1000 data points at an interval of 1 min, were collected at every urea concentration, averaged, and fit to a single-exponential function to obtain the observed rates and amplitudes.

Wako–Saitô–Muñoz–Eaton (WSME) Model

A detailed description of the native-centric statistical mechanical model can be found elsewhere.^28,29 The block approximation of the model is used in this study that considers 2 or 3 contiguous residues as a block, where the block size depends on the size of the protein. Additionally, it is also ensured that residues forming different secondary structures are not incorporated into the same block. This ensures that the residues in the loop regions are segregated separately and assigned additional conformational entropy due to their higher flexibility. Each block is assigned either “1” or “0”, for native-like (or folded) or non-native-like (or unfolded) conformations, respectively. Hence, each conformation of the protein can be imagined as a string of 0s and 1s. The phase space is further reduced by considering only those microstates that can be described via the three approximations: Single Sequence Approximation (SSA; only one stretch of folded blocks, also known as an island, present), Double Sequence Approximation (DSA; two islands with intervening unfolded blocks and no interaction across the islands), DSA with loop (DSAw/L; DSA with interisland interactions allowed). The statistical weights of the “allowed” microstates are calculated by accounting for the van der Waals interactions (with 5 Å heavy-atom cutoff), electrostatics (no cutoff), simplified solvation, and conformational entropy for fixing a block in its native conformation. Free energy profiles were generated from the estimated statistical weights. The pairwise coupling free energies are estimated as described before.³⁰

In this study, a block size of two, van der Waals interaction energy of −77.4 J mol^–1 per native contact, and a heat capacity change per native contact of −0.36 J mol^–1 K^–1 were fixed for both the constructs. No entropic penalty was assigned for proline residues due to their rigidity, whereas a penalty of −6.06 J mol^–1 K^–1 was given for glycine and nonhelical residues³¹ in addition to the entropic penalty per residue of −14.5 J mol^–1 K^–1 assigned to every residue. The structure predicted from AlphaFold2 was used as an input to the model. The contact maps of both constructs were tuned to capture the trends in stability and cooperativity observed in far-UV CD experiments by employing a simple modulation of energetics within and across the domains. Specifically, the strength of van der Waals interactions within FF3 (considered as 1–62 residues) and FF4 (63–136 residues) were reduced to 86.25 and 98.25% of their original number by tuning the number of interactions in an iterative manner. Additionally, the electrostatic interaction between residues 32 and 113 in both constructs was neglected, and the interaction energy between residues 28 and 113 was increased 1.8-fold to precisely capture experimental trends. These calibrated values were arrived at via several trial and error attempts done both separately and in combination, where the strength of van der Waals interactions was modified in the range of 65–125% of its original interactions, and electrostatic interaction strength between 1.5 and 2.5 times. The statistical weights of the conformations in the ensemble were calculated at an ionic strength of 0.15 M and 310 K, similar to experiments.

MD Simulations

Structures of FF34 WT and K113E mutant, predicted from AlphaFold2, were simulated using GROMACS 2019.6³² employing AMBER99SB*-ILDN force field with TIP3P water model (26,832 and 26,836 water molecules for FF34 WT and mutant, respectively) in a dodecahedron box with a padding distance of 15 Å. The charge neutralized system was energy minimized using the steepest-descent algorithm followed by a 100 ps NVT relaxation at 300 K, and subsequently, a 100 ps NPT equilibration run at 300 K and 1 bar pressure using the Parrinello–Rahman barostat. Particle mesh Ewald (PME) scheme at a grid spacing of 1.2 Å was employed for calculating long-range Coulomb interactions, while nonbonded interactions were calculated with a cutoff distance of 10 Å, and covalent bonds were constrained through the LINCS algorithm. Finally, the production runs of 5 μs each for the WT and mutant with a time-step of 2 fs were carried out using the leapfrog integrator, and the trajectories obtained were analyzed using the built-in GROMACS commands. The structure at time t = 0 was employed to calculate native contacts within a heavy-atom distance cutoff of 5 Å and a sequence cutoff of 3. All other contacts formed during the production run with the same distance and sequence cutoff were considered non-native. The fraction of native contacts at time t, Q(t), was calculated as per Best et al.,³³

where the summation is applied over N pairs of native contacts (i, j). The variables d_ij(t) and d^o_ij are the distance between the native pair (i, j) at time t and t = 0, respectively. The smoothing parameter β is 5 Å^–1 and λ is set to 1.8. To quantify changes in residue-level non-native contacts, we define the parameter Θ as the logarithm of the ratio of the contact maps (M) containing only non-native contacts averaged over the entire trajectory

Note that both M and Θ will have the dimensions 136 × 136, where 136 is the number of residues in FF34, similar to a conventional contact map. In cases where ⟨M_x⟩ (i, j) = 0, i.e., no non-native interactions are observed between residues i and j during the entire duration of the trajectory in either the WT or the mutant, this value was set to 1 to enable the calculation of the ratio.

For performing the principal component analysis (PCA), frames with only C_α were extracted from the original all-atom simulations and concatenated to obtain a global trajectory. The concatenated trajectory was used to compute a diagonalized mass-weighted covariance matrix employing built-in GROMACS commands. The structures from the trajectories of the wild-type and mutant were then projected on to the top two eigenvectors (PC1 and PC2, which account for 62% of the total variance) of this covariance matrix.

AlphaFold2-ColabFold-Based Structural Analysis

AlphaFold2-ColabFold platform was used to predict the different conformations of p190A FF34, K113E mutant, and p190B FF34 (Uniprot id: Q13017). The default advanced settings (max_msa: “auto” and 20 number of recycles) were maintained, but the number of seeds (num_seeds) was set to the maximum value of 16, instead of the default option of 1. This resulted in 16 structures for each of the 5 models, resulting in a total of 80 structures for each variant. The χ₁ angle (N–C_α–C_β–C_γ dihedral angle) and χ₂ angle (C_α–C_β–C_γ–C_δ dihedral angle) for each of the troika residues were calculated for both p190A FF34 WT and K113E mutant. For p190B, the χ₁ and χ₂ angles for only E32 and K113 were calculated as there is no third charged residue.

FF34 Orthologs Sequence Retrieval and Comparison

The orthologs of FF34 were retrieved from UniParc, a nonredundant protein database, and only those sequences that belonged to p190A (ARGHAP35 gene) and represented as “active” or nonobsolete were considered, amounting to 750 orthologs of p190A FF34 (Supporting Sheet S1). The sequences were aligned using Clustal Omega,³⁴ and the alignment file was used to generate a sequence logo using WebLogo server.³⁵ The alignment file was also used to calculate the Shannon entropy at each position using Shannon Entropy-One server (https://www.hiv.lanl.gov/content/sequence/ENTROPY/entropy_one.html). The method was repeated for 1095 orthologues of FF34 from the p190B family (ARHGAP5 gene; Supporting Sheet S2).

Results and Discussion

Decoupled Unfolding in WT FF34

Far-UV CD-monitored unfolding of FF34 results in a two-state-like unfolding curve with a melting temperature (T_m) of 318 K, and an enthalpy of unfolding at the midpoint (ΔH_m) of 179 kJ mol^–1 that is employed as a proxy for thermodynamic cooperativity (Figures 1B and S1B). To place these numbers in context, we compare the unfolding features of FF34 with that of FF1, an independently folding domain with a C_α-RMSD of 1.7 and 1.9 Å with the subdomains of FF34 (Figure S1C,D). Despite being half of the length of FF34 (70 residues in FF1 versus 136 in FF34), FF1 is more stable by 6 K and displays very similar unfolding cooperativity (Figure 1C,1D). These observations point to a weakly coupled and marginally stable bilobed FF34.

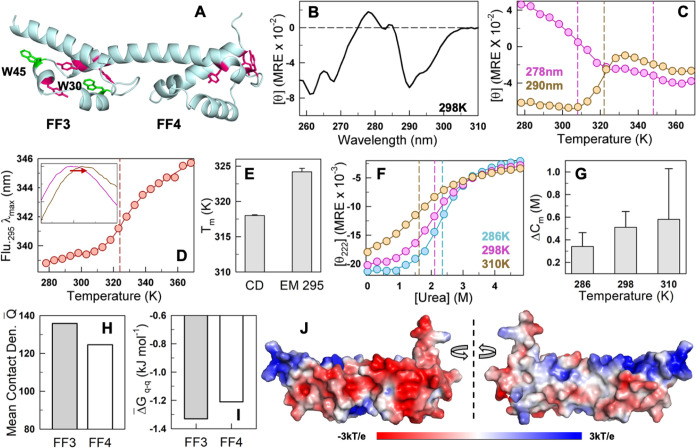
The FF3 subdomain in FF34 exclusively harbors tryptophan residues, while tyrosine residues are equally distributed across both the subdomains, allowing for site-specific studies on FF3 structural changes via near-UV CD and fluorescence (Figure 2A). The near-UV CD spectrum displays fine excitonic coupling bands at ∼260, ∼280, and ∼290 nm, indicating that FF34 does not exist in a molten-globule state (Figure 2B). The unfolding curve, when monitored by near-UV CD at 278 nm, displays a two-stage unfolding with a large amplitude (∼65%) thermodynamically early event and an inflection point of 308 K (Figures 2C and S2A). The smaller amplitude second-stage unfolding shows an inflection point at 348 K. On the other hand, a sigmoidal-like unfolding curve is observed at 290 nm, with an inflection point of 322 K. Near-UV CD, therefore, points to a more complex and thermodynamically decoupled unfolding process that is hidden in far-UV CD thermal melts.

Figure 2.

Subdomains of FF34 display varying intrinsic stabilities. (A) Structure of FF34 highlighting the tryptophan residues in green (W30 and W45) and tyrosine residues in dark magenta. (B) Near-UV CD spectrum at 298 K indicates a well-folded structure of FF34. (C) Near-UV CD-monitored thermal denaturation curves at 278 nm (magenta) and 290 nm (orange) showcase the complex non-two-state behavior of FF34. (D) Fluorescence emission maximum wavelength shifts upon excitation of the protein at 295 nm (EM 295). The inset shows the fluorescence emission spectra at 298 K (magenta) and 353 K (dark yellow) as a function of wavelength between 300 and 450 nm (abscissa). This shift as a function of temperature monitors solely the unfolding of FF3. (E) The difference in melting temperature across experiments showing the different intrinsic stabilities of the subdomains, with far-UV CD (Figure 1B) and EM 295 (D) reporting on global and FF3 unfolding, respectively. (F) Chemical denaturation curves at 286 K (cyan), 298 K (magenta), and 310 K (orange) obtained from far-UV CD experiments. (G) Difference in the chemical denaturation midpoint (C_m from fluorescence spectroscopy – C_m from far-UV CD) confirms the higher stability of FF3. The errors reported here and in other bar graphs correspond to a 68% confidence interval of the parameters from a fit to the two-state model. (H–J) Mean contact density (H; see main text), the Tanford–Kirkwood electrostatic interaction free energy of the individual domains (I) and electrostatic potential show large frustration and weak packing in FF4 (J). The dashed vertical lines in (C), (D), and (F) indicate the inflection point of the unfolding stage, the melting temperature, and the chemical denaturation midpoint, respectively.

The fluorescence emission maximum of tryptophan residues (W30 and W45 in FF3) varies with temperature, enabling us to probe the unfolding of solely FF3 (Figures 2D and S2B,C). The resulting melting temperature is 324 K, 6 K higher than the estimate from far-UV CD and matching that of the FF1 domain (Figure 2E). Employing the far-UV CD melting curve as a measure of global unfolding (i.e., both FF3 and FF4) and the T_m from the fluorescence emission maximum as a measure of FF3 stability, we estimate T_m of FF4 to be 312 K. We thus establish the unfolding mechanism of the bilobed FF34 to be a two-step process, with FF4 unfolding first, followed by FF3, with a difference in melting temperature of nearly 12 K.

To provide further evidence for this mechanism, we monitor urea-dependent unfolding of FF34 employing both far-UV CD and fluorescence as probes for the global (FF3 + FF4) and local (FF3) structure (Figures 2F and S2D). A similar trend is observed with FF3 displaying a consistently higher chemical denaturation midpoint at the three temperatures studied (Figure 2G). Why is FF3 more stable? A comparison of the mean number of native contacts (employing a 5 Å cutoff; mean contact density) indicates that FF3 is more compactly packed than FF4 (Figures 2H and S2E). The presence of more proline residues and their location in the loop region could also enhance the rigidity of FF3 relative to that of FF4 (Figure S2E). Tanford–Kirkwood (TK) electrostatic interaction free energy terms^36,37 follow a similar trend, with FF3 exhibiting relatively more favorable free energies, which can also be visually observed in the electrostatic potential map (Figures 2I,J and S2F). It is possible that the unfavorable charge–charge interactions weaken the overall packing density in FF4, which in turn destabilizes FF4 more and contributes to the earlier unfolding. The decoupled melting (i.e., one domain unfolding at relatively lower temperatures compared to the other) effectively highlights that there is little cross-talk between the two subdomains and hence in the interdomain connectivity or coupling.

Serendipitous Engineering of a Stable-Cooperative Variant

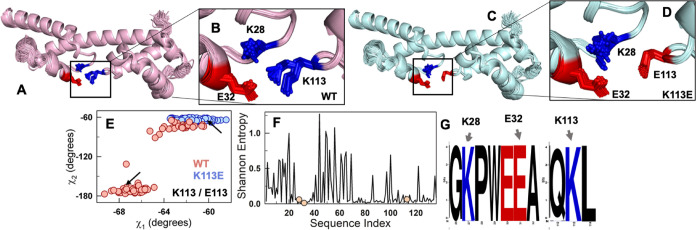
The interface between FF3 and FF4 is primarily formed of three charged residues K28 (located in FF3), E32 (FF3), and K113 (FF4), which we term the charge troika (Figure 3A,3B). The charge troika encompasses three sets of interactions: spatially close favorable interaction between E32 and K113 across the interface and between FF3 and FF4, K28-E32 ionic interaction within FF3, and the “frustrated”³⁸ unfavorable charge–charge interaction between K28 and K113 across the interface. We hypothesize that these interactions effectively determine the conformational behavior of the protein as a whole given their conflicting nature. In other words, thermal fluctuations alone could shift the equilibrium from being favorable to unfavorable due to alternate pairing between the charged residues.

Figure 3.

Charge troika and a mutation at the domain interface that enhances stability and cooperativity. (A, B) The structure of FF34 highlights the charge troika at the interface (A), and the pairwise distance between each troika pair (B). (C) TK electrostatic interaction free energy predicts larger frustration in the mutant K113E. (D) The thermal melt curve obtained at 222 nm from far-UV CD experiment shows higher stability and cooperativity of mutant, compared to the WT. The red and blue circles in (D) and (E) represent the experiment data points for WT and mutant. The solid lines indicate two-state fit. The vertical dashed lines represent the melting temperature, and the horizontal dashed lines represent the pretransition baselines. (E) The changes in fluorescence emission maximum wavelength on excitation at 295 nm (EM 295) as a function of temperature depicts little changes in FF3 stability, following the color code of (D). (F) Melting temperatures estimated from far-UV CD (gray bars; derived from (D)) and fluorescence measurements (white bars; derived from (E)) for the WT and mutant. (G, H) Ratio of unfolding enthalpy at midpoint (G), and the ratio of the slope of the transition or “m-value” in chemical denaturation experiments (H) confirm the higher cooperativity of the mutant. (I, J) The third component of SVD analysis (I) and its corresponding temperature-dependent amplitudes (J) show higher intramolecular FRET for the WT (see text for more details).

To test this hypothesis, we engineered a mutation K113E that is expected to destabilize the protein based on an electrostatic interaction energy calculation solely from the AlphaFold2-predicted structure (Figures 3C and S3A,B). Counterintuitively, we find that the mutation stabilizes the protein by 5 K when monitored by far-UV CD (a measure of global structure) despite no change in the secondary-structure content (Figure 3D). Changes in the unfolding behavior are also observed in near-UV CD experiments where the second unfolding stage is either absent or diminished in the mutant at 278 nm, whereas the signal at 290 nm showed a similar increase in T_m as the far-UV CD experiment (Figure S3C,D). On the other hand, the tryptophan fluorescence emission, which reports on the stability of FF3, exhibits only a marginally higher T_m than the WT (by ∼1 K) (Figure 3E,3F). This in turn suggests that the relative stability of FF4 has increased significantly by a mutation at the interface with the K28-E113 charge–charge interaction dominating over the unfavorable E32–E113 pair.

Employing far-UV CD as a measure of global melting temperature and that from the fluorescence emission of W30/W45 in FF3 as a reporter of FF3 stability, this increase in T_m of FF4 is estimated to be 9 K (from 312 K in the WT to 321 K in the mutant). In addition, the thermodynamic cooperativity increases by 30–60%, as calculated from the thermodynamic cooperativity ratio (ΔH_m of the mutant over the WT, Figure 3G). The increase in cooperativity is higher for the unfolding of tryptophan residues in FF3 compared to far-UV CD, despite the mutation being in the FF4 domain. A similar increase in stability and cooperativity is also observed via urea-based unfolding measurements, though with a larger fitting error due to the poorly defined pretransition baselines (Figures 3H and S3E–G). These results therefore point to the emergence of long-range thermodynamic connectivity between the two subdomains, as tryptophan residues are located in the second shell of K113 (W30) or beyond (W45), and in the FF3 subdomain. Of the two tryptophan residues, W30 is located in the second shell of K113 and fully buried within the FF3 protein core with a relative solvent accessible surface area (rSASA) of 6.3%, while W45 is located farther away from K113 with a rSASA of 26%. Since the effect of K113E mutation is expected to be larger in the second shell as opposed to the third and fourth shells, it is likely that the increase in cooperativity in FF3 is a consequence of W30 exhibiting an altered packing density, apart from the enhanced thermodynamic coupling between FF3 and FF4.

One avenue to extract altered packing patterns within FF3 is to employ the sensitive tyrosine-tryptophan Förster resonance energy transfer (FRET);³⁹ on excitation of the protein at 274 nm, the fluorescence emission band of tyrosine (Y) at ∼305 nm overlaps with the absorption band of tryptophan (W), contributing to enhanced tryptophan fluorescence which could be different in the mutant. Moreover, this technique is highly sensitive to small structural changes, as the Förster distance, R₀, for a Y–W pair is just ca. 9–12 Å. As tryptophan residues are not present in FF4, the intramolecular FRET employing natural probes is sensitive to structural changes solely within FF3. We excite both the WT and K113E at 274 nm independently, collect temperature-dependent emission spectra between 280 and 550 nm, and globally deconvolute them employing singular value decomposition (SVD), which is equivalent to the well-known principal component analysis. In SVD, the concatenated matrix of emission spectra is mathematically deconvoluted into multiple orthonormal basis spectra (or components) and their temperature dependence (or amplitudes), which are rank-ordered according to their singular values (or their relative contribution to the spectra).

In FF34, the resulting first component from a global SVD analysis is the average spectrum that displays an amplitude trend similar to the protein quantum yield with temperature (Figure S3H,I). The second component reports on spectral broadening as observed from the anticorrelated high-intensity bands at 330 and 380 nm (Figure S3J). The temperature dependence of this component is again very similar for both variants but with a slightly higher cooperativity and inflection point for the mutant (Figure S3K). If there are no other structural changes in the protein ensemble, the rest of the SVD components should purely be random experimental noise, and should not display spectral signatures or distinct amplitudes. Interestingly, the third component exhibits spectral features expected of FRET changes with an anticorrelated tyrosine-tryptophan emission spectrum (Figure 3I; note the peaks at 305 and 350 nm corresponding to tyrosine and tryptophan emission maxima). The corresponding temperature-dependent amplitude shows complex patterns, with the WT exhibiting a positive amplitude at temperatures below the T_m; this signals a relatively higher emission from tryptophan as compared to tyrosine, and hence closer tyrosine-tryptophan spacing on average; this can be observed by multiplying the third spectral component with the temperature-dependent amplitudes (Figure 3J). However, the mutant K113E exhibits a higher tyrosine fluorescence than tryptophan at lower temperatures (negative amplitude), suggestive of the tryptophan residues moving farther away and likely pulled toward the FF34 interface by the favorable K28 and E113 interaction. Given that there are two tryptophan residues in FF34, the trends displayed by the amplitude of the third component are the result of an effective FRET between different Y–W pairs. Since W45 is fully exposed to the solvent and ∼12.3 Å (ring centroid distance) from the nearest tyrosine Y43, the amplitude of the third component is likely dominated by FRET between W30 and the cluster of tyrosine residues (Y43, Y51, and Y55) in the FF3 hydrophobic core, all of which are between 5.2 and 8.8 Å from W30.

Weak Cooperativity Translates to a Rough Conformational Landscape in WT

The differences in the thermodynamic features of the two variants should be more apparent from heat capacity (C_p) profiles, which report the overall enthalpy change associated with the unfolding process. We were, however, hampered by the low solubility of the WT and temperature-sensitive aggregation at concentrations required for generating accurate differential scanning calorimetry (DSC) thermograms. To overcome this, we acquired heat capacity profiles at faster scan rates in the range between 2 and 4 K min^–1, and despite this, there is little excess heat capacity peak in the raw data (Figure S4A,B). Figure 4A plots the mean heat capacity profile from several such experiments and is indicative of a broad, weakly cooperative transition in the WT. The K113E mutant, on the other hand, is well behaved in solution, enabling the determination of the absolute heat capacity profile from concentration-dependent scans at a single scan rate of 1.5 K min^–1 (Figure S4C). The resulting C_p versus temperature curve of the mutant is sharp and remarkably different from the WT, in spite of harboring only a single amino-acid change. The back-calculated DSC curve of the WT (with WT T_m and ΔH_m from far-UV CD), but with the baselines of the mutant, agrees reasonably well with the experimental estimates and rules out any scan rate artifacts as a potential reason for the broad thermogram.

Figure 4.

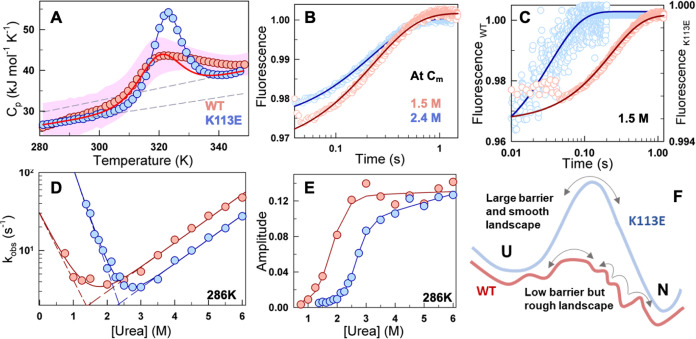
Rough conformational landscape of the WT. (A) The thermogram of the K113E mutant (blue) and the mean heat capacity profile of the WT (red circles) obtained from differential scanning calorimetry (DSC) points to a higher cooperativity and, hence, thermodynamic barrier of the mutant. The dashed gray lines represent the folded and unfolded baselines obtained from a two-state fit to the mutant’s DSC curve. The red solid line is the predicted thermogram of the WT using the T_m and ΔH_m parameters obtained from far-UV CD experiments and the baselines of the mutant. The pink-shaded region indicates the standard deviation obtained from averaging heat capacity profiles measured at various scan rates for the WT. (B) Unfolding kinetic traces of both WT and mutant at their respective chemical denaturation midpoints show similar relaxation rates. (C) Kinetic traces at 1.5 M urea concentration (circles) show faster folding with minor amplitude changes for the mutant (cyan and right axis), compared to the WT (red and left axis), and fit to a single-exponential function (blue and red curves for mutant and WT, respectively). (D, E) The observed relaxation rates (D) and their amplitudes (E) as a function of increasing concentrations of urea indicate a broader chevron for the WT with lower observed rates in the folding arm. The circles in (D) are the relaxation rates obtained from the kinetic traces; the solid lines represent two-state model fits, and the dashed lines represent the urea dependence of the folding and unfolding rate constants. The curves in (E) are shown as a guide to the eye. (F) Graphical representation of the conformational landscape of the WT and mutant.

The sharper thermogram of the mutant is indicative of a higher thermodynamic free energy barrier separating the folded and unfolded states (ΔG^‡), compared to that of the WT, as expected from statistical mechanical analysis of heat capacity profiles.^40,41 This should translate to a relatively slower folding rate in the mutant if the other features of the folding landscape remain identical. Assuming that the folding dynamics can be described as a diffusion process on a one-dimensional free energy profile, the rate of folding k can be written as k = D_eff e^–ΔG‡/RT, where D_eff is the folding diffusion coefficient or the pre-exponential factor (k₀, in inverse time units). D_eff is a measure of landscape roughness as it lumps together dihedral angle rotation barriers, internal friction, and solvent effects.⁴²⁻⁴⁵ To probe whether the higher thermodynamic barrier contributes to slower folding in the mutant, we measured the folding relaxation kinetics as a function of urea employing a stopped flow setup (Methods section; Figure 4B,4C). The folding relaxation rates of both the WT and the mutant exhibit chevron-like behavior with similar slopes in the unfolding limb (Figure 4D). The folding arm of the chevron is steeper in the mutant, translating to a higher kinetic m-value, in agreement with the higher equilibrium m-value (Figure 3H).

To our surprise, both the WT and the mutant display similar relaxation traces at the chemical denaturation midpoint (C_m; iso-stability condition) with an observed rate constant of ∼3 s^–1 (Figure 4B). The faster folding of the mutant despite the higher free energy barrier effectively means that D_eff is faster in the mutant compared to the WT. In other words, the mutation has smoothened the folding conformational landscape, thus speeding up the folding relaxation rate despite a higher free energy barrier. Accordingly, the relaxation rate at a fixed urea concentration of 1.5 M, increases by an order of magnitude: 4 s^–1 for the WT versus 30 s^–1 for the mutant (Figure 4C). Similarly, the extrapolated folding relaxation rate constants in water are estimated to be 24.5 and 1568 s^–1, for the WT and mutant, respectively (Figure 4D). The similarity in the trends of the kinetic amplitudes and quantum yield measurements from fluorescence spectroscopy confirms the reliability of the data (Figure 4E). The contrasting features of the conformational landscape that dictate the folding rate of the WT and the mutant are summarized in Figure 4F, where the rugged landscape, despite a low thermodynamic barrier, leads to a slower folding rate of the former.

Coupling Free Energies Reveal Local and Global Perturbations on Mutation

We map the equilibrium thermodynamics observations on to the structure-based statistical mechanical Wako–Saitô–Muñoz–Eaton (WSME) model to check if our experimental interpretations can be captured in a semiquantitative manner. The only input data we use are the AlphaFold2-predicted structure and the WT/K113E far-UV CD unfolding curves that carry information on the inflection point and the thermodynamic cooperativity (see the Methods section). While the uncalibrated WSME model predicts the weak coupling of the subdomains and the non-two-state folding behavior of FF34 (Figure S5), the experiment-calibrated model accurately captures the difference in melting temperature and cooperativity between the WT and the K113E variants (Figure 5A). Specifically, it can be seen that the melting temperature of FF3 does not change significantly between the two variants, and it is primarily the FF4 that is stabilized by nearly 7 K, compared to 9 K from experiments (Figure 5B).

Figure 5.

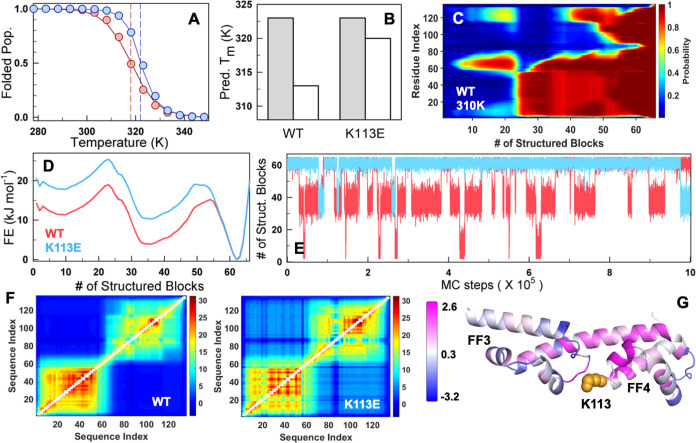
Statistical mechanical modeling and coupling free energy differences. (A) The experiment-calibrated model captures trends in stability and cooperativity of both the WT (red) and K113E mutant (blue). The circles represent the folded population obtained from the far-UV CD experiment thermal melt fit. The solid lines represent the WSME model-predicted trends in the folded population. The dashed vertical lines represent the predicted T_m. (B) The predicted T_m from the mean residue folding probability of helix residues in FF3 (1–62 residues, gray) and FF4 (63–136 residues, white) highlights that it is FF4 that is primarily stabilized on the K113E mutation in agreement with experiments. (C, D) The residue folding probability projected on the reaction coordinate (C) and the predicted 1D free energy profiles (FEPs; D) at 310 K indicates a three-state-like folding mechanism. At the RC value of 35, where panel (D) predicts an intermediate and panel (C) indicates that it is primarily FF3 that is folded (residues 1–70). (E) Monte Carlo simulations on the 1D FEP show frequent transitions of the WT to an intermediate population due to a lower thermodynamic barrier. (F) The thermodynamic coupling free energy matrices of the WT (left) display very little coupling between subdomains and weak coupling within FF4 in the WT, which improves upon K113E mutation (right). (G) The difference in coupling free energies (ΔG_c,K113E – ΔG_c,WT) mapped onto the structure. The regions in magenta and blue indicate increased and decreased coupling with the rest of the structure upon the K113E mutation, respectively. The mutated residue is shown as orange spheres.

The individual residue folding probabilities are projected on to the reaction coordinate (RC), the number of structured blocks, to extract the most probable folding mechanism. Residual structure is observed between residues 60–80 that span the helix connecting both of the domains at low RC values and hence in the unfolded state, which nucleates the formation of FF3 (residues 1–62). Following this event, the C-terminal of FF4 corresponding to residues (120–136) fold to enable the formation of FF4, and hence the fully folded structure in a two-stage manner (Figure 5C). The one-dimensional free energy profile as a function of the reaction coordinate reveals a three-state-like folding mechanism for both the WT and mutant with an intermediate formed by folded FF3 (Figure 5D). However, as expected, the free energy profile of the mutant exhibits a higher free energy, effectively destabilizing the intermediate and hence enabling cooperative folding despite a similar overall folding mechanism. Monte Carlo (MC) simulations on the 1D free energy profile employing the Metropolis criterion reveal the reason for the enhanced aggregation tendency of the WT: the WT protein frequently switches between the fully folded and the partially folded conformation corresponding to the unfolded FF4, and this partial unfolding event is suppressed in the mutant owing to the higher free energy of the intermediate (Figure 5E).

Finally, we examine the extent of coupling between the two subdomains by generating pairwise residue probabilities in free energy terms, termed the effective coupling free energy matrix (ΔG_c). It carries information on both physical (contributions from spatially close interactions) and thermodynamic coupling, i.e., contributions from spatially farther interactions due to coupled folding, and second-/third-shell effects.³⁰ The coupling matrix reveals that FF3 is more strongly coupled with intra-subdomain residues (more sea of red in the bottom left square of Figure 5F) compared to FF4, while very little interdomain FF3-FF4 coupling exists in the native ensemble (note the sea of blue in the off-diagonal regions). However, the FF3 subdomain in the mutant displays more variation in its coupling patterns (compare the bottom left squares in Figures 5F and S6A), likely as a result of the stronger electrostatic interaction across the interface with FF4, than from within the subdomain. This altered coupling pattern is likely the reason for the differential tyrosine-tryptophan FRET observed in experiments. Additionally, the coupling within the FF4 domain increases in the mutant, thus displaying higher stability (Figure S6B). Importantly, one can now explicitly observe the presence of interdomain coupling to the extent of ∼7 kJ mol^–1 in the mutant and not observed in the WT. The increased coupling in FF4 is more evident when the differences in residue-level mean coupling free energies are mapped onto the structure, where regions shaded in magenta exhibit enhanced coupling upon mutation, whereas regions in blue show a reduction in coupling with the rest of the structure (Figure 5G). Effectively, a single-residue mutation at the interface can strongly influence the extent of long-range thermodynamic coupling across the two domains, even when considering only native interactions.

Large-Scale Conformational Transitions in the WT

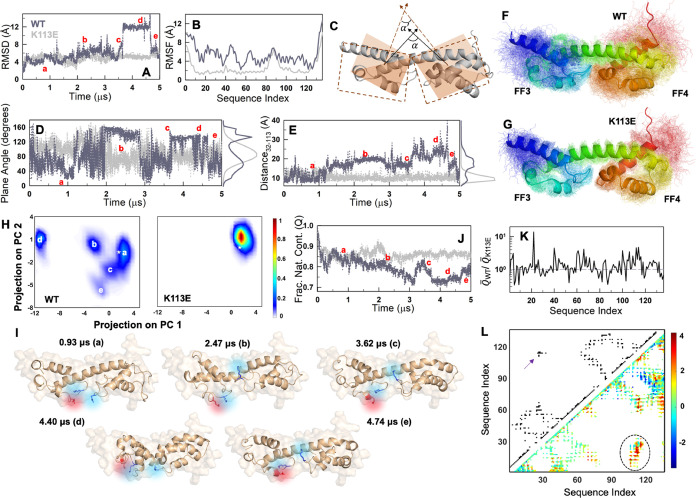
A weaker coupling across the interface is expected to decouple the motions of the two domains, and the stronger coupling observed in the K113E mutant should manifest as coupled but minimal dynamics across the entire structure. We test this hypothesis via 5 μs all-atom molecular dynamics (MD) simulations in explicit solvent. Both WT and the mutant display similar root-mean-squared deviation (RMSD) with respect to the starting structure for the first 3.5 μs (Figure 6A), following which only the WT appears to sample an alternate state with a large RMSD (12–14 Å), although it reverts back to the baseline ensemble at ca. 4.7–5 μs. Even within the first 3.5 μs, it can be seen that the WT undergoes conformational excursions to states of larger RMSD (ca. 8–10 Å). The average fluctuations as estimated by the root-mean-squared fluctuations (RMSF) showcase the rigid nature of the mutant with RMSF values being less than 2 Å for all positions except for the N-terminal and C-terminal residues and the region between 80 and 93 residues (Figure 6B). The WT, on the other hand, exhibits higher dynamics and large variability throughout the entire structure. Interestingly, the trends in RMSF of the mutant agree very well with the pLDDT (predicted local distance difference test) score from AlphaFold2 (Figure S7A), indicating that the predicted structure matches better with the mutant ensemble than the WT.

Figure 6.

Native ensemble of WT FF34 from MD simulations. (A, B) Root-mean-squared deviation (RMSD; A) and fluctuations (RMSF; B) as a function of simulation time and sequence index, respectively. (C) Cartoon of planes superimposed on the two subdomains to calculate the relative plane angle. α and α′ are representative plane angles at the two time points. The points that define the planes are the center of mass (CoM) of the backbone atoms of FF3 (FF4), residue 45 in FF3 (92 in FF4), and a common position as the CoM of the backbone helix (48–82). (D) Plane angle as a function of simulation time. Note the frequent transitions and the bimodal-like distribution (right of the plot) in the WT. (E) Changes in the distance between the CoM of residues 32 and 113 with simulation time. (F, G) Superimposition of snapshots from simulations (thin lines) on to the starting structure (cartoon). (H) Global principal component (PC) analysis of the conformational space sampled for WT (left) and the mutant (right). The WT can be observed to sample distinct pockets of structure as labeled. The corresponding labels are also provided in (A), (D), (E), and (J). (I) Representative snapshots from the WT ensemble (cartoon) superimposed on to the starting structure (surface representation in the background). The charge troika is shown in color. (J) Fraction of native contacts decreases to lower values for the WT (dark gray) compared to that of the mutant (light gray). (K) The ratio of the mean number of non-native contacts for the WT over the mutant. The values are >1 for most residues indicating more non-native interactions in the WT. (L) The contact map (top left triangle) compared with the Θ map (bottom left triangle). The color bar on the right is applicable only to the Θ map. Interaction pairs colored in yellow, orange, or red are indicative of more frequent non-native interactions in the WT. See the main text for more details. The arrow indicates the interface interactions in the contact map, which is more heterogeneous in the Θ map (circled).

Since the stabilizing mutation K113E is at the interface of the two subdomains, FF3 and FF4, we anticipate their relative orientations to be highly variable in the WT. To quantify this, we first define a plane in each of the two subdomains specified by two sets of atoms (see the legend to Figure 6), and then calculate the angle between them through the normal vectors (Figure 6C). The resulting plane angle α transitions between 40 and 140° starting from ∼108° calculated from the AF2 predicted structure (Figure 6D). The mutant is not perfectly rigid either but predominantly fluctuates around a single average plane angle of ∼85°. A second metric, the distance between the center of masses of E32 and K113 (E113 in the mutant), is shown to fluctuate around 10 Å for the mutant, but departs dramatically from the AF2 predicted structure/distances in WT (Figure 6E; also see Figure S7B–D). In fact, the WT samples E32-K113 distances as large as 40 Å and also a second minor distribution at ∼20 Å (apart from native-like conformations). Figure 6F,6G provides an ensemble view of the snapshots from the simulations, highlighting the extent to which electrostatic frustration at the interface dictates conformational behaviors.

To identify subensembles within the native ensembles in an unbiased manner, we perform a global principal component analysis (PCA) of the two trajectories and project the simulation frames on to the first two principal components (Figure 6H). The WT, as expected, displays multiple pockets of structure sampling at least five distinct substates and hence indicative of a rough landscape, while the mutant samples a single well-defined state. Figure 6I depicts representative examples from the subensembles with the starting structure shown in a surface representation for reference (Table S1). It is quite evident that the relative orientations and positions of the charged residues K28, E32, and K113 are highly variable. The series of frames with a large (∼12 Å) RMSD observed in the WT (Figure 6A) effectively corresponds to a state in which the two subdomains collapse onto each other, reducing the overall dimensions dramatically (state “d” in Figure 6I, Supporting Movie S1). For the mutant, the representative conformation derived from the PC analysis corresponds to a structure in which the residue K28 forms a shared salt bridge with E32 and E113 (Figure S7E, Supporting Movie S2), thus stabilizing the overall ensemble. On the other hand, the array of conformations sampled by the WT is likely stabilized by non-native interactions. In fact, the fraction of native contacts (Q, with respect to the t = 0 structure; see the Methods section) is substantially lower by ∼10% for the WT compared to the mutant at longer time scales (Figure 6J). The WT ensemble is therefore characterized by a higher number of non-native contacts (Q̅) on average, with the ratio of non-native contacts between the two (with the mutant as a reference) identified to be greater than one for most of the residues (Figure 6K). We note here that non-native contacts are defined as those interactions that are not present in the starting AlphaFold2-predicted structure.

A more precise picture is generated by considering the pairs of non-native residues that interact (or come closer than the cutoff distance of 5 Å during the simulation time) relatively more frequently in the WT ensemble compared to the mutant, defined by the Θ map (see the Methods section; Figure 6L). The Θ map provides a unique picture of the ensemble features, with positive, zero, and negative values indicative of more frequent non-native contacts in the WT compared to the mutant, no distinction between the two, and fewer non-native contacts in the WT, respectively. Three distinct observations stand out in this comparison. First, the FF3 subdomain displays relatively less frequent non-native contacts (cyan color) compared to FF4 (Θ ∼ 0, and cyan in Figure 6L), while FF4 samples states with more non-native interactions on average (Θ > 2, and red in Figure 6L). This minimal change in FF3 is in agreement with the similar stability of the subdomain in both the variants. Second, the contact map in the upper-left triangle in Figure 6L highlights that the interaction between the two domains is mediated by the charge troika (arrow) as per the static structure. This specific region exhibits a higher and more heterogeneous Θ-value in the simulation ensemble (circled region in Figure 6L), corroborating its importance in mediating non-native interactions but which is suppressed in the mutant (hence Θ > 0). Interestingly, a group of intra-FF4 contacts exhibit negative Θ values (blue in Figure 6L). These primarily correspond to the interactions mediated by the loop region present C-terminal to the backbone helix (83–91 residues), with the residues in the last helix and the C-terminal end of the protein. Both these C-terminal residues and loop regions are highly dynamic (Figure 6B), with the loop also showing lower coupling free energies (Figure 5F, right). The higher number of non-native contacts in the mutant relative to the WT could be the effect of the K113E mutation, whose effects are clearly nonlocalized resulting in modulation of dynamics in distal regions. Finally, compared to the contact map, the Θ map shows a larger spread (more elements in the matrix are colored), attesting to the heterogeneous nature of the WT native ensemble.

AlphaFold2-ColabFold Ensembles and Functional Implications

We have thus convincingly shown that the WT exhibits a conformationally diverse landscape with numerous interconverting conformations. Given the above observations, and the superior performance of AF2 in predicting structures,²⁴ the question remains on why the pLDDT score of the interface region is still high, i.e., predicted with a high accuracy (Figure S7A). Is it possible to extract more information from AF2 about the structure and the electrostatic frustration we observe? To do so, we employed ColabFold²⁵ to predict more models than just the default number (5), for both WT and the mutant (Methods). All 80 models predicted had nearly identical backbone architectures for both variants (Figure 7A–7D). However, differences emerge for K113 located at the interface: the WT K113 is predicted to populate two distinct rotameric states (defined by χ₁ and χ₂ angles; red in Figure 7E), while that of E113 in the mutant is characterized by a unimodal distribution (blue in Figure 7E). The other troika residues do not show significant differences in the rotameric states across the WT and mutant (Figure S8A,B). In WT, one of the χ₁ rotameric states of K113, corresponding to the orientation with χ₁ and χ₂ angles of ca. −68 and ca. −175°, respectively, takes it to be closer to K28 with the repulsion potentially counteracted by stabilizing interactions with E32. In the other rotameric state, K113 is slightly farther from K28 by ∼2 Å (a χ₁ and χ₂ angle of ca. −61 and ca. −73°, respectively). Though these differences are minor, it is obvious that AF2 recognizes the conflicting nature of the interactions at the interface. It is also interesting to note that K28 exhibits a slightly more heterogeneous distribution of rotameric states in the mutant than in the WT, highlighting perturbation to FF3 intradomain interactions in agreement with experimental observations. In order to confirm if the different rotameric states of K113 are due to repulsion by K28, we performed a similar analysis with p190B RhoGAP FF34, whose K28 is replaced by Q28 at the interface (Figure S9A,B). In contrast to the WT, a unimodal distribution of χ₁ and χ₂ angles was observed for the K113 residue (Figure S9C,D). The p190B FF34 domain lacking the charge troika behaves as a rigid system with minimal dynamics over the course of 5 μs MD simulation time (similar to the p190A FF34 K113E mutant), further confirming the link between conflicting electrostatic interactions and ensemble dynamics (Figure S10).

Figure 7.

AlphaFold2-ColabFold ensembles and high sequence conservation in the FF4 subdomain. (A, B) The 80 superimposed AlphaFold2-predicted structures of the WT (A), and the relative orientations of the charge troika, are depicted in sticks to highlight the two rotameric states of K113 (B). (C, D) The superimposed predicted structures of K113E mutant (C), and the orientations of the corresponding troika residues at the interface (D). (E) The χ₁ and χ₂ rotameric dihedral angle distributions for residue 113 of WT (red) and the mutant (blue) show two different orientations in the former construct. The arrows represent the orientation present in the rank 1 model, which was used for all structure-based predictions. (F) Shannon entropy as a function of sequence index, calculated from multiple sequence alignment (MSA) of FF34 orthologs. The orange circles represent the troika residues. (G) The sequence logo obtained from the MSA shows the conservation of troika residues.

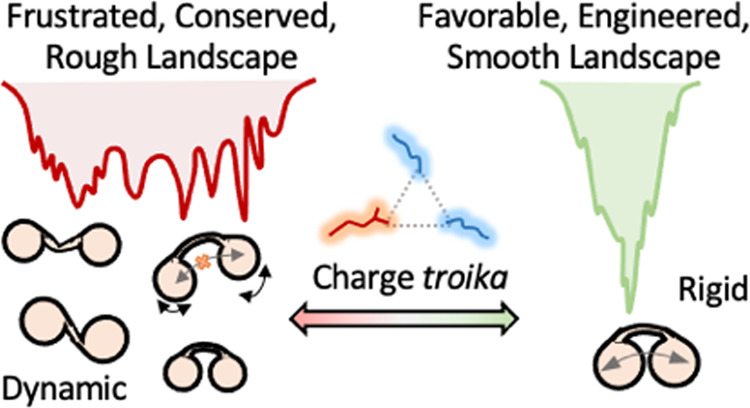
The weak coupling, marginal stability, and cooperativity of the wild-type, despite the possibility of a better variant, raises questions about whether the charge troika is an evolutionarily selected feature and, if yes, why. In order to answer these questions, we performed a multiple sequence alignment of nearly 750 orthologs of p190A FF34 and calculated the Shannon entropy at each position. Surprisingly, while FF3 shows variations in the sequence, FF4 is predominantly conserved across all organisms (Figure 7F). More importantly, the charge troika remains conserved, indicating that the conflicting interactions and hence, the complex conformational behavior of FF34 is evolutionarily selected for in the majority of sequences (Figure 7G). Similar conservation of charged residues at the interface is also observed for p190B (Figure S9E,F). One possible reason underlying the highly conserved nature of FF4 and the charge troika could be its role in FF34 function as a protein interaction module. It is also possible that the selection of conflicting interactions at the interface leading to large dynamics could be important to mediate interactions selectively with one of the lobes in a bilobed protein. Hence, it can be deduced that conserved conflicting interactions at the interface of a bilobed system could influence multiple aspects of the protein conformational behavior, directly or indirectly controlling the function of the individual subdomains and hence the protein as a whole.

Conclusions

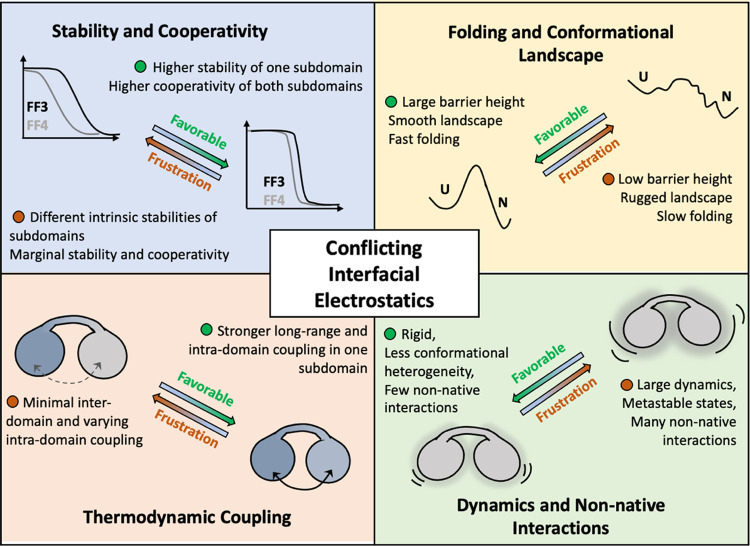
Employing a combination of experiments and simulations, we showcase how the conformational behavior of a bilobed protein is uniquely connected to a network of conflicting electrostatic interactions at the interface between the two lobes or subdomains (Figure 8). The nonoptimal interactions mediated by the charge troika lead to repulsion and destabilization of interdomain packing. As a result, the domains behave in a thermodynamically independent manner, exhibiting weak cooperativity, while contributing to the population of metastable conformations on the native landscape. This in turn, manifests as slow folding despite a lower thermodynamic barrier. The K113E mutation at the interface flips the protein’s behavior into a compact, highly coupled, stable, and cooperative one via optimization of charge–charge interactions. The mutation further eliminates the metastable conformations in the landscape, contributing to faster folding. The WT landscape is dominated by non-native interactions with very many relative positions of the charge troika, while the mutant is stabilized by a shared salt bridge between K28, E32, and E113, which locks the structure and minimizes the overall dynamics. From a folding mechanistic viewpoint, the smoothening of the landscape could lead to a lower thermodynamic barrier between unfolded and intermediate states in the K113E mutant, resulting in an apparent two-state system. A higher time-resolution experiment or a significantly longer simulation is however required to identify if FF34 indeed unfolds through a three-state-like mechanism and to understand the structural changes identified by near-UV CD probes.

Figure 8.

Summary of our findings highlighting the nonintuitive role of interfacial electrostatics on the conformational properties of the bilobed FF34 domain.

Thermodynamic coupling free energies and native ensemble dynamics are two sides of the same coin.³⁰ In fact, active and functional sites of proteins and enzymes are inherently dynamic,⁴⁶⁻⁵⁰ exhibit frustration (due to unfavorable interactions or degeneracy in the interaction states),⁵¹ and are only minimally coupled to the rest of the structure from a thermodynamic perspective.³⁰ Within this framework, the strong conservation of the WT FF4 sequence, and selection for conflicting interactions at the interface (the charge troika), points to functional roles. Experimentally, it is FF4 which is more dynamic and weakly coupled of the two lobes. Taken together with the large dynamics evident from molecular simulations, it is likely that FF4 subdomain dynamics is critical to mediate interactions. In fact, many proteins have been predicted to interact with the FF34 domain including TFII-I, Rnd3, C-terminal region of HPV16 E7, Cortactin, and the C-terminal region of Anillin.^23,52−55 The different conformational modes observable in the WT could therefore determine the moonlighting behavior of this protein, balancing selectivity and affinity across the different partners. Additionally, it should be possible to tune the degree of interdomain coupling, stability, and cooperativity by introducing glycine and proline mutations in the long linker helix without perturbing the interface or potentially even through the FF2 domain, which is located upstream of FF34.

Charged residues on the protein surface play many roles, including enhancing protein solubility, in protein–ligand binding, and in modulating thermodynamic stability. However, it is being increasingly realized that the distribution of charged residues plays additional roles other than the three highlighted above. Specifically, the balance between favorable and unfavorable electrostatics could modulate the thermodynamic cooperativity contributing to a molten-globule-like behavior as opposed to two-state unfolding, as shown before in the comparison of bovine lactalbumin (BLA) and hen egg-white lysozyme (HEWL).⁵⁶ A single charged residue biases the unfolding from N-terminal first to C-terminal first in paralogous bacterial stress response proteins, Hha and Cnu.⁵⁷ Remarkably, a surface lysine in FF1 from the p190A RhoGAP protein controls the extent of structural opening events that determine the phosphorylation of a buried tyrosine.⁵⁸ Similarly, electrostatic interactions at the subunit interface of calmodulin,⁵⁹ lipoxygenase,⁶⁰ pyruvate kinase,⁶¹ DnaK,⁶² and aminopeptidease⁶³ control the ligand binding and activity, despite the salt bridges located far from the functional site. Taken together with the current work, it appears that modulating the strength of interdomain interactions via salt bridges could be a simple avenue to control long-range activity. This could be particularly more advantageous than mutations of buried hydrophobic residues that are oftentimes associated with primarily providing stability and rigidity to protein structures.^64,65

Finally, understanding the molecular basis of interdomain communication, allostery, and modularity is important for the design of new proteins with specific functions.⁶⁶⁻⁶⁸ The ability to engineer proteins with specific functions is particularly important in the field of biotechnology, where proteins are used as catalysts, sensors, and therapeutic agents. However, the design of functional proteins is not always straightforward due to the complexity associated with protein structures and the degeneracy associated with noncovalent interactions. Our work shows that the exploitation of long-range electrostatic interactions, especially at the interface, could be a simple yet powerful approach to modulate both the global and local features of the protein by altering the coupling patterns, both within and across domains. The extent of interdomain communication can be regulated via perturbations at the interface, which we believe could further help create either a system with function compartmentalization or a unified entity with enhanced function. Depending on the location of the charged residues at the interface, the relative orientations, and the nature of pairwise interactions, it is possible to gradually tune the protein characteristics and hence strike a desired balance between stability and flexibility, a trait often challenging to achieve during protein design.

Glossary

Abbreviations

WSME

Wako–Saitô–Muñoz–Eaton

DSC

differential scanning calorimetry

CD

circular dichroism

MD

molecular dynamics

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsbiomedchemau.3c00047.

• Table with RMSD values for specific substates from MD simulations, thermal reversibility of FF34 and structural comparison of the subdomains with FF1, temperature- and urea-dependent unfolding monitored by different experimental probes for the WT and the mutant K113E (far-, near-UV CD, and fluorescence), TK electrostatic interaction free energies for the WT and mutant, the first two SVD components and their amplitudes, raw heat capacity profiles, bWSME model predictions, additional MD simulation results for the WT and K113E mutant, pLDDT scores from AF2-ColabFold-based structure prediction, sequence and structural analysis of p190B FF34 domain, and MD simulation results for p190B FF34 (PDF)

• Movies of MD simulations highlighting the differential dynamics of FF34 WT and the K113E variant (MP4)

• Orthologous sequences of the p190A and p190B FF34 family members (XLSX)

Author Contributions

CRediT: Adithi Kannan data curation, formal analysis, funding acquisition, investigation, methodology, validation, visualization, writing-original draft, writing-review & editing; Dhruv Kumar Chaurasiya formal analysis, investigation, visualization, writing-original draft, writing-review & editing; Athi N. Naganathan conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, supervision, validation, visualization, writing-original draft, writing-review & editing.

The authors declare no competing financial interest.