One Stone, Two Birds: Using High Electric Fields to Enhance the Mobility and the Concentration of Point Defects in Ion-Conducting Solids

Abstract

Improving the ionic conductivity of outstanding, composition-optimized crystalline electrolytes is a major challenge. Achieving increases of orders of magnitude requires, conceivably, highly nonlinear effects. One known possibility is the use of high electric fields to increase point-defect mobility. In this study, we investigate quantitatively a second possibility that high electric fields can increase substantially point-defect concentrations. As a model system, we take a pyrochlore oxide (La₂Zr₂O₇) for its combination of structural vacancies and dominant anti-Frenkel disorder; we perform molecular-dynamics simulations with many-body potentials as a function of temperature and applied electric field. Results within the linear regime yield the activation enthalpies and entropies of oxygen-vacancy and oxygen-interstitial migration, and from three independent methods, the enthalpy and entropy of anti-Frenkel disorder. Transport data for the nonlinear regime are consistent with field-enhanced defect concentrations and defect mobilities. A route for separating the two effects is shown, and an analytical expression for the quantitative prediction of the field-dependent anti-Frenkel equilibrium constant is derived. In summary, we demonstrate that the one stone of a nonlinear driving force can be used to hit two birds of defect behavior.

1. Introduction

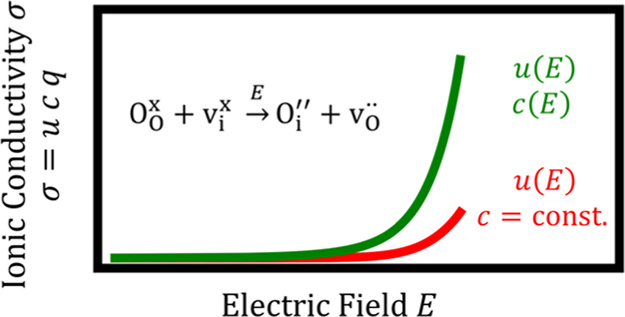
Despite the fairly regular discoveries of new crystalline oxides that exhibit outstanding oxide-ion conductivity and the compositional optimization of these new systems, the conductivities of the new, compositional-optimized systems are not vastly superior to those of the already-known oxide-ion conductors.¹⁻⁹ Evidently, at least as far as crystal chemistry and crystal composition are concerned, there is a limit to the rate of oxide-ion transport in such materials.¹⁰ Other possibilities for improving the conductivity, such as the introduction of faster diffusion paths¹¹⁻¹⁴ or the application of mechanical strain,¹⁵⁻²¹ have caught, therefore, the community’s attention in recent years, but with only moderate success even in the most favorable cases. One promising possibility that has received little attention so far is the use of high electric fields.

The ionic conductivity σ of a material can be expressed as the product of the concentration of the mobile defects c_j, their charge z_je, and their mobility u_j

1

Under high electric fields, an (almost) exponential increase of u_j (and thus σ_j) is expected,²²⁻²⁴ an effect due to the lowering of the migration barrier in the field direction with increasing field strength. This is the first “bird” to be hit with the “stone” of a high electric field, and it is a recognized effect.^4,25−32 A second possibility for increasing the ionic conductivity of a material by applying an electric field—according to eq 1—is to increase the concentration of point defects, c_j. This is the second “bird” to be addressed with the “stone”, and it has been considered far less (see Section 1.1).

In order for the “stone” to hit successfully “birds” one and two, the material’s structure should provide a network within which point defects (vacancies or interstitials) are mobile; and it should allow such point defects to be generated through the action of an electric field. In the case of oxide-ion transport in a crystalline oxide, the most feasible reaction is the anti-Frenkel (aF) disorder reaction, through which oxygen interstitials and oxygen vacancies are generated (in Kröger–Vink notation³³⁻³⁵)

2

Typical crystal structures with highly mobile oxide ions are fluorite oxides (AO₂) and perovskite oxides (ABO₃), but the close-packed nature of such structures gives rise to (prohibitively) high energies for anti-Frenkel disorder.³⁶⁻³⁸ One possibility of providing space for oxygen interstitials while keeping the same basic crystal structure with mobile oxide ions would be to take a material based on an AO₂ fluorite or an ABO₃ perovskite that contains structural vacancies, i.e., sites that are formally vacant in the perfect structure. Structures that fulfill both criteria are thus A₂B₂O₇ pyrochlores, based on AO₂ fluorites, and A₂B₂O₅ brownmillerites, based on ABO₃ perovskites. The latter system will be considered elsewhere;³⁹ the former system is the subject of this study.

The A₂B₂O₇ pyrochlore structure, part of which is shown in Figure 1, can be described in simplified terms as a highly substituted, oxygen-deficient, ordered fluorite structure. Within this structure, the A³⁺ cations occupy the 16d Wyckoff position, the B⁴⁺ cations the 16c position, and the O^2– ions the 48f and 8b positions. Of major importance for anti-Frenkel disorder is the 8a position, the site of the structural oxygen vacancies. Regular oxide ions can be thermally excited to occupy the 8a site, becoming oxygen interstitial ions and creating thereby oxygen vacancies. All theoretical studies agree that the anti-Frenkel disorder reaction [eq 2] is the most favorable defect formation in A₂B₂O₇ pyrochlores and that oxygen diffusion takes place predominantly by a vacancy mechanism between 48f positions.⁴⁰⁻⁴³ It has also been reported⁴⁴ that the interstitial ions are mobile, even though the structural vacancies are not adjacent to each other; details of the underlying mechanism, however, have not been elucidated. In any case, we expect both point defects to contribute to the total oxide-ion conductivity, giving rise to two possible contributions to field-enhanced conductivity. In the work performed to date, simulation and experimental studies agree that significant oxygen diffusion only occurs when the cations become disordered or the systems are doped appropriately.⁴⁵⁻⁴⁹ The main question here is to what extent an electric field can influence the defect formation equilibrium in eq 2 and thus the concentration of charge carriers c_v and c_i without doping or cation disorder.

Figure 1.

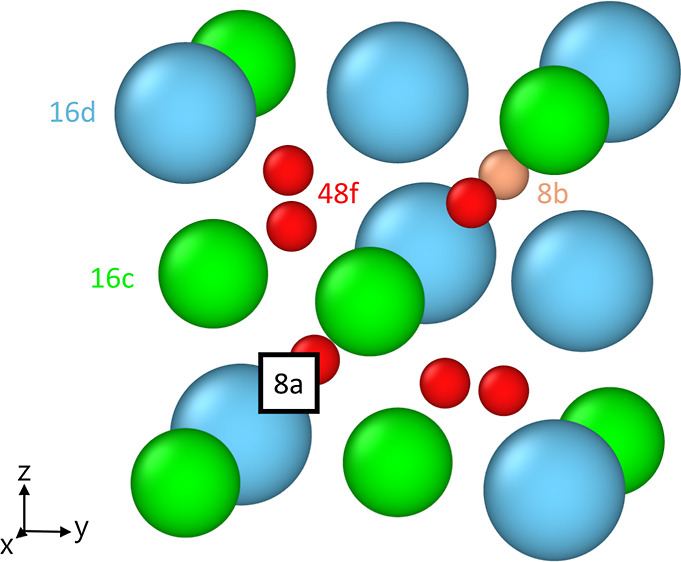
Partial unit cell of the pyrochlore structure with A³⁺ cations in turquoise, B⁴⁺ cations in green, O^2– ions on 48f positions in red, and O^2– ions on 8b positions in light red. The structural vacancy at the 8a position is shown as a square.

In this study, La₂Zr₂O₇ (LZO) is used as a model pyrochlore oxide for two reasons. First, a many-body interatomic potential set suitable for molecular dynamics (MD) simulations is available.^50,51 In preliminary simulations employing Buckingham pair potentials,⁵² only a few point defects were observed (during a reasonably long simulation run) and then only close to the melting temperature. In contrast, in simulations with the many-body potentials, point defects were detected far below the melting point, thus providing a wider range of temperatures for study and also better statistics. Second, according to the many-body potentials, LZO stays in an ordered pyrochlore structure up to its melting point, whereas Gd₂Zr₂O₇, for which a many-body potential is also available, shows extensive cation disordering at elevated temperatures, both results in agreement with experimental and computational findings.⁵³⁻⁵⁶ Maintaining an ordered cation arrangement in the simulations is important in order to focus on the effects on anion transport caused by the field rather than the effects caused by cation defects.

In this study, three different LZO systems—oxygen-poor, oxygen-rich, and stoichiometric—are investigated by means of MD simulations as a function of temperature T and field strength E. The results yield, first, a detailed description of oxide-ion conduction and anti-Frenkel disorder in LZO at low field strengths and, in this way, provide a solid base for the investigation of anion-defect behavior at high field strengths. Subsequently, we derive a mathematical expression to describe the field-enhanced formation of anti-Frenkel defects. It is noted that the emphasis is not on LZO as such. LZO simply provides a suitable system for obtaining the MD data that we require in order to derive the mathematical expression. It also provides us with a suitable system for demonstrating the use of various methods to obtain the enthalpy and entropy of anti-Frenkel disorder.

1.1. Literature Review of Field-Dependent Defect Formation

There are a few computational studies that have investigated point-defect formation in an electric field, but they provide no clear picture. Density-functional-theory (DFT) calculations have been conducted on HfO₂,⁵⁷ SiO₂,⁵⁸ TiO₂,⁵⁹ alkaline-earth-metal binary oxides⁶⁰ and ABO₃ perovskites.⁶¹ The studies that have addressed anti-Frenkel defect formation⁵⁷⁻⁵⁹ are similar in that they predict the electric field has an effect on the formation energy of charged defect pairs (O^″_iv^••_O), but systematic investigations are absent. Furthermore, defect concentrations at finite temperatures were not calculated. (Incidentally, four^57,59−61 of the above studies additionally agree that the formation of neutral oxygen vacancies (v^×_O) is affected by strong electric fields.)

MD simulations, on the other hand, are in principle capable of directly yielding c_def(E,T), since large systems of the order of 10⁴ to 10⁵ particles can evolve over several nanoseconds at finite temperatures in the presence of an electric field. Xu et al.⁶² have performed a field-dependent study on YSZ with grain boundaries and observed small changes in defect concentration with increasing field strength. The field strengths used (10^–3 MV cm^–1) are, however, orders of magnitude lower than would be expected⁶³ for a field effect [(10¹ to 10²)MV cm^–1]. Since the Wigner–Seitz (WS) cell method was used to determine the number of point defects, these results should be viewed with caution since the method tends to falsely identify point defects in simulation cells with complex structures, e.g., cells containing extended defects, such as surfaces or grain boundaries.⁶⁴ In another study by Schie et al.,⁶⁵ field-dependent defect formation was investigated for HfO₂, and a simple model was presented to calculate the critical field strength E^aF_crit required for the formation of an anti-Frenkel (aF) pair by an oxide ion on a regular lattice site moving a distance d_vi to overcome the standard Gibbs formation energy of anti-Frenkel disorder ΔG^⊖_aF

3

While the MD results were consistent with the predicted values of eq 3 (no defect generation observed at lower fields), confirmation was not obtained because E^aF_crit was an order of magnitude higher than the field at which the simulation cells became unstable.

Experimental evidence of a field-dependent defect concentration is rare, as the field strengths required for this are extraordinarily high, and, in addition, field effects must be separated from other voltage-induced effects. Evans et al.⁶⁶ applied high field strengths (up to 6 MV cm^–1)⁶⁷ to hexagonal Er(Mn,Ti)O₃ single crystals and found an increase in electrical conductivity of several orders of magnitude, attributing the increase to the formation of anti-Frenkel pair defects. The possibility of stoichiometry polarization was not excluded, however, nor was the possibility of sample decomposition. The authors claimed that support for the stability of anti-Frenkel pairs was provided by MD simulations, but the simulations were only carried out for tens of ps, whereas with respect to experiment, stability is presumably required for hours at the very least.

1.2. Theoretical Prediction of u_O(E)

It is important to keep in mind the difference between defect mobilities and ion mobilities. Equation 1 was written in terms of defect quantities, but it could equally well be written in terms of ion quantities. Since ion concentrations are orders of magnitude higher than defect concentrations (by definition), and since there is only one measured conductivity, the ion mobility has to be orders of magnitude lower than the defect mobility. Specifically, for an oxide material with two mobile oxygen defects, the mobility of the oxide ions, u_O, can be described as the weighted sum of each defect’s individual mobility (here, oxygen vacancy mobility u_v and oxygen interstitial mobility u_i)

4

The following description of u_O(E) applies individually to vacancy and interstitial contributions.

The theoretical treatment of u_O(E) assumes that the mobility is proportional to the difference in the forward (f) and reverse (r) jump rates. The quantitative treatment yields

5

where d_O is the jump distance, c_def is the number density of defects (vacancies or interstitials), c_O is the number density of oxide ions, ν₀ is the jump attempt frequency, k_B is Boltzmann’s constant, and T is the temperature. The activation free enthalpies for the forward and reverse jumps, ΔG^‡,f_mig and ΔG^‡,r_mig, are obtained by assuming that the free energy landscape is cosinusoidal and that the field is linearly superimposed on the free energy landscape⁶⁸

6

with γ = (|z_O|eEd_O)/(πΔG^‡_mig). This approach is superior to the traditional approach²²⁻²⁴ as it is mathematically exact for a given free energy hypersurface. In the limit of small fields, eq 5 becomes (with ΔG^‡_mig = ΔH^‡_mig – TΔS^‡_mig)

7

i.e., the standard expression for the field-independent mobility is recovered.

The rationale behind this approach, indeed, its specific benefit, is that eq 6 predicts ΔG^‡,f/r_mig(E) from the zero-field quantity ΔG^‡_mig and from the structural quantity d_O. It obviates the need to calculate individually ΔG^‡,f_mig and ΔG^‡,r_mig (and the respective d_O values) for each E value of interest. For exceptionally high field strengths (E ∼ 10^1.5 MV cm^–1), above which the electrons in a solid will be affected,^69,70 discrepancies are to be expected, but such field strengths are not considered in this study. In cases where exact values are required, DFT calculations of ΔH^‡,f/r_mig (see refs (57 and 58)) and ΔS_mig^‡,f/r would need to be performed.

One of the aims of this study is to derive an analogous expression for defect concentrations that would predict quantitatively c_def(E,T) from (easily accessible) zero-field quantities.

2. Computational Methods

We used MD simulations to investigate field-dependent ion transport because the method is efficient, has a comparatively low computational cost, and allows u_def and c_def to be obtained directly from the simulations over large ranges of temperature and field strength. In addition, we need to make no assumptions in advance about the exact migration paths taken (and thus the heights of the migration barriers), and this is important because the pyrochlore structure has a variety of different migration barriers (for vacancies and interstitial transport) due to its three crystallographically different oxygen sites (see Figure 1).

MD simulations were performed by means of the LAMMPS code⁷¹ with periodic boundary conditions in all dimensions. The NpT ensemble with constant particle number N, pressure p, and temperature T was employed, and to ensure this, Nosé–Hoover thermostat and barostat with damping parameters of 0.1 and 10 ps, respectively, were used.^72,73 The pressure of 0 bar was used in all simulations. The long-range Coulombic interactions were calculated with a particle–particle particle–mesh solver⁷⁴ with an accuracy of 10^–5. Newton’s equations of motion were integrated by means of the velocity Verlet algorithm with a time step of 1 fs. The electric field in the simulations was included as an additional force F_j = z_jeE acting on each particle. In all simulations, the electric field was applied in the x-direction, and the drift velocity of oxide ions (v_d,O) in this direction was determined. Specifically, v_d,O is obtained easily and reliably from MD simulations⁷⁵ by evaluating the mean displacement of all oxide ions, ⟨r_O⟩, as a function of simulation time t, according to v_d,O = d⟨r_O⟩(t)/dt (the behavior should be linear, as this indicates steady-state conditions with a constant drift velocity). The mobility u_O is subsequently obtained from

8

Short-range interactions were modeled with the many-body potential derived by Cooper et al.,⁵⁰ which is based on the embedded atom method⁷⁶ and calculates the potential energy U_j of an atom j as

9

The first term in eq 9 describes simple pair interactions between two atoms j and k separated by a distance r_jk. Here, ϕ_αβ(r_jk) is a combination of Morse and Buckingham potentials

10

11

12

The second term in eq 9 calculates the energy required to introduce an atom j with type α into the electron cloud distribution of the surrounding atoms with atom type β. It is comprised of a pairwise interaction σ_β(r_jk) = n_β/r⁸_jk that is passed through a nonlinear embedding function 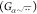. Though usually used for simulations of metals and alloys, it was demonstrated by Cooper et al.(50) that this approach is applicable to ionic systems, too. Specifically, they derived a set of parameters for actinide oxides substituted in CeO₂, including the O–O interactions, and, in a subsequent work,⁷⁷ pair potential contributions of lanthanide oxides, including the La–O interactions. These are combined with a second parameter set⁵¹ that includes a Zr–O interaction and the same O–O interaction (see Table 1).

Table 1. Potential Parameters for the Many-Body Potential Used in This Study^a.

α–β	La–O	Zr–O	O–O	Zr–Zr
Dαβ/eV		1.2269
γαβ/Å–1		1.4482
r0/Å		1.998
Aαβ/eV	36197.135	1147.471	830.283	18,600
ραβ/Å	0.2069536	0.32235	0.3529	0.23066
Cαβ/Å6	0.000	0.000	3.8843	0.000
Gα/Å1.5		1.597	0.69
nβ/Å5		1188.786	106.856

^aShort-range interactions are calculated with eqs 9–12 using values for La–O taken from ref (77), for Zr–O and Zr–Zr from ref (51), and for O–O from ref (50). The charge numbers of the species are z_O = −1.1104, z_Zr = +2.2208, and z_La = +1.6656. The short-range interaction cutoff was set to 11.0 Å.

Oxygen transport in stoichiometric LZO was examined in a supercell containing 45,056 ions (La₈₁₉₂Zr₈₁₉₂O₂₈₆₇₂) for the temperature range 2000 ≤ T/K ≤ 2875 and for the range of field strengths 1.0 ≤ E/MV cm^–1 ≤ 20.0. The cells were first equilibrated for 50 ps, and then mean displacements were monitored for another 450 ps. For E ≤ 3.0 MV cm⁻¹, the time of the production run was increased to 950 ps to improve the jump statistics. Two independent runs were conducted at each field strength, and the obtained mobilities were averaged. For oxygen-rich and oxygen-poor LZO, 30 oxygen ions were randomly introduced into the structural vacancies or removed from 48f oxygen positions, ensuring a dilute solution and negligible defect–defect interactions. The excess charge was compensated by increasing/decreasing the charge of the Zr cations. In these systems, u_O was determined as an average over three independent runs for 1000 ≤ T/K ≤ 2875 and E ≤ 2.0 MV cm^–1. The cells were equilibrated for 50 ps, and production runs lasted 1450 ps for T < 2000 K, 950 ps for 2000 ≤ T/K ≤ 2500, and 450 ps for T > 2500 K.

Since we used potentials^50,51,77 that were not derived specifically for LZO, we confirm in Table 2 that the predicted room-temperature lattice parameter and the high-temperature thermal expansion coefficient agree very well with experimental^54,78−80 and computational⁸¹ data.

Table 2. Comparison of Room-Temperature Lattice Parameter a and High-Temperature Thermal Expansion Coefficient a_L (for the Temperature Range 300 ≤ T/K ≤ 2500) with Values from Other Computational (Comp.) and Experimental (Expt.) Studies^a.

a/Å	aL/10–6 K–1	expt./comp.	references
10.830	10.53	comp., MBP	rhis study
10.7997	9.0	expt.	(78)
10.8128	10.3	expt.	(54)
10.794	7.0	expt.	(79)
10.812	7.76	expt.	(80)
10.828	6.96	comp., EPP	(81)

^aThe value of ref (81) was converted to a room-temperature lattice parameter. (MBP, many-body potentials; EPP, empirical pair potentials).

3. Results and Discussion

Investigating field-dependent defect migration and formation requires, first of all, knowledge of the field-independent parameters that characterize migration (ΔH^‡_mig and ΔS^‡_mig) and formation (ΔH^⊖_aF and ΔS^⊖_aF). This is because increases are relative to the field-independent situation. All these parameters are obtained directly from MD simulations rather than from static (i.e., 0 K) simulations, so they refer to the same temperature of interest and the same concentration range of the defects.

In the following, we first obtain for both oxygen vacancies and oxygen interstitials ΔH^‡_mig and ΔS^‡_mig from u_O at low field strengths. Then, we present and use three methods for extracting ΔH^⊖_aF and ΔS^⊖_aF directly from MD simulations. Subsequently, we analyze the high-field behavior; we show that u_O(E) alone cannot describe the data; we derive a mathematical expression for the description of c_def(E); and we demonstrate that the MD results can be described by a combination of u_O(E) and c_def(E).

3.1. Oxide-Ion Mobilities at Low Field Strengths

Anticipating later results as a function of field strength, we consider in Figure 2 the field-independent oxide-ion mobilities, u_O,E→0, obtained for E ≤ 2.0 MV cm⁻¹. Three different systems are considered: La₂Zr₂O_7−δ with extrinsic oxygen vacancies (LZO+vO); La₂Zr₂O_7+δ with extrinsic oxygen interstitials (LZO+Oi); and stoichiometric La₂Zr₂O₇ (LZO). As expected, the two nonstoichiometric systems exhibit a low-temperature extrinsic regime governed by the purposely introduced defects and a high-temperature intrinsic regime where both systems behave identically to each other and to the stoichiometric system. The extrinsic regimes (at T ≤ 2000 K) are characterized by negligible contributions from intrinsically generated defects.

Figure 2.

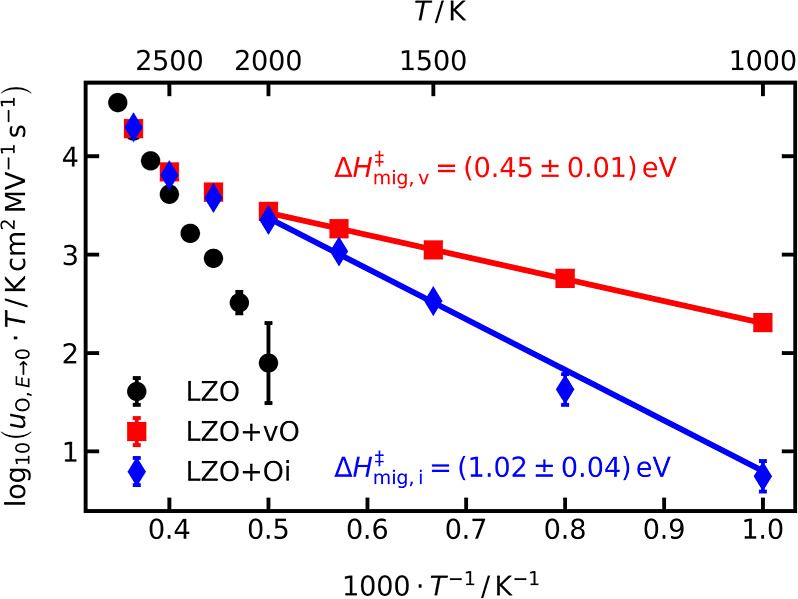
Field-independent oxide-ion mobilities, u_O,E→0, as a function of inverse temperature obtained for the three different systems LZO (stoichiometric), LZO+vO, and LZO+Oi. The activation enthalpies of migration, ΔH^‡_mig,v and ΔH^‡_mig,i, are obtained by weighted linear regression of eq 7 to the data.

Analyzing these regions with eq 7 to extract activation enthalpies and entropies requires the jump length of oxygen vacancies/interstitials, d_v/i, and the attempt frequency ν₀. For the latter, we use the experimentally determined Debye temperature^82,83 of Θ_D ≈ 550 K to obtain ν₀ = Θ_Dk_B/h = 11.5 THz (with h being Planck’s constant). The jump length of oxygen vacancies refers to the shortest distance between two 48f positions, d_v = 2.8 Å. As mentioned in Section 1, interstitial oxide-ion transport in pyrochlores is not well characterized. Analysis of the trajectories of our simulations shows that interstitial ion transport occurs by means of an extended interstitialcy mechanism involving three oxide ions. Specifically, an interstitial ion on the 8a site jumps toward an occupied, adjacent 48f position, pushing this oxide ion away. This displaced ion pushes, in turn, a third oxide ion from its 48f site onto an adjacent, empty 8a site, forming an interstitial. We also observed a few interstitialcy events involving even more oxide ions, but since the time resolution was only 1 ps, it is unclear if such events were in fact two three-oxide-ion interstitialcy events, one after the other; these jumps are ignored since the majority of jumps involved only three oxide ions. Since for ion transport in a field, the distance traveled by the charge is crucial, we define the jump distance of interstitial transport as the distance between the two nearest 8a positions, d_i = 7.7 Å.

Our analysis of the data in Figure 2 with eqs 6 and 7 (and substituting d_O with d_v and d_i, respectively) thus yields ΔH^‡_mig,v = (0.45 ± 0.01) eV and ΔS^‡_mig,v = −(1.24 ± 0.04) k_B for oxygen-vacancy migration in LZO+vO; and ΔH^‡_mig,i = (1.02 ± 0.04) eV and ΔS^‡_mig,i = −(0.05 ± 0.28) k_B for oxygen-interstitial migration in LZO+Oi. Experimental conductivity studies of La_1.95Sr_0.05Zr₂O_6.975 (i.e., a system with oxygen vacancies) report activation energies of (0.4 to 0.6) eV,^84,85 in excellent agreement with our value of ΔH^‡_mig,v = (0.45 ± 0.01) eV.

Extrapolating the data for the extrinsic regimes in Figure 2 to lower and higher temperatures, one recognizes that the vacancies are far more mobile than the interstitials for T ≤ 1000 K and that the two mobilities are comparable for T ≥ 2000 K. Consequently, in the intrinsic regime, thermally generated vacancies and interstitials both contribute to the observed mobility. In the next section, these data are used, as one of three methods, to extract ΔH^⊖_aF and ΔS^⊖_aF.

3.2. Determination of ΔH^⊖_aF and ΔS^⊖_aF from MD Simulations

The equilibrium constant of anti-Frenkel disorder [eq 2] can be written as

13

where ΔH^⊖_aF and ΔS^⊖_aF are the enthalpy and entropy of anti-Frenkel defect formation, respectively. The concentrations of oxygen interstitials, oxygen vacancies, interstitial sites (v^×_i, i.e. structural vacancies), and oxygen ions (O^×_O) are denoted by c_i, c_v, c_is, and c_O, respectively. If no other point-defect reactions occur in the simulation cells, charge neutrality requires that c_v = c_i. The equilibrium concentration of defects formed by the anti-Frenkel disorder reaction is thus

14

In the following, c_def always refers to the concentration of anti-Frenkel defects (c_def ≡ c_v = c_i).

Since, to the best of our knowledge, the direct determination of ΔH^⊖_aF and ΔS^⊖_aF from MD simulations has not been carried out, we employ three different methods to determine these quantities. Achieving good agreement between the three methods would indicate that the methods are reliable.

3.2.1. Comparison of Extrinsic and Intrinsic Systems

The first method we used for determining ΔH^⊖_aF and ΔS^⊖_aF from MD simulations is based on the experimentalist’s approach of comparing the conductivity (or ion mobilities) of systems displaying extrinsic and intrinsic behavior. First, defect mobilities u_i and u_v were calculated from the extrinsic-regime data of the systems LZO+Oi and LZO+vO (Figure 2) with the appropriate forms of eq 4. With this information, the intrinsic-regime data for LZO was analyzed. Specifically, the combination of eqs 4 and 14 gives an expression that was fitted to the u_O data for LZO (see Figure 3), yielding ΔH^⊖_aF = (5.32 ± 0.01) eV and ΔS^⊖_aF = (11.48 ± 0.22) k_B. From the individual contributions, one sees in Figure 3 that, at these high temperatures, the contribution from interstitials is larger than that from vacancies.

Figure 3.

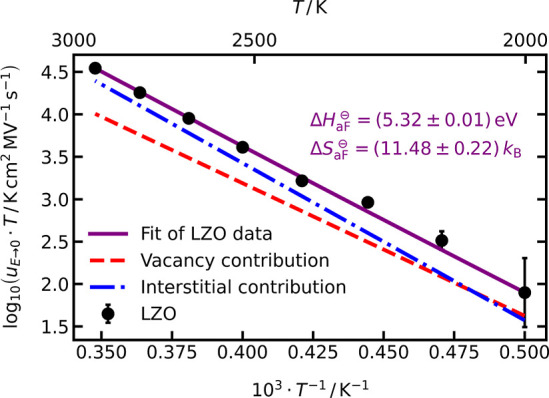
Field-independent oxide-ion mobilities, u_O,E→0, as a function of inverse temperature for stoichiometric LZO. The purple (solid) line is a weighted fit of eqs 4 and 14 to u_O,E→0, and the red (dashed) and blue (dashed-dotted) lines are the individual contributions from vacancy and interstitial mobility, respectively.

3.2.2. WS Analysis

The second method for determining ΔH^⊖_aF and ΔS^⊖_aF from dynamic simulations is unique to the simulator’s toolbox, namely counting the point defects present in the LZO simulation cell at each temperature. While simple in principle, reliably determining the number of defects in a dynamic system is difficult in practice since the ions are in motion and not at fixed points in space.

One easily implemented, and thus frequently applied, solution is the WS cell method. A simulation cell is divided into WS cells based on a reference structure (usually the perfect crystal lattice) so that each WS cell contains exactly one lattice site. Snapshots from MD simulations are subsequently mapped onto the WS cells, and the differences are counted as defects, with unoccupied WS cells being identified as vacancies and doubly occupied WS cells as interstitial ions. The major problem is that large-amplitude vibrational motion of ions may lead to such events being counted erroneously as point defects. As a result, we analyze the two nonstoichiometric systems in addition to the stoichiometric system. The difference between the number of counted defects and intentionally inserted defects in the nonstoichiometric systems should equal the number of defects counted in LZO. If the numbers are different, this is a sign of such falsely identified defects.

For the three systems, c_def was obtained with the WS analysis, as implemented in the postprocessing software OVITO.⁸⁶ Only oxygen vacancies and oxygen interstitials were found (no cation defects), and the results are shown in Figure 4. As expected, we find a steady increase of c_def with increasing temperature in LZO, which can be attributed solely to the anti-Frenkel equilibrium. Fitting eq 14 with a weighted linear regression to the data, ΔH^⊖_aF = (5.21 ± 0.15) eV and ΔS^⊖_aF = (13.14 ± 0.33) k_B are obtained, in good agreement with the values determined with the first method (see Figure 3).

Figure 4.

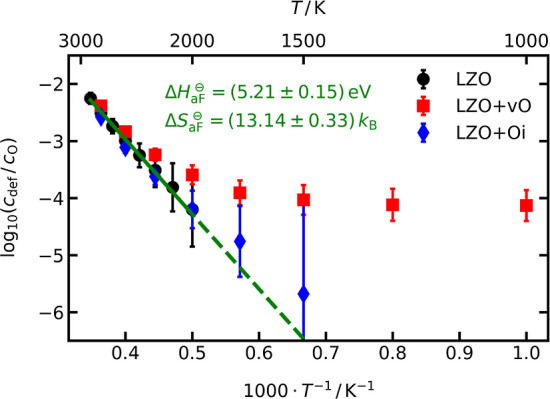
Temperature-dependent relative defect concentration, c_def/c_O, obtained with the WS analysis for the three different systems LZO, LZO+vO, and LZO+Oi. Anti-Frenkel formation enthalpy and entropy, ΔH^⊖_aF and ΔS^⊖_aF, are obtained by fitting eq 14 with a weighted linear regression to the LZO data. For LZO+Oi, data of the lowest two temperatures are not shown because there were no additional defects detected over the whole simulation time.

Tests of the WS cell method revealed for the vacancy system (LZO+vO) a constant offset of c_def at lower temperatures instead of a steady decrease, as observed for LZO. This offset is attributed to large relaxations of oxide ions adjacent to oxygen vacancies. In fact, repeating the simulations with a smaller number of oxygen vacancies led to a reduction of the offset at lower temperatures and thus support the assumption of an artefact. For the interstitial system (LZO+Oi), on the other hand, the WS analysis gave (within error) similar values to the (extrapolated) values of LZO and, in addition, identified no defects below 1500 K. These tests, combined with the similar values of ΔH^⊖_aF and ΔS^⊖_aF compared to the first method, indicate that the application of the WS analysis provides, in the case of LZO, meaningful values, but that the success of the method is not guaranteed, even for a single system.

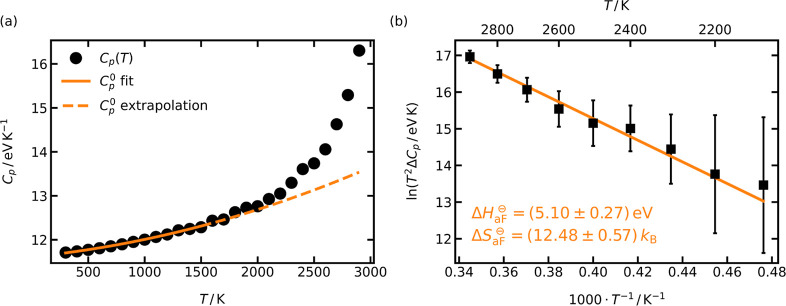
3.2.3. Excess Heat Capacity

Originally proposed by Mott and Gurney²³ in 1940 and first used experimentally in the 1950s,⁸⁷⁻⁸⁹ the third method is also copied from the experimental world. It concerns the anomalous increase in a solid’s heat capacity on account of defect formation as the melting point is approached. The measured heat capacity thus has two contributions

15

C⁰_p(T) refers to the heat capacity of the solid without point defects and ΔC_p(T) to the contribution from point defects (=∂ΔH_def/∂T). In the case of anti-Frenkel disorder, ΔH_def = (c_def/c_O)N_OΔH^⊖_aF (with N_O being the number of oxygen ions), one obtains

16

Thus, a plot of ln(T²ΔC_p) versus 1/T yields ΔH^⊖_aF from the slope and ΔS^⊖_aF from the intercept, once ΔH^⊖_aF is known.

To this end, we conducted short (50 ps) MD simulations of LZO for temperatures 300 ≤ T/K ≤ 2900 and determined the average total energy of the system, U_tot, at each temperature. We then described U_tot(T) over the entire temperature range with cubic splines (not shown); assuming reasonably H_tot ≈ U_tot, we obtained 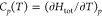by differentiating the spline function. The results are shown in Figure 5a. To extract ΔC_p(T) from C_p(T), one requires C⁰_p(T) for the temperature range of interest, and this is generally obtained by extrapolating C_p(T) from a range of lower temperatures, for which anti-Frenkel disorder is negligible. We identified the relevant temperature range of C⁰_p(T) from Figure 2 (mobility data) and in particular Figure 4 (WS analysis), both of which indicated no anti-Frenkel defects in the simulation cells for T ≤ 1500 K, and we then described these data with a second-order polynomial to obtain C⁰_p(T). Extrapolating, now, C⁰_p(T) to T > 1500 K, we find an increasing difference between the extrapolated C⁰_p and the calculated C_p(T) for T > 2000 K, i.e., ΔC_p(T). A fit of eq 16 to the ΔC_p data, as shown in Figure 5b, yields ΔH^⊖_aF = (5.10 ± 0.27) eV and ΔS^⊖_aF = (12.48 ± 0.57) k_B, values in good agreement with those obtained from the previous two methods.

Figure 5.

(a) Heat capacity at constant pressure, C_p, obtained from differentiating a cubic spline fit of the temperature-dependent cell energies, C_p = dU_tot/dT. The solid line represents a second-order polynomial fit up to 1500 K, the temperature range with negligible amounts of anti-Frenkel defects. The dashed line is an extrapolation of the polynomial fit to 2900 K. (b) Excess heat capacity, ΔC_p, calculated as the difference between the defect-free system [extrapolated values, dashed line in (a)] and the observed system (black circles). The values for ΔH^⊖_aF and ΔS^⊖_aF were obtained by fitting eq 16 with a weighted linear regression to the data. Error bars are based on the uncertainties of the second-order polynomial fit [solid line in (a)].

3.2.4. Summary and Comparison

The very good agreement between the values of ΔH^⊖_aF and ΔS^⊖_aF determined by three methods—combination of defect mobilities, WS analysis, excess heat capacity analysis—is a strong result for the determination of defect numbers from dynamic simulations, and the subsequent calculation of ΔH^⊖_aF and ΔS^⊖_aF is not trivial. Consideration of all three data sets together gives ΔH^⊖_aF ≈ (5.2 ± 0.1) eV and ΔS^⊖_aF ≈ (12 ± 1) k_B.

Since there are no experimental data available for comparison of ΔH^⊖_aF and ΔS^⊖_aF, we turn to values obtained from (static) simulations. DFT calculations predict ΔH^⊖_aF of (0.5 to 1.0) and 1.7 eV,⁹⁰ with EPP calculations predicting (6.4 to 7.2) and 6.12 eV. The DFT calculations were performed with both vacancy and interstitial in the same small supercell of only 88 atoms, and hence the influence of defect–defect interactions on these values is unclear. The EPP results, in contrast, refer to infinite dilution. Our value of ΔH^⊖_aF is much closer to the EPP values, and it was obtained for a finite, but low, defect concentration range of 10^–6 ≤ c_def/c_O < 10^–2 (over a temperature range of 2000 ≤ T/K ⩽ 2875). We consider our value, therefore, to be physically reasonable.

Values of ΔS^⊖_aF are not available for LZO, or indeed, for any pyrochlore material. The two closest cases are CeO₂, for which Grieshammer et al.⁹¹ obtained ΔS^⊖_aF = 10 k_B from DFT calculations, and In₂O₃, for which Walsh et al.⁹² obtained ΔS^⊖_aF = 5.8 k_B from EPP calculations. Since our value of ΔS^⊖_aF ≈ (12 ± 1) k_B is of a similar order of magnitude, we also consider this value to be physically reasonable.

The investigation of the high-field behavior relies on a precise description of the system at low field strengths at the temperatures and defect concentrations examined. With these results, we have such a precise description of the low-field behavior of LZO and can now turn to the influence of high electric fields on defect formation and migration.

3.3. High-Field Behavior of LZO

Oxide-ion mobilities u_O were obtained from MD simulations of LZO at field strengths of 1.0 ≤ E/MV cm^–1 ≤ 20.0 and temperatures of 2000 ≤ T/K ≤ 2875. For some combinations of very high field strengths and high temperatures, the crystalline structure became amorphous during the MD simulation, as indicated by the loss of long-range order in the radial distribution functions (not shown). Closer examination of such cells before amorphization revealed the presence of cation vacancies on both cation sublattices, as well as cation interstitials and cation antisite defects. Since our primary interest in this study is anti-Frenkel disorder, the presence of other point defects in simulation cells would complicate the analysis, and hence we did not consider u_O data from those simulations in which cation point defects were detected. The mobilities obtained from the remaining simulations are shown in Figure 6.

Figure 6.

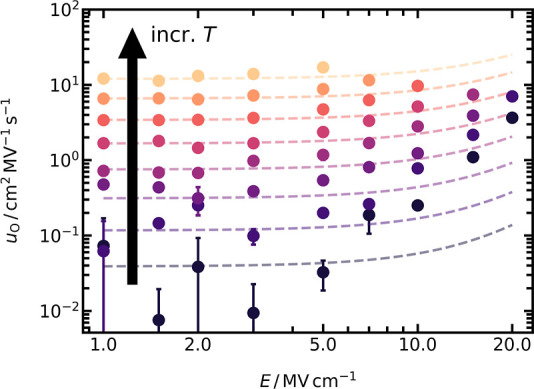
Field-dependent oxide-ion mobilities u_O obtained from MD simulations of LZO in the range of 2000 ≤ T/K ≤ 2875 (with 125 K steps). Every data point is the average of two independent runs, with their standard deviation included as error bars. Dashed lines are predictions of u_O with eqs 4–6.

The qualitative behavior is as expected, that is, constant u_O at low field strengths (here, up to 2.0 MV cm⁻¹) and a nonlinear increase at higher field strengths. The large scatter in u_O for T < 2375 K is a result of poor jump statistics, i.e., only a small number of ion jumps in the field direction took place during the simulation time of 1.5 ns. Returning briefly to those cells that became amorphous during the simulations, we compare the field strength required for amorphization at a given temperature (e.g., E = 20.0 MV cm⁻¹ at T = 2375 K) with E^mig_crit, the critical field strength at which a crystalline phase becomes unstable because the ions are no longer confined to potential wells, i.e., the migration barrier in one direction goes to zero [specifically, γ in eq 6 goes to zero]. Assuming that ΔG^‡_mig,v will be the first barrier to go to zero, we predict with

17

that the critical field strength is much higher, E^mig_crit ≈ 69 MV cm⁻¹. This comparison does not take into account, however, the presence of cation point defects in the simulation cells prior to amorphization. In particular, theoretical and experimental studies show that small amounts of cation disorder reduce the activation barrier of oxide-ion migration by (0.3 to 0.5) eV,^41,93 with the consequence that E^mig_crit ≈ (40 to 26)MV cm^–1, and thus are in better agreement with the observed behavior in the simulations.

Coming back now to the main topic and Figure 6, we compare the simulation data with the predictions of Section 1.2, taking into account u_v(E) and u_i(E). One perceives that there is a substantial discrepancy for E > 7 MV cm⁻¹, which strongly suggests the occurrence of field-enhanced defect formation. Of course, this comparison assumes that the standard treatment of Section 1.2 is applicable to vacancy and interstitial migration in LZO. Since there are no reasons, however, to suspect that the treatment is invalid at these field strengths,^68,75,94 we attribute the discrepancy to the field-enhanced formation of ionic charge carriers.

Unambiguous support for field-enhanced defect formation is provided by a WS analysis (cf. Section 3.2.2) of the same simulation cells from which u_O(E) was obtained (Figure 6). From the analysis, we obtain defect concentrations as a function of E and T, and we plot the results in Figure 7. Also shown (as dashed lines) are the field-independent defect concentrations from Figure 4. Substantial deviations between the symbols and the lines are apparent for E > 7 MV cm⁻¹. The degree of deviation increases with increasing field and with decreasing temperature, reaching 2 orders of magnitude for the lowest temperature and highest field examined. For an increase of 1 order of magnitude at, say, T = 2000 K, a field of 10 MV cm⁻¹ is necessary.

Figure 7.

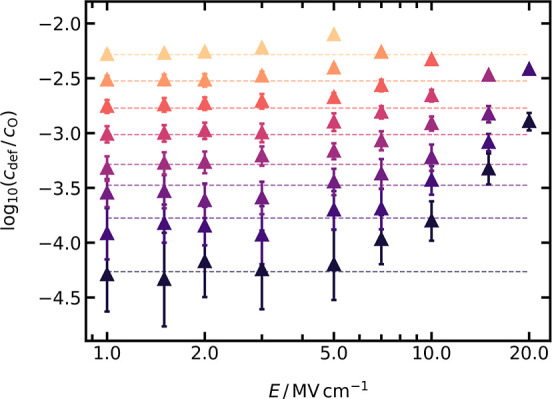
Field-dependent relative defect concentration, c_def/c_O, determined with the WS analysis in the range of 2000 ≤ T/K ≤ 2875 (with 125 K steps). Every data point is the average of two independent runs, with their standard deviation included as error bars. Dashed lines are the field-independent c_def/c_O values determined for LZO from Figure 4.

From the data in Figure 7, an effective defect formation enthalpy can be calculated according to

18

The results are shown in Figure 8, and they indicate that ΔH^⊖_aF,eff is hardly affected by the electric field up to 7 MV cm⁻¹ but decreases strongly at higher field strengths. This is consistent with the deviation of u_O from the prediction of the standard analytical model observed in Figure 6. At E > 7 MV cm⁻¹, the anti-Frenkel disorder reaction is enhanced by the field-induced decrease of ΔH^⊖_aF,eff, and consequently, the charge-carrier concentration increases. It is important to note that the field strength of 7 MV cm⁻¹ is specific to this system and to the examined temperature range.

Figure 8.

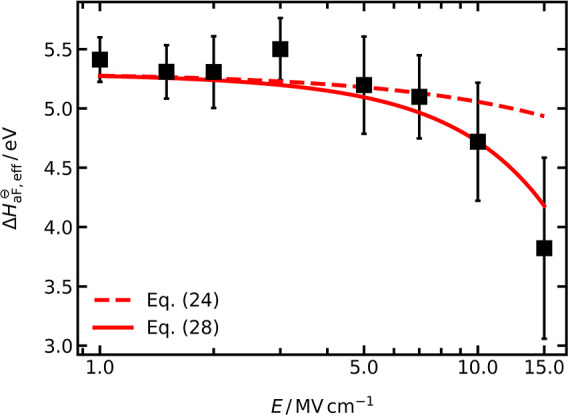
Effective anti-Frenkel defect formation enthalpy, ΔH^⊖_aF,eff, calculated with eq 18 from c_def in Figure 7. The dashed line is a prediction with eq 24, and the solid line is a fit of eq 28 with ΔH^r = 9 meV. For both predictions, ΔH^⊖_aF = 5.3 eV was used.

3.3.1. An Analytical Expression for ΔH^⊖_aF(E)

The formation of v^••_O and O^″_i through anti-Frenkel disorder takes place through a series of steps,⁹² such as

19

That is, it starts [step (i)] with an oxide ion on a regular lattice site moving to a vacant interstitial site, forming the defect associate (v_OO_i)^×. The vacancy and/or the interstitial move subsequently away from each other [step (ii)], but remain at finite separation. Further movement results eventually in the vacancy and interstitial being separated sufficiently far from one another to count as effectively noninteracting [step (iii)]. The Gibbs energy of anti-Frenkel disorder, ΔG^⊖_aF, refers to the difference between the initial and final states, whereas the relevant Gibbs energy for the field-driven process is the difference between the initial and second configuration (or even the initial and third configuration) in eq 19, with v^••_O and O^″_i separated by d_vi.

Before deriving a quantitative expression, we return to the simple equation derived by Schie et al.⁶⁵ [eq 3] to predict the critical field strength needed for enhanced defect formation. As mentioned in the previous paragraph, the critical issue is the values of d_vi and ΔG^⊖_aF used as input. With the inconsistent combination of d_vi = 2.2 Å (i.e., defect associate) and ΔG^⊖_aF (i.e., infinite separation), one finds E^aF_crit in the range of (123 to 85) MV cm^–1 for the temperature range (2000 to 2875) K, roughly an order of magnitude higher than the observed values. A consistent combination of ΔG^⊖_aF and d_vi with both quantities referring to the same configuration, i.e., to the second or third configuration in eq 19, is characterized by a much lower ΔG^⊖_aF,^65,92 thus leading to better agreement. In other words, we find no evidence invalidating eq 3; rather, we draw attention to the problems involved in using it, and we emphasize the need for an improved, quantitative treatment.

A quantitative model encapsulating the three reaction steps of eq 19 would involve a considerable number of parameters since each step would require a few characteristic parameters. It would possibly yield, if at all, an unwieldy expression for ΔH^⊖_aF,eff. Hence, instead of considering such an exact model, we formulate a simpler, effective model in which we assume that anti-Frenkel pair generation can be described approximately by the Gibbs energy landscape shown in Figure 9a. The landscape is characterized by a comparatively high barrier ΔG^‡,f for the formation of the defect pair and a small but nonzero barrier ΔG^‡,r for the recombination (as indicated in the figure, ΔG^‡,f = ΔG^⊖_aF + ΔG^‡,r).

Figure 9.

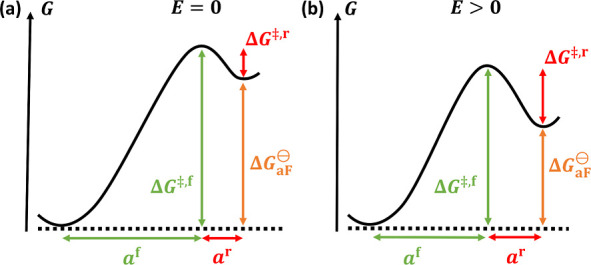
Simple model of field-driven anti-Frenkel disorder, showing Gibbs energy landscapes for the formation and recombination of oxygen vacancies and oxygen interstitials through the anti-Frenkel disorder reaction (a) without applied field and (b) with an applied field E. For the formation, the ion needs to traverse the distance a^f to overcome the barrier ΔG^‡,f, and for the recombination, the distance a^r and the barrier ΔG^‡,r. The difference between the initial and final states equals the free enthalpy of anti-Frenkel defect formation, ΔG^⊖_aF = ΔG^‡,f – ΔG^‡,r.

The reaction rate for anti-Frenkel formation can be written from standard chemical kinetics as

20

with rate constants k^f and k^r for charge-carrier formation and recombination, respectively. Expressing the rate constants k^f/r in terms of the respective attempt frequencies and Gibbs energies, that is, as ν^f/r₀exp[−ΔG^‡,f/r/(k_BT)], one recovers at equilibrium (v = 0)

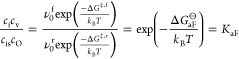21

i.e., the equilibrium constant of anti-Frenkel disorder. If an electric field is applied to the system, this will result in a decrease of ΔG^‡,f and an increase of ΔG^‡,r, as shown in Figure 9b. Assuming that, as in the traditional treatment,²²⁻²⁴ ΔG^‡,f/r is modified by the applied electric field according to

22

and assuming further that a^f ≈ a^r = d_vi/2 and ν₀^f = ν₀^r, one finds that the field-dependent equilibrium constant of anti-Frenkel disorder is

23

By applying eq 18, one then obtains

24

A comparison between this prediction and the MD-derived data for ΔH^⊖_aF,eff in Figure 8 (dashed line) reveals good agreement up to 7 MV cm⁻¹ but an underestimation of the decrease in ΔH^⊖_aF,eff at higher field strengths.

A superior approach to eq 22 is to assume a mathematical form for the Gibbs energy landscape and to superimpose the field linearly onto it. This is analogous to the treatment of field-driven ion mobility by Genreith-Schriever and De Souza⁶⁸ (see Section 1.2). Here, we assume that each Gibbs energy barrier sketched in Figure 9 has a cosinusoidal form, such that a linearly superimposed electric field leads to the equivalent forms of eq 6 for ΔG^‡,f/r(E). Since this does not produce a simple expression for ΔH^⊖_aF,eff, we expand the (f/r) forms of eq 6 to obtain

25

with

26

Truncating eq 25 after the quadratic terms, combining the result with eqs 21 and 26, and assuming a^f ≈ a^r = d_vi/2 gives

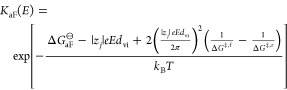27

Since ΔG^‡,r ≪ ΔG^‡,f (see Figure 9) and assuming, for simplicity, ΔG^‡,r ≈ ΔH^‡,r, we finally obtain by applying eq 18

28

With this expression, ΔH^⊖_aF,eff can be described satisfactorily over the whole field-strength range with ΔH^‡,r = 9 meV (solid line in Figure 8), although given the large error bars, descriptions with ΔH^‡,r from 5 up to 18 meV are possible. The difference between the two curves in Figure 8 illustrates the importance of taking the form of the free energy landscape into account, as this leads to an additional (quadratic) field term in eq 28. A second important point illustrated by eq 28 is the nonzero, field-dependent barrier for recombination, ΔH^‡,r. The value of ΔH^‡,r obtained is essentially a doubly effective quantity; it is effective because of the simplified model and because of the assumptions made in the derivation. Nevertheless, from its order of magnitude, it is in agreement with computational studies^65,95 that report fast recombination of neighboring oxygen vacancies and interstitials in AO₂ fluorites, extracting from the recombination kinetics effective activation energies of some tens of meV.

3.3.2. Prediction of Field-Dependent Oxide-Ion Mobilities

Combining eqs 4–6, 14, 28, and using ΔH^‡,r = 18 meV, we predict u_O(E,T) for LZO for the whole temperature and field strength range. As seen in Figure 10 for T > 2125 K, an excellent description of u_O is observed over the entire field strength range. At lower temperatures, it is unclear whether the mobilities are satisfactorily described due to poor data quality. The excellent description at higher temperatures, however, suggests that the predictions at lower temperatures are trustworthy.

Figure 10.

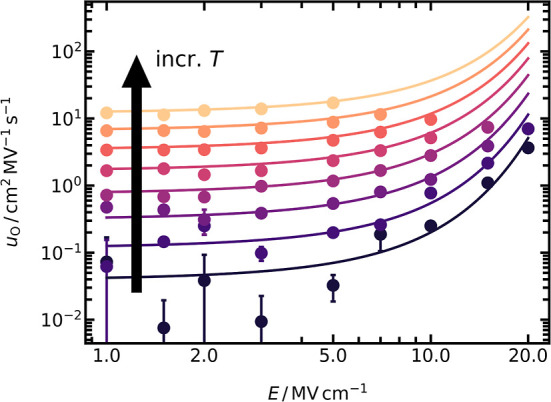
Field-dependent oxide-ion mobilities u_O obtained from MD simulations of LZO in the range of 2000 ≤ T/K ≤ 2875. Every data point is the average of two independent runs, with their standard deviation included as error bars. Solid lines are predictions calculated with a combination of eqs 4–6, 14, 28. For the predictions, ΔH_aF^⊖ = (5.32 ± 0.01) eV and ΔS_aF^⊖ = (11.48 ± 0.22) k_B from Figure 3 are used; and ΔH^‡,r = 18 meV.

We can predict with some confidence, therefore, the behavior at much lower temperatures, i.e., at those more appropriate to experiment or device. At T = 500 K, for example, we predict that a field of 5 MV cm⁻¹ is sufficient to increase the concentration of anti-Frenkel defects by 1 order of magnitude. Such a field is achieved by applying a potential difference of 1 V to a film of 2 nm thickness. It does not involve, therefore, potential differences of several volts, which are sufficient for phase decomposition, or film thickness below a unit cell. Since such a field also increases the vacancy mobility in LZO by a factor of 1.5, one can attain an increase in conductivity by a factor of 15. Consequently, utilizing this effect in actual devices is not limited by physical constraints; instead, we contend that fabricating high-quality, stable devices will be the major problem. Predicting the behavior of other pyrochlore systems,or indeed, other material systems, is difficult since it is unclear how the effective quantity ΔH^‡,r varies from system to system. Simulation studies of a range of pyrochlore compositions are thus required to make the next step of progress toward hitting the two birds of defect behavior with the one stone of an electric field.

4. Conclusions

In this study, we demonstrated how to successfully hit the two birds of defect mobility and defect concentration with the stone of a high electric field. To this end, field- and temperature-dependent ion mobilities u_O for oxygen-deficient, oxygen-rich, and stoichiometric La₂Zr₂O₇ (LZO) were determined from MD simulations employing many-body potentials. Three important points are highlighted:

• (1)Based on an effective free energy landscape of anti-Frenkel formation, we derived an expression to predict quantitatively c_def(E,T). The importance of field-dependent energy barriers for defect formation and recombination is emphasized.
• (2)According to our treatment, ionic charge-carrier concentrations in a pyrochlore oxide can be increased by orders of magnitude without the need for aliovalent doping or cation disorder and within the thermodynamic stability window of the material through the application of a high electric field.
• (3)We present three methods based on three different system properties to obtain oxygen-vacancy and oxygen-interstitial concentrations, and thus ΔH^⊖_aF and ΔS^⊖_aF, directly from MD simulations: combination of defect mobilities, WS analysis, and excess heat capacity analysis. Satisfyingly, all three methods agree very well with each other, yielding ΔH^⊖_aF ≈ (5.2 ± 0.1) eV and ΔS^⊖_aF ≈ (12 ± 1) k_B.

The authors declare no competing financial interest.

Notes

The English idiom is “To kill two birds with one stone”.