Abstract
Using data from the Applied Problems subtest of the Woodcock-Johnson Tests of Achievement (Woodcock & Johnson, 1989/1990, Woodcock-Johnson psycho-educational battery-revised. Allen, TX: DLM Teaching Resources) administered to 1,364 children from the National Institute of Child Health and Human Development (NICHD) Study of Early Childcare and Youth Development (SECCYD), this study measures children’s mastery of three numeric competencies (counting, concrete representational arithmetic and abstract arithmetic operations) at 54 months of age. We find that, even after controlling for key demographic characteristics, the numeric competency that children master prior to school entry relates to important educational transitions in secondary and post-secondary education. Those children who showed low numeric competency prior to school entry enrolled in lower math track classes in high school and were less likely to enrol in college. Important numeracy competency differences at age 54 months related to socioeconomic inequalities were also found. These findings suggest that important indicators of long-term schooling success (i.e., advanced math courses, college enrollment) are evident prior to schooling based on the levels of numeracy mastery.
Keywords: longitudinal, mathematical achievement, numeracy
1 |. INTRODUCTION
The development of mathematical ability in childhood is crucial for later academic and occupational success (Heckman, Humphries, & Veramendi, 2018a, 2018b; Long, Conger, & Iatarola, 2012). Yet, for decades, children in the United States have lagged behind students in other countries with respect to mathematical achievement. In 2018, the United States was ranked 38th out of the 79 countries that participated in the Program for International Student Assessment (PISA) for mathematics (OECD, 2019). While US students did slightly better on the 2019 Trends in International Mathematics and Science Study (TIMSS) math tests, they ranked behind countries such as Ireland, Russia and South Korea (Mullis, Martin, Foy, Kelly, & Fishbein, 2020). According to results from the National Assessment of Educational Progress (NAEP), only 41% of fourth-grade students in the United States reached mathematics proficiency in 2019, and only 9% reached an advanced level of mathematics achievement (NCES, 2019).
In the words of Horace Mann, education should be the ‘great equalizer’ of differences in students backgrounds and previous experiences (Mann, 1848). Yet, recent research using large-scale, nationally representative education data finds a more discouraging situation where achievement gaps that exist at the entry to formal schooling persist across primary and secondary education (Davis-Kean & Jager, 2014; Kuhfeld, Gershoff, & Paschall, 2018; von Hippel & Hamrock, 2019; von Hippel, Workman, & Downey, 2018). However, this research has only looked at early achievement predicting later achievement – all defined by standardized achievement test scores across primary and early secondary education (Watts, Duncan, Siegler, & Davis-Kean, 2014). Even though this approach provides information about the intertemporal relation among achievement scores, it does not tell us whether indicators of later academic success is also driven by early ability skills. Thus, it is unclear if these gaps are meaningful for outcomes such as participation in advanced math course work in high school or college enrollment after high school (Heckman et al., 2018a, 2018b; Heckman, Moon, Pinto, Savelyev, & Yavitz, 2010), which are more qualitative indicators of schooling success. Thus, the goal of this article, using a unique birth cohort study, was to use a measure of early numeracy to see if there were important skills that had already been acquired prior to enrolling in formal schooling (i.e., kindergarten) and explore the possible links between these early numeracy skills and later advanced math course-taking in high school and college enrollment.
1.1 |. Theoretical conceptualizations of early numeracy skills
Early numeracy skills are thought to develop through the acquisition of several key foundational skills followed by incremental increases in deeper mathematical skills that build on that early foundation (Libertus, Odic, Feigenson, & Halberda, 2016; Lyons, Bugden, Zheng, De Jesus, & Ansari, 2018; Matthews & Fuchs, 2020; Matthews, Lewis, & Hubbard, 2016; Sokolowski, Fias, Ononye, & Ansari, 2017). For example, Sarama and Clements (2009) posit a process whereby, after the notion of numeracy has been established, children engage mathematically with physical objects or visual representations of these objects and, over time, learn to generalize from these physical manipulations and conduct more abstract or symbolic mathematical operations. That is, children begin by conducting operations using representations (▲▲▲ + ▲▲ = ▲▲▲▲▲) before progressing to symbolic operations (3 + 2 = 5). Sarama and Clements (2009) argue that this process of ‘cyclic concretization’ occurs in multiple mathematical domains, such as by first recognizing shapes to later being able to understand geometric principles (e.g., area, circumference).
This conceptualization of numerical development implies a predictable sequence of mathematical skill acquisition, in which children move from a concrete understanding of numbers to a more abstract understanding. As such, this theory suggests that an understanding of symbolic numeric representations and facility with adding and subtracting using representations are essential building blocks for later success in mathematics. It implies that there is a progressive nature to numeracy development and that the successful mastery of certain early skills serves as the foundation for success in later advanced mathematical skills (Siegler et al., 2012).
1.2 |. Assessing early numeracy mastery
How, then, are these important early, foundational numeracy skills identified? One method has been to examine overall performance on various standardized achievement tests either at a single time point or across time (Barnard, 2004; Brooks-Gunn & Duncan, 1997; Lee & Bowen, 2006). Another method has been to deconstruct existing achievement scaled into component skills that may differentially predict later achievement and attainment. This approach was taken by Siegler et al. (2012), who categorized, using expert opinion, items on the Woodcock-Johnson Calculation Subtest (Woodcock & Johnson, 1989/1990) into various mathematical skills including addition, subtraction, multiplication, division and fractions. They then used the Woodcock-Johnson Applied Problem Subtest to categorize items that were tapping into algebra knowledge in order to test whether these earlier skills predicted to later algebra ability. They found that both fraction skills and division skills when children were between the ages of 8 and 10 years of age were important for later achievement in high school algebra.
The present study uses a similar approach as Siegler et al. (2012) and uses one of the same measures of achievement, the Woodcock-Johnson Applied Problems scale, to construct different numeracy skill areas. However, instead of using qualitative coding, we use an advanced item response methodology to categorize children’s skills. Also, unique from the research by Siegler and colleagues, we categorize these skills at an earlier age (preschool) and then extend the study to examine the role of these skills in the selection of advanced math classes in high school and later college enrollment. As the available measures focus primarily on capturing children’s facility with numbers – rather than spatial or geographic relations – our discussion focuses on numeracy rather than mathematics skills more generally.
1.3 |. Current study
Drawing from current theories about the building blocks of early numeracy skills as well as the research by Siegler et al. (2012), and using standardized assessments as a way to parse these numeracy skills into competency categories, the current study identifies skills measured at 54 months of age on the Applied Problems subtest of the Woodcock-Johnson Psycho-Educational Battery. We use an innovative quantitative approach based on item response methodology to classify these skills (Diagnostic Classification Model [DCM]; Rupp, Templin, & Henson, 2010). This classification method allows children to be grouped based on their mastery of foundational numeracy concepts, such as counting and adding. Once these 54-month competency groups were established, we documented whether there were demographic differences across the groups in order to document early numeracy skill gaps by early life background factors. We then examined how these established numeric abilities groups at preschool mattered for educational outcomes in adolescence and young adulthood. We built on previous research by Watts et al. (2014) that found that standardized numeracy achievement scores at preschool predicted adolescent achievement scores at age 15 years. We extended this work by identifying specific early skills (rather than a global measure of achievement) and examined whether these categories of numeric competencies also predicted math achievement at age 15 years. We also looked to see if children in the early numeric competency groups differed in the difficulty of the mathematical courses they took in high school. We did so because mathematics courses play a crucial gatekeeping role in the contemporary American educational system. Being proficient or above average in mathematics ability (specifically algebra) allows for the completion of advanced mathematics or calculus courses before graduating high school (Burris, Heubert, & Levin, 2004). Finally, based on the role of mathematical training in predicting college matriculation and graduation (Murnane, Willett, & Levy, 1995), we also examined whether early numeracy ability predicted college enrollment. Thus, our research builds on prior research demonstrating that early numeracy skills predict later mathematical skills by charting the extent to which mastery of some of the most basic early numeracy concepts in early childhood predicts two educational outcomes which, themselves, are important indicators of a successful transition to adulthood (c.f. Attewell & Domina, 2008; Card, 1999; Heckman et al., 2018a, 2018b; Long et al., 2012).
By focusing on numeracy skills at age 54 months, we are identifying the skills children have before they enter formal schooling, which can serve as indicators of what children may have learned in the home and early childhood education environments. Hence, to control for the possibility that early home and preschool environments may have independent effects on later achievement and attainment, we controlled for several potential confounding variables. Specifically, we included the family’s income-to-needs ratio, the quality of the home environment, the mother’s receptive vocabulary and the mother’s highest level of education. To make sure that we are isolating preschool numeric competencies and not just reflecting children’s overall cognitive abilities, we controlled for the child’s cognitive functioning at 24 months and the child’s short-term memory at 54 months in our models.
2 |. METHOD
2.1 |. Participants
Data were drawn from the National Institute of Child Health and Human Development (NICHD) Study of Early Childcare and Youth Development (SECCYD). Researchers recruited mothers over the age of 18 years who spoke English as their first language and delivered full-term, healthy newborn babies in 10 geographically diverse collection sites in the United States. This sampling procedure resulted in a diverse but not nationally representative sample of children born in 1991. Researchers followed these children and their families longitudinally through age 15 years. Additionally, after the end of NICHD sponsorship of the SECCYD, members of the NICHD Early Child Care Research Network collected high school transcripts and conducted a web survey about young adult role transitions when participants were between ages 22 and 23 years. The main time points of focus in the current study are the assessments at 54 months, age 15 years, the end of high school and college age.
The full sample of the NICHD SECCYD data set includes 1,364 children. As with any study that employs longitudinal data with multiple measurements, attrition occurs over time. Of the 1,064 children in the 54-month sample, 467 have high school transcript data and 406 have college enrollment data. The descriptive statistics for the 54-month sample and the final predictive sample are shown in Table 1 and Table S1 (Supplemental Materials). For a more thorough discussion of the full recruitment procedures and related limitations, see NICHD Early Child Care Research Network (2002). This study is based solely on secondary data that are deidentified and available for download through the Interuniversity Consortium for Political and Social Research (ICPSR), thus the research ethics committee at the [blinded for review] declared this study exempt.
TABLE 1.
Comparison between 54-month sample and high school course completion SECCYD sample
| Full sample |
Final predictive sample |
Attrition sample |
Sig. |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Variable | N | M | SD | n | M | SD | n | M | SD | |
| %child race and ethnicity | ||||||||||
| White | 1,064 | 0.79 | 0.41 | 470 | 0.85 | 0.36 | 594 | 0.74 | 0.44 | *** |
| Black | 1,064 | 0.11 | 0.32 | 470 | 0.07 | 0.25 | 594 | 0.15 | 0.36 | *** |
| Hispanic | 1,064 | 0.06 | 0.23 | 470 | 0.05 | 0.21 | 594 | 0.06 | 0.24 | |
| Other | 1,064 | 0.04 | 0.21 | 470 | 0.04 | 0.20 | 594 | 0.05 | 0.22 | |
| Mother’s education (in years) | 1,064 | 14.42 | 2.48 | 470 | 15.14 | 2.45 | 594 | 13.85 | 2.35 | *** |
| Mother’s PPVT score | 1,036 | 99.71 | 18.28 | 463 | 104.59 | 17.9 | 574 | 95.79 | 17.60 | *** |
| Partner in home (EC) | 1,064 | 0.86 | 0.3 | 470 | 0.91 | 0.25 | 594 | 0.82 | 0.33 | *** |
| Stable income to needs (EC) | 1,063 | 3.67 | 2.78 | 470 | 4.16 | 2.92 | 594 | 3.31 | 2.61 | *** |
| Average HOME score (EC) | 1,064 | 40.46 | 4.54 | 470 | 41.61 | 3.82 | 594 | 39.56 | 4.85 | *** |
| Proportion centre care (36–54 m) | 1,064 | 0.41 | 0.39 | 470 | 0.43 | 0.39 | 594 | 0.40 | 0.39 | |
| Memory for sentences 54 m | 1,061 | 91.86 | 18.5 | 470 | 95.39 | 18.2 | 594 | 89.09 | 18.25 | *** |
| Bayley MDI | 1,021 | 92.78 | 14.52 | 461 | 96.51 | 13.94 | 563 | 89.72 | 14.27 | *** |
| Percentage correct | ||||||||||
| Counting | 1,064 | 0.79 | 0.24 | 470 | 0.85 | 0.20 | 594 | 0.74 | 0.26 | *** |
| Concrete representational arithmetic operations | 1,064 | 0.45 | 0.30 | 470 | 0.51 | 0.29 | 594 | 0.40 | 0.30 | *** |
| Abstract arithmetic operations | 1,064 | 0.14 | 0.24 | 470 | 0.19 | 0.27 | 594 | 0.10 | 0.21 | *** |
| Clocks | 1,064 | 0.4 | 0.44 | 470 | 0.5 | 0.45 | 594 | 0.32 | 0.42 | *** |
| WJ-R applied problems | ||||||||||
| 54 months | 1,064 | 424.84 | 19.24 | 467 | 429.97 | 17.63 | 594 | 420.82 | 19.51 | *** |
| First grade | 995 | 470.25 | 15.50 | 454 | 473.11 | 15.42 | 541 | 467.84 | 15.18 | *** |
| Third grade | 943 | 497.72 | 12.70 | 448 | 499.56 | 12.77 | 495 | 496.05 | 12.41 | *** |
| Fifth grade | 918 | 510.14 | 11.98 | 442 | 512.47 | 11.43 | 476 | 507.97 | 12.08 | *** |
| Age 15 | 839 | 525.04 | 16.40 | 433 | 529.05 | 16.53 | 406 | 520.75 | 15.14 | *** |
Note: The full sample is students who had a WJ-R Applied Problem test score at 54 months. The significance test compares the final predictive sample with the attrition sample (who was not observed at the end of high school).
Abbreviations: EC, average of the variable reported at 1-, 6-, 15-, 24-, 36- and 54-month interviews; HOME, home observation for measurement of the environment; m, months; MDI, mental developmental index; PPVT, peabody picture vocabulary test; WJ-R, Woodcock-Johnson revised.
2.2 |. Measures
2.2.1 |. Background characteristics
We drew on data reported by SECCYD mothers when their children were 1 month of age to measure background characteristics, including the child’s sex, the child’s race and ethnicity (white, black, Hispanic, other) and the mother’s highest level of education (reported in years). Family income was provided by the mother during the 1-, 6-, 15-, 24-, 36- and 54-month interviews. We converted income to an income-to-needs ratio based on the federal poverty line at the time of data collection and how many children were living in the household at each time point. For simplicity, we combined these time-varying measures of family income-to-need into a stable family income-to-needs measure, which is calculated as the mean value of each of the available income-to-needs measures. Similarly, we calculated the proportion of time a partner lived in the household across the same six measurement points.
Based on research showing that the home environment may relate to children’s early numeracy ability (Davis-Kean, 2005; Levine, Suriyakham, Rowe, Huttenlocher, & Gunderson, 2010; Susperreguy & Davis-Kean, 2016), we used several additional items to characterize children’s early lives. The quality of the home environment was assessed using the Home Observation for Measurement of the Environment (HOME; Bradley & Caldwell, 1979) at 36 months. The HOME is administered through both observational assessment and structured interviews with the child’s parents or primary caregivers, with higher scores indicating a higher-quality environment. A composite HOME score was calculated using the same measurement time points as family income. The proportion of time (hours per week/total non-maternal care) in centre care between 36 and 54 months of age was used as a measure for children’s experiences in preschool before formal schooling. The mother’s score on the Peabody Picture Vocabulary Test (PPVT; Dunn & Dunn, 1981) was obtained when the child was 36 months old and is used as an indication of the mother’s crystallized intelligence (e.g., NICHD Early Child Care Research Network & Duncan, 2003). We included the Mental Developmental Index (MDI) of the Bayley Scales of Infant Development at 24 months (Bayley, 1993), which is an early assessment of cognitive functioning. The Bayley Scales of Infant Development is administered in a laboratory setting and involves a trained examiner observing the focus child as he or she plays game-like tasks, such as stacking blocks or placing pegs in a hole on a board. The WJ-R Memory for Sentences subtest administered at 54 months was included as a measure of the child’s short-term memory.
2.2.2 |. Mathematical competency
Children’s numeracy skills were assessed by a trained examiner at multiple waves using the Applied Problems subtest of the Woodcock-Johnson Psycho-Educational Battery–Revised, Form A (WJ-AP; Woodcock & Johnson, 1989/1990). The current study focuses on children’s WJ-AP scores at 54 months of age as the key independent variable and their scores at age 15 years as dependent variables; in addition, we examined their scores at first-, third- and fifth-grade descriptively across the skill groups. At each assessment, students answered items in order of difficulty, and basal and ceiling levels were determined for each student in order to ensure efficiency in the testing process. At 54 months, students began the WJ-AP with items focused on counting and continued receiving new items until they incorrectly answered six consecutive items. In the SECCYD, the Applied Problems subtest had strong internal reliability at each wave (60 items; scores ranging from α = .81–.87).
2.2.3 |. High school mathematics course-taking
Youth mathematics course attainment was derived from the high school transcript data collected from students after the end of high school. SECCYD researchers used these data, in conjunction with contextual data collected from the principal or a designated staff member at each respondent’s school on course offerings and graduation requirements, to associate each course that appeared on a student’s transcript with a Classification of Secondary School Courses (CSSC) code. Developed by the National Center for Education Statistics (NCES) and used in the National Education Longitudinal Study of 1988 (NELS) and Education Longitudinal Study of 2002 (ELS) transcript studies, these codes provide a standardized accounting of high school course titles. We simplified these course codes into an ordinal measure of the highest level of mathematics that students reached by the end of high school. The five ranked ordered categories were: ‘Algebra I’, ‘Geometry’, ‘Algebra II’, ‘Advanced Mathematics’ and ‘Calculus’. Students in the ‘Advanced Mathematics’ category completed at least one course beyond Algebra II, such as Trigonometry, Advanced Placement Statistics or Pre-Calculus but had not taken Calculus during high school.
2.2.4 |. College enrollment
Our final outcome was youth’s enrollment in postsecondary education. When the participants in the study were aged 22 or 23 years, they reported whether they had graduated from high school, whether they had enrolled in a two-year college and whether they had enrolled in a four-year college. For ease of interpretation, multivariate analyses focus in particular on the comparison between students who enrolled in a four-year college and those who did not.
2.3 |. Analysis plan
The purpose of our study was to identify early numeracy skills that may be key predictors of later achievement and attainment, using a validated mathematics assessment. The analysis proceeded in four steps. First, an exploratory factor analysis (EFA) was conducted to identify items in the WJ-AP that factored together. Second, we used a Diagnostic Classification Model (DCM; explained in detail below) to classify students into groups based on their mastery of key numerical concepts at 54 months that were identified through the EFA. Third, we examined descriptive analyses of early numeracy concept mastery inequalities by race or ethnicity, parent education and other aspects of their home environments in order to understand the characteristics of students who were classified together. Fourth, multivariate models were used to investigate the link between early concept mastery and later educational outcomes taking into consideration a rich set of background characteristics, as well as the classification groupings that were established by the DCM procedure.
3 |. RESULTS
3.1 |. Identification of early numerical competency factors
We used EFA models to uncover latent factors that explained shared variation in children’s patterns of correct item responses across multiple items. Initially, we allowed for one to six factors to be identified using oblique Geomin rotation to allow the factor analysis to return correlated factors (loadings patterns from the six EFA analyses are shown in Table S2a). Factor analyses were conducted on the first 25 WJ-R Applied Problems items using mean- and variance-adjusted weighted least squares estimation in Mplus (Muthén & Muthén, 2016) with the full sample of 54-month-old children (n = 1,041). As a result of the ceiling rules in the administration of the test, children at this age typically responded to the first 10–20 items before hitting the ceiling, thus 25 seemed likely to capture the abilities of all respondents at 54 months. All of the models showed excellent fit based on traditional standards (RMSEA <.05 and CFI > .90; Hu & Bentler, 1999). Therefore, we compared the EFA results in terms of the conceptual clarity of the item factors and consistency of factor structures across models. The model with four latent factors had conceptual clarity and was more parsimonious and stable than the five or six-factor model (Table S2b).
The first item factor contains items related to counting objects (eight questions; e.g., ‘How many dogs?’, ‘How many cows?’). The second factor contains items that provide visual representations of objects and focus on subtracting objects (six questions; e.g., ‘If you took away five crayons, how many are left?’), and thus we labelled it concrete representational arithmetic operations. The third factor contains items in which children are asked to add objects that are not visually represented (four questions; e.g., ‘If you have five balloons and get one more, how many do you have?’) and thus was labelled abstract arithmetic operations. We conceptualize these three skill-sets as steps in the process that Sarama and Clements (2009) describe as ‘cyclic concretization’, in which children first engage with numerical concepts at a sensory-concrete level before gaining a capacity to make verbally-based or symbolic numeracy generalizations. A fourth factor contained two items that asked children to read the time from diagrams of analog clocks which we labelled clocks. However, since these two items appeared to measure a separate, potentially important skill (i.e., the ability to tell time) but not numerical skills, we calculated the percentage correct on the two items (0 = both wrong, 0.5 = one correct, 1 = both correct) and included this variable in the multiple regression models, but not the DCM. This allowed us to more clearly align the analyses with the Sarama and Clements (2009) hierarchical process of mathematical development but allowed for the relation with the other items to be accounted for in the regressions.
3.2 |. Early numeracy skills mastery groups
After identifying three conceptually consistent factors related to numerical skills, these factors served as the basis for examining groups of children by skill mastery. Some classification models, such as Latent Class Analysis, focus on groups based on a single construct, but in this study, the focus is mastery of a set of specific skills at preschool age. DCMs are a family of confirmatory psychometric models that characterize individuals based on their mastery of a discrete set of narrowly defined skills (e.g., see Gierl, Alves, & Majeau, 2010). This approach contrasts with traditional psychometric approaches such as item response theory (IRT) models, in which the latent variables are continuous and typically somewhat broadly defined, such as ‘mathematics ability’. The DCMs specify the cognitive attributes that examinees must possess in order to answer test items correctly, and the end-product of DCMs is the classification of examinees with respect to the mastery of these attributes (where the cut-points for mastery classification are derived within the model). Following the DCM convention, we use the term ‘attribute’ to refer to the dichotomous latent traits that distinguish between examinees who have mastered and those who have not mastered each skill of interest. For the reliability of DCM examinee estimates, see Templin and Bradshaw (2013). DCMs are considered confirmatory latent class models because the number of attributes and the item-attribute alignment are both defined prior to analyses. The 18 items and three dimensions identified by the EFA were the basis of the DCM structure (shown in Table S3). Child group classifications were determined by the item responses, the item properties and the population-level base rates of examinees that are masters of each attribute.
In the DCM framework, items can be specified to measure a single attribute or multiple attributes. When an item measures multiple attributes or skills, DCM can be estimated under a variety of assumptions regarding how the attributes interact to predict a correct response. For example, a child may be able to get a subtraction item correct by using their counting skills (e.g., counting backward on their hands), even if they have not learned subtraction methods. This would be an example of a compensatory model, where that possession of one attribute could offset the absence of another. Alternatively, there may be other items where it is thought that all relevant attributes are necessary in order for an examinee to have any increase in the probability of a correct response. For instance, an item that asks examinees to add together two fractions may require both adding and fraction knowledge for the examinee to answer the item correctly. If a child has just mastered adding but not fractions, they would be unlikely to get the correct response. In this study, we utilized a compensatory re-parameterized unified model (C-RUM; Choi, Rupp, & Pan, 2012), which when items are tied to multiple attributes, allows for mastery of one attribute to compensate for non-mastery on other attributes. C-RUM is a special case of the log-linear diagnostic classification model (LDCM) in which only the main effects are estimated.
In addition to the specification of how the attributes are theorized to relate to the items, DCM requires the specification of the joint distribution of binary attributes in models. A higher-order latent trait was specified to explain the relationship between the attributes (De La Torre & Douglas, 2004). The higher-order structure assumes that there is a general mathematics aptitude (continuous) dimension that explains the relationship between the categorical attributes, which captures specific numeracy skills.
We used flexMIRT version 3.2 (Cai, 2016) to estimate the DCM with the three attributes: counting, concrete representational arithmetic operations and abstract arithmetic operations. Table S4 presents the population probabilities of the eight potential groups that reflect all combinations of mastery/non-mastery status of the three skill attributes (counting, concrete representational arithmetic and abstract arithmetic). Due to the inherent ordering in numeracy skill development, some combinations are very rarely observed in the population. The three abstract arithmetic items (AP16, AP17, AP21) appear later in the measure than the majority of the concrete representational arithmetic items and were found to be more difficult for the participants in this sample. As a result, only four attribute groups were observed in the 54-month sample.
The descriptive portrait of these early numeracy skill groups that emerges from this analysis can be found in Table 2, with the four skill groups having the following labels: (a) no applied problems mastery (NAP), (b) counting mastery (C), (c) counting and concrete representational arithmetic mastery (CR) and (d) counting, concrete representational and abstract arithmetic mastery (CRA). As shown in the table just 16% of the sample falls into the ‘NAP’ group, 31% falls in the ‘C’ group, 27% in the ‘CR’ group and 26% of children fall into the ‘CRA’ group at 54 months of age. The percentage correct for the counting, concrete representational arithmetic and abstract arithmetic operations items within each mastery group are reported in Table 2. For example, the average student in the ‘C’ group got 79% of the counting items correct, but only 23% of the concrete representational arithmetic operations and 3% of the abstract arithmetic operations items correct. In comparison, the average student in the ‘CRA’ group got 95% of the counting items correct, 70% of the concrete representational arithmetic operations and 48% of the abstract arithmetic operations items correct. The continuing trajectories of these four skill groups across all included timepoints are shown in Figure 1.
TABLE 2.
Descriptive statistics for the numeracy skill groups at the 54-month assessment
| DCM attribute groups at the 54-month assessment |
||||
|---|---|---|---|---|
| NAP | C | CR | CRA | |
| N | 166 | 327 | 285 | 263 |
| %child race and ethnicity | ||||
| White | 0.53 (0.50) | 0.76 (0.43) | 0.87 (0.34) | 0.90 (0.30) |
| Black | 0.30 (0.46) | 0.14 (0.34) | 0.06 (0.24) | 0.01 (0.09) |
| Hispanic | 0.13 (0.33) | 0.05 (0.23) | 0.04 (0.19) | 0.04 (0.19) |
| Other | 0.04 (0.20) | 0.05 (0.21) | 0.03 (0.16) | 0.06 (0.23) |
| Mother’s education (in years) | 12.98 (2.24) | 13.87 (2.38) | 14.95 (2.26) | 15.49 (2.32) |
| Mother’s PPVT score | 86.78 (19.02) | 96.84 (15.84) | 102.88 (16.55) | 107.63 (17.26) |
| Partner in home (EC) | 0.74 (0.38) | 0.83 (0.32) | 0.89 (0.27) | 0.94 (0.19) |
| Stable income to needs (EC) | 2.23 (1.76) | 3.20 (2.35) | 3.94 (2.34) | 4.86 (3.54) |
| Average HOME score (EC) | 36.55 (5.36) | 39.93 (4.46) | 41.49 (3.59) | 42.50 (3.11) |
| Proportion Centre care (36–54 m) | 0.32 (0.36) | 0.39 (0.37) | 0.45 (0.39) | 0.46 (0.40) |
| Memory for sentences 54 m | 75.92 (14.24) | 88.02 (15.98) | 97.27 (15.60) | 101.07 (18.39) |
| Bayley MDI | 77.90 (13.45) | 89.92 (12.89) | 95.95 (12.37) | 101.69 (11.00) |
| Percentage correct | ||||
| Counting | 0.32 (0.18) | 0.79 (0.12) | 0.92 (0.08) | 0.95 (0.07) |
| Concrete representational arithmetic | 0.13 (0.16) | 0.23 (0.16) | 0.66 (0.17) | 0.70 (0.22) |
| Abstract arithmetic | 0.02 (0.07) | 0.03 (0.10) | 0.00 (0.00) | 0.48 (0.21) |
| Clocks | 0.07 (0.21) | 0.25 (0.39) | 0.55 (0.43) | 0.62 (0.43) |
| WJ-R applied problems (W score) | ||||
| 54 months | 391.84 (17.02) | 419.54 (7.25) | 434.51 (5.60) | 441.98 (8.37) |
| First grade | 454.65 (12.83) | 465.58 (13.29) | 472.80 (12.38) | 480.30 (13.01) |
| Third grade | 485.41 (16.02) | 494.82 (11.52) | 501.00 (8.59) | 504.22 (9.37) |
| Fifth grade | 499.58 (13.60) | 507.85 (10.43) | 513.69 (9.18) | 515.79 (9.66) |
| Age 15 | 512.78 (14.67) | 518.64 (13.25) | 528.68 (14.64) | 533.95 (15.96) |
| % high school highest math coursea | ||||
| Algebra 1 | 0.26 (0.45) | 0.07 (0.25) | 0.00 (0.00) | 0.01 (0.11) |
| Geometry | 0.05 (0.22) | 0.09 (0.29) | 0.04 (0.21) | 0.02 (0.13) |
| Algebra 2 | 0.33 (0.48) | 0.22 (0.42) | 0.26 (0.44) | 0.12 (0.33) |
| Advanced math | 0.31 (0.47) | 0.47 (0.50) | 0.36 (0.48) | 0.43 (0.50) |
| Calculus | 0.05 (0.22) | 0.15 (0.36) | 0.34 (0.47) | 0.42 (0.49) |
| % college enrollment | ||||
| Less than HS | 0.05 (0.23) | 0.02 (0.12) | 0.02 (0.07) | 0.01 (0.10) |
| HS graduate | 0.29 (0.46) | 0.17 (0.38) | 0.12 (0.33) | 0.11 (0.31) |
| Two-year college | 0.40 (0.49) | 0.28 (0.45) | 0.24 (0.43) | 0.12 (0.33) |
| Four-year college | 0.26 (0.44) | 0.53 (0.50) | 0.62 (0.49) | 0.76 (0.43) |
Note: Means are reported with standard deviations in parentheses.
Abbreviations: C, counting mastery; CR, counting and concrete representational arithmetic mastery; CRA, counting, concrete representational and abstract arithmetic mastery; DCM, diagnostic classification model; EC, average of the variable reported at 1-, 6-, 15-, 24-, 36- and 54-month interviews; HOME, home observation for measurement of the environment; m, months; MDI, mental developmental index; NAP, no applied problems mastery; PPVT, peabody picture vocabulary test; WJ-R, Woodcock-Johnson revised.
Due to sample attrition, the sample size for the high school’s highest math course variables was lower than that for the remaining variables. See Table 1 for a comparison of the full sample and the high school sample.
FIGURE 1.
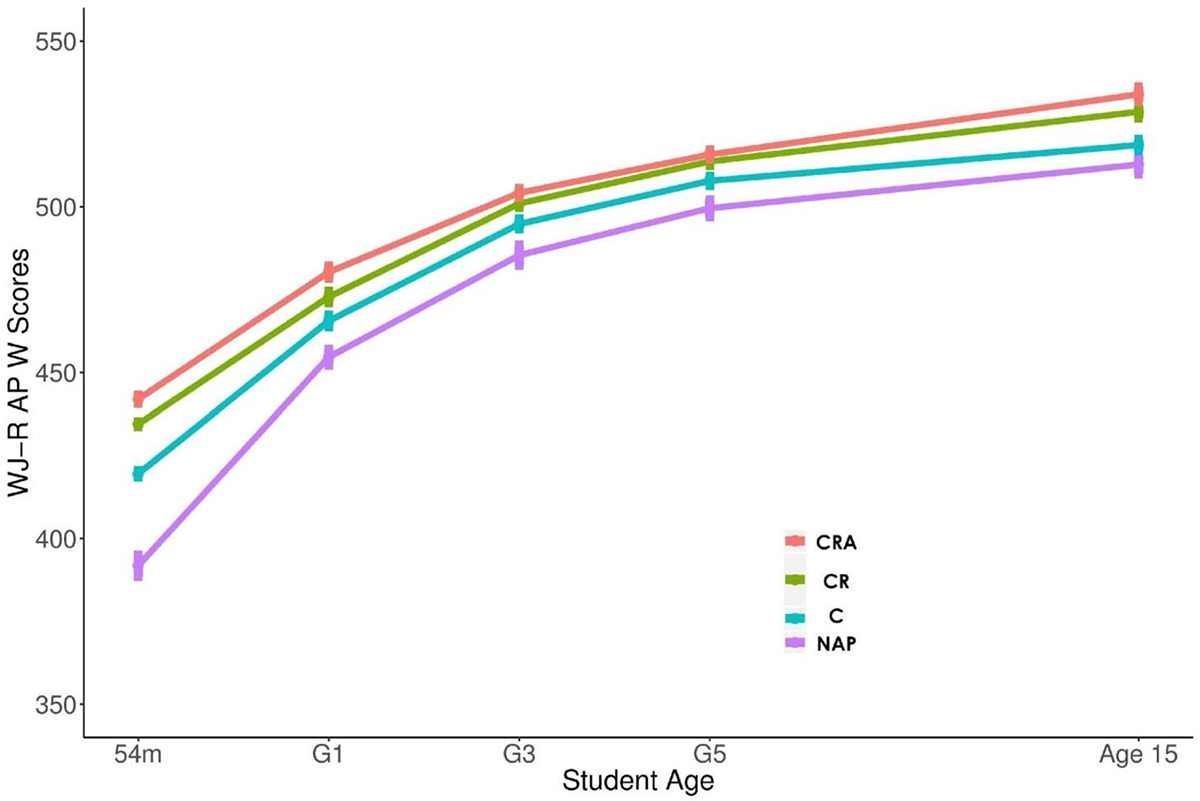
Math achievement trajectories by early numeracy skill group category. NAP = no applied problems mastery, C = counting mastery, CR = counting and concrete representational arithmetic mastery, CRA = counting, concrete representational and abstract arithmetic mastery
3.3 |. Demographic differences in early numeracy skill groups
The descriptive statistics reported in Table 2 allow for an investigation of the potential sources of early inequalities in numeracy skills and for a look at the differences among the early skills groups in their later educational outcomes. Although we found no age differences across the four skills groups, there were substantial race and socioeconomic disparities in skill mastery at 54 months. White children, who make up 79% of the entire SECCYD sample, are overrepresented in the ‘CRA’ group and under-represented in the ‘NAP’ group. Forty-seven percent of the children in the ‘NAP’ group are non-white, compared with 10% of the children in the ‘CRA’ group. Black families makeup 11% of the total analysis sample but are overrepresented in the ‘NAP’ group (30%) and underrepresented in the ‘CRA’ group (1%).
Additionally, we found a positive and monotonic relationship between multiple measures of children’s home environment and resources and membership in the skills groups. As Table 2 indicates, the mean level of educational attainment for mothers of children in the ‘NAP’ group is slightly above 12 years of schooling or high school equivalent, while the mean level of educational attainment for mothers of children in the ‘C’ group is equivalent to a community college education, and mean level of educational attainment for mothers of children in the ‘CRA’ is equivalent to 4 years of college. While 94% of children in the ‘CRA’ group resided with two parents, a smaller percent (74%) of the children in the ‘NAP’ group had two parents residing in the home. The average child in the ‘CRA’ group had parents who had two times more economic resources available for their children in early childhood than did children in the ‘NAP’ group. The average HOME score for children in the ‘CRA’ group was more than 1.5 SD higher than the average HOME score for children in the ‘NAP’ group.
3.4 |. Descriptive data on the links between early numeracy skills and later achievement and attainment
The longitudinal nature of the SECCYD’s data allowed us to examine how children in the skill groups scored relative to each other over time as well as how early skill group membership was linked with later achievement and attainment. As the data reported in Table 2 demonstrate, the gap in WJ-AP scores between children in the ‘NAP’ group and children in the ‘C’ group narrows from 40 points (almost two standard deviations) at 54 months to just five points (less than a third of a standard deviation) at age 15 years. However, the achievement gaps between children who demonstrated ‘NAP’ at 54 months and children in the two highest skills groups remain relatively large throughout the transition to adolescence. Children who demonstrated a mastery of counting and concrete representational arithmetic by 54 months scored 11 points higher in mathematics achievement at age 15 years than did students who demonstrated little numerical mastery at 54 months, which is more than a standard deviation in the WJ-AP achievement scores among 15-year olds. Similarly, children who demonstrated a mastery of all three early numeric skills at 54 months scored 17 points higher, or nearly two standard deviations, at age 15 years than students who demonstrated no numerical mastery at 54 months.
Differences among the four early numerical competency groups in mathematics course selection at the end of high school were even larger. As Figure 2 illustrates, within the ‘NAP’ group, just 36% of students reached a mathematics course higher than Algebra 2. In comparison, approximately 70% of the ‘CR’ group and approximately 85% of students in the ‘CRA’ group completed a mathematics course higher than Algebra 2. Indeed, children who had mastered counting by 54 months completed high school Calculus at nearly three times the rate of children who demonstrated no numerical competencies at 54 months. These course completion gaps were even more pronounced for children in the top two skills groups: children who had mastered ‘CR’ completed Calculus at nearly seven times the rate of children with ‘NAP’, while children in the ‘CRA’ group completed Calculus at eight times the rate of children with ‘NAP’. Figure 3 shows the early childhood numeric skills groups were also highly predictive of college enrollment, such that 76% of children who had mastered all three early numeric preschool skills were enrolled in a 4-year college compared to 26% of young adults who had mastered none of the early numeric skills when in preschool.
FIGURE 2.
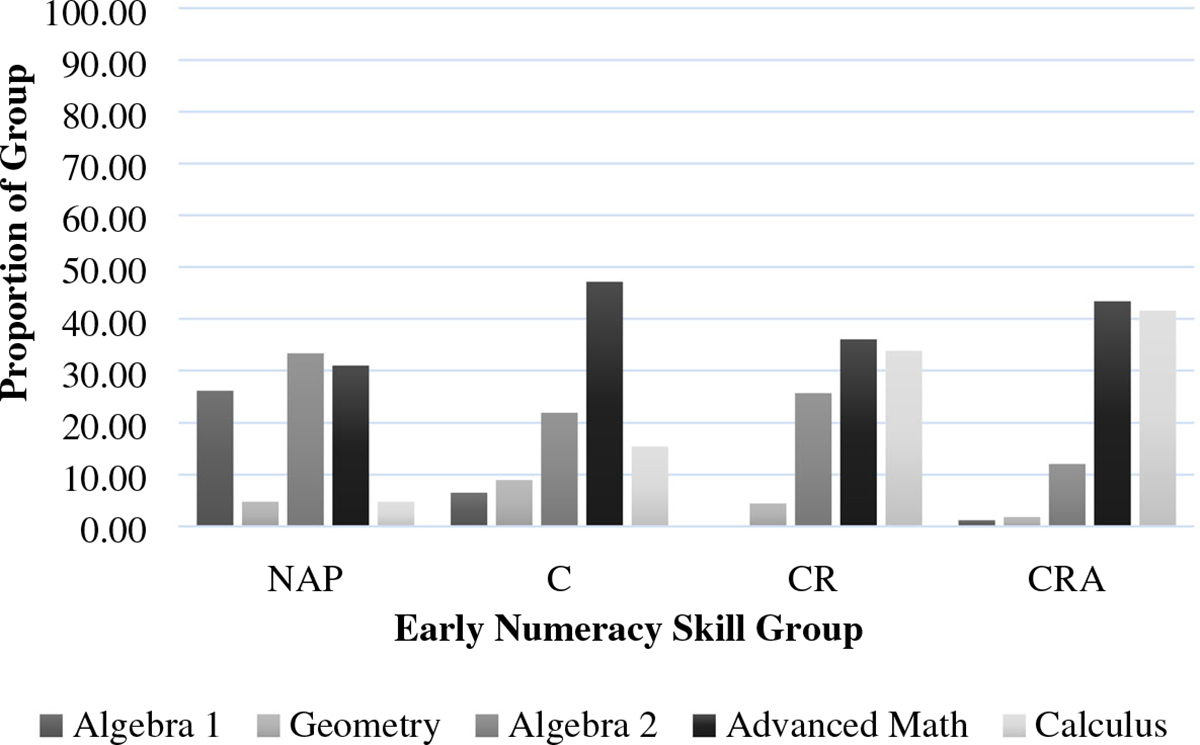
Highest high school math course completion by early numeracy skill groups. NAP = no applied problems mastery, C = counting mastery, CR = counting and concrete representational arithmetic mastery, CRA = counting, concrete representational and abstract arithmetic mastery
FIGURE 3.
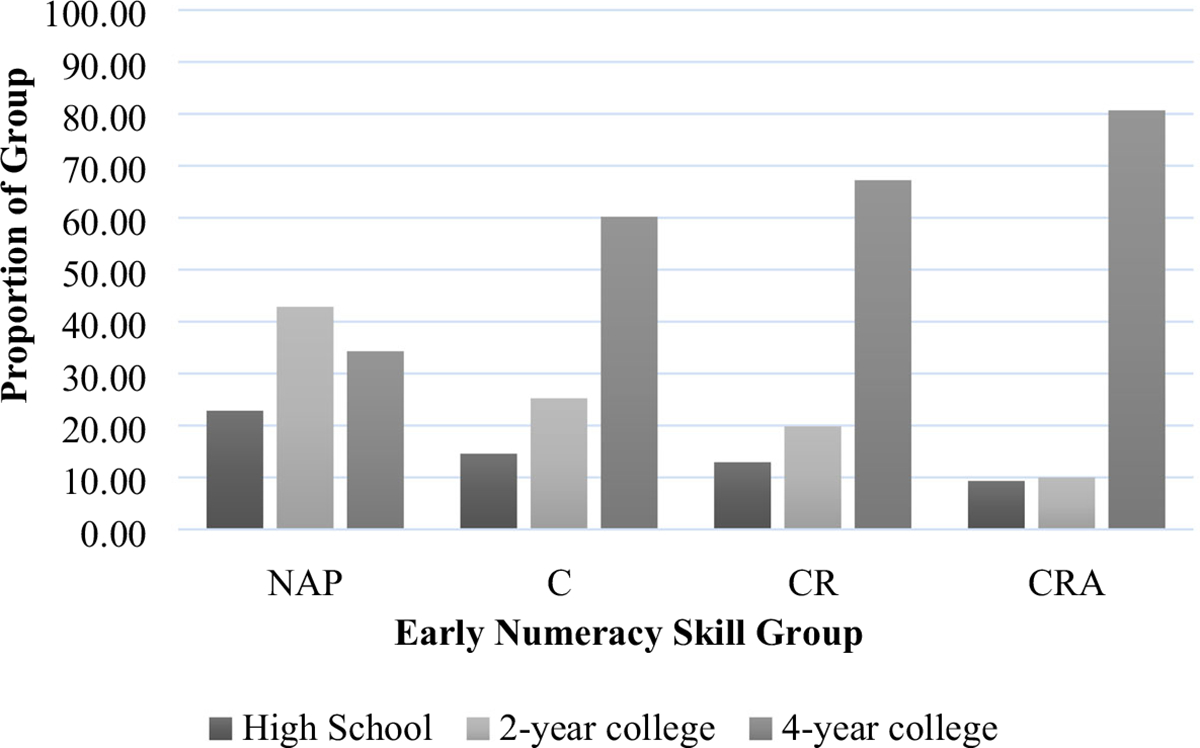
Highest education level in young adulthood by early numeracy skill groups. NAP = no applied problems mastery, C = counting mastery, CR = counting and concrete representational arithmetic mastery, CRA = counting, concrete representational and abstract arithmetic mastery
3.5 |. Predictive multivariate analyses
Part of the relationship between early skills groups and age 15 mathematics achievement is likely a function of students’ home resources, cognitive ability and other potentially confounding factors. Thus, in our models of the relations between these early numeracy skill groups and WJ-AP scores at age 15 years, high school mathematics course-taking and college enrollment, we statistically controlled for the rich set of background characteristics described above and displayed in Table 2. In doing so, we were able to identify the relations between early skills and later outcomes independent of a wide range of potential confounders.
Each of these models was estimated using Mplus (Muthén & Muthén, 2016) on the full sample of students for whom longitudinal data from age 54 months through college enrollment is available (n = 470). Full-Information Maximum Likelihood (FIML) estimation was used to handle data missing at random (Graham, Olchowski, & Gilreath, 2007). The final set of analyses thus examined the relations between students’ early numeracy competencies and (a) their mathematics achievement through age 15 years, (b) their highest level of mathematics course completion by the end of high school and (c) whether they enrolled in a 2-year or 4-year college by age 22 or 23 years.
The first model in Table 3 examined the relation between early numeracy skill groups and adolescent mathematics achievement at age 15 years as measured by standardized scores on the WJ-R. Relative to the ‘NAP’ group, children who had mastered ‘CR’ by 54 months scored approximately half a standard deviation higher on the age 15 test (B = 7.28, SE = 2.65, p < .01), holding constant the other variables in the model. Children who demonstrated a mastery of ‘CRA’ at 54 months scored approximately two-thirds of a standard deviation higher than children with no numerical mastery at 54 months (B = 10.02, SE = 3.94, p < .01).
TABLE 3.
Multivariate models predicting age 15 WJ-R applied problems standardized score, highest math course taken by the end of high school and 4-year college enrollment
| Model 1: Age 15 applied problems scores (ordinary least squares regression) | Model 2: High school highest math course completion (ordered logistic regression) | Model 3: Four-year college enrollment (logistic regression) | |
|---|---|---|---|
| Counting mastery (C) | 1.7 | 1.67 | 1.99 |
| Counting, concrete representational arithmetic mastery (CR) | 7.28** | 2.71* | 1.87 |
| Counting, concrete and abstract arithmetic mastery (CRA) | 10.02*** | 3.88** | 3.63* |
| Skill with clocks | 3.94** | 1.12 | 1.2 |
| WJ-R memory for sentences (54 m) | 0.08 | 1 | 1 |
| Male | 4.92*** | 1.19 | 0.86 |
| Black | −0.77 | 0.86 | 1.23 |
| Other | 0.07 | 0.74 | 3.75 |
| Hispanic | −0.87 | 0.76 | 0.58 |
| Mother’s education (in years) | 0.89** | 1.24*** | 1.21** |
| Mother’s PPVT score | 0.10* | 1.01 | 1 |
| Proportion of epochs in center care (36–54 m) | 2.29 | 1.02 | 1.58 |
| Partner in-home (EC) | 4.19 | 2.21 | 2.57 |
| Stable income to needs (EC) | −0.38 | 1.12* | 0.97 |
| Average HOME score (EC) | 0.1 | 0.98 | 1.11* |
| Bayley MDI | −0.03 | 1.01 | 1 |
| n | 467 | 467 | 467 |
| Pseudo R2 | 0.3 | 0.27 | 0.31 |
| Bayesian information criteria (BIC) | 11,214.922 | 8,925.95 | 8,243.64 |
Note: High school course completion was coded as 1 = ‘Algebra I’, 2 = ‘Geometry’, 3 = ‘Algebra II’, 4 = ‘Advanced Mathematics’ and 5, ‘Calculus’.
Abbreviations: EC, average of the variable reported at 1-, 6-, 15-, 24-, 36- and 54-month interviews; HOME, home observation for measurement of the environment; m, months; MDI, mental developmental index; PPVT, peabody picture vocabulary test; WJ-R, Woodcock-Johnson revised.
p < .05
p < .01
p < .001.
Model 2 reported in Table 3 traced the relation between the early numeracy skills groups and children’s high school mathematics course completion. Given that mathematics course completion is a five-category ordinal variable in which each of the categories has clear rank order (1 = ‘Algebra I’, 2 = ‘Geometry’, 3 = ‘Algebra II’, 4 = ‘Advanced Mathematics’, 5 = ‘Calculus’), we estimated an ordered logit or proportional odds model. Ordered logit models are appropriate when the outcome has a clear ordering, such as remedial courses to advanced mathematics courses. Unlike ordinary least-squares (OLS) regression, these models do not assume that the outcome variable is ordered at equal intervals. Additionally, ordered logit models are more parsimonious than fitting a series of logistic regression models for each mathematics course pair. To develop a single regression model, ordered logit models were used to estimate cumulative probabilities, namely, the probability that the outcome is less than or equal to a given category of the dependent variable. The ordered logit model estimates regression parameters (β) for each independent variable i as well as m − 1 threshold parameters (θm). The ordered logit regression models reported in this manuscript assumed that the coefficients that describe the relationship between the odds of completing Calculus versus the combined lower mathematics courses were the same as those that describe the odds of completing either Geometry or Calculus versus the combined lower categories.
After we controlled for our set of demographics, family and maternal variables, students who had demonstrated a mastery of either two or all three of the early numeric skills at 54 months were significantly more likely to complete high school Calculus than children in the ‘NAP’ group. To make the results from the ordered logistic more interpretable, we also calculated the marginal probabilities of enrolling in Calculus given students’ mastery of early numeric skills at 54 months. The marginal probability is calculated separately for each group, setting all of the other predictors in the model to their sample mean values. The predicted probabilities of completing Calculus by the end of high school for each skill group as well as the corresponding 95% confidence intervals can be found in Figure 4. As the figure shows, the predicted probability of enrolling in Calculus for a hypothetical child in the ‘NAP’ group who is at the sample average on all background characteristics is 13% (adjusted model). On the other hand, the predicted probability of enrolling in Calculus for a hypothetical child in the ‘CRA’ group who is at the sample average on all background characteristics is 34%.
FIGURE 4.
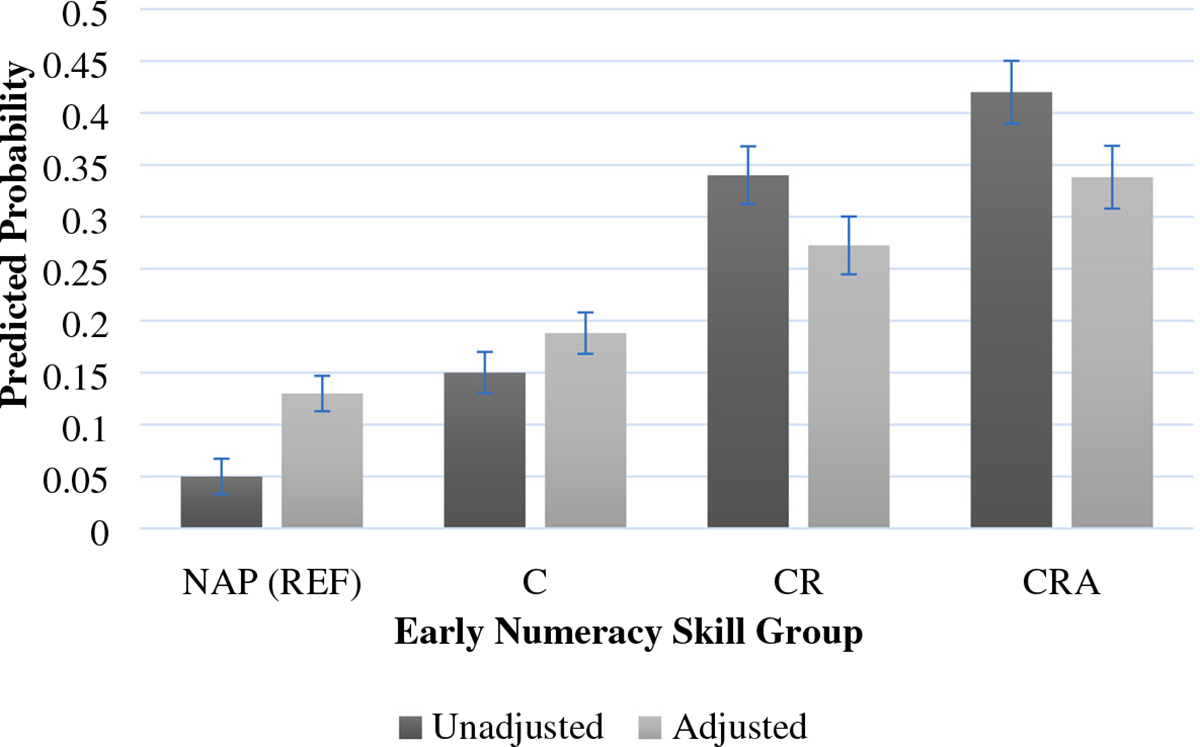
Predicted probabilities of completing calculus in high school by early numeracy skill groups. NAP = no applied problems mastery, C = counting mastery, CR = counting and concrete representational arithmetic mastery, CRA = counting, concrete representational and abstract arithmetic mastery. This figure displays the unadjusted probability of completing Calculus by the end of high school given a child’s 54-month numeracy skill group and then the adjusted probability, setting all covariates in Table 3 to their mean values. The 95% confidence intervals are shown as black vertical bars
Model 3 presented in Table 3 is a logistic regression model predicting enrollment in a four-year college or university given early numeracy skills. After controlling for background characteristics, children who had demonstrated a mastery of all three early numeric skills at 54 months were significantly more likely to enrol in a four-year college than children in the ‘NAP’ group. Using the parameters from Model 3, the predicted probabilities of enrollment in a four-year college or university for each skill group as well as the corresponding 95% confidence intervals can be found in Figure 5. Controlling for mean values of all covariates in both groups, the predicted probability that children in the ‘CRA’ group would enrol in a four-year college was 80% compared with 53% for children in the ‘NAP’ group for the adjusted model.
FIGURE 5.
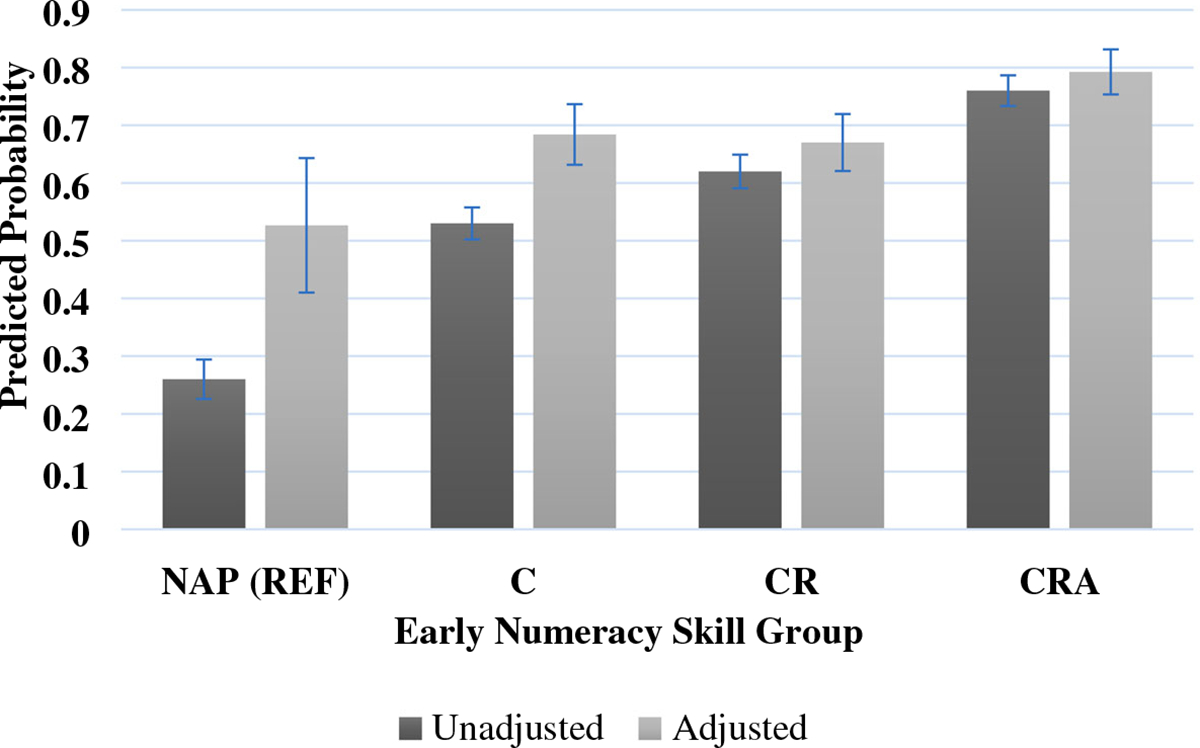
Predicted probabilities of 4-Year college enrollment by early numeracy skill groups. NAP = no applied problems mastery, C = counting mastery, CR = counting and concrete representational arithmetic mastery, CRA = counting, concrete representational and abstract arithmetic mastery. This figure displays the unadjusted probability of enrolling in a 4-year college given a child’s 54-month numeracy skill group as well as the adjusted probability, setting all covariates in Table 3 to their mean values. The 95% confidence intervals are shown as black vertical bars
4 |. DISCUSSION
Education is considered one of the primary avenues to help in equalizing the gaps in income and general resource differences in our society (Mann, 1848). Decades of research, however, have documented an achievement gap at the beginning of mandatory schooling that persists throughout primary and secondary education, even with educational interventions occurring throughout the educational cycle (von Hippel & Hamrock, 2019). Understanding what aspects of achievement may be important to understand for long-term educational outcomes for children. Given the importance of mathematical achievement in later schooling and job market success (Murnane et al., 1995; Watts, Duncan, Clements, & Sarama, 2018), this study investigated the extent to which the development of children’s mastery of early numerical concepts was associated with later mathematics ability and advanced math course selection in high school and college enrollment in young adults.
Our study expanded on previous research tracing the relation between preschool and adolescents’ math achievement test scores (Watts et al., 2014) in two ways – first, we identified numeric skills using a quantitative method for identifying skills that group together. Second, we investigated the extent to which membership in those early mastery groups fared in later pivotal educational outcomes, such as enrolling in advanced math courses in high school and enrolling in college as a young adult. We found that these early numeracy mastery groups are important indicators of later educational outcomes and relate to aspects of the home environment, caregiver cognitive resources and the children’s own early cognitive ability.
This study used classification models to identify latent constructs based on specific items of a well-validated standardized mathematics assessment and then grouped children based on mastery of these numeric skills. Consistent with the theoretical literature, our analyses suggest that children begin with a concrete understanding of numerical concepts and proceed to more abstract, representational understandings (Sarama & Clements, 2009). The vast majority of children in our sample had mastered counting prior to starting school, which is consistent with research that shows over 80% of kindergartners are already skilled in counting (Claessens, Engel, & Curran, 2014). Notably, however, there is substantial variation among children in early numeracy skills mastery. Approximately 16% of children in our study had mastered no basic numeracy skills, as tested by the standardized achievement test, prior to kindergarten, whereas nearly 30% had mastered abstract single-digit addition and subtraction. This heterogeneity in early numeracy mastery replicates earlier longitudinal research by Watts et al. (2014), who found that preschool test scores on a standardized achievement test related to later achievement test scores and educational attainment. Importantly, the findings extend this earlier research by showing that the heterogeneity in the mastery of specific numeracy concepts at 4.5 years of age (not just overall test scores) was strongly predictive of later course selections in high school and college enrollment for this sample, even after controlling for a large set of background characteristics. Thus, not only do we find that there is an autoregressive relation (same achievement test scores predicting each other across time), but we also found that the mastery of early numeracy skills relates to more qualitative educational transitions such as course selection and applying to college. This provides additional support for differences in early skills setting a stable trajectory of achievement, as defined by test scores, but also by other educational choices that put students on certain pathways for educational success (von Hippel & Hamrock, 2019).
We also found children who enter school with few discernable early numeracy skills, as measured by a standardized achievement test, are less likely to take advanced mathematics classes in high school or enrolling in a four-year college. These findings suggest that future research efforts should examine the specific contexts prior to formal schooling that may relate to the development of early mathematics. Based on previous research (Bradley & Corwyn, 2002; Davis-Kean, 2005; Levine et al., 2010; Susperreguy & Davis-Kean, 2016), two possible contexts, the home environment and preschool enrollment were included as covariates. The home environment has been shown to relate to numeracy skill formation. For example, research has shown children who are exposed to more instances of ‘math talk’ conversations in the home have higher scores on standardized mathematics tests a year later, even after controlling for maternal education (Susperreguy & Davis-Kean, 2016). However, children’s numeracy skills at the entry to formal schooling track their achievement across schooling as well as course selection in high school and later college enrollment even after controlling for the home environment and preschool enrollment. This finding suggests that initial differences in numeric skills remain stable and predictive of later achievement (Brooks-Gunn & Duncan, 1997; Davis-Kean & Jager, 2014; Reardon, 2011; von Hippel & Hamrock, 2019) but also predict important qualitative outcomes such as course selection and transition to higher education.
4.1 |. Limitations
These analyses are correlational, and thus we are unable to make statements about the causal nature of early skills to later skills in our inferential analyses. Similarly, our analyses do not explain why numeracy skill differentials are predictive of later achievement and attainment, thus we do not know the mechanisms of the stability we see in the test scores or educational choices. Although we controlled for a range of demographic and home environment factors to rule out the potential influence of selection variables, there are likely unmeasured factors that exert influence both on early numeracy skills and on later achievement and attainment that need to be explored. For example, we do not examine the school or classroom factors that might relate to the stability of achievement and educational choices. It is possible that children from low-resourced homes also attend low-resourced schools, and thus, the stability in these environments is why we see the stability in achievement scores and educational choices. It is further possible that educators discriminate against students who enter into school with relatively few numeracy skills, limiting their ability to grow academically and transition to high-status educational opportunities. It is also the case that black children were overrepresented in the NAP skill group, and thus part of the reason this group fared the worst of the four groups may be their experiences with race-based discrimination throughout elementary, middle and high school. We statistically controlled the models for parent education and mother’s receptive vocabulary; however, we do not know if there are other unmeasured generational transfer (heritability) aspects that may relate to the stability of achievement and educational choices that the analyses have not adequately adjusted. Unfortunately, this data set does not provide either twin or adoptive data for us to assess heritability in a traditional way and so instead we have used the variables available to try and adjust the analyses for this transfer.
Our study is also restricted by our use of one standardized mathematics assessment. Although the Woodcock-Johnson is a widely used assessment in the field, the types of skills it assesses may be limited, particularly for children at age 54 months. For example, the Woodcock-Johnson provides limited information about children’s non-symbolic, symbolic, spatial, geometry and magnitude skills as discrete components; each of which is likely an important contributor to mathematical development (Merkley & Ansari, 2016; Purpura & Simms, 2018; Siegler, 2016). As a result, our analyses and discussion focus on numeracy, rather than mathematical skills more generally.
Our outcome of the highest math course taken in high school was not able to consider the highest level of math courses offered by the school. Thus, it is possible that some students may have had the skills to take those courses, but they were not offered at their high school. We do not have access to that information about their schools, and so it remains a limitation of our study.
Finally, even though we use data from a national study that reflects variation across the country, the study sample was not selected to be representative of the population of the United States. The NICHD-SEYCCD, for example, does not include children who were considered to be born of low birth weight and the mothers could not be teenagers. There is also a potential selection effect related to those who completed the young adulthood questionnaires that asked questions on college enrollment. Even though we adjusted for attrition and missing data, the loss of children from black families and from families in the lowest income groups potentially further restricts the generalizability of the results. Future research is needed to see if these early skills groups can be replicated with a nationally representative sample and to test whether these early skill groups have similar relations with later achievement outcomes.
5 |. CONCLUSION
The current study complements and further emphasizes the previous research demonstrating the importance of improving early childhood education (Heckman et al., 2018a, 2018b; Long et al., 2012). Just as basic research in linguistic and developmental science has helped educators target reading interventions toward phonemic awareness and other crucial early reading skills (Connor et al., 2011; Connor, Morrison, Fishman, Schatschneider, & Underwood, 2007; Connor, Morrison, & Katch, 2004), our results emphasize the need for continued research on numeracy and mathematical development to understand the variety of skills that children bring to school entry. Perhaps a stronger focus on children’s numerical skills at 54 months of age will provide more children with the option of attending college. These findings also emphasize that an important way to prevent the persistence of achievement gaps is to identify them as early as possible and to target them with early intervention, potentially before the start of formal schooling (von Hippel & Hamrock, 2019). Doing so will help to target the exposure to numeracy and mathematics instruction in early childhood settings and begin to address the persistent stability of achievement and attainment gaps documented in the research literature and that have long-term consequences for adult outcomes.
Supplementary Material
Highlights.
Differences in early math ability relate to course selection in high school
There are clear differences in math ability prior to starting formal schooling
Students with no math skills at school entry continue on a low math achievement trajectory throughout schooling
The likelihood of enrolling in college can be predicted from the level of math ability at 54 months.
ACKNOWLEDGEMENTS
This research was funded by a grant from the National Science Foundation (NSF) grant #1519686 to Robert Crosnoe and Elizabeth Gershoff. This research reflects the views of the authors of this study and not the National Science Foundation. Any questions or comments should be addressed to the first author at 530 Church St, Ann Arbor, MI, 48109–1043 pdakean@umich.edu.
Footnotes
SUPPORTING INFORMATION
Additional supporting information may be found in the online version of the article at the publisher’s website.
DATA AVAILABILITY STATEMENT
This research uses the NICHD Study of Early Child Care and Youth Development (SECCYD) Series dataset that is available from ICPSR at https://www.icpsr.umich.edu/web/DSDR/series/233 and contains information on the materials used to age 15 years of this birth cohort study. The information from the adult data is not publicly available and should be requested from the first author. The code used for the analyses will be provided upon request from the first authors.
REFERENCES
- Attewell P, & Domina T (2008). Raising the bar: Curricular intensity and academic performance. Educational Evaluation and Policy Analysis, 30(1), 51–71. [Google Scholar]
- Barnard WM (2004). Parent involvement in elementary school and educational attainment. Children and Youth Services Review, 26(1), 39–62. 10.1016/j.childyouth.2003.11.002 [DOI] [Google Scholar]
- Bayley N (1993). Bayley scales of infant development (2nd ed.). New York, NY: Psychological Corporation. [Google Scholar]
- Bradley RH, & Caldwell BM (1979). Home observation for measurement of the environment: A revision of the preschool scale. American Journal of Mental Deficiency, 84, 235–244. [PubMed] [Google Scholar]
- Bradley RH, & Corwyn RF (2002). Socioeconomic status and child development. Annual Review of Psychology, 53(1), 371–399. 10.1146/annurev.psych.53.100901.135233 [DOI] [PubMed] [Google Scholar]
- Brooks-Gunn J, & Duncan GJ (1997). The effects of poverty on children. The Future of Children, 7(2), 55–71. 10.2307/1602387 [DOI] [PubMed] [Google Scholar]
- Burris CC, Heubert JP, & Levin HM (2004). Math acceleration for all. Educational Leadership, 61(5), 68–72. [Google Scholar]
- Cai L (2016). flexMIRT version 3: Flexible multilevel multidimensional item analysis and test scoring. Seattle, WA: Vector Psychometric Group. [Google Scholar]
- Card D (1999). The causal effect of education on earnings. In Handbook of labor economics (Vol. 3, pp. 1801–1863). Amsterdam, Netherlands: Elsevier. [Google Scholar]
- Choi HJ, Rupp AA, & Pan M (2012). Standardized diagnostic assessment design and analysis: Key ideas from modern measurement theory. In Self-directed learning oriented assessments in the Asia-Pacific (pp. 61–85). Dordrecht: Springer. 10.1007/978-94-007-4507-0_4 [DOI] [Google Scholar]
- Claessens A, Engel M, & Curran FC (2014). Academic content, student learning, and the persistence of preschool effects. American Educational Research Journal, 51(2), 403–434. 10.3102/0002831213513634 [DOI] [Google Scholar]
- Connor CM, Morrison FJ, Fishman BJ, Schatschneider C, & Underwood P (2007). Algorithm-guided individualized reading instruction. Science, 315(5811), 464. 10.1126/science.1134513 [DOI] [PubMed] [Google Scholar]
- Connor CM, Morrison FJ, & Katch LE (2004). Beyond the reading wars: Exploring the effect of child-instruction interactions on growth in early reading. Scientific Studies of Reading, 8(4), 305–336. 10.1207/s1532799xssr0804_1 [DOI] [Google Scholar]
- Connor CM, Morrison FJ, Schatschneider C, Toste JR, Lundblom E, Crowe EC, & Fishman B (2011). Effective classroom instruction: Implications of child characteristics by reading instruction interactions on first graders’ word reading achievement. Journal of Research on Educational Effectiveness, 4(3), 173–207. 10.1080/19345747.2010.510179 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis-Kean PE (2005). The influence of parent education and family income on child achievement: The indirect role of parental expectations and the home environment. Journal of Family Psychology, 19(2), 294–304. 10.1037/0893-3200.19.2.294 [DOI] [PubMed] [Google Scholar]
- Davis-Kean PE, & Jager J (2014). Trajectories of achievement within race/ethnicity: “Catching up” in achievement across time. The Journal of Educational Research, 107(3), 197–208. 10.1080/00220671.2013.807493 [DOI] [Google Scholar]
- De La Torre J, & Douglas JA (2004). Higher-order latent trait models for cognitive diagnosis. Psychometrika, 69(3), 333–353. 10.1007/BF02295640 [DOI] [Google Scholar]
- Dunn L, & Dunn L (1981). PPVT-R Manual. Circle Pines, MN: American Guidance Service. [Google Scholar]
- Gierl MJ, Alves C, & Majeau RT (2010). Using the attribute hierarchy method to make diagnostic inferences about examinees’ knowledge and skills in mathematics: An operational implementation of cognitive diagnostic assessment. International Journal of Testing, 10(4), 318–341. 10.1080/15305058.2010.509554 [DOI] [Google Scholar]
- Graham JW, Olchowski AE, & Gilreath TD (2007). How many imputations are really needed? Some practical clarifications of multiple imputation theory. Prevention Science, 8(3), 206–213. 10.1007/s11121-007-0070-9:10.1007/s11121-007-0070-9 [DOI] [PubMed] [Google Scholar]
- Heckman JJ, Humphries JE, & Veramendi G (2018a). The nonmarket benefits of education and ability. Journal of Human Capital, 12(2), 282–304. 10.1086/697535 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman JJ, Humphries JE, & Veramendi G (2018b). Returns to education: The causal effects of education on earnings, health, and smoking. Journal of Political Economy, 126(S1), S197–S246. 10.1086/698760 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman JJ, Moon SH, Pinto R, Savelyev PA, & Yavitz A (2010). The rate of return to the HighScope Perry preschool program. Journal of Public Economics, 94(1–2), 114–128. 10.1016/j.jpubeco.2009.11.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu L, & Bentler PM (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling: A Multidisciplinary Journal, 6, 1–55. 10.1080/10705519909540118 [DOI] [Google Scholar]
- Kuhfeld M, Gershoff ET, & Paschall KW (2018). The development of racial/ethnic and socioeconomic achievement gaps during the school years. Journal of Applied Developmental Psychology, 57, 62–73. 10.1016/j.appdev.2018.07.001 [DOI] [Google Scholar]
- Lee JS, & Bowen NK (2006). Parent involvement, cultural capital, and the achievement gap among elementary school children. American Educational Research Journal, 43(2), 193–218. 10.3102/00028312043002193 [DOI] [Google Scholar]
- Levine SC, Suriyakham LW, Rowe ML, Huttenlocher J, & Gunderson EA (2010). What counts in the development of young children’s number knowledge? Developmental Psychology, 46(5), 1309. 10.1037/a0019671 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libertus ME, Odic D, Feigenson L, & Halberda J (2016). The precision of mapping between number words and the approximate number system predicts children’s formal math abilities. Journal of Experimental Child Psychology, 150, 207–226. 10.1016/j.jecp.2016.06.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long MC, Conger D, & Iatarola P (2012). Effects of high school course-taking on secondary and postsecondary success. American Educational Research Journal, 49(2), 285–322. 10.3102/0002831211431952 [DOI] [Google Scholar]
- Lyons IM, Bugden S, Zheng S, De Jesus S, & Ansari D (2018). Symbolic number skills predict growth in nonsymbolic number skills in kindergarteners. Developmental Psychology, 54(3), 440. 10.1037/dev0000445 [DOI] [PubMed] [Google Scholar]
- Mann H (1848). Twelfth annual report to the Massachusetts Board of Education. The Republic and the School: Horace Mann and the Education of Free Men. [Google Scholar]
- Matthews PG, & Fuchs LS (2020). Keys to the gate? Equal sign knowledge at second grade predicts fourth-grade algebra competence. Child Development, 91(1), e14–e28. 10.1111/cdev.13144 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews PG, Lewis MR, & Hubbard EM (2016). Individual differences in nonsymbolic ratio processing predict symbolic math performance. Psychological Science, 27(2), 191–202. 10.1177/0956797615617799 [DOI] [PubMed] [Google Scholar]
- Merkley R, & Ansari D (2016). Why numerical symbols count in the development of mathematical skills: Evidence from brain and behavior. Current Opinion in Behavioral Sciences, 10, 14–20. 10.1016/j.cobeha.2016.04.006 [DOI] [Google Scholar]
- Mullis IVS, Martin MO, Foy P, Kelly DL, & Fishbein B (2020). TIMSS 2019 international results in mathematics and science. Retrieved from Boston College, TIMSS & PIRLS International Study Center website. Retrieved from https://timssandpirls.bc.edu/timss2019/international-results/ [Google Scholar]
- Murnane RJ, Willett JB, & Levy F (1995). The growing importance of cognitive skills in wage determination (no. w5076). National Bureau of Economic Research. 10.3386/w5076 [DOI] [Google Scholar]
- Muthén LK, & Muthén BO . (2016). Mplus: Statistical analysis with latent variables. Los Angeles, CA: Muthén & Muthén.1988– [Google Scholar]
- National Center on Education Statistics. (2019). NAEP Report Card: Mathematics. Retrieved 12/7/19 from https://www.nationsreportcard.gov/mathematics/nation/achievement?grade=4
- National Institute of Child Health and Human Development Early Child Care Research Network. (2002). Early child care and children’s development prior to school entry: Results from the NICHD study of early child care. American Educational Research Journal, 39, 133–164. 10.3102/00028312039001133 [DOI] [Google Scholar]
- National Institute of Child Health and Human Development Early Child Care Research Network, & Duncan GJ. (2003). Modeling the impacts of child care quality on children’s preschool cognitive development. Child Development, 74, 1454–1475. 10.1111/1467-8624.00617 [DOI] [PubMed] [Google Scholar]
- OECD. (2019). PISA 2018 results (volume III): What school life means for Students’ lives, PISA. Paris: OECD; Publishing. 10.1787/acd78851-en [DOI] [Google Scholar]
- Purpura DJ, & Simms V (2018). Approximate number system development in preschool: What factors predict change? Cognitive Development, 45, 31–39. 10.1016/j.cogdev.2017.11.001 [DOI] [Google Scholar]
- Reardon SF (2011). The widening academic achievement gap between the rich and the poor: New evidence and possible explanations. Whither Opportunity. 91–116. [Google Scholar]
- Rupp AA, Templin J, & Henson RA (2010). Diagnostic assessment: Theory, methods, and applications. New York: Guilford. [Google Scholar]
- Sarama J, & Clements DH (2009). Early childhood mathematics education research: Learning trajectories for young children. New York: Routledge. [Google Scholar]
- Siegler RS (2016). Magnitude knowledge: The common core of numerical development. Developmental Science, 19(3), 341–361. 10.1111/desc.12395 [DOI] [PubMed] [Google Scholar]
- Siegler RS, Duncan GJ, Davis-Kean PE, Duckworth K, Claessens A, Engel M, … Chen M (2012). Early predictors of high school mathematics achievement. Psychological Science, 23(7), 691–697. 10.1177/0956797612440101 [DOI] [PubMed] [Google Scholar]
- Sokolowski HM, Fias W, Ononye CB, & Ansari D (2017). Are numbers grounded in a general magnitude processing system? A functional neuroimaging meta-analysis. Neuropsychologia, 105, 50–69. 10.1016/j.neuropsychologia.2017.01.019 [DOI] [PubMed] [Google Scholar]
- Susperreguy MI, & Davis-Kean PE (2016). Maternal math talk in the home and math skills in preschool children. Early Education and Development, 27(6), 841–857. 10.1080/10409289.2016.1148480 [DOI] [Google Scholar]
- Templin J, & Bradshaw L (2013). Measuring the reliability of diagnostic classification model examinee estimates. Journal of Classification, 30(2), 251–275. [Google Scholar]
- von Hippel PT, & Hamrock C (2019). Do test score gaps grow before, during, or between the school years? Measurement artifacts and what we can know in spite of them. Sociological Science, 6, 43–80. 10.15195/v6.a3 [DOI] [Google Scholar]
- von Hippel PT, Workman J, & Downey DB (2018). Inequality in reading and math skills forms mainly before kindergarten: A replication, and partial correction, of “are schools the great equalizer?”. Sociology of Education, 91(4), 323–357. 10.1177/0038040718801760 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts TW, Duncan GJ, Clements DH, & Sarama J (2018). What is the long-run impact of learning mathematics during preschool? Child Development, 89(2), 539–555. 10.1111/cdev.12713 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts TW, Duncan GJ, Siegler RS, & Davis-Kean PE (2014). What’s past is prologue: Relations between early mathematics knowledge and high school achievement. Educational Researcher, 43, 352–360. 10.3102/0013189X14553660 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodcock RW, & Johnson MB (1989/1990). Woodcock-Johnson psycho-educational battery-revised. Allen, TX: DLM Teaching Resources. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
This research uses the NICHD Study of Early Child Care and Youth Development (SECCYD) Series dataset that is available from ICPSR at https://www.icpsr.umich.edu/web/DSDR/series/233 and contains information on the materials used to age 15 years of this birth cohort study. The information from the adult data is not publicly available and should be requested from the first author. The code used for the analyses will be provided upon request from the first authors.


