Bending DNA increases its helical repeat

Abstract

In all biological systems, DNA is under high mechanical stress from bending and twisting. For example, DNA is tightly bent in nucleosome complexes, virus capsids, bacterial chromosomes, or complexes with transcription factors that regulate gene expression. A structurally and mechanically accurate model of DNA is therefore necessary to understand some of the most fundamental molecular mechanisms in biology including DNA packaging, replication, transcription and gene regulation. An iconic feature of DNA is its double helical nature with an average repeat $h_0$ of ~10.45 base pairs per turn, which is commonly believed to be independent of curvature. We developed a ligation assay on nicked DNA circles of variable curvature that reveals a strong unwinding of DNA to over 11 bp/turn for radii around 3–4 nm. Our work constitutes a major modification of the standard mechanical model of DNA and requires reassessing the molecular mechanisms and energetics of all processes involving tightly bent DNA.

Introduction

In all cells and viruses, DNA is twisted and bent in a highly dynamic way. For example, two meters of human DNA are tightly wrapped around histone proteins, compacting it into a nucleus measuring mere micrometers across. During DNA replication and transcription, DNA unbinds from the nucleosome and relaxes its mechanical stress. DNA is also tightly bent in nanometer-sized virus capsids, bacteria, or complexes with many transcription factors that regulate gene expression. An accurate physical model of tightly bent DNA is therefore essential to understand the molecular mechanisms and energetics of many fundamental biological processes ^1,2.

The twistable wormlike chain (TWLC) is the standard elastic model for DNA and treats DNA as an inextensible rod with elastic moduli controlling twist and bend deformations ³. It accurately describes circularization probabilities of long linear DNA fragments ^4–8. While some studies postulated extreme bendability for short fragments ^9,10, kinetic effects have likely distorted the results ^11–13. Moreover, sharp kinks at nicks that release bending and torsional stress limit the usefulness of circularization experiments with short fragments and complicate the measurement of the natural helical repeat $h_0$, which is the average number of base pairs that are required to complete a full helical turn in the absence of torsional stress (Supplementary Note 1, ^13–15). B-DNA has an $h_0$ of 10.45 (±0.05) base pairs (bp) per helical turn ^4–8,16,17.

Twisting and bending deformations are treated as independent by the standard TWLC model ³, and the textbook value of $h_0$ is widely considered to be constant for straight and bent DNA alike. This model was challenged 30 years ago by Marko and Siggia ¹⁸ and their prediction of twist-bend coupling (TBC) that would lead to an unwinding, or increase of $h_0$, when DNA is bent into radii of curvatures that are well below the persistence length (50 nm). Such tight curvatures are common in biology. For example, the radius of curvature in the nucleosome is only 4.5 nm—just 10% of its persistence length—with DNA that is considerably overwound at $h=10.1(\pm 0.1)bp/turn$ ^17,19. On the other hand, recent all-atom molecular dynamics (MD) simulations of protein-free DNA circles at similar radii predict $h_0=11.25bp/turn$ ^20–22.

However, there has been no direct experimental quantification of the change of $h_0$ due to TBC, as existing assays cannot precisely control curvature and measure $h_0$ simultaneously.

Nicked minicircle assay

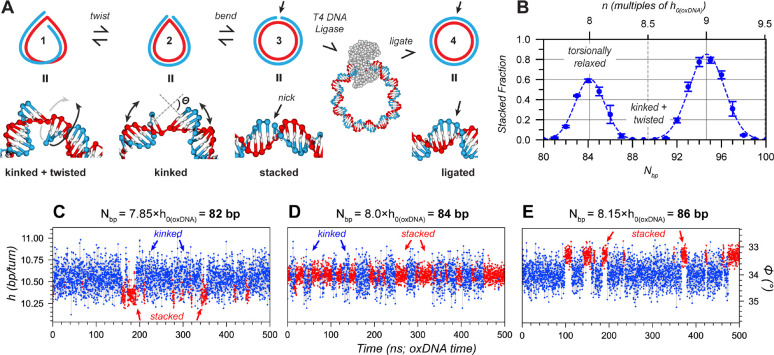
To determine $h_0$ of tightly bent DNA, we developed an assay using nicked DNA circles (Fig. 1). The point where the 5’ and 3’ ends of the linear strand meet is called a nick and is mechanically the weakest point in the structure. Unlike linear fragments in circularization experiments, this complex can neither unloop nor dimerize, which eliminates the impact of bending stress on complex formation (Supplementary Note 1). Three distinct conformations exist: a “stacked” state (Fig. 1A3); a “kinked” state (Fig. 1A2); and a “kinked + twisted” state in which the ends are twisted out of alignment (Fig. 1A1). Stacked states are approximately circular or oval, whereas kinked configurations are sharply bent at the nick which reduces the bending stress by lowering the DNA’s average curvature. The transition from a kinked to a stacked state is stabilized by additional π-stacking between nucleobases, but destabilized by increased bending stress; nevertheless, the energy difference between these states is small compared to the energy required for looping a linear duplex of the same length. In a “kinked + twisted” conformation (Fig 1A1), the two ends cannot be realigned through bending alone, but requires an additional twisting energy that must be overcome for stacking, either by over- or underwinding.

Fig. 1. Conformational states in nicked minicircles.

(A) Representative snapshots from oxDNA simulations of nicked minicircles in a (1) kinked + twisted, (2) kinked, or (3) stacked conformation (rendered with oxView ^23,24). See Fig. S3 for analysis of kink angles $\theta$. In a ligation experiment (Fig. 2), only the ends of stacked configurations (3) can be joined into a fully ligated circle (4). Complex with T4 DNA ligase (PDBID: 6DT1) is for size comparison and illustration only. (B) Plot of the fraction of stacked configurations from 21 different oxDNA simulations of nicked circles between 80–100 bp. Dotted line: Gaussian fits. (C-E) Analysis of dynamics between kinked (blue) and stacked (red) conformations as well as ℎ in oxDNA simulations of nicked circles with 82 (C), 84 (D) and 86 bp (E). $h$ (scale on left) was calculated from the average twist angle $\varphi$ between adjacent base pairs (scale on right; $h=360°⁄\varphi$). Note that kinked conformations fluctuate around the equilibrium $h_0$ of oxDNA (10.55 bp/turn), while stacked conformations can be overwound (C) or underwound (E).

MD simulations

We first simulated nicked minicircles with circumferences of $N_{\mathrm{b}\mathrm{p}}=80-100bp$ with the coarse-grained MD model oxDNA ²⁵. The fraction of stacked configurations in each simulation was determined through a geometrical analysis of the bases around the nick (Fig. 1B, Methods and Fig. S1). Two maxima around $N_{\mathrm{b}\mathrm{p}}=84.1bp$ and 94.6 bp appear roughly at 8 and 9 multiples of the natural helical repeat of oxDNA, $h_{0\left(\text{oxDNA}\right)}=10.55bp/turn$ ²⁶, indicating no significant change in the helical repeat compared to relaxed DNA. The minicircles are generally kinked around $N_{bp}\approx \left(n+\frac{1}{2}\right)h_{0\left(oxDNA\right)}$ for integer $n$ (Fig. 1A1, Fig. S3). Transitions between stacked and kinked conformations occur within nanoseconds to microseconds (Fig. 1C–E and Fig. S6, Fig. S7, Supplementary Movies S1–4). In these simulations of tightly bent circles, $h_0$ is not significantly changed compared to that of relaxed DNA, indicating a weak or absent TBC in the oxDNA model.

Ligation experiments

Next, we determined the helical repeat through ligation experiments of nicked minicircles. For this, we first circularized linear oligonucleotides with all lengths between 67–105 nucleotides (nt) with a ‘splint’ into single-stranded circles (Fig. 2A–B). All strands share the same 13 nt sequences at the ends, so that one common 26 nt splint can be used for all strands. Single-stranded circles formed with near-quantitative yields, as most of the complex is single-stranded and therefore very flexible, entropically favoring circularization over dimerization (Fig. 2B). Addition of the complementary strands (Fig. 2C, blue) forms the respective nicked circles. The sequences in between the common splint-binding domains are unique such that each ss circle can only hybridize to the correct counterstrand. The resulting nicked circles (Fig. 2D) were then enzymatically ligated into topologically closed double-stranded (ds) circles (Fig. 2E). The different species including linear strands, single- and double-stranded circles, can be separated by denaturing PAGE (polyacrylamide gel electrophoresis), (F-H), which also separates ss circles and linear strands of non-ligated complexes Fig. 2E). Four to five oligonucleotides with a length difference of 4 nt were combined into eight different subpools to fit all experiments on one gel and to allow for a better relative comparison between them as indicated in Fig. 2G.

Fig. 2. Experimental ligation of nicked circles of different lengths.

(A) Splint ligation of oligonucleotides (67–105 nt) produces ss minicircles (B). oxDNA simulation snapshot illustrates flexibility of ss region. (C) Respective complementary strands are annealed to yield nicked circles (D), which can then be enzymatically ligated into double-stranded circles (E). (F) Denaturing PAGE gel. (1) Five oligonucleotides (same as pool 7 in (G) and (H)) before and (2) after splint ligation. The splints run out of the gel; (3) Hybridization to the blue complementary strand before and (4) after ligation. M = size marker (linear ds DNA). (G) Denaturing PAGE analysis of the ligation experiment at 37 °C of all nicked circles $N_{bp}=67-105bp$, that are distributed between eight pools as annotated. Note that some circles split into two bands (73, 83, 93, and 103 bp) indicating different topoisomers. We hypothesize that the ligase does not change $h_0$ of DNA and that splitting occurs at half-integer multiples of $h_0$, or $N_{bp}\approx \left(n+\frac{1}{2}\right)h_0$. Ligase concentration in the final ligation step (D to E) was 100-fold lower in experiment H (4 U/μl). Uncropped gel images, an independent repeat of experiment G and of a 0.1X [ligase] experiment are shown in Fig. S4. (I) Helical repeat $h=N_{bp}/Lk$ for theoretically possible (grey) and experimentally observed (blue) ligated circles. Vertical lines indicate $N_{bp}$ where nicked circles form two topoisomers after ligation. Red datapoints: circles that should have been observed for a constant $h_0=10.5bp/turn$. Circles with $h=h_0$ are torsionally relaxed ($\Delta Tw=0),h>h_0$ are underwound ($\Delta Tw<0$), and $h<h_0$ are overwound ($\Delta Tw>0$). (J) The total mechanical energy of DNA in stacked or ligated circles is the sum of twisting energy $E_{Tw}$ and bending energy $E_{bend}$. At the local minima, circles are torsionally relaxed; to the left they are overwound, and to the right underwound. Red: Expected energy landscape if $h_0=10.5bp/turn$ was constant and independent of curvature.

Equilibrium helical repeat is curvature-dependent

As only stacked configurations present the terminal 5’ phosphates and the 3’ OH groups close enough for ligation, we originally expected a band intensity profile like that in Fig. 1B and to detect TBC through a shift of maxima. However, ligation was near-quantitative at all $N_{bp}$ (Fig. 2G). Reducing [ligase] (Fig. 2H, Fig. S4) or increasing [salt] (Fig. S8) increased the difference between ligation maxima and minima and indicate a clear shift towards longer $N_{bp}$, but an accurate determination of $h_0$ from gel band intensities was still difficult. However, at those $N_{bp}$ where ligation produces two topoisomers ($N_{bp}=73,83,92,93$ and 103 bp), the energetical cost (twist energy) for unwinding or overwinding the ends from a torsionally relaxed kinked and twisted starting configuration into a ligatable stacked configuration must have been roughly equal. This is only the case if $N_{bp}\approx \left(n+\frac{1}{2}\right)h_0$, which is equivalent to an excess twist $\Delta Tw\approx \pm \frac{1}{2}turns$. Therefore, $N_{bp}=73bp\approx 6.5h_0$ and $h_0\approx 73bp/6.5turns\approx 11.2bp/turn$. Likewise, for $N_{bp}=83,h_0\approx 83bp/7.5turns\approx 11.1bp/turn$ and so on. If $h_0$ were constant at $h_0=10.5bp/turn$, two topoisomers would have been observed around $N_{bp}\approx 68,79,89$, and $100bp$ instead. For any other circle length, only the topoisomer with the least torsional stress (the lowest $\Delta Tw$) is observed (see Supplementary Note 2).

Fig. 2I shows the helical repeat $h$ of circles with different lengths and linking numbers $Lk$, which is the number helical turns. For a given $Lk,h$ increases linearly with $N_{bp}$ with a slope of $1/Lk$ (Fig. 2I). Rings with $h\ne h_0$ are either over- or underwound. Two topoisomers form at the vertical lines. With additional datapoints from topoisomer splitting at 123, 143 and 164 bp (see Fig. S5), the length-dependent, or rather curvature-dependent, $h_0$ can be fitted through the datapoints at $N_{bp}\approx \left(n+\frac{1}{2}\right)h_0$, where two topoisomers are observed with a function from MS [¹⁸, Fig. 3B, Supplementary Note 4, eq. 31)].

Fig. 3. Extent of change of $h_0$.

(A) A 39 bp DNA fragment is displayed with decreasing radii of curvature ($r=50,12,6.4or4.2nm$). All DNA with a smaller radius of curvature than $r=50nm~l_p$ is considered tightly bent. The fragment with $r=4.2nm$ has $h_0=11.14bp/turn$ and is unwound by ~82° compared to the canonical 10.45 bp/turn (transparent overlay); a full circle is unwound by almost ½ turn. (B) Relaxed helical repeat of a duplex bent with a constant radius of curvature $r$ (top axis) matching that of a minicircle of $N_{bp}$ base pairs (bottom axis). Green: $h_0$ from gel data (topoisomer splitting); black: data from circularization experiments ^5–7; blue: fit using the Marko/Siggia model ¹⁸ with fit parameters $h_{(k=0)}=10.42bp/turn$ (=linear DNA) and G/C = 2.7, where G is the twist-bend coupling parameter and C is the torsional stiffness; red: TBC prediction with parameters from ref. ^28,29. (C) A Nucleosome (PDBID: 3LZ0) has a helical repeat of ~10.1 bp/turn ¹⁷, but a circle with this curvature is torsionally relaxed at ~11.1 bp/turn according to our measurements (D). It follows that $\Delta Tw\approx 1.2turns$.

In Fig. 2J, we plot the sum of the twist and bend deformation energy, $E_{\mathrm{c}\mathrm{i}\mathrm{r}\mathrm{c}}=E_{\mathrm{T}\mathrm{w}}+E_{\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{d}}$ (see Supplementary Note 2). Circles are torsionally relaxed if they lie on the observed $h_0$ curve in Fig. 2I, which connects the helical repeats of circles at the local minima of the energy shown in Fig. 2J. The measured helical repeat is not changed by lowering the ligase concentration, as band splitting is still visible at the same lengths (Fig. 2, Fig. S4). On the other hand, DNA slightly unwinds at high temperatures and low salinity ^16,27, and both trends are captured by oxDNA simulations and ligation experiments (Fig. S8 - Fig. S9). In summary, our data shows that $h_0$ is curvature-dependent and bending unwinds DNA (Fig. 3A–B).

Discussion

DNA is commonly tightly bent or twisted in biology, and the associated mechanical stress influences all molecular mechanisms involving DNA. Physical models often treat DNA as an elastic rod or beam where three fundamental modes of deformation exist: stretching, bending, and twisting. These deformations can in principle be coupled. Entropically coiled DNA can be straightened by forces below 1 pN and allow one to determine the persistence length ^30,31. Higher forces overstretch DNA, causing twist-stretch coupling ^32,33, where DNA counterintuitively first slightly overwinds at small forces (<20–30 pN) and unwinds at higher forces. Tension in minicircles is only ~3–5 pN (see simulation in Fig. S10 and Supplementary Note 5), and the influence of twist-stretch coupling on their helical repeat is therefore negligible. Finally, TBC was theoretically predicted three decades ago by Marko and Siggia (MS) ¹⁸ as an unwinding of tightly bent DNA.

A direct quantification of $h_0$ as in our experiments is difficult with magnetic torque tweezer (MTT) experiments because these require fragments where $L\gg l_b$ and cannot produce tight curvatures in a controllable way. Recent TBC estimates ^28,29 predict an insignificant widening of $h_0$ by only 0.2 % at the curvature of the nucleosome (Fig. 3B, red curve; see Suppl. Note 4), which would be practically indetectable. Our data and the magnitude of the relative difference in helical repeat (~10 %), however, is in almost perfect agreement with the predictions from the original MS paper ¹⁸ and the extrapolation of the trend from some circularization experiments (Fig. 3B, black datapoints ^5–7, discussion in Supplementary Note 4). While the MS equation (Supplementary Note 4, eq. 31) fits excellently to the experimental data in Fig. 3B, the value of the fitted TBC parameters may indicate that additional physics is at play. General stability requirements of the MS model are difficult to satisfy for a linear model when the twist-bend coupling parameter $G$ exceeds the torsional stiffness $C$, and non-linearities might have to be introduced (see Supplementary Note 4). In contrast, the TBC parameter estimates from ref. ^28,29 satisfy $G/C<1$ naturally, but the effect on the helical repeat (Fig. 3B, red curve) is irreconcilably weaker than the experimental results suggest.

In a related assay, Du et al. also observed circles with different topoisomers consistent with our data ³⁴, but interpreted them as a species with internal kinks ($\Delta Tw=-1$) and one without kinks ($\Delta Tw=0$). However, generating circles of these lengths with $\Delta Tw=-1$ ³⁴ through ligation of nicked circles seems implausible due to the high energetical cost of undertwisting and/or the large stabilization energy required for a kink to make the free energy of the delta TW = −1 state and Delta TW = 0 comparable. Moreover, we performed MD simulations that confirm that nicks are the weakest link in the structure (Fig. S12). We therefore apply the conventional interpretation that two topoisomers are found at $N_{bp}=\left(n+\frac{1}{2}\right)h_0$^4–8, which requires a changing $h_0$.

Theoretically, the T4 DNA ligase might also influence the assay results. While $h_0$ of DNA in ligase complexes is not directly significantly changed ^35,36, a stabilization of internal defects by ligase was reported ³⁷. On the other hand, a helical repeat of 11–11.3 bp/turn consistent with TBC and our data also appears in ligation-free circularization experiments where j-factor maxima (Fig. 3E in ref. ¹⁰) and the uncircularization kinetics ¹⁵ are significantly shifted. Different $h_0$ found in other circularization experiments ^9,11 can be explained by sticky end geometries and kinks at nicks (¹⁵, Supplementary Note 1).

Moreover, the helical repeat is also increased in transcription factors that loop DNA including the lac repressor ³⁸, or araCBAD ³⁹ or in HU protein induced loops ⁴⁰ . We therefore conclude that a widening of $h_0$ in tightly bent DNA occurs irrespective of ligase.

Conclusions

DNA in biological systems is commonly under high mechanical stress. Around 72% of eukaryotic DNA is nucleosomal DNA with a radius of curvature of ~4.5 nm (Fig. 3C). Our data suggests that DNA with this curvature would be torsionally relaxed at $h_0=11.1\mathrm{b}\mathrm{p}/\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{n}$, but instead, nucleosomal DNA is overwound to $h=10.1\mathrm{b}\mathrm{p}/\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{n}$ ¹⁷. This results in a $\Delta Tw\approx 1.2turns$ (Fig. 3D) or a twist energy of $E_{Tw}\approx 60k_{B}T\approx 35.4kcal/mol$ (Supplementary Note 2, eq. 13) in addition to a bending stress $E_{bend}\approx 60k_{B}T$ (eq. 15). The total mechanical stress in a nucleosome would therefore be $E_{Tw}+E_{bend}\approx 120k_{B}T$, which must be compensated or modulated through noncovalent interactions between the DNA and highly positively charged histone proteins. The increase of $h_0$ aggravates the linking number paradox (36) and the torsional stress will influence DNA wrapping and unwrapping (37) that are necessary for gene regulation and expression.

Our findings also apply to packing of virus capsids, bacterial genomes ⁴¹ or transcription factors, or the template length-dependent amplification bias in rolling circle amplification ⁴². Next, the curvature-dependence of the helical repeat will also have to be considered in the design of DNA nanostructures that contain small minicircles such as DNA catenanes ⁴³, rotaxanes ⁴⁴, DNA-encircled lipid nanodiscs ⁴⁵, or for tightly bent DNA origami structures ^46,47. Physical models of DNA need to be corrected for tightly bent DNA. Finally, a consequence of TBC is that torque from helicases, polymerases or DNA packing motors will induce bending. We conclude that a changing helical repeat must be considered in all processes where DNA is tightly bent or twisted.

Data and materials availability:

Raw experimental or simulation data as well as code is available upon request.