MRI economics: Balancing sample size and scan duration in brain wide association studies

Abstract

A pervasive dilemma in neuroimaging is whether to prioritize sample size or scan time given fixed resources. Here, we systematically investigate this trade-off in the context of brain-wide association studies (BWAS) using functional magnetic resonance imaging (fMRI). We find that total scan duration (sample size × scan time per participant) robustly explains individual-level phenotypic prediction accuracy via a logarithmic model, suggesting that sample size and scan time are broadly interchangeable up to 20–30 min of data. However, the returns of scan time diminish relative to sample size, which we explain with principled theoretical derivations. When accounting for fixed overhead costs associated with each participant (e.g., recruitment, non-imaging measures), prediction accuracy in many small-scale and some large-scale BWAS might benefit from longer scan time than typically assumed. These results generalize across phenotypic domains, scanners, acquisition protocols, racial groups, mental disorders, age groups, as well as resting-state and task-state functional connectivity. Overall, our study emphasizes the importance of scan time, which is ignored in standard power calculations. Standard power calculations maximize sample size, at the expense of scan time, which can result in sub-optimal prediction accuracies and inefficient use of resources. Our empirically informed reference is available for future study design: WEB_APPLICATION_LINK

Introduction

A fundamental question in systems neuroscience is how individual differences in brain function are related to common variation in phenotypic traits, such as cognitive ability or physical health. Following recent work (Marek et al., 2022), we define brain wide association studies (BWAS) as studies of the associations between phenotypic traits and common inter-individual variability of the human brain. An important subclass of BWAS seeks to predict individual-level phenotypes using machine learning. Individual-level prediction is important for addressing basic neuroscience questions and critical for precision medicine (Finn et al., 2015; Gabrieli et al., 2015; Woo et al., 2017; Bzdok et al., 2019; Eickhoff et al., 2019; Varoquaux et al., 2019).

Many BWAS are underpowered, leading to low reproducibility and inflated prediction performance (Button et al., 2013; Arbabshirani et al., 2017; Bzdok et al., 2018; Kharabian Masouleh et al., 2019; Elliott et al., 2020; Poldrack et al., 2020). Larger sample sizes increase reliability of brain-behavior associations (Tian et al., 2021; Chen et al., 2023) and individual-level prediction accuracy (He et al., 2020; Schulz et al., 2020). Indeed, a recent study suggested that reliable BWAS require thousands of participants (Marek et al., 2022), although certain multivariate approaches might reduce sample size requirements (Chen et al., 2023).

In parallel, other studies have emphasized the importance of longer fMRI scan time per participant during both resting and task states, which leads to improved data quality and reliability (Mumford et al., 2008; Birn et al., 2013; Nee, 2019; Noble et al., 2019; Elliott et al., 2020; Lynch et al., 2020; G. Chen et al., 2022), as well as new insights into the brain (Laumann et al., 2015; Newbold et al., 2020; Gordon et al., 2023). When sample size is fixed, increasing resting-state fMRI scan time per participant improves individual-level prediction accuracy of some cognitive measures (Feng et al., 2023).

Therefore, in a world with infinite resources, fMRI-based BWAS should maximize both sample size and scan time for each participant. However, in reality, BWAS investigators have to decide between scanning more participants (for a shorter duration), or fewer participants (for a longer duration) within a fixed scan budget. Furthermore, there is a fundamental asymmetry between sample size and scan time per participant because of inherent overhead cost associated with each participant, which can be quite substantial, e.g., when recruiting from a rare population. Surprisingly, the exact trade-off between sample size and scan time per participant has never been studied. We emphasize that this trade-off is an issue for the design of small studies, as well as large-scale collection efforts with thousands of participants, given competing interests among multiple investigators and limited participant availability.

Here, we systematically characterize the effects of sample size and scan time of resting-state fMRI on BWAS prediction accuracy, using the Adolescent Brain and Cognitive Development (ABCD) study and the Human Connectome Project (HCP). To explore how overhead cost per participant impacts the trade-off between sample size and scan time in maximizing prediction accuracy within a fixed scan budget, we then expanded the datasets to include the Transdiagnostic Connectome Project (TCP), Major Depressive Disorder (MDD), Alzheimer’s Disease Neuroimaging Initiative (ADNI) and the Singapore geriatric intervention study to reduce cognitive decline and physical frailty (SINGER) datasets. Overall, our results provide an empirical reference for future study design.

Results

Larger sample size can compensate for shorter scan time & vice versa

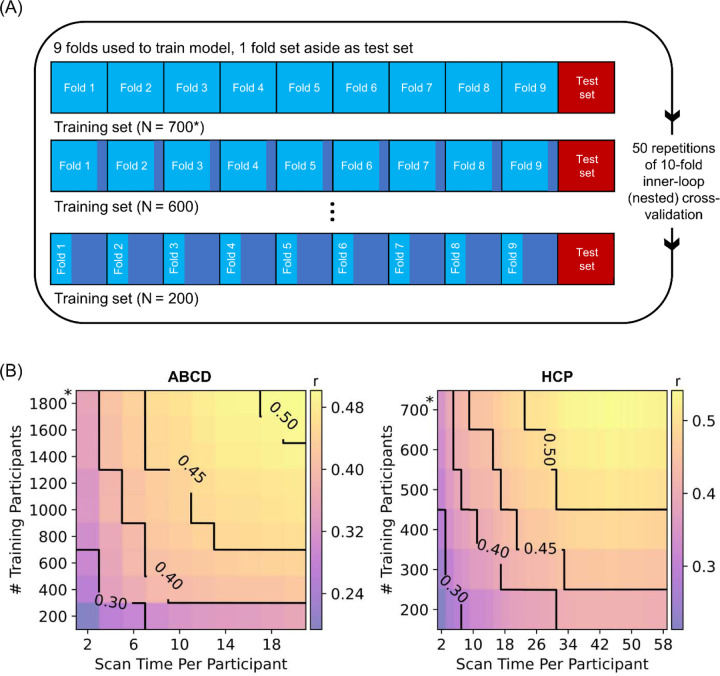
For each participant in the HCP and ABCD datasets, we calculated a 419 × 419 resting-state functional connectivity (RSFC) matrix using the first $T$ minutes of fMRI data (Schaefer et al., 2018). $T$ was varied from 2 minutes to the maximum scan time in each dataset in intervals of 2 minutes. The RSFC matrices (from the first $T$ minutes) served as input features to predict a range of phenotypes in each dataset using kernel ridge regression (KRR) via a nested inner-loop cross-validation procedure. The analyses were repeated with different numbers of training participants (i.e., different training sample size $N$). Within each cross-validation loop, test participants were fixed across different training set sizes, so that prediction accuracy was comparable across different training set sizes (Figure 1A). The whole procedure was repeated multiple times and averaged to yield stable results.

Figure 1. Increasing training participants and scan time per participant lead to higher prediction accuracy of phenotypes.

(A) Prediction workflow for the HCP dataset. The participants were split into 10 folds. One fold was set aside to be the test set. The remaining folds comprised the training set. Cross-validation was performed on the training set to select the best hyperparameter. The best hyperparameter was then used to fit a final model from the full training set, which was then used to predict phenotypes in the test set. To vary training set size, each training fold was subsampled and the whole inner-loop nested cross-validation procedure was repeated with the resulting smaller training set. As shown in the panel, the test set remained the same across different training set sizes, so that prediction accuracy was comparable across different sample sizes. Each fold took a turn to be the test set (i.e., 10-fold inner-loop nested cross-validation) and the procedure was repeated with different amounts of fMRI data per participant $T$ (not shown in panel). For stability, the entire procedure was repeated 50 times and averaged. A similar workflow was used in the ABCD dataset. We note that in the case of HCP, care was taken so siblings were not split across folds, while in the case of ABCD, participants from the same site were not split across folds. (B) Contour plot of prediction accuracy (Pearson’s correlation) of the cognitive factor score as a function of the scan time $T$ used to generate the functional connectivity matrix, and the number of training participants $N$ used to train the predictive model in the Adolescent Brain and Cognitive Development (ABCD) and Human Connectome Project (HCP) datasets. Increasing training participants and scan time both improved prediction performance. The * in both figures indicates that all available participants were used, therefore the sample size will be close to, but not exactly the number shown. Multiple additional control analyses are found in Figures S1 to S5.

We first considered the cognitive factor score from each dataset because the cognitive factor scores were previously found to exhibit the highest prediction accuracy across all phenotypes (Ooi et al., 2022). Figure 1B shows the prediction accuracy (Pearson’s correlation) of the cognitive factors in the HCP and ABCD datasets as a function of both scan time per participant and number of training participants. Along a black iso-contour line, the prediction accuracy is (almost) constant even though scan time and sample size are changing. Consistent with previous literature (He et al., 2020; Schulz et al., 2023), increasing the number of training participants (when scan time per participant is fixed) improved prediction performance. Similarly, increasing scan time per participant (when number of training participants is fixed) also improved prediction performance (Feng et al., 2023).

Similar conclusions were obtained when we measured prediction accuracy using coefficient of determination (COD) instead of Pearson’s correlation (Figure S1), computed RSFC using the first $T$minutes of uncensored data (Figure S2), did not perform censoring of high motion frames (Figure S3), or utilized linear ridge regression (LRR) instead of KRR (Figures S4 & S5). Furthermore, although the cognitive factors were not necessarily comparable across datasets (due to differences in population characteristics and phenotypic measures), there was strong agreement in prediction accuracies between the two datasets for the same sample size and scan time per participant (r = 0.98; Figure S6).

Sample size & scan time per participant are interchangeable

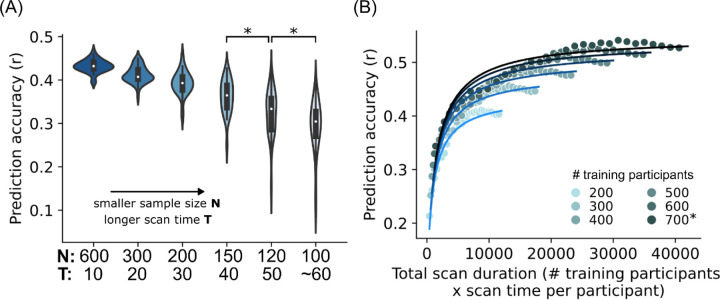
Next, we characterised the relative contributions of sample size and scan time per participant to the prediction of different phenotypes. Figure 2A shows that the prediction accuracy of the cognitive factors increases with total scan duration (# training participants × scan time per participant), suggesting that sample size and scan time per participant were broadly interchangeable.

Figure 2. Sample size and scan time are broadly interchangeable for individual-level phenotypic prediction.

(A) Scatter plot showing prediction accuracy (Pearson’s correlation) of the cognitive factor as a function of total scan duration (defined as # training participants x scan time per participant). Each color shade represents different number of total participants used to train the prediction algorithm. Plots are repeated for the Adolescent Brain and Cognitive Development (ABCD) study and Human Connectome Project (HCP). The * indicates that all available participants were used, therefore the sample size will be close to, but not exactly the number shown. There was a diminishing returns of scan time per participant beyond 30 minutes in the HCP dataset; data points with more than 30 minutes of scan time are shown with black outlines. As shown by the black arrows, scanning 700 participants for 14 minutes and 300 participants for 58 minutes yielded the same prediction accuracy, although the total scan duration of the former was almost 2 times lower: 700 × 14 = 9800 vs 300 × 58 = 17400. In the ABCD dataset, where maximum scan time per participant was 20 minutes, the diminishing returns of scan time was not observed. (B1) Scatter plot showing normalized prediction accuracy of the cognitive factor scores and 34 other phenotypes versus total scan duration ignoring data beyond 20 minutes of scan time. Cognitive, mental health, personality, physicality, emotional and well-being measures are shown in shades of red, grey, blue, yellow, green and pink, respectively. The logarithmic black curve suggests that total scan duration explained prediction performance well across phenotypic domains and datasets. (B2) Same as Figure 2B1, except the horizontal axis (total scan duration) is plotted on a logarithm scale. The linear black line suggests that the logarithm of total scan duration explained prediction performance well across phenotypic domains and datasets.

In the HCP dataset, we observed diminishing returns of scan time with respect to sample size for scan time beyond 30 minutes. For example, scanning 700 participants for 14 minutes per participant (with a total scan duration of 9800 minutes) and scanning 300 participants for 58 minutes (with a total scan duration of 17400 minutes) produced similar prediction accuracy (arrows in Figure 2A). The diminishing returns of scan time was not present in the ABCD study, which had a maximum scan time of 20 minutes.

Looking beyond the cognitive factor scores, we focused on 28 (out of 59) HCP phenotypes and 23 (out of 37) ABCD phenotypes that were reasonably well-predicted with maximum prediction accuracies of r > 0.1 (Table S1A). Upon visual inspection, we found that 89% (i.e., 25 out of 28) HCP phenotypes exhibited diminishing returns of scan time beyond 20–30 minutes. Diminishing returns were not observed for all 23 ABCD phenotypes.

Overall, this suggests that for almost all phenotypic measures (that were reasonably well-predicted), sample size and scan time per participant were broadly interchangeable up to 20–30 minutes in the HCP dataset.

Total scan duration explains prediction accuracy via a logarithmic trend

Among the 25 HCP and all 23 ABCD phenotypes exhibiting broad interchangeability of sample size and scan time, a logarithmic pattern was evident in 76% (19 out of 25) HCP and 74% (17 out of 23) ABCD phenotypes (Table S1A; Figures S7 and S8). To assess the universality of a logarithmic relationship between total scan duration and prediction accuracy, for each of the 19 HCP and 17 ABCD phenotypes, we fitted a logarithm curve (with two free parameters) between prediction accuracy and total scan duration (ignoring data beyond 20 minutes per participant). The logarithm fit allowed phenotypic measures from both datasets to be plotted on the same normalized prediction performance scale (Figures 2B). See Methods for details.

The black curve (Figures 2B) indicated the quality of the logarithmic fit of the phenotypes (dots in Figure 2B). Overall, total scan duration explained prediction accuracy across HCP and ABCD phenotypes remarkably well: coefficient of determination (COD) or R² = 0.88 and 0.89 respectively. For example, scanning 300 participants for 28 minutes (total scan duration = 300 × 28 = 8400 minutes) in the HCP dataset, or 600 participants for 14 minutes (total scan duration = 600 × 14 = 8400 minutes) in the ABCD dataset yielded very similar normalized prediction accuracies for the cognitive factor scores (arrows in Figure S8). Quantitative goodness of fit measures are reported in Table S1B.

The logarithm curve was also able to explain prediction accuracy well across different prediction algorithms (KRR and LRR) and different performance metrics (COD and r), as illustrated for the cognitive factor scores in Figure S9. The logarithm fit was also excellent when we considered 30 minutes of scan time, instead of 20 minutes (Figure S10).

As scan time increases, sample size becomes relatively more important

In the previous sections, we showed that sample size and scan time per participant were broadly interchangeable in the ABCD study and up to 20–30 minutes of scan time per participant in the HCP dataset. To examine this interchangeability more closely, we considered the prediction accuracy of the HCP factor score across six combinations of sample size and scan time totalling 6000 minutes of total scan duration (Figure 3A).

Figure 3. As scan time increases, sample size eventually becomes more important than scan time.

(A) Prediction accuracy of the HCP cognition factor score when total scan duration is fixed at 6000 minutes, while varying scan time per participant from 10 to 60 minutes. Each violin plot shows the distribution of prediction accuracies across 50 random cross-validation splits. * indicates that the distributions of prediction accuracies were significantly different between adjacent pairs of sample sizes (and scan time per participant) after false discovery rate (FDR) q < 0.05 correction. (B) Scatter plot of prediction accuracy against total scan duration for the cognitive factor score in the HCP dataset. The curves were obtained by fitting a theoretical model to the prediction accuracies of the cognitive factor score. The theoretical model explains why sample size is more important than scan time (see main text).

We observed that prediction accuracy decreased with increasing scan time per participant, despite maintaining 6000 minutes of total scan duration (Figure 3A). However, the accuracy reduction was modest below 30 minutes of scan time. Similar conclusions were obtained for all 19 HCP and 17 ABCD phenotypes that followed a logarithmic fit (Figure S11).

The observation that increasing scan time per participant has diminishing returns relative to sample size suggests that a simple logarithmic model does not explain all the factors that contribute to prediction accuracy. In the next section, we derived a mathematical theory that better explains the relative contributions of scan time and sample size to prediction as empirically observed.

Theoretical relationship of prediction accuracy with sample size & scan time explains why sample size is more important than scan time

Even though sample size and scan time are broadly interchangeable, there is a diminishing return of scan time per participant relative to sample size (Figure 3A). To gain insights into this phenomenon, we derived a closed-form mathematical relationship relating prediction accuracy (Pearson’s correlation) with scan time per participant and sample size (see Methods). To provide an intuition for the theoretical derivations, we note that phenotypic prediction can be theoretically decomposed into two components: one component relating to an average prediction (common to all participants) and a second component relating to a participant’s deviation from this average prediction.

The uncertainty (variance) of the first component scales as $1/N$, like a conventional standard error of the mean. For the second component, we note that the prediction can be written as regressions coefficients × FC (for linear regression). The uncertainty (variance) of the regression coefficient estimates scales with $1/N$.The uncertainty (variance) of the FC estimates scales with $1/T$ (i.e. reliability improves with $T$). Thus, the uncertainty of the second component scales with $1/NT$. Overall, our theoretical derivation suggests that prediction accuracy can be expressed as a function of $1/N$ and $1/NT$ with three free parameters.

There were several simplifying assumptions in the theoretical derivations. Furthermore, the theoretical derivations did not tell us the relative importance of the $1/N$ and $1/NT$ terms. Therefore, we fitted the theoretical model to actual prediction accuracies in the HCP and ABCD datasets (Figure 1B). The goal was to determine (1) whether our theoretical model (despite the simplifying assumptions) would still explain the empirical results, and (2) to determine the relative importance of $1/N$ and $1/NT$.

We found an excellent fit with actual prediction accuracies for the 19 HCP and 17 ABCD phenotypes (Figures 3B, S12 & S13): R² = 0.89 and 0.90 respectively (Table S1B). This suggests that our theoretical model was able to explain the observed phenomena despite the simplifying assumptions. When $T$ was small, the $1/NT$ term dominated the $1/N$ term, which explained the almost 1-to-1 interchangeability between scan time and sample size for shorter scan time. The existence of the $1/N$ term ensured that sample size was still slightly more important than scan time even for small $T$. FC reliability eventually saturated with increasing $T$. Therefore, the $1/N$ term eventually dominated the $1/\mathit{NT}$ term, so sample size became much more important than scan time.

We note that for shorter scan time, the logarithmic and theoretical models performed equally well with equivalent goodness of fit (R²) across the 17 ABCD phenotypes (p = 0.57). For longer scan time, the theoretical model exhibited better fit than the logarithmic model (p = 0.002 across the 19 HCP phenotypes; Figure S14). Furthermore, prediction accuracy under the logarithmic model will exceed a correlation of one for sufficiently large N and T, which is obviously wrong. Therefore, we will use the theoretical model to derive a reference for future study design (in a later section).

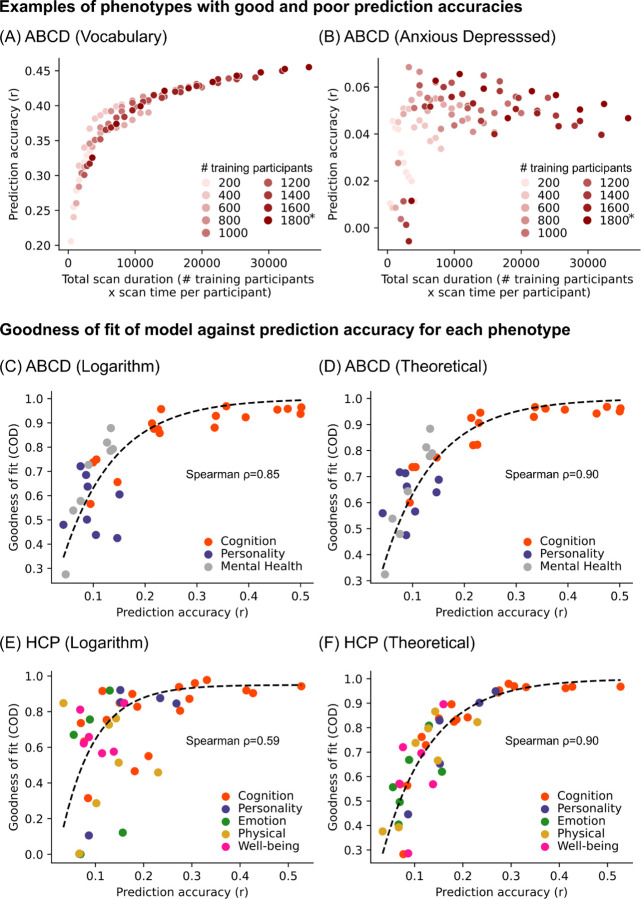
Models work better for well-predicted phenotypes

For phenotypes that were predicted with maximum prediction accuracies of Pearson’s r > 0.1, the logarithmic and theoretical models were able to explain the prediction accuracies well with an average explained variance >75% (Table S1B). If we loosened the prediction threshold to include phenotypes whose prediction accuracies (Pearson’s r) were positive in at least 90% of all combinations of sample size $N$ and scan time $T$ (Table S1A), the model fit was lower but still relatively high with average explained variance >67% (Table S1B).

More generally, phenotypes with high overall prediction accuracies adhered to the logarithmic and theoretical models well (example in Figure 4A), while phenotypes with poor prediction accuracies resulted in poor adherence to both models (example in Figure 4B). Indeed, model fit for both models was strongly correlated with prediction accuracy across phenotypes in both datasets (Figures 4C to 4F). These findings suggest that the imperfect fit of the theoretical and logarithmic models for some phenotypes may be due to their poor predictability, rather than true variation in prediction accuracy with respect to sample size and scan time.

Figure 4. Logarithmic and theoretical models work better for well-predicted phenotypes.

(A) Scatter plot of prediction accuracy against total scan duration for an exemplary phenotype with high prediction accuracy. (B) Scatter plot of prediction accuracy against total scan duration for an exemplary phenotype with low prediction accuracy. (C) Scatter plot of logarithmic model goodness-of-fit (coefficient of determination or COD) against prediction accuracies of different ABCD phenotypes. COD (also known as R²) is a measure of explained variance. Here, we considered phenotypes whose prediction accuracies (Pearson’s r) were positive in at least 90% of all combinations of sample size $N$ and scan time $T$, yielding 42 HCP phenotypes and 33 ABCD phenotypes. Prediction accuracy (horizontal axis) was based on maximum scan time and sample size. For visualization, we plot a dashed black line by fitting to a monotonically increasing function. (D) Same as panel C but using theoretical (instead of logarithmic) model. (E) Same as panel C but using HCP (instead of ABCD) dataset. (F) Same as panel C, but using HCP (instead of ABCD) and using theoretical (instead of logarithmic) model. For all panels, logarithmic model fit was performed using up to 20 minutes of scan time per participant. For theoretical model fit, the maximum scan time per participant was used.

Non-stationarity in fMRI-phenotype relationships weakens model adherence

The theoretical model better matched the empirical data than the logarithmic model. However, there remain discrepancies, particularly in the HCP dataset, which sometimes showed decreases in prediction accuracy with increasing scan time (Figure S7). As noted above, some phenotypes likely fail to match the logarithmic or theoretical models because of intrinsically poor predictability. However, there were phenotypes that were reasonably well-predicted yet still exhibited a low fit to both logarithmic and theoretical models. For example, “Anger: Aggression” was reasonably well-predicted in the HCP dataset, but prediction accuracy was primarily improved by sample size and not scan time (Figure 5A). As scan time per participant increased, prediction accuracy appeared to increase, decrease and then increase again. This pattern was remarkably consistent across sample sizes (Figure 5A).

Figure 5. Non-stationarity in fMRI-phenotype relationship weakens adherence to logarithmic and theoretical models.

(A) Scatter plot of prediction accuracy against total scan duration for the “Anger: Aggression” phenotype in the HCP dataset. Despite relatively high accuracy, the phenotype improved with larger sample size, but not scan time. As scan time per participant increases, prediction accuracy appeared to increase, decrease, then increase again. (B) Scatter plot of prediction accuracy against total scan duration for the “Anger: Aggression” phenotype in the HCP dataset after randomizing fMRI run order for each participant. Observe that the prediction accuracy now adheres strongly to the logarithmic and theoretical models. (C) Box plots showing goodness of fit to logarithmic and theoretical models before and after randomizing fMRI run order for 33 ABCD phenotypes. * indicates that goodness-of-fits were significantly different (after FDR correction with q < 0.05). (D) Same as panel C, but for 42 HCP phenotypes. For all panels, model fit was performed using the maximum scan time per participant. For panels C and D, we considered all phenotypes whose prediction accuracies (Pearson’s r) were positive in at least 90% of all combinations of $N$ and $T$. For each boxplot, the horizontal line indicates the median across 33 ABCD phenotypes or 42 HCP phenotypes. The bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. Outliers are defined as data points beyond 1.5 times the interquartile range. The whiskers extend to the most extreme data points not considered outliers.

This suggests that fMRI-phenotype relationships might be non-stationary for certain phenotypes, which violates an assumption in both theoretical and logarithmic models. To put this in more colloquial terms, the assumption is that the relationship between FC and a phenotypic measure is the same (i.e., stationary) regardless of whether FC was computed based on five minutes of fMRI from the beginning, middle or end of the MRI session. To test the non-stationarity hypothesis, we note that for both HCP and ABCD datasets, the fMRI data was collected over four runs. Therefore, we randomized the fMRI run order independently for each participant and repeated the FC computation (and prediction) using the “first” T minutes of resting-state fMRI data under the randomized run order. The run randomization improved the goodness of fit of both theoretical and logarithmic models (Figures 5B, 5C, S15 and S16).

A reference for future study design

We have shown that investigators have the flexibility of attaining a specified prediction accuracy through different combinations of sample size and scan time per participant. To derive a reference for future studies, we considered four additional datasets – the TCP, MDD, ADNI and SINGER datasets. 34 phenotypes exhibited good fit to the theoretical model (Table S2; Figures S17 to S20). We also considered task-FC of the three ABCD tasks, and found that the number of phenotypes with good fit to the theoretical model ranged from 16 to 19 (Table S2; Figures S21 to S23).

In total, we fitted the theoretical model to 76 phenotypes in the HCP, ABCD, TCP, MDD, ADNI and SINGER datasets, yielding 89% average explained variance (Table S2). For each phenotype, the model was normalized by its maximum achievable accuracy (estimated by the theoretical model), yielding a fraction of maximum achievable prediction accuracy for every combination of sample size and scan time per participant. The fraction of maximum achievable prediction accuracy was then averaged across the phenotypes under a hypothetical 10-fold cross-validation scenario (Figure 6A). We note that the correlations between Figure 6A and Figure 1B across corresponding sample sizes and scan durations were 0.99 for both HCP and ABCD datasets.

Figure 6. Empirical reference for balancing sample size and scan duration while accounting for fixed costs per participant to optimally design BWAS.

(A) Fraction of maximum achievable prediction accuracy as a function of sample size and scan time per participant. Here, we assume a hypothetical 10-fold cross-validation scenario, where 90% of the sample size is used for training a model. The theoretical model was fitted to 76 phenotypes from the HCP, ABCD (rest and task), SINGER, TCP, MDD and ADNI datasets, yielding 89% average explained variance (Table S2). For each phenotype, the model was normalized by its maximum achievable accuracy (based on the theoretical model), yielding a fraction of maximum achievable prediction accuracy for every combination of sample size and scan time per participant. The fraction of maximum achievable prediction accuracy was then averaged across the phenotypes yielding the plot. (B) Fraction of maximum achievable prediction accuracy as a function of total fMRI budget, scan cost per hour and overhead cost per participant. The solid circles indicate location of the maximum prediction accuracy. Circles are not shown if optimal combination of sample size and scan time was beyond the edge of the graph (i.e., more than 200 minutes of scan time). The error bars indicate the optimal range of scan time that can achieve within 1% of the maximum prediction accuracy.

For the purpose of study design, we also need to consider the fundamental asymmetry between sample size and scan time per participant because of inherent overhead cost associated with each participant. These overhead costs might include recruitment effort, manpower to perform neuropsychological tests, additional MRI modalities (e.g., anatomical T1, diffusion MRI), other biomarkers (e.g., position emission tomography or blood tests). Therefore, the overhead cost can be higher than the cost of fMRI itself. Figure 6B illustrates the prediction accuracy achievable with different total fMRI budgets, costs per hour of scan time and overhead cost per participant.

There are three observations. First, larger fMRI budgets, lower scan cost and lower overhead cost facilitates larger sample size and scan time, leading to greater achievable prediction accuracy. Second, optimal scan time (solid circles in Figure 6B) increases with larger overhead cost, lower fMRI budget and lower scan cost. Third, all curves rise steeply with increasing scan time per participant, and then declines slowly with increasing scan time. Therefore, the optimal scan time range (error bars in Figure 6B) needed to achieve within 1% of the maximum prediction accuracy is asymmetric with a longer tail towards longer scan time. This long tail becomes longer when overhead cost is high. The reason is that even though sample size is more important than scan time in the theoretical model, higher overhead cost makes sample size and scan time more interchangeable.

As an example, when total fMRI budget was $100K, scan cost was $500 per hour and overhead cost was $500 for each participant, the optimal prediction accuracy was achieved by scanning 119 participants for 40.8 min per participant. To achieve within 1% of the maximum prediction accuracy, the minimum scan time was 25.5 min, which jumped to 67.5 min when overhead cost was $2000 per participant. As another example, when total fMRI budget was $10M and scan cost was $500 per hour, to achieve within 1% of the maximum prediction accuracy, the minimum scan time per participant were 8 min, 21.9 min and 41.6 min, corresponding to overhead costs of $500, $2000 and $5000 respectively.

Among the six datasets, the optimal scan time was the highest for ABCD and lowest for ADNI, but overall, the 1% optimum scan time ranges were highly overlapping across the six datasets (Figure S24). The consistency across datasets was remarkable given variations across datasets (Table S5), including different phenotypes, acquisitions (single band, multiband, multiecho multiband), coordinate systems (fsLR, fsaverage, MNI152), racial groups (Western and Asian populations), mental disorders (healthy, neurological and psychiatric) and age groups (children, young adults and elderly).

Different phenotypic domains also yielded highly overlapping 1% optimum scan time ranges (Figure S25). Furthermore, replicating previous studies (Greene et al., 2018; J. Chen et al., 2022; Zhao et al., 2023), n-back task-FC yielded better prediction performance for cognitive measures compared with RSFC in the ABCD dataset. However, although the optimal scan time was slightly higher for resting-state and the SST-task, the 1% optimum scan time ranges were highly overlapping across resting-state and the three tasks (Figure S26).

These results (Figure 6) do not account for second-order effects. For example, certain populations (e.g., children) might not be able to handle more than 1 hour of MRI scanning at a time, so longer scans would need to be broken up into multiple sessions, yielding an overhead cost associated with each session, and so on. As another example, beyond a certain sample size, multi-site data collection becomes necessary, which increases overhead cost per participant. Our web application (WEB_APPLICATION_LINK) allows for more flexible usage.

Additional control analyses

Figure S27 shows the 1% optimal scan time ranges for 13 HCP and ABCD phenotypes that exhibited strong agreement with the theoretical model without serious over-shoot or under-shoot. The 1% optimal scan time ranges were similar to the main analyses. Similar results were also obtained with all 36 HCP and ABCD phenotypes after randomizing the run order, as well as a subset of 17 HCP and ABCD phenotypes that exhibited strong agreement with the theoretical model without serious over-shoot or under-shoot after randomizing run order (Figure S27).

A higher resolution cortical parcellation with 1000 parcels yielded highly overlapping optimal scan time ranges with the original analysis (Figures S28 & S29). Given the observed non-stationarity effects (Figure 5), we simulated splitting data collection into two separate sessions. This simulation is possible because the HCP collected resting-state fMRI on two different days (sessions). We found splitting data collection into two sessions slightly increase optimal scan time, but the 1% optimal scan time ranges still highly overlapped when collecting data in a single session versus two sessions (Figure S29).

Our main analyses involved a cortical parcellation with 400 regions and 19 subcortical regions, yielding 419 × 419 RSFC matrices. We also repeated the main analyses using 19 × 419 RSFC matrices (Figures S28 & S29). When overhead cost per participant was low (e.g., $500 or $1000), the 1% optimal scan time range was highly overlapping between subcortical-cortical FC and whole-brain FC. However, when overhead cost per participant was high (e.g., $5000), the optimal scan time for subcortical-cortical FC was somewhat longer than for whole-brain FC, although there was still substantial overlap in the 1% optimal scan time ranges. This might arise because of lower SNR in subcortical regions, resulting in the need for longer scan time to achieve better estimate of subcortical FC.

Finally, we turn our attention to the effects of sample size and scan time per participant on the reliability of BWAS (Marek et al., 2022) using a previously established split-half procedure (Figure S30A; Tian et al., 2021^; Chen et al., 2023). Similar conclusions were obtained for both univariate and multivariate BWAS reliability, except that diminishing returns of scan time occurred beyond 10 minutes per participant, instead of 20–30 minutes of scan time for prediction accuracy (Figures S31 to S46). However, we strongly recommend that prediction accuracy, instead of reliability should be prioritized during study design. The reason is that reliability does not imply validity (Schmidt et al., 2000; Noble et al., 2019). For example, hardware artifacts may appear reliably in measurements without having any biological relevance. In the case of resting-state fMRI, reliable BWAS features do not guarantee accurate prediction of phenotypic measures.

Discussion

Neuroimaging studies are always confronted with the difficult decision of how to allocate fixed resources for an optimal study design. Here, we systematically investigate the trade-off between maximising scan time and sample size in the context of predicting phenotypes from FC. Sample size and scan time per participant are broadly interchangeable up to 20–30 min of scan time, and can be explained with a logarithmic model. A more complex theoretical model is able to explain prediction accuracy for longer scan time. Model fits were excellent across multiple phenotypic domains in six datasets, suggesting strong generalizability of these findings.

When accounting for overhead cost per participant, we found that future study designs might benefit from longer scan time per participant than those employed in existing studies. Our results strongly argue against the common practice of employing traditional power analyses, whose only inputs are sample size, to inform BWAS design. Because such power analyses inevitably point towards maximizing sample size, scan time then become minimized under budget constraints. The resulting prediction accuracies are likely lower than would be produced with alternate designs, thus impeding scientific discovery.

The 1% optimal scan time range provides greater flexibility in modifying study designs based on population- and site-specific characteristics. For example, a researcher seeking to study patients with depression from a minority population (i.e., higher overhead cost per participant) might find it more economical to increase the scan time for each participant in order to achieve the maximum possible prediction accuracy. Indeed, because the 1% optimal scan time range has a longer tail towards longer scan time, erring towards longer scan time (at the expense of sample size) increases the chance that the resulting scan time falls within the 1% optimal scan time range for the particular experiment. On the other hand, when sample size is small (in the low hundreds), there is a lot variability across cross-validation folds (Figure 3A; Varoquaux, 2018). Therefore, a case can also be made to prioritize sample size over scan time (left tail of the optimal scan time range).

To more accurately enable flexible decision making under varying constraints and inform study planning, we have provided a web application (WEB_APPLICATION_LINK) that estimates the fraction of maximum prediction accuracy that can be achieved with different sample size, scan time per participant and overhead cost per participant, together with additional factors. For example, certain demographic and patient populations might not be able to tolerate longer scans, so an additional factor will be the maximum scan time in each MRI session. As another example, beyond a certain sample size, multi-site data collection becomes a necessity, resulting in significantly higher overhead costs. As a third example, our analysis was performed on participants whose data survived quality control. Therefore, we have also provided an option on the web application to allow researchers to specify their estimate of the percentage of participants, whose data might be lost due to poor data quality (or general drop out).

We also emphasize that although the trade-off between scan time and sample size are similar across phenotypic domains, there exists variation within phenotypic domains. Therefore, our web application also allows users to select different phenotypes. Furthermore, the empirically informed reference is less useful for poorly predicted phenotypes, which predominantly included non-cognitive phenotypes (Figure 4). There are two non-exclusive reasons for poorly predicted phenotypes. One reason is that the measurement of the phenotype might not be reliable or valid (Uher, 2015; Nikolaidis et al., 2022; Gell et al., 2023), suggesting the need to improve the measurement of the phenotype. A second reason is that there may be an inherently weak relationship between the phenotype and fMRI, in which case, other imaging modalities might be worth exploring.

Another caveat is that the empirically informed reference is less useful for phenotypes whose prediction accuracies are strongly influenced by non-stationarity in fMRI-phenotype relationships. Arousal changes between or during resting-state scans are well-established (Tagliazucchi et al., 2014; Wang et al., 2016; Bijsterbosch et al., 2017; Laumann et al., 2017; Orban et al., 2020), so we expect the fMRI to be non-stationary especially for longer scans. However, since run randomization affected some phenotypes more than others (Figure 5), this suggests that there is an interaction between fMRI non-stationarity and phenotypes, i.e., there appears to be a non-stationary relationship between fMRI and phenotypes.

However, we should not over-emphasize the effect of non-stationarity in fMRI-phenotype relationship. The primary effect of increasing scan time is increasing FC reliability, while the non-stationarity of fMRI-phenotype relationship is a secondary effect. Indeed, while randomizing run order improves the fit of the theoretical and logarithmic models, the 1% optimal scan time range was similar to the main analyses (Figure S27). Furthermore, explicit state manipulation, such as asking participants to perform a task (Figure S23) or splitting the data collection into two separate days (Figure S26) also yielded highly overlapping optimal scan time range with the main analyses. Nevertheless, it is possible that some other (undiscovered) state manipulation could modify the 1% optimal scan time range significantly.

Finally, we note that beyond economic considerations, the diversity of the data sample and the generalizability of predictive models to subpopulations are also important factors when designing a study (Benkarim et al., 2022; Greene et al., 2022; Li et al., 2022; Kopal et al., 2023; Gell et al., 2024). There might also be studies where extensive scan time per participant is unavoidable. For example, when studying sleep stages, it is not easy to predict how long a participant would need to enter a particular sleep stage. Conversely, some phenomena of interest might be inherently short-lived. For example, if the goal is to study a fast acting drug (e.g., nitrous oxide), then it might not make sense to collect long fMRI scans. Furthermore, not all studies are interested in cross-sectional relationships between brain and non-brain-imaging phenotypes. For example, in the case of personalized brain stimulation (Cash et al., 2021; Lynch et al., 2022) or neurosurgical planning (Boutet et al., 2021), significant quantity of resting-state fMRI data might be necessary for accurate individual-level network estimation (Laumann et al., 2015; Braga et al., 2017; Gordon et al., 2017).

Conclusion

We find that sample size and scan time per participant are broadly interchangeable for brain-wide association studies (BWAS), although there are eventually diminishing returns of scan time per participant with respect to sample sizes. When accounting for fixed overhead costs per participant, we find that most studies (including large-scale studies) might benefit from greater scan time per participant than previously assumed. Our findings establish an empirically informed reference for calibrating scan time and sample sizes to optimize the study of how inter-individual variation in brain network architecture is related with individual differences in behavior.

Methods

Datasets, phenotypes and participants

Following previous studies, we considered 58 HCP phenotypes (Kong et al., 2019; Li et al., 2019) and 36 ABCD phenotypes (Chen et al., 2022; J. Chen et al., 2023). We additionally consider a cognition factor score derived from all phenotypes from each dataset (Ooi et al., 2022), yielding a total of 59 HCP and 37 ABCD phenotypes (Table S4).

In this study, we used resting-state fMRI from the HCP WU-Minn S1200 release. We filtered participants from Li’s set of 953 participants (Li et al., 2019), excluding participants who did not have at least 40 minutes of uncensored data (censoring criteria are discussed under “Image Processing”) and did not have the full set of the 59 non-brain-imaging phenotypes (henceforth referred to as phenotypes) that we investigated. This resulted in a final set of 792 participants with demographics found in Table S5.

We additionally considered resting-state fMRI from the ABCD 2.0.1 release. We filtered participants from Chen’s set of 5260 participants (J. Chen et al., 2023). We excluded participants who did not have at least 15 minutes of uncensored resting-fMRI data (censoring criteria are discussed under “Image Processing”) and did not have the full set of the 37 phenotypes that we investigated. This resulted in a final set of 2565 participants with demographics found in Table S5.

We also utilized resting-state fMRI from the SINGER baseline cohort. We filtered participants from an initial set of 759 participants, excluding participants who did not have at least 10 minutes of resting-fMRI data or did not have the full set of the 19 phenotypes that we investigated (Table S4). This resulted in a final set of 642 participants with demographics found in Table S5.

We utilized resting-state fMRI from the TCP dataset (Chopra et al., 2024). We filtered participants from an initial set of 241 participants, excluding participants who did not have at least 26 minutes of resting-fMRI data or did not have the full set of the 19 phenotypes that we investigated (Table S4). This resulted in a final set of 194 participants with demographics found in Table S5.

We utilized resting-state fMRI from the MDD dataset. We filtered participants from an initial set of 306 participants. We excluded participants who did not have at least 23 minutes of resting-fMRI data or did not have the full set of the 20 phenotypes that we investigated (Table S4). This resulted in a final set of 287 participants with demographics found in Table S5.

We utilized resting-state fMRI from the ADNI datasets (ADNI 2, ADNI 3 and ADNI GO). We filtered participants from an initial set of 768 participants with both fMRI and PET scans acquired within 1 year of each other. We excluded participants who did not have at least 9 minutes of resting-fMRI data or did not have the full set of the 6 phenotypes that we investigated (Table S4). This resulted in a final set of 586 participants with demographics found in Table S5.

In addition, we considered task-fMRI from the ABCD 2.0.1 release. We filtered participants from Chen’s set of 5260 participants (J. Chen et al., 2023). We excluded participants who did not have all 3 task-fMRI data remaining after quality control, and did not have the full set of the 37 phenotypes that we investigated. This resulted in a final set of 2262 participants with demographics found in Table S5.

Image processing

For the HCP dataset, the MSMAll ICA-FIX resting state scans were used (Glasser et al., 2013). Global signal regression has been shown to improve behavioral prediction (Li et al., 2019), so we further applied global signal regression (GSR) and censoring, consistent with our previous studies (Li et al., 2019; He et al., 2020; Kong et al., 2021). The censoring process entailed flagging frames with either FD > 0.2mm or DVARS > 75. The frame immediately before and after flagged frames were marked as censored. Additionally, uncensored segments of data consisting of less than 5 frames were also censored during downstream processing.

For the ABCD dataset, the minimally processed resting state scans were utilized (Hagler et al., 2019). Processing of functional data was performed in line with our previous study (Chen et al., 2022). Specifically, we additionally processed the minimally processed data with the following steps. (1) The functional images were aligned to the T1 images using boundary-based registration (Greve et al., 2009). (2) Respiratory pseudomotion motion filtering was performed by applying a bandstop filter of 0.31–0.43Hz (Fair et al., 2020). (3) Frames with FD > 0.3mm or DVARS > 50 were flagged. The flagged frame, as well as the frame immediately before and two frames immediately after the marked frame were censored. Additionally, uncensored segments of data consisting of less than 5 frames were also censored. (4) Global, white matter and ventricular signals, 6 motion parameters, and their temporal derivatives were regressed from the functional data. Regression coefficients were estimated from uncensored data. (5) Censored frames were interpolated with the Lomb-Scargle periodogram (Power et al., 2014). (6) The data underwent bandpass filtering (0.009Hz – 0.08Hz). (7) Lastly, the data was then projected onto FreeSurfer fsaverage6 surface space and smoothed using a 6 mm full-width half maximum kernel. Task-fMRI data was processed in the same way as the resting-state fMRI data.

For the SINGER dataset, we processed the functional data with the following steps. (1) Removal of the first 4 frames; (2) Slice time correction; (3) Motion correction and outlier detection: frames with FD > 0.3mm or DVARS > 60 were flagged as censored frames. 1 frame before and 2 frames after these volumes were flagged as censored frames. Uncensored segments of data lasting fewer than five contiguous frames were also labeled as censored frames. Runs with over half of the frames censored were removed; (4) Correcting for susceptibility-induced spatial distortion; (5) Multi-echo denoising (DuPre et al., 2021); (6) Alignment with structural image using boundary-based registration (Greve et al., 2009); (7) Global, white matter and ventricular signals, 6 motion parameters, and their temporal derivatives were regressed from the functional data. Regression coefficients were estimated from uncensored data.; (8) Censored frames were interpolated with the Lomb-Scargle periodogram (Power et al., 2014). (9) The data underwent bandpass filtering (0.009Hz – 0.08Hz). (10) Lastly, the data was then projected onto FreeSurfer fsaverage6 surface space and smoothed using a 6 mm full-width half maximum kernel.

For the TCP dataset, the details of data processing can be found elsewhere (Chopra et al., 2024). Briefly, the functional data was processed by following the HCP minimal processing pipeline with ICA-FIX, followed by GSR. The processed data was then projected onto MNI space.

For the MDD dataset, we processed the functional data with the following steps. (1) Slice time correction; (2) Motion correction, (3) Normalization for global mean signal intensity; (4) Alignment with structural image using boundary-based registration (Greve et al., 2009); (5) Linear detrending and bandpass filtering (0.01–0.08 Hz), and (6) Global, white matter and ventricular signals, 6 motion parameters, and their temporal derivatives were regressed from the functional data. (7) Lastly, the data was then projected onto FreeSurfer fsaverage6 surface space and smoothed using a 6 mm full-width half maximum kernel.

For the ADNI dataset, we processed the functional data with the following steps. (1) Slice time correction; (2) Motion correction; (3) Alignment with structural image using boundary-based registration (Greve et al., 2009); (4) Global, white matter and ventricular signals, 6 motion parameters, and their temporal derivatives were regressed from the functional data. (5) Lastly, the data was then projected onto FreeSurfer fsaverage6 surface space and smoothed using a 6 mm full-width half maximum kernel.

We derived a 419 × 419 RSFC matrix for each HCP and ABCD participant using the first $T$ minutes of scan time. The 419 regions consisted of 400 parcels from the Schaefer parcellation (Schaefer et al., 2018), and 19 subcortical regions of interest (Fischl et al., 2002). For the HCP, ABCD and TCP datasets, $T$ was varied from 2 to the maximum scan time in intervals of 2 minutes. This resulted in 29 RSFC matrices per participant in the HCP dataset (generated from using the minimum amount of 2 minutes to the maximum amount of 58 minutes in intervals of 2 minutes), 10 RSFC matrices per participant in the ABCD dataset (generated from using the minimum amount of 2 minutes to the maximum amount of 20 minutes in intervals of 2 minutes), and 13 RSFC matrices per participant in the TCP dataset (generated from using the minimum amount of 2 minutes to the maximum amount of 26 minutes in intervals of 2 minutes).

In the case of the MDD dataset, the total scan time was an odd number (23 minutes), so T was varied from 3 to the maximum of 23 minutes in intervals of 2 minutes, which resulted in 11 RSFC matrices per participant. For SINGER, ADNI and ABCD task-fMRI data, because the scans were relatively short (around 10 minutes), T was varied from 2 minutes the maximum scan time in intervals of 1 minute. This resulted in 9 RSFC matrices per participant in the SINGER datasets (generated from using the minimum amount of 2 minutes to the maximum amount of 10 minutes), 8 RSFC matrices per participant in the ADNI datasets (generated from using the minimum amount of 2 minutes to the maximum amount of 9 minutes), 9 RSFC matrices per participant in the ABCD n-back task (from using the minimum amount of 2 minutes to the maximum amount of 9.65 minutes), 11 RSFC matrices per participant in the ABCD SST task (from using the minimum amount of 2 minutes to the maximum amount of 11.65 minutes) and 10 RSFC matrices per participant in the ABCD MID task (from using the minimum amount of 2 minutes to the maximum amount of 10.74 minutes).

We note that the above preprocessed data was collated across multiple labs, and even within the same lab, datasets were processed by different individuals many years apart. This led to significant preprocessing heterogeneity across datasets. For example, raw FD was used in the HCP dataset because it was processed many years ago, while the more recently processed ABCD dataset utilized a filtered version of FD, which has been shown to more effective. Another variation is that some datasets were projected to fsaverage space, while other datasets were projected to MNI152 and fsLR space. We considered this heterogeneity a strength of our study. Indeed, the consistency of our results across datasets and analyses (Figures S24 to S26) indicate that the robustness of our findings.

Prediction workflow

The RSFC generated from the first $T$ minutes were used to predict each phenotypic measures (previous section) using kernel ridge regression (KRR; He et al., 2020) within an inner-loop (nested) cross-validation procedure.

Let us illustrate the procedure using the HCP dataset (Figure 1A). We began with the full set of participants. A 10-fold nested cross-validation procedure was used. Participants were divided in 10 folds (first row of Figure 1A). We note that care was taken so siblings were not split across folds, so the 10 folds were not exactly the same sizes. For each of 10 iterations, one fold was reserved for testing (i.e., test set), while the remainder was used for training (i.e., training set). Since there were 792 HCP participants, the training set size was roughly 792 × 0.9 ≈ 700 participants. The KRR hyperparameter was selected via a 10-fold cross-validation of the training set. The best hyperparameter was then used to train a final KRR model in the training set and applied to the test set. Prediction accuracy was measured using Pearson’s correlation and coefficient of determination (Chen et al., 2022).

The above analysis was repeated with different training set sizes achieved by subsampling each training fold (second and third rows of Figure 1A), while the test set remained identical across different training set sizes, so the results are comparable across different training set sizes. The training set size was subsampled from 200 to 600 (in intervals of 100). Together with the full training set size of approximately 700 participants, there were 6 different training set sizes, corresponding to 200, 300, 400, 500, 600 and 700.

The whole procedure was repeated with different values of $T$. Since there were 29 values of $T$, there were in total 29 × 6 sets of prediction accuracies for each phenotypic measure. To ensure robustness, the above procedure was repeated 50 times with different splits of the participants into 10 folds to ensure stability (Figure 1A). The prediction accuracies were averaged across all test folds and all 50 repetitions.

The procedure for the other datasets followed the same principle as the HCP dataset. However, the ABCD (rest and task) and ADNI datasets comprised participants from multiple sites. Therefore, following our previous studies (Chen et al., 2022; Ooi et al., 2022), we combined ABCD participants across the 22 imaging sites into 10 site-clusters and combined ADNI participants across the 71 imaging sites into 20 site-clusters (Table S6). Each site-cluster has at least 227, 156 and 29 participants in ABCD (rest), ABCD (task) and ADNI datasets respectively.

Instead of the 10-fold inner-loop (nested) cross-validation procedure in the HCP dataset, we performed a leave-3-site-clusters-out inner-loop (nested) cross-validation (i.e., 7 site-clusters are used for training and 3 site-clusters are used for testing) in the ABCD (rest and task) dataset. The hyperparameter was again selected using a 10-fold CV within the training set. This nested cross-validation procedure was performed for every possible split of the site clusters, resulting in 120 replications. The prediction accuracies were averaged across all 120 replications.

We did not perform a leave-one-site-cluster-out procedure because the site-clusters are “fixed”, so the cross-validation procedure can only be repeated 10 times under a leave-one-site-cluster-out scenario (instead of 120 times). Similarly, we did not go for leave-two-site-clusters-out procedure because that will only yield a maximum of 45 repetitions of cross-validation. On the other hand, if we left more than 3 site clusters out (e.g., leave-5-site-clusters-out), we could achieve more cross-validation repetitions, but at the cost of reducing the maximum training set size. Therefore, we opted for the leave-3-site-clusters-out procedure, consistent with our previous study (Chen et al., 2022).

To be consistent with the ABCD dataset, for the ADNI dataset, we also performed a leave-3-site-clusters-out inner-loop (nested) cross-validation procedure. This procedure was performed for every possible split of the site clusters, resulting in 1140 replications. The prediction accuracies were averaged across all 1140 replications.

We also performed 10-fold inner-loop (nested) cross-validation procedure in the TCP, MDD and SINGER datasets. Although the data from the TCP and MDD datasets were acquired from multiple sites, the number of sites was much smaller (2 and 5 respectively) than that of the ABCD and ADNI datasets. Therefore, we were unable to use the leave-some-site-out cross-validation strategy because that would reduce the training set size by too much. Therefore, we ran a 10-fold nested cross-validation strategy (similar to the HCP). However, we regress sites from the target phenotype in the training set, which were then applied to the test set. In other words, our prediction was performed on the residuals of phenotypes after site regression. Site regression was unnecessary for the SINGER dataset as the data was only collected from a single site. The rest of the prediction workflow was the same as the HCP dataset, except for the number of repetitions. Since TCP, MDD and SINGER datasets had smaller sample size than the HCP dataset, the 10-fold cross-validation was repeated 350 times. The prediction accuracies were averaged across all test folds and all repetitions.

Similar to the HCP, the analyses were repeated with different numbers of training participants, ranging from 200 to 1600 ABCD (rest) participants (in intervals of 200). Together with the full training set size of approximately 1800 participants, there were 9 different training set sizes. The whole procedure was repeated with different values of $T$. Since there were 10 values of $T$ in the ABCD (rest) dataset, there were in total 10 × 9 values of prediction accuracies for each phenotype. In the case of ABCD (task), the sample size was smaller with maximum training set size of approximately 1600 participants, so there were only 8 different training set sizes.

The ADNI and SINGER datasets had less participants than the HCP dataset, so we decided to sample the training set size more finely. More specifically, we repeated the analyses by varying the number of training participants from the minimum sample size of 100 to the maximum sample size in intervals of 100. For SINGER, the full training set size is ~580 participants, so there were 6 different training set sizes in total (100, 200, 300, 400, 500, ~580). For ADNI, the full training set size is ~530, so there were also 6 different training set sizes in total (100, 200, 300, 400, 500, ~530).

Finally, TCP and MDD datasets were the smallest, so the training set size was sampled even more finely. More specifically, we repeated the analyses by varying the number of training participants from the minimum sample size of 50 to the maximum sample size in intervals of 25. For TCP, the full training set size is ~175, so there 6 training set sizes in total (50, 75, 100, 125, 150, 175). For MDD, the full training set size is ~258, so there 10 training set sizes in total (50, 75, 100, 125, 150, 175, 200, 225, 250, 258).

Current best MRI practices suggest that the model hyperparameter should be optimized (Nichols et al., 2017), so in the current study, we did not consider the case where the hyperparameter was fixed. As an aside, we note that for all analyses, the best hyperparameter was selected using a 10-fold cross-validation within the training set. The best hyperparameter was then used to train the model on the full training set. Therefore, the full training set was used for hyperparameter selection and for training the model. Furthermore, we only needed to select one hyperparameter, while training the model required fitting many more parameters. Therefore, we do not expect the hyperparameter selection to be more dependent on the training set size than training the actual model itself.

We also note that our study focused on out-of-sample prediction within the same dataset, but did not explore cross-dataset prediction (Wu et al., 2023). For predictive models to be clinically useful, these models must generalize to completely new datasets. The best way to achieve this goal is by training models from multiple datasets jointly, so as to maximize the diversity of the training data (Abraham et al., 2017; P. Chen et al., 2023). However, we did not consider cross-dataset prediction in the current study because most studies are not designed with the primary aim of combining the collected data with other datasets.

A full table of prediction accuracies for every combination of sample size and scan time per participant can be found in the supplementary spreadsheet.

Logarithmic fit of prediction accuracy with respect to total scan duration

By plotting total scan duration (number of training participants × scan duration per participant) against prediction accuracy for each phenotypic measure, we observed that for most measures, scanning beyond 20–30 minutes per participant did not improve prediction accuracy.

Furthermore, visual inspection suggests that a logarithmic curve might fit well to each phenotypic measure when scan time per participant is 30 minutes or less. To explore the universality of a logarithmic relationship between total scan duration and prediction accuracy, for each phenotypic measure $p$, we fitted the function $y_p=z_{p}log(t_p)+k_p$, where $y_p$ was the prediction accuracy for phenotypic measure $p$, and $t_p$ is the total scan duration. $z_p$ and $k_p$ were estimated from data by minimizing the square error, yielding ${\widehat{z}}_p$ and ${\widehat{k}}_p$.

In addition to fitting the logarithmic curve to different phenotypic measures, the fitting can also be performed with different prediction accuracy measures (Pearson’s correlation or coefficient of determination) and different predictive models (kernel ridge regression and linear ridge regression). Assuming the datapoints are well explained by the logarithmic curve, the normalized accuracies $\left(y_b-{\widehat{k}}_p\right)/{\widehat{z}}_b$ should follow a standard $\left(t\right)$ curve across phenotypic measures, prediction accuracies, predictive models, and datasets. As an example, Figure 2B shows the normalized prediction performance of the cognitive factors for different prediction accuracy measures (Pearson’s correlation or coefficient of determination) and different predictive models (kernel ridge regression and linear ridge regression) across HCP and ABCD datasets.

Here we have chosen to use kernel ridge regression and linear regression because previous studies have shown that they have comparable prediction performance, and also exhibited similar prediction accuracies as several deep neural networks (He et al., 2020; Chen et al., 2022). Indeed, a recent study suggested that linear dynamical models provide better fit to resting-state brain dynamics (as measured by fMRI and intracranial electroencephalogram) than nonlinear models, suggesting that due to the challenges of in-vivo recordings, linear models might be sufficiently powerful to explain macroscopic brain measurements. However, we note that in the current study, we are not making a similar claim. Instead, our results suggest that the trade-off between scan time and sample size are similar for different regression models, and phenotypic domains, scanners, acquisition protocols, racial groups, mental disorders, age groups, as well as resting-state and task-state functional connectivity.

Fit of theoretically-motivated model of prediction accuracy, sample size and scan time

We observed that sample size and scan time per participant did not contribute equally to prediction accuracy, with sample size playing a slightly more important role than scan time. To explain this observation, we derived a mathematical relationship relating the expected Pearson’s correlation between noisy brain measurements and non-brain-imaging phenotype with scan time and sample size.

Based on a linear regression model with no regularization and assumptions including (1) stationarity of fMRI (i.e., autocorrelation in fMRI is the same at all timepoints), and (2) prediction errors are uncorrelated with errors in brain measurements, we found that

$$E\left(\widehat{\rho }\right)\approx K_0\sqrt{\frac{1}{1+\frac{K_1}{N}+\frac{K_2\text{'}}{NT}}}$$

where $E\left(\widehat{\rho }\right)$ is the expected correlation between regression weights estimated from noisy brain measurements and the observed phenotype. $K_0$ is related to the ideal association between brain measurements and phenotypes, attenuated by phenotype reliability. $K_1$ is related to the true association between brain measurements and phenotype. $K_2$ is related to brain-phenotype prediction errors due to brain measurement inaccuracies. Full derivations can be found in Supplementary Methods Sections 1.1 and 1.2.

Based on the above equation, we fitted the following function $y_p=K_{0,p}\sqrt{\frac{1}{1+K_{1,p}/N+K_{2,p}/(NT)\text{'}}}$, where $y_p$ was the prediction accuracy for phenotypic measure $p$, $N$ was the sample size and $T$ was the scan time per participant. $K_{0,p}$, $K_{1,p}$and $K_{2,p}$ were estimated by minimizing the mean squared error between the above functional form and actual observation of $y_p$ using gradient descent.

Analysis of non-stationarity

In the original analysis, FC matrices were generated with increasing time $T$ based on the original run order. To account for the possibility of state effects, we randomized the order in which the runs were considered for each participant. Since both HCP and ABCD datasets contained 4 runs of resting-fMRI, we generated FC matrices from all 24 possible permutations of run order. For each cross-validation split, the FC matrix for a given participant was randomly sampled from one of the 24 possible permutations. We note that the randomization was independently performed for each participant.

To elaborate further, let us consider an ABCD participant with the original run order (run 1, run 2, run 3, run 4). Each run was 5 minutes long. In the original analysis, if scan time $T$ was 5 minutes, then we used all the data from run 1 to compute FC. If scan time $T$ was 10 minutes, then we used run 1 and run 2 to compute FC. If scan time $T$ was 15 minutes, then we used runs 1, 2 and 3 to compute FC. Finally, if scan time $T$ was 20 minutes, we used all 4 runs to compute FC.

On the other hand, after run randomization, for the purpose of this exposition, let us assume this specific participant’s run order had become run 3, run 2, run 4, run 1. In this situation, if scan time $T$ was 5 minutes, then we used all data from run 3 to compute FC. If scan time $T$ was 10 minutes, then we used run 3 and run 2 to compute FC. If scan time $T$ was 15 minutes, then we used runs 3, 2 and 4 to compute FC. Finally, if T was 20 minutes, we used all 4 runs to compute FC.

Brain-wide association reliability workflow

To explore the reliability of univariate brain-wide association analyses (BWAS; Marek et al., 2022), we followed a previously established split-half procedure (Tian et al., 2021; J. Chen et al., 2023).

Let us illustrate the procedure using the HCP dataset (Figure S30A). We began with the full set of participants, which were then divided into 10 folds (first row of Figure S30A). We note that care was taken so siblings were not split across folds, so the 10 folds were not exactly the same sizes. The 10 folds were divided into two non-overlapping sets of 5 folds. For each set of 5 folds and each phenotype, we computed Pearson’s correlation between each RSFC edge and phenotype across participants, yielding a 419 × 419 correlation matrix, which was then converted into a 419 × 419 t-statistic matrix. Split-half reliability between the (lower triangular portions of the symmetric) t-statistic matrices from the two sets of 5 folds was then computed using the intra-class correlation formula (Tian et al., 2021; J. Chen et al., 2023).

The above analysis was repeated with different sample sizes achieved by subsampling each fold (second and third rows of Figure S30A). The split-half sample sizes were subsampled from 150 to 350 (in intervals of 50). Together with the full sample size of approximately 800 participants (corresponding to a split-half sample size of around 400), there were 6 split-half sample sizes corresponding to 150, 200, 250, 300, 350 and 400 participants.

The whole procedure was also repeated with different values of $T$. Since there were 29 values of $T$, there were in total 29 × 6 univariate BWAS split-half reliability values for each phenotype. To ensure robustness, the above procedure was repeated 50 times with different split of the participants into 10 folds to ensure stability (Figure 30A). The reliability values were averaged across all 50 repetitions.

The same procedure was followed in the case of the ABCD dataset, except as previously explained, the ABCD participants were divided into 10 site-clusters. Therefore, the split-half reliability was performed between two sets of 5 non-overlapping site-clusters. In total, this procedure was repeated 126 times since there were 126 ways to divide 10 site-clusters into two sets of 5 non-overlapping site-clusters.

Similar to the HCP, the analyses were repeated with different numbers of split-half participants, ranging from 200 to 1000 ABCD participants (in intervals of 200). Together with the full training set size of approximately 2400 participants (corresponding to a split-half sample size of approximately 1200 participants, there were 6 split-half sample sizes, corresponding to 200, 400, 600, 800, 1000, 1200.

The whole procedure was also repeated with different values of $T$. Since there were 10 values of $T$ in the ABCD dataset, there were in total 10 × 6 values univariate BWAS split-half reliability values for each phenotype.

Previous studies have suggested the Haufe-transformed coefficients from multivariate prediction are significantly more reliable than univariate BWAS (Tian et al., 2021; J. Chen et al., 2023). Therefore, we repeated the above analyses by replacing BWAS with the multivariate Haufe-transform.

A full table of split-half BWAS reliability for each given combination of sample size and scan time per participant can be found in the supplementary spreadsheet.

Data and Code Availability

The prediction accuracies for each phenotype, sample size N, and scan time T in all six datasets are publicly available (LINK_TO_BE_UPDATED). The raw data for HCP (https://www.humanconnectome.org/), ABCD (https://abcdstudy.org/), TCP (https://openneuro.org/datasets/ds005237 and https://nda.nih.gov/edit_collection.html?id=3552) and ADNI (https://ida.loni.usc.edu/) are publicly available. ABCD parcellated time courses can be found on NDA (LINK_TO_BE_UPDATED). HCP and TCP parcellated time courses can be found on GitHub (LINK_TO_BE_UPDATED). The ADNI user agreement does not allow us to share the ADNI derivatives. The SINGER dataset can be obtained via a data-transfer agreement (https://medicine.nus.edu.sg/macc/projects/singer/). The MDD dataset is available upon request to co-author HL (hesheng@biopic.pku.edu.cn).

Code for this study is publicly available in the GitHub repository maintained by the Computational Brain Imaging Group (https://github.com/ThomasYeoLab/CBIG). Processing pipelines of the fMRI data can be found here (https://github.com/ThomasYeoLab/CBIG/tree/master/stable_projects/preprocessing/CBIG_fMRI_Preproc2016).

Code specific to the analyses in this study can be found here (LINK_TO_BE_UPDATED). Code related to this study was reviewed by co-author TWKT to reduce the chance of coding errors.