Statistics of maximum photon penetration depth in a two-layer diffusive medium

Abstract

We present numerical results for the probability density function f(z) and for the mean value of photon maximum penetration depth ‹z _max › in a two-layer diffusive medium. Both time domain and continuous wave regime are considered with several combinations of the optical properties (absorption coefficient, reduced scattering coefficient) of the two layers, and with different geometrical configurations (source detector distance, thickness of the upper layer). Practical considerations on the design of time domain and continuous wave systems are derived. The methods and the results are of interest for many research fields such as biomedical optics and advanced microscopy.

1. Introduction

Light propagation in diffusive or turbid media such as biological tissues is generally ruled by the complex interplay between light absorption and light scattering. In the 600 − 900 nm spectral region the combination of low absorption and high scattering allows near infrared light to penetrate deeply in a diffusive medium and be eventually re-emitted to the surface. In most biomedical applications the information of interest is in the deeper region below the medium surface. This is the case for example for near infrared spectroscopy (NIRS) for monitoring tissue oxygen saturation in cerebral cortex [1], or in skeletal muscle [2], or cancer screening in thyroid [3]. Depth information is important also for other non-clinical fields, such as internal quality assessment of agricultural produce [4], non-destructive monitoring of wood materials [5], or for pharmaceuticals and highly scattering plastics [6]. For these reasons, the study of photon penetration depth in diffusive media is interesting and it can play an active role in the improvement of these applications.

Photon penetration depth in random media has been studied by many research groups with different approaches. A first used metric is the depth at which the fluence rate falls to 1/e of the incident fluence rate [7]. An alternative metric is the depth at which 1/e of the laser radiation has been absorbed [7,8]. The first metric focuses on the intensity distribution inside the medium, while the second one focuses on the absorption depth of the propagated light. A different approach focuses on the mean average depth $⟨\overline{z}⟩$ or the mean maximum depth $⟨z_{\mathit{\text{max}}}⟩$ reached by photons detected at the surface of the medium. A recent comprehensive work on this subject by the Authors [9] gives a general description of the statistics behind the penetration depth of light in a turbid medium within the framework of the Diffusion Approximation for both time domain and continuous wave regime. In that work analytical formulae for the probability density function $f(z)$ of the maximum penetration depth and the corresponding average values $⟨z_{\mathit{\text{max}}}⟩$ have been presented in the case of a homogeneous slab geometry that is often used as a model for biological tissues neglecting their inhomogeneities.

Layered model geometries are also employed in tissue optics, motivated by the fact that some biological tissues have a layered architecture. This is the case of the human arm or leg with the adipose tissue layer typically overlying skeletal muscle, or of the human head with the extra-cerebral compartment (comprising scalp, skull, and cerebrospinal fluid) and the brain (i.e., gray matter and white matter). Thus, the study of photon penetration depth in layered geometries can be very interesting for biomedical applications to optimize biophotonic diagnostic tools or therapeutic strategies. Interestingly, layered configurations for diffusive media can also be found in other fields. For example, nanoparticle-based solar cells composed of a silicon nanoparticle stack as a light trapping absorber for ultra-thin photovoltaics [10]. Understanding how diffusive light propagation, and specifically photon penetration depth, is affected by the optical and geometrical properties of the different layers can provide useful insights for design and development of photonic techniques and devices.

To our knowledge, while several works have investigated light diffusion and the reconstruction of the optical properties in a two-layer medium [11–17], limited studies have been published on photon penetration depth in a layered diffusive medium. In the pioneering works by Nossal et al. [18] and Taitelbaum et al. [19] the average depth probed by photons remitted from a two-layer medium was estimated in the framework of random walk or diffusion equation (DE) models only in the continuous wave regime and for a limited range of optical parameters. In recent works, Monte Carlo (MC) simulations were performed in layered scenarios mimicking the human skin [20–22] or the human head [23]. However, all these studies were focused on a specific set of optical and geometrical properties, therefore these results cannot be used to predict the effect of changes in the optical or geometrical properties. Moreover, the time domain regime was not considered. Finally, in almost all of these works [20,21,23], the focus was on light fluence attenuation in the tissue, therefore no information on the statistical properties of remitted photons could be derived.

The aim of this work is to study the statistics of photon penetration depth in a two-layer geometry with a comprehensive approach. The type of two-layer diffusive medium here considered is characterized by a very high overall thickness of the entire medium, such that the entire medium can also be optically approximated as semi-infinite, as in the case of biomedical applications the human head or the human arm. The probability density for the maximum penetration depth $f(z)$ and the mean value of the maximum penetration depth $⟨z_{\mathit{\text{max}}}⟩$ reached by remitted photons will be calculated both in the time domain and in continuous wave regime for several combinations of the optical properties (absorption coefficient, ${\mu }_a$ , and reduced scattering coefficient, ${\mu }_s^{\mathrm{\prime }}$ ) of the two layers, and for different geometrical configurations (source detector distance, $\rho$ , and thickness of the upper layer, $s_1$ ). Practical considerations on the design of time domain and continuous wave systems will also be derived.

2. Material and methods

We considered a reflectance configuration with source detector distance $\rho$ in a two-layer medium (see Fig. 1). The pivotal condition was selected assuming total thickness $s_{\mathit{\text{tot}}}=90\text{mm}$ , thickness of the upper layer $s_1=15\text{mm}$ , and thickness of the bottom layer $s_2=75\text{mm}$ . The optical properties (absorption coefficient, reduced scattering coefficient, and refractive index) were initially assumed equal in the two layers: ${\mu }_{a1}={\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ , ${\mu }_{s1}^{\mathrm{\prime }}={\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ , $n_1=n_2=1.4$ . Further, the external refractive index was initially assumed equal in the upper and lower external region: $n_{e1}=n_{e2}=1.0$ . This choice aimed at mimicking an adult head configuration with an average radius in the range $8-10\text{cm}$ for a head circumference in the range $54-64\text{cm}$ [24] and average optical properties for head tissue [25,26].

Fig. 1.

Scheme for the implementation of the numerical method. (a) if $z<s_1$ the model for reflectance from a homogeneous slab of thickness z is used; (b) if $z>s_1$ the model for reflectance from a two-layer slab with $s_2=z$ is used.

In the continuous wave the probability density function that the photons emerging from the medium surface at a distance ρ from the injection point have reached a maximum depth $z_{\mathit{\text{max}}}$ between z and $z+dz$ is

$$f(z|\rho )=\frac{1}{R(s_{\mathit{\text{tot}}},\rho )}\frac{\mathrm{\partial }R(z,\rho )}{\mathrm{\partial }z},$$ (1)

where $R(z,\rho )$ and $R(s_{\mathit{\text{tot}}},\rho )$ are the reflectance from a slab of thickness $z<s_{\mathit{\text{tot}}}$ and of thickness $s_{\mathit{\text{tot}}}$ , respectively [9].

Similarly, in the time domain, the probability density function is defined as

$$f(z|\rho ,t)=\frac{1}{R(s_{\mathit{\text{tot}}},\rho ,t)}\frac{\mathrm{\partial }R(z,\rho ,t)}{\mathrm{\partial }z},$$ (2)

where $R(z,\rho ,t)$ and $R(s_{\mathit{\text{tot}}},\rho ,t)$ are the time domain reflectance from a slab of thickness $z<s_{\mathit{\text{tot}}}$ and of thickness $s_{\mathit{\text{tot}}}$ , respectively. For a slab of thickness s in the expression for $R(s,\rho ,t)$ the dependence on $\rho$ is only in a multiplicative exponential factor, therefore the dependence on $\rho$ vanishes in $f(z|\rho ,t)$ and we can simply write $f(z|t)$ for the left term in Eq. (2) [9].

In Eqs. (1) and (2) we have not considered the additional term accounting for possible refractive index mismatch at depth $z=s_{\mathit{\text{tot}}}$ (see Eq. (7.14) in Ref. [27]) since this term in the geometrical configuration here considered gives a negligible contribution in the calculation of the overall maximum penetration depth. The partial current boundary condition (PCBC) was used to derive R from the photon fluence $\mathrm{\Phi }$ according to the formula $R=\mathrm{\Phi }/2A$ , where A is the Fresnel coefficient that considers the refractive index mismatch at the tissue boundary. For $z<s_1$ (see Fig. 1 panel a) the formulas for reflectance from a homogeneous slab with thickness z were used (see Eq. (5.44) and (5.50) in Ref. [27] for time domain and continuous wave, respectively), while for $z>s_1$ (see Fig. 1 panel b) the formulas for reflectance from a two-layer medium were used with thickness of the upper layer $s_1$ and thickness of the lower layer $s_2=z-s_1$ (see Eq. (11.26) and (12.30) in Ref. [27]). In both cases we have modified the formula for R to consider a refractive index matching condition at depth z [9].

To save computational time, the depth z was varied in the range $[z_{\mathit{\text{min}}},z_{\mathit{\text{max}}}]$ with a variable step $z_{\mathit{\text{step}}}$ . The value for $z_{\mathit{\text{max}}}$ corresponded to the total thickness $s_{\mathit{\text{tot}}}$ , while $z_{\mathit{\text{min}}}$ was set to $0.2\text{mm}$ to avoid singularities in the evaluation of R. In the z range $[0.2,15)$ mm, $z_{\mathit{\text{step}}}=0.2\text{mm}$ was used, then a geometric progression with common ratio equal to 2 was used. The resulting $z_{\mathit{\text{step}}}$ was $0.2\text{mm}$ for $zϵ[0.2,15)\text{mm}$ , $0.4\text{mm}$ for $zϵ[15,30)\text{mm}$ , $0.8\text{mm}$ for $zϵ[30,45)\text{mm}$ , $1.6\text{mm}$ for $zϵ[45,60)\text{mm}$ , and $3.2\text{mm}$ for $zϵ[60,90)\text{mm}$ . At each depth z the derivative of R was calculated as $\frac{\mathrm{\partial }R(z,\rho ,t)}{\mathrm{\partial }z}\simeq \frac{[R(z)-R(z-\mathrm{\Delta }z)]}{\mathrm{\Delta }z}$ , with $\mathrm{\Delta }z=0.001\text{mm}$ . The choice of using a backward derivative is to avoid entering in the bottom layer when at the interface between upper and lower layer. Finally, the average value $⟨z_{\mathit{\text{max}}}|t⟩={\int }_0^{s_{\mathit{\text{tot}}}}zf(z|t)dz$ and $⟨z_{\mathit{\text{max}}}|\rho ⟩={\int }_0^{s_{\mathit{\text{tot}}}}zf(z|\rho )dz$ was obtained by numerical integration (trapezoid method). A dedicated script was used in Matlab R2020b [28]. The computation time for a simulation in the continuous wave regime was < 10 s, while for the time domain it was < 10² s on a Windows10 Pro 64-bit laptop equipped with an Intel Core i7-4500U (1.8 GHz CPU and with 8 GB RAM).

Starting from the pivotal configuration, several combinations of optical and geometrical parameters were tested. While keeping fixed the thickness of the upper layer $s_1=15\text{mm}$ , changes in the optical properties were simulated in realistic ranges for biological tissues, separately for the upper layer and the bottom layer. In particular, we simulated changes in ${\mu }_{a1}$ or ${\mu }_{a2}$ to span the range $0.005-0.025\text{m}{\text{m}}^{-1}$ in $0.005\text{m}{\text{m}}^{-1}$ steps, and changes in ${\mu }_{s1}^{\mathrm{\prime }}$ or ${\mu }_{s2}^{\mathrm{\prime }}$ to cover the range $0.5-1.5\text{m}{\text{m}}^{-1}$ in $0.25\text{m}{\text{m}}^{-1}$ steps. Then, for different combination of the optical properties of the upper and lower layers, we also simulated changes in the thickness of the upper layer $s_1$ to cover the range $5-25\text{mm}$ in $5\text{mm}$ steps. For all the above configurations, in the time domain we assumed a fixed source detector distance $\rho =30\text{mm}$ and different time-of-flight $t=0.50,0.75,1.00,1.25,1.50,2.00,3.00,4.00\text{ns}$ . Then we considered also changes in the source detector distance $\rho =10,20,30,40,50\text{mm}$ . In the continuous wave regime, the source detector distance $\rho$ was always varied in the range $5-40\text{mm}$ in $5\text{mm}$ steps.

To check the validity of the DE results, we have used a previously developed MC code [9] to calculate for each detected trajectory i the mean value of the depth at which the photon undergoes scattering events, $z_i$ , and the maximum value of the penetration depth, $z_{\mathit{\text{max}},i}$ . Then we have obtained $⟨z_{\mathit{\text{max}}}⟩$ and $⟨\overline{z}⟩$ in the time domain and in the continuous wave regime. For each MC simulation we used the same geometry as for the DE results, with 10⁶ collected photons.

3. Results

3.1. Time domain

3.1.1. Variation of ${\mu }_{a1}$ or ${\mu }_{a2}$

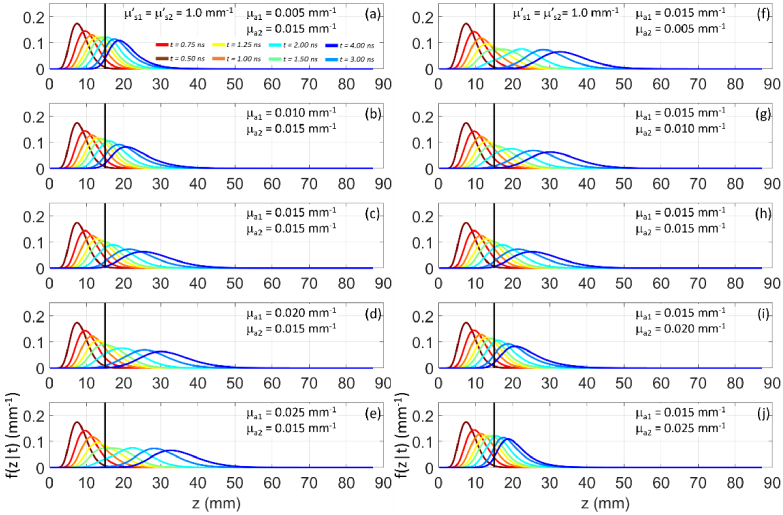
Figure 2 shows the time dependent photon probability density for the maximum penetration depth $f(z|t)$ for increasing ${\mu }_{a1}$ at fixed ${\mu }_{a2}$ (panel a) and increasing ${\mu }_{a2}$ at fixed ${\mu }_{a1}$ (panel b) for different time-of-flight. It is evident how for longer time-of-flight the increase in ${\mu }_{a1}$ results in the spreading of $f(z|t)$ over larger z. Conversely, we have an opposite effect if ${\mu }_{a2}$ increases. The observed behavior has an intuitive explanation: the effect of absorption in one layer selects surviving photons that have migrated primarily to the other layer.

Fig. 2.

$f(z|t)$ as a function of z for $t=0.50,0.75,1.00,1.25,1.5,2.0,3.0,4.0\text{ns}$ (color code from brown to blue) for a two-layer medium ( $s_1=15\text{mm}$ , $s_2=75\text{mm}$ , $n_1=n_2=1.4$ , ${\mu }_{s1}^{\mathrm{\prime }}={\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ). (a)-(e): variable ${\mu }_{a1}=0.005,0.010,0.015,0.020,0.025\text{m}{\text{m}}^{-1}$ , fixed ${\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ; (f)-(j): fixed ${\mu }_{a1}=0.015\text{m}{\text{m}}^{-1}$ , variable ${\mu }_{a2}=0.005,0.010,0.015,0.020,0.025\text{m}{\text{m}}^{-1}$ . In all cases $\rho =30\text{mm}$ , $n_{e1}=n_{e2}=1.0$ .

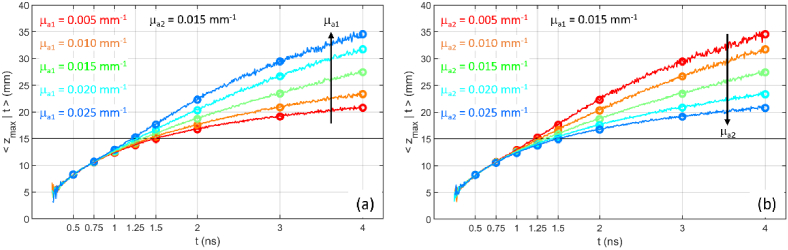
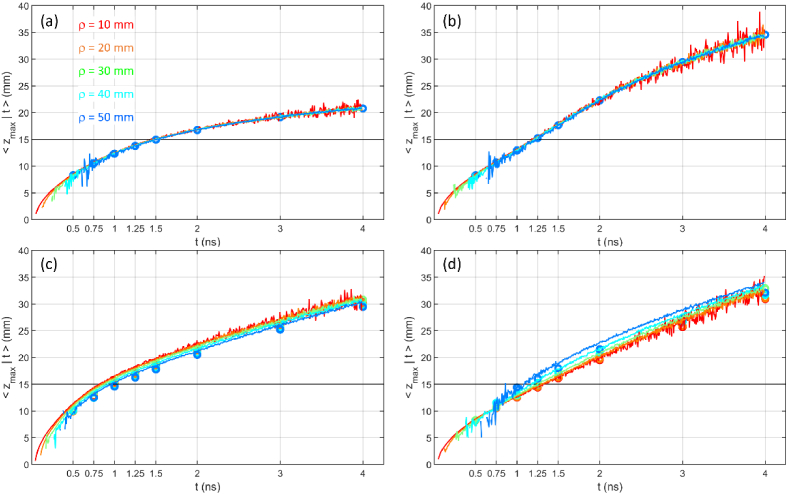
Figure 3 reports the corresponding mean value of the maximum penetration depth $⟨z_{max}|t⟩$ . Differently from the homogeneous case, where $⟨z_{max}|t⟩$ is independent of the absorption coefficient of the medium [7], in the two-layer case we have a dependence from ${\mu }_{a1}$ and ${\mu }_{a2}$ . In particular, $⟨z_{max}|t⟩$ increases with respect to the homogeneous case if $\mathrm{\Delta }{\mu }_{a12}={\mu }_{a1}-{\mu }_{a2}>0$ , while $⟨z_{max}|t⟩$ decreases if $\mathrm{\Delta }{\mu }_{a12}<0$ . These results reflect the fact that photons travelling in the more absorbing medium are preferentially lost with respect to photons travelling in the less absorbing medium. This effect is evident only at long time-of-flight, while at early time-of-flight, when most of the trajectories are confined to the upper medium, the effect of absorption is null (like in a homogeneous slab).

Fig. 3.

$⟨z_{max}|t⟩$ as a function of t for a two-layer medium ( $s_1=15\text{mm}$ , $s_2=75\text{mm}$ , $n_1=n_2=1.4$ , ${\mu }_{s1}^{\mathrm{\prime }}={\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ). (a) variable ${\mu }_{a1}=0.005,0.010,0.015,0.020,0.025\text{m}{\text{m}}^{-1}$ , fixed ${\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ; (b) fixed ${\mu }_{a1}=0.015\text{m}{\text{m}}^{-1}$ , variable ${\mu }_{a2}=0.005,0.010,0.015,0.020,0.025\text{m}{\text{m}}^{-1}$ . In all cases $\rho =30\text{mm}$ , $n_{e1}=n_{e2}=1.0$ . Circles are DE results, lines are MC results.

It is worth noting the symmetry in the results for $f(z|t)$ and $⟨z_{max}|t⟩$ . The case ${\mu }_{a1}=0.005\text{m}{\text{m}}^{-1}$ and ${\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ is equivalent to the case ${\mu }_{a1}=0.015\text{m}{\text{m}}^{-1}$ and ${\mu }_{a2}=0.025\text{m}{\text{m}}^{-1}$ since for both cases $\mathrm{\Delta }{\mu }_{a12}=-0.010\text{m}{\text{m}}^{-1}$ . The same happens of course for the cases with positive $\mathrm{\Delta }{\mu }_{a12}=+0.010\text{m}{\text{m}}^{-1}$ , like ${\mu }_{a1}=0.025\text{m}{\text{m}}^{-1}$ and ${\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ , or ${\mu }_{a1}=0.015\text{m}{\text{m}}^{-1}$ and ${\mu }_{a2}=0.005\text{m}{\text{m}}^{-1}$ . According to this observation we have a kind of similarity of the results for the maximum penetration depth in terms of the coefficient $\mathrm{\Delta }{\mu }_{a12}$ .

3.1.2. Variation of ${\mu }_{s1}^{\mathrm{\prime }}$ or ${\mu }_{s2}^{\mathrm{\prime }}$

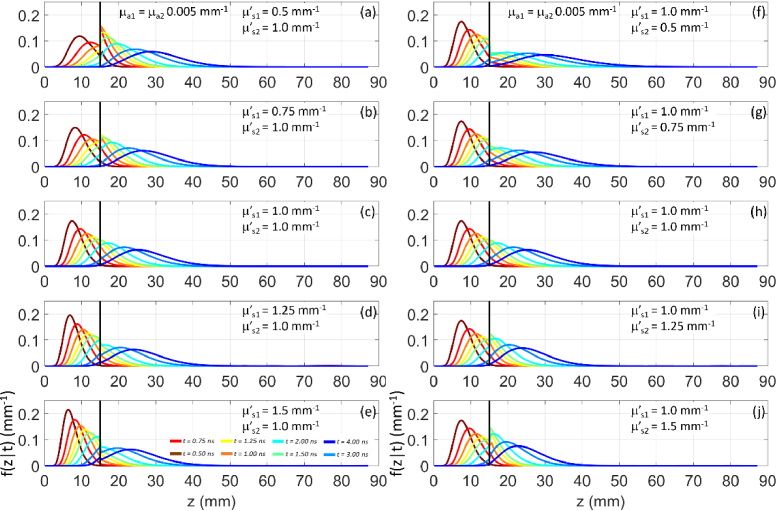
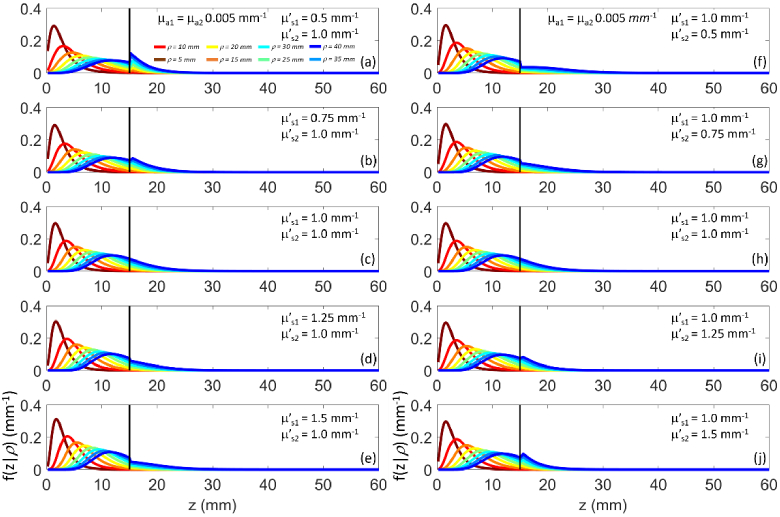
Figure 4 shows $f(z|t)$ for increasing ${\mu }_{s1}^{\mathrm{\prime }}$ at fixed ${\mu }_{s2}^{\mathrm{\prime }}$ (panel a), and for increasing ${\mu }_{s2}^{\mathrm{\prime }}$ at fixed ${\mu }_{s1}^{\mathrm{\prime }}$ (panel b) for different time-of-flight.

Fig. 4.

$f(z|t)$ as a function of z for $t=0.50,0.75,1.00,1.25,1.5,2.0,3.0,4.0\text{ns}$ (color code from brown to blue) for a two-layer medium ( $s_1=15\text{mm}$ , $s_2=75\text{mm}$ , $n_1=n_2=1.4$ , ${\mu }_{a1}={\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ). (a)-(e): variable ${\mu }_{s1}^{\mathrm{\prime }}=0.5,0.75,1.0,1.25,1.5\text{m}{\text{m}}^{-1}$ , fixed ${\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ; (f)-(j): fixed ${\mu }_{s1}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ , variable ${\mu }_{s2}^{\mathrm{\prime }}=0.5,0.75,1.0,1.25,1.5\text{m}{\text{m}}^{-1}$ . In all cases $\rho =30mm$ , $n_{e1}=n_{e2}=1.0$ .

In both cases we observe that $f(z|t)$ is progressively confined to smaller z as ${\mu }_{s1}^{\mathrm{\prime }}$ or ${\mu }_{s2}^{\mathrm{\prime }}$ increases. We also note a discontinuity in the graph of $f(z|t)$ for $z=s_1$ , due to the abrupt change in the (scattering) transport mean free path. For ${\mu }_{s1}^{\mathrm{\prime }}<{\mu }_{s2}^{\mathrm{\prime }}$ we have $f(z=s_1^{-}|t)<f(z=s_1^{+}|t)$ , while for ${\mu }_{s1}^{\mathrm{\prime }}>{\mu }_{s2}^{\mathrm{\prime }}$ we have $f(z=s_1^{-}|t)>f(z=s_1^{+}|t)$ . This agrees with the fact that the continuity of the fluence derivatives at z = s₁ does not hold [27,29]. At the interface between the two layers photons tend to accumulate in the more scattering medium.

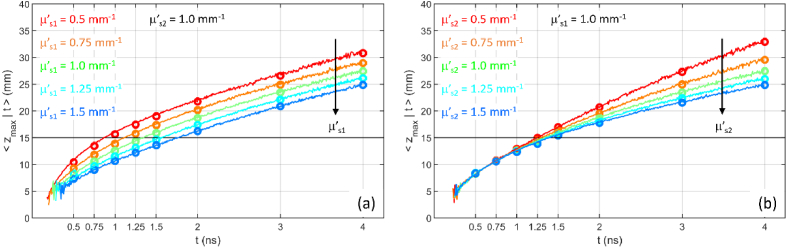
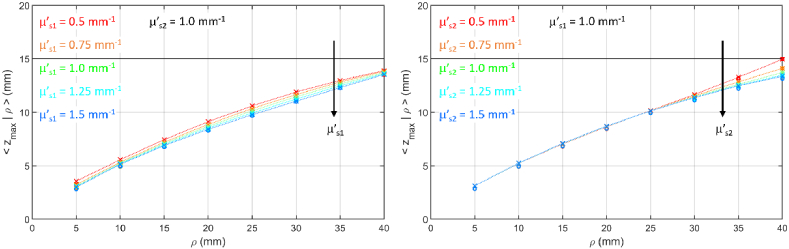
As expected, comparing the results with the homogeneous case ${\mu }_{s1}^{\mathrm{\prime }}={\mu }_{s2}^{\mathrm{\prime }}$ , $⟨z_{max}|t⟩$ decreases as ${\mu }_{s1}^{\mathrm{\prime }}$ or ${\mu }_{s2}^{\mathrm{\prime }}$ increases, and vice versa (see Fig. 5). The variation of ${\mu }_{s1}^{\mathrm{\prime }}$ affects the statistics at every time since all detected photons must travel some distance in the first layer. Conversely, the effect of changes in ${\mu }_{s2}^{\mathrm{\prime }}$ appears only at long time-of-flight, that is only if detected photons have reached the bottom layer.

Fig. 5.

$⟨z_{max}|t⟩$ as a function of t for a two-layer medium ( $s_1=15\text{mm}$ , $s_2=75\text{mm}$ , $n_1=n_2=1.4$ , ${\mu }_{a1}={\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ). (a) variable ${\mu }_{s1}^{\mathrm{\prime }}=0.5,0.75,1.0,1.25,1.5\text{m}{\text{m}}^{-1}$ , fixed ${\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ; (b) fixed ${\mu }_{s1}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ , variable ${\mu }_{s2}^{\mathrm{\prime }}=0.5,0.75,1.0,1.25,1.5\text{m}{\text{m}}^{-1}$ . In all cases $\rho =30\text{mm}$ , $n_{e1}=n_{e2}=1.0$ . Circles are DE results, lines are MC results.

3.1.3. Variation of $\rho$

There is no appreciable effect of the source detector distance $\mathrm{\rho }$ on $f(z|t)$ (data not shown) and on $⟨z_{max}|t⟩$ (see Fig. 6). In particular, the effect is null if ${\mu }_{s1}^{\mathrm{\prime }}={\mu }_{s2}^{\mathrm{\prime }}$ , for any combination of ${\mu }_{a1}$ and ${\mu }_{a2}$ . This agrees with the results for the homogeneous medium [9]. Although these results were predictable, it should be noted that this property is not derived from an exact analytical independence of $⟨z_{max}|t⟩$ from $\mathrm{\rho }$ , however, it is a good approximation.

Fig. 6.

$⟨z_{max}|t⟩$ as a function of t for a two-layer medium ( $s_1=15\text{mm}$ , $s_2=75\text{mm}$ , $n_1=n_2=1.4$ ). for different values of $\rho =10,20,30,40,50\text{mm}$ . (a) different absorption ( ${\mu }_{a1}=0.005\text{m}{\text{m}}^{-1}$ , ${\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ), same scattering ( ${\mu }_{s1}^{\mathrm{\prime }}={\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ); (b) different absorption ( ${\mu }_{a1}=0.015\text{m}{\text{m}}^{-1}$ , ${\mu }_{a2}=0.005\text{m}{\text{m}}^{-1}$ ), same scattering ( ${\mu }_{s1}^{\mathrm{\prime }}={\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ); (c) same absorption ( ${\mu }_{a1}={\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ), different scattering ( ${\mu }_{s1}^{\mathrm{\prime }}=0.5\text{m}{\text{m}}^{-1}$ , ${\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ); (d) same absorption ( ${\mu }_{a1}={\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ), different scattering ( ${\mu }_{s1}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ , ${\mu }_{s2}^{\mathrm{\prime }}=0.5\text{m}{\text{m}}^{-1}$ ). In all cases $n_{e1}=n_{e2}=1.0$ . Circles are DE results, lines are MC results.

3.1.4. Variation of the thickness of the upper layer $s_1$

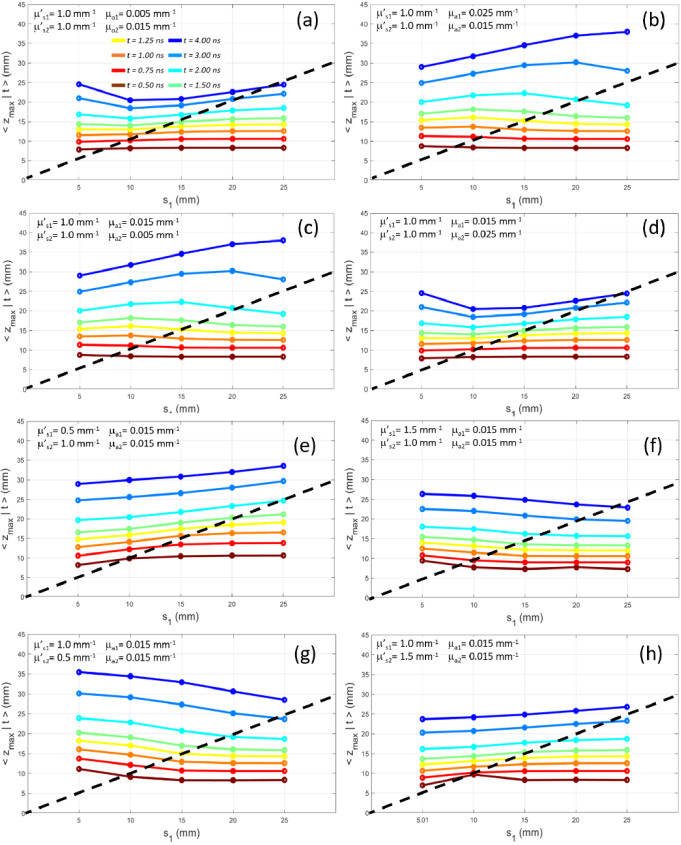
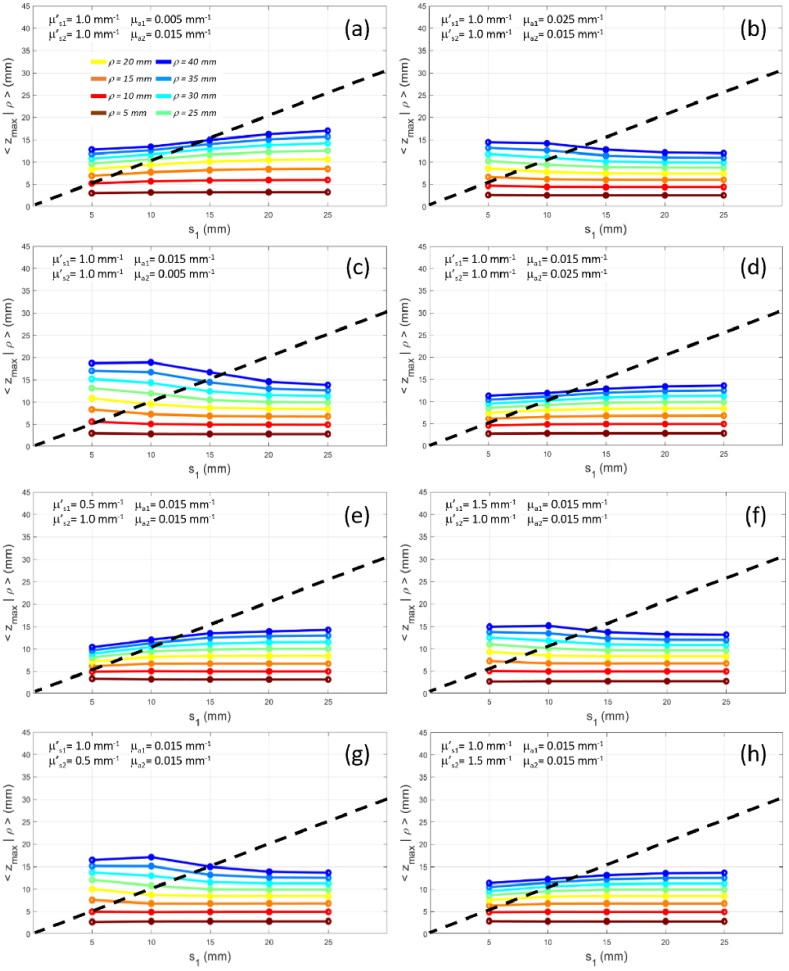
Figure 7 shows the effect on $⟨z_{max}|t⟩$ of the variation of the thickness of the upper layer $s_1$ . If ${\mu }_{s1}^{\mathrm{\prime }}={\mu }_{s2}^{\mathrm{\prime }}$ and ${\mu }_{a1}<{\mu }_{a2}$ (panels (a) and (d)), we observe a non monotonic behavior of $⟨z_{max}|t⟩$ with an initial decrease when $s_1$ increases from $5\text{mm}$ to $15\text{mm}$ , followed by an increase when $s_1$ becomes larger than 20 mm. A similar but opposite behavior is observed when ${\mu }_{s1}^{\mathrm{\prime }}={\mu }_{s2}^{\mathrm{\prime }}$ and ${\mu }_{a1}>{\mu }_{a2}$ (panels (b) and (c)), with an initial increase of $⟨z_{max}|t⟩$ when $s_1$ increases from $5\text{mm}$ to $15\text{mm}$ , followed by a decrease when $s_1$ becomes larger than $20\text{mm}$ . In both absorption scenarios, the case $s_1=5\text{mm}$ , $s_2=85\text{mm}$ and the case $s_1=85\text{mm}$ , $s_2=5\text{mm}$ have very similar values of $⟨z_{max}|t⟩$ . This can be explained by noting that in both cases photons spend the most of their time in the wider medium, being that quite close to a homogeneous slab, therefore $⟨z_{max}|t⟩$ is almost independent of the absorption.

Fig. 7.

$⟨z_{max}|t⟩$ at different time of flight $t=0.50,0.75,1.00,1.25,1.5,2.0,3.0,4.0\text{ns}$ (color code from brown to blue) as a function of the thickness of the upper layer $s_1=5,10,15,20,25\text{mm}$ for a two-layer medium with constant total thickness ( $s_{\mathit{\text{tot}}}=90\text{mm}$ , $n_1=n_2=1.4$ ). Panels (a)-(d) have same scattering ( ${\mu }_{s1}^{\mathrm{\prime }}={\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ) and different absorption: (a) ${\mu }_{a1}=0.005\text{m}{\text{m}}^{-1}$ , ${\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ; (b) ${\mu }_{a1}=0.025\text{m}{\text{m}}^{-1}$ , ${\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ; (c) ${\mu }_{a1}=0.015\text{m}{\text{m}}^{-1}$ , ${\mu }_{a2}=0.005\text{m}{\text{m}}^{-1}$ ; (d) ${\mu }_{a1}=0.015\text{m}{\text{m}}^{-1}$ , ${\mu }_{a2}=0.025\text{m}{\text{m}}^{-1}$ . Panels (e)-(h) have same absorption ( ${\mu }_{a1}={\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ) and different scattering: (e) ${\mu }_{s1}^{\mathrm{\prime }}=0.5\text{m}{\text{m}}^{-1}$ , ${\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ); (f) ${\mu }_{s1}^{\mathrm{\prime }}=1.5\text{m}{\text{m}}^{-1}$ , ${\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ); (g) ${\mu }_{s1}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ , ${\mu }_{s2}^{\mathrm{\prime }}=0.5\text{m}{\text{m}}^{-1}$ ); (h) ${\mu }_{s1}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ , ${\mu }_{s2}^{\mathrm{\prime }}=1.5\text{m}{\text{m}}^{-1}$ ). In all cases we set $\rho =30\text{mm}$ , $n_{e1}=n_{e2}=1.0$ . The dashed line is the unity line for which $⟨z_{max}|t⟩=s_1$ .

If ${\mu }_{a1}={\mu }_{a2}$ and ${\mu }_{s1}^{\mathrm{\prime }}<{\mu }_{s2}^{\mathrm{\prime }}$ (panels (e) and (h)), $⟨z_{max}|t⟩$ increases with $s_1$ since photons travels a greater distance in the less scattering layer and they penetrate more easily in the medium at larger depths. Conversely, if ${\mu }_{a1}={\mu }_{a2}$ and ${\mu }_{s1}^{\mathrm{\prime }}>{\mu }_{s2}^{\mathrm{\prime }}$ (panels (f) and (g)), $⟨z_{max}|t⟩$ decreases with $s_1$ since photons are experiencing a higher number of scattering events in the upper layer and thus they tend to be confined at lower depths. Again, we notice that in Fig. 7 panel (a) and panel (d) show identical results since for both panels $\mathrm{\Delta }{\mu }_{a12}=-0.010\text{m}{\text{m}}^{-1}$ . The same for panel (b) and bottom panel (c) with $\mathrm{\Delta }{\mu }_{a12}=+0.010\text{m}{\text{m}}^{-1}$ .

3.2. Continuous wave

3.2.1. Variation of ${\mu }_{a1}$ or ${\mu }_{a2}$

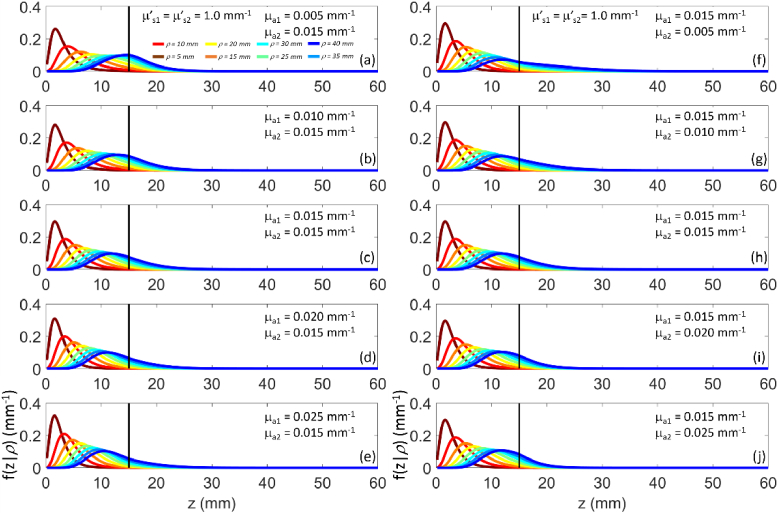
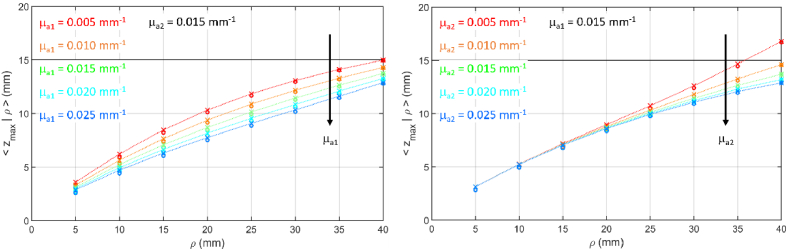
Figure 8 shows the steady state probability density function for the maximum penetration depth $f(z|\rho )$ for different values of the absorption coefficient in the two layers, while Fig. 9 shows the corresponding $⟨z_{max}|\rho ⟩$ values. Differently from the time domain case (see Fig. 2), $f(z|\rho )$ is confined to much lower depth, therefore the resulting $⟨z_{max}|\rho ⟩$ is smaller than $⟨z_{max}|t⟩$ . Moreover, as expected, the increase in the absorption coefficient in either ${\mu }_{a1}$ or ${\mu }_{a2}$ yields a decrease of $⟨z_{max}|\rho ⟩$ , and a shift of $f(z|\rho )$ towards lower z. The effect is evident at all source detector distances in case of changes in ${\mu }_{a1}$ , while it appears only at larger source detector distance for changes in ${\mu }_{a2}$ .

Fig. 8.

$f(z|\rho )$ as a function of z for $\rho =5,10,15,20,25,30,35,40\text{mm}$ (color code from brown to blue) for a two-layer medium ( $s_1=15\text{mm}$ , $s_2=75\text{mm}$ , $n_1=n_2=1.4$ , ${\mu }_{s1}^{\mathrm{\prime }}={\mu }_{s2}^{\mathrm{\prime }}=1.0\text{mm}$ ). (a)-(e) variable ${\mu }_{a1}=0.005,0.010,0.015,0.020,0.025\text{m}{\text{m}}^{-1}$ , fixed ${\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ; (f)-(j) fixed ${\mu }_{a1}=0.015\text{m}{\text{m}}^{-1}$ , variable ${\mu }_{a2}=0.005,0.010,0.015,0.020,0.025\text{m}{\text{m}}^{-1}$ .

Fig. 9.

$⟨z_{max}|\rho ⟩$ as a function of $\rho$ for a two-layer medium ( $s_1=15\text{mm}$ , $s_2=75\text{mm}$ , $n_1=n_2=1.4$ , ${\mu }_{s1}^{\mathrm{\prime }}={\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ). (a) variable ${\mu }_{a1}=0.005,0.010,0.015,0.020,0.025\text{m}{\text{m}}^{-1}$ , fixed ${\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ; (b) fixed ${\mu }_{a1}=0.015\text{m}{\text{m}}^{-1}$ , variable ${\mu }_{a2}=0.005,0.010,0.015,0.020,0.025\text{m}{\text{m}}^{-1}$ . Circles are DE results, crosses are MC results. Lines connect MC results to guide the eye.

3.2.2. Variation of ${\mu }_{s1}^{\mathrm{\prime }}$ or ${\mu }_{s2}^{\mathrm{\prime }}$

Figure 10 shows $f(z|\rho )$ for different values of the reduced scattering coefficient in the two layers, while Fig. 11 shows the corresponding $⟨z_{max}|\rho ⟩$ values. The increase in either ${\mu }_{s1}^{\mathrm{\prime }}$ or ${\mu }_{s2}^{\mathrm{\prime }}$ yields a decrease of $⟨z_{max}|\rho ⟩$ . Like for changes in the absorption coefficient, the effect is present (although very small) at all source detector distances $\rho$ in case of changes occurring in the upper layer, while it appears only at larger $\rho$ for changes in the bottom layer. The weak dependence of $⟨z_{max}|\rho ⟩$ on the scattering properties of the layers deserves a specific remark. It is somewhat surprising, even though the overall effect of scattering on propagation is known. It certainly has a strong impact in penetration depth calculations in real biological tissues, where in many cases the exact determination of scattering properties can be a not so easy task.

Fig. 10.

$f(z|\rho )$ as a function of z for $\rho =5,10,15,20,25,30,35,40\text{mm}$ (color code from brown to blue) for a two-layer medium ( $s_1=15\text{mm}$ , $s_2=75\text{mm}$ , $n_1=n_2=1.4$ , ${\mu }_{a1}={\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ). (a)-(e) variable ${\mu }_{s1}^{\mathrm{\prime }}=0.5,0.75,1.0,1.25,1.5\text{m}{\text{m}}^{-1}$ , from top to bottom) and fixed ${\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ; (f)-(j) fixed ${\mu }_{s1}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ and variable ${\mu }_{s2}^{\mathrm{\prime }}=0.5,0.75,1.0,\text{m}{\text{m}}^{-1}$ , from top to bottom).

Fig. 11.

$⟨z_{max}|\rho ⟩$ as a function of $\rho$ for a two-layer medium ( $s_1=15\text{mm}$ , $s_2=75\text{mm}$ , $n_1=n_2=1.4$ , ${\mu }_{a1}={\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ). (a) variable ${\mu }_{s1}^{\mathrm{\prime }}=0.5,0.75,1.0,1.25,1.5\text{m}{\text{m}}^{-1}$ and fixed ${\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ; (b) fixed ${\mu }_{s1}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ and variable ${\mu }_{s2}^{\mathrm{\prime }}=0.5,0.75,1.0,1.25,1.5\text{m}{\text{m}}^{-1}$ . Circles are DE results, crosses are MC results, lines connect MC results to guide the eye.

As in the time domain case (see Fig. 4) the discontinuity in the reduced scattering coefficient yields a discontinuity of the density function $f(z|\rho )$ . The effect is however not relevant for $⟨z_{max}|\rho ⟩$ .

3.2.3. Variation of the thickness of the upper layer $s_1$

Figure 12 shows the effect on $⟨z_{max}|\rho ⟩$ of the variation of the thickness of the upper layer $s_1$ for different values of the source detector distance $\rho$ .

Fig. 12.

$⟨z_{max}|\rho ⟩$ for $\rho =5,10,15,20,25,30,35,40\text{mm}$ (color code from brown to blue) as a function of the thickness of the upper layer $s_1=5,10,15,20,25\text{mm}$ for a two-layer medium with constant total thickness ( $s_{\mathit{\text{tot}}}=90\text{mm}$ , $n_1=n_2=1.4$ ). Panels (a)-(d) have same scattering ( ${\mu }_{s1}^{\mathrm{\prime }}={\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ) and different absorption: (a) ${\mu }_{a1}=0.005\text{m}{\text{m}}^{-1}$ , ${\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ; (b) ${\mu }_{a1}=0.025\text{m}{\text{m}}^{-1}$ , ${\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ; (c) ${\mu }_{a1}=0.015\text{m}{\text{m}}^{-1}$ , ${\mu }_{a2}=0.005\text{m}{\text{m}}^{-1}$ ; (d) ${\mu }_{a1}=0.015\text{m}{\text{m}}^{-1}$ , ${\mu }_{a2}=0.025\text{m}{\text{m}}^{-1}$ . Panels (e)-(h) have same absorption ( ${\mu }_{a1}={\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ) and different scattering: (e) ${\mu }_{s1}^{\mathrm{\prime }}=0.5\text{m}{\text{m}}^{-1}$ , ${\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ); (f) ${\mu }_{s1}^{\mathrm{\prime }}=1.5\text{m}{\text{m}}^{-1}$ , ${\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ); (g) ${\mu }_{s1}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ , ${\mu }_{s2}^{\mathrm{\prime }}=0.5\text{m}{\text{m}}^{-1}$ ); (h) ${\mu }_{s1}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ , ${\mu }_{s2}^{\mathrm{\prime }}=1.5\text{m}{\text{m}}^{-1}$ ). The dashed line is the unity line for which $⟨z_{max}|\rho ⟩=s_1$ .

Almost for all combinations of optical properties in the two layers if $s_1>15\text{mm}$ for all source detector distances $\rho$ we have $⟨z_{max}|\rho ⟩<s_1$ , therefore photons hardly reach the bottom layer. As expected, larger $\rho$ yield larger $⟨z_{max}|\rho ⟩$ , but apart for the largest $\rho$ values that show a limited change with $s_1$ (slight increase if ${\mu }_{s1}^{\mathrm{\prime }}<{\mu }_{s2}^{\mathrm{\prime }}$ or ${\mu }_{a1}<{\mu }_{a2}$ , and slight decrease if ${\mu }_{s1}^{\mathrm{\prime }}>{\mu }_{s2}^{\mathrm{\prime }}$ or ${\mu }_{a1}>{\mu }_{a2}$ ), the effect of $s_1$ is rather flat.

4. Discussion

4.1. Novelty of this work

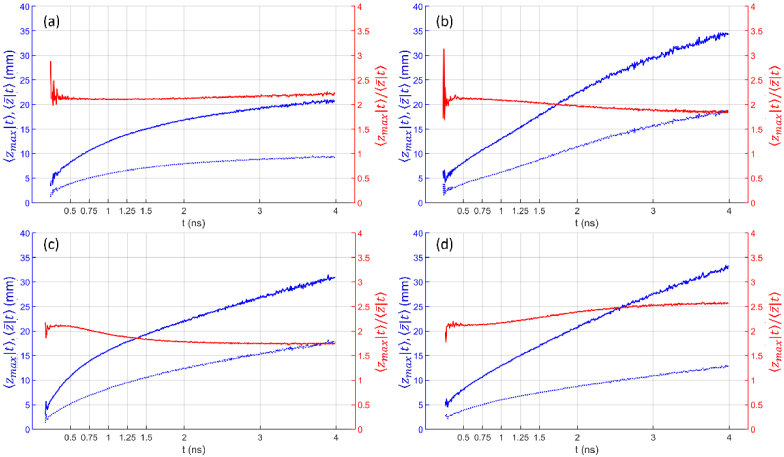
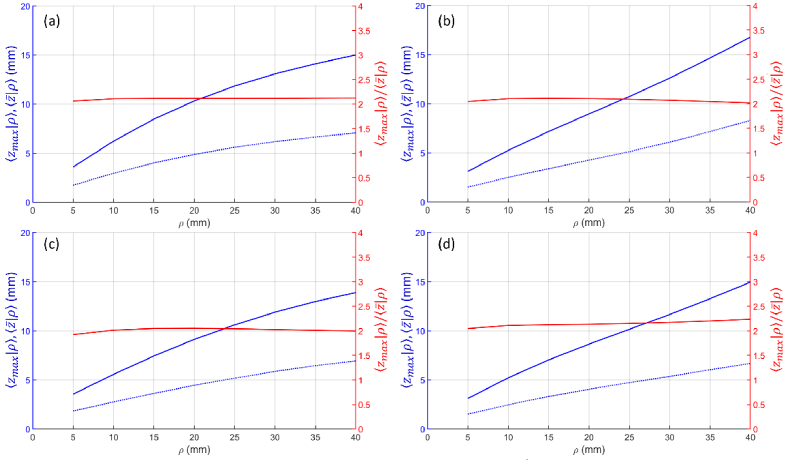
In this work we have extended the results on photon maximum penetration depth obtained for a homogeneous slab by Martelli et al. (2016) [9] to the case of a two-layer diffusive medium. Results are presented for $⟨z_{\mathit{\text{max}}}⟩$ and $f(z)$ , both in time domain and in continuous wave regime, for several combinations of the optical properties (absorption coefficient and reduced scattering coefficient, refractive index) of the two layers, and for different geometrical configurations (e.g., source detector distances and thickness of the upper layer). It is worth noting that the MC results showed [9] that the maximum penetration depth $⟨z_{\mathit{\text{max}}}⟩$ is related to the average penetration depth $⟨\overline{z}⟩$ by a simple relationship, namely $⟨\overline{z}⟩\approx ⟨z_{\mathit{\text{max}}}⟩/2$ . Considering this fact, the results presented here can also be analyzed for the average penetration depth by simply dividing by 2 the reported values for the maximum penetration depth. Figure 13 and Fig. 14 show $⟨z_{\mathit{\text{max}}}⟩$ and $⟨\overline{z}⟩$ , as well as the ratio $⟨z_{\mathit{\text{max}}}⟩/⟨\overline{z}⟩$ obtained from MC simulations for the time domain and for the continuous wave case, respectively, for different combinations of the optical properties of the two layers. The approximate relationship $⟨\overline{z}⟩\approx ⟨z_{\mathit{\text{max}}}⟩/2$ holds well in all cases.

Fig. 13.

$⟨z_{max}|t⟩$ (blue solid line), $⟨\overline{z}|t⟩$ (blue dashed line) and ratio $⟨z_{max}\mid t⟩/⟨\overline{z}\mid t⟩$ (red line) as a function of t for a two-layer medium ( $s_1=15\text{mm}$ , $s_2=75\text{mm}$ , $n_1=n_2=1.4$ ) for $\rho =30\text{mm}$ . (a) different absorption ( ${\mu }_{a1}=0.005\text{m}{\text{m}}^{-1}$ , ${\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ), same scattering ( ${\mu }_{s1}^{\mathrm{\prime }}={\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ); (b) different absorption ( ${\mu }_{a1}=0.015\text{m}{\text{m}}^{-1}$ , ${\mu }_{a2}=0.005\text{m}{\text{m}}^{-1}$ ), same scattering ( ${\mu }_{s1}^{\mathrm{\prime }}={\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ); (c) same absorption ( ${\mu }_{a1}={\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ), different scattering ( ${\mu }_{s1}^{\mathrm{\prime }}=0.5\text{m}{\text{m}}^{-1}$ , ${\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ); (d) same absorption ( ${\mu }_{a1}={\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ), different scattering ( ${\mu }_{s1}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ , ${\mu }_{s2}^{\mathrm{\prime }}=0.5\text{m}{\text{m}}^{-1}$ ). In all cases $n_{e1}=n_{e2}=1.0$ .

Fig. 14.

$⟨z_{max}\mid t⟩$ (blue solid line), $⟨\overline{z}\mid t⟩$ (blue dashed line), and ratio $⟨z_{max}\mid t⟩/⟨\overline{z}\mid t⟩$ (red line) as a function of ρ for a two-layer medium ( $s_1=15\text{mm}$ , $s_2=75\text{mm}$ , $n_1=n_2=1.4$ ). (a) different absorption ( ${\mu }_{a1}=0.005\text{m}{\text{m}}^{-1}$ , ${\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ), same scattering ( ${\mu }_{s1}^{\mathrm{\prime }}={\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ); (b) different absorption ( ${\mu }_{a1}=0.015\text{m}{\text{m}}^{-1}$ , ${\mu }_{a2}=0.005\text{m}{\text{m}}^{-1}$ ), same scattering ( ${\mu }_{s1}^{\mathrm{\prime }}={\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ); (c) same absorption ( ${\mu }_{a1}={\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ), different scattering ( ${\mu }_{s1}^{\mathrm{\prime }}=0.5\text{m}{\text{m}}^{-1}$ , ${\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ ); (d) same absorption ( ${\mu }_{a1}={\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ ), different scattering ( ${\mu }_{s1}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ , ${\mu }_{s2}^{\mathrm{\prime }}=0.5\text{m}{\text{m}}^{-1}$ ). In all cases $n_{e1}=n_{e2}=1.0$ .

Moreover, unlike the previous work, in which the classical extrapolated boundary condition (EBC) was used, in this work we have considered a more flexible and accurate hybrid approach), called EBPC, that relies on both the EBC and the PCBC [27]. With this approach the EBC is used to calculate fluence, while the PCBC is used to calculate flux.

To our knowledge, this is the first comprehensive study on the statistics of penetration depth of photon re-emitted by a two-layer diffusive medium. Previous studies adopting the same approach of this work reported results for $⟨z_{\mathit{\text{max}}}⟩$ , but not for $f(z)$ , only in the continuous wave regime and for a limited range of optical and geometrical properties [18,19]. In more recent works, either focusing on skin or head tissue, penetration depth was gauged by light fluence attenuation in the tissue, therefore no information on the statistical properties of remitted photons could be derived [20,21,23]. Depth information for re-emitted photons were indeed obtained by MC simulations in a layered scenario mimicking the human skin [22], although in a geometrical range far from that described in this work. However, all these studies were focused on a specific set of optical and geometrical properties, therefore these results cannot be used to predict the effect of changes in the optical or geometrical properties. Finally, also in all these recent works the time domain regime was not considered.

4.2. Practical considerations for the time domain case

Some practical considerations can be drawn for the time domain case.

Looking at the effect of the absorption coefficient in the bottom layer, we notice that for early time-of-flight ( $t<1.5\text{ns}$ ) there are no appreciable variations in the calculated parameters $f(z|t)$ and $⟨z_{\mathit{\text{max}}}|t⟩$ suggesting that - as expected - at short time-of-flight only the superficial parameters have influence. At longer time-of-flight ( $t>1.5\text{ns}$ ) an increase in the absorption coefficient of the upper layer results in a larger $⟨z_{\mathit{\text{max}}}|t⟩$ since photons travelling in the upper layer are preferentially lost. Of course, this also results in a lower number of detected photons. Therefore, in the design of a time domain setup care should be taken to optimize system parameters (e.g., pulsed laser repetition rate, detector noise, signal-to-noise ratio (SNR)) to achieve a proper timing and counting dynamics to better exploit the information of the late photons. Conversely, $⟨z_{\mathit{\text{max}}}|t⟩$ decreases if the absorption coefficient in the lower layer increases. In the limiting case of an infinite absorption in the lower layer, $⟨z_{\mathit{\text{max}}}|t⟩$ would be equal to the thickness of the upper layer. Values of the absorption coefficients in the two layers that produce equal relative change $\mathrm{\Delta }{\mu }_{a12}$ yields identical results for the penetration depth parameters $f(z|t)$ and $⟨z_{\mathit{\text{max}}}|t⟩$ . This is true also for the limiting case $\mathrm{\Delta }{\mu }_{a12}=0$ , confirming the previous results obtained for a homogeneous medium.

Looking at the results with different values for the reduced scattering coefficient in the two layers, we notice that the variations in $f(z|t)$ and $⟨z_{\mathit{\text{max}}}|t⟩$ are small. Therefore, considering the medium as homogeneous (from the point of view of the scattering) can be an acceptable approximation that may be properly used in real applications to tissues so that their heterogeneity in the scattering properties in many cases does not significantly affect the calculation of $⟨z_{\mathit{\text{max}}}|t⟩$ . Thus, in vivo applications the exact knowledge of the reduced scattering coefficient in the two layers might not be necessary. The value of ${\mu }_{s1}^{\mathrm{\prime }}$ , obtained e.g., with a homogeneous model, can be a rough estimate also of ${\mu }_{s2}^{\mathrm{\prime }}$ . This result matches previous findings from other groups that showed little sensitivity of diffuse reflectance to ${\mu }_{s2}^{\mathrm{\prime }}$ [16,30]. The time domain results are practically independent of the choice of the source detector distance $\rho$ . The optimal $\rho$ shall be fixed by considering the characteristics of the real time domain setup, like full-width-at-half-maximum (FWHM) of the instrument response function (IRF) and responsivity [31]. As a rule of thumb, unless interested in implementing a null distance time domain setup [32], the largest $\rho$ should be used to minimize the effect of the IRF and to reinforce the robustness of the physical model based on photon diffusion.

The thickness of the upper layer $s_1$ can be easily retrieved in real applications by means of simple measurements with e.g., plicometer or portable ultrasound device, or by data obtained by magnetic resonance imaging, computed tomography data, or anatomical atlases. Knowing $s_1$ it would be possible to optimize the time-of-flight t to ensure that $⟨z_{max}\mid t⟩>s_1$ , if interested in reaching the bottom layer. For example, for $s_1=5\text{mm}$ , $⟨z_{\mathit{\text{max}}}|t⟩$ is greater than $s_1$ at any time-of-flight, while for $s_1=15\text{mm}$ , it is required $t>1.5\text{ns}$ .

We also considered changes in the refractive index $n_1$ or $n_2$ to span the range $1.3-1.5$ in $0.1$ steps, and in the external refractive index $n_{e1}$ or $n_{e2}$ to span the range $1.0-1.8$ in $0.2$ steps. No effect on $⟨z_{\mathit{\text{max}}}|t⟩$ is observed if the internal or external refractive index is varied (data not shown). Therefore, typical values for biological tissues can be used (e.g., $n_1=n_2=1.4$ ) and care should be taken only in considering the proper value for $n_{e1}$ to apply the correct boundary conditions on the side where the light source is injected in the medium.

4.3. Practical considerations for the continuous wave case

As a general observation, we note that, in the selected pivotal configuration ( $s_1=15\text{mm}$ , $s_2=75\text{mm}$ , ${\mu }_{a1}={\mu }_{a2}=0.015\text{m}{\text{m}}^{-1}$ , ${\mu }_{s1}^{\mathrm{\prime }}={\mu }_{s2}^{\mathrm{\prime }}=1.0\text{m}{\text{m}}^{-1}$ , $n_1=n_2=1.4$ ), $⟨z_{\mathit{\text{max}}}|\rho ⟩$ is smaller than $s_1$ for $\rho <40\text{mm}$ . Looking at the effect of $s_1$ , one observes that to reach the condition $⟨z_{\mathit{\text{max}}}|\rho ⟩\ge s_1$ it is approximately needed $\rho >10\text{mm}$ if $s_1=5\text{mm}$ , $\rho >20\text{mm}$ if $s_1=10\text{mm}$ , and $\rho >40\text{mm}$ if $s_1=15\text{mm}$ .

Care should be taken to directly transfer these results to real applications like functional near infrared spectroscopy (fNIRS) of the human brain or tissue oximetry in the human muscle. In adults the mean depth from head to cortical surface is lower than 15 mm in most of the frontal, temporal and occipital position [33] where most of the fNIRS studies are conducted. Indeed the human head anatomy is not perfectly described by plane parallel smooth surfaces since curvature of the skull and corrugation of brain occur. Moreover, the presence of the low scattering cerebrospinal fluid alters photon migration in the head as compared to a highly diffusive medium. Therefore, in the context of photon migration, it is better referring to an effective than a geometrical thickness of the extracerebral tissue, the former being easily lower than 15 mm. Most of fNIRS studies in fact successfully employ $\rho <40\text{mm}$ [34]. Conversely, in tissue oximetry of the muscle the presence of subdermal adipose tissue can be appropriately modelled as a plane parallel layer covering the muscle. Adipose tissue thickness higher than 15 mm can indeed be found and in this case results can be jeopardized if using $\rho <40\text{mm}$ . [35].

Changes in the absorption coefficient of the upper layer will affect $⟨z_{\mathit{\text{max}}}|\rho ⟩$ at any $\rho$ , while changes occurring in the bottom layer can be revealed only at the largest $\rho$ . The use of multiple source detector distances (e.g., short one and long one) is mandatory in continuous wave applications if interested in unravelling absorption changes in the two layers.

Interestingly, like in the time domain case, the effect of changes in the reduced scattering coefficient on $⟨z_{\mathit{\text{max}}}|\rho ⟩$ is limited. Therefore, unless interested in the exact values of ${\mu }_{s1}^{\mathrm{\prime }}$ or ${\mu }_{s2}^{\mathrm{\prime }}$ , a rough guess of ${\mu }_{s1}^{\mathrm{\prime }}$ can be enough to estimate $⟨z_{\mathit{\text{max}}}|\rho ⟩$ .

Finally, like for the time domain case the (internal or external) refractive index yields no effect on $f(z|\rho )$ and $⟨z_{\mathit{\text{max}}}|\rho ⟩$ (data not shown).

4.4. Limitations of this work

We have focused our work mimicking an experimental configuration typical of NIRS measurement on the human head. We modelled the head as a two-layer diffusive medium with an upper layer comprising the extra-cerebral tissues (i.e., scalp, skull and cerebrospinal fluid) and a lower layer for intra-cerebral tissue (i.e., gray matter, white matter). This two-layer approximation might appear as an oversimplification of the real head structure, nonetheless this is the most used approach in practical applications (e.g., monitoring cortical oxygen saturation in adults or neonates, monitoring the hemodynamic response function to external stimuli in functional NIRS) where the interest is discriminating the confounding systemic signals originating from the extra-cerebral region [1,2]. The two layer approach can in fact provide better results than the homogeneous model without the complication of mimicking a real head structure [30]. In the case of other applications (e.g., monitoring the hemodynamic changes occurring in skeletal muscle covered by a superficial adipose tissue layer) the results of this work can provide preliminary hints but for accurate results novel simulations should be run after the optical parameters have been properly adjusted. The use of a planar geometry to interpret data obtained from a curved biological tissue is surely an approximation. The knowledge of the local curvature of the probed tissue would enable the use in the fitting procedure of a cylindrical or spherical model for photon migration, resulting in improved estimation of the optical properties as compared to a planar (semi infinite or slab) model. However, given the typical values for the source detector distance in the range 10-40 mm, the effect of curvature can be disregarded in most applications especially if source and detector fibers are aligned in the direction of the least curvature (e.g., along the axis of a cylinder) [36].

For the time domain case we have considered the ideal configuration with Dirac-delta IRF and unlimited SNR. The effect of a real IRF (with finite FWHM) is to introduce uncertainty in the time-of-flight of detected photons, while a limited SNR will mainly shorten the maximum measurable time-of-flight since at longer time-of-flight system noise will overcome the few detected photons. Both effects will reduce $⟨z_{\mathit{\text{max}}}|t⟩$ . Similarly, for the continuous wave case a real system with a reduced SNR would imply to use shorter source detector distances ρ therefore reducing the achievable $⟨z_{\mathit{\text{max}}}|\rho ⟩$ . However, the study of the ideal case can provide a limiting target for technological development.

5. Conclusion

In this work we have presented numerical results for the probability density function and for the mean value of photon maximum penetration depth in a two-layer diffusive medium. Both time domain and continuous wave regime were considered with several combinations of the optical properties (absorption coefficient, reduced scattering coefficient) of the two layers, and with different geometrical configurations (source detector distance, thickness of the upper layer). Results were obtained within the framework of the DE, and comparisons with MC simulations were also reported for verification of the proposed model. From the study of photon penetration depth, practical considerations on the design of biophotonic time domain and continuous wave systems were also derived to optimize diagnostic tools or therapeutic strategies.

Funding

Ministero dell’Università e della Ricerca10.13039/501100021856 (2022EB4B7E PRIN 2020477RW5PRIN, 20227EPKW2 PRIN2022); European Union Next-GenerationEU (Age-IT, PE0000015, CN00000022; MNESYS, PE0000006); Horizon 2020 Framework Programme10.13039/100010661 (101016087, 863087).

Disclosures

A.P. and A.T. are co-founders of PIONIRS Srl, spin-off company of the Politecnico di Milano.

Data availability

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.