Associative and predictive hippocampal codes support memory-guided behaviors

Abstract

INTRODUCTION:

The brain generates models of the environment that are used to guide flexible behaviors. This process requires learning the states of the world (such as specific locations) as well as the transitional relationships between those states (e.g., successive locations along often-traveled trajectories). The hippocampal cognitive map is believed to be one such internal model, supporting a variety of behaviors, including associative learning, navigational planning, and inference. It remains unknown which facets of hippocampal coding are required for these different behaviors and how they support both associative and predictive memory functions.

RATIONALE:

We hypothesize that two modes of hippocampal activity support learning of world states and state transitions, respectively. On one hand, the synchronous coactivity of groups of hippocampal neurons—cell assemblies—may encode features of individual states, forming an associative code. On the other hand, the ordered activation of these cell assemblies into behaviorally relevant sequences may encode the relational structure between states, forming a predictive code. Previous research has not been able to dissociate these two dynamic codes or provide evidence of their specific functions. We leveraged an optogenetic approach to dissociate these two coding schemes, with the goal of disrupting the predictive code (hippocampal sequences) while preserving the associative code (rate coding and coactivity dynamics) in behaving rats. This dissociation allowed us to examine the different memory functions of these two codes.

RESULTS:

We optogenetically perturbed the fine temporal coordination of hippocampal place cell firing as rats navigated specific spatial trajectories in a novel maze. This manipulation disrupted properties of the predictive code (such as temporally compressed place cell sequences and anticipatory place field shifts), but global network dynamics and single-cell spatial tuning and rate coding properties were preserved.

During sleep after the novel experience, we observed that task-related cell assemblies encoding discrete maze locations were reactivated in sharp wave–ripples (SWRs), unaffected by the manipulation. However, their sequential structure did not reproduce the order in which they were active in the task, resulting in impaired sequential replay for the perturbed trajectories. This result shows a dissociation between assembly reactivation and sequence replay, two phenomena previously assumed to reflect the same underlying process. The same manipulation did not disrupt replay of familiar trajectories, suggesting that the precise temporal coordination of place cell firing during learning mediates initial plasticity required for subsequent replay. Computational simulations suggest that distinct Hebbian plasticity mechanisms mediate assembly reactivation and sequence replay.

We tested the functional role of the predictive code by deploying our optogenetic manipulation in two different hippocampal-dependent memory tasks. Context-reward associative learning in a conditioned place preference task was unaffected and thus does not require a predictive map or memory replay. On the other hand, flexible memory–guided navigation in a foraging task was perturbed by the manipulation and thus depends on hippocampal predictive coding.

CONCLUSION:

Our results provide a mechanistic and functional dissociation between coactivity and sequence codes in the hippocampus. Hippocampal cells with similar responses to behavioral variables fire together, forming functional assemblies during learning, which are reactivated in SWRs during subsequent sleep. These cell assemblies encode discrete states in the environment, an associative code that is sufficient for some types of episodic memories. As these cell assemblies are activated in a specific order during behavior, they form temporally compressed hippocampal sequences and promote Hebbian plasticity. This process enables the replay of behaviorally relevant sequences during SWRs. Hippocampal sequences thus encode transitional structures of world states, generating a predictive model on top of the associative code of individual assemblies. This new framework contributes to our understanding of how memory associations develop into predictive representations of the world and helps reconcile previously disparate views on hippocampal function.

Episodic memory involves learning and recalling associations between items and their spatiotemporal context. Those memories can be further used to generate internal models of the world that enable predictions to be made. The mechanisms that support these associative and predictive aspects of memory are not yet understood. In this study, we used an optogenetic manipulation to perturb the sequential structure, but not global network dynamics, of place cells as rats traversed specific spatial trajectories. This perturbation abolished replay of those trajectories and the development of predictive representations, leading to impaired learning of new optimal trajectories during memory-guided navigation. However, place cell assembly reactivation and reward-context associative learning were unaffected. Our results show a mechanistic dissociation between two complementary hippocampal codes: an associative code (through coactivity) and a predictive code (through sequences).

Graphical Abstract

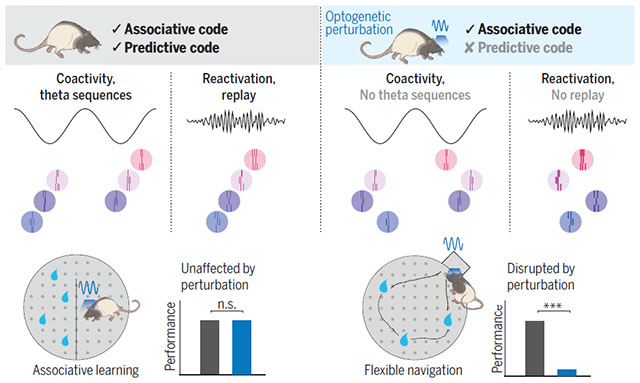
Associative and predictive codes in the hippocampus. Our optogenetic manipulation perturbed hippocampal sequences without affecting cell coactivity, thus selectively disrupting the predictive code. After learning, cell assemblies were reactivated, but their order was not preserved, abolishing sequential replay (right). Perturbing the predictive code had no effect on associative learning (bottom left) but did disrupt the flexible learning of novel optimal trajectories on a maze (bottom right). [Rat illustrations: Yu Kang]

Learning associations from experience and using this knowledge to make novel predictions are integral features of memory-guided behavior. Learning the structure of one’s environment can be conceptualized as two separate processes: learning the states in the world and learning the likely transitions between those states. The hippocampus has been implicated in both processes because it has been shown to be fundamental for encoding spatial-temporal associations (1–5) and supporting flexible memory–guided behaviors, planning, and inference (6–11). Such involvement in diverse types of memory has led to different theories of hippocampal function focused either on its role in the formation and recall of episodic memories (12–15) or in the generation of predictive models to guide behavior (10, 16, 17), while some proposals highlighted the intrinsic relationship between these functions (18, 19). However, it is unclear which facets of hippocampal coding are required for these different behaviors. One prominent candidate is the short-timescale (~10 to 30 ms) coincidental firing of hippocampal neurons with selective responses to external variables (e.g., place cells encoding the same location). This synchronous activation of “cell assemblies” can lead to the strengthening of their connections through Hebbian plasticity, forming a coactivity code (20–22). In addition, hippocampal cell assemblies organize into sequences. During navigation, temporally compressed neuronal sequences on the timescale of a single cycle of the theta oscillations (6 to 12 Hz; i.e., “theta sequences”) sweep ahead of the animal’s current position to encode future routes (23–25). During rest periods, the sequential activation of place cells “replays” past spatial trajectories (26, 27). Coactivity and sequential hippocampal dynamics have been traditionally considered conjoined aspects of the same underlying process, supported by common circuit and synaptic mechanisms to the extent that they are regarded as nondissociable. An alternative possibility is that coactivity and sequential dynamics of hippocampal place cells represent distinct coding schemes (Fig. 1). First, assemblies of coactive cells would encode individual associations, or discrete states in the world. Second, assemblies can be concatenated into sequences reflecting either experienced or inferred behaviorally relevant state transitions, forming a predictive code. Although multiple studies have found deficits in memory-guided behavior by disrupting hippocampal activity (28–32), none have been able to dissociate these two dynamic modes and provide evidence of the specific role of hippocampal sequences in behavior. To overcome this limitation and test our hypothesis, we selectively disrupted hippocampal sequences in rats while preserving place cell expression and coactivity dynamics and investigated their specific contribution to predictive coding and flexible spatial learning.

Fig. 1. Two hypothesized memory codes in the hippocampus.

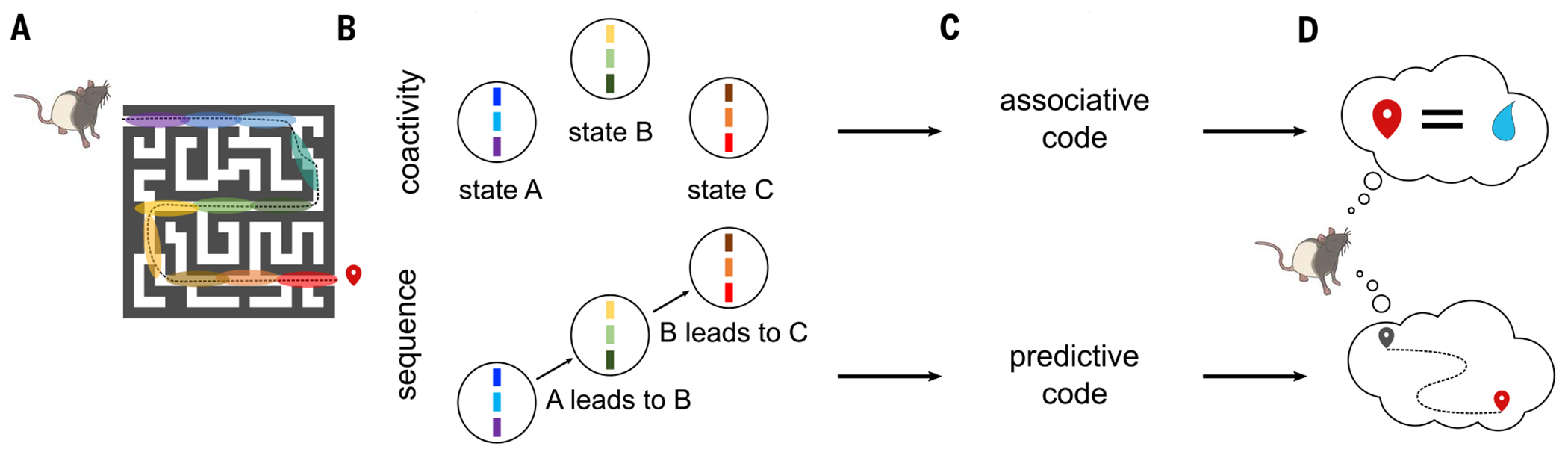
(A) As a rat learns to navigate a maze to find a reward, place cells activate along its spatial trajectory (color areas represent place fields). (B) During navigation, but also during offline periods, place cells with overlapping fields are active together, forming functional assemblies (top), and these assemblies form a sequence that reproduces an animal's learned trajectory (bottom). (C) We propose that the coactivity of cell assemblies represents an associative code to learn discrete states in the world, while their sequential activation forms a predictive code to learn behaviorally relevant state transitions. (D) An associative memory code may be sufficient for some types of memory, such as associating a place with a reward. Other types of memory-guided behavior, such as flexibly navigating a complex environment, would require a predictive model.

Results

Disruption of hippocampal theta sequences impairs the formation of a predictive map

To dissociate assembly coactivation and the sequential organization of assembly activity, we sought to specifically disrupt place cell sequence dynamics while preserving their tuning and coactivity properties in the main hippocampal output region, CA1. Timing of CA1 place cell firing relies on inputs from the medial entorhinal cortex (MEC) (33–35). However, silencing or inactivating the MEC profoundly interferes with hippocampal physiology, affecting place cell expression, coactivity, and phase coding, and thus lacks the necessary specificity to test the role of sequences (36–39). To overcome these limitations, we expressed channel-rhodopsin (ChR2) in rat MEC γ-aminobutyric acid–releasing (GABAergic) cells to optogenetically entrain them at an artificial gamma frequency (40, 41). With this approach, we selectively perturbed the fine temporal structure of MEC outputs while simultaneously recording hippocampal population activity (Fig. 2A and fig. S1). In contrast to previous manipulations (33, 36), our optogenetic perturbation spared theta power, frequency, and the theta phase modulation of CA1 unit firing (fig. S1). To evaluate the effect of our optogenetic perturbation on CA1 place cell properties, we delivered light while rats (n = 5) ran in one direction (“Stim ON”) but not in the opposite direction (“Stim OFF”) on a novel linear track. We aimed to disrupt specific sequences that encoded part of the experience and to leave other sequences intact as a control. The formation, stability, and firing properties of CA1 place cells at the single cell and population levels were preserved for both the Stim ON and Stim OFF directions (Fig. 2, B to F, and figs. S2 to S4). Place cells in the two directions had similar properties and formed a highly directional code such that Stim OFF and Stim ON trajectories could be decoded separately (fig. S3A), and on the population level, the composition, spatial properties, and stability of place cell assemblies were similar in the Stim OFF and Stim ON directions (figs. S4, E to H). Despite preserved place cell tuning curves, the progressive shift in their spike timing in relation to the phase of global theta rhythm [“phase precession” (42)] was impaired in the Stim ON direction (Fig. 2D and fig. S5). Moreover, the sequential firing of pairs of place cells at the theta timescale was disrupted in Stim ON (Fig. 2, G and H). In contrast, across theta cycles, cofiring of CA1 cells was preserved in both directions (Fig. 2, G and I).

Fig. 2. Optogenetic perturbation of MEC gamma timing impairs temporal but not rate coding features of CA1 place cells.

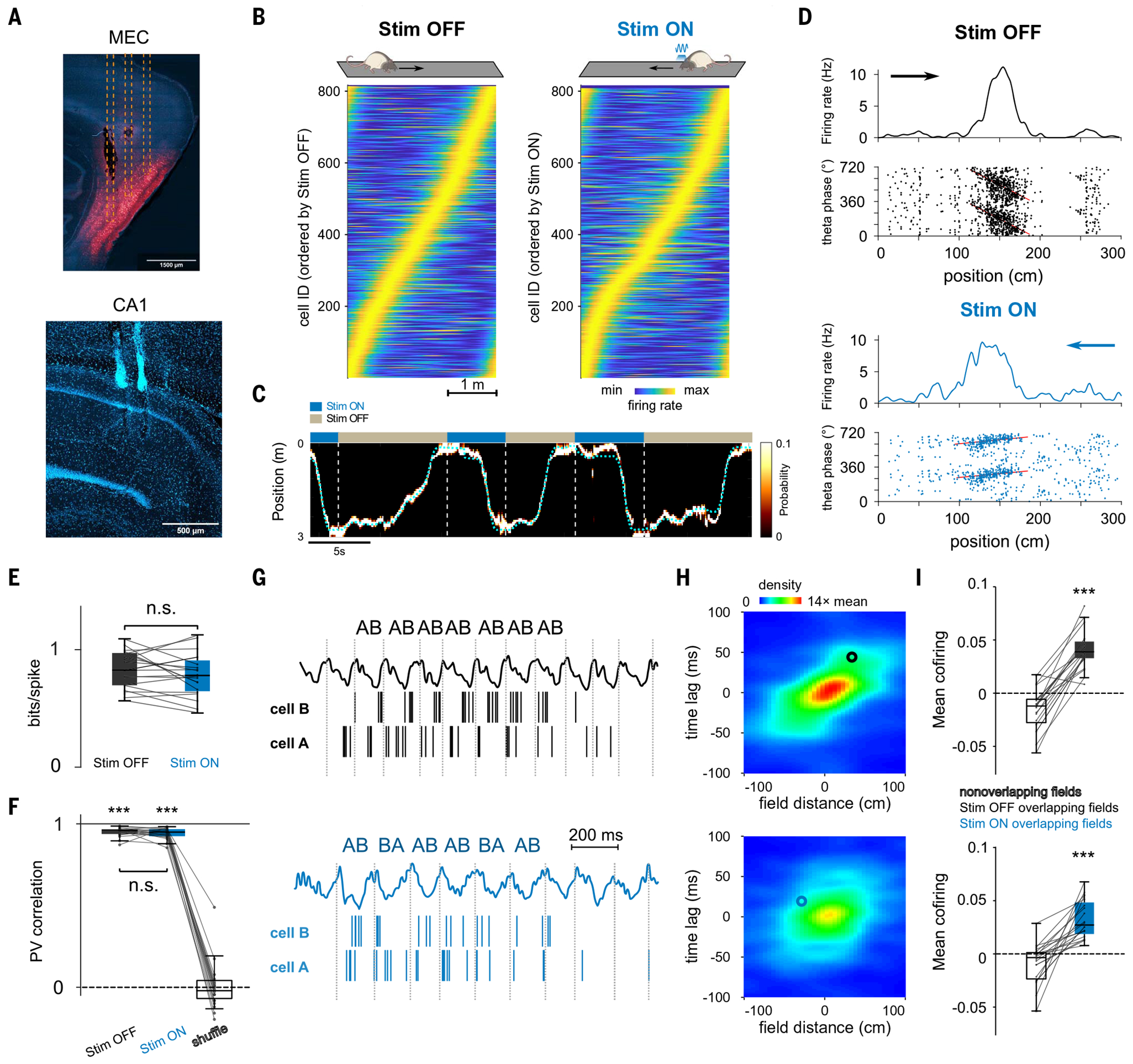
(A) Histological sections showing (top) expression of mDlx-ChR2-mCherry in MEC GABAergic cells (red) and optic fibers’ tracks (dashed lines) and (bottom) probe locations in CA1. (B) Rate maps for CA1 pyramidal cells (n = 815) in the Stim OFF and Stim ON directions. (C) Example Bayesian decoding of CA1 population spike trains during running behavior. Dashed cyan line represents animal’s actual position. The color map indicates probability of a decoded location. (D) Representative place cells for the Stim OFF (top) and Stim ON (bottom) directions. (Top) Firing rate as a function of spatial positions. (Bottom) Theta phase–position raster of place cell spikes. Red line represents the linear circular regression. (E) Spatial information was not significantly different between cells in the Stim OFF and Stim ON directions (P = 0.39; Wilcoxon signed-rank test). (F) Representation stability as measured by the population vector (PV) correlation between even and odd trials in both directions was higher than shuffled data (OFF/ON versus shuffle: P = 6 × 10⁻⁸/P = 6 × 10⁻⁸, Wilcoxon signed-rank test) and not different between the ON and the OFF directions (P = 0.35, Wilcoxon signed-rank test). (G) Examples of theta firing relationships for cell pairs with overlapping place fields in OFF (top) and ON (bottom) directions. The cells cofired in the same theta cycles in both cases, but the order of firing (AB) is only consistent in the OFF direction. (H) Average normalized density plot between place field distance and theta timescale firing lag for all overlapping place cell pairs in OFF (top) and ON (bottom) running directions. Theta compression was disrupted in Stim ON only (P = 9 × 10⁻⁵, Wilcoxon signed-rank test between theta compression slopes; see methods). Circles indicate the cell pairs shown in (G). (I) Cofiring of overlapping place cells in the same theta cycles was preserved in both directions (overlapping versus nonoverlapping place cells in OFF/ON: P = 1 × 10⁻⁴/P = 9 × 10⁻⁵, Wilcoxon signed-rank test; OFF versus ON: P = 0.067). ***P < 0.001.

In our framework, the formation of place fields (PFs) in a novel environment reflects learning the states in the world (e.g., locations), whereas the formation of a predictive map develops as an animal learns the likely transitions between those states (e.g., successive locations along often-traveled trajectories). To test whether the predictive code could be dissociated from the encoding of the individual states with our manipulation, we examined the evolution of place cells and hippocampal predictive coding features in the novel maze. We found that place cell properties in both Stim OFF and Stim ON directions showed experience-dependent development. Place field quality in both directions improved across laps, as measured by both their spatial information (Fig. 3B) and the decoding accuracy of animal position from place cell population activity (fig. S3), indicating that spatial maps were formed and developed with experience, unaffected by our optogenetic perturbation.

Fig. 3. Impaired development of place cell theta sequences and predictive properties.

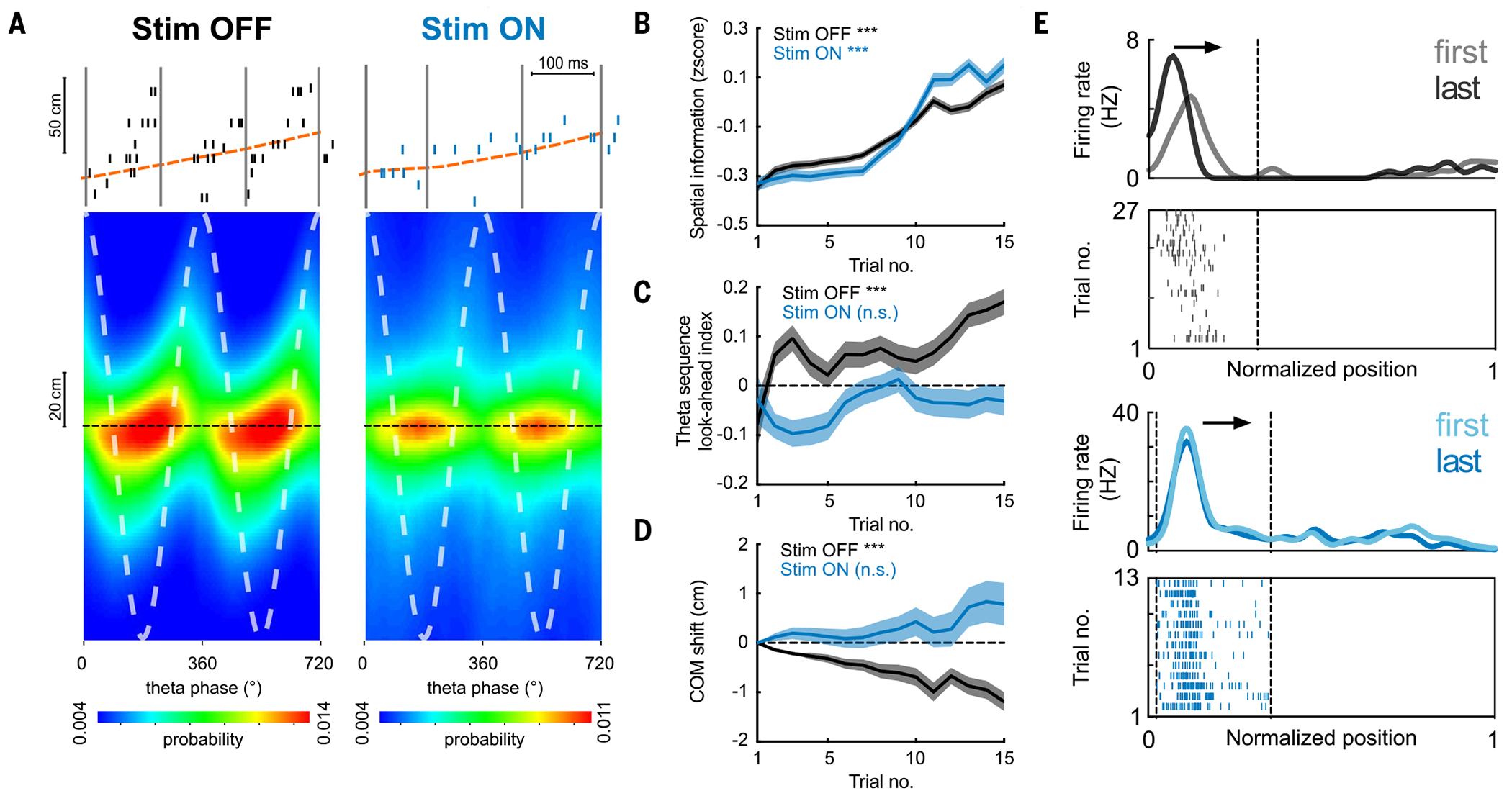
(A) (Top) Example theta sequences. (Bottom) Average (n = 20 sessions in five rats) decoded position estimated across different theta phases, relative to the actual animal position (dashed black line). Stim ON theta sequences were impaired (Stim OFF versus Stim ON quadrant scores: P = 7 × 10⁻¹⁴¹; weighted correlation: P = 4 × 10⁻²², Wilcoxon rank sum test, n = 17,992/13,265 theta cycles). (B) Increase in spatial information of place cells across laps in both Stim ON (blue) and Stim OFF (black) conditions (***P = 1.8 × 10⁻¹¹/1.2 × 10⁻⁵ for Stim OFF/ON, Wilcoxon rank sum tests comparing the 1st versus the 15th lap). (C) Increase in theta sequence look-ahead index in the Stim OFF (***P = 4.0 × 10⁻⁶), but not the Stim ON, direction (P = 0.71, Wilcoxon signed-rank tests). (D) Backward shifting of PF center-of-mass (COM) overlaps on the Stim OFF trajectory (***P = 1.3 × 10⁻⁶⁹) but not the Stim ON trajectory (P = 0.16, Wilcoxon signed-rank tests). COM shift relative to the first lap is shown (>0, forward shifting to future; < 0, backward shifting to past). (E) Example place cells showing backward shifting place fields on the Stim OFF trajectory (top) and stable fields on the Stim ON trajectory (bottom). Arrows depict the animal’s running direction. Curves on top show smoothed firing rate for the first and last laps, and raster plots below show spikes across all laps. For all these analyses, n = 20 sessions from five rats were used.

We then examined the development of a predictive code in two ways. We first analyzed theta sequences, because they are temporally compressed representations of spatial trajectories, reflecting short-term predictions of the immediate future (43–46). In contrast to the preserved spatial map formation, theta sequences were impaired in the Stim ON direction (Fig. 3A). Moreover, we observed a specific experience-dependent development of theta sequences in the Stim OFF direction, such that they became more prospective across laps (encoding longer distances ahead of the animal) (Fig. 3C), a process that could reflect the formation of increasingly predictive internal representations of the maze. This development was not observed in the Stim ON direction (Fig. 3C). Another property of the hippocampal predictive map is the progressive backward shift of place fields toward past states (or locations) with experience (47), so that the early firing reflects the expectation of upcoming states (17). We observed a progressive backward shift across laps of place fields only in the Stim OFF direction, as expected, not the Stim ON direction (Fig. 3, D and E). These changes in the predictive code were not due to differences in animal behavior between the two trajectories (fig. S3G).

Impaired replay with preserved reactivation of a novel experience

Memory formation in the hippocampus is typically measured as both the reactivation of short-timescale coactivity patterns (“assemblies”) and the replay of neuronal sequences during sharp wave–ripples (SWRs) (48–50). We first examined sequential replay of a running experience on a novel linear track. During pauses between track running and during sleep after the task, we observed SWR-associated replay events reproducing place cell sequences of the Stim OFF direction (Fig. 4, A and B). However, replay sequences of the Stim ON trajectory, where hippocampal predictive coding was disrupted, were impaired (Fig. 4B). Compared with baseline sleep sessions before the task, the fraction of SWRs that expressed significant replay of the Stim OFF trajectory and their sequence scores were considerably increased, but no experience-dependent enhancement was observed for the Stim ON trajectory (Fig. 4C and fig. S6). This effect cannot be explained by differences in single neuronal activity during SWRs or decoding quality (fig. S7). Stim ON replay sequences were not observed in either the forward or the reverse direction (fig. S6, B and C), and this result was replicated with different replay methods and decoding parameters (figs. S6 and S7). We also tested whether this disruption of replay of specific trajectories was due to the impaired formation of a predictive map (i.e., encoding the relevant state transitions). We conducted an experiment in which rats (n = 3) first explored a linear track without manipulation to form a predictive map without perturbation and, in a subsequent session, experienced optogenetic perturbation in one direction as previously described. Theta sequences were still impaired in the Stim ON direction, but we observed intact replay for both Stim ON and Stim OFF trajectories (fig. S8), confirming that although predictive coding is key in the initial stages of encoding novel experiences, once the predictive map is established, it does not require further repetitions to generate replay of recent experience.

Fig. 4. Impaired replay with preserved reactivation of a novel experience.

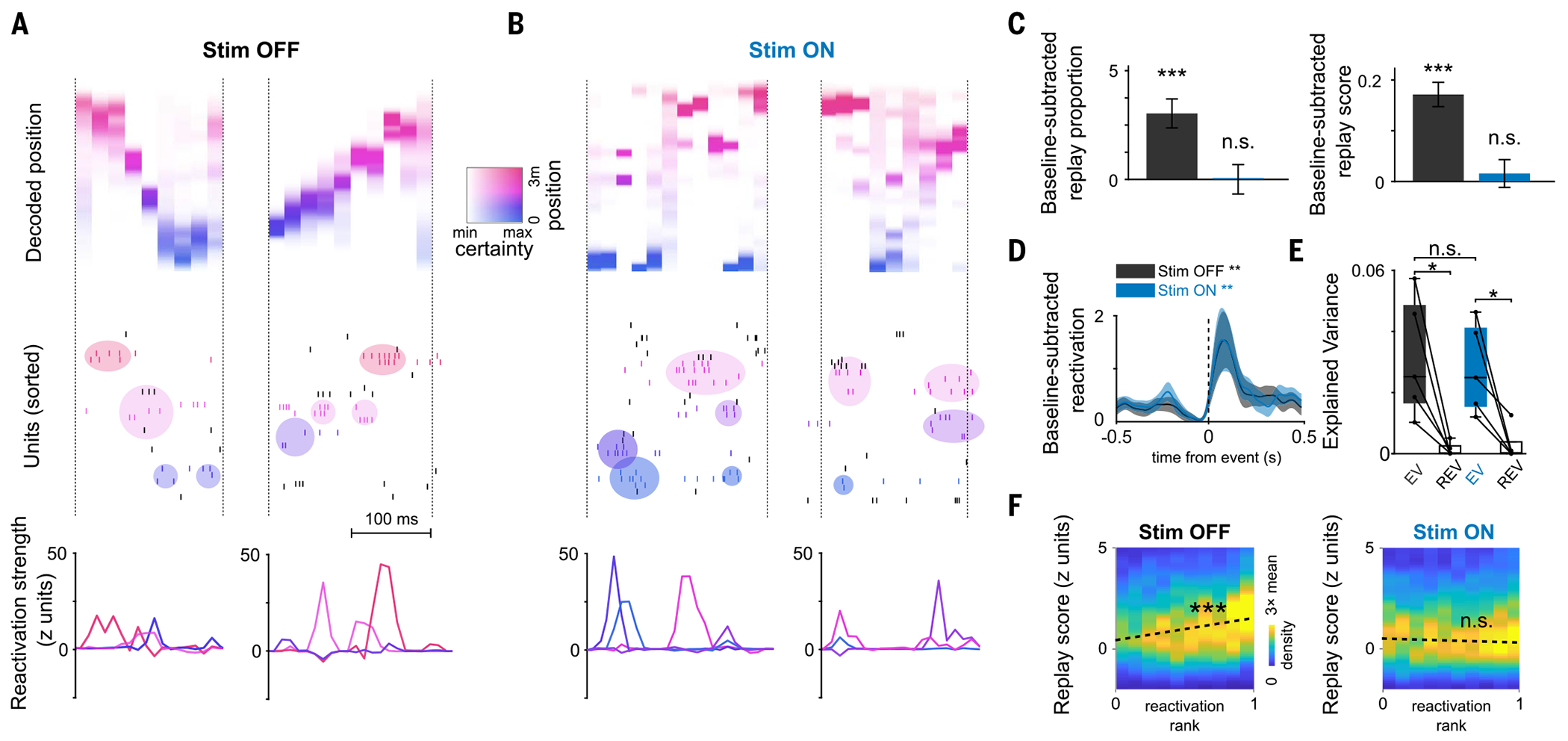
(A and B) Examples of replay and reactivation for (A) the Stim OFF and (B) the Stim ON experience, respectively. (Top) Decoded position during replay events (color coded by decoded position). (Middle) Raster plots of neuronal firing; colored circles indicate activations of assemblies composed of neurons with nearby place fields (colored ticks; colors of assemblies reflect their peak activation position). (Bottom) Assembly reactivation strength curves. (C) Increase in proportion significant replay (left) and sequence scores (right) of SWRs in post-task sleep as compared with pre-task sleep. Unlike the OFF direction, there was no significant replay in the ON direction (n = 4437 events; Stim OFF: studenťs t test, ***P = 7 × 10⁻¹¹; Stim ON: P = 0.29 for proportions; and Wilcoxon signed-rank test: OFF ***P = 3 × 10⁻¹⁷ and ON P = 0.29 for scores). Only the first session in the maze was included (n = 5 sessions). (D) Reactivation strength of task-related assemblies centered on post-task sleep SWR, increased relative to baseline (Stim OFF post-task sleep versus baseline sleep during SWRs: Wilcoxon signed-rank test, n = 31 components, **P = 0.0096; Stim ON post-task sleep versus baseline sleep during SWRs: Wilcoxon signed-rank test, n = 27 components, **P = 0.0026). (E) Reactivation of pairwise neuronal correlation as measured by explained variance (EV) in post-task sleep was significant for both directions (Stim OFF: *P = 0.031; Stim ON: Wilcoxon signed-rank test, *P = 0.031; Stim OFF versus Stim ON, Wilcoxon signed-rank test, P = 0.81; n = 5 sessions). (F) Correlation between replay scores and assembly reactivation strength for post-task SWRs computed independently for Stim OFF and Stim ON replay events. Reactivation and replay were correlated in Stim OFF (Pearson’s correlation coefficient r = 0.11, ***P = 3 × 10⁻¹²) but not in Stim ON (Pearson’s r = −0.028, P = 0.06).

In the novel linear track experience, we next examined reactivation of task coactivity patterns by detecting synchronous cell assemblies that encoded discrete positions along both Stim OFF and Stim ON trajectories (fig. S9). The composition, spatial properties, and stability of assemblies were similar in the Stim OFF and Stim ON directions (fig. S4, E to H). Surprisingly, Stim OFF and Stim ON assemblies reactivated with similar strength during SWRs (Fig. 4, A and B), significantly increasing their activity compared with the preceding sleep (Fig. 4D and fig. S9, B to D). This result indicates an intact memory reactivation of locations along both trajectories, which was also confirmed using other canonical metrics of memory reactivation (Fig. 4E and fig. S9A). We wondered how these stark differences in reactivation and replay can coexist. A closer look at the temporal dynamics of cell assemblies revealed an important difference. Assemblies from the Stim OFF trajectory reactivated during SWRs in a temporal sequence that reproduced the order of their encoded spatial locations in the maze (Fig. 4 and fig. S9A). However, while individual assemblies for the Stim ON trajectory reactivated during SWRs with similar strength to those for the Stim OFF trajectory, their task sequential structure was not preserved in these reactivation events (Fig. 4B and fig. S9E), resulting in the impairment of sequence replay and the preservation of reactivation of the Stim ON trajectories. Indeed, although the strength of assembly reactivation and replay for the Stim OFF direction were correlated at the level of individual SWRs, this correlation was absent for the Stim ON direction (Fig. 4F), dissociating reactivation from replay in the absence of a predictive code.

Associative and predictive codes support different memory-guided behaviors

Next, we asked whether the associative (coactivity) and predictive (sequences) hippocampal codes have different functional roles. A predictive model of the environment would be required to learn tasks that necessitate flexible navigation. To test this prediction, we trained rats (n = 5) to learn a novel spatial configuration of rewards in a familiar “cheeseboard” maze (8, 41, 51). Rats learned to find three hidden water rewards in different locations on the maze, with the reward locations changing every day (Fig. 5, A and B). Each trial started with the animal in the home box and ended when they retrieved the three rewards and came back to the box. The most efficient strategy for the animal in this task was thus to find the optimal route that connected all three reward locations by learning to sequentially navigate from one reward to the next. On half of the days, we performed the same optogenetic perturbation during learning trials (Stim ON sessions), whereas in the other half there was no stimulation (Stim OFF sessions). We observed an intact formation of place fields (fig. S10) and impaired theta sequences (Fig. 5D) in Stim ON sessions. Animal learning performance was impaired in Stim ON compared with Stim OFF sessions (Fig. 5C and fig. S10), supporting a role of the predictive code in the efficient learning of novel optimal trajectories in a familiar environment. We next asked whether replay would be preserved despite the disruption of theta sequences in this familiar environment. We first examined replay of the novel trajectory learned by the end of the current day’s training session. In Stim OFF sessions, we found robust replay in both awake SWRs (during intertrial periods in the home box) and in the post-learning sleep session (Fig. 5F and fig. S11A). In contrast, replay of the novel route to the new goal locations was impaired in Stim ON sessions (Fig. 5F and fig. S11A), suggesting that when learning a new optimal route to goals, even in familiar environments, the transitional structure between locations of the route encoded by theta sequences is required for its subsequent replay. Replay of the familiar routes to previously learned locations was preserved in both Stim OFF and Stim ON sessions (fig. S11B). These effects were not due to differences in SWR properties, single-unit firing dynamics during SWRs, or decoding accuracy of animal position between Stim OFF and Stim ON sessions (figs. S11, D and E, and S10C). The two-dimensional (2D) place field properties of individual cells were also preserved, similar to those on the 1D linear track (fig. S10E).

Fig. 5. Internally generated sequences are needed for memory-guided behavior.

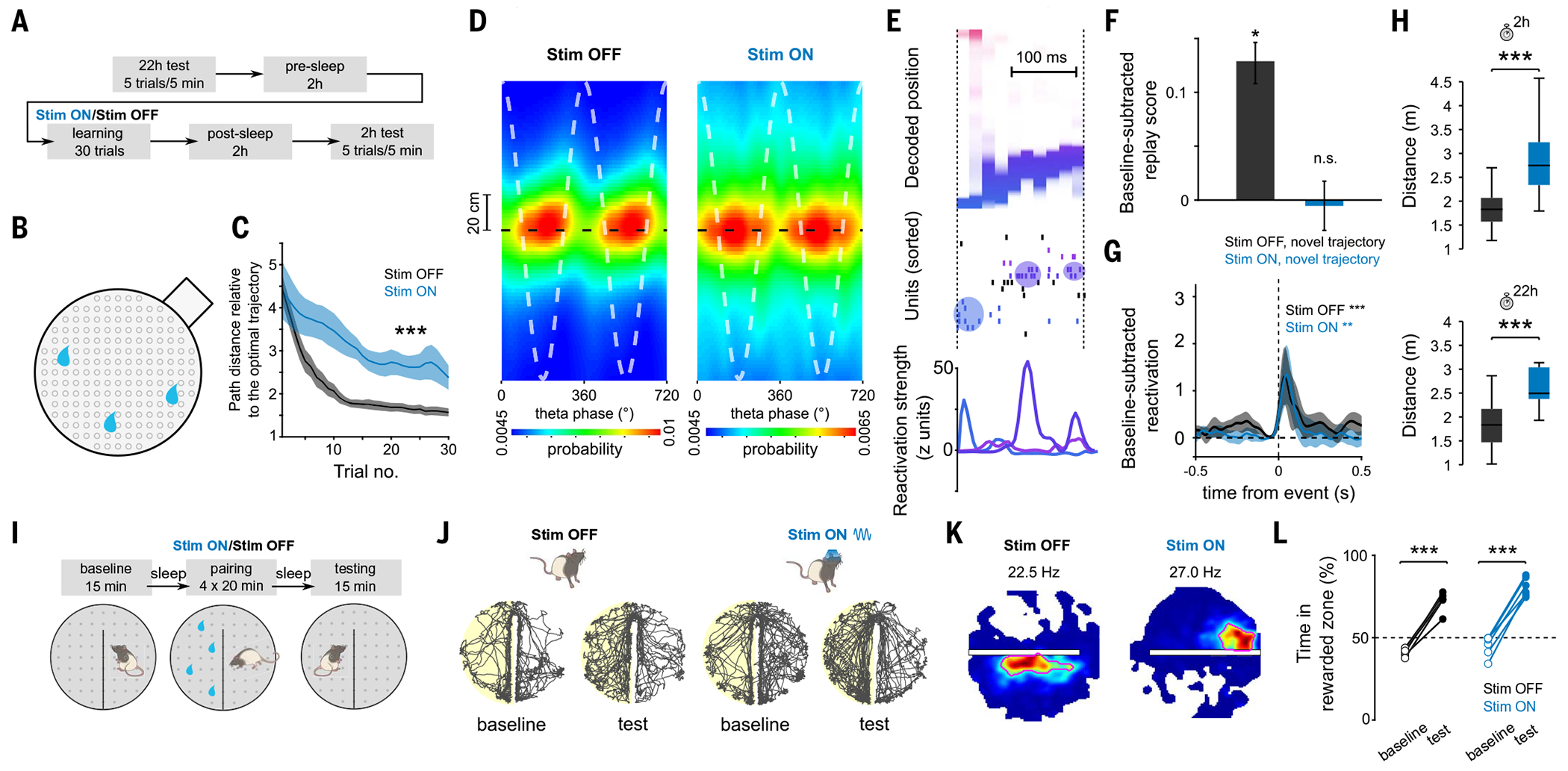
(A) Task structure of the cheeseboard task: Each day, animals learned a novel trajectory to get three hidden rewards in a circular arena. (B) Schematic of the cheeseboard setup. (C) Learning performance measured as distance traveled relative to optimal trajectory. ANOVA with repeated measures showed a significant main effect of group (F_1,43 = 133.4, P < 10⁻¹⁰; n = 33 and 11 sessions for Stim OFF and Stim ON, respectively). (D) Average decoded position versus theta phase, relative to actual animal position (dashed black line). Stim ON theta sequences were degraded (quadrant scores were lower in Stim ON than in Stim OFF: n = 5958/2695 cycles for Stim OFF and Stim ON, respectively, P = 2 × 10⁻³; weighted correlations were lower in Stim ON than in Stim OFF: P = 3 × 10⁻⁴, rank sum test). Two cycles are shown for visibility. (E) Example of a decoded replay event. Decoded linearized position (top), spike raster (middle), and assembly reactivation strength (bottom) were shown for the same replay event. (F) Increase in replay score in post-task sleep as compared with pre-task sleep. Unlike the Stim OFF condition, there was no significant replay in the Stim ON condition (Stim OFF: P = 3 × 10⁻²⁰; signed-rank test, n = 11,460 events; Stim ON: P = 0.41, n = 8689 events). (G) Reactivation strength of task-related assemblies centered on post-task sleep SWR (Stim OFF post-task sleep versus baseline sleep during SWRs: n = 36 components, P = 4.71 × 10⁻⁴; Stim ON post-task sleep versus baseline sleep during SWRs: n = 22 components, P = 3.19 × 10⁻³, signed-rank test). (H) Memory performance during 2 and 22 hour post-learning recall tests (P = 6.8 × 10⁻⁴/7.9 × 10⁻⁴ for 2 and 22 hour tests, rank sum test; n = 25/11 for Stim OFF/ON sessions from five rats). (I) Task structure of CPP task. (J) Example rat paths for Stim OFF (left) and Stim ON (right) baseline and testing sessions on CPP task. The side rewarded during pairing is highlighted in yellow. (K) Example place fields near the boundary for Stim OFF (left) and Stim ON (right) conditions, illustrating place field elongation along the boundary, which was disrupted in the Stim ON condition. Red circles emphasize the shape of the place field. (L) CPP memory performance: both Stim ON and Stim OFF training resulted in animals spending more active time in rewarded versus unrewarded side (Stim OFF: paired t test, n = 5 sessions, P = 2.85 × 10⁻⁴; Stim ON: paired t test, n = 6 sessions, P = 2.10 × 10⁻⁵).

In contrast to the impaired Stim ON replay, reactivation of cell assemblies was maintained in both Stim OFF and Stim ON sessions (Fig. 5G and fig. S11), replicating our results from the linear track. Finally, we tested whether impairment of hippocampal sequences with preserved place cell expression and coactivity affected subsequent memory recall. Memory recall measured 2 and 22 hours after learning was disrupted in Stim ON compared with Stim OFF sessions (Fig. 5H), and animals spent less time exploring around the reward locations after Stim ON than after Stim OFF sessions (fig. S10B). Furthermore, while performance on the 2- and 22-hour tests during Stim OFF sessions remained on par with the final performance reached during learning, in Stim ON sessions, performance was further deteriorated (fig. S10A).

Our hypothesis predicted that in contrast to “model-based” behaviors that require a predictive code, an associative memory code implemented by the coactivity of hippocampal cells would be sufficient to support other types of episodic memory, such as associating spatial context with rewards. We trained rats (n = 5) on a conditioned place preference (CPP) paradigm (Fig. 5I), which depends on intact hippocampal function. Rats were trained to associate one of the two halves of a cheeseboard maze with the presence of water rewards at random locations. After four pairing trials, we tested their preference for either of the two halves of the maze (without reward present). In half of the sessions, we delivered the optogenetic perturbation during all running periods during pairing trials. In line with our previous results, we detected similar assembly reactivation during sleep after both Stim OFF and Stim ON pairing trials (fig. S12). Population activity during SWRs formed distinct memory representations for both contexts (rewarded and nonrewarded maze halves) in both Stim OFF and Stim ON sessions, consistent with an intact associative code (fig. S12). Because the CPP task involves boundaries, it gave us the opportunity to quantify a critical signature of hippocampal predictive coding, which is the elongation of place fields along obstacles in 2D mazes, reflecting the topological structure of the space (17, 52). Similar to previous reports (53, 54), fields near the boundary of our maze tended to elongate parallel to the wall in Stim OFF sessions (Fig. 5K and fig. S12). However, this effect was disrupted during Stim ON (Fig. 5K and fig. S12), providing further support that the predictive map was impaired. To assess replay in the absence of stereotypical trajectories, we examined the degree to which the sequential order of firing in post-task sleep SWRs resembled the sequential order in behavior. The sequential order was preserved in post-task sleep in Stim OFF sessions but not in Stim ON sessions (fig. S12, F and G). Despite these changes in the predictive code, on the test session, where no reward or stimulation was delivered, rats showed an enhanced preference for the previously rewarded context in both Stim OFF and Stim ON conditions (Fig. 5, J and L), confirming that an associative memory code was sufficient for the formation and retrieval of a context-reward association.

Circuit mechanisms for coactivity and sequence memory codes

Given this dissociation, we wondered which distinct circuit mechanisms support the reactivation and replay of memories. The main inputs that modulate the firing dynamics of CA1 pyramidal cells are excitatory projections from CA3 and the entorhinal cortex as well as perisomatic inhibition (Fig. 6A). The relative strength of each of these inputs during behavior can be estimated by measuring layer-specific gamma oscillations (34,35,55,56). MEC optogenetic perturbation specifically disrupted midfrequency gamma oscillations (gamma_M) in the distal CA1 dendrites, the domain innervated by MEC axons (Fig. 6B and fig. S13), while other CA1 gamma oscillations, elicited respectively by CA3 inputs and local inhibition (34, 35, 55–57), remained unaltered (Fig. 6B and fig. S13). The coupling of CA1 spikes to gamma_M, but not to the other two gamma oscillations, was also impaired (fig. S13), consistent with the notion that our manipulation disrupted CA1 pyramidal cell entrainment by MEC inputs but not by CA3 or local interneurons. The disruption of theta sequences during initial experience led to the impairment of replay but not the reactivation of assemblies, raising the question of which mechanisms link these processes. To answer this question, we turned to computational modeling.

Fig. 6. Circuit mechanisms for coactivity and sequence hippocampal dynamics.

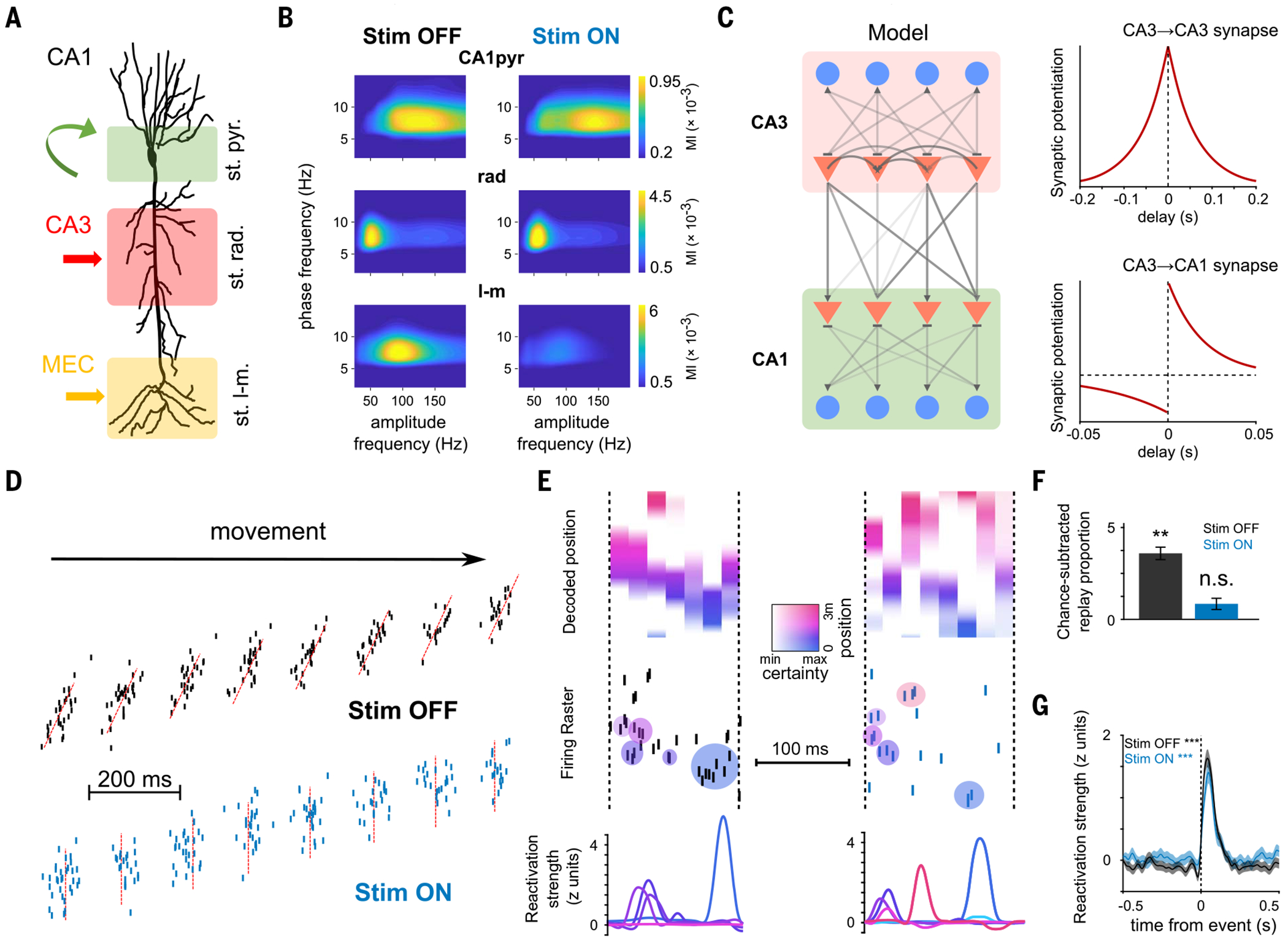
(A) Schema depicting the inputs to CA1 pyramidal neurons stratified along their somatodendritic axis. Local inhibitory inputs are dominant in the pyramidal layer (st. pyr.), CA3 inputs target proximal apical dendrites in the stratum radiatum (st. rad.), and entorhinal inputs target distal dendrites in the stratum lacunosum-moleculare (st. l-m.). (B) Gamma amplitude-theta phase comodulograms for each layer-specific LFP component (see methods) displayed modulation in a specific gamma sub-band (averaged data from n = 10 sessions from four rats): CA1pyr in gamma_F (100 to 160 Hz), rad in gamma_S (30 to 60 Hz), and LM in gamma_M (60 to 110 Hz). (Right) MEC perturbation selectively impaired LM gamma_M but not CA1pyr or rad oscillations (**P = 0.002, Wilcoxon signed-rank test; n = 13 sessions from five rats). (C) (Left) Model schematic depicting a subnetwork of CA3 cells projecting to a subnetwork of CA1 cells. Triangles represent pyramidal neurons, and circles represent inhibitory interneurons. (Right) STDP rules used to train different synapses within the network during learning trials. (D) In Stim OFF simulations (top), place cells displayed phase precession and prominent theta sequences. In Stim ON simulations (bottom), phase precession was disrupted, and theta sequences were abolished. (E) Example replay events simulated by the model after Stim OFF (left) and Stim ON (right) learning. Decoded position, spike raster, and assembly reactivation strength as in Fig. 4. (F) Increase in proportion of “SWR” events with significant replay in post-task “sleep” epochs in Stim OFF and Stim ON protocols. Replay improvement was above chance levels in Stim OFF but not Stim ON simulations (Stim OFF: P = 0.0039, Wilcoxon signed-rank test, n = 6585 events; Stim ON: P = 0.19, n = 6031 events). (G) Reactivation strength of task-related assemblies centered on post-task sleep SWR-like events increase relative to baseline (Stim OFF post-task sleep versus baseline sleep during SWR-like events: Wilcoxon signed-rank test, n = 362 components, ***P = 5 × 10⁻⁴⁴; Stim ON post-task sleep versus baseline sleep during SWR-like events: Wilcoxon signed-rank test, n = 312 components, ***P = 1 × 10⁻²⁷).

Previous work has suggested that the highly recurrent CA3 hippocampal region with its auto-associative network structure is responsible for both the coactivation of CA1 cells forming functional assemblies (22, 58) and the generation of sequential activity (24, 59, 60). We implemented a spiking CA3-CA1 network model capable of generating spontaneous replay. Our CA3 network consisted of recurrently connected leaky integrate-and-fire pyramidal cells and interneurons (61). This network was connected in a feedforward manner to a CA1 network, with a similar composition but lacking recurrent excitation, so every CA1 pyramidal cell integrated inputs from multiple CA3 pyramidal cells (Fig. 6C). We first simulated a learning phase, akin to a rat running on a novel linear track, in which place cells received random spatial inputs. In accordance with experimental observations, CA3-CA1 synaptic weights were updated according to an asymmetric (62, 63) spike time–dependent synaptic plasticity (STDP) rule, whereas CA3-CA3 weights followed a symmetric (64) STDP rule (Fig. 6C). On the basis of our experimental findings, we simulated a Stim OFF condition, in which place cells displayed phase precession and robust theta sequences (Fig. 6D and fig. S14). In a Stim ON condition (mimicking the effects of our optogenetic MEC perturbation), place cells were phase-locked to theta oscillation but lacked phase precession and theta sequences (Fig. 6D and fig. S14), reproducing our experimental findings. We also simulated offline epochs [akin to non–rapid eye movement (non-REM) sleep] before and after spatial learning; in such periods, the network received low-level stochastic spiking inputs to drive activity. We examined CA1 spiking patterns after learning and quantified replay and reactivation as we did with our experimental data. In the Stim OFF condition, synapses between overlapping place cells were potentiated by STDP (fig. S14). Place cell sequences experienced in the learning phase were spontaneously replayed in the following offline epoch (Fig. 6, E and F). In the Stim ON condition, disorganized timing within theta cycles disrupted CA3-CA1 STDP, which relies on a consistent timing between pre- and postsynaptic spike pairs (fig. S14). CA3-CA3 STDP was preserved due to place cell coactivity within theta cycles, regardless of their precise temporal ordering (fig. S14). These effects resulted in an impairment of replay in the Stim ON condition (Fig. 6, E and F) but robust reactivation of place cell assemblies in both conditions (Fig. 6, E and G), mirroring our experimental results. The dissociation between reactivation and replay in our model suggests that reactivation and replay are differently mediated by STDP at CA3 and CA1 synapses, providing a plausible circuit-level mechanism for our findings.

Discussion

In this study, we described two complementary hippocampal circuit mechanisms that support the formation of memory associations and the generation of predictive representations of the environment. First, the coactivity of place cell assemblies encoded discrete states in the environment and, with their subsequent reactivation, supported associative memory. Second, temporally compressed hippocampal sequences encoded transitional structures of states in the environment, supporting the formation of a predictive map. Replay of these sequences provided a mechanism to update and exploit this predictive map, but only after intact encoding of transitional structures of task states during learning. Disruption of trajectory-specific theta sequences impaired their subsequent replay but did not affect the reactivation of neuronal assemblies representing those same locations. Reactivation and sequence replay are therefore dissociable neural processes. The dependence of replay on learning environment transitional structures through theta sequences was highly specific for both space and time: Neither disruption of theta sequences for the same trajectory traveled in the opposite direction nor disruption of previously experienced trajectories affected replay. Furthermore, these results indicate that encoding the specific transitions between place cells along behaviorally relevant trajectories, rather than place field formation per se or global theta-timescale dynamics alone, is an instrumental mechanism for replay, explaining and extending previous observations on the relationship between theta population dynamics and replay (65–67). The disruption of temporally compressed hippocampal sequences impaired flexible memory–guided navigation but did not affect the formation and recall of contextual associations.

Our results advance a framework to unify previously disparate views of hippocampal function, including encoding cognitive maps for spatial and episodic memory (68–70), predictive maps for flexible navigation and planning (10, 16, 17), and multimodal memory representations for relational processing (18, 71). We argue that the hippocampal role in encoding episodic memories relies on two complementary mechanisms. First, the synchronous coactivity of cell assemblies binding different features of experience into cohesive representations enables the fast encoding of discrete states in the world and supports associative memory. Second, the formation of a predictive map is supported by internally generated hippocampal sequences, binding discrete successor states into a relational structure. Moreover, our results can account for two independent lines of evidence supporting previous theories of hippocampal predictive coding: predictive sequences and “successor representation” place fields. Our manipulation impaired the development of theta and replay sequences. Previous studies have shown that both theta and replay sequences not only reproduce animal recent experiences but can also construct novel predictive representations. Theta sequences encode trajectories ahead of the animal’s current location and can represent alternative paths at decision points (44–46). Replay sequences can reproduce never-experienced paths (72, 73) and dynamically change to reflect learned task contingencies (11,74–76) or represent available paths not yet taken (77, 78). In both cases, internally generated hippocampal sequences could be conceptualized as a sampling process between a series of possible future states from a probabilistic generative model, and they were both impaired by our manipulation. In addition, experience-dependent backward expansion and deformation around obstacles of place fields are believed to reflect the encoding of a predictive map over the locations the animal expects to occupy in the near future (17, 52). These features were disrupted by our manipulation, in contrast to place field formation and stability, which may be supported by different plasticity mechanisms (79). Together, these effects of our manipulation suggest that all these “generative” features of hippocampal representations are linked by common circuit mechanisms.

Although numerous processes could contribute to the generation of replay sequences (80–83), our results suggest that initial theta sequence–mediated STDP is necessary for the replay of newly learned spatial trajectories but not for memory reactivation. These results suggest a hierarchical organization of hippocampal assembly and sequence dynamics. Previous work investigating the postnatal development of hippocampal dynamics supports this dissociation. Synchronous cell assemblies are already present around postnatal day 17 in rats, with their reactivation in SWRs reflecting encoding of individual locations on a maze (84). However, theta sequences and replay encoding animal spatial trajectories appear only after postnatal day 21 (66, 84).

The present findings agree with previous studies that investigated the contribution of the temporal coordinatization of hippocampal spike timing to memory. Pharmacological disruption of place cell theta rhythmicity and coordination, while preserving their rate coding properties, impaired spatial memory (85, 86). In addition, disruption of the behavioral timescale (on the order of seconds) sequential structure of CA1 firing responses during temporal delays also impaired memory (31, 87). These studies highlight the importance of the precise temporal coordination of hippocampal spike timing for memory.

Additional research is still needed to elucidate the precise contribution of different input pathways and cell types in the entorhinal-hippocampal network to temporal coding and sequence generation. MEC inputs reach CA1 via direct projections from layer III and also indirectly via layer II inputs to the dentate gyrus, CA3, and CA2 (88). Our manipulation was not restricted to either of these input pathways and therefore cannot precisely determine their contributions to the generation of CA1 sequences. Furthermore, a small subset of MEC GABAergic cells send direct long-range projections to CA1 (89). It is possible that our manipulation also affected these projections; however, their sparsity and the fact that the stronger GABAergic projections to CA1 arise from the lateral rather than the medial entorhinal cortex (90) limit their potential contribution to the results described here.

Overall, this study suggests the coexistence of complementary associative and predictive codes in the hippocampus. This dual code could account for the wide range of behavioral functions attributed to this brain structure in learning, memory, navigation, and planning.

Materials and methods

Surgical procedures

Rats (adult male Long-Evans, 300 to 500 g, 3 to 6 months old) were kept in the vivarium on a 12 hour light/dark cycle and were housed two per cage before surgery and individually after it. All experiments conformed to guidelines established by the National Institutes of Health and have been approved by the Cornell University Institutional Animal Care and Use Committee.

Silicon probe implantation was performed as described previously (41, 51, 91). Animals were anesthetized with isoflurane anesthesia and craniotomies were carried out under stereotaxic guidance. Silicon probes (NeuroNexus, Cambridge Neurotech, or Diagnostic Biosignals) were mounted on custom-made 3D-printed microdrives to allow precise adjustment of the vertical position of sites after implantation. The probes were inserted above the target region. Craniotomies were sealed with sterile wax. Two stainless steel screws were placed bilaterally over the cerebellum to serve as ground and reference electrodes. Several additional screws were driven into the skull and covered with dental cement to strengthen the implant. Finally, a copper mesh mounted on a 3D-printed resin base was attached to the skull with dental cement and connected to the ground screws to act as a Faraday cage, attenuating the contamination of the recordings by environmental electric noise and protecting the headgear. Three doses of analgesic were administered, with the first dose administered prior to surgery in order to cover 72 hours total. After post-surgery recovery, probes were moved gradually in 50- to 150-μm steps per day until the desired position was reached. Hippocampal layers were identified physiologically by unit activity and characteristic local field potential (LFP) patterns (34, 92).

A variety of different silicon probes were implanted in the dorsal hippocampus [−4.0 to 4.5 mm anteroposterior (AP) from Bregma and 2.6 mm from midline (ML)]. Data from some of the animals included in this study have also been included in a previous study, and surgical procedures have been described in more detail there (41).

For optogenetic experiments, rats were also implanted with custom-made optic fiber arrays (three 200-μm core multimode fibers each, ~500 μm apart, connected to a single 2.5-mm steel ferrule; Doric Lenses) in both hemispheres over the MEC (−7.7/−8.4/−9.1 AP; ± 4.6 ML and 4.7/ 4.3/3.2 mm from the surface of the brain, for each fiber respectively).

Optogenetic experiments

For optogenetic experiments, rats were injected with custom-prepared AAV5-mDlx-hChR2(H134R)-mCherry from AddGene [plasmids were a gift from Dr. Gord Fishell (40)]. Three injections per hemisphere were performed along the dorsoventral MEC as follows: (i) −7.7 AP, ±4.6 ML, 4.7 mm depth, 200 nl; (ii) −8.4 AP, ±4.6 ML, 4.3 mm depth, 400 nl; (iii) −9.1 AP, ±4.6 ML, 3.2 depth, 700 nl. After injection, craniotomies were sealed, and animals recovered in the vivarium for 3 weeks. After this period, a second surgical procedure for implanting optic fibers and electrodes was performed, as described above. Optic fiber arrays were implanted in the same craniotomies performed previously for virus injection. For optogenetic stimulation, fiber array ferrules were connected with mating sleeves to 450-nm blue light-emitting laser diodes coupled to 2.5mm steel ferrules (PL-450, Osram).

Optogenetic perturbations were performed by delivering blue light, modulated with a positive 53 Hz current sinusoid using an isolated current driver (Thorlabs). Light intensity was calibrated for each animal during home cage recordings by analyzing the suppression of LFP gamma power in the stratum lacunosum-moleculare during stimulation. A minimum and maximum power of 3 and 6 mW, respectively, was used. In the linear maze task, light stimulation was triggered when the animal crossed an infrared sensor near the end of the track (but before the reward port located at the very end of it) and stopped when it crossed a similar sensor at the other end, resulting in stimulation only during running periods. In the cheeseboard maze and CPP tasks, the same optogenetic stimulation was applied during all running periods in the maze during learning trials.

Behavioral and electrophysiological recordings

After surgery, animals were handled daily and accommodated to the experimenter, recording room, and cables for 1 week before the start of the experiments. Before the start of the behavioral experiment, the animals were water-restricted. Electrophysiological recordings were conducted using Intan RHD2000 interface board or Recording Controller (IntanTech) and 64-channel digital headstages (IntanTech or Diagnostic Biochips), sampled at 20 kHz. For all behavior tasks, animal position was recorded with an overhead camera (Basler) and tracked with DeepLabCut (93) and custom codes.

Linear track task

In the linear track, rats were trained to run back and forth to collect small sugar water rewards at both ends. Animals typically performed between 30 and 80 trials per day. The session was terminated when the animal was satiated, typically alter 40 min. The linear track was placed 1 meter above the floor and was 300 cm long and 7 cm wide with 5- to 10-cm-high walls. Water rewards were automatically delivered in reward wells at both ends of the track. Baseline and post-task sleep were recorded in the home cage before and after the task, respectively.

Cheeseboard maze task

The cheeseboard maze was a circular platform (120 cm diameter), where the animals learned to find three goal wells that contained water rewards. A trial was completed once the animal had retrieved all rewards and returned to the start box to collect an additional food pellet reward. The locations of the goal wells changed daily but were fixed during a given session. This strategy required the animals to update their memory for the new goal locations in an otherwise familiar environment during each session. Note that between trials, there was always a delay of ~30 s. If the rat could not find all three rewards within 2 min, the trial was terminated, and the animal was returned to the start box. A pre-task test session of five trials (with the same configuration as the previous day) was run every day to assess whether the animal remembered the previous day’s positions, followed by a 2-hour sleep session. Next, a 30-trial learning session was conducted (with or without light stimulation). After a 2-hour sleep session after the learning trials, a five-trial post-task test session (with the newly learned reward configuration) was also conducted to examine whether the animal remembered the newly learned locations. Learning performance was evaluated as the distance traveled from the start box to collect the three rewards and divided by the optimal trajectory (shortest possible path). A value of 1 then indicates an optimal path taken by the animal. Performance in the post-task test sessions was computed in the same way (Fig. 5H), and additionally it was compared directly with the learning performance on the final learning trial (fig. S10A). An additional measure of performance was computed as the proportion of exploration time spent within 5 cm the correct wells (fig. S10B). Stim OFF and Stim ON sessions were alternated in a counterbalanced manner across animals. The inclusion of data for the analysis required that the animal be pretrained for a week in this task.

Conditioned place preference task

The CPP task was performed in the same maze as in the cheeseboard maze task but separated into two compartments by a 30-cm-high wall in the midline. Animals had free access to both compartments connected by a common corridor at one end of the maze (Fig. 5I). The task included three stages spanning 3 days: baseline, pairing, and testing. For the baseline stage on day 1, animals were allowed to freely explore the two compartments for 15 min with no reward. A baseline place preference was then measured as the difference in active exploratory time spent in the two compartments. The compartment that animals explored less was selected as the rewarded side for the subsequent pairing sessions. Pairing sessions included one session after the baseline session on day 1, two sessions on day 2, and one session before the testing session (see below) on day 3. During the pairing sessions, animals explored the maze for 20 min, with hidden water reward delivered at random locations on the rewarded side. On day 3, after the final pairing session, a testing session was performed, during which animals again explored the maze without reward for 15 min and the place preference was measured as was done during the baseline session. Optogenetic stimulation was delivered when animals actively explored the maze during pairing sessions. Each CPP session was flanked by sleep recordings (around 2 hours) in the home cage. Learning performance of the CPP task was measured by comparing the place preference during the baseline versus the testing session (Fig. 5L).

Tissue processing and immunohistochemistry

After the termination of the experiments, animals were deeply anesthetized and perfused transcardially, first with 0.9% saline solution followed by 4% paraformaldehyde solution. The brains were sectioned into 70-μm-thick slices (Leica Vibratome). The sections were washed and mounted on glass slides with a fluorescence medium [Fluoroshield with DAPI (4′,6-diamidino-2-phenylindole), product no. F6057, Sigma, USA]. A confocal microscope (Zeiss LSM 800) was used to obtain high-quality photos.

Computational model

Architecture

We built a simplified network model consisting of 1250 pyramidal cells (PYR) and 100 inhibitory interneurons (INT) in area CA3 and 1250 pyramidal cells and 100 inhibitory interneurons in area CA1 using the Brian2 simulation environment (94). Each neuron was modeled as an adaptive exponential leaky integrate-and-fire unit with cellular adaptation (61). Briefly,

$$C_{\text{m}}\frac{dV(t)}{dt}=-(g_{\text{L}}\left(V(t)-V_{\text{rest}}\right)-g_{\text{L}}\Delta T\exp \left(\frac{V(t)-\theta }{\Delta T}\right)+I_{\text{syn}}(t)+w(t))$$

where $V\left(t\right)$ is the membrane potential, $C_m$ is the membrane capacitance, $g_{\text{L}}$ is the leak conductance, $V_{\mathrm{rest}}$ is the reversal potential of the linear leak current, $\theta$ is the spike threshold, $\Delta T$ is the threshold sharpness, $I_{syn}$ is the synaptic current, and $w\left(t\right)$ is the adaptation current, described by

$${\tau }_w\frac{dw(t)}{dt}=a\left(V(t)-V_{\text{rest}}\right)-w(t)$$

where the parameter a describes the strength of the subthreshold adaptation. The synaptic current $I_{\mathrm{syn}}$ was computed as

$$I_{\text{syn}}(t)=g_{\text{AMPA}}(t)\left(V(t)-E_{\text{exc}}\right)+g_{\text{GABA}}(t)\left(V(t)-E_{\text{inh}}\right)$$

where $E_{\mathrm{exc}}=0\text{mV}$ and $E_{\text{inh}}=-70\text{mV}$ are the reversal potentials of excitatory and inhibitory currents, respectively. Synapses were modeled as conductances with biexponential kinetics (61).

Synapses

Within each area, $\mathrm{PYR}\to \mathrm{INT}$ connectivity occurred at 10% probability, and $\mathrm{INT}\to \mathrm{INT}$ and $\mathrm{INT}\to \mathrm{PYR}$ connectivity occurred at 25% probability. Whereas $\mathrm{PYR}\to \mathrm{PYR}$ connectivity was absent from CA1, CA3 PYR cells projected at 10% probability to PYR from both CA3 and CA1, modeling recurrent CA3 connectivity and CA3 inputs into CA1, respectively. Synaptic parameters were used as previously reported (61), with the modification that synaptic weights were initialized to follow a lognormal distribution $\exp \left(N\right(0,1\left)\right)\times w_{\text{init}}$, where $w_{\text{init}}^{\mathrm{C}\mathrm{A}3\to \mathrm{C}\mathrm{A}3}=0.3$ and where $w_{\text{init}}^{\mathrm{C}\mathrm{A}3\to \mathrm{C}\mathrm{A}1}=0.7$. To simulate learning as a result of the activity during exploration, STDP was modeled for $\mathrm{PYR}\to \mathrm{PYR}$ synapses alone, where synaptic weights are updated according to an additive pair-based learning rule as follows

$$\Delta w_{+}=A_{+}\text{exp}\left(-\frac{\Delta t}{{\tau }_{+}}\right)\text{at}{t}_{\text{post}}\text{if}{t}_{\text{pre}}<t_{\text{post}}$$

$$\Delta w_{-}=A_{-}\text{exp}\left(-\frac{\Delta t}{{\tau }_{-}}\right)\text{at}{t}_{\text{pre}}\text{if}{t}_{\text{pre}}>t_{\text{post}}$$

$\mathrm{C}\mathrm{A}3\to \mathrm{C}\mathrm{A}3$ STDP followed a symmetric rule, where $A_{+}=A_{-}=80\mathrm{p}\mathrm{A}$, and ${\tau }_{+}={\tau }_{-}=62.5\mathrm{m}\mathrm{s}$, while $\mathrm{C}\mathrm{A}1\to \mathrm{C}\mathrm{A}3$ STDP followed an asymmetric rule, where $A_{+}=800\mathrm{p}\mathrm{A},A_{-}=-A_{+}\times 0.4,{\tau }_{+}=$ $20\mathrm{m}\mathrm{s}$, and ${\tau }_{-}=40\mathrm{m}\mathrm{s}$. All weights were cropped at $w_{\mathrm{m}\mathrm{a}\mathrm{x}}=40\mathrm{n}\mathrm{S}$.

Exploration phase

Spike trains of PYR cells during exploration were generated as previously described (61). Briefly, 10% of all pyramidal cells in each region were designated as place cells, and place fields were randomly distributed along a 3-m-long simulated linear track. Exploration was simulated as 10 min of exploration time while the rat ran along the linear track at 50 cm/s. Silent cells (nonplace cells) fired at 0.01 Hz, and place cell spikes were sampled from a Poisson process at 20 Hz, with the sampling procedure ensuring an inhomogeneous Poisson process with a time-dependent rate $\lambda \left(t\right)$, which was the product of a Gaussian tuning curve (representing the neuron’s place field) with width $\sigma =7\mathrm{c}\mathrm{m}$ (yielding l = 30 cm place fields) and a theta component. The theta component was either a phase precession component to simulate the sequences of the Stim OFF condition or a phase-locking component to simulate the lack of sequences but preserved theta-cycle coactivity in the Stim ON condition. The Stim OFF theta component was

$${\theta }^{\text{OFF}}(t)=\text{cos}\left(2\pi f_{\theta }t+\frac{\pi }{2\pi \cdot Q}\left(x(t)-x^i\right)\right)$$

where Q represents the proportion of the linear track that the place field spans and takes numeric value of 30-cm field over 300-cm linear track or 0.1, and $x^i$ is the position of the place field of cell i.

The Stim ON theta component was a phase-locking component designed to yield the same phase-locking value as the other condition’s theta precessing component but abolishing sequential order of spikes

$${\theta }^{\text{ON}}(t)=\text{cos}\left(2\pi f_{\theta }t+\frac{\pi }{2\pi \cdot Q}N\left(\frac{\pi }{2},\frac{\sigma }{l}\right)\right)$$

where l is the length of the track (3 m), and $N\left(\frac{\pi }{2},\sigma \right)$ is a normal distribution with mean $\frac{\pi }{2}$ and standard deviation $\frac{\sigma }{l}$.

Offline phase

Before and alter exploration-triggered STDP, the network was simulated using Brian2 to respectively model pre (baseline) and post “sleep” sessions. To drive the network, each CA3 pyramidal cell received random inputs in the form of uncorrelated Poisson spike trains with a pooled mean rate of 15 Hz. Under these conditions, the network spontaneously generated population burst events (akin to SWRs).

Analysis

All the modeling steps described above were performed n =10 times with different randomly generated initial conditions determining place field locations, initial weights, etc. This resulted in n = 10 simulated sessions, in which theta sequences, replay, and reactivation were analyzed applying the same methodology and parameters as we did to analyze experimental data described above.

Spike sorting and unit classification

Spike sorting was performed semiautomatically with KiloSort (95) (https://github.com/cortex-lab/; KiloSort), followed by manual curation using the software Phy (https://github.com/cortex-lab/phy) and custom designed plug-ins (https://github.com/petersenpeter/phy-plugins) to obtain well-isolated single units. Cluster quality was assessed by manual inspection of waveforms and autocorrelograms, and by the isolation distance metric. Multiunit, noise clusters, or poorly isolated units were discarded for analysis. Well-isolated units were classified into putative cell types using the Matlab package CellExplorer (96) (https://github.com/petersenpeter/CellExplorer). Spiking characteristics, including the autocorrelograms, spike waveforms, and putative monosynaptic connections derived from short-term cross-correlograms, were used to select and characterize well-isolated units. Three cell types were assigned: putative pyramidal cells, narrow waveform interneurons, and wide waveform interneurons. Two key metrics used for this separation were burst index and trough-to-peak latency. Burst index was determined by calculating the average number of spikes in the 3- to 5-ms bins of the spike autocorrelogram divided by the average number of spikes in the 200- to 300-ms bins. To calculate the trough-to-peak latency, the average waveforms were taken from the recording site with the maximum amplitude for the averaged waveforms of a given unit.

Detection of brain states

State scoring was performed as previously described (41, 51). Briefly, the LFP was extracted from wide-band data by lowpass filtering (sync filter with a 450 Hz cutoff band) and downsampling to 1250 Hz. Broadband LFP, narrow-band theta frequency LFP, and estimated electromyogram (EMG) were used for state scoring. Spectrograms were computed from broadband LFP with a fast Fourier transform in 10-s sliding windows (at 1 s), and a principal components analysis was computed after a Z-transform. The first principal component reflected power in the low (<20 Hz) frequency range, with oppositely weighted power at higher (>32 Hz) frequencies. Theta dominance was quantified as the ratio of powers in the 5 to 10 Hz and 2 to 16 Hz frequency bands. EMG was estimated as the zero-lag correlation between filtered (300 to 600 Hz) signals across recording sites (55). Soft sticky thresholds on these metrics were used to identify states. High LFP principal component 1 and the low EMG were considered non-REM, the high theta and low EMG were considered REM, and the remaining data were taken to reflect the waking state.

For analysis of neural activity during active behavior (e.g., place cell and theta sequence analysis), only periods in which the animals run faster than 5 cm/s were included.

SWR detection

To detect SWRs, one channel around the CA1 pyramidal layer was chosen for the ripple detection, and one channel from CA1 stratum radiatum was chosen for sharp wave detection. The difference between the two channels was used as the basis for SWR detection. This difference signal was filtered with a low-pass filter at 55 Hz, and then local minima were detected as candidate events. The corresponding ripple power (amplitude of the difference signal in the bandpass 80 to 250 Hz) for each candidate event was recorded. A true event was considered when both a sharp wave and ripple oscillation were detected in the same window. K-means clustering was used to define clustering of SWR from non-SWR events, and manual curation was used to better define the boundary and remove outliers. The events were then expanded until the (nonclipped) ripple power fell below 1 SD; short events (<15 ms) and longer events (>400 ms) were discarded.

To refine the detection of SWR start and end points for reactivation and replay analyses (in order to avoid including empty bins), we detected population burst events as periods when the instantaneous population firing rate (binned in 1-ms bins and smoothed with a Gaussian kernel with 10-ms width) reached a peak of >2 SD and remained greater than the mean. The SWR start and end time points were set as the start and end time points of the population burst within the respective SWR, and SWRs without population bursts were discarded.

Place cell analysis

Spiking data and the tracked animal’s position were binned into 3-cm-wide segments of the camera field projected onto the maze floor, generating raw maps of spike counts and occupancy. A Gaussian kernel (SD = 3 cm) was applied to both raw maps of spike and occupancy, and a smoothed rate map was constructed by dividing the spike map by the occupancy map. Independent rate maps were constructed for the different running directions in the mazes. Only periods in which the animal velocity was >4 cm/s were included. A place field was defined as a continuous region of at least 15 cm², where the mean firing rate was >10% of the peak rate in the maze, and the peak firing rate was >3Hz.

Spatial information (SI) for individual place cells was obtained from the linearized rate maps (97)

$$SI=\sum _{i=1}^N{p}_i\frac{{\lambda }_i}{\lambda }{\text{log}}_2\frac{{\lambda }_i}{\lambda }$$

where N is the total number of spatial bins, $p_i$ is the probability of occupancy, and ${\lambda }_i$ is the firing rate in the ith spatial bin, and $\lambda$ the average firing rate of the cell. To measure the experience-dependent change of SI across laps in each condition, the mean and standard deviation of SI across all cells within a condition group were calculated, and the SI was then z-scored for that condition (Fig. 3B).

To identify cells that discriminate between the two sides of the CPP task, we constructed a vector for each cell containing the mean firing rate for every movement interval that the animal spent in each of the two halves. We then performed a one-tailed Wilcoxon rank sum test between the firing vectors in the two halves, and cells for which this comparison was significant were identified as cells with firing specific to that respective half. To quantify discrimination in post-task sleep, pairwise posttask sleep correlations ($C_{\mathrm{P}\mathrm{O}\mathrm{S}\mathrm{T}}$, see below) were compared between pairs of cells specific for the same half versus pairs of cells that were specific for opposite halves of the environment.

Population vector analysis

To estimate the stability of the population code in the Stim OFF and Stim ON conditions, we performed population vector analysis as described previously (98). Briefly, we measured the correlation between the population firing curves in even and in odd trials for each running direction, and we compared this value with the value obtained in surrogate data, in which cell identity was shuffled across even and odd trials.

In addition, we performed a cross-correlation between the population firing curves in even and odd trials separately for each pair of spatial bins (fig. S3, A and B). To estimate representation stability, we computed the “error” defined as the distance between the peak correlation for each spatial bin (each of the columns of the matrix) to the diagonal. To statistically test the directionality of the hippocampal code, we compared the representation stability within a given direction (even versus odd trajectories in the same direction) to the stability of the representation between the two directions of movement (even trajectories in one direction versus odd trajectories in the other direction).

COM shift

To measure PF shifting across laps (Fig. 3D), we used place cells that had PFs on the linear track, and calculated the center-of-mass (COM) of PFs for each lap $n\left({\mathrm{C}\mathrm{O}\mathrm{M}}_n\right)$ (99)

$${\text{COM}}_n=\frac{{\sum }_{i}F{R}_i{x}_i}{{\sum }_{i}F{R}_i}$$

where $F{R}_i$ is the firing rate in the spatial bin i, and $x_i$ is the distance of the spatial bin i from the start of the running trajectory. For each lap, COM shift was then measured as the difference between the first lap and the current lap. To prevent any edge effect, only PFs with a peak location outside the two ends of the track (i.e., defined by 20% of the track length) were included. For place cells with multiple PFs, only the primary PF (with the maximal peak rate) was included.

Place field eccentricity

To calculate the eccentricity of 2D place fields in the CPP task (fig. S12), we first defined the PF boundary on the 2D rate maps. PF was first defined as the area with firing rates larger than 40% of the peak rate. This area was further refined with a series of morphological operations: opening, closing, and infill, with Matlab functions imopen, imclose, and imfill, respectively. PF boundary was then detected on the resulting binarized image using the Matlab function bwboundaries. The eccentricity of the detected PF was measured using the Matlab function regionprops. For place cells with multiple PFs, only the primary PF (with the maximal peak rate located within the PF boundary with the maximal size) was included. The boundary and nonboundary cells were defined as the cells with the peak of the primary PF located within and outside 15 cm of the wall, respectively.

Phase precession

Phase precession analysis was performed as previously described (34, 100). Circular-linear regression between relative position within the place field and theta phase was applied to calculate the phase-precession slope and correlation strength (101). The slope and correlation strength (r²) of phase precession were derived from this circular-linear regression analysis.

Theta compression

Theta compression analysis was performed as described previously (102), independently for the Stim OFF and the Stim ON direction. Briefly, for each pair of overlapping place cells, we computed (i) the distance between their place field peaks and (ii) the theta time lag. To qualify pairs with a significant theta time lag, we computed a coarse cross-correlogram for each cell pair using for durations ±1 s using 5-ms bins. Cell pairs with a peak in this coarse correlogram within ±100 ms with at least five spikes in the peak bin were deemed significant, and other cell pairs were excluded from this analysis. To compute the theta time lag for the selected cell pairs, cross-correlograms were restricted to in-field spikes during running periods of the respective direction (Stim OFF versus Stim ON) using 1-ms bins, and each cross-correlogram was filtered with a bandpass filter between 2 and 30 Hz. The time of the cross-correlogram peak was defined as the theta time lag of the pair of place cells. Theta compression slopes were computed by performing linear regression between the distance between the place field peaks and the theta time lags.

Linearizing positions on the cheeseboard maze

Positions on the cheeseboard maze were linearized along an optimal trajectory, connecting the start box with the three rewarded locations for that session (with the closest reward locations connecting directly to the start box). The animal’s linearized position was defined as the relative position along the optimal trajectory closest to the animal’s current position. To decode animal position from neuronal activity (for theta sequence and replay analyses), we only retained periods when this linearized position described the current animal’s position well, defined as periods in which (i) the error distance between the optimal trajectory and the actual animal position was within 20 cm and (ii) the animal running speed along the optimal trajectory was at least 10 cm/s. To decode replay of familiar routes to previously learned trajectories (fig. S7), we modified the above procedure to define the linearized trajectory: Instead of using the three currently rewarded locations, we used the three rewarded locations from the previous day’s session.

Decoding animal position from neuronal activity

To decode position from place cell activity during both theta states and replay, we used a Bayesian reconstruction approach as described previously (65). Briefly, we computed the average firing rate probability ${\lambda }_i^{\mathrm{O}\mathrm{F}\mathrm{F}}\left(x\right)$ and ${\lambda }_i^{\mathrm{O}\mathrm{N}}\left(x\right)$ for each pyramidal cell i at position x as the normalized firing rate curve (spatial bin size: 1.5 cm) of the cell during running epochs in the OFF and the ON direction, respectively, which constituted the training step in our decoder. To then decode the animal position from the neuronal activity as expressed by the firing rate vector n in a particular window of width $\tau \mathrm{s}$, we estimate the probability $P(x\mid n)$

$$P(x\mid n)=\frac{P(n\mid x)\cdot P(x)}{P(n)}$$

where spikes are assumed to fire as independent Poisson processes

$$P(n\mid x)={\prod }_{i=1}^N\frac{{\left({\lambda }_i(x)\cdot \tau \right)}^{n_i}}{n_i^{!}}{e}^{-{\lambda }_i(x)\cdot \tau }$$

We applied the same procedure to decode linearized positions on the cheeseboard maze, using periods of movement along the linearized trajectory in which the animal stayed within 20 cm of the optimal trajectory to train the decoder.

Theta sequences

Theta reconstruction matrices

To decode the animal position during theta cycles, we trained Bayesian decoders for the OFF and the ON directions as described above and decoded the animal position during running periods in the OFF and the ON direction, respectively, using τ = 20 ms bins with 5-ms sliding window. We then computed theta reconstruction matrices for each theta cycle while the animal was running in the OFF and the ON direction by dividing the cycle in 500 temporal bins and interpolating the respective (OFF or ON) decoded position. The same procedure was applied to construct theta reconstruction matrices for Stim OFF and Stim ON cheese-board sessions using the linearized cheeseboard position during periods of movement along the linearized trajectory and stayed within 20 cm of the optimal trajectory.

Theta cycles

To detect theta cycles, we first detected deep and superficial CA1 sublayers using the depth profile of SWRs as described previously (51) and selected the deep CA1 channel with the highest theta power in the normalized spectrum. Theta cycles were defined as the peaks in the LFP filtered in the theta band during running periods, and cycles shorter than 100 ms or longer than 200 ms were excluded from further analyses. To correct for the phase shift that can occur in different sublayer depth of the theta channel, the final theta cycles were shifted to ensure that the theta peaks were defined as the phase of maximal uncertainty of the theta reconstruction matrices, where uncertainty u was defined as $u=-\underset{x}{\max }\{P(x|n)\}$. Theta peaks correspond 0° (0 rad.) and 360° ($2\pi$ rad.) and troughs at 180° ($\pi$ rad.) and 540° ($3\pi$ rad.) of theta waves.

Theta sequences

To quantify theta sequence, we applied the measures of quadrant scores and weighted correlation on the theta reconstruction matrices for each cycle. To compute the quadrant score, we divided the central region in the theta reconstruction matrix that was within 50 cm of the animal’s current location and within $\frac{1}{2}\pi$ of the theta trough ($\pi$) into four equal quadrants, and computed the ratio between the probability within quadrants II and IV (representing directions consistent with the animal’s running direction) and the probability within quadrants I and III (representing directions incongruent with the animal’s running direction). The weighted correlation measured the correlation between time t and location l weighted by the decoded probability values p within the reconstruction matrix

$$w=\frac{\text{cov}(t,l\mid p)}{\sqrt{\text{cov}(t,t\mid p)\text{cov}(l,l\mid p)}}$$

where

$$\text{cov}(t,l\mid p)=\frac{{\sum }_i{p}_i\left(t_i-m(t\mid p)\right)\left(l_i-m(l\mid p)\right)}{{\sum }_i{p}_i},$$

$$m(t\mid p)=\frac{{\sum }_i{p}_i{t}_i}{{\sum }_i{p}_i},\text{and}m(l\mid p)=\frac{{\sum }_i{p}_i{l}_i}{{\sum }_i{p}_i}.$$

The look-ahead index of theta sequences is calculated as in previous reports (46). In brief, we recomputed the reconstruction matrix quadrants, this time extending the reach to use all decoded probabilities within 1 m of the animal’s current location. The look-ahead index was measured by comparing the probabilities in the quadrants ahead (quadrant IV, future) and behind (quadrant I, past) in the second half of theta phases, as (IV − I)/(IV + I).

Replay analysis

Candidate replay events

We first detected periods of elevated pyramidal cell population activity as defining periods when the instantaneous firing rate (1-ms bins, smoothed with a Gaussian kernel of width 10 ms) was greater than the mean and reached a peak of >2 SD above the mean during the session. Candidate events were between 100 and 500 ms in duration, and they each overlapped with an independently detected SWR; otherwise they were excluded from further analyses.

Quantifying replay

We decoded the animal position for the OFF and the ON direction during each candidate replay event using non-overlapping τ = 20ms bins (but see fig. S7A for replay results with τ = 40 ms and τ = 60 ms). OFF and ON direction replay were scored independently. To assess replay quality, we computed trajectory scores of the reconstruction matrices (103). Briefly, each reconstruction matrix was fitted with a line (of slope a and intercept b) maximizing the average likelihood R that the animal is located within a distance d (set to 22.5 cm) of the linear trajectory defined by the slope a and intercept b

$$R(v,\rho )=\frac{1}{m}\sum _{k=0}^{m-1}P(|pos-(\rho -v\cdot k\cdot \Delta \xi |\le d))$$

The score of each event was normalized by subtracting the mean and dividing by the standard deviation of a distribution of 500 shuffled scores obtained by independently shifting each of the columns of the event’s reconstruction matrix along the spatial dimension by a random distance. An event with a score exceeding the scores of 95% of its shuffled scores was considered significant. To quantify replay, we normalized the proportion of significant events during awake behavior or post-task sleep by subtracting the mean proportion of significant events in pre-task sleep.

In a control analysis, we corrected for the differences in decoding quality between Stim OFF and Stim ON trajectories (fig. S7C). For this purpose, downsampled units before decoding the Stim OFF trajectories by progressively dropping units until the average decoded error in Stim OFF trajectories was larger than the average decoded error in Stim ON trajectories, and we recomputed replay events for Stim OFF trajectories using this more limited sample (fig. S7C).

We performed an additional quantification of replay, where for each replay event we computed the weighted correlation and the jump distance. The weighted correlation measures the correlation coefficient between time and decoded space, and jump distance was defined as the maximum distance between the peak decoded positions in two successive time bins of the same event. Trajectory events were defined as the events with high weighted correlation (>0.6) and low jump distance (<75 cm), and to assess whether the number of trajectory events exceeded chance, we compared the number trajectory events in the recorded data with the number of trajectory events in surrogate data where cell identities were shuffled 500 times. This comparison yielded a P value (the proportion of shuffled datasets with as many or more trajectory events than those observed in the original dataset), and we generated a significance matrix of P values for progressively stricter weighted correlation thresholds (0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95) and jump distance thresholds (75 cm, 62.5 cm, 50 cm, 37.5 cm, 25 cm, 12.5 cm).

Pairwise bias correlations

The above replay analyses test for the replay of stereotypical trajectories and are not directly applicable to the trajectory-free behavior in the CPP task. To assess whether the order of unit spiking in behavior is preserved in these sessions, we computed the similarity between behavioral sequences and SWR sequences using a pairwise bias correlation method (65). Briefly, we computed a bias matrix $B_k$ for each sequence k

$$B_k=\frac{n_k(i,j)}{n_k(i)\cdot n_k(j)}$$

where $n_k\left(i\right)$ is the number of spikes emitted by neuron $i$ in the kth sequence, and $n_k(i,j)$ is the number of times neuron $i$ spiked before neuron $j$ in the kth sequence (see fig. S12F for an example). $B_k(i,j)$ therefore reflects the bias of $i$ to spike before $j$ in the kth sequence, taking values between 0 ($i$ never precedes $j$) and 1 ($i$ always precedes $j$), with 0.5 representing no bias ($i$ precedes $j$ half of the time). The correlation between two sequences can be estimated as the cosine between their skew-bias matrices as each bias matrix is unwrapped into a vector $2B_k-2$ (this normalization is to achieve a range of values between −1 and 1, assuring that two mirror sequences would have opposite signs with vectors pointing in opposite directions). The activity of cells that are not common to the two sequences is ignored.

To test whether the order of firing in behavior was preserved in post-task sleep, we computed the mean bias matrix of all sequences taking place in theta cycles during the task in a given recording session. We computed the correlation (cosine) between this bias matrix and each of the bias matrices describing sequences in post-task sleep SWRs. We compared this correlation with a shuffled distribution obtained by recomputing the correlation after shuffling the spikes sequence n = 100 times and deemed as significant those sequences with correlations whose absolute value exceeded 5% of the shuffled distribution. We normalized the proportion of significant events by subtracting the mean proportion of significant events in pre-task sleep.

Coactivity and reactivation analysis

Cofiring

Each spike train was binned in individual theta cycles, and the cofiring of a pair of cells was defined as the Pearson correlation coefficient of the binned firing rates of the two cells across all theta cycles in the recorded session. The matrix of Pearson correlation coefficients was called the cofiring matrix C.

Explained variance

Explained variance (EV) was quantified as previously described (104). Briefly, for each session, we computed the proportion of the variance in the population spiking activity in post-task sleep that is explained by task-related activity, after taking into account correlations preexisting in sleep before the experience

$$EV={\left(\frac{r_{C,C_{\text{POST}}}-r_{C,C_{\text{PRE}}}{r}_{C_{\text{POST}},C_{\text{PRE}}}}{\sqrt{\left(1-r_{C,C_{\text{PRE}}}^2\right)\left(1-r_{C_{\text{POST}},C_{\text{PRE}}}^2\right)}}\right)}^2$$

where $C,C_{\mathrm{P}\mathrm{R}\mathrm{E}}$, and $C_{\mathrm{P}\mathrm{O}\mathrm{S}\mathrm{T}}$ refer to the cofiring matrix and the correlation matrices across SWRs in pre- and post-task sleep, respectively, and $r_{A,B}$ describes the correlation coefficient between the pairwise correlation matrices A and B. EV was computed for each recorded session separately, and it was compared with the control value of reverse explained variance (REV) obtained by recomputing EV after swapping $C_{\text{PRE}}$ and $C_{\text{POST}}$.

Pairwise reactivation

For the pairwise reactivation analyses, we used linear regression between $C_{\mathrm{P}\mathrm{O}\mathrm{S}\mathrm{T}}$ and $C_{\mathrm{P}\mathrm{R}\mathrm{E}}$ to remove the portion of the variance in $C_{\mathrm{P}\mathrm{O}\mathrm{S}\mathrm{T}}$ that can be explained by preexisting patterns, and we correlated the resultant residuals $C_{\text{RESIDUAL}}$ with C (105).

For the CPP reactivation analysis, we identified cells that had a preference for each of the two sides of the maze by computing each cell’s firing rate for every movement period that the animal spent moving in each of the two sides of the maze. Cells with a significant preference (Wilcoxon rank sum test, alpha α = 0.05) were divided according to the sign of their preference between rewarded-side responsive cells and unrewarded-side responsive cells. We then compared $C_{\text{RESIDUAL}}$ (see above) in pairs of rewarded-side responsive cells versus pairs of unrewarded-side responsive cells.

Cell assembly analyses

For detecting cell assembly patterns, we used an unsupervised statistical framework based on a hybrid principal components analysis (PCA) followed by independent component analysis (ICA) as previously reported (49, 106–108). In brief, spike trains of each neuron were binned in 25-ms intervals for the whole session (including only task periods during movement), the matrix of firing correlation coefficients for all pairs of neurons were constructed. Next, we calculated the number of assemblies on the basis of those principal components whose eigenvalues exceeded the threshold for random firing correlations (using the Marchenko-Pastur law). This method provides a number of significant patterns smaller than the number of neurons. Each of these patterns explained more variance of the spike train correlation matrix than other patterns that would result from independently firing neurons. Independent component analysis (fast-ICA algorithm) was then used to determine for each assembly (component) the vector of weights with which each neuron’s firing contributes to that assembly. The strength of each assembly i’s activation for a given time bin k was computed as follows

$$S_{ik}=Z_k^{T}P{Z}_k$$

where Z is the population activity matrix of the z-scored firing rate of each unit, and P is the outer product of the component i’s weights, in which the diagonal has been set to zero so that isolated spikes from individual units do not contribute to S.

Most of the detected assembly patterns consisted of a few neurons with high weights and a large group of neurons with weights around zero. Assembly members were thus considered those cells whose weight exceeded the mean weight of the assembly by two standard deviations (107).

To produce the assembly activity profiles in fig. S9B, we took the assembly activation strength during the last hour of cumulative baseline sleep and the first hour of cumulative post-task sleep, excluding periods outside of non-REM sleep. During the task, we took the assembly activation strength during running in Stim OFF and Stim ON trajectories separately. Because the exploration time is variable between sessions, instead of absolute elapsed time, we divided the Stim OFF and Stim ON exploration time into quantiles.

Assembly activation events were detected as peaks in the assembly activation strength exceeding a value of 5 (109). The point process of assembly activation events during behavior in the task was used to compute the spatial information content of assembly activity in fig. S4G. The order of assembly activation events in SWRs was analyzed in fig. S9E as follows. For each SWR in which at least three assemblies were active, we correlated the timing of assembly activations within an event to the respective positions (that is, the location of peak activity for a given assembly). We took the absolute value of the Spearman’s rank-order correlation coefficient $\rho$ to account for reverse replay. To correct for coefficient variation with the number of assemblies (e.g., fewer points yield higher correlation coefficients) and the day of the recording, we subtracted from each coefficient $\rho$ a baseline value ${{\rho }_0}^n$ defined as the mean $\rho$ of SWRs recorded pre-task sleep of the same session with a matching number n of assembly activations.

Spectral analysis, cross-frequency coupling, and spike-LFP coupling

To obtain the phase of the theta rhythm, one LFP channel was selected as explained above. LFP was bandpass-filtered in the range of 5 to 15 Hz. Theta phase was then computed using the Hilbert transform of the filtered LFP.

Cross-frequency coupling

To perform spectral analysis at a high resolution in time and frequency, the complex wavelet transform (CWT) of the LFP (or ICs) was calculated using complex Morlet wavelets. Wavelets were calculated using a logarithmically spaced frequency vector in the band of interest (25 to 200 Hz). Phase-amplitude cross-frequency coupling for a given LFP recording was assessed using the modulation index measure (MI) (110). Phase time-series were binned into phase intervals and the mean wavelet amplitude was calculated for each of them. The MI was obtained by measuring the divergence of the observed amplitude distribution from the uniform distribution. The statistical significance of the MI values (P value) was assessed by a surrogate analysis (n = 1000 surrogates) with random shifts between the phase and amplitude time series. For the presented plots, grand averages were calculated as the mean across all animals, unless otherwise indicated, and MI reported were significant [P < 0.01 compared with surrogate distribution (34, 55)].

Spike-LFP coupling

The phase-locking of spikes to LFP features at each frequency was measured for individual units using the wavelet phase from 25 to 200 Hz (30 logarithmically spaced wavelet scales) at the time of each spike (34, 55). Only neurons that fired at least 100 spikes during the selected task intervals were included in the analysis. Reference LFP was taken 200 to 400 μm away from the electrode, where the unit was recorded to minimize spike energy leakage into the LFP. Modulation indices were calculated using the mean resultant length of the phases, and significance was estimated using the Rayleigh test for nonuniformity (P < 0.05) using circular statistics. Preferred frequency of modulation was determined as the largest mean vector length of each significantly modulated neuron. The mean angle of the phases for a given neuron’s spikes was taken as the preferred phase.

Independent component and current source density analysis of LFPs

To separate the different sources that contribute to the LFP mixed signal, we used an approach based on independent component analysis (ICA) that has been described and validated previously for hippocampal recordings (41, 55, 111). Here, we applied ICA to spatially contiguous LFP channels after filtering in the gamma band (25 to 200 Hz). The ICA algorithm (runinca) (112) takes a time series of data with dimension equal to the number of recording sites and returns a time series of the same dimensionality, but rotated so that each dimension represents a different IC. The inverse of the mixing matrix that transforms the LFP data into the ICs gives the channel weight of each component that is captured for each recording site. When projected back to the anatomical location of the recording site, this corresponds to the spatial voltage loadings of each IC (41, 55, 111). Once ICs have been extracted from the raw LFP traces, they can be analyzed as if they were active independently from activities at other locations.

Hierarchical bootstrap

Hierarchical bootstrap (113) was performed to analyze data with hierarchical structure. Briefly, bootstrap datasets were created by resampling with replacement following levels of hierarchical order (in the order of animals followed by sessions). The mean of each resampled bootstrap data was calculated each time, in a total of 1000 resampling times. The final statistics were done on the populations of resampled data from the different experimental conditions. P value indicated the test result that the values of one condition were higher than the values of the other condition after controlling for the other nesting variables.

Statistical analyses

Statistical analyses were performed with MATLAB functions or custom-made scripts. No specific analysis was used to estimate minimal population sample or group size, but the number of animals, sessions, and recorded cells was larger or similar to those used in previous related works (41, 65, 66, 75, 92). The unit of analysis was typically identified as single neurons or assemblies. In a few cases, the unit of analysis was sessions or animals, and this is stated in the text. Unless otherwise noted, nonparametric two-tailed Wilcoxon rank sum (equivalent to Mann-Whitney U test) or Wilcoxon signed-rank test was used for unpaired and paired data, respectively. For multiple comparisons following analysis of variance (ANOVA), Tukey’s honest significant difference post-hoc test was used. All statistical tests were two-sided, unless otherwise specified. Throughout the manuscript, statistical significance is indicated by asterisks: *P < 0.05, **P < 0.01, ***P < 0.001.

On box plots, the central mark indicates the median; bottom and top edges of the box indicate the 25th and 75th percentiles, respectively; and whiskers extend to the most extreme data points not considered outliers. Outliers are not displayed in some plots but were included in statistical analysis. Owing to experimental design constraints, the experimenter was not blind to the manipulation performed during the experiment (i.e., optogenetic manipulation).

Data and materials availability:

All data are available in the main text or the supplementary materials. Custom scripts used in this study can be downloaded from Zenodo (114).