仿鼠脑内嗅—海马—前额叶信息传递回路的空间导航方法

Abstract

生理学研究发现，大鼠进行空间定位依赖内嗅—海马CA3结构中的网格细胞与位置细胞，而内嗅—海马结构与前额叶皮层之间的动态联系是导航的关键。基于此，本文提出一种仿鼠脑内嗅—海马—前额叶信息传递回路的空间导航方法，旨在为移动机器人赋予强大的空间导航能力。在海马CA3—前额叶空间导航模型的基础上，本文构建以海马CA1区位置细胞为基本单元的动态自组织模型优化导航路径。随后通过海马CA3区位置细胞与前额叶皮层动作神经元将优化后的路径回馈至脉冲神经网络，提高模型收敛速度的同时还有助于建立导航习惯的长期记忆。为验证方法的有效性，本文分别设计了二维仿真实验和三维仿真平台的机器人实验。实验结果表明：本文方法不仅能够在导航效率、收敛速度等方面超越其他算法，而且对动态变化的导航任务具有较好的适应性。同时，本文方法还能够很好地应用在移动机器人平台上。

0. 引言

环境认知与导航是各类高等哺乳动物特有的一种能力^[1]。对于自主移动式机器人来说，具备像高等哺乳动物一样的智能行为是在复杂未知的环境中快速而准确地实现面向目标导航的必要条件。导航包含定位与决策两个部分^[2]。定位是确定自身在环境中的位置，而决策则代表如何正确地指导机器人从当前位置运动至目标点。大鼠作为哺乳动物的一员，也拥有着卓越的导航能力。生理学研究表明，内嗅—海马结构是大鼠实现定位的关键脑区^[3]，其内部存在多种对空间位置有着特异性放电作用的神经元细胞（空间细胞），例如：位置细胞^[4]、网格细胞^[5]、边界细胞^[6]、头朝向细胞^[7]等。其中，自运动信息被认为是输入至内嗅皮层网格细胞结构^[8]，并通过神经网络投射至海马CA3区的位置细胞群，从而实现对自运动信息的路径积分^[9]。随后，海马CA1区位置细胞接收CA3区位置细胞所投射的位置信息，实现对空间位置集合的存储与记忆^[10]。由于位置细胞是定位的主要神经元，其放电活动并不能预测未来行为的方向，而决策是导航过程中必不可少的组成部分，因此可以推断在大鼠脑结构中必定存在承担决策任务的相关脑区。研究表明，前额叶皮层是大脑产生命令和运动控制的关键脑区^[11]，且内嗅—海马结构与前额叶皮层之间的动态联系是决定未来行为的关键因素^[12]。

近年来，基于仿生认知机制的空间导航方法的研究成为热点，主要包括两个研究方向：① 仿生环境认知地图构建与导航。该研究方向旨在构建仿鼠脑运行机制的精确环境认知地图，随后基于认知地图进行路径规划与导航^[13-15]。而基于地图的路径规划与导航方法较为工程化，因而缺乏仿生性。② 基于仿生认知机制的空间认知与导航习惯养成。该研究方向旨在构建导航模型指导机器人对空间环境进行探索，并随着机器人的探索逐渐获得对应环境的导航能力。2004年，Oudeyer等^[16]提出一种智能自适应好奇心学习理论，使机器人在没有先验知识的环境中不断探索，逐渐完成对环境的认知。随后在2018年和2021年，张晓平等^[17]和阮晓钢等^[18]构建了基于好奇心学习理论的环境认知模型，并在此基础上实现移动机器人的路径规划。而仿鼠脑认知机制的导航习惯养成相关研究工作可以追溯到2009年，Kulvicius等^[19]利用简单的前馈神经网络构建海马位置细胞到动作神经元之间的连接关系，并使用Q-learning算法实现面向目标的导航。2013年，Frémaux等^[20]使用脉冲神经网络作为位置细胞到动作神经元之间的连接结构，引入STDP学习规则调整网络的连接权值，提升了导航模型发现目标区域的速度。随后在2017年和2021年，Zannone团队^[21-22]将乙酰胆碱和多巴胺的顺序神经调节机制加入STDP学习规则（Sn-Plast模型），使智能体能够有效地导航到不断变化的奖励位置，增强了模型的适应能力。但上述方法都容易陷入局部最优，导致输出的路径并不是当前导航任务的最优路径。

基于上述研究事实，本文提出一种仿鼠脑内嗅—海马—前额叶信息传递回路的空间导航方法，旨在为移动机器人赋予强大的定位与决策能力。本文的主要贡献如下：① 构建以海马CA1区的位置细胞为基本单元的动态自组织模型，能够根据环境信息优化海马CA3—前额叶脉冲神经网络模型输出的导航路径，从而提高导航效率；② 通过优化后的导航路径得出动作神经元和海马CA3位置细胞群的理论放电率，并以此为监督信号调整脉冲神经网络的连接权值，实现了将优化后的导航路径及时回馈至脉冲神经网络，提高模型收敛速度的同时还有助于建立导航习惯的长期记忆。

1. 模型的建立

1.1. 模型的整体结构

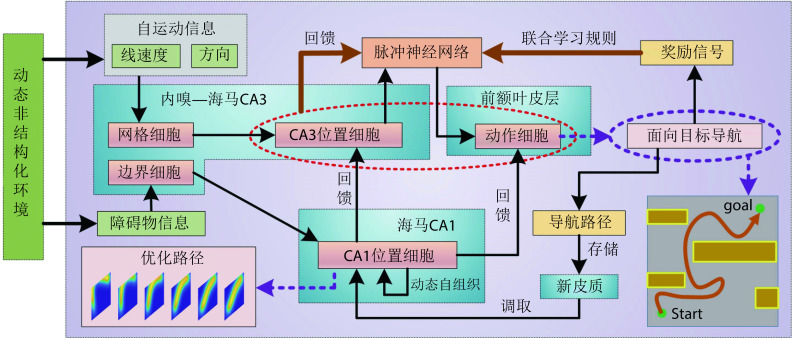
本节对仿鼠脑内嗅—海马—前额叶信息传递回路的空间导航方法的整体结构进行详细说明。随着机器人在环境中探索，自运动信息首先被输入至网格细胞模型，随后通过神经网络连接将空间信息投射至海马CA3区位置细胞模型，实现路径积分功能^[23]。机器人探索过程中，使用联合学习规则Sn-Plast调节海马CA3区位置细胞到前额叶皮层动作神经元之间脉冲神经网络的权值大小^[22]。待探索至目标点时，海马CA1区位置细胞通过动态自组织对形成的导航路径进行优化。由于导航行为需要动作神经元的放电率为指导，而动作神经元的放电率由脉冲神经元的权值和海马CA3区位置细胞群的放电率共同决定，故利用优化后的导航路径计算出动作神经元和海马CA3区位置细胞群的理论放电率序列，并以此为监督信号调整脉冲神经网络的连接权值。导航方法的整体运行机制如图1所示。

图 1.

The overall operating mechanism of navigation method

导航方法的整体运行机制示意图

1.2. 导航路径优化方法

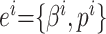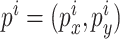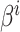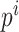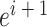导航路径实际上是由多个路径点组成的，每个海马CA1位置细胞可以看作是一个记忆单元，存储一个路径点信息。设第 i 个位置细胞为 。 代表放电野中心坐标。 代表智能体在 处的头朝向角度，其初始值为相邻两个位置细胞 和 放电野中心连线与x轴正方向之间的夹角。设t时刻第i个位置细胞放电野中心位置的更新量为 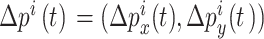，头朝向角度的修正量为 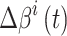，相关数学表达式如下。

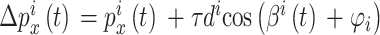1

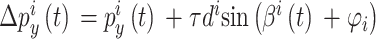2

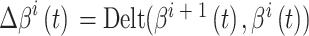3

式(3)中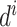， 代表初始时刻位置细胞 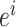和 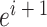放电野中心之间的距离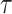， 代表松弛因子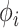， 代表初始时刻 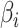与 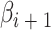之间的差值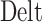， 代表求解角度差的函数。得到修正量之后，即可对放电野中心和头朝向角度进行修正。放电野中心坐标修正的数学表达式如下：

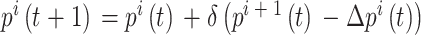4

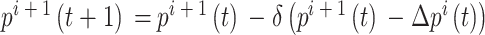5

头朝向角度修正的数学表达式如下：

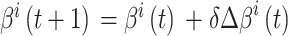6

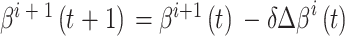7

式(4)~(7)中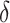， 代表修正增益。然而，实际物理环境中通常存在许多障碍物，因此路径的优化过程也要考虑障碍物的影响。生理学研究表明，内嗅皮层的边界细胞是大鼠感知环境边界和障碍的主要神经元，同样也是海马体的信息输入源之一^[24]。因此，本文基于边界细胞的放电机制对路径优化过程进行分段。首先，将环境中的所有障碍物离散化，并将离散化的障碍物位置集定义为 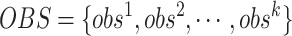。设 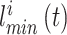代表 t 时刻第 i 个位置细胞放电野中心与障碍物之间的最短距离，其数学表达式如下：

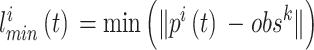8

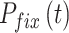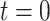在导航路径优化的过程中，当某个位置细胞的放电野中心逐渐靠近障碍物且与障碍物之间的距离足够小的时候，则固定该位置细胞的放电野中心位置（位置不再改变）。设t时刻已经被固定放电野中心的位置细胞集合为 ，当 时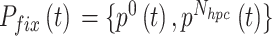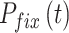，。 随着迭代次数增加的数学表达式如下：

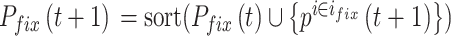9

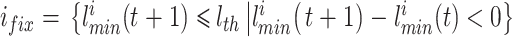10

式(10)和(11)中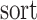， 代表将集合中的元素从小到大排序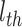， 代表最短距离判据阈值。设函数 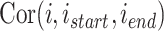代表对第 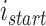个位置细胞到第 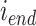个位置细胞之间的所有位置细胞放电野中心进行路径优化，其中 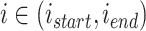。定义集合 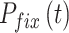中的第 i 个元素为 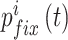，故导航路径的优化过程可以表示为如下公式：

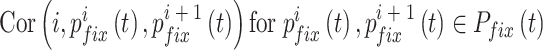11

上述步骤可以对导航路径进行分段校正，以确保模型在有障碍物的环境中仍能实现高效的面向目标的导航。导航路径分段修正的运行机制如图2所示。

图 2.

Operation mechanism of navigation path segment optimization

导航路径分段优化的运行机制

在导航路径优化过程中，随着迭代次数的增加，更新量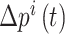的值逐渐减小。此时再继续进行迭代更新所产生的效果不显著且耗费处理器的计算时间，影响算法的实时性。基于此，本文提出一种收敛度的判据方法。首先定义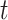时刻的路径收敛量为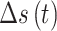，其数学表达式如式(12)所示：

12

设收敛判据比例因子为ρ，当满足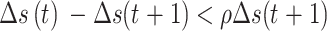 时，判断此时无需再继续进行更新迭代，反之则继续执行更新迭代。导航路径优化方法的收敛性证明过程见附件1。

1.3. 导航路径回馈

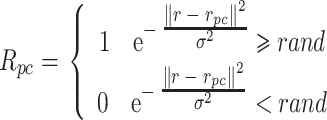
待导航路径优化后，需要将优化后的导航路径回馈至脉冲神经网络。首先计算动作神经元和海马CA3区位置细胞群的理论放电率作为监督信号来调整脉冲神经网络的连接权值，相关数学表达式如式(13)和(14)所示。

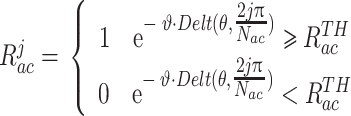13

14

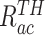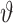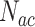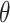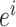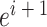式(13)代表第j个动作神经元的放电率表达，其中 代表放电率阈值， 代表动作神经元放电率调整因子， 代表神经元的个数， 代表当前的头朝向角度（路径优化后相邻两个CA1区位置细胞 和 放电野中心连线与x轴正方向之间的夹角）。式(14)代表CA3区位置细胞的放电率表达，其中 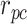代表位置细胞的放电野中心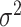， 代表位置野半径调整因子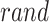， 表示0至1之间随机的一个数。智能体在t时刻的动作 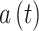由动作神经元的放电活动所决定，其数学表达式如下：

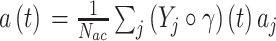15

式(15)中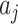， 为第j个动作神经元在t时刻所代表的动作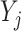， 代表第j个动作神经元的放电脉冲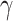， 代表滤波器，相应的数学表达式如式(16)至(18)所示。

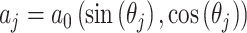16

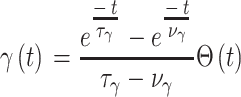17

式(16)中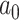， 代表动作步长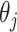， 代表第j个动作神经元的偏好方向。式(17)中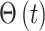， 代表阶跃函数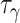， 和 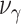均为时间常数。当机器人运动至目标区域时，使用STDP规则与资格迹结合的可塑性规则^[22]对突触权重进行更新，数学表达式如式(18)所示。

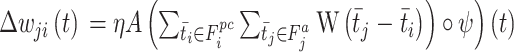18

式(18)中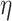， 代表学习率；A代表神经调节函数；W代表STDP窗口函数，其数学表达式为 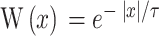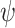； 代表资格迹。 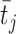和 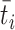分别代表第j个动作神经元和第i个位置细胞所产生脉冲的到达时间。综上，导航方法的工作流程可以简述如下：首先采集机器人的自运动信息，按照信息流顺序依次计算各空间神经元的放电率，并利用全体动作神经元的放电活动指导机器人移动。当机器人运动至目标区域时，利用CA1位置细胞动态自组织模型调整导航路径，并将优化后的导航路径与先前所有路径的长度进行对比。若当前路径是最短路径则计算CA3位置细胞和动作神经元的理论放电率，并作为监督信号调整脉冲神经网络的连接权值。

1.4. 动态导航过程

当机器人处于静态环境中，机器人只需要探索环境并搜索导航路径即可。然而，空间环境或导航任务通常是不断变化的，这就需要机器人拥有较强的适应能力。导航过程发生改变主要包括以下两种情况：① 原导航路径发生阻塞；② 导航终点发生改变。导航过程发生改变后，机器人将以导航路径与障碍物的交点或原导航终点为起点重新探索环境。导航方法的运行流程如图3所示。

图 3.

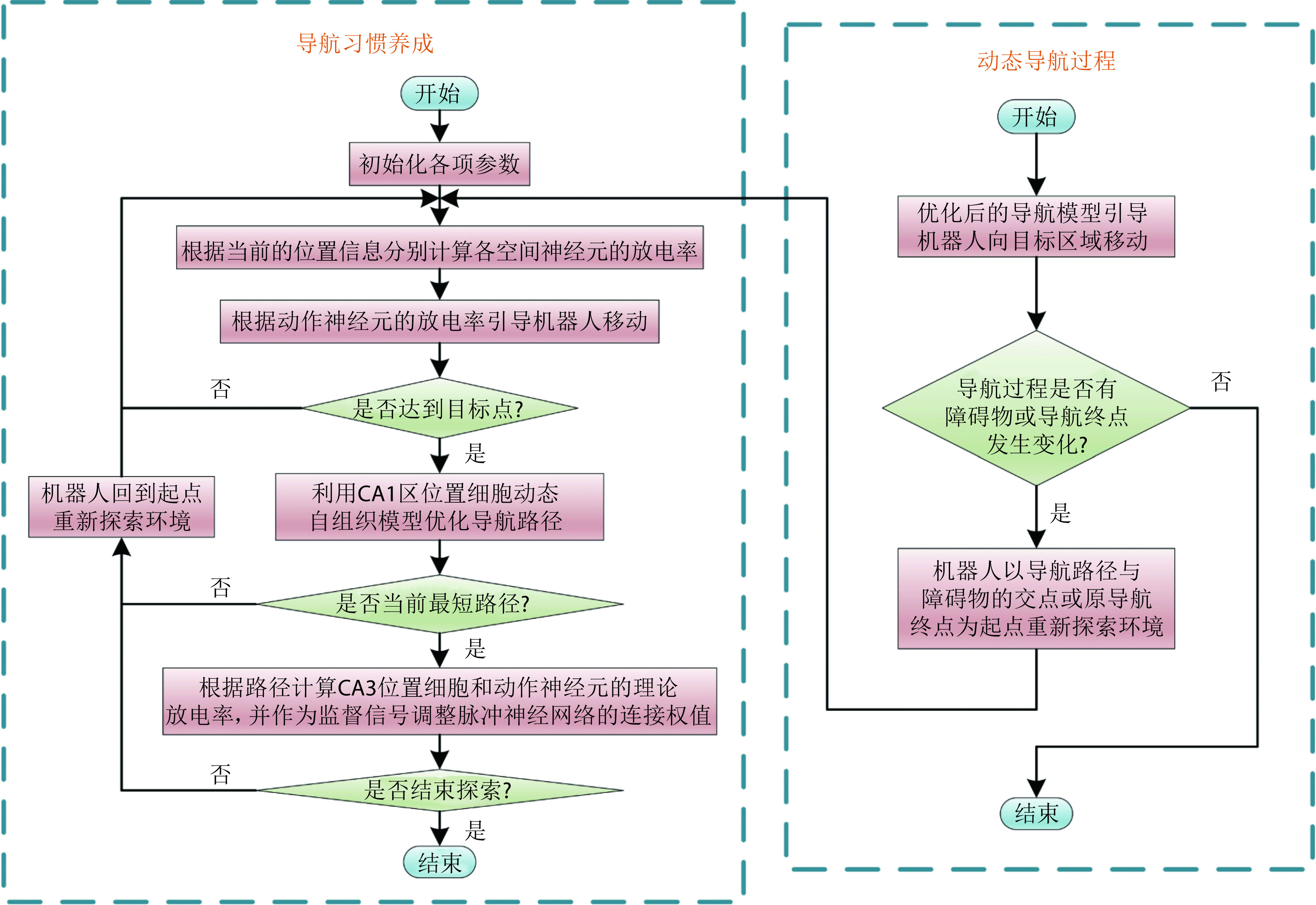
Operation process of the navigation method

导航方法的运行流程图

2. 实验验证

2.1. 实验说明与参数设定

本节通过设计二维仿真实验在模型收敛速度、导航效率、动态导航任务的适应能力等方面进行测试，并在此基础上设计机器人平台的三维仿真实验进一步验证模型的有效性。内嗅—海马CA3信息传递模型的参数设定与文献[23]一致，海马CA3—前额叶空间导航模型的参数设定与文献[22]一致。本文模型涉及的参数设定如下：修正增益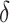设定为0.5，松弛因子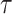设定为0.3，收敛判据比例因子为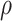设定为0.001，动作神经元放电率阈值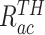设定为0.9，动作神经元放电率调整因子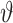设定为1 000，距离判据阈值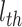设定为0.1。

2.2. 二维仿真实验

2.2.1. 导航习惯养成实验

本节对所提出的模型性能进行二维仿真实验验证，分别构建四个不同的空间区域进行导航实验，区域面积均设定为10 m × 10 m。空间区域内设置障碍物以及导航的起点与终点。以Sn-Plast模型引导智能体在四个空间区域中探索，并养成相应的导航习惯。单次导航习惯养成过程中的探索次数设定为30，单次探索过程的最大路径长度设定为80 m。智能体在空间区域中的导航习惯养成过程如图4所示，其中从左至右代表探索环境次数的增加。

图 4.

The formation process of navigation habits of agents under the guidance of Sn-Plast model

Sn-Plast模型引导下智能体的导航习惯养成过程

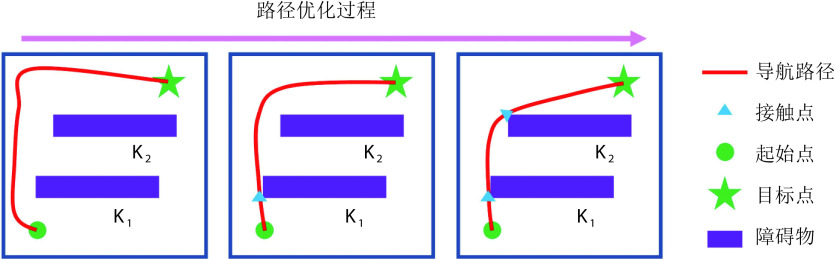
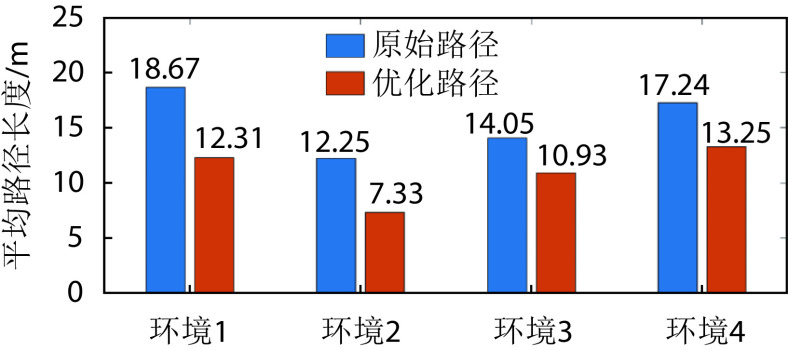
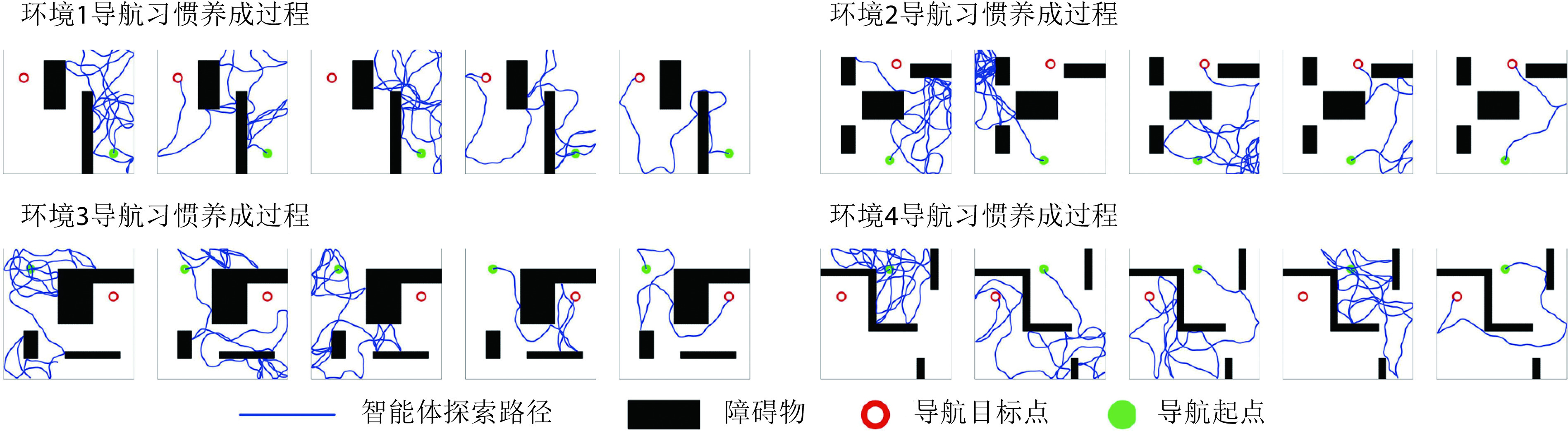
从图4中可以看出，在Sn-Plast模型的引导下机器人能够通过不断探索环境而逐渐习得如何从起点出发运动至目标点，养成对应当前任务的导航习惯。但从导航结果来看也同时存在两点不足：① 模型无法快速收敛（当智能体探索至目标区域时，在接下来的探索任务中依旧会出现无法运动至目标区域的情况）；② 导航路径比较弯曲，并不是最优导航路径。因此本文通过CA1区位置细胞动态自组织模型对导航路径进行优化。随后将优化后的路径通过CA3位置细胞和动作神经元回馈至脉冲神经网络，强化模型对路径的记忆，解决模型无法快速收敛的问题。图5所示为导航路径的优化过程，图中从左至右代表优化模型迭代次数的增加。图6所示为原始路径与优化路径的长度统计结果。从图5和图6中可以看出，随着优化模型迭代次数的增加，优化路径较原始路径显著缩短，验证了模型的有效性。

图 5.

Optimization process of navigation path

导航路径的优化过程

图 6.

Average length statistics of original paths and optimized paths

原始路径和优化路径的平均长度统计

2.2.2. 对比实验与消融实验

为了突出本文方法的优势，将之与Q-learning算法^[19]、SARSA算法^[25]以及智能好奇心算法（intelligent adaptive curiosity，IAC）^[16]进行对比。鉴于本文导航方法由导航习惯养成模块（Sn-Plast）、路径优化模块（path optimization，PO）和路径回馈模块（path feedback，PF）组成，为了体现各模块的作用，增加消融实验以测试每个模块对模型性能的影响。对比的性能指标如下：导航路径平均长度、发现目标区域后收敛的概率、首次发现目标区域所需的探索次数以及完成导航习惯养成所需的平均探索次数。为量化模型的收敛性能，收敛判据如下：当智能体发现目标区域并且在接下来的四次探索任务中均能够运动至目标区域，则判断模型已收敛；反之亦然。定义发现目标区域后收敛的概率为 ，其数学表达式如式(19)所示。

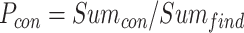19

式(19)中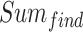，代表发现目标区域的次数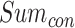，代表发现目标区域且接下来的四次探索任务均能够运动至目标区域的次数。导航路径平均长度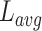代表所有发现目标的路径长度平均值，其数学表达式如式(20)所示。

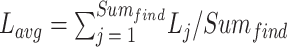20

式(20)中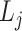，代表第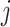次发现目标区域的探索路径长度。完成导航习惯养成所需的平均探索次数代表算法收敛所需的平均探索次数，该指标能够综合反映算法引导智能体发现目标区域的速度和收敛速度。单次导航习惯养成过程中的探索次数设定为20，单次探索过程的最大路径长度设定为80 m。算法导航的实验结果见表1。

表 1. Statistical results of navigation experiments of various algorithms.

各算法导航实验的统计结果

环境	算法	导航路径 平均长度/m	发现目标区域后 收敛的概率	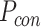首次发现目标所需的 平均探索次数	完成导航习惯养成 所需的平均探索次数
1	Q-learning	16.59	84.2%	9.4	11.2
	SARSA	19.56	67.6%	10.7	16.5
	IAC	17.44	85.8%	11.9	17.3
	Sn-Plast	18.97	73.3%	6.6	13.8
	Sn-Plast + PO	13.02	73.3%	6.6	13.8
	Sn-Plast + PO + PF	12.48	96.1%	6.4	6.7
2	Q-learning	11.87	79.9%	8.5	9.3
	SARSA	12.62	73.5%	9.8	12.4
	IAC	11.14	81.3%	7.7	8.9
	Sn-Plast	12.90	80.7%	6.8	12.9
	Sn-Plast + PO	7.73	80.7%	6.8	12.9
	Sn-Plast + PO + PF	7.52	97.8%	7.0	7.1
3	Q-learning	16.28	76.2%	9.7	14.2
	SARSA	17.55	71.5%	9.3	22.8
	IAC	17.13	89.1%	8.5	16.1
	Sn-Plast	18.93	78.4%	7.9	20.7
	Sn-Plast + PO	11.40	78.4%	7.9	20.7
	Sn-Plast + PO + PF	11.16	97.3%	7.9	8.4
4	Q-learning	18.51	85.7%	9.7	14.1
	SARSA	19.38	70.2%	11.6	20.9
	IAC	18.96	91.5%	8.1	9.6
	Sn-Plast	19.73	74.8%	6.2	17.4
	Sn-Plast + PO	14.06	74.8%	6.2	17.4
	Sn-Plast + PO + PF	13.70	98.2%	5.9	6.1

从表1可以看出，各算法均能够使智能体养成对应空间的导航习惯。SARSA算法具有最差的导航性能，其收敛速度和导航路径长度均不及其他算法。Q-learning算法在导航路径长度上优于SARSA、Sn-Plast和IAC算法，但其发现目标区域的速度较Sn-Plast更慢。这主要是因为Sn-Plast算法融合了改进的STDP学习规则和资格迹，能够在一定程度上减少重复区域探索的次数。但是，虽然Sn-Plast能够更快地发现目标区域，却不能及时收敛（首次发现目标所需探索次数与养成导航习惯所需探索次数之间存在较大差异）。由于PO模块的作用，使得Sn-Plast + PO算法在导航路径长度上优于Q-learning算法，但由于没有信息回馈，导致Sn-Plast + PO算法与Sn-Plast一样无法及时收敛。而Sn-Plast + PO + PF算法在收敛速度、导航路径以及发现目标区域的速度三个方面均表现最佳，不仅能够保持Sn-Plast算法的优点，而且能够对已经生成的导航路径进行优化与回馈，从而快速形成最优导航路径的稳定记忆。

2.2.3. 动态导航实验

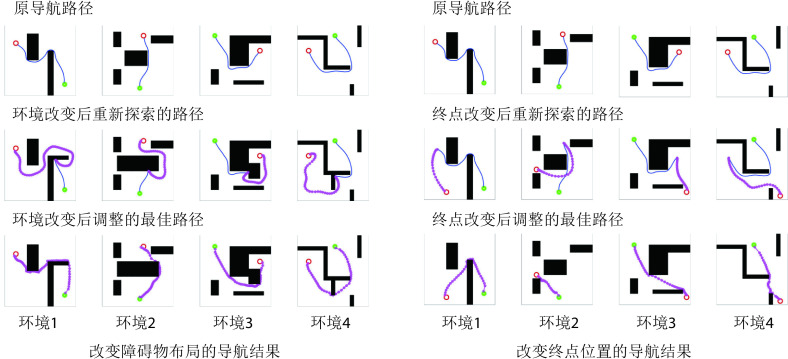
为验证模型对导航任务动态变化的适应能力，分别在原导航路径上增加障碍物以及改变导航任务的终点，以此观察算法应对环境变化与导航任务发生变化时所做出的行为。模型的相关参数设定与前文一致。在智能体沿导航路径运动的过程中，若检测到前方有障碍物则说明空间环境中障碍物的布局已经发生了改变；若达到原导航终点位置时未发现目标则说明导航终点的位置发生了变化。此时算法将根据上述情形分别指导智能体以导航路径与障碍物的交点或原导航终点为起点重新探索环境，并重新养成对应新环境或导航任务的最佳导航习惯。智能体在四个空间区域内进行动态导航实验的部分结果如图7所示，图中各元素的含义与图5中保持一致。

图 7.

Navigation results for dynamic navigation tasks

动态导航任务的实验结果

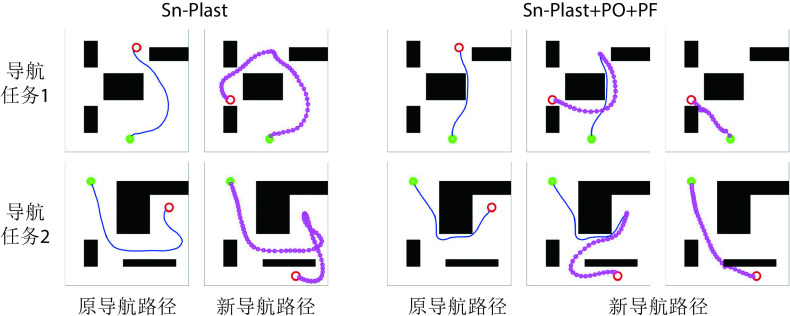
图7左图第二行图片中蓝色线条代表原始导航路径中未接触新障碍物的部分，粉色线条代表以原导航路径与障碍物的交点为起点重新养成的导航习惯。图7右图第二行图片中粉色线条代表以原导航终点为起点重新养成的导航习惯。结果表明，本文算法能够及时有效地指导智能体对已发生改变的环境做出调整。为进一步证明本文算法对于动态导航任务具有较高的灵活性，设计两组容易使算法陷入局部最优的动态导航实验，将本文算法与Sn-Plast算法进行对比，导航轨迹如图8所示。从图中可以看出，当导航任务发生改变时，Sn-Plast算法形成的新导航路径会陷入新起点至目标点导航任务的局部最优，而Sn-Plast+PO+PF算法则能够统筹优化原轨迹与新轨迹所组成的新轨迹，实时判断是否为当前的最优路径，从而生成适应新导航任务的最优路径。此外，关于从原起点和新起点出发对算法性能影响的讨论见附件2。

图 8.

Track comparison of dynamic navigation tasks

动态导航任务的轨迹对比结果

2.3. 机器人平台三维仿真实验

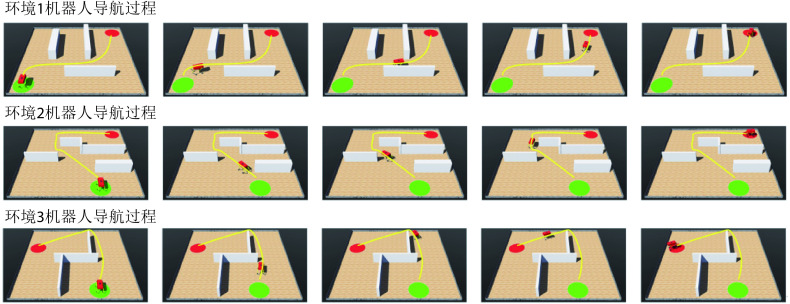
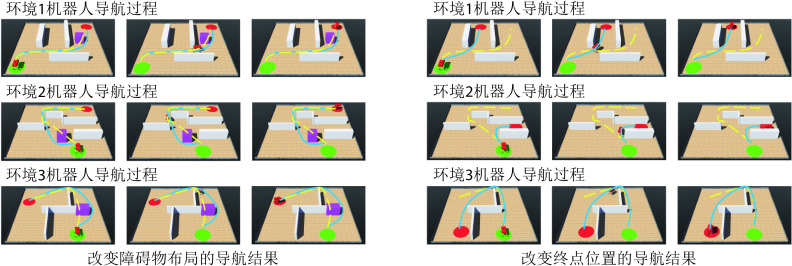
为进一步验证模型的有效性，本文使用Webots仿真软件进行三维仿真实验。在仿真软件中使用刚体、角度传感器、电机、接触传感器、摄像头、GPS传感器以及IMU搭建四足机器人的物理模型。仿真环境的大小为10 m×10 m，四足机器人在该环境中自主探索。通过获取机器人的GPS传感信息来解算自身在环境中的位置。机器人的正前方安装有深度摄像头来判断前方是否有障碍物。利用本文算法计算下一时刻机器人应当达到的位置坐标，随后控制四足机器人到达指定位置，以此引导四足机器人在空间环境中进行探索并养成导航习惯。分别在Webots软件中构建三个仿真环境进行实验，空间中随机设置起点、终点以及围墙、方块等障碍物，算法的各项参数与前文保持一致。导航习惯养成后机器人在算法的引导下完成导航任务的过程如图9所示，图中黄色线条代表机器人的导航轨迹。随后效仿二维实验在环境中原机器人导航路径上增加方块形障碍物以及改变导航终点位置，机器人在算法的引导下完成新导航任务的过程如图10所示，图中黄色虚线和蓝色线条分别代表导航任务发生改变前后的机器人导航轨迹。可以看出，本文算法不但能够引导机器人探索环境并养成对应的导航习惯，而且可以及时有效地指导智能体适应动态变化的环境和导航终点。机器人的物理结构及其在空间环境中导航的视频文件见附件3～6。

图 9.

The process of robot completing navigation task under the guidance of algorithm

机器人在算法的引导下完成导航任务的过程

图 10.

Motion process of robot completing dynamic navigation task

机器人完成动态导航任务的运动过程

3. 结论

本文提出一种仿鼠脑内嗅—海马—前额叶信息传递回路的空间导航方法，其特点在于：① 构建以海马CA1区的位置细胞为基本单元的动态自组织模型以优化导航路径；② 能够通过空间细胞的放电作用将路径信息回馈至脉冲神经网络，提高算法收敛速度的同时还有助于建立导航习惯的长期记忆。实验结果表明了方法的有效性和可行性，且相较于其他导航方法，本文方法在导航效率、收敛速度以及对环境中动态障碍的适应性等方面更有优势。三维仿真平台的机器人实验表明本文方法能够很好地应用在移动机器人平台上。

然而本文方法也存在以下不足：① 导航任务局限于给定空间内进行。② 机器人在运动的过程中通常存在累计误差，导致定位不准。而本文仅在真实位置的引导下进行实验验证，未考虑由于定位不够精确而影响算法导航性能的情况。③ 在环境发生改变的时候还是需要在局部空间内进行探索与路径优化，不能根据改变之后的环境直接对当前路径进行调整。因此下一步的研究方向为：① 将算法扩展到能够在任意大小空间范围内实现导航任务；② 结合多种外源信息作为输入，力求使机器人在与环境的交互过程中渐进地形成和发展对环境的认知能力，提升导航过程的定位精度进而增强模型的鲁棒性。综上，本文研究成果为仿鼠脑认知机制的机器人导航方法奠定了基础。

重要声明

利益冲突声明：本文全体作者均声明不存在利益冲突。

作者贡献声明：于乃功对相关工作进行了调查，发现了现有方法的不足，提出了本文的核心观点与研究思路；廖诣深针对该研究思路进行了实现，并设计了实验对本文方法进行了验证。

本文附件见本刊网站的电子版本（biomedeng.cn）。

Funding Statement

国家自然科学基金资助项目（62076014; 61573029）；北京市自然科学基金资助项目（4162012）；北京市教育委员会科技计划重点项目（KZ202010005004）

The National Natural Science Foundation of China; The Natural Science Foundation of Beijing; Beijing Municipal Education Commission and Municipal Natural Science Foundation