Abstract
电阻抗断层成像（EIT）技术在肺通气监测和区域性肺功能检测中发挥着重要作用。然而，EIT算法固有的病态特性导致从含有噪声的电压数据中求解电导率时存在明显偏差，难以获得准确的电导率变化分布图像以及清晰的边界轮廓。为了提高EIT在肺通气监测中的成像质量，本文提出将EIT算法与深度学习算法相结合的方法。首先，引用优化因子对卡尔曼滤波算法进行修正并将吉洪诺夫（Tikhonov）正则化引入算法的状态空间表达式，以获得初始肺部重建图像；其次将初始成像结果输入生成对抗网络模型，以重构出精确的肺部轮廓。仿真实验结果表明，该方法生成的肺部图像边界清晰，对噪声具有更强的鲁棒性，基本实现了可视化的效果，可为计算机断层扫描等影像的诊断提供参考意义。
Keywords: 电阻抗断层成像, 卡尔曼滤波, 生成对抗网络, 图像重建
Abstract
Electrical impedance tomography (EIT) plays a crucial role in the monitoring of pulmonary ventilation and regional pulmonary function test. However, the inherent ill-posed nature of EIT algorithms results in significant deviations in the reconstructed conductivity obtained from voltage data contaminated with noise, making it challenging to obtain accurate distribution images of conductivity change as well as clear boundary contours. In order to enhance the image quality of EIT in lung ventilation monitoring, a novel approach integrating the EIT with deep learning algorithm was proposed. Firstly, an optimized operator was introduced to enhance the Kalman filter algorithm, and Tikhonov regularization was incorporated into the state-space expression of the algorithm to obtain the initial lung image reconstructed. Following that, the imaging outcomes were fed into a generative adversarial network model in order to reconstruct accurate lung contours. The simulation experiment results indicate that the proposed method produces pulmonary images with clear boundaries, demonstrating increased robustness against noise interference. This methodology effectively achieves a satisfactory level of visualization and holds potential significance as a reference for the diagnostic purposes of imaging modalities such as computed tomography.
Keywords: Electrical impedance tomography, Kalman filter, Generative adversarial network, Image reconstruction
0. 引言
电阻抗断层成像（electrical impedance tomography，EIT）是一种电学测量技术，具有快速成像、无损伤、无辐射等优点[1]。近年来，EIT技术已经被广泛研究和应用于临床检测中，主要用于呼吸系统监测、肺功能成像、肺通气监测等领域。该技术通过测量边界电压并采用适当的成像算法对人体内部电导率分布进行重构，从而实现高分辨率的实时成像[2]。然而在实际测量过程中，由于测量值数量远少于待求未知量的数量，EIT逆问题具有严重的不适定性。传统成像算法对噪声和误差极为敏感，为了提高电导率分布图像的稳定性，通常需要降低空间分辨率，因此导致重构图像出现较大的伪影且成像精度较差。目前常用的重构算法包括线性反投影法[3]、一步线性高斯牛顿法[4]等。1998年Vauhkonen等[5]基于随机游走模型将卡尔曼滤波（Kalman filter，KF）算法引入EIT技术中，将EIT逆问题转化为状态估计问题。然而在实际应用中，人们往往难以建立精确的数学模型，EIT的不适定性导致状态向量的更新过程极易受到噪声干扰，从而导致传统KF算法滤波精度下降，进而影响图像重建的质量。因此，本文提出基于吉洪诺夫（Tikhonov）正则化的修正自适应扩展KF（modified adaptive extended KF with Tikhonov regularization，MAEKF-TR）算法，以期减小过程噪声对实际数据的影响，改善EIT逆问题的不适定性，完成对肺部组织的图像重建。
近年来，深度学习算法在计算机视觉、图像重建等领域取得了长足发展[6]。与传统方法相比，深度学习网络模型可以更有效地捕获图像的复杂特征，获得更高的重建性能。因此，许多国内外学者尝试将深度学习算法用于生物医学图像处理领域[7-8]。经典的深度学习算法如卷积神经网络、U型网络（U-net）、生成对抗网络（generative adversarial network，GAN）等，已在计算机断层扫描（computed tomography，CT）、磁共振成像（magnetic resonance imaging，MRI）等医学图像重建领域取得了显著的成果[9-11]。为了减少传统EIT算法的重构误差，降低人为因素对影像诊断的影响，本文提出将GAN与MAEKF-TR算法相结合的方法。具体而言，首先使用卷积神经网络对包含误差和伪影的EIT阻抗分布数据进行训练，通过GAN中生成器与鉴别器之间的对抗训练所生成的肺部影像能够更清晰地反映肺部大小和形态等信息，从而减小EIT重建算法引起的伪影干扰。
本文构建了人体肺部仿真数据集，来模拟人类胸腔和常见肺部疾病的电导率分布，以评估所提方法的性能。此外，本文还将以仿真实验证实，与传统KF重建算法相比，MAEKF-TR算法与GAN结合，不仅能准确检测出肺部器官的大小和位置，而且所生成的肺部图像轮廓边缘更加清晰，可以降低对EIT重建图像分析的主观性影响和误差。综上，通过仿真实验研究结果，期望本研究提出的方法对肺通气监测相关研究有一定的参考意义。
1. 算法描述
1.1. EIT原理
本文采用16个电极的EIT测量系统，采用相邻电极输入电流，其他相邻电极测量电压值的模式。EIT重建过程可分为两个主要步骤：正问题求解和逆问题求解。正问题求解，是指在已知物体内EIT分布的情况下求解边界电压值；逆问题求解，则是通过边界电压差值求解内部电导率的变化分布。图像重建过程实际上是逆问题的求解过程，EIT线性模型如式(1)所示[12]：
 |
1 |
式中，ΔU为测量电压变化量；J为灵敏度矩阵；Δσ为场域内电导率变化量。逆问题的求解实际是对非线性表达式的求解，而EIT图像重建过程就是将非线性表达式进行线性化来寻找最优解σ，如式(2)所示：
 |
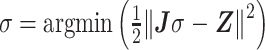2 |
式中，Z为实际测量数据。
1.2. MAEKF-TR算法
求解EIT逆问题的过程，其实质是对电导率分布的求解。KF标准递推方程见文献[13-15]，将KF映射到EIT系统中，电导率σk视为状态估计量，从而将EIT逆问题转化为状态估计问题，如式(3)所示：
 |
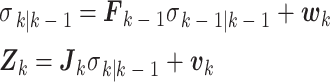3 |
式中，
是k时刻的先验状态估计量；
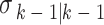是k − 1时刻的先验状态估计量；Fk-1为k–1时刻的状态传递矩阵，wk为k时刻的系统噪声；Zk为k时刻的实际测量值；Jk为k时刻的观测矩阵；vk为k时刻的测量噪声。EIT系统的KF滤波方程如式(4)所示：
 |
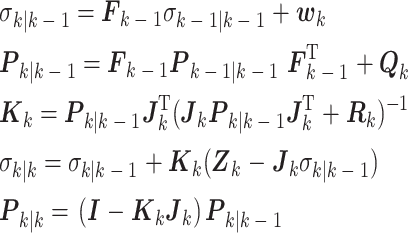4 |
式中，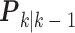
表示估计误差协方差矩阵k时刻的先验估计；
表示估计误差协方差矩阵k – 1时刻的先验估计；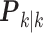
表示估计误差协方差矩阵k时刻的后验估计；
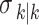是k时刻的后验状态估计量；Rk表示k时刻的测量噪声协方差；Qk表示k时刻的过程噪声协方差；Kk表示k时刻的算法增益；I是单位矩阵，T为转置符号。在实际测量生物组织时，数据信息会发生突变，导致估计的新息矢量发生较大变化。然而算法增益Kk不能实时根据状态变化进行调整，从而导致滤波精度下降、滤波发散等情况出现。要削减测量噪声对算法的干扰，就要调整测量噪声协方差Rk及过程噪声协方差Qk的权重占比。
本文提出引入优化因子δp[δp∈(0，1)]，对过程噪声协方差Qk进行修正，将更新的数据给予更多的权重。Qk调整如式(5)所示：
 |
5 |
式中，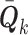
表示修正后k时刻的过程噪声协方差；
表示修正后k – 1时刻的过程噪声协方差；ξk表示在k时刻的新息矢量；Δp表示观测值与先验值之间的残差。以上分析可知，改进后的自适应扩展KF（adaptive extended KF，AEKF）算法考虑了实际噪声的时变特性对系统的影响，并通过实时数据更新的方式实现了对噪声的实时修正。
算法增益Kk是最小二乘估计的最优增益，相当于对后验误差协方差矩阵的迹进行了最小化[16]。在EIT求解过程中，输入数据的微小扰动就会对输出数据产生较大的相对误差，难以准确求出逆问题的解，体现出严重的病态特性。此时AEKF观测矩阵的病态性会导致重建反演的不稳定，使得滤波值与真值之间存在明显偏差。因此本文提出基于Tikhonov正则化来修正AEKF算法以克服这一问题，Tikhonov正则化最小化问题如式(6)所示：
 |
6 |
式中，γ为正则化参数，参数值可以通过L曲线法来确定；y表示为最小化问题的最优解。L曲线法广泛应用于选择最优的正则化参数，参数值越大，其稀疏性约束条件越强。在曲线的拐点处，残差范数和解范数与正则化参数之间呈现出“L”形曲线，因此选用该点作为正则化控制参数的最优值。基于Tikhonov正则化相应的最小二乘估计值如式(7)所示：
 |
7 |
新的正则化观测矩阵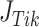
如式（8）所示：
 |
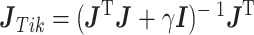8 |
为了将Tikhonov正则化引入改进的算法中，本文采用伪测量方法[17]，将式(8)替换原始方程引入到递推的修正AEKF算法中，MAEKF-TR算法更新过程如式(9)所示：
 |
9 |
2. 结合GAN的后处理
本研究采用MAEKF-TR算法建立边界电压与肺部组织电导率分布之间的预映射关系，利用GAN对图像进行优化，从而提高图像质量。在EIT算法中，输入输出数据必须一一对应，因此使用初始电导率图像δσ0代替随机噪声作为生成器的输入以生成高质量的重构图像δσ。鉴别器在学习大量标签图像δσ1后对图像δσ的真实性进行判断，通过不断交替更新生成器和鉴别器的参数来优化成像结果[18]。网络模型结构如图1所示。
图 1.
The overall network architecture of GAN
GAN模型整体结构
2.1. GAN模型搭建
鉴于图像卷积运算（convolution，Conv）能够有效地利用医学图像中的结构信息，因此本文采用U-net作为生成器的网络结构[19]。输入输出均为3通道图像，网络结构包括下采样、上采样和图像重构过程。使用4×4的卷积核进行4次卷积与反卷积运算，激活函数为线性整流函数（rectified linear unit，ReLu）。使用全卷积网络马尔可夫判别器（PatchGAN）作为模型的鉴别器，将图片分成固定大小的子图像，然后独立处理每个子图像的内容[20]。PatchGAN的输入为两个256 × 256 × 3的数据矩阵，拼接后的数据矩阵先后进行3次组合操作：卷积、批归一化（batch normalization，BN）、激活函数泄露ReLU（Leaky ReLU），最后通过一次卷积操作提取数据特征，采用逻辑激活函数（Sigmoid）映射到(0, 1)区间。鉴别器结构如表1所示。
表 1. Structure of discriminator.
鉴别器结构
| 层数 | 鉴别器结构 |
| 1 | Conv，Leaky ReLU |
| 2 | Conv，BN，Leaky ReLU |
| 3 | Conv，BN，Leaky ReLU |
| 4 | Conv，BN，Leaky ReLU |
| 5 | Conv，Leaky ReLU |
| 6 | Sigmoid |
2.2. GAN损失函数
模型采用的损失函数由对抗损失和回归损失两部分组成，对抗损失函数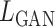 
如式(10)所示：
 |
10 |
式中，D为鉴别器，G为生成器；重建图像的可信度在肺部EIT成像方面非常重要，因此采用L1损失函数来评估重建图像与真实图像之间的差值。回归损失函数 
如式(11)所示：
 |
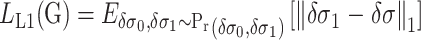11 |
模型采用的损失函数L如式(12)所示：
 |
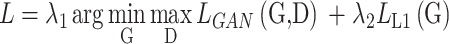12 |
式中，D的目标是将式（10）的值最大化，而G则使其值最小。λ1、λ2是平衡对抗损失和回归损失的加权项，根据经验选择设定λ1的值为100，λ2的值为10。
3. 实验结果与分析
3.1. 数据集构建
为了验证算法的有效性，采用两个肺部公开数据集分别是2016年推出的肺结节分析（lung nodule analysis 16，LUNA 16）数据集[21]和国家肺部筛查试验（the national lung screening trial，NLST）数据集[22]以及公开癌症影像数据库（the cancer imaging archive，TCIA）中的非小细胞肺癌（non‐small cell lung cancer，NSCLC）影像组[23]的肺部CT影像作为EIT仿真模型的样本。
本文通过区域生长法提取CT影像中的胸腔及肺部轮廓信息，使用有限元仿真软件COMSOL Multiphysics 6.0（COMSOL Inc.，瑞典）和科学计算软件MATLAB R2016a（MathWorks Inc.，美国）联合仿真构建了不同胸腔边界和肺部形态的仿真模型，建立了人体肺部仿真模型数据库。在该模型中，将皮下组织电导率设置为0.037 S/m，健康肺部区域电导率设置为0.120～0.142 S/m，病变组织电导率设置为0.200～0.347 S/m [24-25]。在模型边缘均匀放置了16个激励电极，电极采用圆形表示，激励电流设置为1 mA，频率为50 kHz。通过仿真方法生成的训练集数据包含5 000个肺部仿真模型，其中健康肺部样本数与肺部疾病样本数比例为1:1。将70%的健康肺部和患病肺部的样本用于训练集，30%的样本分配到测试集。本研究的网络开发环境如下：使用计算机编程语言python 3.8.16（Guido van Rossum，荷兰）和深度学习框架pytorch 1.4（Facebook Inc，美国）。实验使用显卡GPU为NVIDIA GeForce GTX 2080Ti（Nvidia Inc，美国），处理器CPU为Intel（R）Core（TM）i7-6700 CPU @ 3.40 GHz（Intel Inc，美国）。
3.2. 评价标准
为了直观地展示本研究所提出算法的有效性和优越性，可以从定量的角度来比较仿真数据的成像结果。本文使用结构相似性（structural similarity index，SSIM）、峰值信噪比（peak signal to noise ratio，PSNR）、相对误差（relative error，RE）和相关系数（correlation coefficient，CC）来评估图像重建的效果。评价指标表达式如式(13)所示：
 |
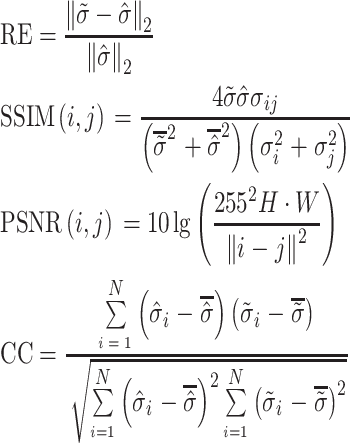13 |
式中，H和W分别为图像的长度和宽度，i、j代表标签与重建图像的像素指数；
表示图像真实阻抗值；
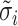表示在第i个单元的真实阻抗值；
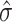表示重建图像的阻抗值；
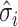表示在第i个单元的重建图像阻抗值；
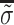和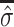 
表示原始图像和重建图像电导率分布的平均值，σi和σj表示原始图像和重建图像电导率分布的方差；σij为协方差矩阵；N为重建图像中像素点的个数。SSIM、PSNR和CC的数值越接近于1，表明重构图像的质量越高；RE值越接近于0，表明重构图像与原始图像之间的相对误差越小，即图像重建效果越好。
3.3. 无噪声情况下重构成像
正则化参数的目的是平衡残差范数和解范数，较小的正则化参数会削弱约束，对残差项施加较大的惩罚；较大的正则化参数会加强约束，导致正则化项在目标函数中占主导地位。如图2所示，为观测到的残差范数和正则化解范数的L曲线，在拐点处残差范数和解范数同时达到最小值，因此选取该点作为最优正则化参数，γ值为0.01。
图 2.
L-curve method for determining regularization parameter
L曲线法确定正则化参数
为了验证本文提出的MAEKF-TR算法的性能，本研究将使用KF算法、AEKF算法和MAEKF-TR算法对人体肺部仿真数据集进行图像重建，如图3所示。图3为六组仿真模型（模型1~模型6）的成像结果，分别展示了EIT阻抗分布数据以及结合GAN模型处理后的肺部影像图。从阻抗分布图中可以看出，KF算法能够检测到肺部组织，但重建图像较为模糊，重建效果不佳；AEKF算法相比于KF算法可以重建大致的肺部轮廓，但存在明显的图像伪影，无法准确地重现出肺部轮廓。MAEKF-TR算法重建效果最佳，可以较为清晰地重建出肺部边缘轮廓，更接近真实目标。将三种EIT算法结合GAN模型后得到可视化的肺部影像，可以看到MAEKF-TR算法与GAN模型的组合相比于其他两种算法能够更清晰地刻画肺部轮廓的边界信息，并且在不同胸腔轮廓模型下成像效果更为稳定，重建图像的位置大小和边缘轮廓都更接近真实数据。
图 3.
Comparison of simulation imaging results of the three algorithms
三种算法的仿真成像结果对比
为了定量描述重建图像质量，本文分别对不同算法的重建图像进行评估。评价结果如图4所示，MAEKF-TR算法的SSIM和CC的值接近0.9，显著优于其他算法，证明了MAEKF-TR算法应用于EIT重建过程的有效性。同时，本文还对三种算法与GAN模型组合后的重建结果进行了评估，结果如图5所示。对比结果表明，结合GAN模型的MAEKF-TR算法能更加准确地表达胸腔内电特性的参数分布，所成图像精度更高，并且不易受到肺部疾病等因素导致的模型复杂程度的影响。
图 4.
Reconstruction performance of various algorithms of traditional EIT
传统EIT不同算法的重建性能
图 5.
Reconstruction performance of various algorithms combined with GAN model
不同算法结合GAN模型的重建性能
3.4. 含噪声情况下重构成像
为了验证MAEKF-TR算法的抗噪性能，本文对仿真数据添加了信噪比为5 dB和12 dB的高斯噪声。如图6所示，结合GAN模型的MAEKF-TR算法在噪声干扰下的重建图像受到扰动最小，能准确地反映肺部位置，边缘区域的重建效果较好。而KF算法和AEKF算法的重建图像受到噪声的影响均发生了不同程度的畸变，抗干扰能力较差。本文提出的方法在噪声条件下依旧表现出良好的重建性能，如表2所示，加粗字体表示三种重建算法在噪声干扰下每个模型的最优性能参数。
图 6.
Comparison of simulation imaging results of various algorithms in the presence of noise
含噪声情况下不同算法的仿真成像结果对比
表 2. Reconstruction performance metrics of various algorithms combined with GAN model in the presence of noise.
含噪声情况下不同算法结合GAN模型的重构性能参数
| 噪声大小 | 算法 | 模型1 | 模型2 | 模型3 |
| SSIM/CC/RE | SSIM/CC/RE | SSIM/CC/RE | ||
| 5 dB | KF | 0.757/0.783/0.359 | 0.860/0.897/0.386 | 0.850/0.865/0.477 |
| AEKF | 0.773/0.779/0.316 | 0.839/0.885/0.311 | 0.845/0.869/0.432 | |
| MAEKF-TR | 0.863/0.867/0.358 | 0.900/0.951/0.341 | 0.917/0.957/0.408 | |
| 12 dB | KF | 0.722/0.772/0.377 | 0.843/0.861/0.335 | 0.814/0.821/0.522 |
| AEKF | 0.746/0.763/0.367 | 0.851/0.878/0.326 | 0.820/0.840/0.441 | |
| MAEKF-TR | 0.830/0.858/0.344 | 0.868/0.934/0.310 | 0.894/0.942/0.412 |
4. 结论
本文提出了一种结合GAN的MAEKF-TR算法应用于肺通气监测。首先构建了人体肺部仿真数据集来评估所提出算法的性能，同时将MAEKF-TR算法生成的EIT阻抗分布数据用于GAN模型进行对抗训练，通过生成器与鉴别器之间的不断博弈，最终得到了近似人体阻抗分布的肺部重构影像。仿真实验结果表明，该方法能显著提升肺部成像的质量，得到边界完整且位置精确的肺部图像。综上，本文所提出的方法为EIT图像重建提供了新的思路，有望进一步推动EIT在肺部疾病检测方面的应用。
重要声明
利益冲突声明：本文全体作者均声明不存在利益冲突。
作者贡献声明：本文工作中，赵明康、刘珺负责算法程序设计、数据收集；郭忠圣、陈祥琪负责数据分析；郑天予负责论文图像处理；刘珺负责论文写作；张帅负责论文审阅。
Funding Statement
国家自然科学基金资助项目（62276089，51877069）；河北省高等学校科学研究资助项目（QN2023230）
References
- 1.叶健安, 田翔, 王普, 等 基于多分支一维卷积神经网络电阻抗断层成像数据后处理方法研究. 空军军医大学学报. 2022;43(7):842–846,851. [Google Scholar]
- 2.田翠杰, 王海播, 张文平, 等 电阻抗断层成像技术在呼吸系统疾病中的临床应用. 中国呼吸与危重监护杂志. 2020;19(6):617–620. doi: 10.7507/1671-6205.201808044. [DOI] [Google Scholar]
- 3.Barber D C A review of image reconstruction techniques for electrical impedance tomography. Med Phys. 1989;16(2):162–169. doi: 10.1118/1.596368. [DOI] [PubMed] [Google Scholar]
- 4.Widodo A, Endarko Experimental study of one step linear Gauss-Newton algorithm for improving the quality of image reconstruction in high-speed electrical impedance tomography. J Phys Conf Ser. 2018;1120:012067. doi: 10.1088/1742-6596/1120/1/012067. [DOI] [Google Scholar]
- 5.Vauhkonen M, Karjalainen P A, Kaipio J P A Kalman filter approach to track fast impedance changes in electrical impedance tomography. IEEE Trans Biomed Eng. 1998;45(4):486–493. doi: 10.1109/10.664204. [DOI] [PubMed] [Google Scholar]
- 6.Wang H, Yang Y Y, Pan Y, et al Detecting thoracic diseases via representation learning with adaptive sampling. Neurocomputing. 2020;406:354–360. doi: 10.1016/j.neucom.2019.06.113. [DOI] [Google Scholar]
- 7.Wang Y, Yu B, Wang L, et al 3D conditional generative adversarial networks for high-quality PET image estimation at low dose. Neuroimage. 2018;174:550–562. doi: 10.1016/j.neuroimage.2018.03.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chen Y, Yang X H, Wei Z, et al Generative adversarial networks in medical image augmentation: a review. Comput Biol Med. 2022;144:105382. doi: 10.1016/j.compbiomed.2022.105382. [DOI] [PubMed] [Google Scholar]
- 9.Faruqui N, Yousuf M A, Whaiduzzaman M, et al LungNet: a hybrid deep-CNN model for lung cancer diagnosis using CT and wearable sensor-based medical IoT data. Comput Biol Med. 2021;139:104961. doi: 10.1016/j.compbiomed.2021.104961. [DOI] [PubMed] [Google Scholar]
- 10.Chan H P, Hadjiiski L M, Samala R K Computer-aided diagnosis in the era of deep learning. Med Phys. 2020;47(5):e218–e227. doi: 10.1002/mp.13764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Goodfellow I J, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets// Proceedings of the 27th International Conference on Neural Information Processing Systems (NIPS’14), Montreal: NIPS, 2014, 2: 2672-2680.
- 12.李佳.电阻抗层析成像的数据融合与正则化算法研究. 天津: 天津大学, 2020.
- 13.Liu D, Smyl D, Du J Nonstationary shape estimation in electrical impedance tomography using a parametric level set-based extended Kalman filter approach. IEEE Transactions on Instrumentation and Measurement. 2019;69(5):1894–1907. [Google Scholar]
- 14.Kim K Y, Kim B, Kim M C, et al Image reconstruction in time-varying electrical impedance tomography based on the extended Kalman filter. Measurement Science and Technology. 2001;12(8):1032. doi: 10.1088/0957-0233/12/8/307. [DOI] [Google Scholar]
- 15.Zhang J, Zhang L, Liu Z, et al Tikhonov regularization-based extended Kalman filter technique for robust and accurate reconstruction in diffuse optical tomography. J Opt Soc Am A Opt Image Sci Vis. 2023;40(1):10–20. doi: 10.1364/JOSAA.476795. [DOI] [PubMed] [Google Scholar]
- 16.Qiu Y, Zhao H Ocean acoustic tomography with moving node based on Tikhonov regularized Kalman filter. Journal of Physics: Conference Series. 2019;1169(1):012027. [Google Scholar]
- 17.Carmi A, Gurfil P, Kanevsky D Methods for sparse signal recovery using Kalman filtering with embedded pseudo-measurement norms and quasi-norms. IEEE Transactions on Signal Processing. 2010;58(4):2405–2409. doi: 10.1109/TSP.2009.2038959. [DOI] [Google Scholar]
- 18.Li X, Zhang R, Wang Q, et al SAR-CGAN: improved generative adversarial network for EIT reconstruction of lung diseases. Biomedical Signal Processing and Control. 2023;81:104421. doi: 10.1016/j.bspc.2022.104421. [DOI] [Google Scholar]
- 19.Garehdaghi F, Meshgini S, Afrouzian R Positron emission tomography image enhancement using magnetic resonance images and U-net structure. Computers & Electrical Engineering. 2021;90:106973. [Google Scholar]
- 20.Isola P, Zhu J Y, Zhou T, et al. Image-to-image translation with conditional adversarial networks//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017: 1125-1134.
- 21.Liao F, Liang M, Li Z, et al Evaluate the malignancy of pulmonary nodules using the 3-D deep leaky noisy-OR network. IEEE Trans Neural Netw Learn Syst. 2019;30(11):3484–3495. doi: 10.1109/TNNLS.2019.2892409. [DOI] [PubMed] [Google Scholar]
- 22.Petousis P, Han S X, Aberle D, et al Prediction of lung cancer incidence on the low-dose computed tomography arm of the national lung screening trial: a dynamic Bayesian network. Artif Intell Med. 2016;72:42–55. doi: 10.1016/j.artmed.2016.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kiser K J, Ahmed S, Stieb S, et al PleThora: pleural effusion and thoracic cavity segmentations in diseased lungs for benchmarking chest CT processing pipelines. Med Phys. 2020;47(11):5941–5952. doi: 10.1002/mp.14424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wang H, Hu L, Wang J, et al An image reconstruction algorithm of EIT based on pulmonary prior information. Frontiers of Electrical and Electronic Engineering in China. 2009;4(2):121–126. doi: 10.1007/s11460-009-0020-3. [DOI] [Google Scholar]
- 25.Li X, Chen X, Wang Q, et al Electrical impedance tomography imaging based on a new three-dimensional thorax model for assessing the extent of lung injury. AIP Advances. 2019;9(12):125310. doi: 10.1063/1.5124353. [DOI] [Google Scholar]