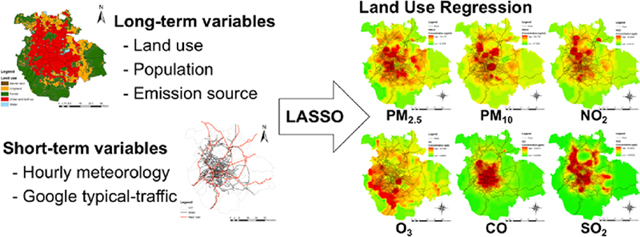
Abstract
The Mexico City Metropolitan Area (MCMA) is one of the largest and most populated urban environments in the world and experiences high air pollution levels. To develop models that estimate pollutant concentrations at fine spatiotemporal scales and provide improved air pollution exposure assessments for health studies in Mexico City. We developed finer spatiotemporal land use regression (LUR) models for PM2.5, PM10, O3, NO2, CO and SO2 using mixed effect models with the Least Absolute Shrinkage and Selection Operator (LASSO). Hourly traffic density was included as a temporal variable besides meteorological and holiday variables. Models of hourly, daily, monthly, 6-monthly and annual averages were developed and evaluated using traditional and novel indices. The developed spatiotemporal LUR models yielded predicted concentrations with good spatial and temporal agreements with measured pollutant levels except for the hourly PM2.5, PM10 and SO2. Most of the LUR models met performance goals based on the standardized indices. LUR models with temporal scales greater than one hour were successfully developed using mixed effect models with LASSO and showed superior model performance compared to earlier LUR models, especially for time scales of a day or longer. The newly developed LUR models will be further refined with ongoing Mexico City air pollution sampling campaigns to improve personal exposure assessments.
Keywords: land use regression, air pollution, exposure, LASSO, Mexico City
Graphical Abstract
1. Introduction
The Mexico City Metropolitan Area (MCMA) is one of the largest and most populated urban environments in the world and experiences high air pollution levels (Molina et al., 2010). A large body of published studies link air pollution exposure in the MCMA to various adverse health outcomes, including inflammation and/or DNA damage (Alfaro-Moreno et al., 2002; Osornio-Vargas et al., 2003), respiratory diseases including asthma (Rojas-Martinez et al., 2007), cardiovascular disease (Shields et al., 2013), suppression of innate antibacterial immunity (Rivas-Santiago et al., 2015) and overall mortality (Bell et al., 2008; O’Neill et al., 2004). Most of these health studies have relied on ambient air pollution data from fixed monitoring stations to estimate exposure. A major disadvantage of this methodological approach is that it may not capture spatial variability in exposure due to local sources, urban topography and local meteorological variables (Jerrett et al., 2005).
Several other methods, such as geostatistical methods and land use regression (LUR), have therefore been proposed to model and account for the within-city spatial distribution of air pollution concentrations in health studies (Brauer et al., 2003; Hoek et al., 2008; Rivera-González et al., 2015; Ryan and LeMasters, 2007). On one hand, geostatistical methods, including inverse distance weighting and ordinary Kriging, have been evaluated as exposure assessment methods in the MCMA (Rivera-González et al., 2015), but these methods cannot deal with local emissions (Jerrett et al., 2005). On the other hand, LUR analyses have not been used widely for air pollution research in the MCMA. Currently available LUR methods developed for the MCMA air pollution study have identified limitations associating with data availability and extrapolation from seasonal variables to annual simulations (Just et al., 2015; Sangrador et al., 2008).
The current effort to improve LUR models in the MCMA with fine spatial and temporal exposure analysis methods was made to advance an ongoing study of the relationship between ambient air pollution exposure and human host immune cell functions among participants in a Mexico City-based study known as ‘MexAir’. Based on data from our lab (Rivas-Santiago et al., 2015; Sarkar et al., 2012), we hypothesize that exposure to poor air quality in the MCMA may increase susceptibility to infection with Mycobacterium tuberculosis (M.tb) and risk of reactivation tuberculosis (TB).
In order to develop a LUR model with fine spatial and temporal scale, two key variables need to be considered. First, traffic data have been identified as an important predictor to improve spatial variability (Beelen et al., 2013; Hoek et al., 2001). However, there are no publicly obtainable traffic data in most cities (Hoek et al., 2008). Indeed, traffic information were not included in the previous MCMA LUR study due to the data availability (Just et al., 2015). Second, meteorological variables might improve the performance of LUR models with short temporal resolution (Ainslie et al., 2008; Just et al., 2015; Liu et al., 2015). However, most LUR models performed to date outside of the MCMA, have focused on long-term air pollutant exposures, and assessments of annual, seasonal and monthly averages of PM2.5 (Henderson et al., 2007; Johnson et al., 2013), PM10 (Hart et al., 2009; Liu et al., 2015), NO2 (Arain et al., 2007; Beelen et al., 2013; Dons et al., 2014; Hart et al., 2009; Henderson et al., 2007; Johnson et al., 2013; Liu et al., 2015; Wang et al., 2013; Wheeler et al., 2008), and SO2 (Wheeler et al., 2008). A limited number of earlier LUR models that predicted shorter-term pollutant levels used temporal calibration approaches (e.g., dummy variables) (Dons et al., 2013; Johnson et al., 2013) but did not consider time-varying meteorological covariates that are useful in the optimization and refinement of LUR models (Ainslie et al., 2008; Liu et al., 2015).
The aim of the current study was to introduce ‘hourly meteorological variables’ and an ‘hourly traffic density variable’ into the LUR model to allow modeling of air quality on a finer temporal resolution scale and integrate the temporal variations found throughout the three major weather seasons in the MCMA: wet, cold-dry, warm-dry (de Foy et al., 2006; Manzano-León et al., 2016).
2. Material and Methods
2.1. Study Areas and Polygonal Regions
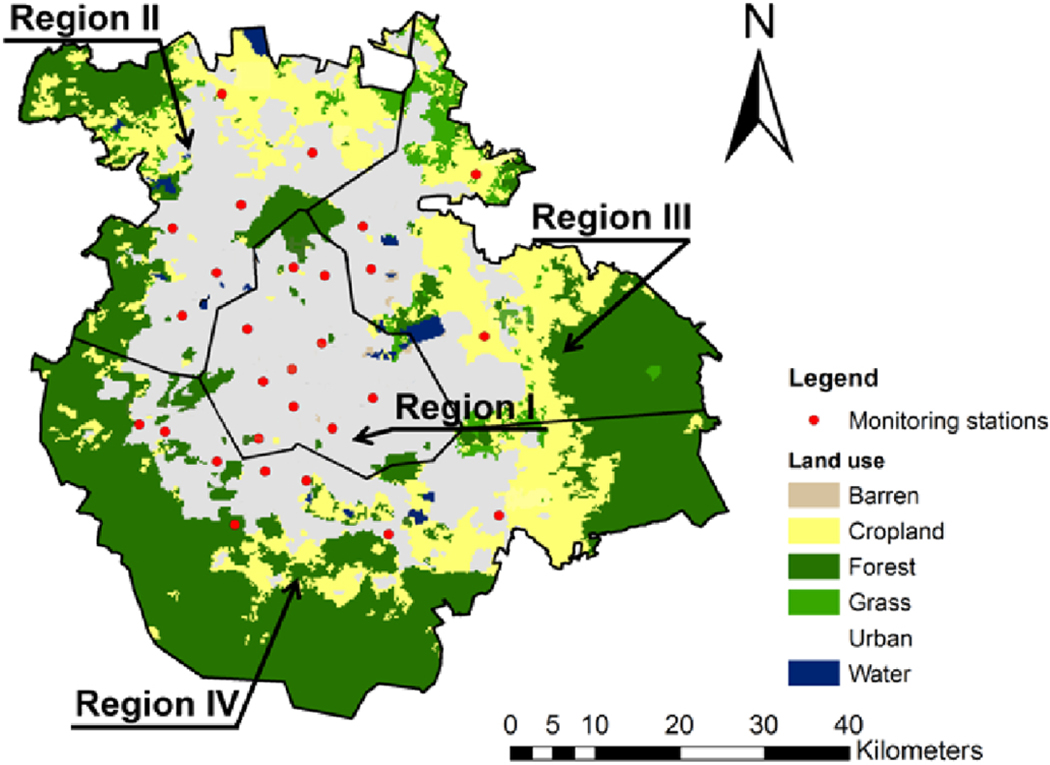
The MCMA includes the states of Mexico and Hidalgo, and the Federal District (Distrito Federal). The current study area (Region I, II, III, and IV) covered a central part of the MCMA with a total area of 4,238 km2 (Figure 1). LUR models were developed to cover the whole MCMA study area with different time scales, and then evaluated using whole and separate air quality monitoring data based on polygonal regions. Thiessen polygons were generated using the locations of the 28 automatic air quality monitoring stations of the Red Automática de Monitoreo Atmosférico (RAMA) in the MCMA. Thiessen polygons were then combined into four regions based on air quality distribution, pollutant emission sources and urban population density. The four regions are defined as: Region I (central MCMA region with large population density; the MexAir study municipalities Iztapalapa and Iztacalco are included in this zone), Region II (north western MCMA region with medium population density and high air pollution levels), Region III (north eastern MCMA region with medium air pollution levels) and IV (southern MCMA region with highest O3 levels and low levels of other air pollutants).
Figure 1.
The study area and polygonal regions
2.2. Data Collection
Data sets for regression analyses are described in the Supplementary Material (Table S1). In brief, ambient air pollution data from 2011 to 2014 was downloaded from the RAMA (SIMAT, 2018). The air quality monitoring stations operate beta-attenuation monitors, UV photometric ambient ozone analyzers, chemiluminescence NO-NO2-NOx analyzers, UV Fluorescence Sulfur Dioxide analyzers, and Infrared CO analyzers to measure particulate matter (PM2.5, PM10), O3, NO2, SO2, and CO, respectively. Outliers (i.e., any pollutant values lower than 5% and higher than 95%) were not excluded in our study as the pollutant data sets had been cleaned and verified by the Mexican government and were therefore considered accurate.
Hourly meteorological data for the same time period was obtained from the meteorology and solar radiation monitoring network (Red de Meteorología y Radiación Solar; REDMET) and the atmospheric deposition monitoring network (Red de Depósito Atmosférico, REDDA), which is operated by the Mexican Ministry of Environment (Secretaría del Medio Ambiente y Recursos Naturales; SEMARNAT) (SIMAT, 2018). Data from a total of 28 RAMA stations, 21 REDMET stations and 16 REDDA stations covering the entire Federal District area and part of Hidalgo and Mexico states are included in the current LUR study (Table S2 and S3).
Traffic density data in past LUR models were either considered as a long-term variable or were not available at all (Hoek et al., 2008; Just et al., 2015). This study included crowd-sourcing traffic data (i.e., Google traffic) that cover the entire MCMA with hourly temporal variation to improve the LUR model. Hourly traffic density was manually coded from the Google traffic website (Google, 2009), which shows historical data as ‘typical traffic’ for seven days of a week and day times from 5:00 a.m. to 11:00 p.m.. The Google typical traffic map covers the entire MCMA with clear spatial and temporal traffic patterns (Figure S1).
Briefly, the Google traffic road map for the MCMA was duplicated using the ArcMap 10.2 software, and then color codes (green, orange, red and dark red for fast to slow traffic speed) from the Google typical traffic were manually recorded as a number code (0–5 scale for no color to dark red) for identical roads. We assumed that slower traffic (red or dark red) would result in a greater car density on a road and that this would lead to the emission of larger quantities of air pollutants in a given time period. As Google does not provide ‘typical traffic’ information for the time interval between midnight and 4:00 a.m., traffic density data for this time interval was defined as the average of the 11:00 p.m. and 5:00 a.m. values from each respective day. Then, coded ‘typical traffic’ density was applied to all days.
Road maps and the Mexican census basic area level population data (Área geoestadística básica; AGEB; an area where approximately 1,500 individual reside) were obtained from the National Institute of Statistics and Geography (Instituto Nacional de Estadística y Geografía; INEGI) in Mexico (INEGI, 2018). A land use map and a digital elevation model (DEM) were downloaded from the United States Geological Survey (USGS, 2016). In addition, residential, industrial and commercial urban land use information was obtained from the OpenStreetMap (OpenStreetMap contributors, 2015). Point values of annual pollutant emission loads (ton/year) for PM2.5, PM10, NO2, SO2, and CO were obtained from SEMARNAT (SIMAT, 2018). Point emission data were divided by the distance between each emission point and monitoring station because pollutant concentrations were inversely correlated with the distance from their sources. Estimated inverse distance weighted emission loads (ton/year/km) were used in all LUR model developments to incorporate the impact of point sources on the Mexico City air quality. We simply incorporated the annual emissions data uniformly into the hourly and monthly assessments, recognizing that this assumes constant emissions across the time period from these sources.
2.3. Development of LUR Models for the MCMA
LUR models were developed for six ambient air pollutants: PM2.5, PM10, O3, NO2, SO2, and CO. In these models, dependent variables were log-transformed hourly air pollutant concentrations. Independent variables were hourly meteorological data, hourly traffic density, road length, land use, emission inventory and population-related data (Table S4) within different radiuses of circular buffers (500 m - 5 km) around the RAMA sampling stations. Large buffers might not represent the diverse spatial distribution of air pollutants emitted by traffic related sources such as particulate matter and NOx (Hoek et al., 2008). We therefore excluded traffic related independent variables for small buffers (< 500 m) in all final LUR models because the small buffers included similar road lengths and traffic densities due to the complex road network and traffic patterns of the MCMA and failed to include sources form the emission inventories and different land uses. Therefore, buffer sizes greater than 500 m were selected to (1) include multiple emission sources from the emission inventory and all roads covered by Google traffic data and (2) to represent the breadth of land use classes (residential, industrial, commercial and green space). Data points without observed pollutant concentrations were excluded from the final dataset. Hourly meteorological data from nearest weather stations were used to fill in the missing values.
The best subsets of the mixed-effect models were selected using the least absolute shrinkage and selection operator (LASSO) method, which is intended to improve the prediction accuracy and interpretability of model (Tibshirani, 1996). Independent variables were fixed at a shrinkage parameter (λ), which represents one standard deviation of a minimum mean square error. Linear mixed-effect models with LASSO corresponding to each time of the days throughout a year were developed using the following equation (Eq. 1):
| (1) |
where denotes the log-transformed hourly pollutant concentration; is the intercept; denote the regression coefficient for the independent variables; are independent variables; and are the random intercepts on hours (h) in jth day (j = 366, h = 24) for a pollutant . Analysis was conducted in R 3.2.1 (R Core Team, 2015) using the lmmlasso package (Schelldorfer et al., 2011). For comparison purposes, the linear mixed-effect (LME) method (lme4 package in R) was applied to the same hourly PM2.5 data set used for the LASSO method. The final subset of the LME model for hourly PM2.5 concentrations was selected by the internal optimization function of lme4 package to obtain maximum likelihood (Bates et al., 2014). In addition, daily, monthly, 6-month and annual LUR models were generated by averaging dependent and temporal independent variables to evaluate the impact of temporal scale on independent variable selection and model performance.
2.4. Evaluation of the LUR Models
The performances of the final LUR models in predicting actual measured air pollution levels were evaluated using coefficients of determinants (R2), Nash-Sutcliffe efficiency (NSE), root mean square error (RMSE), RMSE-observations standard deviation ratio (RSR), and mean fractional error (MFE). R2 and RMSE are the most popular measures of goodness-of-fit and error index but may be over-sensitive to extreme values (Moriasi et al., 2007). NSE, RSR and MFE are standardized indices that are not biased by outliers and used by U.S. EPA to evaluate model performances (EPA, 2007). NSE measures how well the simulated and observed data fits identity line (i.e., x=y line) (Nash and Sutcliffe, 1970). NSE ranges from negative infinity to 1 and NSE values of 1 reflect optimal performance. The RSR standardizes the RMSE using standard deviations of observed data and indicates unbiased error indices (Moriasi et al., 2007). The optimal value of the RSR is 0 representing zero residual variations or RMSE. The MFE indicates a normalized error without biases (Boylan and Russell, 2006). An MFE value of 0 represents no difference between observed and simulated value. Equations for the NSE, RSR and MFE are presented in Supplementary Material.
Spatial validation was performed for the entire study area using a K-fold cross validation (CV) with the LASSO method. First, a monitoring station was excluded from the total number of sampling sites (K) to generate training data sets with K-1 sites. Monitoring sites are K=14, 20, 28, 27, 27 and 26 for PM2.5, PM10, O3, NO2, SO2 and CO monitoring stations, respectively (Table S3). The final LUR models were fitted to the training data sets. Fitted models predicted pollutant concentrations at the excluded sites (test set). Model performance was subsequently calculated using predicted and observed concentrations of the test data and averaged R2 was reported as a result of the cross validation. LUR and validation statistics could not be calculated for each polygonal region due to the limited number of monitoring stations.
3. RESULTS
3.1. Air Quality of the MCMA
Table 1 shows summary statistics of meteorological variables and air pollutant concentrations in the MCMA between 2011 and 2014. Annual average PM2.5, PM10, O3, NO2, SO2 and CO concentrations during the study period (2011–2014) were 24.5 μg/m3, 45.3 μg/m3, 28.3 ppb, 26.3 ppb, 5.56 ppb and 0.80 ppm, respectively. The ambient air quality of the MCMA showed clear temporal patterns. PM2.5, PM10 and O3 concentrations were higher in the warm-dry seasons whereas NO2, CO and SO2 concentrations were higher in the cold-dry seasons. Lower air pollutant concentrations were observed during the wet seasons.
Table 1.
Summary statistics of meteorological and ambient air quality data in the MCMA (2011–2014)
| Parameter | Average | Percentile (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
| Weta | CDb | WDc | Annual | Min | 5 | 25 | 50 | 75 | 95 | Max | |
|
| |||||||||||
| Temperature (°C) | 17.2 | 14.8 | 18.6 | 16.7 | −3.40 | 8.80 | 13.4 | 16.3 | 20.3 | 25.3 | 34.4 |
| Humidity (%) | 63.2 | 49.2 | 39.7 | 52.6 | 0.00 | 15.0 | 35.0 | 53.0 | 71.0 | 89.0 | 100 |
| Precipitation (mm) | 4.35 | 0.00 | 0.59 | 1.97 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.21 | 178 |
| Wind speed (m/s) | 2.13 | 1.87 | 2.10 | 2.04 | 0.00 | 0.60 | 1.20 | 1.80 | 2.60 | 4.30 | 12.1 |
| PM2.5 (μg/m3) | 19.4 | 27.6 | 31.0 | 24.5 | 1.00 | 5.00 | 13.0 | 21.0 | 32.0 | 54.0 | 275 |
| PM10 (μg/m3) | 35.3 | 55.8 | 63.7 | 45.3 | 1.00 | 10.0 | 26.0 | 42.0 | 63.0 | 110 | 1269 |
| O3 (ppb) | 26.0 | 23.2 | 37.9 | 28.3 | 1.00 | 1.00 | 6.00 | 20.0 | 43.0 | 82.0 | 185 |
| NO2 (ppb) | 21.8 | 31.4 | 27.4 | 26.3 | 1.00 | 7.00 | 10.0 | 24.0 | 35.0 | 54.0 | 200 |
| SO2 (ppb) | 4.02 | 7.35 | 5.29 | 5.56 | 1.00 | 1.00 | 2.00 | 3.00 | 5.00 | 19.0 | 348 |
| CO (ppm) | 0.66 | 0.93 | 0.81 | 0.80 | 0.10 | 0.20 | 0.40 | 0.60 | 1.00 | 2.00 | 8.80 |
Wet season: June-October;
CD (Cold-dry season): November-February;
WD (Warm-dry season): March-May
Air pollutant concentrations in the MCMA also showed special patterns (Table S5). Region I showed the highest PM2.5, PM10, NO2 and CO concentrations because this region is located in the middle of MCMA which has the most population, traffic, and industries. The highest SO2 concentration (7.25 ppb) was observed in the northern part of the MCMA (region II) due to the highest number of SO2 emission sources. Whereas, the highest O3 concentration (33.7 ppb) was observed in the southern part (region IV).
3.2. Development of the LUR Models
The developed LUR model equations for the hourly time scale are presented in Table 2 and daily, monthly, 6-month and annual time scales are presented in detail in the Supplementary Material (Table S6). Meteorological variables, including temperature, humidity and wind speed, and the hourly traffic density variable, were selected as covariates in models for all six air pollutants of interest and five temporal scales. Hourly PM10 and NO2 decrease by 1.00 μg/m3 and 0.98 ppb for every increase of 1 °C in temperature. Hourly O3 concentrations would be changed by 1.03 ppb and −0.99 ppb for every increase of 1 °C in temperature and 1% in humidity, respectively. One level increases of hourly traffic density within 5 km radius are expected to increase by 1.21 μg/m3, 1.11 μg/m3 and 1.14 ppb for hourly PM2.5, PM10 and NO2, respectively. Increased air pollutant concentrations were observed on holidays and weekends in both observed data and LUR model results. For instance, 1.13 μg/m3 higher PM2.5 concentrations would be expected on holidays or weekend days than on other days.
Table 2.
Developed land use regression model equations using LASSO for hourly temporal scale
| Pollutant | LUR model |
|---|---|
| PM2.5 | |
| PM10 | |
| O3 | |
| NO2 | |
| SO2 | |
| CO |
3.3. Evaluation of the LUR Model Development Method
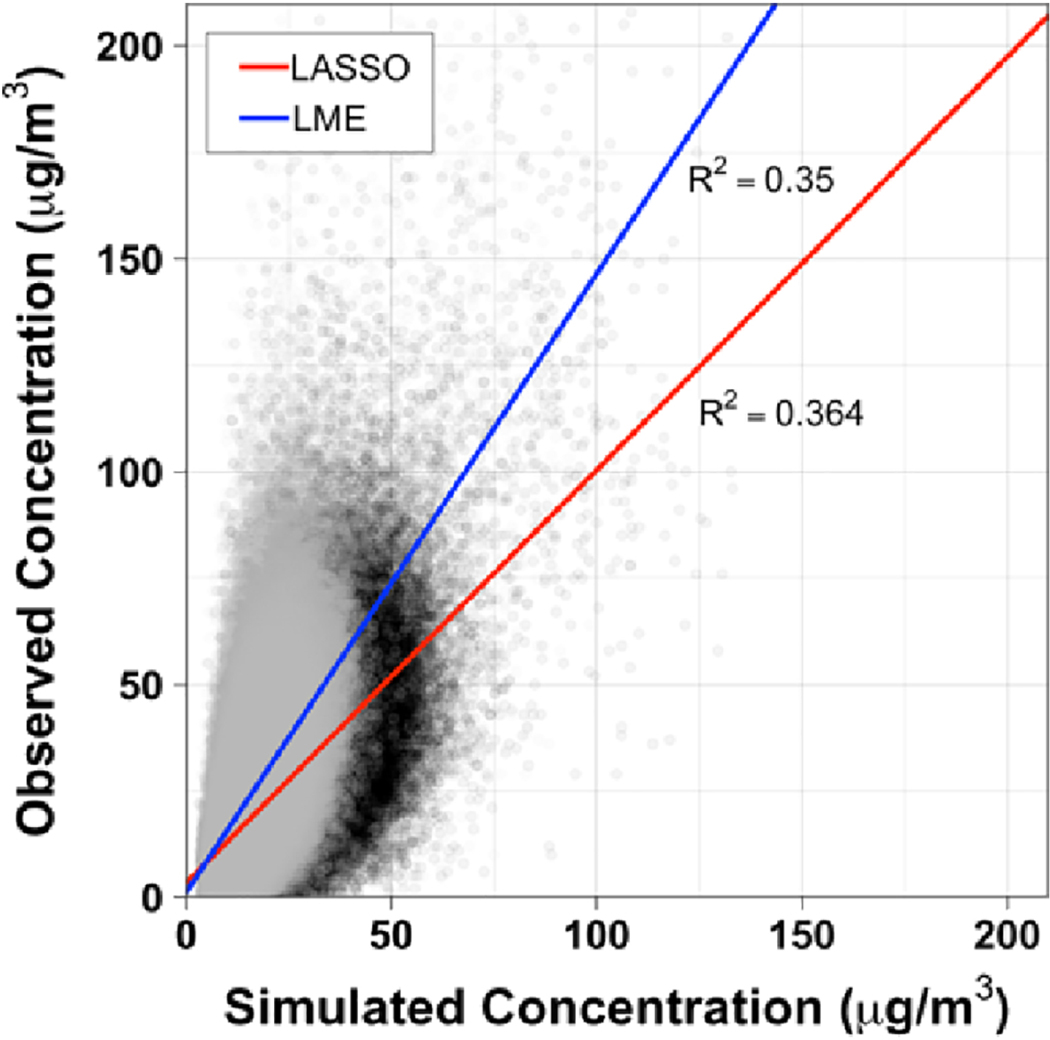
Hourly PM2.5 model performances using LASSO and LME were compared to evaluate the LUR model development method (Figure 2). In general, LASSO method shows better model performance than LME method. R2 and NSE of hourly PM2.5 model using LASSO were 0.364 and 0.335, respectively, and LME method were 0.350 and 0.038, respectively. Error indices of hourly PM2.5 model using LME were 15.84, 0.981, and 0.496 for RMSE, RSR, and MFE, respectively, and LASSO method were 13.27, 0.816, and 0.414 for RMSE, RSR, and MFE, respectively.
Figure 2.
Hourly PM2.5 model performances for the least absolute shrinkage and selection operator (LASSO, black dot) and the linear mixed effect (LME, gray dot) method. Red and blue lines indicate the trend lines for the LASSO and LME method, respectively
3.4. Performance of the LUR Models
The LUR model performances were evaluated by comparing the predicted air pollutant concentrations with observed concentrations obtained from the monitoring network in the MCMA (Table 2 and Table S7). LUR models using longer temporal scales showed better performances than those using shorter temporal scales. For instance, the NSE of hourly PM2.5 model was 0.320, while the NSE of the monthly average of the PM2.5 models was increased to 0.765. The error indices, i.e., RMSE, RSR and MFE, were inversely correlated with the temporal scale. The RSR and MFE of the hourly PM2.5 model was 0.825 and 0.413, respectively, whereas RSR and MFE of the monthly average PM2.5 model were 0.378 and 0.056, respectively. Furthermore, spatial variabilities of developed LUR models were acceptable and validated by differences between cross validation results and the hourly LUR model R2 values of less than 10% (Table S7).
Hourly and monthly averages of the LUR model performances were evaluated in each polygonal geographical region within the MCMA (Table 2). Hourly LUR models in region IV usually showed lower R2 values than other polygonal regions. Higher RMSEs were observed in regions with higher ambient pollutant concentrations; e.g., the highest RMSE for the hourly NO2 model was observed in region I where NO2 concentrations were higher than in other regions, whereas RSR and MFE of NO2 observed in region IV were higher than in other regions.
The simulated average diurnal and monthly LUR model results for the six air pollutants studied here correlated well with the observed trends (Figures S2 and S3). Except O3, all air pollutants displayed highest concentrations in the morning (around 10 a.m.) while the highest O3 concentrations were noted around 3:00 p.m. (Figure S2). Air pollutant concentrations during the months of December and May (cold-dry and warm-dry weather seasons) were higher than during June and November (wet weather season). O3 concentrations were high in May while PM2.5, PM10, NO2, SO2 and CO concentrations were high in the December-January period (Figure S3).
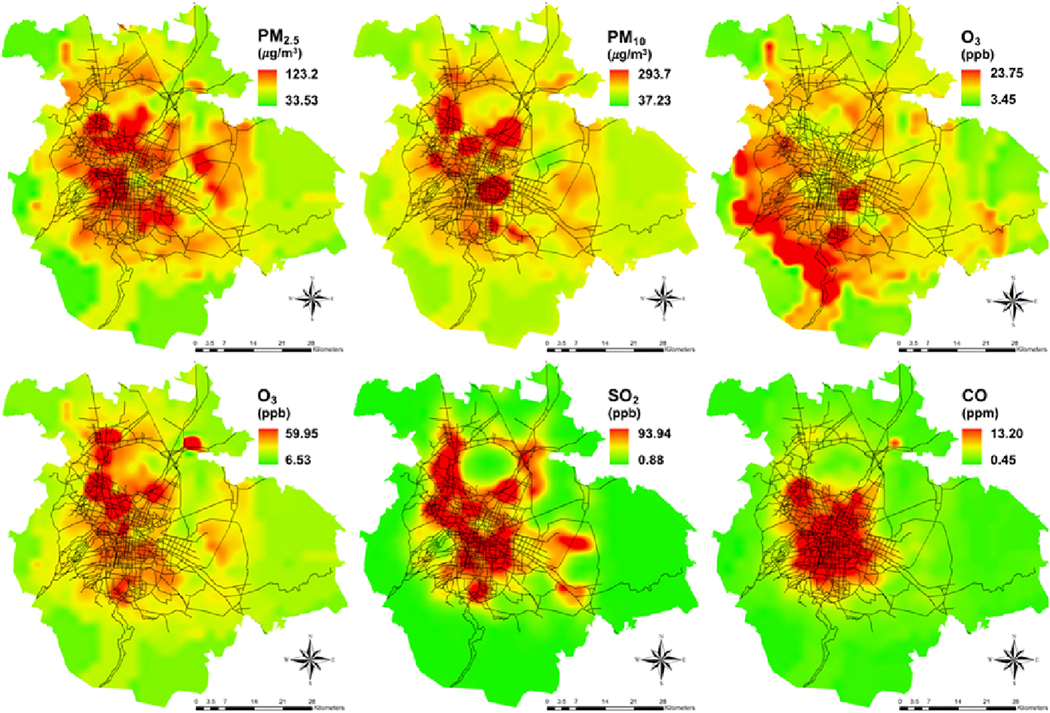
Figure 3 shows the spatial distributions of simulated average ambient air pollution data at 7 a.m. (30×30 m grid cells), which is the time showing the highest air pollutant concentrations except for O3. Our developed LUR models well represented the spatial distributions of six air pollutants. The simulated air quality map shows particulate matter, NO2, and CO concentrations are the highest in the middle of the MCMA (Region I) and are well correlated with the observed air quality (Table S5). The north-western part and the middle of the MCMA (Region II) show higher SO2 concentration than other regions. In addition, the predicted O3 concentration is the highest in the south-western part of the MCMA (Region IV) as observed from the RAMA.
Figure 3.
Spatial distribution of simulated average air pollutant concentrations at 7 a.m.
4. DISCUSSION
This paper contributes to the existing literature by demonstrating a LUR approach to air pollution exposure estimation in the MCMA which incorporates a range of predictors and uses a novel combination of temporal variables (i.e., hourly meteorological variable and hourly traffic density) and statistical techniques for model fitting and performance assessment.
The LASSO method improved the performance of the traditional LUR method. To develop improved spatiotemporal LUR models for the MCMA, we employed the LASSO method which is a variation of linear regression and maximizes overall model efficiency under weak or negligible assumptions (e.g., linearity, constant variance and normality) (Lockhart et al., 2014). In contrast, most previously developed LUR models used the standard linear least squares method (Hoek et al., 2008), for which it is recommended that the investigator apply diagnostic tests to monitor for violations of any assumptions (Jerrett et al., 2005).
The developed LUR model equations interpreted temporal air pollution levels and emission processes satisfactorily. The meteorological variables which are included in all of our hourly LUR models represent seasonal and temporal variation of air pollutants. The temperature variable showed a positive relationship with O3, as expected, since increased temperature, UV radiation, and source pollutants (e.g., VOC, NOx and CO) can generate higher levels of O3 (Singh et al., 2009). Our model results also correlated well with high O3 concentrations in the warm-dry season (Figure S3). In addition, the significant influence of the elevation variable in our hourly O3 model reflects the relationship between radiation and O3 formation because elevation increase was known to provide more UV radiation (Blumthaler et al., 1997). Indeed, the addition of a UV radiation variable, which was not available for this analysis, might further improve the O3 model performance.
The increased relative humidity and precipitation variables that decreased the air pollutant simulation and our model results correlate well with the observed air pollutant concentrations in the wet season (Figure S3). Strong air flows from the Gulf of Mexico that increase humidity and precipitation in the MCMA, are known to enhance the mixing and removal of air pollutants in the region (Molina et al., 2010). In fact, precipitation may be a factor that contributes to the scavenging of particulate matter and hydrophilic air pollutants (Marley et al., 2009).
Next, among the air pollutant emission related variables, traffic density variables were the most influential variables in most of our hourly LUR models except the hourly O3 model. This coincides with the observation that anthropogenic emissions are major sources of particulate matter and NOx in the MCMA (Molina et al., 2010). On-road mobile emissions dominate the total anthropogenic emission in size, followed by point emissions such as industrial production processes. Indeed, in our models, the traffic density variable was the most significant variable to predict diurnal air pollution trend (Figure S2). While traffic density data has been a significant predictor variable in many LUR models developed in European countries and Canada (Beelen et al., 2013; Brauer et al., 2003; Briggs et al., 2000), most of these available data were derived from long-term average traffic counts or were not obtainable at all (Hoek et al., 2008; Just et al., 2015). The current study, in contrast, obtained hourly traffic density data from the Google ‘typical traffic’ website, which is based on crowd-sourcing data (Google, 2009). Hourly traffic density explained 2%−10% of temporal air quality variability in the MCMA. The Google ‘typical traffic’ provides hourly traffic data that cover 61 out of 256 countries worldwide. A difficulty associated with the use of the Google ‘typical traffic’ data for the purpose of the development of LUR models, such as the current one for the MCMA, is that data need to be coded manually.
The holiday variable was found to be another important covariate in the current study that explained temporal variations of air pollution concentrations in the MCMA. Current LUR models showed that air pollutant concentrations were increased on holidays and weekends except for O3. Activity patterns during holidays and weekends are different from that on weekdays. Traffic-related pollutant emission rates may, for example, decrease during holidays and weekends when many residents leave the MCMA (Velasco et al., 2005). In contrast, peaks of PM2.5 concentrations in Mexico City can occur during New Year and Christmas days as a result of fireworks, outdoor cooking or other, unusual, pollution events (Just et al., 2015).
Developed hourly LUR models showed ranges of model performances in different regions of the MCMA (Table 3). Large industrial complexes located in Region II might decrease hourly NO2, SO2, and CO model performances. Even though mobile emissions are the major source of air pollutants, industrial emissions are estimated to contribute 10–50% of the total air pollutant emissions in the MCMA (Molina et al., 2010). For example, the Tula industrial complex located northwest of the MCMA consists of the second largest refinery and the fifth largest thermoelectric power plant in Mexico and largely impacts the SO2 and NO2 levels of the MCMA Region II (Rivera et al., 2011). While the operation of these facilities could affect air pollution concentrations in Region II, short-term emission patterns could not be included in our LUR models due to the lack of data availability. For the same reason, our hourly models could not explain satisfactorily the air pollution concentrations for Region IV. Indeed, the Popocatépetl volcano located on the edge of Region IV might emit substantial amounts of air pollutants into the MCMA but the temporal emission pattern of the volcano is not well known or predictable. The dispersion of these point emission sources in the MCMA are largely depending on wind speed, wind direction, and boundary layer height. Thus, detailed emission patterns from local pollution sources coupled with wind field data need to be accessed to improve current LUR models.
Table 3.
Hourly LUR model performance in different polygonal regions of the MCMA
| Pollutant | Region | Hourly time scale | Monthly time scale | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
| R2 | NSE | RMSE | RSR | MFE | R2 | NSE | RMSE | RSR | MFE | ||
|
| |||||||||||
| PM2.5 | All | 0.364 | 0.320 | 13.32 | 0.825 | 0.413 | 0.765 | 0.764 | 3.266 | 0.486 | 0.097 |
| I | 0.379 | 0.306 | 14.31 | 0.833 | 0.411 | 0.778 | 0.775 | 3.235 | 0.475 | 0.090 | |
| II | 0.368 | 0.336 | 12.94 | 0.815 | 0.391 | 0.651 | 0.620 | 3.765 | 0.617 | 0.103 | |
| III | 0.381 | 0.343 | 12.35 | 0.810 | 0.398 | 0.801 | 0.795 | 2.800 | 0.453 | 0.100 | |
| IV | 0.259 | 0.242 | 12.22 | 0.871 | 0.447 | 0.711 | 0.708 | 3.019 | 0.541 | 0.099 | |
| PM10 | All | 0.381 | 0.350 | 27.23 | 0.807 | 0.397 | 0.381 | 0.350 | 27.23 | 0.807 | 0.397 |
| I | 0.368 | 0.339 | 22.60 | 0.813 | 0.347 | 0.695 | 0.599 | 8.559 | 0.633 | 0.140 | |
| II | 0.414 | 0.371 | 27.24 | 0.793 | 0.432 | 0.887 | 0.869 | 6.745 | 0.362 | 0.089 | |
| III | 0.413 | 0.355 | 26.55 | 0.803 | 0.381 | 0.826 | 0.782 | 8.880 | 0.466 | 0.145 | |
| IV | 0.306 | 0.285 | 23.61 | 0.845 | 0.419 | 0.843 | 0.777 | 5.955 | 0.473 | 0.110 | |
| O3 | All | 0.653 | 0.610 | 16.77 | 0.625 | 0.488 | 0.719 | 0.718 | 3.952 | 0.532 | 0.110 |
| I | 0.727 | 0.691 | 15.32 | 0.556 | 0.510 | 0.730 | 0.717 | 3.612 | 0.532 | 0.110 | |
| II | 0.727 | 0.699 | 13.73 | 0.549 | 0.482 | 0.632 | 0.570 | 3.856 | 0.655 | 0.111 | |
| III | 0.652 | 0.489 | 17.76 | 0.715 | 0.477 | 0.761 | 0.758 | 3.257 | 0.492 | 0.092 | |
| IV | 0.682 | 0.168 | 27.70 | 0.912 | 0.530 | 0.776 | 0.489 | 5.873 | 0.715 | 0.145 | |
| NO2 | All | 0.512 | 0.502 | 10.68 | 0.706 | 0.324 | 0.820 | 0.818 | 3.343 | 0.427 | 0.103 |
| I | 0.459 | 0.427 | 12.60 | 0.757 | 0.283 | 0.714 | 0.660 | 3.849 | 0.583 | 0.088 | |
| II | 0.422 | 0.393 | 10.94 | 0.779 | 0.339 | 0.768 | 0.747 | 3.264 | 0.503 | 0.115 | |
| III | 0.589 | 0.558 | 7.906 | 0.665 | 0.337 | 0.779 | 0.771 | 3.184 | 0.478 | 0.149 | |
| IV | 0.302 | 0.159 | 11.79 | 0.917 | 0.388 | 0.859 | 0.794 | 2.353 | 0.454 | 0.081 | |
| SO2 | All | 0.130 | 0.059 | 10.19 | 0.970 | 0.562 | 0.620 | 0.611 | 1.719 | 0.624 | 0.229 |
| I | 0.165 | 0.063 | 9.990 | 0.968 | 0.544 | 0.637 | 0.608 | 1.625 | 0.626 | 0.189 | |
| II | 0.072 | −0.011 | 13.90 | 1.005 | 0.629 | 0.441 | −0.295 | 3.088 | 1.138 | 0.379 | |
| III | 0.112 | 0.061 | 8.979 | 0.969 | 0.528 | 0.576 | 0.575 | 1.487 | 0.652 | 0.231 | |
| IV | 0.083 | 0.042 | 7.182 | 0.979 | 0.573 | 0.508 | 0.499 | 1.359 | 0.708 | 0.207 | |
| CO | All | 0.530 | 0.497 | 0.426 | 0.709 | 0.379 | 0.593 | 0.588 | 0.167 | 0.642 | 0.168 |
| I | 0.531 | 0.484 | 0.478 | 0.719 | 0.343 | 0.559 | 0.535 | 0.148 | 0.682 | 0.129 | |
| II | 0.528 | 0.409 | 0.492 | 0.769 | 0.408 | 0.440 | 0.388 | 0.164 | 0.782 | 0.156 | |
| III | 0.528 | 0.489 | 0.317 | 0.715 | 0.436 | 0.498 | 0.474 | 0.162 | 0.725 | 0.220 | |
| IV | 0.305 | 0.254 | 0.288 | 0.864 | 0.388 | 0.233 | −0.355 | 0.157 | 1.164 | 0.216 | |
R2 = coefficient of determination, NSE = Nash-Sutcliffe efficiency, RMSE = root mean square error, RSR = RMSE-observations standard deviation ratio, and MFE = mean fractional error; performance criteria are NSE ≥ 0.5, RSR ≤ 0.7 and MFE ≤ 0.5
LUR models with longer timescales showed better model performances because peak observations in the shorter temporal scale data were temporally aggregated (Table S7). For instance, gases and particles emitted from biomass and garbage burning have been shown to contribute significantly to observed air pollution levels in the MCMA (Christian et al., 2010). Shorter timescale models could not reflect such episodic emission events, while longer temporal scale models could decrease relative errors by aggregating these peak events. Therefore, the study of local emission sources and dispersion events can be expected to help improve short-term LUR models.
Despite the fact that direct comparisons between LUR models may not be adequate because of differences in their methodology and data, the performances of our daily LUR models are comparable with or better than that of previous studies developed in different regions of world. The daily NO2 LUR model in this study shows a R2 value of 0.72 while previous studies reported R2 values ranging from 0.43 to 0.82 for NO2 LUR models (Ainslie et al., 2008; Arain et al., 2007; Johnson et al., 2013; Liu et al., 2015). Reported daily LUR model performances (R2) for PM2.5 were 0.88 and for PM10 were 0.47 and 0.89 (Johnson et al., 2013; Liu et al., 2015), respectively. Our daily PM2.5 and PM10 LUR models showed R2 values of 0.51 and 0.58, respectively. Previously reported LUR model performances (R2) for monthly averages were 0.17 for PM2.5, 0.49 for PM10, and 0.51 for NO2, and for annual averages were 0.73 for PM2.5, 0.58 for PM10, and 0.97 for NO2 (Beelen et al., 2013; Dons et al., 2013; Dons et al., 2014; Hart et al., 2009; Hoek et al., 2008; Liu et al., 2015; Wang et al., 2013; Wheeler et al., 2008). The monthly average, 6-month average and annual LUR models presented here show similar or higher R2 values compared with those previously reported (Table S7), although previous studies used large number of saturation monitoring stations. Methodology, data source and, land use may attribute the difference in LUR model performances.
Even though most studies report R2 and RMSE to show model performance, we suggest that standardized model evaluation techniques, i.e., NSE, RSR and MFE, should be used to present LUR model performances. In the current study, differences between R2 and NSE in hourly LUR models were due to the impact of extreme values and/or worse fitting on the identity line compared to longer time scales (Table S7). In past studies, the RMSE was the most popular error index used to evaluate LUR models (Hoek et al., 2008; Jerrett et al., 2005); however, direct comparisons of RMSE values may thus be less meaningful than standardized error indices for LUR models that employ different spatiotemporal scales (e.g., in the current study the NO2 models in region I and region IV, or the LUR models in the wet and the warm-dry seasons). Interestingly, to date there are no clear model performance criteria defined for R2 and RMSE, but NSE, RSR and MFE criteria have been defined as NSE ≥ 0.5, RSR ≤ 0.7 and MFE ≤ 0.5 (Boylan and Russell, 2006; Moriasi et al., 2007) and accepted by U.S. EPA (EPA, 2007). Therefore, standardized evaluation indices can indicate how well LUR model results simulate observed air quality data without the bias of using pre-defined criteria. Our developed LUR model results are within these model performance goals except hourly models for PM2.5, PM10 and SO2 (Table S7).
LUR models employing different time scales can explore multiple health outcomes with outcome-relevant time frames to best reflect acute or chronic adverse health outcomes. For instance, asthma exacerbations and dysrhythmias are inherently measured on shorter time scales and models which can predict short-term air pollution exposures are important to study such acute and sub-chronic health outcomes. Longer time scale models are necessary to investigate for example chronic pulmonary diseases or immunological alterations that may facilitate respiratory infections such as with M.tb. However, for both acute and chronic health outcome studies, smaller time scales appear to improve the reliability of epidemiological studies by reducing within-subject variations and/or by identifying critical windows of exposure (Nethery et al., 2008). Sbihi et al. (2015), for example, found positive correlations between postnatal air pollution exposure and increased risk for atopy using bi-weekly adjusted LUR models. In addition, shorter timescale models will help to understand local air pollution exposures. Short temporal scale model results provide better information on emission sources (e.g., mobile, point, or areal emission) and toxic hot-spots in addition to critical windows. Therefore, developed short timescale models may, in the future, be used both to assess the impact of air pollution exposures on health and inform local air pollution regulation.
The current study has limitations and points to the need for further research. First, buffer sizes of traffic-related independent variables used in this study ranged from 500 m to 5 km and were thus larger than in previous studies in Canada and European countries that employed mobile sampling strategies (Hoek et al., 2008). Large buffer sizes may impair the ability of the current model to accurately predict air pollutant exposures as the impact of traffic-related pollutant sources declines at distances from major urban roads and freeways, beyond 100 m and 500 m, respectively (Hoek et al., 2008). The impact of finer buffer size on LUR model performances will be accessed using the on-going MexAir indoor/outdoor sampling data. Atmospheric boundary layer (ABL) heights may further improve spatial and temporal variations of air pollution. Low ABL heights may trap air pollution in the southern part of the MCMA during the cold weather periods, because the MCMA is located at 2,240 m altitude and its basin is surrounded by three high mountain ridges (de Foy et al., 2006). It is possible that the introduction of dispersion conditions could improve the simulation of spatiotemporal distributions of air pollution concentrations in the MCMA.
5. CONCLUSIONS
We developed LUR models with different temporal scales for the MCMA using mixed effect models with the LASSO method. This approach improved air pollution exposure predictions and made them less dependent on assumptions inherent to the least squares method. The current model employed hourly meteorological variables and hourly traffic density information from Google ‘typical traffic’ and satisfactorily reflects differences in temporal and spatial air pollution trends in the MCMA. Our approach to utilizing the LASSO method with hourly meteorological and crowd-sourcing traffic data can be generalized to any LUR study and may improve air pollution exposure assessments. In the context of the MexAir study, near road and indoor air pollution sampling data from on-going sampling campaigns are expected to improve the performance of the presented LUR models as exposure assessment tools in the MCMA.
Supplementary Material
Highlights.
Air pollution exposures in Mexico City result in adverse health outcomes
Land use regression models for six air pollutants were developed
Hourly meteorology and traffic data facilitated finer timescale simulation
A new regression method improved model performance
ACKNOWLEDGEMENT
We thank the providers of data used in our LUR models: RAMA, Gobierno de la Ciudad de Mexico; INECC, Secretaria del Mdio Ambiente y Recursos Naturales (SEMARNAT), and INEGI, Instituto Nacional de Estadística y Geografía in Mexico. This work was supported by the US National Institutes of Environmental Health Sciences (grant numbers 5R01ES020382 [S. Schwander], P30ES005022, P30ES017885, and R01s ES017022 and ES016932 [M.S. O’Neill and A.R. Osornio-Vargas]). This work was also supported by T42OH008455-09 (M.S. O’Neill).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ainslie B, Steyn D, Su J, Buzzelli M, Brauer M, Larson T, Rucker M.2008. A source area model incorporating simplified atmospheric dispersion and advection at fine scale for population air pollutant exposure assessment. Atmos. Environ 42, 2394–2404. [Google Scholar]
- Alfaro-Moreno E, Martínez L, García-Cuellar C, Bonner JC, Murray JC, Rosas I, de León Rosales SP, Osornio-Vargas ÁR 2002. Biologic effects induced in vitro by PM10 from three different zones of Mexico City. Environ. Health Perspect 110(7), 715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arain M, Blair R, Finkelstein N, Brook J, Sahsuvaroglu T, Beckerman B, Zhang L, Jerrett M.2007. The use of wind fields in a land use regression model to predict air pollution concentrations for health exposure studies. Atmos. Environ 41, 3453–3464. [Google Scholar]
- Bates D, Mächler M, Bolker B, Walker S.2014. Fitting linear mixed-effects models using lme4. J. Stat. Softw 67(1), 1–48. [Google Scholar]
- Beelen R, Hoek G, Vienneau D, Eeftens M, Dimakopoulou K, Pedeli X, Tsai M-Y, Künzli N, Schikowski T, Marcon A.2013. Development of NO2 and NOx land use regression models for estimating air pollution exposure in 36 study areas in Europe-the ESCAPE project. Atmos. Environ 72, 10–23. [Google Scholar]
- Bell ML, O’Neill MS, Ranjit N, Borja-Aburto VH, Cifuentes LA, Gouveia NC 2008. Vulnerability to heat-related mortality in Latin America: a case-crossover study in Sao Paulo, Brazil, Santiago, Chile and Mexico City, Mexico. Int. J. Epidemiol 37, 796–804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blumthaler M, Ambach W, Ellinger R.1997. Increase in solar UV radiation with altitude. J. Photochem. Photobiol. B: Biology, 39(2), 130–134. [Google Scholar]
- Boylan JW, Russell AG 2006. PM and light extinction model performance metrics, goals, and criteria for three-dimensional air quality models. Atmos. Environ 40, 4946–4959. [Google Scholar]
- Brauer M, Hoek G, van Vliet P, Meliefste K, Fischer P, Gehring U, Heinrich J, Cyrys J, Bellander T, Lewne M.2003. Estimating long-term average particulate air pollution concentrations: application of traffic indicators and geographic information systems. Epidemiology. 14, 228–239. [DOI] [PubMed] [Google Scholar]
- Briggs DJ, de Hoogh C, Gulliver J, Wills J, Elliott P, Kingham S, Smallbone K.2000. A regression-based method for mapping traffic-related air pollution: application and testing in four contrasting urban environments. Sci. Total Environ 253, 151–167. [DOI] [PubMed] [Google Scholar]
- Christian TJ, Yokelson RJ, Cárdenas B, Molina L, Engling G, Hsu SC 2010. Trace gas and particle emissions from domestic and industrial biofuel use and garbage burning in central Mexico. Atmospheric Chem. Phys 10, 565–584. [Google Scholar]
- de Foy B, Varela J, Molina L, Molina M.2006. Rapid ventilation of the Mexico City basin and regional fate of the urban plume. Atmospheric Chem. Phys 6, 2321–2335. [Google Scholar]
- Dons E, Van Poppel M, Kochan B, Wets G, Panis LI 2013. Modeling temporal and spatial variability of traffic-related air pollution: Hourly land use regression models for black carbon. Atmos. Environ 74, 237–246. [Google Scholar]
- Dons E, Van Poppel M, Panis LI, De Prins S, Berghmans P, Koppen G, Matheeussen C.2014. Land use regression models as a tool for short, medium and long term exposure to traffic related air pollution. Sci. Total Environ 476, 378–386. [DOI] [PubMed] [Google Scholar]
- EPA. 2007. U.S. Guidance on the Use of Models and Other Analyses for Demonstrating Attainment of Air Quality Goals for Ozone, PM2.5, and Regional Haze U.S. Environmental Protection Agency, Research Triangle Park, North Carolina. [Google Scholar]
- OpenStreetMap contributors. 2015. OpenStreetMap. https://planet.openstreetmap.org
- Google. 2009. The bright side of sitting in traffic: Crowdsourcing road congestion data. https://googleblog.blogspot.com/2009/08/bright-side-of-sitting-in-traffic.html (accessed 6 May 2018). [Google Scholar]
- Hart J, Yanosky J, Puett R, Ryan L, Dockery D, Smith T, Garshick E, Laden F.2009. Spatial Modeling of PM10 and NO2 in the Continental United States, 1985–2000. Environ. Health Perspect 117, 1690–1696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henderson SB, Beckerman B, Jerrett M, Brauer M.2007. Application of land use regression to estimate long-term concentrations of traffic-related nitrogen oxides and fine particulate matter. Environ. Sci. Technol 41, 2422–2428. [DOI] [PubMed] [Google Scholar]
- Hoek G, Beelen R, de Hoogh K, Vienneau D, Gulliver J, Fischer P, Briggs D.2008. A review of land-use regression models to assess spatial variation of outdoor air pollution. Atmos. Environ 42, 7561–7578. [Google Scholar]
- Hoek G, Fischer P, Van Den Brandt P, Goldbohm S, Brunekreef B.2001. Estimation of long-term average exposure to outdoor air pollution for a cohort study on mortality. J. Expo. Anal. Environ. Epidemiol 11, 459–469. [DOI] [PubMed] [Google Scholar]
- INEGI. 2018. National Institute of Statistics and Geography (Instituto Nacional de Estadística y Geografía). http://www.inegi.org.mx (accessed 6 May 2018). [Google Scholar]
- Jerrett M, Arain A, Kanaroglou P, Beckerman B, Potoglou D, Sahsuvaroglu T, Morrison J, Giovis C.2005. A review and evaluation of intraurban air pollution exposure models. J. Expo. Anal. Environ. Epidemiol 15, 185–204. [DOI] [PubMed] [Google Scholar]
- Johnson M, MacNeill M, Grgicak-Mannion A, Nethery E, Xu X, Dales R, Rasmussen P, Wheeler A.2013. Development of temporally refined land-use regression models predicting daily household-level air pollution in a panel study of lung function among asthmatic children. J. Expo. Anal. Environ. Epidemiol 23, 259–267. [DOI] [PubMed] [Google Scholar]
- Just AC, Wright RO, Schwartz J, Coull BA, Baccarelli AA, Tellez-Rojo MM, Moody E, Wang Y, Lyapustin A, Kloog I.2015. Using High-Resolution Satellite Aerosol Optical Depth To Estimate Daily PM2. 5 Geographical Distribution in Mexico City. Environ. Sci. Technol 49, 8576–8584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu W, Li X, Chen Z, Zeng G, León T, Liang J, Huang G, Gao Z, Jiao S, He X.2015. Land use regression models coupled with meteorology to model spatial and temporal variability of NO2 and PM10 in Changsha, China. Atmos. Environ 116, 272–280. [Google Scholar]
- Lockhart R, Taylor J, Tibshirani RJ, Tibshirani R.2014. A significance test for the lasso. Ann. Stat 42(2), 413–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manzano-León N, Serrano-Lomelin J, Sánchez BN, Quintana-Belmares R, Vega E, Vázquez-López I, Rojas-Bracho L, López-Villegas MT, Vadillo-Ortega F, De Vizcaya-Ruiz A, Rosas Perez I, O’Neill M.a., Osornio-Vargas A.2016. TNFα and IL-6 Responses to Particulate Matter in Vitro: Variation According to PM Size, Season, and Polycyclic Aromatic Hydrocarbon and Soil Content. Environ. Health Perspect 124(4), 406–412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marley NA, Gaffney JS, Tackett M, Sturchio NC, Heraty L, Martinez N, Hardy KD, Marchany-Rivera A, Guilderson T, MacMillan A.2009. The impact of biogenic carbon sources on aerosol absorption in Mexico City. Atmospheric Chem. Phys 9, 1537–1549. [Google Scholar]
- Molina LT, Madronich S, Gaffney J, Apel E, Foy B.d., Fast J, Ferrare R, Herndon S, Jimenez JL, Lamb B.2010. An overview of the MILAGRO 2006 Campaign: Mexico City emissions and their transport and transformation. Atmospheric Chem. Phys 10, 8697–8760. [Google Scholar]
- Moriasi D, Arnold J, Van Liew M, Bingner R, Harmel R, Veith T.2007. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 50(3), 885–900. [Google Scholar]
- Nash J, Sutcliffe JV 1970. River flow forecasting through conceptual models part I-A discussion of principles. J. Hydrol 10, 282–290. [Google Scholar]
- Nethery E, Leckie SE, Teschke K, Brauer M.2008. From measures to models: an evaluation of air pollution exposure assessment for epidemiological studies of pregnant women. J. Occup. Environ. Med 65, 579–586. [DOI] [PubMed] [Google Scholar]
- O’Neill MS, Loomis D, Borja-Aburto VH 2004. Ozone, area social conditions, and mortality in Mexico City. Environ. Res 94, 234–242. [DOI] [PubMed] [Google Scholar]
- Osornio-Vargas ÁR, Bonner JC, Alfaro-Moreno E, Martínez L, García-Cuellar C, Rosales S.P.-d.-L., Miranda J, Rosas I. 2003. Proinflammatory and cytotoxic effects of Mexico City air pollution particulate matter in vitro are dependent on particle size and composition. Environ. Health Perspect 111, 1289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team. 2015. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. http://www.R-project.org (accessed 6 May 2018). [Google Scholar]
- Rivera C, Sosa G, Wohrnschimmel H, De Foy B, Johansson M, Galle B.2009. Tula industrial complex (Mexico) emissions of SO2 and NO2 during the MCMA 2006 field campaign using a mobile mini-DOAS system. Atmospheric Chem. Phys 9, 6351–6361. [Google Scholar]
- Rivas-Santiago CE, Sarkar S, Cantarella P, Osornio-Vargas Á, Quintana-Belmares R, Meng Q, Kirn TJ, Strickland PO, Chow JC, Watson JG, Torres M, Schwander S.2015. Air Pollution Particulate Matter Alters Antimycobacterial Respiratory Epithelial Innate Immunity. Infect. Immun 83(6), 2507–2517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivera-González LO, Zhang Z, Sánchez BN, Zhang K, Brown DG, Rojas-Bracho L, Osornio-Vargas A, Vadillo-Ortega F, O’Neill MS 2015. An Assessment of Air Pollutant Exposure Methods in Mexico City, Mexico. J. Air Waste Manag. Assoc 65(5), 581–591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rojas-Martinez R, Perez-Padilla R, Olaiz-Fernandez G, Mendoza-Alvarado L, Moreno-Macias H, Fortoul T, McDonnell W, Loomis D, Romieu I.2007. Lung function growth in children with long-term exposure to air pollutants in Mexico City. Am. J. Respir. Crit. Care Med 176, 377–384. [DOI] [PubMed] [Google Scholar]
- Ryan PH, LeMasters GK 2007. A review of land-use regression models for characterizing intraurban air pollution exposure. Inhal. Toxicol 19, 127–133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sangrador JT, Nuñez ME, Villarreal AB, Cadena LH, Jerrett M, Romieu I.2008. A land use regression model for predicting PM2.5 in Mexico City. Epidemiology. 19, S259. [Google Scholar]
- Sarkar S, Song Y, Sarkar S, Kipen HM, Laumbach RJ, Zhang J, Strickland PAO, Gardner CR, Schwander S.2012. Suppression of the NF-κB pathway by diesel exhaust particles impairs human antimycobacterial immunity. J. Immunol 188, 2778–2793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sbihi H, Allen RW, Becker A, Brook JR, Mandhane P, Scott JA, Sears MR, Subbarao P, Takaro TK, Turvey SE 2015. Perinatal exposure to traffic-related air pollution and atopy at 1 Year of age in a multi-center canadian birth cohort study. Environ. Health Perspect 123(9), 902–908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schelldorfer J, Bühlmann P, Van de Geer S.2011. Estimation for High‐Dimensional Linear Mixed‐Effects Models Using ℓ1‐Penalization. Scand. Stat. Theory Appl 38, 197–214. [Google Scholar]
- Shields KN, Cavallari JM, Hunt M, Lazo M, Molina M, Molina L, Holguin F.2013. Traffic-related air pollution exposures and changes in heart rate variability in Mexico City: A panel study. Environ. Health 12, 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SIMAT. 2018. Mexico City Atmospheric Monitoring System (Sistema de Monitoreo Atmosférico). Mexico City, Mexico. http://www.aire.cdmx.gob.mx/default.php (accessed 6 May 2018). [Google Scholar]
- Singh H, Brune W, Crawford J, Flocke F, Jacob DJ 2009. Chemistry and transport of pollution over the Gulf of Mexico and the Pacific: spring 2006 INTEX-B campaign overview and first results. Atmospheric Chem. Phys 9, 2301–2318. [Google Scholar]
- Tibshirani R.1996. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Series B Stat. Methodol 58(1), 267–288. [Google Scholar]
- USGS. 2016. North American Land Change Monitoring System. 2005 North American Land Cover at 250 m spatial resolution. Produced by Natural Resources Canada/Canadian Center for Remote Sensing (NRCan/CCRS), United States Geological Survey (USGS); Insituto Nacional de Estadística y Geografía (INEGI), Comisión Nacional para el Conocimiento y Uso de la Biodiversidad (CONABIO) and Comisión Nacional Forestal (CONAFOR) https://landcover.usgs.gov/nalcms.php (accessed 6 May 2018).
- Velasco E, Pressley S, Allwine E, Westberg H, Lamb B.2005. Measurements of CO2 fluxes from the Mexico City urban landscape. Atmos. Environ 39, 7433–7446. [Google Scholar]
- Wang R, Henderson SB, Sbihi H, Allen RW, Brauer M.2013. Temporal stability of land use regression models for traffic-related air pollution. Atmos. Environ 64, 312–319. [Google Scholar]
- Wheeler AJ, Smith-Doiron M, Xu X, Gilbert NL, Brook JR 2008. Intra-urban variability of air pollution in Windsor, Ontario-measurement and modeling for human exposure assessment. nviron. Res. 106, 7–16. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.